Électricité/Les associations de résistors

Dans les chapitres précédents, nous avons parlé des résistances et générateurs, qui n'ont plus de secrets pour nous. Les circuits les plus simples sont composés intégralement de résistances et de générateurs, d'où le nom de circuits résistifs qui leur est parfois donné. L'analyse de ces circuits se repose sur seulement trois équations : la loi des mailles, la loi des nœuds et la loi d'Ohm. Elle permet de calculer les tensions et courants en tout point du circuit. L'analyse de ces circuits dépend fortement du nombre de générateurs, et on peut faire la différence entre les circuits résistifs avec un seul générateur et ceux qui en ont plusieurs. Il se trouve que l'analyse des circuits avec plusieurs générateurs peut se rapporter à l'analyse de circuits avec un seul générateur (nous détaillerons cela dans le chapitre prochain). En conséquence, il est important d'étudier les circuits à un seul générateur, de savoir comment les analyser, ce qui est le but de ce chapitre. Dans le chapitre suivant, nous verrons comment analyser des circuits avec plusieurs générateurs. Précisons cependant que nous n’allons étudier le fonctionnement de ces circuits que dans le cas où le générateur fournit un courant ou une tension continus., le cas des tensions ou courants alternatifs étant laissé à plus tard.

Électricité

La physique de l’électricité

Les circuits électriques

Le régime continu et les circuits résistifs/linéaires

Le régime transitoire : bobines et condensateurs

Le régime alternatif

Annexes

Notions de sécurité électrique

Version imprimable

[ Modifier le sommaire ]

Les générateurs

Les circuits linéaires et leurs lois

Dans un circuit résistif à un seul générateur, on peut calculer le courant fournit par un générateur de tension avec l'aide d'un outil mathématique très simple : la résistance équivalente. Derrière ce terme barbare se cache quelque chose de simple : dans la plupart des calculs, il est possible de remplacer le réseau de résistances par une résistance unique, sans changer le comportement du circuit. Cette résistance unique est appelée la résistance équivalente. Celle-ci n'est autre que la tension aux bornes du réseau de résistances $U_{0}$ , divisée par le courant $I$ qui traverse les résistances.

{\frac {U_{0}}{I}}=R_{eq}

Dans ce chapitre, nous allons calculer la résistance équivalente de plusieurs circuits résistifs communs. Nous allons d'abord étudier des circuits où deux résistances sont placées en série ou en parallèle d'un générateur. Ces deux montages sont souvent appelés des diviseurs de tension et de courant, comme nous le verrons à l'instant. Nous allons d'abord étudier le cas simple où deux résistances sont placées en série, avant d'étudier celui où les résistances sont en parallèle. La raison en est que le cas série est le plus simple à étudier, le cas parallèle étant mathématiquement moins simple.

Résistances en série

Diviseur de tension.

Lorsque l'on place deux résistances en série avec une source de tension, on obtient un montage appelé diviseur de tension. Ce terme deviendra plus clair quand vous aurez compris le fonctionnement de ce circuit. L'étude de ce circuit est assez simple, vu qu'il s'agit d'un circuit série. L'application de la loi des nœuds nous dit que le courant est constant dans tout le circuit, vu qu'il s'agit d'un circuit série. Son application n'est donc pas très intéressante. Mais tel n'est pas le cas pour la loi des mailles.

Résistance équivalente

Résistance équivalente d'une association série de deux résistances.

Dans ce qui va suivre, nous allons calculer la résistance équivalente d'une association série de résistances.

Pour cela, nous allons commencer par utiliser la loi des mailles, qui nous dit que la somme des tensions aux bornes des résistances et du générateur est nulle. En utilisant les notations du schéma à votre droite, on obtient :

-U_{0}+U_{1}+U_{2}=0

Ce qui se reformule comme suit :

U_{0}=U_{1}+U_{2}

On peut alors appliquer la loi d'Ohm pour chaque résistance, ce qui permet de reformuler les tensions $U_{1}$ et $U_{2}$ :

U_{0}=I\cdot R_{1}+I\cdot R_{2}

On factorise le courant I :

U_{0}=I\cdot \left(R_{1}+R_{2}\right)

On voit que cette formule est similaire à la loi d'Ohm, mais appliquée aux deux résistances, non à une résistance individuelle. On peut alors diviser la tension par le courant, pour obtenir la résistance équivalente :

{\frac {U_{0}}{I}}=R_{1}+R_{2}

Celle-ci nous dit simplement que la résistance de deux résistances en série est égale à la somme des résistances. En somme, ce circuit est équivalent à une résistance $R_{1}+R_{2}$ , placée en série avec le générateur. Par équivalent, on veut dire que le calcul du courant ou des tensions aux bornes des deux résistances donnera le même résultat. Le résultat précédent nous donne la valeur de la résistance équivalente de deux résistances en série : c'est leur somme.

On peut généraliser le résultat précédent pour un circuit avec plusieurs résistances en série, la démonstration étant similaire à celle pour deux résistances. Pour résumer, la résistance équivalente de plusieurs résistances en série est égale à la somme des résistances.

R_{eq}=\sum _{i}R_{i}

Tension aux bornes d'une résistance

Maintenant, essayons de calculer la tension aux bornes d'une résistance, par exemple aux bornes de la résistance $R_{1}$ . Pour cela, il nous suffit d'appliquer la loi d'Ohm :

U_{1}=R_{1}\cdot I

Le courant $I$ se calcule en appliquant la loi d'Ohm avec la résistance équivalente : $I={\frac {U_{0}}{R_{eq}}}$ . En faisant le remplacement, on a :

U_{1}=R_{1}\cdot {\frac {U_{0}}{R_{eq}}}

En réarrangeant les termes, on trouve :

U_{1}=U_{0}\cdot {\frac {R_{1}}{R_{eq}}}

Cette formule est assez générale et se généralise pour un nombre arbitraire de résistances en série. On peut la reformuler comme suit :

{\frac {U_{R}}{U_{gen}}}={\frac {R}{R_{eq}}}

Elle nous dit que la tension aux bornes d'une résistance est proportionnelle à la tension du générateur. Le coefficient de proportionnalité est le rapport entre la résistance étudiée et la résistance équivalente. On comprend alors pourquoi ce montage est appelé diviseur de tension : il permet de diviser la tension du générateur par la valeur de notre choix : il suffit de bien choisir les résistances pour obtenir le diviseur voulu.

Dans le cas précis où l'on n'a que deux résistances, on trouve :

U_{1}=U_{0}\cdot {\frac {R_{1}}{R_{1}+R_{2}}}

Résistances en parallèle

Diviseur de courant.

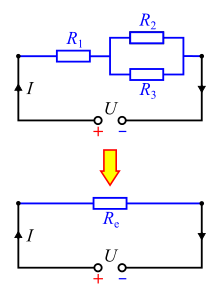
Après avoir étudié le montage avec des résistances en série, nous allons voir ce qui se passe quand on utilise des résistances en parallèle. Le montage obtenu ne fonctionne pas comme un diviseur de tension, mais comme un diviseur de courant, comme nous allons le voir. Cette fois-ci, l'usage de la loi des mailles donne des résultats différents : chaque résistance formant une maille avec le générateur, on voit rapidement que la tension aux bornes du générateur est reproduite aux bornes de chaque résistance.

U_{0}=U_{1}=U_{2}

Résistance équivalente

Résistance équivalente d'une association parallèle de deux résistances.

Comme pour le circuit précédent, on peut calculer une résistance équivalente à ce circuit. On peut utiliser les résistances pour faire cette démonstration, mais les équations se formulent plus simplement en utilisant les conductances. On obtient alors le résultat suivant : dans un circuit parallèle, la conductance équivalente est égale à la somme des conductances. La résistance équivalente est égale à l'inverse de cette conductance équivalente ${\frac {1}{G_{eq}}}$ .

{\frac {I}{U}}=G_{eq}=\sum _{i}G_{i}

R_{eq}={\frac {1}{G_{eq}}}={\frac {1}{\sum _{i}G_{i}}}

Loi des nœuds avec deux résistances en parallèle.

Nous allons démontrer ces relations dans le cas de deux résistances en parallèle, mais sachez que la démonstration que nous allons faire se généralise aisément à plus de deux résistances.

Commençons par appliquer la loi des nœuds, qui dit que le courant qui traverse le circuit est la somme des courants qui traversent chaque résistance. On a alors :

I=I_{1}+I_{2}

On peut calculer le courant qui traverse chaque résistance, en appliquant la loi d'Ohm.

I_{1}=U\cdot G_{1}

I_{2}=U\cdot G_{2}

En injectant combinant les trois équations précédentes, on trouve :

I=U\cdot G_{1}+U\cdot G_{2}=U\cdot \left(G_{1}+G_{2}\right)

En divisant par U, on trouve la conductance équivalente :

G_{eq}={\frac {I}{U}}=G_{1}+G_{2}

La résistance équivalente est égale à ${\frac {1}{G_{eq}}}$ . Dans notre exemple, cela donne :

$R_{eq}={\frac {1}{G_{eq}}}={\frac {1}{G_{1}+G_{2}}}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}$

Cette équation peut encore se simplifier :

$R_{eq}={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}}}={\frac {1}{{\frac {R_{2}}{R_{1}R_{2}}}+{\frac {R_{1}}{R_{1}R_{2}}}}}={\frac {1}{\frac {R_{2}+R_{1}}{R_{1}R_{2}}}}={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}$

Diviseur de courant

Répartition du courant dans deux résistances en parallèle.

On peut comprendre assez facilement pourquoi ce circuit s'appelle un diviseur de courant. Pour cela, on peut comparer le courant sortant du générateur avec le courant passant dans une résistance. Prenons par exemple la résistance $R_{1}$ et calculons le courant qui la traverse.

I_{1}=U\cdot G_{1}

Calculons maintenant le courant total :

I=U\cdot G_{eq}

Le rapport entre les deux vaut :

{\frac {I_{1}}{I}}={\frac {U\cdot G_{1}}{U\cdot G_{eq}}}={\frac {G_{1}}{G_{eq}}}

On voit que le courant qui traverse une résistance est proportionnel au courant sortant du générateur, le coefficient étant le rapport entre conductance et conductance équivalente. Le courant a été divisé par ce rapport, ce qui fait que ce circuit divise bien le courant d'entrée par une valeur donnée, calibrée par le choix des conductances. Intuitivement, on comprend que c'est une conséquence de la loi des nœuds : le courant générateur se divise entre les deux résistances, en proportion de la valeur des conductances.

La formule précédente peut se reformuler comme suit :

I_{1}=I\cdot {\frac {G_{1}}{G_{eq}}}