Les suites et séries/Version imprimable

Les suites et séries

Une version à jour et éditable de ce livre est disponible sur Wikilivres,
une bibliothèque de livres pédagogiques, à l'URL :
https://fr.wikibooks.org/wiki/Les_suites_et_s%C3%A9ries

Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la Licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans Texte de dernière page de couverture. Une copie de cette licence est incluse dans l'annexe nommée « Licence de documentation libre GNU ».

Les suites numériques

Les suites sont des outils mathématiques assez généraux, que l'on peut définir comme des suites d'objets mathématiques, placés dans un certain ordre.. Les exemples les plus simples sont de loin les suites de nombres. Les suites les plus simples sont de banales suites de nombres, comme on peut en trouver dans des tests de QI ou dans diverses énigmes mathématiques. Par exemple, ceci est une suite : 1, 2, 4, 8, 16, 32, 64, ... L'exemple précédent est une suite numérique, à savoir une suite de nombres (numérique = nombre). On a bien des objets mathématiques, ici des nombres, placés dans un certain ordre. Il ne faut pas plus pour obtenir une suite !

Mais les suites numériques ne sont pas les seules : il existe de nombreux autres types de suites, comme des suites de fonctions, de polynômes, ou autres. Après tout, rien n’empêche de ranger des fonctions mathématiques dans un certain ordre, ou d'ordonner des polynômes, bref : tant que l'on met des truc mathématiques dans un certain ordre, on obtient une suite. Le terme objet mathématique est volontairement vague, l'objet mathématique en question pouvant être n'importe quoi. Les objets mathématiques d'une suite, qu'ils soient des nombres ou non, sont nommés les termes de la suite. Une suite est donc un ensemble de termes rangés dans un certain ordre.

Pour définir une suite, il faut naturellement préciser ses termes, mais pas seulement : il faut aussi préciser dans quel ordre sont rangés les objets mathématiques. Pour rendre compte de cet ordre, les termes de la suite sont numérotés dans leur ordre dans la suite. Chaque terme est associé à un nombre qui définit sa place dans la suite, ce nombre étant appelé le rang du terme dans la suite, ou encore son indice. Dans la quasi-totalité des cas, la numérotation des termes commence à partir de 1. Cette convention est intuitive : le premier terme a pour rang 1, le second est de rang 2, et ainsi de suite. Cependant, rien n’empêche de commencer à compter non à partir de 1, mais à partir d'un autre rang. Il est par exemple possible de commencer à compter les rangs à partir de 0 : cette convention est notamment très utilisée par les informaticiens, quand ils doivent manipuler des suites. Dans tous les cas, le énième terme de la suite est appelé le terme de rang $n$. Une petite remarque au niveau des notations :

• le terme de rang $n$ est noté $u_{n}$ ;
• la suite en elle-même est notée $(u_{n})$.

Exemple de suite numérique

Rang $n$	1	2	3	4	5	6	7	...
Terme $u_{n}$	1	2	4	8	16	32	64	...

Exemple de suite de fonctions

Rang $n$	1	2	3	4	5	6	7	8	...
Terme $u_{n}$	$x^{0}$	$x^{1}$	$x^{2}$	$x^{3}$	$x^{4}$	$x^{5}$	$x^{6}$	$x^{7}$	...

Les suites récurrentes et paramétrées

Supposons que vous souhaitiez créer une suite quelconque. Pour cela, vous avez deux méthodes qui fonctionnent bien, la première donnant des suites paramètres, l'autre des suites récurrentes. Il faut noter que les deux types de suites ne sont pas mutuellement exclusifs : certaines suites sont à la fois récurrentes et paramétrées. La plupart des suites que nous allons étudier dans la suite du cours sont dans ce cas.

Les suites paramétrées

Les suites paramétrées sont simplement des suites définies par une fonction mathématique $u_{n}=f(n)$. En clair, construire la suite demande simplement de dire que tel rang est associé à tel terme de manière univoque. Comme exemple de suite paramètres, on peut citer la suite définie par $f(n)=n^{2}$. Celle-ci est illustrée dans le tableau ci-dessous.

La suite numérique définie par $f(n)=n^{2}$

Rang $n$	1	2	3	4	5	6	7	...
Terme $u_{n}$	1	4	9	16	25	36	49	...

Comme autres exemples de suites paramétrées, nous allons prendre les suites de Riemann, des suites où chaque terme est une puissance de l'inverse d'un entier... Pour le dire plus clairement, ce sont des suites de la forme :

$u_{n}={\frac {1}{n^{r}}}$, avec r un coefficient appelé la raison de la suite.

suite harmonique alternée

La suite de Riemann la plus simple est la suite harmonique, la suite de l'inverse des entiers naturels.

$S_{h}=1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}},{\frac {1}{5}},{\frac {1}{6}},...$

On peut modifier la suite harmonique en inversant les signes d'un terme à l'autre : on obtient alors la suite harmonique alternée.

$S_{h}=1,-{\frac {1}{2}},{\frac {1}{3}},-{\frac {1}{4}},{\frac {1}{5}},-{\frac {1}{6}},...$

Une autre suite de Riemann, que nous étudierons dans les chapitres suivants, est la suite de l'inverse des carrés. Elle est définie par :

$u_{n}={\frac {1}{n^{2}}}=1,{\frac {1}{2^{2}}},{\frac {1}{3^{2}}},{\frac {1}{4^{2}}},{\frac {1}{5^{2}}},...$

Les suites récurrentes

Une autre méthode consiste à définir comment passer d'un terme au suivant. Dans ce cas, la suite est définie par une fonction de la forme $u_{n}=f(u_{n-1})$. On voit que le cas précédent marche dans le cas où chaque terme dépend de la valeur du terme précédent. Mais on peut généraliser au cas où chaque terme dépend de plusieurs termes précédents, avec des fonctions de la forme $u_{n}=f(u_{n-1},u_{n-2},u_{n-3},u_{n-4}...)$. Ces suites sont appelées des suites récurrentes.

Ces suites sont définies par la fonction qui permet de calculer un terme en fonction des précédents, mais pas seulement ! En effet, une même fonction peut donner plusieurs suites, selon le premier terme utilisé. Par exemple, la fonction $u_{n}=2\times u_{n-1}$ peut donner les deux suites (1, 2, 4, 8, 16, 32, 64, ...) et (3, 6, 12, 24, 48, 96, ...). En plus de préciser la fonction, on doit préciser le ou les premiers termes.

Comme exemple de suite récurrente, nous donnant dans le tableau ci-dessous un exemple de suite récurrente assez simple : celle définie par la fonction $u_{n}=u_{n-1}/2$ et le premier terme 1.

La suite numérique définie par $u_{n}=u_{n-1}/2$ et $u_{1}=1$

Rang $n$	1	2	3	4	5	6	7	...
Terme $u_{n}$	1	0.5	0.25	0.125	0.0625	0.03125	0.015625	...

L'étude des suites récurrentes se limite souvent à trouver une expression non-récurrente (paramétrée), plus simple à manipuler. Quand cela n'est pas possible, il est intéressant d'étudier le comportement de la suite quand n devient grand, pour savoir si les termes grandissent, diminuent, si la suite se stabilise, etc.

L'exemple de la suite de Fibonnaci

Un exemple très connu de suite récurrente est la suite de Fibonnaci, une suite souvent abordée dans les livres de mathématiques récréatives. Elle est apparue pour la première fois dans un problème de mathématiques récréatives impliquait un problème de lapins qui se reproduisent dans un enclos. Ce problème était l’œuvre de par Leonardo Fibonacci, qui donna son nom à cette suite. Voici l'énoncé de ce problème :

«
	Quelqu’un a déposé un couple de lapins dans un certain lieu, clos de toutes parts, pour savoir combien de couples seraient issus de cette paire en une année, car il est dans leur nature de générer un autre couple en un seul mois, et qu’ils enfantent dans le second mois après leur naissance.
	»
	— Leonardo Fibonacci

Si on fait un graphique, on devrait trouver ceci :

Évolution du nombre de lapins en fonction des mois dans le problème de Fibonnaci.

Mais une autre manière de résoudre le problème est de concevoir une suite dont le énième terme donne le nombre de lapins dans l'enclos à l’énième mois. Pour le mois numéro n, on peut calculer le nombre de couples présents dans l'enclos assez simplement : il est la somme du nombre de couples au mois précédent, qui sont encore vivants, et du nombre de nouveaux couples ajoutés par la reproduction. Et ce dernier est égal au nombre de lapins d'il y a deux mois auparavant, car les lapins mettent deux mois à se reproduire. Les deux dernières phrases se résument mathématiquement avec la relation de récurrence suivante :

$u_{n}=u_{n-1}+u_{n-2}$

L'énoncé nous dit que le premier terme de la suite est 1, car il n'y a qu'un seul couple pour le premier mois. Le second terme est identique, car il faut deux mois aux lapins pour se reproduire. Les deux premiers termes de la suite de Fibonacci sont respectivement 1 et 1, ce qui donne la suite suivante. On peut faire commencer la suite avec 0 et 1, mais il s'agit d'une définition alternative presque totalement équivalente.

Fibonacci sequence - optional starting with zero

La suite de Fibonnaci ne paye pas de mine au premier abord, mais elle a des propriétés assez intéressantes, avec notamment des liens avec le nombre d'or. Mais n'en disons pas plus pour le moment.

Les propriétés d'une suite

Les suites ont divers propriétés assez simples, basées sur des définitions somme toute triviales, que nous allons décrire dans cette section. Ces propriétés sont souvent assez importantes mathématiquement et leur présence est source de beaucoup de propriétés ou de théorèmes intéressants. Pour donner un exemple simple, on peut parler de la distinction entre suite finie et infinie. Les suites finies ont un nombre de termes fini et se terminent sur un dernier terme, alors que ce n'est pas le cas des suites infinies, qui ont autant de termes qu'il y a d'entiers naturels. Cette propriété est assez simple à comprendre, mais elle est à l'origine de grandes différences : là où les suites finies possèdent très peu de propriétés mathématiques intéressantes, les suites infinies sont un sujet d'étude très riche. C'en est au point que ce cours ne parlera que des suites infinies, tant elles possèdent de propriétés supplémentaires par rapport aux suites finies ! Et d'autres propriétés simples donnent le même résultat, d'où l'importance de détailler ces propriétés. Les propriétés que nous allons voir permettent de distinguer les suites bornées, croissantes, décroissantes, constantes, monotones, stationnaires, etc.

Les suites majorées, minorées et bornées

Une suite majorée est une suite dont tous les termes sont plus petits qu'une constante définie. Dit autrement, pour tout $u_{n}$, $u_{n}<k$. La constante, plus grande que tous les termes de la suite, est appelée un majorant. On peut cependant préciser que toute suite qui a un majorant en a une infinité ! Par exemple, prenons une suite quelconque qui est majorée par 100 : elle est aussi majorée par 101, 102, 103, etc. Tous les nombres supérieurs à un majorant sont eux-mêmes des majorants. Parmi tous ces majorants, il en existe un qui est plus petit que les autres, ce qui lui vaut le nom de borne supérieure de la suite.

Une suite minorée est une suite dont tous les termes sont plus grands qu'une constante définie. Dit autrement, pour tout $u_{n}$, $u_{n}>k$. La constante, plus petite que tous les termes de la suite, est appelée un minorant. Encore une fois, toute suite qui a un minorant en a une infinité : tout nombre plus petit qu'un minorant est lui-même un minorant. Parmi tous ces minorants, il en existe un qui est plus petit que les autres, ce qui lui vaut le nom de borne inférieure de la suite.

Une suite bornée est une suite qui est à la fois minorée et majorée, ce qui fait que tous les termes de la suite sont pris dans un intervalle.

Illustration d'une suite bornée, qui montre bien les bornes supérieures et inférieures.

Les suites monotones et constantes

Les suites numériques ont souvent des propriétés que d’autres suites n’ont pas forcément, la raison étant que les nombres peuvent être ordonnés : on peut dire si un nombre est supérieur, inférieur ou égal à un autre. Cela permet donc de comparer les termes consécutifs d'une suite. Dans quelques cas, les termes consécutifs d'une suite sont les mêmes, que ce soit dès le début de la suite, ou alors au-delà d'un certain rang.

• Si chaque terme est égal au précédent, la suite est dite constante.
• Il existe des suites qui sont constantes au-delà d'un certain rang, mais pas avant celui-ci : on les appelle des suites stationnaires.

D'autres suites ont des termes différents : chaque terme est plus grand ou plus petit que le précédent.

• Dans le cas où chaque terme de la suite est plus grand que le précédent (pour tout rang $n$, on a : $u_{n+1}>u_{n}$), la suite est dite strictement croissante.
• Dans le cas contraire, on a $u_{n+1}<u_{n}$ pour tout rang $n$ et la suite est dite strictement décroissante.
• Si $u_{n+1}\leq u_{n}$, la suite est dite décroissante.
• Si $u_{n+1}\geq u_{n}$, la suite est dite croissante.

Certaines suites récurrentes sont soit croissantes, soit décroissantes, selon leur premier terme ou la fonction utilisée. Tel est le cas de la suite définie par la relation $u_{n}=u_{n-1}\times 5$ : la fonction est décroissante avec $u_{0}<0$ et croissante avec $u_{0}>0$. Pour éviter de dire qu’une catégorie de suite est soit croissante, soit décroissante, on préfère dire qu’elle est monotone. À noter que certaines suites deviennent monotones au-delà d'un certain rang, mais ne le sont pas forcément avant. Ces suites sont aux suites monotones ce que les suites stationnaires sont aux suites constantes. Mais il faut avouer que ces suites sont assez rares et que nous n'aurons pas à en manipuler beaucoup dans ce cours.

Démontrer qu'une suite est constante, croissante ou décroissante est généralement assez facile.

• Si une suite est croissante, pour tout rang $n$, $u_{n}<u_{n+1}$.
• Si une suite décroissante, pour tout rang $n$, $u_{n}>u_{n+1}$.
• Si une suite est constante, pour tout rang $n$, $u_{n}=u_{n+1}$, on est face à une suite constante.

Une bonne manière pour déterminer la croissance/constance/décroissance d'une suite est de calculer la différence $u_{n}-u_{n+1}$. Son signe varie selon le rang si elle n'est pas monotone, alors qu'il est le même si la suite est monotone. Elle est toujours nulle pour une suite constante, toujours positive si la suite est strictement décroissante, toujours négative pour une suite strictement décroissante. Pour vous donner un exemple type de démonstration de ce genre, nous allons prendre le cas de la suite harmonique, la suite de l'inverse des entiers naturels. La voici :

$S_{h}=1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}},{\frac {1}{5}},{\frac {1}{6}},...$

Pour montrer qu'elle est décroissante, nous allons calculer $u_{n}-u_{n+1}$, qui vaut alors :

$u_{n}-u_{n+1}={\frac {1}{n}}-{\frac {1}{n+1}}={\frac {1}{n(n+1)}}$

On voit bien que la différence $u_{n}-u_{n+1}$ est positive : la suite harmonique est donc décroissante.

Les suite périodiques et ultimement périodiques

Une suite périodique forme un cycle, les mêmes valeurs revenant périodiquement au-delà d'un certain rang. De manière générale, une suite périodique est une suite telle que les termes forment une séquence de la forme : $u_{1},u_{2},u_{3},...,u_{p-1},u_{p},u_{1},u_{2},u_{3},...,u_{p-1},u_{p},...$. Le nombre de termes répétés $p$ est appelé la période de la suite. Au fait, si une suite est (ultimement ou non) périodique de période $p$, alors elle est aussi périodique de période $2p$, $3p$, $4p$, $5p$, ... Les suites périodiques sont définies de telle sorte que, quel que soit le rang $n$ : $a_{n+p}=a_{n}$. En voici quelques exemples :

• Les suites constantes sont des suites périodiques de période 1.
• Un autre exemple de suite périodique est la suite définie par $u_{n}=(-1)^{n}$ : $1,-1,1,-1,1,-1,1,-1,...$, qui a une période de 2.

Les suites ultimement périodiques sont similaires aux suites périodiques, à un détail près : le début de la suite n'est pas périodique, la suite n'étant périodique qu'au-delà d'un certain rang. Par exemple, les suites stationnaires (constantes au-delà d'un certain rang) sont des suites ultimement périodiques de période 1.

Les suites périodiques et quasi-périodiques sont toutes bornées. Cela parait évident à démontrer : chaque période, chaque cycle, ne renferme qu'un nombre limité de valeurs différentes ($p$ valeurs pour être exact), ce qui est incompatible avec une suite non-bornée. Les suites périodiques sont donc bornées entre la plus grande de ces valeurs et la plus petite. Quant aux suites quasi-périodiques, elles possèdent fatalement un nombre fini de termes avant de devenir périodique, ce qui fait que le même raisonnement s'applique.

Il existe des suites pour lesquelles on n'a pas encore réussit à prouver si elles sont ou non (quasi-)périodiques. Le meilleur exemple est la suite de Syracuse, définie par la relation de récurrence suivante  :

$u_{0}=N$

$u_{n+1}={\begin{cases}{\dfrac {u_{n}}{2}}&{\mbox{si }}u_{n}{\mbox{ est pair,}}\\3u_{n}+1&{\mbox{si }}u_{n}{\mbox{ est impair.}}\end{cases}}$

Dans la totalité des cas connus, la suite de Syracuse se stabilise au bout d’un certain temps : la fin de la suite sera une succession de 1, 4, 2, 1, 4, 2, etc. Les tentatives de trouver des contre-exemples se sont retrouvées infructueuses, même en utilisant des ordinateurs très puissants pour tester N jusqu’à des valeurs extraordinairement grandes. Faute de contre-exemples connus à l'heure actuelle, les mathématiciens ont conjecturé que la suite est quasi-périodique pour toutes les valeurs possibles du N initial. Mais à ce jour, les mathématiciens n'en ont pas la preuve et ils n'arrivent pas non plus à démontrer le contraire. La situation est telle que le grand mathématicien feu Paul Erdős a déclaré à propos de cette suite que "Les mathématiques ne sont pas encore prêtes pour de tels problèmes".

Un exemple : les suites arithmético-géométriques

Tout cours sur les suites aborde rapidement les fameuses suites arithmétiques, géométriques et arithmético-géométriques. Il faut dire que ces suites sont assez utilisées dans de nombreux domaines et il est important de les connaître par cœur. Elles sont de plus assez simples à comprendre, ce qui fait que nous allons les étudier maintenant.

Les suites arithmétiques

Les suites arithmétiques sont des suites où les termes augmentent d'un pas régulier : on compte de 2 en 2, de 3 en 3, de 1.6 en 1.6, de 39 en 39, etc.

Exemple de suite arithmétique de raison 4.

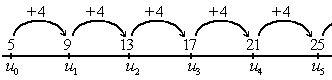
Dit autrement, la différence entre un terme et le suivant est une constante et chaque terme s’obtient en additionnant une constante au terme précédent. En clair, on a :

$u_{n+1}=u_{n}+k$

L'équation précédente peut aussi se réécrire comme suit :

$u_{n}=u_{0}+n\times k$

La constante $k$, le pas de la suite, est appelée la raison de la suite La raison d'une suite arithmétique peut être aussi bien positive que négative, et même nulle ! Et le signe de la raison influence la croissance ou décroissance de la suite.

• Si la raison est nulle, chaque terme est égal au précédent : la suite est constante.
• Si la raison est positive, les termes de la suite ne cessent d'augmenter avec le rang : la suite est croissante.
• Si la raison est négative, les termes diminuent progressivement quand le rang augmente : la suite est décroissante.

Les suites arithmétiques sont donc soit croissantes, soit décroissantes : ce sont donc des suites monotones.

Les suites géométriques

Les suites géométriques sont assez similaires aux suites arithmétiques, la seule différence étant que l'addition est remplacée par une multiplication : chaque terme est un multiple du précédent

Suite géométrique

Une suite de ce type est définie par la fonction de récurrence suivante :

$u_{n+1}=u_{n}\times k$

L'équation précédente peut se réécrire comme suit :

$u_{n}=u_{0}\times k^{n}$

La constante $k$ est encore une fois appelée la raison de la suite et elle peut être aussi bien positive que négative.

Contrairement aux suites arithmétiques, les suites géométriques ne sont pas forcément monotones. Et cette fois-ci, la croissance ou décroissance de la suite ne dépend pas que du signe de la raison, mais aussi de sa valeur. Dans les grandes lignes, tout dépend si la raison est négative ou positive, et si sa valeur absolue est comprise entre 0 et 1.

• Si la raison est positive, la suite est obligatoirement monotone.
  • Si la raison est supérieure à 1, chaque terme sera plus grand que le précédent et la suite est croissante.
  • Si la raison est de 1, chaque terme est égal au précédent : la suite est constante.
  • Si la raison est plus petite que 1 mais malgré tout positive, chaque terme sera plus petit que le précédent, mais reste positif : la suite est décroissante.
• Si la raison est négative, chaque terme positif est suivi d'un négatif et réciproquement : la suite est alors dite alternée.

Cas où la raison est positive.

|

Cas où la raison est négative.

Les suites arithmético-géométriques

Les suites arithmético-géométriques sont des généralisations des suites géométriques et arithmétiques : elles sont en quelque sorte les deux à la fois. Chaque terme se calcule en multipliant le précédent, avant d'ajouter une autre constante. La constante par laquelle on multiplie le terme précédent est appelé la raison de la suite, alors que l'autre constante additionnée est appelée la constante additive.

$u_{n+1}=a\times u_{n}+b$

On peut signaler qu'une suite arithmétique est une suite arithmético-géométrique de raison multiplicative 1, alors qu'une suite géométrique est une suite arithmético-géométrique où la constante additive nulle.

Obtenir l'expression paramétrée de la suite est possible, bien que compliqué. Pour cela, nous allons déterminer la différence entre la suite arithmético-géométrique voulue et une suite géométrique de même raison et de premier terme identique. Nous allons voir ce que cela donne sur un exemple, avant de généraliser.

Rang	Suite géométrique	Suite arithmético-géométrique	Différence entre les deux suites
1	$u_{0}$	$u_{0}$	0
2	$u_{0}\times a$	$u_{0}\times a+b$	$a$
3	$u_{0}\times a^{2}$	$u_{0}\times a^{2}+ab+b$	$ab+b$
4	$u_{0}\times a^{3}$	$u_{0}\times a^{3}+a^{2}b+ab+a$	$a^{2}b+ab+a$
5	$u_{0}\times a^{4}$	$u_{0}\times a^{4}+a^{3}b+a^{2}b+ab+a$	$a^{3}b+a^{2}b+ab+a$
...	...	...	...
n	$u_{0}\times a^{n}$	$u_{0}\times a^{n}+b(a^{n}+a^{n-1}+...+a^{2}+a^{1}+a^{0})$	$b(a^{n}+a^{n-1}+...+a^{2}+a^{1}+a^{0})$
...	...	...	...

On verra dans le chapitre sur les sommes partielles, que $(a^{n}+a^{n-1}+...+a^{2}+a^{1}+a^{0})={\frac {a^{n+1}-1}{a-1}}$. En faisant le remplacement, on a :

$u_{n}=u_{0}\times b^{n}+b\left({\frac {a^{n+1}-1}{a-1}}\right)$

On obtient avec pas mal de manipulations algébriques :

$u_{n}=a^{n}\left(u_{0}-{\frac {b}{1-a}}\right)+{\frac {b}{1-a}}$

Il est possible de démontrer cette relation autrement, bien que la démonstration soit moins intuitive. En voici une démonstration juste en-dessous.

Démonstration

Pour faire cette démonstration, nous allons tenter de nous ramener d'une suite arithmético-géométrique à une simple suite géométrique, que l'on sait traiter. Pour cela, nous allons étudier la suite définie par : $u_{n}=v_{n}+t$ avec $t={\frac {b}{1-a}}$ On a alors : $u_{n+1}=au_{n}+b=a(v_{n}+t)+b$ Vu que $u_{n+1}=v_{n+1}+t$ : $v_{n+1}=a(v_{n}+t)+b-t=av_{n}+at+b-t=av_{n}$ La suite $v_{n}$ est donc une suite géométrique. On a donc : $u_{n}=v_{n}+t=a^{n}v_{0}+t=a^{n}(u_{0}-t)+t$ En remplaçant $t$ par sa valeur $t={\frac {b}{1-a}}$, on trouve : $u_{n}=a^{n}\left(u_{0}-{\frac {b}{1-a}}\right)+{\frac {b}{1-a}}$

Les opérations sur les suites

Les mathématiques sont le royaume des généralisations. On ne compte les fois où une opération ou un type d'objet mathématique a été étendu pour en donner une version plus générale. Les nombres fractionnaires ont été complémentés par les réels, eux-mêmes complétés par les nombres complexes. Même chose pour les opérations comme l'addition ou la multiplication : initialement inventées pour les nombres, elles ont été étendues aux matrices, aux vecteurs et à bien d'autres objets mathématiques beaucoup plus complexes. Les suites ne font pas exception : il est possible de les additionner, de les soustraire, de les multiplier, les diviser, etc.

Les comparaisons entre suites et limites

Il est possible de comparer deux suites, ce qui permet de dire si une suite est "supérieure" ou "inférieure" à une autre. Si on compare deux suites $(a_{n})$ et $(b_{n})$ :

• $(a_{n})=(b_{n})$ si, pour rang n, $a_{n}=b_{n}$.
• $(a_{n})>(b_{n})$ si, pour rang n, $a_{n}>b_{n}$.
• $(a_{n})<(b_{n})$ si, pour rang n, $a_{n}<b_{n}$.
• $(a_{n})\leq (b_{n})$ si, pour rang n, $a_{n}\leq b_{n}$.
• $(a_{n})\geq (b_{n})$ si, pour rang n, $a_{n}\geq b_{n}$.

Les opérations "arithmétiques" sur les suites et limites

Comme dit plus haut, il est possible de faire les quatre opérations arithmétiques sur deux suites. Précisément, soit deux suites notées $(a_{n})$ et $(b_{n})$ :

• La somme est la suite $(s_{n})$ définie par : $s_{n}=a_{n}+b_{n}$.
• La différence est la suite $(s_{n})$ définie par : $s_{n}=a_{n}-b_{n}$.
• La multiplication d'une suite par un nombre réel $k$ est la suite définie par : $s_{n}=k\times a_{n}$.
• Le produit est la suite $(s_{n})$ définie par : $s_{n}=a_{n}\times b_{n}$.
• Le quotient est la suite $(s_{n})$ définie par : $s_{n}={\frac {a_{n}}{b_{n}}}$.

Les deux annexes qui suivent peuvent être sautées en première lecture.

Annexe : l'espace vectoriel des suites réelles

Avec les opérations définies ci-dessus, on peut montrer que l'ensemble des suites réelles est un espace vectoriel.

Pour rappel, un espace vectoriel est défini comme le regroupement : d'un ensemble E, d'une addition + et d'une multiplication par un réel $\times$. De plus, les conditions suivantes sont respectées. On note x et y des membres quelconques de l'ensemble E. Addition : L'addition de deux membres de l'ensemble doit donner un résultat qui appartient à l'ensemble : $+:E\times E\rightarrow E$ L'addition est associative et commutative. $y+x=x+y$ $(y+x)+z=x+(y+z)$ Il existe un élément neutre pour l'addition, noté $\nu _{+}$, qui est un membre de l'ensemble E tel que : $\nu _{+}+x=x+\nu _{+}=x$ Tout membre de E possède un opposé par rapport à l'addition, cet opposé étant tel que : ${\overline {x}}+x=x+{\overline {x}}=\nu$ Multiplication par un réel : Comme pour l'addition, la multiplication par un réel d'un membre de l'ensemble, qui donne un résultat dans l'ensemble : $\times :R\times E\rightarrow E$ Le réel 1 est un élément neutre pour la multiplication, noté $\nu _{*}$, définit tel que : $\nu _{*}\times x=x$ La multiplication est distributive par rapport à l'addition.

On a vu dans la section précédente que l'on peut additionner deux suites réelles ou en multiplier une par un réel. De plus, ces opérations donnent pour résultat une suite réelle. On dispose donc des opérations idoines. On vérifie assez facilement que les autres conditions sont vérifiées, les seules difficultés étant l’élément neutre de l'addition et la détermination de l'opposé. L’élément neutre n'est autre que la suite nulle, une suite constante dont tous les termes sont nuls. La suite opposée d'une suite $(u_{n})$ est simplement la suite $(v_{n})$ définie par $v_{n}=-u_{n}$.

Annexe : Les sous-espaces vectoriels de suites

Certains sous-ensembles de suites réelles sont eux aussi des espaces vectoriels, et plus précisément, des sous-espaces vectoriels.

Pour rappel, un sous-espace vectoriel est un sous-ensemble d'un espace vectoriel, qui est lui-même un espace vectoriel. Pour un espace vectoriel E, un sous-ensemble $F\in {E}$ est un sous-espace vectoriel si : il contient l’élément neutre : $\nu _{+}\in {F}$ ; et si l'addition et la multiplication donne un résultat dans F : $+:F\times F\rightarrow F$ et $\times :R\times F\rightarrow F$.

En guise d'exercice, essayez de trouver quels ensembles suivants sont des espaces vectoriels :

• l'ensemble des suites constantes ;
• l’ensemble des suites croissantes ;
• l’ensemble des suites monotones ;
• l’ensemble des suites géométriques.

Solution :

• L'ensemble des suites constantes est bien un espace vectoriel. Il contient l’élément neutre, et la somme de deux suites constantes donne bien une suite constante, de même que le produit d'une suite constante par un réel.
• L'ensemble des suites croissantes n'est pas un espace vectoriel. Le produit d'une suite croissante par -1 ne donne pas une suite croissante, mais décroissante. La multiplication par un réel ne respecte pas la condition $\times :R\times F\rightarrow F$.
• L'ensemble des suites monotones n'est pas un espace vectoriel. La somme d'une suite croissante et d'une décroissante n'est pas systématiquement monotone.
• L'ensemble des suites géométriques n'est pas un espace vectoriel. La somme de deux suites géométriques ne donne pas toujours une suite géométrique.

Les sommes partielles

Dans ce chapitre, nous allons étudier ce qui se passe quand on additionne tous les termes d'une suite jusqu’à un certain rang. Le résultat de cette opération est ce qu'on appelle une somme partielle, qui est notée comme suit pour la somme des termes allant du terme numéro 0 à k  :

$S_{k}=\sum _{n=0}^{k}u_{n}$.

Dans ce chapitre, nous allons voir quelques généralités sur les sommes partielles, avant de voir quelques exemples simples mais sans grande importance. Les sommes partielles de suites importantes seront vues dans les chapitres suivants. Nous y verrons quelques sommes partielles de suites classiques, comme la somme des n premiers entiers, la somme partielle d'une suite arithmétique ou géométrique, et bien d'autres.

Les sommes partielles sont un premier tremplin vers le concept final de ce cours : les séries. La différence entre somme partielle et série est assez simple à comprendre : une série additionne tous les termes d'une suite infinie, alors que la somme partielle n'en additionne qu'un nombre fini. Vous vous doutez bien qu'il vaut mieux voir le cas le plus simple, fini, avant de passer aux sommes infinies que sont les séries.

Les opérations sur les sommes partielles

Avant de voir un exemple de somme partielle, nous allons voir rapidement les opérations que l'on peut faire avec les sommes partielles. Vous avez vu dans les chapitres précédents qu'il est possible d'additionner deux suites, de multiplier une suite par une constante, et de faire bien d'autres opérations. Beaucoup de suites peuvent s'écrire comme la somme de deux suites plus simples, ou d'un multiple d'une autre suite. Il est intéressant d'étudier ce qui se passe quand on prend la somme partielle de telles suites. Dans les grandes lignes, les sommes partielles sont juste un enchainement d'additions, en nombre fini. Les propriétés de commutativité, d'associativité et de distributivité tiennent donc, ce qui permet de faire quelques simplifications.

La somme partielle du multiple d'une suite

Pour le multiple d'une suite, sa somme partielle est la suivante :

$\sum _{i=0}^{n}(k\cdot u_{n})=k\cdot \left(\sum _{i=0}^{n}u_{n}\right)$

En clair, on peut sortir la constante de la somme, la factoriser comme avec une somme normale.

Précisons aussi que l'on peut faire d'autres raccourcis. Par exemple, la somme partielle d'une suite constante est égal au produit du nombre de rang par la constante. Dit autrement, on a :

$\sum _{i=0}^{n-1}k=n\cdot k$

Un cas particulier de l'expression précédente est le cas où $k=1$ :

$\sum _{i=0}^{n-1}1=n$

La somme partielle d'une somme de suites

Pour la somme de deux suites, sa somme partielle est la suivante :

$\sum _{i=0}^{n}(u_{n}+v_{n})=\left(\sum _{i=0}^{n}u_{n}\right)+\left(\sum _{i=0}^{n}v_{n}\right)$

Là encore, le résultat est intuitif et est lié à la commutativité de l'addition : on peut changer l'ordre des additions comme on le souhaite sans changer le résultat.

La somme partielle du produit de deux suites

Pour le produit de deux suites, le calcul naïf ne marche pas : la somme du produit de deux suites n'est pas la somme des produits.

$\sum _{i=0}^{n}(u_{n}\cdot v_{n})\neq \left(\sum _{i=0}^{n}u_{n}\right)\cdot \left(\sum _{i=0}^{n}v_{n}\right)$

Le calcul de la somme partielle est beaucoup plus compliqué et il n'existe pas vraiment de formule générale qui fonctionne.

Exemples de sommes partielles

Il est maintenant temps de voir quelques exemples de suites assez simples.

La somme de la suite des nombres oblongs

Pour commencer, nous allons étudier la suite des nombres oblongs. Un nombre oblong est, par définition, le produit de deux entiers consécutifs, en clair un nombre n tel que $n=i(i+1)$, avec i un entier. Ces nombres ont été beaucoup étudiés dans l'antiquité car ils peuvent se représenter visuellement sans difficultés (ils forment un rectangle). Mais ce qui va nous intéresser ici est la somme des n premiers nombres oblongs. En clair, nous allons calculer la somme partielle suivante :

$S_{n}=\sum _{i=0}^{n-1}i(i+1)$

Partons de la définition de la suite des nombres oblongs et développons.

$\sum _{i=0}^{n-1}i(i+1)=\sum _{i=0}^{n-1}(i^{2}+i)=\sum _{i=0}^{n-1}(i^{2})+\sum _{i=0}^{n-1}i$

On démontrera dans quelques chapitres que $\sum _{i=0}^{n-1}(i^{2})={\frac {n(n+1)(2n+1)}{6}}$ et que $\sum _{i=0}^{n-1}i={\frac {n(n+1)}{2}}$ En faisant le remplacement, on a :

$\sum _{i=0}^{n-1}i(i+1)={\frac {n(n+1)(2n+1)}{6}}+{\frac {n(n+1)}{2}}$

On met au même dénominateur :

$\sum _{i=0}^{n-1}i(i+1)={\frac {n(n+1)(2n+1)}{6}}+{\frac {3n(n+1)}{6}}$

On additionne les termes au numérateur :

$\sum _{i=0}^{n-1}i(i+1)={\frac {n(n+1)(2n+4)}{6}}$

Puis on simplifie :

$\sum _{i=0}^{n-1}i(i+1)={\frac {n(n+1)(n+2)}{3}}$

L'inverse de la suite précédente

Maintenant, nous allons reprendre la même suite, si ce n'est que nous allons prendre l'inverse de chaque terme. En clair, nous allons étudier la suite suivante :

$S_{n}=\sum _{i=1}^{n}{\frac {1}{i(i+1)}}$

On peut démontrer que :

$\sum _{i=1}^{n}{\frac {1}{i(i+1)}}={\frac {n}{n+1}}=1-{\frac {1}{n+1}}$

Démonstration

Cette propriété se démontre assez facilement en utilisant une preuve par induction. Initialisation : On doit commencer par vérifier que cette relation se vérifie pour le premier terme. C'est le cas, comme le prouvent les calculs suivants : Pour $n=1$, $\sum _{i=1}^{n}{\frac {1}{i(i+1)}}={\frac {1}{2}}$ Pour $n=1$, ${\frac {n}{n+1}}={\frac {1}{2}}$ Récurrence : Si on suppose que la relation à prouver est valable pour n, alors elle doit l'être aussi pour n + 1. Il faut donc prouver la relation suivante : $\sum _{i=1}^{n+1}{\frac {1}{i(i+1)}}={\frac {n+1}{n+2}}$ Par définition, on a : $\sum _{i=1}^{n+1}{\frac {1}{i(i+1)}}=\sum _{i=1}^{n}{\frac {1}{i(i+1)}}+{\frac {1}{(n+1)(n+2)}}$ On suppose alors que la relation est valable pour n, ce qui fait que le premier terme à droite du signe égal vaut $n \over n+1$ : $\sum _{i=1}^{n+1}{\frac {1}{i(i+1)}}={\frac {n}{n+1}}+{\frac {1}{(n+1)(n+2)}}$ On met au même dénominateur : $\sum _{i=1}^{n+1}{\frac {1}{i(i+1)}}={\frac {n(n+2)}{(n+1)(n+2)}}+{\frac {1}{(n+1)(n+2)}}$ On additionne et on développe : $\sum _{i=1}^{n+1}{\frac {1}{i(i+1)}}={\frac {n^{2}+2n+1}{(n+1)(n+2)}}$ On peut remarquer que $n^{2}+2n+1=(n+1)^{2}$ : $\sum _{i=1}^{n+1}{\frac {1}{i(i+1)}}={\frac {(n+1)^{2}}{(n+1)(n+2)}}$ On simplifie alors par $n+1$ : $\sum _{i=1}^{n+1}{\frac {1}{i(i+1)}}={\frac {n+1}{n+2}}$

La suite de Fibonacci

Maintenant, calculons la somme partielle de la suite de Fibonnaci. Pour rappel, cette suite est une suite dont chaque terme est la somme des deux termes précédents, dont les premiers termes sont 0 et 1.

Fibonacci sequence - optional starting with zero

La somme partielle des n premiers nombres de Fibonacci a une expression assez simple. Si on note $F_{n}$ le énième nombre de Fibonacci, on a :

Pour $n>1$, $\sum _{i=0}^{n}F_{i}=F_{n+2}-1$

Démonstration

Cette propriété se démontre assez facilement en utilisant une preuve par induction. Initialisation : On doit commencer par vérifier que cette relation se vérifie pour les trois premiers termes : $F_{0}+F_{1}=F_{2}=F_{3}-1$ Ce qui est le cas : $0+1=1=2-1$ Récurrence : Si on suppose que la relation $\sum _{i=0}^{n}F_{i}=F_{n+2}-1$ est valable pour n, alors elle doit l'être aussi pour n + 1. Il faut donc prouver la relation suivante : $\sum _{i=0}^{n+1}F_{i}=F_{n+3}-1$ Par définition, on a : $\sum _{i=0}^{n+1}F_{i}=F_{n+1}+\sum _{i=0}^{n}F_{i}$ Or, on a, par supposition : $\sum _{i=0}^{n}F_{i}=F_{n+2}-1$. On peut faire le remplacement dans l'équation précédente, ce qui donne : $\sum _{i=0}^{n+1}F_{i}=F_{n+2}+F_{n+1}-1$ On applique alors la définition des nombres de Fibonacci, qui dit que : $F_{n+2}+F_{n+1}=F_{n+3}$. On a alors : $\sum _{i=0}^{n+1}F_{i}=F_{n+3}-1$

La suite harmonique

La suite harmonique est le nom donné à la suite de des inverses des entiers naturel, à savoir la suite définie par :

$u_{n}={\frac {1}{n}}$

Ses sommes partielles donnent ce qu'on appelle les nombres harmoniques. Le énième nombre harmonique est simplement la somme des n premiers termes de la suite harmonique, à savoir :

$H_{n}=\sum _{x=1}^{n}{\frac {1}{x}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+...+{\frac {1}{n}}$

Si on écrit les nombres harmoniques sous forme de fraction, on obtient ceci :

$1$, ${\frac {3}{2}}$, ${\frac {11}{3}}$, ${\frac {25}{12}}$, ${\frac {137}{60}}$, ${\frac {49}{20}}$, ${\frac {363}{140}}$, ${\frac {761}{280}}$, $\cdots$

Le numérateur est toujours un nombre impair, alors que le dénominateur est toujours pair. Or, les fractions de type impair/pair ne correspondent jamais à des nombres entiers, contrairement aux fractions de type pair/pair, pair/impair ou impair/impair. En conséquence, les nombres harmoniques sont tous des nombres non-entiers, à l'exception de 1 qui est son propre inverse.

La constante d'Euler–Mascheroni

Ce graphique montre en rouge la suite des nombres harmoniques, et en bleu la fonction logarithme népérien. On voit que les deux suites/fonctions sont assez proches.

La suite des nombres harmoniques forme une suite croissante. Si on compare les nombres harmoniques avec $\ln n$, on trouve que les deux sont proches et qu'elles le sont d'autant plus que le rang augmente. Mieux : la différence entre un nombre harmonique et $\ln n$ converge vers une constante appelée constante d'Euler–Mascheroni, notée $\gamma$.

$\gamma =\lim _{n\rightarrow \infty }\left(H_{n}-\ln {n}\right)$

Elle vaut approximativement :

$\gamma \approx 0.5772156649015328606065120900824024310421...$

Euler-Mascheroni constant.

Tout cela est lié au fait que l'intégrale de la fonction 1/x est égale à :

$\int {\frac {1}{x}}dx=\ln x+K$, avec K une constante

Si on fait la différence entre la fonction $f(x)={\frac {1}{x}}$ et la suite $u_{n}={\frac {1}{n}}$ qui correspond à la fonction $g(x)=\left\lfloor {\frac {1}{x}}\right\rfloor$, on obtient le graphe si-contre. L'aire sous la courbe de 1/X est égale à $\ln x$, alors que l'aire sous la courbe de la suite harmonique est égale à $\sum _{i=0}^{n}{\frac {1}{i}}$. La différence entre les deux est l'aire coloriée en rouge. Plus on augmente le rang n, plus l'aire bleue converge vers la constante d'Euler-Mascheroni .

La suite des entiers et les nombres polygonaux

La suite des entiers naturels donne un exemple assez simple de somme partielle. Très facile à étudier, sa somme partielle est aussi très utile pour établir les sommes partielles d'autres suites, comme les suites arithmétiques.

La suite des entiers (nombres triangulaires)

La suite des nombres entiers est la suite suivante :

$\sum _{x=1}^{n}x=1+2+3+4+5+...+n$

On peut calculer la somme partielle de cette suite, qui n'est autre que la somme des n premiers entiers. La suite formée à partir des sommes partielles donne ce qu'on appelle la suite des nombres triangulaires. Les nombres triangulaires peuvent être représentés par un triangle équilatéral formé par des boules. Le nombre de boules dans le triangle est égal au nombre triangulaire voulu. Le énième terme de la suite des nombres triangulaires donne le nombre de boules pour un triangle de n boules de côté.

Les premiers nombres triangulaires

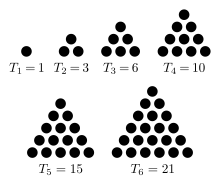
La relation de récurrence

Cette suite est tout simplement de la somme des n premiers entiers. Cette définition nous permet d'obtenir aisément sa forme récurrente. Il s'agit d'une suite définie par :

$u_{0}=0$

$u_{n}=u_{n-1}+n$

Un bon moyen de s'en rendre compte est de calculer les termes de cette suite et de calculer la différence entre termes consécutifs. Le tableau ci-dessous montre que cette différence entre termes consécutifs est égale au rang.

La suite des nombres triangulaires

Terme $u_{n}$	1	3	6	10	15	21	28	...
Rang $n$	1	2	3	4	5	6	7	...
$u_{n}-u_{n-1}$	1	2	3	4	5	6	7	...

La relation paramétrée

Calculer la forme paramétrée de cette suite est assez simple pour qui est suffisamment ingénieux. La légende veut que le mathématicien Gauss ait découvert cette formule alors qu’il était au primaire, bien que ce soit sans doute une idée reçue. Cette légende prétend que son professeur avait donné comme exercice le calcul des 100 premiers entiers. Là où ses camarades de classe firent les calculs à la main, Gauss procéda autrement. Il prit la suite des nombres entiers jusqu’à 100 et créa une seconde suite identique, mais de sens inverse. Il additionna alors les deux et trouva ceci :

• 1 + 100 = 101 ;
• 2 + 99 = 101 ;
• 3 + 98 = 101 ;
• … ;
• 49 + 52 = 101 ;
• 50 + 51 = 101 ;
• … ;
• 98 + 3 = 101 ;
• 99 + 2 = 101 ;
• 100 + 1 = 101.

En additionnant la suite des n premiers entiers avec elle-même, il se retrouvait avec 100 fois 101 : $2S=100\times 101$. Le calcul de la somme partielle est alors aisé.

Illustration géométrique de la somme des n premiers entiers.

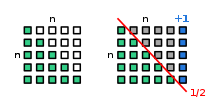
On peut généraliser ce raisonnement pour toute suite de n nombres entiers consécutifs. Pour cette suite, on a :

$1+n=2+(n-1)=3+(n-2)=...$

Donc, si on additionne la suite S avec elle-même, on a :

$2S=n(1+n)$

D'où :

$u_{n}={\frac {n(n+1)}{2}}$

Pour précision, le terme $n(n+1)$ est ce qu'on appelle un nombre oblong, à savoir le produit de deux entiers consécutifs. Il existe une suite des nombres oblongs, définie par $u_{n}=n(n+1)$. L'équation démontrée précédemment nous dit donc que le énième nombre oblong est égal au double de la somme des n premiers entiers. En clair, la suite des nombres oblongs est égal au double de la suite des nombres triangulaires.

Les suites arithmétiques

Raisonnement généralisé dans le cas d'une progression arithmétique quelconque.

Démonstration visuelle de la somme des n premiers termes d'une progression arithmétique.

Après avoir vu les multiples des entiers, nous allons voir le cas où chaque entier est multiplié par une constante, avant de se voir ajouter une autre constante. En clair, les suites de la forme :

$u_{n}=k\cdot n+u_{0}$, avec k la raison de la suite et $u_{0}$ le premier terme.

Il se trouve que ces suites ne sont autre que les suites arithmétiques. Nous allons donc calculer la somme partielle d'une suite arithmétique, de la forme :

$\sum _{i=0}^{n}(k\cdot i+u_{0})$

On peut déduire, avec quelques développements assez simples, que cette somme partielle vaut :

$S_{n}=k\cdot {\frac {n(n+1)}{2}}+n\cdot u_{0}$

Démonstration

La somme partielle d'une suite arithmétique se calcule en additionnant les n premiers termes de la suite : $S_{n}=u_{0}+u_{1}+u_{2}+u_{3}+u_{4}+...+u_{n}$ Remplaçons chaque terme par sa valeur paramétrée dans l'équation précédente : $S_{n}=u_{0}+(u_{0}+k)+(u_{0}+2k)+(u_{0}+3k)+(u_{0}+4k)+...+(u_{0}+nk)$ Factorisons le terme $u_{0}$ : $S_{n}=n\times u_{0}+(k+2k+3k+4k+5k+6k+...+nk)$ Factorisons maintenant $k$ : $S_{n}=n\times u_{0}+k\times (1+2+3+4+5+6+...+n)$ On a vu plus haut que $(1+2+3+4+5+6+...+n)={\frac {n(n+1)}{2}}$. On a alors : $S_{n}=n\times u_{0}+k\times {\frac {n(n+1)}{2}}$

Démonstration

Partons de la définition de la somme partielle voulue : $S_{n}=\sum _{i=0}^{n}(k\cdot i+u_{0})$ On applique la formule $\sum _{i=0}^{n}(u_{n}+v_{n})=\left(\sum _{i=0}^{n}u_{n}\right)+\left(\sum _{i=0}^{n}v_{n}\right)$ : $S_{n}=\left(\sum _{i=0}^{n}k\cdot i\right)+\left(\sum _{i=0}^{n}u_{0}\right)$ Par définition, le terme de droite $\sum _{i=0}^{n}k_{2}$ est égal à $n\cdot u_{0}$ : $S_{n}=\left(\sum _{i=0}^{n}k\cdot i\right)+n\cdot u_{0}$ Puis, on applique la formule $\sum _{i=0}^{n}(k\cdot u_{n})=k\cdot \left(\sum _{i=0}^{n}u_{n}\right)$ : $S_{n}=k\cdot \left(\sum _{i=0}^{n}i\right)+n\cdot u_{0}$ On a vu plus haut que $\sum _{i=0}^{n}i={\frac {n(n+1)}{2}}$ : $S_{n}=k\cdot {\frac {n(n+1)}{2}}+n\cdot u_{0}$

On peut aussi reformuler la formule précédente comme suit :

$S_{n}=n{\frac {u_{0}+u_{n+1}}{2}}$

Démonstration

Pour cela, partons de la formule précédente : $S_{n}=k\cdot {\frac {n(n+1)}{2}}+n\cdot u_{0}$ Factorisons $n \over 2$ : $S_{n}=n{\frac {2u_{0}+k(n+1)}{2}}$ On peut alors utiliser l'équation $u_{n+1}=u_{0}+k(n+1)$, ce qui simplifie l'équation précédente en : $S_{n}=n{\frac {u_{0}+u_{n+1}}{2}}$

La somme des n premiers nombres pairs et la suite des nombres oblongs

Commençons par nous intéresser à la somme des n premiers nombres pairs. Par définition, la suite des nombres pairs, à savoir la somme :

$\sum _{i=0}^{n}(2i)$

En appliquant la formule sur le produit d'une suite par une constante, on trouve :

$\sum _{i=0}^{n}(2i)=2\times \sum _{i=0}^{n}i=n(n+1)$

En clair, la somme des n premiers pairs est la somme de deux entiers consécutifs. Pour rappel, la somme de deux entiers consécutifs est ce qu'on appelle un nombre oblong. Le résultat précédent nous dit que la somme des n premiers nombres pairs est le énième nombre oblong.

La somme des n premiers nombres impairs

Maintenant, étudions le cas de la suite des nombres impairs, dont la somme partielle est la suivante :

$\sum _{i=0}^{n}(2i+1)=(n+1)^{2}$

La somme des n-1 premiers nombres impairs donne donc le énième carré !

Démonstration

La suite des nombres impairs est par définition une suite arithmétique de premier terme 1 et de raison 2. Le énième nombre impair est donc égal à $u_{n}=2n-1$, alors que $u_{0}=1$. En injectant dans la formule générale, on a : $S_{n}=n{\frac {1+2n-1}{2}}=n^{2}$

Démonstration

$\sum _{i=0}^{n-1}(2i+1)=2\sum _{i=0}^{n-1}i+\sum _{i=0}^{n-1}1=2\left({\frac {n(n-1)}{2}}\right)+n=n(n-1)+n=n^{2}$

On peut remarquer que cette somme partielle donne aussi des nombres figurés, que l'on peut représenter par des figures géométriques, comme pour les nombres triangulaires. Sauf que cette fois-ci, le triangle est remplacé par un carré.

Nombres figurés carrés.

La somme des n premiers nombres de la forme 3n + 1

Nombres pentagonaux.

Maintenant, il est temps de voir la somme partielle de la suite arithmétique de raison 3 et de premier terme 1. Cette série donne aussi des nombres figurés, qui peuvent être représentés par un pentagone. La figure de droite illustre ce point. Cette suite est celle des nombres pentagonaux.

Cette série est obtenue en additionnant les n premiers nombres de la forme 3n + 1. Voici sa formule :

$S_{n}=\sum _{x=0}^{n}(3x+1)$

L'application de la formule générale nous donne :

$S_{n}=3\times {\frac {n(n+1)}{2}}+n$

Ce qui se reformule en :

$u_{n}={\frac {n(3n-1)}{2}}+n$

Les autres nombres polygonaux

Nombres hexagonaux.

On pourrait poursuivre et parler des nombres hexagonaux et heptagonaux et de bien d'autres. Mais nous n’allons pas le faire, ce qui serait trop répétitif. Tout ce que l'on peut dire, c'est que les suites de nombres de la forme 4n + 1, 5n + 1, 6n + 1 et autres ont des sommes partielles représentables sous la forme de polygones réguliers (pour rappel, les polygones réguliers sont des figures géométriques avec des côtés de même longueur et des angles identiques). La formule des sommes partielles arithmétiques permet de calculer leur valeur assez simplement. Elle est de la forme :

$S_{n}=k\cdot {\frac {n(n+1)}{2}}+n\cdot u_{0}$

Ici, k est égal au nombre de côtés du polygone, moins 2. En notant s le nombre de côtés, on a donc :

$S_{n}=(s-2)\cdot {\frac {n(n+1)}{2}}+n\cdot u_{0}$

Ce qui peut aussi s'écrire comme suit :

$S_{n}={\frac {(s-2)n^{2}-(s-4)n}{2}}$

La somme partielle d'une suite arithmético-géométrique

Dans ce chapitre, nous allons voir comment calculer la somme partielle d'une suite géométrique, et d'une suite arithmético-géométrique. Nous allons d'abord voir les suites arithmétiques, avant de passer aux suites géométriques et enfin aux suites arithmético-géométriques. Pour chaque type de suite, nous verrons quelques exemples particuliers qui ont un intérêt intellectuel ou ludique. Par exemple, nous verrons la somme des entiers pairs, de leurs inverses, etc.

Les suites géométriques

|r| < 1, n → ∞ ⇒ S_∞ = a/(1 − r)

Dans la section précédente, nous avons montré que la formule d'une somme partielle arithmétique se déduisait d'un cas particulier : le cas de la somme des n premiers entiers. Toute somme partielle arithmétique a pour résultat une fonction affine de la somme des n premiers entiers : on doit multiplier cette somme par la raison et ajouter le premier terme (multiplié par le rang). Pour les séries géométriques, la situation est similaire, à savoir que toute somme partielle géométrique est un multiple d'un cas particulier. Ce cas particulier correspond au cas où le premier terme vaut 1.

Les suites avec premier terme unitaire

Dans ce qui va suivre, nous allons démontrer le résultat pour les séries géométriques où le premier terme vaut 1, qui sont de la forme :

$S_{n}=1+r+r^{2}+r^{3}+r^{4}+\cdots +r^{n-1}=\sum _{i=0}^{n-1}r^{i}$

Multiplions l'expression précédente par la raison. On a alors :

$r\times S_{n}=r+r^{2}+r^{3}+r^{4}+\cdots +r^{n-1}+r^{n}=\sum _{i=0}^{n-1}r^{i+1}$

Soustrayons cette expression à la valeur de la suite initiale :

$S_{n}-r\times S_{n}=1-r^{n}$

Factorisons le terme de gauche :

$S_{n}(1-r)=1-r^{n}$

Isolons le terme $S_{n}$ :

$S_{n}={\frac {1-r^{n}}{1-r}}$

Le cas général

La somme partielle d'une suite géométrique se calcule, par définition, en additionnant les n premiers termes de la suite (qui vont des rangs 0 à $n-1$) :

$S_{n}=u_{0}+u_{1}+u_{2}+u_{3}+u_{4}+...+u_{n-1}$

Remplaçons chaque terme par son expression paramétrée $u_{n}=u_{0}\times r^{n}$.

$S_{n}=u_{0}+(u_{0}\times r^{1})+(u_{0}\times r^{2})+(u_{0}\times r^{3})+(u_{0}\times r^{4})+(u_{0}\times r^{5})...++(u_{0}\times r^{n-1})=\sum _{i=0}^{n}u_{0}\cdot r^{n}$

Factorisons $u_{0}$ :

$S_{n}=u_{0}(1+r+r^{2}+r^{3}+r^{4}+\cdots +r^{n-1}+r^{n})=u_{0}\cdot \sum _{i=0}^{n}r^{n}$

Le second terme n'est autre que le cas particulier étudié dans la section précédente. Il vient alors :

$S_{n}=u_{0}{\frac {1-r^{n}}{1-r}}$

À noter qu'il existe d'autres démonstrations de cette formule. Ceux qui souhaitent en prendre connaissance peuvent consulter celles-ci sur le site proofwiki, en suivant ce lien : Somme d'une progression géométrique.

Un exemple : la somme partielle des puissances de deux

Étudions maintenant un cas particulier assez intéressant pour les informaticiens : la somme des n premières puissances de deux. Toute personne qui s'y connaît suffisamment en numération binaire voit où je veux en venir avec cet exemple. Par définition, la suite des puissances de deux est une suite géométrique de raison 2 et de premier terme 1. La formule plus haut nous dit alors que la somme des n premières puissances de deux vaut :

$S_{n}={\frac {1-2^{n}}{1-2}}={\frac {1-2^{n}}{-1}}=-(1-2^{n})=2^{n}-1$

On voit donc que la somme des n premières puissances de deux est égale à la puissance de deux immédiatement supérieure, retranchée de 1 :

$\sum _{i=0}^{n-1}2^{i}=2^{n}-1$

Il s'agit d'une propriété absolument essentielle de la numération binaire, qui est très utile pour simplifier certains calculs en binaire ou faire quelques démonstrations importantes.

Un second exemple : la somme partielle des inverses des puissances de deux

Maintenant, nous allons voir un second exemple : la somme partielle des inverses de $2^{n}$, définie par :

$\sum _{i=1}^{n}{\frac {1}{2^{i}}}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\cdots +{\frac {1}{2^{n}}}$

Il s'agit d'une suite géométrique de raison $1 \over 2$ et de premier terme égal à $1 \over 2$. La formule donne donc :

$S_{n}={\frac {1}{2}}{\frac {1-{\frac {1}{2}}^{n}}{1-{\frac {1}{2}}}}={\frac {1}{2}}{\frac {1-{\frac {1}{2^{n}}}}{\frac {1}{2}}}=1-{\frac {1}{2^{n}}}$

On peut prouver cette équation d'une autre manière, donnée dans la démonstration suivante.

Démonstration

Repartons de l'équation : $\sum _{i=1}^{n}{\frac {1}{2^{i}}}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\cdots +{\frac {1}{2^{n-1}}}+{\frac {1}{2^{n}}}$ Mettons tout au même dénominateur : $\sum _{i=1}^{n}{\frac {1}{2^{i}}}={\frac {2^{n-1}}{2^{n}}}+{\frac {2^{n-2}}{2^{n}}}+{\frac {2^{n-3}}{2^{n}}}+\cdots +{\frac {2^{1}}{2^{n}}}+{\frac {1}{2^{n}}}={\frac {2^{n-1}+2^{n-2}+2^{n-3}+\cdots +2^{1}+1}{2^{n}}}$ Or, on a vu juste dans la précédente section que : $2^{n-1}+2^{n-2}+2^{n-3}+\cdots +2^{1}+1=2^{n}-1$. En faisant le remplacement, on a : $\sum _{i=1}^{n}{\frac {1}{2^{i}}}={\frac {2^{n}-1}{2^{n}}}=1-{\frac {1}{2^{n}}}$

Les suites arithmético-géométriques

La somme partielle d'une suite arithmético-géométrique est assez simple à calculer quand on sait comment calculer une somme partielle arithmétique et une somme partielle géométrique. Reprenons la formule pour le calcul du terme d'une suite arithmético-géométrique :

$u_{n}=a^{n}\left(u_{0}-t\right)+t$ avec $t={\frac {b}{1-a}}$

Faisons la somme des n premiers termes :

$\sum _{i=0}^{n-1}u_{n}=\sum _{i=0}^{n-1}\left(a^{n}\left(u_{0}-t\right)+t\right)$

On applique la formule $\sum _{i=0}^{n}(u_{n}+v_{n})=\left(\sum _{i=0}^{n}u_{n}\right)+\left(\sum _{i=0}^{n}v_{n}\right)$ :

$\sum _{i=0}^{n-1}u_{n}=\sum _{i=0}^{n-1}\left(a^{n}\left(u_{0}-t\right)\right)+\sum _{i=0}^{n-1}t$

Par définition, le terme de droite $\sum _{i=0}^{n-1}t$ est égal à $n\cdot t$ :

$\sum _{i=0}^{n-1}u_{n}=\sum _{i=0}^{n-1}\cdot \left(a^{n}\left(u_{0}-t\right)\right)+n\cdot t$

Puis, on applique la formule $\sum _{i=0}^{n}(k\cdot u_{n})=k\cdot \left(\sum _{i=0}^{n}u_{n}\right)$ :

$\sum _{i=0}^{n-1}u_{n}=\left(u_{0}-t\right)\cdot \sum _{i=0}^{n-1}\left(a^{n}\right)+n\cdot t$

En faisant le remplacement avec $t={\frac {b}{1-a}}$, on trouve :

$\sum _{i=0}^{n-1}u_{n}=\left(u_{0}-{\frac {b}{1-a}}\right){\frac {1-a^{n}}{1-a}}+n{\frac {b}{1-a}}$

Les suites de puissances et la formule de Faulhaber

La suite des carrés des entiers naturels, celle des cubes, et bien d'autres se dérivent aussi à partir de la suite des entiers. Dans cette section, nous allons étudier les suites de puissances, à savoir les suites de la forme :

$1^{k}+2^{k}+3^{k}+4^{k}+...+n^{k}=\sum _{i=0}^{n}i^{k}$

Nous avons déjà vu le cas où k=1, qui n'est autre que la suite des entiers naturels. Et nous savons déjà que la somme associée vaut :

$\sum _{i=0}^{n}i={\frac {n(n+1)}{2}}\approx {\frac {n^{2}}{2}}$

Dans ce chapitre, nous allons voir les autres cas. Nous allons commencer par la suite des carrés, puis voir la suite des cubes, puis le cas général.

La suite des carrés (nombres pyramidaux carrés)

Après avoir vu la somme des n premiers entiers, nous allons poursuivre en voyant la somme de leurs carrés. Encore une fois, il s'agit d'une suite de Riemann, dont la forme est la suivante :

$\sum _{x=1}^{n}x^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}+...+n^{2}$

La somme des n premiers carrés, qui n'est autre que le énième nombre pyramidal carré, vaut :

$\sum _{x=1}^{n}x^{2}={\frac {n(n+1)(2n+1)}{6}}={\frac {n(n+1)}{2}}{\frac {2n+1}{3}}={\frac {2n^{3}+3n^{2}+n}{6}}={\frac {n^{3}}{3}}+{\frac {n^{2}}{2}}+{\frac {n}{6}}$

Démonstration

Illustration du quatrième nombre pyramidale. Cette somme peut se représenter sous la forme d'une figure géométrique, comme les nombres triangulaires. Mais cette forme est en trois dimensions : c'est une pyramide dont la base est carrée. D'où le nom de nombres pyramidaux carrés donné aux nombres provenant d'une somme des n premiers carrés. On voit que la pyramide est composée de plusieurs couches (n couches pour être précis), chaque couche étant un carré. La somme des carrés correspond donc au volume de la pyramide et ce fait nous permet de trouver une formule pour le calculer. Prenons trois de ces pyramides, et assemblons-les comme illustré ci-dessous. On voit que le résultat ressemble à un pavé de côtés (n, n, n+1), si ce n'est qu'il y a quelques cubes en trop au sommet (n gris ans le schéma ci-dessous). Les cubes qui manquent forment un triangle de côté n, ce qui fait qu'il y a exactement $n(n+1) \over 2$ (le énième nombre triangulaire) cubes en trop. Preuve géométrique de la formule de la somme des carrés. L'observation géométrique précédente peut se traduire en équation. Le pavé est composé de trois pyramides, plus du énième nombre triangulaire. En notant $V_{pyramide}$ le volume d'une pyramide et $T_{n}$ le énième nombre triangulaire, on a : $3\cdot V_{pyramide}=V_{pave}+T_{n}$ Le pavé a un volume de $n^{2}\cdot (n+1)=n^{3}+n^{2}$. $3\cdot V_{pyramide}=n^{3}+n^{2}+T_{n}$ Le énième nombre triangulaire vaut ${\frac {n(n+1)}{2}}={\frac {n^{2}+n}{2}}={\frac {n^{2}}{2}}+{\frac {n}{2}}$ : $3\cdot V_{pyramide}=n^{3}+n^{2}+{\frac {n^{2}}{2}}+{\frac {n}{2}}$ Enfin, le volume d'une pyramide est la somme des n premiers carrés. $3\cdot \left(\sum _{i=0}^{n-1}i^{2}\right)=n^{3}+n^{2}+{\frac {n^{2}}{2}}+{\frac {n}{2}}$ Simplifions : $3\cdot \left(\sum _{i=0}^{n-1}i^{2}\right)=n^{3}+{\frac {3n^{2}}{2}}+{\frac {n}{2}}$ On divise par trois : $\sum _{i=0}^{n-1}i^{2}={\frac {n^{3}}{3}}+{\frac {3n^{2}}{6}}+{\frac {n}{6}}$ Simplifions : $\sum _{i=0}^{n-1}i^{2}={\frac {n^{3}}{3}}+{\frac {n^{2}}{2}}+{\frac {n}{6}}$

Démonstration

Pour démontrer cette formule, nous allons utiliser les notations suivantes pour la somme des n premiers entiers, des n premiers carrés et des n premiers cubes : $S_{n}^{1}=1+2+3+4+5+6+...+n$ $S_{n}^{2}=1+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}+...+n^{2}$ $S_{n}^{3}=1+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}+...+n^{3}$ Pour faire la démonstration, nous allons partir du développement du cube de n+1 : $(n+1)^{3}=(n+1)\times (n+1)^{2}=n^{3}+3n^{2}+3n+1$ Appliquons maintenant cette formule sur tous les nombres de 1 à n + 1 : $(n+1)^{3}=(n+1)+(n+1)^{2}=n^{3}+3n^{2}+3n+1$ ... $2^{3}=1^{3}+3(1)^{2}+3(1)+1$ $1^{3}=0^{3}+3(0)^{2}+3(0)+1$ Additionnons le tout en colonnes. On trouve alors : $S_{n+1}^{3}=S_{n}^{3}+3S_{n}^{2}+3S_{n}+n+1$ $S_{n+1}^{3}-S_{n}^{3}=3S_{n}^{2}+3S_{n}+n+1$ Or, on voit que $S_{n+1}^{3}-S_{n}^{3}$ vaut, par définition $(n+1)^{3}$. Faisons le remplacement : $(n+1)^{3}=3S_{n}^{2}+3S_{n}+n+1$ $3S_{n}^{2}=(n+1)^{3}-(3S_{n}+n+1)$ Développons $(n+1)^{3}$ : $3S_{n}^{2}=(n^{3}+3n^{2}+3n+1)-(3S_{n}+n+1)$ $3S_{n}^{2}=n^{3}+3n^{2}+2n-3S_{n}$ $S_{n}^{2}={\frac {n^{3}+3n^{2}+2n-3S_{n}}{3}}$ $S_{n}^{2}={\frac {n^{3}+3n^{2}+2n}{3}}-S_{n}$ Or, on sait que : $u_{n}={\frac {n(n+1)}{2}}={\frac {n^{2}+n}{2}}$, ce qui donne : $S_{n}^{2}={\frac {n^{3}+3n^{2}+2n}{3}}-{\frac {n^{2}+n}{2}}$ Mettons au même dénominateur : $S_{n}^{2}={\frac {2n^{3}+6n^{2}+4n}{6}}-{\frac {3n^{2}+3n}{6}}$ $S_{n}^{2}={\frac {2n^{3}+3n^{2}+n}{6}}$

La suite des cubes (nombres triangulaires carrés)

Représentation visuelle de l'identité de Nicomaque de Gérase.

Maintenant, passons à la suite de l'inverse des cubes, définie par :

$\sum _{x=1}^{n}x^{3}=1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}+...+n^{3}$

On peut prouver que :

$\sum _{x=1}^{n}x^{3}=\left(\sum _{x=1}^{n}x\right)^{2}$

Ce qui peut s’écrire comme suit, sachant que $\sum _{x=1}^{n}x={\frac {n(n+1)}{2}}$ :

$\sum _{x=1}^{n}x^{3}={\frac {n^{2}(n+1)^{2}}{4}}={\frac {n^{4}+2n^{3}+n^{2}}{4}}$

Cette identité est connue sous le nom d'identité de Nicomaque, en l'honneur du découvreur de cette formule, Nicomaque de Gérase. Il existe plusieurs démonstrations de cette formule, mais la plus simple est clairement la démonstration par induction.

Démonstration

Pour commencer, la formule est valable pour n = 1 : $1={\frac {1^{2}(1+1)^{2}}{4}}$ Maintenant, supposons que la formule soit valable pour n, et regardons ce que cela donne pour n+1. Partons de la formule de la somme des cubes jusqu’à n+1, écrite comme suit : $\sum _{x=1}^{n+1}x^{3}=\sum _{x=1}^{n}x^{3}+(n+1)^{3}$ Vu qu'on suppose que la formule de Nicomaque est valide pour n, appliquons-la : $\sum _{x=1}^{n+1}x^{3}={\frac {n^{2}(n+1)^{2}}{4}}+(n+1)^{3}$ Mettons le tout au même dénominateur : $\sum _{x=1}^{n+1}x^{3}={\frac {n^{2}(n+1)^{2}}{4}}+{\frac {4(n+1)^{3}}{4}}$ Factorisons $(n+1)^{2} \over 4$ : $\sum _{x=1}^{n+1}x^{3}={\frac {(n+1)^{2}}{4}}\left[n^{2}+4(n+1)\right]$ Développons le terme entre parenthèses : $\sum _{x=1}^{n+1}x^{3}={\frac {(n+1)^{2}}{4}}\left[n^{2}+4n+4\right]$ On utilise alors l'identité remarquable $(n+2)^{2}=n^{2}+4n+4$ : $\sum _{x=1}^{n+1}x^{3}={\frac {(n+1)^{2}(n+2)^{2}}{4}}$ On voit donc que la formule de Nicomaque est respectée pour n+1, si elle est respectée pour n. L'induction est donc valide.

Démonstration

A plus b au carre. Il existe aussi une démonstration géométrique de l'identité de Nicomaque. Cette démonstration se base sur l'étude d'un carré de côté (a+b) bien particulier. Rappelons l'identité remarquable suivante : $(a+b)^{2}=a^{2}+2\cdot a\cdot b+b^{2}$ Dans le cas qui nous intéresse, nous allons prendre $a=\sum _{i=0}^{n-1}i$ et $b=n$, ce qui donne $(a+b)=\sum _{i=0}^{n}i$. On a donc : $\left(\sum _{i=0}^{n}i\right)^{2}=\left(\sum _{i=0}^{n-1}i\right)^{2}+2\cdot n\cdot \left(\sum _{i=0}^{n-1}i\right)+n^{2}$ En faisant le remplacement $\sum _{i=0}^{n-1}={\frac {n^{2}-n}{2}}$, on a : $\left(\sum _{i=0}^{n}i\right)^{2}=\left(\sum _{i=0}^{n-1}i\right)^{2}+2\cdot n\cdot {\frac {n^{2}-n}{2}}+n^{2}$ Simplifions le terme de droite : $\left(\sum _{i=0}^{n}i\right)^{2}=\left(\sum _{i=0}^{n-1}i\right)^{2}+n^{3}$ Maintenant, examinons le terme : $\left(\sum _{i=0}^{n-1}i\right)^{2}$. En utilisant la formule précédente, on peut l'écrire de la manière suivante : $(n-1)^{3}+\left(\sum _{i=0}^{n-2}i\right)^{2}$. En injectant dans l'équation précédente, on a : $\left(\sum _{i=0}^{n}i\right)^{2}=\left(\sum _{i=0}^{n-2}i\right)^{2}+(n-1)^{3}+n^{3}$ Et on répéte le procédé autant de fois qu'il le faut, jusqu'à ne plus avoir que des cubes dans le terme de droite. On a alors : $\left(\sum _{i=0}^{n}i\right)^{2}=1^{3}+2^{3}+3^{3}+...+(n-1)^{3}+n^{3}$ En clair, on a : $\left(\sum _{i=0}^{n}i\right)^{2}=\sum _{i=0}^{n}i^{3}$

Le cas général : la méthode récursive

Dans cette section, nous allons voir une méthode générale pour calculer la somme :

$1^{k}+2^{k}+3^{k}+4^{k}+...+n^{k}=\sum _{i=0}^{n}i^{k}$

La méthode en question demande cependant de connaitre les sommes pour la puissance immédiatement inférieure k-1. En clair, pour calculer la somme pour k=5, il faut connaitre la formule pour k=4. La formule en question est la suivante :

$(n+1)\sum _{i=0}^{n}i^{k-1}=\sum _{i=0}^{n}i^{k}+\sum _{p=0}^{n}\sum _{i=0}^{p}i^{k-1}$

Le cas de la somme des carrés

La formule se comprend assez bien sous forme géométrique. Pour l'étudier, commençons par le cas le plus simple, où l'on cherche à avoir la somme des carrés. Pour cela, étudions un rectangle tel que sa hauteur soit égale à $n+1$ et sa longueur soit égale à la somme $\sum _{i=0}^{n}i$ des premiers entiers. Le tout est illustré ci-dessous, dans le cas où n = 8. Sa surface est donc de :

$S_{rectangle}=(n+1)\cdot \sum _{i=0}^{n}i$

Sur sa longueur, on a découpé les distances égales à 1, 2, 3, 4, etc. En jaune, on représente les carrés de côté 1, 2, 3, 4, etc. L'aire en jaune est donc égale à :

$S_{carres}=\sum _{i=0}^{n}i^{2}$

Il ne reste qu'à calculer la différence entre rectangle et somme des carrés. Sur la première ligne, on voit qu'il manque (1+2+3+4+..+n). Sur la seconde ligne, il manque (1+2+3+4+5+ ... + (n-1). Et ainsi de suite. En clair, la surface totale manquante est égale à :

$S_{manquante}=\sum _{p=0}^{n}\sum _{i=0}^{p}i$

En combinant le tout, on obtient la formule vue plus haut, mais dans le cas où k=2:

$(n+1)\sum _{i=0}^{n}i=\sum _{i=0}^{n}i^{2}+\sum _{p=0}^{n}\sum _{i=0}^{p}i$

Démonstration géométrique de la somme partielle des carrés - illustration avec k = 2 et n=8.

On peut alors combiner la formule précédente avec la formule $\sum _{i=0}^{n}i={\frac {n^{2}+n}{2}}$. On a alors :

$(n+1)\sum _{i=0}^{n}i=\sum _{i=0}^{n}i^{2}+\sum _{p=0}^{n}{\frac {p^{2}+p}{2}}$

On sort le 1/2 du dernier terme :

$(n+1)\sum _{i=0}^{n}i=\sum _{i=0}^{n}i^{2}+{\frac {1}{2}}\sum _{p=0}^{n}(p^{2}+p)$

On développe la dernière somme :

$(n+1)\sum _{i=0}^{n}i=\sum _{i=0}^{n}i^{2}+{\frac {1}{2}}\sum _{p=0}^{n}p^{2}+{\frac {1}{2}}\sum _{p=0}^{n}p$

On soustrait la somme ${\frac {1}{2}}\sum _{p=0}^{n}p$ des deux côtés :

$\left(n+{\frac {1}{2}}\right)\sum _{i=0}^{n}i=\sum _{i=0}^{n}i^{2}+{\frac {1}{2}}\sum _{p=0}^{n}p^{2}$

Le terme de droit se factorise en :

$\left(n+{\frac {1}{2}}\right)\sum _{i=0}^{n}i={\frac {3}{2}}\sum _{i=0}^{n}i^{2}$

On multiplie par $2 \over 3$ des deux côtés :

${\frac {2n+1}{3}}\sum _{i=0}^{n}i=\sum _{i=0}^{n}i^{2}$

En faisant le remplacement, on trouve :

$\sum _{i=0}^{n}i^{2}={\frac {n(n+1)}{2}}{\frac {2n+1}{3}}$

Soit le même résultat que nous avions trouvé plus haut.

Le cas de la somme des cubes

Le raisonnement précédent marche aussi pour la somme des cubes, sous réserve que l'on change la longueur du rectangle. On garde une hauteur de (n+1), sauf que cette fois-ci la longueur du rectangle est changée pour la somme des carrés $\sum _{i=0}^{n}i^{2}$. Sa surface totale est donc de :

$S_{rectangle}=(n+1)\sum _{i=0}^{n}i^{2}$

On peut ensuite découper la longueur en segments de longueur $1^{2},2^{2},3^{2},4^{2},...,n^{2}$. On peut alors créer des rectangles avec chaque segment, dont la hauteur est de k. Leur surface est donc égale à $1^{3},2^{3},3^{3},4^{3},...,n^{3}$. La somme totale de ces rectangles a une surface de :

$S_{sous-rectangles}=\sum _{i=0}^{n}i^{3}$

La différence entre les deux sommes précédentes est composé d'une somme de lignes. Chaque ligne a pour surface la somme des carrés jusqu’à un certain rang, tous les rangs étant représentés. La surface totale occupée par ces lignes est donc de :

$S_{lignes}=\sum _{p=0}^{n}\sum _{i=0}^{p}i^{2}$

En combinant tout cela, on a la formule générale :

$S_{rectangle}=S_{sous-rectangles}+S_{lignes}$

En faisant le remplacement avec les équations précédentes, on trouve :

$(n+1)\sum _{i=0}^{n}i^{2}=\sum _{i=0}^{n}i^{3}+\sum _{p=0}^{n}\sum _{i=0}^{p}i^{2}$

Démonstration géométrique de la somme partielle des cubes - illustration avec n=4.

Le cas général

le raisonnement peut se généraliser pour un k quelconque. Il suffit de prendre un rectangle de hauteur $n+1$ et de longueur égale à $\sum _{i=0}^{n}i^{k-1}$ (donc une puissance en-dessous de celle voulue). Sa surface totale est donc de :

$S_{rectangle}=(n+1)\sum _{i=0}^{n}i^{k-1}$

On peut ensuite découper la longueur en segments de longueur $1^{k-1},2^{k},3^{k-1},4^{k-1},...,n^{k-1}$. On peut alors créer des rectangles avec chaque segment, dont la hauteur est de k. Leur surface est donc égale à $1^{k},2^{k},3^{k},4^{k},...,n^{k}$. La somme totale de ces rectangles a une surface de :

$S_{sous-rectangles}=\sum _{i=0}^{n}i^{k}$

La différence entre les deux sommes précédentes est composé d'une somme de ligne qui ont pour surface $1^{k-1},2^{k},3^{k-1},4^{k-1},...,n^{k-1}$. La surface totale occupée par ces lignes est donc de :

$S_{lignes}=\sum _{p=0}^{n}\sum _{i=0}^{p}i^{k-1}$

En combinant tout cela, on a la formule générale :

$S_{rectangle}=S_{sous-rectangles}+S_{lignes}$

En faisant le remplacement avec les équations précédentes, on trouve :

$(n+1)\sum _{i=0}^{n}i^{k-1}=\sum _{i=0}^{n}i^{2}+\sum _{p=0}^{n}\sum _{i=0}^{p}i^{k-1}$

Le cas général : la formule de Faulhaber

Maintenant, étudions le cas général, mais sans recourir à une récursion.

$1^{k}+2^{k}+3^{k}+4^{k}+...+n^{k}=\sum _{i=0}^{n}i^{k}$

Et pour cela, commençons par étudier quelques exemples.

$\sum _{x=1}^{n}x^{0}=n$

$\sum _{x=1}^{n}x^{1}={\frac {1}{2}}n^{2}+{\frac {1}{2}}n$

$\sum _{x=1}^{n}x^{2}={\frac {1}{3}}n^{3}+{\frac {1}{2}}n^{2}+{\frac {1}{6}}n$

$\sum _{x=1}^{n}x^{3}={\frac {1}{4}}n^{4}+{\frac {1}{2}}n^{3}+{\frac {1}{4}}n^{2}$

$\sum _{x=1}^{n}x^{4}={\frac {1}{5}}n^{5}+{\frac {1}{2}}n^{4}+{\frac {1}{3}}n^{3}+{\frac {1}{30}}n$

$\sum _{x=1}^{n}x^{5}={\frac {1}{6}}n^{6}+{\frac {1}{2}}n^{5}+{\frac {5}{12}}n^{4}+{\frac {1}{12}}n^{2}$

$\sum _{x=1}^{n}x^{6}={\frac {1}{7}}n^{7}+{\frac {1}{2}}n^{6}+{\frac {1}{2}}n^{5}+{\frac {1}{6}}n^{3}+{\frac {1}{42}}n$

Les exemples montrent que la formule finale est toujours un polynôme de degré égal à $k+1$ et on peut démontrer que cela se généralise à toute somme de puissance. De plus, le premier terme est toujours de la forme $n^{k+1} \over k+1$. On peut donc établir l'approximation suivante :

$\sum _{i=0}^{n}i^{k}\approx {\frac {n^{k+1}}{k+1}}$

On peut même aller plus loin en regardant le second terme, qui est toujours de la forme $n^{k} \over 2$. On a donc :

$\sum _{i=0}^{n}i^{k}\approx {\frac {n^{k+1}}{k+1}}+{\frac {n^{k}}{2}}$

Par contre, il ne semble pas y avoir de règle évidente pour les autres termes.

Maintenant, cherchons une formule non pas approchée, mais exacte.

Une approche intuitive de la formule de Faulhaber

Il existe une formule qui permet de calculer le cas général, appelée la formule de Faulhaber, du nom de son découvreur. Pour comprendre comment elle a été découverte, étudions les premiers exemples. Nous allons supposer que les formules sont des polynômes de degré $k+1$ et allons tenir compte des termes nuls.

$\sum _{x=1}^{n}x^{0}=n$

$\sum _{x=1}^{n}x^{1}={\frac {1}{2}}n^{2}+{\frac {1}{2}}n$

$\sum _{x=1}^{n}x^{2}={\frac {1}{3}}n^{3}+{\frac {1}{2}}n^{2}+{\frac {1}{6}}n$

$\sum _{x=1}^{n}x^{3}={\frac {1}{4}}n^{4}+{\frac {1}{2}}n^{3}+{\frac {1}{4}}n^{2}+0\cdot n$

$\sum _{x=1}^{n}x^{4}={\frac {1}{5}}n^{5}+{\frac {1}{2}}n^{4}+{\frac {1}{3}}n^{3}+0\cdot n^{2}+{\frac {1}{30}}n$

$\sum _{x=1}^{n}x^{5}={\frac {1}{6}}n^{6}+{\frac {1}{2}}n^{5}+{\frac {5}{12}}n^{4}+0\cdot n^{3}+{\frac {1}{12}}n^{2}+0\cdot n$

$\sum _{x=1}^{n}x^{6}={\frac {1}{7}}n^{7}+{\frac {1}{2}}n^{6}+{\frac {1}{2}}n^{5}+0\cdot n^{4}+{\frac {1}{6}}n^{3}+0\cdot n^{2}+{\frac {1}{42}}n$

Le premier terme est égal à $n^{k+1} \over k+1$. En factorisant $k+1$, on obtient :

$\sum _{x=1}^{n}x^{0}={\frac {1}{1}}\left[n\right]$

$\sum _{x=1}^{n}x^{1}={\frac {1}{2}}\left[n^{2}+2\cdot {\frac {1}{2}}\cdot n\right]$

$\sum _{x=1}^{n}x^{2}={\frac {1}{3}}\left[n^{3}+3\cdot {\frac {1}{2}}\cdot n^{2}+3\cdot {\frac {1}{6}}\cdot n\right]$

$\sum _{x=1}^{n}x^{3}={\frac {1}{4}}\left[n^{4}+4\cdot {\frac {1}{2}}\cdot n^{3}+6\cdot {\frac {1}{6}}\cdot n^{2}+0\cdot n\right]$

$\sum _{x=1}^{n}x^{4}={\frac {1}{5}}\left[n^{5}+5\cdot {\frac {1}{2}}\cdot n^{4}+10\cdot {\frac {1}{6}}\cdot n^{3}+5\cdot {\frac {1}{30}}\cdot n^{2}+0\cdot n\right]$

$\sum _{x=1}^{n}x^{5}={\frac {1}{6}}\left[n^{6}+6\cdot {\frac {1}{2}}\cdot n^{5}+15\cdot {\frac {5}{6}}\cdot n^{4}+0\cdot n^{3}+15\cdot {\frac {1}{30}}\cdot n^{2}+0\cdot n\right]$

$\sum _{x=1}^{n}x^{6}={\frac {1}{7}}\left[n^{7}+7\cdot {\frac {1}{2}}\cdot n^{6}+21\cdot {\frac {1}{6}}\cdot n^{5}+0\cdot n^{4}+0\cdot n^{3}+35\cdot {\frac {1}{30}}\cdot n^{2}+7\cdot {\frac {1}{42}}\cdot n\right]$

Triangle de Pascal.

Reste à trouver un moyen de calculer les coefficients, dont on voit qu'ils sont le produit de deux termes : un terme entier et une fraction. Maintenant, comparons les termes entiers avec ceux du triangle de Pascal, un triangle de nombres très connu en mathématiques et souvent utilisé dans des domaines divers. On voit que les termes entiers correspondent exactement à ceux du triangle de Pascal. Un triangle de pascal est donné ci-contre pour que vous puissiez comparer avec les termes des polynômes précédents. Par définition, le nombre situé à la ligne numéro $i$ et la colonne $j$ est égal à ce qu'on appelle le coefficient binomial ${i \choose j}$. Pour rappel, le coefficient binomial ${i \choose j}$ donne le nombre de configurations de $i$ éléments parmi un ensemble de $j$ éléments. On les calcule avec la formule suivante :

${n \choose k}={\frac {n!}{k!\cdot (n-k)!}}$.

Les polynomes précédents se reformulent donc :

$\sum _{x=1}^{n}x^{0}={\frac {1}{1}}\left[{1 \choose 0}n\right]$

$\sum _{x=1}^{n}x^{1}={\frac {1}{2}}\left[{2 \choose 0}n^{2}+{2 \choose 1}\cdot {\frac {1}{2}}\cdot n\right]$

$\sum _{x=1}^{n}x^{2}={\frac {1}{3}}\left[{3 \choose 0}n^{3}+{3 \choose 1}\cdot {\frac {1}{2}}\cdot n^{2}+{3 \choose 2}\cdot {\frac {1}{6}}\cdot n^{1}\right]$

$\sum _{x=1}^{n}x^{3}={\frac {1}{4}}\left[{4 \choose 0}n^{4}+{4 \choose 1}\cdot {\frac {1}{2}}\cdot n^{3}+{4 \choose 2}\cdot {\frac {1}{6}}\cdot n^{2}+{4 \choose 3}\cdot 0\cdot n\right]$

$\sum _{x=1}^{n}x^{4}={\frac {1}{5}}\left[{5 \choose 0}n^{5}+{5 \choose 1}\cdot {\frac {1}{2}}\cdot n^{4}+{5 \choose 2}\cdot {\frac {1}{6}}\cdot n^{3}+{5 \choose 3}\cdot 0\cdot n^{2}+{5 \choose 4}\cdot {\frac {1}{30}}\cdot n\right]$

$\sum _{x=1}^{n}x^{5}={\frac {1}{6}}\left[{5 \choose 0}n^{6}+{6 \choose 1}\cdot {\frac {1}{2}}\cdot n^{5}+{6 \choose 2}\cdot {\frac {1}{6}}\cdot n^{4}+{6 \choose 3}\cdot 0\cdot n^{3}+{6 \choose 4}\cdot {\frac {1}{30}}\cdot n^{2}+{6 \choose 5}\cdot 0\cdot n\right]$

$\sum _{x=1}^{n}x^{6}={\frac {1}{7}}\left[{7 \choose 0}n^{7}+{7 \choose 1}\cdot {\frac {1}{2}}\cdot n^{6}+{7 \choose 2}\cdot {\frac {1}{6}}\cdot n^{5}+{7 \choose 3}\cdot 0\cdot n^{4}+{7 \choose 4}\cdot {\frac {1}{30}}\cdot n^{3}+{7 \choose 5}\cdot 0\cdot n^{2}+{7 \choose 6}\cdot {\frac {1}{42}}\cdot n\right]$

Graphe des premiers nombres de Bernoulli.

Les coefficients fractionnaires placés juste avant les coefficients binomiaux sont appelés les nombres de Bernoulli , en référence à leur découvreur. En soi, les nombres de Bernoulli sont conçus de manière à ce que la méthode présentée au-dessus marche. On peut les fabriquer par des séries génératrices ou d'autres méthodes assez complexes, mais ils n'ont rien de particulier à eux seuls. Du moins, c'est ce qui apparaît au premier abord, mais ils sont utilisés dans divers développements mathématiques, comme en analyse, en théorie des nombres et dans d'autres domaines. Le énième nombre de la suite de Bernoulli sera notés $B_{n}$ dans ce qui suit. Les premiers nombres de Bernoulli sont : $B_{0}=1,\quad B_{1}=-{\tfrac {1}{2}},\quad B_{2}={\tfrac {1}{6}},\quad B_{3}=0,\quad B_{4}=-{\tfrac {1}{30}}\quad \dots$ Tous les termes impairs au-delà de $B_{1}$ sont égaux à zéro, ce qui élimine beaucoup de termes. Ils sont définis par la formule récursive suivante :

$B_{0}=1$

$B_{1}={1 \over 2}$

${\frac {1}{m+1}}\sum _{i=0}^{m}{m+1 \choose i}B_{i}=1$

La formule de Faulhaber : formalisation

Formalisons les observations précédentes. Pour commencer, les premières observations nous disent que la formule est un polynôme de degré $k+1$ :

$\sum _{i=0}^{n}i^{k}=\sum _{i=0}^{n}\left(a_{i}\cdot n^{k+1-i}\right)=a\cdot n^{k+1}+b\cdot n^{k}+c\cdot n^{k-1}+d\cdot n^{k-2}+...$

On factorise alors $k+1$, ce qui donne des polynômes obtenus de la forme :

$\sum _{i=0}^{n}i^{k}={\frac {1}{k+1}}\sum _{i=0}^{n}\left(k_{i}\cdot n^{k+1-i}\right)={\frac {1}{k+1}}\left[k_{1}\cdot n^{k+1}+k_{2}\cdot n^{k}+k_{2}\cdot n^{k-1}+k_{3}\cdot n^{k-2}+...\right]$

On sait que les coefficients $k_{i}$ sont le produit d'un coefficient binomial ${k+1 \choose i}$ par le nombre de Bernoulli $B_{i}$.

$\sum _{i=0}^{n}i^{k}={\frac {1}{k+1}}\sum _{i=0}^{n}\left[{k+1 \choose i}\cdot B_{i}\cdot n^{k+1-i}\right]={\frac {1}{k+1}}\left[n^{k+1}+{\frac {k+1}{2}}n^{k}+{\frac {1}{6}}{k+1 \choose 2}n^{k-1}-{\frac {1}{30}}{k+1 \choose 4}n^{k-3}+{\frac {1}{42}}{k+1 \choose 6}n^{k-5}+...\right]$

Une formule équivalente, mais plus lisible, est la suivante :

$\sum _{i=0}^{n}i^{k}={\frac {n^{k+1}}{k+1}}+{\frac {n^{k}}{2}}+\sum _{i=2}^{n}\left[{\frac {B_{i}}{i!}}\cdot {\frac {k!}{(k-i-1)!}}\cdot n^{k+1-i}\right]$

Les suites télescopiques

Les sommes télescopiques sont les sommes partielles de la forme :

Pour $\sum _{i=0}^{n}(u_{i+1}-u_{i})$

Le calcul d'une somme partielle télescopique

On peut facilement démontrer la formule suivante :

Pour $\sum _{i=0}^{n}(u_{i+1}-u_{i})=u_{n+1}-u_{0}$

De manière informelle, le raisonnement est le suivant. On part de la définition d'une somme télescopique :

$\sum _{i=0}^{n}(u_{i+1}-u_{i})$

Développons l'expression :

Pour $\sum _{i=0}^{n}(u_{i+1}-u_{i})=(u_{1}-u_{0})+(u_{2}-u_{1})+(u_{3}-u_{2})+(u_{4}-u_{3})+(u_{5}-u_{4})+(u_{6}-u_{5})+\cdots$

On peut changer l'ordre des termes, ce qui donne :

Pour $\sum _{i=0}^{n}(u_{i+1}-u_{i})=-u_{0}+(u_{1}-u_{1})+(u_{2}-u_{2})+(u_{3}-u_{3})+\cdots +(u_{n}-u_{n})+u_{n+1}=u_{n+1}-u_{0}$}}

Une démonstration plus formelle, équivalent à ce qui vient d'être dit, serait la suivante :

Démonstration

Partons de la définition d'une somme télescopique : $\sum _{i=0}^{n}(u_{i+1}-u_{i})$ Appliquons la formule $\sum _{i=0}^{n}(u_{n}+v_{n})=\left(\sum _{i=0}^{n}u_{n}\right)+\left(\sum _{i=0}^{n}v_{n}\right)$ : $\left(\sum _{i=0}^{n}u_{i+1}\right)-\left(\sum _{i=0}^{n}u_{i}\right)$ En simplifiant, cela donne : $\left(\sum _{i=1}^{n+1}u_{i}\right)-\left(\sum _{i=0}^{n}u_{i}\right)$ Le calcul donne donc : Pour $\sum _{i=0}^{n}(u_{i+1}-u_{i})=u_{n+1}-u_{0}$

Le produit d'un suite telescopique par une autre suite

On a vu plus haut que le calcul de la somme partielle est beaucoup plus compliqué et il n'existe pas vraiment de formule générale qui fonctionne. On peut cependant déduire un résultat pour le cas particulier suivant :

$\sum _{i=0}^{n}\left[u_{i}\cdot (v_{i+1}-v_{i})\right]$

On voit que le cas particulier en question est le produit d'une suite par une somme télescopique $v_{n}-v_{n-1}$. Dans ce cas particulier, on peut alors utiliser la sommation par partie, que voici :

$\sum _{i=0}^{n}\left[u_{i}\cdot (v_{i+1}-v_{i})\right]=u_{n}\cdot v_{n+1}-u_{0}\cdot v_{0}-\sum _{i=1}^{n}\left[v_{n}\cdot (u_{n}-u_{n-1})\right]$

On peut appliquer cette formule dans le cas général, en transformant une suite en suite télescopique. Pour montrer comment, partons du cas général :

$P=\sum _{n=0}^{N}\left(a_{n}\cdot b_{n}\right)$

On peut alors définir la suite suivante :

$B_{n}=\sum _{k=0}^{n}b_{k}$.

Par définition, on a $b_{n}=B_{n}-B_{n-1}$, ce qui permet de réécrire le produit P comme ceci :

$P=a_{0}b_{0}+\sum _{n=1}^{N}a_{n}(B_{n}-B_{n-1})$

En faisant une sommation par partie, on trouve alors :

$P=a_{0}b_{0}-a_{0}B_{0}+a_{N}B_{N}+\sum _{n=0}^{N-1}B_{n}(a_{n}-a_{n+1}).$

Un exemple d'utilisation

Un exemple d'utilisation des théorèmes sur les suites télescopiques est le suivant. On peut retrouver la somme partielle de la suite de l'inverse des nombres oblongs, soit la somme partielle suivante, sans recourir à une démonstration par récurrence :

$S_{n}=\sum _{i=1}^{n}{\frac {1}{i(i+1)}}=1-{\frac {1}{n+1}}$

Pour cela, il suffit de réécrire la suite initiale sous la forme d’une suite télescopique. Pour cela, partons de la suite initiale :

$S_{n}=\sum _{i=1}^{n}{\frac {1}{i(i+1)}}$

On applique alors la formule ${\frac {1}{i(i+1)}}={\frac {1}{i}}-{\frac {1}{i+1}}$

$S_{n}=\sum _{i=1}^{n}\left({\frac {1}{i}}-{\frac {1}{i+1}}\right)$

La formule précédente s'identifie à la limite de la suite télescopique $u_{i}={\frac {1}{i}}-{\frac {1}{i+1}}$. En appliquant la formule des suites télescopiques, on trouve que :

$S_{n}=1-{\frac {1}{n+1}}$

Les limites de suites

L'étude des suites porte le plus souvent sur la manière dont les termes se comportent quand le rang augmente. Par exemple, les mathématiciens ou physiciens cherchent souvent à savoir si les termes finaux d'une suite se rapprochent d'une valeur précise. Beaucoup de suites sont dans ce cas : les termes se rapprochent de plus en plus d'une valeur précise quand on augmente le rang. D'autres ne sont pas dans ce cas et voient leurs termes devenir de plus en plus grands ou petits avec le rang. C'est le cas de la suite $u_{n}=n$, par exemple. Le comportement d'une suite quand n grandit a beaucoup été étudié par les mathématiciens, qui lui ont donné le nom de comportement asymptotique.

La convergence/divergence d'une suite

Comme on le voit, le comportement des termes quand on augmente le rang vers l'infini varie beaucoup selon la suite. Cette intuition peut être formalisée assez simplement par le concept de limite d'une suite. Intuitivement, on peut se retrouver dans trois cas différents :

• Soit les termes se rapprochent, tendent, vers une valeur précise.
• Soit les termes tendent vers une valeur infinie.
• Soit les termes ne tendent vers aucune valeur, qu'elle soit finie ou infinie : c'est le cas par exemple de la suite 1, -1, 1, -1, 1, -1 ...

Dans le premier cas, on dit que la suite est convergente. Les deux autres cas correspondent à ce qu'on appelle une suite divergente. On voit qu'il existe deux types de suites divergentes, les premières tendent vers l'infini alors que les autres sont es suites un peu à part. Ces dernières sont appelées des suites sautantes. Elles sont définies par la condition suivante : soit a < b, la suite $(u_{n})$ est dite sautante si une infinité de termes est supérieur à b ($u_{n}>b$) et une autre infinité est inférieur à a ($u_{n}<a$).

Les suites divergentes

Une suite est dite divergente si ses termes finissent par devenir aussi grands que possible quand le rang augmente. Si on choisit une constante précise, aussi grande que l'on veut, alors tous les termes au-delà d'un certain rang dépasseront cette constante. Dit autrement, pour tout nombre M, il existe un rang n tel que $u_{n}>M$. La suite diverge alors vers l'infini $+\infty$. Le cas où la suite diverge vers $-\infty$ est similaire, si ce n'est que $u_{n}<M$ au-delà d'un rang n.

Les suites convergentes

Pour une suite qui converge, la logique est similaire au cas où la suite diverge, à quelques différences près. Pour une suite convergente, ses termes sont circonscrits dans un intervalle que l'on peut rendre aussi petit que possible quand le rang augmente. Le centre de cet intervalle est la limite de la suite. Précisément, si on choisit un nombre $\epsilon$, aussi petit que l'on veut, alors il y a un rang au-delà duquel les termes de la suite sont tous compris dans l'intervalle $[limite-\epsilon ,limite+\epsilon ]$.

Définition de la limite d'une suite.

On peut reformuler cette définition de la manière suivante : les suites convergentes sont bornées au-delà d'un certain rang, les bornes étant les valeurs $limite-\epsilon$ et $limite+\epsilon$. Cette définition montre plus clairement que la convergence d'une suite ne dépend pas de ses premiers termes.

On peut noter que si une suite converge, sa limite est unique : une suite ne peut pas converger vers deux limites différentes en même temps. Un bon moyen de le "démontrer" est simplement d'utiliser un raisonnement par l'absurde. Pour commencer, on suppose qu'une suite (peu importe laquelle) converge vers deux suites $l$ et $l'$. Au bout d'un certain rang, on sait que tout terme la de suite sera donc compris dans les intervalles $[l-\epsilon ,l+\epsilon ]$ et $[l'-\epsilon ,l'+\epsilon ]$. Évidemment, si l et l' sont différents, ces intervalles seront disjoints. Vu que chaque terme de la suite au-delà d'un certain rang ne peut pas appartenir à deux intervalles disjoints, on fait face à une contradiction.

Quelques exemples types de limites

Dans l'enseignement secondaire et/ou universitaire, vous aurez certainement à faire des calculs de limites. Dans ces calculs, certaines limites particulières ont tendance à revenir, à être fortement utiles. Dans ce qui va suivre, nous allons voir quelques exemples classiques de limites assez courants.

Nom de la suite	Formule paramétrée de la suite	Limite
Suite constante	$u_{n}=x$	$\lim \limits _{x\rightarrow +\infty }u_{n}=x$
Suite identité	$u_{n}=n$	$\lim \limits _{x\rightarrow +\infty }u_{n}=+\infty$
Suite harmonique	$u_{n}={\frac {1}{n}}$	$\lim \limits _{x\rightarrow +\infty }u_{n}=0$
Suite de l'inverse des carrés	$u_{n}={\frac {1}{n^{2}}}$	$\lim \limits _{x\rightarrow +\infty }u_{n}=0$
Suite d'une puissance	$u_{n}=n^{a}$	Si $a>0$, la suite est croissante et sans majorant : elle diverge vers $+\infty$. Si $a=0$, la suite est constante et converge vers $1$. Si $a<0$, la suite est décroissante et avec une borne inférieure nulle : elle converge vers $0$.

Démontrer les limites du tableau précédent est assez simple : il suffit d'appliquer la définition.

Le cas des suites constantes est trivial. Pour la suite identité, on remarque rapidement qu'elle n'est pas bornée, ce qui signifie qu'elle n'a pas de limite et donc diverge.

Le cas de la suite harmonique est plus intéressant, bien qu'une simple application de la définition d'une suite suffise à donner le résultat.

L'exemple de la suite harmonique

Dans cette section, nous allons démontrer que la suite harmonique converge bien vers zéro. Pour cela, il suffit d'appliquer la définition de la limite d'une suite. Déjà, on sait que chaque terme de la suit ne peut être négatif : tout terme est positif ou nul : $u_{n}\geq 0$. Il ne reste plus qu'à prouver que si on choisit un $\epsilon$ aussi petit que l'on veut, on peut trouver un rang $n$ à partir duquel tous les termes de la suite sont plus petits que $\epsilon$. Déjà, on peut remarquer que la suite est décroissante : chaque terme est plus petit que le précédent. Donc, si on trouve un rang pour lequel $u_{n}<\epsilon$, alors les rangs suivants respectent aussi cette propriété. Dit autrement, on souhaite trouver $n$ tel que :

$0\leq u_{n}<\epsilon$

Appliquons l'équation $u_{n}={\frac {1}{n}}$ et faisons le remplacement :

$0\leq {\frac {1}{n}}<\epsilon$

On trouve alors qu'il faut que :

$0\leq {\frac {1}{\epsilon }}<n$

Or, un tel rang existe toujours. Vu que chaque terme de la suite ne peut être négatif, mais qu'on peut les rendre aussi petits que l'on veut, tant qu'ils restent à zéro ou plus, alors la limite de la suite est nulle.

Les critères de convergence usuels

Exemple de suite convergente.

Pour établir si une suite converge ou diverge, l'application de la définition d'une limite est rarement facile. Pour faire des démonstrations plus facilement, il existe de nombreux critères qui permettent de savoir si une suite converge ou non. Une simple analyse de la suite avec ces critères permet de déterminer si elle converge ou diverge. Ces critères sont nombreux et permettent surtout de savoir si une suite diverge, sans pour autant préciser si elle converge effectivement. D'autres permettent de comparer des suites à d'autres suites dont on sait qu'elles convergent ou divergent. Cette section va donner quelques critères de convergences usuels, simples à appliquer.

Les suites convergentes sont bornées

Une propriété importante des suites convergentes est qu'elles sont toutes bornées (pour rappel, cela signifie qu'elles ont un minimum et un maximum). Mais il faut faire attention à la réciproque, qui est fausse : une suite bornée n'est pas forcément convergente. Un bon contre-exemple est la suite définie par : $u_{n}=(-1)^{n}$. Celle-ci est bornée dans l'intervalle $[-1,1]$, mais elle ne converge pas. Pour résumer, les suites convergentes sont bornées. On peut donc déterminer si une suite diverge en vérifiant qu'elle est bornée. Si on démontre que ce n'est pas le cas, elle diverge. Si c'est le cas, on ne sait pas si elle diverge ou si elle converge.

Démonstration

Cette propriété n'est pas étonnante et découle directement de la définition d'une limite. Pour rappel, cette définition dit qu'il existe un rang $n$ tel que les termes de la suite sont bornés par l'intervalle : $[limite-\epsilon ,limite+\epsilon ]$ Avant ce rang $n$, il n'y a qu'un nombre fini de termes. Parmi ces termes, il y en a un qui est plus grand que les autres et un autre qui est plus petit que tous les autres. Notons ceux-ci max et min. Par définition, les termes de la suite avant le rang $n$ sont naturellement bornés dans l'intervalle suivant : $[min,max]$ La suite est donc bornée avant le rang : $n$, prendant et après : elle est donc bornée.

Le théorème des gendarmes

Illustration du théorème des gendarmes.

Le théorème des gendarmes, aussi appelé théorème du sandwich ou théorème d'encadrement, est un critère qui concerne les suites adjacentes. Si une suite est encadrée par deux suites qui convergent vers la même limite, alors on sait que les trois suites convergent vers la même limite. Cet encadrement est plus précisément un encadrement de chaque terme de la suite entre les termes de même rang des deux autres. Dit d'une manière plus claire, chaque terme $u_{n}$ de la suite encadré est compris entre les termes $v_{n}$ et $w_{n}$ des deux autres suites : $w_{n}\leq u_{n}\leq v_{n}$. Si à partir d'un certain rang, l'égalité précédente est respectée pour tous les termes, on sait que la suite encadrée converge et que sa limite est la même que celle des deux autres suites.

Pour résumer, supposons que l'on ait la condition suivante :

$v_{n}\leq u_{n}\leq w_{n}$, au-delà d'un certain rang n.

Alors on peut en déduire que :

$\left(\lim _{n\rightarrow \infty }v_{n}\right)\leq \left(\lim _{n\rightarrow \infty }u_{n}\right)\leq \left(\lim _{n\rightarrow \infty }w_{n}\right)$

Démonstration

Démontrer ce critère se démontre avec les concepts que nous verrons dans le chapitre suivant, qui porte sur les opérations entre limites de suites. Il s'agit d'une simple application du théorème de prolongement des inégalités larges. Celui-ci dit simplement que si $(a_{n})\leq (b_{n})$, alors $\lim _{n\to \infty }(a_{n})\leq \lim _{n\to \infty }(b_{n})$.

Le critère de Cauchy

Illustration d'une suite de Cauchy.

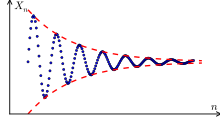
Le critère de Cauchy permet de déterminer si une suite converge ou non, assez simplement. Ce critère permet de définir une classe de suites particulières, appelées suites de Cauchy. On peut démontrer, avec des outils mathématiques compliqués, que toute suite convergente est obligatoirement une suite de Cauchy. Pour les suites réelles, les suites de Cauchy convergent toutes, sans exception. Démontrer qu'une suite réelle est de Cauchy suffit donc pour dire qu'elle converge.

Une suite de Cauchy est une suite telle que pour deux rangs $a$ et $b$, avec $a>n,b>n$, on a :

$|u_{a}-u_{b}|<\epsilon$

Ce qui est équivalent à :

$\lim _{n\to \infty }|u_{a}-u_{b}|=0$

Il faut préciser que cette condition doit valoir pour tout a et b supérieur à n. Le fait que la condition fonctionne avec a et b convenablement choisis ne marche pas. Par exemple, prendre a et b consécutif ne donnera pas une application correcte du théorème de Cauchy. Il existe en effet des suites divergentes dont suite dont la différence entre deux termes consécutifs tend vers zéro. Ainsi, on ne peut pas dire qu'une suite est convergente si elle respecte la condition suivante :

$\lim _{n\to \infty }|u_{n+1}-u_{n}|=0$

Les opérations sur les limites de suites

Il est intéressant de regarder quelle est la limite d'une somme de deux suites, ou de leur produit. Dans une telle condition, on peut dire si la limite de la somme converge ou diverge selon le comportement des deux suites. Pour les suites qui convergent, le résultat est plutôt simple : la limite de la somme est la somme des limites, idem pour le produit ou le quotient.. Pour deux suites $(a_{n})$ et $(b_{n})$ qui convergent respectivement vers $a$ et $b$, leur somme converge vers $a+b$, leur différence vers $a-b$, leur produit vers $a\times b$ et leur quotient vers $a \over b$. Le résultat pour les suites divergentes est assez compliqué, mais le résultat diverge dans la plupart des cas, sauf dans quelques cas où le résultat n'est pas connu qui portent le nom de formes indéterminées. Dans les tableaux qui suivent, ces formes indéterminées seront notées "F.I".

Les comparaisons entre suites

Le résultat d'une comparaison entre deux suites n'est pas forcément conservée lors du passage à la limite. Tout dépend de la comparaison considérée. Précisément, il faut faire la différence entre les inégalités strictes, à savoir $<$ et $>$, et les inégalités non-strictes, à savoir $=$, $\leq$ et $\geq$.

Le passage à la limite des inégalités strictes entre suites

Le passage à la limite ne conserve pas les inégalités strictes entre suites. Il suffit de considérer les deux suites suivantes pour ce convaincre du fait que le passage à la limite ne conserve pas les inégalités strictes :

$\forall n\in \mathbb {N} ^{*},\quad U_{n}:=1+{\frac {1}{n}}\qquad V_{n}:=1-{\frac {1}{n}}$

Leur limite est 1 pourtant pour $n>0,U_{n}>V_{n}$.

Comme autre exemple, on peut citer les deux suites $u_{n}={1 \over n}$ et $b_{n}={2 \over n}$. On a bien $u_{n}<v_{n}$, mais ces deux suites ont la même limite (ici, 0).

Pour les inégalités strictes, on peut prouver les relations suivantes :

• Si $(a_{n})<(b_{n})$, alors $\lim _{n\to \infty }(a_{n})\leq \lim _{n\to \infty }(b_{n})$.
• Si $(a_{n})>(b_{n})$, alors $\lim _{n\to \infty }(a_{n})\geq \lim _{n\to \infty }(b_{n})$.

En clair, une inégalité stricte entre deux suites se transforme en une inégalité non-stricte lors du passage à la limite. Par contre, le sens de l'inégalité ne s'inverse pas. Si une suite est inférieure à une autre, impossible que sa limite soit supérieure (et réciproquement).

On peut démontrer les deux relations suivantes de la même manière. Dans ce qui suit, nous allons faire la démonstration pour $(a_{n})<(b_{n})\implies \lim _{n\to \infty }(a_{n})\leq \lim _{n\to \infty }(b_{n})$.

Démonstration

Notons $l_{a}$ et $l_{b}$ les limites respectives $\lim _{n\to \infty }(a_{n})$ et $\lim _{n\to \infty }(b_{n})$. On pose aussi $\epsilon >0$. Vu que $(a_{n})$ converge vers $l_{a}$, alors il existe un rang $N_{a}$ au-delà duquel on a : $l_{a}+\epsilon >a_{n}>l_{a}-\epsilon$. Même chose pour la suite $(b_{n})$, où on a un rang $N_{b}$ au-delà duquel $l_{b}+\epsilon >b_{n}>l_{b}-\epsilon$. Dans ce qui va suivre, nous allons seulement utiliser les inégalités suivantes : $l_{a}+\epsilon >a_{n}$, pour $N_{a}<n$. $l_{b}+\epsilon >b_{n}$, pour $N_{b}<n$. Si on suppose que $a_{n}<b_{n}$, on a : $a_{n}+\epsilon <b_{n}+\epsilon$ En combinant les trois inégalités précédentes, on trouve : $l_{a}<a_{n}+\epsilon <b_{n}+\epsilon <l_{b}+2\cdot \epsilon$ En simplifiant, on trouve que : $l_{a}<l_{b}+2\cdot \epsilon$ On a alors : $l_{a}\leq l_{b}$. On voit que le passage d'une inégalité stricte à une inégalité non-stricte se fait dans la toute dernière étape, et est lié à $\epsilon$.

Le passage à la limite des inégalités non-strictes entre suites

Les inégalités larges (non-strictes) sont conservées lors du passage à la limite. On a alors :

• Si $(a_{n})=(b_{n})$, alors $\lim _{n\to \infty }(a_{n})=\lim _{n\to \infty }(b_{n})$.
• Si $(a_{n})\leq (b_{n})$, alors $\lim _{n\to \infty }(a_{n})\leq \lim _{n\to \infty }(b_{n})$.
• Si $(a_{n})\geq (b_{n})$, alors $\lim _{n\to \infty }(a_{n})\geq \lim _{n\to \infty }(b_{n})$.

Ces relations sont connues sous le nom de théorème de prolongement des inégalités larges (sous entendu, entre deux suites et lors d'un passage à la limite).

Ces trois relations peuvent se démontrer par un raisonnement par l'absurde assez simple.

Les résultats d'opérations sur les suites

Voyons maintenant comment se comporte la limite lorsque l'on effectue une opération sur deux suites. Les résultats sont donnés pour des suites divergentes et convergentes notées $u_{n}$ et $v_{n}$.

Multiplication d'une suite par un réel

Le résultat du produit d'une suite avec un réel est assez trivial à établir. Tout dépend si la suite diverge ou converge :

• Dans le cas d'une suite convergente $(a_{n})$ de limite $a$, la limite du produit $k\times (a_{n})$ a pour limite $k\times a$. En clair, la limite du produit est le produit des limites.
• Dans le cas d'une suite divergente, le produit avec un réel ne change rien : la suite diverge toujours et sa "limite" reste la même si elle en a une. Une suite qui diverge vers $\infty$ continuera à diverger ainsi après multiplication par un réel.

Par contre, il faut faire attention quand le réel $k$ est négatif : le signe de la limite peut changer.

$\lim u_{n}$		$\ell$	$-\infty$	$+\infty$
$\lim(k\times u)_{n}$	$k>0$	$k\times \ell$	$-\infty$	$+\infty$
	$k<0$		$+\infty$	$-\infty$

Démonstration

Prenons une suite convergente $u_{n}$ et $K$ une constante réelle ou complexe. Nous voulons prouver que : $\lim _{n\rightarrow \infty }(K\cdot u_{n})=K\cdot \lim _{n\rightarrow \infty }u_{n}$ Notons $L$ la limite de la suite $u_{n}$. Pour prouver l'égalité plus haut, il faut trouver un rang $N$ tel que : $|C\cdot u_{n}-C\cdot L|<\epsilon$ Du fait des propriétés des valeurs absolues, on a : $|C|\cdot |u_{n}-L|<\epsilon$ Si la constante C est non-nulle, l'inégalité précédente peut se reformuler comme suit : $|u_{n}-L|<{\frac {\epsilon }{|C|}}$ Or, vu que la suite $u_{n}$ converge, l'égalité précédente est toujours respectée au-delà d'un certain rang. La division par C ne change pas grand chose, vu que l'on peut prendre epsilon aussi petit que l'on souhaite. Notons que la démonstration ne vaut pas si $C=0$, mais ce cas est trivial et donne une suite nulle, qui converge par définition.

L'inverse d'une suite

Prenons une suite $u_{n}$ dont on connait la limite $\lim _{n\rightarrow \infty }u_{n}$. On peut calculer la limite de l'inverse de cette suite $\lim _{n\rightarrow \infty }\left({\frac {1}{u_{n}}}\right)$, si elle existe. On peut se retrouver face à trois situations, selon que la limite tend vers zéro, tend vers un nombre fini non-nul, ou tend vers l'infini.

Limite de la suite	Limite de l'inverse
$\lim _{n\rightarrow \infty }u_{n}=0$	$\lim _{n\rightarrow \infty }\left({\frac {1}{u_{n}}}\right)=\infty$
$\lim _{n\rightarrow \infty }u_{n}=L\neq 0$	$\lim _{n\rightarrow \infty }\left({\frac {1}{u_{n}}}\right)={\frac {1}{L}}$
$\lim _{n\rightarrow \infty }u_{n}=+/-\infty$	$\lim _{n\rightarrow \infty }\left({\frac {1}{u_{n}}}\right)=0$

Somme et différence de deux suites

Additionner deux suites donne des résultats assez différents selon les suites $(a_{n})$ et $(b_{n})$. En effet, l'addition de deux suites convergentes ne donnera pas le même résultat que l'addition de deux suites divergentes, ou qu'une suite divergente avec une convergente.

Le cas le plus simple est de loin l'addition de deux suites convergentes $(a_{n})$ et $(b_{n})$ qui convergent respectivement vers $a$ et $b$. Leur somme $(a_{n}+b_{n})$ converge vers $a+b$ : la limite d'une somme est égale à la somme des limites

Démonstration

Prenons deux suites convergentes $u_{n}$ et $v_{n}$. Nous voulons prouver que : $\lim _{n\rightarrow \infty }(v_{n}+u_{n})=\lim _{n\rightarrow \infty }v_{n}+\lim _{n\rightarrow \infty }u_{n}$ Notons $L_{1}$ la limite de la suite $v_{n}$ et $L_{2}$ la limite de la suite $u_{n}$. Pour prouver l'égalité plus haut, il faut trouver un rang $N$ tel que : $|(v_{n}+u_{n})-(L_{1}+L_{2})|<\epsilon$ Du fait de l'inégalité triangulaire, on a : $|(v_{n}+u_{n})-(L_{1}+L_{2})|<|v_{n}-L_{1}|+|u_{n}-L_{2}|$ Vu que les deux suites convergent, on peut toujours trouver un rang tel que $|v_{n}-L_{1}|<{\frac {\epsilon }{2}}$ et $|u_{n}-L_{2}|<{\frac {\epsilon }{2}}$. On a alors : $|(v_{n}+u_{n})-(L_{1}+L_{2})|<|v_{n}-L_{1}|+|u_{n}-L_{2}|<{\frac {\epsilon }{2}}+{\frac {\epsilon }{2}}$ Ce qui se réécrit, après quelques simplifications : $|(v_{n}+u_{n})-(L_{1}+L_{2})|<\epsilon$ Cette inégalité n'est autre que la définition du fait que $(v_{n}+u_{n})$ converge vers $L_{1}+L_{2}$.

Ce principe est cependant remis en question quand une des deux suites $(a_{n})$ et $(b_{n})$ diverge : la somme des suites va elle aussi diverger. Dans le cas où une des suites $(a_{n})$ et $(b_{n})$ n'a pas de limite, alors la somme $(a_{n}+b_{n})$ ne peut pas avoir de limite. Le cas le plus simple à étudier est celui où la suite divergente tend vers $+\infty$ ou $-\infty$. Dans ce cas, la suite diverge aussi vers $\infty$, à une exception près : celui où une des suite tend vers $+\infty$ et l'autre vers $-\infty$. Dans ce dernier cas, on ne sait pas si les deux infinis se compensent (donnant un zéro), ou si l'un des deux infini l'emporte sur l'autre. Le résultat de la somme ne peut donc pas être connu avec certitude, tout du moins sans techniques particulières : c'est une forme indéterminée.

$u+v$		$\lim v$ (resp. $\lim g$)
		$\ell '$	$-\infty$	$+\infty$
$\lim u$ (resp. $\lim f$)	$\ell$	$\ell +\ell '$	$-\infty$	$+\infty$
	$-\infty$	$-\infty$	$-\infty$	FI
	$+\infty$	$+\infty$	FI	$+\infty$

Avec ce qui vient d'être dit, on peut démontrer que les relations suivantes sont équivalentes :

$\lim _{n\rightarrow \infty }u_{n}=L$

$\lim _{n\rightarrow \infty }(u_{n}-L)=0$

Pour le dire en mots, dire que la suite $(u_{n})$ converge vers L est équivalent à dire que la suite $(u_{n}-L)$ converge vers 0.

Produit de deux suites

Maintenant, étudions la limite du produit de deux suites.

Si les deux suites convergent, alors leur produit converge lui aussi.

Démonstration

On veut prouver que : $\lim _{n\rightarrow \infty }(u_{n}\cdot v_{n})=(\lim _{n\rightarrow \infty }u_{n})\cdot (\lim _{n\rightarrow \infty }v_{n})$ Dit autrement, on veut prouver qu'il existe un rang N tel que : $|u_{n}\cdot v_{n}-L_{1}\cdot L_{2}|<\epsilon$, avec $L_{1}$ la limite de $u_{n}$ et $L_{2}$ la limite de $v_{n}$. Le terme de gauche peut se reformuler comme suit : $|u_{n}\cdot v_{n}-L_{1}\cdot L_{2}|=|L_{2}|\cdot |u_{n}-L_{1}|+|u_{n}|\cdot |v_{n}-L_{2}|$ On peut alors choisir le rang N tel que $|u_{n}-L_{1}|<{\frac {\epsilon }{2\cdot |T|+1}}$ et $|v_{n}-L_{2}|<{\frac {\epsilon }{2\cdot |u_{n}|+1}}$. En combinant cela avec la formule précédente, on a alors : $|u_{n}\cdot v_{n}-L_{1}\cdot L_{2}|<|L_{2}|\cdot {\frac {\epsilon }{2\cdot |L_{2}|+1}}+|u_{n}|\cdot {\frac {\epsilon }{2\cdot |u_{n}|+1}}$ Réorganisons les termes et factorisons epsilon : $|u_{n}\cdot v_{n}-L_{1}\cdot L_{2}|<\epsilon \left[{\frac {|L_{2}|}{2\cdot |L_{2}|+1}}+{\frac {|u_{n}|}{2\cdot |u_{n}|+1}}\right]$ Par définition, on a ${\frac {|u_{n}|}{2\cdot |u_{n}|+1}}<{\frac {1}{2}}$ et ${\frac {L_{2}}{2\cdot |L_{2}|+1}}<{\frac {1}{2}}$, ce qui donne : $|u_{n}\cdot v_{n}-L_{1}\cdot L_{2}|<{\frac {\epsilon }{2}}+{\frac {\epsilon }{2}}$ Ce qui se simplifie en : $|u_{n}\cdot v_{n}-L_{1}\cdot L_{2}|<\epsilon$ Cette expression n'est autre que la définition $\lim _{n\rightarrow \infty }(u_{n}\cdot v_{n})=(\lim _{n\rightarrow \infty }u_{n})\cdot (\lim _{n\rightarrow \infty }v_{n})$.

Si une des deux suites diverge, on a droit soit à un résultat indéterminé, soit à une suite divergente. Quand on multiplie deux suites qui divergent, la suite résultat diverge elle aussi. Même chose quand une suite divergente est multipliée avec une suite convergente dont la limite est non-nulle. Mais les problèmes surviennent quand une des deux suites converge vers zéro. Dans ce cas, on ne sait pas si c'est le zéro ou l'infini qui l'emporte. Le résultat est alors ce qu'on appelle une forme indéterminée. Nous reparlerons de ces formes indéterminée plus bas, mais pour résumer : la suite peut converger ou diverger suivant le cas étudié. Le résultat exact peut se calculer, mais cela demande de reformuler le quotient d'une manière ou d'une autre.

$u\times v$		$\lim v$ (resp. $\lim g$)
		$\ell '$	$0$	$\infty$
$\lim u$ (resp. $\lim f$)	$\ell$	$\ell '\times \ell$	$0$	$\infty$
	$0$	$0$		FI
	$\infty$	$\infty$	FI	$\infty$

N'oublions pas que les limites/infinis peuvent avoir un signe, ce qui se transmet par la multiplication et le passage à la limite. En tenant compte des signes des limites et des infinis, le tableau précédent devient :

$u\times v$		$\lim v$ (resp. $\lim g$)
		$\ell '<0$	$\ell '>0$	$0$	$-\infty$	$+\infty$
$\lim u$ (resp. $\lim f$)	$\ell <0$	$\ell \times \ell '$		$0$	$+\infty$	$-\infty$
	$\ell >0$				$-\infty$	$+\infty$
	$0$	$0$			FI
	$-\infty$	$+\infty$	$-\infty$	FI	$+\infty$	$-\infty$
	$+\infty$	$-\infty$	$+\infty$		$-\infty$	$+\infty$

Quotient de deux suites

Le quotient de deux suites est un peu plus compliqué que le produit de deux suites. Pour le calculer, on prend en compte le fait que ${\frac {u_{n}}{v_{n}}}=u_{n}\cdot {\frac {1}{v_{n}}}$. On peut donc appliquer les formules sur la limite d'un produit de suite, ce qui donne :

$\lim _{n\rightarrow \infty }\left({\frac {u_{n}}{v_{n}}}\right)=\left(\lim _{n\rightarrow \infty }u_{n}\right)\cdot \left(lim_{n\rightarrow \infty }{\frac {1}{v_{n}}}\right)$

Il y a trois possibilités pour le calcul de l'inverse, suivant que la suite inversée tend vers zéro, une limite finie non-nulle ou l'infini (vers $L\neq 0$, vers 0 ou vers $\infty$.

• Si la suite diviseur converge vers $L\neq 0$, alors le quotient converge comme la suite divisée.
• Si la suite diviseur converge vers zéro, alors le quotient diverge, sauf dans le cas $0 \over 0$ qui est une forme indéterminée.
• Si la suite diviseur diverge, alors le quotient converge vers zéro, sauf dans le cas $\infty \over \infty$ qui est une forme indéterminée.

Pour résumer, on fait donc face à neuf cas différents, du moins si on ne tient pas compte des signes.

$u \over v$		$\lim v$ (resp. $\lim g$)
		$\ell '\neq 0$	$0$	$\infty$
$\lim u$ (resp. $\lim f$)	$\ell \neq 0$	${\frac {\ell }{\ell '}}$	$+\infty$	$0$
	$0$	$0$	FI
	$\infty$	$\infty$		FI

En tant compte des signes, le tableau précédent devient :

$u \over v$		$\lim v$ (resp. $\lim g$)
		$\ell '<0$	$\ell '>0$	$0^{-}$	$0^{+}$	$-\infty$	$+\infty$
$\lim u$ (resp. $\lim f$)	$\ell <0$	${\frac {\ell }{\ell '}}$		$+\infty$	$-\infty$	$0^{(+)}$	$0^{(-)}$
	$\ell >0$			$-\infty$	$+\infty$	$0^{(-)}$	$0^{(+)}$
	$0^{-}$	$0^{(+)}$	$0^{(-)}$	FI		$0^{(+)}$	$0^{(-)}$
	$0^{+}$	$0^{(-)}$	$0^{(+)}$			$0^{(-)}$	$0^{(+)}$
	$-\infty$	$+\infty$	$-\infty$	$+\infty$	$-\infty$	FI
	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$+\infty$

Les formes indéterminées

Les formes indéterminées surviennent quand on se retrouve devant un calcul impossible en tentant de calculer le produit ou la somme de deux limites. Par exemple, vous pouvez essayer de diviser deux suites qui divergent : vous vous retrouvez à diviser l'infini par lui-même. Le résultat est alors indéterminé et la suite quotient peut aussi bien diverger que converger ! Voici les sept formes indéterminées possibles :

Formes indéterminées
$\infty -\infty$	$0\times \infty$	$\infty \over \infty$	$0 \over 0$	$1^{\infty }$	$\infty ^{0}$	$0^{0}$

Lever l'indétermination

Le seul moyen de trouver la vraie valeur d'une forme indéterminée est de reformuler le calcul, en utilisant des techniques spéciales comme le changement de variable. Pour donner un exemple simple, nous allons prendre l'exemple de la suite définie par :

$u_{n}={\frac {n^{2}+n}{n^{2}}}$

Les deux suites : $u_{n}=n^{2}+n$ et : $u_{n}=n^{2}$ divergent toutes les deux, ce qui fait que la limite est la suivante :

$\lim _{n\to \infty }(u_{n})={\frac {\lim _{n\to \infty }(n^{2}+n)}{\lim _{n\to \infty }(n^{2})}}={\frac {\infty }{\infty }}$

Une solution pour lever l'indétermination est de simplifier la fraction initiale :

$u_{n}={\frac {n^{2}+n}{n^{2}}}=1+{\frac {1}{n}}$

On voit alors immédiatement que la suite converge vers :

$\lim _{n\to \infty }(u_{n})=1+\lim _{n\to \infty }{\frac {1}{n}}=1$

Les suites monotones réelles

Pour rappel, les suites monotones regroupent les suites constantes, croissantes et décroissantes.

• Dans le cas où chaque terme de la suite est plus grand que le précédent (pour tout rang $n$, on a : $u_{n+1}>u_{n}$), la suite est dite strictement croissante.
• Dans le cas contraire, on a $u_{n+1}<u_{n}$ pour tout rang $n$ et la suite est dite strictement décroissante.
• Si $u_{n+1}\leq u_{n}$, la suite est dite décroissante.
• Si $u_{n+1}\geq u_{n}$, la suite est dite croissante.

Certaines suites récurrentes sont soit croissantes, soit décroissantes, selon leur premier terme ou la fonction utilisée. Tel est le cas de la suite définie par la relation $u_{n}=u_{n-1}\times 5$ : la fonction est décroissante avec $u_{0}<0$ et croissante avec $u_{0}>0$.

La convergence des suites monotones (qui sont soit croissantes, soit décroissantes) est assez simple à étudier, car il existe des critères de convergence spécifiques à ce type de suites.

Les suites majorées/minorées

Dans le cas le plus simple, il suffit de déterminer si elles sont croissantes ou décroissantes et de vérifier si elles ont un minorant/majorant. On peut se retrouver avec quatre cas bien précis :

	Croissante	Décroissante
Pas de majorant (mais un minorant)	$\infty$	Limite égale à la borne inférieure
Pas de minorant (mais un majorant)	Limite égale à la borne supérieure	$-\infty$

Démonstration

Les propriétés précédentes ne sont que des corolaires du fait que toute suite convergente est bornée. Commençons par le cas d'une suite croissante. Celle-ci est naturellement minorée par son premier terme, qui est le plus petit terme de la suite. Si la suite n'a pas de majorant, elle n'est pas bornée : elle doit donc diverger. Mais si elle a un majorant, alors elle est bornée. Vu son caractère croissant, on sait qu'il existe un rang au-delà duquel la différence avec la borne supérieure sera négligeable. Par définition de la borne supérieure, on a un rang au-delà duquel : $u_{n}-limite_{sup}<\epsilon$. Dit autrement, la suite converge. Le raisonnement pour la suite décroissante est l'exact copier-coller du raisonnement précédent, en changeant borne supérieure par borne inférieure et en intervertissant majorant et minorant.

Les suites adjacentes

La propriété précédente a une conséquence assez intéressante dans le cas de suites dites adjacentes. Les suites adjacentes sont deux suites $(a_{n})$ et $(b_{n}$ qui respectent les propriétés suivantes :

• $(a_{n})$ est croissante alors que $(b_{n}$ est décroissante ;
• $a_{n}\leq b_{n}$ pour tout rang $n$ ;
• $\lim _{n\to \infty }(b_{n}-a_{n})=0$.

Par définition des suites adjacentes, on sait que tout terme de la suite croissante est plus petit que n'importe quel terme de la suite décroissante.

$a_{n}\leq b_{p}$, pour tout n et tout p.

Cela a deux conséquences :

• La suite $(a_{n})$ est majorée : tout terme de $(b_{n})$ est un majorant de la suite.
• La suite $(b_{n})$ est minorée : tout terme de $(a_{n})$ est un minorant de la suite.

Grâce à cela, on peut prouver que deux suites adjacentes ont la même limite.

Démonstration

Prenons deux suites adjacentes : une suite croissante $(a_{n})$ et une suite décroissante $(b_{n})$. Prouvons que les deux suites convergent : $(a_{n})$ est une suite croissante majorée : elle converge donc vers une limite $\lim _{n\to \infty }(a_{n})=L_{1}$ $(b_{n})$ est une suite décroissante minorée : elle converge donc vers une limite $\lim _{n\to \infty }(b_{n})=L_{2}$ Prouvons ensuite que ces deux limites sont les mêmes. Pour cela, partons de la formule : $\lim _{n\to \infty }(b_{n}-a_{n})=0$. On sait, depuis le chapitre sur les opérations sur les limites, que $\lim _{n\to \infty }(a_{n}-b_{n})=\lim _{n\to \infty }(a_{n})-\lim _{n\to \infty }(b_{n})$. En faisant le remplacement, on a : $L_{2}-L_{1}=0$ Donc, les deux limites sont égales : les deux suites convergent vers la même limite.

Exemples : suites suites arithmétiques et géométriques

Les suites arithmétiques et géométriques sont les exemples les plus simples de suites monotones (sauf pour certaines suites géométriques, qui sont alternées). Aussi, nous pouvons démontrer leur convergence avec les théorèmes vus dans ce chapitre.

Les suites arithmétiques non-constantes divergent

Il est intéressant d'étudier la convergence/divergence des suites arithmétiques. On peut éliminer un cas assez simple : celui des suites constantes, qui convergent systématiquement. Pour les suites croissantes et décroissantes, c'est autre chose : elles divergent systématiquement. Pour résumer :

• Si $r=0$, la suite est constante et converge vers $u_{0}$.
• Si $r>0$, la suite diverge vers $+\infty$.
• Si $r<0$, la suite diverge vers $-\infty$.

On peut démontrer la divergence des suites arithmétiques non-constantes de plusieurs manières.

Démonstration

La première méthode utilise ce théorème : Les suites croissantes et sans majorant divergent, de même que les suites décroissantes et sans minorants. Or, les suites arithmétiques croissantes (décroissantes) n'ont pas de majorants (minorants) : elles divergent donc.

Démonstration

Une autre méthode consiste à appliquer la définition de la divergence vers $+\infty$ ou $-\infty$. Une suite diverge vers $+\infty$ si, pour tout nombre $M$, il existe un rang $n$ tel que : $u_{n}>M$. Dans le cas des suites arithmétiques, il suffit de prendre le rang tel que : $u_{n}=u_{0}+r\cdot n>M$ Il suffit pour cela de prendre un rang tel que : $n>{\frac {M-u_{0}}{r}}$ Et un tel rang existe toujours. La démonstration pour les suites décroissantes est similaire, si ce n'est que la définition à appliquer est la suivante : Une suite diverge vers $-\infty$ si, pour tout nombre $M$, il existe un rang $n$ tel que : $u_{n}<M$. Le raisonnement est alors similaire au précédent, avec seulement quelques changements au niveau des calculs.

La convergence/divergence des suites géométriques

Toutes les suites géométriques ne convergent pas, bien que certaine le font. On peut éliminer directement le cas des suites géométriques qui sont alternées, qui ne peuvent pas converger par définition. Les suites géométriques constantes convergent aussi, par définition. Les autres suites convergent ou divergent, selon la valeur de la raison.

• Si $r>1$, la suite est diverge vers $+\infty$ ou $-\infty$ selon le signe du premier terme.
• Si $r=1$, la suite est constante et converge vers $u_{0}$.
• Si $-1<r<1$, la suite converge vers $0$.
• Si $-1\leq r$, la suite est alternée (les termes consécutifs changent de signe) : elle n'a pas de limite.

On peut démontrer la divergence des suites géométriques non-constantes et non-alternées avec les mêmes raisonnements que pour les suites arithmétiques.

Démonstration

La première méthode utilise deux théorèmes, que nous démontrerons dans le chapitre suivant. Pour les suites géométriques croissantes, on utilise ce théorème : Les suites croissantes et sans majorant divergent, de même que les suites décroissantes et sans minorants. Or, les suites géométriques croissantes n'ont pas de majorants : elles divergent donc. Pour les suites géométriques décroissantes, on utilise ce théorème : Les suites croissantes et avec un majorant convergent, de même que les suites décroissantes et avec un minorant. Les suites géométriques décroissantes avec -1 < r < 1 sont minorées par zéro (leurs termes sont tous positifs) : elles convergent donc. Les autres divergent vers moins l'infini.

Les sous-suites (suites extraites)

Dans les chapitres précédents, nous avons vu des suites lambda et quelques opérations que l'on peut faire sur celles-ci. Mais nous avons volontairement omis de parler d'une opération assez simple : l'extraction. Cette opération permet de créer une nouvelle suite à partir d'une suite donnée en opérande. Elle prend une suite et n'en garde qu'une partie des termes, les autres étant retirés de la suite. L'extraction est définie par une fonction, la fonction extractrice, qui détermine quels sont les termes à conserver et ceux à oublier. Le résultat de cette opération d'extraction est appelée une sous-suite ou encore une suite extraite (sous-entendu, extraite d'une suite donnée).

La définition formelle d'une suite extraite est la suivante :

Une suite $(v_{n})$ est une sous-suite de $(u_{n})$ si il existe une fonction strictement croissante $f:N\rightarrow N$ (la fonction extractrice) telle que : $v_{n}=u_{f(n)}$

Prenons quelques exemples, pour que vous compreniez mieux cette définition.

• Supposons que l'on veuille ne conserver que les rangs pairs de la suite $(u_{n})$. Dans ce cas, la fonction extractrice est la fonction : $f:f(n)=2\cdot n$, ce qui donne : $v_{n}=u_{2\cdot n}$, qui ne conserve que les rangs pairs.
• Supposons maintenant que l'on veuille ne conserver que les rangs impairs de la suite $(u_{n})$. Dans ce cas, la fonction extractrice est la fonction : $f:f(n)=2\cdot n+1$, ce qui donne : $v_{n}=u_{2\cdot n+1}$, soit seulement les rangs impairs.

La convergence d'une sous-suite

Si une suite converge vers L, toutes ses sous-suites convergent vers la même limite.

Démonstration

Prenons une suite $(u_{n})$ qui converge vers L et une de ses sous-suites $(v_{n})$ d'extractrice $f$. Dire que la suite converge vers L signifie, pour rappel, que pour tout $\epsilon >0$, il existe $n_{0}$ tel que pour tout $n\geq n_{0},\vert u_{n}-L\vert <\epsilon$. Vu que la fonction extractrice est croissante, on a : $f(n)\geq n$ (ce lemme se démontre aisément par récurrence). On a alors $f(n)\geq n\geq n_{0}$ et donc $\vert u_{f(n)}-L\vert <\epsilon$, c'est-à-dire $\vert v_{n}-L\vert <\epsilon$

Les sous-suites de suites bornées

Les sous-suites ont quelques propriétés intéressantes, et les suites bornées sont de loin les plus intéressantes à étudier.

Extraction d'une sous-suite monotone

Une première propriété intéressante est celle-ci :

De toute suite bornée, on peut extraire une suite monotone.

Démonstration

Prenons une suite $(u_{n})$. Un terme est un pic si tous les termes suivants sont plus petits que lui. En clair, un pic est défini par : $u_{n}>u_{p}$, pour tout $p>n$. On peut se retrouver dans plusieurs cas : Si la suite a une infinité de pics, alors la suite des pics forme une sous-suite décroissante. Sinon, on peut construire une sous-suite croissante. On prend comme premier terme un terme d'indice supérieur à tous les pics, puis un terme d'indice encore supérieur, etc. La suite ainsi construite est de facto croissante, par définition des pics.

Le théorème de Bolzano-Weierstrass

Le théorème de Bolzano-Weierstrass, appliqué aux suites réelles, nous dit que l'on peut en extraire une sous-suite convergente de n'importe quelle suite bornée. Le théorème nous dit qu'une telle sous-suite existe toujours, mais il ne nous dit pas comment trouver cette sous-suite. Il ne nous dit pas non plus qu'il n'en existe qu'une seule : il existe des situations où l'on peut extraire plusieurs sous-suites convergentes d'une même suite bornée.

Il existe plusieurs démonstrations du théorème.

• La première est simplement une application de la propriété précédente, qui dit que l'on peut extraire une sous-suite monotone de toute suite bornée. Or, toute suite monotone et bornée converge vers sa borne supérieure/inférieure, et cette sous-suite ne fait pas exception.
• La seconde est reproduite ci-dessous.

Démonstration

Prenons une suite $(u_{n})$ dont les termes sont bornés dans l'intervalle $[m,M]$ - m est la borne inférieure de la suite, alors que M en est la borne supérieure. Pour démontrer le théorème, nous allons construire deux suites adjacentes, par extraction de la suite $(u_{n})$. Ces deux suites adjacentes sont les suites $(a_{n})$ et $(b_{n})$. Construction des suites adjacentes par dichotomie : On pose, comme premier terme pour chaque sous-suite adjacente : $a_{0}=m$ et $b_{0}=M$. Par la suite, on procède par dichotomie. Partageons l'intervalle [m,M] en deux parties égales, respectivement les intervalles : $\left[m,{\frac {m+M}{2}}\right]$ et $\left[{\frac {m+M}{2}},M\right]$ Un de ces deux intervalles contient un nombre infini de termes, l'autre regroupant au contraire un nombre fini de termes. Si l'intervalle $\left[m,{\frac {m+M}{2}}\right]$ contient un nombre infini de termes, on pose : $a_{1}=m$ et $b_{1}={\frac {m+M}{2}}$. Si au contraire, c'est l'intervalle $\left[{\frac {m+M}{2}},M\right]$ contient un nombre infini de termes, on pose : $a_{1}={\frac {m+M}{2}}$ et $b_{1}=M$. A cette étape, on peut remarquer que l'intervalle choisit est deux fois plus petit que l'intervalle initial. En clair, $a_{1}-b_{1}={\frac {a_{0}-b_{0}}{2}}$. Et on recommence ainsi de suite avec l'intervalle choisit à l'étape précédente... Démonstration de l'adjacence des deux sous-suites : On peut démontrer que les deux suites $(a_{n})$ et $(b_{n})$ sont adjacentes. On sait que : $(a_{n})$ est croissante et majorée par M : elle converge donc vers une limite L ; $(a_{n})$ est décroissante et minorée par m : elle converge donc vers une limite L'. A chaque étape, l'intervalle choisit est deux fois plus petit que l'intervalle initial. La différence $a_{n}-b_{n}$ est, par construction, égale à : $a_{n}-b_{n}={\frac {a_{n-1}-b_{n-1}}{2}}={\frac {a_{n-2}-b_{n-2}}{4}}={\frac {a_{n-3}-b_{n-3}}{8}}=...=={\frac {a_{0}-b_{0}}{2^{n}}}$ On peut donc en déduire que : $\lim _{n\rightarrow \infty }(a_{n}-b_{n})=\lim _{n\rightarrow \infty }{\frac {a_{0}-b_{0}}{2^{n}}}=0$ Ce qui montre que les deux suites $(a_{n})$ et $(b_{n})$ sont adjacentes. Elles ont donc la même limite L. Construction de la suite extraite convergente : Construire la suite extraite convergente $(x_{n})$ est trivial : il suffit de prendre des termes qui sont entre les deux suites adjacentes, c'est-à-dire des termes $x_{n}$ tels que $u_{n}<x_{n}<v_{n}$. Par le théorème des gendarmes, cette suite converge vers la même limite que les deux suites adjacentes.

Les suites récurrentes linéaires

Les suites vues dans le premier chapitre sont des suites récurrentes, qui calculent chaque terme en fonction du précédent. Certaines suites vont cependant un peu plus loin et calculent chaque terme en fonction des deux précédents, des trois précédents, voire de tous les termes précédents ! Le cas les plus simples vont se contenter d'additionner les termes précédents. D'autres suites vont encore plus généraliser les fonctions précédentes, on ajoutant une caractéristique des suites géométriques : l'usage d'une multiplication par une constante. Pour cela, les termes sont tous additionnés, mais seulement après avoir été multipliés par une constante. Ces suites sont les suites récurrentes linéaires. On peut les voir comme une généralisation des suites arithmético-géométriques, ce qui transparaît dans leur définition.

Les propriétés générales des suites récurrentes linéaires

Le suites récurrentes linéaires sont décrites par une équation de récurrence qui a la forme suivante :

$u_{n}=u_{n-1}\times a_{n-1}+u_{n-2}\times a_{n-2}+u_{n-3}\times a_{n-3}+...+u_{n-k}\times a_{n-k}$

Le nombre $k$ de l'équation précédente est le nombre de termes précédents utilisés pour calculer le prochain. Il porte un nom : c'est l'ordre de la suite, ou encore son degré.

Au passage, les suites arithmético-géométriques sont des suites récurrentes linéaires d'ordre 1. Et en conséquence, les suites géométriques et arithmétiques en sont aussi : les suites géométriques sont des suites récurrentes linéaires d'ordre 1, les suites arithmétiques et constantes sont d'ordre 0. Dans la suite du cours, nous allons surtout nous concentrer sur les suites d'un ordre supérieur, au moins égal à 2.

Les opérations sur les suites récurrentes linéaires

Les suites récurrentes linéaires peuvent être additionnées, soustraites, multipliées et divisées, tout comme les autres suites. À ce propos, il est facile de prouver que, pour des suites récurrentes linéaires $(u_{n})$ et $(v_{n})$ :

$(u_{n})+(v_{n})$ est une suite récurrente linéaire ;

$\lambda \cdot (u_{n})$ est une suite récurrente linéaire ;

$(u_{n})*(v_{n})$ est une suite récurrente linéaire.

Prenons par exemple la multiplication d'une suite récurrente linéaire par une constante.

Démonstration

Pour cela, prenons une suite $(u_{n})$ et multiplions par une constante. Regardons ce qui se passe au niveau de la relation de récurrence. Par définition, la relation de récurrence de la suite $(u_{n})$ est de la forme : $u_{n}=u_{n-1}\times a_{n-1}+u_{n-2}\times a_{n-2}+u_{n-3}\times a_{n-3}+...+u_{n-k}\times a_{n-k}$ Multiplions maintenant par $\lambda$ : $\lambda \cdot u_{n}=\lambda \cdot (u_{n-1}\times a_{n-1}+u_{n-2}\times a_{n-2}+u_{n-3}\times a_{n-3}+...+u_{n-k}\times a_{n-k})$ Développons : $\lambda \cdot u_{n}=u_{n-1}\times (\lambda \cdot a_{n-1})+u_{n-2}\times (\lambda \cdot a_{n-2})+u_{n-3}\times (\lambda \cdot a_{n-3})+...+u_{n-k}\times (\lambda \cdot a_{n-k})$ On voit que le terme de droite peut se mettre sous la forme suivante, qui est la relation de récurrence d'une suite récurrente linéaire : $u_{n}=u_{n-1}\times b_{n-1}+u_{n-2}\times b_{n-2}+u_{n-3}\times b_{n-3}+...+u_{n-k}\times b_{n-k}$

Des développements similaires permettent de prouver la même chose, mais pour l'addition ou la multiplication de deux suites récurrentes linéaires. En sachant cela, on peut démontrer que l'ensemble des suites récurrentes linéaires respecte toutes les conditions pour être qualifié d'espace vectoriel.

Le polynôme caractéristique d'une suite récurrente linéaire

Le nombre de termes utilisés pour calculer le prochain porte un nom : c'est l'ordre de la suite, ou encore son degré. Vous avez peut-être remarqué que le terme "ordre" est aussi utilisé pour les polynômes, et ce n'est pas un hasard. Il y a un lien assez franc entre les polynômes et les suites récurrentes linéaires. L'étude de ces dernières se base essentiellement sur l'étude de leur polynôme caractéristique. Celui-ci est un polynôme dont le degré est le même que celui de la suite et dont les coefficients sont les mêmes que ceux de l'équation de récurrence qui définit la suite. En clair, il vaut, pour une suite d'ordre n :

$P(x)=a_{n}\times x^{n}+a_{n-1}\times x^{n-1}++a_{n-2}\times x^{n-2}...+a_{2}\times x^{2}+a_{1}\times x+a_{0}$

Les racines de ce polynôme sont d'une importance capitale pour l'étude de la suite associée. Pour rappel, les racines d'un polynôme $P(x)$ sont les solutions de l'équation $P(x)=0$. Les racines du polynômes caractéristiques permettent de déterminer la limite de la suite, ainsi que son expression paramétrée. Prenons le cas d'une suite récurrente linéaire quelconque. Supposons que le polynôme caractéristique associé a $i$ racines, notées $r_{1}$, $r_{2}$, $r_{3}$, ..., $r_{i}$. Dans ce cas, on sait qu'il existe $i$ coefficients constants $\lambda _{i}$ tels que :

$u_{n}=\lambda _{1}\cdot r_{1}^{n}+\lambda _{2}\cdot r_{2}^{n}+\lambda _{3}\cdot r_{3}^{n}+...+\lambda _{i}\cdot r_{i}^{n}$

Déterminer la valeur des coefficients $\lambda _{i}$ n'est pas si difficile. Il suffit de résoudre un système à n équations, qui s'obtient en testant les $i$ premières valeurs de la suite.

$u_{0}=\lambda _{1}+\lambda _{2}+\lambda _{3}+...+\lambda _{i}$, où $n=0$.

$u_{1}=\lambda _{1}\cdot r_{1}+\lambda _{2}\cdot r_{2}+\lambda _{3}\cdot r_{3}+...+\lambda _{i}\cdot r_{i}$, où $n=1$.

$u_{2}=\lambda _{1}\cdot r_{1}^{2}+\lambda _{2}\cdot r_{2}^{2}+\lambda _{3}\cdot r_{3}^{2}+...+\lambda _{i}\cdot r_{i}^{2}$, où $n=2$.

...

$u_{i}=\lambda _{1}\cdot r_{1}^{i}+\lambda _{2}\cdot r_{2}^{i}+\lambda _{3}\cdot r_{3}^{i}+...+\lambda _{i}\cdot r_{i}^{i}$, où $n=i$.

Les suites récurrentes linéaires d'ordre 2

Dans ce qui va suivre, nous allons surtout étudier les suites d'ordre 2, à savoir celles de la forme suivante :

$u_{n}=a\times u_{n-1}+b\times u_{n-2}$

Le polynôme caractéristique associé à ces suites est :

$r^{2}+ar+b=0$

Les racines de cette équation sont notées $r_{1}$ et $r_{2}$. On se retrouve alors dans deux cas :

• les deux racines sont différentes : la formule paramétrée est alors égale à : $u_{n}=\lambda \cdot r_{1}^{n}+\gamma \cdot r_{2}^{n}$.
• les deux racines sont égales : la formule paramétrée est alors égale à : $u_{n}=(\lambda +\gamma )\times r_{1}^{n}$.

Les constantes $\lambda$ et $\gamma$ sont deux constantes qui se déterminent à partir de la valeur des deux premiers termes de la suite. On a naturellement les conditions suivantes :

• $\lambda +\gamma =u_{0}$ ;
• $\lambda \cdot r_{1}+\gamma \cdot r_{2}=u_{1}$.

Les suites de type "Lucas"

Le cas le plus simple de suite récurrente linéaire d'ordre 2 est celui où chaque terme est la somme des deux précédents.

$u_{n}=u_{n-1}+u_{n-2}$

Toutes les équations de ce genre ont un rapport avec le nombre d'or $\varphi$, un nombre égal à $\varphi \approx 1.61803398874989$, très souvent abordé dans les ouvrages de mathématiques amusantes. Ce lien vient du fait que ce nombre d'or est une des deux racines de l'équation caractéristique. Il apparaît donc naturellement dans la recherche d'une forme paramétrée des suites de Lucas.

La formulation des suites de Lucas fait qu'il s'agit de suites récurrentes linéaires d'ordre 2 dont les coefficient a et b valent tous deux 1. Le polynôme caractéristique de cette récurrence est :

$r^{2}-r-1=0$

Ce polynôme possède deux racines, la première étant le fameux nombre d'or $\varphi$ et la seconde son inverse.

$r_{1}={\frac {1+{\sqrt {5}}}{2}}=\varphi$

$r_{2}={\frac {1-{\sqrt {5}}}{2}}=1-\varphi ={\frac {1}{\varphi }}$

Vu qu'il y a deux racines différentes, l'équation paramétrée des suites de Lucas est la suivante :

$u_{n}=\lambda \cdot \varphi ^{n}+\gamma \cdot {\frac {1}{\varphi ^{n}}}$.

On peut remarquer que si le rang n est assez grand, le terme : ${\frac {1}{\varphi ^{n}}}$ tend vers zéro, le dénominateur devant très grand. Dans ce cas, on peut le négliger, ce qui donne :

$u_{n}\approx \lambda \times \varphi ^{n}$.

Maintenant, étudions le rapport entre deux termes consécutifs : ${\frac {u_{n+1}}{u_{n}}}$. Ce rapport vaut, par définition :

${\frac {u_{n+1}}{u_{n}}}={\frac {\lambda \varphi ^{n+1}+\gamma {\frac {1}{\varphi ^{n+1}}}}{\lambda \varphi ^{n}+\gamma {\frac {1}{\varphi ^{n}}}}}$

Si l'on prend la limite, les termes ${\frac {1}{\varphi ^{n+1}}}$ et ${\frac {1}{\varphi ^{n}}}$ s'annulent. Dit autrement, peut remplacer numérateur et dénominateur par l'approximation précédente ($u_{n}\approx \lambda \times \varphi ^{n}$). On obtient alors une formule qui dit que lorsque l'on prend la limite $n\rightarrow \infty$, le rapport ${\frac {u_{n+1}}{u_{n}}}$ tend vers le nombre d'or.

$\lim _{n\to \infty }{\frac {u_{n+1}}{u_{n}}}={\frac {\lambda \times \varphi ^{n+1}}{\lambda \times \varphi ^{n}}}={\frac {\varphi ^{n+1}}{\varphi ^{n}}}=\varphi$

Les deux résultats précédents sont tout ce qu'on peut déduire de l'étude des suites de Lucas dans le cas général. On peut déterminer leur expression paramétrée et trouver la limite du rapport ${\frac {u_{n+1}}{u_{n}}}$, mais on ne peut pas faire plus sans connaître les deux coefficients $\lambda$ et $\gamma$. Pour aller plus loin, on doit étudier des cas particuliers, où l'on a précisé les deux premiers termes. Or, il existe plusieurs suites avec cette relation récurrente, mais qui différent par leurs deux premiers termes. La plus connue est la suite de Fibonacci, une suite avec une certaine renommée, qui est souvent abordée dans les livres de mathématiques récréatives. Celle-ci est apparue pour la première fois dans un problème de mathématiques récréatives crée par Leonardo Fibonacci, qui donna son nom à cette suite. Ce problème impliquait un problème de lapins qui se reproduisent dans un enclos, ce problème étant assez connu. Une autre suite de ce genre est la suite de Lucas. Mais la plus simple est de loin la suite des puissances du nombre d'or.

La suite des puissances du nombre d'or

La suite des puissances du nombre d'or est la suite définie par

$u_{n}=\varphi ^{n}$

Il s'agit du cas particulier où $\lambda =1$ et $\gamma =0$. Ses premiers termes sont naturellement :

$u_{0}=\varphi ^{0}=1$ et $u_{1}=\varphi ^{1}=\varphi$

Cette suite respecte bien la relation de récurrence $u_{n}=u_{n-1}+u_{n-2}$, ce qui fait qu'on a :

$\varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}$

Vous pouvez vérifier cela par vous-même en calculant les premières puissances du nombre d'or :

$\varphi ^{0}=1$

$\varphi ^{1}=1,6180339887$

$\varphi ^{2}=\varphi ^{1}+\varphi ^{0}=2,6180339887$

$\varphi ^{3}=\varphi ^{2}+\varphi ^{1}=4.2360679775$

$\varphi ^{4}=\varphi ^{3}+\varphi ^{2}=6.85410196625$

$\varphi ^{5}=\varphi ^{4}+\varphi ^{3}=11.0901699437$

$\varphi ^{6}=\varphi ^{5}+\varphi ^{4}=17.94427191$

$\varphi ^{7}=\varphi ^{6}+\varphi ^{5}=29.0344418537$

$\cdots$

La suite de Lucas

La suite de Lucas a pour premiers termes $u_{0}=2$ et $u_{1}=1$. On peut alors calculer les coefficients gamma et lambda avec les conditions suivantes :

• $\lambda +\gamma =2$ ;
• $\lambda r_{1}+\gamma r_{2}=1$.

Ce qui donne :

$\lambda =1$ et $\gamma =-1$

On a alors la pièce finale, l'équation paramétrée de la suite de Lucas :

$u_{n}=\left(\varphi ^{n}+{\frac {1}{\varphi ^{n}}}\right)\approx \varphi ^{n}$

La voici :

$2,1,3,4,7,11,18,29,47,76,123,199,322,521,843,1364,2207,3571,5778,9349,15127,24476,39603,64079,\cdots$

La suite de Fibonacci

La suite de Fibonacci la même relation de récurrence que la suite de Lucas, sauf que ses premiers termes sont respectivement 0 et 1, ce qui donne la suite suivante :

Fibonacci sequence - optional starting with zero

Vu qu'elle a la même relation de récurrence que la suite de Lucas, elle a la même équation caractéristique et a donc les mêmes racines. Seuls les coefficients gamma et lambda changent, eux seuls étant influencés par les deux premiers termes. Dans le cas de la suite de Fibonacci, ceux-ci valent :

• $\lambda +\gamma =0$ ;
• $\lambda r_{1}+\gamma r_{2}=1$.

Ce qui donne :

$\lambda ={\frac {1}{\sqrt {5}}}$ et $\gamma =-{\frac {1}{\sqrt {5}}}$

On a alors la pièce finale, l'équation paramétrée de la suite de Fibonacci :

$u_{n}={\frac {1}{\sqrt {5}}}\left(\varphi ^{n}+{\frac {1}{\varphi ^{n}}}\right)\approx {\frac {\varphi ^{n}}{\sqrt {5}}}$

On voit que chaque terme de la suite de Fibonacci est un multiple du même terme de la suite de Lucas : la seule différence est le facteur ${\frac {1}{\sqrt {5}}}$. Après tout, les deux suites partagent la même relation de récurrence. Pas étonnant que les propriétés de la suite de Lucas se retrouvent donc dans la suite de Fibonnaci.

Les suites récurrentes (cas général)

Dans le premier chapitre, nous avons vu qu'il existe deux manières de décrire une suite, l'une donnant les suites paramétrées et l'autre les suites récurrentes (les deux n'étant pas exclusives). Dans ce chapitre, nous allons parler des suites récurrentes dans le cas général. Celles-ci sont très nombreuses et font clairement partie des plus étudiées, loin devant les simples suites paramétrées. Dans les grandes lignes, il existe deux choses importantes à propos des suites récurrentes : leur trouver une expression paramétrée et étudier leur comportement quand le rang grandit. Trouver leur limite, si elle existe, est aussi intéressant pour certaines suites récurrentes. Pour rappel, les suites récurrentes sont définies pour tout rang n par une fonction de récurrence, comme suit :

$u_{n}=f(u_{n-1},u_{n-2},u_{n-3},...,u_{2},u_{1},u_{0})$

Comme on le voit, ces suites sont intégralement définies par une fonction, qui détermine la relation de récurrence. Étudier ces suites, c'est simplement étudier la fonction qui les définit : est-elle croissante, décroissante, stationnaire au-delà d'un point, continue, dérivable, linéaire, etc. Par exemple, on peut savoir si la suite est croissante ou décroissante en calculant la dérivée de la fonction f : la suite est croissante si cette dérivée est positive, décroissante si elle est négative, constante si elle est nulle. Malheureusement, il n'existe pas de méthode à tout faire qui puisse traiter toute suite récurrente existante et nous allons donc nous rabattre sur des cas particuliers de suites récurrentes.

Les concepts de base des suites récurrentes du premier ordre

Dans ce chapitre et le suivant, nous allons étudier deux cas particuliers : les suites récurrentes linéaires et certaines suites non-linéaires. Nous verrons les suites récurrentes linéaires dans le prochain chapitre. Dans ce chapitre, nous allons nous intéresser aux suites définies par une relation de la forme :

$u_{n+1}=f(u_{n})$

Dans ce qui suit, la fonction f est choisie pour avoir quelques propriétés qui simplifient l'analyse : elle est supposée continue, éventuellement dérivable.

Les intervalles stables

On pourrait croire que choisir une relation de récurrence $u_{n+1}=f(u_{n})$ et une valeur $u_{0}$ suffise à donner une suite. Mais il existe cependant quelques exceptions qui viennent compliquer la situation. Par exemple, regardez l'exemple suivant :

${\begin{cases}u_{0}=2\\u_{n+1}={\frac {1}{u_{n}-1}}\end{cases}}$

Les termes $u_{0}$ et $u_{1}$ existent, mais le terme $u_{2}$ non ! Il suffit de faire les calculs pour s'en rendre compte.

$u_{0}=2$

$u_{1}={\frac {1}{2-1}}=1$

$u_{2}={\frac {1}{1-1}}={\frac {1}{0}}\ldots$

Le calcul donne une belle division par zéro qui stoppe net la progression de la suite. Le problème est alors que les opérations utilisées pour le calcul de la fonction ne donnent pas un nombre, alors qu'on s'attend à ce que ce soit le cas dans une suite numérique. On pourrait trouver d'autres exemples du même genre , mais pour des suites plus complexes, voire des suites qui ne sont pas numériques. Et bien évidemment, les problèmes peuvent survenir pour d'autres raisons que des divisions par zéro : que pensez-vous d'une suite dont un terme donnerait $0^{0}$ ? Pour comprendre quand ce genre de problème peut arriver, nous devons introduire la notion d'intervalle stable. Un intervalle stable est défini comme suit :

Soit une fonction $f(x)$ et un intervalle $I$, ce dernier est un intervalle stable si $f(I)\in I$.

Cette définition nous donne une explication assez intuitive des problèmes mentionnés plus haut. Tout vient du fait que la fonction donne un résultat qui n'est ni un entier ni un réel, alors que la suite récurrente associée est censée être une suite d'entiers ou de réels. Pour reprendre l'exemple cité plus haut de la suite définie par $u_{n+1}={\frac {1}{u_{n}-1}}$. Le problème est que certains opérandes vont donner une division par zéro : les opérandes de la fonction sont censés être des entiers ou des réels ($u_{n}\in \mathbb {R}$), mais ce n'est pas le cas du résultat ! L'intervalle utilisé n'est pas stable, ce qui permet à ces problèmes de se manifester (ou du moins, ces problèmes peuvent potentiellement se manifester, vu que certains opérandes ne posent pas de problèmes).

Les suites récurrentes associées

Maintenant, prenons les deux hypothèses suivantes :

• la relation de récurrence est $u_{n+1}=f(u_{n})$ ;
• le terme $u_{0}$ appartient à un intervalle stable par f, que nous noterons I.

Alors une simple relation de récurrence nous permet de dire que la suite existe, qu'elle est définie pour tout entier n. Intuitivement, cela s'explique par le fait qu'à chaque passage par la fonction, le résultat sera bien dans l'intervalle I. Une véritable démonstration demande simplement de faire une démonstration par récurrence triviale. La suite alors définie est appelée la suite récurrente associée à f.

Si une fonction possède un intervalle stable fini (borné), alors la suite récurrente associée l'est tout autant. Ses termes sont dans l'intervalle stable, par définition, ce qui rend la suite bornée entre la borne inférieure et supérieure de l'intervalle. Par exemple, si une fonction $f$ a [0,1] pour intervalle stable, on sait que la suite récurrente associée est bornée entre 0 et 1. Là où les choses deviennent intéressantes, c'est que cette propriété évidente permet de déterminer rapidement si la suite associée converge ou non. Le cas le plus simple est celui où la suite associée est monotone (croissante ou décroissante). Dans ce cas, on sait que la limite va converger et on peut calculer sa limite facilement : c'est tout simplement la borne supérieure ou inférieure de l'intervalle (selon que la suite est croissante ou décroissante). Aussi, ne vous étonnez pas si beaucoup de démonstrations sur les suites récurrentes utilisent les théorèmes de convergence des fonctions monotones.

Les points fixes d'une suite

Ce qui va nous intéresser chez ces suites est l'étude des points fixes de la fonction f. Par point fixe on entend un nombre x tel que :

$x=f(x)$

Exemple de fonction avec plusieurs points fixes. On voit que son graphe coupe la ligne identité en plusieurs points fixes.

Évidemment, toutes les fonctions n'ont pas de point fixe, bien que cela soit quand même assez courant.

On peut trouver les points fixes d'une fonction en regardant son graphe. Formellement, les points fixes sont ceux où le graphe de la fonction $y=f(x)$ coupe la droite identité ($y=x$).

Évidemment, toutes les fonctions n'ont pas de point fixe et il n'y a alors aucun point d'intersection entre le graphe de la fonction et la droite identité. À l'inverse, une fonction peut aussi avoir plusieurs points d'intersection, et donc plusieurs points fixes, comme le montre le graphe ci-contre. On peut se demander si les fonctions admettant au moins un point fixe sont courantes ou non. Eh bien c'est le cas : toute fonction continue définie sur un intervalle stable admet au moins un point fixe. Cette propriété capture un grand nombre de fonctions, y compris des fonctions courantes comme les puissances, les logarithmes, l'exponentielle, etc.

Démonstration

On part d'une fonction $f(x)$ définie sur un intervalle stable $I=[a;b]$. On souhaite démontrer qu'il existe un point pour lequel $x=f(x)$, ce qui se reformule comme suit : $x-f(x)=0$. Considérons donc la fonction $g(x)=x-f(x)$. On déduit facilement que la fonction est continue sur l'intervalle $I=[a;b]$, cette propriété étant héritée de la fonction $f(x)$. Maintenant, regardons ce qui se passe aux bords $a$ et $b$ de l'intervalle. Vu que $g(a)\in I$ et $g(b)\in I$, on a : $g(a)=a-f(a)\leq 0$ $g(b)=b-f(b)\geq 0$ D’après le théorème des valeurs intermédiaires, on déduit que $g(x)$ doit s'annuler en une valeur précise de $x$. Ce qu'il fallait démontrer.

Les points périodiques d'une suite

Les points périodiques sont une sorte de généralisation des points fixes, la différence étant que la fonction est appliquée plusieurs fois au lieu d'une seule pour les points fixes. Par exemple, prenons le cas d'un point périodique pour lequel une fonction est appliquée deux fois. On a alors :

$x=f(f((x))$

En toute généralité, un point périodique est une valeur x telle que :

$x=f_{n}(x)$, où $f_{n}(x)=f(f(f(f(f(f(...(x))))))$ avec f appliquée sur elle-même $n$ fois.

Si $f$ possède un ou plusieurs points périodiques, alors la suite associée appartient à une classe de suite particulière : les suites périodiques ou quasi-périodiques. Si on omet les suites constantes ou stationnaires, aucune suite périodique ou ultimement périodique n'a de point fixe vers lequel elles peuvent converger. Ce qui signifie que toute suite (ultimement) périodique de période > 1 diverge.

La convergence d'une suite récurrente associée

La présence de points fixes fait que la suite peut devenir stationnaire (constante au-delà d'un certain rang). Il suffit qu'il existe un rang $n$ tel que $u_{n}=x$ : tous les rangs supérieurs donneront une sous-suite stationnaire. Mais ce qui est intéressant est que cela permet de déterminer la limite de la suite si celle-ci converge. En effet, on peut démontrer que la limite d'une suite récurrente est aussi un cas particulier de point fixe.

La limite, si elle existe, est un point fixe

Si une suite récurrente associée possède une limite $l$, alors cette limite est un des points fixes de f. En clair, on a : $l=f(l)$.

Démonstration

Partons de la relation de récurrence d'une suite, définie comme suit : $u_{n+1}=f(u_{n})$ Passons à la limite quand $n$ tend vers l'infini : $\lim _{n\rightarrow \infty }u_{n+1}=\lim _{n\rightarrow \infty }f(u_{n})$ On peut alors écrire : $\lim _{n\rightarrow \infty }u_{n+1}=f\left(\lim _{n\rightarrow \infty }u_{n}\right)$ Les deux limites sont égales à la limite de la suite, par définition. Si on note $l$ la limite de la suite, on a : $l=f(l)$ Ce qui nous dit que la limite $l$ est bien un point fixe.

Faisons quelques remarques, histoire de bien comprendre la portée de ce résultat.

1. On doit s'assurer que la suite converge pour utiliser ce théorème. Il existe en effet des suites qui divergent, mais qui admettent quand même un ou plusieurs points fixes. Trouver les points fixes d'une fonction ne suffit pas à dire que la suite récurrente associée converge vers ce point fixe : il faut encore prouver que la suite converge effectivement. Dit autrement : l'existence d'un point fixe est une condition nécessaire, mais pas suffisante pour la convergence. Par contre, on sait que la réciproque est vraie : si la fonction $f$ n'a pas de point fixe, alors la suite récurrente associée ne converge pas. L'inexistence d'un point fixe implique de facto la divergence. Pour donner un exemple, la fonction $f(x)={\sqrt {1+x^{2}}}$ n'a pas de point fixe, ce qui fait que toute suite définie par $u_{n+1}={\sqrt {1+{u_{n}}^{2}}}$ ne converge pas.
2. Le point fixe peut ne s'exprimer que pour certains $u_{0}$ bien précis, qui sont les seuls à faire converger la fonction. Par exemple, la suite définie par $u_{n+1}={\frac {1}{u_{n}}}$ ne converge que si le premier terme vaut 1 et diverge systématiquement sinon.
3. Un autre problème est le cas où la fonction f a plusieurs points fixes. Dans ce cas, on sait que la limite de la suite est un de ces points fixes, mais on ne sait pas lequel. Pour en donner un exemple, prenons la suite définie par la relation suivante (un exemple de suite logistique, dont nous reparlerons plus tard) : $u_{n+1}={\frac {3}{2}}u_{n}(1-u_{n})$. Cette suite possède deux points fixes : 0 et 1/3. La limite, si elle existe, ne peut être qu'un de ces deux points fixes, mais on ne sait pas l'avance lequel. Pour cet exemple, la suite converge effectivement et sa limite est de 1/3, mais l'analyse des points fixes seule ne nous permet pas de le déduire.

Les points précédents sont assez importants et font que la découverte d'un point fixe ne suffit pas à déterminer la limite d'une suite récurrente. Il faut d'abord s'assurer que la suite converge effectivement, avant de déterminer quel point fixe est le bon. Dans les démonstrations qui suivront, nous aurons à respecter ces deux étapes, dans cet ordre. D'abord on prouvera la convergence, avant de dire quel est le point fixe qui sert de limite. Pour cette seconde étape, il arrivera qu'on prouve que la fonction ne dispose que d'un seul point fixe, ce qui rend la tâche assez aisée.

Les différents types de points fixes

On peut classer les points fixes d'une fonction en deux types, selon la manière dont la limite converge vers ce point fixe.

• Avec un point fixe répulsif, la suite ne converge vers un point fixe $l$ que si elle est constante et égale à $l$ au-delà d'un certain rang. En clair, la suite doit non seulement être stationnaire, mais les termes de sa portion constante doivent être égaux à $l$.
• Avec un point fixe attractif, ce n'est pas nécessairement le cas : la suite peut converger vers $l$ progressivement, sans pour autant être stationnaire. Un point attractif $a$ cause la convergence de toutes les suites construites avec la fonction f, sous condition que le premier terme soit suffisamment proche de $a$.

Ils se distinguent par la valeur absolue de la dérivée de la fonction $f$, $|f'(x)|$, selon qu'elle est inférieure, supérieure ou égale à 1.

• Si $|f'(x)|>1$, les points fixes de la suite sont répulsifs ;
• Si $|f'(x)|<1$, les points fixes de la suite sont attractifs ;
• Si $|f'(x)|=1$, la suite peut converger ou non vers ses points fixes, qui peuvent être autant attractifs que répulsifs.

Un exemple : la suite de Héron

Dans la suite de ce chapitre, nous allons étudier quelques exemples emblématiques de suites récurrentes de premier ordre. Pour commencer, nous allons étudier un exemple classique de suite récurrente : la suite de Héron, définie par :

$u_{n+1}={\frac {1}{2}}\left(u_{n}+{\frac {A}{u_{n}}}\right)$, avec $A$ un nombre constant positif.

Voici une autre formulation équivalente, qui nous sera utile par la suite :

$u_{n+1}={\frac {1}{2}}{\frac {u_{n}^{2}+A}{u_{n}}}={\frac {u_{n}^{2}+A}{2u_{n}}}$

Le premier terme $u_{0}$ est choisi plus ou moins arbitrairement, mais cela ne change pas grand-chose à sa limite. Dans ce qui va suivre, nous allons étudier la convergence de cette suite et démontrer qu'elle converge vers ${\sqrt {A}}$. Nous allons utiliser pour cela quelques arguments, dont l'étude du point fixe de cette suite.

Avant toute chose, on peut donner l'intuition qui se cache derrière cette suite, expliquer pourquoi elle converge vers ${\sqrt {A}}$. Pour comprendre pourquoi, imaginons que l'on choisisse un premier terme $u_{0}$ tel que $u_{0}<{\sqrt {A}}$. Dans ce cas, le terme ${\frac {A}{u_{n}}}$ sera tel que : ${\frac {A}{u_{n}}}>{\sqrt {A}}$. Le premier terme est donc inférieur à la racine carrée, tandis que le second est supérieur. On peut appliquer le même raisonnement avec un premier terme tel que $u_{0}>{\sqrt {A}}$. Pour obtenir une meilleure approximation de ${\sqrt {A}}$, on peut prendre la moyenne des deux termes. C'est ce que fait la relation de récurrence : c'est la moyenne de deux termes $u_{n}$ et ${\frac {A}{u_{n}}}$. Il suffit ensuite d'itérer ce calcul de moyenne avec l'approximation obtenue, le raisonnement précédent valant pour toutes les étapes. Ce raisonnement intuitif ne vaut cependant pas une démonstration en bonne et due forme, chose que nous allons faire dans ce qui suit.

Avant d'utiliser les points fixes de cette suite, nous devons avoir vérifié si celle-ci converge effectivement. On pourrait imaginer un cas où la suite ne converge pas, ce qui rendrait l'utilisation du point fixe inutile. Il nous faut donc démontrer que la suite de Héron converge, avant de crier victoire. Heureusement, cette démonstration est très simple, vu que la suite est monotone. On peut alors utiliser les théorèmes vus dans le chapitre sur les limites pour dire si elle converge ou non.

Preuve de la monotonie de la suite de Héron

Pour commencer, vérifions si la suite est croissante, décroissante ou constante. Pour cela, calculons simplement le terme $u_{n+1}-u_{n}$ :

$u_{n+1}-u_{n}={\frac {1}{2}}\left(u_{n}+{\frac {A}{u_{n}}}\right)-u_{n}$

Développons et réarrangeons les termes :

$u_{n+1}-u_{n}=\left[{\frac {1}{2}}u_{n}-u_{n}\right]+{\frac {1}{2}}{\frac {A}{u_{n}}}$

Simplifions :

$u_{n+1}-u_{n}={\frac {1}{2}}{\frac {A}{u_{n}}}-{\frac {1}{2}}u_{n}$

$u_{n+1}-u_{n}={\frac {1}{2}}\left({\frac {A}{u_{n}}}-u_{n}\right)$

Multiplions par $u_{n}$ :

$u_{n+1}-u_{n}={\frac {1}{2}}\left(A-{u_{n}}^{2}\right)$

Le terme de droite est nul si $u_{n}={\sqrt {A}}$, positif quand $u_{n}<{\sqrt {A}}$ et négatif avec $u_{n}>{\sqrt {A}}$. La suite est donc constante si $u_{n}={\sqrt {A}}$, croissante quand $u_{n}<{\sqrt {A}}$ et décroissante avec $u_{n}>{\sqrt {A}}$. Reste enfin à trouver des minorants et des majorants à la suite.

Les minorants et majorants de la suite

Pour finir la démonstration, il nous reste à trouver des minorants et des majorants à la suite. Il se trouve que, quel que soit le premier terme, tous les termes suivants de la suite seront tels que $x_{n}\geq {\sqrt {A}}$, ou encore $x_{n}-{\sqrt {A}}\geq 0$. Pour simplifier les calculs, nous allons calculer le carré de l'inégalité précédente, à savoir :

$x_{n+1}^{2}-A$

On remplace $x_{n+1}$ par sa valeur déterminée par récurrence. Cela signifie que les calculs qui vont suivre ne seront valables qu'au-delà du premier rang, le premier terme n'étant pas concerné.

$\left({\frac {u_{n}^{2}+A}{2u_{n}}}\right)^{2}-A$

Développons le terme au carré :

$\left({\frac {u_{n}^{4}+A^{2}+2Au_{n}^{2}}{4u_{n}^{2}}}\right)-A$

Mettons au même dénominateur :

$\left({\frac {u_{n}^{4}+A^{2}+2Au_{n}^{2}}{4u_{n}^{2}}}\right)-{\frac {4u_{n}^{2}A}{4u_{n}^{2}}}$

Factorisons :

${\frac {u_{n}^{4}+A^{2}-2Au_{n}^{2}}{4u_{n}^{2}}}$

En faisant appel à une identité remarquable, on trouve :

$\left({\frac {u_{n}^{2}-A}{2u_{n}}}\right)^{2}$

Vu que cette expression est un carré, elle est toujours positive ou nulle. Ce qu'il fallait démontrer.

$\left({\frac {u_{n}^{2}-A}{2u_{n}}}\right)^{2}\geq 0$

Cette inégalité n'étant qu'une reformulation de l'inégalité $x_{n}-{\sqrt {A}}\geq 0$, on peut en déduire que pour tout rang au-delà du premier terme : $x_{n}\geq {\sqrt {A}}$. La suite est donc minorée par ${\sqrt {A}}$ au-delà du premier rang. Sachant qu'on a démontré au-dessus que la suite est alors décroissante, on en déduit qu'elle converge. La suite de Héron converge donc vers la racine carrée du nombre A.

Le point fixe de la suite de Héron

D'après ce qu'on a vu en introduction, on sait que la limite de la suite de Héron est un point fixe de la fonction de récurrence. Calculons donc la valeur de ce point fixe, définit par :

$l={\frac {1}{2}}\left(l+{\frac {A}{l}}\right)$

Multiplions par $2l$ :

$2l^{2}=l^{2}+A$

En isolant A et en prenant la racine carrée, on trouve :

$l={\sqrt {A}}$

Ce résultat nous dit que si cette suite converge, elle converge vers ${\sqrt {A}}$.

Les suites récurrentes k-contractantes

Il existe quelques cas particuliers de fonctions pour lesquelles on peut prouver qu'une suite récurrente associée converge systématiquement. Un cas particulier bien connu, souvent introduit dans les cours de mathématiques du supérieur, est celui des fonctions dites K-contractantes.

Les fonctions K-contractantes sont celles qui respectent la propriété suivante : Une fonction est dite K-contractante si, pour tout x et tout y : $|f(x)-f(y)|\leq K\cdot |x-y|$, avec $K\in [0,1[$. On peut réécrire la formule précédente comme suit : ${\frac {|f(x)-f(y)|}{|x-y|}}\leq K$ Cette formule ressemble à s'y méprendre à la formule d'une dérivée, et nous verrons que ce n'est pas un hasard : diverses propriétés impliquant la dérivée de f sont liées au caractère K-contractant de la fonction. Tel est le cas du théorème suivant : Prenons une fonction f dérivable sur un intervalle I. Si $\max _{x\in I}{|f'(x)|}=K<1$, alors la fonction f est strictement contractante sur l'intervalle I.

Le théorème du point fixe de Picard et Banach

Cette propriété implique, sous certaines conditions, que la suite récurrente associée à f converge. Ces conditions sont les suivantes :

• f est K-contractante.
• I est un intervalle stable par f.
• f admet un unique point fixe $x_{0}$.

On peut démontrer que les deux premières conditions impliquent la troisième, mais cette démonstration aurait plus sa place dans un cours sur les fonctions que dans un cours sur les suites, aussi nous la mettons de côté pour le moment.

Si ces conditions sont remplies, la suite récurrente associée à f converge vers le point fixe $x_{0}$. Ce résultat est un théorème qui porte le doux nom de Théorème du point fixe de Picard et Banach. Le démontrer est assez aisé et demande de procéder comme indiqué plus haut : d'abord on prouve que la suite associée converge, avant de montrer que le point fixe est bien celui qui sert de limite. Ici, nous allons procéder dans l'ordre inverse : nous allons d'abord démontrer que le point fixe en question est unique, avant de montrer que la suite associée converge. La raison à cela est que la démonstration de l'unicité du point fixe est particulièrement simple : c'est un simple raisonnement par l'absurde qui ne demande que quelques manipulations algébriques triviales. Par contre, démontrer que la suite converge vers le point fixe est plus compliqué et demande un raisonnement mathématique à plusieurs étapes assez longues.

Démonstration de l'unicité de la limite

Commençons par démontrer l'unicité par l'absurde.

Démonstration

Supposons que la fonction accepte deux points fixes différents nommés $x_{0}$ et $x_{1}$. Par définition, on a : $x_{0}=f(x_{0})$ $x_{1}=f(x_{1})$ En soustrayant les deux équations, on trouve alors : $|x_{0}-x_{1}|=|f(x_{0})-f(x_{1})|$ Dire que f est K-contractante signifie, par définition, que $|f(x_{0})-f(x_{1})|\leq K\cdot |x_{0}-x_{1}|$, ce qui donne : $|x_{0}-x_{1}|\leq K\cdot |x_{0}-x_{1}|$ Et vu que, d'après l'énoncé, $K\in [0,1[\implies K<1$, on a : $|x_{0}-x_{1}|<|x_{0}-x_{1}|$ Ce qui est absurde.

Démonstration de la convergence de la suite

Il existe deux démonstrations différentes du fait que la suite converge.

Démonstration

Une première démonstration montre que la suite est une suite de Cauchy, à savoir une suite telle que $\lim _{(p,q)\rightarrow \infty }u_{n}-u_{p}=0$, qui converge donc forcément (dans R ou C, du moins). Du fait que la fonction g est K-contractante, on a immédiatement: $|u_{n+1}-u_{n}|\leq |g(u_{n})-g(u_{n-1})|\leq K\left[|g(u_{n-1})-g(u_{n-2})|\right]\leq ...\leq K^{n}\left[|g(u_{1})-g(u_{0})|\right]$ On a aussi, par définition : $u_{n}-u_{p}=(u_{n}-u_{n-1})-(u_{n-1}-u_{n-2})-(u_{n-2}-u_{n-3})-...-(u_{1}-u_{0})$ En combinant les deux équations précédentes, on a : $|u_{n}-u_{p}|\leq \sum _{0}^{n-1}K^{n+1}(|u_{1}-u_{0}|)\leq {\frac {K^{n}}{1-K}}(|u_{1}-u_{0}|)$ En prenant la limite vers l'infini de l'expression précédente, on trouve bien que : $\lim _{(p,q)\rightarrow \infty }|u_{n}-u_{p}|=0$

Démonstration

Une autre démonstration utilise le théorème de Boltzano-Weistrass. La suite est bornée : En premier lieu, la démonstration prouve que la suite K-contractante est bornée. En effet, on a : $|u_{n+1}-u_{n}|=|f(u_{n})-f(u_{n-1})|<K\cdot |f(u_{n-1})-f(u_{n-2})|<K^{2}\cdot |f(u_{n-2})-f(u_{n-3})|<K^{3}\cdot |f(u_{n-3})-f(u_{n-4})|<...<K^{n}\cdot |f(u_{1})-f(u_{0})|$ On peut alors démontrer que : $|u_{n}-u_{0}|<{\frac {1-K^{n}}{1-K}}\cdot |u_{1}-u_{0}|$ Vu que $K\in {[0,1]}$, on a : $|u_{n}-u_{0}|<{\frac {1-K^{n}}{1-K}}\cdot |u_{1}-u_{0}|<{\frac {1}{1-K}}\cdot |u_{1}-u_{0}|$ Inégalité qu'on peut reformuler comme suit : $-{\frac {1}{1-K}}\cdot |u_{1}-u_{0}|\leq |u_{n}-u_{0}|\leq {\frac {1}{1-K}}\cdot |u_{1}-u_{0}|$ Les termes de la suite $(u_{n})$ sont donc bornés dans l'intervalle : $\left[u_{0}-{\frac {|u_{1}-u_{0}|}{1-K}},u_{0}+{\frac {|u_{1}-u_{0}|}{1-K}}\right]$ Application de Boltzano-Weirstrass : Vu que la suite est bornée, on peut en extraire une suite convergente, que l'on notera $u_{\Sigma (n)}$. Sa limite sera notée L dans ce qui suit. Prouver que $L$ est un point fixe de f : Il faut ensuite prouver que L est un point fixe de f, ce qui est fait par le développement suivant. On sait que, par définition de la limite L : $\lim _{n\rightarrow \infty }|u_{\Sigma (n)}-L|\rightarrow 0$ On a alors : $|f(L)-L|=|f(L)-f(u_{\Sigma (n)})+f(u_{\Sigma (n)})-u_{\Sigma (n)}+u_{\Sigma (n)}-L|$ $|f(L)-L|\leq |f(L)-f\left(u_{\Sigma (n)}\right)|+|f\left(u_{\Sigma (n)}\right)-u_{\Sigma (n)}|+|u_{\Sigma (n)}-L|$ $|f(L)-L|\leq K\cdot |L-\left(u_{\Sigma (n)}\right)|+|u_{\Sigma (n)+1}-u_{\Sigma (n)}|+|u_{\Sigma (n)}-L|$ $|f(L)-L|\leq (K+1)\cdot |\left(u_{\Sigma (n)}\right)-L|+K^{\Sigma (n)+1}|u_{1}-u_{0}|$ On a alors : $\lim _{n\rightarrow \infty }u_{\Sigma (n)}\rightarrow 0$ $\lim _{n\rightarrow \infty }K^{\Sigma (n)}\rightarrow 0$ Le second terme tend donc vers zéro, ce qui donne : $|f(L)-L|\leq 0$ En clair, on la limite L est bien un point fixe de la fonction f. Prouver que $L$ est la limite de $u_{\Sigma (n)}$ : Enfin, il reste à prouver que : $|u_{n}-L|\leq K^{n}\cdot |u_{0}-L|$ La démonstration est une simple démonstration par récurrence. Pour n = 1, la propriété est évidente. $|u_{1}-L|=|f(u_{0})-f(L)|\leq K\cdot |u_{0}-L|$ Ensuite, il reste à prouver que si la propriété est vraie pour n, elle l'est aussi pour n+1 : $|u_{n+1}-L|=|f(u_{n})-f(L)|\leq K\cdot |u_{n}-L|\leq K\times K^{n}|u_{0}-L|=K^{n+1}|u_{n}-L|$

Les suites logistiques

Dans ce chapitre, nous allons voir les suites logistiques, des suites très utilisées dans divers domaines (en biologie dans le modèle proie-prédateur, en dynamique des populations, dans la théorie des systèmes dynamiques, et ainsi de suite). Elles sont définies par la fonction relation de récurrence suivante :

$u_{n+1}=\mu \cdot u_{n}(1-u_{n})$

Le paramètre µ détermine le comportement asymptotique de la suite. Suivant sa valeur, la suite va soit converger, soit être périodique, soit être une suite dite chaotique. C'est surtout ce dernier comportement qui intéresse les mathématiciens, surtout ceux qui travaillent sur la théorie du chaos ou la théorie des systèmes dynamiques. Dans les grandes lignes, on peut distinguer les trois situations (convergence, périodicité, chaos) selon la valeur du paramètre µ :

• Si µ est compris entre 0 et 3, la suite converge. La limite dépend cependant de la valeur exacte de µ :
  • Si µ est compris entre 0 et 1, la suite converge vers 0.
  • Si µ est compris entre 1 et 3, la suite converge vers $\mu -1 \over \mu$.
• Si µ est compris entre 3 et 3,57 , la suite est périodique.
• Si µ est entre 3,57 et 4, la suite a un comportement chaotique.
• Si µ est au-delà de 4, la suite diverge.

Le domaine de convergence des suites logistiques

Commençons par étudier la convergence potentielle de ces suites. Pour cela, nous devons calculer les points fixes de la fonction associés, qui respectent donc :

$x=\mu \cdot x(1-x)$.

On voit immédiatement que 0 est un point fixe. On peut aussi, après quelques manipulations algébriques, trouver que l'autre point fixe vaut :

$x={\frac {\mu -1}{\mu }}=1-{\frac {1}{\mu }}$

La fonction associée est la fonction $f(x)=\mu \cdot x(1-x)$.

Une autre manière de déterminer les deux points fixes est de tracer le graphe de la fonction f. Par simplicité, nous allons illustrer celui-ci ci-contre, mais seulement pour $x\in [0,1]$, par souci de simplicité. On voit que le graphe de la fonction f est une parabole, dont la hauteur dépend du paramètre µ : plus µ est grand, plus la parabole sera haute.

Graphe de la fonction logistique pour plusieurs valeurs de µ (ici noté alpha).

Pour trouver les points fixes, on regarde où le graphe précédent coupe la droite identité $y=x$. On voit qu'il existe entre zéro et deux points d'intersection. En-dehors de l'intervalle [0,1], la fonction donne des résultats négatifs, dont aucun ne passe par la droite identité : il n'y a donc pas de points fixes en-dehors de cet intervalle. Le nombre de points d'intersection dépend de la valeur de µ. Si $\mu \in [0,1]$, alors la parabole reste sous la droite $y=x$ et il n'existe qu'un seul point d'intersection : l'origine. Par contre, si $\mu >1$, alors le second point d'intersection apparait à $x={\frac {\mu -1}{\mu }}$.

Points fixes de la fonction associée à une suite logistique.

Maintenant, regardez le tracé des valeurs successives, la ligne en forme de serpentin : on voit qu'il y a un comportement différent entre les deux schémas du milieu (pour lesquels µ > 1). Le premier montre une convergence assez souple, les valeurs de la suite augmentant progressivement pour atteindre la limite $\mu -1 \over \mu$. Ce comportement est celui obtenu quand $1<\mu <2$. Le second schéma montre que les valeurs de la suite convergent vers la même limite, mais le font d'une manière différente : ils vont fluctuer autour de cette valeur, en faisant une sorte d'oscillation amortie.

Suite logistique pour µ = 0.95

Suite logistique pour µ = 1.6

Suite logistique pour µ = 2.8

On peut résumer le tout comme suit :

• Avec 0 < µ < 1, la suite converge vers 0.
• Avec 1 < µ < 2, la suite converge de manière monotone vers $\mu -1 \over \mu$.
• Avec 2 < µ < 3, la suite converge vers $\mu -1 \over \mu$, les valeurs $u_{n}$ oscillant autour de la limite.

Cas où 0 < µ < 1

Graphe de la fonction logistique pour plusieurs valeurs de µ (ici noté alpha).

Commençons par étudier le cas où $0<\mu <1$. Si on étudie la parabole de la fonction avec $0<\mu <1$, on trouve que la valeur maximale atteinte par la parabole est de $\mu \over 4$, et elle est atteinte pour $x={\frac {1}{2}}$. On peut le démontrer en dérivant la fonction $f(x)=\mu \cdot x(1+x)$ et en regardant quelle valeur l'annule, ce que nous ne ferons pas ici. L'intuition nous dit que le comportement de la suite est donc différent selon que $u_{0}\leq {\frac {1}{2}}$ ou que $u_{0}\geq {\frac {1}{2}}$ (on omet les cas où $u_{0}$ vaut 0 ou 1, qui donnent une suite constante).

• Si $u_{0}\leq {\frac {1}{2}}$, alors la suite décroit de manière géométrique, tout en étant minorée par zéro : elle converge donc vers 0.
• Si $u_{0}>{\frac {1}{2}}$, $u_{n+1}<{\frac {1}{2}}$ et on revient au cas précédent.

Cas où 1 < µ < 2

On peut se ramener au cas $0<\mu <1$ avec un changement de variable.

Le domaine périodique des suites logistiques

Ce diagramme montre les différents termes d'une suite logistique, en fonction des valeurs de µ. La valeur µ est placée en abscisse, l'ordonnée donnant la valeur du ou des points périodiques (comprise entre 0 et 1). On voit qu'il n'existe d'un seul point périodique non-nul pour µ < 3, et que celui-ci augmente avec µ. Au-delà, la suite ne peut prendre que deux valeurs, qui sont les deux points périodiques de f(x). Puis la suite passe à une période de 4, etc. Les distances L0, L1, L2, ... sont reliées par la constante de Feigenbaum.

Pour $3<\mu <3,57$, la suite logistique devient périodique. Il est alors possible d'étudier deux choses : la période de la suite, mais aussi les valeurs prises dans un cycle. Il se trouve que les deux dépendent fortement de la valeur de µ choisie. Il existe des relations assez intéressantes entre µ et les valeurs choisies, ainsi qu'avec la période. On peut déduire tout cela de l'étude des points périodiques de la fonction $f(x)=\mu \cdot x(1-x)$. Il se trouve que plus µ augmente, plus la période de la suite augmente : elle double régulièrement, quand µ passe des paliers précis. Le premier palier est égal à ${\sqrt {6}}+1$, le second de $\approx 3.54409$, etc.

• Pour µ compris entre 3 et ${\sqrt {6}}+1$, la suite a une période de 2. Les deux valeurs prises lors d'un cycle sont les solutions de l'équation $x=f(f(x))$. Cette équation possède quatre points périodiques : les deux points fixes, ainsi que les deux racines ${\frac {1}{2}}\left({\frac {1+\mu }{\mu }}+{\frac {1}{\mu }}{\sqrt {\mu ^{2}-2\mu -3}}\right)$ et ${\frac {1}{2}}\left({\frac {1+\mu }{\mu }}-{\frac {1}{\mu }}{\sqrt {\mu ^{2}-2\mu -3}}\right)$. Si on observe la suite obtenue, on voit qu'au-delà d'un certain rang, la suite oscille entre ces deux valeurs.
• Au-delà de ${\sqrt {6}}+1$, la suite voit sa période doubler (passer à 4), avec l'apparition de deux valeurs supplémentaires. Cette fois-ci, les valeurs prises lors d'un cycle sont les solutions de l'équation $x=f(f(f(f(x))))$, points fixes exclus.
• La même chose se reproduit au-delà d'une nouvelle limite, où la période double encore.
• Et ainsi de suite, jusqu’à la valeur limite de 3.56995, où la suite n'est plus périodique.

La convergence d'une série

Les sommes partielles, vues au chapitre précédent, se limitent à faire la somme des premiers termes d'une suite. Pour les suites finies, cela ne change pas grand-chose : le résultat sera naturellement fini, quoiqu'il arrive, même si la suite est elle-même très longue. Mais avec les suites infinies, on peut pousser le concept de somme partielle à son paroxysme : on peut faire la somme de tous les termes de la suite, sans exception. La somme ainsi obtenue n'est pas une somme partielle, vu qu'elle additionne une quantité infinie de termes. À la place, on lui donne le nom de série. Cette définition de série est quelque peu imprécise, la définition formelle est la suivante : une série est la limite de la somme partielle quand le rang n tend vers l’infini : $\sum _{i=0}^{\infty }u_{n}$.

On pourrait croire que ces séries donnent toutes un résultat infini, sauf dans quelques exceptions triviales (suite dont tous les termes sont nuls) : additionner une infinité de termes non-nuls doit naturellement donner un résultat infini, nous dit l'intuition. Mais l’intuition se trompe : certaines séries ont un résultat fini. Par exemple, Euler a montré que la base des logarithmes népériens est le résultat de la série associée à la suite des inverses des factorielles :

$e=1+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+{\frac {1}{5!}}+...$

Les mathématiciens distinguent donc les séries dont le résultat est infini ou indéterminé, appelées séries divergentes, des autres au résultat fini qui portent le nom de séries convergentes.

Quelques suites problématiques

Diverses subtilités se font jour avec les séries, subtilités qui n'existaient pas avec les suites "normales". La raison est que l'addition d'un nombre infini de termes peut jouer des tours lors des calculs. L'addition d'une infinité de termes est en effet quelque peu différente de l'addition usuelle : elle n'est pas forcément associative, distributive et commutative. Ce qui pose problème lors de l'addition d'une suite infinie de termes.

La suite de Grandi

Pour donner un exemple de problèmes qui peuvent survenir avec certaines séries, prenons la suite de Grandi, une suite définie comme suit :

$u_{n}=(-1)^{n+1}$

$(u_{n})=1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,\cdots$

Si l'on souhaite en calculer la série, on peut remarquer qu'il y a plusieurs manières de faire l'addition des termes. Les deux plus simples donnent respectivement 0 et 1 :

$\sum _{n}(u_{n})=(1-1)+(1-1)+(1-1)+(1-1)+(1-1)+(1-1)+(1-1)+(1-1)+(1-1)+\cdots =0$

$\sum _{n}(u_{n})=1+(-1+1)+(-1+1)+(-1+1)+(-1+1)+(-1+1)+(-1+1)+(-1+1)+\cdots =1$

Une autre manière de faire les calculs donne 1/2 :

$\sum _{n}(u_{n})=1-(1-1+1-1+1-1+1-1+1-1+1-1+1+\cdots )$

$\sum _{n}(u_{n})=1-\sum _{n}(u_{n})$

$2\cdot \sum _{n}(u_{n})=1$

$\sum _{n}(u_{n})={\frac {1}{2}}$

Remarquons que cette valeur est compatible avec la formule ${\frac {1}{1+x}}=1-x+x^{2}-x^{3}+x^{4}-x^{5}+\cdots$, avec $x=1$.

D'autres exemples

La suite de Grandi n'est pas la seule suite problématique. On peut aussi citer l'exemple de la suite des entiers alternée, qui est divergente, mais dont la somme des termes a un comportement plus complexe. Là encore, on peut additionner les termes de plusieurs manières différentes, qui donnent chacune un résultat différent. Par exemple, Euler a écrit l'identité suivante :

$\sum _{n}(u_{n})=1-2+3-4+5-6+7-8+9-10+11-12+\cdots ={\frac {1}{4}}$

Ou encore, on peut citer la série des nombres entiers que l'on peut faire converger vers -1/12 si l'on s'y prend bien :

$\sum _{n}(u_{n})=1+2+3+4+5+6+7+8+9+10+11+12+\cdots =-{\frac {1}{12}}$

Pour retrouver ces résultats, nous utiliserons les notations suivantes :

$A=1-1+1-1+1-\cdots$ (série de Grandi).

$B=1-2+3-4+5-\cdots$ (série alternée des entiers naturels).

$S=1+2+3+4+5+\cdots$ (série des entiers naturels).

Calculons maintenant la somme $B-A$ :

${\begin{aligned}B&=&1-2+3-4+5-6+\cdots \\-A&=&-1+1-1+1-1+1-\cdots \\B-A&=&0-1+2-3+4-5+\cdots \end{aligned}}$

On voit que :

$B-A=-B$

Ce qui se reformule en :

$2\cdot B=A$

En utilisant la formule $A={\frac {1}{2}}$, on trouve bien :

$B=1-2+3-4+5-6+7-8+9-10+11-12+\cdots ={\frac {1}{4}}$

Ensuite, calculons $S-B$ :

${\begin{aligned}S&=&1+2+3+4+5+6+\cdots \\-B&=&-1+2-3+4-5+6-\cdots \\S-B&=&0+4+0+8+0+12+\cdots \end{aligned}}$

En simplifiant les zéros, on trouve :

$S-B=4+8+12+16+\cdots$

Ce qui donne :

$S-B=4\cdot S$

$S-4\cdot S=B$

$-3\cdot S=B$

En utilisant la formule $B={\frac {1}{4}}$, on a :

$S=1+2+3+4+5+6+7+8+9+10+11+12+\cdots =-{\frac {1}{12}}$

La convergence absolue et conditionnelle

Dans la section précédente, on a vu que l'ordre dans lequel on effectue les calculs change le résultat d'une série. L'addition n'est donc pas associative, distributive et commutative quand on additionne une infinité de termes. La série converge donc vers deux limites différentes selon la situation et on peut même réussir à la faire diverger si l'on s'y prend assez bien. Heureusement, certaines suites ne sont pas concernées par ce genre de problèmes : elles convergent toujours ou divergent toujours, peu importe l'ordre des calculs. On doit donc distinguer les séries qui convergent toujours de celles qui convergent seulement si les calculs sont faits dans un certain ordre.

Les séries qui sont épargnées par les phénomènes vus plus haut sont appelées les séries absolument convergentes. Elles convergent vers une seule limite finie, qui est toujours la même, peu importe l'ordre dans lequel on fait les calculs. Les séries qui convergent ou divergent selon l'ordre des calculs sont appelées des séries semi-convergentes ou encore séries conditionnellement convergentes. Enfin, il existe certaines séries qui divergent, peu importe l'ordre des calculs, qui sont naturellement appelées séries absolument divergentes.

Toutes les séries qui ne contiennent que des nombres positifs ou nuls sont des séries absolument convergentes ou absolument divergentes. Même chose pour les séries qui ne contiennent que des nombres négatifs ou nuls, qui convergent toujours vers une seule limite ou divergent toujours. Pour qu'une série puisse diverger ou converger vers plusieurs limites, il faut impérativement que la suite contienne des nombres négatifs et positifs. Et encore, cela ne suffit pas pour que le phénomène apparaisse.

Déterminer si une série est absolument convergente

Les séries absolument convergentes respectent toutes la propriété suivante : si on remplace tous les nombres négatifs de la suite par leur valeur absolue, la série doit converger. En clair :

• Une série $\sum _{n=0}^{\infty }u_{n}$ converge si $\sum _{n=0}^{\infty }|u_{n}|$ converge.

On peut comprendre l'intuition derrière ce résultat avec un raisonnement heuristique assez simple. Prenons une suite $u_{n}$, qui contient à la fois des termes positifs et des termes négatifs. Nous allons la décomposer en deux sous-suites, une suite qui contient uniquement les termes positifs et une autre avec les termes négatifs. Nous les noterons respectivement $u_{n}^{+}$ et $u_{n}^{-}$. La série $<u_{n}>$ vaut donc :

$\sum _{n=0}^{\infty }u_{n}=\sum _{n=0}^{\infty }u_{n}^{+}+\sum _{n=0}^{\infty }u_{n}^{-}$

Si la série $\sum _{n=0}^{\infty }u_{n}$ converge absolument, les deux sous-séries $\sum _{n=0}^{\infty }u_{n}^{+}$ et $\sum _{n=0}^{\infty }u_{n}^{-}$ convergent toutes deux. Il n'y a alors pas d’ambiguïté sur la convergence de la série. Mais si les deux sous-séries divergent, alors le résultat est indéterminé : $\infty -\infty$ peut donner un résultat aussi bien fini qu'infini. La série est alors semi-convergente.

Un exemple de série semi-convergente

Pour donner un exemple de série conditionnellement convergente, on peut prendre la série harmonique alternée, une variante de la suite harmonique où les signes sont inversés d'un terme à l'autre. La série de cette suite est la suivante :

$S_{h}=\sum _{n=1}^{\infty }{\frac {-1^{n+1}}{n^{1}}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-{\frac {1}{6}}+...$

Si on applique le critère précédent, on se retrouve en face de la série harmonique, connue pour diverger.

$|S_{h}|=\sum _{n=1}^{\infty }|{\frac {-1^{n+1}}{n}}|=\sum _{n=1}^{\infty }{\frac {1}{n}}=+\infty$

La série ne peut donc qu'être conditionnellement convergente.

Le théorème de réarrangement de Riemann et les méthodes de sommation

Les séries conditionnellement convergentes ont une particularité : on peut obtenir n'importe quel résultat, si l'on sait s'y prendre correctement. En effet, le théorème de Riemann nous dit qu'il est possible d'obtenir n'importe quel résultat déterminé à l'avance, tant que l'on effectue l'addition des termes dans le bon ordre. Dit autrement : les séries conditionnellement convergentes n'ont pas vraiment de résultat.

Les méthodes de sommation

Le théorème de Riemann n'a pas empêché les mathématiciens de définir des techniques de calculs pour ces suites, qui permettent d'obtenir des résultats reproductibles et déterministes à de telles additions. Ces techniques, qui indiquent comment faire l'addition d'une infinité de nombres, sont appelées des méthodes de sommation. Celles-ci doivent respecter certains critères pour avoir le nom de méthode de sommation. Ceux-ci sont donnés ci-dessous :

• Critère de stabilité : La méthode de sommation doit donner le même résultat que l'addition normale, quand on ne prend en compte que les $n$ premiers termes de la suite.
• Critère de régularité : La méthode de sommation doit donner le résultat correct pour les suites absolument convergentes.
• Critère de linéarité  : Si on note $A$ et $B$ le résultat des séries $(a_{n})$ et $(b_{n})$, la méthode donne le résultat $\lambda \times A+B$ à la série de terme $\lambda \times \sum a_{n}+\sum b_{n}$.

La méthode de Cesàro

Les méthodes de sommation les plus connues sont les méthodes de Cesàro et d’Abel. La méthode de Cesàro consiste à faire la moyenne des sommes partielles. La limite de ces suites est prise comme valeur de la suite. Ainsi, la série $S$ associé à une suite $u_{n}$ est égale à la formule suivante. Le terme $S_{n}$ est la somme partielle des n premiers termes.

$S=\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=1}^{n}S_{n}=A$.

Les critères de convergence d'une série

Comme on l'a dit il y a quelques chapitres, certaines séries convergent alors que d'autres non. Nous avons notamment prouvé que la série harmonique diverge en utilisant une méthode asse idiosyncratique. Mais heureusement, il existe des méthodes plus générales pour déterminer si une série converge ou non. Ces méthodes sont souvent appelées des critères de convergence. Il en existe beaucoup, aussi ce chapitre ne vous présentera que les principaux, ceux les plus facilement utilisables. Nous verrons les critères de Cauchy, d'Abel, le test du ratio et de la racine carrée, et quelques autres.

Le test de la limite de la suite

Une condition nécessaire pour qu'une série converge est que son terme générale tende vers 0 avec le rang : si $\sum _{n=0}^{\infty }u_{n}$ converge, alors $\lim _{n\to \infty }u_{n}=0$.

La contraposée de ce résultat donne un critère simple de divergence : une série dont le terme général ne tend pas vers 0 diverge.

Attention toutefois : le fait que le terme général d'une série tende vers 0 ne signifie pas que celle-ci est forcément convergente. Par exemple, la série harmonique, de terme général $u_{n}={\tfrac {1}{n}}$ qui tend vers 0 lorsque $n$ tend vers l'infini, diverge :

$1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+...=+\infty$

(ceci sera démontré dans la chapitres suivants).

Exemple d'une suite dont les membres tendent vers zéro. Il s'agit d'une suite géométrique de raison 2/3 et de premier terme 1. On voit sur le schéma que les termes de la suite diminuent progressivement, tout en restant positifs.

Un premier exemple : la suite ${\frac {n}{n+1}}$

Comme premier exemple, nous allons prouver que la série suivante diverge :

$\sum _{n}{\frac {n}{n+1}}=+\infty$

Calculons la limite de la suite ${\frac {n}{n+1}}$ :

$\lim _{n\to \infty }{\frac {n}{n+1}}=\lim _{n\to \infty }{\frac {(n+1)-1}{n+1}}=\lim _{n\to \infty }1-{\frac {1}{n+1}}=1$

Vu que la limite de la suite n'est pas nulle, la série ne peut pas converger.

Un second exemple : la convergence des suites entières

Dans cette section, nous allons voir le cas des séries naturelles. Les séries naturelles sont formées à partir de suites naturelles, des suites dont tous les termes sont des nombres entiers naturels (positifs ou nuls), sans exception. Le critère précédent nous dit que, pour que sa série converge, la suite naturelle doit tendre vers zéro. Ce critère peut se reformuler en disant que toute suite naturelle qui converge doit n'avoir que des termes nuls au-delà d'un certain rang : les seuls termes non-nuls se situent avant ce rang, mais en aucun cas après. On peut reformuler encore une fois en disant que la suite naturelle doit avoir un nombre fini de termes non-nuls. Si ce n'est pas le cas, la série diverge complètement.

Pour vous donner un exemple, prenons la suite définie par :

$u_{n}={\begin{cases}1{\mbox{ si }}n=2^{k}\\0{\mbox{ sinon }}\end{cases}}$

La série qui correspond diverge. Il y a beau avoir une quantité infinie de termes nuls, il y a aussi une infinité de termes non-nuls : le critère nous dit que la suite ne peut pas converger.

Le critère de condensation de Cauchy

Le critère de condensation de Cauchy s'applique à un nombre limité de suites, qui doivent avoir certaines caractéristiques. Dans le détail, ce critère s'applique aux suites décroissantes, qui tendent vers zéro. Un bon exemple serait la suite harmonique, qui est strictement décroissante (nous l'avons démontré dans le premier chapitre) et qui tend vers zéro (nous l'avons aussi démontré dans le second chapitre). Cette suite est donc parfaitement applicable au critère que nous allons aborder. Comme autre exemple, nous pourrions citer la suite de l'inverse des carrés ou des cubes, ou les autres suites harmoniques. Mais la suite harmonique alternée ne serait pas éligible pour ce critère : elle a beau avoir une limite nulle, elle n'est pas décroissante : c'est une suite alternée.

Le critère de condensation de Cauchy s'applique donc à une suite $<u_{n}>$ décroissante et de limite nulle. Celui-ci permet de dire si la série suivante converge :

$\sum _{n=0}^{\infty }u_{n}$

Elle converge si et seulement si la série dérivée suivante converge :

$\sum _{n=0}^{\infty }\left(2^{n}\times u_{2^{n}}\right)$

Exemple d'application : la série harmonique

Ce critère peut sembler assez abscons, aussi nous allons l'illustrer par un exemple. Nous allons démontrer que la série harmonique diverge, encore une fois. Comme dit plus haut, la suite harmonique respecte les critères d'éligibilité. Nous voulons calculer la série

$\sum _{n=0}^{\infty }{\frac {1}{n}}$

Le critère nous dit qu'elle converge si et seulement si la série dérivée suivante converge :

$\sum _{n=0}^{\infty }2^{n}\times {\frac {1}{2^{n}}}$

Quelques simplifications algébriques triviales donnent :

$\sum _{n=0}^{\infty }1=\infty$

La série dérivée diverge, ce qui fait que la série harmonique initiale aussi. CQFD !

Démonstration

Une démonstration de ce théorème est accessible via le lien suivant :

• démonstration du critère de concentration de Cauchy (en anglais).

Les critères pour les séries réelles à termes positifs

Les critères que nous allons voir dans cette section ne sont valables uniquement pour certaines suites de nombres réels, celles dont les termes sont tous positifs et/ou nuls. Ils ne sont pas applicables aux séries dont certains termes sont négatifs.

L'application du théorème des suites croissantes

Le premier critère se base sur le fait que, pour les suites à termes positifs ou nuls, toute somme partielle est croissante. Ce lemme se démontre assez facilement : la différence entre deux sommes partielles consécutives vaut : $\sum _{n=0}^{n}u_{n}=u_{n}+\sum _{n=0}^{n-1}u_{n}$. Vu que, par définition, $u_{n}\geq 0$, on a : $\sum _{n=0}^{n}u_{n}\geq \sum _{n=0}^{n-1}u_{n}$. Ce qui, traduit en langage humain, dit que la suite des sommes partielles est croissante.

On peut alors appliquer le théorème des suites monotones : la suite des sommes partielles étant croissante, elle converge seulement si elle est majorée. La série diverge si ce n'est pas le cas, et converge si ce l'est.

Le test de comparaison

Le test de comparaison permet de comparer deux suites entre elles : si l'on sait que l'une converge ou diverge, on peut alors savoir ce qu'il en est pour l'autre. Cette comparaison compare une série cible avec une série test. La comparaison s'effectue terme à terme : on cherche à savoir, pour deux suites $a_{n}$ et $b_{n}$, si :

• $a_{n}\geq b_{n}\geq 0$ pour tout rang $n$ ;
• $0\leq a_{n}\leq b_{n}$ pour tout rang $n$ ;
• $a_{n}=b_{n}$ pour tout rang $n$.

Si l'une des trois conditions est représentée, on peut parfois déterminer si $a_{n}$ converge ou diverge selon la convergence/divergence de $b_{n}$. Le cas le plus simple à étudier est clairement le cas où $a_{n}=b_{n}$ pour tout rang $n$. Soit les deux suites divergent, soit elles convergent. Les deux autres cas sont plus intéressants à étudier.

Si $a_{n}\leq b_{n}$ pour tout rang $n$ et que $b_{n}$ converge, alors $a_{n}$ converge elle aussi. Dans le cas où $b_{n}$ diverge, on ne peut cependant pas conclure : la série $<a_{n}>$ peut aussi bien converger que diverger.

Si $a_{n}\geq b_{n}$ pour tout rang $n$ et que $b_{n}$ diverge, alors $a_{n}$ diverge elle aussi. Dans le cas où $b_{n}$ converge, on ne peut cependant pas conclure : la série $<a_{n}>$ peut aussi bien converger que diverger.

	$b_{n}$ converge	$b_{n}$ diverge
$a_{n}=b_{n}$	$a_{n}$ converge	$a_{n}$ diverge
$a_{n}\geq b_{n}$	On ne sait pas	$a_{n}$ diverge
$a_{n}\leq b_{n}$	$a_{n}$ converge	On ne sait pas

Une généralisation du résultat

Le résultat peut se généraliser aux cas où :

• $a_{n}\geq k\times b_{n}$ pour tout rang $n$ ;
• $a_{n}\leq k\times b_{n}$ pour tout rang $n$ ;
• $a_{n}=k\times b_{n}$ pour tout rang $n$.

La raison en est simple : multiplier une série par une constante ne fait que multiplier son résultat par cette même constante. Si une série converge, son résultat sera simplement multiplié par la constante en question : le résultat convergera aussi.

Le critère de comparaison des limites

Le critère de comparaison des limites est utile si l'on sait que l'une des deux converge/diverge et que l'on veut savoir ce qu'il en est de la seconde.

Prenons deux suites $(a_{n})$ et $(b_{n})$, dont les termes sont positifs ou nuls. De plus, leur quotient tend vers une limite finie, non-nulle. En clair, on a :

$\lim \limits _{n\to \infty }{\frac {a_{n}}{b_{n}}}=q$ avec $q>0$

Dans ce cas, le théorème que nous allons voir nous dit que soit les deux convergent, soit les deux divergent. Précisément, trois cas permettent de conclure :

• Si $q=0$ et que la suite $(b_{n})$ converge, alors $(a_{n})$ converge aussi.
• Si $0<q<+\infty$ et qu'une des suites converge, alors l'autre converge aussi.
• Si $q=+\infty$ et que la suite $(b_{n})$ diverge, alors $(a_{n})$ diverge aussi.

On peut remarquer que ce critère n'est qu'un corolaire du critère précédent.

Exemple d'application

Pour illustrer ce théorème, nous allons prendre le cas de la suite de l'inverse des entiers pairs. Nous allons la comparer à la suite harmonique, ce qui nous dit que les deux sont multiples d'une de l'autre. En effet :

$\sum _{n=0}^{\infty }{\frac {1}{2n}}=\sum _{n=0}^{\infty }{\frac {1}{2}}{\frac {1}{n}}={\frac {1}{2}}\sum _{n=0}^{\infty }{\frac {1}{n}}$

On a donc :

$\lim \limits _{n\to \infty }{\frac {a_{n}}{b_{n}}}={\frac {1}{2}}$

Or, l'on sait que la série $<b_{n}>$ (ici, la série harmonique) diverge : l'autre série (ici la série de l'inverse des entiers pairs) diverge aussi.

La règle d'Alembert

Le critère qui va suivre permet de savoir si une série converge, sans avoir à la comparer à une suite déjà connue. Ce critère se contente d'analyser la suite $u_{n}$. Précisément, il demande de calculer le rapport :

$\lim _{n\to \infty }|{\frac {u_{n+1}}{u_{n}}}|=l$

• Si $l>1$, la série diverge ;
• Si $l<1$, la série converge ;
• Dans les autres cas, on ne peut pas conclure.

Démonstration

Il est facile de démontrer ce critère, qui n'est en réalité que l'application de la définition d'une limite couplée à quelques formules assez simples. On peut notamment remarquer que ce critère est fortement semblable au critère de convergence d'une série géométrique : le critère du ratio ne fait que calculer une « raison géométrique » à une suite quelconque (pas forcément géométrique). Rappelons ce que signifie la formule : $\lim _{n\to \infty }|{\frac {u_{n+1}}{u_{n}}}|=l$. Cette formule signifie qu'au-delà d'un rang $N$, on a : $l-\epsilon \leq |{\frac {u_{n+1}}{u_{n}}}|\leq l+\epsilon$ Donc : $|u_{n}|=|{\frac {u_{n}}{u_{n-1}}}|\times |{\frac {u_{n-1}}{u_{n-2}}}|\times |{\frac {u_{n-2}}{u_{n-3}}}|\times |{\frac {u_{n-3}}{u_{n-4}}}|\cdots$ On en déduit l'inégalité suivante : $|u_{n}|\leq (l+\epsilon )^{n-N-1}|u_{n+1}|$ Le terme de droite est une suite géométrique de raison $l+\epsilon$, qui converge si $l+\epsilon <1$ et diverge si $l+\epsilon >1$. Donc, par comparaison, le terme de gauche fait de même. CQFD !

Exemple d'application : la suite du rapport puissance/factorielle

Le critère précédent permet de démontrer que la série suivante converge :

$\sum _{n}{\frac {x^{n}}{n!}}$

Pour cela, calculons le rapport : ${\frac {u_{n+1}}{u_{n}}}$ :

${\frac {u_{n+1}}{u_{n}}}={\frac {x^{(n+1)}}{(n+1)!}}{\frac {n!}{x^{n}}}={\frac {x^{(n+1)}}{x^{n}}}{\frac {n!}{(n+1)!}}={\frac {x}{n+1}}$

Or, $x$ est une constante, ce qui fait que ce rapport tend vers 0.

$\lim _{n\to \infty }{\frac {u_{n+1}}{u_{n}}}=\lim _{n\to \infty }{\frac {x}{n+1}}=0$

En conséquence, la série converge !

La règle de Cauchy

Le critère de Cauchy (différent du critère de Cauchy pour les suites) permet de savoir si une série converge, sans avoir à la comparer à une suite déjà connue. Ce critère se contente d'analyser, pour une suite $u_{n}$, la limite suivante :

$\lim _{n\to \infty }{\sqrt[{n}]{|u_{n}|}}=L$

• Si $L>1$, la série diverge ;
• Si $L<1$, la série converge ;
• Dans les autres cas, on ne peut pas conclure.

Démonstration

Démonstration de la convergence pour $L<1$ : Si on a $L<1$, alors il existe un entier $r$ tel que : ${\sqrt[{n}]{|u_{n}|}}<r<1$ On élève alors les deux termes à la puissance n : $u_{n}<r^{n}$ Or, la suite $r^{n}$ est une suite géométrique de premier terme 1 et de raison $r<1$ : elle converge donc. La suite $u_{n}$, par le critère de comparaison converge aussi. CQFD !

Démonstration

Démonstration de la divergence pour $L>1$ : Si on a $L<1$, alors il existe un entier $r$ tel que : ${\sqrt[{n}]{|u_{n}|}}>r>1$ On élève alors les deux termes à la puissance n : $u_{n}>r^{n}>1$ La suite $r^{n}$ est une suite géométrique de premier terme 1 et de raison $r>1$ : elle diverge donc. La suite $u_{n}$, par le critère de comparaison diverge aussi. CQFD !

Les opérations sur les séries

On a vu dans le chapitre "Les opérations sur les multiplications de la suite", qu'il est possible d'additionner des suites entre elles, de les multiplier, les soustraire, les diviser, etc. Et les suites de sommes partielles ne font pas exception : ce sont des suites, de sommes partielles certes, mais des suites quand même. Les séries n'étant que les limites de ces sommes partielles, les théorèmes sur les limites de sommes/produit de suites s'appliquent parfaitement. Cela a des conséquences assez intéressantes, que nous allons détailler dans cette section.

Les opérations arithmétiques sur les suites

Dans ce qui va suivre, nous allons voir comment additionner, soustraire, multiplier et diviser des séries.

La série d'une somme de suites

Ce résultat peut permettre de calculer la série d'une somme de suites. Il suffit de mettre $\alpha$ et $\beta$ à 1 pour obtenir une somme. On a alors le résultat suivant. Soit deux séries convergentes $\sum _{n}a_{n}=A$ et $\sum _{n}b_{n}=B$, alors :

$\sum _{n}(a_{n}+b_{n})=A+B$

Ce résultat est simplement une application du théorème sur la limite d'une somme de suites, dans le cas où la suite est une série.

La série du produit d'une suite par une constante

Soit une constante $\alpha$ et une série convergente $\sum _{n}a_{n}=A$, alors :

$\sum _{n}(\alpha \times a_{n})=\alpha \sum _{n}a_{n}=\alpha A$

Ce résultat est simplement une application du théorème sur le produit d'une suite par une constante, dans le cas où la suite est une série.

La série d'une combinaison linéaire de suites

Soit deux séries convergentes $\sum _{n}a_{n}=A$ et $\sum _{n}b_{n}=B$, alors :

$\sum _{n}(\alpha \times a_{n}+\beta \times b_{n})=\alpha \sum _{n}a_{n}+\beta \sum _{n}b_{n}=\alpha A+\beta B$

Ce résultat est simplement une application des deux théorèmes précédents.

La série d'un produit

Soit deux séries convergentes $\sum _{n}a_{n}=A$ et $\sum _{n}b_{n}=B$, dont l'une des deux est absolument convergente, alors :

$\sum _{n}(a_{n}\times b_{n})=A\times B$

Ce résultat est simplement le théorème sur la limite d'un produit de suites, dans le cas où la suite est une série.

Les séries de nombres complexes

Les théorèmes précédents ont une application assez importante, dans le cas où la suite étudiée est une suite de nombres complexes. Prenons la suite de nombres complexes $(u_{n})$ et calculons sa suite. Chaque terme est la somme d'une partie réelle et d'une partie imaginaire : $u_{n}=a+ib$. Créons une suite $a_{n}$ qui ne comprend que la partie réelle de chaque terme, et une autre suite $b_{n}$ qui n'a que les parties imaginaires. On suppose que les deux suites convergent vers les limites respectives $A$ et $B$. On a alors :

$\sum _{n}u_{n}=\sum _{n}(a_{n}+ib_{n})$

$\sum _{n}u_{n}=\sum _{n}a_{n}+\sum _{n}(ib_{n})$

$\sum _{n}u_{n}=\sum _{n}a_{n}+i\sum _{n}(b_{n})$

$\sum _{n}u_{n}=A+iB$

On voit donc que la série $\sum _{n}u_{n}$ ne peut converger que si $\sum _{n}a_{n}$ et $\sum _{n}b_{n}$ convergent toutes deux.

Les séries télescopiques

Les séries télescopiques sont des séries dont les sommes partielles ne conservent qu'un nombre fini de termes, une fois qu'on a compensé les termes opposés. Dans de telles suites, les sommes partielles sont telles que certains termes se compensent, dans le sens où leur somme s'annule.

Les séries télescopiques simples

Les plus simples sont de la forme :

$\sum _{i=0}^{\infty }(u_{i+1}-u_{i})$

On peut démontrer que la limite de telles séries n'est autre que :

$\sum _{i=0}^{\infty }(u_{i+1}-u_{i})=\left(\lim _{n\rightarrow \infty }u_{n+1}\right)-u_{0}$

Pour démontrer cette formule, il faut partir de la formule obtenue dans le chapitre sur les sommes partielles. On a en effet démontré que :

$\sum _{i=0}^{n}(u_{i+1}-u_{i})=u_{n+1}-u_{0}$

En prenant la limite de cette somme partielle quand n tend vers l'infini, on a :

$\lim _{n\rightarrow \infty }\sum _{i=0}^{n}(u_{i+1}-u_{i})=\lim _{n\rightarrow \infty }\left(u_{n+1}-u_{0}\right)$

On peut alors sortir la constante $u_{0}$ :

$\sum _{i=0}^{\infty }(u_{i+1}-u_{i})=\left(\lim _{n\rightarrow \infty }u_{n+1}\right)-u_{0}$

La formule précédente implique que la limite $\lim _{n\rightarrow \infty }u_{n+1}$ existe bel et bien. Si ce n'est pas le cas, alors la série diverge.

Pour donner un exemple où une série télescopique diverge, on peut prendre la série suivante :

$\sum _{i=0}^{\infty }{\frac {\ln(n+1)}{\ln n}}=\sum _{n\rightarrow \infty }[\ln(n+1)-\ln n]$

On trouve alors :

$\sum _{i=0}^{\infty }{\frac {\ln(n+1)}{\ln n}}=\lim _{n\rightarrow \infty }[\ln(n+1)]-\ln 1$

Le premier terme $\lim _{n\rightarrow \infty }[\ln(n+1)]$ diverge, ce qui fait que la série au total diverge elle aussi.

D'autres séries télescopiques

Toutes les séries télescopiques ne s'écrivent pas sous la forme précédente, à savoir :

$\sum _{i=0}^{\infty }(u_{i+1}-u_{i})$

Comme premier exemple, nous allons étudier la série suivante :

$\sum _{i=0}^{\infty }{\frac {k}{i(i+k)}}$

On peut la réécrire comme ceci :

$\sum _{i=0}^{\infty }{\frac {(i+k)-i}{i(i+k)}}$

En factorisant, on a :

$\sum _{i=0}^{\infty }\left[{\frac {i+k}{i(i+k)}}-{\frac {i}{i(i+k)}}\right]$

En simplifiant, on a :

$\sum _{i=0}^{\infty }\left[{\frac {1}{i}}-{\frac {1}{i+k}}\right]$

Ce qui se réécrit comme suit :

$\left(\sum _{i=0}^{\infty }{\frac {1}{i}}\right)-\left(\sum _{i=0}^{\infty }{\frac {1}{i+k}}\right)$

Cela est équivalent à :

$\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+\cdots \right)-\left({\frac {1}{k}}+{\frac {1}{k+1}}+{\frac {1}{k+2}}+{\frac {1}{k+3}}+{\frac {1}{k+4}}+\cdots \right)$

On peut le réécrire comme suit :

$1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{k-1}}+\left({\frac {1}{k}}-{\frac {1}{k}}+{\frac {1}{k+1}}-{\frac {1}{k+1}}+{\frac {1}{k+2}}-{\frac {1}{k+2}}+\cdots \right)$

On voit que tous les termes à partir de ${\frac {1}{k}}$ s'annulent. Au final, il ne reste qu'un nombre fini de termes, ce qui fait que la série est techniquement parlant une série télescopique. Le tout se simplifie en :

$1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{k-1}}=H_{k}$, avec $H_{k}$ le k-ième nombre harmonique.

En divisant la série précédente par k, on trouve la limite de la suite suivante :

$\sum _{i=0}^{\infty }{\frac {1}{i(i+k)}}={\frac {H_{k}}{k}}$

Dans le cas particulier où k=1, on trouve la série suivante. Celle-ci est la série de l’inverse des nombres oblongs. Pour rappel, un nombre oblong est la somme de deux nombres consécutifs et le énième nombre oblong est égal à n(n+1).

$\sum _{i=0}^{\infty }{\frac {1}{i(i+1)}}=H_{1}=1$

La formule précédente nous permet de calculer la série de l'inverse des nombres triangulaires. Car si la suite et la série des nombres triangulaires divergent, ce n'est pas le cas de leur inverse. Pour le montrer, il suffit de se rappeler que le énième nombre triangulaire est égal à la moitié du énième nombre oblong : $\sum _{i=0}^{n}i={\frac {n(n+1)}{2}}$. En prenant l'inverse, on trouve alors :

$\sum _{i=0}^{\infty }\left(\sum _{n=0}^{i}{\frac {1}{n}}\right)=\sum _{i=0}^{\infty }{\frac {2}{i(i+1)}}=2\cdot \sum _{i=0}^{\infty }{\frac {1}{i(i+1)}}=2$

Les séries géométriques

Les séries géométriques sont simplement des séries qui additionnent tous les termes d'une suite géométrique. Toutes ne convergent pas, la plupart divergeant franchement ! Par exemple, la suite géométrique de raison 10 et de premier terme 1 va naturellement diverger, vu que ses termes n'ont de cesse d'augmenter avec le rang. Dans les grandes lignes, il n'y a qu'un seul moyen pour que les termes tendent vers zéro avec le rang : la raison doit être comprise entre -1 et 1. Si c'est le cas, chaque terme sera plus petit (en valeur absolue) que le précédent : les termes diminuant de plus en plus, ils tendent bien vers zéro. Il se trouve que dans ce cas, la série va alors converger. Par contre, une raison de valeur absolue supérieure ou égale à 1 fait diverger la série. Si la raison est égale à 1, la suite est une suite constante, qui va naturellement diverger. Une raison supérieure à 1 va faire que les terme augmentent avec le rang, rendant la série divergente.

Dans la suite du chapitre, nous allons voir le cas général, avant de voir des cas particuliers qui méritent d'être étudiés pour eux même.

Le cas général

Pour démontrer le cas général, partons de la formule de la somme partielle d'une suite géométrique, qui est la suivante :

$\sum _{k=0}^{n}u_{k}=\sum _{k=0}^{n}u_{0}\cdot r^{k}=u_{0}{\frac {1-r^{n}}{1-r}}$

On peut réorganiser les termes comme suit :

$\sum _{k=0}^{n}u_{0}\cdot r^{k}={\frac {u_{0}}{1-r}}\times \left(1-r^{n}\right)$

Faisons tendre n vers l'infini :

$\sum _{k=0}^{\infty }u_{0}\cdot r^{k}=\lim _{n\rightarrow \infty }{\frac {u_{0}}{1-r}}\times \left(1-r^{n}\right)$

le terme ${\frac {u_{0}}{1-r}}$ étant constant et indépendant de n, on peut le sortir de la limite :

$\sum _{k=0}^{\infty }u_{0}\cdot r^{k}={\frac {u_{0}}{1-r}}\times \lim _{n\rightarrow \infty }\left(1-r^{n}\right)$

Si $r>1$, la limite diverge. Mais si $0\leq r<1$, le terme $r^{n}$ tend vers 0, ce qui donne :

$\sum _{k=0}^{\infty }u_{0}\cdot r^{k}={\frac {u_{0}}{1-r}}$

La suite des puissances des entiers

Comme premier exemple de série géométrique, nous allons prendre le cas de la suite des puissances d'un nombre (compris entre 0 et 1), à savoir la suite suivante :

$1,r,r^{2},r^{3},r^{4},\cdots$

Cette suite n'est autre que la suite définie par la relation de récurrence suivante :

$u_{0}=1$

$u_{n}=r^{n}=u_{n-1}\times r$

On voit qu'il s'agit d'un cas particulier de suite géométrique, où le premier terme est égal à 1.

La série qui correspond a donc pour résultat :

${\frac {1}{1-r}}$

La suite de l'inverse des puissances des entiers

Comme second exemple de série géométrique, nous allons prendre le cas de l'inverse des puissances d'un nombre entier. Par exemple, nous allons étudier la suite de l'inverse des puissances de deux, l'inverse des puissances de trois, etc. Formellement, nous allons étudier les suites définies par :

$u_{0}=1$ ou $u_{0}={\frac {1}{x}}$

$u_{n}={\frac {1}{x^{n}}}=u_{n-1}\times {\frac {1}{x}}$

La suite de l'inverse des puissances de deux

Illustration de la somme de l'inverse des puissance de deux.

Pour commencer, nous allons prendre l'exemple de la suite de l'inverse des puissances de deux définie par :

$u_{0}=1$

$u_{n}={\frac {1}{2^{n}}}=u_{n-1}\times {\frac {1}{2}}$

La série associée est la suivante :

$1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+{\frac {1}{32}}+...$

Si on applique la formule du dessus, on trouve :

$S={\frac {1}{1-1/2}}=2$

Cette série donne donc un résultat fini quand on fait la somme de tous ses termes : le résultat vaut 2 !

---

On peut aussi étudier la suite précédente, en remplacant le premier terme par 1/2 et en gardant la même relation de récurrence. On obtient alors la suite définie ainsi :

$u_{0}={\frac {1}{2}}$

$u_{n}={\frac {1}{2^{n+1}}}=u_{n-1}\times {\frac {1}{2}}$

La formule nous dit que le résultat de la série est tout simplement 1 !

$S={\frac {1}{2}}{\frac {1}{1-1/2}}=1$

Illustration de la somme de l'inverse des puissance de deux.

On peut aussi déduire cette limite d'une autre manière. On a vu dans le chapitre sur les sommes partielles que :

$\sum _{i=1}^{n}{\frac {1}{2^{i}}}={\frac {2^{n}-1}{2^{n}}}=1-{\frac {1}{2^{n}}}$

En prenant la limite vers l'infini, on retrouve bien le résultat précédent.

Mine de rien, cette série est contre-intuitive : l'intuition nous dit que cette suite devrait diverger, pas converger. Historiquement, le premier a avoir été trahit ainsi par son intuition a été le philosophe Zénon, auteur des célèbres paradoxes de Zénon, censés démontrer que le mouvement est une impossibilité (des trucs de philosophes ! ). Le paradoxe le plus connu est le suivant. Imaginons que me tient à une certaine distance d'un arbre. Pour l'atteindre, je dois parcourir la moitié de la distance qui me sépare de celui-ci. Puis, je dois parcourir la moitié du chemin restant. Puis je dois encore parcourir encore une nouvelle moitié, et ainsi de suite à l'infini. Il est impossible que j'atteigne l'arbre, vu que je devrais traverser une infinité de distances, chacune étant une des moitié mentionnée plus haut. On voit que ce paradoxe est résolu par le calcul vu plus haut : la somme des moitiés converge !

Paradoxe de la dichotomie de Zénon.

La suite de l'inverse des puissances de quatre

On peut maintenant passer au dernier exemple, à savoir la suite de l'inverse des puissances de quatre, définie par :

$u_{0}=1$

$u_{n}={\frac {1}{4^{n}}}=u_{n-1}\times {\frac {1}{4}}$

Cette suite est la suivante :

$1,{\frac {1}{4}},{\frac {1}{16}},{\frac {1}{64}},{\frac {1}{256}},{\frac {1}{1024}},...$

Si on applique la formule du dessus, on trouve :

$S={\frac {1}{1-1/4}}=1+{\frac {1}{3}}$

---

Preuve visuelle de la série de l'inverse des puissances de quatre.

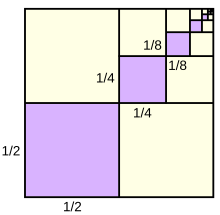
On peut aussi étudier la suite précédente, en remplaçant le premier terme par 1/4 et en gardant la même relation de récurrence. On obtient alors la suite définie ainsi :

$u_{0}={\frac {1}{4}}$

$u_{n}={\frac {1}{4^{n+1}}}=u_{n-1}\times {\frac {1}{4}}$

La formule nous dit que le résultat de la série est tout simplement 1/3 !

$S={\frac {1}{4}}{\frac {1}{1-1/4}}={\frac {1}{3}}$

Il existe une belle preuve visuelle de ce résultat, illustré dans le schéma à votre droite, qui illustre le calcul ${\frac {1}{4}}+{\frac {1}{16}}+{\frac {1}{64}}+{\frac {1}{256}}+{\frac {1}{1024}}+...$.

Le cas général

Preuve visuelle du résultat de la série de l'inverse des puissances de quatre.

Exemples de série géométriques convergentes.

On peut étudier les cas de l'inverse des puissances de trois, de cinq, de six, et de bien d'autres. Voici ce que l'on obtient pour les premiers entiers naturels :

$\sum _{n=1}^{\infty }{\frac {1}{2^{n}}}=1$	$\sum _{n=1}^{\infty }{\frac {1}{3^{n}}}={\frac {1}{2}}$	$\sum _{n=1}^{\infty }{\frac {1}{4^{n}}}={\frac {1}{3}}$	$\sum _{n=1}^{\infty }{\frac {1}{5^{n}}}={\frac {1}{4}}$
$\sum _{n=1}^{\infty }{\frac {1}{6^{n}}}={\frac {1}{5}}$	$\sum _{n=1}^{\infty }{\frac {1}{7^{n}}}={\frac {1}{6}}$	$\sum _{n=1}^{\infty }{\frac {1}{8^{n}}}={\frac {1}{7}}$	$\sum _{n=1}^{\infty }{\frac {1}{9^{n}}}={\frac {1}{8}}$

Il y a là un motif assez évident et l'on peut généraliser la formule suivante :

$\sum _{n=1}^{\infty }{\frac {1}{x^{n}}}={\frac {1}{x-1}}$

Les décimaux périodiques

Tous les nombres fractionnaires ont un développement décimal périodique. C'est à dire que si on regarde leurs décimales, on remarque que celles-ci finissent par faire un cycle au bout d'un certain temps. Un même cycle de décimale se répète à l'infini à partir d'un certain rang.

Exemples :

• ${\frac {1}{2}}=0.500000...$
• ${\frac {1}{3}}=0.333333...$
• ${\frac {1}{4}}=0.250000...$
• ${\frac {2}{7}}=0.285714285714...$
• ...

On ne considère que les séries de décimales répétées non nulles. On peut noter ces nombres en surlignant le groupe de décimales qui se répètent. Par exemple, $0.1271717171...=0.12{\overline {71}}$. Le cas le plus simple est certainement la fraction ${\frac {1}{3}}=0.33333333{\overline {3}}$. En voici d'autres exemples :

${\begin{array}{l}1/9=0{,}111111\ldots \\1/3=0{,}333333\ldots \\13/6=2{,}166666\ldots \\1/37=0{,}027027\ldots \\26/37=0{,}702702\ldots \\2/37=0{,}054054\ldots \end{array}}$

Ces nombres peuvent s'étudier assez simplement avec le formalisme des séries. En effet, ces nombres décimaux périodiques peuvent être vus comme le résultat d'une série géométrique et l'on peut déterminer leur fraction à partir de leur développement décimal à partir de la formule d'une série géométrique.

Le développement décimal de l'unité

0.999... = 1, illustration.

Le cas le plus étonnant est clairement le cas du nombre $0.999999999999{\overline {9}}$. Celui-ci est tout simplement la somme des termes de la suite suivante :

$0.9,0.09,0.009,0.0009,0.00009,...$

Cette suite est définie comme suit :

$u_{n}={\frac {9}{10^{n+1}}}$, ou de manière équivalente : ${\begin{cases}u_{0}={\frac {9}{10}}\\u_{n}=u_{n-1}\times {\frac {1}{10}}\end{cases}}$

Si l'on souhaite calculer la série qui correspond, on doit retrouver le résultat initial :

$S=0.99999999999...$

Cependant, il est intéressant de regarder le résultat obtenu avec la formule des séries géométriques :

$S={\frac {9}{10}}{\frac {1}{1-1/10}}=1$

Les deux résultats doivent être égaux, ce qui donne :

$1=0.99999999999...$

Ce résultat fortement contre-intuitif est cependant vérifiable par une petite démonstration assez simple.

Démonstration

Partons du nombre : $S=0.99999999999...$ Multiplions-le par l'inverse de la raison de la suite, à savoir 10. $10S=9.99999999999...$ Soustrayons maintenant le nombre S initial : $10S-S=9.99999999999...-0.99999999999...$ $9S=9$ Donc, on a : $S=0.99999999999...=1$ CQFD!

Une série de zéros peut se remplacer par une série de 9 en retranchant 1 au chiffre précédent :

${\frac {1}{2}}=0.500000...=0.49999...$

Car en utilisant le résultat $0.999...=1$ ci-dessus :

${\frac {1}{2}}={\frac {5}{10}}={\frac {4}{10}}+{\frac {1}{10}}$

${\frac {1}{2}}={\frac {4}{10}}+{\frac {0.99999999...}{10}}$

${\frac {1}{2}}=0.4+0.099999999...$

Le développement des décimaux à chiffres périodiques

Après avoir vu le cas du développement de l'unité, on peut passer à des décimaux périodiques de la forme : $0.11111111{\overline {1}}$ ou $0.55555555{\overline {5}}$. Par exemple, le nombre $0.77777777777{\overline {7}}$ est la somme totale de la série géométrique suivante : $0.7,0.07,0.007,0.0007,$. On voit que cet exemple est une suite géométrique de raison l/10 et de premier terme 7/10. La formule d'une série géométrique nous dit que cette série vaut :

$S={\frac {7}{10}}{\frac {1}{1-1/10}}={\frac {7}{9}}$

Si on applique le même raisonnement aux nombres dont un seul chiffre est répété infiniment, on trouve :

${\frac {1}{9}}$	${\frac {2}{9}}$	${\frac {3}{9}}$	${\frac {4}{9}}$	${\frac {5}{9}}$	${\frac {6}{9}}$	${\frac {7}{9}}$	${\frac {8}{9}}$	${\frac {9}{9}}$
$0.11111111{\overline {1}}$	$0.22222222{\overline {2}}$	$0.33333333{\overline {3}}$	$0.44444444{\overline {4}}$	$0.55555555{\overline {5}}$	$0.66666666{\overline {6}}$	$0.77777777{\overline {7}}$	$0.88888888{\overline {8}}$	$0.99999999{\overline {9}}=1$

On voit clairement qu'il y a un certain motif qui se dégage, un motif suffisamment évident pour ne pas le détailler plus.

Les séries de Riemann

Dans ce chapitre, nous allons voir les séries de Riemann et leurs liens avec les nombres premiers. Ces séries peuvent sembler assez peu intéressantes, mais il n'en est rien. Par exemple, les séries de Riemann sont impliquées dans diverses conjectures encore non-résolues sur les nombres premiers. Précisément, de telles suites ont un lien très fort avec la répartition des nombres premiers quand la raison est un nombre complexe. Nous aurons l'occasion de reparler de la fameuse fonction zéta de Riemann, qui n'est autre qu'une série associée à une suite de Riemann. Quelques suites de Riemann particulières donnent aussi des résultats assez intéressants quand on prend leur série (nous verrons cela dans quelques chapitres). Bref, laissons tout cela à plus tard. Nous étudierons ces suites dans les chapitres sur les sommes partielles et les séries.

La série harmonique et ses dérivées

Nous allons commencer par voir la série harmonique et ses dérivées. Nous allons voir la série harmonique, puis les séries harmoniques généralisées. Dans cette section, nous ne parlerons pas des séries harmoniques alternées. La raison est qu'un futur chapitre est complètement dédié à l'analyse des séries alternées, et que nous avons décider de parler des séries harmoniques alternées dans ce dernier. Mais il y a une autre raison : vu que la série harmonique et ses dérivées divergent, leurs versions alternées convergent conditionnellement. On peut donc les faire diverger ou converger vers n'importe quelle valeur avec les manipulations adaptées.

La série harmonique

Premiers membres de la suite harmonique.

La série de Riemann la plus connue est incontestablement la série harmonique. Pour rappel, la suite harmonique est la suite de l'inverse des entiers naturels :

$S_{h}=\sum _{n=0}^{\infty }{\frac {1}{n^{1}}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+...$

Cette série a une limite qui tend vers zéro avec le rang, ce qui fait qu'on pourrait croire qu'elle converge. Mais rappelez-vous : si les suites convergentes ont une limite qui tend vers zéro, la réciproque n'est pas vraie. Et la série harmonique est justement un contre-exemple parfait : elle diverge alors que sa limite est nulle !

$\sum _{n=0}^{\infty }{\frac {1}{n^{1}}}=\infty$

Démonstration

Pour démontrer que la série harmonique diverge, nous allons la comparer avec une suite qui diverge elle aussi. Dans les grandes lignes, nous allons prendre une suite dont chaque terme est inférieur au terme de même rang dans la suite harmonique. Si on additionne tous les termes de la suite harmonique, on sait que la somme des termes de l'autre suite sera donc inférieure : tous les termes de l'autre suite sont plus petits, donc leur somme doit aussi l'être. Si cette suite, plus petite, diverge, alors la série harmonique doit aussi diverger. Il s'agit d'une méthode de démonstration de divergence assez stéréotypée et assez utile. Il faut préciser qu'il existe une variante pour démontrer qu'une suite converge : on doit trouver une série convergente dont tous les termes sont plus grands que la suite étudiée. Or, voici une suite dont tous les termes sont plus petits que ceux de la suite harmonique (à rang égal), mais qui diverge : $S=1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+...$ Pour vérifier qu'elle diverge, regroupons les termes par paquets de deux, puis quatre, puis huit, etc. $S=1+\left({\frac {1}{2}}+{\frac {1}{2}}\right)+\left({\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{4}}\right)+\left({\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right)+...$ $S=1+1+1+1+1+...$ Cette série est équivalente à une série constante, quand on additionne tous ses termes : elle diverge ! Donc la série harmonique, dont tout les termes sont plus grands que la série précédente, diverge aussi. CQFD !

Les séries harmoniques généralisées

Les séries harmoniques généralisées sont des séries de la forme :

$S_{h}=\sum _{n=0}^{\infty }{\frac {1}{a\cdot n+b}}$

Par exemple, on pourrait citer la série de l'inverse des entiers impairs.

Toutes divergent, sans exceptions. Le démontrer demande d'étudier deux cas : celui où $a\geq b$ et celui où $a<b$.

Démonstration

Supposons que : $a\geq b$ Ajoutons $a\cdot n$ à l'inégalité précédente : $a\cdot n+a\geq a\cdot n+b$ Si on prend l'inverse, l'inégalité s'inverse : ${\frac {1}{a\cdot n+a}}\leq {\frac {1}{a\cdot n+b}}$ On utilise la formule ${\frac {1}{a\cdot n+a}}={\frac {1}{a}}{\frac {1}{n+1}}$ : ${\frac {1}{a}}{\frac {1}{n+1}}\leq {\frac {1}{a\cdot n+b}}$ Prenons la série : $\sum _{n=0}^{\infty }{\frac {1}{a}}{\frac {1}{n+1}}\leq \sum _{n=0}^{\infty }{\frac {1}{a\cdot n+b}}$ On factorise $1 \over a$ ${\frac {1}{a}}\sum _{n=0}^{\infty }{\frac {1}{n+1}}\leq \sum _{n=0}^{\infty }{\frac {1}{a\cdot n+b}}$ On sait que la série $\sum _{n=0}^{\infty }{\frac {1}{n+1}}$ diverge, ce qui fait que le terme de gauche diverge. La série harmonique généralisée étant encore supérieure, elle diverge elle aussi.

Démonstration

Supposons que : $a<b$ Ajoutons $b\cdot n$ à l'inégalité précédente : $b\cdot n+a<b\cdot n+b$ Si on prend l'inverse, l'inégalité s'inverse : ${\frac {1}{b\cdot n+a}}>{\frac {1}{b\cdot n+b}}$ On utilise la formule ${\frac {1}{b\cdot n+b}}={\frac {1}{b}}{\frac {1}{n+1}}$ : ${\frac {1}{b\cdot n+a}}>{\frac {1}{b}}{\frac {1}{n+1}}$ Prenons la série : $\sum _{n=0}^{\infty }{\frac {1}{b\cdot n+a}}>\sum _{n=0}^{\infty }{\frac {1}{b}}{\frac {1}{n+1}}$ On factorise $1 \over b$ $\sum _{n=0}^{\infty }{\frac {1}{b\cdot n+a}}>{\frac {1}{b}}\sum _{n=0}^{\infty }{\frac {1}{n+1}}$ On sait que la série $\sum _{n=0}^{\infty }{\frac {1}{n+1}}$ diverge, ce qui fait que le terme de gauche diverge. La série harmonique généralisée étant encore supérieure, elle diverge elle aussi.

Les séries de Riemann (non-harmonique)

Les séries de Riemann ne sont autre que les séries des suites de Riemann. Pour rappel, ces dernières sont des suites de la forme :

$u_{n}={\frac {1}{n^{r}}}$

Le coefficient r est appelé la raison de la suite, par analogie avec les suites géométriques. Elle peut être un nombre réel ou complexe et elle est souvent notée r pour un nombre réel et s pour un nombre complexe.

Les séries de Riemann sont notées $\zeta (r)$ et sont de la forme suivante :

$\zeta (r)=\sum _{n=0}^{\infty }{\frac {1}{n^{r}}}$

La série harmonique est un cas particulier de série de Riemann pour laquelle r = 1.

Plus la raison est grande, plus la limite obtenue est petite, ce qui fait que la fonction $\zeta (r)$ est décroissante, comme indiquée ci-dessous. Les théorèmes que nous verrons dans le prochain chapitre nous disent que cette série converge ou diverge selon la valeur de sa raison : une raison inférieure ou égale à 1 fait diverger la série, alors qu'une raison supérieure à 1 la fait converger. On peut aussi prouver que :

$\lim _{r\rightarrow \infty }\zeta (r)=1$

Fonction zéta de Riemann.

La série de l'inverse des carrés

Une autre série intéressante est la série de l’inverse des carrés.

$\zeta (2)=\sum _{n=0}^{\infty }{\frac {1}{n^{2}}}=1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+...$

Un des mathématiciens les plus connu du 18ème siècle, Euler, a démontré que cette série valait :

$\zeta (2)=\sum _{n=0}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}$

La série de l'inverse des cubes

Une autre série intéressante, bien qu'un peu moins que la précédente est la série de l’inverse des cubes.

$\zeta (3)=\sum _{n=0}^{\infty }{\frac {1}{n^{3}}}=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+{\frac {1}{5^{3}}}+...$

Le résultat de cette série est une constante, appelée constante d'Apéry. On sait qu'il s'agit d'un nombre irrationnel, ce résultat ayant été démontré par Apéry lui-même, mais on ne sait pas encore s'il est transcendant ou non.

$\zeta (3)=\sum _{k=1}^{\infty }{\frac {1}{k^{3}}}\approx 1{,}202\,056\,903.$

Les séries de Riemann à exposants pairs

Prenons les séries de Riemann dont l'exposant est un nombre pair. En clair, les suites de la forme : $\zeta (2n)=\sum _{i=0}^{\infty }{\frac {1}{n^{2k}}}$.

Il se trouve que toutes ces séries ont un résultat de la forme suivante avec $a$ un nombre rationnel (fractionnaire) :

$\zeta (2n)\propto \pi ^{2k}$

Par exemple, on a :

$\sum _{n=1}^{+\infty }{1 \over n^{2}}={\frac {\pi ^{2}}{6}}$

$\sum _{n=1}^{+\infty }{1 \over n^{4}}={\frac {\pi ^{4}}{90}}$

$\sum _{n=1}^{+\infty }{1 \over n^{6}}={\frac {\pi ^{6}}{945}}$

$\sum _{n=1}^{+\infty }{1 \over n^{8}}={\frac {\pi ^{8}}{9450}}$

Une formule plus détaillée est la suivante :

$\zeta (2n)=(-1)^{k+1}\times {\frac {(2\pi )^{2k}}{2\cdot (2k)!}}\times B_{2k}$, avec $B_{n}$ le énième nombre de Bernouilli (nous avions déjà introduit les nombres de Bernouilli dans le chapitre sur les sommes de puissance).

Croissance des nombres de Bernoulli.

Cette expression nous permet de trouver une approximation du énième nombre de Bernoulli, pour un n assez grand. En effet, prenons la limite de l'équation précédente quand 2n tend vers l'infini :

$\lim _{r\rightarrow \infty }\zeta (2n)=\lim _{r\rightarrow \infty }\left[(-1)^{k+1}\times {\frac {(2\pi )^{2k}}{2\cdot (2k)!}}\times B_{2k}\right]$

Oublions le terme : $(-1)^{k+1}$ pour simplifier les calculs :

$\lim _{r\rightarrow \infty }\zeta (2n)=\lim _{r\rightarrow \infty }\left[{\frac {(2\pi )^{2k}}{2\cdot (2k)!}}\times B_{2k}\right]$

Or, on sait que $\lim _{r\rightarrow \infty }\zeta (r)=1$. En faisant le remplacement, on trouve :

$1=\lim _{r\rightarrow \infty }\left[{\frac {(2\pi )^{2k}}{2\cdot (2k)!}}\times B_{2k}\right]$

On réorganise les termes :

$\lim _{r\rightarrow \infty }B_{2k}=\lim _{r\rightarrow \infty }{\frac {2\cdot (2k)!}{(2\pi )^{2k}}}$

Si n est assez grand, on peut remplacer la limite par une approximation.

$B_{2k}\approx {\frac {2\cdot (2k)!}{(2\pi )^{2k}}}$

Les séries liées aux nombres premiers

Certaines séries sont fabriquées à partir de nombres premiers, comme la suite de l'inverse des nombres premiers. Celles-ci sont très utiles pour étudier les nombres premiers, sans compter que la plupart ont des propriétés assez intéressantes.

La série de l'inverse des nombres premiers

Comparaison entre la somme de l'inverse des nombres premiers et une autre fonction divergente.

La série de l'inverse des nombres premiers est de loin la plus simple à étudier. Cette série n'est autre qu'une variante de la suite harmonique, dans laquelle on n'aurait conservé que les termes au dénominateur premier. Et il se trouve que cette série diverge !

$\sum _{p{\text{ prime}}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+\cdots =\infty$

Un bon moyen de le prouver est de comparer cette série à une autre série, dont tous les termes sont inférieurs à la série des nombres premiers, qui est de plus connue pour diverger. Cette seconde série est la suivante :

$\sum \ln \ln(n+1)-\ln {\frac {\pi ^{2}}{6}}$

On sait que chaque terme de la suite de l'inverse des nombres premiers est supérieur au terme de même rang de l'autre suite :

$\sum _{\scriptstyle p{\text{ prime}} \atop \scriptstyle p\leq n}{\frac {1}{p}}\geq \ln \ln(n+1)-\ln {\frac {\pi ^{2}}{6}}$

Vu que la seconde suite a une série qui diverge, celle des nombres premiers aussi.

La constante de Meissel–Mertens

Constante de Meissel–Mertens.

Il est intéressant de comparer la somme partielle de l'inverse des premiers à d'autres fonctions/suites. Le fait que la suite de l'inverse des entiers soit une sorte de variante de la suite harmonique nous est utile pour choisir à quelle suite la comparer. On a vu plus haut que la différence entre la série harmonique et la série de la suite $u_{n}=\ln(\ln n)$ est une constante, appelée constante d'Euler-Mascheroni. Et bien on peut comparer la suite de l'inverse des premiers avec la suite $u_{n}=\ln(\ln n)$, mais dont on n'aurait conservé que les termes premiers. Et le résultat est plus ou moins le même avec seulement les premiers qu'avec tous les entiers : la différence converge vers une constante. Mais dans le cas avec seulement les termes premiers, la constante est différente de la constante d'Euler-Mascheroni. Pour résumer, la série de l'inverse des premiers et la série du double logarithme ne différent que d'une constante, appelée constante de Meissel–Mertens. Cette constante a pour définition la formule suivante, avec $\gamma$ la constante d'Euler-Mascheroni :

$M=\lim _{n\rightarrow \infty }\left(\sum _{p\leq n}{\frac {1}{p}}-\ln(\ln n)\right)=\gamma +\sum _{p}\left[\ln \!\left(1-{\frac {1}{p}}\right)+{\frac {1}{p}}\right]$

Sa valeur approchée est la suivante :

$M\approx 0.26149/72128/47642/78375/54268/38608/69585/90516/\cdots$

La série de l'inverse des nombres premiers jumeaux

Illustration de la convergence de la série des nombres premiers jumeaux.

Si la série des nombres premiers diverge, ce n'est pas le cas pour la série des nombres premiers jumeaux. Pour rappel, les nombres premiers jumeaux sont des nombres premiers tels que leur différence est égale à 2 (en clair, ce sont des couples de la forme $(p,p+2)$). Cette série se construit en prenant deux nombres premiers jumeaux et en additionnant leurs inverses. Cette série converge vers une constante appelée la constante de Brun.

$\sum \limits _{p,\,p+2\in \mathbb {P} }{\left({{\frac {1}{p}}+{\frac {1}{p+2}}}\right)}=\left({{\frac {1}{3}}+{\frac {1}{5}}}\right)+\left({{\frac {1}{5}}+{\frac {1}{7}}}\right)+\left({{\frac {1}{11}}+{\frac {1}{13}}}\right)+\cdots$

Les séries alternées

Une suite est dite alternée si des termes consécutifs n'ont pas le même signe. Dit autrement, le signe change quand on passe d'un terme au suivant. La moitié des termes de la suite sont positifs, les autres étant négatifs. Les suites alternées sont donc des suites de la forme :

$u_{n}=(-1)^{n}|u_{n}|$ ou $u_{n}=(-1)^{n+1}|u_{n}|$

Les séries alternées sont des séries obtenues en additionnant les termes d'une suite alternée. Ce sont des séries de la forme :

$\sum _{n=0}^{\infty }(-1)^{n}|u_{n}|$ ou $\sum _{n=0}^{\infty }(-1)^{n+1}|u_{n}|$

Une particularité de ces suites est qu'elles ont des termes négatifs (ce ne sont pas les seules, évidemment), ce qui fait que leur convergence absolue n'est pas garantie. Rappelez-vous la différence entre convergence absolue et conditionnelle : la suite converge toujours dans le premier cas, seulement si on additionne les termes dans le bon ordre dans le second. Les suites à convergence conditionnelle peuvent diverger ou converger vers une limite arbitraire, suivant comment on additionne les termes. Et nous avons vu une condition pour qu'une suite converge absolument : la suite composée des valeurs absolues de chaque terme doit converger. Si ce n'est pas le cas, la convergence de la suite est conditionnelle. Là où une suite de termes positifs converge absolument ou diverge, une suite avec des termes négatifs peut avoir une convergence conditionnelle. Les suites alternées sont dans ce cas, ce qui rend l'étude de leur convergence plus compliquée que pour les suites vues dans les chapitres précédents.

Les critères de convergence pour les suites alternées

Il est parfaitement possible d'appliquer les critères de convergence généraux sur les suites alternées. Mais certains critères de convergence sont spécifiques à de telles suites et ne peuvent pas s'appliquer aux suites non-alternées. Et dans de nombreux cas, ces critères spécifiques sont plus faciles à manier que les critères généraux. Voyons rapidement quels sont ces critères spécifiques aux suites alternées.

La règle de Leibniz

Le premier critère porte le nom de règle de Leibniz. Il nous dit que pour une suite alternée qui tend vers zéro et dont la valeur absolue des termes forme une suite décroissante, la série alternée associée converge. Dit autrement, on doit avoir $|u_{n+1}|<|u_{n}|$, ainsi que $\lim _{n\rightarrow 0}u_{n}\rightarrow 0$.

Le reste d'une suite alternée

Sous ces hypothèses, on peut aussi prouver quelques propriétés liées à la quantité $R_{n}=\sum _{i=n+1}^{\infty }u_{i}=\sum _{i=0}^{\infty }u_{i}-\sum _{i=0}^{n}u_{i}$. Celle-ci n'est autre que la différence entre la série et une somme partielle de la suite et est appelée le reste. On peut alors prouver que :

• Le reste a le même signe que son premier terme $u_{n+1}$.
• Sa valeur absolue est majorée par ce même premier terme : $R_{n}<u_{n+1}$.

Les séries harmoniques alternées

Après avoir vu les critères de convergence usuel, pour les suites alternées, nous allons analyser quelques suites alternées assez simples. Dans cette section, nous allons voir les différentes suites harmoniques alternées.

La série harmonique alternée

Prenons un exemple très simple de suite qui peut s'analyser avec respecte la règle de Liebniz : la série harmonique alternée. Pour rappel, la suite harmonique alternée est définie par :

$u_{n}={\frac {(-1)^{n}}{n}}=1,-{\frac {1}{2}},{\frac {1}{3}},-{\frac {1}{4}},{\frac {1}{5}},-{\frac {1}{6}},...$

Rappelons que la série harmonique ne converge pas. En conséquence, on sait que si la suite harmonique alternée converge, sa convergence ne peut être que conditionnelle et non absolue. Il n’empêche que l'on peut quand même lui appliquer le critère de Liebniz. Déjà, si on prend les valeurs absolues, la suite devient la suite harmonique qu'on sait décroissante. La première condition, à savoir $|u_{n+1}|<|u_{n}|$ pour tout rang n, est donc remplie. Ensuite, la suite tend bien vers zéro, comme la suite harmonique (le changement de signes à chaque terme n'y change pas grand-chose). La série harmonique converge donc, même si sa convergence est conditionnelle.

La série de Leibniz

La série de Leibniz est assez similaire à la série harmonique alternée, une variante de la série harmonique où des termes consécutifs sont de signes opposés. La différence est que les inverses des entiers sont remplacés par les inverses des entiers impairs. Comme pour la série harmonique alternée, les signes des termes s'inversent d'un terme à l'autre. Cette série vaut :

$\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+...={\frac {\pi }{4}}$

Démonstration

Pour le démontrer, nous allons partir de la fonction sinus. Rien d'étonnant à cela, ${\frac {\pi }{4}}$ étant une valeur beaucoup utilisée en trigonométrie, notamment avec la fonction sinus. On verra dans quelques chapitres que la fonction sinus peut s'écrire comme un polynôme infini (le terme exact est "série entière", mais nous y reviendrons plus tard). Pour le moment, admettons que la fonction sinus s'écrive bien comme suit, avec un nombre infini de termes : $sin(x)=a_{0}+a_{1}\cdot x+a_{2}\cdot x^{2}+a_{3}\cdot x^{3}+a_{4}\cdot x^{4}+a_{5}\cdot x^{5}+...$ Quand un polynôme dispose de plusieurs zéros notés $z_{1}$, $z_{2}$, $z_{3}$, $z_{4}$, ... ; alors le polynôme s'écrit comme suit : $P(x)=a\cdot (x-z_{1})(x-z_{2})(x-z_{3})(x-z_{4})...$ Or, la fonction sinus s'annule pour tous les multiples de $\pi$, ce qui signifie que les multiples de $\pi$ sont les zéros de ce polynôme infini. On peut écrire le polynôme infini de sinus comme suit, en tenant compte des zéros négatifs, positifs et nuls : $\sin(x)=x(x-\pi )(x+\pi )(x-2\pi )(x+2\pi )(x-3\pi )(x+3\pi )(x-4\pi )(x+4\pi )...$ Factorisons x : $\sin(x)=x\cdot \left[\left(1-{\frac {\pi }{x}}\right)\left(1+{\frac {\pi }{x}}\right)\left(1-{\frac {2\pi }{x}}\right)\left(1+{\frac {2\pi }{x}}\right)\left(1-{\frac {3\pi }{x}}\right)\left(1+{\frac {3\pi }{x}}\right)\left(1-{\frac {4\pi }{x}}\right)\left(1+{\frac {4\pi }{x}}\right)...\right]$ Prenons maintenant le logarithme de l'expression précédente : $\ln \sin(x)=\ln \left[x\cdot \left(1-{\frac {\pi }{x}}\right)\left(1+{\frac {\pi }{x}}\right)\left(1-{\frac {2\pi }{x}}\right)\left(1+{\frac {2\pi }{x}}\right)\left(1-{\frac {3\pi }{x}}\right)\left(1+{\frac {3\pi }{x}}\right)\left(1-{\frac {4\pi }{x}}\right)\left(1+{\frac {4\pi }{x}}\right)...\right]$ On applique la formule $\ln(a\cdot b)=\ln a+\ln b$, qui dit que le logarithme d'un produit est la somme des logarithmes : $\ln \sin(x)=\ln x+\ln \left(1-{\frac {\pi }{x}}\right)+\ln \left(1+{\frac {\pi }{x}}\right)+\ln \left(1-{\frac {2\pi }{x}}\right)+\ln \left(1+{\frac {2\pi }{x}}\right)+\ln \left(1-{\frac {3\pi }{x}}\right)+\ln \left(1+{\frac {3\pi }{x}}\right)+\ln \left(1-{\frac {4\pi }{x}}\right)+\ln \left(1+{\frac {4\pi }{x}}\right)+...$ Prenons maintenant la dérivée. On sait que $[\ln u]'={\frac {u'}{u}}$. En appliquant ce théorème sur le premier terme, on a $[\ln \sin(x)]'={\frac {(\sin x)'}{\sin x}}={\frac {\cos x}{\sin x}}$. On a alors : ${\frac {\cos x}{\sin x}}={\frac {1}{x}}-{\frac {1}{\pi -x}}+{\frac {1}{\pi +x}}-{\frac {1}{2\pi -x}}+{\frac {1}{2\pi +x}}-{\frac {1}{3\pi -x}}+{\frac {1}{3\pi +x}}-{\frac {1}{4\pi -x}}+{\frac {1}{4\pi +x}}...$ En prenant $x={\frac {\pi }{4}}$, on a : ${\frac {\cos {\frac {\pi }{4}}}{\sin {\frac {\pi }{4}}}}={\frac {1}{\frac {\pi }{4}}}-{\frac {1}{\pi -{\frac {\pi }{4}}}}+{\frac {1}{\pi +{\frac {\pi }{4}}}}-{\frac {1}{2\pi -{\frac {\pi }{4}}}}+{\frac {1}{2\pi +{\frac {\pi }{4}}}}-{\frac {1}{3\pi -{\frac {\pi }{4}}}}+{\frac {1}{3\pi +{\frac {\pi }{4}}}}-{\frac {1}{4\pi -{\frac {\pi }{4}}}}+{\frac {1}{4\pi +{\frac {\pi }{4}}}}...$ Simplifions : ${\frac {\cos {\frac {\pi }{4}}}{\sin {\frac {\pi }{4}}}}={\frac {1}{\frac {\pi }{4}}}-{\frac {1}{\frac {3\pi }{4}}}+{\frac {1}{\frac {5\pi }{4}}}-{\frac {1}{\frac {7\pi }{4}}}+{\frac {1}{\frac {9\pi }{4}}}-{\frac {1}{\frac {11\pi }{4}}}+{\frac {1}{\frac {13\pi }{4}}}-...$ Simplifions encore : ${\frac {\cos {\frac {\pi }{4}}}{\sin {\frac {\pi }{4}}}}={\frac {4}{\pi }}-{\frac {4}{3\pi }}+{\frac {4}{5\pi }}-{\frac {4}{7\pi }}+{\frac {4}{9\pi }}-{\frac {4}{11\pi }}+{\frac {4}{13\pi }}-...$ Factorisons ${\frac {4}{\pi }}$ : ${\frac {\cos {\frac {\pi }{4}}}{\sin {\frac {\pi }{4}}}}={\frac {4}{\pi }}\left[1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-...\right]$ Sachant que ${\frac {\cos {\frac {\pi }{4}}}{\sin {\frac {\pi }{4}}}}=1$, on a : $1={\frac {4}{\pi }}\left[1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-...\right]$ Multiplions maintenant par ${\frac {\pi }{4}}$ : ${\frac {\pi }{4}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-...$

Les séries entières

Dans le chapitre précédent, nous avons étudié les séries géométriques, à savoir des séries de la forme :

$\sum _{n}k\cdot x^{n}$

Ces séries ont cependant une particularité : le coefficient $k$ est le même pour tous les termes de la suite géométrique. Cependant, on peut imaginer des séries plus générales que les suites géométriques, où le coefficient $k$ changerait à chaque rang. Ces généralisations des séries géométriques sont appelées des séries de puissances, souvent mal nommées séries entières. On peut voir les séries entières comme un polynôme avec une infinité de termes, bien que la formulation ne soit pas très rigoureuse.

Dans leur forme la plus simple, les séries entières sont de la forme suivante :

$\sum _{n}a_{n}\cdot x^{n}=a_{0}+a_{1}\cdot x+a_{2}\cdot x^{2}+a_{3}\cdot x^{3}+a_{4}\cdot x^{4}+a_{5}\cdot x^{5}+...$

De telles séries sont centrées sur zéro. Cela signifie que pour $x=0$, les termes disparaissent à l'exception du tout premier, $a_{0}$.

Plus généralement, les séries entières sont les suivantes :

$\sum _{n}a_{n}\cdot (x-c)^{n}$

De telles séries entières sont centrées sur c. Là encore, cela veut dire que pour $x=c$, les termes disparaissent à l'exception du tout premier, $a_{0}$.

La différence entre série centrée sur zéro et série centrée sur c est utile pour simplifier certaines démonstrations. On peut en effet généraliser les résultats obtenus avec les séries centrées sur zéro, aux séries centrées sur c, par un simple changement de variable. Il suffit pour cela d'étudier la série $\sum _{n}a_{n}\cdot y^{n}$, naturellement centrée sur zéro, en posant $y=x-c$.

De nombreuses séries de ce genre sont utilisées, les plus connues étant de loin les séries de Taylor ou de Laurent, qui en sont les cas particuliers les plus connues.

La convergence des séries entières

Les séries entières peuvent converger ou diverger, selon la valeur de leur raison ou de leurs coefficients $a_{n}$. On est certain qu'il existe au moins une valeur pour laquelle la série converge toujours : le centre de la série. Une série centrée sur zéro converge forcément pour $x=0$, de même qu'une série centrée sur a converge pour $x=a$. Mais pour les autres valeurs de x, le comportement varie grandement suivant la série. Si l'on prend une série centrée sur a, on peut se retrouver dans trois cas distincts :

• soit la série converge pour tout x ;
• soit la série converge pour a et diverge pour toute autre valeur ;
• soit la série converge quand x appartient à un intervalle bien précis, appelé l'intervalle de convergence.

Le dernier cas est celui qui va nous intéresser. L'intervalle de convergence a plusieurs propriétés intéressantes. Déjà, on sait qu'il contient la valeur a, sur laquelle la série est centrée. Mais on peut ajouter que a est au milieu de l'intervalle, qui est symétrique par rapport à a. La distance entre a et les bornes de l'intervalle est appelé le rayon de convergence de la série, et sera notée R dans ce qui suit. Avec ce qu'on vient de dire, la série converge quand $|x-a|<R$ et diverge pour tout $|x-a|>R$. Pour $|x-a|=R$, la série peut diverger ou converger, tout dépend de la série étudiée.

L'application du critère l'Alembert

Le comportement décrit plus haut peut faire penser aux séries géométriques. Comme pour les séries entières, elles convergent forcément pour $x=0$, et leur convergence dans les autres cas dépend de la valeur de la raison. Suivant la valeur de la raison, elles peuvent converger ou non. Nous allons voir que les propriétés de convergence de ces séries entières sont assez similaires à celles des séries géométriques, à quelques détails près. Pour nous en rendre compte, nous allons étudier divers exemples.

Un premier exemple

Comme premier exemple, nous allons utiliser la suite définie par :

$\sum _{n}{\frac {x^{n}}{n}}$, à savoir une série entière où $a_{n}={\frac {1}{n}}$

On peut alors utiliser le test du quotient pour vérifier si cette suite converge ou non. Calculons :

$\lim _{n\to \infty }{\frac {u_{n+1}}{u_{n}}}=\lim _{n\to \infty }\left({\frac {x^{n+1}}{n+1}}/{\frac {x^{n}}{n}}\right)=\lim _{n\to \infty }{\frac {x^{n+1}}{n+1}}{\frac {n}{x^{n}}}=\lim _{n\to \infty }x{\frac {n}{n+1}}=\lim _{n\to \infty }x\left(1-{\frac {1}{n+1}}\right)=x$

On voit que la série converge si la limite, donc $x$, est inférieure à 1. Elle diverge si elle est supérieure à 1. Dans le cas où $x=1$, on retombe sur la série harmonique qui est divergente. Pour les valeurs négatives de $x$, les résultats sont identiques, si ce n'est que le cas où $x=-1$ donne la série harmonique alternée, qui diverge elle aussi.

Un second exemple

On peut aussi étudier la série suivante, assez semblable à la série précédente :

$\sum _{n}{\frac {x^{n}}{n!}}$

On a montré il y a quelques chapitres que la série converge quelle que soit la valeur donnée à $x$. La démonstration avait été réalisée avec la méthode du quotient, illustrée plus haut. Nous reproduisons ici cette démonstration, pour montrer la ressemblance avec la démonstration pour la série précédente.

Calculons le rapport : ${\frac {u_{n+1}}{u_{n}}}$ :

${\frac {u_{n+1}}{u_{n}}}={\frac {x^{(n+1)}}{(n+1)!}}{\frac {n!}{x^{n}}}={\frac {x^{(n+1)}}{x^{n}}}{\frac {n!}{(n+1)!}}={\frac {x}{n+1}}$

Or, $x$ est une constante, ce qui fait que ce rapport tend vers 0.

$\lim _{n\to \infty }{\frac {u_{n+1}}{u_{n}}}=\lim _{n\to \infty }{\frac {x}{n+1}}=0$

En conséquence, la série converge !

Dans le cas où $x=1$, la série se simplifie en la série de l'inverse des factorielles, qui vaut :

$\sum _{n}{\frac {1^{n}}{n!}}=1+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+{\frac {1}{5!}}+\cdots =e$

Le cas général

Comme vous l'avez peut-être remarqué, l'application de la règle d'Alembert donne des démonstrations extrêmement similaires pour toutes les séries entières. En effet, prenons le cas général, à savoir :

$\lim _{n\to \infty }{\frac {u_{n+1}}{u_{n}}}=\lim _{n\to \infty }{\frac {a_{n+1}x^{n+1}}{a_{n}x^{n}}}=\lim _{n\to \infty }{\frac {a_{n+1}}{a_{n}}}{\frac {x^{n+1}}{x^{n}}}=x\left(\lim _{n\to \infty }{\frac {a_{n+1}}{a_{n}}}\right)=xL$

Le critère d'Alembert dit que la série converge toujours pour :

$|x|\cdot L<1$

On vient d'établir que la série converge si :

$|x|<{\frac {1}{L}}$

La convergence de la série entière dépend donc de la convergence de la suite $a_{n}$, même si celle-ci ne converge pas. On a bien le cas de la série : $\sum _{n}{\frac {x^{n}}{n}}$ où la suite des $a_{n}$ ne converge pas. Un autre paramètre important pour la convergence est la valeur de la raison $x$.

Le rayon de convergence

La valeur $1 \over L$ est appelée le rayon de convergence et est définie comme la valeur maximale de la raison qui permette à la série de converger. Plus précisément, le rayon de convergence $R$ est définie comme la valeur telle que :

• Si $0\leq |r|\leq R$, la série converge.
• Si $|r|>R$, la série diverge.
• Si $|r|=R$, la série peut diverger ou converger selon la série.

Le rayon de convergence peut être nul, non-nul ou infini et ces trois cas donnent des résultats différents en termes de convergence. Les cas où $L=0$ et $L=\infty$ donnent une forme indéterminée, dont on peut trouver facilement la solution. Mais hormis ces cas pathologiques, il existe toujours une valeur de la raison qui permette de faire converger la série. Pour résumer :

• Si $R$ est non-nul et pas infini, les valeurs comprises dans l'intervalle $\left]-{\frac {1}{L}},{\frac {1}{L}}\right[$ font converger la série.
• Si $R=+\infty \equiv L=0$, alors la série converge pour toute valeur de la raison.
• Si $R=0$, la série converge uniquement pour $r=0$.

Ce qui nous amène au point suivant, nommé lemme d'Abel par les mathématiciens :

Prenons une valeur $r$ telle que la série entière $\sum _{n}a_{n}r^{n}$ converge (en fait, il suffit qu'elle soit bornée, mais laissons ce détail de côté). Alors, pour toute raison comprise dans l'intervalle $[0,r]$, la série sera convergente.

Démonstration

Si $r_{1}<r$, on a : $\sum _{n}a_{n}r_{1}^{n}=\sum _{n}a_{n}r^{n}\left({\frac {r_{1}}{r}}^{n}\right)$ La série $\sum _{n}a_{n}r^{n}$ converge vers une valeur que nous allons noter M, ce qui donne : $\sum _{n}a_{n}r_{1}^{n}=\sum _{n}M\left({\frac {r_{1}}{r}}^{n}\right)$ Vu que $r_{1}<r\equiv {\frac {r_{1}}{r}}<1$, le second terme $\sum _{n}{\frac {r_{1}}{r}}^{n}=$ va converger. Chaque terme du produit converge, ce qui fait que la suite complète converge elle aussi.

Les fonctions analytiques

Les séries entières ont un lien avec une classe de fonctions bien particulières : les fonctions analytiques. Ces dernières sont des fonctions que l'on peut approximer par une série entière. L'intérêt de cette approximation est qu'elle permet d'étudier des fonctions assez simplement. Transformer une fonction compliquée en un polynôme facilite grandement les calculs. L'analyse d'un polynôme ne demande que les quatre opérations de base et des manipulations de puissances, choses qui sont à la portée de tout lycéen. On peut ainsi dériver ou intégrer une fonction analytique sans faire de calculs compliqués. La plupart des fonctions que vous connaissez sont analytiques. C’est le cas pour les polynômes, les fonctions trigonométriques, l'exponentielle, le logarithme, et quelques autres. Par contre, certaines fonctions comme la valeur absolue ne le sont pas.

Une fonction analytique $f(x)$ peut se calculer avec une série entière telle que :

$f(x)=\sum _{n=0}^{\infty }a_{n}\cdot (x-x_{0})^{n}=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})^{2}+a_{3}(x-x_{0})^{3}+a_{4}(x-x_{0})^{4}+...$

Précisons que l'égalité ne vaut que si x est dans l'intervalle de convergence, pas ailleurs. En dehors de cet intervalle, la série diverge et l'égalité avec la fonction cède. En clair, on sait que la formule précédente est valable pour $x_{0}$, éventuellement pour d'autres valeurs. Si la série a un rayon de convergence non-nul, alors l'égalité fonction-série tient tant que x reste dans l'intervalle de convergence : la formule n'est valable que dans le voisinage de $x_{0}$ (pour les valeurs proches). Dans de rares cas, le rayon de convergence est infini et la série converge pour tout x réel/complexe, la formule est alors valable pour tout x.

Pour donner un exemple, prenons la fonction $f(x)={\frac {1}{1-x}}$. On sait que la série géométrique $1+x+x^{2}+x^{3}+x^{4}+x^{5}+...=\sum _{i=0}^{\infty }x^{i}$ converge vers $1 \over 1-x$ pour $|x|<1$. On peut donc écrire :

$\sum _{i=0}^{\infty }x^{i}=f(x)$

Ce qui est équivalent à écrire :

$1+x+x^{2}+x^{3}+x^{4}+x^{5}+...={\frac {1}{1-x}}$

Mais l'égalité ne vaut que pour $|x|<1$, condition nécessaire pour que la série converge au-delà, la fonction et la série n'ont plus aucun rapport entre elles.

Les coefficients d'une série entière et les dérivées de la fonction analytique associée

Les coefficients $a_{n}$ peuvent se calculer de plusieurs manières différentes. Le cas le plus courant est celui où l'on calcule les coefficients à partir des dérivées de la fonction f(x). Pour être précis, on a besoin de la fonction, de ses dérivées première, seconde, troisième, quatrième, cinquième et ainsi de suite. On a besoin de toutes les autres dérivées d'ordre n, jusqu'à l'infini, ce qui implique que de telles dérivées existent toutes. Dit autrement, la fonction doit être de classe $C^{\infty }$. La méthode que nous allons voir ne marche pas pour les fonctions qui ne respectent pas cette condition.

Les coefficients d'une série entière ont un rapport avec les dérivées de la fonction associée. On sait déjà que le premier coefficient est égal à f(0) pour une série centrée sur zéro, et à f(a) pour une série centrée sur a.

$a_{0}=f(a)$

Maintenant, essayons de calculer le premier coefficient. Prenons une fonction f(x) et considérons sa série entière associée, en supposant que la série entière soit centrée sur zéro.

$f(x)=\sum _{n=0}^{\infty }a_{n}\cdot x^{n}=a_{0}+a_{1}\cdot x+a_{2}\cdot x^{2}+a_{3}\cdot x^{3}+a_{4}\cdot x^{4}+...$

Maintenant, dérivons l'équation précédente. On sait que la dérivée d'un polynôme est la somme des dérivées de chaque terme, de chaque monôme.

$f'(x)=(a_{0})'+\left(a_{1}\cdot x\right)'+\left(a_{2}\cdot x^{2}\right)'+\left(a_{3}\cdot x^{3}\right)'+\left(a_{4}\cdot x^{4}\right)'+...$

On utilise la formule $(k\cdot f(x))'=k\cdot f(x)'$ :

$f'(x)=a_{1}\cdot \left(x\right)'+a_{2}\cdot \left(x^{2}\right)'+a_{3}\cdot \left(x^{3}\right)'+a_{4}\cdot \left(x^{4}\right)'+...$

On applique la formule $\left(x^{n}\right)'=n\cdot x^{n-1}$ :

$f'(x)=a_{1}+a_{2}\cdot 2x+a_{3}\cdot 3x^{2}+a_{4}\cdot 4x^{3}+...$

Regardons la valeur pour x = 0. Les coefficients multiples de x s'annulent et ne laissent que le coefficient $a_{1}$.

$f'(0)=a_{1}$

Le résultat se généralise pour les séries qui ne sont pas centrées sur zéro, mais sur a : il suffit de remplacer zéro par a dans les formules.

$f'(a)=a_{1}$

Maintenant, calculons la dérivée seconde. Pour cela, repartons de la formule de la dérivée première établie plus haut :

$f'(x)=a_{1}+a_{2}\cdot 2x+a_{3}\cdot 3x^{2}+a_{4}\cdot 4x^{3}+a_{5}\cdot 5x^{4}...$

Le calcul de la dérivée est similaire aux calculs précédents, ce qui donne :

$f''(x)=2\cdot a_{2}+a_{3}\cdot (3\times 2)+a_{4}\cdot (4\times 3)x^{2}+...$

En prenant x = 0, on trouve :

$f''(0)=2\cdot a_{2}$

Le résultat se généralise pour les séries qui ne sont pas centrées sur zéro, mais sur a : il suffit de remplacer zéro par a dans les formules.

$a_{2}={\frac {f''(a)}{2}}$

Le calcul du troisième coefficient procède de la même manière, en calculant la dérivée troisième à partir de la formule de la dérivée seconde établie auparavant. Cela donne :

$f'''(x)=a_{3}\cdot (3\times 2)+a_{4}\cdot (4\times 3\times 2)x+...$

En prenant x=0, on trouve :

$f'''(x)=a_{3}\cdot (3\times 2)$

Notons que le produit est égal à la factorielle de 3.

Le résultat se généralise pour les séries qui ne sont pas centrées sur zéro, mais sur a : il suffit de remplacer zéro par a dans les formules.

$a_{3}={\frac {f''(a)}{3!}}$

Même chose pour le quatrième coefficient. On part de la dérivée troisième :

$f'''(x)=a_{3}\cdot (3\times 2)+a_{4}\cdot (4\times 3\times 2)x+...$

On dérive une nouvelle fois et on trouve :

$f'''(x)=a_{4}\cdot (4\times 3\times 2)x+...$

En prenant x=0, on trouve :

$f'''(0)=a_{4}\cdot (4\times 3\times 2)x$, avec le produit entre parenthèse la factorielle de 4.

On a donc :

$a_{4}={\frac {f'''(a)}{4!}}$

Et on peut poursuivre ainsi de suite. On aura toujours la formule suivante :

$a_{n}={\frac {f^{(n)}(a)}{n!}}$

L'expansion en série de Taylor

Avec ce que l'on vient de voir, on a :

$a_{n}={\frac {f^{(n)}(x_{0})}{n!}}$, avec $f^{(n)}$ la dérivée d'ordre n de la fonction f(x) et $n!$ la factorielle de n.

Avec cette méthode, la fonction f(x) est donc approximée par une série appelée série de Taylor :

$f(x)=\sum _{n=0}^{\infty }{\frac {f^{(n)}(x_{0})}{n!}}(x-x_{0})^{n}$

Une série de Taylor nous permet de calculer la fonction au point x, si l'on connait sa valeur et ses dérivées au point $x_{0}$. L'avantage est que la plupart des fonctions ont un point où calculer leurs propriétés est très facile. Dans le cas particulier où $x_{0}=0$, une série de Taylor est appelée une série de Maclaurin.

$f(x)=\sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!}}x^{n}=\sum _{n=0}^{\infty }f^{(n)}(0){\frac {x^{n}}{n!}}$

On connait les séries de Taylor pour de nombreuses fonctions. Voici quelques autres exemples très connus.

Exponentielle	$\exp(x)=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}$	$1+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+...$
Logarithmes (les formules ne convergent pas toujours)	$\ln(1-x)=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}$	$-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}-{\frac {x^{5}}{5}}-...$
	$\ln(1+x)=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}$	$x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-...$
Fonctions trigonométriques	$\sin(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{(2n+1)!}}$	$1-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{7}}{7!}}+...$
	$\cos(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n)!}}$	$1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+{\frac {x^{8}}{8!}}+...$
	...	...

L'approximation d'une fonction analytique par une série de Taylor partielle

Approximation de la fonction exponentielle, au fur et à mesure qu'on ajoute les premiers termes de la série de Maclaurin.

Les fonctions non-polynomiales ont un nombre infini de termes, alors que les fonctions polynomiales n'ont qu'un nombre fini de termes (sous-entendu, de termes non-nuls). D'ailleurs, la série de Taylor d'une fonction polynomiale est la fonction elle-même. En fait, le principe qui se cache derrière les séries de Taylor est d'approximer la fonction par un polynôme, polynôme décrit par la série de Taylor. Si la fonction est polynomiale, alors la série de Taylor est le polynôme lui-même. Pour d'autres fonctions, la correspondance marche localement, à savoir qu'au voisinage d'un point, la fonction est décrite à la perfection par un polynôme en un point x, mais que l’approximation se fait de moins en moins bonne quand on s'en éloigne.

Notons que les séries de Taylor sont des séries infinies, mais que l'on peut ne prendre en compte que les premiers termes pour des applications pratiques. Par exemple, les séries de Taylor sont utilisées pour faire des approximations en physique ou en ingénierie. Si un phénomène est décrit par une fonction assez compliquée, ou mal connue, on peut l'approximer par une série de Taylor et ne prendre en compte que les premiers termes (souvent les plus importants). Prenons par exemple celui de la fonction sinus et de sa série de Taylor associée. Sur le schéma ci-dessous, on voit la fonction sinus, avec la courbe obtenue avec les 7 premiers termes de la série de Taylor associée. On voit que la fonction est pas trop mal approximée par le polynôme, mais seulement à proximité du point étudié.

Approximation de sinus par les 7 premiers termes de la série de Taylor.

Annexe : la vitesse de convergence d'une suite

Si toutes les suites convergent, certaines le font plus rapidement que d'autres. Les termes des suites rapides arrivent rapidement à des valeurs proches de leur limite, alors que ce n'est pas le cas pour les suites lentes. Cette description intuitive n'est cependant pas facile à formaliser. Mais sa formalisation est particulièrement utile quand on doit analyser la convergence de certaines suites. C'est notamment le cas en analyse numérique, un domaine des mathématique assez complexe. C'est aussi utilisé dans le domaine du calcul numérique (à savoir le calcul sur ordinateur), qui fait un grand usage de suites pour calculer certains nombres. Par exemple, il existe des suites qui permettent de calculer certaines constantes mathématiques , comme pi, e, ou bien d'autres constantes utiles. Pour donner un autre exemple, la constante de Majorana, une constante de la physique des particules, se calcule avec une suite de ce genre. Il est préférable d'utiliser des suites qui convergent rapidement pour faire les calculs et c'est là que l'analyse de la vitesse de convergence devient utile.

L'erreur d'approximation

La définition formelle de la vitesse de convergence fait intervenir la différence $u_{n}-L$ entre un terme $u_{n}$ et la limite $L$. Si $n$ est assez grand, $u_{n}$ est assez proche de la limite $L$. On peut alors considérer que $u_{n}\approx L$. Il est alors intéressant d'étudier l'erreur d'approximation, à savoir de combien le terme approximé $u_{n}$ se trompe par rapport à la valeur exacte de L. Intuitivement, on devine que :

$u_{n}=L+\epsilon$, avec $\epsilon$ l'erreur d'approximation.

L'erreur d'approximation de l'équation précédente peut être aussi bien positive que négative. Par exemple, si j'ai $u_{n}=2.23$ et L = 2, l'erreur d'approximation est positive et égale à 0.23. Par contre, si j'ai $u_{n}=1.50$ et $L=2$, l'erreur d'approximation est négative et égale à -0.5. Ce qui nous intéresse dans la suite du cours est la valeur absolue de l'erreur d'approximation. Celle-ci porte le nom d'erreur absolue.

L'erreur absolue est la valeur absolue de l'erreur d'approximation, comme mentionnée plus haut. Dans le cas général, elle vaut :

$\epsilon _{a}=|a-b|$, avec a la valeur exacte et b une valeur approchée de a.

L'erreur relative est l'erreur absolue, mais rapportée en valeur de a. Dans le cas général, elle vaut :

$\epsilon _{r}={\frac {|a-b|}{|a|}}$, avec a la valeur exacte et b une valeur approchée de a.

Appliqué à une suite $u_{n}$ qui converge vers L, on trouve alors :

$\epsilon _{a}=|u_{n}-L|$, avec L la limite.

$\epsilon _{r}={\frac {|u_{n}-L|}{|L|}}={\frac {|u_{n}|}{|L|}}-1$, avec L la limite.

C'est l'erreur d'approximation absolue qui est utilisée pour définir la convergence de la suite. Cependant, l'erreur relative n'est pas inutile et nous servira quand on parlera du nombre de chiffres significatifs de l'approximation.

La vitesse de convergence

L'erreur d'approximation absolue diminue avec le rang, ce qui fait que les deux erreurs d'approximation absolues $|u_{n}-L|$ et $|u_{n+1}-L|$ seront différentes. Plus l'erreur d'approximation diminue d'un rang au suivant, plus l'erreur d'approximation diminue rapidement avec le rang n et plus la suite $(u_{n})$ converge rapidement. L'idée est de comparer ces deux différences entre deux rangs, en utilisant leur rapport $|u_{n+1}-L| \over |u_{n}-L|$. La vitesse de convergence est définie par la limite de ce quotient quand n tend vers l’infini.

$Q=\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|}}$

On distingue plusieurs vitesses de convergences, selon que la limite $0=Q$, $0<Q<1$, $Q=1$ (le cas où $Q>1$ implique une suite divergente).

• Si la limite est égale à 1, alors la suite a une convergence infra-linéaire, aussi appelée convergence lente.
• Si la limite est une constante K telle que $K\in {]0,1[}$, la suite a une convergence linéaire, aussi appelée convergence géométrique (on verra qu'il y a un lien avec les suites géométriques dans ce qui suit).
• Si la limite est égale à 0, alors la suite a une convergence supra-linéaire, aussi appelée convergence rapide.

Convergence infralinéaire	$\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|}}=1$
Convergence linéaire	$0<\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|}}<1$
Convergence supralinéaire	$\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|}}=0$

Convergence linéaire

Pour le dire autrement, une suite a une convergence linéaire si, au-delà d'un certain rang, il existe $k\in {]0,1[}$ tel que :

$|u_{n+1}-L|\leq k\cdot |u_{n}-L|$

Cette équation nous dit qu'une suite $(u_{n})$ est linéairement convergente si $(|u_{n}-L|)$ est bornée par une suite géométrique. Pour le dire en français, l'erreur d'approximation (sa valeur absolue, pour être précis) est bornée par une suite géométrique. L'erreur d'approximation diminue donc en passant au rang suivant, avec un taux de décroissance $k$ plus petit que 1, mais positif. Le coefficient $k$ est appelé le taux de convergence de la suite.

Convergence supra-linéaire

Il est possible de classer les convergences supra-linéaires en modifiant quelque peu l'équation. Il suffit d'élever le dénominateur de l'expression précédente à une certaine puissance $\alpha$, qui dépend de la suite.

$\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|^{\alpha }}}=k$

On peut reformuler cette équation de la même manière que pour les suites linéairement convergentes, ce qui donne :

$|u_{n+1}-L|\leq k\cdot |u_{n}-L|^{\alpha }$

Suivant la valeur du coefficient $\alpha$, on distingue

• les suites à convergence quadratique, pour lesquelles $\alpha =2$ ;
• les suites à convergence cubique, pour lesquelles $\alpha =3$ ;
• les suites à convergence quartique, pour lesquelles $\alpha =4$ ;
• etc.

Convergence quadratique	$\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|^{2}}}=K$	$|u_{n+1}-L|\leq k\cdot |u_{n}-L|^{2}$
Convergence cubique	$\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|^{3}}}=K$	$|u_{n+1}-L|\leq k\cdot |u_{n}-L|^{3}$
Convergence quartique	$\lim _{n\to \infty }{\frac {|u_{n+1}-L|}{|u_{n}-L|^{4}}}=K$	$|u_{n+1}-L|\leq k\cdot |u_{n}-L|^{4}$

Comparer la vitesse de convergence de deux suites

Il est parfois intéressant de comparer la vitesse de convergence de deux suites, pour savoir laquelle converge le plus vite. Les informaticiens font cela souvent, sans même le savoir, en comparant le comportement asymptotique de deux algorithmes (leur complexité algorithmique, pour être précis). Dans ce qui va suivre, nous allons comparer une suite $(u_{n})$ à une suite de référence $(v_{n})$. Les suites de références auxquelles on compare les suites sont les suivantes :

Convergence lente		Convergence géométrique	Convergence rapide
$u_{n}={\frac {1}{(\ln n)^{a}}}$	$u_{n}={\frac {1}{n^{a}}}$	$u_{n}=k^{n}$, avec $0<k<1$	$u_{n}={\frac {1}{n!}}$	$u_{n}={\frac {1}{n^{n}}}$	$u_{n}=k^{2^{n}}$, avec $0<k<1$

Chaque suite converge plus rapidement que les précédentes. On peut déterminer si une suite converge lentement, rapidement ou de manière géométrique en la comparant aux suites du tableau. Par exemple, on sait qu'une suite en $O\left({\frac {1}{n^{a}}}\right)$ (dominée par la suite définie par $u_{n}={\frac {1}{n^{a}}}$) converge lentement.

Suites dominées, équivalentes et négligeables

Nous allons maintenant introduire les notions qui permettent de comparer les vitesses de convergence de deux suites. Prenons deux suites $(u_{n})$ et $(v_{n})$, avec $(v_{n})$ la suite de référence, à laquelle on compare $(u_{n})$. Les relations de dominance, négligeabilité et d'équivalence sont déterminée par la valeur de la limite : $\lim _{n\to \infty }{\frac {u_{n}}{v_{n}}}$. Tout dépend si elle est finie, nulle ou égale à 1.

	Notation	Première définition	Seconde définition	Troisième définition
$(u_{n})$ est dominée par $(v_{n})$	$u_{n}=O(v_{n})$	$\lim _{n\to \infty }{\frac {u_{n}}{v_{n}}}\rightarrow K$, avec K un réel quelconque.	Au-delà d'un certain rang $N$, il existe une constante M telle que : $u_{n}<M\cdot v_{n}$	Il existe une suite $a_{n}$ bornée telle que : $u_{n}=a_{n}\cdot v_{n}$
$(u_{n})$ est négligeable devant $(v_{n})$	$u_{n}=o(v_{n})$	$\lim _{n\to \infty }{\frac {u_{n}}{v_{n}}}\rightarrow 0$	Il existe un rang au-delà duquel on a, pour tout $\epsilon >0$ : $u_{n}<\epsilon \cdot v_{n}$	Il existe une suite $\epsilon _{n}$ qui converge vers zéro telle que : $u_{n}=\epsilon _{n}\cdot v_{n}$
$(u_{n})$ est équivalente à $(v_{n})$	$u_{n}\sim v_{n}$	$\lim _{n\to \infty }{\frac {u_{n}}{v_{n}}}\rightarrow 1$		Il existe une suite $\nu _{n}$ qui converge vers 1 telle que : $u_{n}=\nu _{n}\cdot v_{n}$

À partir de la définition de l'équivalence, on peut démontrer que deux suites équivalentes ont la même limite. Ainsi, si $\lim _{n\rightarrow \infty }u_{n}=L$ et que $u_{n}\sim v_{n}$, alors on sait que $\lim _{n\rightarrow \infty }v_{n}=L$.

Les relations entre dominance, négligeabilité et équivalence

Vous remarquerez que la négligeabilité et l'équivalence sont deux cas particuliers de dominance. Ce qui est à l'origine des deux propriétés suivantes :

• Si une suite $(u_{n})$ est négligeable devant $(v_{n})$, alors elle est aussi dominée par $(v_{n})$.

$u_{n}=o(v_{n})\implies u_{n}=O(v_{n})$

• Si deux suites sont équivalentes, alors l'une domine l'autre et réciproquement.

$u_{n}\sim v_{n}\implies u_{n}=O(v_{n}),v_{n}=O(u_{n})$

Attention : la réciproque est fausse. Il existe des suites qui se dominent mutuellement, sans pour autant être équivalentes.

On peut démontrer que la négligeabilité est transitive :

$a_{n}=o(b_{n}),b_{n}=o(c_{n})\implies a_{n}=o(c_{n})$

L'équivalence de deux suites est, quant à elle, une relation transitive, réflexive (une suite est équivalente à elle-même) et symétrique (c'est donc une relation dite d'équivalence, d'où son nom).

Transitivité : $a_{n}\sim b_{n},b_{n}\sim c_{n}\implies a_{n}\sim c_{n}$

Réflexivité : $a_{n}\sim a_{n}$

Symétrie : $a_{n}\sim b_{n}\equiv b_{n}\sim a_{n}$

Opérations avec l'équivalence, la négligeabilité et la dominance

Négligeabilité :

On peut démontrer qu'une combinaison linéaires de suites négligeables devant $(u_{n})$ est aussi négligeable devant $(u_{n})$ :

$a\times (a_{n})+\times (b_{n})=o(u_{n})$, sous condition que $a_{n}=o(u_{n})/math>et<math>b_{n}=o(u_{n})$.

Il en est de même pour le produit d'une suite $(a_{n})$ par une suite négligeable devant $(u_{n})$ :

$b_{n}\times (a_{n})=o(u_{n})$, sous condition que $a_{n}=o(u_{n})$ (mais on n'a pas besoin que $b_{n}=o(u_{n})$).

Équivalence :

On peut noter que les relations suivantes sont équivalentes :

• $u_{n}\sim v_{n}$
• $u_{n}=v_{n}+o(v_{n})$
• $v_{n}=u_{n}+o(u_{n})$
• $u_{n}-v_{n}=o(v_{n})$
• $v_{n}-u_{n}=o(u_{n})$

Les relations au-delà de la première sont appelées des développements asymptotiques de l'équivalence. On voit avec ces relations que l'on ne peut pas additionner ou soustraire des suites équivalentes. Par exemple, si $u_{n}\sim w_{n}$ et $v_{n}\sim w_{n}$, on ne peut PAS en déduire que $u_{n}+v_{n}\sim 2\cdot w_{n}$. Les seules opérations que l'on peut faire dans ce genre de situation sont les multiplications, les quotients et les élévations à la puissance. Ainsi, si on a : $u_{n}\sim a_{n}$ et $v_{n}\sim b_{n}$ :

• $u_{n}\cdot v_{n}\sim a_{n}\cdot b_{n}$
• ${\frac {u_{n}}{a_{n}}}\sim {\frac {v_{n}}{b_{n}}}$
• $u_{n}^{a}\sim v_{n}^{a}$

Les chiffres significatifs de l'approximation

Si l'approximation est suffisante, $u_{n}$ et L ont des chiffres en communs et ne différent que par des chiffres les plus à droite. Pour rappel, les chiffres communs entre l'approximation $u_{n}$ et la cible (la limite L) sont appelés des chiffres significatifs. Plus le rang augmente, plus le nombre de chiffres significatifs augmente : des chiffres qui étaient erronés aux rangs précédents vont devenir corrects. L'approximation s'affinera progressivement, d'un rang à l'autre. Par exemple, prenons une suite qui me permet de calculer $\pi =3.141592653589793238462643383279502884...$. Si j'ai $u_{7}=3.1415926719457$, je n'ai que 8 chiffres significatifs corrects. En augmentant le rang, je vais avoir de plus en plus de chiffres qui vont devenir significatifs. Par exemple, je vais avoir $u_{1}0=3.14159265357817$, puis $u_{1}5=3.141592653589793235$, etc.

Si on connaît l'erreur d'approximation et la limite, on peut calculer le nombre de chiffres significatifs de $u_{n}$ après la virgule.

Celui-ci est défini par le logarithme de l'erreur relative (en fait, son opposé) :

$\sigma _{n}=-\log {\epsilon _{r}}=-\log _{10}{\frac {|u_{n}-L|}{|L|}}$

Attention : cette formule ne vaut que si la limite est non-nulle, sans quoi on obtient une division par zéro.

Le lien avec la vitesse de convergence

Il existe un lien entre le nombre de chiffres significatifs et la vitesse de convergence.

Pour une convergence linéaire, au-delà d'un certain rang :

$\sigma _{n+1}=\sigma _{n}+k$, avec k une constante positive non-nulle (k > 0).

Pour une convergence supra-linéaire :

$\lim _{n\to \infty }\sigma _{n+1}-\sigma _{n}=0$

Pour une convergence infra-linéaire, au-delà d'un certain rang :

$\lim _{n\to \infty }{\frac {\sigma _{n+1}}{\sigma _{n}}}\geq \alpha$, avec $\alpha$ l'ordre de convergence.

Démonstration

Pour le démontrer, partons de l'équation : $|u_{n+1}-L|\leq k\cdot |u_{n}-L|^{\alpha }$ Divisons des deux côtés par L : ${\frac {|u_{n+1}-L|}{L}}\leq k\cdot {\frac {|u_{n}-L|^{\alpha }}{L}}$ En prenant l'opposé du logarithme, on a : $-\log _{10}{\frac {|u_{n+1}-L|}{L}}\geq -\log _{10}\left(k\cdot {\frac {|u_{n}-L|^{\alpha }}{L}}\right)$ On utilise la formule $\log {(x\cdot y)}=\log {x}+\log {y}$ : $-\log _{10}{\frac {|u_{n+1}-L|}{L}}\geq -\left(\log _{10}{\frac {|u_{n}-L|^{\alpha }}{L}}+\log _{10}k\right)$ Simplifions : $-\log _{10}{\frac {|u_{n+1}-L|}{L}}\geq -\left(\alpha \cdot \log _{10}{\frac {|u_{n}-L|}{L}}+\log _{10}[L^{\alpha -1}k]\right)$ On applique la formule $\sigma _{n}=-\log _{10}{\frac {|u_{n}-L|}{L}}$ : $\sigma _{n+1}\geq \alpha \cdot \sigma _{n}-\log _{10}[L^{\alpha -1}k]$ Divisons maintenant par $\sigma _{n}$ : ${\frac {\sigma _{n+1}}{\sigma _{n}}}\geq \alpha -{\frac {\log _{10}[L^{\alpha -1}k]}{\sigma _{n}}}$ Puisque $\sigma _{n}$ tend vers l'infini par hypothèse, on déduit en passant à la limite que: $\lim _{n\to \infty }{\frac {\sigma _{n+1}}{\sigma _{n}}}\geq \alpha$, ce qu'il fallait démontrer.

GFDL

Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans texte de dernière page de couverture.