Électronique/La rétroaction linéaire et l'amplification

Les AOP sont rarement utilisés seuls, mais sont souvent utilisés dans des circuits qui combinent un AOP avec des résistances, des bobines, des condensateurs, ou d'autres composants passifs. Dans beaucoup de cas, la sortie de l'AOP est envoyée dans un circuit passif, qui lui-même est relié à l'entrée. Ce genre de circuit est un cas particulier de ce qu'on appelle des circuits à rétroaction. Ce sont des circuits dans lesquels la sortie du circuit est traitée, puis renvoyée sur l'entrée. Renvoyer la sortie sur l'entrée est ce qu'on appelle une rétroaction, d'où le nom donné à ces circuits. En soit, la rétroaction peut s'utiliser pour des raisons très différentes.

Les circuits à rétroaction ont une forme illustrée ci-dessous. La tension d'entrée est notée X(s) et la tension de sortie est notée Y(s). On voit qu'il y a deux circuits distincts. Le premier circuit transforme l'entrée X(s) en sa sortie Y(s) et il a une transmittance notée G(s). Nous l’appellerons le circuit direct, car il connecte directement l'entrée à la sortie. Le second circuit, de transmittance H(s), traite la sortie et renvoie son résultat sur l'entrée. Nous l’appellerons le circuit de rétroaction. Il existe deux types de rétroaction, suivant comment on traite le résultat du circuit de rétroaction. Avec la rétroaction positive, l'entrée est additionnée au signal de rétroaction. Avec la rétroaction négative, le signal de rétroaction est soustrait du signal d'entrée.

Dans ce qui suit, nous allons supposer que le circuit direct et le circuit de rétroaction sont des circuits linéaires, c'est à dire que la sortie et l'entrée sont proportionnels. Le circuit direct multiplie son entrée par un coefficient $\alpha$ , alors que le circuit de rétroaction multiplie sa sortie par $\beta$ . Le coefficient $\alpha$ est appelé le gain en boucle ouverte et correspond ni plus moins qu'au gain de l'amplificateur. Il est à différencier du gain du circuit complet, qui est défini par le rapport entre entrée et sortie du circuit, soit Y(s)/X(s). Ce dernier est appelé le gain en boucle fermée. Les noms gain en boucle fermée et gain en boucle ouverte parlent d'eux-mêmes : le premier est mesuré sans la rétroaction, donc avec la boucle ouverte, alors que le second est mesuré avec le circuit de rétroaction, donc quand la boucle est fermée.

Dans ce chapitre, nous allons voir comment fonctionnent les circuits à rétroaction de manière générale. Nous verrons dans le chapitre suivant quels montages on peut obtenir avec une rétroaction simple. Nous utiliserons aussi les acquis de ce chapitre dans les chapitres sur les filtres et les oscillateurs. Dans ce qui va suivre, nous allons voir la rétroaction négative avant de voir la rétroaction positive.

La rétroaction négative

Avec la rétroaction négative, le résultat de la rétroaction est soustrait au signal d'entrée. Dans le cas des AOP, elle peut servir à corriger les défauts de l'AOP utilisé. Cela peut permettre de rendre le gain moins sensible aux défauts de l'AOP, à augmenter la bande passante, à réduire l'effet du bruit et des perturbations, à réduire les distorsions non-linéaires, où à modifier les résistances d'entrée et de sortie. Mais, si elle est utilisée intelligemment, elle permet de créer des circuits complexes en utilisant un AOP central. On peut ainsi créer des filtres, des oscillateurs ou des circuits additionneur/soustracteurs/multiplieurs/intégrateur/dérivateurs/autres.

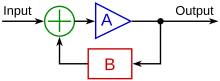
Un circuit à rétroaction négative a la forme donnée ci-dessous. Il prend un signal d'entrée $S(\omega )$ (Signal) et fournit un signal de sortie $O(\omega )$ (Output), le signal de rétroaction est noté $R(\omega )$ .

Le signal O(s) est multiplié par $\beta$ par le circuit de rétroaction, ce qui donne :

R(\omega )=\beta \cdot O(\omega )

Le signal d'entrée S se voit soustrait le signal de rétroaction R, de qui donne un résultat temporaire I qui vaut :

I(\omega )=S(\omega )-R(\omega )=S(\omega )-\beta \cdot O(\omega )

Ce dernier est amplifié par l'AOP, qui a un gain $\alpha$ , ce qui donne une sortie égale à :

O(\omega )=\alpha \cdot I=\alpha \cdot \left[S(\omega )-\beta \cdot O(\omega )\right]

Diagramme d'un circuit linéaire à rétroaction négative.

La transmittance d'un circuit à rétroaction

Maintenant, reprenons l'équation précédente et développons.

O(\omega )=\alpha \cdot S(\omega )-\alpha \beta \cdot O(\omega )

Divisons par S :

{\frac {O(\omega )}{S(\omega )}}=\alpha -\alpha \beta \cdot {\frac {O(\omega )}{S(\omega )}}

Par définition, ${\frac {O(\omega )}{S(\omega )}}$ n'est autre que la transmittance du circuit complet. En notant celle-ci $T(\omega )$ , on a :

T(\omega )=\alpha -\alpha \beta \cdot T(\omega )

Regroupons les termes avec la transmittance :

T(\omega )+\alpha \beta \cdot T(\omega )=\alpha

Factorisons la transmittance :

T(\omega )\left(1+\alpha \beta \right)=\alpha

Et isolons la transmittance :

T(\omega )={\frac {\alpha }{1+\alpha \beta }}

Le terme $\alpha \beta$ est appelé le gain de boucle. Pour que la rétroaction soit négative, il faut que celui-ci soit positif. Le terme $1+\alpha \beta$ , au dénominateur de la transmittance est appelé la quantité de rétroaction.

Circuit à rétroaction originel.

Circuit équivalent au circuit à rétroaction précédent.
Le circuit illustré a une transmittance égale à

T(\omega )={\frac {\alpha }{1\pm \alpha \beta }}

.

Au passage, dans la plupart des applications, on a $\alpha \beta >>1$ . Dans de telles conditions, la transmittance devient :

T(\omega )\approx {\frac {1}{\beta }}

Cela signifie que le comportement du circuit est totalement déterminé par le circuit de rétroaction, pas par l'amplificateur. Cela ne signifie pas que le circuit direct est inutile, mais que la sortie sera peu sensible au gain de l'AOP central.

Usage de la rétroaction négative

Maintenant, nous allons voir quels sont les avantages de la rétroaction négative, ce à quoi elle peut servir.

Une augmentation de la bande passante

La rétroaction négative augmente la bande passante de l'AOP. Notons que cette augmentation de la bande passante est proportionnelle à la réduction du gain en boucle fermée. Plus le gain en boucle fermée est réduit, par rapport au gain en boucle ouverte, plus la bande passante sera élargie. On peut prouver, à partir de résultats mathématiques non-triviaux, que le produit bande passante $\times$ gain est une constante. En conséquence, une réduction de x% du gain en boucle fermée se traduira par une augmentation de x% de la bande passante.

Compromis entre gain et bande passante d'un circuit à rétroaction.

Traditionnellement, on étudie le cas où le gain de l'AOP diminue avec la fréquence. Le gain de l'amplificateur dépend de la fréquence en suivant l'équation suivante :

\alpha (f)={\frac {\alpha _{0}}{1+j(f/f_{o})}}

On peut alors combiner cette équation avec la formule de la transmittance $T(\omega )={\frac {\alpha }{1-\alpha \beta }}$ . On obtient alors :

T(\omega )={\frac {\alpha _{0}/(1+j(f/f_{o}))}{1-\beta \cdot \alpha _{0}[1+j(f/f_{o})]}}

En simplifiant, on a :

T(\omega )={\frac {\alpha _{0}}{1+j(f/f_{o})+\beta \cdot \alpha _{0}}}

La situation étudiée est illustrée dans le schéma ci-dessous.

Comparaison entre la bande passante en boucle ouverte (en bleu) et en boucle fermée (en rouge).

Réduction de la sensibilité à l'AOP du gain

La première utilisation est la réduction du gain du circuit, de sa sensibilité au gain de l'AOP. Une variation massive du gain de l'AOP se traduit par une réduction beaucoup plus faible du gain du circuit total. Pour comprendre en quoi, partons de la transmittance du circuit à rétroaction :

T(\omega )={\frac {\alpha }{1+\alpha \beta }}

Dérivons l'équation précédente, pour voir comment le gain varie.

dT(\omega )={\frac {d\alpha }{(1+\alpha \beta )^{2}}}

Divisons par la transmittance :

{\frac {dT(\omega )}{T(\omega )}}={\frac {1}{(1+\alpha \beta )^{2}}}{\frac {d\alpha }{\alpha }}

Le terme ${\frac {dT(s)}{T(s)}}$ correspond à une modification en pourcentage du gain en boucle fermée, alors que le terme ${\frac {d\alpha }{\alpha }}$ est une variation en pourcentage du gain en boucle ouverte. On voit que le terme ${\frac {1}{(1+\alpha \beta )^{2}}}$ est le coefficient de proportionnalité entre les deux gains en boucle fermée et ouverte. Ce terme est généralement plus petit que 1, beaucoup plus petit. Le gain en boucle fermée du circuit est donc stabilisé, il dépend peu du gain en boucle ouverte de l'AOP.

La réduction des interférences

Une autre utilité de la rétroaction est qu'elle permet de réduire l'intensité des perturbations extérieures. Pour comprendre pourquoi, imaginons qu'une perturbation D survienne et perturbe la sortie. Intuitivement, le circuit de rétroaction amplifiera la perturbation D et le signal de rétroaction sera de $\beta \cdot D$ . Le signal intermédiaire I est donc amputé de $\beta \cdot D$ , ce qui fait que la sortie est approximativement réduite de $\alpha \beta \cdot D$ . Si on $\alpha \beta \approx 1$ , alors la perturbation est supprimée immédiatement après son apparition. Il suffit que la distorsion se propage dans le circuit de rétroaction, puis dans l'AOP central, et la sortie revient à la normale.

Diagramme d'un circuit linéaire à rétroaction négative avec un bruit.

Au niveau mathématique, on peut comparer ce qui se passe avec une perturbation D, avec et sans rétroaction.

Si la rétroaction n'avait pas d'effet sur la perturbation, alors la perturbation s'ajouterait à la sortie directement. Ce qui fait que l'on aurait :

O(\omega )=S(w)\cdot {\frac {\alpha }{1+\alpha \beta }}+D

Or, les calculs nous disent qu'avec la perturbation, le circuit à rétroaction négative a une sortie égale à :

O(\omega )=S(w)\cdot {\frac {\alpha }{1+\alpha \beta }}+D\cdot {\frac {1}{1+\alpha \beta }}


Démonstration
Pour cela, on suppose que la perturbation s'ajoute à la sortie de l'AOP, pour donner la sortie. En clair, on a : $O=\alpha I+D$ . On combine alors avec $I=S-\beta O$ $O=\alpha (S-\beta \cdot O)+D$ On développe : $O=\alpha \cdot S-\alpha \beta \cdot O+D$ On regroupe les termes avec O : $O+\alpha \beta \cdot O=\alpha \cdot S+D$ On factorise O : $O(1+\alpha \beta )=\alpha \cdot S+D$ On divise par $1+\alpha \beta$ : $O=+S\cdot {\frac {\alpha }{1+\alpha \beta }}+D{\frac {1}{1+\alpha \beta }}$

On voit que l'effet de la perturbation est multiplié par ${\frac {1}{1+\alpha \beta }}$ , qui est généralement inférieur à 1. En clair : l'effet de la perturbation est réduit du fait de la rétroaction. Si jamais une interférence électromagnétique peu intense survient, un circuit à rétroaction se comportera normalement. Sa sortie restera relativement stable et ne sera pas trop perturbée par la perturbation.

La rétroaction positive

Un circuit à rétroaction positive est identique au circuit à rétroaction négative, sauf que le signal de rétroaction est ajouté au signal d'entrée. Dans ces conditions, on a :

O(\omega )=\alpha \cdot \left[S(\omega )+\beta \cdot O(\omega )\right]

Développons l'équation précédente :

O(\omega )=\alpha \cdot S(\omega )+\alpha \beta \cdot O(\omega )

Divisons par S pour obtenir la transmittance :

T(\omega )=\alpha +\alpha \beta \cdot T(\omega )

Regroupons les termes avec la transmittance :

T(\omega )-\alpha \beta \cdot T(\omega )=\alpha

Factorisons la transmittance :

T(\omega )\left(1-\alpha \beta \right)=\alpha

Et isolons la transmittance :

T(\omega )={\frac {\alpha }{1-\alpha \beta }}

Effets de la rétroaction positive

La rétroaction positive a divers effets que nous allons aborder ici.

Réduction de la sensibilité à l'AOP du gain

Comme pour la rétroaction négative, la rétroaction positive tend à réduire la sensibilité du gain en boucle fermée au gain en boucle ouverte. Pour le prouver, reprenons le gain en boucle fermée :

T(\omega )={\frac {\alpha }{1-\alpha \beta }}

Dérivons l'équation précédente et divisons par la transmittance :

{\frac {dT(\omega )}{T(\omega )}}={\frac {1}{(1-\alpha \beta )^{2}}}{\frac {d\alpha }{\alpha }}

Comme pour la rétroaction négative, le terme ${\frac {1}{(1-\alpha \beta )^{2}}}$ est un coefficient de proportionnalité qui relie les gains en boucle fermée et ouverte. Ce terme est généralement plus petit que 1, ce qui fait le des variations du gain en boucle ouverte n'ont que peu d'effet sur le gain en boucle fermée.

Réduction de la bande passante

Contrairement à la rétroaction négative, la rétroaction positive réduit la bande passante. Il faut dire que l'augmentation du gain doit forcément se traduire par une réduction de la bande passante, du fait de la constante du produit gain $\times$ bande passante.

Amplification des perturbations

Un autre défaut est que la rétroaction positive augmente l'effet des perturbations. Pour le montrer, procédons comme auparavant et ajoutons une perturbation sur la sortie du circuit. Comparons maintenant le résultat avec et sans la rétroaction.

Sans la rétroaction, le circuit a une sortie égale à :

O(\omega )=S(w)\cdot {\frac {\alpha }{1-\alpha \beta }}+D

Or, les calculs nous disent qu'avec la perturbation, le circuit à rétroaction positive a une sortie égale à :

O=S\cdot {\frac {\alpha }{1-\alpha \beta }}+D\cdot {\frac {1}{1-\alpha \beta }}


Démonstration
Pour cela, on suppose que la perturbation s'ajoute à la sortie de l'AOP, pour donner la sortie. En clair, on a : $O=\alpha I+D$ . On combine alors avec $I=S+\beta O$ $O=\alpha (S+\beta \cdot O)+D$ On développe : $O=\alpha \cdot S+\alpha \beta \cdot O+D$ On regroupe les termes avec O : $O-\alpha \beta \cdot O=\alpha \cdot S+D$ On factorise O : $O(1-\alpha \beta )=\alpha \cdot S+D$ On divise par $1-\alpha \beta$ : $O=S\cdot {\frac {\alpha }{1-\alpha \beta }}+D{\frac {1}{1-\alpha \beta }}$

On voit que les perturbations sont amplifiées, du fait du terme $D\cdot {\frac {1}{1-\alpha \beta }}$ .

La stabilité d'un circuit à rétroaction négative

Il existe des valeurs de $\alpha \beta$ pour lesquelles la transmittance peut s'annuler ou au contraire devenir infinie. La transmittance est toujours écrite sous la forme d'une fraction avec un numérateur et un dénominateur. Elle s'annule si le numérateur est égal à 0, alors qu'elle devient infinie/indéfinie si le dénominateur s'annule. Les valeurs pour lesquelles $T(f)=0$ sont appelées les zéros de la transmittance, alors que celles où $T(f)=+\infty$ sont appelées des pôles. Si la présence de zéros n'est pas en soi un problème, la présence de pôle en est un. Dans un cas pareil, le circuit est dit instable. On pourrait croire que les pôles n'ont pas de signification physique. Mais il n’en est rien ! Il est parfaitement possible de créer des circuits avec des pôles. En effet, certains oscillateurs (des générateurs de fréquences) sont fabriqués en utilisant cette possibilité. Concrètement, sur un pôle, la sortie du circuit est finie et non-nulle alors que l'entrée est nulle. Dans la plupart des cas, le circuit se met à osciller, à savoir que sa sortie est une tension sinusoïdale ou tout du moins une tension périodique. Ce n'est pas systématique, mais c'est une possibilité, tout dépend du circuit.

Si on compare les circuits à rétroaction positive et négative, on voit que les pôles surviennent pour des valeurs différentes de $\alpha \beta$ . Rappelons que pour le dénominateur est égal à $1-\alpha \beta$ et $1+\alpha \beta$ , respectivement. Pour un circuit à rétroaction négative, un pôle correspond au cas où $\alpha \beta =-1$ . Cela demande que la condition suivante soit respectée : $\beta =-{\frac {1}{\alpha }}$ . Pour un circuit à rétroaction positive, il faut que la quantité de rétroaction $1-\alpha \beta$ s'annule, ce qui arrive si $\alpha \beta =1$ . Cela demande que la condition suivante soit respectée : $\beta ={\frac {1}{\alpha }}$ .

Un problème similaire survient si la transmittance devient négative. Le cas est un petit peu plus complexe, mais le circuit est là aussi instable. Dans ce cas, la transmittance reste finie, mais la tension de sortie a quelques propriétés bizarres. Les méthodes classiques d'analyse des circuits linéaires ne fonctionnent pas et il faut utiliser d'autres méthodes d'analyse spécifiques. Les circuits qui fonctionnent avec cette condition sont les circuits oscillateurs, comme les multivibrateurs, les circuits bistables, etc. Cela arrive si $1+\alpha \beta$ devient négatif, pour un circuit à rétroaction négative. Pour un circuit à rétroaction positive, il faut que $\alpha \beta >1$ . Avec cette condition, la quantité de rétroaction est négative et la transmittance aussi.

En théorie, il suffirait de choisir $\alpha$ et $\beta$ pour éviter un tel cas d'instabilité. C'est simple à faire si les deux coefficients ne dépendant pas de la fréquence et sont des constantes. Mais dans la réalité, les AOP et circuits linéaires ne se comportent pas ainsi. Dans la réalité, les circuits ont une transmittance qui dépend de la fréquence. Et il est possible que, pour certaines fréquences, on ait $\alpha (\omega )\cdot \beta (\omega )=+/-1$ . Il faut absolument éviter ce cas de figure lors de la conception du filtre. Pour cela, il existe quelques techniques, dont l'usage du critère de Nyquist, qui permettent de détecter la présence d'une instabilité ou son absence. L'analyse de la stabilité d'un circuit à rétroaction positive se fait avec les mêmes outils que pour un circuit à rétroaction négative, avec quelques petites différences mineures (la valeur de $\alpha \beta$ n'est pas la même pour obtenir un pôle).

Le diagramme de Nyquist

Le diagramme de Nyquist est relativement simple. Il s'agit d'une courbe dessinée dans le plan complexe. Rappelons que la transmittance est un nombre complexe, son module correspondant au rapport entre tension d'entrée et de sortie, alors que l'argument donne le déphasage entre les deux tensions. Mais contrairement à ce que l'on peut penser, on ne trace par la transmittance du circuit sur ce diagramme, ce qui ne nous permettrait pas de détecter les situations où elle devient infinie. À la place, chaque point de la courbe est associée au produit $\alpha \beta$ mesuré à une fréquence, différente en chaque point.

Pour un circuit à rétroaction, le circuit devient instable pour une valeur finie de $\alpha \beta$ , ce qui peut se voir sur le plan complexe. Rappelons que la valeur est égale à -1 pour un circuit à rétroaction négative. La courbe dessinée sur le diagramme de Nyquist donne donc toutes les valeurs possibles de ce produit, et l'on peut vérifier si la courbe passe par -1. Si le circuit peut être instable, alors il passe forcément par le point de coordonnées (-1,0).

Exemples de diagramme de Nyquist.

La réponse impulsionnelle d'un circuit à rétroaction

Précisons maintenant comment se comporte un circuit suivant ce que l'on voit sur le diagramme de Nyquist. Nous allons voir comment il se comporte quand on place un échelon de tension sur son entrée. Par échelon de tension, on veut dire que l'on place une tension finie sur son entrée, durant un temps très faible, trop faible pour être considéré comme un signal d'entrée clair. Si le circuit est stable, la sortie du circuit va dépasser zéro durant un certain temps, avant de diminuer et de repasser à 0. La réduction de la tension de sortie peut être progressive, ou se faire par oscillations progressives, mais celles-ci sont amorties. Si le circuit instable, la sortie du circuit peut soit osciller de manière périodique, soit s’emballer et diverger totalement. Ci-dessous, on voit ce qui se passe suivant la valeur du facteur de rétroaction. Si il reste supérieur à -1, le circuit reste stable suite à un échelon de tension. Si il passe par -1, la sortie du circuit se met à osciller périodiquement. Et enfin, si jamais il devient inférieur à -1, la sortie du circuit diverge totalement.

Analyse de stabilité - Lieux de Nyquist et conséquences sur la réponse indicielle

Les quatre topologies des circuits à rétroaction à amplificateurs opérationnels

Dans ce qui précède, nous avons parlé de la rétroaction dans le cas général. Tout ce que l'on a dit marche pour beaucoup de choses, en électronique, mais aussi en mécanique, en électromécanique, en hydraulique, voire en dehors de l’ingénierie. Nous avons abordé la rétroaction dans le cadre général de la théorie du contrôle des systèmes dynamiques. Il est maintenant temps d'aborder des connaissances plus ancrées dans l'électronique.

Montage en série et en shunt de l'AOP central et du circuit de rétroaction

Quadripôle idéal (pas de résistance d'entrée et de sortie).

Quadripôle réel, avec résistance d'entrée et de sortie.

Dans un circuit à rétroaction électronique, on trouve un AOP central bouclé à un circuit de rétroaction. Les deux, l'AOP central et le circuit de rétroaction, sont des quadripôles, à savoir des circuits qui ont quatre bornes. Deux de ces bornes sont des bornes d'entrée, sur lesquelles on peut placer une tension ou un courant, alors que les deux autres fournissent la sortie. En théorie, un quadripôle (idéal ou réel) a pour circuit équivalent les deux circuits ci-contre.

Suivant que l'on mette une tension ou un courant sur l'entrée, on dit que le circuit est en série ou en shunt. Dans le cas en série, on place une tension sur l'entrée. Dans le cas qui nous intéresse, on place la tension d'entrée sur une borne, alors que l'autre reçoit la tension fournie par le circuit de rétroaction. En faisant cela, on est certain que c'est la différence entre ces deux tensions qui est envoyée en entrée de l'AOP. Dans le cas en shunt, on place des courants sur l'entrée. Le courant sur la première borne est le courant du signal d'entrée, celui sur la seconde borne est fourni par le circuit de rétroaction.

Montage en série et en shunt d'un AOP.

Il est possible de faire la même chose, mais pour le circuit de rétroaction. Ce faisant, on peut se retrouver avec quatre possibilités :

Un shunt sur l'entrée de l'AOP central et du circuit de rétroaction.
Une série sur l'entrée de l'AOP central et du circuit de rétroaction.
Un shunt sur l'entrée de l'AOP central et une série sur l'entrée du circuit de rétroaction.
Une série sur l'entrée de l'AOP central et un shunt sur l'entrée du circuit de rétroaction.

Les explications précédentes peuvent sembler très techniques, en raison du jargon utilisé. Pour le dire autrement, le circuit à rétroaction peut prendre en entrée soit un courant, soit une tension. Et c'est la même chose pour ce qui est fourni en sortie du circuit : c'est soit une tension, soit un courant. Ces quatre possibilités correspondent aux cas suivants :

L'amplificateur en tension, aussi appelé cas série-shunt, où le circuit prend en entrée une tension et fournit en sortie une tension.
L'amplificateur en courant, aussi appelé cas shunt-série, où le circuit prend en entrée un courant et fournit en sortie un courant.
L'amplificateur en transimpédance, aussi appelé cas série-série, où le circuit prend en entrée un courant et fournit en sortie une tension.
L'amplificateur en transconductance, aussi appelé cas shunt-shunt, où le circuit prend en entrée une tension et fournit en sortie un courant.

Pour résumer, il y a quatre façons de relier entre eux deux quadripôles, qui sont illustrées ci-dessous. Elles correspondent respectivement à l'amplificateur en tension (droite, haut), à l’amplificateur en courant (gauche, bas), à l'amplificateur en transconductance (droite, bas) et l'amplificateur en transimpédance (gauche, haut).

Topologies des circuits électroniques à AOP, avec rétroaction.

Le montage série-shunt

Commençons par étudier l'amplificateur en tension, le montage série-shunt. Nous allons voir que l'amplificateur en tension est censé avoir une résistance d'entrée forte, alors que sa résistance de sortie doit être la plus faible possible. Et l'usage de la rétroaction permet justement de réduire la résistance de sortie, tout en augmentant la résistance d'entrée.

Pour commencer, nous allons préciser qu'il faut faire la distinction entre la tension $V_{s}$ et la tension $V_{i}$ : la première est celle envoyée en entrée du circuit, alors que la seconde est celle en entrée de l'AOP. Pareil pour les courants d'entrée : il y en a deux, que nous noterons $i_{s}$ et $i_{i}$ , qui correspondent aux courants d'entrée du circuit et de l'AOP. Même chose pour les résistances d'entrée du circuit et de l'AOP qui sont respectivement notées $R_{of}$ et $R_{o}$ .

Dans ce qui suit, nous supposons que l'AOP est un quadripôle réel, alors que le circuit de rétroaction est un quadripôle idéal.

La résistance d'entrée du montage

Dans ce qui suit, nous supposons que l'AOP central est un quadripôle réel, avec une résistance d'entrée $R_{i}$ et une résistance de sortie $R_{o}$ . Par définition, cette résistance est définie par le rapport entre la tension en entrée de l'AOP et le courant d'entrée, par la relation :

i_{i}={\frac {V_{i}}{R_{i}}}

Maintenant, calculons la résistance d'entrée du circuit complet, pas celle de l'AOP, mais celle du circuit complet. Elle est égale, par définition, au rapport entre la tension d'entrée $V_{s}$ et le courant d'entrée. Si l'on suppose que le circuit de rétroaction est un quadripôle idéal, alors le courant d'entrée est égal au courant d'entrée de l'AOP (il n'y a pas d'autre résistance sur l'entrée du circuit). Dans ce cas, la résistance d'entrée du circuit vaut :

R_{s}={\frac {V_{s}}{i_{i}}}

On combine les deux équations précédentes :

R_{s}={\frac {V_{s}}{V_{i}/R_{i}}}=R_{i}{\frac {V_{s}}{V_{i}}}

Maintenant, on applique la formule $V_{s}=V_{i}(1+\alpha \beta )$ :

R_{s}=R_{i}{\frac {V_{i}(1+\alpha \beta )}{V_{i}}}=R_{i}(1+\alpha \beta )

On voit que ce montage augmente la résistance d'entrée.

La résistance de sortie du montage

Maintenant, étudions la résistance de sortie du montage, et formulons-la à partir de la résistance d'entrée de l'AOP. Nous supposons que l'AOP est un quadripôle réel, alors que le circuit de rétroaction est un quadripôle idéal. L'AOP est composé d'une résistance $R_{o}$ en série avec un générateur de tension. Le générateur de tension en question fournit une tension égale à :

V_{o}=V_{i}\cdot \alpha =V_{s}{\frac {\alpha }{1+\alpha \beta }}

Si on met la sortie en court-circuit, la tension de sortie est nulle. La tension de rétroaction s'annule elle aussi, en conséquence. La tension d'entrée de l'AOP est donc la tension d'entrée du circuit, ce qui donne :