Électronique/Les montages à amplificateurs opérationnels

Les AOP sont rarement utilisés seuls, mais sont souvent utilisés dans des circuits qui combinent un AOP avec des résistances, des bobines, des condensateurs, ou d'autres composants passifs. Dans presque tous les cas, la sortie de l'AOP est reliée à une entrée, ce qui porte le nom de rétroaction. On a alors deux cas : soit l'entrée $e_{+}$, soit la $e_{-}$. Dans le premier cas, la rétroaction est dite positive, alors qu'elle est dite négative pour le second cas. Les deux situations sont très différentes et l'AOP fonctionne dans deux modes différent selon que la rétroaction est positive ou négative.

• Avec une rétroaction négative, une augmentation de la tension de sortie réduit la différence des entrées, ce qui tend à réduire la tension de sortie. La tension tend à se stabiliser à une valeur précise, d'équilibre. L'AOP est alors dit en mode linéaire, ce qui trahit le fait que la tension de sortie ne sature pas (du moins, pas systématiquement).
• Avec une rétroaction positive, une augmentation de la tension de sortie augmente la différence entre entrée, ce qui augmente encore la tension de sortie et rebelote. La tension augmente ou baisse alors jusqu’à ce qu'elle arrive à la tension de sortie maximale/minimale.

Contre-réaction.

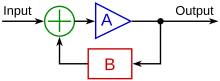
Les montages en mode linéaire (rétroaction négative)

Dans ce chapitre, nous allons voir les montages les plus utilisés, en supposant l'AOP idéal. Pour rappel, un AOP parfait respecte les hypothèses suivantes :

• Il n'a pas de courants d'entrée : $I_{+}=I_{-}=0$.
• Son gain différentiel est infini : $G_{diff}=\infty$.
• On néglige les tensions d'offset et le gain en mode commun, ce qui donne : $U_{s}=G_{diff}(U_{+}-U_{-})$.

En combinant les deux expressions, et en supposant le mode linéaire (contre-réaction négative), on a :

$U_{+}-U_{-}={\frac {U_{s}}{G_{diff}}}={\frac {U_{s}}{\infty }}=0$

Les deux tensions d'entrée sont donc égales, sous condition qu'il y ait une contre-réaction sur l'entrée $e_{-}$. Intuitivement, on peut interpréter ce résultat comme suit.

Pour commencer, étudions le cas où l'AOP a un gain égal à 1. Supposons que les deux tensions d'entrée soient égales : la sortie est alors égale à 0. Maintenant, imaginons que la tension $U_{+}$ augmente : cela entraine l'apparition d'une tension différentielle $(U_{+}-U_{-})$ et la tension de sortie prend la même valeur (si le gain est de 1). Cette tension différentielle est envoyée sur l'entrée $e_{-}$ par l'intermédiaire de la contre-réaction : $U_{-}$ augmente et les augmentations de $U_{+}$ et $U_{-}$ se compensent exactement (dans le cas où le gain est de 1).

Si l'AOP a un gain différent de 1, le principe reste valable, même si le déroulement des faits est plus compliqué. On retrouve la même logique qui veut que si $U_{+}$ augmente, alors $U_{-}$ fait de même. Par contre, les deux tensions ne se compensent pas exactement du premier coup : à la place, on voit apparaitre une nouvelle tension différentielle, qui modifie elle aussi la tension $U_{-}$ et ainsi de suite. Le circuit évolue donc continuellement, mais finir par atteindre un état d'équilibre au bout d'un temps assez court. Et à l'équilibre, les augmentations de $U_{+}$ et $U_{-}$ se compensent parfaitement et les tensions d'entrée sont égales.

Le montage suiveur

Montage suiveur.

Le montage le plus simple à étudier est le montage suiveur, illustré ci-contre. Il se limite à une contre-réaction négative, à savoir une liaison de la sortie sur l'entrée $e_{-}$.

En appliquant la loi des mailles, on trouve :

$U_{s}=U_{e}+U_{diff}$, avec $U_{diff}$ la différence de tension entre $U_{+}$ et $U_{-}$.

Vu que cette dernière vaut zéro, on a :

$U_{s}=U_{e}$

En clair, ce montage reproduit la tension d'entrée sur sa sortie.

Démonstration

On peut aussi analyser ce circuit en utilisant les équations vues au chapitre précédent. Rappelons que l'on a vu que la transmittance d'un circuit à rétroaction négative est donnée par la formule suivante, avec $\alpha$ le gain de l'AOP et $\beta$ le gain du circuit de rétroaction. $T(\omega )={\frac {\alpha }{1+\alpha \beta }}$ Dans le montage suiveur, le circuit de rétroaction est un simple, ce qui fait que sa transmittance est de 1 (le signal d'entrée est égal au signal de sortie). On a donc : $T(\omega )={\frac {\alpha }{1+\alpha }}\approx 1$

Le montage non-inverseur

Montage non-inverseur.

Le montage non-inverseur est illustré dans le schéma ci-contre.

Montage non-inverseur, avec les courants.

Rappelons que le courant d'entrée d'un AOP parfait est nul. Avec cette hypothèse, on peut calculer la tension $U_{-}$ par un simple pont diviseur de tension :

$U_{-}=U_{s}{\frac {R_{1}}{R_{1}+R_{2}}}$

On a aussi, de par les hypothèses de l'AOP parfait :

$U_{-}=U_{+}=U_{e}$

Ce qui donne :

$U_{e}=U_{s}{\frac {R_{1}}{R_{1}+R_{2}}}$

Multiplions par $R_{1}+R_{2}$ :

$U_{e}(R_{1}+R_{2})=U_{s}\cdot R_{1}$

Divisons par $R_{1}$

$U_{s}=U_{e}\cdot {\frac {R_{1}+R_{2}}{R_{1}}}$

Simplifions la fraction :

$U_{s}=U_{e}\cdot \left(1+{\frac {R_{2}}{R_{1}}}\right)$

Démonstration

Illustration du circuit non-inverseur, qui met en avant la sortie du circuit de rétroaction. Faire les calculs avec la formule : $T(\omega )={\frac {\alpha }{1+\alpha \beta }}$ donne des résultats assez compliqués, la formule étant : $T(\omega )={\frac {\alpha (R_{1}+R_{2})}{(1+\alpha )R_{1}+R_{2}}}$ Mais si on pose l'approximation $\alpha \beta >>1$, on a : $T(\omega )={\frac {1}{\beta }}$ Dans le montage non-inverseur, le circuit de rétroaction est un pont diviseur de tension, ce qui fait que : $\beta ={\frac {R_{1}}{R_{1}+R_{2}}}$ En combinant les deux équations précédente, on trouve : $T(\omega )\approx {\frac {1}{\frac {R_{1}}{R_{1}+R_{2}}}}=1+{\frac {R_{2}}{R_{1}}}$

Le montage suiveur peut être vu comme un cas particulier du montage non-inverseur, pour lequel on aurait : $R_{2}=0$ et $R_{1}=\infty$. Les calculs redonnent bien ce qu'on a établi pour le montage suiveur, à savoir :

: $U_{s}=U_{e}\cdot \left(1+{\frac {0}{\infty }}\right)=U_{e}$

Le montage convertisseur courant-tension

Montage convertisseur courant-tension.

La particularité de ce montage est que l'entrée ne reçoit pas une tension, mais un courant d'entrée $I_{e}$. Vu que l'AOP n'absorbe pas de courant (ses courants sur les entrées sont nuls), tout le courant $I_{e}$ passe dans la résistance.

L'entrée $e_{+}$ est reliée à la masse, ce qui fait que $U_{+}=0$. Si l'AOP est parfait, on a donc :

$U_{-}=U_{+}=0$

La loi des mailles donne alors :

$U_{r}+U_{s}=0$, avec $U_{r}$ la tension aux bornes de la résistance R.

Dit autrement, on a :

$U_{s}=-I_{e}\times R$

Ce montage convertit donc le courant d'entrée $I_{e}$ en une tension, par l'intermédiaire de la résistance R.

Le montage inverseur

Montage inverseur.

Le montage illustré ci-contre est appelée le montage inverseur. Ce nom vient de ce que fait ce montage. Sa tension de sortie est l'inverse (en réalité l'opposée) de la tension d'entrée, pondérée par un coefficient lié aux résistances.

Montage inverseur avec les courants.

La démonstration la plus simple utilise les approximations du début du chapitre. Vu que les courants d'entrée de l'AOP sont nuls, le circuit est alors composé de deux résistances en séries, alimentées aux deux bouts par une tension : $U_{e}$ d'un côté, $U_{s}$ de l'autre. C'est la situation parfaite pour utiliser le théorème de superposition (aussi appelé théorème de Millmann). Si on ne garde que $U_{e}$ et qu'on met $U_{s}$ à 0, le circuit devient un simple pont diviseur. Idem si l'on met $U_{e}$ à 0 en conservant $U_{s}$. La tension d'entrée est la somme de ces deux ponts diviseurs, ce qui donne :

$U_{-}=U_{s}{\frac {R_{1}}{R_{1}+R_{2}}}+U_{e}{\frac {R_{2}}{R_{1}+R_{2}}}$

Mais vu que l'entrée $e_{+}$ est connectée à la masse, on a :

$U_{-}=U_{+}=0$

Ce qui donne :

$0=U_{s}{\frac {R_{1}}{R_{1}+R_{2}}}+U_{e}{\frac {R_{2}}{R_{1}+R_{2}}}$

$U_{s}{\frac {R_{1}}{R_{1}+R_{2}}}=-U_{e}{\frac {R_{2}}{R_{1}+R_{2}}}$

On multiplie par : $R_{1}+R_{2}$ des deux côtés :

$U_{s}\cdot R_{1}=-U_{e}\cdot R_{2}$

On divise par $R_{1}$ des deux côtés :

$U_{s}=-U_{e}{\frac {R_{2}}{R_{1}}}$}}

Il existe aussi un autre moyen de faire la démonstration, sans faire d'approximations simplificatrices.

Démonstration

La tension de sortie de l'AOP est donnée, par définition, par la formule suivante : $U_{s}=G_{diff}\times (U_{+}-U_{-})$ Le schéma montre que l'entrée $U_{+}$ est reliée à la masse et vaut donc 0, ce qui simplifie la formule précédente en : $U_{s}=-G_{diff}\times U_{-}$ La tension $U_{-}$ provient de la somme de deux ponts diviseur entre la tension d'entrée et de sortie, ce qui donne : $U_{s}=U_{e}\times {\frac {R_{in}}{R_{in}+R_{f}}}+U_{s}\times {\frac {R_{f}}{R_{in}+R_{f}}}$ On combine alors avec la formule qui donne la tension $V_{out}$ : $U_{s}=-G_{diff}\times \left(U_{e}\times {\frac {R_{in}}{R_{in}+R_{f}}}+U_{s}\times {\frac {R_{f}}{R_{in}+R_{f}}}\right)$ On développe : $U_{s}=-G_{diff}\times U_{e}\times {\frac {R_{in}}{R_{in}+R_{f}}}-G_{diff}\times U_{s}\times {\frac {R_{f}}{R_{in}+R_{f}}}$ On réorganise les termes : $U_{s}+U_{s}\times {\frac {G_{diff}\times R_{f}}{R_{in}+R_{f}}}=-U_{e}\times {\frac {G_{diff}\times R_{in}}{R_{in}+R_{f}}}$ On factorise le terme de gauche : $U_{s}\left(1+{\frac {G_{diff}\times R_{f}}{R_{in}+R_{f}}}\right)=-U_{e}\times {\frac {G_{diff}\times R_{in}}{R_{in}+R_{f}}}$ On met au même dénominateur dans le terme de gauche : $U_{s}\left({\frac {R_{in}+R_{f}}{R_{in}+R_{f}}}+{\frac {G_{diff}\times R_{f}}{R_{in}+R_{f}}}\right)=-U_{e}\times {\frac {G_{diff}\times R_{in}}{R_{in}+R_{f}}}$ On simplifie : $U_{s}\left({\frac {R_{in}+R_{f}+G_{diff}\times R_{f}}{R_{in}+R_{f}}}\right)=-U_{e}\times {\frac {G_{diff}\times R_{in}}{R_{in}+R_{f}}}$ On isole alors $U_{s}$ : $U_{s}=-U_{e}\times {\frac {G_{diff}\times R_{in}}{R_{in}+R_{f}}}\times {\frac {R_{in}+R_{f}}{R_{in}+R_{f}+G_{diff}\times R_{f}}}$ On simplifie : $U_{s}=-V_{in}\times {\frac {G_{diff}\times R_{in}}{R_{in}+R_{f}+G_{diff}\times R_{f}}}$ Si on suppose que $G_{diff}$ est très grand par rapport aux valeurs des résistances, on a alors : $U_{s}\approx -U_{e}\times {\frac {R_{in}}{R_{f}}}$

Circuit équivalent d'un montage inverseur.

On peut aussi reformuler ce développement comme suit. On peut voir ce montage inverseur comme une amélioration du montage précédent, auquel on aurait rajouté une résistance sur l'entrée. Cette résistance convertit la tension d'entrée en un courant, qui est convertit par le reste du montage en une tension. Cela fonctionne parce que la tension sur l'entrée $e_{-}$ est nulle, ce qui fait que schéma équivalent du montage est celui illustré ci-contre. Vu que le courant d'entrée de l'AOP est nul, tout le courant passe dans les deux résistances. On a donc :

$i={\frac {U_{s}}{R_{2}}}={\frac {U_{e}}{R_{1}}}$

Quelques manipulations algébriques redonnent bien l'équation précédente.

On peut reformuler cette équation de manière à obtenir le gain de l'amplificateur :

$G={\frac {U_{s}}{U_{e}}}=-{\frac {R_{2}}{R_{1}}}$

On voit que le gain obtenu n'est pas égal au gain différentiel (ou au gain en mode commun). D'un côté le gain différentiel est supposé infini, de l'autre le gain réel dépend de la valeur des résistances. Cela nous amène à faire la distinction entre deux gains : le gain différentiel vu précédemment, et le gain obtenu avec les calculs de cette section. Le gain différentiel est une propriété de l'AOP quand celui-ci n'a pas de rétroaction, ce qui lui vaut son appellation de gain en boucle ouverte. Par contre, le gain mesuré dans un montage avec une rétroaction est différent. Ce gain est appelé gain en boucle fermée, pour signifier qu'il implique une boucle de rétroaction (négative).

Le montage sommateur-inverseur

Montage sommateur.

Le montage sommateur-inverseur est une amélioration du montage précédent, la différence étant que l'on a plusieurs tensions/résistances reliées à l'entrée $e_{-}$. Le montage additionne les tensions placées sur cette entrée et fournit en sortie l'inverse de cette somme. Pour le démontrer, repartons du second développement du montage inverseur. On sait que la tension $U_{-}$ est nulle.

Pour le courant qui circule dans la résistance $R_{f}$, on a :

$i=-{\frac {U_{s}}{R_{f}}}$

On peut aussi calculer la somme des courants qui circulent dans chaque résistance d'entrée, ce qui donne :

$i={\frac {U_{1}}{R_{1}}}+{\frac {U_{2}}{R_{2}}}+{\frac {U_{3}}{R_{3}}}+...+{\frac {U_{n}}{R_{n}}}$

Vu que le courant d'entrée de l'AOP est nul, les deux courants sont égaux :

$-{\frac {U_{s}}{R_{f}}}={\frac {U_{1}}{R_{1}}}+{\frac {U_{2}}{R_{2}}}+{\frac {U_{3}}{R_{3}}}+...+{\frac {U_{n}}{R_{n}}}$

En multipliant par $-R_{f}$, on a :

$U_{s}=-R_{f}\left({\frac {U_{1}}{R_{1}}}+{\frac {U_{2}}{R_{2}}}+{\frac {U_{3}}{R_{3}}}+...+{\frac {U_{n}}{R_{n}}}\right)=U_{1}{\frac {R_{f}}{R_{1}}}+U_{2}{\frac {R_{f}}{R_{2}}}+U_{3}{\frac {R_{f}}{R_{3}}}+...+U_{n}{\frac {R_{f}}{R_{n}}}$

Ce circuit additionne donc les tensions pondérées par chaque résistance.

Le montage amplificateur différentiel

Montage amplificateur différentiel.

Le montage en amplificateur différentiel est le même que le montage inverseur, si ce n'est qu'on a ajouté un pont diviseur sur la tension d'entrée.

La tension $U_{-}$ se calcule exactement comme avec le montage inverseur (théorème de Millmann/superposition), ce qui donne :

$U_{-}=U_{s}{\frac {R_{1}}{R_{1}+R_{f}}}+U_{1}{\frac {R_{f}}{R_{1}+R_{f}}}$

La tension $U_{+}$ se calcule avec un pont diviseur de tension :

$U_{+}=U_{2}{\frac {R_{g}}{R_{g}+R_{2}}}$

Les deux tensions sont égales, par les hypothèses de l'AOP parfait :

$U_{s}{\frac {R_{1}}{R_{1}+R_{f}}}+U_{1}{\frac {R_{f}}{R_{1}+R_{f}}}=U_{2}{\frac {R_{g}}{R_{g}+R_{2}}}$

On soustrait : $U_{1}{\frac {R_{f}}{R_{1}+R_{f}}}$ des deux côtés :

$U_{s}{\frac {R_{1}}{R_{1}+R_{f}}}=U_{2}{\frac {R_{g}}{R_{g}+R_{2}}}-U_{1}{\frac {R_{f}}{R_{1}+R_{f}}}$

On divise des deux côtés par : ${\frac {R_{1}}{R_{1}+R_{f}}}$ :

$U_{s}={\frac {R_{1}+R_{f}}{R_{1}}}\left(U_{2}{\frac {R_{g}}{R_{g}+R_{2}}}-U_{1}{\frac {R_{f}}{R_{1}+R_{f}}}\right)$

On développe :

$U_{s}=U_{2}\left({\frac {R_{1}+R_{f}}{R_{1}}}{\frac {R_{g}}{R_{g}+R_{2}}}\right)-U_{1}\left({\frac {R_{1}+R_{f}}{R_{1}}}{\frac {R_{f}}{R_{1}+R_{f}}}\right)$

On simplifie et on réarrange les termes :

$U_{s}=U_{2}\left({\frac {R_{1}+R_{f}}{R_{g}+R_{2}}}{\frac {R_{g}}{R_{1}}}\right)-U_{1}{\frac {R_{f}}{R_{1}}}$

Deux cas particuliers sont intéressants à étudier :

• Quand $R_{1}=R_{2}$ et $R_{f}=R_{g}$, on a :

$U_{s}={\frac {R_{f}}{R_{1}}}(U_{2}-U_{1})$

• Quand $R_{1}=R_{f}$ et $R_{2}=R_{g}$, on obtient le montage soustracteur :

$U_{s}=U_{2}-U_{1}$

Le montage amplificateur d'instrumentation

Le montage amplificateur d'instrumentation est une amélioration de l'amplificateur différentiel. Il suffit d'ajouter deux suiveurs sur les deux entrées du circuit pour obtenir un amplificateur d'instrumentation. Ce faisant, on est certain que les courants d'entrée de l'AOP (qui sont non-nuls pour un AOP réel) ne perturbent pas le fonctionnement du circuit.

Sur certains montages, on ajoute quelques résistances : une dans chaque boucle du suiveur, et une autre pour relier les deux boucles, afin d'améliorer le fonctionnement du circuit.

Montage amplificateur d'instrumentation sans résistances additionnelles.

Montage amplificateur d'instrumentation avec les résistances additionnelles.

Second montage avec les résistances additionnelles.

Le montage intégrateur

Montage intégrateur.

Le montage intégrateur ressemble au montage inverseur, si ce n'est qu'on a remplacé une résistance par un condensateur. Le montage est illustré ci-contre.

Si on suppose l'AOP parfait, il n'y a pas de courants d'entrée.

Aux bornes de la résistance, on a :

$i={\frac {U_{e}-U_{-}}{R}}={\frac {U_{e}}{R}}$

Au bornes du condensateur, on a :

$i=C{\frac {d(U_{s}-U_{-})}{dt}}=C{\frac {dU_{s}}{dt}}$

Le courant circule dans le circuit série formé par la résistance et le condensateur, ce qui fait qu'il est identique en tout point du circuit. Les deux courants des équations précédentes sont égaux, ce qui donne :

$C{\frac {dU_{s}}{dt}}={\frac {U_{e}(t)}{R}}$

Divisons par C :

${\frac {dU_{s}}{dt}}={\frac {U_{e}(t)}{RC}}$

Intégrons pour trouver $U_{s}$ :

$U_{s}=\int {\frac {U_{e}(t)}{RC}}dt$

Simplifions :

$U_{s}={\frac {1}{RC}}\int U_{e}(t)dt$

Ce circuit calcule donc l'intégrale de la tension d'entrée au cours du temps (pondérée par le produit RC). D'où son nom de montage intégrateur.

Le montage dérivateur

Montage dérivateur.

Si on inverse de place la résistance et le condensateur, le comportement du montage est changé du tout au tout. De montage intégrateur, il passe à un montage dérivateur, qui calcule la dérivée de la tension d'entrée. Pour le démontrer, il faut refaire les développements de la section précédente. La seule différence est que la tension d'entrée et de sortie seront inversées. Évidemment, on suppose l'AOP parfait, ce qui fait qu'il n'y a pas de courants d'entrée.

Aux bornes de la résistance, on a :

$i={\frac {U_{s}-U_{-}}{R}}={\frac {U_{s}}{R}}$

Au bornes du condensateur, on a :

$i=C{\frac {d(U_{e}-U_{-})}{dt}}=C{\frac {dU_{e}}{dt}}$

Les deux courants précédents sont égaux, ce qui donne :

${\frac {U_{s}(t)}{R}}=C{\frac {dU_{e}}{dt}}$

Multiplions par R :

$U_{s}(t)=RC{\frac {dU_{e}}{dt}}$

Ce circuit calcule donc la dérivée de la tension d'entrée au cours du temps (pondérée par le produit RC).

Le montage exponentiel

Montage exponentiel.

Le montage exponentiel est une amélioration du montage convertisseur courant-tension : on a rajouté une diode sur l'entrée du montage. Et cette fois-ci, on envoie une tension sur l'entrée du montage, et non un courant.

La diode ne change pas grand chose au fonctionnement du montage, vu que la chute de tension à ses bornes est négligeable. On a toujours :

$U_{s}=-R\times I_{e}$

Par contre, on peut le courant qui parcourt le circuit est le courant fournit par la diode (en fonction de la tension d'entrée). Celui-ci vaut, d'après l'équation de Schokley vue il y a quelques chapitres :

$I_{e}\approx I_{s}\times e^{\frac {U_{e}}{U_{t}}}$

En combinant les deux expressions précédentes, on a :

$U_{s}=-R\times I_{s}\times e^{\frac {U_{e}}{U_{t}}}$

En clair, ce montage calcule l'exponentielle de la tension d'entrée, à un coefficient de proportionnalité près.

En réalité, l'équation de Schokley d'une diode n'est pas $I_{e}\approx I_{s}\times e^{\frac {U_{-}}{U_{t}}}$, mais : $I_{e}=I_{s}\times \left(e^{\frac {U_{-}}{U_{t}}}-1\right)$. Cela modifie quelque peu les calculs, ce qui donne l'équation suivante :

$U_{s}=-R\times I_{s}\times e^{\left({\frac {U_{e}}{U_{t}}}-1\right)}$

Le montage logarithmique

Montage logarithmique.

Le montage logarithmique est une variante du montage précédent, dans lequel la diode et la résistance échangent leurs places.

Ici, la diode est alimentée par la tension $U_{-}$, ce qui fait que le courant qui traverse le circuit est de :

$I_{e}\approx I_{s}\times e^{\frac {U_{-}}{U_{t}}}$

On a toujours $U_{+}=U_{-}=U_{s}$, ce qui donne :

$U_{e}=-R\times I_{e}$

En combinant les deux expressions précédentes, on a :

$U_{e}=R\times I_{s}\cdot e^{\frac {U_{-}}{U_{t}}}$

On peut reformuler l'expression comme suit :

$e^{\frac {U_{-}}{U_{t}}}=-{\frac {U_{e}}{R\times I_{s}}}$

Prenons le logarithme des deux côtés :

${\frac {U_{-}}{U_{t}}}=-\log {\left({\frac {U_{e}}{R\times I_{s}}}\right)}$

Multiplions par la tension de seuil de la diode $U_{t}$ :

$U_{s}=-U_{t}\times \log {\left({\frac {U_{e}}{R\times I_{s}}}\right)}$

En clair, ce montage calcule le logarithme de la tension d'entrée, à un coefficient de proportionnalité près.

En réalité, l'équation de Schokley d'une diode n'est pas $I_{e}\approx I_{s}\times e^{\frac {U_{-}}{U_{t}}}$, mais : $I_{e}=I_{s}\times \left(e^{\frac {U_{-}}{U_{t}}}-1\right)$. Cela modifie quelque peu les calculs, ce qui donne l'équation suivante :

$U_{s}=-U_{t}\times \log {\left({\frac {U_{e}}{R\times I_{s}}}+1\right)}$

Nous en aurons besoin dans la section suivante.

Le montage multiplieur

Le montage multiplieur fournit en sortie le produit des deux tensions d'entrée. Il est composé avec l'aide des circuits exponentiels, logarithmiques, inverseurs et sommateurs vus plus haut. L'idée qui se cache derrière ce circuit est redoutablement simple, pour qui connait les propriétés des logarithmes. On sait que le logarithme d'un produit est égal à la somme des logarithmes. Cette propriété a durant longtemps été exploitée pour faire des multiplications à la main, pour des opérandes étaient assez grandes. Il suffit de réutiliser ce principe ici : on prend les logarithmes de chaque entrée, on les additionne, puis on prend l'exponentielle du résultat pour obtenir le résultat final. En clair, on a un montage logarithmique sur chaque entrée, un circuit sommateur, et enfin un montage exponentiel. Le circuit final est illustré ci-dessous.

Montage multiplieur analogique.

On peut créer le circuit sommateur de plusieurs manières. La méthode la plus évidente est d'utiliser un montage inverseur-sommateur, suivi par un montage inverseur (pour compenser l'inversion réalisée par le montage inverseur-sommateur). Mais il existe une autre solution, bien plus élégante. Avec elle, les sorties des montages logarithmiques sont placées en série avec une résistance, pour transformer la tension (le logarithme), en un courant proportionnel. Puis, les deux fils sont reliés/fusionnés : la loi des nœuds fait que les deux courants sont additionnés. Enfin, on fait passer le courant obtenu (la somme des courants logarithmiques) dans un montage de conversion courant-tension. Le circuit total, montages exponentiels et logarithmiques inclus, est celui-ci :

Montage multiplieur analogique avec sommation des courants.

En réalité, ce montage ne marche pas parfaitement, pour une raison simple : le montage logarithmique ne calcule pas exactement le logarithme, mais fait le calcul suivant :

$U_{1}=-U_{t}\times \log {\left({\frac {U_{e}}{R\times I_{s}}}+1\right)}$

La somme des deux logarithmes donne donc :

$U_{sum}=-U_{t}\times \left[\log {\left({\frac {U_{1}}{R\times I_{s}}}+1\right)}+\log {\left({\frac {U_{1}}{R\times I_{s}}}+1\right)}\right]$

En appliquant la règle $\log {(a+b)}=\log {a}+\log {b}$ on a :

$U_{sum}=-U_{t}\times \log {\left[\left({\frac {U_{1}}{R\times I_{s}}}+1\right)\times \left({\frac {U_{1}}{R\times I_{s}}}+1\right)\right]}$

En appliquant le montage exponentiel, on trouve :

$U_{s}=-R\times I\times e^{\left({\frac {U_{sum}}{U_{t}}}-1\right)}$

Ce qui se simplifie en :

$U_{s}=-{\frac {U_{1}\times U_{2}}{R\times I}}-(U_{1}+U_{2})$

Il faut donc ajouter les deux tensions d'entrée au résultat pour obtenir le bon résultat. Il suffit d'ajouter un montage sommateur, ce qui donne le circuit suivant :

Circuit multiplieur complet.

Les montages en mode comparateur (rétroaction positive ou absence de rétroaction)

Les montages précédents utilisent tous une contre-réaction négative, à savoir qu'ils relient la sortie à l'entrée $e_{-}$. Cette contre-réaction négative fait fonctionner l'AOP dans le régime linéaire et la sortie tend à être stable autour d'une valeur d'équilibre. Mais il est aussi possible de relier la sortie à l'entrée positive $e_{+}$. Dans ce cas, le circuit fonctionne tout autrement. Le circuit fonctionne alors en mode de saturation, à savoir que sa sortie est égale à la valeur maximale ou minimale que peut fournir l'AOP. Les circuits qui utilisent cette propriété sont généralement des comparateurs de tension, qui comparent les deux tensions d'entrée entre elles, ou qui comparent une tension d'entrée à un seuil prédéfini. Dans cette section, nous allons voir les montages qui utilisent une contre-réaction positive, et notamment les comparateurs.

Le comparateur à un seuil (absence de rétroaction)

Pour commencer cette section, je me dois de faire une digression sur l'AOP en mode de saturation. Un AOP parfait est, par définition, un comparateur. En effet, son comportement en régime de saturation est défini par les deux équations suivantes :

Si $U_{+}>U_{-}$ : $U_{s}=+VCC$

Si $U_{+}<U_{-}$ : $U_{s}=-VCC$

Un simple AOP, sans contre-réaction, permet de réaliser un circuit qui compare la tension d'entrée à un seuil. Si la tension est sous le seuil, $U_{s}=-VCC$. Mais si la tension d'entrée dépasse ce seuil : $U_{s}=+VCC$. Pour cela, il suffit de placer la tension de seuil sur l'entrée $e_{-}$ et de mettre la tension d'entrée sur l'entrée $e_{+}$. Ce circuit est appelé un comparateur à un seuil.

Le schéma ci-dessous illustre un comparateur à un seuil qui compare la tension d'entrée au seuil $VCC \over 2$.

Exemple d'un comparateur à un seuil qui compare la tension d'entrée au seuil $VCC \over 2$.

Le circuit comparateur à deux seuils (trigger de Schmitt)

Le circuit précédent n'utilise pas de rétroaction. Les circuits que nous allons voir dans cette section utilisent une rétroaction positive, qui garantit qu'ils fonctionnent en saturation. Pour comprendre pourquoi l'AOP fonctionne en saturation, étudions ce qui se passe quand la tension différentielle est positive. En clair la tension d'entrée du circuit est telle que la sortie de l'AOP est positive. La tension de sortie positive est alors renvoyée en entrée, où elle s'ajoute à la tension d'entrée préexistante. La tension d'entrée finale augmente donc, ce qui fait encore augmenter la tension de sortie de l'AOP. Et la boucle recommence, la tension de sortie augmentant jusqu’à ce que l'AOP atteigne sa tension maximale. Pour le cas où la tension d'entrée fait que la tension d'entrée est négative, c'est le même raisonnement, si ce n'est que la tension de sortie sera négative. On voit donc que la rétroaction fait que le processus 'emballe : de petites différences d'entrées s'amplifient de plus en plus, jusqu’à ce que l'AOP atteigne sa tension maximale ou minimale.

Courbe d’hystérésis.

Le comparateur à deux seuils est un comparateur un peu spécial. Il dispose non pas d'un seuil, mais de deux seuils de basculement. Lorsque le premier seuil est franchit, le circuit voit sa sortie passer de -VCC à +VCC. Le second seuil est pour l'opération inverse : quand la tension d'entrée descend en-dessous de ce second seuil, la sortie passe de +VCC à -VCC. Le premier seuil (passage de -VCC à +VCC) est appelé le seuil positif, alors que l'autre est appelé le seuil négatif. La raison est, pour la majorité des montages, ces deux seuils ont la même valeur absolue, mais des signes différents.

Le fonctionnement de ce circuit est résumé dans le schéma ci-contre. Ce schéma est appelé une courbe d'Hystérésis. L'interprétation de cette courbe est la suivante. Supposons que la tension d'entrée soit comprise au-delà du seuil T : la sortie est donc égale à +VCC. Imaginons maintenant qu'elle descende en-dessous du seuil T, mais reste supérieure à -T. Dans ce cas, la sortie restera à +VCC. Ce n'est que quand elle descendra sous le seuil - T que la sortie basculera à -VCC. Ensuite, imaginons que l'entrée, initialement sous le seuil -T, dépasse ce seuil et augmente progressivement. Rien ne se passe tant que l'entrée n'a pas dépassé le seuil de basculement T et la sortie reste à -VCC. Ce n'est qu'une fois le seuil T dépassé que la sortie bascule à +VCC. Les flèches indiquent comment interpréter ces basculements et les hausses/baisses de tension de sortie selon l'entrée.

Pour résumer :

• Si l'entrée est en-dessous du seuil négatif -T, la sortie est à -VCC.
• Si l'entrée est au-dessus du seuil positif +T, la sortie est à +VCC.
• Entre les deux, la sortie garde sa valeur précédente, qui est de +VCC ou de -VCC selon l'histoire du circuit.

Le comparateur à deux seuils inverseur

Comparateur à deux seuils inverseur

Il existe deux circuits comparateurs à deux seuils, qui ressemblent aux circuits inverseur et non-inverseur obtenus avec contre-réaction négative. La seule différence est que la contre-réaction est ici placée sur la borne $e_{+}$ et non $e_{-}$. Le circuit inverseur est montré ci-contre.

On voit immédiatement que la tension $U_{+}$ est obtenue par un pont diviseur de tension, ce qui donne :

$U_{+}=U_{s}{\frac {R_{1}}{R_{2}+R_{1}}}$

Vu que l'AOP est en mode de saturation, $U_{s}$ peut prendre deux valeurs possibles : +VCC et -VCC. En injectant ces deux valeurs dans l'équation précédente, on trouve l'expression des deux seuils :

$U_{seuil^{+}}=VCC{\frac {R_{1}}{R_{2}+R_{1}}}$ : seuil positif.

$U_{seuil^{-}}=-VCC{\frac {R_{1}}{R_{2}+R_{1}}}$ : seuil négatif.

Le comparateur à deux seuils non-inverseur

Comparateur à deux seuils non-inverseur

Passons maintenant au circuit non-inverseur.

Cette fois-ci, on doit utiliser le théorème de superposition (ou de Milmann, c'est selon) pour analyser ce circuit (comme on l'avait fait avec le montage non-inverseur). On a alors :

$U_{+}=U_{s}{\frac {R_{1}}{R_{2}+R_{1}}}+U_{in}{\frac {R_{2}}{R_{2}+R_{1}}}$

Vu que l'AOP est en mode de saturation, $U_{s}$ peut prendre deux valeurs possibles : +VCC et -VCC. En injectant ces deux valeurs dans l'équation précédente, on trouve a :

$U_{+}=VCC{\frac {R_{1}}{R_{2}+R_{1}}}+U_{in}{\frac {R_{2}}{R_{2}+R_{1}}}$

$U_{+}=-VCC{\frac {R_{1}}{R_{2}+R_{1}}}+U_{in}{\frac {R_{2}}{R_{2}+R_{1}}}$

Reste alors à trouver la tension $U_{in}$ qui annule la tension différentielle (et donc la tension $U_{+}$), pour trouver les tensions de seuil. Quelques manipulations algébriques triviales donnent alors :

$U_{seuil^{+}}=VCC\left({\frac {R_{1}}{R_{2}}}\right)$ : seuil positif.

$U_{seuil^{-}}=-VCC\left({\frac {R_{1}}{R_{2}}}\right)$ : seuil positif.