Cosmologie/Version imprimable

Cosmologie

Une version à jour et éditable de ce livre est disponible sur Wikilivres,
une bibliothèque de livres pédagogiques, à l'URL :
https://fr.wikibooks.org/wiki/Cosmologie

Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la Licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans Texte de dernière page de couverture. Une copie de cette licence est incluse dans l'annexe nommée « Licence de documentation libre GNU ».

Le paradoxe d'Olbers

Nous allons commencer ce cours avec une question simple, qui est paradoxalement une excellente introduction à la cosmologie :

Pourquoi la nuit est-elle noire ?

Cette question peut sembler étrange, tant nous sommes habitués à voir les étoiles sur un fond noir. Bien que la lumière artificielle nous cache les étoiles et éclaire le ciel nocturne, nous savons que cette lumière cache le noir de la nuit, ses étoiles et la Lune. Mais pour un scientifique, même les choses évidentes sont dignes d'intérêt et demandent à être expliquées.

Les astronomes de l'antiquité n'étaient eux-mêmes pas surpris par l'obscurité de la nuit. Pour simplifier, ils pensaient les étoiles attachées à une sphère céleste, une sorte de sphère/coupole géante qui recouvre le ciel. S'ils supposaient que la Terre tourne sur elle-même, ils supposaient la sphère céleste fixe, expliquant le mouvement des étoiles au cours de la nuit et des saisons. Pour être plus précis, leur pensée utilisait plusieurs sphères : une pour le Soleil, une pour la Lune, une pour les étoiles proches, une pour les étoiles fixes des constellations (la plus lointaine) et bien d'autres. L'explication au noir de la nuit était que les étoiles étaient en nombre limitées et à des endroits bien précis, elles ne recouvraient pas entièrement le ciel. Beaucoup de savants avaient compris que ce modèle de sphères concentriques était un artifice de calcul utile, mais fondamentalement faux. Néanmoins, l'explication fondamentale au noir de la nuit restait valide : il n'y avait pas assez d'étoiles pour illuminer le ciel.

Terre dans la sphère céleste.

Sphères célestes emboîtées d'Anaximandre.

Avec les progrès de l'astronomie, et notamment l'arrivée des modèles géocentriques et héliocentriques, ce modèle de sphères emboîtées fût remis en cause. Pour les astronomes du moyen-âge et de la renaissance, les étoiles et astres n'étaient pas fixés sur des sphères proches, mais peuvent emplir tout l'espace. Leur vision de l'univers évolua vers un modèle d'univers infini, immobile, éternel, homogène. Par immobile, on veut dire que les effets de la gravité des astres s'annulent mutuellement sur de grandes distances. Chaque galaxie s'éloigne ou se rapproche de la nôtre, mais dans l'ensemble, ces différents mouvements se compensent et la moyenne des vitesses des galaxies est nulle. Par infini, on veut dire que l'univers a un volume infini : il n'a pas de début ni de fin, pas de frontières ou de bords, etc. Par éternel, on veut dire qu'il a un âge infini, qu'il n'a pas de début et de fin. Et par homogène, on veut dire que la répartition des étoiles est supposée globalement uniforme à grande échelle.

Mais les astronomes du moyen-âge et de la renaissance comprirent rapidement que le noir de la nuit était incompatible avec ce qu'ils savaient de l'univers.

Le paradoxe d'Olbers

Le modèle d'un univers infini, immobile, éternel, homogène est assez logique, limite intuitive, mais elle entre en conflit avec le noir de la nuit. Plusieurs savant ont en effet montré qu'un tel univers devrait avoir une nuit extrêmement lumineuse, et certainement pas une nuit noire. Cela peut paraitre étonnant, mais plusieurs astronomes l'ont déduit mathématiquement ou sur la base d'arguments logiques. C'est un paradoxe, appelé paradoxe d'Olbers, nommé ainsi en l'honneur d'Olbers , un des astronomes à avoir évoqué ce paradoxe. D'autres astronomes avaient autrefois évoqué ce paradoxe, comme Thomas Digges en 1576, Johannes Kepler en 1605 ou Edmond Halley au XVIIIe siècle, mais pas aussi explicitement qu'Olbers.

Nombre d'étoiles visibles depuis la Terre en fonction de leur distance.

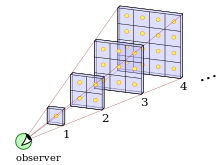
Logiquement, on s'attend à ce que la nuit soit noire car les étoiles lointaines nous envoient directement moins de lumière que les étoiles proches. Après tout, la lumière émise par un objet est répartie dans toutes les directions, ce qui fait que plus un objet est lointain, moins on reçoit sa lumière. La luminosité perçue depuis la Terre diminue avec la distance, et plus précisément avec le carré de la distance. Mais il se trouve que le diamètre apparent fait de même. Le résultat est que pour une portion du ciel d'une surface bien précise, on peut mettre soit peu d'étoiles proches, soit beaucoup d'étoiles lointaines. Il se trouve que sous certaines conditions, respectées dans l'univers infini, éternel et homogène, les deux phénomènes se compensent et que la luminosité d'une portion du ciel est globalement constante.

La lumière des étoiles se déplaçant dans le vide intersidéral en ligne droite, les étoiles sont visibles depuis la Terre tant qu'il n'y a pas d'obstacle entre elles et la Terre. Or, si l'univers est infini, éternel et homogène, alors on est certain qu'en tout point du ciel, on tombera sur au moins une étoile. Si l’univers est infini, il contient une infinité d'étoiles. Et s'il existe depuis un temps infini, la lumière de toutes ces étoiles a eu le temps d'atteindre la Terre. En conséquence, le ciel devrait être éclairé par une infinité d'étoiles. La répartition homogène des étoiles assure que ces étoiles soient réparties équitablement sur la sphère céleste, ce qui fait que peu importe où on regarde de la voûte céleste, on devrait y voir une étoile à cet endroit.

Avec ces conditions, la baisse de quantité de lumière reçue avec la distance est compensée par le plus grand nombre d'étoiles observables. Le schéma ci-contre illustre ce fait. Pour résumer, le ciel devrait être empli de lumière, cachant totalement le Soleil. C'était pour eux un paradoxe, appelé paradoxe d'Olbers, du nom de l'astronome qui le formalisa (d'autres astronomes, comme Kepler, avaient cependant mentionné ce paradoxe dans certains écrits, mais pas aussi explicitement qu'Olbers).

Pour mieux comprendre le problème, nous allons reprendre un développement mathématique assez connu qui formalise l'argument d'Olbers.

Modélisation de la répartition des étoiles

En premier lieu, on découpe l'univers en sphères concentriques. Chaque couche, chaque sphère, a une épaisseur $D$ égale à la distance moyenne entre deux étoiles. De plus, chaque couche est à une distance $R$ de la Terre.

Illustration d'une couche sphérique dans la démonstration d'Olbers.

Calcul du nombre d'étoile dans chaque couche

En second lieu, on calcule le nombre d'étoiles présentes dans chaque "sphère", dans chaque coque.

Pour cela, on utilise l'hypothèse suivante :

H1 : Les étoiles sont uniformément réparties.

Cette hypothèse dit que la densité d'étoile, à savoir le nombre d'étoiles par unité de volume, est constante. Dans ce qui suit, nous allons la noter $n$.

Chaque "sphère", chaque coque, contient un nombre d'étoile égal à son volume multiplié par $n$ :

$N=n\times V$

Le volume d'une coque est approximativement égal à sa surface S multipliée par son épaisseur (la distance moyenne entre deux étoiles, notée D), ce qui donne :

$V=S\times R=4\pi R^{2}\times D$

En combinant les deux équations précédentes, on a :

$N=n\times 4\pi R^{2}\times D$

Calcul du flux de lumière émis par les étoiles d'une couche

En troisième lieu, on calcule le flux de lumière émis par une couche.

Pour cela, on part de l'hypothèse suivante :

H2 : Toutes les étoiles ont la même luminosité L.

On va utiliser cette hypothèse pour calculer le flux de lumière de chaque étoile. La physique du rayonnement nous dit que ce flux est égal à :

$f_{etoile}={\frac {L}{4\pi R^{2}}}$

Le flux émis par toutes les étoiles d'une couche est la somme des flux de chaque étoile de la couche :

$f_{couche}=f_{etoile}\times N=N\times {\frac {L}{4\pi R^{2}}}$

On utilise alors l'équation $N=n\times 4\pi R^{2}\times D$, démontrée plus haut :

$f_{couche}=(n\times 4\pi R^{2}\times D)\times {\frac {L}{4\pi R^{2}}}$

On simplifie :

$f_{couche}=n\times D\times L$

Cette équation nous dit que toutes les couches émettent la même quantité de lumière, ce qui n'est pas intuitif...

Calcul de la luminosité du ciel

En quatrième lieu, on combine la luminosité de toutes les couches pour trouver la luminosité totale du ciel.

Pour cela, on utilise les hypothèses suivantes :

H3 : Toutes les étoiles sont visibles depuis la Terre, il n'y a pas d'obstacle entre une étoile et la Terre.

Cela signifie qu'il faut prendre en compte toutes les couches dans le calculs.

H4 : L'univers est infini.

Le fait que l'univers est infini nous dit qu'il existe une infinité de couches concentriques.

H4 : L'univers est éternel.

Le fait que l'univers est éternel nous dit que la lumière de toutes les étoiles a eu le temps d'atteindre la Terre.

Illustration du paradoxe d'Olbers, en ajoutant progressivement chaque couche d'étoiles.

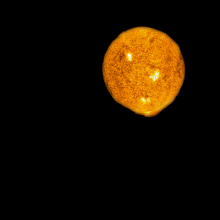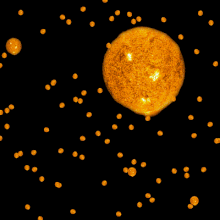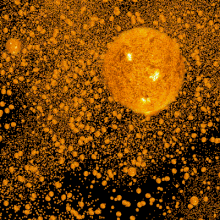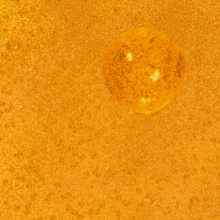
Il faut donc additionner la luminosité de toutes les couches existantes pour trouver le flux de lumière visible dans le ciel, en faisant une intégrale. Nous n'allons pas faire le calcul, car il se trouve qu'on obtient un résultat infini. Intuitivement, la troisième étape suffit à comprendre pourquoi : chaque couche a une luminosité finie et identique à celle des autres couches, et il y a une infinité de couches. Le ciel devrait être infiniment lumineux !

Les "solutions" du paradoxe d'Olbers

Divers savants se sont écharpés sur le paradoxe d'Olbers et de nombreuses réponses y ont été apportées. La démonstration d'Olbers n'ayant pas de problèmes mathématiques particuliers, il fallu se rendre à l'évidence : certaines hypothèses utilisées dans la démonstration sont fausses. Reste à trouver lesquelles.

On peut remettre en cause l'hypothèse de la luminosité fixe des étoiles, mais cela ne mène à rien. Même en supposant que certaines étoiles émettent peu ou pas de lumière, on se retrouve quand même avec une somme infinie.

Remettre en cause la répartition des étoiles a été envisagé, notamment dans des théories qui supposaient que la répartition des étoiles/galaxies était une distribution fractale. Ces théories sont cependant restées au stade de théories irréalistes, dont l'utilité est de montrer que telle piste de recherche est envisageable. La raison à cela est que les résultats empiriques ne suivent pas : dans ces théories, on devrait avoir des endroits du ciel qui seraient extrêmement lumineux, bien plus que le Soleil. Les observations astronomiques montrent de plus que si l'univers est assez hétérogène à petite distance, il est fortement homogène à grande distance.

Une première possibilité "crédible" était que les étoiles lointaines ne sont pas visibles depuis la Terre. Leur lumière est bien émise mais n'arrive pas à destination, reste à en trouver la raison. Une première explication fût que la lumière était absorbée par des nuages de gaz, de poussière, ou tout autre obstacle entre les étoiles et la Terre. Mais cette explication était incorrecte. L'obstacle en question absorbe le rayonnement de l'étoile, ce qui le chauffe. Or, tout corps chauffé émet un rayonnement dit de corps noir, dont l'intensité augmente avec la température. À force de chauffer, l'obstacle atteint une température d'équilibre, où le rayonnement absorbé par l'obstacle est intégralement réémis vers la Terre. L'obstacle est alors aussi lumineux que l'étoile qui le chauffe. Retour à la case départ.

La seule solution est que l'univers n'est pas infini et/ou qu'il a un âge fini. Les deux solutions font que l'on ne doit additionner que les couches les plus proches de la Terre, situées en-dessous d'un rayon maximal $R_{max}$.

• Si l'univers a un volume fini, il a de de facto un rayon maximal $R_{max}$.
• S'il a un âge fini $T_{univers}$, la lumière des étoiles très éloignées n'a pas eu le temps d'arriver sur Terre. Au-delà de la distance $R_{max}=T_{univers}\times c$ ($c$ est la vitesse de la lumière), la lumière n'a pas encore pu arriver jusqu’à la Terre.

Le décalage vers le rouge (redshift)

Peu après la découverte des galaxies, à la moitié des années 20, les astronomes ont entrepris d'étudier les étoiles et les galaxies à partir de la lumière qu'elles émettent. Les observations actuelles utilisent soit des étoiles variables (des céphéides), soit des étoiles qui explosent : les supernovas. Plus précisément, les astronomes utilisent une classe bien précise de supernovas, qui ont pour particularité de générer systématiquement la même luminosité : les supernovas de type Ia. La luminosité perçue depuis la Terre de ces supernovas est proportionnelle à la distance.

Les astronomes analysent la lumière émise par les étoiles et galaxies, afin d'en déduire énormément de chose. Ils ne se contentent pas d'analyser la luminosité ou la couleur des objets, ils étudient le spectre de la lumière émise. Par spectre, on veut dire l'ensemble des fréquences présente dans la lumière émise. Les galaxies et étoiles émettent de la lumière qui est une superposition d'onde électromagnétiques aux fréquences très diverses. L'ensemble forme ce qu'on appelle le spectre de la lumière et il ressemble à ceci :

Spectre électromagnétique de l'étoile Altair (01F8GF7Z3Q28EJBC051YNTMJ2X).

Les trous dans le spectre, les bandes noires, s'expliquent par l'absorption de la lumière par les atomes. Les atomes absorbent la lumière dans des bandes de fréquence très précises, bandes qui sont des endroits très précis suivant l’élément chimique en question. La position des bandes permet de déterminer la composition chimique des étoiles/galaxies. L'étude des spectres de la lumière s'appelle la spectroscopie et astronomes l'utilisent beaucoup dans leurs observations astronomiques.

Mystery star spectrum

Illustration du redshift. La lumière émise par l'objet est à gauche, alors que la lumière reçue par l'observateur est à droite. On voit que la lumière émise est perçue comme décalée, du point de vue du spectre, entre émetteur et observateur.

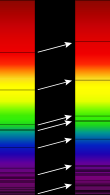
Le redshift des galaxies

Si vous étudiez le spectre d'une galaxie, bous allez tomber sur la situation ci-contre. Les bandes semblent décalées par rapport à la fréquence habituelle. Les distances entre les bandes sont conservées, toutes les bandes semblent s'être décalées en bloc. Tout se passe comme si la lumière semble être décalée vers les basses fréquences (le rouge), comparée à sa couleur d'émission. Ce phénomène s'appelle le décalage vers le rouge ou encore le redshift.

Il est possible de quantifier le redshift par un paramètre mathématique noté $z$. Pour quantifier ce phénomène, les physiciens utilisent le rapport entre le décalage des longueurs d'onde, et la longueur d'onde normale, attendue, celle mesurée sur Terre. Cette quantité, notée $z$, est appelée le décalage vers le rouge, ou encore le redshift.

$z={\frac {\lambda (t)-\lambda (t_{0})}{\lambda (t_{0})}}={\frac {\lambda (t)}{\lambda (t_{0})}}-1$, avec $\lambda (t)$ la longueur d'onde actuelle, mesurée lors d'une observation, et $\lambda (t_{0})$ la longueur d'onde lors de l'émission du rayonnement.

Les observations sur les galaxies ont montré la présence de ce décalage vers le rouge, sans pour autant pouvoir l'expliquer. Un point intriguant est que le redshift varie fortement avec la distance. Plus une galaxie est éloignée, plus son spectre sera décalé vers le rouge.

La loi de Hubble

Hubble a été le premier astronome à mettre en équation ce comportement, dans son article daté de 1929. Il étudia un grand nombre d'observations provenant de ses collègues, ainsi que les observations qu'il avait effectuées lui-même. De ces observations, il induit une loi statistique, du nom de loi de Hubble. Dans sa formulation la plus fiable, elle dit que pour les galaxies proches, le redshift est proportionnel à la distance.

$z(D)\propto D$

Suite à la découverte de Hubble, de nombreuses campagnes d'observations ont suivi et se sont poursuivies durant des décennies. Un exemple de résultats obtenus est le suivant. On voit que la relation de Hubble

Hubble constant

La loi de Hubble ne fonctionne pas à longue distance

Insistons sur le fait que la loi de Hubble ne fonctionne que pour des objets cosmologiques "proches". Par proche, on veut dire que leur décalage vers le rouge est proche de 1, guère plus. Pour de tels objets astronomiques, la concordance est franchement bonne. Mais pour les objets astronomiques plus lointains, la loi de Hubble ne fonctionne tout simplement pas et la relation entre distance et redshift devient tout autre. Elle cesse d'être linéaire, et devient alors beaucoup plus complexe.

Idéalement, il faudrait trouver une équation du redshift qui marche tout le temps. De telles formules empiriques existent, de même que d'autres formules basées sur la théorie de la relativité générale. Les scientifiques ont des logiciels dédiés pour faire les calculs et on peut trouver des calculateurs en ligne pour. Par exemple, vous pouvez utiliser ce site pour faire quelques calculs de distance en fonction du redshift :

• Calculateur cosmologique

L'interprétation de la relation redshift-distance

Maintenant que nous connaissons la relation entre distance et redshift, encore faut-il l'expliquer. Et c'est là que le bât blesse ! Pour expliquer le décalage vers le rouge, il existe plusieurs solutions. Mais, comme nous allons le voir, les explications classiques sont rapidement mises en défaut.

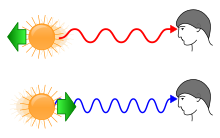
L'explication par l'effet Doppler

Pour expliquer le décalage vers le rouge des galaxies, Hubble pensa à l'effet Doppler-Fizeau, que les étudiants en physique connaissent bien. Quand un objet s'éloigne de nous à une certaine vitesse, la fréquence de la lumière qu'il émet baisse et la lumière parait rougie par rapport à la normale. Et réciproquement, un objet qui s'approche émettra une lumière plus bleuie, dont la fréquence a légèrement augmenté. Le redshift est alors causé par la vitesse de l'objet qui s'approche ou s'éloigne.

Illustration de l'effet Doppler-Fizeau.

La loi de Hubble proprement dite

Il existe une formule qui associe la vitesse de l'objet et le décalage vers le rouge, qui est différente selon que l'on travaille en physique newtonienne, en relativité restreinte ou en relativité générale. La physique classique donne la formule suivante, entre la vitesse de l'objet en mouvement et le décalage vers le rouge qui en découle.

$z(v)={\frac {v}{c}}$

On peut réécrire la formule précédente de manière à obtenir la vitesse de l'objet à partir de son redshift :

$v(z)={\frac {z(t)}{c}}$

En utilisant cette formule et en combinant celle-ci à ses observations sur le redshift, Hubble formula une loi statistique, du nom de loi de Hubble, dit que la vitesse d'éloignement d'une galaxie est proportionnelle à sa distance. Le facteur de proportionnalité nommée paramètre de Hubble, il est noté H.

$v=H\times d$, où v est la vitesse extrapolée du redshift, d la distance de la galaxie et H le facteur de Hubble.

La formule précédente est en réalité une extrapolation basée sur l'hypothèse que le redshift est bien causé par une vitesse. En réalité, ce qu'Hubble avait observé, c'est que le redshift était égal à :

$z(v)={\frac {H}{c}}\cdot d(t)$

La loi de Hubble est approximative, car les galaxies ne s'éloignent pas toutes à la même vitesse. Certaines vont plus vite, d'autres moins vite. Il faut faire la différence entre la vitesse donnée par la loi de Hubble, qui est une moyenne, et la différence avec la vitesse moyenne.

Distance v velocity

L'interprétation en termes de vitesse était tout simplement fausse et il n'a pas fallu longtemps pour s'en rendre compte. Appliquées de manière naïve à des galaxies lointaines, les redshift observés correspondent à des vitesses supérieures à celle de la lumière dans le vide. De telles vitesses supraluminiques sont un signe que la cause du décalage vers le rouge demande une explication relativiste. Une manière de sauver le tout serait d'utiliser des formules d'effet Doppler tirées de la relativité restreinte, plus adaptées aux forts redshifts, mais nous verrons plus bas que de telles explications ne marchent pas.

L'expansion de l'univers

Expansion de l'univers, image d'artiste.

L'interprétation initiale, à base d'effet Doppler, indique que les galaxies s'éloignent toutes de nous, comme si nous étions au centre de l'univers, et que les galaxies tentaient de le fuir. La conclusion est claire : l'univers s'étend, gonfle. Les astronomes ont appelé ce phénomène l'expansion de l'univers. Pourtant, on aurait dû s'attendre à l'inverse : la gravité est censée rapprocher les galaxies les unes des autres.

A cause de l'expansion de l'univers, il est évident que l'univers devait être plus "petit" par le passé (plus précisément, la portion de l'univers qui correspond aujourd'hui à l'univers observable). En renversant l'écoulement du temps, l'univers se contracte progressivement, et on peut facilement imaginer qu'après un certain temps, tout le contenu de l'univers soit rassemblé en un seul point : la singularité initiale. L'univers serait alors né d'une dilatation de cette singularité initiale, dilatation qui porte le nom de big-bang.

Mais cette vue de l'esprit pose de nombreux problèmes mathématiques. En effet, cette singularité implique que de nombreux calculs dépendant des distances donnent des divisions par zéro. Par exemple, le calcul de la pression, de la température, de la densité, ou d'autres paramètres physiques ne sont pas calculables. Tout ce que peuvent faire les scientifiques, c'est étudier ce qu'il s'est passé quelques secondes ou minutes après le temps qui correspond à cette singularité hypothétique. Les calculs actuels ne donnent plus de résultats crédibles au-delà d'une certaine durée, la durée de Planck. Celle-ci vaut environ $5{,}391\ 06(32)\times 10^{-44}$ secondes.

L'expansion de l'univers est une manière d'expliquer les observations de Hubble, qui est compatible avec l'interprétation du redshift comme un effet Doppler. Cependant, le fait que les redshift donnent des vitesses supra-luminiques semblent indiquer qu'il faut expliquer tout cela avec une théorie relativiste. Voyons ce que la relativité peut dire là dessus.

L'explication par le décalage vers le rouge gravitationnel

Une autre explication est le décalage vers le rouge gravitationnel, aussi appelé décalage d'Einstein. Il s'agit d'une conséquence de la relativité générale, observé expérimentalement. Sans rentrer dans les détails, il dit que la fréquence de la lumière change quand elle traverse un champ gravitationnel. Précisément, si on prend une masse M qui génère un champ de gravité, la lumière bleuit en se rapprochant de la masse, elle rougit en s'en éloignant.

Décalage vers le rouge gravitationnel.

Vous avez peut-être pensé que c'était le candidat idéal pour expliquer le redshift des galaxies, mais c'est en réalité le pire. La gravité de la terre ou de notre galaxie est une mauvaise explication : elle a tendance à faire bleuir la lumière qui s'approche de nous, sans compter que les calculs montrent que cela n'explique pas la relation redshift-distance.

En réalité, la lumière émise par les galaxies se rapproche de nous, elle rougit, ce qui signifie qu'elle s'éloigne de la source de gravité responsable du décalage vers le rouge. Et le redshift est observé pour toutes les galaxies, dans tous les sens, peu importe où on regarde sur la voute céleste. Cela signifie que la distribution des masses serait franchement bizarre, avec la terre au beau milieu d'un creux gravitationnel. Chose étrange, sachant qu'on est dans une galaxie et que la distribution des galaxies est assez homogène dans l'univers... Le décalage d'Einstein n'est pas la solution.

L'hypothèse de la lumière fatiguée

Les deux idées précédentes font que l'univers n'est pas statique :, il est en expansion avec l'explication par l'effet Doppler, en contraction gravitationnelle avec le décalage d'Einstein. Mais l'intuition nous ferait plutôt penser à un univers statique, sans expansion ni contraction. Aussi, diverses théories ont tenté d'expliquer les redshifts galactiques sans recourir à un univers en expansion/contraction.

La théorie de la lumière fatiguée est une ancienne hypothèse visant à expliquer le redshift et sa variation en fonction de la distance avec un univers statique. L'idée est que sur de longues distances, la lumière interagit avec la matière, ce qui lui fait perdre de l'énergie, ce qui réduit sa fréquence et la décale vers le rouge. Plus la distance est grande, plus la lumière a interagit avec la matière et plus le décalage vers le rouge serait grand. L'idée a été formalisée dans de nombreuses théories différentes, qui se distinguaient par des détails. Mais l'idée de base est la même pour toutes ces théories.

Mais elle a de nombreux défaut, comme le fait que les images de galaxies lointaines devraient être plus floues qu'observé, du fait de la dispersion de la lumière lors des interactions lumière-matière. Cela ne veut pas dire que la lumière n'a pas interagit avec la matière lors de son trajet, mais cela ne suffit pas à expliquer la loi de Hubble.

De plus, d'autres observations vont contre ce mécanisme. Par exemple, la luminosité angulaire des galaxies devrait être constante dans un univers sans expansion avec lumière fatiguée, alors que les observations montrent qu'elle diminue avec la distance. La formalisation de cet argument a donné naissance au test empirique nommé le test de luminosité surfacique de Tolamn (Tolman surface brightness test). Et les résultats de ce test ont montré que les théories de la lumière fatiguée ne tiennent pas la route. D'autres observations plus complexes à expliquer vont à l'encontre des théories de la lumière fatiguée, comme des observations sur les courbes de luminosité des Supernovae, mais surtout : les observations du fond diffus cosmologique qu'on verra dans quelques chapitres.

Tolman surface brightness test

L'explication du redshift cosmologique par la relativité générale

Aussi bizarre que cela puisse paraitre, les savants de l'époque n'étaient pas étonnés de voir apparaitre loi de Hubble, ni des galaxies aux vitesses supra-luminiques. La théorie de la relativité générale, qui existait déjà à l'époque, avait déjà permis de prédire que de telles situations pouvaient arriver. Et la relativité générale fournit un cadre explicatif parfait pour rendre compte des observations sur le redshift. De plus, la théorie de la relativité générale, appliquée à l'univers, explique parfaitement le paradoxe d'Olbers vu au chapitre précédent.

L'interprétation du redshift comme un effet Doppler son aujourd'hui abandonnée, au profit d'une explication totalement différente, basée sur la relativité générale. Dans cette interprétation, la relation $v=H\times d$ est toujours valable, c'est l'équation pour le redshift $z(v)={\frac {H}{c}}\cdot d(t)$ qui est fausse. Et nous allons détailler cette explication dans le chapitre suivant.

L'expansion de l'univers

Analogie de l'expansion de l'univers.

Expansion de l'univers.

Les équations de la relativité expliquent le redshift cosmologique avec le concept d'expansion de l'univers : les corps matériels de l'univers s'éloignent les uns des autres au fil du temps. Les interprétations de la relativité disent que l'expansion de l'univers ne provient pas d'un mouvement des objets dans l'espace, mais d'une modification de la manière de calculer les distances avec le temps. L'image qui est souvent donnée dans la vulgarisation scientifique compare l'univers avec un gâteau au raisin qui gonfle progressivement, les raisins étant les galaxies.

Le facteur d'échelle, les distances, et le facteur d'échelle

Mettre en équation le phénomène d'expansion de l'univers est assez trivial. Du fait de l'expansion, toute distance entre deux points sera multipliée par un facteur multiplicatif après une durée t. Pour calculer ce facteur multiplicatif, les physiciens font intervenir ce qu'on appelle le facteur d'échelle, noté $a(t)$. Dans ce qui va suivre, nous allons supposer que nous prenons toutes les mesures dans un référentiel d'origine O, et que nous suivons la distance $x(t)$ d'un objet matériel en fonction du temps. Nous allons comparer les distances entre un instant $t_{0}$ et un instant ultérieur$t$. L'augmentation des distances à cause de l'expansion de l'univers se calcule comme suit :

$x(t)=x(t_{0}){\frac {a(t)}{a(t_{0})}}$

Le rapport des facteurs d'échelle est un coefficient multiplicateur qui dit par combien les distances ont été multipliées entre l'époque actuelle et l'instant $t_{0}$. Dit autrement, le facteur d'échelle est ce par quoi il faut diviser les distances actuelles pour obtenir les distances à l'instant $t_{0}$.

Notons que le facteur d'échelle est sans dimensions (il n'a pas d'unité).

Pour simplifier les calculs, on considère souvent que le facteur d'échelle vaut 1 à un instant idéal pour simplifier les calculs. Sous cette hypothèse, l'équation précédente se simplifie :

$x(t)=x(t_{0})\cdot a(t)$

L’interprétation de cette équation est assez simple : si le facteur d'échelle augmente de X %, les distances font de même.

Les distances propres et comobiles

Différence entre distance comobile et distance propre. Sur ce schéma, les deux points sont immobiles, hors effet de l'expansion de l'univers. On voit que l'expansion éloigne les deux points en distance propre, si on mesure la distance avec une règle, sans tenir compte de la grille. Mais si on mesure la distance comobile, c'est à dire la distance mesurée avec les unités de la grille, la distance reste la même.

Reprenons la définition du facteur d'échelle vue précédemment :

$x(t)=x(t_{0}){\frac {a(t)}{a(t_{0})}}$

Il est possible de réécrire la formule précédente comme suit :

${\frac {x(t)}{a(t)}}={\frac {x(t_{0})}{a(t_{0})}}$

Les distances ${\frac {x(t)}{a(t)}}$ et ${\frac {x(t_{0})}{a(t_{0})}}$ sont égale à une distance corrigée de l'influence des facteurs d'échelle. $a(t_{0})$ et $a(t)$. Elle peut s'interpréter comme la distance qu'auraient deux objets s'il n'y avait pas d'expansion. Elle est appelée la distance comobile. À contrario, la distance $x(t)=x(t_{0})\cdot a(t)$ tient compte de l'expansion, qui augmente les distances entre deux objets. Les distances qui tiennent compte de l'expansion, opposées aux distances comobiles, sont appelées des distances propres. Par définition, les distances propres sont celles que l'on peut mesurer, qui ne sont pas corrigées de l'influence du facteur d'échelle.

Il existe une définition alternative de la distance comobile. C'est la distance mesurée à l'instant où $a(t)=1$.

Expansion de l'Univers illustré avec deux galaxies : on voit que la distance comobile montrée par la grille ne change pas, mais que la distance propre augmente.

L'augmentation des distances liée au facteur d'échelle n'est pas très intuitive. Dans le monde réel, une expansion a un centre, un point central d'où s'éloignent les autres. Mais avec l'expansion de l'univers, ce n'est pas du tout le cas. Peu importe où l'on soit dans l'univers, tous les autres objets semblent s'éloigner de nous. Un habitant de la Terre verra toutes les galaxies lointaines s'éloigner de la Terre, mais un habitant de la galaxie d'Andromède verra lui aussi l'ensemble des galaxies s'éloigner de lui et non de la Terre ! C'est cette particularité qui fait que l'on doit recourir à un facteur d'échelle pour expliquer l'expansion.

Schéma de l'expansion de l'univers. Les deux premiers schémas illustrent l'effet de l'expansion sur un ensemble de points, dont un point bleu et un point vert. Les deux schémas du bas montrent cette expansion du point de vue d'un observateur situé respectivement au point bleu, puis au point vert. On voit que chaque observateur voit les autres points s'éloigner de lui.

Le lien entre vitesse et facteur d'échelle

La distinction entre distance comobile et propre peut aussi se faire pour les vitesses, volumes, surfaces et autres. Par exemple, il est possible de calculer une vitesse propre en dérivant la distance propre. Pour cela, on pourrait partir de la définition de la distance propre et en calculer la dérivée.

Par souci de lisibilité, nous noterons parfois la dérivée première d'une variable $x$, à savoir ${\frac {dx}{dt}}$, comme ceci : $x'$. Le remplacement ne sera pas systématique, la notation ${\frac {dx}{dt}}$ étant plus courante et donc plus claire. La notation $x'$ sera utilisée quand la notation ${\frac {dx}{dt}}$ est trop lourde, par exemple pour simplifier les formules de ce style : ${\frac {1}{x}}{\frac {dx}{dt}}$ en ${\frac {x'}{x}}$.

$x(t)'=\left(x(t_{0})\cdot {\frac {a(t)}{a(t_{0})}}\right)'=x(t_{0})'\cdot {\frac {a(t)}{a(t_{0})}}+x(t_{0})\cdot {\frac {a(t)}{a(t_{0})}}'$

Mais les calculs seraient alors un petit peu longs, bien que pas difficiles. Pour éviter ce petit désagrément, nous allons ruser. À la place, nous allons calculer la dérivée de la distance comobile. La dérivée de la distance comobile est naturellement une vitesse, appelée la vitesse comobile. Elle correspond à la vitesse qu'aurait un objet s'il n'y avait pas d'expansion. Elle traduit le fait que les objets s'éloignent ou se rapprochent même sans expansion. Sachant que la distance comobile est définie par $x_{comobile}={\frac {x(t)}{a(t)}}$, on a :

$v_{comobile}=x_{comobile}'=\left({\frac {x(t)}{a(t)}}\right)'$

On utilise la formule de la dérivée d'un quotient :

$v_{comobile}={\frac {x(t)'\cdot a(t)-x(t)\cdot a(t)'}{a(t)^{2}}}={\frac {x(t)'\cdot a(t)}{a(t)^{2}}}-{\frac {x(t)\cdot a(t)'}{a(t)^{2}}}$

On simplifie par $a(t)$ :

$v_{comobile}={\frac {x(t)'}{a(t)}}-{\frac {x(t)\cdot a(t)'}{a(t)^{2}}}$

Les deux termes : ${\frac {x(t)'}{a(t)}}$ et $x(t)\cdot {\frac {a(t)'}{a(t)^{2}}}$ sont techniquement des vitesses. Mais elles sont écrites en coordonnées comobiles, dans le référentiel où $a(t)=1$. Ce sont donc des vitesses que l'on ne peut pas mesurer. Pour passer dans le référentiel général, on doit multiplier par le facteur d'échelle :

$v_{comobile}\cdot a(t)=x(t)'-x(t)\cdot {\frac {a(t)'}{a(t)}}$

Le terme $x(t)'$ n'est autre que la vitesse propre, la vitesse totale de l'objet qui incorpore les effets de l'expansion.

$v_{comobile}\cdot a(t)=v_{propre}-x(t)\cdot {\frac {a(t)'}{a(t)}}$

Cette équation peut se reformuler comme suit :

$v_{propre}(t)=v_{comobile}\cdot a(t)+x(t)\cdot {\frac {a(t)'}{a(t)}}$

Le terme $v_{comobile}\cdot a(t)$ est ce qu'on appelle la vitesse locale. C'est la vitesse qu'a l'objet quand on retire l'effet de l'expansion, mais qu'on prend quand même en compte le facteur d'échelle. En effet, la vitesse comobile est mesurée dans un référentiel particulier, où $a(t)=1$. Et ce référentiel est situé arbitrairement dans le temps, pas forcément dans le temps présent. Pour obtenir la vitesse indépendante de l'expansion, on doit multiplier la vitesse comobile par $a(t)$, afin de tenir compte de la multiplication des distances au cours du temps.

$v_{propre}(t)=v_{locale}(t)+x(t)\cdot {\frac {a(t)'}{a(t)}}$

On voit que la vitesse propre est la somme de deux vitesses. Une vitesse indépendante du facteur d'échelle et une autre qui dépend du facteur d'échelle. En clair, une vitesse indépendante de l'expansion et une qui y est proportionnelle. La première est une vitesse locale indépendante de l'expansion, alors que le second terme a pour origine l'expansion. Nous allons l'appeler la vitesse d'expansion, bien que ce ne soit pas une vitesse.

En réalité, les seules vitesses sont des vitesses comobiles. Qui dit vitesse dit déplacement d'un objet dans l'espace, donc dans les coordonnées comobiles. L'extension de l'espace n'est pas une vitesse, elle correspond à une modification de l'espace lui-même, pas quelque chose qui se passe dedans, ce n'est pas le déplacement d'un objet matériel ou d'une onde. Si la vitesse locale ne peut dépasser la vitesse de la lumière, la vitesse de l'expansion n'est pas contrainte par $c$ car ce n'est pas une vitesse.

Le paramètre de Hubble

Tous les développements précédents permettent de retrouver la loi de Hubble. Pour les objets éloignés, la vitesse locale est négligeable par rapport à la vitesse d'expansion. Il est donc utile, de supposer la vitesse locale nulle. Sous cette hypothèse, l'équation précédente se simplifie comme suit :

$v(t)=x(t)\cdot {\frac {a(t)'}{a(t)}}$

La loi de Hubble ressemble trait pour trait à l'équation précédente, jugez plutôt :

$v(t)=x(t)\cdot H(t)$

En combinant les deux équations, on trouve :

$H(t)={\frac {a(t)'}{a(t)}}$

La loi de Hubble est donc un pur dérivé de l'expansion de l'univers. La vitesse mesurée par la loi de Hubble est donc une pseudo-vitesse liée à l'expansion, pas une vitesse propre. Cela explique pourquoi certaines galaxies très lointaines semblent s'éloigner de nous plus vite que la lumière avec la loi de Hubble. En réalité, il ne s'agit pas d'une vitesse propre, limitée par la vitesse c. En réalité, il s'agit d'une pseudo-vitesse liée à l'expansion de l'espace, c'est la vitesse d'expansion. Ainsi, la vitesse supraluminique des galaxies lointaines provient de la vitesse de l'expansion et ne reflète pas une véritable vitesse supraluminique.

Au passage, cela explique pourquoi la loi de Hubble ne fonctionne pas pour les grandes distances. Les développements précédents permettent de calculer une vitesse instantanée, calculée avec des dérivées. Mais dans les faits, rien ne dit que le paramètre de Hubble H est constant dans le temps. Si celui-ci a varié, alors la loi de Hubble finit fatalement par être fausse. La variation de H a été assez lente dans le temps, ce qui fait que la loi de Hubble marche bien avec les galaxies proches, pour lesquelles la lumière a mis peu de temps à nous parvenir. Pour les galaxies lointaines, H a varié durant le temps de trajet de la lumière, ce qui fausse le lien entre distance et redshift.

Notons une grande différence entre la loi de Hubble $v(t)=H\cdot d(t)$, qui est une relation fondamentale, et la loi de Hubble liée au redshift. La relation entre vitesse et redshift dans un univers relativiste est assez complexe. Aussi, l'application de la loi de Hubble aux observations astronomique est assez complexe.

Le paramètre de Hubble est la rapidité instantanée de l'expansion de l'univers

L'équation précédente peut se reformuler comme suit :

$H(t)={\frac {d}{dt}}\ln {a(t)}$

Comme on le voit, la démonstration précédente nous donne une nouvelle interprétation du facteur de Hubble : c'est la dérivée logarithmique du facteur d'échelle.

Pour rappel, la dérivée logarithmique d'une fonction $x(t)$ se note ${\mathcal {L}}$ et est définie par : ${\mathcal {L}}(x)={\frac {x'}{x}}$ Elle porte ce nom car elle est égale à la dérivée du logarithme de la fonction initiale : ${\mathcal {L}}(x(t))={\frac {x(t)'}{x(t)}}={\frac {d}{dt}}\ln {x(t)}$ Cela nous permet de faire une remarque importante dans la suite du cours : l'intégrale d'une dérivée logarithmique est tout simplement le logarithme de la fonction. Nous ferons ce raccourci très souvent dans le cours. $\int {\mathcal {L}}(x(t))dt=\ln {x(t)}+{\text{Constante d'intégration}}$

Pour le dire plus clairement, le facteur de Hubble est le taux, du pourcentage auquel l'expansion a lieu. Pour information, la dérivée ${\frac {da}{dt}}$ s’interprète comme la vitesse de l'expansion de l'univers, la vitesse à laquelle croît le facteur d'échelle. Plus la vitesse de l'expansion est grande, plus l'univers grandit vite et s'étend rapidement. De même, la dérivée seconde de $a(t)$ est l'accélération de l'expansion de l'univers : plus elle est grande, plus l'expansion devient de plus en plus rapide avec le temps. Le facteur de Hubble est donc la vitesse de l’expansion divisée par le facteur d'échelle, soit le taux de variation du facteur d'échelle. Intuitivement, il indique approximativement si le facteur d'échelle augmente de 5 %, 10 % ou 20 % par unité de temps. Si H vaut 0,015, cela signifie que les distances augmentent de 1,5 % par seconde.

Faites attention à ne pas confondre la vitesse de l'expansion avec la vitesse d'expansion qui est la vitesse d'un objet acquiert à cause de l'expansion.

Maintenant, partons de l'équation précédente et intégrons-la :

$\int H(t)dt=\ln {a(t)}$

On prend l'exponentielle et on réorganise l'équation :

$a(t)=\exp \left(\int H(t)dt\right)$

Cette équation permet de calculer le facteur d'échelle quand on connait le facteur de Hubble. L'utilité de cette équation est qu'estimer le facteur de Hubble au cours du temps est possible, même si c'est par des moyens indirects. Les observations astronomiques permettent d'avoir une estimation précise de la valeur actuelle du facteur de Hubble, ainsi que de ses valeurs anciennes. Alors que l'évolution du facteur d'échelle ne l'est pas.

Le redshift cosmologique

On vient de démontrer la loi de Hubble $v=H\times d$, ce qui signifie qu'elle est valable en tout lieu, à tout instant. Mais n'en déduisez pas que les formules du redshift vues dans le chapitre précédents le sont. En réalité, la relation redshift-distance n'est pas celle obtenue en combinant la loi de Hubble avec la formule $z={v \over c}$ de l'effet Doppler, elle est un peu différente, même si elle ressemble. Dans cette section, nous allons montrer comment l'expansion de l'univers explique le décalage vers le rouge, sans recourir à un effet Doppler.

Effect of the stretching of light on the light wavefront.

Le redshift cosmologique est causé par une modification du facteur d'échelle, valable quel que soit le référentiel. En effet, l'expansion de l'univers impacte aussi la longueur d'onde de la lumière, qui est une distance comme une autre. En clair, il influence la lumière lors de son trajet, mais n'a rien à voir avec la vitesse de l'objet émetteur.

Si une onde lumineuse est émise avec la longueur d'onde $\lambda _{0}$ à un instant $t_{0}$, sa longueur d'onde $\lambda$ à un instant $t$ sera égale à :

$\lambda =\lambda _{0}{\frac {a(t)}{a(t_{0})}}$

La fréquence d'une onde lumineuse étant proportionnelle à sa longueur d'onde, on a alors :

$f=f_{0}{\frac {a(t_{0})}{a(t)}}$

La relation entre redshift et facteur d'échelle

Il est possible de démontrer une relation entre le facteur d'échelle et le redshift. Pour cela, partons de la définition du redshift z :

$z(t)+1={\frac {\lambda (t)}{\lambda (t_{0})}}$

On utilise alors l'équation $\lambda (t)=\lambda (t_{0}){\frac {a(t)}{a(t_{0})}}$, réécrite comme ceci :

${\frac {\lambda (t)}{\lambda (t_{0})}}={\frac {a(t)}{a(t_{0})}}$

En combinant les deux équations précédentes, on déduit la valeur du décalage vers le rouge en fonction du facteur d'échelle. Dans ce qui suit, on suppose que $t_{0}$ est l'instant d'émission de la lumière, alors que l'observation a lieu à l'instant $t$.

$1+z(t)={\frac {a(t)}{a(t_{0})}}$

Posons que le facteur d'échelle actuel vaut 1. L'équation obtenue est alors la suivante :

$z(t)={\frac {1}{a(t_{0})}}-1$

$z(t)+1={\frac {1}{a(t_{0})}}$

$a(t_{0})={\frac {1}{z(t)+1}}$

La relation entre redshift et paramètre de Hubble

Quelques manipulations algébriques à partir des équations précédentes permettent d'exprimer le facteur de Hubble en fonction du redshift. Pour cela, partons de l'équation suivante :

$z(t)={\frac {1}{a(t_{0})}}-1$

Prenons la dérivée par rapport au temps :

${\frac {dz(t)}{dt}}=\left({\frac {1}{a(t_{0})}}-1\right)'$

Le calcul de la dérivée donne :

${\frac {dz(t)}{dt}}=-{\frac {a(t_{0})'}{a(t_{0})^{2}}}$

On applique la formule $H={\frac {a'(t)}{a(t)}}$ :

${\frac {dz(t)}{dt}}=-{\frac {H(t_{0})}{a(t_{0})}}$

On multiplie les deux côtés par $a(t_{0})$

$-{\frac {dz(t)}{dt}}\times a(t_{0})=H(t_{0})$

Maintenant, utilisons l'équation $a(t_{0})={\frac {1}{z(t)+1}}$ :

$-{\frac {1}{z(t)+1}}{\frac {dz(t)}{dt}}=H(t)$

La relation entre redshift et temps écoulé depuis l'émission d'un photon

L'équation précédente permet de calculer quel temps temps s'est écoulé depuis qu'un photon a été émis, en fonction de son redshift. Pour cela, prenons l'équation précédente et isolons dt, en multipliant par ${\frac {dt}{H(t)}}$. On obtient alors le temps dt qu'il faut pour obtnir un incrément de redshift dz.

$dt=-{\frac {1}{H(t)}}{\frac {dz(t)}{z(t)+1}}$

Intégrons cette formule entre O et z :

$t=-\int _{0}^{z}{\frac {1}{H(t)}}{\frac {dz(t)}{z(t)+1}}$

Il est possible de mettre l'équation précédente sous la forme suivante :

$t={\frac {1}{H(0)}}\int _{0}^{z}{\frac {dz(t)}{z(t)+1}}{\frac {1}{E(z)}}$, avec $E(z)=H(z)/H(0)$

Le signe moins disparait car z est négatif, vu que t=0 correspond à maintenant et que z est localisé dans le passé.

Évidemment, résoudre cette équation demande de connaitre E(z), ce qui demande d'avoir un modèle cosmologique sous la main. En utilisant le modèle actuel, on trouve la relation suivante :

Temps de parcours d'un photon et redshift.

La relation entre redshift et distance d'une source

La distance parcourue par la lumière lors de son trajet n'est autre que le temps précédent multiplié par la vitesse c. La distance en question s'appelle la light-travel distance.

$d_{l}(z)={\frac {c}{H(0)}}\int _{0}^{z}{\frac {dz(t)}{z(t)+1}}{\frac {1}{E(z)}}$, avec $E(z)=H(z)/H(0)$

Remarquez que le terme ${\frac {c}{H(0)}}$ n'est autre que la distance telle que calculée par la loi de Hubble. Si on note celle-ci $d_{H}$, on a :

$d_{l}(z)=d_{H}\int _{0}^{z}{\frac {dz(t)}{z(t)+1}}{\frac {1}{E(z)}}$, avec $E(z)=H(z)/H(0)$

Mais il s'agit là d'une distance un peu trompeuse. Il s'agit de la distance parcourue par le photon, mais pas de la distance actuelle à laquelle se situe la source qui a émis la lumière. En effet, l'expansion agit tout le temps et fait que la source s'est éloignée pendant que le photon faisait son voyage.

Il est cependant possible de calculer la distance comobile parcourue par le photon, ce qui demande de diviser le contenu de l'intégrale par le facteur d'échelle a(t), ce qui donne :

$d_{c}=d_{H}\int _{0}^{z}{\frac {1}{a(t)}}{\frac {dz(t)}{z(t)+1}}{\frac {1}{E(z)}}$, avec $E(z)=H(z)/H(0)$

Or, $a(t)={\frac {1}{z(t)+1}}$, ce qui fait que l'équation précédente se simplifie en :

$d_{c}=d_{H}\int _{0}^{z}{\frac {dz(t)}{E(z)}}$

On peut obtenir la distance actuelle entre source et récepteur de la lumière en multipliant l'équation précédente par le facteur d'échelle.

$d_{t0}=d_{H}\times a(t)\times \int _{0}^{z}{\frac {dz(t)}{E(z)}}$

Pour exploiter cette équation, toute la difficulté consiste à connaitre E(z), et donc de savoir comment le facteur de Hubble a évolué dans le temps.

Le redshift des galaxies proches et la loi de Hubble

Nous allons maintenant supposer que le facteur de Hubble H est resté constant. Dans ce cas, les équations précédentes se simplifient un peu. Les équations pour le temps de parcours et la distance sont donc égales à :

$t={\frac {1}{H}}\int _{0}^{z}{\frac {dz(t)}{z(t)+1}}$

$d_{c}={\frac {c}{H}}\int _{0}^{z}dz(t)$

En faisant l'intégrale, on trouve :

$d_{c}={\frac {c}{H}}z(t)$

En reformulant retrouve la loi de Hubble :

$z(t)={\frac {H}{c}}\cdot d(t)$

En clair, la loi de Hubble ne fonctionne que dans les cas où le paramètre de Hubble n'a pas trop varié entre l’émission du photon et sa réception. En clair, elle marche pour des petites distances et/ou des durées assez courtes, ce qui correspond aux galaxies proches. Mais pour les observations de galaxies très éloignées, cette formule ne tient juste plus la route. Plus E(z) s'éloigne de 1, plus la relation précédente donne des résultats erronés. L'observation de galaxies à fort redshift et le calcul de leur distance doit se faire avec l'aide d'un modèle cosmologique qui dit comment E(z) a évolué dans le temps, sous peine d'obtenir des résultats invalides.

L'accélération de l'expansion de l'univers

Il est intéressant de savoir si l'expansion se fait à vitesse constante, ou si l'expansion accélère/décélère. Pour simplifier les calculs, nous allons omettre la vitesse de la lumière et nous concentrer sur la vitesse de l'expansion de l'univers. Cela ne change rien aux résultats que nous allons obtenir vu que la vitesse de la lumière est constante : sa dérivée est donc nulle, ce qui la rend inutile dans les calculs de dérivée qui vont suivre.

L'accélération de l'expansion en fonction du paramètre de Hubble

Une première étape pour savoir si l'expansion ralentit ou accélère, est de calculer l'accélération de l'expansion de l'univers. Cette accélération est simplement égale à la dérivée de la vitesse de l'expansion.

$a_{c}={\frac {d}{dt}}(H(t)\times r)$

En développant, on a :

$a_{c}={\frac {dH(t)}{dt}}\times r+H(t)\times {\frac {dr}{dt}}$

Or, ${\frac {dr}{dt}}$ est simplement la vitesse d'expansion calculée avec la loi de Hubble, ce qui donne :

$a_{c}={\frac {dH(t)}{dt}}\times r+H(t)^{2}\times r$

Le tout se simplifie en :

$a_{c}=r\left(H(t)^{2}+{\frac {dH(t)}{dt}}\right)$

L'accélération de l'expansion en fonction du facteur d'échelle

Une autre manière de quantifier l'accélération de l'expansion est de calculer la dérivée du facteur de Hubble. Le raisonnement derrière cette définition est assez simple. Le facteur de Hubble dit à quel taux les distances dans l'univers augmentent avec le temps. Si la dérivée est nulle, le facteur de Hubble est constant : l'expansion n’accélère pas plus qu'elle ne décélère. Inversement, une dérivée non-nulle nous dit comment le facteur de Hubble varie, et donc comment évolue l'expansion. Si la dérivée est positive, l’expansion accélère, et elle décélère pour le cas négatif.

Sachant que $H={\frac {a(t)'}{a(t)}}$, la dérivée du facteur de Hubble est la suivante :

${\frac {dH(t)}{dt}}={\frac {d}{dt}}\left[{\frac {a(t)'}{a(t)}}\right]$

On utilise alors la formule ${\frac {d}{dx}}\left[{\frac {u(x)}{v(x)}}\right]={\frac {u(x)'}{v(x)}}-{\frac {u(x)v(x)'}{v(x)^{2}}}$

${\frac {dH(t)}{dt}}={\frac {a(t)''}{a(t)}}-{\frac {a(t)'^{2}}{a(t)^{2}}}$

Ce qui se simplifie, en utilisant le facteur de Hubble :

${\frac {dH(t)}{dt}}={\frac {a(t)''}{a(t)}}-H(t)^{2}$

On peut réorganiser les termes pour obtenir l'équation suivante :

${\frac {a(t)''}{a(t)}}={\frac {dH(t)}{dt}}+H(t)^{2}$

On peut en profiter pour identifier cette équation avec l'équation $a_{c}=r\left(H(t)^{2}+{\frac {dH(t)}{dt}}\right)$, ce qui donne :

$a_{c}=r(t)\cdot {\frac {a(t)''}{a(t)}}$

Le facteur de décélération

Il est courant que les cosmologistes utilisent ce qu'on appelle le facteur de décélération, un nombre calculé à partir du facteur de Hubble. Celui-ci est positif si l'expansion est décélérée, négatif si elle accélère, et reste constant si la vitesse d'expansion reste constante. Par définition, ce facteur de décélération q vaut :

$q=-{\frac {a(t)''/a(t)'}{a(t)'/a(t)}}=-{\frac {a(t)''\cdot a(t)}{a(t)'^{2}}}$

En utilisant la formule $H(t)=a(t)'/a(t)$, la formule précédente se reformule comme suit :

$q=-{\frac {a(t)''/a(t)'}{H(t)}}=-{\frac {a(t)''}{a(t)'\cdot H(t)}}=-{\frac {a(t)''}{a(t)\cdot H(t)^{2}}}=-{\frac {a(t)''}{a(t)}}\cdot {\frac {1}{H(t)^{2}}}$

On utilise alors la formule ${\frac {a(t)''}{a(t)}}={\frac {dH(t)}{dt}}+H(t)^{2}$ :

$q=-\left({\frac {dH(t)}{dt}}+H(t)^{2}\right)\cdot {\frac {1}{H(t)^{2}}}$

Quelques manipulations algébriques donnent alors :

$q=-\left(1+{\frac {H(t)'}{H(t)^{2}}}\right)$

Les formules précédentes peuvent se réécrire sous la forme ci-dessous. Cette formule sera importante dans la suite du cours, car les deux termes $H(t)^{2}$ et ${\frac {a(t)''}{a(t)}}$ peuvent se calculer assez facilement. Dans les chapitres sur les équations de Friedmann, nous verrons que le premier terme se calcule à partir de la première équation de Friedmann et le second terme à partir de la seconde équation de Friedmann. Autant dire que l'étude des modèles cosmologiques est fortement facilitée quand on connaît cette relation.

${\frac {a(t)''}{a(t)}}=-q\cdot H(t)^{2}$

Une autre formulation est la suivante :

$q={\frac {d}{dt}}{\frac {1}{H(t)}}-1$

La formule se démontre facilement si on calcule la dérivée suivante :

${\frac {d}{dt}}{\frac {1}{H(t)}}=-{\frac {H(t)'}{H(t)^{2}}}$

En combinant avec les équations précédentes qui donnent le facteur de décélération en fonction de ${\frac {H(t)'}{H(t)^{2}}}$, on retrouve l'équation précédente.

Le lien entre expansion et facteur de Hubble

L'expansion, de part son action sur les distances, entraîne naturellement une variation des surfaces, volumes et densités. Prenons par exemple une sphère de rayon $r$ et de volume $V$ : son rayon augmentant avec le facteur d'échelle, son volume fera de même. Quelques calculs triviaux nous disent que son volume évolue avec le facteur d'échelle selon la formule suivante, avec $V_{0}$ le volume de la sphère à l'instant $t_{0}$.

$V=V_{0}\times a^{3}$

Cette équation nous permet de déduire le rapport entre le facteur de Hubble et l'expansion des volumes. Pour cela, commençons par calculer la dérivée du volume :

${\frac {dV}{dt}}={\frac {d(V_{0}\cdot a^{3})}{dt}}=V_{0}{\frac {d(a^{3})}{dt}}=V_{0}\left(3\cdot a^{2}\cdot {\frac {da}{dt}}\right)$

Divisons ensuite par V, ce qui revient à diviser par : $V_{0}\times a^{3}$ :

${\frac {V'}{V}}={\frac {V_{0}(3\cdot a^{2}\cdot a')}{V_{0}\cdot a^{3}}}$

On simplifie par $V_{0}$ et par $a^{3}$ :

${\frac {V'}{V}}=3{\frac {a'}{a}}=3H$

La formule précédente peut aussi s'écrire de manière moins compacte comme ceci : ${\frac {1}{V}}{\frac {dV}{dt}}=3H$.

Cette équation sera réutilisée plus tard dans le cours, quand nous démontrerons l'équation du fluide de Friedmann.

Le facteur de Hubble

Le facteur de Hubble est d'abord né des observations de Hubble, et précisément de la loi de Hubble, dit que la vitesse d'éloignement d'une galaxie est proportionnelle à sa distance.

$v(D)=H\times D$, où v est la vitesse extrapolée du redshift, D la distance de la galaxie et H un facteur de proportionnalité nommée paramètre de Hubble.

Nous avons vu qu'en réalité, cette relation est approximative et ne marche pas sur les galaxies lointaines. La véritable définition est plus profonde : le facteur de Hubble est un taux d'accroissement du facteur d'échelle, définit par :

$H(t)={\frac {a(t)'}{a(t)}}={\frac {d}{dt}}\ln {a(t)}$

Vous avez peut-être déjà entendu parler de la constante de Hubble pour désigner le paramètre de Hubble. C'était le terme utilisé au tout début de la cosmologie moderne, on pensait que H était constant, mais on sait aujourd'hui que ce n'est pas le cas. Ce n'est donc pas une constante, d'où le fait que nous parlerons de paramètre de Hubble dans de cours. La valeur actuelle de H est sous notée $H_{0}$, et nous utiliserons cette notation dans ce cours.

La mesure du facteur de Hubble

Formellement, le paramètre de Hubble est égal à une vitesse divisée par une distance, ce qui fait qu'elle est l'inverse d'un temps. Le paramètre de Hubble H a donc pour unité $s^{-1}$, soit l'inverse d'une seconde. Mais dans les faits, les astronomes l'expriment en kilomètres par seconde par mégaparsecs (km/s/Mpc ou $km\cdot s^{-1}\cdot Mpc^{-1}$. Pour rappel, le mégaparsec est une unité astronomique qui vaut environ 3,26 millions d'années-lumière. Avec de telles unités, le paramètre de Hubble actuel, mesuré aujourd'hui, vaudrait approximativement :

$H\approx 70\cdot km\cdot s^{-1}\cdot Mpc^{-1}$

L'interprétation de cette valeur est que chaque seconde, l'univers grandit de 70 kilomètres par mégaparsecs.

Les mesures du paramètre de Hubble sont assez nombreuses, mais elles semblent converger vers la valeur de 70 mentionnée plus haut, avec cependant des incertitudes de mesure non-négligeables. Pour vous donner quelques exemples, les graphiques ci-dessous et ci-contre vous donnent les valeurs mesurées pour plusieurs compagnes d'observation assez anciennes. Vous voyez que la valeur n'est pas connue avec certitude.

Mesures du paramètre de Hubble par plusieurs campagnes scientifiques.

À l'heure actuelle, les cosmologistes ne savent pas expliquer pourquoi les mesures du paramètre de Hubble sont aussi différentes. Ce qui est sûr, c'est que le résultat dépend fortement de la méthode de mesure. Sans rentrer dans les détails techniques, il existe plusieurs méthodes indirectes pour estimer le paramètre de Hubble, qui estiment les distances des objets lointains en analysant la luminosité des supernovæ, des galaxies, des céphéides (des étoiles pulsatiles), et d'autres objets astronomiques. Et suivant la méthode utilisée ou l'objet observé, le paramètre de Hubble n'a pas la même valeur. Peut-être que les mesures sont entachées d'un biais systématique qui dépend de la mesure, peut-être que la valeur du paramètre de Hubble varie suivant la distance des objets considérés, peut-être que l'hypothèse d'un univers isotrope et homogène doit être abandonné, peut-être qu'une nouvelle physique se cache derrière ces résultats disparates, personne ne le sait.

Les valeurs précédentes sont obtenues avec des objets situés à des distances très différentes, pour lesquels la lumière a mis du temps à nous parvenir. Aussi, vous avez peut-être pensé que les différences dans les mesures sont liés aux variations du paramètre de Hubble. Manque de chance, les scientifiques ne sont pas stupides et ils ont pris cela en compte. Les valeurs des graphiques précédents sont des valeurs qui corrigent l'évolution du paramètre de Hubble, à partir d'hypothèses très crédibles sur son évolution.

Le temps de Hubble

Comme dit plus haut, le paramètre de Hubble est l'inverse d'un temps. Ce temps en question est appelé le temps de Hubble et nous le noterons $T_{H}$. Par définition, il vaut :

$T_{H}(t)={\frac {1}{H(t)}}$

Il vaut environ 14,4 milliards d'années et cette valeur est très proche de celle actuellement admise par les scientifiques pour l'âge de l'univers (13,6 milliards d'années environ). Précisons que si les estimations actuelles nous disent que les deux sont assez proches, mais rien ne nous dit qu'ils sont exactement identiques. Les mesures et estimations sont en effet entachées d'une marge d'erreur assez large, ce qui fait que les deux mesures peuvent sembler se confondre alors qu'elles sont peut-être légèrement différentes.

Le temps de Hubble n'est pas l'âge de l'univers, attention à ne pas confondre ! Un bon moyen de s'en rendre compte est de regarder ce qui se passe dans un univers où $H(t)$ serait constant, mais positif et non-nul. Le temps de Hubble serait alors constant, alors que l'univers serait en expansion.

La théorie nous dit que temps de Hubble et âge de l'univers n'ont pas de raison de coïncider. Dans la plupart des théories mathématiques de la cosmologie, $T_{H}$ et âge de l'univers ne coïncident qu'en un seul instant $t$ bien précis. À tous les autres instants, ces deux valeurs sont différentes. Dans de nombreuses théories cosmologiques, le temps de Hubble est plusieurs fois inférieur ou supérieur à l'âge de l'univers.

La seule exception est un modèle théorique appelé le modèle $R_{H}(t)=c\cdot t$ (oui, le nom de cette théorie est bien une formule mathématique...), dans lequel le temps de Hubble et l'âge de l'univers se confondent à tout instant. Mais c'est l'exception qui confirme la règle. À l'heure actuelle, on ne sait pas si ce modèle décrit correctement l'univers actuel. Aussi, les scientifiques ne savent pas si la coïncidence actuelle entre temps de Hubble et âge de l'univers en est une ou est valide en permanence.

Le lien entre temps de Hubble et facteur de décélération

Le temps de Hubble a un lien assez important avec le facteur de décélération. Pour nous en rendre compte, prenons la formule suivante pour le facteur de décélération :

$q={\frac {d}{dt}}{\frac {1}{H(t)}}-1={\frac {d}{dt}}T_{H}-1$

L'interprétation de cette équation est assez simple, si on regarde comment évolue la dérivée ${\frac {d}{dt}}T_{H}$. Le cas où ${\frac {d}{dt}}T_{H}=1$ correspond au cas où le temps de Hubble augmente au même rythme que l'âge de l'univers, ce qui signifie que les deux sont égaux. Or, nous verrons dans quelques chapitres que ce n'est possible que si l'expansion de l'univers se fait à vitesse constante. Plus précisément, cela implique que le facteur d'échelle augmente linéairement avec le temps ($a(t)=k\cdot t$), donc que sa dérivée première soit constante et sa dérivée seconde nulle.

Les cas où ${\frac {d}{dt}}T_{H}>1$ et ${\frac {d}{dt}}T_{H}<1$ correspondent alors à une expansion supra- et infra-linéaire. Or, le facteur de décélération est définit de manière à valoir 0 pour un univers en expansion linéaire (à vitesse constante), positif pour une expansion supra-linéaire et négatif pour une expansion infra-linéaire. On voit que pour passer de la dérivée ${\frac {d}{dt}}T_{H}$ au facteur de décélération, il faut retrancher 1.

Une autre manière de réécrire cette formule, qui sera utile dans la suite du cours, est la suivante :

$q+1={\frac {d}{dt}}{\frac {1}{H(t)}}={\frac {d}{dt}}T_{H}$

Le facteur de décélération moyen

Rien n'implique que le facteur de décélération soit une constante. Il peut très bien varier dans le temps, si le facteur de Hubble varie lui aussi. Rien n’empêche d'avoir un univers dont l'expansion accélère, puis stoppe et décéléré, par exemple. Il est alors utile de calculer un facteur de décélération moyen, qui est définit par :

${\overline {q}}(t_{0})={\frac {1}{t_{0}}}\int _{0}^{t_{0}}q(t)dt$, avec $t_{0}$ l'âge de l'univers.

On utilise alors l'équation $q={\frac {d}{dt}}T_{H}-1$ :

${\overline {q}}(t_{0})={\frac {1}{t_{0}}}\int _{0}^{t_{0}}\left[{\frac {d}{dt}}T_{H}-1\right]dt$

L'intégrale d'une somme est la somme des intégrales :

${\overline {q}}(t_{0})={\frac {1}{t_{0}}}\left[\int _{0}^{t_{0}}\left({\frac {d}{dt}}T_{H}\right)dt-\int _{0}^{t_{0}}1dt\right]$

On calcule la dernière intégrale :

${\overline {q}}(t_{0})={\frac {1}{t_{0}}}\left[\int _{0}^{t_{0}}\left({\frac {d}{dt}}T_{H}\right)dt-t_{0}\right]$

On développe :

${\overline {q}}(t_{0})={\frac {1}{t_{0}}}\left[\int _{0}^{t_{0}}\left({\frac {d}{dt}}T_{H}\right)dt\right]-1$

L'intégrale et la dérivée s'annulent si on néglige les constantes d'intégration, ce qui donne :

${\overline {q}}(t_{0})={\frac {T_{H}(t_{0})}{t_{0}}}-1$

On voit que le facteur de décélération moyen dépend de l'âge de l'univers et du facteur de Hubble actuel, rien de plus. C'est un résultat très intéressant, qui permet soit de calculer le facteur de décélération moyen à partir de l'âge de l’univers, ou de faire l'inverse. L'âge de l'univers vaut donc :

$t={\frac {T_{H}}{{\overline {q}}(t)+1}}$

Plus haut, nous avons dit que l'âge de l'univers qui fait actuellement consensus est proche du temps de Hubble. Si on en croit l'équation précédente le seul moyen d'avoir $t\approx T_{H}$ est que ${\overline {q}}(t)\approx 0$. En clair, l'univers a eu une expansion approximativement constante, en moyenne. Mais attention, cela ne signifie pas que l'expansion s'est faite de manière régulière tout le temps. Le consensus actuel est que l'univers a alterné entre décélération et d'expansion. Mais nous reparlerons de cela plus tard dans le cours, quand nous parlerons des modèles cosmologiques, de l'accélération de l'expansion de l'univers et de l'inflation.Toute la difficulté de la cosmologie est d'établir comment s'est déroulée l'expansion.

Le rayon de Hubble

Le rayon de Hubble, noté $R_{H}$, est la distance que parcourt la lumière pendant le temps de Hubble. Il vaut donc, par définition :

$R_{H}=c\cdot T_{H}={\frac {c}{H(t)}}$

Notons que cette dernière formule est une tautologie sans grande importance, sans sens physique. Dans la plupart des modèles cosmologiques, temps de Hubble et rayon associé n'ont pas de sens physique et ne sont que des conventions. Par exemple, si on suppose que le facteur de Hubble est constant, le rayon de Hubble est constant, alors que l'univers est en expansion.

Un autre point important est que le rayon de Hubble n'est en rien la limite au-delà de laquelle la lumière n'a pas eu le temps de nous parvenir (en termes scientifiques, ce n'est pas un horizon). On peut parfaitement voir des objets qui sont situés au-delà du rayon de Hubble, et les astronomes l'ont déjà fait. Bref, temps et rayon de Hubble sont des conventions.

La relation entre redshift et rayon de Hubble

On a vu que pour les faibles redshift, la loi de Hubble donne une relation entre distance et redshift qui s'écrit comme suit :

$z(t)={\frac {H}{c}}\cdot d(t)$

Le terme ${\frac {H}{c}}$ n'est autre que l'inverse du rayon de Hubble, ce qui donne :

$z(t)={\frac {d(t)}{R_{H}}}$

Rappelons que cette relation ne vaut que pour des distances assez faibles, des galaxies proches.

L'évolution du rayon de Hubble

On peut s'amuser à calculer dans quelles circonstances le rayon de Hubble est constant. Pour cela, prenons sa dérivée :

${\frac {d}{dt}}R_{H}(t)={\frac {d}{dt}}(c\cdot T_{H})=c\cdot {\frac {d}{dt}}T_{H}$

On utilise alors la formule qui relie la dérivée du temps de Hubble au facteur de décélération :

$q+1={\frac {d}{dt}}{\frac {1}{H(t)}}={\frac {d}{dt}}T_{H}$

En combinant les deux équations précédentes, on trouve :

${\frac {d}{dt}}R_{H}(t)=c\cdot (q+1)$

Cette dérivée s'annule quand $q=-1$. En analysant la dérivée, on remarque que le rayon de Hubble se contracte pour $q<-1$, augmente quand $q>-1$, et reste stationnaire pour $q=-1$. En clair, le rayon de Hubble augmente quand l'expansion qui ralentit, diminue quand l'expansion accélère, reste constante si l'expansion se fait à taux constante.

Le rayon de Hubble et les vitesses de fuite supra-luminiques

Au-delà du rayon de Hubble, le produit $H\times D$ dépasse la vitesse de la lumière. En effet, calculons la distance à laquelle la vitesse calculée avec la loi de Hubble vaut c :

$c=H\times d$

On a alors :

$d={c \over H}=c\times T_{H}$

Prenons n'importe quel objet qui émet de la lumière vers nous. La lumière va a une vitesse c vers nous, mais l'expansion fait que la lumière s'éloigne de nous à une vitesse $v_{rec}$ qui se calcule avec la loi de Hubble. La vitesse des photons venant vers nous, en coordonnées non-comobiles, est donc de $v_{rec}-c$.

Pour les objets au-delà du rayon de Hubble, $v_{rec}>c$ : ils s'éloignent de nous plus vite que la lumière. Ce qui fait que leur lumière ne devrait pas nous rejoindre si le rayon de Hubble restait statique, car elle est supérieure à c. Mais il faut maintenant prendre en compte que le rayon de Hubble grandit à la vitesse qu'on vient de calculer plus haut. Ce qui fait que ces photons dont $v_{rec}>c$ se retrouvent quand même dans la sphère de Hubble, s'ils respectent la condition suivante :

${\frac {d}{dt}}R_{H}(t)\geq v_{rec}-c$

Utilisons la formule suivante :

${\frac {d}{dt}}R_{H}(t)=c\cdot (q+1)$

Combinons les deux équations précédentes :

$c\cdot (q+1)\geq v_{rec}-c$

Simplifions :

$c\cdot q\geq v_{rec}$

En clair, le rayon de Hubble finit par rattraper ces photons, ce qui fait qu'ils finissent par arriver chez nous.

Le rayon comobile de Hubble

Notons que l'on peut calculer le rayon de Hubble comobile, c'est à dire en supprimant l'effet de l'expansion. Ce rayon n'a pas plus de sens physique que le rayon de Hubble normal. Il est définit comme toute distance comobile, en divisant par le facteur d'échelle. Cela donne :

${\frac {R_{H}(t)}{a(t)}}={\frac {c}{a(t)\cdot H(t)}}$

En utilisant la formule $H={\frac {a'(t)}{a(t}}$ et en simplifiant, on trouve :

${\frac {R_{H}(t)}{a(t)}}={\frac {c}{a'(t)}}$

Le rayon comobile est constant si la dérivée du facteur d'échelle est constante, ce qui correspond à une expansion linéaire, où le facteur d'échelle augmente proportionnellement avec le temps.

L'univers observable

L'univers observable est la portion de l'univers que nous pouvons observer, compte tenu de la limite de la vitesse de la lumière. Des objets situés très loin ne peuvent pas être vus pour une raison très simple : la lumière qu'ils émettent n'a pas eu le temps de nous parvenir. La distance maximale à laquelle nous pouvons voir des objets (sans tenir compte d'éventuelles limitations techniques) dépend de l'âge de l'univers. S'il faut un temps supérieur à l'âge de l'univers pour nous parvenir, il nous est actuellement impossible de les voir, ce qui n'est pas le cas pour des objets situés plus près. Cette distance maximale est donc le rayon de l'univers observable. L'ensemble des points situés à la distance maximale des objets observables, à savoir la surface de l'univers observable, porte un nom : c'est l'horizon cosmologique.

Le rayon de Hubble

On pourrait croire que le rayon de Hubble est une bonne estimation de la taille de l'univers observable. Pour rappel, ce rayon de Hubble est définit à partir du facteur de Hubble comme suit :

$R_{H}(t)=c\cdot T_{H}$, avec c la vitesse de la lumière et $T_{H}$ le temps de Hubble définit par $T_{H}={\frac {1}{H}}$.

Il s'agit de la distance parcourue par la lumière pendant le temps de Hubble, lui-même définit comme l'inverse du facteur de Hubble. Mais le rayon de Hubble n'est malheureusement pas une bonne estimation du rayon de l'univers observable, pas plus que le temps de Hubble ne donne l'âge de l'univers. En effet, le rayon de Hubble n'est en rien la limite de l'univers observable : on voit des objets sont situés au-delà et on peut calculer leur redshift ou tout autre mesure pertinente.

Pourtant, sa définition semble indiquer que le rayon de Hubble soit la limite de l'univers observable. Par définition, tout ce qui est au-delà du rayon de Hubble va plus vite que la lumière. Donc la lumière émise au-delà de ce rayon n'est pas censée nous atteindre. Sauf que ce raisonnement par du principe que le rayon de Hubble est stable. Or, rappelez-vous l'équation du chapitre précédent, qui dit comment évolue le rayon de Hubble :

${\frac {d}{dt}}R_{H}(t)=c\cdot (q+1)$

Pour notre univers, tout semble indiquer qu'il augmente avec le temps. Et cela explique pourquoi on peut voir des objets qui se déplacent "plus vite que la lumière", dans le sens où l'expansion les éloignait de nous plus vite que la lumière. La raison est que, vu que le rayon de Hubble grandit, certains photons hors du rayon de Hubble finissent par y rentrer. Ils sont en quelque sorte rattrapés par le rayon de Hubble et nous finiront donc par les voir une fois arrivés sur Terre. Par contre, les objets qui ont émis cette lumière s'éloignent bien de nous plus vite que la lumière et restent au-delà du rayon de Hubble.

Le rayon de l'univers observable

Le calcul du rayon cosmologique actuel est assez simple sur le principe, mais compliqué en pratique. Une méthode assez simple se base sur la vitesse d'éloignement de l'horizon, à savoir la vitesse à laquelle l'horizon cosmologique s'éloigne de nous. Une fois cette vitesse connue, il suffit de l'intégrer sur l'âge de l'univers.

La vitesse d'éloignement du rayon observable est définie par :

$v(t)={\frac {d}{dt}}r(t)$, avec $r(t)$ le rayon de l'univers à l'instant t.

On réutilise l'équation du chapitre précédent, qui donne la vitesse en fonction de la distance: $v(t)=v(t_{0})a(t)+x(t_{0})\cdot H(t)$. Dans le cas de l'horizon cosmologique, la distance est égale au rayon de l'univers et la vitesse locale est égale à la vitesse de la lumière, ce qui donne :

${\frac {d}{dt}}r(t)=c+H(t)\times r(t)$

On peut reformuler le tout en divisant par $r(t)$, ce qui donne :

${\frac {r'(t)}{r(t)}}={\frac {c}{r(t)}}+H(t)$

On peut alors intégrer cette expression sur l'âge de l'univers pour obtenir le rayon de l'horizon cosmologique, du moins dans certaines conditions. Faire les calculs demande de connaître la loi d'évolution du facteur de Hubble $H(t)=...$. Mais dans les faits, elle nous est inconnue et on n'en a que quelques bribes. La théorie ne nous est pas d'un grand secours et le seul cas que l'on peut calculer simplement est celui où le facteur de Hubble est constant. En général, les modèles cosmologiques les plus simples supposent que le facteur d'échelle suit une loi de puissance, de type $a(t)=a_{0}\cdot (t/t_{0})^{\beta }$, ce qui fait que l'équation peut se résoudre avec quelques développements analytiques. Mais des modèles plus réalistes ne suivent pas vraiment une loi de puissance, ce qui complique les calculs. Pour nous éviter de longs calculs fastidieux, nous allons étudier le cas général, en utilisant quelques raisonnements astucieux.

Le rayon comobile de l'univers observable

Une autre façon de faire les calculs est de passer par l'intermédiaire du rayon comobile. Pour rappel, ce rayon comobile est le rayon corrigé de l'influence du facteur d'échelle (et donc de l'expansion). Il vaut, par définition : $r(t) \over a(t)$.

La vitesse comobile est la dérivée de ce rayon comobile, qui est égale à :

${\frac {d}{dt}}\left({\frac {r(t)}{a(t)}}\right)={\frac {r(t)'}{a(t)}}-{\frac {r(t)\cdot a(t)'}{a(t)^{2}}}={\frac {r(t)'}{a(t)}}-H(t){\frac {r(t)}{a(t)}}$

On peut alors factoriser le rayon comobile $r(t) \over a(t)$ :

${\frac {d}{dt}}\left({\frac {r(t)}{a(t)}}\right)={\frac {r(t)}{a(t)}}\left[{\frac {r(t)'}{a(t)}}{\frac {a(t)}{r(t)}}-H(t)\right]$

On simplifie :

${\frac {d}{dt}}\left({\frac {r(t)}{a(t)}}\right)={\frac {r(t)}{a(t)}}\left[{\frac {r(t)'}{r(t)}}-H(t)\right]$

En injectant l'équation ${\frac {r(t)'}{r(t)}}={\frac {c}{r(t)}}+H(t)$ dans la précédente, on a :

${\frac {d}{dt}}\left({\frac {r(t)}{a(t)}}\right)={\frac {r(t)}{a(t)}}\left[{\frac {c}{r(t)}}+H(t)-H(t)\right]$

En développant, on trouve :

${\frac {d}{dt}}\left({\frac {r(t)}{a(t)}}\right)={\frac {c}{a(t)}}$

On voit que la dérivée est égale à ce qu'on appelle la vitesse comobile de la lumière. Par définition, la vitesse de la lumière est de $c=299792,458Km/S$, mais il s'agit d'une vitesse propre. On peut calculer sa vitesse comobile en divisant par le facteur d'échelle, ce qui n'est autre que le premier terme de l'équation précédente. $c_{com}={c \over a}$. En intégrant l'équation précédente sur l'âge de l'univers, on a la distance comobile de l'horizon, celle à laquelle se situait l'horizon cosmologique quand la lumière de l'horizon a été émise. On se retrouve alors avec une équation très générale, qui marche même quand le facteur de Hubble est variable.

Seule la vitesse comobile de la lumière devant être prise en compte. On trouve alors que le rayon comobile se calcule avec la formule suivante, avec $t_{u}$ l'âge de l'univers :

${\frac {r(t)}{a(t)}}=\int _{0}^{t_{u}}{c \over a(t)}dt=c\int _{0}^{t_{u}}{dt \over a(t)}$

Il est possible de simplifier fortement la formule précédente en faisant intervenir une variable particulière, appelée le temps conforme, définie par $\eta ={\frac {dt}{a(t)}}$. On peut voir ce temps conforme comme l'équivalent de la distance comobile, mais pour les durées. Il n'a pas vraiment d'interprétation physique digne de ce nom et sert plus d'intermédiaire pour les calculs. Avec le temps conforme, la formule précédente devient alors :

${\frac {r(t)}{a(t)}}=c\cdot (\eta _{0}-\eta _{t_{u}})$

On peut voir la formule précédente comme la généralisation de la formule $D=c\cdot \Delta T$, mais où le temps est remplacé par le temps conforme.

Le rayon actuel de l'univers observable

On peut obtenir la distance propre par un calcul très simple, à partir de la distance comobile. Le passage de la distance comobile à la distance propre se fait simplement en multipliant par $a(t)$. On obtient alors la distance propre suivante :

$r(t)=a(t)\cdot \int _{0}^{t_{u}}{c \over a(t)}dt$

Dans l'équation précédente, on peut factoriser la vitesse de la lumière, ce qui donne :

$r(t)=c\cdot \left[a(t)\cdot \int _{0}^{t}{1 \over a(t_{i})}dt_{i}\right]$

Comme pour le rayon comobile, on peut voir la formule précédente comme la généralisation de la formule $D=c\cdot \Delta T$, mais où la durée $\Delta T$ est remplacée par la valeur temporelle $\left[a(t)\cdot \int _{0}^{t}{1 \over a(t_{i})}dt_{i}\right]$.

Les intégrales précédentes ne sont pas solubles telles quelles. Il faut préciser comment le facteur d'échelle évolue avec le temps, sans quoi les intégrales ne peuvent pas être calculées exactement. Manque de chance, la loi d'évolution du facteur d'échelle nous est inconnue. Nous sommes obligés de postuler des fonctions particulières, en espérant qu'elles collent au mieux aux observations. Nous ferons cela plus en détail dans le chapitre sur les modèles cosmologiques.

Une introduction aux modèles cosmologiques

Les chapitres précédents nous ont appris beaucoup de choses. Ils ont fourni une description de l'expansion de l'univers basée sur le facteur d'échelle, de quoi calculer le rayon de l'univers observable, et ont décrit comment la matière et le rayonnement réagissent à l'expansion. Maintenant, nous allons voir une portion bien plus intéressante de la cosmologie. Nous allons étudier les modèles cosmologiques, des modèles théoriques qui décrivent comment l'univers lui-même a évolué au cours du temps. Les modèles cosmologiques que nous allons voir dans ce cours donnent au minimum les résultats suivants : l'évolution du facteur d'échelle au cours du temps (la fonction $a(t)$, le rayon observable de l'univers, son âge (s'il en a un), une formule pour le facteur de Hubble, et parfois d'autres données supplémentaires (T(t) : température à tout instant, ...).

Dans ce chapitre, nous allons voir quelques modèles cosmologiques ad hoc. Par ad hoc, on veut dire qu'on fait des hypothèses purement arbitraires pour démontrer le modèle. De tels modèles sont à contraster avec des modèles démontrés à partir de principes physiques fondamentaux. Les modèles démontrés à partir de lois physiques plus fondamentales sont en effet un peu plus compliqués et seront vus dans les chapitres qui suivent. Le prochain chapitre porte d'ailleurs sur les modèles de Friedmann, qui sont les modèles les plus utilisés en cosmologie physique. Dans ce chapitre, nous allons voir des modèles plus simples. La démarche de ce chapitre consistera simplement à postuler une loi d'évolution pour le facteur d'échelle, à postuler la fonction $a(t)$. Une fois cela fait, nous pourrons établir une formule pour le facteur de Hubble, le rayon cosmologique, etc. Une telle démarche demande de choisir une fonction $a(t)$ en fonction de ses propriétés mathématiques, de sa facilité pour faire les calculs, etc. Dans les modèles cosmologiques physiques, cette loi $a(t)$ est démontrée à partir de principes physiques plus fondamentaux.

Dans ce chapitre, nous allons voir plusieurs modèles. Le premier est celui pour lequel la loi $a(t)$ est linéaire. Il s'agit d'un modèle très simple, mais qui n'est pas réaliste du tout. Cependant, ce modèle permet d'introduire deux grandeurs fondamentales : le temps et le rayon de Hubble. De plus, il sert de point de comparaison avec le second type de modèles : ceux pour lesquels la loi $a(t)$ est une loi de puissance. Enfin, nous verrons ce qui se passe quand le facteur d'échelle croit de façon exponentielle. En soit, ces trois modèles font que l'univers est en expansion, mais de manière différente. Une croissance linéaire n'a rien à voir avec une croissance exponentielle, ni avec une croissance en loi de puissance. Nous verrons cependant que les modèles cosmologiques physiques, ceux de Friedmann, donnent une croissance soit exponentielle, soit en loi de puissance. Nous pourrons donc réutiliser les résultats de ce chapitre dans les chapitres ultérieurs sur les modèles physiques. Les modèles ad hoc que nous allons voir vont nous donner des résultats qui faciliteront l'étude de modèles plus physiques, plus compliqués.

Le modèle à croissance linéaire

Pour commencer, nous allons étudier un premier modèle : le modèle à croissance linéaire. Il est aussi appelé modèle $R_{h}=ct$, en raison d'une des équations du modèle. Les cosmologistes ont étudié ce modèle à partir de l'année 2012, car de nombreux problèmes des autres modèles disparaissent dans ce modèle, mais il semble qu'il ne colle pas trop aux observations actuelles. Quoi qu’il en soit, ce modèle est intéressant à étudier et il sert de bonne introduction, avant de passer à des modèles plus compliqués.

Avec ce modèle, on suppose que l'univers gonfle de manière relativement constante avec le temps. Mathématiquement, cela se traduit par la loi d'évolution suivante pour le facteur d'échelle :

$a(t)=k\cdot t$, avec $t$ le temps, $k$ une constante quelconque.

Une autre formulation, souvent utilisée, est la suivante :

$a(t)=a(t_{0})\cdot {\frac {t}{t_{0}}}$, avec $t_{0}$ l'origine de temps choisie arbitrairement et $a(t_{0})$ le facteur d'échelle à ce même instant.

Notons que les deux sont équivalentes, sous réserve que $k={\frac {a(t_{0})}{t_{0}}}$. Dans ce qui va suivre, nous utiliserons la première formulation, sauf pour ce qui est l'étude du décalage vers le rouge. Avec ces formules, nous allons calculer quelle est la valeur du facteur de Hubble qui correspond, quel est l'âge de l'univers, quel est son rayon, la vitesse de l'expansion de l'univers, etc.

Avant de poursuivre, on peut calculer la dérivée première et seconde du facteur d'échelle, deux résultats qui seront utiles pour la suite. Le calcul de la dérivée première donne :

${\frac {d}{dt}}a(t)={\frac {d}{dt}}(k\cdot t)=k$

Celle-ci étant une constante, la dérivée seconde est donc nulle.

${\frac {d}{dt}}^{2}a(t)=0$

Rappelons que la dérivée seconde du facteur d'échelle nous dit si l'expansion de l'univers accélère, ralentit ou reste constante. Pour une valeur nulle, l'expansion se fait à rythme constant.

Le calcul du facteur de Hubble et de l'âge de l'univers

Pour calculer le facteur de Hubble, nous allons partir de la dérivée du facteur d'échelle, qui est égale à :

${\frac {d}{dt}}a(t)=k$

En divisant par a(t), le terme de gauche devient le facteur de Hubble. On a alors :

$H(t)={\frac {k}{a(t)}}={\frac {k}{k\cdot t}}={\frac {1}{t}}$

On peut comparer l'équation précédente avec l'identité $H(t)={\frac {1}{T_{H}}}$ vue dans le second chapitre. On obtient alors :

$t=T_{H}$

L'âge de l'univers est égal au temps de Hubble dans ce modèle.

L'évolution du facteur de Hubble dans le temps

De l'équation $H={\frac {1}{t}}$, on peut déduire comment le facteur de Hubble H évolue au cours du temps. Pour cela, il suffit d'étudier ce qui se passe quand l'âge de l'univers augmente. Au fur et à mesure que le temps passe, l'âge de l'univers augmente. Ce faisant, le dénominateur de $H={\frac {1}{t}}$ croit et le facteur de Hubble diminue donc. Pour le dire en termes mathématiques, le facteur de Hubble est une fonction décroissante du temps. Un bon moyen de s'en rendre compte est de calculer la dérivée du facteur de Hubble :

${\frac {d}{dt}}H(t)=\left({\frac {1}{t}}\right)'=-{\frac {1}{t^{2}}}$

La dérivée étant négative, on en déduit que le facteur de Hubble décroit au cours du temps. Et cette décroissance est d'autant plus rapide que l'univers est âgé.

Le calcul du paramètre de décélération

À partir des résultats précédents, on peut calculer la valeur du paramètre de décélération. Pour rappel, celui-ci est un nombre qui dit à quelle vitesse l'expansion de l'univers accélère ou ralentit. L'expansion est décélérée s'il est positif, accélère s'il est négatif et reste constante sinon. Il se calcule en utilisant la formule suivante, vue dans le chapitre sur l'univers observable :

$q=-\left(1+{\frac {H(t)'}{H(t)^{2}}}\right)$

On injecte alors les équations $H={\frac {1}{t}}$ et $H'(t)=-{\frac {1}{t^{2}}}$, ce qui donne :

$q=-\left(1-{\frac {1}{t^{2}}}t^{2}\right)=-(1-1)=0$

En clair, l'expansion garde un rythme constant, elle n’accélère pas et ne ralentit pas, comme dit précédemment.

Le rayon de Hubble

Par définition, le rayon de Hubble est égal à :

$R_{H}(t)={\frac {c}{H(t)}}$

En combinant avec l'équation $H(t)={\frac {1}{t}}$, on a :

$R_{H}(t)=c\cdot t$

Le modèle à expansion linéaire est aussi appelé modèle $R_{h}=ct$, en raison de ce résultat. D'ailleurs, c'est le seul modèle dans lequel cette égalité est tout le temps vraie. Si l'on a pas une expansion linéaire, alors le rayon de Hubble n'est égal à $c\cdot t$ que pour une valeur de $t$ bien précise et fausse pour toutes les autres.

Le rayon comobile de Hubble est définit par la formule :

${\frac {R_{H}(t)}{a(t)}}={\frac {c}{a'(t)}}$

Par définition, on a $a'(t)=k$, qui est une constante.

${\frac {R_{H}(t)}{a(t)}}={\frac {c}{k}}$

On remarque que toute la partie de droite ne contient que des termes constants (c et k sont tous deux constants). Ce qui signifie que le rayon comobile de l'univers est lui aussi constant. Certes, le rayon de Hubble grandit, mais il le fait au rythme que le facteur d'échelle. Les deux se compensent, donnant un rayon comobile constant.

Le calcul du rayon de l'univers observable

Dans ce modèle, calculer le rayon de l'univers observable n'est pas une mince affaire. On a vu dans le chapitre sur l'univers observable qu'il faudrait idéalement utiliser cette formule :

$R(t)=c\cdot \left[a(t)\cdot \int _{0}^{t}{1 \over a(t_{i})}dt_{i}\right]$

Malheureusement, si on se met à faire les calculs à la main, on s’aperçoit rapidement que l'intégrale ne converge pas ! Le modèle nous dit donc que le rayon observable de l'univers est infini. Cela est un avantage, car cela résout un problème majeur, appelé problème de l'horizon, qui touche les autres modèles cosmologiques. Nous en reparlerons vers la fin du cours plus en détail.

Le calcul du décalage vers le rouge

Dans ce qui suit, nous allons supposer qu'un objet à une distance $d$ émet de la lumière à un instant $t_{0}$, lumière qui est reçue par l'observateur à un instant $t$. Nous allons calculer le décalage vers le rouge de cette lumière, le redshift. Pour gérer ce cas, nous allons devoir utiliser la formule suivante, vue dans le chapitre sur le rayonnement, qui donne le redshift en fonction du facteur d'échelle :

$1+z={\frac {a(t_{0})}{a(t)}}$

On injecte alors l'équation $a(t)=k\cdot t$ :

$1+z={\frac {k\cdot t_{0}}{k\cdot t}}$

En simplifiant, on trouve :

$1+z={\frac {t_{0}}{t}}$

Il est aussi possible d'écrire le facteur de Hubble en fonction du décalage vers le rouge et réciproquement. Par exemple, imaginons qu'un objet émette de la lumière à un instant $t-0$, quand le facteur de Hubble est égal à $H_{0}$ et le facteur d'échelle à $a_{0}$. Sa lumière est reçue par l'observateur à l'instant $t$, quand le paramètre de Hubble et le facteur d'échelle valent $H(t)$ et $a(t)$. On peut alors démontrer l'équation suivante :

$1+z={H(z) \over H_{0}}$

Qui peut se reformuler comme suit :

$H(z)=H_{0}\cdot (1+z)$

Démonstration

Pour démontrer la formule précédente, partons de la relation : $1+z={\frac {t_{0}}{t}}$ Or, on sait que $H(t)={1 \over t}$. On a donc $t={1 \over H(t)}$ et $t_{0}={1 \over H_{0}}$ En faisant le remplacement dans l'équation précédente, on trouve : $1+z={1 \over H_{0}}/{\frac {1}{H(t)}}$ En réarrangeant les termes, on trouve la formule à démontrer, mais sous une forme légèrement différente : $1+z={H(z) \over H_{0}}$

Un modèle trop simplifié pour être réaliste

Les scientifiques ont estimé le rayon de l'univers observable, et leurs résultats semblent relativement proches du rayon de Hubble. Là encore, comme pour la coïncidence entre âge de l'univers estimé et temps de Hubble, personne ne sait si c'est une coïncidence ou quelque chose de plus important. En théorie, l'égalité $R(t)=c\cdot T_{H}$ est respectée en permanence dans le modèle linéaire. Par contre, elle n'est respectée que pour un instant $t$ bien précis dans les autres et violée dans tous les autres cas. Le fait que l'égalité soit respectée dans notre monde est donc soit une grosse coïncidence, soit elle trahit quelque chose de fondamental qui est encore mal compris. Par contre, les résultats empiriques concernant les mesures de redshift, ou via d'autres mesures indirectes, ne collent pas du tout avec ce modèle. Autant l'égalité $R(t)=c\cdot T_{H}$ est respectée, autant les autres prédictions du modèle ne le sont pas.

Et les mesures ne sont pas seules à nous dire que ce modèle est trop simpliste pour décrire fidèlement l'univers. La théorie nous dit que ce modèle n'est valide que pour un univers vide, c'est à dire en absence de matière. Toute présence de matière biaise les résultats du modèle. Et aux dernières nouvelles, la matière existe...

Le modèle à croissance en loi de puissance

Maintenant, nous allons étudier le cas d'une expansion en loi de puissance. En clair, nous allons étudier le cas où le facteur d'échelle est égal à :

$a(t)=k\cdot t^{n}$, avec $t$ le temps, $k$ une constante quelconque et $n$ une puissance quelconque.

Une autre formulation, souvent utilisée, est la suivante :

$a(t)=a(t_{0})\cdot \left({\frac {t}{t_{0}}}\right)^{n}$, avec $t_{0}$ l'origine de temps choisie arbitrairement et $a(t_{0})$ le facteur d'échelle à ce même instant.

Les deux formulations sont équivalentes si l'on postule $k=a_{0}\cdot \left({\frac {1}{t_{0}}}\right)^{n}$. Dans ce qui suit, nous utiliserons la première formulation.

On peut d'or et déjà remarquer que l'expansion linéaire n'est qu'un cas particulier d'expansion en loi de puissance, où $n=1$. Ne vous étonnez donc pas si les calculs se ressemblent quelque peu.

Le calcul du facteur de Hubble et des paramètres associés

Pour calculer le facteur de Hubble, nous allons partir de la dérivée du facteur d'échelle, qui est égale à :

${\frac {d}{dt}}a(t)={\frac {d}{dt}}(k\cdot t^{n})=k\cdot {\frac {d(t^{n})}{dt}}=k\cdot n\cdot t^{n-1}$

On divise alors par a(t) pour obtenir le facteur de Hubble :

$H={\frac {k\cdot n\cdot t^{n-1}}{k\cdot t^{n}}}=n\cdot t^{-1}={\frac {n}{t}}$

Pour résumer :

$H={\frac {n}{t}}$

L'évolution du facteur de Hubble

Pour savoir comment évolue le facteur de Hubble dans le temps, le mieux est encore une fois de calculer sa dérivée. La dérivée du facteur de Hubble est égale à :

$H'(t)=\left({\frac {n}{t}}\right)'=-{\frac {n}{t^{2}}}$

On pourrait croire qu'elle est négative, en raison du signe -, mais tout dépend de la valeur de n. C’est le cas si n est positif ou nul, mais il peut être négatif.

Le calcul du paramètre de décélération

À partir des résultats précédents, on peut calculer la valeur du paramètre de décélération. Pour le calculer, on applique la formule suivante, vue dans le chapitre sur l'univers observable :

$q=-\left(1+{\frac {H(t)'}{H(t)^{2}}}\right)$

On injecte l'équation $H'(t)=-{\frac {n}{t^{2}}}$ dans l'équation précédente, ce qui donne :

$q=-\left(1-{\frac {n}{t^{2}}}{\frac {1}{H(t)^{2}}}\right)$

On injecte alors l'équation $H={\frac {n}{t}}$, ce qui donne :

$q=-\left(1-{\frac {n}{t^{2}}}\cdot {\frac {t^{2}}{n^{2}}}\right)$

Ce qui se simplifie en :

$q=-\left(1-{\frac {1}{n}}\right)$

On peut réécrire le tout comme suit :

$q={\frac {1}{n}}-1={\frac {1-n}{n}}$

En clair, l'expansion dépend du coefficient $n$.

• Si $n=1$, alors on retombe sur le cas de l'expansion linéaire. L'expansion a un rythme constant : elle n’accélère pas et ne ralentit pas.
• Si $n>1$, l'expansion accélère.
• Enfin, si $n<1$, l'expansion de l'univers ralentit.

Le calcul de l'âge de l'univers

L'équation : $H={\frac {n}{t}}$ permet de calculer l'âge de l'univers $t$ à partir du facteur de Hubble. En isolant $t$ dans l'équation précédente, on trouve en effet :

$t={\frac {n}{H}}$

Reformulons en utilisant le temps de Hubble :

$t=n\cdot T_{H}$

On voit que l'âge de l'univers est un multiple du temps de Hubble, le coefficient de proportionnalité n'étant autre que l'exposant de la loi de puissance.

Le calcul du rayon de Hubble

Il est possible, à partir des résultats précédents, de calculer le rayon de Hubble assez facilement. Pour rappel, celui-ci est la distance à partir de laquelle les objets semblent aller plus vite que la lumière à cause de l'expansion. Pour rappel, il vaut :

$R_{H}(t)={\frac {c}{H(t)}}$

On injecte alors l'équation : $H={\frac {n}{t}}$ :

$R_{H}(t)={\frac {c\cdot t}{n}}$

Dans ce modèle, le rayon de Hubble augmente avec le temps.

Le calcul du rayon de l'univers observable

À partir des résultats précédents, nous pouvons trouver le rayon de l'univers observable, qui n'est pas le même que le rayon de Hubble. Pour cela, il faut cependant se rappeler ce qu'on a vu dans le chapitre sur l'univers observable. Pour calculer le rayon de l'univers observable, il faut procéder en deux étapes. Premièrement, il faut calculer le rayon comobile, le rayon calculé en supprimant l'effet de l'expansion. Ensuite, on corrige ce rayon comobile pour ajouter l'expansion de l'univers. Si on note $R(t)$ le rayon de l'univers à l'instant t, alors le rayon comobile est égal à $r(t)={R(t) \over a(t)}$. Le passage du rayon comobile au rayon observé se fait donc simplement en multipliant par le facteur d'échelle $a(t)$. La deuxième étape est donc triviale. Par contre, la première étape, le calcul du rayon comobile, fait intervenir une intégrale assez compliquée. Pour rappel, le rayon comobile se calcule avec la formule suivante :

$R(t)=c\cdot \left[a(t)\cdot \int _{0}^{t}{1 \over a(t_{i})}dt_{i}\right]$

Pour calculer le rayon comobile, nous allons introduire l'équation $a(t)=k\cdot t^{n}$ dans la précédente, ce qui donne :

$r(t)=c\int _{0}^{t}{\frac {1}{k\cdot t_{i}^{n}}}dt_{i}$

La constante k peut être sortie de l'intégrale, ce qui donne :

$r(t)={\frac {c}{k}}\int _{0}^{t}{\frac {1}{t_{i}^{n}}}dt_{i}$

On utilise alors la formule $\int {\frac {1}{t^{n}}}dt={\frac {t^{1-n}}{1-n}}$ :

$r(t)={\frac {c}{k}}{\frac {t_{u}^{1-n}}{1-n}}$

On utilise alors la formule $t_{u}^{1-n}={\frac {t}{t^{n}}}$ :

$r(t)={\frac {c}{k}}{\frac {t}{t^{n}}}{\frac {1}{1-n}}$

On regroupe les termes comme suit :

$r(t)={\frac {ct}{1-n}}{\frac {1}{k\cdot t^{n}}}$

Par définition, le terme ${\frac {1}{k\cdot t^{n}}}$ est égal à $1 \over a(t)$, ce qui donne :

$r(t)={\frac {ct}{1-n}}{\frac {1}{a(t)}}$

On peut donc en déduire le rayon propre de l'univers observable en multipliant des deux côtés par $a(t)$ :

$R(t)={\frac {c\cdot t}{1-n}}$

Si on prend $n=1$, on retombe sur les résultats du modèle $R_{h}=ct$ vus précédemment. Et encore une fois, on voit que le rayon de l'univers diverge : l'application de la formule précédente donne une division par zéro.

La relation entre rayon de Hubble et rayon de l'univers observable

Les équations précédentes montrent que le rayon de l'univers observable n'est pas égal au rayon de Hubble ! Il y a une différence entre $R_{H}={\frac {c\cdot t}{n}}$ et le rayon de l'univers observable $R(t)={\frac {c\cdot t}{1-n}}$. La relation entre les deux variables se calcule comme suit :

$R_{H}={\frac {c\cdot t}{n}}$

Multiplions au numérateur et au dénominateur par 1 - n :

$R_{H}={\frac {1-n}{1-n}}{\frac {c\cdot t}{n}}$

En réorganisant les termes, on trouve :

$R_{H}={\frac {1-n}{n}}{\frac {c\cdot t}{1-n}}$

Le terme le plus à droite n'est autre que le rayon de l'univers observable :

$R_{H}={\frac {1-n}{n}}r(t)$

On peut aussi inverser la relation, ce qui donne :

$r(t)={\frac {n}{1-n}}R_{H}$

Les deux rayons sont égaux seulement dans le cas où $n=1-n$, ce qui donne $n={\frac {1}{2}}$.

On peut aussi remarquer que l'on a :

${\frac {1}{R_{H}}}+{\frac {1}{R(t)}}=c\cdot t$

Le calcul du décalage vers le rouge

Voyons maintenant le calcul du redshift. Dans ce qui suit, nous allons supposer qu'un objet à une distance $d$ émet de la lumière à un instant $t_{0}$, lumière qui est reçue par l'observateur à un instant $t$. Pour calculer le décalage vers le rouge de cette lumière, le redshift, on utilise la formule suivante, vue dans le chapitre sur le rayonnement :

$1+z={\frac {a(t_{0})}{a(t)}}$, avec $t_{0}$ l'origine de temps choisie arbitrairement et $a(t_{0})$ le facteur d'échelle à ce même instant.

On injecte alors l'équation $a(t)=k\cdot t^{n}$ :

$1+z={\frac {k\cdot {t_{0}}^{n}}{k\cdot t^{n}}}$

On simplifie :

$1+z=\left({\frac {t_{0}}{t}}\right)^{n}=\left({\frac {t}{t_{0}}}\right)^{-n}$

Sachant que $H(t)={\frac {n}{t}}$, on a aussi :

$1+z=\left({\frac {H(t_{0})}{H(t)}}\right)^{n}$

En remarquant que ${t_{0}}^{n}$ est une constante, les équations précédentes se simplifient en :

$1+z\propto t^{-n}$

Le modèle à croissance exponentielle

Pour terminer, nous allons étudier le cas d'une expansion exponentielle, décrite par :

$a(t)=k\cdot e^{r\cdot t}$, avec $t$ le temps, $k$ et $r$ deux constantes quelconques.

Précisons que nous prenons $r>0$, sans quoi la fonction serait décroissante, ainsi que $k>0$, pour garantir que l'univers n'a pas de volume négatif. Voir le graphique ci-dessous pour comprendre pourquoi.

Illustration de la courbe de la fonction exponentielle.

Précisons que les propriétés mathématiques de l'exponentielle ont une conséquence assez intéressante. En effet, une exponentielle ne peut pas s'annuler, ce qui fait qu'il n'existe pas de temps t où le facteur d'échelle s'annule. En conséquence, on n'a pas d'instant où tout l'univers est rassemblé en un unique point, on n'a pas de singularité initiale. L'univers n'a donc pas d'âge, il existe depuis un temps infini. Ce modèle est donc un petit peu particulier, dans le sens où il n'y a pas de big-bang dedans. Cela peu sembler bizarre que les cosmologistes utilisent un tel modèle, mais nous verrons dans certains chapitres que ce modèle est plus réaliste qu'il n'y parait. Et à bien y penser, l'absence de singularité est plus un avantage qu'un inconvénient.

Le calcul du paramètre de Hubble

Une démonstration simple part du principe que le facteur de Hubble est la dérivée logarithmique du facteur d'échelle, c'est à dire la dérivée du logarithme. Pour en faire le calcul, on commence par prendre le logarithme du facteur d'échelle, ce qui colle parfaitement avec la formule exponentielle.

$\ln a(t)=\ln \left[k\cdot e^{r\cdot t}\right]$

Le logarithme d'un produit est égal à la somme des logarithmes des opérandes :

$\ln a(t)=\ln k+\ln \left[e^{r\cdot t}\right]$

Le logarithme et l'exponentielle s'annulent, ce qui donne :

$\ln a(t)=\ln k+r\cdot t$

On prend ensuite la dérivée, ce qui donne :

$H(t)={\frac {d}{dt}}\ln k+{\frac {d}{dt}}(r\cdot t)=0+r=r$

Démonstration

Une démonstration alternative part de la dérivée du facteur d'échelle : ${\frac {da}{dt}}={\frac {d(k\cdot e^{r\cdot t})}{dt}}=k\cdot {\frac {d(e^{r\cdot t})}{dt}}=k\cdot r\cdot e^{r\cdot t}$ On divise par $a(t)=k\cdot e^{r\cdot t}$, ce qui donne : $H={\frac {k\cdot r\cdot e^{r\cdot t}}{k\cdot e^{r\cdot t}}}=r$

Le paramètre de Hubble est donc la constante r de l'exponentielle. On peut donc reformuler la loi d'expansion comme suit :

$a(t)=k\cdot e^{H\cdot t}$

Le calcul du temps et du rayon de Hubble

À partir du facteur de Hubble calculé juste avant, on peut calculer le temps de Hubble :

$T_{H}={\frac {1}{H}}={\frac {1}{r}}$

Même chose pour le rayon de Hubble :

$R_{H}={\frac {c}{H}}={\frac {c}{r}}$

On voit que vu que le paramètre de Hubble est constant, le temps de Hubble et le rayon de Hubble le sont aussi. Cela peut paraître bizarre que le rayon de Hubble soit constant, mais rappelez-vous qu'il ne s'agit que du rayon au-delà duquel la vitesse de fuite d'un objet est égale à $c$. Il n'a pas de signification physique.

Le calcul du rayon de l'univers observable

Pour trouver le rayon de l'univers observable, on utilise encore une fois l'équation suivante :

$R(t)=c\cdot \left[a(t)\cdot \int _{0}^{t}{1 \over a(t_{i})}dt_{i}\right]$

On fait le remplacement avec $a(t)=k\cdot e^{H\cdot t}$ :

$R(t)=c\cdot k\cdot e^{H\cdot t}\cdot \int _{0}^{t}{1 \over k\cdot e^{H\cdot u}}du$

Vu que k est une constante, on la sort de l'intégrale :

$R(t)=c\cdot k\cdot e^{H\cdot t}\cdot {1 \over k}\int _{0}^{t}{1 \over e^{H\cdot u}}du$

On simplifie :

$R(t)=c\cdot e^{H\cdot t}\cdot \int _{0}^{t}e^{-H\cdot u}du$

Le calcul de l'intégrale donne :

$R(t)=c\cdot e^{H\cdot t}\cdot \left({1-e^{-H\cdot u} \over H}\right)$

On reformule :

$R(t)={\frac {c}{H}}\cdot e^{H\cdot t}\cdot \left(1-e^{-H\cdot u}\right)$

On simplifie :

$R(t)={\frac {c}{H}}\left(e^{H\cdot t}-1\right)$

Le terme ${\frac {c}{H}}$ n'est autre que le rayon de Hubble $R_{H}$ :

$R(t)=R_{H}\left(e^{H\cdot t}-1\right)$

On voit que le rayon de l'univers observable est plus grand que le rayon de Hubble.

Le calcul du paramètre de décélération

À partir des résultats précédents, on peut calculer la valeur du paramètre de décélération. Pour cela, on utilise la formule vue dans le chapitre sur l'univers observable :

$q=-\left(1+{\frac {H(t)'}{H(t)^{2}}}\right)$

Le facteur de Hubble est constant, ce qui fait que sa dérivée est nulle. En injectant $H'(t)=0$ dans l'équation précédente, on trouve :

$q=-1$

Ce résultat nous dit que l'expansion de l'univers accélère.

Le calcul du décalage vers le rouge

Passons maintenant au calcul du redshift. Pour le calculer, on utilise la formule suivante, vue dans le chapitre sur le rayonnement :

$1+z={\frac {a(t_{0})}{a(t)}}$, avec $t_{0}$ l'origine de temps choisie arbitrairement et $a(t_{0})$ le facteur d'échelle à ce même instant.

On injecte alors l'équation $a(t)=k\cdot e^{rt}$ :

$1+z={\frac {k\cdot e^{rt_{0}}}{k\cdot e^{rt}}}$

On simplifie :

$1+z=e^{r(t_{0}-t)}$

On voit que le redshift augmente exponentiellement.

Les équations de Friedmann newtoniennes

Armé de la loi de Hubble et du facteur d'échelle, nous pouvons aborder des équations très importantes de la cosmologie actuelle : les équations de Friedmann. Elles décrivent un univers de densité homogène, sans préférence au niveau de la direction (isotrope), et permettent de calculer le facteur de Hubble en fonction de la densité de l'univers et du facteur d'échelle. Elles sont au nombre de trois et portent les noms de "première équation de Friedmann", "seconde équation de Friedmann" et "équation du fluide cosmologique".

Démontrer ces équations demande d'utiliser la relativité générale, ce qui est affreusement compliqué. Heureusement, il existe une autre manière de déduire cette équation, nettement plus simple et intuitive, en utilisant la physique newtonienne. Les deux approches donnent des résultats similaires, avec cependant quelques différences que nous expliquerons plus tard. Dans ce chapitre, nous allons démontrer ces équations dans un cadre newtonien. Nous n'allons pas faire usage de la relativité et nous utiliserons seulement les outils de la physique classique. Ce qu'on verra dans le chapitre est donc assez simple et accessible.

Dans ce qui suit, les notations sont les suivantes : $\rho$ est la densité de matière, $G$ est la constante de gravitation et $K$ est un terme dont nous verrons la signification dans ce qui suit.

Les trois équations de Friedmann, en version non-relativiste, sont les suivantes :

Première équation de Friedmann	$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {K}{a^{2}}}$
Seconde équation de Friedmann	${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\rho$
Équation du fluide cosmologique de Friedmann	${\frac {d\rho }{dt}}+3H\rho =0$

La première équation de Friedmann

Pour démontrer la première équation de Friedmann, nous allons considérer que l'univers observable est une sphère de rayon R, de masse M, de volume V, de masse volumique homogène ρ, qui grossit à une vitesse v (la vitesse de l'expansion de l'univers). Le centre de cette sphère est situé là où se trouve l'observateur (la Terre, donc). Prenons maintenant une galaxie située sur le bord de l'univers observable, et posons que son énergie mécanique est notée $E$. Ses énergies potentielle et cinétique sont donc respectivement égales à $E_{pot}=-{\frac {GMm}{R}}$ et $E_{cin}={\frac {1}{2}}mv^{2}$, ce qui donne :

$E=E_{cin}+E_{pot}={\frac {1}{2}}mv^{2}-{\frac {GMm}{R}}$

Modifions l'ordre des termes :

${\frac {1}{2}}mv^{2}={\frac {GMm}{R}}+E$

Nous pouvons alors utiliser la loi de Hubble $v=H\times R$, pour remplacer la vitesse de la galaxie.

${\frac {1}{2}}mR^{2}H^{2}={\frac {GMm}{R}}+E$

Isolons maintenant $H^{2}$ en divisant des deux membres par ${\frac {1}{2}}mR^{2}$.

$H^{2}={\frac {2GM}{R^{3}}}+{\frac {2E}{mR^{2}}}$

Ensuite, rappelons-nous que par définition, $R=R_{t0}\times {\frac {a(t)}{a(t0)}}$. En posant qu'à l'instant t0, le facteur d'échelle est égal à 1, nous avons : $R=R_{0}\times a(t)$. Nous n'allons cependant faire le remplacement que dans le second terme et pas dans le premier. Quelques simplifications ultérieures permettront de se débarrasser du rayon dans le premier terme.

$H^{2}={\frac {2G}{R^{3}}}M+{\frac {2E}{mR_{0}^{2}a^{2}}}$

Nous allons maintenant poser que $-{\frac {2E}{mR_{0}^{2}}}$ est une constante, que nous allons noter $K$. Prenez garde au signe de cette formule !

$H^{2}={\frac {2G}{R^{3}}}M-{\frac {K}{a^{2}}}$

Exprimons maintenant la masse de l'univers comme étant égale à sa masse volumique multipliée par le volume : $M={\frac {4\pi }{3}}R^{3}\rho$. On a alors :

$H^{2}={\frac {2G}{R^{3}}}{\frac {4\pi }{3}}R^{3}\rho -{\frac {K}{a^{2}}}$

Après quelques simplifications algébriques, nous obtenons la première équation de Friedmann.

$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {K}{a^{2}}}$

La seconde équation de Friedmann

Par souci de lisibilité, nous noterons la dérivée première d'une variable $x$ comme ceci : $x'$. Même chose pour la dérivée seconde, notée $x''$. De plus, toutes les dérivées sont par rapport au temps. En clair, $x'={\frac {dx}{dt}}$ et $x''={\frac {d^{2}x}{dt^{2}}}$.

La seconde équation de Friedmann est la suivante.

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\rho$

Celle-ci nous dit comment varie la dérivée seconde du facteur d'échelle, qui elle-même dit si l'expansion de l'univers accélère, ralentit ou reste constante. Il s'agit donc d'une équation très importante pour comprendre la dynamique de l'expansion et comment celle-ci évolue avec le temps.

On peut la démontrer comme suit.

Démonstration

Supposons que nous soyons au centre de l'univers observable et prenons un point situé à sa surface, à la limite de l'univers observable. Ce point s'éloigne de nous à une vitesse égale à $v=H\cdot d(t)$, avec $R(t)$ le rayon de l'univers observable. Maintenant, essayons de calculer son accélération. Partons du principe que l'accélération de ce point est intégralement liée à la gravité, c'est à dire qu'il est attiré vers le centre de l'univers observable (on néglige les masses qui ne sont pas dans l'univers observable, bien que ce soit un peu de la triche). L'accélération de ce point se calcule avec la formule de Newton et vaut : $R(t)''={\frac {GM}{R(t)^{2}}}$, avec M la masse totale de l'univers. Divisons par R(t) : ${\frac {R(t)''}{R(t)}}={\frac {GM}{R(t)^{3}}}$ La masse de l'univers observable est égale au produit de sa densité par son volume : ${\frac {R(t)''}{R(t)}}={\frac {G\cdot \rho \cdot V}{R(t)^{3}}}$ L’univers observable est une sphère, donc son volume est de ${\frac {4}{3}}\pi \cdot R(t)^{3}$. En injectant cette formule dans la précédente, on trouve : ${\frac {R(t)''}{R(t)}}={\frac {G\cdot \rho \cdot {\frac {4}{3}}\pi \cdot R(t)^{3}}{R(t)^{3}}}$ En simplifiant, on trouve : ${\frac {R(t)''}{R(t)}}={\frac {4\pi G}{3}}\cdot \rho$ On applique ensuite la formule $R(t)=R_{0}\cdot a(t)$, valable pour toutes les distances : ${\frac {[R_{0}\cdot a(t)]''}{R_{0}\cdot a(t)}}={\frac {4\pi G}{3}}\cdot \rho$ En simplifiant, on a : ${\frac {a(t)''}{a(t)}}={\frac {4\pi G}{3}}\cdot \rho$

Une autre démonstration, équivalente, fait appel à l'équation de Poisson pour le champ gravitationnel.

Démonstration

Pour rappel, l'équation de Poisson relie l'accélération de la pesanteur à la densité du corps qui génère la gravité. L'équation en question utilise l'opérateur divergence, défini par : $\nabla \cdot {\vec {A}}={\frac {dA}{dx}}+{\frac {dA}{dy}}+{\frac {dA}{dz}}$ Dans le cas qui nous intéresse, l'accélération n'est autre que l'accélération de l'expansion de l'univers. L'équation de Poisson est donc la suivante : $\nabla \cdot {\vec {a_{c}}}=4\pi G\rho$ Nous avons vu il y a quelques chapitres l'équation suivante, qui donne l'accélération de l'expansion en fonction du facteur de Hubble et du rayon de l'univers r : ${\vec {a_{c}}}={\vec {r(t)}}\cdot {\frac {a(t)''}{a(t)}}$ En combinant les deux équations, on trouve : $\nabla \cdot \left[{\vec {r}}{\frac {a(t)''}{a(t)}}\right]=4\pi G\rho$ L'opérateur $\nabla$ est une dérivée, ce qui fait qu'on peut utiliser la formule ${\frac {d(k\cdot f(x))}{dx}}=k\cdot {\frac {df(x)}{dx}}$. ${\frac {a(t)''}{a(t)}}\left[\nabla \cdot {\vec {r}}\right]=4\pi G\rho$ Maintenant, appliquons la définition de $\nabla$ : ${\frac {a(t)''}{a(t)}}\left[{\frac {d{\vec {r}}}{dx}}+{\frac {d{\vec {r}}}{dy}}+{\frac {d{\vec {r}}}{dz}}\right]=4\pi G\rho$ Par définition, on a ${\frac {d{\vec {r}}}{dx}}={\frac {d{\vec {r}}}{dy}}={\frac {d{\vec {r}}}{dz}}=1$, ce qui donne : $3\cdot {\frac {a(t)''}{a(t)}}=4\pi G\rho$ On réorganise les termes : ${\frac {a(t)''}{a(t)}}={\frac {4\pi G}{3}}\rho$

L'équation du fluide

Enfin, on peut aussi démontrer une troisième équation, appelée l'équation du fluide de Friedmann. Pour la démontrer, partons du principe que l'univers a une masse M égale au produit de son volume par sa densité :

$M=V\cdot \rho (t)$

Le volume de l'univers dépend du cube du facteur d'échelle, comme nous l'avons vu dans les chapitres précédents :

$M=V_{0}\cdot a(t)^{3}\cdot \rho (t)$

Divisons des deux côtés par $V_{0}$ :

${\frac {M}{V_{0}}}=a(t)^{3}\cdot \rho (t)$

Prenons la dérivée :

${\frac {d}{dt}}\left({\frac {M}{V_{0}}}\right)={\frac {d}{dt}}\left(a(t)^{3}\cdot \rho (t)\right)$

Maintenant, supposons que la masse de l'univers est conservée. Vu que $V_{0}$ est une constante, ${\frac {M}{V_{0}}}$ l'est alors aussi, ce qui fait que sa dérivée est nulle. L'équation précédente devient donc :

${\frac {d}{dt}}\left(a(t)^{3}\cdot \rho (t)\right)=0$

Le calcul de la dérivée donne :

$a(t)^{3}\cdot {\frac {d\rho (t)}{dt}}+{\frac {da(t)^{3}}{dt}}\cdot \rho =0$

La dérivée d'un cube vaut ${\frac {dx^{3}}{dt}}=3x^{2}x'$ :

$a(t)^{3}\cdot {\frac {d\rho (t)}{dt}}+3a(t)^{2}a(t)'\cdot \rho =0$

On divise par $a(t)^{3}$  :

${\frac {d\rho (t)}{dt}}+3{\frac {a(t)'}{a(t)}}\cdot \rho =0$

Sachant que $H={\frac {a(t)'}{a(t)}}$, on a :

${\frac {d\rho (t)}{dt}}+3H\rho =0$

Résoudre les équations de Friedmann newtoniennes

Nous avons établi les trois équations newtoniennes de Friedmann dans le chapitre précédent. Pour rappel, les voici :

$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {K}{a^{2}}}$

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\rho$

${\frac {d\rho }{dt}}+3H\rho =0$

La résolution des deux équations de Friedmann

Maintenant que nous avons ces trois équations, nous allons tenter de les résoudre. La première étape pour cela passe par l'équation du fluide de Friedmann. Avec cette équation, on peut trouver une équation qui relie la densité avec le facteur d'échelle. On peut ensuite injecter cette équation dans la première et la seconde équation de Friedmann, effectuer des simplifications très appréciables.

La résolution de l'équation du fluide

Commençons donc par la première étape, en partant de l'équation du fluide, écrite comme suit :

${\frac {d\rho }{dt}}=3H\rho$

Divisons par $\rho$ :

${\frac {\rho (t)'}{\rho (t)}}=3H$

Il faut alors se rappeler que le facteur de Hubble dépend du facteur d'échelle, qui lui-même dépend du temps, d'après l'équation suivante, vue dans les chapitres précédents :

${\frac {\rho (t)'}{\rho (t)}}=-3{\frac {a(t)'}{a(t)}}$

On utilise alors la formule $\int {\frac {x(t)'}{x(t)}}=\ln {x}+Cst$ :

$\ln {\rho (t)}+K_{1}=-3\times \ln {a(t)}+K_{2}$, avec $K_{1}$ et $K_{2}$ deux constantes d'intégration.

On réorganise les termes, ce qui donne :

$\ln {\rho (t)}=-3\times \ln {a(t)}+K$, avec $K=K_{2}-K_{1}$.

On prend l'exponentielle :

$\rho (t)=e^{-3\times \ln {a(t)}}\times e^{K}$

On utilise alors la formule $x^{y}=exp^{y\ln {x}}$ :

$\rho (t)=a(t)^{-3}\times e^{K}$

Pour conserver la cohérence des unités, $e^{K}$ correspond à une densité. Et plus précisément, l'équation n'a de sens que s'il s'agit de la densité quand $a(t)^{3}=1$. Notons-la $\rho _{0}$. On a donc :

$\rho (t)=\rho _{0}\times a(t)^{-3}$

Cette équation peut se reformuler comme ceci :

${\frac {d}{dt}}[\rho (t)\times a(t)^{3}]=0$

Cette équation n'est autre que l'équation de conservation de la masse de l'univers. En effet, rappelons que le volume de l'univers est proportionnel au terme $a(t)^{3}$. En supposant une masse constante et en la divisant par le volume, on retrouve bien l'équation précédente après quelques simplification.

$\rho (t)={\frac {M}{V}}={\frac {M}{V_{0}\times a(t)^{3}}}={\frac {M}{V_{0}}}\times {\frac {1}{a(t)^{3}}}=\rho _{0}\times a(t)^{-3}$

De plus, cette équation est valable quelle que soit la courbure, ce qui est important à remarquer.

La reformulation de la première équation de Friedmann

Maintenant que l'on a obtenu l'équation précédente, on peut l'injecter dans la première équation de Friedmann et dans la seconde. Commençons par la première. On a alors :

$H^{2}={\frac {8\pi G}{3}}(\rho _{0}\times a(t)^{-3})-{\frac {K}{a^{2}}}$

Ce qui s'écrit aussi comme suit :

$H^{2}={\frac {8\pi G}{3}}{\frac {\rho _{0}}{a(t)^{3}}}-{\frac {K}{a^{2}}}$

Maintenant, remplaçons H par son expression dépendant du facteur d'échelle, vue plus haut :

$\left({\frac {a(t)'}{a(t)}}\right)^{2}={\frac {8\pi G}{3}}{\frac {\rho _{0}}{a(t)^{3}}}-{\frac {K}{a^{2}}}$

Simplifions le terme de gauche :

${\frac {a(t)'^{2}}{a(t)^{2}}}={\frac {8\pi G}{3}}{\frac {\rho _{0}}{a(t)^{3}}}-{\frac {K}{a^{2}}}$

On multiplie par $a(t)^{2}$ :

$a(t)'^{2}={\frac {8\pi G}{3}}{\frac {\rho _{0}}{a(t)}}-K$

On prend la racine carrée :

$a(t)'={\sqrt {{\frac {8\pi G}{3}}{\frac {\rho _{0}}{a(t)}}-K}}$

L’univers dominé par la matière

L'équation précédente est difficile à résoudre en raison du terme de courbure, qui pose quelques problèmes. Mais en postulant une courbure nulle, on peut aller plus loin. Le modèle cosmologique obtenu sous ces hypothèses est appelé l'univers dominé par la matière, ce qui trahit le fait que l'univers en question ne contient que de la matière, sans courbure.

La détermination de la loi d'évolution du facteur d'échelle

Avec l'hypothèse d'une courbure nulle, l'équation précédente devient la suivante en réorganisant les termes :

$a(t)'={\sqrt {{\frac {8\pi G\rho _{0}}{3}}a(t)^{-1}}}$

On utilise alors la formule ${\sqrt {a\times b}}={\sqrt {a}}\times {\sqrt {b}}$ :

$a(t)'={\sqrt {{\frac {8\pi G}{3}}\rho _{0}}}\times {\sqrt {a(t)^{-1}}}$

Prendre la racine carrée est équivalent à élever à la puissance 1/2, ce qui fait qu'on peut faire le remplacement :

$a(t)'={\sqrt {{\frac {8\pi G}{3}}\rho _{0}}}\times a(t)^{-{\frac {1}{2}}}$

Le tout se reformule comme suit :

${\frac {da}{dt}}={\frac {K}{a(t)^{1/2}}}$, avec $K={\sqrt {{\frac {8\pi G}{3}}\rho _{0}}}$.

On réorganise les termes :

$a(t)^{1/2}da=Kdt$

On intègre :

$\int a(t)^{1/2}da=\int Kdt$

On utilise la formule $\int a^{x}=(x+1)a^{x+1}$ :

${\frac {3}{2}}a(t)^{3/2}=K\times t$

La réorganisation des termes donne :

$a(t)={\frac {3K}{2}}^{\frac {2}{3}}\times t^{\frac {2}{3}}$

On peut simplifier le tout en :

$a(t)=a_{0}\cdot t^{\frac {2}{3}}$

L'équation précédente est une loi de puissance. Or, nous avons vu les modèles cosmologiques basés sur des lois de puissance dans le chapitre "Une introduction aux modèles cosmologiques", ce qui fait que l'on pourrait réutiliser les résultats de ce chapitre directement. On a en effet établi des formules pour le facteur de Hubble, le décalage vers le rouge, le rayon de l'univers observable et bien d'autres pour de tels modèles. En appliquant ces formules, on trouve les résultats du tableau suivant :

Paramètre	Formule du cas général	Formule dans le cas de l'univers dominé par la matière
Facteur de Hubble	$H={\frac {n}{t}}$	$H={\frac {2}{3}}{\frac {1}{t}}$
Temps de Hubble	$T_{H}={\frac {t}{n}}$	$T_{H}={\frac {3}{2}}t$
Rayon de Hubble	$R_{H}={\frac {c\cdot t}{n}}$	$R_{H}={\frac {3}{2}}\cdot c\cdot t$
Rayon de l'univers observable	$r(t)={\frac {c\cdot t}{1-n}}$	$r(t)=3\cdot c\cdot t=2\cdot R_{H}$
Age de l'univers	$t=n\cdot T_{H}$	$t={\frac {2}{3}}\cdot T_{H}$
Paramètre de décélération	$q={\frac {3}{2}}w+{\frac {1}{2}}$	$q={\frac {1}{2}}$

Ce qu'on peut tirer de ces formules, est surtout que l'expansion de l'univers ralentit avec le temps. En effet, le facteur de décélération est positif.

La relation entre densité et âge de l'univers

On peut aussi déterminer une relation entre l'âge de l'univers et la densité dans ce modèle. Pour cela, partons de l'équation suivante :

$H={\frac {2}{3}}\cdot {\frac {1}{t}}$

En élevant l'équation au carré, on a :

$H^{2}={\frac {4}{9}}\cdot {\frac {1}{t^{2}}}$

On peut alors combiner cette équation avec l'équation suivante :

$H^{2}={\frac {8\pi G}{3}}\rho$

En égalisant les deux équations, on trouve :

${\frac {8\pi G}{3}}\rho ={\frac {4}{9}}\cdot {\frac {1}{t^{2}}}$

En divisant par ${\frac {8\pi G}{3}}$, on trouve :

$\rho ={\frac {1}{6\pi G}}\cdot {\frac {1}{t^{2}}}$

Pour simplifier, on a :

$\rho \propto {\frac {1}{t^{2}}}$

On voit que la densité diminue avec le carré du temps et que la constante de proportionnalité est assez simple.

L'univers dominé par la courbure

Le second modèle que nous allons voir est celui d'un univers vide, avec seulement de la courbure. Les équations de Friedmann se simplifient alors fortement. L'équation du fluide et la deuxième équation disparaissent complètement, et il ne reste que la première. Voici le résultat :

$H^{2}=-{\frac {k}{a^{2}}}$

Le calcul de la dérivée du facteur d'échelle

On peut alors utiliser la formule $H={\frac {a'}{a}}$ :

${\frac {a'^{2}}{a^{2}}}=-{\frac {k}{a^{2}}}$

On multiplie par $a^{2}$ :

${a'}^{2}=-k$

On prend la racine carrée :

$a'={\sqrt {-k}}$

L'équation n'a de solution réelle que dans le cas où la courbure est négative ou nulle. Attention : cela ne signifie pas qu'une courbure positive n'est pas possible. Elle est parfaitement possible, mais à condition que l'univers contienne de la matière ou du rayonnement. La présence de matière/rayonnement en quantités suffisante fait que la racine carrée ait bien un paramètre positif. Par contre, dans le cas d'un univers vide de matière/rayonnement, ce n'est pas le cas.

Le calcul du facteur d'échelle

En supposant que la courbure est négative et est égale à $k=-|k|$, on a alors :

$a(t)'={\sqrt {-(-|k|)}}$

Ce qui se simplifie en :

$a(t)'={\sqrt {|k|}}$

Là encore, on pose $K={\sqrt {|k|}}$ :

$a(t)'=K$

En intégrant, on trouve :

$a(t)=K\cdot t+a_{0}$

Un univers à croissance linéaire ou statique

En négligeant la constante d'intégration $a_{0}$, on a alors :

$a(t)\approx K\cdot t$

Traduit en langage commun, cela veut dire que l'univers est en expansion linéaire, à rythme constant. Le modèle obtenu n'est autre que le modèle à expansion linéaire que nous avions étudié dans le chapitre "Introduction aux modèles cosmologiques".

Précisons que si on suppose que l'univers a une courbure nulle, on trouve que :

$a(t)=a_{0}$

Traduit en langage commun, cela signifie que l'univers est statique, sans expansion. Mais ce cas est celui d'un univers complètement vide, sans courbure, ni constante cosmologique, ni matière, ni rayonnement, ni quoique ce soit. La présence de matière ou de tout autre composant rend la solution instable et brise la stabilité de l'univers, sauf coïncidence extraordinaire et/ou choix bien précis de paramètres. Un univers statique n'existe donc que si l'effet de la matière est compensé par quelque chose ayant un effet inverse de même ampleur.

L'univers avec matière et courbure

Il est maintenant temps de voir le cas général, celui d'un univers courbe qui contient de la matière. Le cas général n'a pas de solution analytique (sous forme de formule simple), sauf dans les cas où la courbure est respectivement égale à -1, 0 et 1. Cependant, on peut comparer un univers à courbure non-nulle avec l'univers de courbure nulle et en tirer quelques conséquences. Pour faire cette comparaison, nous allons devoir parler du concept de densité critique, qui n'est autre que la densité compatible avec le facteur de Hubble pour un univers à courbure nulle.

Pour rappel, dans un univers à courbure nulle, la première équation de Friedmann est la suivante :

$H_{c}^{2}={\frac {8\pi G}{3}}\rho _{c}$

On peut alors isoler la densité, ce qui donne :

$\rho _{c}={\frac {3H_{c}^{2}}{8\pi G}}$

La densité d'un tel univers de courbure nulle s'appelle la densité critique. Vous remarquerez qu'il existe une valeur de densité différente pour chaque valeur de la constante de Hubble et qu'elle évolue donc avec le temps.

Les cosmologistes utilisent souvent le rapport entre la densité mesurée expérimentalement et la densité critique, ce rapport étant appelé le paramètre de densité. Celui-ci vaut, par définition :

$\Omega (t)={\frac {\rho (t)}{\rho _{c}}}={\frac {8\pi G}{3H_{c}^{2}}}\cdot \rho (t)$

À partir de cette équation, on peut montrer que $\Omega -1$ est la déviation par rapport la densité critique, exprimée en proportion de la densité critique.

$\Omega (t)-1={\frac {\rho (t)}{\rho _{c}}}-1={\frac {\rho (t)-\rho _{c}}{\rho _{c}}}$

Rappelons que la densité varie avec le temps comme $\rho (t)=\rho _{0}\cdot a^{-3}$, et que cela vaut aussi pour la densité critique. En clair, le terme $\Omega (t)$ fait pareil. On a donc :

$\Omega (t)=\Omega _{0}\cdot a^{-3}$.

La reformulation de la première équation de Friedmann avec la densité critique

Armé de ce concept de densité critique, on peut reformuler la première équation de Friedmann avec celle-ci, même dans le cas d'un univers avec courbure. Pour cela, on part de la première équation de Friedmann sous cette forme :

$H(t)^{2}={\frac {8\pi G}{3}}\rho (t)-{\frac {K}{a(t)^{2}}}$

Par définition, on a : ${\frac {8\pi G}{3}}\rho =\Omega (t)\cdot H_{c}^{2}$, ce qui donne :

$H(t)^{2}=\Omega (t)\cdot H_{c}(t)^{2}-{\frac {K}{a(t)^{2}}}$

Divisons par $H_{c}^{2}$ :

${\frac {H(t)^{2}}{H_{c}^{2}}}=\Omega (t)-{\frac {K}{a(t)^{2}H_{c}^{2}}}$

On utilise alors l'équation $\Omega (t)=\Omega _{0}\cdot a^{-3}$ :

${\frac {H(t)^{2}}{H_{c}^{2}}}={\frac {\Omega _{0}}{a(t)^{3}}}-{\frac {K}{a(t)^{2}H_{c}^{2}}}$

Le tout peut se reformuler comme suit :

${\frac {H(t)^{2}}{H_{c}^{2}}}={\frac {\Omega _{0}}{a(t)^{3}}}-{\frac {1-\Omega _{0}}{a(t)^{2}}}$

Le destin de l'univers et le scénario du Big-Crunch

Fort de l'équation précédente, trouvons les conditions pour lesquelles le facteur de Hubble s'annule à un moment bien précis. Pour cela, on pose simplement $H(t)=0$. On a alors :

$0={\frac {\Omega _{0}}{a(t)^{3}}}-{\frac {1-\Omega _{0}}{a(t)^{2}}}$

On a alors :

${\frac {1-\Omega _{0}}{a(t)^{2}}}={\frac {\Omega _{0}}{a(t)^{3}}}$

On multiplie par $a(t)^{3} \over 1-\Omega _{0}$ :

$a(t)={\frac {\Omega _{0}}{1-\Omega _{0}}}$

Maintenant, étudions pour quelles valeurs de $\Omega _{0}$ cela peut se produire. On voit que cette équation n'a de sens que si $\Omega _{0}>1$, sans quoi le facteur d'échelle est soit nul, soit négatif.

• Si on pose que $\Omega _{0}>1$, le facteur de Hubble s'annule pour un facteur d'échelle positif. Une analyse simple nous dit que le facteur de Hubble est positif mais décroit progressivement, avant de s'annuler quand $a(t)={\frac {\Omega _{0}}{1-\Omega _{0}}}$, avant de décroitre jusqu’à ce que l'univers atteindre un volume nul.
• Si on pose que $\Omega _{0}<1$, c'est à que l'univers a une courbure négative, les seules solutions sont un facteur d'échelle négatif, ce qui n'a aucun sens. Il n'est donc pas possible que l'expansion de l'univers s'arrête dans un univers à courbure négative.
• Si on pose que $\Omega _{0}=1$, c'est à dire quand l'univers a une courbure nulle, l'équation précédente est une division par zéro. On peut interpréter ce résultat comme le fait que le facteur de Hubble tend vers zéro quand le facteur d'échelle est infini.

Les trois scénarios pour le destin de l'univers en fonction de la courbure k.

On voit donc que trois scénarios sont possibles, suivant la courbure de l'univers :

• Dans le premier scénario, l'expansion de l'univers finit par cesser et s'inverse, l'univers se contracte et le volume de l'univers observable diminue. En clair, l'univers s'effondre sur lui-même dans un grand big-crunch.
• Dans le second cas, l'expansion de l'univers ne s’arrête jamais et ralentit, mais sans pour autant que le facteur de Hubble s'annule, sauf après un temps infini. C'est le scénario du big-rip.
• Et enfin, dans le dernier scénario, l'expansion de l'univers ne s’arrête jamais, mais celle-ci ralentit progressivement. L'univers commence par s'étendre, mais son rythme de croissance diminue peu à peu, jusqu’à s'annuler après un temps infini. Dans ce scénario, l'univers ne grossit pas indéfiniment et verra son volume tendre progressivement vers un volume maximum. Ce scénario est appelé le big chill.

Courbure	$\Omega$	Destin de l'univers	Comportement de l'expansion
Positive	$\Omega _{0}>1$	Big-Crunch	L'expansion ralentit, s'annule et s'inverse.
Nulle	$\Omega _{0}=1$	Big-Chill	L'expansion ralentit et tend vers zéro avec le temps.
Négative	$\Omega _{0}<1$	Big-Rip	L'expansion ralentit et mais tend vers une limite non-nulle avec le temps.

Univers à courbure positive	Univers de courbure nulle	Univers de courbure négative

À l'heure actuelle, il semblerait que la courbure soit nulle, ou tout du moins tellement faible qu'on peut la considérer comme nulle. Toutes les mesures, réalisées par les satellites WMAP et Planck donnent bien une valeur quasiment nulle, aux imprécisions expérimentales près. Les mesures les plus récentes, provenant du satellite Planck, nous disent qu'il y a 95% de chances pour que le paramètre de densité soit compris entre 1.0008 et −1.0029.

La masse et la relativité générale

Avant de passer au prochain chapitre, nous devons parler rapidement de la masse. Vous avez peut-être l'intuition de ce qu'est la masse d'un objet, en lien avec son poids. Vous savez aussi que la masse est ce que l'on trouve dans la formule de Newton, à savoir ce qui relie l'accélération d'un objet à la force auquel on le soumet. Mais en réalité, il faut être plus précis que cela et distinguer plusieurs sortes de masses. De plus, nous allons voir que masse et énergie ont des liens assez profonds.

Les différents types de masse

Comme dit juste auparavant, il existe plusieurs sortes de masse : la masse inertielle, la masse propre et les deux masses graves (active et passive). La masse inertielle est celle de la loi de Newton, alors que les masses graves sont liées à la gravité. Ces distinctions, que nous allons voir en détail, auront une importance capitale dans de futurs chapitres.

La masse propre

La masse propre est définie par la loi de Newton, à savoir par la relation :

${\vec {F}}=m\cdot {\vec {a}}$, avec ${\vec {F}}$ la force et ${\vec {a}}$ l'accélération.

Dans le cadre de la relativité restreinte, la formule de Newton devient :

${\vec {F}}=m\cdot \gamma \cdot {\vec {a}}$, avec $\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$.

L'équation précédente peut se reformuler de deux manières différentes. La première est la suivante, où l'on regroupe le terme $\gamma$ et le terme ${\vec {a}}$. C'est de loin la version la plus correcte du point de vue physique, vu que les termes $\gamma$ et le terme ${\vec {a}}$ sont tous deux des termes cinématiques (liés au déplacement de l'objet) :

${\vec {F}}=m\cdot {\frac {\vec {a}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$, avec $\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$.

La masse inertielle

La masse inertielle est définie à partir de l'impulsion, la quantité de mouvement.

Dans la théorie de Newton, l'impulsion n'est autre que le produit suivant :

${\vec {p}}=m\cdot {\vec {v}}$

Dans la relativité restreinte, elle est égale à :

${\vec {p}}=m\cdot \gamma \cdot {\vec {v}}$

Ces deux définitions sont intéressantes, car la masse inertielle semble strictement identique à la masse propre. En effet, la force est par définition la dérivée de l'impulsion par rapport au temps. On a donc, par définition :

${\vec {F}}={\frac {d{\vec {p}}}{dt}}$

En supposant la masse inertielle et la masse propre constantes, les deux masses s'égalisent. Mais un point de la définition de la masse inertielle est qu'elle peut se définir à partir de la loi de la conservation de l'impulsion. Mais il existe quelques circonstances où les deux masses ne s'égalisent pas et où l'on a :

${\frac {d{\vec {p}}}{dt}}\neq m\cdot {\frac {d{\vec {v}}}{dt}}$

La masse grave

La masse grave se décline en deux types : la masse grave passive et la masse grave active.

La masse grave passive est la masse sur laquelle la gravité agit. Rappelons que dans la théorie de Newton, la gravité agit sur les objets qui ont une masse et seulement ceux-ci. La gravité est considérée comme étant une force parmi tant d'autres. Si un objet est soumis à une force de gravité ${\vec {F_{g}}}$, il subira une accélération ${\vec {g}}$ dans la direction de la force de gravité. L'accélération en question est appelée l'accélération de la pesanteur. La loi de Newton nous dit qu'il existe une masse m telle que :

${\vec {F_{g}}}=m\cdot {\vec {g}}$

La masse grave active est la source de la gravité. Un objet ayant une masse grave active attire les autres objets vers lui, sous l'effet de sa gravitation. Prenons la loi de gravitation de Newton, qui donne la force qu'un objet de masse M impose à un autre objet de masse m. La masse M est la masse grave active, alors que la masse grave passive est m. La formule est la suivante :

${\vec {F_{g}}}={\frac {G\cdot m\cdot M}{r^{2}}}$, avec G la constante de gravitation de Newton et r la distance entre les deux objets.

L'objet attiré subit une accélération égale à :

${\vec {g}}={\frac {GM}{r^{2}}}$

On voit que la masse grave active est la source de la force de gravité, et de l'accélération que les objets alentours subiront.

De l'équivalence des différentes formes de masse

Dans la théorie de Newton, toutes les formes de masses sont équivalentes. Mais dans la relativité restreinte, c'est autre chose. La raison à cela est que Einstein a montré que la masse et l'énergie sont reliées par des équations assez simples.

Dans ce qui suit, la masse inertielle et la masse propre seront confondues, par simplicité. De plus, nous confondrons aussi les masses grave, passive et active. Masses inertielle et propre seront toutes deux notées $m_{i}$, alors que la masse grave sera notée $m_{g}$

La masse en relativité restreinte

Relation masse-énergie en relativité restreinte.

Pour simplifier, quitte à dire des choses fausses, la masse et l'énergie sont deux choses presque équivalentes. L'équivalence masse-énergie d'Einstein dit que l'énergie d'un corps (ici l'univers) est reliée à sa masse. Si l'objet est en mouvement, on a :

$E^{2}=\left(M\cdot c^{2}\right)^{2}+\left(p\cdot c\right)^{2}$, avec E l'énergie, M la masse et c la vitesse de la lumière et p son impulsion.

On voit que la masse n'est pas tout à fait confondue avec l'énergie. Cependant, quand la vitesse de l'objet est faible, son impulsion est négligeable. L'équation précédente devient alors :

$E\approx M\cdot c^{2}$

Dans le cas d'un objet immobile, l'impulsion est nulle et l'approximation précédente devient une égalité exacte. On a alors :

$E=M\cdot c^{2}$

On voit que l'énergie est proportionnelle à la masse, pour un objet immobile.

Maintenant, divisons l'équation précédente par le volume.

${\frac {E}{V}}={\frac {M}{V}}\cdot c^{2}$

Par définition, le terme de gauche n'est autre que la densité d'énergie, alors que le premier terme de droite est la densité de masse.

$\rho _{e}=\rho \cdot c^{2}$

On vient donc de trouver une relation entre densité de masse et densité de matière, dans le cas d'un système immobile. Ce système peut être un fluide, un solide ou tout autre corps. Mais précisons que cette relation n'est qu'approximative, dans le sens où nous avons négligé l'impulsion. Dans le cas d'un système immobile, ce n'est pas un problème, tant qu'on reste dans le cadre de la relativité restreinte. Mais Dans le cadre de la relativité générale, même un fluide immobile contient de l'impulsion, ce qui change les calculs, comme nous allons le voir dans ce qui suit.

La masse en relativité générale

La définition de la masse grave est presque impossible en relativité générale. Pour comprendre pourquoi, partons de la formule newtonienne suivante, qui relie le potentiel gravitationnel $\phi$ à la densité de masse grave active :

$\nabla ^{2}\cdot \phi =4\pi G\cdot \rho _{mg}$

Le terme de gauche regroupe tout ce qui a trait au potentiel gravitationnel. Le terme de droite regroupe tout ce qui a trait à la masse grave active : il est composé de la masse grave active, multipliée par un coefficient constant. Dans la relativité générale, la formule précédente n'est pas valable, mais il existe une formule équivalente. Elle relie un équivalent du potentiel gravitationnel, à un équivalent de la masse grave. Dans la théorie d'Einstein, il y a plusieurs potentiels gravitationnels, qui sont regroupés dans ce qu'on appelle le tenseur d'Einstein, noté $G_{u\nu }$. L'équivalent de la masse grave active est ce qu'on appelle le tenseur énergie-impulsion $T_{\mu \nu }$. C'est un objet mathématique qui regroupe divers termes liés à l'énergie et l'impulsion de objet gravitant. L'équation de champ d'Einstein s'écrit comme suit :

$G_{\mu \nu }={\frac {8\pi G}{c^{2}}}\cdot T_{\mu \nu }$

En soi, cette équation ne permet pas de définir une masse grave active, du fait de l'absence de force de gravité dans les équations d'Einstein. Mais on peut, avec quelques approximations, calculer une approximation semi-classique de la force de gravité. Ce faisant, les équations nous donnent une relation équivalente à la loi de Newton, mais tirée de la relativité générale. Le tenseur énergie-impulsion regroupe plusieurs termes, dont l'énergie, l'impulsion et la pression (pour un fluide). Chacun de ces termes joue un rôle dans la masse grave active.

En premier lieu, la masse grave active se confond avec l'énergie. L'énergie a un effet gravitationnel, peu importe que cette énergie corresponde à de la masse grave newtonienne, à de l'énergie cinétique, ou à de l'énergie potentielle. Pour simplifier, on a donc :

$\rho _{g}\approx {\frac {\rho _{e}}{c^{2}}}$, avec $\rho _{g}$ la densité de masse grave active.

L'équation précédente n'est cependant qu'une approximation, qu'on retrouve dans beaucoup de contextes, mais qui échoue dans certains cas. En plus de l'énergie proprement dite, il faudrait aussi rajouter la pression comme sources de masse. On a donc :

$\rho _{g}\approx {\frac {\rho _{e}}{c^{2}}}+f\left({\frac {P}{c^{2}}}\right)$, avec $P$ la pression.

En supposant que les relations sont linéaires, on devrait trouver quelque chose du genre :

$\rho _{g}\approx {\frac {\rho _{e}}{c^{2}}}+k\cdot {\frac {P}{c^{2}}}$, avec $\rho _{g}$ la densité de masse grave active.

En relativité générale, on n'est pas certain que masse inertielle, masse grave passive et masse grave active soient identiques. Elles sont censées être identiques localement, pour un objet, en vertu du principe d'équivalence. Mais les calculs ne sont pas vraiment d'accord. Dans certains cas particuliers, les trois masses sont complètement différentes. Par exemple, prenons l'exemple de la lumière, d'un photon pour être précis. La lumière n'a pas de masse inertielle, que ce soit dans la théorie de la relativité ou dans la physique de Newton. Par contre, elle dispose d'une énergie et a donc une masse grave active non-nulle (même si l'effet n'a jamais été mesuré). Elle a aussi une masse grave passive, vu que la lumière est déviée par la gravité ! On a donc un cas où masse grave et masse inertielle sont différentes. Un autre exemple est le cas des fluides, qui sont abondamment utilisés dans la cosmologie relativiste, qu'il nous faut aborder pour comprendre les chapitres qui vont suivre.

La densité de masse grave d'un fluide relativiste : démonstration intuitive

La densité d'énergie d'un fluide n'est pas si difficile à comprendre. En théorie, l'énergie d'un fluide est la somme de plusieurs contributions : l'énergie de masse du fluide, son énergie cinétique et son énergie potentielle. L'énergie potentielle est souvent négligée, et ce sera le cas dans les développements qui vont suivre. Nous allons supposer que l'énergie du fluide est la somme de son énergie de masse et de son énergie cinétique. Cette simplification est peu rigoureuse, mais elle permet de comprendre ce qui va suivre sans recourir à des développements rigoureux. On a donc :

$E=M\cdot c^{2}+E_{\text{cinétique}}$

On divise alors par le volume :

${\frac {E}{V}}={\frac {M}{V}}\cdot c^{2}+{\frac {E_{\text{cinétique}}}{V}}$

Le terme de gauche est la densité d'énergie, par définition, alors que le premier terme à droite est la densité de matière.

$\rho _{e}=\rho \cdot c^{2}+{\frac {E_{\text{cinétique}}}{V}}$

En mécanique classique, on peut prouver que la densité d'énergie cinétique d'un fluide est proportionnelle à la pression (même si les deux ne sont pas exactement la même chose), le coefficient de proportionnalité dépendant du fluide. Par exemple, pour un gaz de photons, la pression est égale au tiers de la densité d'énergie. Pour un gaz parfait matériel, le coefficient de proportionnalité est de $2 \over 3$. Et pour de la matière solide, il est de zéro. En clair, on a :

$\rho _{e}=\rho \cdot c^{2}+k\cdot P$

Pour obtenir la densité de masse grave active, on peut, bien que ce ne soit pas rigoureux, appliquer bêtement la formule $\rho _{g}\approx {\frac {\rho _{e}}{c^{2}}}$. Il suffit donc de diviser l'équation précédente par $c^{2}$ :

$\rho _{g}=\rho +k{\frac {P}{c^{2}}}$

La densité de masse grave d'un fluide relativiste : explications rigoureuses

Le développement précédent n'est cependant pas rigoureux. La dérivation relativiste exacte de cette formule est assez compliquée, le concept même de masse étant ambigu dans la relativité générale. Cependant, dans certains cas, on peut définir une masse particulière, appelée la masse de Komar. Dans le cas d'un fluide idéal, la masse de Komar du fluide est égale à :

$M_{\text{Komar}}\approx {\frac {E+3\cdot PV}{c^{2}}}$, avec E l'énergie du fluide, P sa pression et V son volume.

La densité de masse grave devrait être donc égale à :

$\rho _{g}\approx {\frac {\rho _{e}}{c^{2}}}+3{\frac {P}{c^{2}}}=\rho +3{\frac {P}{c^{2}}}$

Pour aller plus loin, les calculs relativistes donnent aussi des valeurs différentes pour la masse grave active et la masse grave passive. Les calculs en hydrodynamique relativistes donnent :

$\rho _{g}^{\text{active}}\approx \rho +3{\frac {P}{c^{2}}}$, où $\rho$ est la densité de matière inertielle.

$\rho _{g}^{\text{passive}}\approx \rho +{\frac {P}{c^{2}}}$, avec $\rho$ la densité de matière inertielle.

On voit que masse inertielle, masse grave active et masse grave passive sont différentes. On devra donc les utiliser à bon escient dans les chapitres suivants.

Quoi qu'il en soit, cela nous permet de comprendre pourquoi la démonstration de la section précédente n'était pas rigoureuse. Elle est imparfaite du fait de plusieurs erreurs majeures :

• Elle intervertit la place de $\rho$ et $\rho _{e} \over c^{2}$ dans les équations.
• Elle confond $\rho _{g}$ et $\rho _{e} \over c^{2}$, alors que l'équation précédente nous dit que les deux valeurs ne sont pas égales.
• Elle intègre le terme $3{\frac {P}{c^{2}}}$ dans la densité d'énergie volumique, alors que la pression est avant tout un phénomène de surface.

La pression et la masse grave active

Les équations précédentes nous montrent que la pression est une forme particulière de masse grave active. Néanmoins, la gravité liée à la pression nous pose un problème. Imaginons que l'on ait une sphère (une étoile, par exemple), remplie d'un gaz quelconque, autour de laquelle gravite un satellite. La masse grave active de cette sphère est égale à l'intégrale sur son volume de sa densité de masse grave active.

$m_{g}=\int \rho _{mg}dV$

Cette dernière vaut, comme on l'a vu, $\rho _{mg}={\frac {\rho _{e}}{c^{2}}}+3{\frac {P}{c^{2}}}$. On injecte donc dans l'intégrale :

$m_{g}=\int \left({\frac {\rho _{e}}{c^{2}}}+3{\frac {P}{c^{2}}}\right)dV$

Dans le cas d'une matière sans pression, on trouve :

$m_{g}=\int {\frac {\rho _{e}}{c^{2}}}dV$

Mais dans le cas du rayonnement, la masse est nulle et la pression vaut le tiers de la densité d'énergie. En clair, $P={\frac {1}{3}}\rho _{e}$. En calculant l'intégrale, on trouve :

$m_{g}=\int \left({\frac {\rho _{e}}{c^{2}}}+3{\frac {P}{c^{2}}}\right)dV=\int \left({\frac {\rho _{e}}{c^{2}}}+3{\frac {\rho _{e}/3}{c^{2}}}\right)dV=2\cdot \int {\frac {\rho _{e}}{c^{2}}}dV$

On voit que la masse grave active n'est pas la même pour une densité d'énergie identique. La même quantité d'énergie n'a pas la même masse grave active, selon qu'elle est sous la forme de matière ou de rayonnement. Et cela pose un grave paradoxe. Imaginons qu'il se passe quelque chose dans la sphère, et que cette transformation transforme toute la matière en rayonnement. La masse grave active double du fait de cette transformation. Deux conséquences contradictoires sont possibles : soit la conservation de l'énergie est violée lors de la transformation, soit énergie et masse grave ne sont pas synonyme et la relativité générale est fausse. À l'heure actuelle, personne ne sait réellement comment résoudre correctement ce paradoxe, appelé le paradoxe de Tolman. Il y a bien quelques pistes, mais rien de bien folichon. Peut-être que le tenseur énergie-impulsion est incorrectement défini, peut-être que les équations mentionnées dans le chapitre sont fausses, peut-être que la théorie des fluides relativistes est à revoir, ou peut-être que tout simplement que les démonstrations actuelles oublient de prendre en compte des détails techniques subtils.

Les équations de Friedmann relativistes

Dans un chapitre précédent, nous avons vu les équations de Friedmann, mais avions fourni des versions newtoniennes de ces équations.

Première équation de Friedmann	$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {K}{a^{2}}}$
Seconde équation de Friedmann	${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\rho$
Équation du fluide cosmologique de Friedmann	${\frac {d\rho }{dt}}+3H\rho =0$

Dans ce qui va suivre, nous allons voir les versions relativistes de ces équations. Nous allons voir comment passer des versions newtoniennes aux équations relativistes, en appliquant les concepts vus dans le chapitre précédent.

Dans ce qui suit, les notations sont les suivantes : $\rho _{e}$ est la densité d'énergie, $\rho$ est la densité de matière, $P$ est la pression et $K$ est un terme de courbure, qui décrit la géométrie de l'univers (nous reviendrons sur l'interprétation de ce terme dans ce qui suit).

Les trois équations de Friedmann relativistes sont les suivantes :

Première équation de Friedmann	$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {k\cdot c^{2}}{a^{2}}}$
Équation du fluide cosmologique de Friedmann	${\frac {d\rho }{dt}}+3H\left(\rho +{\frac {P}{c^{2}}}\right)=0$
Seconde équation de Friedmann	${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)$

Les équations de Friedmann relativistes ressemblent à leurs cousines newtoniennes, si ce n'est que la densité masse est remplacée par les équations du chapitre précédent. Mais il y a un problème : quelle est la masse utilisée dans les équations de Friedmann ? En toute généralité, les densités de masse inertielle, masse grave active et masse grave passive ne sont pas égales. Pire : leur valeur dépend de la situation considérée, ce qui fait qu'il faut faire le remplacement intelligemment. Il existe un cas où l'on sait calculer exactement ces trois densités de masse : le cas d'un fluide parfait. Aussi, on va supposer que l'univers observable est rempli d'un fluide qui regroupe la matière, le rayonnement, les galaxies, et de manière générale tout le contenant de l'univers. On postule que ce fluide est homogène, c'est à dire que sa température est la même partout, de même que la densité, la pression, et toutes les variables du même genre. On peut alors utiliser les équations vues au chapitre précédent pour faire le remplacement.

La première équation de Friedmann

La première équation de Friedmann, en version non-relativiste, est la suivante :

$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {K}{a(t)^{2}}}$

La relation entre densité de masse et densité d'énergie se déduit de l'équivalence masse-énergie d'Einstein, même si cette démonstration est loin d'être rigoureuse. Pour convertir l'équation de Friedmann dans sa version relativiste, il suffit de remplacer la masse volumique $\rho$ par $\rho _{e} \over c^{2}$. Pour le terme $K$, il faut faire l'inverse, à savoir la multiplier par $c^{2}$, pour des raisons techniques assez compliquées.

$H^{2}={\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a(t)^{2}}}$

L'interprétation de cette formule est assez simple à comprendre. Elle nous dit que l'expansion de l'univers dépend de deux forces opposées. Le premier terme correspond à l'influence gravitationnelle de la matière, alors que l'autre traduit l'effet de la courbure de l'univers.

Avant de passer à la suite, je tiens à faire remarquer une chose assez subtile, mais très importante. Dans le chapitre sur les équations de Friedmann newtoniennes, nous avions démontré la première équation de Friedmann, à partir d'un raisonnement newtonien simple. Dans cette démonstration, la masse utilisée pour calculer la densité de masse était la masse grave active, et non la masse inertielle. Le raisonnement tenu juste auparavant est donc faux. Il aurait fallu utiliser la relation $\rho _{g}^{\text{active}}\approx \rho +3{\frac {P}{c^{2}}}$. Mais la démonstration dans le cadre de la relativité générale donne bien l'équation obtenue plus haut, en remplaçant la densité de masse par la densité de masse inertielle. Cela est sans doute lié au fait que les trois types de masse sont égaux dans la théorie newtonienne.

Le paramètre de courbure

La géométrie de l'univers peut prendre trois formes, selon que le paramètre de densité est nul, positif ou négatif.

Dans la démonstration newtonienne, nous avions posé $K=-{\frac {2E}{m}}{\frac {1}{R_{0}^{2}}}$ pour simplifier les calculs. Mais ce paramètre a une interprétation totalement différente dans la relativité générale. Dans la relativité générale, ce terme s'appelle le paramètre de courbure. Il décrit la courbure, un paramètre qui décrit la géométrie de l'espace-temps :

• un espace de courbure nulle a une géométrie euclidienne ;
• un espace de courbure positive a une géométrie qui équivaut en trois dimensions à la surface d'une sphère en deux dimensions ;
• un espace de courbure négative a une géométrie qui équivaut en trois dimensions à la surface d'une « selle de cheval » en deux dimensions (cette selle de cheval étant à une hyperbole ce que la sphère est au cercle).

Pour simplifier, la courbure décrit comment varie le facteur d'échelle dans l'espace et dans le temps. Avec un espace-temps courbe, le facteur d'échelle varie en fonction de la position et du temps. Pour simplifier les explications, imaginons que l'espace seul soit courbé. Un espace de courbure nulle a un facteur d'échelle identique partout et a donc une géométrie euclidienne. Avec un espace courbé, le facteur d'échelle varie en fonction de la position et les calculs de distance euclidiens ne marchent plus. La courbure décrit avec quelle intensité le facteur d'échelle varie en fonction de la direction, à quel point les calculs de distance varient des calculs euclidiens. Cependant, dans la relativité générale, c'est l'espace-temps qui est courbé, et pas seulement l'espace. Ce qui fait que le facteur d'échelle varie en fonction de la position, mais aussi du temps considéré. On verra dans quelques chapitres qu'une courbure positive fait décroître linéairement le facteur d'échelle avec le temps, alors qu'une courbure négative entraîne une croissance linéaire du facteur d'échelle. Mais passons.

Précisons que le paramètre de courbure décrit la courbure qu'aurait l'univers s'il était vide. Il s'agit d'un paramètre global, qui décrit l’univers tout entier. Mais il peut y avoir des variations locales, liées à la gravité. La gravité n'est autre qu'une variation de la courbure à proximité d'une masse. Toute masse grave active déforme l’espace-temps et le courbe, ce qui fait que le facteur d'échelle varie à proximité d'une masse. Le facteur d'échelle à proximité d'une masse décroît continuellement, ce qui fait que les distances se réduisent. Ainsi, un objet placé à proximité d'une masse se rapprochera progressivement de la masse considérée, non pas parce qu'elle bouge dans l'espace, mais parce que l'espace ne cesse de se contracter à proximité d'une masse grave active. On pourrait décrire la gravité comme l'expansion, avec une variation du facteur d'échelle avec le temps et la distance, ce que fait la relativité générale d’Einstein, mais cela demande une artillerie mathématique des plus élaborées. Pour résumer, on a :

Masse (grave active) $\rightarrow$ Courbure locale $\rightarrow$ Variation spatiale et temporelle du facteur d'échelle.

Le rayon de courbure

En relativité générale, la formule pour le paramètre de courbure est différente. Déjà, les formules ne sont pas identiques et on a l'équation suivante :

$K=k\cdot c^{2}$, avec K la pseudo-courbure newtonienne et k la courbure telle que décrite dans la théorie de la relativité générale.

À comparer avec la formule newtonienne :

$K=-{\frac {2E}{m}}{\frac {1}{R_{0}^{2}}}$

En combinant les deux équations précédentes, on trouve :

$k=-{\frac {2E}{mc^{2}}}{\frac {1}{R_{0}^{2}}}$, avec $R_{0}$ le rayon de l'univers observable dans la démonstration newtonienne.

En utilisant la formule $E=Mc^{2}$, on trouve alors :

$k=-{\frac {2}{R_{0}^{2}}}$

Ce qui se simplifie en :

${\frac {1}{R}}\propto {\sqrt {k}}$, avec R un rayon dont l'interprétation est donnée plus bas.

On voit que la courbure est proportionnelle à l'inverse d'un rayon. Dans la démonstration newtonienne, le rayon en question est celui de l'univers. Mais en relativité générale, ce rayon n'est pas le rayon de l'univers, mais un rayon dit "rayon de courbure".

Cercle osculateur.

Rayon de courbure.

Pour comprendre ce qu'est ce rayon, prenons une courbe en une dimension, dessinée sur un plan. En ce point, on peut décrire la courbure de cette courbe en faisant une analogie avec la courbure d'un cercle. Un cercle est en effet une ligne dont la courbure est constante. Qui plus est, plus un cercle est grand, plus sa courbure est faible (plus on courbe une ligne uniformément, plus elle forme un cercle petit). Pour la courbe prise en exemple, et sur le point choisi, on peut définir un cercle tangent en ce point, appelé le cercle osculateur. Le rayon de ce cercle. La courbure en ce point est alors définie comme la courbure du cercle tangent, qui est elle-même inversement proportionnelle au rayon du cercle osculateur. Cela permet de définir la courbure comme l'inverse du rayon du cercle osculateur.

Courbure locale de la courbe $=$ Courbure du cercle osculateur $\propto$ ( 1 / Rayon du cercle osculateur )

En deux, trois, quatre dimensions, on peut définir la même chose, ce qui permet de décrire un cercle osculateur et le lier avec la courbure locale/globale. Sauf que le coefficient de proportionnalité n'est pas le même, sans compter que les puissances changent. Pour résumer, la courbure de l'univers est proportionnelle à l'inverse de son rayon de courbure (plus précisément de son carré).

L'interprétation de la densité dans la version relativiste

Formellement, la densité d'énergie prend en compte aussi bien la densité de matière $\rho _{m}(t)$ que la densité d'énergie liée au rayonnement (lumière) $\rho _{r}(t)$, et potentiellement d'autres formes d'énergie. Pour simplifier, la densité d'énergie est la somme de la densité de matière, la densité de rayonnement, et quelques autres termes.

$H^{2}={\frac {8\pi G}{3c^{2}}}\left[\rho _{m}(t)+\rho _{r}(t)\right]-{\frac {K}{a(t)^{2}}}$

Il est possible aussi de rendre compte de la courbure $K$ via une densité d'énergie de courbure. En effet, nous avons vu que celle-ci est proportionnelle à une énergie dans la démonstration newtonienne. En appliquant l'équivalence masse-énergie, nous nous retrouvons donc avec une densité d'énergie de courbure $\rho _{k}$ dans l'équation de Friedmann. En injectant le tout dans l'équation de Friedmann, nous trouvons :

$H^{2}={\frac {8\pi G}{3c^{2}}}\left[\rho _{m}(t)+\rho _{r}(t)-\rho _{k}(t)\right]$, avec $\rho _{k}(t)={\frac {K}{a(t)^{2}}}$

Si on pose $K=\rho _{k0}$, on peut reformuler cette équation comme ceci :

$H^{2}={\frac {8\pi G}{3c^{2}}}\left[\rho _{m}(t)+\rho _{r}(t)-{\frac {\rho _{k0}}{a(t)^{2}}}\right]$

On verra dans les chapitres suivants que les densités de rayonnement et de matière dépendent du facteur d'échelle.

• La densité de matière varie selon l'équation : $\rho _{m}(t)={\frac {\rho _{m0}}{a(t)^{3}}}$.
• Pour la densité d'énergie du rayonnement, l'équation a été vue dans le chapitre sur le rayonnement : $\rho _{k}(t)={\frac {\rho _{k0}}{a(t)^{4}}}$.

La première équation de Friedmann se reformule ainsi, quand on injecte les relations précédentes dans l'équation :

$H^{2}={\frac {8\pi G}{3c^{2}}}\left(-{\frac {\rho _{k0}}{a(t)^{2}}}+{\frac {\rho _{m0}}{a(t)^{3}}}+{\frac {\rho _{r0}}{a(t)^{4}}}\right)$

Il est aussi possible de reformuler la première équation de Friedmann avec le paramètre de densité, à savoir le rapport entre la densité réelle et la densité critique obtenue quand on considére un univers de courbure nulle. Cependant, cela demande de fournir plusieurs paramètres de densité. En effet, il ne faut pas oublier l'influence différentielle du facteur d'échelle sur la matière, l'énergie de rayonnement et la courbure. Pour cela, il faut utiliser différents paramètres de densité : un pour la matière, un autre pour le rayonnement, et un autre pour la courbure. Le premier est égal à la densité de matière divisée par la densité critique et est noté $\Omega _{m}$. Le second est égal à la densité de rayonnement divisée par la densité critique et est noté $\Omega _{r}$. Même principe pour le rapport entre densité de courbure et densité critique $\Omega _{k}$.

$H(a)^{2}=H_{0}^{2}\left(\Omega _{k}\cdot a^{-2}+\Omega _{m}\cdot a^{-3}+\Omega _{r}\cdot a^{-4}\right)$

L'équation du fluide de Friedmann

L'équation du fluide de Friedmann est, dans sa version relativiste, reformulée de la même manière que la première équation. On remplace la densité de masse par sa valeur compatible avec la relativité, obtenue dans le chapitre précédent.

L'équation du fluide de Friedmann newtonienne est la suivante :

${\frac {d\rho }{dt}}+3H\rho =0$

Dans la démonstration de l'équation de Friedmann d'il y a deux chapitres, on peut remarquer que la masse utilisée est indéterminée. Mais on retrouve l'équation relativiste si on suppose qu'il s'agit de la masse grave passive. Or, on a vu dans le chapitre précédent que celle-ci est égale, pour un fluide relativiste, à :

$\rho _{g}^{\text{passive}}=\rho +{\frac {P}{c^{2}}}$, où $\rho$ est la densité de matière inertielle.

En faisant le remplacement, on a :

${\frac {d\rho }{dt}}+3H\left(\rho +{\frac {P}{c^{2}}}\right)=0$

Démonstration

Dans cette section, nous allons donner une dérivation de la version relativiste, qui n'est cependant pas très rigoureuse. En faire une véritable dérivation demanderait de passer par les mathématiques de la relativité générale, ce que nous ne ferons pas dans ce cours. Nous allons considérer que l'univers est un système isolé, à savoir qu'il n'y a pas d'échange de matière ou d'énergie avec l'extérieur (il est en effet difficile de donner un sens à l'« extérieur de l'univers »). Dans ces conditions, la première loi de la thermodynamique s'applique. Celle-ci dit que toute variation de l'énergie interne de l'univers provient des variations de chaleur et de volume/pression. De plus, on va supposer que l'expansion est adiabatique : il n'y a pas d'échange de chaleur entre l'univers observable et un éventuel extérieur. Dans ces conditions, toute variation de l'énergie interne de l'univers se calcule avec la formule suivante, avec P la pression et V le volume de l'univers. $dE+PdV=0$ Utilisons ensuite la relation $E=Mc^{2}$ : $d(Mc^{2})+PdV=0$ Le facteur $c^{2}$ étant constant, nous pouvons le sortir de la dérivée. $c^{2}\cdot d(M)+PdV=0$ Divisons par $c^{2}$ : $d(M)+{\frac {P}{c^{2}}}dV=0$ Reformulons la masse de l'univers en fonction du volume et de la densité de matière $d(V\times \rho )+{\frac {P}{c^{2}}}dV=0$ Appliquons la formule sur la dérivée d'un produit. $dV\times \rho +V\times d\rho +{\frac {P}{c^{2}}}dV=0$ Factorisons maintenant le terme $dV$. $V\times d\rho +\left(\rho +{\frac {P}{c^{2}}}\right)dV=0$ Divisons maintenant par V. $d\rho +\left(\rho +{\frac {P}{c^{2}}}\right){\frac {dV}{V}}=0$ Puis divisons par dt. ${\frac {d\rho }{dt}}+\left(\rho +{\frac {P}{c^{2}}}\right){\frac {V'}{V}}=0$ Appliquons maintenant l'égalité suivante, vue dans le premier chapitre : ${\frac {V'}{V}}=3H$. ${\frac {d\rho }{dt}}+3H\left(\rho +{\frac {P}{c^{2}}}\right)=0$

On peut la récrire de la manière suivante, sous certaines hypothèses :

${\frac {d\rho _{e}}{dt}}+3H(\rho _{e}+P)=0$, où $\rho _{e}$ est la densité d'énergie.

Démonstration

Démonstration de la deuxième version. Partons de la première équation de Friedmann : $H^{2}={\frac {a'}{a}}={\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {kc^{2}}{a^{2}}}$ Et la deuxième : ${\frac {a''}{a}}=-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$ Prenant la dérivée temporelle de la première des deux équations : ${\frac {d}{dt}}H^{2}={\frac {d}{dt}}\left(\left({\frac {a'}{a}}\right)^{2}\right)={\frac {2a''a'}{a^{2}}}-{\frac {2a'^{2}a'}{a^{3}}}={\frac {8\pi G}{3c^{3}}}\rho _{e}'+{\frac {2kc^{2}a'}{a^{3}}}$ Que l'on peut mettre sous la forme : ${\frac {a''}{a}}{\frac {a'}{a}}-{\frac {a'^{3}}{a^{3}}}={\frac {4\pi G}{3c^{2}}}\rho _{e}'+kc^{2}{\frac {a'}{a^{3}}}$ Et donc : ${\frac {a''}{a}}={\frac {4\pi G}{3c^{2}}}{\frac {a}{a'}}\rho _{e}'+kc^{2}{\frac {a'}{a^{3}}}{\frac {a}{a'}}+{\frac {a'^{3}}{a^{3}}}{\frac {a}{a'}}$ En identifiant avec la seconde équation de Friedmann : $-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)+{\frac {\Lambda c^{2}}{3}}={\frac {4\pi G}{3c^{2}}}{\frac {a}{a'}}\rho _{e}'+{\frac {kc^{2}}{a^{2}}}+{\frac {a'^{2}}{a^{2}}}$ On bouge un peu les termes et on identifie le dernier terme avec la première équation de Friedmann : ${\frac {4\pi G}{3c^{2}}}{\frac {a}{a'}}\rho _{e}'=-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)+{\frac {\Lambda c^{2}}{3}}-{\frac {kc^{2}}{a^{2}}}-\left({\frac {8\pi G\rho _{e}}{3c^{2}}}-{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}\right)$ Il reste à simplifier comme : ${\frac {a}{a'}}\rho _{e}'=-(\rho _{e}+3P)-2\rho _{e}$ On trouve donc enfin : $\rho _{e}'=-3{\frac {a'}{a}}(\rho _{e}+P)=-3H(\rho _{e}+P)$

La seconde équation de Friedmann

La seconde équation de Friedmann est la suivante, dans sa forme newtonienne.

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\rho$

Dans la démonstration newtonienne, la masse utilisée était la masse grave active, ce qui fait qu'on doit utiliser l'équation suivante :

$\rho _{g}^{\text{active}}=\rho +3{\frac {P}{c^{2}}}$, avec $\rho$ la densité de masse inertielle et P la pression.

En combinant les deux équations précédentes, on retrouve la seconde équation de Friedmann :

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)$

Cette seconde équation de Friedmann nous dit quelque chose d'assez contre-intuitif concernant la pression : celle-ci lutte contre l'expansion. L'intuition nous dirait pourtant le contraire, mais celle-ci est trompeuse. La pression de la matière ou du rayonnement ne pousse pas sur les bords de l'univers, et ne peut donc guider l'expansion. Rappelons que l'horizon cosmologique n'est pas une barrière matérielle sur laquelle la pression pourrait pousser, mais une simple limite liée à la vitesse de la lumière. L'effet de la pression sur l'expansion ne peut donc provenir de ce mécanisme intuitif.

Pour comprendre l'effet contre-expansionniste de la pression, il faut se rappeler que la pression est proportionnelle à la densité d'énergie. Par exemple, on peut facilement démontrer que la pression d'un gaz parfait est égale aux deux tiers de sa densité d'énergie interne. Même chose pour le rayonnement, quoique le coefficient de proportionnalité soit différent. Or, rappelez-vous que l'énergie et la masse sont reliées dans la théorie de la relativité, l'équation $E=Mc^{2}$ en étant la plus simple expression. Pour simplifier, l'énergie a un poids, un effet gravitationnel qui va lutter contre l'expansion. Plus la pression et donc la densité d'énergie sont grandes, plus cet effet gravitationnel sera fort, plus l'expansion sera contrecarrée.

On peut démontrer la seconde équation de Friedmann (relativiste) à partir de la première équation et de l'équation du fluide.

Démonstration

Partons de la première équation de Friedmann, écrite comme ceci : ${\frac {(a')^{2}}{a^{2}}}={\frac {8\pi G}{3}}\rho -{\frac {K}{a^{2}}}$ Multiplions des deux côtés par $a^{2}$ : $(a')^{2}={\frac {8\pi G}{3}}(\rho a^{2})-K$ Dérivons maintenant par rapport au temps : $2\cdot a'\cdot a''={\frac {8\pi G}{3}}(\rho \cdot a^{2})'$ Divisons par 2 les deux membres de l'équation : $a'\cdot a''={\frac {4\pi G}{3}}(\rho \cdot a^{2})'$ Calculons la dérivée dans le second terme : $a'\cdot a''={\frac {4\pi G}{3}}\left[\rho \cdot (a^{2})'+(\rho '\cdot a^{2})\right]$ Divisons par $a^{2}$ : ${\frac {a'\cdot a''}{a^{2}}}={\frac {4\pi G}{3}}\left[\rho {\frac {(a^{2})'}{a^{2}}}+\rho '\right]$ On utilise alors la relation $(a^{2})'=2a\cdot a'$ pour simplifier le second terme : ${\frac {a'\cdot a''}{a^{2}}}={\frac {4\pi G}{3}}\left[\rho {\frac {2a'\cdot a}{a^{2}}}+\rho '\right]$ Simplifions par $a$ : ${\frac {a'\cdot a''}{a^{2}}}={\frac {4\pi G}{3}}\left[2\rho {\frac {a'}{a}}+\rho '\right]$ Divisons par $a'/a$ : ${\frac {a''}{a}}={\frac {4\pi G}{3}}\left(2\rho +\rho '{\frac {a}{a'}}\right)$ Or, l'équation du fluide nous dit que $\rho '=-3{\frac {a'}{a}}\left({\frac {P}{c^{2}}}+\rho \right)$. Nous pouvons donc faire la substitution dans l'équation précédente, ce qui donne : ${\frac {a''}{a}}={\frac {4\pi G}{3}}\left[2\rho -3{\frac {a'}{a}}\left({\frac {P}{c^{2}}}+\rho \right){\frac {a}{a'}}\right]$ En simplifiant, nous obtenons : ${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)$

Les équations de Friedmann pour un univers plat

Par souci de lisibilité, nous noterons la dérivée première d'une variable $x$ comme ceci : $x'$. Même chose pour la dérivée seconde, notée $x''$. De plus, toutes les dérivées sont par rapport au temps. En clair, $x'={\frac {dx}{dt}}$ et $x''={\frac {d^{2}x}{dt^{2}}}$.

Dans le chapitre précédent, nous avons vu les équations de Friedmann relativiste, mais nous ne les avons pas résolues. Et leur résolution dans le cas général est assez complexe. La raison est que les équations ont entre deux et trois termes. Et une solution pour résoudre ce problème serait de diminuer le nombre de termes, quitte à n'étudier que des cas particuliers.

La première simplification est de négliger le terme de courbure. En clair, nous allons étudier le cas d'un univers plat (c.a.d sans courbure. On étudie donc un cas particulier, mais ce n'est pas un problème, car les mesures observationnelles suggèrent très fortement que la courbure est nulle ! Faire cette hypothèse est donc très réaliste. Notons qu'en supprimant le terme de courbure, on simplifie seulement la première équation de Friedmann, qui donne la vitesse de l'expansion, mais la seconde équation qui donne l'accélération de l'expansion. Avec un tel univers, la première équation de Friedmann se simplifie et devient :

$H^{2}={\frac {8\pi G}{3}}\rho$

Les équations obtenues demandent de manipuler la pression et la densité de la matière, ce qui en fait des équations différentielles à deux inconnues, bien plus complexes que celles à une seule inconnue. Mais il est possible de ruser, en postulant une relation entre la densité d'énergie et la pression, à savoir une équation d'état. La plupart des gaz disposent d'une telle équation d'état simple, qui permet d'éliminer le terme de pression dans la plupart des équations. Généralement, on postule que la pression est proportionnelle à la densité d'énergie. La relation entre pression et densité est donc de la forme :

$P=w\times (\rho \cdot c^{2})$

Le cas général, avec w indéterminé

Pour commencer, nous allons étudier le cas général, dans lequel la valeur de $w$ n'est pas précisée. Nous allons étudier comment les équations de Friedmann se reformulent quand on injecte l'équation $P=w\times (\rho \cdot c^{2})$ à l'intérieur. Les trois équations obtenues sont donc :

$H^{2}={\frac {8\pi G}{3}}\rho$

${\frac {a''}{a}}=-4\pi G\rho \left(w+{\frac {1}{3}}\right)$

$\rho '+3H(1+w)\rho =0$

Remarquons que la première équation de Friedmann ne change pas, vu qu'elle n'a pas de terme de pression.

Pour obtenir cette version de la seconde équation de Friedmann, partons de la seconde équation de Friedmann originelle :

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)=-4\pi G\left({\frac {\rho }{3}}+{\frac {P}{c^{2}}}\right)$

Injectons la formule $P=w\times \rho c^{2}$ :

${\frac {a''}{a}}=-4\pi G\left({\frac {\rho }{3}}+{\frac {w\times \rho c^{2}}{c^{2}}}\right)$

On simplifie par $c^{2}$ et on factorise $\rho$ :

${\frac {a''}{a}}=-4\pi G\rho \left(w+{\frac {1}{3}}\right)$

La détermination de l'équation de la densité en fonction du facteur d'échelle

Pour la troisième équation de Friedmann, on part de l'équation relativiste :

${\frac {d\rho }{dt}}+3H\left(\rho +{\frac {P}{c^{2}}}\right)=0$

On fait le remplacement :

${\frac {d\rho }{dt}}+3H\left(\rho +{\frac {w\times \rho c^{2}}{c^{2}}}\right)=0$

On simplifie par $c^{2}$, et on factorise $\rho$ :

$\rho '+3H(1+w)\rho =0$

On divise par $\rho$ et on réorganise les termes :

${\frac {\rho '}{\rho }}=-3H(1+w)$

On utilise alors la relation $H={\frac {a'(t)}{a(t)}}$, qui relie facteur de Hubble et facteur d'échelle :

${\frac {\rho '}{\rho }}=-3(1+w){\frac {a'(t)}{a(t)}}$

On utilise alors la formule $\int {\frac {x(t)'}{x(t)}}dt=\ln {x(t)}+Cst$ :

$\ln {\rho (t)}+K_{1}=-3(1+w)\times \ln {a(t)}+K_{2}$, avec $K_{1}$ et $K_{2}$ deux constantes d'intégration.

On réorganise les termes, ce qui donne :

$\ln {\rho (t)}=-3(1+w)\times \ln {a(t)}+K$, avec $K=K_{2}-K_{1}$.

On prend l'exponentielle :

$\rho (t)=e^{-3(1+w)\times \ln {a(t)}}\times e^{K}$

On utilise alors la formule $x^{y}=exp^{y\ln {x}}$ :

$\rho (t)=a(t)^{-3(1+w)}\times e^{K}$

Pour conserver la cohérence des unités, $e^{K}$ correspond à une densité. Et plus précisément, l'équation n'a de sens que s'il s'agit de la densité quand $a(t)^{3}=1$. Il s'agit d'une densité de base que l'on notera $\rho _{0}$. On a donc :

$\rho (t)=\rho _{0}\times a(t)^{-3(1+w)}$

De plus, cette équation est valable quelle que soit la courbure, ce qui est important à remarquer.

La détermination de l'équation du facteur d'échelle

Maintenant, essayons de trouver une équation pour le facteur d'échelle en fonction du temps. Pour cela, partons de l'équation précédente, reformulée comme suit :

$\rho (t)\propto a(t)^{-3(1+w)}$

Maintenant, prenons la première équation de Friedmann écrite comme suit :

$H(t)^{2}\propto \rho (t)$

En combinant les deux, on a :

$H(t)^{2}\propto a(t)^{-3(1+w)}$

On prend alors la racine carrée, ce qui est équivalent à élever à la puissance 1/2. Cela donne l'équation suivante :

$H(t)\propto a(t)^{-{\frac {3(1+w)}{2}}}$

On utilise alors la formule $H={\frac {a(t)'}{a(t)}}$ :

${\frac {a(t)'}{a(t)}}\propto a(t)^{-{\frac {3(1+w)}{2}}}$

On multiplie par a(t), ce qui revient à ajouter 1 à l'exposant pour le terme de droite :

$a(t)'\propto a(t)^{-{\frac {3(1+w)}{2}}+1}$

On simplifie l'exposant :

$a(t)'\propto a(t)^{-{\frac {3w+1}{2}}}$

Résoudre cette équation différentielle dans le cas général est quelque peu complexe. Toujours est-il que le résultat est le suivant :

$a(t)=a_{0}\cdot t^{\frac {2}{3(1+w)}}$

Les équations générales du modèle

L'équation précédente nous dit que le facteur d'échelle suit une loi de puissance, ce qui fait qu'on peut utiliser les formules du chapitre "Une introduction aux modèles cosmologiques". On trouve donc les résultats suivants :

$H={\frac {2}{3(1+w)}}\cdot {\frac {1}{t}}$

$t={\frac {2}{3(1+w)}}\cdot T_{H}$

$R_{H}={\frac {3(1+w)}{2}}\cdot c\cdot t$

$r(t)={\frac {c\cdot t}{1-{\frac {2}{3(1+w)}}}}=c\cdot t\cdot {\frac {3(1+w)}{3(1+w)-2}}$

$q={\frac {3(1+w)}{2}}-1={\frac {3}{2}}w+{\frac {1}{2}}$

La relation entre densité et âge de l'univers

On peut aussi déterminer une relation entre l'âge de l'univers et la densité. Pour cela, partons de l'équation suivante :

$H={\frac {2}{3(1+w)}}\cdot {\frac {1}{t}}$

En élevant l'équation au carré, on a :

$H^{2}={\frac {4}{9}}{\frac {1}{(1+w)^{2}}}\cdot {\frac {1}{t^{2}}}$

On peut alors combiner cette équation avec l'équation suivante :

$H^{2}={\frac {8\pi G}{3}}\rho$

En égalisant les deux équations, on trouve :

${\frac {8\pi G}{3}}\rho ={\frac {4}{9}}{\frac {1}{(1+w)^{2}}}\cdot {\frac {1}{t^{2}}}$

En divisant par ${\frac {8\pi G}{3}}$, on trouve :

$\rho ={\frac {1}{6\pi G(1+w)^{2}}}\cdot {\frac {1}{t^{2}}}$

Pour simplifier, on a :

$\rho \propto {\frac {1}{t^{2}}}$

On voit que la densité diminue avec le carré du temps, mais que la constante de proportionnalité dépend du paramètre de l'équation d'état.

Le facteur de décélération et les équations de Friedmann

Maintenant, étudions le comportement de l'accélération de l'univers, à partir du facteur de décélération. Nous avons vu plus haut quelle était la valeur du facteur de décélération dans le cas général, mais sachez qu'il est possible de démontrer la valeur du facteur de décélération autrement.

Démonstration

Pour rappel, la définition du facteur de décélération est la suivante : ${\frac {a(t)''}{a(t)}}=-q\cdot H(t)^{2}$ Le terme de gauche se calcule à partir de la seconde équation de Friedmann, alors que $H(t)^{2}$ se calcule à partir de la première. Dans le cas qui nous intéresse, on a alors : $H(t)^{2}={\frac {8\pi G}{3}}\rho$, vu que la courbure est considérée comme nulle. ${\frac {a''}{a}}=-4\pi G\rho \left(w+{\frac {1}{3}}\right)$, du fait de l'hypothèse $P=w\times \rho c^{2}$. On a alors : $-4\pi G\rho \left(w+{\frac {1}{3}}\right)=q\cdot {\frac {8\pi G}{3}}\rho$ On simplifie par $4\pi G\rho$ : $w+{\frac {1}{3}}={\frac {2}{3}}\cdot q$ D'où on dérive : $q={\frac {3}{2}}w+{\frac {1}{2}}$

Pour rappel, ce dernier nous dit sous quelles condition l'expansion ralentit, accélère ou reste stable. Pour cela, calculons la valeur de $w$ pour laquelle $q=0$. On a donc :

$0={\frac {3}{2}}w+{\frac {1}{2}}$

On trouve alors que :

$w=-{\frac {1}{3}}$

En étudiant un petit peu la relation $q=f(w)$, on en déduit le tableau suivant.

$w<-{\frac {1}{3}}$	$w=-{\frac {1}{3}}$	$w>-{\frac {1}{3}}$
L'expansion accélère	L'expansion est constante (modèle à croissance linéaire)	L'expansion ralentit

Faisons maintenant le rapprochement avec les valeurs de $w$ obtenues pour le rayonnement et la matière. Pour la matière et le rayonnement, on a $w>-{\frac {1}{3}}$, ce qui fait qu'un univers composé intégralement de matière et de rayonnement doit voir son expansion décélérer. Pour un univers qui contient un mélange d'énergie noire et de matière/rayonnement, tout dépend des parts respectives de chaque composant.

Le modèle cosmologique dominé par la matière

Pour la matière, on part du principe que celle-ci est un gaz parfait qui emplit l'espace. La pression d'un tel gaz est alors définie par la formule $P={\frac {1}{3}}\rho v^{2}$, avec $\rho$ la densité du gaz et v la vitesse moyenne de ses particules. Cependant, par souci de simplification, il est supposé que la vitesse des particules du gaz est très faible, au point qu'on peut la supposer nulle (ce qui marche bien pour de la matière qui va à faible vitesse). Dans ces conditions, la pression s'annule, peu importe la densité. On a alors : $w=0$.

Cette hypothèse est crédible dans le sens où les amas de galaxies sont relativement éloignés et interagissent peu. Comme autre simplification, nous allons prendre le cas d'une matière froide, au zéro absolu. Cette autre hypothèse n'est pas si abusive vu l'état actuel de l'univers : seul 10% de la matière sert à fabriquer des étoiles, le reste étant localisé dans des nébuleuses et des nuages moléculaires dont la température ne dépasse pas la dizaine de degrés au-dessus du zéro absolu.

Les équations du modèle

Avec cette hypothèse, les équation de Friedmann deviennent les suivantes :

$H^{2}={\frac {8\pi G}{3}}\rho$

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\rho$

${\frac {d\rho }{dt}}+3H\rho =0$

On remarque qu'on retrouve les équations de Friedmann newtoniennes dans le cas où la courbure est nulle. Et nous avions vu que ce modèle permettait de démontrer les formules suivantes :

Paramètre	Formule dans le cas de l'univers dominé par la matière
Densité en fonction du facteur d'échelle	$\rho (t)=\rho (t_{0})\cdot a(t)^{-3}$
Facteur d'échelle en fonction du temps	$a(t)=a_{0}\cdot t^{\frac {2}{3}}$
Facteur de Hubble	$H={\frac {2}{3}}{\frac {1}{t}}$
Temps de Hubble	$T_{H}={\frac {3}{2}}t$
Rayon de Hubble	$R_{H}={\frac {3}{2}}\cdot c\cdot t$
Rayon de l'univers observable	$r(t)=3\cdot c\cdot t=2\cdot R_{H}$
Age de l'univers	$t={\frac {2}{3}}\cdot T_{H}$
Paramètre de décélération	$q={\frac {1}{2}}$
Densité	$\rho ={\frac {1}{6\pi G}}\cdot {\frac {1}{t^{2}}}$

Le modèle cosmologique dominé par le rayonnement

Dans le cas où on considère un univers entièrement rempli de rayonnement, on postule que le rayonnement est formé d'un gaz parfait de photons. Dans ces conditions, le comportement des photons fait que :

$w={\frac {1}{3}}$

Les équations du modèle

Avec cette valeur, les équations du cas général se simplifient comme suit :

Paramètre	Formule du cas général	Formule dans le cas de l'univers dominé par le rayonnement
Densité en fonction du facteur d'échelle	$\rho (t)=\rho (t_{0})\cdot a(t)^{-3(1+w)}$	$\rho (t)=\rho (t_{0})\cdot a(t)^{-4}$
Facteur d'échelle en fonction du temps	$a(t)=a_{0}\cdot t^{\frac {2}{3(1+w)}}$	$a(t)=a_{0}\cdot t^{\frac {1}{2}}$
Facteur de Hubble	$H={\frac {n}{t}}$	$H={\frac {1}{2}}{\frac {1}{t}}$
Temps de Hubble	$T_{H}={\frac {t}{n}}$	$T_{H}=2t$
Rayon de Hubble	$R_{H}={\frac {c\cdot t}{n}}$	$R_{H}=2\cdot c\cdot t$
Rayon de l'univers observable	$r(t)={\frac {c\cdot t}{1-n}}$	$r(t)=2\cdot c\cdot t$
Age de l'univers	$t=n\cdot T_{H}$	$t={\frac {1}{2}}T_{H}$
Paramètre de décélération	$q={\frac {3}{2}}w+{\frac {1}{2}}$	$q=1$
Densité	$\rho ={\frac {1}{6\pi G(1+w)^{2}}}\cdot {\frac {1}{t^{2}}}$	$\rho ={\frac {3}{32\pi G}}\cdot {\frac {1}{t^{2}}}$

On peut noter que le rayon de Hubble et le rayon de l'univers observable sont égaux dans l'univers dominé par le rayonnement.

Le paramètre de décélération étant positif, on en déduit que l'expansion de l'univers ralentit progressivement avec le temps.

Les équations précédentes disent que l'univers a une expansion plus rapide qu'avec l'univers dominé par la matière. La raison est que le rayonnement se dilue plus vite que la matière, comme le dit l'équation $\rho (t)=\rho (t_{0})\cdot a(t)^{-4}$, en raison de la dilution par l'expansion de l'univers, mais aussi de l'expansion des longueurs d'onde. La dilution étant plus grande, la gravité perd plus rapidement en importance et l'expansion est donc plus rapide.

L'interprétation physique de la variation de densité énergétique du rayonnement

On a vu que la densité d'énergie du rayonnement varie selon la puissance quatrième du facteur d'échelle :

$\rho (t)=\rho (t_{0})\cdot a(t)^{-4}$

On peut donner un sens physique à cette équation. Premièrement, l'énergie du rayonnement est diluée dans un volume plus grand, égal à la puissance troisième du volume initial, comme pour la matière. La densité est donc divisée par la puissance troisième. À cela, il faut ajouter la diminution de la longueur d'onde causée par le facteur d'échelle. La somme de ces deux contributions donne la formule précédente. Pour nous en rendre compte, on peut partir de la définition de la densité d'énergie du rayonnement :

${E \over V}={E \over N}\times {N \over V}$

La variation de la densité d'énergie provient de deux sources : l'une est la variation de ${N \over V}$ et l'autre est la diminution de ${E \over N}$. La première varie comme $a^{-3}$, car le nombre de photons reste globalement constant et que l'expansion fait augmenter le volume en $V=V_{0}a^{3}$. Cela sera justifié dans la section suivante, mais le résultat est le même que celui vu dans le chapitre précédent. Si l'énergie par particule demeurait constante lors de l'expansion, on aurait l'équation $\epsilon \propto a^{-3}$. Quant au second terme, il évolue en $a^{-1}$.

On peut l'expliquer avec un argument qualitatif (et peu rigoureux) nous permet de justifier pourquoi l'expansion réduit l'énergie par particule. Rappelons qu'un photon de fréquence f a une énergie égale à $E_{\text{photon}}=h\times f$, avec h la constante de Planck. Or, on a vu que la fréquence varie avec l'inverse du facteur d'échelle, l'énergie par photon doit faire de même, ce qui donne : math>{E \over N} \propto f \propto a^{-1}</math>. En clair, l'expansion étire la longueur d'onde des photons, ce qui leur fait perdre de l'énergie. Cependant, cette dérivation n'est pas parfaite, vu qu'on mélange la fréquence d'un photon unique avec la température d'un gaz de plusieurs photons. Ce qui nuit à la généralité de l'argument.

Cela a une conséquence assez importante : l'énergie de l'univers ne se conserve pas, mais diminue avec le temps ! Et ce n'est pas un problème qui serait réglé en relativité générale : il y a réellement une perte d'énergie quel que soit le modèle utilisé. À l'heure actuelle, on ne sait pas comment résoudre ce problème (si tant est que ce soit vraiment un problème).

L'énergie noire et la constante cosmologique

Les équations de Friedmann nous disent une chose assez importante : l'univers est en expansion. La première équation de Friedmann donne la vitesse de l'expansion, la seconde donne l'accélération de l'expansion de l'univers. Elle nous dit si l'expansion accélère ou ralentit, en fonction de la densité de la pression de l'univers.

$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {k\cdot c^{2}}{a^{2}}}$

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)$

Rien de surprenant en soi, nous savons aujourd'hui que l'univers est en expansion. Mais à l'époque où ces équations ont été déduites à partir de la relativité générale, c'était une surprise. L'expansion de l'univers n'était pas encore connue et la loi de Hubble n'avait pas encore été découverte. Le consensus commun de l'époque était que l'univers était statique et un univers en expansion paraissait contre-intuitif. Il fallait réconcilier un univers statique avec ces équations, ce qu'a fait Einstein.

Quand Einstein vit que les équations de Friedmann impliquaient un univers en expansion, il leur ajouta un terme censé corriger ce qui était un "problème" à l'époque. Le terme $\Lambda$, ajouté aux équations de Friedmann, a reçu le nom de constante cosmologique. L'existence de cette constante était totalement justifiée par la relativité générale, où elle sert de constante d'intégration lors de certains calculs. Les équations de Friedmann étaient modifiées par la prise en compte de ce terme, ce qui donnait ceci :

$H^{2}={\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}$

${\frac {a''}{a}}={\frac {\Lambda c^{2}}{3}}-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$

L'ajout de la constante cosmologique permet d'obtenir un univers statique sous certaines conditions, qui sont détaillées dans un chapitre annexe de ce wikilivres, mais qui ne sont pas très intéressantes à étudier. Toujours est-il que la découverte de l'expansion de l'univers a mis au placard la constante cosmologique. Cependant, quelques décennies plus tard, les physiciens la réutilisèrent pour expliquer un autre phénomène : l'accélération de l'expansion.

L'accélération de l'expansion : la réintroduction de la constante cosmologique

Il a longtemps été cru que l'expansion de l'univers devait décélérer avec le temps, car c'était une conséquences des équations de Friedmann. Mais quelques observations ont remis cette affirmation en cause. Deux expériences ont fait voler en éclat ce consensus, en faisant état d'une accélération de l'expansion : le Supernova Cosmology Project et le High-Z supernovae search team. Ces observations ont été confirmées par des observations faites avec le télescope Hubble, à l'heure où j'écris ces lignes (fin 2016). Autant dire que la découverte de l'accélération de l'univers remettait en question les équations de Friedmann telles qu'elles sont formulées dans les chapitres précédents.

Illustration schématique de l'accélération de l'expansion de l'univers.

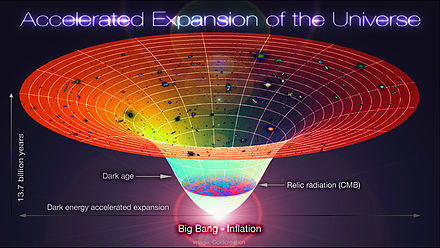
La réintroduction de la constante cosmologique

Pour comprendre en quoi l'accélération de l'expansion pose problème, rappelons que l'accélération de l'expansion est donnée par la dérivée seconde du facteur d'échelle. Or, la seconde équation de Friedmann sans constante cosmologique nous donne justement cette dérivée seconde, qui vaut :

$a''(t)\propto -\left(\rho (t)+3{\frac {P(t)}{c^{2}}}\right)$

La densité et la pression sont forcément positives pour la matière et le rayonnement, le terme entre parenthèses est donc positif, ce qui fait que la dérivée seconde est négative en raison du signe moins. Et un $a''$ négatif signifie que l'expansion décélère.

Pour résoudre le problème, les physiciens ont ressorti la constante cosmologique du placard. On peut rendre compte de l'accélération de l'expansion assez facilement en réutilisant les équations de Friedmann avec une constante cosmologique. Pour rappel, il s'agit des deux équations suivantes :

$H^{2}={\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}$

${\frac {a''}{a}}={\frac {\Lambda c^{2}}{3}}-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$

L'accélération de l'expansion est donnée par la seconde équation, avec la dérivée seconde du facteur d'échelle. On peut remarquer que cette équation ne contient pas de terme de courbure. En effet, la courbure cause une expansion constante, linéaire, sans accélération ni décélération. Et vu que le terme s'additionne aux autres termes, il n'a pas d'effet sur l'accélération de l'expansion, juste sur la vitesse de l'expansion. Par contre, la constante cosmologique apparaît comme un terme positif, qui permet de faire passer la dérivée seconde au-dessus de zéro. Le terme de densité est positif, ce qui donne une décélération. La dérivée seconde est positive sous la condition suivante :

${\frac {\Lambda c^{2}}{3}}>{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$

Il est en théorie possible de rendre le terme de densité négatif en faisant des hypothèses hardies, comme une matière à pression négative, mais cela serait équivalent à une constante cosmologique.

L'univers dominé par la constante cosmologique

Étudions maintenant le cas d'un univers avec une constante cosmologique, mais sans matière, ni rayonnement, ni courbure, ni quoique ce soit d'autre. Un tel univers hypothétique est appelé un univers de De Sitter. Sous ces hypothèses, les équations de Friedmann deviennent celles-ci :

$H^{2}={\frac {\Lambda c^{2}}{3}}$

${\frac {a''}{a}}={\frac {\Lambda c^{2}}{3}}$

Tous les paramètres de cette équation, $\Lambda$, c et les autres, sont tous constants, ce qui fait que le facteur de Hubble l'est aussi. Le fait que le facteur de Hubble est constant est à la base des développements mathématiques qui vont suivre.

La constance du facteur de Hubble a des conséquences assez intéressantes, qui peuvent se déduire de la définition du facteur de Hubble. Pour rappel, la définition du facteur de Hubble en fonction du facteur d'échelle donne :

$H={\frac {1}{a(t)}}{\frac {da(t)}{dt}}$

Multiplions par $dt$ des deux côtés :

$H\cdot dt={\frac {da(t)}{a(t)}}$

Intégrons sur $t$ :

$\int _{t}H\cdot dt=\int _{t}{\frac {da(t)}{a(t)}}$

Dans le premier terme, H est une constante, ce qui donne :

$H\cdot \int _{t}dt=\int _{t}{\frac {da(t)}{a(t)}}$

Dans le second terme, l'intégrale $\int dt$ n'est autre que l'âge de l'univers. Dans ce qui suit, nous noterons l'âge de l'univers $t$. Le calcul de l'intégrale de droite donne :

$H\cdot t=\ln {a(t)}$

Prenons l'exponentielle des deux côtés :

$a(t)=e^{H\cdot t}$

En injectant l'équation $H={\sqrt {\frac {\Lambda c^{2}}{3}}}$, on a alors :

$a(t)=e^{{\sqrt {\frac {\Lambda }{3}}}ct}$

Dans ce modèle, le facteur d'échelle suit une relation exponentielle avec le temps. Il s'agit donc d'un cas particulier de modèle à croissance exponentielle, ces derniers ayant déjà été abordés dans le chapitre "Une introduction aux modèles cosmologiques". Tout ce qui a été dit sur ces modèles peut donc s'adapter à ce modèle d'univers dominé par la constante cosmologique. Par exemple, leur facteur de décélération est toujours positif, égal à -1. Un tel univers va donc une croissance exponentiellement croissante, ce qui est beaucoup plus rapide que dans les deux prochains modèles, où la croissance est plus lente. Ce plus, on sait aussi qu'un tel l'univers a un âge infini : vu qu'une exponentielle ne peut être nulle, le facteur d'échelle et le volume de l'univers ne peuvent pas être nuls. Dit autrement : la singularité initiale est totalement évitée !

Les univers vides, avec constante cosmologique et courbure

Évidemment, le modèle précédent est irréaliste car l'univers contient aussi de la matière et du rayonnement. Mais le cas général n'a pas de solutions analytiques et il faut recourir à des calculs sur ordinateurs. Les rares solutions analytiques sont connues dans le cas d'un univers vide, à savoir sans matière ni rayonnement, mais avec une courbure positive ou négative. Dans les équations de Friedmann, il suffit de poser que la densité et la pression sont nulles. Sous ces conditions, l'équation du fluide disparaît et les deux autres équations de Friedmann deviennent alors :

$H^{2}={\frac {\Lambda c^{2}}{3}}-{\frac {k\cdot c^{2}}{a^{2}}}$

${\frac {a''}{a}}={\frac {\Lambda c^{2}}{3}}$

La disparition de l'équation du fluide est assez simple à comprendre. Cette équation décrit comment la matière et le rayonnement sont dilués par l'expansion. Mais sans matière et rayonnement, il n'y a rien à diluer avec l'expansion, et donc cette équation devient inutile. La dilution de la matière et du rayonnement avec l'expansion n'existant pas, on devine que cela a des conséquences sur la dynamique de l'expansion.

Résoudre ces équations dans le cas général, avec une courbure non-nulle et une constante cosmologique, est assez difficile et donne des équations relativement complexes. Mais il est beaucoup plus facile d'obtenir des résultats simples dans le cas où la courbure vaut soit 1, soit 0, soit -1. On obtient alors les résultats suivants :

$a(t)=\left\{{\begin{matrix}\cosh(Ht)\;si\;k=1\\\exp(Ht)\;si\;k=0\\\sinh(Ht)\;si\;k=-1\\\end{matrix}}\right.$

L'énergie noire

Pour expliquer l'accélération de l'expansion, il existe une solution alternative à la constante cosmologique. Elle part du principe que les équations de Friedmann du chapitre précédent sont valides, mais que l'univers est empli d'une forme de matière/énergie aux propriétés particulières. Précisément, l'équation d'état est calibrée de manière à ce que la seconde équation de Friedmann donne une expansion accélérée.

Pour cela, prenons la seconde équation de Friedmann et posons la condition que l'univers soit en expansion. On a alors :

$-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)>0$

En simplifiant, on trouve :

$\rho +3{\frac {P}{c^{2}}}>0$

Cette condition est remplie si et seulement si :

$P=-{\frac {1}{3}}\rho c^{2}$

Contenu de l'univers.

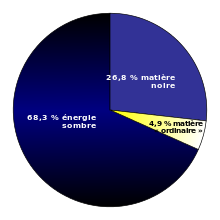
En clair, l'univers peut être en expansion à condition que l'univers contienne quelque chose qui a une densité positive, mais une pression négative. Ce quelque chose, ils l'ont appelé l'énergie noire. Cette énergie noire assez mal connue serait quelque chose de physique, qui contient une certaine densité d'énergie, sous la forme de masse et de pression. Mais les caractéristiques de cette énergie noire font qu'elle ne se comporte pas comme de la matière ordinaire ou du rayonnement. Les observations semblent indiquer que 30% de l'univers est composé de matière, tandis que le reste de la densité d'énergie est intégralement composé d'énergie noire.

Les propriétés de l'énergie noire

L'énergie noire a une masse positive, mais a aussi une pression négative. Or, la relativité générale nous dit que la pression est une forme d'énergie, qui a donc un effet gravitationnel. Dans cette théorie, toute énergie a un poids, une sorte de masse fictive, et la pression ne fait pas exception. Mais pour la matière ordinaire, la pression est positive, c'est à dire qu'elle a un effet gravitationnel normal, similaire à une masse positive. Elle a donc tendance à ralentir l'expansion, dans une certaine mesure. Mais l'énergie noire a une pression négative, ce qui est particulièrement original (même si on observe des phénomènes similaires dans certains cristaux ou lors de changements de phases). Du point de vue de la relativité générale, une pression négative implique un effet anti-gravitationnel, une attraction gravitaire dirigée vers l'extérieur. En clair, elle agit comme une force répulsive qui contrecarre la gravité et augmente l'expansion au lieu de la ralentir.

L'énergie noire se caractériserait par une densité constante au cours du temps, même en tenant compte de l'expansion de l'univers. La constance de la densité d'énergie noire a une conséquence assez intéressante : la densité étant constante, le facteur de Hubble est constant lui aussi. On peut remarquer que cela implique que l'énergie de l'univers ne se conserve pas, vu que cette densité constante est couplée à une augmentation du volume de l'univers par l'expansion.

Les scientifiques ont tenté d'expliquer cette énergie noire de plusieurs manières. La tentative la plus connue se base sur une prédiction assez singulière de la théorie quantique des champs., à savoir que le vide est censé être rempli d'une énergie appelé énergie du vide. C'était le candidat idéal pour expliquer l'énergie noire, jusqu'à ce que les calculs montrent que l'expansion mesurée implique une énergie du vide près de $10^{120}$ fois plus grande qu'observée. Ce résultat est aujourd'hui considéré comme la "pire prédiction théorique de l'histoire de la physique".

Il faut préciser que l'énergie noire et la constante cosmologique sont quasiment équivalentes en terme d'équation de Friedmann. La constante cosmologique est équivalente à une énergie noire d'équation $P=-pc^{2}$.

Énergie noire et équations de Friedmann

La constante de la densité d'énergie noire permet de simplifier la première équation de Friedmann, en utilisant la densité d'énergie noire $\rho _{\Lambda }$.

$H(t)^{2}={\frac {8\pi G}{3c^{2}}}\left(\rho _{\Lambda }-\rho _{k}(t)+\rho _{m}(t)+\rho _{r}(t)\right)$

Rappelons que la densité de matière, de rayonnement et de courbure suivent les relations suivantes : $\rho _{m}(t)={\frac {\rho _{m0}}{a(t)^{3}}}$, $\rho _{r}(t)={\frac {\rho _{r0}}{a(t)^{4}}}$ et $\rho _{k}(t)={\frac {K}{a(t)^{2}}}$. En substituant dans l'équation de Friedmann, on trouve :

$H(t)^{2}={\frac {8\pi G}{3c^{2}}}\left(\rho _{\Lambda }-{\frac {\rho _{k}0}{a(t)^{2}}}+{\frac {\rho _{m}0}{a(t)^{3}}}+{\frac {\rho _{r}0}{a(t)^{4}}}\right)$

Par définition, $H={\frac {a'(t)}{a(t)}}$. En faisant le remplacement dans l'équation précédente et en faisant quelques manipulations algébriques, on trouve :

${\frac {a'(t)^{2}}{a(t)^{2}}}={\frac {8\pi G}{3c^{2}}}\left(\rho _{\Lambda }-{\frac {\rho _{k}0}{a(t)^{2}}}+{\frac {\rho _{m}0}{a(t)^{3}}}+{\frac {\rho _{r}0}{a(t)^{4}}}\right)$

On multiplie par $a(t)^{2}$ :

$\left({\frac {da}{dt}}\right)^{2}={\frac {8\pi G}{3c^{2}}}\left(a^{2}\rho _{\Lambda }-\rho _{k}0+{\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)$

À l'heure actuelle, la constante cosmologique n'est qu'un paramètre ad-hoc qui permet de faire coller prédictions théoriques et observations. On ne connaît pas encore son origine, même si les physiciens ont quelques pistes. L'interprétation de ce terme varie suivant les physiciens.

Il est possible de reformuler la première équation de Friedmann avec le paramètre de densité, à savoir le rapport entre la densité réelle et la densité critique obtenue quand on considère un univers de courbure nulle.

$H(a)^{2}=H_{0}^{2}\left(\Omega _{k}\cdot a^{-2}+\Omega _{m}\cdot a^{-3}+\Omega _{r}\cdot a^{-4}+\Omega _{\Lambda }\right)$

Le destin de l'univers

Dans les chapitres précédents, nous avons établi les deux équations de Friedmann. Pour rappel, les voici :

$H^{2}={\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}$

${\frac {a''}{a}}={\frac {\Lambda c^{2}}{3}}-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$

On peut déduire bien des choses à partir de ces équations, notamment comment le facteur de Hubble évolue au cours du temps. Cela nous permet de déduire ce qu'il adviendra de l'univers. Continuera-t-il à s'étendre indéfiniment ? Ou au contraire, l'expansion cessera-t-elle au bout d'un certain temps ? L'univers finira-t-il par s'effondrer sur lui-même ? Il n'y a pas 36 possibilités et seuls trois scénarios sont possibles :

• Dans le premier scénario, l'expansion de l'univers s'inverse après un certain temps, l'univers se contracte et s'effondre sur lui-même : c'est le big-crunch.
• Dans le second cas, l'expansion de l'univers ne cesse jamais : c'est le scénario du big-rip.
• Et enfin, dans le dernier scénario, l'expansion de l'univers ne s’arrête jamais, mais celle-ci ralentit progressivement jusqu’à s'annuler après un temps infini : c'est le scénario du big chill.

Trois possibilités pour l'évolution de l'univers.

Dans le second chapitre sur les équations de Friedmann newtonienne, nous avions vu que le destin de l'univers dépendait uniquement de sa courbure, mais pas de son contenu en matière. Et autant ce résultat marche avec seulement de la matière, autant cela change quand on ajoute la constante cosmologique. Nous allons refaire les calculs et l'analyse dans le cas général, avec les équations de Friedmann relativistes.

Facteur de Hubble, facteur d'échelle et destin de l'univers

Le scénario qui se matérialise dépend du facteur de Hubble. Rappelons en effet que le facteur de Hubble est le taux d'expansion de l'univers, le taux auquel l'univers augmente de volume. Un H négatif signifie que l'univers se contracte, un H positif signifie que l'univers est en expansion, et un H nul signifie que l'univers est stationnaire. Pour l'étude du destin de l'univers, on se préoccupe du facteur de Hubble obtenu après un temps assez long, pour un âge de l'univers très important. Idéalement, on doit étudier la limite de H quand le temps tend vers l'infini : $\lim _{t\rightarrow \infty }H(t)$. On distingue les trois scénarios précédents selon que la limite de H est positive, négative ou nulle.

• Positive : l'expansion de l'univers ne s’arrête jamais et c'est le big rip qui se matérialise.
• Nulle : le big chill se matérialise si la limite tend vers 0.
• Négative : l'expansion s'inverse si la limite devient négative et l'univers finit en big-crunch.

Il est aussi possible de voir les choses à partir du facteur d'échelle, en utilisant la dérivée du facteur d'échelle. Quand ${\frac {da}{dt}}>0$, le facteur d'échelle augmente au cours du temps, ce qui implique un univers en expansion. Par contre, ${\frac {da}{dt}}<0$ implique un facteur d'échelle qui se réduit au cours du temps et donc un univers qui se contracte. Enfin, ${\frac {da}{dt}}=0$ implique un univers stable, qui n'est ni en expansion ni en contraction.

En théorie, on devrait étudier le destin de l'univers, ce qui veut dire son état quand l'âge de l'univers est très avancé, voire à la limite $t\rightarrow \infty$. Mais les équations précédentes sont écrites avec le facteur d'échelle, pas avec le temps. Cependant, le facteur d'échelle dépend du temps et on peut l'utiliser en remplacement, sous certaines hypothèses.

• Dans le cas du big crunch, l'univers gonfle avant de se rétracter. Au niveau du facteur d'échelle, cela signifie que le facteur d'échelle est initialement croissant, cesse de croître à un temps bien précis, et décroît au-delà. Au niveau du facteur de Hubble, cela signifie qu'il est d'abord positif (univers en expansion), puis s'annule, et enfin devient négatif. On est donc dans le cas où la dérivée du facteur d'échelle s'annule pour un temps fini.
• Dans le cas du big chill, la dérivée s'annule, mais seulement pour la limite $t\rightarrow \infty$. L'univers ne cesse de croître et ce n'est qu'après un temps infini qu'il se stabilise.
• Dans le cas du big rip, la dérivée reste positive quand on passe à la limite $t\rightarrow \infty$. L'univers ne cesse de croître et ne se stabilise pas, même après un temps infini.

	$\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)$	$\lim _{t\rightarrow \infty }a(t)$
Big Crunch	Négative	Nulle
Big Chill	Nulle	Infinie
Big Rip	Positive

On peut calculer la dérivée du facteur d'échelle en utilisant la formule $a'(t)={\frac {da}{dt}}$. Et donc, on peut la calculer indirectement à partir de la première équation de Friedmann. Celle-ci s'écrit en effet, comme on l'a vu dans le chapitre sur l'énergie noire :

$\left({\frac {da}{dt}}\right)^{2}=a^{2}\left[{\frac {8\pi G}{3c^{2}}}\rho _{e}+{\frac {\Lambda c^{2}}{3}}\right]-k\cdot c^{2}$

Pour rappel, la densité d'énergie est égale à la densité de matière et la densité de rayonnement :

$\left({\frac {da}{dt}}\right)^{2}=a^{2}\left[{\frac {8\pi G}{3c^{2}}}(\rho _{m}(t)+\rho _{r}(t))+{\frac {\Lambda c^{2}}{3}}\right]-k\cdot c^{2}$

Pour rappel, la densité de matière et de rayonnement évoluent comme suit : $\rho _{m}(t)=\rho _{m}0\cdot a^{(}t){-3}$ et $\rho _{r}(t)=\rho _{r}0\cdot a(t)^{-4}$. En injectant dans l'équation précédente, on a :

$\left({\frac {da}{dt}}\right)^{2}=a^{2}\left[{\frac {8\pi G}{3c^{2}}}\left({\frac {\rho _{m}0}{a^{3}}}+{\frac {\rho _{r}0}{a^{4}}}\right)+{\frac {\Lambda c^{2}}{3}}\right]-k\cdot c^{2}$

On simplifie :

$\left({\frac {da}{dt}}\right)^{2}={\frac {8\pi G}{3c^{2}}}\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)+a^{2}{\frac {\Lambda c^{2}}{3}}-k\cdot c^{2}$

On prend alors la limite quand t tend vers l'infini :

$\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)^{2}=\lim _{t\rightarrow \infty }\left[{\frac {8\pi G}{3c^{2}}}\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)+a^{2}{\frac {\Lambda c^{2}}{3}}-k\cdot c^{2}\right]$

En sortant les termes indépendants de t de la limite, on a :

$\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}$

Le cas du big crunch

Dans le cas du big crunch, l'univers décroît au-delà d'un certain temps et se ratatine sur lui-même au point d'atteindre un volume nul. Traduit mathématiquement, cela se traduit par les équations suivantes :

$\lim _{t\rightarrow \infty }a(t)=0$

$\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)^{2}<0$

On part de l'équation des sections précédentes :

$\lim _{t\rightarrow \infty }{\frac {da}{dt}}^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}$

On combine les deux équations précédentes :

${\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}<0$

On réorganise :

${\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a(t)}}+{\frac {\rho _{r}0}{a(t)^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a(t)^{2}\right]<k\cdot c^{2}$

Or, on a vu que le big crunch impliquait que : $\lim _{t\rightarrow \infty }a(t)=0$. En injectant dans l'équation précédente, on trouve :

${\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a(t)}}+{\frac {\rho _{r}0}{a(t)^{2}}}\right)\right]<k\cdot c^{2}$

Cette inégalité nous dit que le big crunch n'est possible que si l'univers a une courbure positive et que celle-ci a une intensité suffisante. Il faut alors que l'effet de la constante cosmologique et de la gravité soient compensés quand l'âge de l'univers a atteint une valeur suffisante.

Le cas du big rip

Pour le big-rip, on a, par définition du big rip :

$\lim _{t\rightarrow \infty }a(t)=\infty$.

$\lim _{t\rightarrow \infty }{\frac {da}{dt}}>0$.

On part de l'équation des sections précédentes :

$\lim _{t\rightarrow \infty }{\frac {da}{dt}}^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}$

On combine les deux équations précédentes :

${\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}>0$

On réorganise :

${\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]>k\cdot c^{2}$

On utilise alors la condition $\lim _{t\rightarrow \infty }a(t)=\infty$. On en déduit que les facteurs ${\frac {\rho _{m}}{a(t)}}$ et ${\frac {\rho _{r}}{a(t)^{2}}}$ deviennent très petits, au point d'être négligeables, et vont s'annuler avec l'augmentation progressive de $a$. On a alors :

${\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]>k\cdot c^{2}$

L'équation nous dit que la présence d'une constante cosmologique non-nulle suffit à elle seule pour que le big-rip survienne. Mais dans le cas où elle est nulle, le big rip dépend de la valeur de la courbure. Supposons que la constante cosmologique soit nulle, ce qui donne :

${\frac {0\cdot c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]>k\cdot c^{2}$

Ce qui se simplifie en :

$0>k\cdot c^{2}$

On voit que le big rip est possible si $\lambda =0$, mais à condition que la courbure soit négative.

Pour résumer, le big rip a lieu soit si la constante cosmologique est positive, soit si la courbure est négative (et même suffisamment négative pour compenser l'effet de la gravité/densité). Dit autrement, le destin de l'univers dépend uniquement de la valeur de la constante cosmologique et de la courbure.

Le cas du big chill

Dans le cas du big chill, le facteur d'échelle tend vers l'infini et sa dérivée tend vers zéro :

$\lim _{t\rightarrow \infty }a(t)=\infty$.

$\lim _{t\rightarrow \infty }{\frac {da}{dt}}=0$.

On part de l'équation des sections précédentes :

$\lim _{t\rightarrow \infty }{\frac {da}{dt}}^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}$

On combine les deux équations précédentes :

${\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}=0$

On réorganise :

${\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]=k\cdot c^{2}$

On ajoute alors la contrainte $\lim _{t\rightarrow \infty }a(t)=\infty$. Dans ce cas, on a $\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)=0$ et $\lim _{t\rightarrow \infty }a^{2}=\infty$. On a alors :

${\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]=k\cdot c^{2}$

Ce qui n'est possible que si la constante cosmologique est nulle, idem pour la courbure. Un univers en big chill ne peut atteindre un volume infini que si sa courbure et sa constante cosmologique sont toutes les deux nulles, en présence de matière et/ou de rayonnement.

Résumé

Dans les paragraphes précédents, on sait quel est le destin de l'univers en fonction de son contenu. Tout dépend de la valeur de la constante cosmologique et de sa courbure, la présence de matière et de rayonnement important peu. On peut donc résumer le tout dans un tableau à deux entrées, qui donne le destin de l'univers en fonction du signe de la courbure et de la constante cosmologique.

	$\lambda$ Nul	$\lambda$ Positif
Courbure négative	Big Rip	Big Rip
Courbure nulle	Big chill
Courbure positive	Big Crunch	Dépend de qui l'emporte

Le fluide cosmologique

On peut modéliser l'ensemble matière + rayonnement comme un fluide non relativiste (en clair, un fluide dont la vitesse des particules est petite devant la vitesse de la lumière). Un tel fluide est gouverné par les équations de la mécanique des fluides, et on pourrait penser qu'il suffit de réutiliser les équations de la mécanique des fluides telles quelles. Cependant, les équations de la mécanique des fluides usuelle ne s'appliquent pas sans modifications, du fait de l'expansion de l'univers.

Pour comprendre pourquoi, il faut savoir que les équations de la mécanique des fluides décrivent l'évolution d'un petit volume infinitésimal de fluide, appelé particule de fluide. Ce volume est pris très très petit, de manière à donner l'illusion que le fluide est un milieu continu. Dans le cas de l'univers, le très très petit signifie une taille petite comparée à l'horizon cosmologique, ce qui fait que les volumes des particules fluides peuvent être extrêmement grands comparés à la normale. Dans ces conditions, tenir compte du volume des particules fluides est absolument primordial. Or, les équations de la mécanique des fluides "usuelle" sont démontrées en partant du principe que ce volume infinitésimal de fluide reste constant. Ce serait le cas si l'expansion de l'univers n'existait pas, mais l'expansion fait que ce volume augmente avec l'expansion. Et il en est de même avec la surface des particules fluides, ainsi que des distances parcourues par le fluide... Autant dire qu'il faudra donc redémontrer les équations de la mécanique des fluides pour tenir compte de ce phénomène.

Rappels sur les opérateurs vectoriels

Le gradient est aux vecteurs ce que la dérivée est aux scalaires/fonctions. Dans le cas des nombres, les deux se confondent d'ailleurs. $\operatorname {grad} {\vec {A}}=\nabla {\vec {A}}=\left({\frac {\partial {A_{x}}}{\partial {x}}},{\frac {\partial {A_{y}}}{\partial {y}}},{\frac {\partial {A_{z}}}{\partial {z}}}\right)$

La divergence est la somme des termes du gradient : $\operatorname {div} {\vec {(}}A)=\nabla \cdot {\vec {A}}={\frac {\partial {A_{x}}}{\partial {x}}}+{\frac {\partial {A_{y}}}{\partial {y}}}+{\frac {\partial {A_{z}}}{\partial {z}}}$ On peut remarquer que sa notation $\nabla \cdot {\vec {A}}$ explicite bien la nature de la divergence. L'opérateur $\nabla$ n'est autre que l'opérateur gradient, alors que l'opérateur $\cdot$ signifie que l'on fait la somme de tous les termes d'un vecteur. Attention : l'opérateur $\cdot$ se place après le $\nabla$ dans l'écriture, mais il est en réalité appliqué après que le gradient ait été calculé. La divergence est un opérateur dit linéaire, ce qui veut dire que : La divergence d'une somme est la somme des divergences. $\operatorname {div} ({\vec {A}}+{\vec {B}})=\operatorname {div} ({\vec {A}})+\operatorname {div} ({\vec {B}})$ La divergence d'un multiple est le multiple de la divergence. $\operatorname {div} (f{\vec {A}})=f\cdot \operatorname {div} ({\vec {A}})+\nabla f\cdot {\vec {A}}$ Si f est un scalaire constant et uniforme, la formule précédente se simplifie et devient alors : $\operatorname {div} (f{\vec {A}})=f\cdot \operatorname {div} ({\vec {A}})$

Le laplacien est tout simplement la divergence du gradient. Ce qui revient à appliquer deux fois l'opérateur gradient, avant d'additionner les termes du vecteur obtenu. $\operatorname {div} (\operatorname {grad} {\vec {(}}A))=\nabla ^{2}\cdot {\vec {A}}={\frac {\partial ^{2}{A_{x}}}{\partial ^{2}{x}}}+{\frac {\partial ^{2}{A_{y}}}{\partial ^{2}{y}}}+{\frac {\partial ^{2}{A_{z}}}{\partial ^{2}{z}}}$

Les équations de conservation "usuelles"

Les trois équations de la mécanique des fluides sont des équations de conservation. Elles portent d'ailleurs les noms d'équation de conservation de la masse, d'équation de conservation de l'énergie et d'équation de conservation de la quantité de mouvement. Elles disent que la masse, l'énergie et la quantité de mouvement se conservent lors de l'évolution d'un fluide. Démontrer ces équations de conservation demande de simplement faire le bilan des variations, entrées et sorties de la particule fluide.

Variation interne + Entrées/sorties = ...

Le terme de variation interne est naturellement un terme de la forme :

${\frac {\partial x}{\partial t}}$

Le flux entrant/sortant d'une quantité $A$ se calcule en multipliant la vitesse par un opérateur appelé divergence, qui donne l'intégrale du flux entrant à travers la surface de la particule fluide :

$\operatorname {div} {\vec {A}}=\left({\frac {\partial {A_{x}}}{\partial {x}}}+{\frac {\partial {A_{y}}}{\partial {y}}}+{\frac {\partial {A_{z}}}{\partial {z}}}\right)$

Pour résumer, toute équation de la mécanique des fluides prend la forme suivante. Elle décrit une quantité A, entraînée à la vitesse v, et dont une quantité S est produite à chaque instant $t$ :

${\frac {\partial A}{\partial t}}+\nabla \cdot (A\cdot v)=S$

La conservation de la masse

Par exemple, l'équation de conservation de la masse s'établit en faisant la somme des entrées/sorties de masse du volume (flux entrant/sortant) et de la variation de la masse de la particule fluide (variation interne). Vu que la masse se conserve, toute variation interne de masse de la particule doit provenir d'un flux entrant ou sortant : la masse de la particule diminue avec un flux sortant et augmente avec un flux entrant. La somme des deux termes est nulle, ce qui traduit le fait que toute variation de ces grandeurs provient d'un flux égal à travers la surface du volume.

Vu qu'il n'y a pas de source de masse, on a l'équation suivante :

Variation interne = Flux entrant/sortant, ou encore : Variation interne + Entrées/sorties = 0.

On a donc :

${\frac {\partial m}{\partial t}}+\operatorname {div} (m\cdot {\vec {v}})=0$

En divisant le tout par le volume infinitésimal, on a :

${\frac {\partial \rho }{\partial t}}+\operatorname {div} (\rho \cdot {\vec {v}})=0$

On peut sortir la densité des parenthèses :

${\frac {\partial \rho }{\partial t}}+\rho \cdot \operatorname {div} ({\vec {v}})=0$

La conservation de la quantité de mouvement

Pour la quantité de mouvement, les choses sont plus compliquées. Le fait est que du point de vue de la particule de fluide, les forces sont des sources de quantité de mouvement, qui donnent l'illusion que de la quantité de mouvement est créée. La somme entre variation interne et flux ne peut pas être nulle en présence de forces, celles-ci s'ajoutant à la quantité conservée de quantité de mouvement. Dans ce cas, la variation de quantité de mouvement et son flux sont causées par des forces, ce qui donne :

Variation interne + Entrées/sorties = Forces.

${\frac {\partial (mv)}{\partial t}}+\operatorname {div} (mv\cdot {\vec {v}})=F$

On suppose l'existence de deux forces : la force causée par le gradient de pression et la gravité. L'accélération liée à la gravité est elle-même liée à un gradient : le gradient du potentiel gravitationnel $\phi$. On a donc :

${\frac {\partial (mv)}{\partial t}}+\operatorname {div} (mv\cdot {\vec {v}})=\rho \cdot \nabla P+m\cdot \nabla (\Phi )$

La masse étant constante, on peut simplifier par celle-ci :

${\frac {\partial (v)}{\partial t}}+\operatorname {div} (v\cdot {\vec {v}})={\frac {\nabla P}{\rho }}+\nabla \Phi$

Les équations au complet

Il y a une équation de conservation pour la masse et la quantité de mouvement, à laquelle on pourrait ajouter une équation de conservation de l'énergie. À ces équations, il faut ajouter une équation qui décrit le champ de gravité.

En supposant que le volume de la particule fluide est constant, les équations obtenues sont alors les suivantes :

L'équation de conservation de la masse du fluide :

${\frac {\partial \rho }{\partial t}}+\rho (\nabla \cdot v)=0$

L'équation de bilan de la quantité de mouvement :

${\frac {\partial v}{\partial t}}+v(\nabla \cdot {\vec {v}})={\frac {\nabla P}{\rho }}+\nabla \Phi$

Les équations du fluide avec l'expansion

On peut retrouver les équations de Friedmann à partir des équations précédentes : il suffit d'utiliser l'équation $v=H\cdot r$, et de faire quelques manipulations algébriques. Dit autrement, on ne prend en compte que l'effet de l'expansion et on néglige l'effet des vitesses locales. Les équations se simplifient alors.

Dérivation de l'équation du fluide de Friedmann

Par exemple, prenons l'équation de conservation de la masse :

${\frac {\partial \rho }{\partial t}}+\rho \cdot \operatorname {div} ({\vec {v}})=0$

Injectons la loi de Hubble :

${\frac {\partial \rho }{\partial t}}+\rho \cdot \operatorname {div} (H\cdot {\vec {r}})=0$

Appliquons maintenant la définition de la divergence : $\operatorname {div} {\vec {A}}=\left({\frac {\partial {A_{x}}}{\partial {x}}}+{\frac {\partial {A_{y}}}{\partial {y}}}+{\frac {\partial {A_{z}}}{\partial {z}}}\right)$.

$\operatorname {div} H\cdot {\vec {r}}=\left(H\cdot {\frac {\partial {r}}{\partial {x}}}+H\cdot {\frac {\partial {r}}{\partial {y}}}+H\cdot {\frac {\partial {r}}{\partial {z}}}\right)=3H$

On a alors l'équation :

${\frac {\partial \rho }{\partial t}}+3H\rho =0$

Cette équation ressemble à l'équation du fluide de Friedmann, bien qu'il manque la pression.

Dérivation de la seconde équation de Friedmann

La seconde équation de Friedmann se dérive en prenant la divergence de l'équation d'Euler et en utilisant l'équation dite de Poisson pour calculer le terme gravitationnel.

Mais avant de faire cela, nous devons simplifier l'équation d'Euler. Il nous faut notamment déterminer la valeur du terme $v\times (\nabla \cdot {\vec {v}})$. Il se trouve que la première équation de conservation nous a permis de déduire que :

$\operatorname {div} ({\vec {v}})=-{\frac {1}{\rho }}{\frac {\partial \rho }{\partial t}}=-3H$

En injectant dans l'équation d'Euler, on trouve :

${\frac {\partial v}{\partial t}}-3H\cdot v={\frac {\nabla P}{\rho }}+\nabla \Phi$

Il ne reste plus qu'à prendre la divergence. De laborieux calculs permettent alors de retrouver la seconde équation de Friedmann.

Les équations de conservation en coordonnées comobiles

Pour décrire l'évolution du fluide dans un univers en expansion, il faut prendre en compte le fait que le volume de la particule fluide augmente avec le facteur d'échelle. Ce que les équations précédentes ne faisaient pas, supposant un volume constant. Les équations précédentes ne fonctionnent pas telles quelles. Par exemple, prenons l'équation de conservation de la masse et supposons qu'il n'y ait pas de flux entrant ou sortant de matière. On devrait avoir ${\frac {\partial \rho }{\partial t}}=\operatorname {div} (\rho \cdot {\vec {v}})=0$. Cependant, l'expansion va faire gonfler la particule fluide, ce qui diluera son contenu : sa masse restant constante, sa densité va diminuer avec le temps, ce qui contredit l'équation précédente ! Les équations précédentes ne donnent pas une version correcte de la conservation de la masse, de la quantité de mouvement et de l'énergie.

L'utilisation des coordonnées comobiles

On peut cependant remarquer que l'on peut utiliser des distances, vitesses et volumes comobiles pour résoudre ce problème. Le volume comobile de la particule fluide ne change pas avec l'expansion, pas plus que sa surface comobile ou sa vitesse comobile. Intuitivement, la densité comobile (masse / volume comobile) se comporte comme la densité dans les équations précédentes. Même chose pour les autres grandeurs comobiles. Cependant, les opérateurs divergence et gradient doivent tenir compte du fait qu'on travaille en coordonnées comobiles, ce qui demande de les reformuler. Nous allons donc devoir reformuler les équations de manière à utiliser des coordonnées comobiles $x=a{\overline {x}}$. La reformulation du gradient est assez simple :

$\nabla {\vec {A}}=\left({\frac {\partial {A_{x}}}{\partial {x}}},{\frac {\partial {A_{y}}}{\partial {y}}},{\frac {\partial {A_{z}}}{\partial {z}}}\right)=\left({\frac {\partial {A_{x}}}{\partial {(a\times {\overline {x}})}}},{\frac {\partial {A_{y}}}{\partial {(a\times {\overline {y}})}}},{\frac {\partial {A_{z}}}{\partial {(a\times {\overline {z}})}}}\right)={\frac {1}{a}}\left({\frac {\partial {A_{x}}}{\partial {\overline {x}}}},{\frac {\partial {A_{y}}}{\partial {\overline {y}}}},{\frac {\partial {A_{z}}}{\partial {\overline {z}}}}\right)={\frac {1}{a}}\nabla {\vec {A}}$

La divergence n'est que la somme des termes du gradient, ce qui donne :

$\nabla .{\vec {A}}={\frac {1}{a}}(\nabla .{\vec {\overline {A}}})$

Enfin, la vitesse à utiliser doit être la vitesse locale, à savoir :

$u=v-H\cdot r$

Sa dérivée est la suivante :

${\frac {du}{dt}}={\frac {dv}{dt}}-{\frac {d}{dt}}(H\cdot r)={\frac {dv}{dt}}-H{\frac {dr}{dt}}={\frac {dv}{dt}}-H\cdot u$

La reformulation des équations précédentes

Maintenant, reformulons les équations précédentes avec les opérateurs définis dans la section précédente.

Prenons la première équation, celle de la conservation de la masse du fluide.

${\frac {\partial \rho }{\partial t}}+\rho \times (\nabla \cdot v)=0$

La seule modification à faire est de remplacer la divergence usuelle par celle en coordonnées comobiles, ce qui demande juste de diviser par le facteur d'échelle a(t). On a alors :

${\frac {\partial \rho }{\partial t}}+{\frac {\rho }{a}}(\nabla \cdot u)=0$

Modifions ensuite la seconde équation, celle de la conservation de l'impulsion, que voici :

${\frac {\partial v}{\partial t}}+v\times (\nabla \cdot {\vec {v}})={\frac {\nabla P}{\rho }}+\nabla \Phi$

Premièrement, on doit remplacer la dérivée, en utilisant l'équation ${\frac {du}{dt}}={\frac {dv}{dt}}-H\cdot u$. On a alors :

${\frac {du}{dt}}-H\cdot u+v\times (\nabla \cdot {\vec {v}})={\frac {\nabla P}{\rho }}+\nabla \Phi$

Ensuite, on divise par le facteur d'échelle a(t), ce qui permet de remplacer la vitesse usuelle par la vitesse comobile, sans compter que cela fait de même pour la divergence. On a alors :

${\frac {\partial u}{\partial t}}-Hu+{\frac {1}{a}}(u\cdot \nabla )u={\frac {1}{a}}\left({\frac {\nabla P}{\rho }}+\nabla \Phi \right)$

Pour résumer, on obtient les équations suivantes :

${\frac {\partial \rho }{\partial t}}+{\frac {\rho }{a}}(\nabla \cdot u)=0$

${\frac {\partial u}{\partial t}}-Hu+{\frac {1}{a}}(u\cdot \nabla )u={\frac {1}{a}}\left({\frac {\nabla P}{\rho }}+\nabla \Phi \right)$

Les perturbations cosmologiques

L'origine des galaxies et autres super-structures de plusieurs milliards d'étoiles est encore assez mal connue. Cependant, on sait que divers processus sont à leur origine. La gravité a naturellement joué un rôle prédominant, en forçant les étoiles à se rapprocher en amas de plusieurs millions/milliards d'étoiles. Mais la nature exacte et le déroulement de ce processus sont encore assez mal connus : les étoiles se sont-elles formées en premier avant de se regrouper en galaxies ou bien les galaxies se sont-elles formées avant de se fragmenter en amas puis en étoiles ? Personne ne le sait à l'heure actuelle. La seule chose qui est certaine est que ces structures se sont formées à partir de zones de surdensités, qui ont grossit de plus en plus sous l'effet de la gravité au point de donner des structures comme des galaxies. Il existe une théorie qui explique les grandes lignes de cette évolution des surdensités : c'est la théorie des perturbations cosmologiques. Nous allons l'aborder dans ce chapitre.

Les précurseurs des galaxies, amas de galaxies et autres "structures cosmologiques" sont des zones où la densité est plus grande qu'aux alentours. La densité n'était en effet pas uniforme et on observait des zones où la densité était plus faible ou plus grande que la moyenne. Ces petites variations de densité ont reçu le nom d'inhomogénéités. La densité dans une surdensité est modélisée comme une petite perturbation $\delta p(x,t)$ par rapport à la densité moyenne $\rho _{m}(t)$, ce qui donne :

$\rho (x,t)=\rho _{m}(t)\cdot (1+\delta )$

${\frac {\rho (x)}{\rho _{m}}}=1+\delta$

$\delta ={\frac {\rho (x)-\rho _{m}}{\rho _{m}}}$

Gaussian 2d

Les inhomogénéités sont supposées provenir d'agitations aléatoires de la matière et du rayonnement dans l'univers primordial. Les scientifiques ont de bonnes raisons de penser que ces fluctuations aléatoires étaient des fluctuations dites gaussiennes : la probabilité d'observer la perturbation $\delta$ en un endroit est définie par une fonction gaussienne, la fameuse courbe en cloche. Mais peu importe la manière dont elles sont générées, cela ne change rien à leur évolution future. Ces fluctuations de densité vont ensuite évoluer : certaines vont grossir, d'autres vont diminuer, etc. L'évolution des perturbations est gouvernée par divers processus que nous aborderons dans les chapitres suivants. Quoiqu'il en soit, la distribution initiale sera modifiée au cours du temps. On peut résumer cela en disant qu'on peut obtenir la distribution à un instant $t'$ à partir de la distribution à un instant t en multipliant cette dernière par une fonction de transfert. Celle-ci va atténuer ou accentuer certaines perturbations initiales, donnant une nouvelle distribution statistique des perturbations.

Les équations du "fluide primordial" avec les inhomogénéités

Pour rendre compte de l'évolution des inhomogénéités, on réutilise les équations en coordonnées comobiles du chapitre précédent. Celles-ci sont, pour rappel :

${\frac {\partial \rho }{\partial t}}+{\frac {\rho }{a}}(\nabla \cdot u)=0$

${\frac {\partial u}{\partial t}}-H\cdot u+{\frac {1}{a}}u(\nabla \cdot u)={\frac {1}{a}}\left({\frac {\nabla P}{\rho }}+\nabla \Phi \right)$

On doit injecter $\rho (x,t)=\rho _{m}(1+\delta )$ dans ces équations.

L'équation de conservation de la masse perturbée

Prenons l'équation :

${\frac {\partial \rho }{\partial t}}+{\frac {\rho }{a}}(\nabla \cdot u)=0$

Injectons l’équation $\rho (x,t)=\rho _{m}(1+\delta )$ :

${\frac {\partial [\rho _{m}(1+\delta )]}{\partial t}}+{\frac {\rho _{m}(1+\delta )}{a}}(\nabla \cdot u)=0$

Le terme $p_{m}$ étant constant, on peut le sortir de la dérivée du terme de gauche.

$\rho _{m}{\frac {\partial (1+\delta )}{\partial t}}+{\frac {(1+\delta )\rho _{m}}{a}}(\nabla \cdot u)=0$

Divisons par $\rho _{m}$ :

${\frac {\partial (1+\delta )}{\partial t}}+{\frac {1+\delta }{a}}(\nabla \cdot u)=0$

Simplifions la dérivée :

${\frac {\partial \delta }{\partial t}}+{\frac {1+\delta }{a}}(\nabla \cdot u)=0$

Les équations linéarisées

Les équations obtenues sont les suivantes :

${\frac {\partial \delta }{\partial t}}+{\frac {1+\delta }{a}}(\nabla \cdot u)=0$

${\frac {\partial u}{\partial t}}-H\cdot u+{\frac {1}{a}}u(\nabla \cdot u)={\frac {1}{a}}\left({\frac {\nabla P}{\rho _{m}(1+\delta )}}+\nabla \Phi \right)$

Ces équations ne peuvent cependant pas être résolues à l'heure actuelle, car ce ne sont pas des équations linéaires. On peut cependant supposer que la perturbation est petite : $\delta <<1$. Si l'on prend cette approximation, on a immédiatement : $1+\delta \approx 1$. Les équations deviennent alors :

${\frac {\partial \delta }{\partial t}}+{\frac {1}{a}}(\nabla \cdot u)=0$

${\frac {\partial u}{\partial t}}-H\cdot u+{\frac {1}{a}}u(\nabla \cdot u)={\frac {1}{a}}\left({\frac {\nabla P}{\rho _{m}}}+\nabla \Phi \right)$

De plus, cette approximation fait que les termes non-linéaires peuvent être négligés et supprimés des équations. Dit autrement, on ne conserve que les termes linéaires, en supprimant tout carré ou terme de puissance > 1. La conséquence est que le terme ${\frac {1}{a}}(u\cdot \nabla )u$ dans l'équation d'Euler disparaît. Les équations après linéarisation sont les suivantes :

${\frac {\partial \delta }{\partial t}}+{\frac {1}{a}}(\nabla \cdot u)=0$

${\frac {\partial u}{\partial t}}-H\cdot u={\frac {1}{a}}\left({\frac {\nabla P}{\rho _{m}}}+\nabla \Phi \right)$

La divergence de l'équation d'Euler

Dans la suite des calculs, nous aurons à faire de nombreuses linéarisations, ce qui fait que les calculs se simplifieront progressivement. La première simplification, consiste à prendre la divergence de l'équation d'Euler. L'utilité de cette reformulation deviendra évidente sous peu. Prenons donc l'équation d'Euler et prenons sa divergence des deux côtés de l'équation :

$\nabla .\left[{\frac {\partial u}{\partial t}}-H\cdot u\right]=\nabla .\left[{\frac {1}{a}}\left({\frac {\nabla P}{\rho _{m}}}+\nabla \Phi \right)\right]$

La divergence d'une somme est la somme des divergences, ce qui simplifie le terme de gauche :

$\nabla .{\frac {\partial u}{\partial t}}-\nabla .(H\cdot u)=\nabla .\left[{\frac {1}{a}}\left({\frac {\nabla P}{\rho _{m}}}+\nabla \Phi \right)\right]$

On utilise ensuite la formule ${\displaystyle }$, ce qui simplifie le terme de droite, ainsi que le terme : $\nabla .(Hu)$.

$\nabla .{\frac {\partial u}{\partial t}}-H\cdot (\nabla .u)={\frac {1}{a}}\left[{\frac {\nabla .(\nabla P)}{\rho _{m}}}+\nabla .(\nabla \Phi )\right]$

La divergence d'un gradient est identique au laplacien, ce qui donne :

$\nabla .{\frac {\partial u}{\partial t}}+H\cdot (\nabla .u)={\frac {1}{a}}\left[{\frac {\Delta P}{\rho _{m}}}+\Delta \Phi \right]$

On applique alors l'identité suivante : $\nabla .{\frac {\partial u}{\partial t}}={\frac {\partial (\nabla .u)}{\partial t}}$

${\frac {\partial (\nabla .u)}{\partial t}}+H\cdot (\nabla .u)={\frac {1}{a}}\left[{\frac {\Delta P}{\rho _{m}}}+\Delta \Phi \right]$

Les relations entre densité et autres paramètres de l'équation d'Euler

Les inhomogénéités vont naturellement influencer la pression et le potentiel gravitationnel, ainsi que la vitesse du fluide. Les zones plus denses que leur voisinage auront naturellement une gravité plus grande que leur entourage. Elles vont donc attirer de la matière et grossir, se densifier. La sur-densité se creuse, elle s'accroit. Par contre, en se densifiant, la pression va augmenter. Au-delà d'une densité limite, la pression augmente tellement qu'elle repousse la matière et dilate la sur-densité.En se dilatant, la sur-densité diminue, et la pression fait de même. Et on revient au point de départ.

Le tout donne un comportement oscillant dans le plasma. Mais les équations précédentes ne permettent pas de rendre compte de ce phénomène, pour deux raisons. Premièrement, elles font usage de la vitesse locale de la matière, qu'il faudrait idéalement faire dépendre de la densité. Deuxièmement, les termes de pression et de potentiel gravitationnel ne sont pas exprimés en fonction de la densité. On doit donc trouver des relations entre densité, pression et potentiel gravitationnel. Avec ces relations, on pourra reformuler les équations du fluide avec seulement la densité.

Notons que la matière noire n'est pas concernée par la pression, elle reste dans les sur-densités initiales, ce qui tend à amortir les oscillations. Mais laissons cela pour plus tard.

La relation entre densité et vitesse locale

Le premier paramètre de l'équation précédente est la divergence de la vitesse locale $\partial (\nabla .u)$. On peut relier cette divergence à la densité en utilisant l'équation de conservation de la masse. Celle-ci donne en effet une relation entre la divergence de la vitesse et la densité. Ce n'est pas une relation directe avec la vitesse locale, mais c'est déjà un bon début.

${\frac {\partial \delta }{\partial t}}+{\frac {1}{a}}(\nabla \cdot u)=0$

On réorganise :

${\frac {\partial \delta }{\partial t}}={\frac {1}{a}}(\nabla \cdot u)$

On multiplie par $a$ :

$a{\frac {\partial \delta }{\partial t}}=\nabla \cdot u$

On injecte alors cette équation dans les équations linéarisées :

${\frac {\partial }{\partial t}}\left(a{\frac {\partial \delta }{\partial t}}\right)+H\left(a{\frac {\partial \delta }{\partial t}}\right)={\frac {1}{a}}\left({\frac {\Delta P}{\rho _{m}}}+\Delta \Phi \right)$

Le calcul des dérivées donne :

$\left(a{\frac {\partial ^{2}\delta }{\partial ^{2}t}}+{\frac {\partial a}{\partial t}}{\frac {\partial \delta }{\partial t}}\right)+H\left(a{\frac {\partial \delta }{\partial t}}\right)={\frac {1}{a}}\left({\frac {\Delta P}{\rho _{m}}}+\Delta \Phi \right)$

On divise alors par $a$ pour simplifier :

$\left({\frac {\partial ^{2}\delta }{\partial ^{2}t}}+H{\frac {\partial \delta }{\partial t}}\right)+H{\frac {\partial \delta }{\partial t}}={\frac {1}{a^{2}}}\left({\frac {\Delta P}{\rho _{m}}}+\Delta \Phi \right)$

On simplifie :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}={\frac {1}{a^{2}}}\left({\frac {\Delta P}{\rho _{m}}}+\Delta \Phi \right)$

L'équation de Poisson

Maintenant, nous allons traiter le terme lié à la gravité, à savoir le gradient du potentiel gravitationnel. Il est relié à la densité par la fameuse équation de Poisson, une forme alternative de la loi de la gravité de Newton que vous avez peut-être déjà étudié dans vos cours de physique. La voici :

$\Delta \Phi =4\pi G\rho$

En injectant la relation $\rho =\rho _{m}(1+\delta )$, on a:

$\Delta \Phi =4\pi G\rho _{m}(1+\delta )$

Si on linéarise l'équation, seul le terme proportionnel à $\delta$ est conservé, ce qui donne :

$\Delta \Phi =4\pi G\rho _{m}\delta$

On peut alors injecter cette équation dans l'équation finale de la section précédente, ce qui donne :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}={\frac {1}{a^{2}}}\left[{\frac {\Delta P}{\rho _{m}}}+4\pi G\rho _{m}\delta \right]$

La relation entre pression et densité

Il ne nous reste plus qu'à calculer le terme $\Delta P$. Il se trouve que, par définition du laplacien $\Delta$, celle-ci est simplement la dérivée seconde de la pression. Avant de calculer cette dérivée seconde, nous allons calculer la dérivée première, avant d'en déduire la dérivée seconde. De manière générale, la pression dépend de la densité et uniquement de celle-ci dans un gaz parfait et on a donc :

$dP={\frac {\partial P}{\partial \rho }}d\rho$

Fait intéressant, le terme ${\frac {\partial P}{\partial \rho }}$ est, par définition, proportionnel au carré de la vitesse du son $c_{s}$ dans le fluide considéré. En effet, les formules nous disent que pour un gaz parfait, on a la relation suivante :

$c_{s}^{2}=\gamma \cdot {\frac {P}{\rho }}={\frac {k_{B}T}{\mu }}$, avec $\gamma$ le coefficient d'expansion adiabatique.

Dans ce qui suit, on négligera le coefficient d'expansion adiabatique $\gamma$, en supposant qu'il vaut 1. En notant $\alpha$ le terme ${\frac {\partial P}{\partial S}}$ et $c_{s}$ la vitesse du son, on a :

$dP=c_{s}^{2}\cdot d\rho$

En dérivant une seconde fois, on trouve la dérivée seconde, qui n'est autre que le terme $\Delta P$ :

$\Delta P=c_{s}^{2}\cdot d^{2}\rho$

En injectant l'équation précédente dans l'équation d'Euler, on a :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}={\frac {1}{a^{2}}}\left[{\frac {c_{s}^{2}\cdot d^{2}\rho }{p_{m}}}+4\pi G\rho _{m}\delta \right]$

L'équation finale

En simplifiant l'équation précédente, on obtient l'équation finale :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}={\frac {1}{a^{2}}}\left[c_{s}^{2}\cdot d^{2}\delta +4\pi G\rho _{m}\delta \right]$

On peut voir que cette équation fait intervenir un terme ${\frac {\partial ^{2}\delta }{\partial ^{2}t}}$qui décrit à quelle vitesse l'inhomogénéité grandit. Les autres termes décrivent la manière dont la croissance de la perturbation va ensuite retentir sur sa pression et son champ de gravité.

• Le terme $c_{s}^{2}\cdot (\nabla ^{2}\delta )$ est un terme de pression hydrostatique. On voit que plus la perturbation est importante, plus sa pression tendra à repousser les flux entrants de masse, et dont à contrecarrer la croissance de la perturbation.
• Le terme : $4\pi G\rho _{m}\delta$ est un terme gravitationnel, qui dit que plus la perturbation est grande, plus elle sera massive et attirera de nouvelle matière. La perturbation va donc, sous l'influence de ce facteur seul, tendre à grossir de plus en plus, à une "accélération" constante.
• Enfin, le terme : $2H{\frac {\partial \delta }{\partial t}}$ décrit l'effet de dilution de la perturbation suite à l'expansion. L'expansion tend à diluer la perturbation dans un espace plus grand et donc à réduire celle-ci de plus en plus vite. Ce phénomène est appelé l'entraînement de Hubble. Il tend à lutter contre la croissance de la perturbation, du fait de son signe négatif.

Si les termes de pression et l’entraînement de Hubble étaient nuls, toute perturbation ne ferait que grossir de plus en plus vite. La moindre surdensité aurait une gravité supérieure à son entourage, ce qui attire de la matière et fait grossir la perturbation progressivement. Ce faisant, elle aurait une masse encore plus grande, ce qui augmenterait sa gravité, et ainsi de suite. La croissance d'une telle inhomogénéité serait exponentielle. Mais la pression et l’entraînement de Hubble limitent ce phénomène, dans une certaine mesure. Pour décrire plus en détail l'évolution des inhomogénéités, il faut étudier les solutions de l'équation précédente, qui disent ce qu'il advient des inhomogénéités. On pourra ainsi savoir si celle-ci vont se contracter ($\delta$ va augmenter), ou osciller. Tout le challenge tient dans le fait que nous avons étudié des perturbations ponctuelles, là où les grumeaux de matière cosmologiques ont une certaine taille, une extension spatiale. Il nous faut donc étudier ce qui se passe quand les grumeaux de matière/rayonnement ont une taille non-nulle.

L'évolution adiabatique et isotherme des perturbations

Dans les chapitres précédents, nous avons utilisé des équations où la densité était un terme unique. Celle-ci n'est autre que la densité d'énergie, qui est elle-même la somme de la densité de matière, du rayonnement et de la courbure. La courbure moyenne est considérée comme homogène, identique en tout point de l'univers. Les modifications locales de courbures sont causées par l'accumulation de matière et/ou de rayonnement, pas par une fluctuation locale de densité de courbure. Toute surdensité peut ainsi être une surdensité de matière et/ou de rayonnement.

$\rho (x,t)=\rho _{matiere}(x,t)+\rho _{rayonnement}(x,t)$

$\delta (x,t)=\delta _{matiere}(x,t)+\delta _{rayonnement}(x,t)$

Reste à expliquer comment les surdensités de matière sont liées avec les surdensités de rayonnement. Il existe plusieurs possibilités : soit les surdensités de matières sont liées à des surdensités de rayonnement, soit les surdensités de matières sont compensées par des sous-densités de rayonnement, soit les surdensités de matière et de rayonnement sont indépendantes. Ces trois possibilités sont étudiées dans des modèles théoriques différents, notamment dans l'étude de l'inflation ou de l'univers primordial. Dans ce qui va suivre, nous allons nous intéresser à deux types de perturbations, résumées dans le tableau ci-dessous.

Les types de perturbations

Nom	Description	Équations
Perturbations adiabatiques	Surdensité à la fois de matière et de rayonnement. Le rapport entre densité de rayonnement et de matière reste le même dans la surdensité et en-dehors. De même, l'entropie reste la même dans et en-dehors de la perturbation, ce qui fait qu'on donne parfois le nom d'isentropique donné à ce type de perturbation.	$\delta (x,t)=\delta _{matiere}(x,t)+\delta _{rayonnement}(x,t)$
Perturbations isothermes (d'isocourbure)	Les surdensités de matière sont compensées par une sous-densité de lumière. Du fait de cette compensation, la densité totale reste constante partout. En conséquence, la gravité/courbure reste la même dans la perturbation et dans son environnement, d'où le nom d'isocourbure donné à ce type de perturbation.	$\delta (x,t)=\delta _{matiere}(x,t)+\delta _{rayonnement}(x,t)=0$

Dans ce chapitre, nous allons voir que les perturbations adiabatiques rendent bien compte de l'état de la matière avant le découplage des photons, alors que le découplage a rendu les perturbations de matière et de rayonnement indépendantes.

Le rapport entre densités de matière et de rayonnement

Dans la suite du cours, nous allons avoir besoin du rapport entre densité de matière et de rayonnement avant et après le découplage pour rendre compte de ces perturbations. Dans les quatre premiers chapitres du cours, nous avons établit que :

$\rho (t)=\rho (t_{0})\cdot a(t)^{-3}$ pour la matière.

$\rho (t)=\rho (t_{0})\cdot a(t)^{-4}$ pour le rayonnement.

De ces équations, on peut déduire :

${\frac {p_{r}'}{p_{r}}}=4$ et ${\frac {p_{m}'}{p_{m}}}=3$

Les équations précédentes peuvent s'écrire comme suit :

$p_{r}'=4\cdot p_{r}$ et $p_{m}'=3\cdot p_{m}$

Il est intéressant d'utiliser le rapport suivant, pour simplifier certaines équations qui vont suivre :

$R={\frac {p_{m}'}{p_{r}'}}={\frac {3\cdot p_{m}}{4\cdot p_{r}}}$

La vitesse du son dans l'univers primordial

Pour calculer la vitesse du son, partons de sa définition :

$c_{s}^{2}={\frac {dP}{dp}}$

Sachant que l'univers primordial contient du rayonnement et de la matière (l'énergie noire n'a pas encore un effet notable), on a :

$c_{s}^{2}={\frac {dP_{r}+dP_{m}}{dp_{r}+dp_{m}}}$

La matière n'ayant pas de pression, la formule se simplifie en :

$c_{s}^{2}={\frac {dP_{r}}{dp_{r}+dp_{m}}}$

On peut ensuite utiliser la formule $P={\frac {pc^{2}}{3}}$ pour le rayonnement, ce qui donne :

$c_{s}^{2}={\frac {dp_{r}c^{2}/3}{dp_{r}+dp_{m}}}={\frac {c^{2}}{3}}{\frac {dp_{r}}{dp_{r}+dp_{m}}}$

On sait que $dp_{r}=4\cdot p_{r}$, $dp_{m}=3\cdot p_{m}$. En injectant dans l'équation précédente, on a :

$c_{s}^{2}={\frac {c^{2}}{3}}{\frac {4p_{r}}{4p_{r}+3p_{m}}}$

Divisons par $4p_{r}$ en haut et en bas de la fraction :

$c_{s}^{2}={\frac {c^{2}}{3}}{\frac {1}{1+(3p_{m}/4p_{r})}}$

On utilise alors le rapport R :

$c_{s}^{2}={\frac {c^{2}}{3}}{\frac {1}{1+R}}$

L'horizon sonore

Chaque zone de surdensité, supposée sphérique, a créé des ondes sonores dont le front d'onde a une forme sphérique. La taille maximale que peut prendre cette sphère dépend du temps écoulé depuis le big-bang et la recombinaison. La sphère de taille maximale correspond à une onde sonore créée lors du big-bang et figée lors de la recombinaison : c'est pour cela qu'on l'appelle l'horizon sonore. Le rayon de cette sphère se calcule en faisant l'intégrale de la vitesse du son dans le plasma primordial sur l'âge de l'univers au moment de la recombinaison.

$R_{s}=\int c_{s}(1+z)dt$

La vitesse du son dans un gaz de photons est égale à $c \over {\sqrt {3}}$. Elle augmente quelque peu du fait de la présence des baryons dans la réalité.

$R_{s}={\frac {c}{\sqrt {3}}}\int (1+z)dt$

Il se trouve que l'horizon sonore correspond à la longueur de l'onde sonore de plus grande amplitude possible : la surdensité a eu le temps maximal pour se compresser.

Prenons le cas où deux régions de l'espace sont à une distance inférieure à l'horizon sonore. Dans ce cas, une onde sonore a pût se transmettre de la première région à la seconde, avant la recombinaison. Dans le cas inverse, où les deux régions sont plus éloignées que l'horizon sonore, c'est l'inverse. On est certain que les deux régions sont trop éloignées pour qu'une onde sonore ait pu passer d'une région à l'autre.

Avant le découplage : les perturbations adiabatiques

Pour décrire le comportement de la matière et du rayonnement avant le découplage, il faut étudier les interactions entre matière ionisée et rayonnement. Avant le découplage des photons, les interactions entre photons et électrons libres étaient fréquentes, suffisamment pour redistribuer l'énergie des photons aux électrons (et réciproquement). Voyons dans le détail ces interactions, avant de voir leurs conséquences sur la densité de l'univers.

Le processus de diffusion Compton sans expansion

Illustration du processus de diffusion Compton.

Avant le découplage, le processus d'interaction principal était la diffusion Compton, ainsi que le processus inverse, la diffusion Compton inverse. Celle-ci est une collision entre un photon et un électron libre, où les deux particules échangent de la quantité de mouvement et de l'énergie cinétique.

Les physiciens rendent compte de la fréquence de ces collisions par deux paramètres : le temps moyen entre deux collisions et la distance moyenne entre deux collisions. Le temps moyen entre deux collisions est appelé le temps de libre parcours moyen, tandis que la distance moyenne entre deux collisions est appelée le libre parcours moyen. Évidemment, les deux sont liés entre eux par la vitesse des particules du gaz : la distance de libre parcours moyen est ainsi égale au produit de la vitesse moyenne par le temps de libre parcours moyen. Ainsi, plus un gaz est froid, plus le temps et la distance entre deux collisions sont faibles. Il en est de même pour les gaz denses : ceux-ci ont un libre parcours moyen assez faible, vu que les particules sont plus proches.

Il est possible de calculer le libre parcours moyen en utilisant une relation très simple entre celui-ci et deux autres variables : le nombre de particules par unités de volume et la probabilité moyenne d'une collision. Le nombre de particules par unité de volume remplace en quelque sorte la densité : plus il y a de particules par unité de volume, plus celles-ci ont de chances d'entrer en collision. Quant à la probabilité d'une collision, elle se calcule à partir des équations de la diffusion Compton. Nous ne ferons pas ces calculs ici, d'autres articles sur la diffusion Compton le feront certainement mieux que moi. Elle se calcule avec la formule suivante, avec $\alpha$ la constante de structure fine et $m_{e}$ la masse d'un électron.

$\sigma ={\frac {8\pi \alpha ^{2}}{2m_{e}^{2}}}$

Le libre parcours moyen est égal, par définition, à l'équation suivante :

$\lambda _{t}={\frac {1}{n_{e}\sigma }}$, avec $\lambda _{t}$ le libre parcours moyen, $n_{e}$ le nombre d'électrons par unité de volume et $\sigma$ la probabilité d'interaction Compton entre deux particules.

Le temps de libre parcours moyen se calcule en divisant cette distance par la vitesse d'un photon, ce qui donne :

$T={\frac {1}{cn_{e}\sigma }}$

Avec expansion, les équations de la diffusion Compton change un petit peu. Avec l'expansion, le libre parcours moyen va naturellement augmenter, à cause de l'évolution du facteur d'échelle. On peut remarquer que l'expansion n'influence pas la section efficace d'interaction Compton : son influence se fait sur la densité des électrons, qui diminue d'un facteur $a^{3}$ avec l'expansion. Suite à l'expansion, il arrive un moment où le libre parcours moyen devient plus grand que l'horizon cosmologique, que l'univers observable. Lorsque cela arrive, la diffusion Compton entre un photon du CMB et un électron libre devient "impossible", ou tout du moins fortement improbable. Les photons cessent d'interagir complètement avec les électrons libres, qui sont alors libres de former des atomes avec les noyaux. C'est ainsi qu'à lieu le découplage. Et cela a des conséquences sur l'évolution des perturbations.

Avant le découplage, les perturbations étaient adiabatiques, isentropiques. La diffusion Compton redistribuait la quantité de mouvement entre matière et rayonnement, et le couplage fort liait les densités de photons et de baryons entre elles. Du fait des interactions entre rayonnement et matière, le rayonnement restait prisonnier des surdensités de matière. Là où il y avait de la matière, le rayonnement devait suivre. Ne pouvant s'échapper sous forme de rayonnement, la chaleur restait coincée dans les surdensités. La chaleur ne pouvant s'échapper, l'entropie reste constante dans ces perturbations adiabatiques. Ce n'est qu'après le découplage des photons que la matière et le rayonnement ont commencé à évoluer indépendamment l'une de l'autre. Le rayonnement a pu alors quitter les zones de surdensité, vu qu'il n'interagissaient plus avec elles, et échanger de la chaleur avec l'environnement. Le rayonnement s'est progressivement dilué dans l'espace, alors que les surdensités de matière sont restées, donnant des perturbations de matière pure. Les perturbations ne sont alors ni isothermes, ni adiabatiques.

L'approximation du couplage fort

La diffusion Compton ne faisait pas que redistribuer la quantité de mouvement : elle couplait aussi fortement le nombre de photons et de baryons. Si on prenait un volume d'espace fini, le nombre de photons et de baryons ne différait pas sensiblement l'un de l'autre. Il y avait bien quelques variations ci et là, mais on peut parfaitement supposer qu'en moyenne, le nombre de particules par unité de volume était le même pour les photons et les baryons. Le résultat est ce qu'on appelle l'approximation du couplage fort : le nombre de baryons et de photons dans un volume d'espace fini est approximativement le même. La densité de baryon et de rayonnement étaient alors fortement liés par une relation que nous allons démontrer.

L'approximation du couplage fort nous dit que, avec $n_{r}$ et $n_{b}$ le nombre de photons et de baryons par unité de volume, on a :

$n_{r}=n_{b}$

On sait de plus que $n_{r}\propto {\frac {p_{r}}{a^{4}}}$ et que $n_{b}\propto {\frac {p_{b}}{a^{3}}}$, ce qui donne :

$4\cdot p_{r}=3\cdot p_{m}$

Ces informations nous sont utiles pour calculer la vitesse du son. Pour rappel, la vitesse du son se calcule avec la formule suivante :

$c_{s}^{2}={\frac {c^{2}}{3}}{\frac {1}{1+(3p_{m}/4p_{r})}}$

En combinant les deux équations précédentes, on trouve :

$c_{s}^{2}={\frac {c^{2}}{6}}$

Après le découplage : les perturbations isothermes et leur évolution

Après le découplage, la matière et le rayonnement ne sont plus couplées. Les densités de matière et de rayonnement deviennent indépendantes l'une de l'autre et évoluent chacun dans leur coin. Elles suivent alors les relations vues dans les premiers chapitres :

$p_{m}=p_{m0}{\frac {1}{a^{3}}}$

$p_{r}=p_{r0}{\frac {1}{a^{4}}}$

Une vitesse du son en chute libre

Rappelons que la vitesse du son est la suivante :

$c_{s}^{2}={\frac {c^{2}}{3}}{\frac {1}{1+R}}$, avec $R={\frac {3p_{m}}{4p_{r}}}$.

Calculons le rapport R :

$R={\frac {3}{4}}{\frac {p_{m}}{p_{r}}}={\frac {3}{4}}{\frac {p_{m0}\cdot a^{-3}}{p_{r0}\cdot a^{-4}}}={\frac {3\cdot p_{m0}}{4\cdot p_{r0}}}\cdot a=R_{0}\cdot a$

En combinant les deux équations précédentes, on trouve :

$c_{s}^{2}={\frac {c^{2}}{3}}{\frac {1}{1+R_{0}\cdot a}}$

L'équation précédente dit que la vitesse du son diminue avec l'expansion, du moins après le découplage.

On peut s'en rendre compte avec l'approximation $R_{0}\cdot a>>1$, qui transforme l'équation précédente en :

$c_{s}^{2}\approx {\frac {c^{2}}{3}}{\frac {1}{R_{0}\cdot a}}$

Si on attend suffisamment longtemps après le découplage, le facteur d'échelle sera devenu suffisamment grand pour que l'on ait : ${\frac {1}{R_{0}\cdot a}}\approx 0$. On obtient alors :

$c_{s}^{2}\approx 0$

La réduction de la vitesse du son n'est pas sans conséquences sur la formation des perturbations et leur évolution. En effet, les ondes sonores sont en effet des ondes de pression (compression/décompression). Elles naissent quand la pression varie en un point d'un objet et transmettent cette variation aux alentours. La vitesse du son est aussi la vitesse de transmission des forces de pression. Or, la pression est ce qui permet de lutter contre la gravité dans les surdensités. Si la vitesse de transmission de la pression est trop faible, les forces de gravité peuvent l'emporter sur la pression dans certaines circonstances. Une surdensité peut ainsi s'effondrer si les ondes de pression sont trop lentes et ne permettent pas de lutter assez rapidement contre leur contraction gravitaire.

L'évolution des perturbations avant le découplage

Dans ce chapitre, nous allons utiliser la décomposition en séries de Fourier du champ de densité. Celle-ci décrit le champ de densité comme la somme/intégrale d'une infinité d'ondes périodiques simples. Si on note chaque onde élémentaire ${\overline {\delta }}(x,t)$, le théorème de Fourier nous donne l'équation suivante :

$\delta (x,t)={\frac {1}{(2\pi )^{3}}}\int {\overline {\delta }}({\vec {k}})\cdot e^{-i({\vec {k}}\cdot {\vec {x}})}d{\vec {k}}$, avec ${\vec {k}}$ le vecteur d'onde, un vecteur de norme $k={\frac {2\pi }{\lambda }}$.

On peut alors combiner cette équation avec l'équation suivante, dérivée il y a quelques chapitres :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}={\frac {1}{a^{2}}}\left[c_{s}^{2}\cdot d^{2}\delta +4\pi G\rho _{m}\delta \right]$

On peut combiner les deux équations. Le résultat, très difficile à obtenir, est pourtant surprenamment simple :

${\frac {\partial ^{2}{\overline {\delta }}(k)}{\partial ^{2}t}}+2H{\frac {\partial {\overline {\delta }}(k)}{\partial t}}-{\frac {1}{a^{2}}}\left[c_{s}^{2}k^{2}+4\pi G\rho _{m}\right]{\overline {\delta }}(k)=0$

L'équation différentielle précédente ressemble formellement à une équation d'oscillateur harmonique amorti. On rappelle qu'un oscillateur harmonique est un système soumis à une force de rappel proportionnelle à la distance : $F_{r}=k\cdot x(t)$. La force de rappel est ici la somme de la pression et de la gravité, qui poussent le système à osciller de manière périodique. Pour obtenir un système amorti, il faut ajouter un terme de friction, qui tend à réduire l'amplitude des oscillations au fil du temps. Ici, la force de friction est le poids des baryons, qui force le système à se compresser. La forme générale d'une équation d’oscillateur harmonique est la suivante :

${\frac {d^{2}A}{d^{2}t}}+2\lambda {\frac {dA}{dt}}+\omega ^{2}A=0$

On voit que les deux équations précédentes sont identiques si on pose : $A=\delta (x,t)$, $\lambda =H$ et $\omega ^{2}=-{\frac {1}{a^{2}}}\left[c_{s}^{2}k^{2}+4\pi G\rho _{m}\right]$.

Les solutions de cette équation sont de la forme :

${\overline {\delta }}(k)=A\cdot e^{r_{1}t}+B\cdot e^{r_{2}t}$, avec $r_{1}$ et $r_{2}$ les solutions de l'équation du second degré $r^{2}+2\lambda r+\omega ^{2}=0$.

Le comportement de la solution dépend selon la valeur des racines. On distingue trois cas, qui sont décrits dans le tableau ci-dessous.

	Discriminant	Interprétation dans l'équation du fluide cosmologique
Cas périodique amorti	Le discriminant de l'équation du second degré est positif.	La pression et la gravité se compensent l'une l'autre.
Cas apériodique	Le discriminant de l'équation du second degré est négatif.	La pression est plus forte que la gravité.
Cas critique	Le discriminant de l'équation du second degré est nul.	La gravité est plus forte que la pression.

Nous allons voir chaque cas l'un après l'autre.

Le cas stable : la distance de Jeans

Lorsque la pression est égale à la gravité, on a :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}=0$

Cette équation dit simplement que la perturbation est stable : elle s'accentue au même rythme que l'expansion la dilue (terme d’entraînement de Hubble). En clair : la perturbation est stable et ne change pas. Mais rappelons-le, cela n'arrive que pour une longueur d'onde précise, appelée rayon de Jeans. Cette longueur d'onde donne la taille de la surdensité pour laquelle la perturbation se stabilise. Cela fonctionne pour les perturbations sphériques, même si elles ne sont pas périodiques (la magie des fonctions de Fourier...).

Le rayon de Jeans

Le rayon de Jeans se calcule comme suit :

$(c_{s}k)^{2}=4\pi G\rho _{m}$

On utilise alors l'équation $k={\frac {2\pi }{\lambda }}$ :

$\left({\frac {2\pi c_{s}}{\lambda }}\right)^{2}=4\pi G\rho _{m}$

On développe le carré :

${\frac {4\pi ^{2}c_{s}^{2}}{\lambda ^{2}}}=4\pi G\rho _{m}$

Simplifions par $4\pi ^{2}c_{s}^{2}$ :

${\frac {1}{\lambda ^{2}}}={\frac {G\rho _{m}}{\pi c_{s}^{2}}}$

Prenons l'inverse de l'équation précédente :

$\lambda ^{2}={\frac {\pi c_{s}^{2}}{G\rho _{m}}}$

Prenons la racine carrée :

$\lambda ={\sqrt {\frac {\pi c_{s}^{2}}{G\rho _{m}}}}$

Simplifions :

$\lambda =c_{s}{\sqrt {\frac {\pi }{G\rho _{m}}}}$

Démonstration

On peut donner une autre démonstration du rayon de Jeans. Pour cela, imaginons une surdensité sphérique et homogène de rayon $R$ et de masse $M$. Et prenons le cas où il n'y a aucune force de pression. Toute surdensité va alors s'effondrer sur elle-même en mettant un certain temps, que l'on va appeler temps d'effondrement. Les équations de la physique classique disent que ce temps est proportionnel à : $t_{collapse}={\frac {1}{\sqrt {G\rho }}}$ Maintenant, ajoutons les forces de pression, dont on suppose qu'elles contrecarrent totalement la gravité. La transmission des forces de pression se fait à la même vitesse que le son. Une surdensité ne peut pas s'effondrer si le temps d'effondrement est égal au temps que met la pression pour parcourir la surdensité. Dit autrement, une surdensité s'effondre sur elle-même si : $t_{pression}>t_{collapse}$ Pour une surdensité de rayon $R$ et une vitesse $c_{s}$ pour la pression, le temps de parcours vaut : $t_{pression}={\frac {R}{c_{s}}}$ En combinant les deux équations précédentes, on a: ${\frac {R}{c_{s}}}>{\frac {1}{\sqrt {G\rho }}}$ On peut alors calculer le rayon R, appelé rayon de Jeans. Celui-ci est simplement le rayon au-delà duquel la surdensité ne peut pas s'effondrer sur elle-même. $R>{\frac {c_{s}}{\sqrt {G\rho }}}$

L'évolution du rayon de Jeans avant et après le découplage

Les calculs précédents nous disent que le rayon de Jeans dépend de la vitesse du son. Or, rappelez-vous que la vitesse du son dépend du rapport $R={\frac {3p_{m}}{4p_{r}}}$. La relation exacte est la suivante :

$c_{s}^{2}={\frac {c^{2}}{3(1+R)}}$

Avant le découplage, le rapport R vaut 1, et ce durant toute la période avant le découplage. La vitesse du son est constante et le rayon de Jeans fait de même.

Mais après le découplage, le rapport R diminue progressivement et la vitesse du son évolue comme ceci :

$c_{s}^{2}\approx {\frac {c^{2}}{3R_{0}}}{\frac {1}{a}}$

Cela impacte le rayon de Jeans, qui évolue avec le facteur d'échelle et donc avec l'expansion. Celui-ci se calcule alors comme suit :

$\lambda ^{2}={\frac {\pi }{G\rho _{m}}}{\frac {c_{0}^{2}}{3R_{0}}}{\frac {1}{a}}$

Ou encore :

$\lambda \approx c{\sqrt {\frac {\pi }{3G\rho _{m}R_{0}}}}{\frac {1}{\sqrt {a}}}$

Ce qui se simplifie en :

$\lambda \propto {\frac {1}{\sqrt {a}}}$

On voit que le rayon de Jeans diminue avec l'expansion.

Le cas où G > P : la croissance/décroissance infinie

Prenons maintenant une perturbation dont la taille est supérieure à la longueur de Jeans, où la gravité l'emporte sur la pression. Il n'y a qu'une seule solution à cette équation différentielle, qui est de la forme :

$\delta (x,t)=Ae^{r_{1}t}+Be^{-r_{2}t}$

On voit que cette solution est la somme de deux solutions particulières :

• la première est une fonction $\delta (x,t)=Ae^{r_{1}t}$, strictement croissante ;
• la seconde est une fonction $\delta (x,t)=Be^{-r_{2}t}=B{\frac {1}{e^{r_{2}t}}}$, strictement décroissante.

Dit autrement, toute structure d'une taille supérieure au rayon de Jeans va soit s'effondrer sur elle-même sous l'effet de sa propre gravité, soit gonfler à cause de l'expansion.

Le cas où P < G : les oscillations acoustiques de baryons

Une perturbation dont la taille est inférieure au rayon de Jeans correspond au cas amorti. Dans celui-ci, la solution de l'équation est une fonction d'onde de la forme :

$\delta (x,t)=\left[\delta (x,t_{0})+(1+R)\Phi \right]\cos {(kr_{s})}+{\frac {1}{kr_{s}}}\sin {(kr_{s})}-(1+R)\Phi$

Illustration de l’oscillation de densité - équation d'un oscillateur harmonique amorti.

L'équation n'a que des solutions ondulatoires dont l'amplitude diminue au cours du temps. Dit autrement, la perturbation pulse, elle grossit avant de dégonfler et ainsi de suite, indéfiniment. On peut interpréter cette solution physiquement comme suit. Sous l'effet de la gravité, de petites zones de surdensités vont se former et vont se contracter sous l'effet de la gravité. Cette contraction va réchauffer la matière dans la zone de surdensité, ce qui en augmentera la pression de radiation (on néglige totalement la pression de la matière baryonique). Cette pression luttera contre la force de gravité, forçant la surdensité à gonfler et à se dilater. Cette dilatation fait chuter sa température, et sa pression fait alors de même. La gravité reprend alors ses droits, en devenant plus forte que la pression, et un nouveau cycle commence.

Ce gonflement/dégonflement périodique de la surdensité va retentir sur son environnement : elle va former des ondes de compression/décompression qui se propagent dans le plasma primordial. Ces ondes ne sont autres que des ondes sonores ! En clair : l'évolution des inhomogénéités cause des ondes sonores primordiales, aussi appelées oscillations acoustiques de baryons.

Lors du découplage, ces ondes sonores se sont figées, les photons n'agissant plus sur la matière. La pression de radiation reste la même, mais celle-ci influence relativement peu la matière, laissant la gravité faire son travail. Ne pouvant plus contrecarrer la gravité, la pression de radiation cesse de donner naissance aux oscillations acoustiques de baryons. Les zones de surdensité cessent d’osciller et s'effondrent sur elles-mêmes, donnant naissance à diverses structures : de futures galaxies pour les surdensités de grande échelle, notamment. Cependant, on trouve encore une trace des oscillations acoustiques de baryons dans le fond diffus cosmologique. On verra que ces oscillations acoustiques de baryons ont laissé de petites perturbations de température dans le fond diffus. Nous en reparlerons dans le prochain chapitre.

L'évolution des perturbations après le découplage

Dans ce chapitre, nous allons étudier ce qui se passe après le découplage. Pour cela, on repart de l'équation habituelle :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}={\frac {1}{a^{2}}}\left[c_{s}^{2}\cdot d^{2}\delta +4\pi G\rho _{m}\delta \right]$

On a vu il y a deux chapitres que, après le découplage, le terme dépendant de la vitesse du son disparaît. L'équation précédente devient alors :

${\frac {\partial ^{2}\delta }{\partial ^{2}t}}+2H{\frac {\partial \delta }{\partial t}}-{\frac {1}{a^{2}}}\left[4\pi G\rho _{m}\cdot \delta \right]=0$

La raison à cela est assez simple à comprendre. Vu que la matière n'a par définition pas de pression, seul le rayonnement est à l'origine du terme de pression dans l'équation originale. Après le découplage, le rayonnement se dilue avec l'expansion et la pression diminue donc. Au bout d'un moment, la pression disparaît. Par contre, même si la matière n'a pas de pression, elle a une masse qui influence l'évolution des perturbations, de par sa gravité. Le terme de gravité reste donc, alors que le terme de pression s'annule.

Dans ce chapitre, nous allons voir quelle est la dynamique de cette équation, ce qui nous enseignera comment les perturbations ont été affectées par l’expansion.

Une croissance/décroissance linéaire

L'équation différentielle précédente n'a aucun coefficient dépendant des coordonnées spatiales, sans compter qu'il n'y a pas de dérivées par rapport à ces coordonnées. Seul le terme $\delta$ dépend des coordonnées spatiales. Dans ce cas, on est assuré par les lois mathématiques que la solution est égale au produit de delta par un terme indépendant des coordonnées spatiales. Par contre, ce terme dépend du temps, vu que les dérivées et les coefficients dépendent du temps. On a donc une solution de la forme :

$\delta (x,t)=D(t)\times {\delta }(x,t_{0})$

L'équation a précisément deux solutions qui ont une croissance ou décroissance linéaire. Mais la solution décroissante peut être oubliée et l'on peut se concentrer sur la solution croissante. Celle-ci nous dit qu'après le découplage, les inhomogénéités gonflent au même rythme que l'expansion. En coordonnées comobile, leur forme est restée figée après le découplage, sans aucune modification autres que celles liées à l'expansion.

En injectant cette solution croissante, l'équation originale devient :

${\frac {\partial ^{2}(D(t)\times \delta (x))}{\partial ^{2}t}}+2H{\frac {\partial (D(t)\times \delta (x))}{\partial t}}-4\pi G\rho _{m}\cdot D(t)\cdot \delta (x)=0$

Le terme $\delta (x)=\delta (x,t_{0})$ étant indépendant du temps, il est une constante du point de vue des dérivées temporelles. On peut donc le sortir des dérivées, ce qui donne :

$\delta (x){\frac {\partial ^{2}D(t)}{\partial ^{2}t}}+2H\delta (x){\frac {\partial D(t)}{\partial t}}-4\pi G\rho _{m}\delta (x)\cdot D(t)=0$

On divise alors par $\delta (x)$ :

${\frac {\partial ^{2}D(t)}{\partial ^{2}t}}+2H{\frac {\partial D(t)}{\partial t}}-4\pi G\rho _{m}\cdot D(t)=0$

Ce qui peut d’écrire d'une manière plus succincte comme suit :

${\ddot {D}}(t)+2H\cdot {\dot {D}}(t)-4\pi G\rho _{m}\cdot D(t)=0$

Les cas particuliers : univers dominé par la matière, le rayonnement ou l'énergie noire

Formellement, la fonction $D$ correspond à la vitesse de croissance des structures. On peut démontrer qu'elle est proportionnelle au facteur d'échelle dans un univers de densité critique (Einstein-de Sitter) :

$D(t)\propto a(t)$

On peut alors comparer la vitesse de croissance entre un univers dominé par la matière, un autre dominé par le rayonnement et un dernier dominé par l'énergie noire. Petit détail : on pourrait croire que le passage d'univers dominé par le rayonnement à un univers dominé par la matière correspond à peu-près au découplage. Il correspond à l'égalité de la densité d'énergie de la matière et du rayonnement (donc le moment de passage d'un univers dominé par le rayonnement à un univers de matière). Mais dans les faits, cette intuition est mise en défaut. Les deux sont en réalité séparés par une durée qui dépend du modèle d'univers considéré.

A l'heure actuelle, on estime que le point de bascule a eu lieu il y a environ 47000 ans après le big-bang. Soit bien avant les 380.000 ans du découplage. Le découplage a donc eu lieu dans un univers dominé par la matière, cas que nous allons voir dans ce qui suit.

L'univers dominé par la matière

Pour l'univers de densité critique (Einstein-de Sitter), les équations vues dans le chapitre sur les modèles cosmologiques de Friedmann-Lemaître nous disent que :

$p_{m}(t)=a^{-3}\cdot p_{\text{critique}}(t)={\frac {3H^{2}}{8\pi G}}{\frac {1}{t^{2}}}$

$a(t)=t^{\frac {2}{3}}$

$H(t)={\frac {2}{3}}$

Rappelons l'équation originale :

${\ddot {D}}(t)+2H\cdot {\dot {D}}(t)-4\pi G\rho _{m}\cdot D(t)=0$

Injectons l'équation $p_{m}(t)=a^{-3}\cdot p_{\text{critique}}(t)={\frac {3H^{2}}{8\pi G}}{\frac {1}{t^{2}}}$ :

${\ddot {D}}(t)+2H\cdot {\dot {D}}(t)-4\pi G\cdot {\frac {3H^{2}}{8\pi G}}{\frac {1}{t^{2}}}\cdot D(t)=0$

Simplifions par $4\pi G$ :

${\ddot {D}}(t)+2H\cdot {\dot {D}}(t)-{\frac {3}{2}}{\frac {H^{2}}{t^{2}}}\cdot D(t)=0$

Puis, injectons l'équation $H(t)={\frac {2}{3}}$ :

${\ddot {D}}(t)+2\cdot {\frac {2}{3}}\cdot {\dot {D}}(t)-{\frac {3}{2}}\left({\frac {2}{3}}\right)^{2}{\frac {1}{t^{2}}}\cdot D(t)=0$

Simplifions :

${\ddot {D}}(t)+{\frac {4}{3}}\cdot {\dot {D}}(t)-{\frac {2}{3}}{\frac {1}{t^{2}}}\cdot D(t)=0$

En supposant que $D\propto t^{p}$, on a :

$(t^{p})''+{\frac {4}{3}}\cdot (t^{p})'-{\frac {2}{3}}{\frac {t^{p}}{t^{2}}}=0$

En calculant les dérivées, on trouve :

$p(p-1)t^{p-2}+{\frac {4}{3}}pt^{p-1}-{\frac {2}{3}}t^{p-2}=0$

On divise par $t^{p-2}$ :

$p(p-1)+{\frac {4}{3}}p\cdot t-{\frac {2}{3}}=0$

Les deux solutions possibles sont respectivement $p=-1$ et $p={2 \over 3}$. La première correspond à des fluctuations qui décroissent avec le temps, la seconde est plus intéressante. En injectant dans $D\propto t^{p}$, on trouve :

$D_{+}\propto t^{\frac {2}{3}}$

L'évolution de la matière

Dans le chapitre précédent, nous avons vu que les équations de Friedmann relient le facteur d'échelle ou le facteur de Hubble, avec la densité de l'univers et sa pression. Pour simplifier ces équations, nous avons supposé que le contenu de l'univers est régit par les lois de la thermodynamique, ce qui fait que son contenu est décrit par un ensemble de plusieurs équations d'état, qui relient sa pression, sa densité, sa température, etc. Et justement, une de ces équations d'état relie la densité et la pression, qui permet d'éliminer un terme des équations de Friedmann, de les simplifier. Mais il existe beaucoup d'autres équations d'état, qui permettent de comprendre comment la pression et la température de l'univers a évolué avec le temps. Elles permettent notamment de comprendre l'historique thermique de l'univers, comment sa température à évolué dans le temps.

Reste à justifier que le contenu de l'univers primordial est bien régit par les lois de la thermodynamique. Pour le moment, nous savons que l'univers est peuplé de matière et de rayonnement. La matière est essentiellement composée de particules massives : baryons, quarks, électrons, etc. Pour plus de simplicité, on peut supposer que la matière de l'univers est un gaz. Cette hypothèse n'est pas si abusive vu l'état actuel de l'univers : 10% de la matière sert à fabriquer des étoiles, le reste étant localisé dans des nébuleuses et des nuages moléculaires dont la température ne dépasse pas la dizaine de degrés au-dessus du zéro absolu.

L'univers est donc essentiellement composé de gaz, le rayonnement n'étant qu'un gaz de photons, comme on le verra dans le prochain chapitre. Évidemment, ce gaz de matière a une pression, un volume, une densité, une énergie, etc. Il reste de plus soumis aux lois de la thermodynamique. L'expansion va cependant faire varier continument sa densité (l'univers se dilue avec l'expansion), sa pression, sa température, etc. Dans ce chapitre, nous allons voir comment évolue ce gaz cosmologique en utilisant les relations de la thermodynamique, sous la contrainte de la loi de Hubble.

Rappels sur le gaz parfait

Dans ce chapitre, et dans tous les chapitres suivants, nous allons supposer que la matière qui remplit l'univers est ce qu'on appelle un gaz parfait. Pour rappel, un gaz parfait est un gaz qui respecte la loi suivante :

$PV=N\cdot k_{B}T$, avec P la pression, V le volume, N le nombre de particules, T la température et $k_{B}$ la constante de Boltzmann.

La densité de particules

On peut simplifier cette équation en utilisant la densité de particule, à savoir la quantité de particule présente par unité de volume, qui sera notée $\epsilon$. Si on note V un volume et N le nombre de particules qu'il y a dedans, la densité de particules est définie par la formule suivante :

$\epsilon ={\frac {N}{V}}$

En combinant les deux équations précédentes, on a :

$P=\epsilon \cdot k_{B}T$, avec $\epsilon$ la densité de particules.

L'expansion affecte surtout les termes de droite, à savoir la densité de particule et la température. Cette influence se répercute ensuite sur la pression. Notons que cette équation fonctionne pour un gaz d'atomes, de molécules, mais aussi pour décrire le rayonnement, la lumière, qui n'est autre qu'un gaz parfait de photons ! Mais avant d'étudier le cas du rayonnement, ce qui sera le fait du prochain chapitre, nous allons étudier le cas d'un gaz parfait composé de matière, de particules avec une masse, soumis à l'expansion.

L'énergie moyenne par particule d'un gaz parfait

La température d'un gaz parfait est la somme des énergies cinétiques de chaque particule. La physique statistique nous donnent des formules pour relier la température et l'énergie cinétique moyenne d'une particule du gaz. Les formules en question dépendent du gaz, mais elles prennent toutes la forme d'une équation de la forme :

$E=k\cdot PV$

$E=k\cdot N\cdot k_{B}T$

Le coefficient $k$ est appelé la capacité calorifique spécifique à volume constant. C'est l'énergie qu'il faut pour augmenter d'un degré la température du gaz, en considérant que son volume et sa masse sont constantes. La capacité calorifique est considérée comme constante avec un gaz parfait. Mais dans le monde réel, elle n'est pas totalement constante et peut varier suivant la température et la pression. Les variations les plus soudaines de la capacité calorifique impliquant souvent des transitions de phase elles-mêmes liées à des baisses/hausses de température.

A partir de l'équation précédente, on peut calculer la densité d'énergie et l'énergie moyenne par particule. L'énergie moyenne par particule se calcule en divisant l'équation précédente par N, ce qui donne :

${E \over N}=k\cdot k_{B}T$

En supposant que la capacité calorifique est constante, on peut reformuler cette équation comme suit :

${E \over N}\propto T$

La densité d'énergie d'un gaz parfait

Partons maintenant de la formule suivante :

$E=k\cdot PV$

La formule précédente, une fois divisée par le volume, donne ceci :

${E \over V}=k\cdot P$

La densité d'énergie est notée $\rho$ :

$\rho _{e}=k\cdot P$

En clair, la densité d'énergie, l'énergie moyenne par unité de volume, est proportionnelle à la pression. On peut aller plus loin en reformulant l'équation précédente en inversant la relation, ce qui donne la pression en fonction de la densité d'énergie :

$P={\frac {\rho _{e}}{k}}$

Les équations d'état de la matière en relativité

Au début du big-bang, les particules allaient très vite, leur énergie cinétique était très importante. Puis, avec le refroidissement de l'univers, les particules ont perdu en vitesse, leur énergie cinétique a chuté. Le truc est que les lois de la thermodynamique et de la physique statistique disent que les particules se comportent différemment entre la haute et basse énergie. Les physiciens utilisent des équations approximées qui sont différentes pour la haute énergie.

Les régimes non-relativiste, relativiste, et ultra-relativiste

Aussi, pour simplifier les choses, les physiciens distinguent trois régimes, dans lesquels les équations ne sont pas exactement les mêmes. La différence entre les trois régimes se fait en comparant l'énergie de masse de la particule avec son énergie cinétique. En notant $E_{m}$ l'énergie de masse et $E_{c}$ l'énergie cinétique, on a donc :

• Le régime non-relativiste est celui où l'énergie de masse est bien plus grande que l'énergie cinétique : $E_{m}>>E_{c}$.
• Le régime relativiste est celui où l'énergie de masse est proche l'énergie cinétique : $E_{m}\approx E_{c}$.
• Le régime ultra-relativiste est celui où l'énergie cinétique est bien plus grande que l'énergie cinétique : $E_{m}<<E_{c}$.

La matière usuelle, fait d'atomes, est dans le régime non-relativiste. A l'inverse, le cas ultra-relativiste extrême est celui des photons, qui n'ont pas d'énergie de masse. Toute l'énergie est alors de l'énergie cinétique. Le rayonnement est donc le cas parfait de particule en régime ultra-relativiste. Pour eux, on a :

$E_{c}=p\cdot c$, avec p l'impulsion, la quantité de mouvement relativiste égale à $p=mv\cdot \gamma$.

Le cas intermédiaire ne nous intéressera pas dans les prochains chapitres. En effet, les premiers instants de l'univers, les premières heures, les premières semaines, se sont déroulées dans le régime ultra-relativiste. La température était tellement élevée que les particules avaient une énergie cinétique énorme, dans lesquelles l'énergie de masse était ridiculement petit en comparaison.

En cosmologie, il est souvent fait l'abus de langage suivant : on appelle rayonnement toute particule en régime ultra-relativiste. Même si la particule en question est un proton, un neutron, un électron, ou toute autre particule matérielle avec une masse. A l'inverse, on appelle matière toute particule en régime non-relativiste. Le cas relativiste est quelque peu ignoré ou ambigu.

Les équations d'état d'un gaz ultra-relativiste

Peu après le big-bang, l'univers était remplit d'un gaz de particules ultra-relativistes. Aussi, pour décrire l'évolution de l'univers, il nous faut connaitre les équations qui gouvernent les gaz ultra-relativistes. Nous allons simplement vous donner les équations et les commenter, sans en donner de démonstrations, qui appartiennent plus à un cours de physique statistique quantique relativiste, ce qui n'est pas pour tout le monde.

Pour un gaz ultra-relativiste, on peut prouver que les relations du gaz parfait fonctionnent toujours. Un gaz ultra-relativiste parfait respectera toujours les relations de la thermodynamique usuelles. Cela simplifie grandement les choses, on sait qu'on peut se baser sur la relation suivante :

$PV=N\cdot k_{B}T$

De plus, on sait que la relation suivante est elle-aussi valide :

$E=k\cdot N\cdot k_{B}T$

Pour un gaz de photons, on peut prouver que $k=3$, soit le double de ce qu'on a pour un gaz non-relativiste mono-atomique pour lequel on a $k={\frac {3}{2}}$. En mélangeant les deux équations précédentes en utilisant $k=3$ ou $k={\frac {3}{2}}$, on peut déduire un ensemble d'équations, qui sont résumées dans le tableau suivant :

	Gaz non-relativiste mono-atomique	Gaz ultra-relativiste	Gaz de photon (rayonnement)
Énergie interne	${\frac {3}{2}}\cdot N\cdot k_{B}T$	$\approx 3\cdot N\cdot k_{B}T$	$3\cdot N\cdot k_{B}T$
Densité de particules	${\frac {3}{2}}\cdot k_{B}T$	$\approx 3\cdot k_{B}T$	$3\cdot k_{B}T$
Densité d'énergie	${\frac {3}{2}}\cdot \epsilon \cdot k_{B}T$ (densité d'énergie)	$\approx 3\cdot \epsilon \cdot k_{B}T$ (densité d'énergie)	$3\cdot \epsilon \cdot k_{B}T$ (densité d'énergie)
Pression	${\frac {3}{2}}\cdot \rho _{e}$	$\approx {\frac {1}{3}}\cdot \rho _{e}$	${\frac {1}{3}}\cdot \rho _{e}$

On voit qu'entre un gaz non-relativiste et un gaz de photons, la différence est un simple a un facteur 2 introduit dans les équations, mais que les équations ne changent pas au-delà de ça. Pour un gaz ultra-relativiste, k est proche de 3 et l'est d'autant plus que la température est élevée. Les relations d'un gaz de photon sont donc valide, mais seulement en tant qu'approximation.

Dans la suite de ce chapitre, nous allons expliquer plus en détail quelles sont les conséquences de cela.

L'expansion adiabatique d'un gaz ultra-relativiste

Maintenant, prenons un gaz ultra-relativiste stocké dans un réservoir fermé. Le réservoir est tel que la chaleur ne peut pas s'en échapper, il n'y a pas d'échange d'énergie thermique entre extérieur et intérieur du réservoir. Maintenant, augmentons progressivement le volume du réservoir, en bougeant ses parois. On fait en sorte que lors de l'expansion du réservoir, aucun échange de chaleur n'ai lieu entre intérieur et extérieur, pas d'échange d'énergie thermique. Une telle expansion est appelée une expansion adiabatique. Il s'agit d'un processus étudié dans les cours de thermodynamique, et on peut prouver que lors d'une telle expansion, le produit suivant reste constant :

$PV^{\alpha }={\text{constante}}$

Comparons les résultats entre un gaz relativiste et non-relativiste :

	Gaz non-relativiste	Gaz ultra-relativiste
$\alpha$	$\alpha ={\frac {5}{3}}$	$\alpha ={\frac {4}{3}}$
Relation volume-température	$V\cdot T^{\frac {3}{2}}={\text{constante}}$	$V\cdot T^{3}={\text{constante}}$

L'expansion de l'univers est une expansion adiabatique

Dans ce qui suit, nous allons faire une hypothèse assez intuitive : l'expansion de l'univers entraine une expansion adiabatique de son contenu. On peut alors étudier deux régimes : celui où l'expansion affecte un gaz ultra-relativiste, et celle où le gaz est non-relativiste. Le premier est clairement le plus important, car il décrit l'état de la matière après le big-bang. Le second cas n'est pas beaucoup étudié dans les cours introductifs car il correspond au cas d'un univers bien refroidit, où les atomes se sont formés, qui est affecté par la nucléosynthèse primordiale, où les structures comme les galaxies et autres structures de grande échelle commencent à se former.

Pour un gaz ultra-relativiste, la relation suivante s'applique :

$V\cdot T^{3}={\text{constante}}$

On a donc :

$T^{3}={\frac {\text{constante}}{V}}$

Ce qui se simplifie en :

$T^{3}\propto {\frac {1}{V}}$

Maintenant, rappelons-nous de la relation $V(t)=V_{0}\times a(t)^{3}$. En injectant dans l'équation précédente, on a :

$T^{3}\propto {\frac {1}{V_{0}\times a(t)^{3}}}$

Ce qui se simplifie en :

$T^{3}\propto a(t)^{-3}$

En prenant la racine cubique, on trouve :

$T(t)=T_{0}\times a(t)^{-1}=T_{0}\times {\frac {1}{a(t)}}$

L'expression exacte est la suivante :

$T(t)=T_{0}\cdot {\frac {a(t_{0})}{a(t)}}$

En clair, la température chute au rythme inverse de celui du facteur d'échelle. Rappelons que ce résultat, obtenu pour un gaz de photon en toute rigueur, fonctionne approximativement pour un gaz de particules massives ultra-relativistes. Il est intéressant de comparer ce résultat avec un gaz non-relativiste. Nous n'allons pas refaire les calculs, ce qui serait superfétatoire, et allons simplement donner les résultats. Pour un gaz non-relativiste, on a $T(t)=T_{0}\times a(t)^{-2}$. En clair, un gaz ultra-relativiste refroidit plus lentement qu'un gaz non-relativiste.

L'expansion de l'univers refroidit le plasma primordial

Pour résumer, l'équation précédente nous dit que la température du plasma primordial diminue au même rythme que l'augmentation du facteur d'échelle. Ainsi, le plasma primordial refroidit progressivement au fur et à mesure que l'univers s'étend. La chute de température se fait proportionnellement à l'inverse du facteur d'échelle. La chute de température avec l'expansion est donc assez rapide.

Il faut noter que cette chute de température se poursuit au même rythme tant que la matière est très chaude, donc ultra-relativiste. Au fur et à mesure que l'univers refroidit, le gaz passe en régime relativiste, puis non-relativiste. Une fois dans le régime non-relativiste, la chute de température ne se poursuit pas au même rythme, comme on l'a vu juste avant. La conséquence est que l'univers refroidit plus vite. L'évolution thermique de l'univers est donc celle d'un refroidissement initialement modéré, mais qui accélère progressivement, avant d'atteindre une sorte de rythme de croisière.

Il y a cependant un cas particulier pour lequel le refroidissement ne s'applique pas : le rayonnement pur. Le rayonnement pur est censé se refroidit en suivant la relation $T(t)=T_{0}\times a(t)^{-1}$, qui est une égalité pure dans le cas d'un gaz de photons. Alors que la matière refroidie après quelques milliards d'années après le big-bang est censée se refroidir au rythme de : $T(t)=T_{0}\times a(t)^{-2}$. Et nous verrons que c'est le cas aujourd'hui, mais que ce comportement a nécessité un phénomène assez particulier, qui a permis aux photons et à la matière d'avoir des température divergentes. Nous en parlerons plus dans le chapitre sur le découplage des photons.

Les processus de baryogenèse et nucléosynthèse

Au tout début de sa formation, l'univers était clairement chaud et dense. Les températures quelques microsecondes après le big-bang dépassaient le million voire le milliard de degrés. L'univers était en première approximation un gaz parfait de particules très différentes : neutrons, protons, neutrinos, électrons, photons, quarks, et autres. Les températures étaient tellement fortes que toutes les populations de particules réagissaient entre elles. N'importe quelle particule pouvait échanger de l'énergie avec n'importe quelle autre, homogénéisant les températures. Le mélange était tel que l'on pouvait définir une température moyenne valable pour tous les types de particules : les neutrons avaient une température moyenne similaire à celle des protons, elle-même identiques à celle des quarks, etc. On dit que l'équilibre thermique est respecté.

Pendant cette phase, l'univers était dominé par le rayonnement, avec énormément plus de photons que de particules. Les calculs disent qu'il y avait plusieurs milliards de photons pour une seule particule matérielle. De plus, la température était très élevée et les autres particules étaient ultra-relativistes. Or, rappelez-vous le résultat du chapitre précédent : la température du rayonnement diminue comme l'inverse du facteur d'échelle ($T(t)=T_{0}/a(t)$), et c'est approximativement la même chose pour les particules ultra-relativistes. Le gaz de particules élémentaires s'est donc progressivement refroidit à cause de l'expansion.

Du fait du refroidissement, le plasma primordial s'est progressivement condensé, donnant naissance à des particules composites. D'une soupe de particules se sont ainsi formés les nucléons, puis les noyaux et enfin les atomes. Puis, l'univers s'est refroidi en raison de l'expansion. En se diluant avec l'expansion, sa densité a diminué, les particules se sont espacées entre elles. Elles se sont éloignées au point que leurs interactions sont devenues plus rares. Leur proximité rendait leurs interactions faciles, chaque particule ayant rapidement accès à une voisine pour échanger de la quantité de mouvement. Mais avec la dilution, les particules se sont progressivement isolées les unes des autres, rendant les échanges de plus en plus difficiles. De nombreuses interactions ont disparues, perturbant les processus de mélange thermique.

La distribution de Maxwell-Boltzmann

Avant toute chose, précisons que lorsque la température n'est pas trop forte, un gaz de particules peut être décrit par ce qu'on appelle la distribution de Maxwell-Boltzmann. Elle permet de savoir quelle est la quantité de particules par unité de volume N, pour une particule de masse $m$, en fonction de la température. L'équation qui lie ces trois paramètres, température, densité de particule, et masse, est la suivante :

$N\propto \exp \left({\frac {mc^{2}}{k_{B}T}}\right)$

Une équation plus précise est la suivante :

$N=m^{3/2}\times \exp \left({\frac {mc^{2}}{k_{B}T}}\right)$

Elle ne peut s'appliquer qu'à la condition que $k_{B}T<<mc^{2}$. En clair, l'énergie de masse de la particule doit être largement supérieure à l'énergie thermique ambiante. De ce fait, la particule peut se former sans être complétement détruite par le chaos thermique ambiant.

Notons que cette relation permet de calculer des rapports, comme le nombre de protons pour un neutron, combien il y a de neutrinos pour un proton, etc. Sauf pour les particules sans masse, comme les photons, évidemment. Elle permet de calculer des choses comme le rapport protons/neutrons, etc. Pour comparer la densité d'une particule $N_{1}$ avec celle d'une particule $N_{2}$, on calcule le rapport ${N_{1} \over N_{2}}$. On a alors :

${N_{1} \over N_{2}}={\frac {m_{1}^{3/2}\times \exp \left[{\frac {m_{1}c^{2}}{k_{B}T}}\right]}{m_{2}^{3/2}\times \exp \left[{\frac {m_{2}c^{2}}{k_{B}T}}\right]}}$

En simplifiant, on a :

${N_{1} \over N_{2}}={\frac {m_{1}}{m_{2}}}^{3/2}\times \exp \left[{\frac {(m_{1}-m_{2})c^{2}}{k_{B}T}}\right]$

La baryogenèse et le découplage des neutrinos

Au tout début, on pouvait voir l'univers comme un mélange de plusieurs gaz composés de particules élémentaires. Du temps des fortes températures, quelques micro-secondes avant le big-bang, l'univers était peuplé par un plasma quark-gluons, à savoir un gaz de quarks et de particules liées, accompagné de photons et de neutrinos très énergétiques. Les protons et neutrons ne pouvaient pas se former à partir de quarks. La température trop intense faisait que les particules composites étaient brisées par le chaos ambiant quelques microsecondes après leur formation. C'était essentiellement les photons et neutrinos qui réagissaient avec la matière et brisaient les structures ainsi formées.

Il a fallu attendre que la température du rayonnement baisse pour que les quarks puissent s'assembler en protons et neutrons sans interagir avec un photon qui passe sur le chemin. Ce processus de formation des protons et neutrons s'appelle la baryogenèse, ce qui signifie formation des baryons (les protons et neutrons sont des exemples de baryons, d'où le nom). La théorie du big-bang nous permet de déterminer comment s'est produit ce processus. Une réussite de la théorie tient dans le fait qu'elle prédit le rapport entre le nombre de protons et de neutrons dans l’univers.

Juste après la baryogenèse

Pour décrire ce qui se passe après la baryogenèse, nous devons d'abord parler du fait que les protons se transforment parfois en neutrons et réciproquement.

Les transformations les plus connues sont des réactions nucléaires appelées désintégrations bêta, qui sont souvent présentées dans les manuels de physique qui parlent de la radioactivité. La transformation d'un proton en neutron est connue sous le nom de désintégration bêta +, la transformation d'un neutron en proton est une désintégration beta -. Ce sont des réactions spontanées, qui impliquent l'émission ou la de particules assez diverses, à savoir : des électrons, des positrons (l'anti-particule associée à l'électron), ainsi que des particules très légères appelées des neutrinos.

• Avec radioactivité bêta plus, un proton se transforme en un neutron, un positron et un neutrino.
• Avec la radioactivité bêta moins, un neutron se transforme en un proton, un électron et un anti-neutrino.

Radioactivité Beta-plus.

Radioactivité Beta-moins.

Mais il existe aussi des désintégration bêta inverses, où un proton/neutron absorbe un neutrino, ce qui le transmute. Par exemple, il est possible de transformer un proton en neutron en lui faisant absorber un anti-neutrino : le résultat est un neutron accompagné de l'émission d'un électron.

${\text{proton + anti-neutrino}}\rightarrow {\text{neutron + anti-électron}}$

Il existe une relation inverse, qui transforme un neutron en proton :

${\text{neutron + neutrino}}\rightarrow {\text{proton + électron}}$

Enfin, il existe aussi une relation où un proton capture un électron, donnant un neutron :

${\text{proton + électron}}\rightarrow {\text{neutron + neutrino}}$

L'existence des réactions bêta peut vous paraitre surprenante, car les neutrinos ont la réputation de très peu interagir avec la matière. Et c'est sans doute pour cela que les manuels de physique sur la radioactivité n'en parlent pas, vu que ces réactions sont très fortement improbables sur Terre. Mais tout cela n'est valide que pour les neutrinos peu énergétiques. Les neutrinos très énergétiques interagissent assez facilement avec la matière, leur section efficace est beaucoup plus importante. Les conséquences à cela sont variées, mais n'impactent que la physique des supernovas et surtout : la baryogenèse !

A forte température, les neutrinos sont très énergétiques et ils interagissent facilement avec les protons/neutrons. Les réactions bêta inverses ont donc lieu assez facilement si les neutrinos sont assez énergétiques, si la température est très élevée. A fortes températures, les désintégrations bêta inverses étaient très fréquentes, aussi fréquentes que les désintégrations bêta usuelles. Le résultat est que le rapport entre protons et neutrons était approximativement égal. De plus, le nombre d'électron est aussi égal au nombre de positrons.

Par la suite, en à peine quelques secondes, la température du plasma a diminué avec l'expansion, ce qui a réduit la température des neutrinos assez rapidement. Les réactions bêta inverses se sont alors faites plus rares, alors que les désintégrations bêta se sont poursuivies normalement, au même rythme. Le résultat est que le nombre de protons et de neutrons a évolué. Le résultat de ces réactions est un déséquilibre entre protons et neutrons, qui s'est aggravé avec la baisse de température.

Dans le plasma primordial, la distribution de Maxwell-Boltzmann s'applique. Ainsi, on peut calculer le rapport entre protons et neutrons, en utilisant l'équation vue au début de ce chapitre, qui est la suivante :

${\frac {N_{p}}{N_{n}}}={\frac {m_{p}}{m_{n}}}^{3/2}\times \exp \left[{\frac {(m_{p}-m_{n})c^{2}}{k_{B}T}}\right]$

Si on fait les calculs à des températures différentes, on voit que le rapport augmente progressivement, en partant d'un rapport proche de 1 à forte température, vers un rapport de plus en plus grand quand la température baisse.

Le découplage des neutrinos

Mais cela ne se poursuit pas indéfiniment. Quand le produit $K_{b}T$ descend en-dessous d'environ 1 Mev, les neutrinos ne sont plus assez énergétiques pour interagir avec la matière. Ils cessent d'interagir avec les protons et les neutrons, les réactions bêta inverses deviennent de plus en plus rares et s’arrêtent. La conséquence est que l'équilibre thermique du plasma est brisé : la température des neutrinos se découple de la température du reste du plasma, car il n'y a pas d'échange d'énergie entre neutrinos et le reste du plasma. La température des neutrinos évolue dans son coin, sans lien avec l'évolution thermique de la matière. Le phénomène porte le nom de découplage des neutrinos.

Au moment du découplage des neutrinos, les réactions bêta inverse cessent, la quantité de protons et de neutrons n'évolue plus. Le rapport proton/neutron gèle, il cesse d'évoluer avec le temps. Le rapport proton/neutron final peut se calculer en prenant l'équation précédente, et en y injectant la température du découplage des neutrinos. Les calculs donnent 6 protons pour 1 neutron : ${\frac {N_{p}}{N_{n}}}\approx 7$. Dit autrement, $1 \over 8$ ème de la matière baryonique est sous la forme de neutrons, alors que $7 \over 8$ ème sont des protons. Cela correspond à environ 12% de neutrons pour 88% de protons.

Un autre point est que malgré le découplage, la température des neutrinos va évoluer au même rythme que celle des photons, du moins au début. La raison est que les neutrinos et les photons ont une température qui évolue de la même manière. L'expansion agit sur les photons et les neutrinos de la même manière, les deux ont une température qui diminue au même rythme. Et vu que neutrinos et photons partent de la même température, leurs températures seront égales, du moins durant un certain temps. Mais à une température égale au double de la masse de l'électron, un phénomène physique va changer la donne.

L'arrêt du phénomène de production de paires

Au-dessus d'une certaine température, les réactions entre électrons, positrons et photons sont assez simples. Les principales sont les suivantes :

• La réaction dite de production de paires, qui transforme un photons en une paire contenant un électron et un positron.
• La réaction inverse, dite d'annihilation électron-positron, où un électron et un positron s'annihilent tous deux, pour donner deux photons.

Pair Production

La réaction de production de paires n'est cependant possible que si le photon est assez énergétique. La conservation de l'énergie dit que le photon doit avoir autant d'énergie que la paire produite. De fait, l'énergie minimale du photon est la somme de l'énergie de masse de l'électron et de celle du positron.

$E_{gamma}>m_{\text{electron}}c^{2}+m_{\text{positron}}c^{2}$

La masse d'un électron et d'un positron étant égales, on a alors :

$E_{gamma}>2\cdot m_{e}c^{2}$, avec $m_{e}$ la masse de l'électron.

L'énergie de masse d'un électron est proche de 500 kilo-électron-volt (0.511 MeV, pour être précis), ce qui donne :

$E_{gamma}>1.022MeV$, avec $m_{e}$ la masse de l'électron.

Et cela n'est possible que si la température est suffisamment élevée. Il faut au minimum une température proche de $k_{B}T\approx 2\times m_{electron}c^{2}$. Sous cette température, le phénomène de production de paire n'est plus possible, les photons n'ont plus assez d'énergie. Le résultat est que seul le phénomène d’annihilation électron-positron a lieu.

Le résultat est que les électrons disparaissent, mais que l'univers se remplit de photons assez énergétiques, ce qui réchauffe le plasma primordial, en augmentant sa température. On peut voir la réaction d'annihilation de paires comme un phénomène endothermique (qui absorbe de la chaleur), alors que la réaction de production de paire est exothermique (elle dégage de la chaleur). L'arrêt des productions de paire fait que le plasma absorbe moins la chaleur, sa température augmente donc. Le résultat est que la température des photons augmente, ce qui fait qu'elle se découple effectivement de celle des neutrinos. Les neutrinos ne sont pas concernés par l'arrêt de la production de paire, les photons le sont.

Il est possible de calculer la température après et avant l'arrêt de la production de paire. L'équation est la suivante :

$T_{\text{après}}={\frac {11}{4}}^{\frac {1}{3}}\times T_{\text{avant}}$

La température avant est celle que les neutrinos vont conserver, alors que celle d'après sera celle des photons. Le résultat est donc que la température des photons et des neutrinos sera donc la suivante :

$T_{\text{photons}}={\frac {11}{4}}^{\frac {1}{3}}\times T_{\text{neutrinos}}$

L'équation restera la même par la suite, l'expansion n'y changera rien. L'expansion va faire baisser la température des photons et des neutrinos, mais au même rythme, ce qui fait que l'équation restera valable.

La nucléosynthèse primordiale

Une fois les protons et neutrons formés, l'univers était rempli de protons, de neutrons, d'électrons et de neutrinos, qui formaient un gaz à haute température. Durant un temps assez court, protons et neutrons ne pouvaient pas s'assembler pour former des noyaux, la température brisant les noyaux qui avaient l'occasion de se former. Mais, la température diminuant, cela ne dura guère. Après un certain temps, protons et neutrons ont pu s'assembler pour former des noyaux, quand la température a atteint un certain seuil.

La formation des premiers noyaux porte le nom de nucléosynthèse primordiale. Un nom barbare assez simple à comprendre : nucléosynthèse veut dire "synthèse de noyaux atomiques", et primordiale pour dire qu'elle a eu lieu peu après le big-bang. Ce terme sert à la distinguer de la nucléosynthèse qui a lieu actuellement au cours des étoiles, la nucléosynthèse stellaire. Les différences entre les deux sont assez nombreuses. Déjà, la nucléosynthèse primordiale s'est faite sur un temps très court, d'à peine quelques secondes grand maximum, alors que la nucléosynthèse des étoiles est un processus continu qui dure durant plusieurs milliards d'années. Ensuite, la nucléosynthèse primordiale a majoritairement créé des éléments chimiques légers, mais guère plus. Elle a permis de fabriquer de l'hydrogène, de l'hélium, du béryllium et du lithium, mais pas plus. Les autres éléments chimiques ont été fabriqués ultérieurement par la nucléosynthèse stellaire, qui a donné naissance à du carbone, de l'oxygène, de l'azote, et d'autres noyaux lourds.

Isotopes de l'hydrogène.

Suite à la nucléosynthèse primordiale, la quasi-totalité de la matière est composée d’hydrogène et d'hélium : environ 3/4 d'hydrogène et 1/4 d'hélium, le reste étant présent en quantités négligeables. C'est pour cela que la quasi-totalité de la matière des étoiles et planètes est sous la forme d'hélium et d'hydrogène, des particules formées par l'assemblage de neutrons et de protons. Pour rappel, Un noyau d'hydrogène est formé d'un simple proton, le nombre de neutrons variant de zéro à deux neutrons. La plupart de l'hydrogène ne contient pas de neutron, cette forme d'hydrogène étant appelé du protium. L'isotope avec un neutron est appelé le deutérium, alors que celui avec deux neutrons est appelé le tritium. Le protium est de loin la forme d’hydrogène dominante, les autres formes n'étant présentes que dans les étoiles, rarement dans le milieu interstellaire. Quant à l'hélium, il possède deux protons, avec un nombre variable de neutrons. Ses deux isotopes les plus fréquents possèdent deux neutrons pour l'hélium-4, un seul pour l'hélium-3.

Les réactions de la nucléosynthèse primordiale

Résumé des réactions nucléaires principales de la nucléosynthèse primordiale, sous forme de liste.

La nucléosynthèse commence avec la fabrication de deutérium, un des isotopes de l'hydrogène. C'est à partir du deutérium que peuvent s'enclencher les réactions qui donnent naissance au tritium, à l'hélium, au lithium et au béryllium.

Dans ce qui suit, on notera D un noyau de deutérium, T un noyau de tritium, p un proton et n un neutron.

Illustration des réactions nucléaires donnant naissance au deutérium, au tritium et à l'hélium (3 et 4).

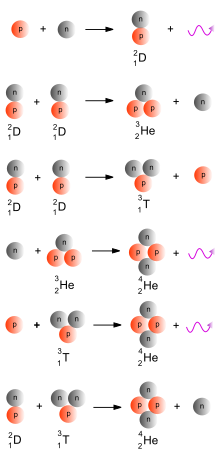
Le deutérium se forme en fusionnant un proton avec un neutron. La formation du deutérium ne s'est produite qu'une fois la température suffisamment basse. Au-dessus de cette température, les noyaux de deutérium ne survivent pas bien longtemps, à cause de la photodissociation. Les photons énergétiques brisent ces noyaux en quelques microsecondes, ne laissant que des protons et des neutrons. Mais une fois que la température descend sous la température critique du deutérium, les photons ne sont plus assez énergétiques pour briser les noyaux de deutérium, qui survivent.

$n+p=D$

Une fois le deutérium formé, des réactions donnent naissance soit à de l'hélium-3, soit à du tritium. L'hélium-3 peut se former de deux manières : soit par addition d'un proton, soit par fusion de deux noyaux de deutérium.

$D+D=n+^{3}\operatorname {H_{e}}$

$D+p=\gamma +^{3}\operatorname {H_{e}}$

Le tritium peut lui aussi se former de deux manières différentes. Dans le premier cas, il est formé par la fusion de deux noyaux de deutérium. Dans le second cas, il est formé à partir d'un noyau d'hélium-3, dans lequel on remplace un proton par un neutron (par désintégration bêta, ou par capture/émission de nucléons).

$D+D=p+T$

$^{3}\operatorname {H_{e}} +p=n+T$

Une fois le tritium ou l'hélium-3 formé, l'hélium-4 peut enfin apparaître. Il se forme soit à partir d'hélium-3, soit à partir de tritium. Et les méthodes pour ce faire assez diverses. Dans les deux cas, il se forme en ajoutant un noyau de deutérium, suivi par l'émission d'un nucléon. Le nucléon émit est un proton pour la fusion avec l'hélium-3, un neutron pour la fusion avec le tritium. Une autre manière consiste à ajouter un proton à du tritium, ou du neutron à de l'hélium-3.

$^{3}\operatorname {H_{e}} +D=p+^{4}\operatorname {H_{e}}$

$T+D=n+^{4}\operatorname {H_{e}}$

$^{3}\operatorname {H_{e}} +n=^{4}\operatorname {H_{e}}$

$T+p=^{4}\operatorname {H_{e}}$

Enfin, les autres éléments légers peuvent se former à partir de l'hélium-4. En fusionnant de l'hélium-4 avec soit du tritium, soit de l'hélium-3, on obtient respectivement du lithium et du béryllium. Le lithium peut aussi se former à partir du béryllium, par remplacement d'un neutron en proton. De plus, le lithium peut fusionner avec un proton pour donner deux noyaux d'hélium-4.

$^{4}\operatorname {H_{e}} +^{3}\operatorname {H_{e}} =^{7}\operatorname {B_{e}}$

$^{4}\operatorname {H_{e}} +T=^{7}\operatorname {L_{i}}$

$^{7}\operatorname {B_{e}} +n=p+^{7}\operatorname {L_{i}}$

$p+^{7}\operatorname {L_{i}} =^{4}\operatorname {H_{e}} +^{4}\operatorname {H_{e}}$

L'ensemble de ces réactions est résumé dans le schéma ci-dessous.

Réactions nucléaires principales de la nucléosynthèse primordiale, en schéma.

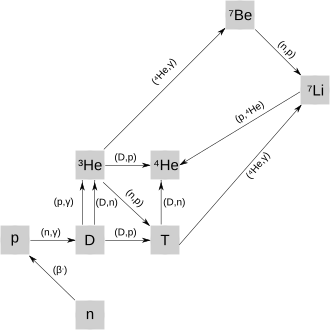
Le calcul de l'abondance de l'Hélium

Des calculs théoriques poussés, basés sur la physique nucléaire, nous disent que la concentration en éléments chimiques a évolué rapidement au cours de la nucléosynthèse primordiale, avant de stabiliser. Le résultat est que les deux éléments majoritaires sont l'hydrogène (le protium) et l'hélium-4. Le deutérium et l'hélium-3 sont plus rares et ont une concentration assez similaire. Le tritium et les neutrons libres sont eux encore plus rares. Enfin, le lithium et le béryllium ferment la marche et sont les éléments les plus rares. Pour simplifier, on peut dire que l'univers est rempli presque exclusivement d'hydrogène et d'hélium-4. Les autres éléments sont tellement rares qu'ils sont presque négligeables.

Évolution de la concentration de chaque élément chimique dans l'univers, au cours de la nucléosynthèse primordiale.

Sans recourir à ces calculs compliqués, on peut calculer l'abondance des éléments principaux. L'idéal est de se concentrer sur l'hydrogène (le protium) et l'hélium-4 uniquement. Négliger les autres éléments n'est pas un problème tant ils sont rares. En faisant cela, on doit considérer que tous les neutrons ont été capturés dans les noyaux d'hélium-4, vu qu'il n'y en a pas dans les noyaux de protium.

Rappelons que le rapport protons/neutrons est de 1/7. Cela veut dire que sur 16 baryons, 2 sont des neutrons et 14 sont des protons (ce qui est équivalent à dire que sur 8 baryons, 1 est un neutron et 7 sont des protons). Avec ces 16 baryons, on peut créer un atome d'hélium-4 avec 2 neutrons et 2 protons, ce qui laisse 12 protons. On a donc 12 noyaux d’hydrogènes pour un noyau d'hélium-4. Vous avez peut-être vu d'autres chiffres dans la vulgarisation, notamment un rapport de 75% d'hydrogène contre 25% d'hélium. Mais ces pourcentages sont exprimés en termes de masse, non de nombre d'atomes. Pour retrouver ce rapport 75%/25%, il faut prendre en compte la masse relative des noyaux d'hélium-4 et d'hydrogène. Un noyau d'hélium-4 étant approximativement 4 fois plus massif qu'un noyau d'hydrogène, il faut diviser le nombre de noyaux d'hydrogène par 4 pour utiliser la même unité de masse. En faisant cela, on trouve alors que 75% de la masse de l'univers est composée d'hydrogène et les 25% restants d'hélium-4.

Abondance des éléments chimiques suite à la nucléosynthèse primordiale.

Il est possible de retrouver ces résultats par le calcul, ce que nous allons faire de ce pas. Dans les calculs qui vont suivre, nous noterons le nombre d'atomes d'hélium $n_{He}$ alors que le nombre d'atomes de protium sera noté $n_{H}$. Les nombres de neutrons et de protons seront notés $n_{n}$ et $n_{p}$. L'hypothèse comme quoi tous les neutrons sont capturés dans les noyaux d'hélium-4 signifie que :

$n_{n}=2\cdot n_{He}$, car il y a deux neutrons dans un noyau d'hélium-4.

La première étape est de calculer la quantité totale de baryons enfermés dans les noyaux d'hélium-4. Un atome d'hélium-4 contient 4 baryons, deux neutrons et deux protons. En multipliant par le nombre de noyaux, on obtient cette quantité totale, égale à :

$N^{He}=n_{He}\cdot 4$

Pour la seconde étape, on a besoin du nombre total de baryons dans l'univers. Par définition, il est égal à la somme $n_{n}+n_{p}$ (la somme du nombre de protons et de neutrons). En combinant les deux équations précédentes, on obtient le rapport entre le nombre de baryons dans les atomes d'hélium et le nombre total de noyaux, que nous noterons $Y$.

$Y={\frac {N^{He}}{N^{total}}}={\frac {4\cdot n_{He}}{n_{n}+n_{p}}}$

On utilise alors l'équation $n_{n}=2\cdot n_{He}$ :

$Y={\frac {2\times n_{n}}{n_{n}+n_{p}}}$

On peut réécrire cette équation en utilisant uniquement le rapport protons/neutrons calculé dans la section précédente. Il suffit pour cela de diviser l'équation précédente par le nombre de protons. On a alors :

$Y={\frac {2\times (n_{n}/n_{p})}{1+(n_{n}/n_{p})}}$

On a vu dans la section précédente que le le rapport protons/neutrons suite au big-bang est de $1 \over 7$. En utilisant cette valeur, on trouve que $Y\approx {\frac {1}{4}}$, ce qui veut dire que 75% de la masse de l'univers est composé d'hydrogène et 25% d'hélium-4. Cette valeur est très proche de la valeur observée. À l'heure actuelle, 74% de la masse de l'univers est composée d'hydrogène et 25% d'hélium-4, le reste se partageant le 1 % restant. Précisons qu'il s'agit d'un pourcentage en masse, non en nombre d'atomes.

Le découplage des photons

Dans les chapitres précédents, nous avons vu quelque chose de très important : la température du rayonnement diminue avec l'expansion. Un point important est que l'univers, à ses débuts, est composé d'un plasma, à savoir un gaz de particules chargées. L'univers ne comprend au départ par d'atomes, mais seulement des électrons, des protons et neutrons, etc. La matière était composée d'un plasma d'électrons libres, de baryons et de photons. A cette époque, le rayonnement interagissait fortement avec les électrons libres, les noyaux d'atomes, les électrons liés aux atomes, bref : avec la matière au sens général. Vu que le rayonnement et la matière interagissaient beaucoup, les deux étaient à la même température. Matière et rayonnement étaient en équilibre thermique, à la même température. Si la matière chauffait trop, elle redistribuait l'excès au rayonnement, et réciproquement. Ce plasma formait un fluide unique, avec une pression, une température, une densité d'énergie, etc.

Les photons interagissaient fortement avec les électrons, par diverses processus (diffusion Compton, et autres), ce qui redistribuait la température. Les photons chauffaient les électrons et réciproquement. Un équilibre thermique s'était ainsi installé entre photons et électrons libres, les deux ayant la même température/énergie cinétique moyenne. Cet équilibre incluait aussi les baryons, bien que les baryons n'interagissaient pas directement avec les photons. Les baryons interagissaient fortement avec les électrons, qui servaient d'intermédiaires avec les photons. Ce plasma avait naturellement des propriétés thermodynamiques simples : une pression, une température, un volume, etc. Sa pression était essentiellement causée par la pression de radiation des photons, avec une participation mineure de la pression des électrons libres et des baryons.

La matière neutre est transparente, ce qui induit un découplage des photons.

Mais la température baissant avec l'expansion, elle a fini par atteindre une température suffisamment basse pour que les atomes se forment. La matière est alors passée de l'état de plasma à un gaz d'atomes. Cela s'est produit 380 000 ans après le big bang, à une température d'environ 3000 degrés. Le résultat est que les interactions entre rayonnement et matière se sont faites plus rares, et surtout que la redistribution d'énergie entre matière et rayonnement s'est faite plus rare, plus lente.On nomme découplage de telles situations où deux populations de particules n'interagissent plus à la suite d'une baisse de température. Et ici, il s'agit du découplage des photons.

Après le découplage, le rayonnement et la matière font leur vie chacun de leur côté et cela s'est ressenti sur leur température et leur évolution. La première conséquence du découplage est que l'équilibre thermique est rompu : les deux populations de particules s'isolent thermiquement et leur températures deviennent indépendantes. La température de la matière est devenue différente de la température des photons. De plus, elles ne se sont pas refroidies de la même manière. La matière garda sa température constante lors de l'expansion, alors que celle du rayonnement chuta avec l'expansion. Le rayonnement s'est refroidi plus vite que la matière, à cause de la diminution de fréquence des photons, abordées il y a quelques chapitres.

Le fond diffus cosmologique

Pour résumer, le plasma s'est divisé en deux gaz indépendants : un gaz de matière et un gaz de photon. Le gaz de matière s'est condensé pour donner des galaxies et autres structures, alors que le gaz de photons a subsisté jusqu’à aujourd'hui sous la forme d'un ensemble de photons de faible température, que l'on peut capter avec certains instruments. Ce gaz est appelé le fond diffus cosmologique, aussi appelé le rayonnement de fond diffus cosmologique, ou encore le CMB (Cosmic Microwave Background).

La même chose a eu lieu pour les neutrinos et anti-neutrinos qui se sont découplés de la matière et des photons un peu avant les photons. Ce fond diffus de neutrinos est malheureusement nettement moins étudié que le fond diffus cosmologique, car les neutrinos n'interagissent pas beaucoup avec la matière, et qu'ils sont donc difficiles à détecter. Nous n'en parlerons donc pas dans ce cours, par manque d'informations à leur sujet. Pour le moment, concentrons-nous sur le découplage des photons.

COBE monopole dipole and primordial perturbations

Le CMB a été théorisé avant d'être découvert. Dans un article de 1948, Alpher et ses collègues théorisèrent l'existence du CMB à partir d'un modèle de big-bang usuel. Mais il fallut attendre 1965 pour que ce signal soit observé pour la première fois, par Penzias et Wilson. Ceux-ci utilisaient une antenne de grandes dimensions, pour tester la fiabilité des communications entre satellites, et étudiaient des interférences radio qui apparaissaient à haute fréquence. Leurs investigations leur ont permis de capter un signal dans la bande de 4Ghz, qui avait des caractéristiques étranges : isotrope, non-polarisé et libre de toute variation saisonnière. L'origine de ce signal est restée inconnue durant quelques années, mais les scientifiques (dont Penzias et Wilson) avaient éliminé toute origine terrestre. Il fallu que Dicke et ses collaborateurs fassent le lien avec l'article d'Alpher. Par la suite, diverses campagnes d'observation ont permis d'obtenir une carte assez détaillée du fond diffus. De nombreux projets d'observations scientifiques ont ainsi observé le fond diffus cosmologique avec une précision de plus en plus grande : COBE, puis WMAP, et enfin la mission PLANCK.

Les observations de Penzias et Wilson montraient un CMB relativement uniforme. Par la suite, les observations du satellite COBE ont montré que le CMB a l'air d'avoir une structure en forme de dipôle, à savoir qu'il a un pôle chaud opposé à un pôle froid. Les observations plus récentes éliminent cet effet Doppler par divers traitements informatiques, et montrent un CMB sans dipôle, mais avec quelques inhomogénéités. On observe notamment une zone plus chaude au niveau de l'équateur, liée à la présence de la voie lactée (notre galaxie), qui réchauffe quelque peu le CMB de par son rayonnement.

La surface de dernière diffusion

Surface de dernière diffusion.

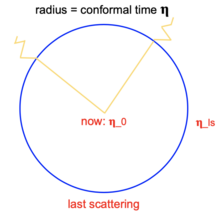
Le fond diffus capté à l'heure actuelle correspond aux photons émis lors du découplage, environ 380 000 ans après le big-bang. Du point de vue de la Terre, les photons du CMB captés par les instruments de mesure sont répartis sur une sphère centrée sur la Terre, appelée la surface de dernière diffusion, dont le diamètre correspond à la distance parcourue par ces photons depuis le découplage.

Pour comprendre pourquoi on parle de surface de dernière diffusion, il faut faire un petit rappel sur les interactions entre photons et matière. Les photons ont en effet tendance se cogner sur les particules qui croisent leur chemin, et à rebondir dessus. Typiquement, ils rebondissent sur des électrons dans un processus appelé la diffusion Compton. Lors de ce choc entre électron et photon,une partie de l'énergie du photon est transférée à l'électron, ou inversement.

Diffusion Compton

Les photons du CMB sont soit des photons qui ont été émis au moment du découplage, soit des photons qui existaient avant, mais ont rebondit une ou plusieurs fois sur des particules de matière. Les diffusions Compton étaient très fréquentes avant le découplage, car les électrons libres étaient très nombreux. Les photons ne pouvaient pas faire un pas sans interagir avec un électron libre, leur temps de libre parcours moyen (temps entre deux collisions avec un électron libre) était très faible. Le mouvement d'un photon dans le plasma primordial était chaotique : les photons ne pouvaient pas aller en ligne droite, mais n'avaient de cesse de se cogner sur les atomes au point où leur trajectoire ressemblait à marche aléatoire, à un mouvement brownien. En conséquence, le plasma primordial avant le CMB était opaque, dans le sens où il ne laissait pas traverser la lumière facilement.

Mais après le découplage, les électrons se sont liés aux atomes, ne laissant presque aucun électron libre pour participer à des diffusions Compton. Les photons du CMB, autrefois diffusés fréquemment, n'ont ensuite plus été diffusé par diffusion Compton, ou presque. Leur libre parcours moyen, la distance parcoure entre deux collisions/diffusions est devenus beaucoup plus grande. Les photons ont alors pu se déplacer en ligne droite entre quelques rares collisions, et donc le plasma primordial est devenu transparent. Le découplage est le moment où ils ont diffusé pour la dernière fois, d'où le fait que l'on parle de surface de dernière diffusion.

Précisons cependant que le découplage ne s'est pas fait instantanément, mais est un processus progressif qui s'est étalé sur un temps non-négligeable. Et cela a un effet sur la surface de dernière diffusion. Il s'agirait bien d'une surface sphérique si le découplage était instantané, mais la réalité est que la surface de dernière diffusion a une certaine épaisseur. Son épaisseur est égale à la distance parcourue par un photon durant la durée du découplage. Cela a des effets mesurables, notamment dans le spectre de puissance du fond diffus, mais nous en reparlerons dans quelques chapitres.

Le CMB est un rayonnement de corps noir

Les observations montrent que, peu importe à quel endroit on le regarde, le CMB est un rayonnement de corps noir quasiment parfait, ce qui est en accord avec la théorie. Le fait que le CMB soit un rayonnement de corps noir signifie que l'on peut lui attribuer une température, une température en chaque point du ciel pour être précis.

Comparaison du CMB avec un rayonnement de corps noir.

Le dipôle du CMB

CMB vu par COBE, sans traitement (en haut), en retirant le dipôle (milieu) et en retirant la luminosité de la voie lactée (en bas).

Le fait que le CMB aie une forme approximativement dipolaire est en soi un gros problème, que l'on arrive pas à bien expliquer théoriquement. On pourrait croire que cela réfute l'idée d'un univers isotrope, mais ce n'est pas forcément le cas.

L'explication usuelle quant à l'existence de ce dipôle est qu'il serait d'origine cinématique, lié au mouvement de la Terre par rapport au CMB. L'explication détaillée part du principe qu'il y aurait un référentiel dans lequel le CMB serait isotrope et sans aucun dipôle. Cependant, la Terre se déplacerait à une certaine vitesse notée v par rapport à ce référentiel. Rappelons que le CMB est avant tout un rayonnement électromagnétique avec une certaine fréquence, fréquence qui dépend de sa température. Or, la fréquence du CMB est alors déformée par une sorte d'effet Doppler, ce qui fait que la température dépend de la direction dans laquelle on se déplace, par rapport au référentiel où le CMB est isotrope. Les zones du CMB qui s'éloignent de nous sont vues comme refroidies, alors que les zones qui s'approchent (opposées, donc) sont vues comme plus chaudes.

Pour rappel, à de faibles vitesse, le CMB subit un décalage vers le rouge de :

$z(v)={\frac {v}{c}}$

La relativité restreinte donne une formule encore plus précise :

$z(v)={\frac {\sqrt {1+{\frac {v}{c}}}}{\sqrt {1-{\frac {v}{c}}}}}-1$

Une explication beaucoup plus détaillée est cependant encore inconnue. On fait face à un cas assez mal compris théoriquement : établir la température d'un objet alors qu'on se déplace par rapport à lui à grande vitesse. Et outre la température, on peut aussi analyser la forme du rayonnement de corps noir observée. Température et corps noirs sont deux concepts de la thermodynamique, une branche de physique parfaitement maitrisée tant qu'on reste dans le cadre de la physique classique de Newton. Mais le cas qui nous intéresse, à savoir à quoi ressemble le fond diffus quand on se déplace à grande vitesse, demande qu'on utilise la relativité restreinte d'Einstein. Et c'est là que le bas blesse : on n'a pas de théorie validée pour la thermodynamique relativiste. La thermodynamique relativiste vise à reformuler les lois de thermodynamique dans le cadre de la relativité restreinte d'Einstein. A l'heure actuelle, les physiciens ont plusieurs théories pour cela, mais elles donnent des résultats complètement contradictoires !

Et pour comprendre pourquoi, faisons quelques rappels de relativité restreinte. La relativité nous dit que quand on se déplace par rapport à un référentiel immobile, les distances et les durées sont modifiées par un facteur appelé le facteur de Lorentz. Ce dernier vaut :

$\gamma ={\frac {c}{\sqrt {c^{2}-v^{2}}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$, avec $v$ est la vitesse de déplacement, et $c$ est la vitesse de la lumière dans le vide.

Concrètement, si je mesure une distance L dans un référentiel immobile, la même distance mesurée en allant à la vitesse v sera de $L \over \gamma$. La distance mesurée est plus petite que dans un référentiel immobile et elle est d'autant plus petite que l'on va vite. C'est l'effet de contraction des longueurs. L'effet est inverse pour les durées, à savoir que la durée d'un évènement/phénoméne n'est pas la même selon la vitesse du référentiel de mesure. La durée mesurée dans un référentiel en mouvement est plus longue que celle mesurée dans un référentiel immobile. Cette fois-ci, une durée D devient $D\times \gamma$. C'est l'effet de dilatation des durées.

Maintenant, prenons le cas où on cherche à calculer la température observée du CMB, ou même de tout autre rayonnement de corps noir observé depuis un objet en mouvement. Le CMB, dans son référentiel où il est isotrope (immobile dirait-on), a une température notée $T_{0}$. L'observateur se déplace à une vitesse $v$ dans une direction bien précise. En théorie, plusieurs situations sont possibles.

• La température observée est égale à $T_{0}\times \gamma$.
• La température observée est égale à $T_{0} \over \gamma$.
• La température observée est égale à $T_{0}$.

A l'heure actuelle, nous ne savons pas quelle est la bonne solution. Les trois possibilités sont impossibles à distinguer expérimentalement, et les trois sont défendues par des arguments théoriques solides. Une revue de ces arguments est disponible dans le document nommé "Black Body Radiation in Moving Frames", par Kamran Derakhshani. Mais l'explication actuelle du dipole du CMB part du principe que l'on a une variante de la seconde solution. En 1968, Bracewell et Conklin ont sorti une étude où ils montraient que, si leur démonstration était correcte, alors un observateur en mouvement dans le CMB mesurait une température anisotrope, à savoir dépendante de la direction. La température mesurée en un point du CMB était la suivante :

$T={\frac {T_{0}}{\gamma \left[1-{v \over c}\times \cos {(\alpha )}\right]}}$, avec $\alpha$ l'angle par rapport à la direction de déplacement.

L'équation nous dit que le CMB doit semble plus chaud à l'avant, et plus froid, par rapport à la direction de déplacement. On retrouve donc le dipole observé dans le CMB, à condition que la vitesse de déplacement ait la bonne valeur. Elle serait d'environ 300 kilomètres par secondes. C'est l'explication actuelle du dipole du CMB.

L'explication précédente du dipôle du CMB est actuellement contestée. A vrai dire, il s'agit d'une hypothèse parmi beaucoup d'autres et elle est juste un consensus assez mou, que les astrophysiciens cherchent à vérifier ou infirmer depuis longtemps. Diverses expériences ont tenté de vérifier l'origine cinétique du dipôle, de plusieurs façons. La première est de vérifier si ce dipôle apparait non seulement dans le CMB, mais aussi dans les observations des quasars et des sources radio lointaines. En théorie, si l'explication cinétique est bonne, alors on devrait retrouver un effet similaire en observant la positions des galaxies très lointaines. Diverses études ont tenté de vérifier cela, mais les résultats ne sont pas encore très fiables. De plus, l'explication cinétique implique qu'il y ait un référentiel dans lequel le CMB serait quasi-uniforme et sans dipôle. Cela pourrait en faire un référentiel privilégié et briserait le principe de relativité avec l'invariance galiléenne/lorentzienne, mais rien n'est moins sûr.

Outre l'existence de ce dipôle, d'autres observations semblent indiquer que le CMB aurait un axe privilégié, nommé l'axe du mal (axis of evil en anglais), qui impacterait le CMB, mais aussi l'expansion de l'univers. Mais le fait que l'axe soit aligné avec le plan de écliptique (le plan sur lequel la Terre tourne autour du Soleil) met le doute quant à son origine. Une origine cinématique locale est en tout cas plus probable qu'une origine cosmologique, sauf coïncidences. Mais là encore, rien n'est moins sûr et il se pourrait que les données soient biaisées, d'autres études n'ayant pas retrouvé cet axe du mal dans leurs données.

L'axe du mal du CMB.

Le découplage et le fond diffus

Au moment du découplage, on sait que le gaz de photons devait avoir la même température que le plasma. Sans expansion, cette température serait égale à la température du plasma au moment du découplage, qui a été conservée par le gaz de photons. Mais l'expansion a décalé ce rayonnement de corps noir vers le rouge, diminuant sa température. La température du fond diffus a donc diminué en conséquence. De nos jours, les mesures donnent une température d'environ 2,735 Kelvin. Mais on est en droit de se demander quelle était sa température au moment de sa formation. On peut aussi se demander combien de temps de refroidissement du CMB a duré.

L'âge de la recombinaison

La température du fond diffus au moment du découplage est estimée à 3000 degrés Kelvin, température de condensation d'un plasma en atomes. À partir de la température mesurée actuellement, et de la valeur théorique de formation d'un plasma, on peut déduire l'âge qui s'est écoulé depuis la formation du CMB. En théorie, on peut déduire la température du CMB en utilisant la formule suivante, établie dans le chapitre "L'évolution de a matière" :

$T(t)=T(t_{0})\cdot {\frac {a(t_{0})}{a(t)}}$

Mais utiliser cette formule présuppose de connaître $a(t_{0})$ et $a(t)$. Cependant, on peut ruser en remplaçant le facteur d'échelle par le redshift. Pour cela, on utilise la formule vue dans le chapitre "L'évolution du rayonnement". Le décalage vers le rouge $z(t)$ est mesuré entre l'époque actuelle et la recombinaison, ce qui fait qu'on le notera $z_{rec}$.

Dans ce qui suit, on suppose que $t_{0}$ est l'instant d'émission de la lumière, alors que l'observation a lieu à l'instant $t$. Avec cette convention, on sait que $1+z(t)={\frac {a(t)}{a(t_{0})}}$. En faisant le remplacement dans l'équation précédente, on trouve :

$T(t)={\frac {T(t_{0})}{1+z}}$

Rappelons que cette formule utilise la convention $t_{0}=t_{emission}$. Ici, le temps d'émission est l'instant où a eu lieu la recombinaison. En clair, la température $T(t_{0})$ est la température de découplage $T_{rec}$.

$T(t)={\frac {T_{rec}}{1+z_{rec}}}$

La température au moment du découplage était d'environ 3000 degrés Kelvin, alors que la température actuelle du fond diffus est d'environ 2,735 degrés Kelvin.

$2,735K={\frac {3000K}{1+z_{rec}}}$

Le redshift calculé ainsi est de :

$z\approx 1100$.

En utilisant un modèle cosmologique, on peut déduire une relation âge-redshift, et donc calculer combien d'années se sont écoulées entre le big-bang et la formation du CMB.

La température de recombinaison

La recombinaison a eu lieu quand l'univers a atteint une certaine température, qu'il est important de connaître. En effet, grâce à elle, on peut calculer quand a eu lieu le découplage, et donc dater le CMB. Autant dire que calculer celle-ci est d'une importance primordiale. En théorie, la température du CMB est la température à laquelle un plasma se condense en atomes quand on le refroidit. Dit autrement, c'est la température d'une transition de phase. Vous avez peut-être déjà entendu que cette température est d'environ 3000 degrés Kelvin, ce qui est la température mesurée sur Terre. Reste qu'il vaut mieux la calculer et en rendre compte théoriquement. Les mesures réalisées sur Terre ne sont peut-être pas représentatives des conditions de l'univers primordial : la pression est plus élevée, la densité différente et j'en passe. Dans cette section, nous allons calculer la température théorique à laquelle le découplage a eu lieu.

L'approximation par l'énergie photonique moyenne

Une première méthode est de comparer l'énergie d'ionisation de l'hydrogène avec l'énergie d'un photon. Dans un gaz de photons de température $T$, l'énergie moyenne d'un photon est de $3k_{B}T$. L'énergie d'ionisation d'un atome d'hydrogène (la plus faible de toutes) est de 13,6 électrons-Volts (l'EV est une unité d'énergie). Si l'énergie moyenne des photons est supérieure à l'énergie d'ionisation de l'hydrogène, alors la matière restera ionisée. Si ce n'est pas le cas, les photons ne sont pas assez énergétiques pour ioniser la matière, qui se condense. On peut alors calculer une approximation de la température de découplage avec le quotient suivant :

$T={\frac {13,6eV}{3k_{B}}}=50000K$

On voit que la température obtenue est diablement haute, comparée aux valeurs réelles : plus de 10 fois la valeur réelle. Cela vient d'un phénomène simple : l'énergie moyenne n'est qu'une moyenne, qui cache le fait que certains photons sont plus énergétiques que la moyenne. Même si l'énergie moyenne d'un photon est de 13,6 eV, de nombreux photons ont une énergie suffisante pour ioniser un atome dans le gaz de photon.

On peut obtenir une approximation plus crédible en étudiant plus en détail la dispersion des énergies des photons. Dans un gaz de photons, tous les photons n'ont pas la même énergie. Et l'énergie n'est pas répartie équitablement entre les photons, mais suit une loi assez compliquée. Mais pour simplifier, on peut estimer que le nombre de photons suit la loi de Boltzmann. Pour résumer, le nombre de photons qui a au moins une énergie $E_{\gamma }$ est proportionnel à l'exponentielle de leur énergie. Mis sous forme de formule, cela donne :

$N_{\gamma }\propto e^{-{\frac {E_{\gamma }}{KT}}}$.

Supposons maintenant qu'il faille un photon par atome à ioniser pour que l'ionisation se fasse. Sachant qu'il y a environ $1,7\times 10^{9}$ photons par baryon.atome, on peut trouver la température de découplage suivante :

$T={\frac {13,6eV}{k_{B}\times \ln {(1,7\times 10^{9})}}}=7400K$

L'approximation par l'équation de Saha

Il est possible d'obtenir une approximation plus précise avec l'équation de Saha. Celle-ci permet de déduire le degré d'ionisation d'un gaz. Le gaz en question correspond à un gaz d'hydrogène, composant principal de l'univers, qui s'est justement formé lors du découplage. Avant le découplage, on peut considérer que l'univers était rempli d'un plasma formé par ionisation du gaz d'hydrogène, à savoir un gaz qui mélangeait protons et électrons. L'équation de Saha nous dit que, si on note :

• $n_{e}$, $n_{p}$ et $n_{H}$ la concentration en électrons, protons et hydrogène ;
• $m_{e}$ la masse de l'électron ;
• $E_{I}$ l'énergie d'ionisation d'un atome d'hydrogène.

${\frac {n_{e}\cdot n_{p}}{n_{H}}}=\left({\frac {m_{e}kT}{2\pi \hbar ^{2}}}\right)^{\frac {3}{2}}\cdot \exp \left({\frac {E_{I}}{kT}}\right)$

Vous remarquerez que l'équation de Saha ressemble beaucoup à la distribution de Boltzmann.

Pour diverses raisons techniques, les physiciens décrivent souvent l'ionisation d'un gaz en utilisant la fraction d'électrons libres. Elle correspond au rapport en nombre d'électrons libres et nombre de protons (libres ou appartenant à un atome d'hydrogène). Elle vaut donc :

$x_{e}={\frac {n_{e}}{n_{p}+n_{H}}}$

Le plasma primordial est neutre électriquement. Or, la neutralité électrique de la matière signifie que $n_{e}=n_{p}$. Avec cette contrainte, l'équation de Saha se réécrit comme suit :

${\frac {x_{e}^{2}}{1-x_{e}}}={\frac {1}{n_{H}+n_{p}}}\cdot \left({\frac {m_{e}kT}{2\pi \hbar ^{2}}}\right)^{\frac {3}{2}}\cdot \exp \left({\frac {E_{I}}{kT}}\right)$

L'équation nous dit que le découplage n'est pas un évènement qui a eu lieu à une température bien précise, mais un processus continu dans lequel l'ionisation a baissé lentement. À 5000 Kelvins, la matière est ionisée à près de 99%. Le taux d'ionisation chute ensuite progressivement avec la température, pour atteindre 50% à 4000 Kelvins, puis 1% à 3000 Kelvins. Les scientifiques estiment, par pure convention, que le découplage a eu lieu quand le degré d'ionisation descend en-dessous de 1%, c'est à dire à une température d'environ 3700 Kelvin.

Les approximations plus précises

Les observations ne sont pas complètement compatibles avec cette approximation, bien que le modèle de Saha colle à-peu-près. Les mesures semblent indiquer non seulement que la température calculée n'est pas tout à fait exacte, mais qu'en plus, le découplage a pris plus de temps, s'est déroulé plus lentement. Pour obtenir des résultats plus précis, divers modèles ont été inventés par les physiciens. Le plus simple de ces modèles est le modèle de Peebles, aussi connu sous le nom de modèle d'atome à trois étages. Il a été complété par de nombreux modèles, qui sont devenus de plus en plus complexes avec le temps, incluant de plus en plus d'acquis théoriques provenant de la physique atomique. Nous ne parlerons pas de ces modèles, qui sont assez compliqués pour ce cours et qui font notamment appel à quelques concepts de physique quantique.

Le spectre de puissance des perturbations

Dans le chapitres précédent, nous avions éliminé la pression des équations, afin de les rendre plus simples. Il faut dire que résoudre ces équations avec la pression est compliqué, mais c'est faisable en utilisant un formalisme mathématique précis. Celui-ci est le formalisme de la transformée de Fourier. Et quitte à introduire ce formalisme, autant parler plus en détail de la manière de modéliser le champ de densité, qui a un lien très fort avec le formalisme de Fourier. Faisons donc une petite parenthèse sur le sujet.

Nous sommes parti du principe que la distribution de la densité $\delta (x,t)$ nous était inconnue. Nous supposions simplement qu'elle existe, mais sans en savoir plus sur ses propriétés. Et il est vrai que dans le cas général, on ne peut rien dire sur la distribution des perturbations. Par contre, on peut en donner quelques propriétés statistiques plus ou moins pertinentes. Ce champ de densité, peu importe sa forme exacte, a une densité moyenne, une certaine dispersion autour de cette moyenne, et ainsi de suite. Dans ce chapitre, nous allons voir diverses mesures statistiques du champ de densité et voir comment elles se marient avec les équations du chapitre précédent.

La fonction de corrélation

Pour commencer, prenons un exemple assez simple, mais en apparence détaché des perturbations cosmologiques. Si je regarde un point $x$ de l'espace et un volume $dV$ autour de ce point (supposé assez gros à l'échelle cosmologique). Il y a une probabilité $P(x)$ que dans le volume $dV$, je trouve une galaxie. Si on suppose qu'il y a en moyenne ${\overline {n}}$ galaxies par unité de volume, alors cette probabilité est de :

$P(x)={\overline {n}}\cdot dV$

De même, en un point $y$, cette probabilité est de :

$P(y)={\overline {n}}\cdot dV$

Maintenant, on souhaite savoir quelle est la probabilité que j'observe une galaxie à la fois au point $x$ et au point $y$. Intuitivement, on penserait avoir :

$P(x,y)=\left({\overline {n}}\cdot dV\right)^{2}$

Mais cela ne vaut que si les positions des galaxies sont totalement indépendantes, ce qui n'est pas garanti. Dans les faits, il est possible qu'il y ait une relation dans la distribution des galaxies qui fait que si on observe une galaxie en x, alors sa présence en y est plus probable, en fonction des positions x et y. On doit donc tenir compte de telles corrélations. La formule exacte, qui en tient compte, est la suivante :

$P(x,y)=\left({\overline {n}}\cdot dV\right)^{2}\left[1+\epsilon (x,y)\right]$, où $\epsilon (x,y)$ est la fonction de corrélation.

Par analogie, on peut utiliser le même formalisme, mais pour prédire non pas la présence d’une galaxie, mais l'intensité d'une fluctuation de densité. On a alors :

$<\rho (x)\rho (y)>={\overline {\rho }}^{2}\left[1+\epsilon (x,y)\right]$, où ${\overline {\rho }}$ est la densité moyenne du champ de densité.

Il est possible de définir des fonctions de corrélation pour trois points, quatre points, voire beaucoup plus.

L'hypothèse d’homogénéité statistique

Si on considère que l'univers est statistiquement homogène, alors la fonction de corrélation ne dépend que de la distance entre x et y, mais pas de la position exacte de x et y.

$<\rho (x)\rho (y)>={\overline {\rho }}^{2}\left[1+\epsilon (|x-y|)\right]$

Ce qui peut s'écrire comme suit :

$<\rho (x)\rho (y)>={\overline {\rho }}^{2}\left[1+\epsilon (d)\right]$, avec r la distance entre les deux points x et y.

Sous cette hypothèse, le calcul de la densité moyenne est assez simple. Il suffit de prendre la moyenne spatiale de la densité. La corrélation moyenne entre deux points peut se calculer en prenant un grand nombre de points x et y et en calculant la corrélation pour chaque paire de points. Il suffit de faire la moyenne des corrélations obtenues, pour obtenir la corrélation moyenne. les mesures semblent montrer que la fonction de corrélation suit une loi de puissance de la forme suivante :

$\epsilon (d)\approx k\cdot d^{-\gamma }$, avec $\gamma \approx 1,8$.

La transformée de Fourier du champ de densité

Outre la fonction de corrélation, on peut aussi utiliser le formalisme dit des harmoniques sphériques. Pour rappel, le terme $\delta (x,t)$ est une fonction qui associe une perturbation de densité à tout endroit de l'espace et à chaque instant. On dit aussi que cette fonction décrit un champ de densité. Or, il existe un théorème qui nous dit que tout champ peut être décomposée en champs périodiques.

Vous connaissez sans doute la transformée de Fourier des fonctions continues, qui permet de découper un signal en une somme d'ondes de forme cosinusoïdales ou sinusoïdales. Il en existe un équivalent en deux dimensions pour le plan, et en trois dimensions. En additionnant un certain nombre (potentiellement infini) de ces ondes de base, pondérées par un coefficient, on peut obtenir n'importe quel champ résultant.

Illustration des séries de Fourier.

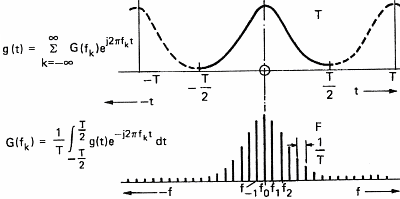
Le champ de densité ne fait pas exception et on peut utiliser ce théorème pour décomposer le champ de densité en une somme d'ondes. Sauf que le champ est plaqué sur une sphère, la surface de dernière diffusion est une sphère. Et l'équivalent de la transformée de Fourier pour une sphère porte le nom d'harmoniques sphériques.

Harmoniques spéhriques sur une sphère tournante.

Le spectre de puissance des perturbations

Décrire le champ de densité avec des séries de Fourier ou avec des harmoniques sphériques permet de définir le spectre de puissance du champ de densité. En temps de normal, il donne l'ensemble des amplitudes de chaque onde sinusoïdale et s'obtient avec la transformée de Fourier. Ici, il s'obtient en prenant la transformée de Legendre et donnent les coefficients pour chaque harmonique sphérique.

Dans le cas qui nous intéresse, la longueur d'onde correspond à la taille d'une perturbation périodique. Le spectre de puissance donne donc l'intensité de la surdensité en fonction de sa taille et est donc une fonction du type :

$P(k)=...$, avec $k$ le nombre d'ondes qui est défini par $k={\frac {2\pi }{\lambda }}$.

Le spectre de puissance et la fonction de corrélation sont reliés l'un à l'autre, par la relation suivante :

$P(k)={\frac {k^{3}}{2\pi ^{2}}}\int \epsilon (r){\mathrm {d} }^{3}{\mathbf {x} }$.

Qui peut aussi s'écrire comme suit :

$P(k)=2\pi \int _{0}^{\infty }r^{2}\cdot {\frac {\sin kr}{kr}}\cdot \epsilon (r)dr$

Les deux équations précédentes nous disent que le spectre de puissance et la fonction de corrélation (en fait son intégrale) sont proportionnels.

Les spectres en loi de puissance et le spectre de Harrison-Zeldovitch

Dans le cas général, connaître le spectre de puissance n'est pas suffisant pour décrire complètement le champ de densité, du moins d'un point de vue statistique. Il en est de même avec la fonction de corrélation qui est elle aussi un résumé imparfait de la distribution. Cependant, il existe des distributions statistiques pour lesquelles la connaissance du spectre de puissance et/ou de la fonction de corrélation suffit à décrire totalement les propriétés statistiques du champ décrit. Ce sont les champs aléatoires gaussiens, pour lesquels la densité suit une distribution gaussienne (la fameuse courbe en cloche). Et ce sont ces gaussiennes qui sont utilisées pour modéliser le champ de densité cosmologique, faute de mieux. Le spectre de puissance de tels champs aléatoires gaussiens suit une loi de puissance de la forme :

$P(k)=A\cdot k^{n}$

Quand l'exposant vaut 1, l'amplitude des fluctuations ne dépend pas de l'échelle. Le spectre de puissance avec $n=1$ est appelé le spectre de Harrison-Zeldovitch, quand il est utilisé en cosmologie.

Précisons que si le spectre de puissance est une loi de puissance, alors la fonction de corrélation est aussi une loi de puissance de la forme :

$\epsilon (d)=k\cdot d^{-\gamma }$, avec $\gamma =n+3$.

Un avantage de ce spectre de puissance est qu'il est invariant si les perturbations sont stables en coordonnées comobiles. Par exemple, c'est le cas après le découplage, où toutes les perturbations évoluent linéairement avec l'expansion, c'est à dire qu'elles grossissent au même rythme que l'expansion. Dit autrement, elles ont toujours la même taille en coordonnées comobiles et sont figées. Dans ce cas, on peut décrire de telles perturbations comme suit :

$\delta (x,t)=D(t)\cdot \delta (x)$

La fonction de corrélation associée devient alors :

$\epsilon (r,t)=D(t)^{2}\cdot \epsilon (r,t_{0})$

Et le spectre de puissance est de :

$P(k,t)=D(t)^{2}\cdot P_{0}(k)$

En clair, avec l'expansion, le spectre de puissance évolue, mais cette évolution est prévisible. Il est simplement multiplié par une valeur qui dépend du carré du temps écoulé. Cela veut dire deux choses. Premièrement, le spectre de puissance est décalé avec le temps. Deuxièmement, les amplitudes sont réduites par un coefficient multiplicatif dépendant du temps. Du moins, c'est le cas pour les structures qui suivent cette loi d'évolution.

Les défauts des spectres en loi de puissance

Les spectres en loi de puissance ont des propriétés intéressantes. Cependant, des arguments techniques nous font dire que le spectre des perturbations ne peut pas être en loi de puissance sur l'ensemble des longueurs d'onde possibles. Ce n'est pas compatible avec l’homogénéité du CMB, qui impose que :

$P(k)\rightarrow 0$ si $k\rightarrow 0$

La relation entre spectre de puissance et fonction de corrélation impose alors que :

$\int _{0}^{\infty }\epsilon (r)r^{2}dr=0$

En clair, si il y a des corrélations en loi de puissance pour un intervalle de k précis, alors il existe des anti-corrélations en-dehors de cette intervalle. Les corrélations et anti-corrélations se compensent et annulent l'intégrale précédente.

Les anisotropies du fond diffus

Carte du fond diffus cosmologique, qui illustre les anisotropies.

Le fond diffus capté à l'heure actuelle correspond aux photons émis 380 000 ans après le big-bang environ, sur une sphère centrée sur la Terre : cette sphère est appelée la surface de dernière diffusion. Si on regarde le fond diffus, on peut remarquer que celui-ci n'est pas totalement homogène, avec quelques variations de température assez aléatoires et dispersées appelées anisotropies. Les scientifiques définissent les anisotropies comme toute déviation de la température CMB par rapport à sa température moyenne. Dans une anisotropie, il existe une petite différence de température en pourcentage par rapport à la moyenne du fond diffus, qui est égale à :

${\frac {T(x)-T_{moyenne}}{T_{moyenne}}}={\frac {T(x)}{T_{moyenne}}}-1={\frac {\Delta T}{T_{moyenne}}}$

L'origine des anisotropies du CMB

Les anisotropies ont diverses origines, les scientifiques font ainsi la différence entre anisotropies primaires et secondaires. Les anisotropies primaires se sont formées lors du découplage, de petites variations de densité ayant laissé leur trace dans le fond diffus. Les anisotropies secondaires après le découplage, quand la matière des étoiles a interagi avec ce fond diffus (rappelez-vous que la matière est à l'état de plasma dans une étoile, plasma qui interagit fortement avec les photons). Les anisotropies secondaires ne sont pas importantes pour le cosmologiste qui étudie la théorie du big-bang. De plus, ces anisotropies secondaires sont de petite taille, peu visibles sur les résultats actuels (à l'exception des anisotropies formées par effet Sache-Wolfe). On peut donc les omettre sans perdre en généralité.

Les empreintes des perturbations de densité dans le CMB

La formation des anisotropies primaires est liée aux perturbations cosmologiques, à la présence de régions de surdensité ou de sous-densité. Les perturbations de densité se traduisent par des perturbations de température, vu que la densité et la température sont reliées par l'équation suivante :

${\frac {\Delta T}{T}}={\frac {1}{4}}{\frac {\Delta p}{p}}+x$

On verra à quoi correspond la variable x plus tard, quand nous aborderons l'effet Sache-Wolfe. Toujours est-il qu'on peut la négliger pour le moment, ce qui donne :

${\frac {\Delta T}{T}}={\frac {1}{4}}{\frac {\Delta p}{p}}$

Démonstration

On a vu dans le chapitre sur l'évolution du rayonnement que pour le rayonnement : ${\frac {d\epsilon }{\epsilon }}=-4{\frac {da}{a}}=-4H$ ${\frac {dT}{T}}=-H$ Quelques manipulations algébriques donnent le résultat voulu.

L'effet Sache-Wolfe

Les surdensités à l'origine des anisotropies sont des zones où la température est plus élevée qu'alentour, cette différence de température entraînant un surcroît de luminosité. Néanmoins, ce sont aussi des zones où la gravité est plus importante. Or, la relativité générale nous dit qu'un photon qui part d'une zone de forte gravité est décalé vers le rouge. Ce décalage gravitationnel est d'origine gravitationnelle, purement lié à la relativité générale. Cela vient du fait que la gravité, dans la relativité générale, est une déformation de la géométrie de l'espace. On peut simplifier en disant que les distances ne se calculent pas de la même manière dans un champ de gravité qu'en dehors. On peut rendre compte de ce phénomène d'une manière simplifiée (et même fausse) en disant que la gravité entraîne une modification stable du facteur d'échelle, par rapport aux environs (c'est une modification "locale"). En sortant d'un champ gravitationnel, un photon garde la même longueur d'onde comobile, ce qui se traduit par une modification de la longueur d'onde perçue (qui tient compte de la modification locale du facteur d'échelle). La modification fait que la longueur d'onde augmente en "sortant" du champ gravitationnel.

Dans le détail, la différence locale de facteur d'échelle est égale au potentiel gravitationnel $\Phi$.

$z_{gravite}={\frac {\Delta a_{locale}}{a_{moyen}}}=-\Phi$

Du fait de ce décalage vers le rouge, la surdensité semble avoir une température inférieure par rapport à celle qu'elle aurait sans ce décalage vers le rouge. C'est ce qu'on appelle l'effet Sache-Wolfe. Pour résumer, on peut décomposer la température perçue par un observateur lointain comme étant la somme du décalage vers le rouge avec la température locale (sans décalage vers le rouge). En notant $T_{p}$ et $T_{l}$ les températures perçues et locales, on a :

${\frac {\Delta T_{p}}{T_{p}}}={\frac {\Delta T_{l}}{T_{l}}}-z_{gravite}={\frac {\Delta T_{l}}{T_{l}}}+\Phi$

Dans leur article original, Sache et Wolfe ont postulé que la valeur de ${\frac {\Delta T_{l}}{T_{l}}}$ était proportionnelle à $\Phi$. Rien d'étonnant à cela : la température dépend de la densité, qui dépend elle-même du potentiel gravitationnel. Leurs calculs et approximations leur ont donné : ${\frac {\Delta T_{l}}{T_{l}}}=-{\frac {2}{3}}\Phi$. On peut en faire une démonstration relativement simple, basée sur quelques arguments physiques.

Par définition, on sait que :

${\frac {\Delta T_{l}}{T_{l}}}=-{\frac {\Delta a}{a}}$

On a vu dans le chapitre sur les modèles cosmologiques que dans un univers où se mélangent rayonnement et matière, on a :

${\frac {\Delta a}{a}}={\frac {2}{3(1+w)}}{\frac {\Delta t}{t}}$

On combine les équations précédentes, on a :

${\frac {\Delta T_{l}}{T_{l}}}=-{\frac {2}{3(1+w)}}{\frac {\Delta t}{t}}$

On peut alors se demander à quoi correspond le terme ${\frac {dt}{t}}$. Il faut savoir que dans un champ de gravitation, le temps s'écoule plus lentement : c'est le phénomène de dilatation des durées. La relativité générale nous dit que ce ralentissement du temps est approximativement proportionnel au potentiel gravitationnel. Autrement dit : ${\frac {\Delta t}{t}}=\Phi$. En combinant les deux équations précédentes, on a :

${\frac {\Delta T_{l}}{T_{l}}}=-{\frac {2}{3(1+w)}}\Phi$

En supposant que la matière domine au fond diffus, on trouve :

${\frac {\Delta T_{l}}{T_{l}}}=-{\frac {2}{3}}\Phi$

En injectant dans l'équation précédente, on trouve :

${\frac {\Delta T_{p}}{T_{p}}}=-{\frac {2}{3}}\Phi +\Phi$

Ce qui se simplifie en :

${\frac {\Delta T_{p}}{T_{p}}}={\frac {1}{3}}\Phi$

Le spectre de puissance du fond diffus

La taille des anisotropies a beaucoup de choses à nous dire concernant la courbure de l'univers, le rapport entre masse visible et énergie noire, et ainsi de suite. Pour comprendre pourquoi, il faut faire appel à ce que l'on appelle le spectre de puissance du fond diffus. Pour rappel, la surface de dernière diffusion est une sphère. La localisation d'un point sur cette sphère demande d'utiliser un système de cordonnées avec : un méridien et un équateur : on peut alors déterminer une latitude et une longitude pour chaque point, celles-ci permettant de localiser le point sur la surface de la sphère. Tout point du fond diffus est donc identifié par une longitude $\theta$ et une latitude $\varphi$. En chaque point, l'intensité de la lumière qui compose le fond diffus varie, à cause de différences de température liées aux anisotropies. Les scientifiques cartographient le fond diffus en notant pour chaque point, la différence de température en pourcentage par rapport à la moyenne du fond diffus :

$\Delta T(\theta ,\varphi ) \over T_{moyenne}$

Illustration de quelques harmoniques sphériques.

Les différences de température entre chaque point sont causées par des différences de densité et de pression, elles-mêmes décrites par un champ de densité. Il y a quelques chapitres, nous avions vu que le champ de perturbation peut se décrire comme la somme de plusieurs champs de densité d'amplitudes différentes. En effet, un théorème très utilisé en physique, le théorème de Fourier, nous dit que toute fonction peut être décomposée en fonctions plus simples, de formes sinusoïdales. En additionnant un certain nombre (potentiellement infini) de ces ondes de base, pondérées par un coefficient, on peut obtenir n'importe quelle fonction résultante. Dans le cas du CMB, qui est de forme sphérique, ces ondes simples sont appelées des harmoniques sphériques.

${\frac {\Delta T(\theta ,\varphi )}{T}}=\sum _{l=0}^{+\infty }\sum _{m=-l}^{+l}\left(a_{l}^{m}\times Y_{l}^{m}(\theta ,\varphi )\right)$

Il est possible d'analyser l'amplitude de chaque harmonique sphérique du CMB en fonction de leur fréquence. Il suffit de reporter ces amplitudes sur un graphique, dont l'abscisse donne la fréquence de chaque harmonique, et l'ordonnée son amplitude. Dit autrement, ce graphique donne l'amplitude de chaque anisotropie en fonction de sa taille : telle anisotropie d'une taille de quelques kilomètres aura une amplitude de tant, telle anisotropie plus grosse aura une amplitude de température plus élevée, etc. Le tout est ce qu'on appelle le spectre de puissance du CMB. Le résultat donne la figure suivante, bien connue des cosmologistes :

Spectre de puissance du CMB.

Le spectre de puissance du CMB peut se déduire des développements des chapitres précédents. Pour résumer rapidement les chapitres précédents, les perturbations ont évolué de deux manières différentes en fonction de leur taille. Les grosses perturbations sont restées figées si on les regarde en coordonnées comobiles, ce qui signifie qu'elles ont grossi en même temps que l'expansion. Dans le chapitre où nous avions introduit le concept de spectre de puissance, nous avions vu que pour de telles perturbations, le spectre de puissance était décalé par l'expansion et que les amplitudes étaient multipliées par un coefficient dépendant du temps, mais le spectre de puissance n'était pas déformé. À l'inverse, pour les petites longueur d'onde, les oscillations acoustique modifient le spectre de puissance et forment des pics assez visibles.

Le plateau de Sachs-wolfe

Comme dit plus haut, les grosses perturbations n'évoluent plus et ne sont affectées que par l'expansion, elles restent figées en coordonnées comobiles. Leur spectre de puissance est assez stable et ne montre pas de pics particuliers, vu qu'il n'y a pas de taille prépondérante pour de telles perturbations. Il n'y a pas de longueur caractéristique qui se démarque. Le spectre de puissance, dans cette portion, suit une loi de puissance.

La taille minimale de ces perturbations se dérive à partir du calcul de l'horizon sonore, la distance à partir de laquelle les oscillations acoustiques n'ont pas d'effet. Pour une distance angulaire inférieure à 100 (l < 100), on est certain que les deux points étudiés sont séparés par une distance supérieure à l’horizon sonore. Précisons que cette distance angulaire tient compte de l'effet Sachs-Wolfe. On est donc certain que les oscillations acoustiques de baryons n'ont pas pu agir dans cette région du spectre, pas plus que les autres phénomènes. Seules les fluctuations primordiales ont laissé leur trace dans cette région du spectre. Le spectre initial de ces fluctuations a été perturbé par l'effet Sachs-Wolfe, ainsi que par des parasites liés aux anisotropies secondaires. Sur le spectre, on voit que cette région est relativement plate et se trouve juste avant le premier pic. Ce qui lui a valu le nom de plateau de Sachs-Wolfe.

Les pics du CMB

Lorsqu'on observe le spectre de puissance du CMB, on observe la présence de plusieurs pics à certains endroits. Les mathématiques nous disent que ces pics sont localisés à des fréquences bien précises, multiples d'une fréquence dite fondamentale. Les pics sont situés respectivement à la fréquence fondamentale pour le premier pic et aux harmoniques pour les suivants. On observe plusieurs de ces pics sur le CMB, dont l'amplitude nous renseigne sur certains paramètres, comme la courbure ou le rapport entre masse visible et matière noire. Les deux premiers sont déterminés par la taille des oscillations acoustiques de baryons, alors que ce n'est pas le cas des suivants.

Le premier pic donne des indications sur la fréquence fondamentale des ondes sonores, qui est liée à la courbure de l'univers K. Précisément, la fréquence fondamentale correspond à une surdensité dont l'extension était maximale au moment du big-bang, et qui s'est compressée avant le découplage. Au moment du découplage, celle-ci a atteint sa compression maximale et s’apprêtait à se détendre. La fréquence fondamentale ayant l'amplitude maximale, sa longueur d'onde est donc égale à l'horizon sonore. Depuis, cet horizon sonore a gonflé du fait de l’expansion de l'univers, ce qui se traduit par une diminution de sa taille. La fréquence fondamentale actuelle est tout simplement le rapport entre distance de la surface de dernière diffusion et rayon de l'horizon sonore. L'analyse du premier pic donne une courbure nulle.

Le second pic correspond au double de la fréquence fondamentale, qui correspond à une surdensité qui a eu le temps de faire une période complète entre le big-bang et le découplage. Il donne des indications sur la quantité de matière baryonique, à savoir formée de protons et de neutrons (en réalité, de baryons, des particules composites formées de quarks et gluons). Cela vient du fait que la valeur moyenne des ondes sonores vaut, comme on l'a vu plus haut : $-(1+R)\Phi$. Le rapport entre densité de matière baryonique et de rayonnement modifie la valeur de R, et donc la valeur moyenne. Pour comprendre le mécanisme exact, rappelons que la fréquence des oscillations dépend de la différence entre pression et gravité dans les surdensités. La pression dépend essentiellement de la pression de radiation, mais pas du tout de la pression de la matière baryonique. La gravité par contre, dépend autant de la matière baryonique que du poids du rayonnement. Sans matière baryonique, les amplitudes des compressions et décompressions devraient être égales, symétriques par rapport à la valeur moyenne. Si on ajoute de la matière baryonique, l'amplitude maximale (des décompressions) reste la même, vu qu'elle dépend surtout de la pression de radiation. Mais l'amplitude maximale des compressions est amplifiée par le poids de la matière baryonique. Les amplitudes sont alors inégales, plus amples pour les compressions. Ainsi, le rapport entre matière baryonique et rayonnement influence l'amplitude des ondes sonores, ce qui se remarque dans le spectre de puissance, sur le second pic.

Les pics après le troisième sont quelque peu atténués. Pour comprendre pourquoi, il faut se rappeler, les ondes sonores se propagent par des collisions entre particules. Avant et au moment de la recombinaison, les photons et autres particules avaient un temps de libre parcours moyen très élevé. Dans les unités de distance actuelle, le libre parcours moyen serait de 10 000 années lumières. Il va de soi que sur le CMB actuel, les ondes sonores dont la longueur d'onde est plus petite sont atténuées. Vu que seule une portion des particules a pu entrer en collision, les particules n'ont pas eu le temps de transmettre totalement l'onde sonore par collisions. Cela en réduit l'amplitude. La région du spectre dans laquelle se manifeste cet effet, localisée pour des longueurs l tels que l > 1000, est appelée la queue amortie.

En savoir plus

• Site sur l'effet Sche-Wolfes

Preuves de la théorie du big-bang

Dans les chapitres précédents, nous avons abordé en détail les bases théoriques de la cosmologie. En soit, la théorie cosmologique actuelle est un petit peu plus compliquée. Dans le détail, les observations astronomiques sont utilisées pour déterminer la valeur de nombreux paramètres, laissés libres dans les chapitres précédents. Le modèle actuel, le modèle LCDM, précise la valeur du facteur de Hubble, l'âge de l'univers, la courbure spatiale de l'univers, la densité de matière ordinaire, la densité de matière noire, la densité d'énergie noire et quelques autres paramètres dérivés. Ce modèle permet d'expliquer de nombreuses observations, mais il faut face à quelques problèmes. Des théories concurrentes existent, comme le modèle Rh=ct, et bien d'autres. Dans ce qui va suivre, nous allons voir quelles sont les preuves en faveur de la théorie LCDM et de la théorie de l'expansion en général. Puis, nous allons voir quels sont les problèmes rencontrés par le modèle LCDM.

Les observations en faveur de la théorie du big-bang

On peut se demander quelles sont les preuves de l’expansion de l'univers (et donc, indirectement, du big-bang). On sait que la loi de Hubble et le phénomène de décalage vers le rouge de la lumière sont des prédictions de la théorie de l'expansion qui sont confirmées expérimentalement depuis belle lurette. Mais d'autres témoins sont demandés à la barre, pour que le jury puisse se faire son opinion !

La nucléosynthèse primordiale

La première preuve tient dans les conséquences du découplage thermique sur la formation des noyaux et des baryons. Les équations permettent de calculer exactement le rapport entre le nombre de protons et de neutrons né de ce découplage, ainsi que le rapport du nombre d'atomes d'hydrogènes, d'hélium et de lithium. La théorie prédit que 92% des atomes de l'univers est composé d'hydrogène, 7% des atomes d’hélium, et le reste est composé d'autres éléments chimiques. Malheureusement, les étoiles ont produit de l’hélium et d'autres éléments chimiques, modifiant les rapports de proportion dans les galaxies récentes : les supernovas ont enrichi le milieu interstellaire en Carbone, Oxygène, Hélium, etc. C'est pour cela qu'on observe des rapports de l'ordre de 75% d'hydrogène, et 24% d'hélium. Pour éliminer le problème, il suffit d'observer la composition chimique des toutes premières galaxies formées, que l'on peut observer à la lisière de l'univers observable (les fameux quasars). Les observations montrent que dans ces galaxies, on observe des rapports exactement identiques à ceux prédits par la théorie du big-bang.

Les mêmes équations permettent de calculer le rapport nombre de protons sur nombre de neutrons. Là encore, celui-ci a été modifié par certaines désintégrations radioactives, mais on peut quantifier le phénomène et prédire les rapports actuels en fonction des rapports prédits lors du découplage. Et là encore, les conclusions sont exactement celles prédites par la théorie de l’expansion de l'univers.

Le fond diffus cosmologique

La théorie du big-bang est la seule à prédire l'existence du fond diffus cosmologique de photons, abordé il y a quelques chapitres. Le fond diffus capté à l'heure actuelle correspond aux photons émis sur une sphère centrée sur la Terre, 380 000 ans après le big-bang environ : cette sphère est appelée la surface de dernière diffusion. Si on regarde le fond diffus, on peut remarquer que celui-ci n'est pas totalement homogène, avec quelques variations de température assez aléatoires et dispersées appelées anisotropies. On a vu il y a quelques chapitres que ces anisotropies sont les traces laissées par des ondes sonores qui se propageaient dans le plasma primordial. Diverses campagnes d'observation ont déterminé la taille des surdensités, des grumeaux de matière, et ont réussi ce qui a permis d'induire les valeurs des paramètres utilisés pour calculer la taille des surdensités.

On a vu il y a quelques chapitres que le spectre du fond diffus possède quelques pics, chacun ayant une signification relativement précise. En postulant un univers sans courbure, et avec quelques hypothèses supplémentaires, on arrive à avoir un accord parfait avec les données observationnelles, comme le montre la courbe ci-dessous. La théorie arrive ainsi à déterminer la taille des zones de surdensité en fonction de certains paramètres comme l'âge de l'univers, le facteur de Hubble, etc. C'est la première réussite de la théorie du big-bang : réussir à prédire l'état du fond diffus cosmologique, seulement à partir des équations vues plus haut. Les campagnes d'observation du fond diffus se succèdent les unes aux autres, pour tenter d'invalider ou de valider divers modèles d’univers, ou théories spéculatives sur le big-bang et les mécanismes thermodynamiques en place avec la recombinaison.

Les problèmes de la théorie cosmologique LCDM

La théorie moderne de la cosmologie n'est pas sans défauts. En utilisant les paramètres mesurés par les astronomes, le modèle cosmologique marche bien pour prédire la plupart des variables cosmologiques pertinentes. Mais aucune théorie n'est parfaite et les scientifiques doivent chercher leurs défauts, en vue de les réfuter ou de les améliorer. À l'heure actuelle, l'existence de l'énergie noire, ainsi que de la matière noire, est un challenge que les théories ne peuvent pas encore expliquer correctement. Aucun mécanisme physique, aucune particule, aucun champ physique ne permet d'expliquer énergie et matière noire. Mais outre ces problèmes, le modèle standard de la cosmologie fait face à deux autres problèmes principaux : le problème de la platitude et le problème de l'horizon.

Le problème de la platitude

Le premier problème de la théorie du big-bang est que l'univers est plat. On pourrait croire que ce n'est qu'une coïncidence, mais les physiciens ne sont pas vraiment satisfaits par cette explication. Beaucoup pensent que le fait que la courbure soit nulle n'est pas naturel et que c'est quelque chose qui doit être expliqué. C'est ce qu'on appelle le problème de la platitude : pourquoi la courbure semble-t-elle nulle ?

Le problème de l'horizon

Problème de l'horizon.

Les observations montrent que le CMB a une température relativement uniforme, proche d'un équilibre thermique. Même des points opposés sur la surface de dernière diffusion ont des températures similaires et sont relativement homogènes entre eux. En soi, cette observation n'est pas un problème dans tous les modèles cosmologiques. Par exemple, un univers en expansion linéaire est parfaitement compatible avec un CMB en équilibre thermique total, de même qu'un univers en expansion exponentielle. Mais dans le modèle cosmologique LCDM, qui fait consensus parmi la communauté des cosmologistes, un tel équilibre thermique parfait ne peut pas exister. Des points éloignés n'ont pas pu interagir entre eux pour harmoniser leurs températures, même indirectement, sauf à supposer que l'on puisse dépasser la vitesse de la lumière. On voit ainsi apparaître le problème de l'horizon : pourquoi le fond diffus est-il si homogène ? C'est là un des points que la théorie LCDM ne peut pas expliquer.

Pour comprendre pourquoi, il faut remarquer que même en allant à la vitesse de la lumière, les photons n'ont pût parcourir qu'une certaine distance entre le big-bang et la recombinaison. On peut calculer cette distance assez simplement. Pour cela, on peut soustraire le rayon de l'univers observable actuel du rayon de l'univers observable lors de la recombinaison. Dit autrement, on souhaite calculer la différence suivante :

$\Delta r=r(t)-r(t_{0})$, avec $t$ l'âge actuel de l'univers et $t_{0}$ l'âge de l'univers lors de la recombinaison.

Utilisons alors la formule qui donne le rayon de l'univers observable :

$r(t)=c\cdot a(t)\cdot \int _{0}^{t_{u}}{dt \over a(t)}$

En combinant ces deux équations, on trouve :

$\Delta r=c\cdot a(t)\cdot \int _{0}^{t_{u}}{dt \over a(t)}-c\cdot a(t)\cdot \int _{0}^{t_{u}}{dt \over a(t)}$

On factorise et on simplifie les intégrales, ce qui donne :

$\Delta r=c\cdot a(t)\cdot \left[\int _{0}^{t_{u}}{dt \over a(t)}-\int _{0}^{t_{u}}{dt \over a(t)}\right]=\int _{t_{0}}^{t_{u}}{dt \over a(t)}$

Après le découplage, l'univers était dominé par la matière, ce qui fait que l'on a :

$a(t)\propto t^{\frac {2}{3}}$

En combinant les deux équations précédentes, on trouve que le tout vaut :

$r(t)-r(t_{0})=3\cdot c\cdot t\left[1-\left({\frac {t_{0}}{t}}\right)^{\frac {2}{3}}\right]$

Le calcul donne une distance approximativement égale à :

$r(t)-r(t_{0})\approx 3\cdot c\cdot t=6000\cdot h^{-1}\cdot Mpc$

Cette distance donne, quand elle est projetée sur la surface de dernière diffusion, un angle maximal bien précis estimé à 2°. Pour le dire plus simplement, sur ce qu'on voit du CMB depuis la Terre, deux points séparés de plus de 2° ne peuvent pas avoir communiqué entre eux et ne peuvent pas être en équilibre thermique. Pourtant, tout le CMB est à l'équilibre thermique et a une température relativement uniforme ! Même des points aux antipodes du CMB ont une température assez similaire et suivent la même loi du rayonnement de corps noir.

Rappelons que ce problème n’apparaît que pour un univers dont l'expansion ralentit dans le temps, c'est à dire un univers dominé par la matière, le rayonnement ou les deux. Ce qui colle avec le modèle LCDM actuel, qui a successivement été dominé par le rayonnement puis par la matière, avant que l'énergie noire commence à faire son effet sur une période récente. Les calculs disent que dans un univers en expansion constante (modèle linéaire) ou croissante, voire exponentielle (dominé par la constante cosmologique), le problème de l'horizon n’apparaît pas. Et cela a une importance capitale pour le prochain chapitre.

L'hypothèse de l'inflation

Inflation comparée à un modèle sans inflation.

Les problèmes du modèle LCDM peuvent être résolus par une hypothèse appelée l'inflation cosmologique. Celle-ci postule que l'univers a subi une phase d’expansion avant la recombinaison, avec une vitesse d'expansion supérieure à celle de la lumière. Avec l'inflation, la surface de dernière diffusion correspond à une portion d'espace suffisamment petite pour harmoniser les températures. Cette portion d'espace homogène a subi l'inflation cosmologique, jusqu'à devenir la surface de dernière diffusion. Le tout est illustré dans le schéma ci-contre, qui montre bien que la surface de dernière diffusion correspond à un espace assez grand sans inflation cosmologique, et à un espace bien plus petit avec elle.

Dans cette théorie, l'évolution de l'univers s'est déroulée en plusieurs étapes :

• une étape antérieure à l'inflation, qu'on ne connaît pas très bien ;
• une étape d'inflation exponentielle ;
• une étape où l'univers est dominé par le rayonnement ;
• une étape où l'univers est dominé par la matière.

Inflation

À l'heure actuelle (début 2016), il n'existe pas de preuve certaine de l'existence d'une inflation. À vrai dire, les scientifiques ne sont même pas certains du déroulement des évènements. On ne sait pas si cette inflation a eu lieu, ni quand. Par quand, on veut dire qu'elle peut avoir eu lieu n'importe quand avant la recombinaison. Dans le cas le plus simple, l'inflation aurait eu lieu avant la phase dominée par le rayonnement, mais il est aussi possible qu'elle ait eu lieu en plein milieu. Dans les faits, on ne peut pas encore discerner ces scénarios avec les observations dont on dispose et la théorie ne nous éclaire pas plus que cela... Au mieux, il s'agit d'une théorie qui fait des prédictions sur certains paramètres du fond diffus, mais ces derniers n'ont pas encore été mesurés. En 2014, la coopération internationale BICEP2 a effectuée des mesures du CMB, espérant trouver des traces de l'inflation dans le CMB, prévues par la théorie. Les résultats étaient initialement favorables et il semblait que l'inflation venait d'être validée scientifiquement, mais des analyses ultérieures ont montré que ce n'était pas le cas. Les analyses statistiques avaient omis divers effets parasites, comme l'influence de la poussière interstellaire/intergalactique et divers autres biais, réduisant les résultats à néant. Reste à voir ce que nous réserve l'avenir !

Le problème de la platitude et l'inflation

Cette hypothèse résout le problème de l'horizon, mais aussi le problème de la platitude : la zone a tellement gonflé que les effets de la géométrie de l'univers seraient presque invisibles. Pour faire une analogie, imaginez que la zone gonflée par l'expansion est la surface de la Terre : vous êtes si petits par rapport à la Terre que vous ne vous rendez pas compte de sa rotondité et voyez un sol plat. Pour une explication plus mathématique, il faut recourir à la première équation de Friedmann, que voici :

$H^{2}={\frac {8\pi G}{3c^{2}}}\rho -{\frac {K}{a(t)^{2}}}$

Vous voyez que dans l'équation précédente, l'effet de la courbure sur l'expansion correspond au terme ${\frac {K}{a(t)^{2}}}$, où l'intensité de la courbure $K$ est modulée par le terme ${\frac {1}{a(t)^{2}}}$. Plus le facteur d'échelle augmente, plus le terme ${\frac {K}{a(t)^{2}}}$ diminue et moins le terme de courbure a d'effet sur l'expansion. Sans inflation, on s'attend à ce que le facteur d'échelle suive une loi de puissance dont les exposants sont connus. D'abord on a une phase d'expansion dominée par le rayonnement avec un exposant proche de 1/2, qui dure environ 300 000 ans, puis une phase dominée par la matière de près de 13 milliards d'années où l'exposant est de 2/3. Les calculs nous disent que la courbure K devait être particulièrement basse pour coller avec les données observationnelles actuelles connues. Mais si l'inflation a bien eu lieu, a(t) aurait connu une hausse très importante pendant ou avant la phase dominée par le rayonnement, réduisant le terme ${\frac {K}{a(t)^{2}}}$ à presque rien, en accord avec les données observationnelles.

Le mécanisme de l'inflation

Le mécanisme supposé pour l'inflation est assez simple à comprendre à partir des équations de Friedmann. À vrai dire, une expansion accélérée s'explique déjà dans ce modèle par la constante cosmologique. Mais en supposant que la constante cosmologique permet d'expliquer l'inflation, on est face à un problème : l'inflation ne s’arrête jamais ! En effet, une constante cosmologique entraîne une expansion exponentielle de l'univers ad vitam æternam, alors que l'inflation a été un phénomène temporaire. La constante cosmologique ne peut donc pas expliquer l'inflation, et il faut trouver autre chose qui se comporte comme une constante cosmologique à un détail près : elle doit varier dans le temps, histoire d'être assez grand lors de la phase d'inflation, et disparaître ensuite.

Au niveau des équations, on peut rendre compte de cela de la même manière que pour la constante cosmologique : en rajoutant une densité d'énergie $\rho _{inflaton}$ dans la première équation de Friedmann. Celle-ci s'écrit alors comme suit :

$H(t)^{2}={\frac {8\pi G}{3c^{2}}}\left(\rho _{inflaton}+\rho _{\Lambda }-{\frac {\rho _{k}0}{a(t)^{2}}}+{\frac {\rho _{m}0}{a(t)^{3}}}+{\frac {\rho _{r}0}{a(t)^{4}}}\right)$

Il suffit juste que $\rho _{inflaton}$ augmente pendant la phase d'inflation avant de se réduire à peau de chagrin ensuite et le tour est joué. Reste à inventer le mécanisme d'inflation qui se cache derrière $\rho _{inflaton}$. Et là, les théories sont assez nombreuses ! Il faut dire que n'importe quelle fonction mathématique ad hoc peut fonctionner tant qu'elle a quelques propriétés mathématiques peu contraignantes. La majorité des tentatives se basent sur la présence de ce qu'on appelle un champ scalaire. Un champ scalaire est quelque chose qui attribue un nombre à tout point dans l'espace à chaque instant, appelé le potentiel, noté $\phi$. De plus, ce champ a une densité d'énergie en chaque point de l'espace, qui dépend du potentiel : celle-ci sera notée $V(\phi )$. Si on suppose que le champ a la même valeur en tout point, les équations nous donnent la densité d'énergie et la pression associée à ce champ.

La densité d'énergie causée par le champ dépend du potentiel $V(\phi )$ et de sa variation dans le temps (qui est un "équivalent" de l'énergie cinétique pour un champ scalaire). La formule exacte est la suivante :

$\rho _{\phi }={\frac {1}{2}}{\dot {\phi }}^{2}+V(\phi )$, avec ${\dot {\phi }}={\ddot {\phi }}^{2}+{\dot {\phi }}^{2}$.

La pression est de :

$P_{\phi }={\frac {1}{2}}{\dot {\phi }}^{2}-V(\phi )$

On peut alors en déduire ${\frac {d}{dt}}\rho _{\phi }$, $\rho _{\phi }+P_{\phi }$ et $\rho _{\phi }+3P_{\phi }$, qui seront utilisées dans ce qui suit :

${\frac {d}{dt}}\rho _{\phi }={\frac {d}{dt}}\left({\frac {1}{2}}{\dot {\phi }}^{2}+V(\phi )\right)={\ddot {\phi }}^{2}+{\frac {d}{dt}}V(\phi )$

$\rho _{\phi }+P_{\phi }=\left({\frac {1}{2}}{\dot {\phi }}^{2}+V(\phi )\right)+\left({\frac {1}{2}}{\dot {\phi }}^{2}-V(\phi )\right)={\dot {\phi }}^{2}$

$\rho _{\phi }+3P_{\phi }=\left({\frac {1}{2}}{\dot {\phi }}^{2}+V(\phi )\right)+3\left({\frac {1}{2}}{\dot {\phi }}^{2}-V(\phi )\right)={\frac {1}{2}}{\dot {\phi }}^{2}+V(\phi )+{\frac {3}{2}}{\dot {\phi }}^{2}-3V(\phi )=2\left({\dot {\phi }}^{2}-V(\phi )\right)$

Injectons ces équations dans les équations de Friedmann, ce qui donne :

$H^{2}={\frac {8\pi G}{3}}\left({\frac {1}{2}}{{\phi }'}^{2}+V(\phi )\right)$

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\left[2\left({\dot {\phi }}^{2}-V(\phi )\right)\right]=-{\frac {8\pi G}{3}}\left[{\dot {\phi }}^{2}-V(\phi )\right]$

${\ddot {\phi }}^{2}+{\frac {d}{dt}}V(\phi )+3H{\dot {\phi }}^{2}=0$

Maintenant, négligeons le terme ${\frac {1}{2}}{\dot {\phi }}^{2}$, supposé bien plus petit que le potentiel $V(\phi )$ et faisons de même pour la dérivée seconde. En clair, on suppose que ${\dot {\phi }}<<V(\phi ))$, hypothèse souvent complémentée avec ${\ddot {\phi }}<<V(\phi ))$. Les équations précédentes deviennent ceci :

$H^{2}={\frac {8\pi G}{3}}V(\phi )$

${\frac {a''}{a}}={\frac {8\pi G}{3}}V(\phi )$

${\frac {d}{dt}}V(\phi )=0$

Les équations précédentes nous disent que l'univers est en expansion pour la première équation, que cette expansion est accélérée pour la seconde, et que le potentiel et la densité d'énergie restent constants malgré l'expansion pour l'équation du fluide. Les trois propriétés sont ce qu'on attend d'un univers dominé par une constante cosmologique, ou par de l'énergie noire de pression négative. Pour résumer, on obtient bien une expansion accélérée dans le cas où ${\dot {\phi }}<<V(\phi ))$, hypothèse souvent complémentée avec ${\ddot {\phi }}<<V(\phi ))$.

Précisons cependant que si le potentiel a une valeur nulle, il ne cause aucune expansion : on peut alors modéliser l'inflation en supposant que $V(\phi )$ diminue avec le temps, l'inflation s’arrêtant quand le champ est nul. Tout champ qui respecte ces conditions peut déclencher une inflation, ce qui laisse beaucoup de possibilités. Le champ lié au boson de Higgs est une solution possible, par exemple.

Les solutions statiques des équations de Friedmann

Les équations de Friedmann basiques nous disent une chose assez importante : l'univers est en expansion. La première équation de Friedmann donne la vitesse de l'expansion, la seconde donne l'accélération de l'expansion de l'univers. Elle nous dit si l'expansion accélère ou ralentit, en fonction de la densité de la pression de l'univers.

$H^{2}={\frac {8\pi G}{3}}\rho -{\frac {k\cdot c^{2}}{a^{2}}}$

${\frac {a''}{a}}=-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)$

Rien de surprenant en soi, nous savons aujourd'hui que l'univers est en expansion. Mais à l'époque où ces équations ont été déduites à partir de la relativité générale, c'était une surprise. L'expansion de l'univers n'était pas encore connue et la loi de Hubble n'avait pas encore été découverte. Le consensus commun de l'époque était que l'univers était statique et un univers en expansion paraissait contre-intuitif.

L'univers statique sans constante cosmologique

Pour avoir un univers statique, il faut que le facteur d'échelle soit constant, ce qui implique que $H(t)=0$, $a(t)'=0$ et $a(t)''=0$ à tout instant t. En injectant ces conditions dans les équations de Friedmann, on trouve :

${\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}=0$

$-{\frac {4\pi G}{3}}\left(\rho +3{\frac {P}{c^{2}}}\right)=0$

Notez que l'équation du fluide de Friedmann disparait tout simplement. En effet, dans un univers statique, la matière n'est pas diluée, et donc la densité reste constante. Le terme avec la dérivée de la densité vaut donc 0. De plus, le facteur de Hubble vaut aussi zéro : tous les termes de l'équation valent zéro, ce qui fait disparaitre l'équation.

Les deux équations précédentes se simplifient, ce qui donne :

${\frac {8\pi G}{3c^{2}}}\rho _{e}={\frac {k\cdot c^{2}}{a^{2}}}$

$\rho +3{\frac {P}{c^{2}}}=0$

La première équation dit qu'un univers statique est possible, à condition que la courbure compense l'effet de la matière et du rayonnement. Ce qui est assez intuitif : la présence de matière/rayonnement fait s'effondrer l'univers sur lui-même sous l'effet de la gravité. Pour compenser cela, on doit avoir une courbure qui crée une expansion exactement opposée.

La seconde équation nous dit que si matière il y a, sa densité doit être compensée par sa pression. La matière doit donc avoir une pression négative, ce qui n'a pas de sens physique. Précisémment, il faut que l'équation qui relie densité et pression soit la suivante :

$P=-{\frac {1}{3}}\rho c^{2}$

L’univers statique d'Einstein : l'invention de la constante cosmologique

Les équations de Friedmann de base ne permettent pas d'avoir un univers statique sans recourir à des hypothèses physiques complètement tordues. Il fallait réconcilier un univers statique avec ces équations, ce qu'a fait Einstein. Il leur ajouta un terme censé corriger ce qui était un "problème" à l'époque. Pour obtenir un univers stationnaire (stable, sans expansion), il pris les équations de la relativité générale et ajouta un terme au bon endroit (dans le tenseur énergie-impulsion, pour les connaisseurs). Le terme $\Lambda$, ajouté aux équations de Friedmann, a reçu le nom de constante cosmologique. Les équations de Friedmann étaient alors modifiées, et sont devenues ceci :

$H^{2}={\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}$

${\frac {a''}{a}}={\frac {\Lambda c^{2}}{3}}-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$

L'ajout de la constante cosmologique modifie la dynamique des équations. Dans la première équation de Friedmann, la constante sert à compenser l'effet de la gravité. L'idée est que la somme courbure + constante cosmologique compense exactement la densité, ce qui annule l'expansion. En soi, on pouvait faire la même chose avec la courbure, mais avec un défaut : la courbure n'est pas présente dans la seconde équation de Friedmann, ce qui ne réglait qu'une partie du problème. Mais la constante cosmologique n'a pas ce problème. Elle est bien présente dans la seconde équation de Friedmann et peut compenser l'effet de la densité avec la valeur appropriée.

Pour un univers statique, on a :

${\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}=0$

${\frac {\Lambda c^{2}}{3}}-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)=0$

Le calcul de la valeur de la constante cosmologique pour un univers statique

La seconde équation se reformule alors comme suit :

${\frac {\Lambda c^{2}}{3}}={\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$

On multiplie par ${\frac {3}{c^{2}}}$ :

$\Lambda ={\frac {4\pi G}{c^{4}}}(\rho _{e}+3P)$

Le calcul de la courbure pour un univers statique

Partons de la seconde équation de Friedmann avec constante cosmologique :

${\frac {\Lambda c^{2}}{3}}={\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)$

En injectant dans la première équation de Friedmann, on trouve :

${\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)=0$

On développe :

${\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {4\pi G}{3c^{2}}}\rho _{e}+{\frac {4\pi G}{3c^{2}}}(3P)=0$

On regroupe les termes et on simplifie :

${\frac {4\pi G}{c^{2}}}\rho _{e}+{\frac {4\pi G}{c^{2}}}P-{\frac {k\cdot c^{2}}{a^{2}}}=0$

On factorise et on réorganise les termes :

${\frac {4\pi G}{c^{2}}}(\rho _{e}+P)=k\cdot {\frac {c^{2}}{a^{2}}}$

Ce qui donne :

$k=a^{2}{\frac {4\pi G}{c^{4}}}(\rho _{e}+P)$

Le lien entre constante cosmologique et courbure dans le modèle d'Einstein

Les deux sections précédentes nous ont démontré les deux équations suivantes :

$k=a^{2}{\frac {4\pi G}{c^{4}}}(\rho _{e}+P)$

$\Lambda ={\frac {4\pi G}{c^{4}}}(\rho _{e}+3P)$

Si on suppose que la pression est négligeable, on peut combiner les deux équations précédentes pour trouver :

$\Lambda ={\frac {k}{a^{2}}}$

En clair, la constante cosmologique implique que l'univers soit courbe. L'obligation d'avoir un univers courbe est un des défauts des univers statiques avec constante cosmologique, mais il est loin d'être le seul. Mais dans les grandes lignes, tous ces défauts pointent vers un même problème : pour obtenir un univers statique, la valeur de la constante cosmologique et de la courbure doivent être minutieusement calibrées pour obtenir un univers statique. L'ensemble de ces défauts font que la constante cosmologique est une réponse imparfaite pour ceux qui veulent un univers statique avec les équations de Friedmann. Aussi, Einstein a abandonné son idée de constante cosmologique pour obtenir un univers statique.

GFDL

Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans texte de dernière page de couverture.