Fonctionnement d'un ordinateur/Version imprimable 2

Un ordinateur est un appareil électronique parmi tant d'autres. La conception de ces appareils est un domaine appelé l’électronique et les gens qui conçoivent ces appareils sont appelés des électroniciens. Tous les appareils électroniques contiennent plusieurs composants électroniques simples, qui sont placés sur un support plat, en plastique ou en céramique, appelé la carte électronique. Les composants sont soudés sur la carte, histoire qu’ils ne puisse pas s’en décrocher. Ils sont reliés entre eux par des fils conducteurs, le plus souvent du cuivre ou de l’aluminium, ce qui leur permet de s’échanger des données. Sur les cartes simples, ces fils sont intégrés dans la carte électroniques, dans des creux du plastique. Ils portent le nom de pistes. Évidemment, tous les composants ne sont pas tous reliés entre eux. Par exemple, si je prends un ordinateur, l’écran n’est pas relié au clavier.
Les composants d'un ordinateur de type PC
modifierDe l'extérieur, l'ordinateur est composé d'une unité centrale sur laquelle on branche des périphériques.
Les périphériques regroupent l'écran, la souris, le clavier, l'imprimante, et bien d'autres choses. Ils permettent à l'utilisateur d'interagir avec l'ordinateur : un clavier permet de saisir du texte sous dans un fichier, une souris enregistre des déplacements de la main en déplacement du curseur, un écran affiche des données d’images/vidéos, un haut-parleur émet du son, etc. Tout ce qui est branché sur un ordinateur est, formellement un périphérique.


1 : Écran ;
2 : Carte mère ;
3 : Processeur ;
4 : Câble Parallel ATA ;
5 : Mémoire vive (RAM) ;
6 : Carte d'extension ;
7 : Alimentation électrique ;
8 : Lecteur de disque optique ;
9 : Disque dur ;
10 : Clavier ;
11 : Souris.
L'unité centrale est là où se trouvent tous les composants importants d'un ordinateur, ceux qui font des calculs, qui exécutent des logiciels, qui mémorisent vos données, etc. Dans les ordinateurs portables, l'unité centrale est bien là, située sous le clavier ou dans l'écran (le plus souvent sous le clavier). À l'intérieur de l'unité centrale, on trouve trois composants principaux : le processeur, la mémoire et les entrée-sorties.
- Le processeur traite les données, les modifie, les manipule. Pour faire simple, il s’agit d’une grosse calculatrice hyper-puissante. Il comprend à la fois un circuit qui fait des calculs, et un circuit de contrôle qui s'occupe de séquencer les calculs dans l'ordre demandé.
- La mémoire vive conserve des informations/données temporairement, tant que le processeur en a besoin.
- La carte mère n'est autre que le circuit imprimé, la carte électronique, sur laquelle sont soudés les autres composants.
Outre ces composants dits principaux, un ordinateur peut comprendre plusieurs composants moins importants, surtout présents sur les ordinateurs personnels. Ils sont techniquement facultatifs, mais sont très présents dans les ordinateurs personnels. Cependant, certains ordinateurs spécialisés s'en passent. Les voici :
- L'alimentation électrique convertit le courant de la prise électrique en un courant plus faible, utilisable par les autres composants.
- Diverses cartes d'extension sont branchées sur la carte mère. Elles permettent d’accélérer certains calculs ou certaines applications, afin de décharger le processeur. Par exemple, la carte graphique s'occupe des calculs graphiques, qu'il s'agisse de graphismes 3D de jeux vidéos ou de l'affichage en 2D du bureau. Dans un autre registre, la carte son prend en charge le microphone et les haut-parleurs.
- Les disques durs sont des mémoires de stockage, qui mémorisent vos données de manière permanente.
- Les lecteurs CD-ROM ou DVD-ROM permettent de lire des CD ou des DVD.
- Et ainsi de suite.
Les appareils électroniques programmables et non-programmables
modifierUn ordinateur comprend donc une unité centrale sur laquelle on connecte des périphériques. Et l'unité centrale contient un processeur, plusieurs mémoires, des cartes d'extension et une carte mère pour connecter le tout. Mais il s'agit là d'une description assez terre-à-terre de ce qu'est un ordinateur. Une autre description, plus générale, se base sur le fait qu'un ordinateur est une énorme calculatrice programmable. Elle permet d'expliquer pourquoi il y a une distinction entre processeur et mémoire, entre unité centrale et périphériques.
La séparation entre entrées-sorties et traitement
modifierL'unité centrale peut être vue comme une énorme calculatrice ultra-puissante, qui exécute des commandes/opérations. Mais à elle seule, elle ne servirait à rien, il faut interagir avec par l'intermédiaire de plusieurs périphériques. Il existe deux types de périphériques, qui sont conceptuellement différents. Les périphériques comme le clavier ou la souris permettent d'envoyer des informations à l'ordinateur, d'agir sur celui-ci. A l'inverse, les écrans transmettent des informations dans le sens inverse : de l'ordinateur vers l'utilisateur. Les premiers sont appelés des entrées, les seconds des sorties.
Un ordinateur reçoit des informations sur des entrées, effectue des opérations/traitements dessus, puis envoie le résultat sur ses sorties. Les informations sont représentées sous la forme de nombres. Toute donnée dans un ordinateur est codée avec un ou plusieurs nombres regroupés dans une donnée, un fichier, ou autre. Par exemple, quand vous appuyez sur votre clavier, le clavier envoie un numéro de touche à l'unité centrale, qui indique quelle touche a été appuyée. L'ordinateur effectue alors des traitements, et détermine quoi afficher à l'écran. L'image à afficher à l'écran est codée sous la forme d'une suite de nombres (un par pixel). L'image est envoyée à l'écran, qui traduit la suite de nombre en image à afficher.
Les entrées traduisent des actions utilisateurs en nombres, qui sont ensuite traités par l'ordinateur. On dit que les entrées encodent les actions utilisateur. Les sorties font la traduction inverse, elles transforment des suites de nombres en une action physique. On dit qu'elles décodent des informations. Pour résumer, toute appareil électronique est composé par :
- Des entrées sur lesquelles l'utilisateur agit sur l'ordinateur. Les entrées transforment les actions de l'utilisateur en nombres, qui sont interprétés par l'ordinateur.
- Une unité de traitement, qui manipule des nombres et fait des calculs/opérations dessus. Les nombres proviennent des entrées, du disque dur, ou d'autres sources, peu importe. L'unité de traitement effectue des calcul et mémorise des nombres.
- Des sorties, qui va récupèrent le résultat calculé par l'unité de traitement pour en faire quelque chose : écrire sur une imprimante ou sur un moniteur, émettre du son,...

L'unité centrale d'un ordinateur est découpée en deux grands composants. Une unité de traitement proprement dite qui fait les calculs, une mémoire qui mémorise les opérandes et résultats des calculs. La séparation entre processeur et mémoire est nécessaire pour qu'un appareil électronique soit qualifié d'ordinateur. De nombreux appareils n'ont pas de séparation entre unité de traitement et mémoire, comme certaines vielles radios AM/FM.

Un ordinateur est un appareil programmable
modifierLes appareils simples sont non-programmables, ce qui veut dire qu’ils sont conçus pour une utilisation particulière et qu’ils ne peuvent pas faire autre chose. Par exemple, les circuits électroniques d’un lecteur de DVD ne peuvent pas être transformé en lecteur audio ou en console de jeux... Les circuits non-programmables sont câblés une bonne fois pour toute, et on ne peut pas les modifier. On peut parfois reconfigurer le circuit, pour faire varier certains paramètres, via des interrupteurs ou des boutons, mais cela s’arrête là. Et cela pose un problème : à chaque problème qu'on veut résoudre en utilisant un automate, on doit recréer un nouveau circuit.
À l'inverse, un ordinateur n’est pas conçu pour une utilisation particulière, contrairement aux autres objets techniques. Il est possible de modifier leur fonction du jour au lendemain, on peut lui faire faire ce qu’on veut. On dit qu'ils sont programmables. Pour cela, il suffit d’utiliser un logiciel, une application, un programme (ces termes sont synonymes), qui fait ce que l'on souhaite. La totalité des logiciels présents sur un ordinateur sont des programmes comme les autres, même le système d'exploitation (Windows, Linux, ...) ne fait pas exception.
Un programme est une suite de d'instructions, chaque instruction effectuant une action dans l'ordinateur. Sur les ordinateurs modernes, la majorité de ces instructions effectuent une opération arithmétique, comme une addition, une multiplication, une soustraction, etc. Les ordinateurs modernes sont donc de grosses calculettes très puissantes, capables d'effectuer des millions d'opérations par secondes. Et qui dit opération dit nombres : un ordinateur gère nativement des nombres, qui sont codés en binaire sur la quasi-totalité des ordinateurs modernes.
Une instruction est représentée dans un ordinateur par une série de nombres : un nombre qui indique quelle opération/commande effectuer et des autres nombres pour coder les données (ou de quoi les retrouver dans l'ordinateur). L'ordinateur récupére les commandes une par une, les traduit en opération à effectuer, exécuter l'opération, et enregistre le résultat. Puis il recommence avec la commande suivante.

Les ordinateurs à programme mémorisé ou programme externe
modifierUn programme informatique est une suite de commande, à exécuter dans l'ordre, l'une après l'autre. Les premiers ordinateurs mémorisaient les programmes sur un support externe, lu par un périphérique. Au tout début de l'informatique, on utilisait des cartes perforées en plastique, sur lesquelles on inscrivait le programme. Par la suite, les premiers ordinateurs grand public, comme les Amstrad ou les Commodore, utilisaient des cassettes audio magnétiques pour stocker les programmes. De même, les consoles de jeu utilisaient autrefois des cartouches de jeu, qui contenaient le programme du jeu à exécuter. Les anciens PC utilisaient des disquettes, de petits supports magnétiques qu’on insérait dans l’ordinateur le temps de leur utilisation. De tels ordinateurs sont dits à programme externe.
- Sur d’anciens ordinateurs personnels, comme l’Amstrad ou le Commodore, on pouvait aussi taper les programmes à exécuter à la main, au clavier, avant d’appuyer une touche pour les exécuter.
Mais de nos jours, les programmes sont en réalité enregistrés sur le disque dur de l'ordinateur ou dans une mémoire intégrée à l'ordinateur. On dit qu'ils sont installés, ce qui est un mot bien compliqué pour dire que le programme est enregistré sur le disque dur de l’ordinateur. A défaut de disque dur, le programme/logiciel est enregistré dans une mémoire spécialisée pour le stockage. Par exemple, sur les cartes électroniques grand public de marque Arduino, les programmes sont envoyés à la carte via le port USB, mais les programmes sont enregistrés dans la carte Arduino, dans une mémoire FLASH dédiée. Disque dur ou non, le programme est mémorisé dans la mémoire de l'ordinateur. Il est possible d'installer ou de désinstaller les programmes en modifiant le contenu de la mémoire. Le terme utilisé est alors celui de programme stocké en mémoire.
Les programmes à installer sont disponibles soit sur un périphérique, comme un DVD ou une clé USB, soit sont téléchargés depuis internet. Les premiers PC fournissaient les logiciels sur des disquettes, qui contenaient un programme d'installation pour enregistrer le programme sur le disque dur de l'ordinateur. Par la suite, le support des logiciels a migré vers les CD et DVD, les logiciels devenant de plus en plus gros. De nos jours, la majorité des applications sont téléchargées depuis le net, l'usage de périphériques est devenu obsolète, même les consoles de jeu abandonnent cette méthode de distribution.
Résumé
modifierDe nombreux appareils sont programmables, mais tous ne sont pas des ordinateurs. Par exemple, certains circuits programmables nommés FPGA n'en sont pas. Pour être qualifié d'ordinateur, un appareil programmable doit avoir d'autres propriétés. L'une d'entre elle est d'avoir un processeur séparé de la mémoire. Pour résumer, les ordinateurs sont des appareils électroniques qui ont les propriétés suivantes.
- Ils sont programmables.
- Ils contiennent un processeur et une mémoire, reliés à des périphériques.
- Ils utilisent un codage numérique, chose que nous allons aborder dans le chapitre suivant.
Ces points peuvent paraitre assez abstraits, mais rassurez-vous : nous allons les détailler tout au long de ce cours, au point qu'ils n'auront plus aucun secret pour vous d'ici quelques chapitres.
L'organisation du cours : les niveaux d'abstractions en architecture des ordinateurs
modifierLe fonctionnement d'un ordinateur est assez complexe à expliquer car les explications peuvent se faire sur plusieurs niveaux. Par plusieurs niveaux, on veut dire qu'un ordinateur est composé de composants très simples, qui sont assemblés pour donner des composants eux-même plus complexes, qui sont eux-même regrouper, etc. Étudier tout cela demande de voir plusieurs niveaux, allant de transistors très petits à des processeurs multicœurs. Les niveaux les plus bas sont de l'électronique pur et dure, alors que ceux plus haut sont à mi-chemin entre électronique et informatique.
Les niveaux d'abstraction en architecture des ordinateurs
modifierLes trois premiers niveaux sont de l'électronique pur et dure. Ils correspondent aux premiers chapitres du cours, qui porteront sur les circuits électroniques en général.
- Le premier niveau est celui des transistors, des circuits intégrés, des wafer et autres circuits de très petite taille.
- Le second niveau est celui des portes logiques, des circuits très basiques, très simples, à la base de tous les autres.
- Le troisième niveau est celui dit de la Register Transfer Level, où un circuit électronique est construit à partir de circuits basiques, dont des registres et autres circuits dits combinatoires.
Les deux niveaux suivants sont de l'informatique proprement dit. C'est dans ces deux niveaux qu'on étudie les ordinateurs proprement dit, les circuits qu'il y a dedans et non l'électronique en général.
- Le quatrième niveau est celui de la microarchitecture, qui étudie ce qu'il y a à l'intérieur d'un processeur, d'une mémoire, des périphériques et autres.
- Le cinquième niveau est celui de l'architecture externe, qui décrit l'interface du processeur, de la mémoire, d'un périphérique ou autre. Par décrire l'interface, on veut dire : comment un programmeur voit le processeur et la mémoire, comment il peut les manipuler. Une architecture externe unique peut avoir plusieurs microarchitecture, ce qui fait qu'on sépare les deux. Tout cela sera plus clair quand on passera aux chapitres sur le processeur et les mémoires.
Nous n'allons pas voir les 5 niveaux dans l'ordre, des transistors vers l'architecture externe. En réalité, nous allons procéder autrement. La première partie du cours portera sur les trois premiers niveaux, le reste sur les deux autres. Les 5 niveaux seront vus dans des chapitres séparés, du moins le plus possible. Au niveau pédagogique, tout est plus simple si on scinde les 5 niveaux. Bien sûr, il y a quelques explications qui demandent de voir plusieurs niveaux à la fois. Par exemple, dans le chapitre sur les mémoires caches, nous auront des explications portant sur la RTL, la microarchitecture du cache et son architecture externe. Mais le gros du cours tentera de séparer le plus possible les 5 niveaux.
Les trois parties principales du cours
modifierNous allons commencer par parler du binaire, avant de voir les portes logiques. Avec ces portes logiques, nous allons voir comment fabriquer des circuits basiques qui reviendront très souvent dans la suite du cours. Nous verrons les registres, les décodeurs, les additionneurs et plein d'autres circuits. Puis, nous reviendrons au niveau des transistors pour finir la première partie. La raison est que c'est plus simple de faire comme cela. Tout ce qui a trait aux transistors sert à expliquer comment fabriquer des portes logiques, et il faut expliquer les portes logiques pour voir le niveau de la RTL.
Une fois la première partie finie, nous allons voir les différents composants d'un ordinateur. Une première partie expliquera ce qu'il y a dans un ordinateur, quels sont ses composants. Nous y parlerons de l'architecture de base, de la hiérarchie mémoire, des tendances technologiques, et d'autres généralités qui serviront de base pour la suite. Puis, nous verrons dans l'ordre les bus électroniques, les mémoires RAM/ROM, le processeur, les périphériques, les mémoires de stockage (SSD et disques durs) et les mémoires caches. Pour chaque composant, nous allons voir leur architecture externe, avant de voir leur microarchitecture. La raison est que la microarchitecture ne peut se comprendre que quand on sait quelle architecture externe elle implémente.
Enfin, dans une troisième partie, nous allons voir les optimisations majeures présentes dans tous les ordinateurs modernes, avec une partie sur le pipeline et le parallélisme d'instruction, et une autre sur les architectures parallèles. Pour finir, les annexes de fin parlerons de sujets un peu à part.
Le codage des informations
modifierVous savez déjà qu'un ordinateur permet de faire plein de choses totalement différentes : écouter de la musique, lire des films/vidéos, afficher ou écrire du texte, retoucher des images, créer des vidéos, jouer à des jeux vidéos, etc. Pour être plus général, on devrait dire qu'un ordinateur manipule des informations, sous la forme de fichier texte, de vidéo, d'image, de morceau de musique, de niveau de jeux vidéos, etc. Dans ce qui suit, nous allons appeler ces informations par le terme données. On pourrait définir les ordinateurs comme des appareils qui manipulent des données et/ou qui traitent de l'information, mais force est de constater que cette définition, oh combien fréquente, n'est pas la bonne. Tous les appareils électroniques manipulent des données, même ceux qui ne sont pas des ordinateurs proprement dit : les exemples des décodeurs TNT et autres lecteurs de DVD sont là pour nous le rappeler. Même si la définition d’ordinateur est assez floue et que plusieurs définitions concurrentes existent, il est évident que les ordinateurs se distinguent des autres appareils électroniques programmables sur plusieurs points. Notamment, ils stockent leurs données d'une certaine manière (le codage numérique que nous allons aborder).
Le codage de l'information
modifierAvant d'être traitée, une information doit être transformée en données exploitables par l'ordinateur, sans quoi il ne pourra pas en faire quoi que ce soit. Eh bien, sachez qu'elles sont stockées… avec des nombres. Toute donnée n'est qu'un ensemble de nombres structuré pour être compréhensible par l'ordinateur : on dit que les données sont codées par des nombres. Il suffit d'utiliser une machine à calculer pour manipuler ces nombres, et donc sur les données. Une simple machine à calculer devient une machine à traiter de l'information. Aussi bizarre que cela puisse paraitre, un ordinateur n'est qu'une sorte de grosse calculatrice hyper-performante. Mais comment faire la correspondance entre ces nombres et du son, du texte, ou toute autre forme d'information ? Et comment fait notre ordinateur pour stocker ces nombres et les manipuler ? Nous allons répondre à ces questions dans ce chapitre.
Toute information présente dans un ordinateur est décomposée en petites informations de base, chacune représentée par un nombre. Par exemple, le texte sera décomposé en caractères (des lettres, des chiffres, ou des symboles). Pareil pour les images, qui sont décomposées en pixels, eux-mêmes codés par un nombre. Même chose pour la vidéo, qui n'est rien d'autre qu'une suite d'images affichées à intervalles réguliers. La façon dont un morceau d'information (lettre ou pixel, par exemple) est représenté avec des nombres est définie par ce qu'on appelle un codage, parfois appelé improprement encodage. Ce codage va attribuer un nombre à chaque morceau d'information. Pour montrer à quoi peut ressembler un codage, on va prendre trois exemples : du texte, une image et du son.
Texte : standard ASCII
modifierPour coder un texte, il suffit de savoir coder une lettre ou tout autre symbole présent dans un texte normal (on parle de caractères). Pour coder chaque caractère avec un nombre, il existe plusieurs codages : l'ASCII, l'Unicode, etc.

Le codage le plus ancien, appelé l'ASCII, a été inventé pour les communications télégraphiques et a été ensuite réutilisé dans l'informatique et l'électronique à de nombreuses occasions. Il est intégralement défini par une table de correspondance entre une lettre et le nombre associé, appelée la table ASCII. Le standard ASCII originel utilise des nombres codés sur 7 bits (et non 8 comme beaucoup le croient), ce qui permet de coder 128 symboles différents.
Les lettres sont stockées dans l'ordre alphabétique, pour simplifier la vie des utilisateurs : des nombres consécutifs correspondent à des lettres consécutives. L'ASCII ne code pas seulement des lettres, mais aussi d'autres symboles, dont certains ne sont même pas affichables ! Cela peut paraitre bizarre, mais s'explique facilement quand on connait les origines du standard. Ces caractères non-affichables servent pour les imprimantes, FAX et autres systèmes de télécopies. Pour faciliter la conception de ces machines, on a placé dans cette table ASCII des symboles qui n'étaient pas destinés à être affichés, mais dont le but était de donner un ordre à l'imprimante/machine à écrire... On trouve ainsi des symboles de retour à la ligne, par exemple.

La table ASCII a cependant des limitations assez problématiques. Par exemple, vous remarquerez que les accents n'y sont pas, ce qui n'est pas étonnant quand on sait qu'il s'agit d'un standard américain. De même, impossible de coder un texte en grec ou en japonais : les idéogrammes et les lettres grecques ne sont pas dans la table ASCII. Pour combler ce manque, des codages ASCII étendus ont rajouté des caractères à la table ASCII de base. Ils sont assez nombreux et ne sont pas compatibles entre eux. Le plus connu et le plus utilisé est certainement le codage ISO 8859 et ses dérivés, utilisés par de nombreux systèmes d'exploitation et logiciels en occident. Ce codage code ses caractères sur 8 bits et est rétrocompatible ASCII, ce qui fait qu'il est parfois confondu avec ce dernier alors que les deux sont très différents.
Aujourd'hui, le standard de codage de texte le plus connu est certainement l’Unicode. L'Unicode est parfaitement compatible avec la table ASCII : les 128 premiers symboles de l’Unicode sont ceux de la table ASCII, et sont rangés dans le même ordre. Là où l'ASCII ne code que l'alphabet anglais, les codages actuels comme l'Unicode prennent en compte les caractères chinois, japonais, grecs, etc.
Image
modifier
Le même principe peut être appliqué aux images : l'image est décomposée en morceaux de même taille qu'on appelle des pixels. L'image est ainsi vue comme un rectangle de pixels, avec une largeur et une longueur. Le nombre de pixels en largeur et en longueur définit la résolution de l'image : par exemple, une image avec 800 pixels de longueur et 600 en largeur sera une image dont la résolution est de 800*600. Il va de soi que plus cette résolution est grande, plus l'image sera fine et précise. On peut d'ailleurs remarquer que les images en basse résolution ont souvent un aspect dit pixelisé, où les bords des objets sont en marche d'escaliers.
Chaque pixel a une couleur qui est codée par un ou plusieurs nombres entiers. D'ordinaire, la couleur d'un pixel est définie par un mélange des trois couleurs primaires rouge, vert et bleu. Par exemple, la couleur jaune est composée à 50 % de rouge et à 50 % de vert. Pour coder la couleur d'un pixel, il suffit de coder chaque couleur primaire avec un nombre entier : un nombre pour le rouge, un autre pour le vert et un dernier pour le bleu. Ce codage est appelé le codage RGB. Mais il existe d'autres méthodes, qui codent un pixel non pas à partir des couleurs primaires, mais à partir d'autres espaces de couleur.
Pour stocker une image dans l'ordinateur, on a besoin de connaitre sa largeur, sa longueur et la couleur de chaque pixel. Une image peut donc être représentée dans un fichier par une suite d'entiers : un pour la largeur, un pour la longueur, et le reste pour les couleurs des pixels. Ces entiers sont stockés les uns à la suite des autres dans un fichier. Les pixels sont stockés ligne par ligne, en partant du haut, et chaque ligne est codée de gauche à droite. Les fichiers image actuels utilisent des techniques de codage plus élaborées, permettant notamment décrire une image en utilisant moins de nombres, ce qui prend moins de place dans l'ordinateur.
Son
modifierPour mémoriser du son, il suffit de mémoriser l'intensité sonore reçue par un microphone à intervalles réguliers. Cette intensité est codée par un nombre entier : si le son est fort, le nombre sera élevé, tandis qu'un son faible se verra attribuer un entier petit. Ces entiers seront rassemblés dans l'ordre de mesure, et stockés dans un fichier son, comme du wav, du PCM, etc. Généralement, ces fichiers sont compressés afin de prendre moins de place.
Le support physique de l'information codée
modifierPour pouvoir traiter de l'information, la première étape est d'abord de coder celle-ci, c'est à dire de la transformer en nombres. Et peu importe le codage utilisé, celui-ci a besoin d'un support physique, d'une grandeur physique quelconque. Et pour être franc, on peut utiliser tout et n’importe quoi. Par exemple, certains calculateurs assez anciens étaient des calculateurs pneumatiques, qui utilisaient la pression de l'air pour représenter des chiffres ou nombres : soit le nombre encodé était proportionnel à la pression, soit il existait divers intervalles de pression correspondant chacun à un nombre entier bien précis. Il a aussi existé des technologies purement mécaniques pour ce faire, comme les cartes perforées ou d'autres dispositifs encore plus ingénieux. De nos jours, ce stockage se fait soit par l'aimantation d'un support magnétique, soit par un support optique (les CD et DVD), soit par un support électronique. Les supports magnétiques sont réservés aux disques durs magnétiques, destinés à être remplacés par des disques durs entièrement électroniques (les fameux Solid State Drives, que nous verrons dans quelques chapitres).
Pour les supports de stockage électroniques, très courants dans nos ordinateurs, le support en question est une tension électrique. Ces tensions sont ensuite manipulées par des composants électriques/électroniques plus ou moins sophistiqués : résistances, condensateurs, bobines, amplificateurs opérationnels, diodes, transistors, etc. Certains d'entre eux ont besoin d'être alimentés en énergie. Pour cela, chaque circuit est relié à une tension qui l'alimente en énergie : la tension d'alimentation. Après tout, la tension qui code les nombres ne sort pas de nulle part et il faut bien qu'il trouve de quoi fournir une tension de 2, 3, 5 volts. De même, on a besoin d'une tension de référence valant zéro volt, qu'on appelle la masse, qui sert pour le zéro.
Dans les circuits électroniques actuels, ordinateurs inclus, la tension d'alimentation varie généralement entre 0 et 5 volts. Mais de plus en plus, on tend à utiliser des valeurs de plus en plus basses, histoire d'économiser un peu d'énergie. Eh oui, car plus un circuit utilise une tension élevée, plus il consomme d'énergie et plus il chauffe. Pour un processeur, il est rare que les modèles récents utilisent une tension supérieure à 2 volts : la moyenne tournant autour de 1-1.5 volts. Même chose pour les mémoires : la tension d'alimentation de celle-ci diminue au cours du temps. Pour donner des exemples, une mémoire DDR a une tension d'alimentation qui tourne autour de 2,5 volts, les mémoires DDR2 ont une tension d'alimentation qui tombe à 1,8 volts, et les mémoires DDR3 ont une tension d'alimentation qui tombe à 1,5 volts. C'est très peu : les composants qui manipulent ces tensions doivent être très précis.
Les différents codages : analogique, numérique et binaire
modifier
Le codage, la transformation d’information en nombre, peut être fait de plusieurs façons différentes. Dans les grandes lignes, on peut identifier deux grands types de codages.
- Le codage analogique utilise des nombres réels : il code l’information avec des grandeurs physiques (quelque chose que l'on peut mesurer par un nombre) comprises dans un intervalle. Par exemple, un thermostat analogique convertit la température en tension électrique pour la manipuler : une température de 0 degré donne une tension de 0 volts, une température de 20 degrés donne une tension de 5 Volts, une température de 40 degrés donnera du 10 Volts, etc. Un codage analogique a une précision théoriquement infinie : on peut par exemple utiliser toutes les valeurs entre 0 et 5 Volts pour coder une information, même des valeurs tordues comme 1, 2.2345646, ou pire…
- Le codage numérique n'utilise qu'un nombre fini de valeurs, contrairement au codage analogique. Pour être plus précis, il code des informations en utilisant des nombres entiers, représentés par des suites de chiffres. Le codage numérique précise comment coder les chiffres avec une tension. Comme illustré ci-contre, chaque chiffre correspond à un intervalle de tension : la tension code pour ce chiffre si elle est comprise dans cet intervalle. Cela donnera des valeurs de tension du style : 0, 0.12, 0.24, 0.36, 0.48… jusqu'à 2 volts.
Les avantages et désavantages de l'analogique et du numérique
modifierUn calculateur analogique (qui utilise le codage analogique) peut en théorie faire ses calculs avec une précision théorique très fine, impossible à atteindre avec un calculateur numérique, notamment pour les opérations comme les dérivées, intégrations et autres calculs similaires. Mais dans les faits, aucune machine analogique n'est parfaite et la précision théorique est rarement atteinte, loin de là. Les imperfections des machines posent beaucoup plus de problèmes sur les machines analogiques que sur les machines numériques.
Obtenir des calculs précis sur un calculateur analogique demande non seulement d'utiliser des composants de très bonne qualité, à la conception quasi-parfaite, mais aussi d'utiliser des techniques de conception particulières. Même les composants de qualité ont des imperfections certes mineures, qui peuvent cependant sévèrement perturber les résultats. Les moyens pour réduire ce genre de problème sont très complexes, ce qui fait que la conception des calculateurs analogiques est diablement complexe, au point d'être une affaire de spécialistes. Concevoir ces machines est non seulement très difficile, mais tester leur bon fonctionnement ou corriger des pannes est encore plus complexe.
De plus, les calculateurs analogiques sont plus sensibles aux perturbations électromagnétiques. On dit aussi qu'ils ont une faible immunité au bruit. En effet, un signal analogique peut facilement subir des perturbations qui vont changer sa valeur, modifiant directement la valeur des nombres stockés ou manipulés. Avec un codage numérique, les perturbations ou parasites vont moins perturber le signal numérique. La raison est qu'une variation de tension qui reste dans un intervalle représentant un chiffre ne changera pas sa valeur. Il faut que la variation de tension fasse sortir la tension de l'intervalle pour changer le chiffre. Cette sensibilité aux perturbations est un désavantage net pour l'analogique et est une des raisons qui font que les calculateurs analogiques sont peu utilisés de nos jours. Elle rend difficile de faire fonctionner un calculateur analogique rapidement et limite donc sa puissance.
Un autre désavantage est que les calculateurs analogiques sont très spécialisés et qu'ils ne sont pas programmables. Un calculateur analogique est forcément conçu pour résoudre un problème bien précis. On peut le reconfigurer, le modifier à la marge, mais guère plus. Typiquement, les calculateurs analogiques sont utilisés pour résoudre des équations différentielles couplées non-linéaires, mais n'ont guère d'utilité pratique au-delà. Mais les ingénieurs ne font cela que pour les problèmes où il est pertinent de concevoir de zéro un calculateur spécialement dédié au problème à résoudre, ce qui est un cas assez rare.
Le choix de la base
modifierAu vu des défauts des calculateurs analogiques, on devine que la grosse majorité des circuits électronique actuels sont numériques. Mais il faut savoir que les ordinateurs n'utilisent pas la numération décimale normale, celle à 10 chiffres qui vont de 0 à 9. De nos jours, les ordinateurs n'utilisent que deux chiffres, 0 et 1 (on parle de « bit ») : on dit qu'ils comptent en binaire. On verra dans le chapitre suivant comment coder des nombres avec des bits, ce qui est relativement simple. Pour le moment, nous allons justifier ce choix de n'utiliser que des bits et pas les chiffres décimaux (de 0 à 9). Avec une tension électrique, il y a diverses méthodes pour coder un bit : codage Manchester, NRZ, etc. Autant trancher dans le vif tout de suite : la quasi-intégralité des circuits d'un ordinateur se basent sur le codage NRZ.
Naïvement, la solution la plus simple serait de fixer un seuil en-dessous duquel la tension code un 0, et au-dessus duquel la tension représente un 1. Mais les circuits qui manipulent des tensions n'ont pas une précision parfaite et une petite perturbation électrique pourrait alors transformer un 0 en 1. Pour limiter la casse, on préfère ajouter une sorte de marge de sécurité, ce qui fait qu'on utilise en réalité deux seuils séparés par un intervalle vide. Le résultat est le fameux codage NRZ dont nous venons de parler : la tension doit être en dessous d'un seuil donné pour un 0, et il existe un autre seuil au-dessus duquel la tension représente un 1. Tout ce qu'il faut retenir, c'est qu'il y a un intervalle pour le 0 et un autre pour le 1. En dehors de ces intervalles, on considère que le circuit est trop imprécis pour pouvoir conclure sur la valeur de la tension : on ne sait pas trop si c'est un 1 ou un 0.
- Il arrive que ce soit l'inverse sur certains circuits électroniques : en dessous d'un certain seuil, c'est un 1 et si c'est au-dessus d'un autre seuil c'est 0.

L'avantage du binaire par rapport aux autres codages est qu'il permet de mieux résister aux perturbations électromagnétiques mentionnées dans le chapitre précédent. À tension d'alimentation égale, les intervalles de chaque chiffre sont plus petits pour un codage décimal : toute perturbation de la tension aura plus de chances de changer un chiffre. Mais avec des intervalles plus grands, un parasite aura nettement moins de chance de modifier la valeur du chiffre codé ainsi. La résistance aux perturbations électromagnétiques est donc meilleure avec seulement deux intervalles.

Dans le chapitre précédent, nous avons vu que les ordinateurs actuels utilisent un codage binaire. Ce codage binaire ne vous est peut-être pas familier. Aussi, dans ce chapitre, nous allons apprendre comment coder des nombres en binaire. Nous allons commencer par le cas le plus simple : les nombres positifs. Par la suite, nous aborderons les nombres négatifs. Et nous terminerons par les nombres à virgules, appelés aussi nombres flottants.
Le codage des nombres entiers positifs
modifierPour coder des nombres entiers positifs, il existe plusieurs méthodes : le binaire, l’hexadécimal, le code Gray, le décimal codé binaire et bien d'autres encore. La plus connue est certainement le binaire, secondée par l'hexadécimal, les autres étant plus anecdotiques. Pour comprendre ce qu'est le binaire, il nous faut faire un rappel sur les nombres entiers tel que vous les avez appris en primaire, à savoir les entiers écrits en décimal. Prenons un nombre écrit en décimal : le chiffre le plus à droite est le chiffre des unités, celui à côté est pour les dizaines, suivi du chiffre des centaines, et ainsi de suite. Dans un tel nombre :
- on utilise une dizaine de chiffres, de 0 à 9 ;
- chaque chiffre est multiplié par une puissance de 10 : 1, 10, 100, 1000, etc. ;
- la position d'un chiffre dans le nombre indique par quelle puissance de 10 il faut le multiplier : le chiffre des unités doit être multiplié par 1, celui des dizaines par 10, celui des centaines par 100, et ainsi de suite.
Exemple avec le nombre 1337 :
Pour résumer, un nombre en décimal s'écrit comme la somme de produits, chaque produit multipliant un chiffre par une puissance de 10. On dit alors que le nombre est en base 10.
Ce qui peut être fait avec des puissances de 10 peut être fait avec des puissances de 2, 3, 4, 125, etc : n'importe quel nombre entier strictement positif peut servir de base. En informatique, on utilise rarement la base 10 à laquelle nous sommes tant habitués. On utilise à la place deux autres bases :
- La base 2 (système binaire) : les chiffres utilisés sont 0 et 1 ;
- La base 16 (système hexadécimal) : les chiffres utilisés sont 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9 ; auxquels s'ajoutent les six premières lettres de notre alphabet : A, B, C, D, E et F.
Le système binaire
modifierEn binaire, on compte en base 2. Cela veut dire qu'au lieu d'utiliser des puissances de 10 comme en décimal, on utilise des puissances de deux : n'importe quel nombre entier peut être écrit sous la forme d'une somme de puissances de 2. Par exemple 6 s'écrira donc 0110 en binaire : . On peut remarquer que le binaire n'autorise que deux chiffres, à savoir 0 ou 1 : ces chiffres binaires sont appelés des bits (abréviation de Binary Digit). Pour simplifier, on peut dire qu'un bit est un truc qui vaut 0 ou 1. Pour résumer, tout nombre en binaire s'écrit sous la forme d'un produit entre bits et puissances de deux de la forme :
Les coefficients sont les bits, l'exposant n qui correspond à un bit est appelé le poids du bit.
La terminologie du binaire
modifierEn informatique, il est rare que l'on code une information sur un seul bit. Dans la plupart des cas, l'ordinateur manipule des nombres codés sur plusieurs bits. Les informaticiens ont donné des noms aux groupes de bits suivant leur taille. Le plus connu est certainement l'octet, qui désigne un groupe de 8 bits. Moins connu, on parle de nibble pour un groupe de 4 bits (un demi-octet), de doublet pour un groupe de 16 bits (deux octets) et de quadruplet pour un groupe de 32 bits (quatre octets).
Précisons qu'en anglais, le terme byte n'est pas synonyme d'octet. En réalité, le terme octet marche aussi bien en français qu'en anglais. Quant au terme byte, il désigne un concept complètement différent, que nous aborderons plus tard (c'est la plus petite unité de mémoire que le processeur peut adresser). Il a existé dans le passé des ordinateurs où le byte faisait 4, 7, 9, 16, voire 48 bits, par exemple. Il a même existé des ordinateur où le byte faisait exactement 1 bit ! Mais sur presque tous les ordinateurs modernes, un byte fait effectivement 8 bits, ce qui fait que le terme byte est parfois utilisé en lieu et place d'octet. Mais c'est un abus de langage, attention aux confusions ! Dans ce cours, nous parlerons d'octet pour désigner un groupe de 8 bits, en réservant le terme byte pour sa véritable signification.
À l'intérieur d'un nombre, le bit de poids faible est celui qui est le plus à droite du nombre, alors que le bit de poids fort est celui non nul qui est placé le plus à gauche, comme illustré dans le schéma ci-dessous.


Cette terminologie s'applique aussi pour les bits à l'intérieur d'un octet, d'un nibble, d'un doublet ou d'un quadruplet. Pour un nombre codés sur plusieurs octets, on peut aussi parler de l'octet de poids fort et de l'octet de poids faible, du doublet de poids fort ou de poids faible, etc.
La traduction binaire→décimal
modifierPour traduire un nombre binaire en décimal, il faut juste se rappeler que la position d'un bit indique par quelle puissance il faut le multiplier. Ainsi, le chiffre le plus à droite est le chiffre des unités : il doit être multiplié par 1 (). Le chiffre situé immédiatement à gauche du chiffre des unités doit être multiplié par 2 (). Le chiffre encore à gauche doit être multiplié par 4 (), et ainsi de suite. Mathématiquement, on peut dire que le énième bit en partant de la droite doit être multiplié par . Par exemple, la valeur du nombre noté 1011 en binaire est de .

La traduction décimal→binaire
modifierLa traduction inverse, du décimal au binaire, demande d'effectuer des divisions successives par deux. Les divisions en question sont des divisions euclidiennes, avec un reste et un quotient. En lisant les restes des divisions dans un certain sens, on obtient le nombre en binaire. Voici comment il faut procéder, pour traduire le nombre 34 :

Quelques opérations en binaire
modifierMaintenant que l'on sait coder des nombres en binaire normal, il est utile de savoir comment faire quelques opérations usuelles en binaire. Nous utiliserons les acquis de cette section dans la suite du chapitre, bien que de manière assez marginale.
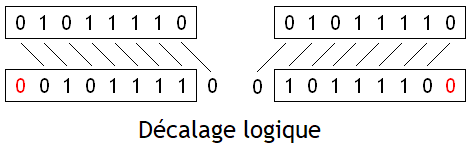
La première opération est assez spécifique au binaire. Il s'agit d'une opération qui inverse les bits d'un nombre : les 0 deviennent des 1 et réciproquement. Par exemple, le nombre 0001 1001 devient 1110 0110. Elle porte plusieurs noms : opération NOT, opération NON, complémentation, etc. Nous parlerons de complémentation ou d'opération NOT dans ce qui suit. Beaucoup d'ordinateurs gèrent cette opération, ils savent la faire en un seul calcul. Il faut dire que c'est une opération assez utile, bien que nous ne pouvons pas encore expliquer pourquoi.

La seconde opération à aborder est l'addition. Elle se fait en binaire de la même manière qu'en décimal : Pour faire une addition en binaire, on additionne les chiffres/bits colonne par colonne, une éventuelle retenue est propagée à la colonne d'à côté. Sauf que l'on additionne des bits. Heureusement, la table d'addition est très simple en binaire :
- 0 + 0 = 0, retenue = 0 ;
- 0 + 1 = 1, retenue = 0 ;
- 1 + 0 = 1, retenue = 0 ;
- 1 + 1 = 0, retenue = 1.
La troisième opération est une variante de l'addition appelée l'opération XOR, notée . Il s'agit d'une addition dans laquelle on ne propage pas les retenues. L'addition des deux bits des opérandes se fait normalement, mais les retenues sont simplement oubliées, on n'en tient pas compte. Le résultat est que l'addition se résume à appliquer la table d'addition précédente :
- 0 0 = 0 ;
- 0 1 = 1 ;
- 1 0 = 1 ;
- 1 1 = 0.
Pour résumer, le résultat vaut 1 si les deux bits sont différents, 0 s'ils sont identiques. L'opération XOR sera utilisée rapidement dans le chapitre suivant, quand nous parlerons rapidement du mot de parité. Et elle sera beaucoup utilisée dans la suite du cours, nous en feront fortement usage. Pour le moment, mémorisez juste cette opération, elle n'a rien de compliqué.
Une dernière opération est l'opération de population count. Il s'agit ni plus ni moins que de compter le nombre de bits qui sont à 1 dans un nombre. Par exemple, pour le nombre 0110 0010 1101 1110, elle donne pour résultat 9. Elle est utilisée dans certaines applications, comme le calcul de certains codes correcteurs d'erreur, comme on le verra dans le chapitre suivant. Elle est supportée sur de nombreux ordinateurs, encore que cela dépende du processeur considéré. Il s'agit cependant d'une opération assez courante, supportée par les processeurs ARM, les processeurs x86 modernes (ceux qui gèrent le SSE), et quelques autres.
L'hexadécimal
modifierL’hexadécimal est basé sur le même principe que le binaire, sauf qu'il utilise les 16 chiffres suivants :
| Chiffre hexadécimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre décimal correspondant | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Notation binaire | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Dans les textes, afin de différencier les nombres décimaux des nombres hexadécimaux, les nombres hexadécimaux sont suivis par un petit h, indiqué en indice. Si cette notation n'existait pas, des nombres comme 2546 seraient ambigus : on ne saurait pas dire sans autre indication s'ils sont écrits en décimal ou en hexadécimal. Avec la notation, on sait de suite que 2546 est en décimal et que 2546h est en hexadécimal.
Dans les codes sources des programmes, la notation diffère selon le langage de programmation.
Certains supportent le suffixe h pour les nombres hexadécimaux, d'autres utilisent un préfixe 0x ou 0h.
La conversion hexadécimal↔décimal
modifierPour convertir un nombre hexadécimal en décimal, il suffit de multiplier chaque chiffre par la puissance de 16 qui lui est attribuée. Là encore, la position d'un chiffre indique par quelle puissance celui-ci doit être multiplié : le chiffre le plus à droite est celui des unités, le second chiffre le plus à droite doit être multiplié par 16, le troisième chiffre en partant de la droite doit être multiplié par 256 (16 * 16) et ainsi de suite. La technique pour convertir un nombre décimal vers de l’hexadécimal est similaire à celle utilisée pour traduire un nombre du décimal vers le binaire. On retrouve une suite de divisions successives, mais cette fois-ci les divisions ne sont pas des divisions par 2 : ce sont des divisions par 16.
La conversion hexadécimal↔binaire
modifierLa conversion inverse, de l'hexadécimal vers le binaire est très simple, nettement plus simple que les autres conversions. Pour passer de l'hexadécimal au binaire, il suffit de traduire chaque chiffre en sa valeur binaire, celle indiquée dans le tableau au tout début du paragraphe nommé « Hexadécimal ». Une fois cela fait, il suffit de faire le remplacement. La traduction inverse est tout aussi simple : il suffit de grouper les bits du nombre par 4, en commençant par la droite (si un groupe est incomplet, on le remplit avec des zéros). Il suffit alors de remplacer le groupe de 4 bits par le chiffre hexadécimal qui correspond.
Interlude propédeutique : la capacité d'un entier et les débordements d'entiers
modifierDans la section précédente, nous avons vu comment coder des entiers positifs en binaire ou dans des représentations proches. La logique voudrait que l'on aborde ensuite le codage des entiers négatifs. Mais nous allons déroger à cette logique simple, pour des raisons pédagogiques. Nous allons faire un interlude qui introduira des notions utiles pour la suite du chapitre. De plus, ces concepts seront abordés de nombreuses fois dans ce wikilivre et l'introduire ici est de loin la solution idéale.
Les ordinateurs manipulent des nombres codés sur un nombre fixe de bits
modifierVous avez certainement déjà entendu parler de processeurs 32 ou 64 bits. Et si vous avez joué aux jeux vidéos durant votre jeunesse et êtes assez agé, vous avez entendu parler de consoles de jeu 8 bits, 16 bits, 32 bits, voire 64 bits (pour la Jaguar, et c'était un peu trompeur). Derrière cette appellation qu'on retrouvait autrefois comme argument commercial dans la presse se cache un concept simple. Tout ordinateur manipule des nombres entiers dont le nombre de bits est toujours le même : on dit qu'ils sont de taille fixe. Une console 16 bits manipulait des entiers codés en binaire sur 16 bits, pas un de plus, pas un de moins. Pareil pour les anciens ordinateurs 32 bits, qui manipulaient des nombres entiers codés sur 32 bits.
Aujourd'hui, les ordinateurs modernes utilisent presque un nombre de bits qui est une puissance de 2 : 8, 16, 32, 64, 128, 256, voire 512 bits. Mais cette règle souffre évidemment d'exceptions. Aux tout débuts de l'informatique, certaines machines utilisaient 3, 7, 13, 17, 23, 36 et 48 bits ; mais elles sont aujourd'hui tombées en désuétude. De nos jours, il ne reste que les processeurs dédiés au traitement de signal audio, que l'on trouve dans les chaînes HIFI, les décodeurs TNT, les lecteurs DVD, etc. Ceux-ci utilisent des nombres entiers de 24 bits, car l'information audio est souvent codée par des nombres de 24 bits.
Anecdote amusante, il a existé des ordinateurs de 1 bit, qui sont capables de manipuler des nombres codés sur 1 bit, pas plus. Un exemple est le Motorola MC14500B, commercialisé de 1976.
Le lien entre nombre de bits et valeurs codables
modifierÉvidemment, on ne peut pas coder tous les entiers possibles et imaginables avec seulement 8 bits, ou 16 bits. Et il parait intuitif que l'on ait plus de valeurs codables sur 16 bits qu'avec 8 bits, par exemple. Plus le nombre de bits est important, plus on pourra coder de valeurs entières différentes. Mais combien de plus ? Par exemple, si je passe de 8 bits à 16 bits, est-ce que le nombre de valeurs que l'on peut coder double, quadruple, pentuple ? De même, combien de valeurs différentes on peut coder avec bits. Par exemple, combien de nombres différents peut-on coder avec 4, 8 ou 16 bits ? La section précédente vous l'expliquer.
Avec bits, on peut coder valeurs différentes, dont le , ce qui fait qu'on peut compter de à . N'oubliez pas cette formule : elle sera assez utile dans la suite de ce tutoriel. Pour exemple, on peut coder 16 valeurs avec 4 bits, qui vont de 0 à 15. De même, on peut coder 256 valeurs avec un octet, qui vont de 0 à 255. Le tableau ci-dessous donne quelques exemples communs.
| Nombre de bits | Nombre de valeurs codables |
|---|---|
| 4 | 16 |
| 8 | 256 |
| 16 | 65 536 |
| 32 | 4 294 967 296 |
| 64 | 18 446 744 073 709 551 615 |
Inversement, on peut se demander combien de bits il faut pour coder une valeur quelconque, que nous noterons N. Pour cela, il faut utiliser la formule précédente, mais à l'envers. On cherche alors tel que . L'opération qui donne est appelée le logarithme, et plus précisément un logarithme en base 2, noté . Le problème est que le résultat du logarithme ne tombe juste que si le nombre X est une puissance de 2. Si ce n'est pas le cas, le résultat est un nombre à virgule, ce qui n'a pas de sens pratique. Par exemple, la formule nous dit que pour coder le nombre 13, on a besoin de 3,70043971814 bits, ce qui est impossible. Pour que le résultat ait un sens, il faut arrondir à l'entier supérieur. Pour l'exemple précédent, les 3,70043971814 bits s'arrondissent en 4 bits.
Le lien entre nombre de chiffres hexadécimaux et valeurs codables
modifierMaintenant, voyons combien de valeurs peut-on coder avec chiffres hexadécimaux. La réponse n'est pas très différente de celle obtenue en binaire, si ce n'est qu'il faut remplacer le 2 par un 16 dans la formule précédente. Avec chiffres hexadécimaux, on peut coder valeurs différentes, dont le , ce qui fait qu'on peut compter de à . Le tableau ci-dessous donne quelques exemples communs.
| Nombre de chiffres héxadécimaux | Nombre de valeurs codables |
|---|---|
| 1 (4 bits) | 16 |
| 2 (8 bits) | 256 |
| 4 (16 bits) | 65 536 |
| 8 (32 bits) | 4 294 967 296 |
| 16 (64 bits) | 18 446 744 073 709 551 615 |
Inversement, on peut se demander combien faut-il de chiffres hexadécimaux pour coder une valeur quelconque en hexadécimal. La formule est là encore la même qu'en binaire, sauf qu'on remplace le 2 par un 16. Pour trouver le nombre de chiffres hexadécimaux pour encoder un nombre X, il faut calculer . Notons que le logarithme utilisé est un logarithme en base 16, et non un logarithme en base 2, comme pour le binaire. Là encore, le résultat ne tombe juste que si le nombre X est une puissance de 16 et il faut arrondir à l'entier supérieur si ce n'est pas le cas.
Une propriété mathématique des logarithmes nous dit que l'on peut passer d'un logarithme en base X et à un logarithme en base Y avec une simple division, en utilisant la formule suivante :
Dans le cas qui nous intéresse, on a Y = 2 et X = 16, ce qui donne :
Or, est tout simplement égal à 4, car il faut 4 bits pour coder la valeur 16. On a donc :
En clair, il faut quatre fois moins de chiffres hexadécimaux que de bits, ce qui est assez intuitif vu qu'il faut 4 bits pour coder un chiffre hexadécimal.
Les débordements d'entier
modifierOn vient de voir que tout ordinateur manipule des nombres dont le nombre de bits est toujours le même : on dit qu'ils sont de taille fixe. Et cela limite les valeurs qu'il peut encoder, qui sont comprises dans un intervalle bien précis. Mais que ce passe-t-il si jamais le résultat d'un calcul ne rentre pas dans cet intervalle ? Par exemple, pour du binaire normal, que faire si le résultat d'un calcul atteint ou dépasse ? Dans ce cas, le résultat ne peut pas être représenté par l'ordinateur et il se produit ce qu'on appelle un débordement d'entier.
On peut imaginer d'autres codages pour lesquels les entiers ne commencent pas à zéro ou ne terminent pas à . On peut prendre le cas où l'ordinateur gère les nombres négatifs, par exemple. Dans le cas général, l'ordinateur peut coder les valeurs comprises dans un intervalle, qui va de la valeur la plus basse à la valeur la plus grande . Et encore une fois, si un résultat de calcul sort de cet intervalle, on fait face à un débordement d'entier.
La valeur haute de débordement désigne la première valeur qui est trop grande pour être représentée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 0 et 7, la valeur haute de débordement est égale à 8. Pour les nombres entiers, la valeur haute de débordement vaut , avec la plus grande valeur codable par l'ordinateur.
On peut aussi définir la valeur basse de débordement, qui est la première valeur trop petite pour être codée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 8 et 250, la valeur basse de débordement est égale à 7. Pour les nombres entiers, la valeur basse de débordement vaut , avec la plus petite valeur codable par l'ordinateur.
La gestion des débordements d'entiers
modifierFace à un débordement d'entier, l'ordinateur peut utiliser deux méthodes : l'arithmétique saturée ou l'arithmétique modulaire.
L'arithmétique saturée consiste à arrondir le résultat pour prendre la plus grande ou la plus petite valeur. Si le résultat d'un calcul dépasse la valeur haute de débordement, le résultat est remplacé par le plus grand entier supporté par l'ordinateur. La même chose est possible quand le résultat est inférieur à la plus petite valeur possible, par exemple lors d'une soustraction : l'ordinateur arrondit au plus petit entier possible.
Pour donner un exemple, voici ce que cela donne avec des entiers codés sur 4 bits, qui codent des nombres de 0 à 15. Si je fais le calcul 8 + 9, le résultat normal vaut 17, ce qui ne rentre pas dans l'intervalle. Le résultat est alors arrondi à 15. Inversement, si je fais le calcul 8 - 9, le résultat sera de -1, ce qui ne rentre pas dans l'intervalle : le résultat est alors arrondi à 0.

L'arithmétique modulaire est plus compliquée et c'est elle qui va nous intéresser dans ce qui suit. Pour simplifier, imaginons que l'on décompte à partir de zéro. Quand on arrive à la valeur haute de débordement, on recommence à compter à partir de zéro. L'arithmétique modulaire n'est pas si contre-intuitive et vous l'utilisez sans doute au quotidien. Après tout, c'est comme cela que l'on compte les heures, les minutes et les secondes. Quand on compte les minutes, on revient à 0 au bout de 60 minutes. Pareil pour les heures : on revient à zéro quand on arrive à 24 heures. Divers compteurs mécaniques fonctionnent sur le même principe et reviennent à zéro quand ils dépassent la plus grande valeur possible, l'image ci-contre en montrant un exemple.
Mathématiquement, l'arithmétique modulaire implique des divisions euclidiennes, celles qui donnent un quotient et un reste. Lors d'un débordement, le résultat s'obtient comme suit : on divise le nombre qui déborde par la valeur haute de débordement, et que l'on conserve le reste de la division. Au passage, l'opération qui consiste à faire une division et à garder le reste au lieu du quotient est appelée le modulo. Prenons l'exemple où l'ordinateur peut coder tous les nombres entre 0 et 1023, soit une valeur haute de débordement de 1024. Pour coder le nombre 4563, on fait le calcul 4563 / 1024. On obtient : . Le reste de la division est de 467 et c'est lui qui sera utilisé pour coder la valeur de départ, 4563. Le nombre 4563 est donc codé par la valeur 467 dans un tel ordinateur en arithmétique modulaire. Au passage, la valeur haute de débordement est toujours codée par un zéro dans ce genre d'arithmétique.
Les ordinateurs utilisent le plus souvent une valeur haute de débordement de , avec n le nombre de bits utilisé pour coder les nombres entiers positifs. En faisant cela, l'opération modulo devient très simple et revient à éliminer les bits de poids forts au-delà du énième bit. Par exemple, reprenons l'exemple d'un ordinateur qui code ses nombres sur 4 bits. Imaginons qu'il fasse le calcul , soit 1101 + 0011 = 1 0000 en binaire. Le résultat entraîne un débordement d'entier et l'ordinateur ne conserve que les 4 bits de poids faible. Cela donne : 1101 + 0011 = 0000. Comme autre exemple l'addition 1111 + 0010 ne donnera pas 17 (1 0001), mais 1 (0001).
L'avantage est que les calculs sont beaucoup plus simples avec cette méthode qu'avec les autres. L'ordinateur a juste à ne pas calculer les bits de poids fort. Pas besoin de faire une division pour calculer un modulo, pas besoin de corriger le résultat pour faire de l'arithmétique saturée.
Aparté : quelques valeurs particulières en binaire
modifierPlus haut, on a dit qu'avec n bits, on peut encoder toutes les valeurs allant de à . Ce simple fait permet de déterminer quelle est la valeur de certains entiers à vue d’œil. Dans ce qui va suivre, nous allons poser quelques bases que nous réutiliserons dans la suite du chapitre. Il s'agit de quelques trivias qui sont cependant assez utiles.
Le premier trivia concerne la valeur maximale : elle est encodée par un nombre dont tous les bits sont à 1.
Le deuxième trivia concerne les nombres de la forme 000...000 1111 1111, à savoir des nombres dont les x bits de poids faible sont à 1 et tous les autres valent 0. Par définition, de tels nombres codent la plus grande valeur possible sur x bits, ce qui fait qu'ils valent .
Le troisième trivia concerne les nombres de la forme 11111...0000. En clair, des nombres où on a une suite consécutive de 1 dans les bits de poids fort et les x bits de poids faibles à 0. De tels nombres valent : . La preuve est assez simple : ils s'obtiennent en prenant la valeur maximale , et en soustrayant un nombre de la forme .

Si on utilise l'arithmétique modulaire, la valeur n'est autre que la valeur de débordement haute pour les nombres stockés sur n bits, et se code comme le zéro (il faudrait 1 bit de plus pour stocker le 1 de poids fort de ). Les 1er et 3ème nombres évoqués dans les paragraphes précédents peuvent donc se passer de dans leur expression :
- est codé 1111111111111111...111 (n bits à 1)
- est codé 11111...111000..000000 (x bits à 0 précédés de n-x bits à 1)
Les nombres entiers négatifs
modifierPassons maintenant aux entiers négatifs en binaire : comment représenter le signe moins ("-") avec des 0 et des 1 ? Eh bien, il existe plusieurs méthodes :
- la représentation en signe-valeur absolue ;
- la représentation en complément à un ;
- la représentation en complément à deux;
- la représentation par excès ;
- la représentation dans une base négative ;
- d'autres représentations encore moins utilisées que les autres.
La représentation en signe-valeur absolue
modifierLa solution la plus simple pour représenter un entier négatif consiste à coder sa valeur absolue en binaire, et rajouter un bit qui précise si c'est un entier positif ou un entier négatif. Par convention, ce bit de signe vaut 0 si le nombre est positif et 1 s'il est négatif. On parle alors de représentation en signe-valeur absolue, aussi appelée représentation en signe-magnitude.
Avec cette technique, il y autant de nombres positifs que négatifs. Mieux : pour chaque nombre représentable en représentation signe-valeur absolue, son inverse l'est aussi. Ce qui fait qu'avec cette méthode, le zéro est codé deux fois : on a un -0, et un +0. Cela pose des problèmes lorsqu'on demande à notre ordinateur d'effectuer des calculs ou des comparaisons avec zéro.

La représentation en complément à un
modifierLa représentation en complément à un peut être vue, en première approximation, comme une variante de la représentation en signe-magnitude. Et je dis bien : "em première approximation", car il y a beaucoup à dire sur la représentation en complément à un, mais nous verrons cela dans la section suivante sur le complément à deux. Conceptuellement, la représentation en signe-magnitude et celle du complément à un sont drastiquement différentes et sont basées sur des concepts mathématiques totalement différents. Mais elles ont des ressemblances de surface, qui font que faire la comparaison entre les deux est assez utile pédagogiquement parlant.
En complément à un, les nombres sont codés en utilisant un bit de signe qui indique si le nombre de positif ou négatif, couplé à une valeur absolue. Par contre, la valeur absolue est codée différemment en binaire. Pour les nombres positifs, la valeur absolue est codée en binaire normal, pas de changement comparé aux autres représentations. Mais pour les valeurs négatives, la valeur absolue est codée en binaire normal, puis tous les bits sont inversés : les 0 deviennent des 1 et réciproquement. En clair, on utilise une opération de complémentation pour les nombres négatifs.
Prenons un exemple avec un nombre codé sur 4 bits, avec un cinquième bit de signe. La valeur 5 est codée comme suit : 0 pour le bit de signe, 5 donne 0101 en binaire, le résultat est 0 0101. Pour la valeur -5, le bit de signe est 1, 5 donne 0101 en binaire, on inverse les bits ce qui donne 1010 : cela donne 11010. Notez qu'on peut passer d'un résultat à l'autre avec une opération de complémentation, à savoir en inversant les bits de l'autre et réciproquement.
Il s'agit là d'une propriété générale avec le complément à 1 : l'opposé d'un nombre, à savoir passer de sa valeur positive à sa valeur négative ou inversement, se calcule avec une opération NOT, une opération de complémentation (d'où son nom). L'avantage est que les ordinateurs gèrent naturellement d'opération de complémentation. Par contre, en signe-magnitude, inverser le bit de signe est une opération spécifique et ne sert qu'à ça. Il faut donc rajouter une opération en plus pour calculer l'opposé d'un nombre.
La représentation en complément à un garde les défauts de la représentation en signe-magnitude. Le zéro est codé deux fois, avec un zéro positif et un zéro négatif. La différence est que les valeurs négatives sont dans l'ordre inverse, il y a une symétrie un peu meilleure. Les deux zéros sont d'ailleurs totalement éloignés, ils correspondent aux valeurs extrêmes encodables : le zéro positif a tous ses bits à 0, le zéro négatif a tous ses bits à 1. Le résultat est que l'implémentation des comparaisons et de certains calculs est plus complexe qu'avec le signe-magnitude, mais de peu.

La représentation par excès
modifierLa représentation par excès consiste à ajouter un biais aux nombres à encoder afin de les encoder par un entier positif. Pour encoder tous les nombres compris entre -X et Y en représentation par excès, il suffit de prendre la valeur du nombre à encoder, et de lui ajouter un biais égal à X. Ainsi, la valeur -X sera encodée par zéro, et toutes les autres valeurs le seront par un entier positif, le zéro sera encodé par X, 1, par X+1, etc. Par exemple, prenons des nombres compris entre -127 et 128. On va devoir ajouter un biais égal à 127, ce qui donne :
| Valeur avant encodage | Valeur après encodage |
|---|---|
| -127 | 0 |
| -126 | 1 |
| -125 | 2 |
| … | … |
| 0 | 127 |
| … | … |
| 127 | 254 |
| 128 | 255 |
La représentation en complément à deux
modifierLa représentation en complément à deux est basée sur les mêmes mathématiques que le complément à un, mais fonctionne très différemment en pratique. Si on regarde de loin, son principe est assez différent : il n'y a pas de bit de signe ni quoi que ce soit d'autre. A la place, un nombre en complément à deux est encodé comme en binaire normal, à un point près : le bit de poids fort est soustrait, et non additionné aux autres. Il a une valeur négative : on soustrait la puissance de deux associée s'il vaut 1, on ne la tient pas en compte s'il vaut 0.
Par exemple, la valeur du nombre noté 111001 en complément à deux s'obtient comme suit :
| -32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 1 |
Sa valeur est ainsi de (−32×1)+(16×1)+(8×1)+(4×0)+(2×1)+(1×1) = −32+16+8+1 = -7.
- Avec le complément à deux, comme avec le complément à un, le bit de poids fort vaut 0 pour les nombres positifs et 1 pour les négatifs.
L'avantage de cette représentation est qu'elle n'a pas de double zéro : le zéro n'est encodé que par une seule valeur. Par contre, la valeur autrefois prise par le zéro négatif est réutilisée pour encoder une valeur négative. La conséquence est que l'on a un nombre négatif en plus d'encodé, il n'y a plus le même nombre de valeurs strictement positives et de valeurs négatives encodées. Le nombre négatif en question est appelé le nombre le plus négatif, ce nom trahit le fait que c'est celui qui a la plus petite valeur (la plus grande valeur absolue). Il est impossible de coder l'entier positif associé, sa valeur absolue.

Le calcul du complément à deux : première méthode
modifierLes représentations en complément à un et en complément à deux sont basées sur le même principe mathématique. Leur idée est de remplacer chaque nombre négatif par un nombre positif équivalent, appelé le complément. Par équivalent, on veut dire que tout calcul donne le même résultat si on remplace un nombre négatif par son complément (idem avec un nombre positif, son complément aura un signe inverse). Et pour faire cela, elles se basent sur les débordements d'entier pour fonctionner, et plus précisément sur l'arithmétique modulaire abordée plus haut.
Si on fait les calculs avec le complément, les résultats du calcul entraînent un débordement d'entier, qui sera résolu par un modulo : l'ordinateur ne conserve que les bits de poids faible du résultat, les autres bits sont oubliés. Par exemple, prenons l'addition 15 + 2, 1111 + 0010 en binaire : le résultat ne sera pas 17 (10001), vu qu'on n'a pas assez de bits pour encoder le résultat, mais 1 (0001). Et le résultat après modulo sera identique au résultat qu'on aurait obtenu avec le nombre négatif sans modulo. En clair, c'est la gestion des débordements qui permet de corriger le résultat de manière à ce que l'opération avec le complément donne le même résultat qu'avec le nombre négatif voulu. Ainsi, on peut coder un nombre négatif en utilisant son complément positif.
- Cela ressemble beaucoup à la méthode de soustraction basée sur un complément à 9 pour ceux qui connaissent, sauf que c'est une version binaire qui nous intéresse ici.
Prenons un exemple, qui permettra d'introduire la suite. Encore une fois, on utilise un codage sur 4 bits dont la valeur haute de débordement est de 16. Prenons l'addition de 13 + 3 = 16. Avec l'arithmétique modulaire, 16 est équivalent à 0, ce qui donne : 13 + 3 = 0 ! On peut aussi reformuler en disant que 13 = -3, ou encore que 3 = -13. Dit autrement, 3 est le complément de -13 pour ce codage. Et ne croyez pas que ça marche uniquement dans cet exemple : cela se généralise assez rapidement à tout nombre négatif.
Prenons un nombre N dont un veut calculer le complément à deux K. Dans le cas général, on a :
- , vu que en utilisant le modulo.
En réorganisant très légèrement les termes pour isoler K, on a :
La formule précédent permet de calculer la complément à deux assez simplement, en faisant le calcul à la main.
Avant de poursuivre, prenons un exemple très intéressant : le cas où N = -1. Son complément à deux vaut donc :
Le terme devrait vous rappeler quelque chose : il s'agit d'un nombre dont tous les bits sont à 1. En clair, le complément à deux de -1 est un nombre de la forme 1111...111. Et cela vaut quelque soit le nombre de bits n. La représentation de -1 est similaire, peu importe que l'on utilise des nombres de 16 bits, 32 bits, 64 bits, etc.
Voyons maintenant le cas des puissance de deux, par exemple 2, 4, 8, 16, etc. Leur complément à deux vaut :
Nous avions vu précédemment dans le chapitre que ces nombres sont de la forme 11111...0000. En clair, des nombres dont les x bits de poids faible sont à 0, et tous les autres bits sont à 1. Par exemple, le complément à deux de -2 est un nombre dont les bits sont à 1, sauf le bit de poids faible. De même, le complément à deux de -4 a tous ses bits à 1, sauf les deux bits de poids faible. Et le complément à deux de -8 a tous ses bits à 1, sauf les trois bits de poids faible. Pour résumer, tout nombre de la forme a tous ses bits à 1, sauf les x bits de poids faible qui sont à 0.
| -1 | 1111 1111 |
|---|---|
| -2 | 1111 1110 |
| -4 | 1111 1100 |
| -8 | 1111 1000 |
| -16 | 1111 0000 |
| -32 | 1110 0000 |
| -64 | 1100 0000 |
| -128 | 1000 0000 |
| 0 / - 256 | 0000 0000 |
Le calcul du complément à deux : seconde méthode
modifierIl existe une seconde méthode pour calculer le complément à deux d'un nombre, la voici. Pour les nombres positifs, encodez-les comme en binaire normale. Pour les nombres négatifs, faites pareil, puis inversez tous les bits, avant d'ajouter un. La procédure est identique à celle du complément à un, sauf que l'on incrémente le résultat final. Et ce n'est pas une coïncidence, comme nous allons le voir immédiatement.
Pour comprendre pourquoi la méthode marche, repartons de la formule précédente . Elle peut se reformuler comme suit :
La valeur est par définition un nombre dont tous les bits sont à 1. À cette valeur, on soustrait un nombre dont certains bits sont à 1 et d'autres à 0. En clair, pour chaque colonne, on a deux possibilités : soit on doit faire la soustraction , soit la soustraction . Or, les règles de l'arithmétique binaire disent que et . En regardant attentivement, on se rend compte que le bit du résultat est l'inverse du bit de départ. De plus, les deux cas ne donnent pas de retenue : le calcul pour chaque bit n'influence pas les bits voisins.
Le terme est donc le complément à un du nombre N, un nombre égal à sa représentation en binaire dont tous les bits sont inversés. Notons le nombre formé en inversant tous les bits de N. On a alors :
En clair, le complément à deux s'obtient en prenant le complément à un et en ajoutant 1. Dit autrement, il faut prendre le nombre N, en inverser tous les bits et ajouter 1.
Une autre manière équivalente consiste à faire le calcul suivant :
On prend le nombre dont on veut le complément, on soustrait 1 et on inverse les bits.
- Notons que tout ce qui a été dit plus haut marche aussi pour le complément à un, avec cependant une petite différence : la valeur haute de débordement n'est pas la même, ce qui change les calculs. Pour des nombres codés sur bits, la valeur haute de débordement est égale à en complément à deux, alors qu'elle est de en complément à un. De ce fait, la gestion des débordements est plus simple en complément à deux.
L'extension de signe
modifierDans les ordinateurs, tous les nombres sont codés sur un nombre fixé et constant de bits. Ainsi, les circuits d'un ordinateur ne peuvent manipuler que des nombres de 4, 8, 12, 16, 32, 48, 64 bits, suivant la machine. Si l'on veut utiliser un entier codé sur 16 bits et que l'ordinateur ne peut manipuler que des nombres de 32 bits, il faut bien trouver un moyen de convertir le nombre de 16 bits en un nombre de 32 bits, sans changer sa valeur et en conservant son signe. Cette conversion d'un entier en un entier plus grand, qui conserve valeur et signe s'appelle l'extension de signe.
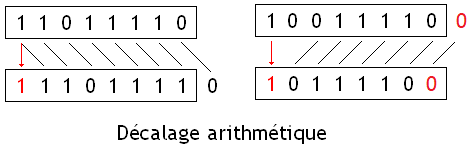
L'extension de signe des nombres positifs consiste à remplir les bits de poids fort avec des 0 jusqu’à arriver à la taille voulue : c'est la même chose qu'en décimal, où rajouter des zéros à gauche d'un nombre positif ne changera pas sa valeur. Pour les nombres négatifs, il faut remplir les bits à gauche du nombre à convertir avec des 1, jusqu'à obtenir le bon nombre de bits : par exemple, 1000 0000 (-128 codé sur 8 bits) donnera 1111 1111 1000 000 après extension de signe sur 16 bits. L'extension de signe d'un nombre codé en complément à 2 se résume donc en une phrase : il faut recopier le bit de poids fort de notre nombre à convertir à gauche de celui-ci jusqu’à atteindre le nombre de bits voulu.
L'explication plus simple tient dans la manière de coder le bit de poids fort. Prenons l'exemple de la conversion d'un entier de 5 bits en un entier de 8bits. Les 4 bits de poids faible ont un poids positif (on les additionne), alors que le bit de poids fort a un poids négatif. Le nombre encodé vaut : . La valeur encodée sur 4 bits reste la même après extension de signe, car les poids des bits de poids faible ne changent pas. Par contre, le bit de poids fort change. Sur 8 bits, la valeur -16 est encodée par un nombre de la forme 1111 0000. En remplaçant le bit de poids fort par sa valeur calculée sur plus de bits, on remarque que les bits de poids fort ont été remplacés par des 1.
La représentation négabinaire
modifierEnfin, il existe une dernière méthode, assez simple à comprendre, appelée représentation négabinaire. Dans cette méthode, les nombres sont codés non en base 2, mais en base -2. Oui, vous avez bien lu : la base est un nombre négatif. Dans les faits, la base -2 est similaire à la base 2 : il y a toujours deux chiffres (0 et 1), et la position dans un chiffre indique toujours par quelle puissance de 2 il faut multiplier, sauf qu'il faudra ajouter un signe moins une fois sur 2. Concrètement, les puissances de -2 sont les suivantes : 1, -2, 4, -8, 16, -32, 64, etc. En effet, un nombre négatif multiplié par un nombre négatif donne un nombre positif, ce qui fait qu'une puissance sur deux est négative, alors que les autres sont positives. Ainsi, on peut représenter des nombres négatifs, mais aussi des nombres positifs dans une puissance négative.
Par exemple, la valeur du nombre noté 11011 en base -2 s'obtient comme suit :
| … | -32 | 16 | -8 | 4 | -2 | 1 |
|---|---|---|---|---|---|---|
| … | 1 | 1 | 1 | 0 | 1 | 1 |
Sa valeur est ainsi de (−32×1)+(16×1)+(−8×1)+(4×0)+(−2×1)+(1×1)=−32+16−8−2+1=−25.
Les nombres à virgule
modifierOn sait donc comment sont stockés nos nombres entiers dans un ordinateur. Néanmoins, les nombres entiers ne sont pas les seuls nombres que l'on utilise au quotidien : il nous arrive d'en utiliser à virgule. Notre ordinateur n'est pas en reste : il est lui aussi capable de manipuler de tels nombres. Dans les grandes lignes, il peut utiliser deux méthodes pour coder des nombres à virgule en binaire : La virgule fixe et la virgule flottante.
Les nombres à virgule fixe
modifierLa méthode de la virgule fixe consiste à émuler les nombres à virgule à partir de nombres entiers. Un nombre à virgule fixe est codé par un nombre entier proportionnel au nombre à virgule fixe. Pour obtenir la valeur de notre nombre à virgule fixe, il suffit de diviser l'entier servant à le représenter par le facteur de proportionnalité. Par exemple, pour coder 1,23 en virgule fixe, on peut choisir comme « facteur de conversion » 1000, ce qui donne l'entier 1230.
Généralement, les informaticiens utilisent une puissance de deux comme facteur de conversion, pour simplifier les calculs. En faisant cela, on peut écrire les nombres en binaire et les traduire en décimal facilement. Pour l'exemple, cela permet d'écrire des nombres à virgule en binaire comme ceci : 1011101,1011001. Et ces nombres peuvent se traduire en décimal avec la même méthode que des nombres entier, modulo une petite différence. Comme pour les chiffres situés à gauche de la virgule, chaque bit situé à droite de la virgule doit être multiplié par la puissance de deux adéquate. La différence, c'est que les chiffres situés à droite de la virgule sont multipliés par une puissance négative de deux, c'est à dire par , , , , , ...
Cette méthode est assez peu utilisée de nos jours, quoiqu'elle puisse avoir quelques rares applications relativement connue. Un bon exemple est celui des banques : les sommes d'argent déposées sur les comptes ou transférées sont codés en virgule fixe. Les sommes manipulées par les ordinateurs ne sont pas exprimées en euros, mais en centimes d'euros. Et c'est une forme de codage en virgule fixe dont le facteur de conversion est égal à 100. La raison de ce choix est que les autres méthodes de codage des nombres à virgule peuvent donner des résultats imprécis : il se peut que les résultats doivent être tronqués ou arrondis, suivant les opérandes. Cela n'arrive jamais en virgule fixe, du moins quand on se limite aux additions et soustractions.
Les nombres flottants
modifierLes nombres à virgule fixe ont aujourd'hui été remplacés par les nombres à virgule flottante, où le nombre de chiffres après la virgule est variable. Le codage d'un nombre flottant est basée sur son écriture scientifique. Pour rappel, en décimal, l’écriture scientifique d'un nombre consiste à écrire celui-ci comme un produit entre un nombre et une puissance de 10. Ce qui donne :
- , avec
Le nombre est appelé le significande et il est compris entre 1 (inclus) et 10 (exclu). Cette contrainte garantit que l'écriture scientifique d'un nombre est unique, qu'il n'y a qu'une seule façon d'écrire un nombre en notation scientifique. Pour cela, on impose le nombre de chiffre à gauche de la virgule et le plus simple est que celui-ci soit égal à 1. Mais il faut aussi que celui-ci ne soit pas nul. En effet, si on autorise de mettre un 0 à gauche de la virgule, il y a plusieurs manières équivalentes d'écrire un nombre. Ces deux contraintes font que le significande doit être égal ou plus grand que 1, mais strictement inférieur à 10. Par contre, on peut mettre autant de décimales que l'on veut.
En binaire, c'est la même chose, mais avec une puissance de deux. Cela implique de modifier la puissance utilisée : au lieu d'utiliser une puissance de 10, on utilise une puissance de 2.
- , avec
Le significande est aussi altéré, au même titre que la puissance, même si les contraintes sont similaires à celles en base 10. En effet, le nombre ne possède toujours qu'un seul chiffre à gauche de la virgule, comme en base 10. Vu que seuls deux chiffres sont possibles (0 et 1) en binaire, on s'attend à ce que le chiffre situé à gauche de la virgule soit un zéro ou un 1. Mais rappelons que le chiffre à gauche doit être non-nul, pour les mêmes raisons qu'en décimal. En clair, le significande a forcément un bit à 1 à gauche de la virgule. Pour récapituler, l'écriture scientifique binaire d'un nombre consiste à écrire celui-ci sous la forme :
- , avec
La partie fractionnaire du nombre , qu'on appelle la mantisse.

Traduire un nombre en écriture scientifique binaire
modifierPour déterminer l'écriture scientifique en binaire d'un nombre quelconque, la procédure dépend de la valeur du nombre en question. Tout dépend s'il est dans l'intervalle , au-delà de 2 ou en-dessous de 1.
- Pour un nombre entre 1 (inclus) et 2 (exclu), il suffit de le traduire en binaire. Son exposant est 0.
- Pour un nombre au-delà de 2, il faut le diviser par 2 autant de fois qu'il faut pour qu'il rentre dans l’intervalle . L'exposant est alors le nombre de fois qu'il a fallu diviser par 2.
- Pour un nombre plus petit que 1, il faut le multiplier par 2 autant de fois qu'il faut pour qu'il rentre dans l’intervalle . L'exposant se calcule en prenant le nombre de fois qu'il a fallu multiplier par 2, et en prenant l'opposé (en mettant un signe - devant le résultat).
Le codage des nombres flottants et la norme IEEE 754
modifierPour coder cette écriture scientifique avec des nombres, l'idée la plus simple est d'utiliser trois nombres, pour coder respectivement la mantisse, l'exposant et un bit de signe. Coder la mantisse implique que le bit à gauche de la virgule vaut toujours 1, mais nous verrons qu'il y a quelques rares exceptions à cette règle. Quelques nombres flottants spécialisés, les dénormaux, ne sont pas codés en respectant les règles pour le significande et ont un 0 à gauche de la virgule. Un bon exemple est tout simplement la valeur zéro, que l'on peut coder en virgule flottante, mais seulement en passant outre les règles sur le significande. Toujours est-il que le bit à gauche de la virgule n'est pas codé, que ce soit pour les flottants normaux ou les fameux dénormaux qui font exception. On verra que ce bit peut se déduire en fonction de l'exposant utilisé pour encoder le nombre à virgule, ce qui lui vaut le nom de bit implicite. L'exposant peut être aussi bien positif que négatif (pour permettre de coder des nombres très petits), et est encodé en représentation par excès sur n bits avec un biais égal à .

Le standard pour le codage des nombres à virgule flottante est la norme IEEE 754. Cette norme va (entre autres) définir quatre types de flottants différents, qui pourront stocker plus ou moins de valeurs différentes.
| Classe de nombre flottant | Nombre de bits utilisés pour coder un flottant | Nombre de bits de l'exposant | Nombre de bits pour la mantisse | Décalage |
|---|---|---|---|---|
| Simple précision | 32 | 8 | 23 | 127 |
| Double précision | 64 | 11 | 52 | 1023 |
| Double précision étendue | 80 ou plus | 15 ou plus | 64 ou plus | 16383 ou plus |
IEEE754 impose aussi le support de certains nombres flottants spéciaux qui servent notamment à stocker des valeurs comme l'infini. Commençons notre revue des flottants spéciaux par les dénormaux, aussi appelés flottants dénormalisés. Ces flottants ont une particularité : leur bit implicite vaut 0. Ces dénormaux sont des nombres flottants où l'exposant est le plus petit possible. Le zéro est un dénormal particulier dont la mantisse est nulle. Au fait, remarquez que le zéro est codé deux fois à cause du bit de signe : on se retrouve avec un -0 et un +0.
| Bit de signe | Exposant | Mantisse |
|---|---|---|
| 0 ou 1 | Valeur minimale (0 en binaire) | Mantisse différente de zéro (dénormal strict) ou égale à zéro (zéro) |
Fait étrange, la norme IEEE754 permet de représenter l'infini, aussi bien en positif qu'en négatif. Celui-ci est codé en mettant l'exposant à sa valeur maximale et la mantisse à zéro. Et le pire, c'est qu'on peut effectuer des calculs sur ces flottants infinis. Mais cela a peu d'utilité.
| Bit de signe | Exposant | Mantisse |
|---|---|---|
| 0 ou 1 | Valeur maximale | Mantisse égale à zéro |
Mais malheureusement, l'invention des flottants infinis n'a pas réglé tous les problèmes. Par exemple, quel est le résultat de ? Ou encore ? Autant prévenir tout de suite : mathématiquement, on ne peut pas savoir quel est le résultat de ces opérations. Pour pouvoir résoudre ces calculs, il a fallu inventer un nombre flottant qui signifie « je ne sais pas quel est le résultat de ton calcul pourri ». Ce nombre, c'est NaN. NaN est l'abréviation de Not A Number, ce qui signifie : n'est pas un nombre. Ce NaN a un exposant dont la valeur est maximale, mais une mantisse différente de zéro. Pour être plus précis, il existe différents types de NaN, qui diffèrent par la valeur de leur mantisse, ainsi que par les effets qu'ils peuvent avoir. Malgré son nom explicite, on peut faire des opérations avec NaN, mais cela ne sert pas vraiment à grand chose : une opération arithmétique appliquée avec un NaN aura un résultat toujours égal à NaN.
| Bit de signe | Exposant | Mantisse |
|---|---|---|
| 0 ou 1 | Valeur maximale | Mantisse différente de zéro |
Les arrondis et exceptions
modifierLa norme impose aussi une gestion des arrondis ou erreurs, qui arrivent lors de calculs particuliers. En voici la liste :
| Nom de l’exception | Description |
|---|---|
| Invalid operation | Opération qui produit un NAN. Elle est levée dans le cas de calculs ayant un résultat qui est un nombre complexe, ou quand le calcul est une forme indéterminée. Pour ceux qui ne savent pas ce que sont les formes indéterminées, voici en exclusivité la liste des calculs qui retournent NaN : , , , , . |
| Overflow | Résultat trop grand pour être stocké dans un flottant. Le plus souvent, on traite l'erreur en arrondissant le résultat vers Image non disponible ; |
| Underflow | Pareil que le précédent, mais avec un résultat trop petit. Le plus souvent, on traite l'erreur en arrondissant le résultat vers 0. |
| Division par zéro | Le nom parle de lui-même. La réponse la plus courante est de répondre + ou - l'infini. |
| Inexact | Le résultat ne peut être représenté par un flottant et on doit l'arrondir. |
La gestion des arrondis pose souvent problème. Pour donner un exemple, on va prendre le nombre 0,1. En binaire, ce nombre s'écrit comme ceci : 0,1100110011001100... et ainsi de suite jusqu'à l'infini. Notre nombre utilise une infinité de décimales. Bien évidemment, on ne peut pas utiliser une infinité de bits pour stocker notre nombre et on doit impérativement l'arrondir. Comme vous le voyez avec la dernière exception, le codage des nombres flottants peut parfois poser problème : dans un ordinateur, il se peut qu'une opération sur deux nombres flottants donne un résultat qui ne peut être codé par un flottant. On est alors obligé d'arrondir ou de tronquer le résultat de façon à le faire rentrer dans un flottant. Pour éviter que des ordinateurs différents utilisent des méthodes d'arrondis différentes, on a décidé de normaliser les calculs sur les nombres flottants et les méthodes d'arrondis. Pour cela, la norme impose le support de quatre modes d'arrondis :
- Arrondir vers + l'infini ;
- vers - l'infini ;
- vers zéro ;
- vers le nombre flottant le plus proche.
Les nombres flottants logarithmiques
modifierLes nombres flottants logarithmiques sont une spécialisation des nombres flottants IEEE754, ou tout du moins une spécialisation des flottants écrits en écriture scientifique. Un nombre logarithmique est donc composé d'un bit de signe et d'un exposant, sans mantisse. La mantisse est totalement implicite : tous les flottants logarithmiques ont la même mantisse, qui vaut 1.
Pour résumer, il ne reste que l'exposant, qui est tout simplement le logarithme en base 2 du nombre encodé, d'où le nombre de codage flottant logarithmique donné à cette méthode. Attention toutefois : l'exposant est ici un nombre fractionnaire, codé en virgule fixe. Le choix d'un exposant fractionnaire permet de représenter pas mal de nombres de taille diverses.
| Bit de signe | Exposant | |
|---|---|---|
| Représentation binaire | 0 | 01110010101111 |
| Représentation décimale | + | 1040,13245464 |
L'utilité de cette représentation est de simplifier certains calculs, comme les multiplications, divisions, puissances, etc. En effet, les mathématiques nous disent que le logarithme d'un produit est égal à la somme des logarithmes : . Or, il se trouve que les ordinateurs sont plus rapides pour faire des additions/soustractions que pour faire des multiplications/divisions. Donc, la représentation logarithmique permet de remplacer les multiplications/divisions par des additions/soustractions, plus simples et plus rapides pour l'ordinateur.
Évidemment, les applications des flottants logarithmiques sont rares, limitées à quelques situations bien précises (traitement d'image, calcul scientifique spécifiques).
Les nombres à virgule non-représentables en binaire
modifierQuel que soit la façon de représenter les nombres à virgules, il existe des nombres qui ne peuvent être représentés de manière exacte, à savoir avec un nombre fini de décimales après la virgule. En soi, ce n'est pas spécifique au binaire, on a la même chose en décimal. Par exemple, la fraction 1/3 en décimal s'écrit 0.3333333..., avec une infinité de 3. La même chose existe en binaire, mais pour des nombres différents.
Déjà, évacuons le cas des nombres irrationnels, à savoir les nombres qui ne peuvent pas s'écrire sous la forme d'une fraction, comme ou . Ils ont une infinité de décimales que ce soit en binaire, en décimal, en hexadécimal, ou autre. Ils ne sont pas représentables avec un nombre fini de décimales quelle que soit la base utilisée. Concentrons-nous sur des nombres qui ne sont pas dans ce cas, et qui ont un nombre fini ou infini de décimales.
Le passage de la base 10 à la base 2 change le nombre de décimales, et peut faire passer d'un nombre fini de décimales à un nombre infini. Par exemple, est représenté en binaire avec une séquence infinie de bits : . Les nombres étant en base binaire et représenté avec un nombre limité de bits, il existe certains nombres décimaux triviaux qui ne sont pas représentables avec un nombre fini de décimales.
Et la réciproque n'est pas vraie : tout nombre binaire avec un nombre fini de décimales en binaire est représentable avec un nombre fini de décimales en base 10. Ceci est lié à la décomposition en facteur premier des bases utilisées :
Le nombre 10 possède tous les facteurs premiers de 2, mais 2 n'a pas de 5 dans sa décomposition.
Les encodages hybrides entre décimal et binaire
modifierDans cette section, nous allons voir les représentations qui mixent binaire et décimal. Il s'agit en réalité d'encodage qui permettent de manipuler des nombres codés en décimal, mais les chiffres sont codés en utilisant des bits. L'encodage Binary Coded Decimal est le plus connu de cette catégorie, mais il y en a quelques autres, qui sont moins connus. De telles représentations étaient très utilisées au début de l'informatique, mais sont aujourd'hui tombées en désuétude. Pour désigner ces encodages, nous parlerons d'encodages bit-décimaux : décimaux pour préciser qu'ils encodent des nombres codés en décimal, bit pour préciser que les chiffres sont codés avec des bits.
De tels encodages étaient utilisés sur les tous premiers ordinateurs pour faciliter le travail des programmeurs, mais aussi sur les premières calculettes. Ils sont utiles dans les applications où on doit manipuler chaque chiffre décimal séparément des autres. Un exemple classique est celui d'une horloge digitale. Ils ont aussi l'avantage de bien se marier avec les nombres à virgule. Les représentations des nombres à virgule fixe ou flottante ont le défaut que des arrondis peuvent survenir. Par exemple, la valeur 0,2 est codée comme suit en binaire normal : 0.00110011001100... et ainsi de suite jusqu’à l'infini. Avec les encodages bit-décimaux, on n'a pas ce problème, 0,2 étant codé 0000 , 0010.
Il a existé des ordinateurs qui travaillaient uniquement avec de tels encodages, appelés des ordinateurs décimaux. Ils étaient assez courants entre les années 60 et 70, même s'ils ne représentent pas la majorité des architectures de l'époque. Avec eux, la mémoire n'était pas organisée en octets, mais elle stockait des chiffres décimaux codés sur 5-6 bits. Le processeur faisait des calculs sur des chiffres bit-décimaux directement.
Leur grand avantage est leur très bonne performance dans les taches de bureautique, de comptabilité, et autres. Les processeurs de l'époque recevaient des entiers codés en bit-décimal de la part des entrées-sorties, et devaient les traiter. Les processeurs binaires devaient faire des conversions décimal-binaire pour communiquer avec les entrées-sorties, mais pas les processeurs décimaux. Le gain en performance pouvait être substantiel dans certaines applications.
Les ordinateurs décimaux se classent en deux sous-types bien précis. Les premiers gèrent des entiers qui ont un nombre de chiffres fixes. Par exemple, l'IBM 7070 gérait des entiers de 10 chiffres, plus un signe +/- pour les entiers signés. Le processeur faisait les calculs directement en bit-décimal, il gérait des entiers faisant environ 10-15 chiffres décimaux et savait faire des calculs avec de tels nombres. Le second sous-type effectue les calculs chiffre par chiffre et géraient des nombres de taille variable, sans limite de chiffres ! Nous reparlerons de ces derniers dans un chapitre ultérieur, quand nous parlerons de la différence entre byte et mot. Pour le moment, ne gardez à l'esprit que les processeurs gérant un nombre fixe de chiffres décimaux, plus simples à comprendre.
Le Binary Coded Decimal
modifierLe Binary Coded Decimal, abrévié BCD, est une représentation qui mixe binaire et décimal. Avec cette représentation, les nombres sont écrits en décimal, comme nous en avons l'habitude dans la vie courante, sauf que chaque chiffre décimal est directement traduit en binaire sur 4 bits. Prenons l'exemple du nombre 624 : le 6, le 2 et le 4 sont codés en binaire séparément, ce qui donne 0110 0010 0100.
| Nombre encodé (décimal) | BCD | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
On peut remarquer que 4 bits permettent de coder 16 valeurs, là où il n'y a que 10 chiffres. Dans le BCD proprement dit, les combinaisons de bits qui correspondent à 10, 11, 12, 13, 14 ou 15 ne sont tout simplement pas prises en compte. Sur quelques ordinateurs, ces combinaisons codent des chiffres décimaux en double : certains chiffres pouvaient être codés de deux manières différentes. Il est aussi possible d'utiliser ces valeurs pour coder quelque chose d'autre que des chiffres. Par exemple, il est possible de les utiliser pour coder un signe + ou -, afin de gérer les entiers relatifs. Une autre possibilité, complémentaire de la précédente, utilise ces valeurs en trop pour coder une virgule, afin de gérer les nombres non-entiers. Les possibilités sont nombreuses.
Le support du BCD implique souvent que le processeur supporte des opérations BCD, à savoir des opérations capables de travailler sur des opérandes en BCD et de donner un résultat en BCD. Il faut bien faire la différence entre les opérations en binaire et les opérations en BCD. Par exemple, on n'effectue pas une addition de la même manière en binaire et en décimal/BCD, même si les grandes lignes sont presque identiques. Les différences font que les processeurs doivent avoir des opérations différentes pour les deux encodages, de la même manière que les processeurs gèrent les opérations sur les flottants et les entiers séparément.
Le support du codage BCD est abandonné de nos jours, c'est surtout quelque chose qu'on trouve sur les anciens processeurs. Les architectures 8 et 16 bits supportaient à la fois des opérations binaires et des opérations BCD. Mais il a aussi existé une méthode intermédiaire, qui utilisait des additions binaires normales sur des opérandes BCD. L'idée est que le résultat de l'addition est incorrect, car les valeurs 10 à 15 peuvent apparaître comme chiffre dans le résultat. Mais on peut le corriger pour obtenir le résultat exact en BCD. Pour résumé, les processeurs faisaient des additions en binaire, et corrigeaient le résultat avec une opération spécifique pour obtenir un résultat en BCD. Nous en reparlerons dans le chapitre sur le langage machine et l'assembleur, dans lequel nous étudierons les différentes opérations que supporte un processeur.
Les encodages compacts du BCD
modifierDes variantes du BCD visent à réduire le nombre de bits utilisés pour encoder un nombre décimal. Nous allons les appeler les encodages BCD compacts. Avec certaines variantes, on peut utiliser seulement 7 bits pour coder deux chiffres décimaux, au lieu de 8 bits en BCD normal. Idem pour les nombres à 3 chiffres décimaux, qui prennent 10 bits au lieu de 12. Cette économie est réalisée par une variante du BCD assez compliquée, appelée l'encodage Chen-Ho. Une alternative, appelée le Densely Packed Decimal, arrive à une compression identique, mais avec quelques avantages au niveau de l'encodage. Ces encodages sont cependant assez compliqués à expliquer, surtout à ce niveau du cours, aussi je me contente de simplement mentionner leur existence.
Les encodages BCD compacts sont utilisés par les programmeurs pour stocker des données dans un fichier, en mémoire, mais guère plus. Ils ne sont pas gérés par le processeur directement, on ne peut pas faire de calculs avec, le processeur ne gére pas d'opération BCD supportant de tels encodages. C'est théoriquement possible, mais ça n'a jamais été implémenté dans un processeur, le cout en circuit n'en valait pas la chandelle. Pour faire des calculs sur des nombres en BCD compact, on doit les décompresser et les convertir en BCD normal ou en binaire, puis faire les calculs avec des opérations BCD/binaire usuelles.
L'encodage Excess-3
modifierLa représentation Excess-3 (XS-3) est une variante du BCD, qui a autrefois était utilisée sur d'anciens ordinateurs décimaux. Il s'agit d'une sorte d'hybride entre une représentation par excès et BCD. Chaque chiffre décimal est codé sur plusieurs bits en utilisant une représentation binaire par excès. Le biais est de 3 pour la représentation XS-3, il en existe des variantes avec un excès de 4, 5, mais elles sont moins utilisées. Avec elle, la conversion d'un chiffre décimal se fait comme suit : on prend le chiffre décimal, on ajoute 3, puis on traduit en binaire.
| Décimal | Binaire | |||
|---|---|---|---|---|
| -3 | 0 | 0 | 0 | 0 |
| -2 | 0 | 0 | 0 | 1 |
| -1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 0 | 1 |
| 7 | 1 | 0 | 1 | 0 |
| 8 | 1 | 0 | 1 | 1 |
| 9 | 1 | 1 | 0 | 0 |
| 10 | 1 | 1 | 0 | 1 |
| 11 | 1 | 1 | 1 | 0 |
| 12 | 1 | 1 | 1 | 1 |
L'avantage de cette représentation est que l'on peut facilement calculer les soustractions en utilisant une méthode bien précise (celle du complément à 10, je ne détaille pas plus). Le défaut est que le calcul des additions est légèrement plus complexe.
L'XS-3 a été utilisé sur quelques ordinateurs décimaux assez anciens, notamment sur l'UNIVAC I et II.
Le code 2 parmi 5
modifierLes codes 2 parmi 5 permettent d'encoder 10 chiffres décimaux sur 5 bits. Le code garantit que sur les 5 bits, deux sont à 1, les trois restants sont à 0, les bits à 0/1 n'étant pas les mêmes selon le chiffre encodé et le code utilisé. Il existe plusieurs codes 2 parmi 5, la plupart sont utilisés sur les codes barres dans les magasins, mais ce ne sont pas ceux utilisés dans les ordinateurs d'antan.
L'ordinateur IBM 7070 et ses déclinaisons utilisait un code 2 parmi 5 qui codait les 10 chiffres décimaux, ainsi que les signes + et -, et un caractère . Il gérait des entiers décimaux codés sur 10 chiffres plus un caractère +/- pour le signe. Les caractères pour le texte étaient codés en utilisant un code à deux chiffres décimaux, c’est-à-dire sur 10 bits.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | - | + |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01100 | 11000 | 10100 | 10010 | 01010 | 00110 | 10001 | 01001 | 00101 | 00011 | 1––10 | 1––01 | 0––11 |
Les codes bi-quinaires
modifierLes codes bi-quinaires codent des chiffres sur 7 bits. Les 7 bits sont découpés en deux sections : 2 bits pour la première, 5 pour l'autre. Les 5 bits permettent de compter de 0 à 4 ou de 5 à 9, un seul bit est à 1, les quatre autres sont à 0. Le bit mis à 1 indique la valeur encodée. Les deux bits restants déterminent si la valeur est inférieure ou supérieure/égale à 5, un seul des deux bits est à 1. Voici les deux encodages les plus courants :
 |
 |
L'originalité de ce codage est qu'il permet de facilement compter sur ses doigts : on a deux mains, cinq doigts. De nombreuses langues utilisent ce système pour coder des nombres, comme le Wolof. Et ce système est utilisé dans certains pays pour compter sur ses doigts, voire dans la vie de tous les jours. Et il a été utilisé sur d'anciens ordinateurs, dont l'IBM 650, l'UNIVAC Solid State et le UNIVAC LARC.
Pour rentrer vraiment dans le détail, voici les encodages utilisés sur ces machines. La lecture est facultative, il est possible de passer directement à la section suivante :
| IBM 650 | Remington Rand 409 | UNIVAC Solid State | UNIVAC LARC | |
|---|---|---|---|---|
| Chiffre | 1357-9 bits | 05-01234 | p-5-421 bits | p-5-qqq bits |
| 0 | 10-10000 | 0000-0 | 1-0-000 | 1-0-000 |
| 1 | 10-01000 | 1000-0 | 0-0-001 | 0-0-001 |
| 2 | 10-00100 | 1000-1 | 0-0-010 | 1-0-011 |
| 3 | 10-00010 | 0100-0 | 1-0-011 | 0-0-111 |
| 4 | 10-00001 | 0100-1 | 0-0-100 | 1-0-110 |
| 5 | 01-10000 | 0010-0 | 0-1-000 | 0-1-000 |
| 6 | 01-01000 | 0010-1 | 1-1-001 | 1-1-001 |
| 7 | 01-00100 | 0001-0 | 1-1-010 | 0-1-011 |
| 8 | 01-00010 | 0001-1 | 0-1-011 | 1-1-111 |
| 9 | 01-00001 | 0000-1 | 1-1-100 | 0-1-110 |
Les encodages alternatifs
modifierOutre le binaire et le BCD que nous venons de voir, il existe d'autres manières de coder des nombres en binaires. Et nous allons les aborder dans cette section. Parmi celle-ci, nous parlerons du code Gray, de la représentation one hot, du unaire et du ternaire. Nous en parlons car elles seront utiles dans la suite du cours, bien que de manière assez limitée. Autant nous passerons notre temps à parler du binaire normal, autant les représentations que nous allons voir sont aujourd'hui utilisées dans des cas assez spécifiques. Et elles sont plus courantes que vous ne le pensez.
Le code Gray
modifierLe code Gray est un encodage binaire qui a une particularité très intéressante : deux nombres consécutifs n'ont qu'un seul bit de différence. Pour exemple, voici ce que donne le codage des 8 premiers entiers sur 3 bits :
| Décimal | Binaire naturel | Codage Gray |
|---|---|---|
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
Les utilisations du code Gray sont assez nombreuses, bien qu'on n'en croise pas tous les jours. Un exemple : le code Gray est très utile dans certains circuits appelés les compteurs, qui mémorisent un nombre et l'incrémentent (+1) ou le décrémentent (-1) suivant les besoins de l'utilisateur. Il est aussi utilisé dans des scénarios difficiles à expliquer ici (des codes correcteurs d'erreur ou des histoires de passages de domaines d'horloge). Mais le point important est que ce code sera absolument nécessaire dans quelques chapitres, quand nous parlerons des tables de Karnaugh, un concept important pour la conception de circuits électroniques. Ne passez pas à côté de cette section.
Pour construire ce code Gray, on peut procéder en suivant plusieurs méthodes, les deux plus connues étant la méthode du miroir et la méthode de l'inversion.

La méthode du miroir est relativement simple. Pour connaître le code Gray des nombres codés sur n bits, il faut :
- partir du code Gray sur n-1 bits ;
- symétriser verticalement les nombres déjà obtenus (comme une réflexion dans un miroir) ;
- rajouter un 0 au début des anciens nombres, et un 1 au début des nouveaux nombres.
Il suffit de connaître le code Gray sur 1 bit pour appliquer la méthode : 0 est codé par le bit 0 et 1 par le bit 1.
Une autre méthode pour construire la suite des nombres en code Gray sur n bits est la méthode de l'inversion. Celle-ci permet de connaître le codage du nombre n à partir du codage du nombre n-1, comme la méthode du dessus. On part du nombre 0, systématiquement codé avec uniquement des zéros. Par la suite, on décide quel est le bit à inverser pour obtenir le nombre suivant, avec la règle suivante :
- si le nombre de 1 est pair, il faut inverser le dernier chiffre.
- si le nombre de 1 est impair, il faut localiser le 1 le plus à droite et inverser le chiffre situé à sa gauche.
Pour vous entraîner, essayez par vous-même avec 2, 3, voire 5.
Les représentations one-hot et unaire
modifierLa représentation one-hot et la représentation unaire sont deux représentations assez liées, mais légèrement différentes. Avec les deux représentations, les nombres sont codés avec un seul bit à 1, tous les autres sont à 0. Cela laisse peu de valeurs possibles : pour N bits, on peut encoder seulement N valeurs, voire N+1 valeurs en comptant le 0.
La représentation unaire est assez intuitive. Un zéro est codé en mettant tous les bits du nombre à zéro, la valeur 1 est encodée avec la valeur 000...0001, le deux avec 000...0010, etc. Pour résumer, le nombre N est encodé en mettant le énième bit à 1, à l'exception du zéro qui est encodé...par un zéro. Elle permet d'encoder N+1 valeurs sur N bits, car le zéro est encodé à part.
| Décimal | Binaire | Unaire |
|---|---|---|
| 0 | 000 | 0000 0000 |
| 1 | 001 | 0000 0001 |
| 2 | 010 | 0000 0010 |
| 3 | 011 | 0000 0100 |
| 4 | 100 | 0000 1000 |
| 5 | 101 | 0001 0000 |
| 6 | 110 | 0010 0000 |
| 7 | 111 | 0100 0000 |
| 8 | 1000 | 1000 0000 |
La représentation one-hot utilise N bits pour encoder N valeurs, zéro inclus. La différence avec le unaire est que dans cette représentation, le zéro est n'est PAS codé en mettant tous les bits à 0. En one-hot, la valeur 00000...0000 n'encode aucune valeur, c'est une valeur interdite. A la place, le zéro est codé en mettant le bit de poids faible à 1. Et pour ça, tout est décalé d'un cran comparé à la représentation unaire. Par exemple, si le bit de poids faible (celui de poids 0) est à 1, alors on code la valeur 0. Si le bit de poids numéro 1 est à 1, alors on code la valeur 1. Et ainsi de suite. En conséquence, on peut coder une valeur en moins avec le même nombre de bits.
| Décimal | Binaire | One-hot |
|---|---|---|
| 0 | 000 | 00000001 |
| 1 | 001 | 00000010 |
| 2 | 010 | 00000100 |
| 3 | 011 | 00001000 |
| 4 | 100 | 00010000 |
| 5 | 101 | 00100000 |
| 6 | 110 | 01000000 |
| 7 | 111 | 10000000 |
L'utilité de ces deux représentations n'est pas évidente. Mais sachez qu'elle le deviendra quand nous parlerons des circuits appelés les "compteurs", tout comme ce sera le cas pour le code Gray. Elles sont très utilisées dans des circuits appelés des machines à état, qui doivent incorporer des circuits compteurs efficients. Et ces représentations permettent d'avoir des circuits pour compter qui sont très simples, efficaces, rapides et économes en circuits électroniques. La représentation unaire sera aussi utile à la toute fin du cours, dans les chapitres liés à l'exécution dans le désordre. Il en sera fait référence quand nous parlerons de fenêtres d'instruction, d'émission dans l'ordre, de scoreboarding, etc.
Les encodages ternaires
modifierAprès avoir vu le binaire, il est temps de finir en beauté avec le ternaire ! Le ternaire n'a en soi rien à voir avec le binaire, c'est un encodage au même titre que le binaire, le décimal, l'hexadécimal, ou autre. Il encode un nombre non pas en base 10 comme le décimal, en base 2 comme le binaire, ou en base 16 comme l'hexadécimal, mais en base 3 ! Il encode un nombre en utilisant non pas des chiffres, ni des bits, mais des trits qui peuvent prendre trois valeurs.
Dans le ternaire normal, les trois valeurs d'un trit sont 0, 1 et 2. L'encodage multiple un trit par une puissance de 3, à savoir 1, 3, 9, 27, etc. On parle alors de ternaire non-équilibré. Inutile de développer plus, le principe est le même qu'en binaire ou en décimal, mais en base 3. De plus, un tel encodage n'est pas très utilisé en informatique, aucun ordinateur ne l’utilise, contrairement aux suivants.
Le ternaire non-équilibré est une variante du ternaire normal, où chaque trit encode les trois valeurs suivantes : 0, 1 et -1. Le trit est donc signé ! L'équivalent en binaire serait d'encoder les trois valeurs sur deux bits : un bit de signe et un bit pour coder 0/1. La différence est qu'utiliser deux bits fait qu'on a un zéro positif et un zéro négatif.
| Valeurs encodables par un trit | |||
|---|---|---|---|
| Ternaire non-équilibré | 0 | 1 | 2 |
| Ternaire équilibré | −1 | 0 | 1 |
Le ternaire non-équilibré a été utilisé sur d'anciens ordinateurs ternaires, dont le plus connu est l'ordinateur ETUN de l'université de Moscou. Il s'agissait de véritables ordinateurs ternaires, qui utilisaient des mémoires et des processeurs ternaires, qui géraient des trits directement. Il ne s'agit pas d'équivalents aux ordinateurs décimaux, qui encodaient des chiffres décimaux en binaire, qui étaient des hybrides entre ordinateurs décimaux et binaire, avec une interface décimale, mais une conception fondamentalement binaire. Les ordinateurs ternaires sont fondamentalement ternaires, il n'y a de bit nulle part dans de tels ordinateurs, seulement des trits !
Les ordinateurs ternaires utilisaient tous le ternaire équilibré. L'avantage de cet encodage est qu'il permet de représenter des entiers positifs comme négatifs, sans compter que certaines opérations sont bien plus simples à implémenter qu'en binaire. Par exemple, calculs l'opposé d'un nombre, son complément, est très simple : il suffit d'inverser tous les trits du nombre : les trits à 1 sont remplacés par des -1, et inversement, les zéros sont laissés tels quels. La soustraction demande de calculer le complément de l'opérande à soustraire, et d'additionner, encore plus simple qu'en complément à deux. L'addition et la multiplication sont plus simples, car la gestion des retenues et des tables de multiplication est légèrement plus simple.
Dans le chapitre précédent, nous avons vu comment l'ordinateur faisait pour coder des nombres. Les nombres en question sont mémorisés dans des mémoires plus ou moins complexes. Les mémoires les plus simples sont des registres, qui mémorisent un nombre. D'autres mémoires plus complexes mémorisent plusieurs nombres, un grand nombre. Et ces mémoires ne sont pas des dispositifs parfaits, elles peuvent subir des corruptions. Les corruptions en question se traduisent le plus souvent par l'inversion d'un bit : un bit censé être à 0 passe à 1, ou inversement. Pour donner un exemple, on peut citer l'incident du 18 mai 2003 dans la petite ville belge de Schaerbeek. Lors d'une élection, la machine à voter électronique enregistra un écart de 4096 voix entre le dépouillement traditionnel et le dépouillement électronique. La faute à un rayon cosmique, qui avait modifié l'état d'un bit de la mémoire de la machine à voter.
Mais qu'on se rassure : certains codages des nombres permettent de détecter et corriger ces erreurs. Les codes de détection et de correction d'erreur, qui ajoutent tous des bits de correction/détection d'erreur aux données. Les bits en question sont calculés à partir des données à transmettre/stocker et servent à détecter et éventuellement corriger toute erreur de transmission/stockage. Plus le nombre de bits ajoutés est important, plus la fiabilité des données sera importante. Ils sont peu utilisées dans les ordinateurs grand public, mais elles sont très importantes dans les domaines demandant des ordinateurs fiables, comme dans l'automobile, l'aviation, le spatial, l'industrie, etc. Et ce chapitre va expliquer ce qu'elles sont, et aussi comment les circuits élaborés permettent de s'en protéger.
Dans ce qui suit, nous parlerons parfois de codes ECC, bien que ce soit un abus de langage : ECC est l'abréviation de Error Correction Code, mais certains de ces codes se contentent de détecter qu'une erreur a eu lieu, sans la corriger. Ceci étant dit, les codes ECC sont utilisés sur les mémoires comme les mémoires RAM, parfois sur les disques durs ou les SSDs, afin d'éviter des corruptions de données. Ils sont aussi utilisés quand on doit transmettre des données, que ce soit sur les bus de communication ou sur un support réseau. Par exemple, les données transmises via internet incorporent un code ECC pour détecter les erreurs de transmission, idem pour les transmissions sur un réseau local.
Le bit de parité
modifierNous allons commercer par aborder le bit de parité/imparité. Le bit de parité est un bit ajouté à la donnée à mémoriser/transmettre. Sa valeur est telle que le nombre stocké (bit de parité inclus) contient toujours un nombre pair de bits à 1. Ainsi, le bit de parité vaut 0 si le nombre contient déjà un nombre pair de 1, et 1 si le nombre de 1 est impair.
Si un bit s'inverse, quelle qu'en soit la raison, la parité du nombre total de 1 est modifié : ce nombre deviendra impair si un bit est modifié. Et ce qui est valable avec un bit l'est aussi pour 3, 5, 7, et pour tout nombre impair de bits modifiés. Mais tout change si un nombre pair de bit est modifié : la parité ne changera pas. Il permet de détecter des corruptions qui touchent un nombre impair de bits. Si un nombre pair de bit est modifié, il est impossible de détecter l'erreur avec un bit de parité. Ainsi, on peut vérifier si un bit (ou un nombre impair) a été modifié : il suffit de vérifier si le nombre de 1 est impair. Il faut noter que le bit de parité, utilisé seul, ne permet pas de localiser le bit corrompu.
Le bit d'imparité est similaire au bit de parité, si ce n'est que le nombre total de bits doit être impair, et non pair comme avec un bit de parité. Sa valeur est l'inverse du bit de parité du nombre : quand le premier vaut 1, le second vaut 0, et réciproquement. Mais celui-ci n'est pas meilleur que le bit de parité : on retrouve l'impossibilité de détecter une erreur qui corrompt un nombre pair de bits.

Il est maintenant temps de parler de si un bit de parité est efficace ou non. Que ce soit avec un bit de parité ou d'imparité, environ la moitié des valeurs encodées sont invalides. En effet, si on prend un nombre codé sur N bits, bit de parité, inclut, on pourra encoder 2^n valeurs différentes. La moitié d'entre elle aura un bit de parité à 0, l'autre un bit de parité à 1. Et la moitié aura un nombre de bit à 1 qui soit pair, l'autre un nombre impair. En faisant les compte, seules la moitié des valeurs seront valides. Le diagramme ci-contre montre le cas pour trois bits, avec deux bits de données et un bit de parité.
L'octet/mot de parité et ses variantes
modifierL'octet de parité est une extension de la technique du bit de parité, qui s'applique à plusieurs octets. L'idée de base est de calculer un bit de parité par octet, et c'est plus ou moins ce que fait le mot de parité, mais avec quelques subtilités dans les détails.

La technique s'applique en général sur toute donnée qu'on peut découper en blocs d'une taille fixe. Dans les exemples qui vont suivre, les blocs en question seront des octets, pour simplifier les explications, mais il est parfaitement possible de prendre des blocs plus grands, de plusieurs octets. La méthode fonctionne de la même manière. On parle alors de mot de parité et non d'octet de parité.
Le calcul du mot de parité
modifierLe calcul du mot de parité se calcule en disposant chaque octet l'un au-dessus des autres, le tout donnant un tableau dont les lignes sont des octets. Le mot de parité se calcule en calculant le bit de parité de chaque colonne du tableau, et en le plaçant en bas de la colonne. Le résultat obtenu sur la dernière ligne est un octet de parité.
- 1100 0010 : nombre ;
- 1000 1000 : nombre ;
- 0100 1010 : nombre ;
- 1001 0000 : nombre ;
- 1000 1001 : nombre ;
- 1001 0001 : nombre ;
- 0100 0001 : nombre ;
- 0110 0101 : nombre ;
- ------------------------------------
- 1010 1100 : octet de parité.
Le calcul de l'octet de parité se fait en utilisant des opérations XOR. Pour rappel, une opération XOR est équivalente à une addition binaire dans laquelle on ne tiendrait pas compte des retenues. L'opération prend deux bits et effectue le calcul suivant :
- 0 0 = 0 ;
- 0 1 = 1 ;
- 1 0 = 1 ;
- 1 1 = 0.
En faisant un XOR entre deux octets, on obtient l'octet de parité des deux octets opérandes. Et cela se généralise à N opérandes : il suffit de faire un XOR entre les opérandes pour obtenir l'octet de parité de ces N opérandes. Il suffit de faire un XOR entre les deux premières opérandes, puis de faire un XOR entre le résultat et la troisième opérande, puis de refaire un XOR entre le nouveau résultat et le quatrième opérande, et ainsi de suite. Le calcul du mot de parité se fait aussi avec des opérations XOR, cela marche au-delà de l'octet.
La récupération des données manquantes/effacées
modifierL'avantage de cette technique est qu'elle permet de reconstituer une donnée manquante. Par exemple, dans l'exemple précédent, si une ligne du calcul disparaissait, on pourrait la retrouver à partir du mot de parité. Il suffit de déterminer, pour chaque colonne, quel valeur 0/1 est compatible avec la valeur du bit de parité associé. C'est d'ailleurs pour cette raison que le mot de parité est utilisé sur les disques durs montés en RAID 3, 5 6, et autres. Grâce à elle, si un disque dur ne fonctionne plus, on peut retirer le disque dur endommagé et reconstituer ses données.
Pour cela, il faut faire faire XOR entre les données non-manquantes et le mot de parité. Pour comprendre pourquoi cela fonctionne, il faut savoir deux choses : faire un XOR entre un nombre et lui-même donne 0, faire un XOR entre une opérande et zéro redonne l'opérande comme résultat. Si on XOR un nombre avec le mot de parité, cela va annuler la présence de ce nombre (son XOR) dans le mot de parité : le résultat correspondra au mot de parité des nombres, nombre xoré exclu. Ce faisant, en faisant un XOR avec tous les nombres connus, ceux-ci disparaîtront du mot de parité, ne laissant que le nombre manquant. Un exemple sera certainement plus parlant.
Prenons le cas où on calcule l'octet de parité de quatre octets nommés O1, O2, O3 et O4, et notant le résultat . On a alors :
Maintenant, imaginons que l'on veuille retrouver la valeur du second octet O2, qui a été corrompu ou perdu. Dans ce cas, on fait un XOR avec O1, O3 et enfin O4 :
On injecte alors l'équation .
On réorganise les termes :
On se rappelle que A XOR A = 0, ce qui simplifie grandement le tout :
On retrouve bien l'octet manquant.
La combinaison d'un mot de parité avec plusieurs bits de parité
modifierAvec un octet/mot de parité, on peut détecter qu'une erreur a eu lieu, mais aussi récupérer un octet/mot effacé. Mais si un bit est modifié, on ne peut pas corriger l'erreur. En effet, on ne sait pas détecter quel octet a été modifié par l'erreur. Maintenant, ajoutons un bit de parité à chaque octet, en plus de l'octet de parité.
| Octets | Bit de parité de chaque octet | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Octet 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Octet 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| Octet 3 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| Octet 4 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| Octet de parité | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
En faisant cela, on peut détecter qu'un bit a été modifié, mais aussi corriger l'erreur assez simplement. En cas d'erreur, deux bits de parité seront faussés : celui associé à l'octet, celui dans l'octet de parité. On peut alors détecter le bit erroné. Une autre méthode est de regarder les bits de parité associés aux octets, pour détecter l'octet erroné. Reste alors à corriger l'erreur, en supprimant l'octet invalide et en récupérant l'octet initial en utilisant le mot de parité.
| Octets | Bit de parité de chaque octet | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Octet 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Octet 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| Octet 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| Octet 4 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| Octet de parité | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
Le nombre de bits de parité total est élevé
modifierLe tout demande d'utiliser beaucoup de bits de parité. Pour N octets, il faut un bit de parité par octet et un octet de parité, ce qui donne N + 8 bits de parité. Pour 64 bits, soit 8 octets, cela fait 16 bits de parité nécessaires, soit 25% de bits en plus. Maintenant, prenons le cas général où on n'utilise pas des octets, mais des mots de M bits, plus longs ou plus courts qu'un octet. Dans ce cas, on a N + M bits de parité.
Notons que la technique peut s'appliquer avec des octets ou des nibbles, si on organise les bits correctement. Par exemple, prenons un nibble (4 bits). On peut l'organiser en un carré de deux bits de côté et ajouter : un bit de parité par colonne, un bit de parité par colonne (le mot de parité). Le tout donne 4 bits de parité, pour 4 bits de données : on double la taille de la donnée. Il est aussi possible de faire pareil avec un octet, l'organisant en deux lignes de 4 bits. Le résultat est de 6 bits de parité, ce qui est un petit peu mieux qu'avec un nibble : on passe à 3/4 de bits de plus.
| 0 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
Il est possible de faire la même chose pour des données de plusieurs octets. Pour un nombre de 16 bits, l'idéal est de faire 4 lignes de 4 bits chacune, ce qui fait 8 bits de parité au total. Pour 32 bits, on passe à 12 bits de parité, etc. Au total, voici la quantité de bits de parité nécessaires suivant la longueur de la donnée :
| 4 | 8 | 16 | 32 | 64 | 128 | 256 | ... |
|---|---|---|---|---|---|---|---|
| 4 | 6 | 8 | 12 | 16 | 24 | 32 | ... |
Il existe cependant des techniques plus économes, que nous allons voir dans ce qui suit. Par plus économes, il faut comprendre qu'elles utilisent moins de bits de parité, pour une fiabilité identique, voire meilleure. C'est là un défaut de la technique précédente : elle utilise beaucoup de bits de parités pour pas grand chose.
Les capacités de correction de la technique
modifierNotons que cette solution permet de corriger plus d'une erreur. Dans le pire des cas, on peut détecter et corriger une erreur. Si toutes les erreurs sont toutes dans le même mot/octet, alors on peut récupérer l'octet manquant. Le bit de parité permet de détecter un nombre impair d'erreur, soit 1, 3, 5, 7, ... erreurs. Il faut donc que le nombre d'erreurs dans l'octet soit impair.
| Octets | Bit de parité de chaque octet | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Octet 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Octet 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| Octet 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| Octet 4 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| Octet de parité | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
Par contre, si le nombre d'erreurs dans un octet est pair, alors le bit de parité associé à l'octet ne remarque pas l'erreur. On sait sur quelles colonnes sont les erreurs, pas la ligne.
| Octets | Bit de parité de chaque octet | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Octet 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Octet 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| Octet 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| Octet 4 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| Octet de parité | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
De même, si les erreurs touchent deux octets, alors on ne peut rien corriger. On peut détecter les erreurs, mais pas les corriger.
| Octets | Bit de parité de chaque octet | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Octet 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Octet 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| Octet 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| Octet 4 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| Octet de parité | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
Pour résumer, pour des mots de M bits, on peut corriger entre 1 et M/2 erreurs. Pour un octet, cela permet de détecter 1 erreur, 3/5/7 erreurs si elles ont lieu dans le même octet.
La protection des bits de parité
modifierAvec la méthode précédente, les bits de parité ne sont pas protégés : la moindre corruption des bits de parité fait que la méthode ne marche plus. Pour cela, il y a une solution toute simple : calculer un bit de parité qui tient compte de tous les bits de parité. Ainsi, si un bit de parité est corrompu, alors ce super-bit de parité détecterait l'erreur.
Dans les tableaux précédents, cela revient à ajouter un bit de parité dans la case tout en bas à droite. Le bit de parité calculé à partie des autres bits de parité est en rouge dans le tableau suivant. Il peut se calculer de plusieurs manières. La plus simple est calculer le bit de parité des 6 bits de parité, ceux de l'octet de parité et les autres. En faisant ainsi, on ganratit que tous les bits de parités sont protégés.
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
Avec cette technique, il faut faire la différence entre les bits de parité primaire, qui calculent la parité de tout ou partie des données, et le bit de parité secondaire, qui est calculé à partie des bits de parité primaire. Généralement, les codes correcteurs/détecteurs d'erreur avec des bits de parité secondaires sont assez peu efficaces, que ce soit en termes de fiabilité ou d'économies de bits. Ils utilisent beaucoup de bits et ne protègent que peu contre les erreurs. De plus, les bits de parité secondaires ne font que repousser le problème : le bit de parité secondaire peut être modifié lui aussi ! Les bits de parité secondaires ne protègent que contre la modification des bits de parité primaire, mais pas de leurs modifications propres. Mais qu'on se rassure : on peut protéger les bits de parité primaire sans recourir à des bits de parité secondaires, avec le codage que nous allons voir dans ce qui suit.
Les codes de Hamming
modifierLe code de Hamming se base sur l'usage de plusieurs bits de parité pour un seul nombre. Chaque bit de parité est calculé à partir d'un sous-ensemble des bits. Chaque bit de parité a son propre sous-ensemble, tous étant différents, mais pouvant avoir des bits en commun. Le but étant que deux sous-ensembles partagent un bit : si ce bit est modifié, cela modifiera les deux bits de parité associés. Et la modification de ce bit est la seule possibilité pour que ces deux bits soient modifiés en même temps : si ces deux bits de parité sont modifiés en même temps, on sait que le bit partagé a été modifié.
Pour résumer, un code de Hamming utilise plusieurs bits de parité, calculés chacun à partir de bits différents, souvent partagés entre bits de parité. Mais cela est aussi vrai pour la technique précédente. Un point important est que si un bit de parité est corrompu et change de valeur, les autres bits de parité ne le seront pas et c'est ce qui permettra de détecter l'erreur. Si un bit de données est inversé, plusieurs bits de parité sont touchés, systématiquement. Donc si un seul bit de parité est incompatible avec les bits de données, alors on sait qu'il a été inversé et qu'il est l'erreur. Pas besoin de faire comme avec la technique précédente, avec un mot de parité complété avec des bits de parité, avec un bit de parité secondaire.

Le code de Hamming le plus connu est certainement le code 7-4-3, un code de Hamming parmi les plus simples à comprendre. Celui-ci prend des données sur 4 bits, et leur ajoute 3 bits de parité, ce qui fait en tout 7 bits : c'est de là que vient le nom de 7-4-3 du code. Chaque bit de parité se calcule à partir de 3 bits du nombre, mais aussi des autres bits de parité. Pour poursuivre, nous allons noter les bits de parité p1, p2 et p3, tandis que les bits de données seront notés d1, d2, d3 et d4.
| Bits de parité incorrects | Bit modifié |
|---|---|
| Les trois bits de parité : p1, p2 et p3 | Bit d4 |
| p1 et p2 | d1 |
| p2 et p3 | d3 |
| p1 et p3 | d2 |
Il faut préciser que toute modification d'un bit de donnée entraîne la modification de plusieurs bits de parité. Si un seul bit de parité est incorrect, il est possible que ce bit de parité a été corrompu et que les données sont correctes. Ou alors, il se peut que deux bits de données ont été modifiés, sans qu'on sache lesquels.
Le code 8-4-4 est un code 7-4-3 auquel on a ajouté un bit de parité supplémentaire. Celui-ci est calculé à partir de tous les bits, bits de parités ajoutés par le code 7-4-3 inclus. Ainsi, on permet de se prémunir contre une corruption de plusieurs bits de parité.

Évidemment, il est possible de créer des codes de Hamming sur un nombre plus grand que bits. Le cas le plus classique est le code 11-7-4.

Les codes de Hamming sont généralement plus économes que la technique précédente, avec un mot de parité combiné à plusieurs bits de parité. Par exemple, pour 4 bits, le code de Hamming 7-4-3 n'utilise que 3 bits de parité, contre 4 avec l'autre technique. Pour 7 bits, elle n'en utilise que 4, contre 6. Voici un tableau qui donne combien on peut protéger avec N bits de parité en utilisant un code de Hamming. On voit que les codes de Hamming sont bien plus économes que le mot de parité, tout en étant tout aussi puissant (ou presque).
| Bits de parité | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| Données | 1 | 4 | 11 | 26 | 57 | 120 | 247 | 502 |
Les sommes de contrôle
modifierLes sommes de contrôle sont des techniques de correction d'erreur, où les bits de correction d'erreur sont ajoutés à la suite des données. Les bits de correction d'erreur, ajoutés à la fin du nombre à coder, sont appelés la somme de contrôle. La vérification d'une erreur de transmission est assez simple : on calcule la somme de contrôle à partir des données transmises et on vérifie qu'elle est identique à celle envoyée avec les données. Si ce n'est pas le cas, il y a eu une erreur de transmission.
Techniquement, les techniques précédentes font partie des sommes de contrôle au sens large, mais il existe un sens plus restreint pour le terme de somme de contrôle. Il est souvent utilisé pour regrouper des techniques telle l'addition modulaire, le CRC, et quelques autres. Toutes ont en commun de traiter les données à coder comme un gros nombre entier, sur lequel on effectue des opérations arithmétiques pour calculer les bits de correction d'erreur. La seule différence est que l'arithmétique utilisée est quelque peu différente de l'arithmétique binaire usuelle. Dans les calculs de CRC, on utilise une arithmétique où les retenues ne sont pas propagées, ce qui fait que les additions et soustractions se résument à des XOR.
La première méthode consiste à diviser les données à envoyer par un nombre entier arbitraire et à utiliser le reste de la division euclidienne comme somme de contrôle. Cette méthode, qui n'a pas de nom, est similaire à celle utilisée dans les Codes de Redondance Cyclique.
Avec cette méthode, on remplace la division par une opération légèrement différente. L'idée est de faire comme une division, mais dont on aurait remplacé les soustractions par des opérations XOR. Nous appellerons cette opération une pseudo-division dans ce qui suit. Une pseudo-division donne un quotient et un reste, comme le ferait une division normale. Le calcul d'un CRC pseudo-divise les données par un diviseur et on utilise le reste de la pseudo-division comme somme de contrôle.
Il existe plusieurs CRC différents et ils se distinguent surtout par le diviseur utilisé, qui est standardisé pour chaque CRC. La technique peut sembler bizarre, mais cela marche. Cependant, expliquer pourquoi demanderait d'utiliser des concepts mathématiques de haute volée qui n'ont pas leur place dans ce cours, comme la division polynomiale, les codes linéaires ou encore les codes polynomiaux cycliques.
Les circuits électroniques
modifierGrâce au chapitre précédent, on sait enfin comment sont représentées nos données les plus simples avec des bits. On n'est pas encore allés bien loin : on ne sait pas comment représenter des bits dans notre ordinateur ou les modifier, les manipuler, ni faire quoi que ce soit avec. On sait juste transformer nos données en paquets de bits (et encore, on ne sait vraiment le faire que pour des nombres entiers, des nombres à virgule et du texte...). C'est pas mal, mais il reste du chemin à parcourir ! Rassurez-vous, ce chapitre est là pour corriger ce petit défaut. On va vous expliquer quels traitements élémentaires notre ordinateur va effectuer sur nos bits.
Les portes logiques de base
modifierLes portes logiques sont des circuits qui reçoivent plusieurs bits en entrée, et fournissent un bit en guise de résultat. Tous les composants d'un ordinateur sont fabriqués avec ce genre de circuits. Elles possèdent des entrées sur lesquelles on va placer des bits, et une sortie sur laquelle se trouve le bit de résultat. Les entrées ne sont rien d'autre que des morceaux de « fil » conducteur sur lesquels on envoie un bit (une tension). La sortie est similaire, si ce n'est qu'on récupère le bit de résultat.
- Sur les schémas qui vont suivre, les entrées des portes logiques seront à gauche et les sorties à droite !
Les portes logiques ont différent symboles selon le pays et l'organisme de normalisation :
- Commission électrotechnique internationale (CEI) ou International Electrotechnical Commission (IEC),
- Deutsches Institut für Normung (DIN, Institut allemand de normalisation),
- American National Standards Institute (ANSI).
La porte OUI/BUFFER
modifierLa première porte fondamentale est la porte OUI, qui agit sur un seul bit : sa sortie est exactement égale à l'entrée. En clair, elle recopie le bit en entrée sur sa sortie. Pour simplifier la compréhension, je vais rassembler les états de sortie en fonction des entrées pour chaque porte logique dans un tableau que l'on appelle table de vérité.
Mine de rien, la porte OUI est parfois utile. Elle sert surtout pour recopier un signal électrique qui risque de se dissiper dans un fil trop long. On place alors une porte OUI au beau milieu du fil, pour éviter tout problème, la porte logique régénérant le signal électrique, comme on le verra dans le chapitre suivant. Cela lui vaut parfois le nom de porte BUFFER, ce qui veut dire tampon. Les portes OUI sont aussi utilisées dans certaines mémoires RAM (les mémoires SRAM), comme nous le verrons dans quelques chapitres.
La porte NON
modifierLa seconde porte fondamentale est la porte NON, qui agit sur un seul bit : la sortie d'une porte NON est exactement le contraire de l'entrée. Son symbole ressemble beaucoup au symbole d'une porte OUI, la seule différence étant le petit rond au bout du triangle.
La porte ET
modifierLa porte ET possède plusieurs entrées, mais une seule sortie. Cette porte logique met sa sortie à 1 quand toutes ses entrées valent 1.
La porte NAND
modifierLa porte NAND donne l'exact inverse de la sortie d'une porte ET. En clair, sa sortie ne vaut 1 que si au moins une entrée est nulle. Dans le cas contraire, si toutes les entrées sont à 1, la sortie vaut 0.
Au fait, si vous regardez le schéma de la porte NAND, vous verrez que son symbole est presque identique à celui d'une porte ET : seul un petit rond (blanc pour ANSI, noir pour DIN) ou une barre (CEI) sur la sortie de la porte a été rajouté. Il s'agit d'une sorte de raccourci pour schématiser une porte NON.
La porte OU
modifierLa porte OU est une porte dont la sortie vaut 1 si et seulement si au moins une entrée vaut 1. Dit autrement, sa sortie est à 0 si toutes les entrées sont à 0.
La porte NOR
modifierLa porte NOR donne l'exact inverse de la sortie d'une porte OU.
La porte XOR
modifierAvec une porte OU, deux ET et deux portes NON, on peut créer une porte nommée XOR. Cette porte est souvent appelée porte OU exclusif. Sa sortie est à 1 quand les deux bits placés sur ses entrées sont différents, et vaut 0 sinon.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La porte XNOR
modifierLa porte XOR possède une petite sœur : la XNOR. Sa sortie est à 1 quand les deux entrées sont identiques, et vaut 0 sinon (elle est équivalente à une porte XOR suivie d'une porte NON).
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Interlude propédeutique : combien il y a-t-il de portes logiques différentes ?
modifierLes portes logiques que nous venons de voir ne sont pas les seules. En fait, il existe un grand nombre de portes logiques différentes, certaines ayant plus d'intérêt que d'autres. Mais avant toute chose, nous allons parler d'un point important : combien y a-t-il de portes logiques en tout ? La question a une réponse très claire, pour peu qu'on précise la question. Les portes que nous avons vu précédemment ont respectivement 1 et 2 bits d'entrée, mais il existe aussi des portes à 3, 4, 5, bits d’entrée, voire plus. Il faut donc se demander combien il existe de portes logiques, dont les entrées font N bits. Par exemple, combien y a-t-il de portes logiques avec un bit d'entrée ? Avec deux bits d'entrée ? Avec 3 bits ?
Pour cela, un petit raisonnement peut nous donner la réponse. Vous avez vu plus haut qu'une porte logique est définie par une table de vérité, qui liste le bit de sortie pour chaque combinaison possible des entrées. Le raisonnement se fait en deux étapes. La première détermine, pour n bits d'entrée, combien il y a de lignes dans la table de vérité. La seconde détermine combien de tables de vérité à c lignes existent.

Le nombre de lignes de la table de vérité se calcule facilement quand on se rend compte qu'une porte logique reçoit en entrée un "nombre" codé sur n bits, et fournit un bit de résultat qui dépend du "nombre" envoyé en entrée. Chaque ligne de la table de vérité correspond à une valeur possible pour le "nombre" envoyé en entrée. Pour n bits en entrée, la table de vérité fait donc lignes.
Ensuite, calculons combien de portes logiques en tout on peut créer c lignes. Là encore, le raisonnement est simple : chaque combinaison peut donner deux résultats en sortie, 0 et 1, le résultat de chaque combinaison est indépendant des autres, ce qui fait :
- .
Pour les portes logiques à 1 bit d’entrée, cela fait 4 portes logiques. Pour les portes logiques à 2 bits d’entrée, cela fait 16 portes logiques.
Les portes logiques à un bit d'entrée
modifierIl existe quatre portes logiques de 1 bit. Il est facile de toutes les trouver avec un petit peu de réflexion, en testant tous les cas possibles.
- La première donne toujours un zéro en sortie, c'est la porte FALSE ;
- La seconde recopie l'entrée sur sa sortie, c'est la porte OUI, aussi appelée la porte BUFFER ;
- La troisième est la porte NON vue plus haut ;
- La première donne toujours un 1 en sortie, c'est la porte TRUE.
| Entrée | FALSE | OUI | NON | TRUE | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 1 |
On peut fabriquer une porte OUI en faisant suivre deux portes NON l'une à la suite de l'autre. Inverser un bit deux fois redonne le bit original.

Les portes logiques TRUE et FALSE sont des portes logiques un peu à part, qu'on appelle des portes triviales. Elles sont absolument inutiles et n'ont même pas de symbole attitré. Il est possible de fabriquer une porte FALSE à partir d'une porte TRUE suivie d'une porte NON, et inversement, de créer une porte TRUE en inversant la sortie d'une porte FALSE. Pour résumer, toutes les portes à une entrée peuvent se fabriquer en prenant une porte NON, couplée avec soit une porte FALSE, soit une porte TRUE. C'est étrange que l'on doive faire un choix arbitraire, mais c'est comme ça et la même chose arrivera quand on parlera des portes à deux entrées.
Les portes logiques à deux bits d'entrée
modifierLes portes logiques à 2 bits d'entrée sont au nombre de 16. Nous avions déjà vu les portes OU, NOR, ET, NAND, XOR et NXOR. À part ces 6 là, peu de portes logiques sont réellement utiles. La liste complète des tables de vérité est regroupée dans le tableau ci-dessous.
| Entrée | FALSE | NOR | NCONVERSE | NON A | NIMPLY | NON (B) | XOR | NAND | ET | NXOR | OUI (B) | IMPLY | OUI (A) | CONVERSE | OU | TRUE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 01 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 10 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Dans ce tableau, on retrouve les deux portes logiques triviales, à savoir la porte FALSE et TRUE, qui donnent toujours respectivement 0 et 1 en sortie. De plus, on retrouve aussi les portes OUI et NON, mais elles sont chacune en double. En cherchant dans le tableau, on trouve une porte qui recopie l'entrée A, une autre qui recopie l'entrée B. De même, on trouve une porte qui inverse l'entrée A et une autre qui inverse l'entrée B.
En clair, sur les 16 portes logiques à deux entrées, 6 d'entre elles sont de fausses portes à deux entrées : elles ont deux entrées, mais l'une d'entre elle ne sert à rien et l'est pas prise en compte pour calculer le résultat. Seules 10 sont de vraies portes à deux entrées, et non des portes à une entrée déguisées. Le tout est illustré dans le tableau ci-dessous, avec les portes à une entrée illustrées en jaune.
| Entrée | FALSE | NOR | NCONVERSE | NON A | NIMPLY | NON (B) | XOR | NAND | ET | NXOR | OUI (B) | IMPLY | OUI (A) | CONVERSE | OU | TRUE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 01 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 10 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
On vient de voir que sur les 16 portes logiques à deux entrées, 6 d'entre elles sont des portes à une entrée déguisées. Reste à étudier les portes logiques restantes. Toutes les portes logiques peuvent se fabriquer en combinant d'autres portes logiques de base.
Par exemple, certaines portes sont l'inverse l'une de l'autre. La porte ET et la porte NAND sont l'inverse l'une de l'autre : il suffit d'en combiner une avec une porte NON pour obtenir l'autre. Même chose pour les portes OU et NOR, ainsi que les portes XOR et NXOR.
| Porte ET | 
|
|---|---|
| Porte OU | 
|
De fait, si on dispose de la porte NON, on peut diviser par 2 le nombre de portes logique, la moitié des portes logiques étant l'inverse de l'autre. Il ne reste alors que les portes logiques suivantes, appelées portes de base :
- TRUE ou FALSE (le choix ne change pas grand chose)
- NON ;
- ET/OU/XOR ;
- CONVERSE ;
- IMPLY.
Mais d'autres possibilités existent et nous allons les voir dans le détail dans ce qui suit. Nous allons voir que certaines de ces portes logiques ne sont en fait que des dérivées des portes ET et des portes OU. En combinant une porte ET/OU avec une ou plusieurs portes NON, on arrive à émuler ces portes logiques restantes. Les portes logiques dérivées de la porte ET sont illustrées en rouge dans le tableau suivant, celles dérivées de la porte OU sont en vert, les portes XOR/NXOR sont en jaune, le reste est les portes à une entrée.
| Entrée | FALSE | NOR | NCONVERSE | NON A | NIMPLY | NON (B) | XOR | NAND | ET | NXOR | OUI (B) | IMPLY | OUI (A) | CONVERSE | OU | TRUE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 01 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 10 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Les portes dérivées de la porte OU
modifierLes portes dérivées de la porte OU regroupent les deux portes OU et NAND, ainsi que deux nouvelles portes : IMPLY et CONVERSE.
La porte CONVERSE a la table de vérité suivante :
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
La porte IMPLY a la table de vérité suivante :
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Leur comportement se comprend facilement quand on sait qu'elles sont équivalentes à une porte OU dont on aurait inversé une des entrées. La porte CONVERSE met sa sortie à 1 soit quand l'entrée 1 est à 1, soit quand l'entrée 2 est à 0. La porte IMPLY fait la même chose, sauf qu'il faut que l'entrée 2 soit à 1 et l'entrée 1 à 0. Leurs symboles trahissent cet état de fait, jugez-en vous-même :
 |
 |
Vous vous demandez certainement ce qui se passe quand on inverse les deux entrées avant le OU. Pour cela, regardons ce que fait le circuit en étudiant sa table de vérité.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
C'est la table de vérité d'une porte NAND. En clair, une porte NAND est équivalente à une porte OU dont on aurait inversé les deux entrées.

Les portes dérivées d'un OU mettent leur sortie à 1 pour trois lignes de la table de vérité, pour trois entrées possibles. Aussi, on les appellera des portes 3-combinaisons.
| Entrée | NAND | OR | CONVERSE | IMPLY |
|---|---|---|---|---|
| 00 | 1 | 0 | 1 | 1 |
| 01 | 1 | 1 | 0 | 1 |
| 10 | 1 | 1 | 1 | 0 |
| 11 | 0 | 1 | 1 | 1 |
Les portes dérivées de la porte ET
modifierLes portes dérivées de la porte ET regroupent les deux portes NOR et ET, ainsi que deux nouvelles portes : NCONVERSE et NIMPLY, qui sont respectivement l'inverse des portes CONVERSE et IMPLY.
La porte NCONVERSE a la table de vérité suivante :
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
La porte NIMPLY a la table de vérité suivante :
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Vous pouvez le voir, elles ont une sortie à 1 à condition que l'une des entrées soit à 1, et l'autre entrée soit à 0. On devine rapidement que ces deux portes peuvent se fabriquer en prenant une porte ET et une porte NON. Il suffit de mettre la porte NON devant l'entrée devant être à 0, et de mettre un ET à la suite. Au passage, cela se ressent dans les symboles utilisés pour ces deux portes, qui sont les suivants :


Vous vous demandez certainement ce qui se passe quand on inverse les deux entrées avant le ET. Pour cela, regardons ce que fait le circuit en étudiant sa table de vérité.
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
C'est la table de vérité d'une porte NOR. En clair, une porte NOR est équivalente à une porte ET dont on aurait inversé les deux entrées.

Les portes dérivées d'un ET mettent leur sortie à 1 pour une seule combinaison d'entrée, une seule ligne de la table de vérité. Aussi, nous allons les appeler des portes 1-combinaison.
| Entrée | NOR | NCONVERSE | NIMPLY | ET |
|---|---|---|---|---|
| 00 | 1 | 0 | 0 | 0 |
| 01 | 0 | 1 | 0 | 0 |
| 10 | 0 | 0 | 1 | 0 |
| 11 | 0 | 0 | 0 | 1 |
Les liens entre portes 1 et 3-combinaisons
modifierLa section précédente a montré qu'on pouvait en théorie créer toute porte logique avec seulement des portes NON, ET et OU. Mais en réalité, on peut faire avec beaucoup moins. Dans cette section, nous allons montrer que toute porte peut être créée avec seulement des portes ET et NON, sans porte OU. Et il est possible de faire de même, mais avec seulement des portes NON et des portes OU, sans porte ET.
Pour comprendre pourquoi, regardez le tableau suivant, qui liste les portes 1 et 3-combinaison en paires. On voit que chaque porte 1-combinaison est l'exact inverse d'une porte 3-combinaison et inversement ! La conséquence est que l'on peut créer n'importe quelle porte 3-combinaison à partie d'une porte 1-combinaison et inversement.
| Entrée | NOR | OU | NCONVERSE | CONVERSE | IMPLY | NIMPLY | ET | NAND | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| 01 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |||
| 10 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | |||
| 11 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
Par exemple, nous avions vu plus haut que la porte NOR est une porte dérivée d'une porte ET. On peut créer une porte OU en ajoutant une porte NON à une porte NOR basée sur un ET, ce qui donne le circuit ci-dessous.

Ou encore, nous avions vu plus haut que la porte NAND est une porte dérivée d'une porte OU. On peut créer une porte ET en ajoutant une porte NON à une porte NAND basée sur un OU, ce qui donne le circuit ci-dessous.

Les portes XOR/NXOR sont "superflues"
modifierDans cette section, nous allons montrer que les portes XOR/NXOR peuvent se fabriquer à partir d'autres portes logiques. Il y a deux grandes manières pour concevoir une porte XOR/NXOR à partir de portes plus simples. Les deux méthodes peuvent servir à créer n'importe quelle porte logique, pas seulement les XOR/NXOR. Aussi, il est intéressant de les étudier. La première méthode combine plusieurs portes 1-combinaison, leur résultat étant combiné avec une porte OU. L'autre méthode fait l'inverse : on prend plusieurs portes 3-combinaisons, on combine les résultats avec une porte ET. Voyons en détail ces deux techniques.
La première méthode : combiner des portes dérivée d'un ET avec un OU
modifierLa première technique part d'un raisonnement assez simple, qui se comprend bien quand on étudie quelques exemples.
Commençons par le cas d'une porte XOR. La sortie d'une porte XOR est à 1 dans deux situations : soit la première entrée est à 1 et l'autre à 0, soit c'est l'inverse. Les deux cas correspondent respectivement aux portes NCONVERSE et NIMPLY, vue précédemment.
| Entrée 1 | Entrée 2 | NCONVERSE | NIMPLY | (NCONVERSE) OU (NIMPLY) = XOR | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | ||
| 1 | 1 | 0 | 0 | 0 |
La sortie des deux circuits est combinée avec une porte OU, car une seule des deux situations rencontrées met la sortie à 1. Les deux portes sont conçues à partir d'une porte ET et de portes NON. Le circuit obtenu est le suivant :

- Notons que ce circuit nous donne une idée pour créer une porte NXOR : il suffit de remplacer la porte OU finale par une porte NOR.
La porte NXOR peut se concevoir à parti du même raisonnement. La porte NXOR sort un 1 dans deux cas : soit quand ses deux entrées sont à 1, soit quand elles sont toutes deux à 0. La porte ET a sa sortie à 1 dans le premier cas, alors que la porte NOR (une OU suivie d'une NOT) a sa sortie à 1 dans le second cas.
| Entrée 1 | Entrée 2 | NOR | ET | NXOR | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | ||
| 0 | 1 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | 1 |
Il faut ajouter une porte pour combiner le résultat de la porte NOR avec celui de la porte ET pour obtenir un résultat valide. Vu que la sortie doit être à 1 dans l'un des deux cas, c’est-à-dire quand l'une des deux portes ET/NOR est à 1, la porte finale est naturellement une porte OU. Le circuit obtenu est le suivant :

- Notons que ce circuit nous donne une troisième possibilité pour créer une porte XOR : il suffit de remplacer la porte OU finale par une porte NOR.
Il s'agit là d'une technique qui marche au-delà des portes XOR, et qui marche pour toutes les portes logiques. L'idée est de lister toutes les lignes de la table de vérité où la porte sort un 1. Pour chaque ligne, on prend la porte 1-combinaison adéquate : celle qui sort un 1 pour cette ligne. On effectue ensuite un OU entre toutes les portes dérivées d'un ET.
Prenons comme exemple la porte logique qui met la sortie à 1 pour la seconde et quatrième ligne de la table de vérité. On peut la concevoir en prenant deux portes 1-combinaison : celle qui a sa sortie à 1 pour la seconde ligne de la table de vérité, et celle pour la quatrième ligne. En faisant un OU entre ces deux portes, le résultat sera la porte demandé. Et on peut appliquer le même raisonnement pour n'importe quelle porte logique. Il suffit alors d'utiliser un OU à 2, 3 ou 4 entrées.
| Entrée 1 | Entrée 2 | NCONVERSE | ET | Porte voulue | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | 1 | ||
| 1 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | 1 |
Cette technique permet de fabriquer directement toutes les portes logiques à deux entrées, sauf la porte FALSE. C'est la seule qui ne puisse être fabriquée à partir de portes 1-combinaison seules et qui demande d'utiliser une porte NON pour. On peut donc, en théorie, fabriquer toutes les portes logiques à partir de seulement les portes ET, OU et NON.
La seconde méthode : combiner des portes dérivées d'un OU avec un ET
modifierUne autre possibilité fait l'inverse de la méthode précédente. Elle conçoit une porte logique en prenant plusieurs portes logiques, mais la combinaison des résultats de celles-ci est différente. Au lieu de procéder par addition, on procède par soustraction. Cette méthode demande de prendre des portes 3-combinaison et de les combiner avec une porte ET. Elle permet de fabriquer toutes les portes logiques, sauf la porte TRUE.
Par exemple, prenons la porte XOR. On part du principe qu'un XOR est un OU, sauf dans le cas où les deux entrées sont à 1, cas qui peut se détecter avec une porte ET. Voici ce que cela donne :
| Entrée 1 | Entrée 2 | OU | ET | XOR | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | ||
| 1 | 1 | 1 | 1 | 0 |
La porte à choisir pour combiner les deux résultats n'est pas évidente en regardant le tableau. Une alternative est de remplacer la porte ET par une porte NAND :
| Entrée 1 | Entrée 2 | OU | NAND | XOR | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 0 | 0 |
On voit qu'en faisant un ET entre les sortie des portes OU et NAND, on obtient le résultat voulu.

- Notons que ce circuit nous donne une idée pour créer une porte NXOR : il suffit de remplacer la porte ET finale par une porte NAND.
Les portes NAND et NOR permettent de fabriquer toutes les autres portes
modifierDans la section précédente, nous avons vu qu'il existe deux possibilités : soit on supprime les portes ET/NAND et on garde les portes OU/NOR, soit on fait l'inverse. Les deux possibilités sont équivalentes et permettent chacune de fabriquer toutes les portes logiques restantes. Cependant, supposons que je conserve les portes ET/NAND : dois-je conserver la porte ET, ou la porte NAND ? Les deux solutions ne sont pas équivalentes, car l'une permet de se passer de porte NON et pas l'autre ! Pour comprendre pourquoi, nous allons essayer de créer toutes les portes à une entrée à partir de portes ET/OU/NAND/NOR.
Il est possible de créer une porte OUI en utilisant une porte ET ou encore une porte OU, comme illustré ci-dessous. La raison est que si on fait un ET/OU entre un bit et lui-même, on retrouve le bit initial. Il s'agit d'une propriété particulière de ces portes sur laquelle nous reviendrons rapidement dans le chapitre sur les circuits combinatoires, et qui sera très utile dans le chapitre sur les opérations bit à bit. De plus, elle sera très utile vers la fin du chapitre.
 |
 |
Il est aussi possible de créer des portes TRUE et FALSE en modifiant les montages précédents. D'ailleurs, en guise d'exercice, essayez de créer des portes TRUE et FALSE à partir des deux montages précédents. Un indice : vous aurez besoin d'une à deux portes NON. Par contre, impossible de créer une porte NON facilement.
Mais que se passe-t-il si on utilise une porte NAND/NOR ? La réponse est simple : on obtient une porte NON ! Pour comprendre pourquoi cela marche, il faut imaginer que la porte NAND/NOR est composée d'une porte ET/OU suivie par une porte NON. Le bit d'entrée va subir un ET/OU avec lui-même, avant d'être inversé. Mais le passage dans le ET/OU ne changera pas le bit (cette étape se comporte comme une porte OUI), alors que la porte NON l'inversera.
| Circuit équivalent avec des NAND | Circuit équivalent avec des NOR | |
|---|---|---|
| Porte NON |  |
 |
- Vous vous demandez peut-être ce qu'il se passe quand on fait la même chose avec une porte XOR, en faisant un XOR entre un bit et lui-même. Et bien le résultat est une porte FALSE. En effet, la porte XOR fournit un zéro quand les deux bits d'entrée sont identiques, ce qui est le cas quand on XOR un bit avec lui-même. Et inversement, une porte TRUE peut se fabriquer en utilisant une porte NXOR. Il s'agit là d'une propriété particulière de la porte XOR/NXOR sur laquelle nous reviendrons rapidement dans le chapitre sur les circuits combinatoires, et qui sera très utile dans le chapitre sur les opérations bit à bit.
Créer les autres portes logiques est alors un jeu d'enfant avec ce qu'on a appris dans les sections précédentes. Il suffit de remplacer les portes NON et ET par leurs équivalents fabriqués avec des NAND.
On vient de voir qu'il est possible de fabriquer tout circuit avec seulement un type de porte logique : soit on construit le circuit avec uniquement des NAND, soit avec uniquement des NOR. Pour donner un exemple, sachez que les ordinateurs chargés du pilotage et de la navigation des missions Appollo étaient intégralement conçus avec des portes NOR.
Les portes logiques à plus de deux entrées
modifierEn théorie, les portes logiques regroupent tous les circuits à une ou deux entrées, mais pas au-delà. Mais dans les faits, certains circuits assez simples sont considérés comme des portes logiques, même s'ils ont plus de deux entrées. En fait, une porte logique est un circuit simple, qui sert de brique de base pour d'autres circuits. Il doit être raisonnablement simple et doit se fabriquer sans recourir à des portes logiques plus simples. En clair, les portes logiques sont des circuits élémentaires, et sont aux circuits électroniques ce que les atomes sont aux molécules. Dans ce qui suit, nous allons voir des portes logiques qui ont plus de 2 entrées, et en ont 3, 4, 5, voire plus. S'il est difficile d'expliquer en quoi ce sont des portes logiques, tout deviendra plus évident dans le chapitre suivant, quand nous verrons comment sont fabriquées ces portes logiques avec des transistors. Nous verrons que les circuits que nous allons voir se fabriquent très simplement en quelques transistors, sans recourir à des portes ET/OU/NAND/NOR. De plus, beaucoup de ces circuits sont très utiles et reviendront régulièrement dans la suite du cours.
Les portes ET/OU/NAND/NOR à plusieurs entrées
modifierLes premières portes logiques à plusieurs entrées que nous allons voir sont les portes ET/OU/NAND/NOR à plus de 2 entrées.
Il existe des portes ET qui ont plus de deux entrées. Elles peuvent en avoir 3, 4, 5, 6, 7, etc. Comme pour une porte ET normale, leur sortie ne vaut 1 que si toutes les entrées valent 1 : dans le cas contraire, la sortie de la porte ET vaut 0. Dit autrement, si une seule entrée vaut 0, la sortie de la porte ET vaut 0.
 |
 |
De même, il existe des portes OU/NOR à plus de deux entrées. Pour les portes OU à plusieurs entrées, leur sortie est à 1 quand au moins une de ses entrées vaut 1. Une autre manière de le dire est que leur sortie est à 0 si et seulement si toutes les entrées sont à 0.
 |
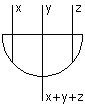 |
Les versions NAND et NOR existent elles aussiet leur sortie/comportement est l'inverse de celle d'une porte ET/OU à plusieurs entrées. Pour les portes NAND, leur sortie ne vaut 1 que si au moins une entrée est nulle : dans le cas contraire, la sortie de la porte NAND vaut 0. Dit autrement, si toutes les entrées sont à 1, la sortie vaut 0.
 |
 |


Bien sur, ces portes logiques peuvent se créer en combinant plusieurs portes ET/OU/NOR/NAND à deux entrées. Cependant, faire ainsi n'est pas la seule solution et nous verrons dans le chapitre suivant que l'on peut faire nettement mieux avec quelques transistors. Elles sont très utiles dans la conception de circuits électroniques, mais elles sont aussi fortement utiles au niveau pédagogique. Nous en ferons un grand usage dans la suite du cours, car elles permettent de simplifier fortement les schémas et les explications pour certains circuits complexes. Sans elles, certains circuits seraient plus compliqués à comprendre et certains schémas seraient trop chargés en portes ET/OU pour être lisibles.
Les portes ET-OU-NON
modifierLes portes ET/OU/NON sont des portes logiques qui combinent plusieurs portes ET et une porte NOR en une seule porte logique. Il en existe de nombreux types, mais nous allons voir les deux principaux : les portes 2-2 et 2-1.
La porte 2-1 est une porte à 3 entrées, que nous allons appeler A, B, C, D. Elle fait un ET entre les entrées A et B, puis fait un NOR entre le résultat et la troisième entrée. Et le tout peut encore une fois s'implémenter en une seule porte logique, pas forcément en enchainant deux ou trois portes à la suite.
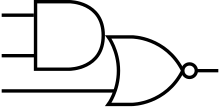
La porte 2-2 est une porte à 4 entrées, que nous allons appeler A, B, C, D. Elle fait un ET entre les entrées A et B, un autre ET entre C et D, puis fait un NOR entre le résultat des deux ET. Et le tout peut s'implémenter en une seule porte logique, pas forcément en enchainant deux ou trois portes à la suite.

Et il s'agit là des versions les plus simples de la porte, mais on peut imaginer des versions plus complexes, où les ET et les OU sont à 3, 4, voire 5 entrées.

Il existe aussi des portes OU-ET-NON, où la position des portes ET et OU sont inversées.
Ces portes combinées permettent de grandement simplifier certains circuits. Mais nous les utiliserons assez peu, sauf dans le chapitre sur les additionneurs où nous y ferons référence. La raison est que les portes ET/OU/NON et assimilées étaient utilisées uniquement sur d'anciens circuits assez anciens, appelés circuits TTL. Ils utilisaient une ancienne technologie de fabrication, ils utilisaient des transistors spécialisés, ce qui fait que concevoir de telles portes était assez facile. Mais avec les technologies de fabrication CMOS actuelles, ce n'est plus le cas. Cependant, il est intéressant de savoir que de telles portes ont existé.
La porte à majorité
modifierLa porte à majorité est une porte à plusieurs entrées, qui met sa sortie à 1 quand une plus de la moitié des entrées sont à 1, et sort un 0 sinon. En général, le nombre d'entrée de cette porte est toujours impair, afin d'éviter une situation où exactement la moitié des entrées sont à 1 et l'autre à 0. Avec un nombre impair d'entrée, il y a toujours un déséquilibre des entrées, pas une égalité parfaite. Il existe cependant des portes logiques à 4, 6, 8 entrées, mais elles sont plus rares.
Dans tous les cas, une porte à majorité est actuellement fabriquée à partir de portes logiques simples (ET, OU, NON, NAND, NOR). Mais on considère que c'est une porte logique car c'est un circuit simple et assez utile. De plus, il est possible de créer une grande partie des circuits électroniques possibles en utilisant seulement des portes à majorité ! C'est surtout cette possibilité qui fait que la porte à majorité est considérée comme une porte logique, pas comme un circuit simple et utile.
Une porte à majorité à trois entrées mettra sa sortie quand deux sorties sont à 1. Il existe plusieurs possibilités pour cela, qui sont presque toutes plus simples que le circuit précédent. La plus simple utilise une couche de portes ET suivie par une porte OU à plusieurs entrées. En voici une autre :

Voici le circuit d'une porte à majorité à 4 bits d'entrées :

Les deux circuits précédents nous disent comment fabriquer une porte à majorité générale. Pour la porte à trois entrée, on prend toutes les paires d'entrées possibles, on fait un ET entre les bits de chaque paire, puis on fait un OU entre le résultat des ET. Pareil pour la porte à 4 entrées : on prend toutes les combinaisons de trois entrées possibles, on fait un ET par combinaison, et on fait un OU entre tout le reste. Pour une porte à 5 entrées, on devrait utiliser là encore les combinaisons de trois entrées possibles. En fait, la recette générale est la suivante : pour une porte à N entrées, on toutes les combinaisons de (N+1)/2 entrées, on fait un ET par combinaison, puis on fait un OU entre les résultats des ET.
La porte à transmission
modifierLa porte à transmission est une porte logique assez particulière, qui mérite d'être vue dans ce chapitre. Pour simplifier, il s'agit d'un interrupteur commandable. Le circuit peut soit connecter l'entrée et la sortie, soit les déconnecter. Pour rappel, un interrupteur fermé laisse passer le courant, alors qu'un interrupteur fermé ne le laisse pas passer. Pour choisir entre les deux, une porte à transmission possède une entrée de commande sur laquelle on envoie un bit de commande, qui ouvre ou ferme l'interrupteur. La porte est typiquement fermée si le bit de commande est à 1, ouvert s'il est à 1.

Il est possible de la voir comme une porte OUI améliorée dont la table de vérité est celle-ci :
| Commande | Entrée | Sortie |
|---|---|---|
| 0 | 0 | Déconnexion |
| 0 | 1 | Déconnexion |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

Les portes à transmission sont très utilisés dans certains circuits très communs, que nous aborderons dans quelques chapitres, comme les multiplexeurs ou les démultiplexeurs.
Un défaut de ces portes logique est qu'elles sont électriquement équivalentes à des interrupteurs. Les autres portes logiques peuvent générer un 1 ou un 0 distinct de ce qu'il y a sur leur entrée. Et ce n'est pas un prodige, c'est juste que les portes logiques sont toutes reliées à la tension d'alimentation et à la masse (le 0 volt). Elles sont alimentées en électricité, pour fournir un 1 en sortie si l'entrée est à 0. Pas les portes à transmission, qui ne sont pas reliées à l'alimentation. Ce détail ne pose pas de problèmes tant qu'on n'enchaine pas de portes à transmission les unes à la suite des autres.
Les circuits combinatoires
modifierDans ce chapitre, nous allons aborder les circuits combinatoires. Ces circuits font comme tous les autres circuits : ils prennent des données sur leurs entrées, et fournissent un résultat en sortie. Le truc, c'est que ce qui est fourni en sortie ne dépend que du résultat sur les entrées, et de rien d'autre (ce n'est pas le cas pour tous les circuits). Pour donner quelques exemples, on peut citer les circuits qui effectuent des additions, des multiplications, ou d'autres opérations arithmétiques du genre.
Quelle que soit la complexité du circuit combinatoire à créer, celui-ci peut être construit en reliant des portes logiques entre elles. La conception d'un circuit combinatoire demande cependant de respecter quelques contraintes. La première est qu'il n'y ait pas de boucles dans le circuit : impossible de relier la sortie d'une porte logique sur son entrée, ou de faire la même chose avec un morceau de circuit. Si une boucle est présente dans un circuit, celui-ci n'est pas un circuit combinatoire, mais appartient à la classe des circuits séquentiels, que nous verrons dans le prochain chapitre.
Dans ce qui va suivre, nous allons voir comment concevoir ce genre de circuits. Il existe des méthodes et procédures assez simples qui permettent à n'importe qui de créer n'importe quel circuit combinatoire. Nous allons voir comment créer des circuits combinatoires à plusieurs entrées, mais à une seule sortie. Pour simplifier, on peut considérer que les bits envoyés en entrée sont un nombre, et que le circuit calcule un bit à partir du nombre envoyé en entrée.

C'est à partir de circuits de ce genre que l'on peut créer des circuits à plusieurs sorties : il suffit d'assembler plusieurs circuits à une sortie. La méthode pour ce faire est très simple : chaque sortie est calculée indépendamment des autres, uniquement à partir des entrées. Ainsi, pour chaque sortie du circuit, on crée un circuit à plusieurs entrées et une sortie : ce circuit déduit quoi mettre sur cette sortie à partir des entrées. En assemblant ces circuits à plusieurs entrées et une sortie, on peut ainsi calculer toutes les sorties.

Décrire un circuit : tables de vérité et équations logiques
modifierDans ce qui va suivre, nous aurons besoin de décrire un circuit électronique, le plus souvent un circuit que l'on souhaite concevoir ou utiliser. Et pour cela, il existe plusieurs grandes méthodes : la table de vérité, les équations logiques et un schéma du circuit. Les schémas de circuits électroniques ne sont rien de plus que les schémas avec des portes logiques, que nous avons déjà utilisé dans les chapitres précédents. Reste à voir la table de vérité et les équations logiques. La différence entre les deux est que la table de vérité décrit ce que fait un circuit, alors qu'une équation logique décrit la manière dont il est câblé. D'un côté la table de vérité considère le circuit comme une boite noire dont elle décrit le fonctionnement, de l'autre les équations décrivent ce qu'il y a à l'intérieur.
La table de vérité
modifierLa table de vérité décrit ce que fait le circuit, mais ne se préoccupe pas de dire comment. Elle ne dit pas quelles sont les portes logiques utilisées pour fabriquer le circuit, ni comment celles-ci sont reliées. Il s'agit d'une description du comportement du circuit, pas du circuit lui-même. En effet, elle se borne à donner la valeur de la sortie pour chaque entrée. Pour l'obtenir, il suffit de lister la valeur de chaque sortie pour toute valeur possible en entrée : on obtient alors la table de vérité du circuit. Pour créer cette table de vérité, il faut commencer par lister toutes les valeurs possibles des entrées dans un tableau, et écrire à côté les valeurs des sorties qui correspondent à ces entrées. Cela peut être assez long : pour un circuit ayant entrées, ce tableau aura lignes. Mais c'est la méthode la plus simple, la plus facile à appliquer.
Un premier exemple
modifierLe premier exemple sera très simple. Le circuit que l'on va créer sera un inverseur commandable, qui fonctionnera soit comme une porte NON, soit se contentera de recopier le bit fournit en entrée. Pour faire le choix du mode de fonctionnement (inverseur ou non), un bit de commande dira s'il faut que le circuit inverse ou non l'autre bit d'entrée :
- quand le bit de commande vaut zéro, l'autre bit est recopié sur la sortie ;
- quand il vaut 1, le bit de sortie est égal à l'inverse du bit d'entrée (pas le bit de commande, l'autre).
La table de vérité obtenue est celle d'une porte XOR :
| Entrées | Sortie |
|---|---|
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 0 |
Un second exemple
modifierPour donner un autre exemple, on va prendre un circuit calculant le bit de parité d'un nombre. Ce bit de parité est un bit qu'on ajoute aux données à stocker afin de détecter des erreurs de transmission ou d’éventuelles corruptions de données. Le but d'un bit de parité est que le nombre de bits à 1 dans le nombre à stocker, bit de parité inclus, soit toujours un nombre pair. Ce bit de parité vaut : zéro si le nombre de bits à 1 dans le nombre à stocker (bit de parité exclu) est pair et 1 si ce nombre est impair. Détecter une erreur demande de compter le nombre de 1 dans le nombre stocké, bit de parité inclus : si ce nombre est impair, on sait qu'un nombre impair de bits a été modifié. Dans notre cas, on va créer un circuit qui calcule le bit de parité d'un nombre de 3 bits.
| Entrées | Sortie |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 1 |
| 011 | 0 |
| 100 | 1 |
| 101 | 0 |
| 110 | 0 |
| 111 | 1 |
Un troisième exemple
modifierPour le dernier exemple, nous allons prendre en entrée un nombre de 3 bits. Le but du circuit à concevoir sera de déterminer le bit majoritaire dans ce nombre : celui-ci contient-il plus de 1 ou de 0 ? Par exemple :
- le nombre 010 contient deux 0 et un seul 1 : le bit majoritaire est 0 ;
- le nombre 011 contient deux 1 et un seul 0 : le bit majoritaire est 1 ;
- le nombre 000 contient trois 0 et aucun 1 : le bit majoritaire est 0 ;
- le nombre 110 contient deux 1 et un seul 0 : le bit majoritaire est 1 ;
- etc.
| Entrées | Sortie |
|---|---|
| 000 | 0 |
| 001 | 0 |
| 010 | 0 |
| 011 | 1 |
| 100 | 0 |
| 101 | 1 |
| 110 | 1 |
| 111 | 1 |
Les équations logiques
modifierIl peut être utile d'écrire un circuit non sous forme d'une table de vérité, ou d'un schéma, mais sous forme d'équations logiques. Mais attention : il ne s'agit pas des équations auxquelles vous êtes habitués. Ces équations logiques ne font que travailler avec des 1 et des 0, et n'effectuent pas d'opérations arithmétiques mais seulement des ET, des OU, et des NON. Dans le détail, les variables sont des bits (les entrées du circuit considéré), alors que les opérations sont des ET, OU et NON. Voici résumé dans ce tableau les différentes opérations, ainsi que leur notation. a et b sont des bits.
| Opérateur | Notation 1 | Notation 2 |
|---|---|---|
| NON a | ||
| a ET b | a.b | |
| a OU b | a+b | |
| a XOR b |
Avec ce petit tableau, vous savez comment écrire des équations logiques… Enfin presque, il ne faut pas oublier le plus important : les parenthèses, pour éviter quelques ambiguïtés. C'est un peu comme avec des équations normales : donne un résultat différent de . Avec nos équations logiques, on peut trouver des situations similaires : par exemple, est différent de .
Les formes normales conjonctives et disjonctives
modifierDans la jungle des équations logiques, deux types se démarquent des autres. Ces deux catégories portent les noms barbares de formes normales conjonctives et de formes normales disjonctives. Derrière ces termes se cache cependant deux concepts assez simples. Il s'agit d'équations qui impliquent uniquement des portes ET, OU et NON. Pour simplifier, ces équations décrivent des circuits composés de trois couches de portes logiques : une couche de portes NON, une couche de portes ET et une couche de portes OU. La couche de portes NON est placée immédiatement à la suite des entrées, dont elle inverse certains bits. Les couches de portes ET et OU sont placées après la couche de portes NON, et deux cas sont alors possibles : soit on met la couche de portes ET avant la couche de OU, soit on fait l'inverse. Le premier cas, avec les portes ET avant les portes OU, donne une forme normale disjonctive. La forme normale conjonctive est l'exact inverse, à savoir celui où la couche de portes OU est placée avant la couche de portes ET.
Les équations obtenues ont une forme similaire aux exemples qui vont suivre. Ces exemples sont donnés pour un circuit à trois entrées nommées a, b et c, et une sortie s. On voit que certaines entrées sont inversées avec une porte NON, et que le résultat de l'inversion est ensuite combiné avec des portes ET et OU.
- Exemple de forme normale conjonctive : .
- Exemple de forme normale disjonctive : .
Il faut savoir que tout circuit combinatoire peut se décrire avec une forme normale conjonctive et avec une forme normale disjonctive. Mais l'équation obtenue n'est pas forcément la manière idéale de concevoir un circuit. Celui-ci peut par exemple être simplifié en utilisant des portes XOR, ou en remaniant le circuit. Mais obtenir une forme normale est très souvent utile, quitte à simplifier celle-ci par la suite. D'ailleurs, les méthodes que nous allons voir plus bas ne font que cela : elles traduisent une table de vérité en forme normale conjonctive ou disjonctive, avant de la simplifier et de traduire le tout en circuit.
Conversions entre équation, circuit et table de vérité
modifier
Une équation logique se traduit en circuit assez facilement : il suffit de substituer chaque terme de l'équation avec la porte logique qui correspond. Les parenthèses et priorités opératoires indiquent l'ordre dans lequel relier les différentes portes logiques. Elles donnent une idée de comment doit être faite cette substitution. Les schémas ci-dessous montrent un exemple d'équation logique et le circuit qui correspond, tout en montrant les différentes substitutions intermédiaires. À ce propos, concevoir un circuit demande simplement d'établir son équation logique : il suffit de traduire l'équation obtenue en circuit, et le tour est joué !
La signification symboles sur les exemples est donnée dans la section « Les équations logiques » ci-dessus.
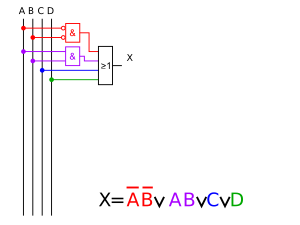
|

|
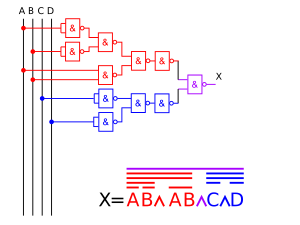
|
 |
Il est aussi intéressant de parler des liens entre tables de vérité et équation logique. Il faut savoir qu'il est possible de trouver l'équation d'un circuit à partir de sa table de vérité, et réciproquement. C'est d'ailleurs ce que font les méthodes de conception de circuit que nous allons voir plus bas : elles traduisent la table de vérité d'un circuit en équation logique. On commence par établir la table de vérité, ce qui est assez simple, avant d'établir une équation logique et de la traduire en circuit. On pourrait croire qu'à chaque table de vérité correspond une seule équation logique, mais ce n'est pas le cas. En réalité, il existe plusieurs équations logiques différentes pour chaque table de vérité. La raison à cela est que des équations différentes peuvent donner des circuits qui se comportent de la même manière. Après tout, on peut concevoir un circuit de différente manières et des circuits câblés différemment peuvent parfaitement faire la même chose. Des équations logiques qui décrivent la même table de vérité sont dites équivalentes. Par équivalente, on veut dire qu'elles décrivent des circuits différents, mais qui ont la même table de vérité - ils font la même chose. À ce propos, il faut savoir qu'il est possible de convertir une équation logique en une autre équation équivalente., chose que nous apprendrons à faire dans la suite de ce chapitre.
Concevoir un circuit combinatoire avec la méthode des minterms
modifierComme dit plus haut, créer un circuit demande d'établir sa table de vérité, avant de la traduire en équation logique, puis en circuit. Nous allons maintenant voir la première étape, celle de la conversion entre table de vérité et équation. Il existe deux grandes méthodes de ce type, pour concevoir un circuit intégré, qui portent les noms de méthode des minterms et de méthode des maxterms. La différence entre les deux est que la première donne une forme normale disjonctive, alors que la seconde donne une forme normale conjonctive. Dans cette section, nous allons voir la méthode des minterms, avant de voir la méthode des maxterms. Pour chaque méthode, nous allons commencer par montrer comment appliquer ces méthodes sans rentrer dans le formalisme, avant de montrer le formalisme en question. Précisons cependant que ces deux méthodes font la même chose : elles traduisent une table de vérité en équation logique. La première étape de ces deux méthodes est donc d'établir la table de vérité. Voyons un peu de quoi il retourne.
La méthode des minterms, expliquée sans formalisme
modifierLa méthode des minterms est de loin la plus simple à comprendre. Ses principes sont en effet assez intuitifs et elle est assez facile à appliquer, pour qui connaît ses principes sous-jacents. Pour l'expliquer, nous allons commencer par voir un circuit, qui compare son entrée avec une constante, dépendante du circuit. Par la suite, nous allons voir comment combiner ce circuit avec des portes logiques pour obtenir le circuit désiré.
Les minterms (comparateurs avec une constante)
modifierNous allons maintenant étudier un comparateur qui vérifie si le nombre d'entrée est égal à une certaine constante (2, 3, 5, 8, ou tout autre nombre) qui dépend du circuit et renvoie un 1 seulement si c’est le cas. Ainsi, on peut créer un circuit qui mettra sa sortie à 1 uniquement si on envoie le nombre 5 sur ses entrées. Ou encore, créer un circuit qui met sa sortie à 1 uniquement quand l'entrée vaut 126. Et ainsi de suite : tout nombre peut servir de constante à vérifier. Le circuit possède plusieurs entrées, sur lesquelles on place les bits du nombre à comparer. Sa sortie est un simple bit, qui vaut 1 si le nombre en entrée est égal à la constante et 0 sinon. Nous allons voir qu'il y en a deux types, qui ressemblent aux deux types de comparateurs avec zéro. Le premier type est basé sur une porte NOR, à laquelle on ajoute des portes NON. Le second est basé sur une porte ET précédée de portes NON.
Le premier circuit de ce type est composé d'une couche de portes NON et d'une porte ET à plusieurs entrées. Créer un tel circuit se fait en trois étapes. En premier lieu, il faut convertir la constante à vérifier en binaire : dans ce qui suit, nous nommerons cette constante k. En second lieu, il faut créer la couche de portes NON. Pour cela, rien de plus simple : on place des portes NON pour les entrées de la constante k qui sont à 0, et on ne met rien pour les bits à 1. Par la suite, on place une porte ET à plusieurs entrées à la suite de la couche de portes NON.

Pour comprendre pourquoi on procède ainsi, il faut simplement regarder ce que l'on trouve en sortie de la couche de portes NON :
- si on envoie la constante, tous les bits à 0 seront inversés alors que les autres resteront à 1 : on se retrouve avec un nombre dont tous les bits sont à 1 ;
- si on envoie un autre nombre, soit certains 0 du nombre en entrée ne seront pas inversés, ou alors des bits à 1 le seront : il y aura au moins un bit à 0 en sortie de la couche de portes NON.
Ainsi, on sait que le nombre envoyé en entrée est égal à la constante k si et seulement si tous les bits sont à 1 en sortie de la couche de portes NON. Dit autrement, la sortie du circuit doit être à 1 si et seulement si tous les bits en sortie des portes NON sont à 1 : il ne reste plus qu'à trouver un circuit qui prenne ces bits en entrée et ne mette sa sortie à 1 que si tous les bits d'entrée sont à 1. Il existe une porte logique qui fonctionne ainsi : il s'agit de la porte ET à plusieurs entrées.

Le second type de comparateur avec une constante est fabriqué avec une porte NOR précédée de portes NON. Il se fabrique comme le comparateur précédent, sauf que cette fois-ci, il faut mettre une porte NON pour chaque bit à 1 de l'opérande, et non chaque bit à zéro. En clair, la couche de portes NON est l'exact inverse de celle du circuit précédent. Le tout est suivi par une porte NOR.

Pour comprendre pourquoi on procède ainsi, il faut simplement regarder ce que l'on trouve en sortie de la couche de portes NON :
- si on envoie la constante, tous les bits à 0 seront inversés alors que les autres resteront à 1 : on se retrouve avec un zéro en sortie ;
- si on envoie un autre nombre, soit certains 1 du nombre en entrée ne seront pas inversés, ou alors des bits à 0 le seront : il y aura au moins un bit à 1 en sortie de la couche de portes NON.
La porte NOR, quant à elle est un comparateur avec zéro, comme on l'a vu plus haut. Pour résumer, la première couche de portes NON transforme l'opérande et que la porte NOR vérifie si l'opérande transformée vaut zéro. La transformation de l'opérande est telle que son résultat est nul seulement si l’opérande est égale à la constante testée.

Combiner les comparateurs avec une constante
modifierOn peut créer n'importe quel circuit à une seule sortie avec ces comparateurs, en les couplant avec une porte OU à plusieurs entrées. Pour comprendre pourquoi, rappelons que les entrées du circuit peuvent prendre plusieurs valeurs : pour une entrée de bits, on peut placer valeurs différentes sur l'entrée. Mais seules certaines valeurs doivent mettre la sortie à 1, les autres la laissant à 0. Les valeurs d'entrée qui mettent la sortie 1 sont aussi appelées des minterms. Ainsi, pour savoir s’il faut mettre un 1 en sortie, il suffit de vérifier que l'entrée est égale à un minterm. Pour savoir si l'entrée est égale à un minterm, on doit utiliser un comparateur avec une constante pour chaque minterm. Par exemple, pour un circuit dont la sortie est à 1 si son entrée vaut 0000, 0010, 0111 ou 1111, il suffit d'utiliser :
- un comparateur qui vérifie si l'entrée vaut 0000 ;
- un comparateur qui vérifie si l'entrée vaut 0010 ;
- un comparateur qui vérifie si l'entrée vaut 0111 ;
- et un comparateur qui vérifie si l'entrée vaut 1111.
Reste à combiner les sorties de ces comparateurs pour obtenir une seule sortie, ce qui est fait en utilisant un circuit relativement simple. On peut remarquer que la sortie du circuit est à 1 si un seul comparateur a sa sortie à 1. Or, on connaît un circuit qui fonctionne comme cela : la porte OU à plusieurs entrées. En clair, on peut créer tout circuit avec seulement des comparateurs et une porte OU à plusieurs entrées.

Méthode des minterms, version formalisée
modifierOn peut formaliser la méthode précédente, ce qui donne la méthode des minterms. Celle-ci permet d'obtenir un circuit à partir d'une description basique du circuit. Mais le circuit n'est pas vraiment optimisé et peut être fortement simplifié. Nous verrons plus tard comment simplifier des circuits obtenus avec la méthode que nous allons exposer.
Lister les entrées de la table de vérité qui valident l'entrée
modifierLa première étape demande d'établir la table de vérité du circuit, afin de déterminer ce que fait le circuit voulu. Maintenant que l'on a la table de vérité, il faut lister les valeurs en entrée pour lesquelles la sortie vaut 1. On rappelle que ces valeurs sont appelées des minterms. Il faudra utiliser un comparateur avec une constante pour chaque minterm afin d'obtenir le circuit final. Pour l'exemple, nous allons reprendre le circuit de calcul d'inverseur commandable, vu plus haut.
| Entrées | Sortie |
|---|---|
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 0 |
Listons les lignes de la table où la sortie vaut 1.
| Entrées | Sortie |
|---|---|
| 01 | 1 |
| 10 | 1 |
Pour ce circuit, la sortie vaut 1 si et seulement si l'entrée du circuit vaut 01 ou 10. Dans ce cas, on doit créer deux comparateurs qui vérifient si leur entrée vaut respectivement 01 et 10. Une fois ces deux comparateurs crée, il faut ajouter la porte OU.
Établir l'équation du circuit
modifierLes deux étapes précédentes sont les seules réellement nécessaires : quelqu'un qui sait créer un comparateur avec une constante (ce qu'on a vu plus haut), devrait pouvoir s'en sortir. Reste à savoir comment transformer une table de vérité en équations logiques, et enfin en circuit. Pour cela, il n'y a pas trente-six solutions : on va écrire une équation logique qui permettra de calculer la valeur (0 ou 1) d'une sortie en fonction de toutes les entrées du circuit. Et on fera cela pour toutes les sorties du circuit que l'on veut concevoir. Pour ce faire, on peut utiliser ce qu'on appelle la méthode des minterms, qui est strictement équivalente à la méthode vue au-dessus. Elle permet de créer un circuit en quelques étapes simples :
- lister les lignes de la table de vérité pour lesquelles la sortie vaut 1 (comme avant) ;
- écrire l'équation logique pour chacune de ces lignes (qui est celle d'un comparateur) ;
- faire un OU entre toutes ces équations logiques, en n'oubliant pas de les entourer par des parenthèses.
Pour écrire l'équation logique d'une ligne, il faut simplement :
- lister toutes les entrées de la ligne ;
- faire un NON sur chaque entrée à 0 ;
- et faire un ET avec le tout.
Vous remarquerez que la succession d'étapes précédente permet de créer un comparateur qui vérifie que l'entrée est égale à la valeur sur la ligne sélectionnée.
Pour illustrer le tout, on va reprendre notre exemple avec le bit de parité. La première étape consiste donc à lister les lignes de la table de vérité dont la sortie est à 1.
| Entrées | Sortie |
|---|---|
| 001 | 1 |
| 010 | 1 |
| 100 | 1 |
| 111 | 1 |
On a alors :
- la première ligne où l'entrée vaut 001 : son équation logique vaut ;
- la seconde ligne où l'entrée vaut 010 : son équation logique vaut ;
- la troisième ligne où l'entrée vaut 100 : son équation logique vaut ;
- la quatrième ligne où l'entrée vaut 111 : son équation logique vaut .
On a alors obtenu nos équations logiques. Reste à faire un OU entre toutes ces équations, et le tour est joué !
Nous allons maintenant montrer un deuxième exemple, avec le circuit de calcul du bit majoritaire vu juste au-dessus. Première étape, lister les lignes de la table de vérité dont la sortie vaut 1 :
| Entrées | Sortie |
|---|---|
| 011 | 1 |
| 101 | 1 |
| 110 | 1 |
| 111 | 1 |
Seconde étape, écrire les équations de chaque ligne. Essayez par vous-même, avant de voir la solution ci-dessous.
- Pour la première ligne, l'équation obtenue est : .
- Pour la seconde ligne, l'équation obtenue est : .
- Pour la troisième ligne, l'équation obtenue est : .
- Pour la quatrième ligne, l'équation obtenue est : .
Il suffit ensuite de faire un OU entre les équations obtenues au-dessus.
Traduire l'équation en circuit
modifierEnfin, il est temps de traduire l'équation obtenue en circuit, en remplaçant chaque terme de l'équation par le circuit équivalent. Notons que les parenthèses donnent une idée de comment doit être faite cette substitution.
Concevoir un circuit avec la méthode des maxterms
modifierLa méthode des minterms, vue précédemment, n'est pas la seule qui permet de traduire une table de vérité en équation logique. Elle est secondée par une méthode assez similaire : la méthode des maxterms. Les deux donnent des équations logiques, et donc des circuits, différents. Les deux commencent par une couche de portes NON, suivie par deux couches de portes ET et OU, mais l'ordre des portes ET et OU est inversé. Dit autrement, la méthode des minterms donne une forme normale disjonctive, alors que celle des maxterms donnera une forme normale conjonctive.
La méthode des maxterms : formalisme
modifierLa méthode des maxterms fonctionne sur un principe assez tordu, mais qui fonctionne cependant. Avec celle-ci, on effectue trois étapes, chacune correspondant à l'exact inverse de l'étape équivalente avec les minterms. Les 0 sont remplacés par des 1 et les portes ET par des portes OU.
- Premièrement on doit lister les lignes de la table de vérité qui mettent la sortie à 0, ce qui est l'exact inverse de l'étape équivalente avec les minterms.
- Ensuite, on traduit chaque ligne en équation logique. La traduction de chaque ligne en équation logique est aussi inversée par rapport à la méthode des minterms : on doit inverser les bits à 1 avec une porte NON et faire un OU entre chaque bit.
- Et enfin, on doit faire un ET entre tous les résultats précédents.
Un exemple d'application
modifierPar exemple, prenons la table de vérité suivante :
| Entrée a | Entrée b | Entrée c | Sortie S | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
La première étape est de lister les entrées associées à une sortie à 0. Ce qui donne :
| Entrée a | Entrée b | Entrée c | Sortie S | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 0 |
Vient ensuite la traduction de chaque ligne en équation logique. Cette fois-ci, les bits à 1 dans l'entrée sont ceux qui doivent être inversés, les autres restants tels quels. De plus, on doit faire un OU entre ces bits. On a donc :
- pour la première ligne ;
- pour la seconde ligne ;
- pour la troisième ligne.
Et enfin, il faut faire un ET entre ces maxterms. Ce qui donne l'équation suivante :
Quelle méthode choisir ?
modifierOn peut se demander quelle méthode choisir entre minterms et maxterms. L'exemple précédent nous donne un indice. Si on applique la méthode des minterms sur l'exemple précédent, vous allez prendre du temps et obtenir une équation logique bien plus compliquée, avec beaucoup de minterms. Alors que c'est plus rapide avec les maxterms, l'équation obtenue étant beaucoup plus simple. Cela vient du fait que dans l'exemple précédent, il y a beaucoup de lignes associées à une sortie à 1. On a donc plus de minterms que de maxterms, ce qui rend la méthode des minterms plus longue. Par contre, on pourrait trouver des exemples où c'est l'inverse. Si un circuit a plus de lignes où la sortie est à 0, alors la méthode des minterms sera plus rapide. Bref, tout dépend du nombre de minterms/maxterms dans la table de vérité. En comptant le nombre de cas où la sortie est à 1 ou à 0, on peut savoir quelle méthode est la plus rapide : minterm si on a plus de cas avec une sortie à 0, maxterm sinon.
Le principe caché derrière la méthode des maxterms
modifierLa méthode des maxterms fonctionne sur un principe un peu différent de la méthode des minterms. Rappelons que chaque valeur d'entrée qui met une sortie à 0 est appelée un maxterm, alors que celles qui la mettent à 1 sont des minterms. Un circuit conçu selon avec des minterms vérifie si l'entrée met la sortie à 1, alors qu'un circuit maxterm vérifie si l'entrée ne met pas la sortie à 0. Dit autrement, ils vérifient soit que l'entrée est un minterm, soit que l'entrée n'est pas un maxterm.
L’aperçu complet de la méthode
modifierPour cela, un circuit conçu avec la méthode des maxterms procède en deux étapes : il compare l'entrée avec chaque maxterm possible, et combine les résultats avec une porte à plusieurs entrées.
- Pour commencer, le circuit vérifie si l'entrée est un maxterm avec plusieurs comparateurs avec une constante modifiée : un pour chaque maxterm. Chaque comparateur dit si l'entrée est différente du maxterm associé : il renvoie un 1 si l'entrée ne correspond pas au maxterm et 0 sinon.
- La seconde étape combine les résultats de tous les maxterms pour déduire la sortie. Si tous les comparateurs renvoient un 1, cela signifie que l'entrée est différente de tous les maxterms : ce n'en est pas un. La sortie doit alors être mise à 1. Si l'entrée correspond à un maxterm, alors le comparateur associé au maxterm donnera un 0 en sortie : il y aura au moins un comparateur qui donnera un 0. Dans ce cas, la sortie doit être mise à 0. On remarque rapidement que ce comportement est celui d'une porte ET à plusieurs entrées.

Le circuit de comparaison
modifierLe circuit de comparaison fonctionne sur le principe suivant : il compare l'entrée avec le maxterm bit par bit, chaque bit étant comparé indépendamment des autres, en parallèle. Les résultats des comparaisons sont ensuite combinées pour donner le bit de résultat.
Le circuit de comparaison donne un 1 quand les bits sont différents et un 0 s'ils sont égaux. La comparaison bit à bit est effectuée par une simple porte logique, qui n'est autre que la porte NON en entrée du circuit (ou son absence). Pour comprendre pourquoi, regardons la table de vérité du circuit de comparaison, illustré ci-dessous. On voit que si le bit du maxterm est 0, alors la sortie est égale au bit d'entrée. Mais si le bit du maxterm est à 1, alors la sortie est l'inverse du bit d'entrée.
| Bit du maxterm | Bit d'entrée | Bit de sortie | |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
Maintenant, passons à la combinaison des résultats. Si au moins un bit d'entrée est différent du bit du maxterm, alors l'entrée ne correspond pas au maxterm. On devine donc qu'on doit combiner les résultats avec une porte OU.
Simplifier un circuit
modifierComme on l'a vu, la méthode précédente donne une équation logique qui décrit un circuit. Mais quelle équation : on se retrouve avec un gros paquet de ET et de OU ! heureusement, il est possible de simplifier cette équation. Pour donner un exemple, sachez que cette équation : ; peut se simplifier en : avec les règles de simplifications que nous allons voir. Dans cet exemple, on passe donc de 17 portes logiques à seulement 3 ! Bien sûr, on peut simplifier cette équation juste pour se simplifier la vie lors de la traduction de cette équation en circuit, mais cela sert aussi à autre chose : cela permet d'obtenir un circuit plus rapide et/ou utilisant moins de portes logiques. Autant vous dire qu'apprendre à simplifier ces équations est quelque chose de crucial, particulièrement si vous voulez concevoir des circuits un tant soit peu rapides.
L'algèbre de Boole
modifierPour simplifier une équation logique, on peut utiliser certaines propriétés mathématiques simples pour factoriser ou développer comme on le ferait avec une équation mathématique normale. Ces propriétés forment ce qu'on appelle l’algèbre de Boole. En utilisant ces règles algébriques, on peut factoriser ou développer certaines expressions, comme on le ferait avec une équation normale, ce qui permet de simplifier une équation logique assez intuitivement. Le tout est de bien faire ces simplifications en appliquant correctement ces règles, ce qui peut demander un peu de réflexion.
Les théorèmes de base de l’algèbre de Boole peuvent se classer en plusieurs types séparés, qui sont les suivantes :
- l'associativité, la commutativité et la distributivité ;
- la double négation et les lois de de Morgan ;
- les autres règles, appelées règles bit à bit.
L'associativité, la distributivité et la commutativité des opérateurs logiques
modifierL'associativité, la commutativité et la distributivité ressemblent beaucoup aux règles arithmétiques usuelles, ce qui fait qu'on ne les détaillera pas ici.
| Commutativité |
|
|---|---|
| Associativité |
|
| Distributivité |
|
Les autres règles sont par contre plus importantes.
Les règles de type bit à bit
modifierLes règles bit à bit ne sont utiles que dans le cas où certaines entrées d'un circuit sont fixées, ou lors de la simplification de certaines équations logiques. Elles regroupent plusieurs cas distincts :
- soit on fait un ET/OU/XOR entre un bit et lui-même ;
- soit on fait un ET/OU/XOR entre un bit et son inverse ;
- soit on fait un ET/OU/XOR entre un bit et 1 ;
- soit on fait un ET/OU/XOR entre un bit et 0.
Le premier cas regroupe les trois formules suivantes :
Le second cas regroupe les trois formules suivantes :
- ,
- .
Le troisième cas regroupe les trois formules suivantes :
- ,
- .
Le dernier cas regroupe les trois formules suivantes :
- ,
- .
Voici la liste de ces règles, classées par leur nom mathématique :
| Idempotence |
|
|---|---|
| Élément nul |
|
| Élément Neutre |
|
| Complémentarité |
|
Ces relations permettent de simplifier des équations logiques, mais peuvent avoir des utilisations totalement différentes.
Nous avons déjà utilisé implicitement les formules du premier cas, à savoir et dans le chapitre sur les portes logiques. En effet, nous avions vu qu'il est possible de fabriquer une porte NON à partir d'une porte NAND ou d'une porte NOR. L'idée était d'envoyer le bit à inverser sur les deux entrées d'une NOR/NAND, le ET/OU recopiant le bit sur sa sortie et le NON l'inversant. Pour retrouver ce résultat, il suffit d'ajouter une porte NON dans les formules et , ce qui donne :
Au passage, la formule nous dit pourquoi cela ne marcherait pas du tout avec une porte XOR.
Pour la formule , elle sert dans certaines situations particulières, où l'on veut initialiser un nombre à zéro, peu importe que ce nombre soit une variable, la sortie d'un circuit combinatoire ou un registre. La formule nous dit que le résultat d'un XOR entre un bit et lui-même est toujours zéro. Et cela s'applique aussi à des nombres : si on XOR un nombre avec lui-même, chacun de ses bits est XORé avec lui-même et est donc mis à zéro. Conséquence : un nombre XOR lui-même donnera toujours zéro. Cette propriété est utilisée pour mettre à zéro un registre, pour le calcul des bits de parité ou pour échanger une valeur entre deux registres. Les formules du second cas, à savoir , et , permettent de faire quelque chose de similaire. La première formule dit que faire un ET entre un nombre et son inverse donnera toujours zéro, comme un XOR entre un nombre et lui-même. Pour les deux autres formules, elles disent que le résultat sera toujours un bit à 1. Cela sert cette fois-ci si on veut initialiser une variable, un registre ou une sortie de circuit à une valeur où tous les bits sont à 1.
Les formules du troisième et quatrième cas seront utilisées dans le chapitre sur les circuits de calcul logique et bit à bit, dans la section sur les masques. C'est dans cette section que nous verrons en quoi ces formules sont utiles en dehors du cas d'une simplification de circuit. Pour le moment, nous ne pouvons pas en dire plus.
Les lois de de Morgan et la double négation
modifierParmi les règles de l’algèbre de Boole, les lois de de Morgan et la double négation sont de loin les plus importantes à retenir. Elles sont les seules à impliquer les négations. Voici ces deux règles :
| Double négation | |
|---|---|
| Loi de De Morgan |
|
La première loi de de Morgan nous dit simplement qu'une porte NAND peut se fabriquer avec une porte OU précédée de deux portes NON, comme nous l'avions vu au chapitre précédent.

La seconde loi, quant à elle, dit qu'une porte NOR peut se fabriquer avec une porte ET précédée de deux portes NON, comme nous l'avions vu au chapitre précédent.

Les règles de Morgan pour deux entrées sont résumées dans le tableau ci-dessous.

| |

|
Les lois de de Morgan peut se généraliser pour plus de deux entrées.
- 1ère loi de de Morgan :
- 2nd loi de de Morgan :
En les combinant avec la loi de la double négation, les lois de de Morgan permettent de transformer une équation écrite sous forme normale conjonctive en une équation équivalente sous forme normale disjonctive, et réciproquement. Elles permettent de passer d'une équation obtenue avec les minterms à l'équation obtenue avec les maxterms.
La formule équivalente de la porte XOR et de la porte NXOR
modifierAvec les règles précédentes, il est possible de démontrer que les portes XOR et NXOR peuvent se construire avec uniquement des portes ET/OU/NON. Nous l'avions vu dans le chapitre précédent, et montré quelques exemples de circuits équivalents.
En utilisant la méthode des minterms, on arrive à l'expression suivante pour la porte XOR et la porte NXOR :
- XOR :
- NXOR :
La formule obtenue avec les minterms pour la porte XOR donne ce circuit :

La formule obtenue avec les minterms pour la porte NXOR donne ce circuit :

Il est possible d'obtenir une formule équivalente pour la porte XOR, en utilisant l’algèbre de Boole sur les formules précédentes. Pour cela, partons de l'équation de la porte NXOR obtenue avec la méthode des minterms :
Appliquons une porte NON pour obtenir la porte XOR :
Appliquons la loi de de Morgan entre les parenthèses :
Appliquons la loi de de Morgan dans les parenthèses :
Simplifions les doubles négations :

Il est possible de faire la même chose, mais pour la porte NXOR. Pour cela, partons de l'équation de la porte XOR obtenue avec la méthode des minterms :
Une porte NXOR est, par définition, l'inverse d'une porte XOR. En appliquant un NON sur l'équation précédente, on trouve donc :
On applique la loi de de Morgan pour le OU entre les parenthèses :
On applique la loi de de Morgan, mais cette fois-ci à l'intérieur des parenthèses :
On simplifie les doubles inversions :
La formule est similaire à celle d'un XOR, la seule différence étant qu'il faut inverser de place les ET et les OU : le ET est dans les parenthèses pour le XOR et entre pour le NXOR, et inversement pour le OU.
Dans les deux exemples précédents, on voit que l'on a pu passer d'une forme normale conjonctive à une forme normale disjonctive et réciproquement, en utilisant la loi de de Morgan. C'est un principe assez général qui se retrouve souvent dans les démonstrations d'équations logiques.
Exemples complets
modifierComme premier exemple, nous allons travailler sur cette équation : . On peut la simplifier en trois étapes :
- Appliquer la règle de distributivité du ET sur le OU pour factoriser le facteur e1.e0, ce qui donne ;
- Appliquer la règle de complémentarité sur le terme entre parenthèses , ce qui donne 1.e1.e0 ;
- Et enfin, utiliser la règle de l’élément neutre du ET, qui nous dit que a.1=a, ce qui donne : e1.e0.
En guise de second exemple, nous allons simplifier . Cela se fait en suivant les étapes suivantes :
- Factoriser e0, ce qui donne : ;
- Utiliser la règle du XOR qui dit que , ce qui donne .
Les tableaux de Karnaugh
modifierIl existe d'autres méthodes pour simplifier nos circuits. Les plus connues étant les tableaux de Karnaugh et l'algorithme de Quine Mc Cluskey. On ne parlera pas de la dernière méthode, trop complexe pour ce cours. Ces deux méthodes possèdent quelques défauts qui nous empêchent de créer de très gros circuits avec. Pour le dire franchement, elles sont trop longues à utiliser quand le nombre d'entrée du circuit dépasse 5 ou 6. Nous allons cependant aborder la méthode du tableau de Karnaugh, qui peut être assez utile pour des circuits simples. La simplification des équations avec un tableau de Karnaugh demande plusieurs étapes, que nous allons maintenant décrire.
Première étape : créer le tableau de Karnaugh
modifier
D'abord, il faut créer une table de vérité pour chaque bit de sortie du circuit à simplifier, qu'on utilise pour construire ce tableau. La première étape consiste à obtenir un tableau plus ou moins carré à partir d'une table de vérité, organisé en lignes et colonnes. Si on a n variables, on crée deux paquets avec le même nombre de variables (à une variable près pour un nombre impair de variables). Par exemple, supposons que j'aie quatre variables : a, b, c et d. Je peux créer deux paquets en regroupant les quatre variables comme ceci : ab et cd. Ou encore comme ceci : ac et bd. Il arrive que le nombre de variables soit impair : dans ce cas, il y a aura un paquet qui aura une variable de plus.
Seconde étape : remplir ce tableau
modifierEnsuite, pour le premier paquet, on place les valeurs que peut prendre ce paquet sur la première ligne. Pour faire simple, considérez ce paquet de variables comme un nombre, et écrivez toutes les valeurs que peut prendre ce paquet en binaire. Rien de bien compliqué, mais ces variables doivent être encodées en code Gray : on ne doit changer qu'un seul bit en passant d'une ligne à sa voisine. Pour le second paquet, faites pareil, mais avec les colonnes. Là encore, les valeurs doivent être codées en code Gray.
Pour chaque ligne et chaque colonne, on prend les deux paquets : ces deux paquets sont avant tout des rassemblements de variables, dans lesquels chacune a une valeur bien précise. Ces deux paquets précisent ainsi les valeurs de toutes les entrées, et correspondent donc à une ligne dans la table de vérité. Sur cette ligne, on prend le bit de la sortie, et on le place à l'intersection de la ligne et de la colonne. On fait cela pour chaque case du tableau, et on le remplit totalement.
Troisième étape : faire des regroupements
modifierTroisième étape de l'algorithme : faire des regroupements. Par regroupement, on veut dire que les 1 dans le tableau doivent être regroupés en paquets de 1, 2, 4, 8, 16, 32, etc. Le nombre de 1 dans un paquet doit TOUJOURS être une puissance de deux. De plus, ces regroupements doivent obligatoirement former des rectangles dans le tableau de Karnaugh. De manière générale, il vaut mieux faire des paquets les plus gros possible, afin de simplifier l'équation au maximum.
 |
 |

Il faut noter que les regroupements peuvent se recouvrir. Non seulement c'est possible, mais c'est même conseillé : cela permet d'obtenir des regroupements plus gros. De plus, ces regroupements peuvent passer au travers des bords du tableau : il suffit de les faire revenir de l'autre côté. Et c'est possible aussi bien pour les bords horizontaux (gauche et droite) que pour les bords verticaux (haut et bas). Le même principe peut s'appliquer aux coins.
Quatrième étape : convertir chaque regroupement en équation logique
modifierTrouver l'équation qui correspond à un regroupement est un processus en plusieurs étapes, que nous illustrerons dans ce qui va suivre. Ce processus demande de :
- trouver la variable qui ne varie pas dans les lignes et colonnes attribuées au regroupement ;
- inverser la variable si celle-ci vaut toujours zéro dans le regroupement ;
- faire un ET entre les variables qui ne varient pas.
- faire un OU entre les équations de chaque regroupement, et on obtient l'équation finale de la sortie.
Dans ce chapitre, nous allons voir les opérations bit à bit, un ensemble d'opérations qui appliquent une opération binaire sur un ou deux nombres. La plus simple d'entre elle est l'opération NON, aussi appelée opération de complémentation, qui inverse tous les bits d'un nombre. Il s'agit de l'opération la plus simple et nous en avions déjà parlé dans les chapitres précédents. Mais il existe des opérations bit à bit un chouia plus complexes, comme celles qui font un ET/OU/XOR entre deux nombres. Pour être plus précis, elles font un ET/OU/XOR entre les deux bits de même poids. L'exemple du OU bit à bit est illustré ci-dessous, les exemples du ET et du XOR sont similaires.

De telles opérations sont appelées bit à bit car elles combinent les bits de même poids de deux opérandes. Par contre, il n'y a pas de calculs entre bits de poids différents, les colonnes sont traitées indépendamment. Elles sont très utilisées en programmation, et tout ordinateur digne de ce nom contient un circuit capable d'effectuer ces opérations. Dans ce chapitre, nous allons voir divers circuits capables d'effectuer des opérations bit à bit, et voir comment les combiner.
Les opérations bit à bit classiques peuvent prendre une ou deux opérandes. La plupart en prenant deux comme les opérations ET/OU/XOR, l'opération NON en prend une seule. Les opérations bit à bit sur deux opérandes sont au nombre de 16, ce qui correspond au nombre de portes logiques à deux entrées possibles. Mais ce chiffre de 16 inclut les opérations bit à bit sur une opérande unique, qui sont au nombre de 4. Les opérations bit à bit sur une seule opérande sont plus simples à voir, nous verrons les opérations bit à bit à deux opérandes plus tard.
Les opérations bit à bit à une opérande
modifierLes opérations bit à bit sur une opérande sont au nombre de quatre :
- Mettre à zéro l'opérande (porte FALSE).
- Mettre à 11111...11111 l'opérande (porte TRUE).
- Inverser les bits de l'opérande (porte NON).
- Recopier l'opérande (porte OUI).
Dans ce qui va suivre, nous allons créer un circuit qui prend en entrée une opérande, un nombre, et applique une des quatre opérations précédente sur chacun de ses bits. On peut choisir l'opération voulue grâce à plusieurs bits de commande, idéalement deux. Le circuit est composé à partir de circuits plus simples, au maximum trois : un circuit qui inverse le bit d'entrée à la demande, un autre qui le met à 1, un autre qui le met à 0. Ces trois circuits ont une entrée de commande qui détermine s'il faut faire l'opération, ou si le circuit doit se comporter comme une simple porte OUi, qui recopie sont entrée sur sa sortie et ne fait donc aucune opération. Le circuit recopie le bit d'entrée si cette entrée est à 0, mais il inverse/set/reset le bit d'entrée si elle est à 1.
Pour comprendre comment concevoir ces circuits, il faut rappeler les relations suivantes, qui donnent le résultat d'un ET/OU/XOR entre un bit quelconque noté a et un bit qui vaut 0 ou 1.
| Opération | Interprétation du résultat | |
|---|---|---|
| Porte ET | Mise à zéro du bit d'entrée | |
| Recopie du bit d'entrée | ||
| Porte OU | Mise à 1 du bit d'entrée | |
| Recopie du bit d'entrée | ||
| Porte XOR | Recopie du bit d'entrée | |
| Inversion du bit d'entrée |
Pour résumer ce qui va suivre :
- Le circuit de mise à 1 commandable est une porte simple OU.
- Le circuit d’inversion commandable est une simple porte XOR.
- Le circuit de Reset, qui permet de mettre à zéro un bit si besoin, est une porte ET un peu modifiée.
Le circuit de mise à la valeur maximale
modifierDans cette section, nous allons voir un circuit qui prend en entrée un nombre et met sa sortie à la valeur maximale si une condition est respectée. Pour le dire autrement, le circuit va soit recopier l'entrée telle quelle sur sa sortie, soit la mettre à 11111...111. Le choix entre les deux situations est réalisé par une entrée Set de 1 bit : un 1 sur cette entrée met la sortie à la valeur maximale, un 0 signifie que l'entrée est recopiée en sortie.
La porte OU est toute indiquée pour cela. La mise à 1 d'un bit d'entrée demande de faire un OU de celui-ci avec un 1, alors que recopier un bit d'entrée demande de faire un OU de celui-ci avec un 0.

Ce circuit est utilisé pour gérer les débordements d'entier dans les circuits de calculs qui utilise l'arithmétique saturée (voir le chapitre sur le codage des entiers pour plus d'explications). Les circuits de calculs sont souvent suivis par ce circuit de mise à 111111...111, pour gérer le cas où le calcul déborde, afin de mettre la sortie à la valeur maximale. Évidemment, le circuit de calcul doit non seulement faire le calcul, mais aussi détecter les débordements d'entiers, afin de fournir le bit pour l'entrée Set. Mais nous verrons cela dans le chapitre sur les circuits de calcul entier.
Le circuit de mise à zéro
modifierLe circuit de Reset prend entrée le bit d'entrée, puis un bit de commande qui indique s'il faut mettre à zéro le bit d'entrée ou non. Le bit de commande en question est appelé le bit Reset. Si le signal Reset est à 1, alors on met à zéro le bit d'entrée, mais on le laisse intact sinon.
Le tableau ci-dessus nous dit que la porte ET est adaptée : elle recopie le bit d'entrée si le bit de commande vaut 1, et elle le met à 0 si le bit de commande vaut 0. Cependant, rappelons que l'on souhaite que le le circuit fasse un Reset si le bit de commande est à 1, pas 0, et la porte ET fait l'inverse. Pour corriger cela, on doit ajouter une porte NON. Le tout donne le circuit ci-dessous.

Un circuit qui met à zéro un nombre est composé de plusieurs circuits ci-dessus, à la différence que la porte NON est potentiellement partagée. Par contre, chaque bit est bien relié à une porte ET.

L'inverseur commandable
modifierDans cette section, nous allons voir un inverseur commandable, un circuit qui, comme son nom l'indique, inverse les bits d'un nombre passé en entrée. Ce circuit inverse un nombre quand le bit de commande, souvent nommé Invert, vaut 1.
La porte XOR est toute indiquée pour, ce qui fait que le circuit d'inversion commandable est composé d'une couche de portes XOR, chaque porte ayant une entrée connectée au bit de commande.

Le circuit qui combine les trois précédents
modifierVoyons maintenant un circuit qui combine les trois circuits précédents. L'implémentation naïve met les trois circuits les uns à la suite des autres, ce qui donne pour chaque bit d'opérande trois portes logiques ET/OU/XOR en série. Le problème est qu'il faut préciser trois bits de commandes, alors qu'on peut en théorie se débrouiller avec seulement 2 bits. Il faut alors ajouter un circuit combinatoire pour calculer les trois bits de commande à partir des deux bits initiaux.

Mais il y a moyen de se passer d'une porte logique ! L'idée est que mettre à 0 et mettre à 1 sont deux opérations inverses l'une de l'autre. Mettre à 1 revient à mettre à 0, puis à inverser le résultat. Et inversement, mettre à 0 revient à mettre à 1 avant d'inverser le tout. Il suffit donc de mettre le circuit d'inversion commandable à la fin du circuit, juste après un circuit de mise à 0 ou de mise à 1, au choix. En faisant comme cela, il ne reste que deux portes logiques, donc deux entrées. En choisissant bien les valeurs sur l'entrée de commande, on peut connecter les entrées de commande directement sur les opérandes des deux portes, sans passer par un circuit combinatoire.

Les opérations bit à bit à deux opérandes
modifierLes opérations bit à bit à deux opérandes effectuent un ET, un OU, ou un XOR entre deux opérandes. Ici, le ET/OU/XOR se fait entre deux bits de même poids dans une opérande. Les circuits qui effectuent ces opérations sont assez simples, ils sont composés de portes logiques placées les unes à côté des autres. Il n'y a pas de possibilité de combiner des portes comme c'était le cas dans la section précédente.

Les opérations de masquage
modifierIl est intéressant de donner quelques exemples d'utilisation des opérations bit à bit ET/OU/XOR. L'utilité des opérations bit est bit est en effet loin d'être évidente. L'exemple que nous allons prendre est celui des opérations de masquage, très connue des programmeurs bas niveau. Leur but est de modifier certains bits d'un opérande, mais de laisser certains intouchés. Les bits modifiés peuvent être forcés à 1, forcés à 0, ou inversés. Pour cela, on combine l'opérande avec un second opérande, qui est appelée le masque. Les bits à modifier sont indiqués par le masque : chaque bit du masque indique s'il faut modifier ou laisser intact le bit correspondant dans l'opérande.
Pour donner un exemple d'utilisation, parlons des droits d'accès à un fichier. Ceux-ci sont regroupés dans une suite de bits : un des bits indique s'il est accessible en écriture, un autre pour les accès en lecture, un autre s'il est exécutable, etc. Bref, modifier les droits en écriture de ce fichier demande de modifier le bit associé à 1 ou à 0, sans toucher aux autres. Cela peut se faire facilement en utilisant une instruction bit à bit avec un masque bien choisie.
Un autre cas typique est celui où un développeur compacte plusieurs données dans un seul entier. Par exemple, prenons le cas d'une date, exprimée sous la forme jour/mois/année. Un développeur normal stockera cette date dans trois entiers : un pour le jour, un pour le mois, et un pour la date. Mais un programmeur plus pointilleux sera capable d'utiliser un seul entier pour stocker le jour, le mois et l'année. Pour cela, il raisonnera comme suit :
- un mois comporte maximum 31 jours : on doit donc encoder tous les nombres compris entre 1 et 31, ce qui peut se faire en 5 bits ;
- une année comporte 12 mois, ce qui tient dans 4 bits ;
- et enfin, en supposant que l'on doive gérer les années depuis la naissance de Jésus jusqu'à l'année 2047, 11 bits peuvent suffire.
Dans ces conditions, notre développeur décidera d'utiliser un entier de 32 bits pour le stockage des dates :
- les 5 bits de poids forts serviront à stocker le jour ;
- les 4 bits suivants stockeront le mois ;
- et les bits qui restent stockeront l'année.
Le développeur qui souhaite modifier le jour ou le mois d'une date devra modifier une partie des bits, tout en laissant les autres intacts. Encore une fois, cela peut se faire facilement en utilisant une instruction bit à bit avec un masque bien choisi.
Le résultat d'une opération de masquage
modifierMaintenant, regardons ce que l'on peut faire avec une opération bit à bit entre un opérande et un masque. Le résultat dépend suivant que l'opération est un ET, un OU ou un XOR. Nous allons vous demander d'accepter les résultats sans les comprendre, vous allez comprendre comment cela fonctionne dans la section suivante.
Faire un ET entre l'opérande et le masque va mettre certains bits de l’opérande à 0 et va recopier les autres. Les bits mis à 0 sont ceux où le bit du masque correspondant est à 0, tandis que les autres sont recopiés tels quels.
La même chose a lieu avec l'opération OU, sauf que cette fois-ci, les bits de l'opérande sont soit recopiés, soit mis à 1. Les bits mis à 1 sont ceux pour lesquels le bit du masque correspondant est un 1.
Dans le cas d'un XOR, les bits sont inversés. Les bits inversés sont ceux pour lesquels le bit du masque correspondant est un 1.

Dans les chapitres précédents, nous avons vu comment fabriquer des circuits relativement généraux. Il est maintenant temps de voir quelques circuits relativement simples, très utilisés. Ces circuits simples sont utilisés pour construire des circuits plus complexes, comme des processeurs, des mémoires, et bien d'autres. Les prochains chapitres vont se concentrer exclusivement sur ces circuits simples, mais courants. Nous allons donner quelques exemples de circuits assez fréquents dans un ordinateur et voir comment construire ceux-ci avec des portes logiques.
Dans ce chapitre, nous allons nous concentrer sur quelques circuits, que j'ai décidé de regrouper sous le nom de circuits de sélection. Les circuits que nous allons présenter sont utilisés dans les mémoires, ainsi que dans certains circuits de calcul. Il est important de bien mémoriser ces circuits, ainsi que la procédure pour les concevoir : nous en aurons besoin dans la suite du cours. Ils sont au nombre de quatre : le décodeur, l'encodeur, le multiplexeur et le démultiplexeur.
Le décodeur
modifier
Le premier circuit que nous allons voir est le décodeur, un composant qui contient un grand nombre d'entrées et de sorties, avec des sorties qui sont numérotées. Un décodeur possède une entrée sur laquelle on envoie un nombre codé bits et sorties de 1 bit. Par exemple, un décodeur avec une entrée de 2 bits aura 4 sorties, un décodeur avec une entrée de 3 bits aura 8 sorties, un décodeur avec une entrée de 8 bits aura 256 sorties, etc. Généralement, on précise le nombre de bits d'entrée et de sortie comme suit : on parle d'un décodeur X vers Y pour X bits d'entrée et Y de sortie. Ce qui fait qu'on peut parler de décodeur 3 vers 8 pour un décodeur à 3 bits d'entrée et 8 de sortie, de décodeur 4 vers 16, etc.
Le fonctionnement d'un décodeur est très simple : il prend sur son entrée un nombre entier x codé en binaire, puis il positionne à 1 la sortie numérotée x et met à zéro toutes les autres sorties. Par exemple, si on envoie la valeur 6 sur ses entrées, il mettra la sortie numéro 6 à 1 et les autres à zéro.
Pour résumer, un décodeur est un circuit :
- avec une entrée de bits ;
- avec sorties de 1 bit ;
- où les sorties sont numérotées en partant de zéro ;
- où on ne peut sélectionner qu'une seule sortie à la fois : une seule sortie devra être placée à 1, et toutes les autres à zéro ;
- et où deux nombres d'entrée différents devront sélectionner des sorties différentes : la sortie de notre contrôleur qui sera mise à 1 sera différente pour deux nombres différents placés sur son entrée.
Une autre manière d'expliquer leur fonctionnement est qu'il traduisent un nombre encodé en binaire vers la représentation one-hot. Pour rappel, sur cette dernière, le nombre N est encodé en mettant le énième bit à 1, les autres sont à 0. Le bit de poids faible compte pour le zéro.
Les décodeurs sont très utilisés, au point que faire la liste de leurs utilisations serait bien trop long. Par contre, on peut d'or et déjà prévenir que les décodeurs sont utilisés dans toutes les mémoires RAM et ROM, présentes dans tout ordinateur. La RAM de votre ordinateur contient un ou plusieurs décodeurs, idem pour la mémoire caché intégrée dans le processeur, etc. C'est donc un circuit absolument primordial à étudier, qui reviendra souvent dans ce cours.
La table de vérité d'un décodeur
modifierAu vu de ce qui vient d'être dit, on peut facilement écrire la table de vérité d'un décodeur. Pour l'exemple, prenons un décodeur 2 vers 4, pour simplifier la table de vérité. Voici sa table de vérité complète, c’est-à-dire qui contient toutes les sorties regroupées :
| E0 | E1 | S0 | S1 | S2 | S3 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 |
Vous remarquerez que la table de vérité est assez spéciale. Les seuls bits à 1 sont sur la diagonale. Et cela ne vaut pas que dans l'exemple choisit, mais cela se généralise pour tous les décodeurs. Sur chaque ligne, il n'y a qu'un seul bit à 1, ce qui traduit le fait qu'une entrée ne met qu'une seule sortie est à 1 et met les autres à 0. Si on traduit la table de vérité sous la forme d'équations logiques et de circuit, on obtient ceci :

Il y a des choses intéressantes à remarquer sur les équations logiques. Pour rappel, l'équation logique d'une sortie est composée, dans le cas général, soit d'un minterm unique, soit d'un OU entre plusieurs minterms. Chaque minterm est l'équation d'un circuit qui compare l'entrée à un nombre bien précis et dépendant du minterm. Si on regarde bien, l'équation de chaque sortie correspond à un minterm et à rien d'autre, il n'y a pas de OU entre plusieurs minterms. Les minterms sont de plus différents pour chaque sortie et on ne trouve pas deux sorties avec le même minterm. Enfin, chaque minterm possible est présent : X bits d'entrée nous donnent 2^X entrées différentes possibles, donc 2^X minterms possibles. Et il se trouve que tous ces minterms possibles sont représentés dans un décodeur, ils ont tous leur sortie associée. C'est une autre manière de définir un décodeur : toutes ses sorties codent un minterm, deux sorties différentes ont des minterms différents et tous les minterms possibles sur n bits sont représentés.
Ces informations vont nous être utiles pour la suite. En effet, grâce à elles, nous allons en déduire une méthode générale pour fabriquer un décodeur, peu importe son nombre de bits d'entrée et de sortie. Mais elles permettent aussi de montrer que l'on peut créer n'importe quel circuit combinatoire quelconque à partir d'un décodeur et de quelques portes logiques. Dans ce qui suit, on suppose que le circuit combinatoire en question a une entrée de n bits et une seule sortie de 1 bit. Pour rappel, ce genre de circuit se conçoit en utilisant une table de vérité qu'on traduit en équations logiques, puis en circuits. Le circuit obtenu est alors soit un simple minterm, soit un OU entre plusieurs minterms. Or, le décodeur contient tous les minterms possibles pour une entrée de n bits, avec un minterm par sortie. Il suffit donc de prendre une porte OU et de la connecter aux minterms/sorties adéquats.

Fabriquer un circuit combinatoire avec un décodeur gaspille pas mal de portes logiques. En effet, le décodeur fournit tous les minterms possibles, alors que seule une minorité est réellement utilisée pour fabriquer le circuit combinatoire. Les minterms en trop correspondent à des paquets de portes NON et ET reliées entre elles, qui ne servent à rien. De plus, les minterms ne sont pas simplifiés. On ne peut pas utiliser les techniques vues dans les chapitres précédents pour simplifier les minterms et réduire le nombre de portes logiques utilisées. Le décodeur reste tel qu'il est, avec l'ensemble des minterms non-simplifiés. Mais la simplicité de conception du circuit reste un avantage dans certaines situations. Notamment, les circuits avec plusieurs bits de sortie sont faciles à fabriquer, notamment si les sorties partagent des minterms (si un minterm est présent dans l'équation de plusieurs sorties différentes, l'usage d'un décodeur permet de facilement factoriser celui-ci).
Ceci étant dit, passons à la conception d'un décodeur avec des portes logiques.
L'intérieur d'un décodeur
modifierOn vient de voir que chaque sortie d'un décodeur correspond à son propre minterm, et que tous les minterms possibles sont représentés. Rappelons que chaque minterm est associé à un circuit qui compare l'entrée à une constante X, X dépendant du minterm. En combinant ces deux informations, on devine qu'un décodeur est simplement composé de comparateurs avec une constante que de minterms/sorties. Par exemple, si je prends un décodeur 7 vers 128, cela veut dire qu'on peut envoyer en entrée un nombre codé entre 0 et 127 et que chaque nombre aura son propre minterm associé : il y aura un minterm qui vérifie si l'entrée vaut 0, un autre vérifie si elle vaut 1, un autre qui vérifie si elle vaut 2, ... , un minterm qui vérifie si l'entrée vaut 126, et enfin un minterm qui vérifie si l'entrée vaut 127.
Pour reformuler d'une manière bien plus simple, on peut voir les choses comme suit. Si l'entrée du décodeur vaut N, la sortie mise à 1 est la sortie N. Bref, déduire quand mettre à 1 la sortie N est facile : il suffit de comparer l'entrée avec N. Si l'adresse vaut N, on envoie un 1 sur la sortie, et on envoie un zéro sinon. Pour cela, j'ai donc besoin d'un comparateur pour chaque sortie, et le tour est joué. Précisons cependant que cette méthode gaspille beaucoup de circuits et qu'il y a une certaine redondance. En effet, les comparateurs ont souvent des portions de circuits qui sont identiques et ne diffèrent parfois que ce quelques portes logiques. En utilisant des comparateurs séparés, ces portions de circuits sont dupliquées, alors qu'il serait judicieux de partager.

Comme autre méthode, plus économe en circuits, on peut créer un décodeur en assemblant plusieurs décodeurs plus simples, nommés sous-décodeurs. Ces sous-décodeurs sont des décodeurs normaux, auxquels on a ajouté une entrée RAZ, qui permet de mettre à zéro toutes les sorties : si on met un 0 sur cette entrée, toutes les sorties passent à 0, alors que le décodeur fonctionne normalement sinon. Construire un décodeur demande suffisamment de sous-décodeurs pour combler toutes les sorties. Si on utilise des sous-décodeurs à n entrées, ceux-ci prendront en entrée les n bits de poids faible de l'entrée du décodeur que l'on souhaite construire (le décodeur final). Dans ces conditions, les n décodeurs auront une de leurs sorties à 1. Pour que le décodeur final se comporte comme il faut, il faut désactiver tous les sous-décodeurs, sauf un avec l'entrée RAZ. Pour commander les n bits RAZ des sous-décodeurs, il suffit d'utiliser un décodeur qui est commandé par les bits de poids fort du décodeur final.

Le démultiplexeur
modifierLes décodeurs ont des cousins : les multiplexeurs et les démultiplexeurs. Un démultiplexeur a plusieurs sorties et une seule entrée. Les sorties sont numérotées de 0 à la valeur maximale. Il permet de sélectionner une sortie et de recopier l'entrée dessus, les autres sorties sont mises à 0. Pour séléctionner la sortie, le démultiplexeur possède une entrée de commande, sur laquelle on envoie le numéro de la sortie de destination. Comme le nom l'indique, le démultiplexeur fait l'exact inverse du multiplexeur, que nous verrons plus bas.
Le démultiplexeur à deux sorties
modifierLe démultiplexeur le plus simple est le démultiplexeur à deux sorties. Il possède une entrée de donnée, une entrée de commande et deux sorties, toutes de 1 bit. Suivant la valeur du bit sur l'entrée de commande, il recopie le bit d'entrée, soit sur la première sortie, soit sur la seconde. Les deux sorties sont numérotées respectivement 0 et 1.

On peut le concevoir facilement en partant de sa table de vérité.
| Entrée de commande Select | Entrée de donnée Input | Sortie 1 | Sortie 0 | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 |
Le circuit obtenu est le suivant :

Les démultiplexeurs à plus de deux sorties
modifierIl est parfaitement possible de créer des démultiplexeurs en utilisant les méthodes du chapitre sur les circuits combinatoires, comme ma méthode des minterms ou les tableaux de Karnaugh. On obtient alors un démultiplexeur assez simple, composé de deux couches de portes logiques : une couche de portes NON et une couche de portes ET à plusieurs entrées.
Mais cette méthode n'est pas pratique, car elle utilise beaucoup de portes logiques et que les portes logiques avec beaucoup d'entrées sont difficiles à fabriquer. Pour contourner ces problèmes, on peut ruser. Ce qui a été fait pour les multiplexeurs peut aussi s'adapter aux démultiplexeurs : il est possible de créer des démultiplexeurs en assemblant des démultiplexeurs 1 vers 2. Évidemment, le même principe s'applique à des démultiplexeurs plus complexes : il suffit de rajouter des couches.

Un démultiplexeur peut aussi se fabriquer en utilisant un décodeur et quelques portes ET. Pour comprendre pourquoi, regardons la table de vérité d'un démultiplexeur à quatre sorties. Si vous éliminez le cas où l'entrée de donnée Input vaut 0, et que vous tenez compte uniquement des entrées de commande, vous retombez sur la table de vérité d'un décodeur. Cela correspond aux cases en rouge.
| Input | E0 | E1 | S0 | S1 | S2 | S3 | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
En réalité, Le fonctionnement d'un démultiplexeur peut se résumer comme suit : soit l'entrée Input est à 1 et il fonctionne comme un décodeur dont l'entrée est l'entrée de commande, soit l'entrée Input vaut 0 et sa sortie est mise à 0. On devine donc qu'il faut combiner un décodeur avec le circuit de mise à zéro vu dans le chapitre précédent. On devine rapidement que l'entrée Input commande la mise à zéro de la sortie, ce qui donne le circuit suivant :

La couche de portes ET en aval du décodeur peut être remplacée par une couche de portes à transmission, ce qui est plus simple. Chaque entrée est connectée à la sortie à travers une porte à transmission, la commande de chaque porte à transmission étant le fait du décodeur.
Le multiplexeur
modifierLes décodeurs ont des cousins : les multiplexeurs et les démultiplexeurs. Les multiplexeurs sont des composants qui possèdent un nombre variable d'entrées, mais une seule sortie. Un multiplexeur permet de sélectionner une entrée et de recopier son contenu sur sa sortie, les entrées non-sélectionnées étant ignorées. Sélectionner l'entrée à recopier sur la sortie se fait en configurant une entrée de commande du multiplexeur. Les entrées sont numérotées de 0 à la valeur maximale. Configurer l'entrée de commande demande juste d'envoyer le numéro de l'entrée sélectionnée dessus.

Les multiplexeurs sont très utilisés et on en retrouve partout : dans les mémoires RAM, dans les processeurs, dans les circuits de calcul, dans les circuits pour communiquer avec les périphériques, et j'en passe. Il s'agit d'un composant très utilisé, qu'il est primordial de bien comprendre avant de passer à la suite du cours.
Le multiplexeur à deux entrées
modifierLe multiplexeur le plus simple est le multiplexeur à deux entrées et une sortie. Il est facile de le construire avec des portes logiques, dans les implémentations les plus simples. Sachez toutefois que les multiplexeurs utilisés dans les ordinateurs récents ne sont pas forcément fabriqués avec des portes logiques, mais qu'on peut aussi les fabriquer directement avec des transistors.

Pour commencer, établissons sa table de vérité. On va supposer qu'un 0 sur l'entrée de commande sélectionne l'entrée a. La table de vérité devrait être la suivante :
| Entrée de commande | Entrée a | Entrée b | Sortie |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Sélectionnons les lignes qui mettent la sortie à 1 :
| Entrée de commande | Entrée a | Entrée b | Sortie |
|---|---|---|---|
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
On sait maintenant quels comparateurs avec une constante utiliser. On peut, écrire l'équation logique du circuit. La première ligne donne l'équation suivante : , la seconde donne l'équation , la troisième l'équation et la quatrième l'équation . L'équation finale obtenue est donc :
L'équation précédente est assez compliquée, mais il y a moyen de la simplifier assez radicalement. Pour cela, nous allons utiliser les règles de l’algèbre de Boole. Pour commencer, nous allons factoriser et :
Ensuite, factorisons dans le premier terme et dans le second :
Les termes et valent 1 :
On sait que , ce qui fait que l'équation simplifiée est la suivante :
Le circuit qui correspond est :

Il est aussi possible de fabriquer un multiplexeur 2 vers 1 en utilisant des portes à transmission. L'idée est de relier chaque entrée à la sortie par l'intermédiaire d'une porte à transmission. Quand l'une sera ouverte, l'autre sera fermée. Le résultat n'utilise que deux portes à transmission et une porte NON. Voici le circuit qui en découle :

Les multiplexeurs à plus de deux entrées
modifierIl est possible de concevoir un multiplexeur quelconque à partir de sa table de vérité. Le résultat est alors un circuit composé d'une porte OU à plusieurs entrées, de plusieurs portes ET, et de quelques portes NON. Un exemple est illustré ci-dessous. Vous remarquerez cependant que ce circuit a un défaut : la porte OU finale a beaucoup d'entrées, ce qui pose de nombreux problèmes techniques. Il est difficile de concevoir des portes logiques avec un très grand nombre d'entrées. Aussi, les applications à haute performance demandent d'utiliser d'autres solutions.

Une solution alternative est de concevoir un multiplexeur à plus de deux entrées en combinant des multiplexeurs plus simples. Par exemple, en prenant deux multiplexeurs plus simples, et en ajoutant un multiplexeur 2 vers 1 sur leurs sorties respectives. Le multiplexeur final se contente de sélectionner une sortie parmi les deux sorties des multiplexeurs précédents, qui ont déjà effectué une sorte de présélection.

Il existe toutefois une manière bien plus simple pour créer des multiplexeurs : il suffit d'utiliser un décodeur, quelques portes OU, et quelques portes ET. L'idée est de :
- sélectionner l'entrée à recopier sur la sortie ;
- mettre les autres entrées à zéro ;
- faire un OU entre toutes les entrées : vu que toutes les entrées non-sélectionnées sont à zéro, la sortie de la porte OU aura la même valeur que l'entrée sélectionnée.
Pour sélectionner l'entrée adéquate du multiplexeur, on utilise un décodeur : si la sortie n du décodeur est à 1, alors l'entrée numéro n du multiplexeur sera recopiée sur sa sortie. Dans ces conditions, l'entrée de commande du multiplexeur correspond à l'entrée du décodeur. Pour mettre à zéro les entrées non-sélectionnées, on adapte le circuit de mise à zéro précédent, basé sur une couche de portes ET, sauf que chaque porte ET est connectée à sa propre entrée. En fait, les entrées forment un nombre, tous les bits sauf un doivent être mis à 0. Pour cela, on applique un masque calculé par le décodeur.


Il est possible de remplacer les portes ET par des interrupteurs, comme on l'a fait pour le démultiplexeur. Les interrupteurs peuvent être des portes à transmission, ou des tampons trois-états. Les deux circuits en question sont une amélioration de la porte OUI. Suivant ce qu'on met sur leur entrée de commande, soit ils se comportent comme une porte OUI normale, soit ils déconnectent l'entrée de la sortie. Ils fonctionnent donc comme des interrupteurs, en un peu améliorés.
Remplacer les portes ET par des portes à transmission permet de se passer de la porte OU, qui est remplacée par un simple fil. Il n'y a qu'une seule entrée qui est connectée à la sortie à chaque instant, pas besoin d'utiliser de porte OU. Le résultat est le circuit suivant :

L'encodeur
modifier
Il existe un circuit qui fait exactement l'inverse du décodeur : c'est l'encodeur. Là où les décodeurs ont une entrée de bits et sorties de 1 bit, l'encodeur a à l'inverse entrées de 1 bit avec une sortie de bits. Par exemple, un encodeur avec une entrée de 4 bits aura 2 sorties, un décodeur avec une entrée de 8 bits aura 3 sorties, un décodeur avec une entrée de 256 bits aura 8 sorties, etc. Comme pour les décodeurs, on parle d'un encodeur X vers Y pour X bits d'entrée et Y de sortie. Ce qui fait qu'on peut parler de décodeur 8 vers 3 pour un décodeur à 8 bits d'entrée et 3 de sortie, de décodeur 16 vers 4, etc.

De plus, contrairement au décodeur, ce sont les entrées qui sont numérotées de 0 à N et non les sorties. Dans ce qui suit, on va supposer qu'une seule des entrées est à 1. Il existe des encodeurs capables de traiter le cas où plusieurs bits d'entrée sont à 1, qui sont appelés des encodeurs à priorité, mais nous les laissons pour le chapitre suivant. Le chapitre suivant sera totalement dédié aux encodeurs à priorité, aussi nous préférons nous focaliser sur le cas d'un encodeur simple, capable de traiter uniquement le cas où une seule entrée est à 1. En sortie, l'encodeur donne le numéro de l'entrée qui est à 1. Par exemple, si l'entrée numéro 5 est à 1 et les autres à 0, alors l'encodeur envoie un 5 sur sa sortie.
Une autre manière d'expliquer son fonctionnement est la suivant : un encodeur traduit un nombre codé en représentation one-hot vers du binaire normal.
L'utilité d'un encodeur n'est pas très évidente à ce moment du cours, mais nous pouvons déjà dire qu'ils seront utiles dans certaines formes de mémoires RAM appelées des mémoires associatives, qui sont utilisées dans des routeurs, switchs et autre matériel réseau. La majorité des mémoires caches de nos ordinateurs sont de ce type, bien que leur implémentation exacte ne fasse pas usage d'un encodeur. Une autre utilisation est la transformation d'un nombre codé en représentation one-hot vers du binaire normal, chose marginalement utile.
L'encodeur 4 vers 2
modifierPrenons l'exemple d'un encodeur à 4 entrées et 2 sorties. Écrivons sa table de vérité. D'après la description du circuit, on devrait trouver ceci :
| E3 | E2 | E1 | E0 | S1 | S0 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 1 |
Vous voyez que la table de vérité est incomplète. En effet, l'encodeur fonctionne tant qu'une seule de ses entrées est à 1. L'encodeur dit alors quelle est la sortie à 1, mais cela suppose que les autres soient à 0. Si plusieurs entrées sont à 1, le comportement de l'encodeur est potentiellement erroné. En effet, il donnera un résultat incorrect sur certaines entrées. Mais passons cela sous silence et ne tenons compte que de la table de vérité partielle précédente. On peut traduire cette table de vérité en circuit logique. On obtient alors les équations suivantes :
Le tout donne le circuit suivant :

Les encodeurs à plus de deux sorties
modifierIl est possible de créer un encodeur complexe en combinant plusieurs encodeurs simples. C'est un peu la même chose qu'avec les décodeurs, pour lesquels on peut créer un décodeur 8 vers 256 à base de deux décodeurs 7 vers 128, ou de quatre décodeurs 6 vers 64. L'idée de découper le nombre d'entrée en morceaux séparés, chaque morceau étant traité par un encodeur à priorité distinct des autres. Les résultats des différents encodeurs sont ensuite combinés pour donner le résultat final.
Pour comprendre l'idée, prenons la table de vérité d'un encodeur 8 vers 3; donnée dans le tableau ci-dessous.
| E7 | E6 | E5 | E4 | E3 | E2 | E1 | E0 | S2 | S1 | S0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
En regardant bien, vous verrez que vous pouvez trouver la table de vérité d'un encodeur 4 vers 2 en deux exemplaires, indiquées en rouge.
| E7 | E6 | E5 | E4 | E3 | E2 | E1 | E0 | S2 | S1 | S0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
On voit que les deux bits de poids faibles correspondent à la sortie de l'encodeur activé par l'entrée. Si le premier encodeur est activé, c'est lui qui fournit les bits de poids faibles. Inversement, si c'est le second encodeur qui a un résultat non-nul, c'est lui qui fournit les bits de poids faible. Notons que seul un des deux encodeurs a une sortie non-nulle à la fois : soit le premier a une sortie non-nulle, soit c'est le second, mais c'est impossible que ce soit les deux en même temps. Cela permet de déduire quelle opération permet de mixer les deux résultats : un simple OU logique suffit. Car, pour rappel, 0 OU X donne X, quelque que soit le X en question. Les bits de poids faible du résultat se calculent en faisant un OU entre les deux résultats des encodeurs.
Ensuite, il faut déterminer comment fixer le bit de poids fort du résultat. Il vaut 0 si le premier encodeur a une entrée non-nulle, et 1 si c'est le premier encodeur qui a une entrée non-nulle. Pour cela, il suffit de vérifier si les bits de poids forts, associés au premier encodeur, contiennent un 1. Si c'est le cas, alors on met la troisième sortie à 1.

Notons que cette procédure, à savoir faire un OU entre les sorties de deux encodeurs simples, puis faire un OU pour calculer le troisième bit, marche pour tout encodeur de taille quelconque. À vrai dire, le circuit obtenu plus haut d'un encodeur 4 vers 2 est conçu ainsi, mais en combinant deux encodeurs 2 vers 1.
La procédure consiste à ajouter trois portes OU à deux encodeurs. Mais ceux-ci sont eux-même composés de portes OU associées à des encodeurs plus petits, et ainsi de suite. On peut poursuivre ainsi jusqu’à tomber sur des encodeurs 4 vers 2, qui sont eux-mêmes composés de deux portes OU. Au final, on se retrouve avec un circuit conçu uniquement à partir de portes OU. Notons qu'il est possible de simplifier le circuit obtenu avec la procédure en fusionnant des portes OU. Si on simplifie vraiment au maximum, le circuit consiste alors en une porte OU à plusieurs entrées par sortie, chacune étant connectée à certaines entrées bien précises. Pour un encodeur 8 vers 3, la simplification du circuit devrait donner ceci :

L'encodeur à priorité
modifierL'encodeur à priorité est un dérivé du circuit encodeur, vu dans la section précédente. La différence ne se situe pas dans le nombre d'entrée ou de sortie, ni même dans son interface extérieure. Comme pour l'encodeur normal, l'encodeur à priorité possède entrées numérotées de 0 à et N sorties. Une autre manière plus intuitive de le dire est qu'il possède N entrées et sorties. Pas de changement de ce point de vue. La différence entre encodeur simple et encodeur à priorité tient dans leur fonctionnement, dans le calcul qu'ils font. Avec un encodeur normal, on a supposé que seul un bit d'entrée pouvait être à 1, les autres étant systématiquement à 0. Si cette condition est naturellement remplie dans certains cas d’utilisation, ce n'est pas le cas dans d'autres. L'encodeur à priorité est un encodeur amélioré dans le sens où il donne un résultat valide même quand plusieurs bits d'entrée sont à 1. Il donne donc un résultat pour n'importe quel nombre passé en entrée.
Mais avant de passer aux explications, un peu de terminologie utile. Dans ce qui suit, nous aurons à utiliser des expressions du type "le 1 de poids faible", "le 1 de poids fort" et quelques autres du même genre. Quand nous parlerons du 1 de poids faible, nous voudrons parler du premier 1 que l'on croise dans un nombre en partant de sa droite. Par exemple, dans le nombre 0110 1000, le 1 de poids faible est le quatrième bit. Quant au "1 de poids fort", c'est le premier 1 que l'on croise quand on parcourt le nombre à partir de sa gauche. Dans le cas le plus fréquent, l'encodeur à priorité prend en entrée un nombre et donne la position du 1 de poids fort. Mais dans d'autres cas, l'encodeur à priorité donne la position du 1 de poids faible. Il existe des équivalents, mais qui trouvent cette fois-ci les zéros de poids fort/faible, mais nous n'en parlerons pas dans ce chapitre.
L'encodeur à priorité conçu à partir de sa table de vérité
modifierIl est possible de concevoir l'encodeur à priorité à partir de sa table de vérité, mais les méthodes des minterms ou des maxterms ne donnent pas de très bons résultats.
Notons que ces encodeurs ont souvent une nouvelle entrée notée V, qui indique si la sortie est valide, et qui indique qu'au moins une entrée est à 1. Elle vaut 1 si au moins une entrée est à 1, 0 si toutes les entrées sont à 0.
À titre d'exemple, la table de vérité d'un encodeur à priorité 4 vers 2 est illustré ci-dessous. Le signe X signifie que le bit peut prendre la valeur 0 ou 1 sans que cela change quoique ce soit à l'entrée.
| E3 | E2 | E1 | E0 | S1 | S0 | V | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 1 | X | 0 | 1 | 1 | |
| 0 | 1 | X | X | 1 | 0 | 1 | |
| 1 | X | X | X | 1 | 1 | 1 |
Les équations logiques obtenues sont donc les suivantes :
On voit quelle est la logique de chaque équation. Pour chaque ligne de la table de vérité, il faut vérifier si les bits de poids fort sont à 0, suivi par un 1, les bits de poids faible après le 1 étant oubliées. Pour le bit de validité, il suffit de faire un OU entre toutes les entrées. Les deux dernières équations se simplifient en :
- ,
Le circuit obtenu est le suivant :

La table de vérité d'un encodeur à priorité 8 vers 3 est illustré ci-dessous. Le signe X signifie que le bit peut prendre la valeur 0 ou 1 sans que cela change quoique ce soit à l'entrée.

Utiliser la table de vérité a des défauts. Premièrement, ce n'est pas la meilleure des solutions pour des circuits avec un grand nombre d'entrée. Faire cela donne des tables de vérité rapidement importantes, mêmes pour des encodeurs avec peu de sorties. Le circuit final utilise beaucoup de portes logiques comparé aux autres méthodes. Les solutions alternatives que nous allons voir dans ce qui suit permettent de résoudre ces deux problèmes en même temps.
Les encodeurs à priorité récursifs
modifierUne première solution consiste à créer un gros encodeur à base d'encodeurs plus petits.L'idée de découper le nombre d'entrée en morceaux séparés, chaque morceau étant traité par un encodeur à priorité distinct des autres. Les résultats des différents encodeurs sont ensuite combinés pour donner le résultat final. Naturellement, il est préférable d'utiliser plusieurs exemplaires d'un même encodeur, c'est à dire que pour une entrée de 256 bits, il vaut mieux utiliser soit deux décodeurs 7 vers 128, soit quatre décodeurs 6 vers 64, etc. La construction est similaire à celle vue dans le chapitre précédent, dans la section sur les encodeurs. La différence est que le OU entre les sorties des encodeurs est remplacé par un multiplexeur. Une version générale est illustrée ci-dessous. On voit que les encodeurs ont une sortie de résultat de X bits notée idx et une sortie de validité notée vld.
La sortie de validité finale se calcule en combinant les sorties de validité de chaque encodeur. La sortie est par définition à 1 tant qu'un seul encodeur a une sortie non-nulle, donc quand un seul encodeur a un bit de validité à 1. En clair, c'est un simple OU entre les bits de validité. Reste à déterminer la sortie de donnée, celle qui donne la position du 1 de poids fort. On peut dire que si l'on utilise des encodeurs avec N bits de sortie, alors les N bits de poids faible du résultat seront donnés par le premier encodeur avec une sortie non-nulle. Les résultats de chaque encodeur donnent doncles X bits de poids faible, un seul résultat devant être sélectionné. Le résultat à sélectionner est le premier à avoir un résultat non-nul, donc à avoir un bit de validité à 1. En clair, on peut déterminer quel est le bon encodeur, le bon résultat, en analysant les bits de validité. Mieux : d'après ce qui a été dit, on peut deviner que l'analyse réalisée correspond à trouver la position du premier encodeur à avoir un bit de validité à 1. En clair, c'est l'opération réalisée par un encodeur à priorité lui-même.
Tout cela permet de déterminer les N bits de poids faible, amis les autres bits, ceux de poids fort, sont encore à déterminer. Pour cela, on peut remarquer que ceux-ci sont eux-même fournit par l'encodeur à priorité qui commande le MUX.

Notons qu'avec cette méthode, il est possible, mais pas très intuitif, de fabriquer un encodeur configurable, capable de se comporter soit comme un encodeur de type Find Highest Set, soit de type Find First Set. L'implémentation la plus simple demande de modifier le circuit qui combine les résultats pour qu'il soit configurable et puisse faire les deux opérations à la demande.
L'encodeur à priorité avec un circuit d'isolation du 1 de poids fort/faible
modifierUne autre solution part d'un encodeur normal, auquel on ajoute un circuit qui se charge de sélectionner un seul des bits passé sur son entrée. Le circuit de gestion des priorités a pour fonction de trouver sélectionner un bit et de mettre les autres 1 à 0. Suivant le circuit de priorité considéré, le bit sélectionné est soit le 1 de poids fort, soit le 1 de poids faible. Dans certains cas, le circuit de priorité est configurable et peut trouver l'un ou l'autre suivant ce qu'on lui demande. Dans ce qui va suivre, nous allons partir du principe que l'on souhaite avoir un encodeur qui trouve le 1 de poids fort, sauf indication contraire.

Une méthode assez pratique découpe le circuit de gestion des priorité en petites briques de bases, reliées les unes à la suite des autres. L'idée est que les briques de base sont connectées de manière à propager un signal de mise à zéro. Si une brique détecte un 1, elle envoie un signal aux briques précédentes/suivantes, qui leur dit de mettre leur sortie à zéro. Ce faisant, une fois le premier 1 trouvé, on est certain que les autres bits précédents/suivants sont mis à zéro. Suivant les connexions des briques de base, on peut obtenir soit un encodeur qui effectue l'opération Find First Set, soit encodeur de type Find Highest Set et réciproquement. En fait, suivant que les briques soient reliées de droite à gauche ou de gauche à droite, on obtiendra l'un ou l'autre de ces deux encodeurs.

Chaque brique de base peut soit recopier le bit en entrée, soit le mettre à zéro. Pour décider quoi faire, elle regarde le signal d'entrée RAZ (Remise A Zéro). Si le bit RAZ vaut 1, la sortie est mise à zéro automatiquement. Dans le cas contraire, le bit passé en entrée est recopié. De plus, chaque brique de base doit fournir un signal de remise à zéro RAZ à destination de la brique suivante. Ce signal RAZ de sortie est mis à 1 dans deux cas : soit si le bit d'entrée vaut, soit quand le signal d'entrée RAZ est à 1. Si vous cherchez à la concevoir à partir d'un table de vérité, vous obtiendrez ceci :
 |
 |
Le circuit complet d'un encodeur à priorité peut être déduit facilement à partir des raisonnements précédents. Après quelques simplifications, on peut obtenir le circuit suivant. On voit qu'on a ajouté une ligne de briques RAZ à l'encodeur 8 vers 3 vu plus haut.

Le défaut de cette méthode est que le circuit de gestion des priorité est assez lent. Dans le pire des cas, le signal de remise à zéro traverse toutes les briques de base, soit autant qu'il y a de bits d'entrée. Si chaque brique de base met un certain temps, le temps mis pour que le circuit de priorité fasse son travail est proportionnel au nombre de bits de l'entrée. Cela n'a l'air de rien, mais cela peut prendre un temps rédhibitoire pour les circuits de haute performance, destinés à fonctionner à haute fréquence. Pour ces circuits, on préfère que le temps de calcul soit proportionnel au logarithme du nombre de bits d'entrée, un temps proportionnel étant considéré comme trop lent, surtout pour des opérations simples comme celles étudiées ici.
Une version légèrement différente de ce circuit est utilisée dans le processeur ARM1, un des tout premiers processeur ARM. L'encodeur à priorité était bidirectionnel, à savoir capable de déterminer soit la place du 1 de poids faible, soit du 1 de poids fort. Pour ceux qui veulent en savoir plus, et qui ont déjà un bagage solide en architecture des ordinateurs, voici un lien à ce sujet :
Dans ce chapitre et les suivants, nous allons voir comment implémenter sous forme de circuits certaines opérations extrêmement courantes dans un ordinateur. Les quelques circuits que nous allons voir seront réutilisés massivement dans les chapitres qui suivront, aussi nous allons passer quelque temps sur ces bases. Pour simplifier, les opérations réalisées par un ordinateur se classent en trois types :
- Les opérations arithmétiques, à savoir les additions, multiplications et autres, qui auront chacune leur propre chapitre.
- Les décalages et rotations, où on décale tous les bits d'un nombre d'un ou plusieurs crans vers la gauche/droite, qui feront l'objet d'un futur chapitre.
- Les opérations logiques qui font l'objet de ce chapitre.
Les portes logiques universelles commandables
modifierIl y a quelques chapitres, nous avions parlé des opérations bit à bit et vu quelques circuits capables d'effectuer ces opérations. Ici, nous allons revenir sur ces circuits, mais allons en proposer une implémentation plus complexe et plus efficiente. Nous allons profiter du fait que l'on ne soit plus limités à quelques portes logiques, mais que nous pouvons maintenant utiliser des multiplexeurs, des démultiplexeurs et d'autres circuits pour améliorer les circuits de calcul bit à bit.
Dans cette section, nous allons voir comment créer un circuit capable d'effectuer plusieurs opérations logiques, le choix de l'opération étant le fait d'une entrée de commande. Par exemple, imaginons un circuit capable de faire à la fois un ET, un OU, un XOR et un NXOR. Le circuit contiendra une entrée de commande de 2 bits, et la valeur sur cette entrée permet de sélectionner quelle opération faire : 00 pour un ET, 01 pour un OU, 11 pour un XOR, 01 pour le NXOR Nous allons créer un tel circuit, sauf qu'il est capable de faire toutes les opérations entre deux bits et regroupe donc les 16 portes logiques existantes. Nous allons aussi voir la même chose, mais pour les portes logiques de 1 bit.
Les circuits de calcul bit à bit, le retour !
modifierSachez qu'avec un simple multiplexeur, on peut créer un circuit qui effectue toutes les opérations bit à bit possible avec deux bits. Et cela a déjà été utilisé sur de vrais ordinateurs. Pour deux bits, divers théorèmes de l’algèbre de Boole nous disent que ces opérations sont au nombre de 16, ce qui inclus les traditionnels ET, OU, XOR, NAND, NOR et NXOR. Voici la liste complète de ces opérations, avec leur table de vérité ci-dessous (le nom des opérations n'est pas indiqué) :
- Les opérateurs nommés 0 et 1, qui renvoient systématiquement 0 ou 1 quel que soit l'entrée ;
- L'opérateur OUI qui recopie l'entrée a ou b, et l'opérateur NON qui l'inverse : , , , ;
- L’opérateur ET, avec éventuellement une négation des opérandes : , , , ;
- La même chose avec l’opérateur OU : , , , ;
- Et enfin les opérateurs XOR et NXOR : , .
| a | b | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | - | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | - | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | - | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Le circuit à concevoir prend deux bits, que nous noterons a et b, et fournit sur sa sortie : soit a ET b, soit a OU b, soit a XOR b, etc. Pour sélectionner l'opération, une entrée du circuit indique quelle est l'opération à effectuer, chaque opération étant codée par un nombre. On pourrait penser que concevoir ce circuit serait assez complexe, mais il n'en est rien grâce à une astuce particulièrement intelligente. Regardez le tableau ci-dessus : vous voyez que chaque colonne forme une suite de bits, qui peut être interprétée comme un nombre. Il suffit d'attribuer ce nombre à l'opération de la colonne ! En faisant ainsi, le nombre attribué à chaque opération contient tous les résultats de celle-ci. Il suffit de sélectionner le bon bit parmi ce nombre pour obtenir le résultat. Et on peut faire cela avec un simple multiplexeur, comme indiqué dans le schéma ci-dessous !

Il faut noter que le raisonnement peut se généraliser avec 3, 4, 5 bits, voire plus ! Par exemple, il est possible d'implémenter toutes les opérations bit à bit possibles entre trois bits en utilisant un multiplexeur 8 vers 3.
Les unités de calcul logique
modifierMaintenant que nous sommes armés des portes logiques universelles, nous pouvons implémenter un circuit généraliste, qui peut effectuer la même opération logique sur tous les bits. Ce circuit est appelé une unité de calcul logique. Elle prend en entrée deux opérandes, ainsi qu'une entrée de commande sur laquelle on précise quelle opération il faut faire.
Elle est simplement composée d'autant de portes universelles 2 bits qu'il n'y a de bits dans les deux opérandes. Par exemple, si on veut un circuit qui manipule des opérandes 8 bits, il faut prendre 8 portes universelles deux bits. Toutes les entrées de commande des portes sont reliées à la même entrée de commande.

Les opérations FFS, FFZ, CTO et CLO
modifierDans cette section, nous allons aborder plusieurs opérations fortement liées entre elles, illustrées dans le schéma ci-dessous. Elles sont très courantes sur la plupart des ordinateurs, surtout dans les ordinateurs embarqués. Beaucoup d'ordinateurs, comme les anciens mac avec des processeurs type Power PC et les processeurs MIPS ou RISC ont des instructions pour effectuer ces opérations.
Mais avant de passer aux explications, un peu de terminologie utile. Dans ce qui suit, nous aurons à utiliser des expressions du type "le 1 de poids faible", "les 0 de poids faible" et quelques autres du même genre. Quand nous parlerons du 0 de poids faible, nous voudrons parler du premier 0 que l'on croise dans un nombre en partant de sa droite. Par exemple, dans le nombre 0011 1011, le 0 de poids faible est le troisième bit en partant de la droite. Quand nous parlerons du 1 de poids faible, c'est la même chose, mais pour le premier bit à 1. Par exemple, dans le nombre 0110 1000, le 1 de poids faible est le quatrième bit. Quant aux expressions "le 1 de poids fort" et "les 0 de poids fort" elles sont identiques aux précédentes, sauf qu'on parcourt le nombre à partir de sa gauche.
Par contre, les expressions "LES 1 de poids faible" ou "LES 0 de poids faible" ne parlent pas de la même chose. Quand nous voudrons parler des 1 de poids faible, au pluriel, nous voulons dire : tous les bits situés avant le 0 de poids faible. Par exemple, prenons le nombre 0011 0011 : les 1 de poids faible correspondent ici aux deux premiers bits en partant de la droite. Même chose quand on parle des zéros de poids faible au pluriel. Quant aux expressions "les 1 de poids fort" ou "les 0 de poids fort" elles sont identiques aux précédentes, sauf qu'on parcourt le nombre à partir de sa gauche.
Les opérations bit à bit complexes
modifierLa première opération que nous allons aborder, Find First Set, donne la position du 1 de poids faible. Cette opération est liée à l'opération Count Trailing Zeros, qui donne le nombre de zéros situés à droite de ce 1 de poids faible. L'opération Find First Set est opposée au calcul du Find highest set, qui donne la position du 1 de poids fort. Le nombre de zéros situés à gauche de ce bit à 1 est appelé le Count Leading Zeros.
Ces quatre opérations ont leur équivalents en remplaçant les 0 par des 1 et réciproquement. Par exemple, l'opération Find First Zero donne la position du 0 de poids faible (le plus à droite) et l'opération Find Highest Zero donne la position du 0 de poids fort (le plus à gauche). L'opération Count Trailing Ones donnent le nombre de 1 situés à gauche du 0 de poids fort, tandis que l'opération Count Leading Ones donne le nombre de 1 situés à droite du 0 de poids faible.

La numérotation des bits et l'équivalence de certaines opérations
modifierDans toutes ces opérations, les bits sont numérotés, leur numéro étant appelé leur position ou leur indice. La position d'un bit est donc donnée par ce numéro. Ces opérations varient selon la méthode utilisée pour numéroter les bits. On peut commencer à compter les bits à partir de 0, le 0 étant le numéro du bit de poids faible. Mais on peut aussi compter à partir de 1, le bit de poids faible étant celui de numéro 1. Ces deux conventions ne sont pas équivalentes. Si on choisit la première convention, certaines opérations sont équivalentes. Par exemple, les opérations Count Trailing Zeros et Find First Set donnent toutes les deux le même résultat. Avec l'autre convention, les deux différent de 1 systématiquement.
Avec la première convention, pour un nombre codé sur bits, on a :
On voit que certaines opérations sont équivalentes, ce qui nous arrange bien. De plus, on peut calculer le résultat de l'opération FHS à partir de l'opération CLZ et réciproquement. De même le résultat de FHZ peut se calculer à partir du résultat de CLO et inversement. Il suffit d'effectuer une simple soustraction, avec une constante qui plus est, ce qui est simple à fabriquer. Ce qui revient à ajouter un circuit pour faire le calcul .
De fait, nous n'aurons qu'à aborder quatre calculs :
- le Find First Set, abréviée FFS ;
- le Find highest set, abrévié FHS ;
- le Find First Zero, abréviée FFZ ;
- le Find highest Zero, abrévié FHZ.
On peut même aller plus loin et éliminer encore plus le nombre d'opérations différentes à effectuer. En effet, les opérations FHS et FHZ peuvent se déduire l'une de l'autre, en changeant le nombre passé en entrée. Pour cela, il suffit d'inverser les bits de l'entrée, avec un inverseur commandable. Avec l'inversion, le 1 de poids fort deviendra le 0 de poids fort et inversement. Idem pour les opérations FFS et FFZ. En inversant l'entrée, le 1 de poids faible deviendra le 0 de poids faible et inversement.

L'encodeur à priorité
modifierReste à voir comment effectuer les deux opérations restantes, à savoir Find Highest Set et Find First Set. Et pour cela, nous devons utiliser un encodeur à priorité. Dans le cas le plus fréquent, l'encodeur à priorité prend en entrée un nombre et donne la position du 1 de poids fort. Ces encodeurs à priorité réalisent l'opération Find Highest Set, qui est reliée à l’opération count leading zeros. Ce qui leur vaut le nom anglais de leading zero detector (LZD) ou encore de leading zero counter (LZC). Mais dans d'autres cas, l'encodeur à priorité donne la position du 1 de poids faible, ce qui correspond à l'opération Count Trailing Zeros. Il existe aussi des encodeurs qui donnent la position du zéro de poids faible, voire du zéro de poids fort, ce qui correspond respectivement aux opérations Find First Zero et Find highest Zero. En clair, pour les quatre opérations précédentes, il existe un encodeur à priorité qui s'en charge.
Les circuits générateurs/vérificateurs d'ECC
modifierAu tout début de ce cours, nous avions vu les codes ECC, qui détectent ou corrigent des corruptions de données. Si un bit est altéré, ils permettent de détecter que le bit en question a été inversé, et peuvent éventuellement le corriger pour retrouver la donnée initiale. Les deux codes ECC les plus connus sont le bit de parité et les codes de Hamming. Dans ce qui suit, nous allons voir des circuits qui calculent soit un bit de parité, soit le code de Hamming d'un nombre.
Le générateur de parité
modifierPour rappel, le bit de parité est une technique qui permet de détecter si une donnée a été corrompue. Elle permet de détecter qu'un bit a été inversé, à savoir qu'un bit censé être à 1 est passé à 0 ou inversement. Pour cela, on ajoute un bit de parité aux données à sécuriser, afin que le nombre de bits à 1 soit pair, bit de parité inclu. En clair, si la donnée a un nombre de bit à 1 pair, alors le bit de parité vaut 0. Mais si le nombre est impair, alors le bit de parité vaut 1. Dans cette section, nous allons voir un circuit qui calcule le bit de parité d'une opérande.
Intuitivement, on se dit qu'il faut compter les 1 dans l'opérande, avant de calculer sa parité et d'en déduire le bit de parité. Compter les 1 dans un nombre est une opération tellement courante qu'elle porte un nom : on l'appelle la population count, ou encore poids de Hamming. Malheureusement, son calcul demande de faire des additions, ce qui fait qu'on le verra dans quelques chapitres. Mais heureusement, il existe une autre méthode bien plus simple, plus rapide, et plus économe en circuits.
Pour comprendre comment, nous allons commencer avec un cas simple : le calcul à partir d'une opérande de 2 bits. Le circuit étant simple, il suffit d'utiliser les techniques vues précédemment, avec la table de vérité. En écrivant la table de vérité du circuit, on remarque rapidement que la table de vérité donne la table de vérité d'une porte XOR.
| Bit 1 | Bit 2 | Bit de parité |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Pour la suite, nous allons partir d'un nombre de trois bits. On pourrait tenter de créer ce circuit à partir d'une table de vérité, mais nous allons utiliser une autre méthode, qui nous donnera un indice important. Ce nombre de 3 bits est composé d'un nombre de 2 bits auquel on a jouté un troisième bit. L'ajout de ce troisième bit modifie naturellement le bit de parité du nombre précédent. Dans ce qui va suivre, nous allons créer un circuit qui calcule le bit de parité final, à partir : du bit de parité du nombre de 2 bits, et du bit ajouté. On voit alors que la table de vérité est celle d'une porte XOR.
| Bit de parité précédent | Bit ajouté | Bit de parité final |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Chose assez intéressante, ce mécanisme fonctionne quel que soit le nombre de bits de l'opérande. Ajouter un bit à un nombre modifie sa parité, celle-ci état alors égale à : bit ajouté XOR bit-parité du nombre. L’explication est relativement simple : ajouter n 0 ne modifie pas le nombre de 1, et donc le bit de parité, tandis qu'ajouter un 1 inverse le bit de parité.
Avec cette logique, on peut créer un générateur de parité parallèle., un circuit qui calcule le bit de parité d'une opérande, en faisant un XOR entre tous ses bits. Effectué naïvement, il suffit d’enchaîner des portes XOR les unes à la suite des autres. En réfléchissant, on devien qu'on peut structurer les portes XOR comme ceci :

Le circuit précédent calcule le bit de parité d'une opérande. Pour ce qui est de vérifier si une donnée est corrompue, rien de plus simple : il suffit de générer le bit de parité de la donnée seule, et de le comparer avec le bit de parité stocké dans la donnée avec la porte logique adaptée. Le circuit qui génère un bit de parité et celui qui vérifie si le bit de parité est valide sont donc très similaires.
Le générateur/checker d'ECC
modifierPour ce qui est des codes de Hamming, ils calculent plusieurs bits de parité, qui sont calculé en prenant en compte une partie des bits de l'opérande. Un circuit qui génère le code de Hamming est donc composé de plusieurs circuits de génération de parité. Idem pour un circuit qui vérifie le code de Hamming d'une opérande.

Par exemple, voici ci-dessous le circuit pour vérifier un code de Hamming de type 7,4. Pour rappel, celui-ci prend des données sur 4 bits, et leur ajoute 3 bits de parité, ce qui fait en tout 7 bits : c'est de là que vient le nom de 7-4-3 du code. Chaque bit de parité se calcule à partir de 3 bits du nombre. Le schéma ci-contre indique quels sont les bits de données utilisés pour calculer un bit de parité : les bits de parité sont noté p, les bits de données d.
Le circuit est composé d'une première couche de portes XOR qui calculent le code de Hamming des 4 bits de données. Une seconde couche de portes XOR compare ce code calculé avec les trois bits d'ECC présents dans l'opérande. Si les deux valeurs correspondent, il n'y a pas d'erreur. Mais si les bits ne correspondent pas, alors on sait quel bit est erroné en regardant quel bit d'ECC est invalide. Uen couche de portes ET/NON sert de pseudo-décodeur, qui sélectionne le bit à corriger. Elle génére un masque de 4 bits qui indique quel bit inverser : celui dont le bit du masque est à 1. La dernière couche de portes XOR prend ce masque et l'applique aux 4 bits de données, ce qui inverse le bit adéquat.

Les circuits séquentiels
modifierLa totalité de l'électronique grand public est basée sur des circuits combinatoires auxquels on ajoute des mémoires. Pour le moment, on sait créer des circuits combinatoires, mais on ne sait pas faire des mémoires. Pourtant, on a déjà tout ce qu'il faut. Il est en effet parfaitement possible de créer des mémoires avec des portes logiques. Toutes les mémoires sont conçues à partir de circuits capables de mémoriser un ou plusieurs bits. Ces circuits sont ce qu'on appelle des bascules, ou flip-flops. Pour une question de simplicité, ce chapitre parlera des circuits capables de mémoriser un bit seulement, pas plusieurs. Nous verrons comment combiner ces bits pour former une mémoire ou des compteurs dans le chapitre suivant.
L'interface d'une bascule
modifierAvant de voir comment sont fabriquées les bascules, nous allons voir quelles sont leurs entrées et leurs sorties. La raison à cela est que des bascules aux entrées-sorties similaires peuvent être construites sur des principes suffisamment différents pour qu'on les voie à part. Si on ne regarde que les entrées-sorties, on peut grosso-modo classer les bascules en quelques grands types principaux : les bascules RS, les bascules JK et les bascules D. Nous ne parlerons pas des bascules JK dans ce qui va suivre, car elles sont très peu utilisées et que nous n'en ferons pas usage dans le reste du cours.
Les bascules D
modifier
En premier lieu, on trouve les bascules D, les bascules les plus simples, qui ont deux entrées et deux sorties. Les deux entrées sont appelées D et E : D pour Data, E pour Enable. Le bit à mémoriser est envoyé directement sur l'entrée D. L'entrée Enable permet d'autoriser ou d'interdire les écritures dans la bascule. Ainsi, tant que cette entrée Enable reste à 0, le bit mémorisé par la bascule reste le même, peu importe ce qu'on met sur l'entrée D : il faut que l'entrée Enable passe à 1 pour que l'entrée soit recopiée dans la bascule et mémorisée. On trouve ensuite deux sorties complémentaires qui sont simplement l'inverse l'une de l'autre. La première sortie permet de lire le bit mémorisé dans la bascule RS, la seconde est simplement l'inverse de ce bit.
Les bascules RS
modifier
En second lieu, on trouve les bascules RS, qui possèdent deux entrées et deux sorties. La première sortie permet de lire le bit mémorisé dans la bascule RS, la seconde est simplement l'inverse de ce bit. Les deux sorties sont simplement l'inverse l'une de l'autre. Les deux entrées permettent de placer un 1 ou un 0 dans la bascule. L'entrée R permet de mettre un 1, l'entrée S permet d'y injecter un 0. Pour vous en rappeler, sachez que les entrées de la bascule ne sont nommées ainsi par hasard : R signifie Reset (qui signifie mise à zéro en anglais) et S signifie Set (qui veut dire mise à un en anglais).
Le principe de ces bascules est assez simple :
- si on met un 1 sur l'entrée R et un 0 sur l'entrée S, la bascule mémorise un zéro ;
- si on met un 0 sur l'entrée R et un 1 sur l'entrée S, la bascule mémorise un un ;
- si on met un zéro sur les deux entrées, la sortie Q sera égale à la valeur mémorisée juste avant.
- Si on met un 1 sur les deux entrées, on ne sait pas ce qui arrivera sur ses sorties. Après tout, quelle idée de mettre la bascule à un en même temps qu'on la met à zéro !
| Entrée Reset | Entrée Set | Sortie Q |
|---|---|---|
| 0 | 0 | Bit mémorisé par la bascule |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | Dépend de la bascule |
Le comportement obtenu quand on met deux 1 en entrée dépend de la bascule. Sur certaines bascules, appelées bascules à entrées non-dominantes, la combinaison est interdite : elle fait dysfonctionner le circuit et le résultat est imprédictible. Il faut dire que cette combinaison demande de mettre le circuit à la fois à 0 (entrée R) et à 1 (entrée S). Mais sur d'autres bascules dites à entrée R ou S dominante, l'entrée R sera prioritaire sur l'entrée S ou inversement. Sur les bascules à entrée R dominante, l'entrée R surpasse l'entrée S : la bascule est mise à 0 quand les deux entrées sont à 1. A l'inverse, sur les bascules à entrée S dominante, l'entrée S surpasse l'entrée R : la bascule est mise à 1 quand les deux entrées sont à 1.
Les bascules RS inversées
modifier
Il existe aussi des bascules RS inversées, où les entrées doivent être mises à 0 pour faire ce qu'on leur demande. Ces bascules fonctionnent différemment de la bascule précédente :
- si on met un 1 sur l'entrée R et un 0 sur l'entrée S, la bascule mémorise un 1 ;
- si on met un 0 sur l'entrée R et un 1 sur l'entrée S, la bascule mémorise un 0 ;
- si on met un 1 sur les deux entrées, la sortie Q sera égale à la valeur mémorisée juste avant ;
- si on met un 0 sur les deux entrées, le résultat est indéterminé.
| Entrée /R | Entrée /S | Sortie Q |
|---|---|---|
| 0 | 0 | Interdit |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Bit mémorisé par la bascule |
Là encore, quand les deux entrées sont à 0, on fait face à trois possibilités, comme sur les bascules RS normales : soit le résultat est indéterminé, soit l'entrée R prédomine, soit l'entrée S prédomine.
Les bascules JK
modifier
Les bascules JK peuvent être vues comme des bascules RS améliorées. La seule différence est ce qui se passe quand on envoie un 1 sur les entrées R et S. Sur une bascule RS, le résultat dépend de la bascule, il est indéterminé. Sur les bascules JK, le contenu de la bascule est inversée.
| Entrée J | Entrée K | Sortie Q |
|---|---|---|
| 0 | 0 | Bit mémorisé par la bascule |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | inversion du bit mémorisé |
Les bascules JK, RS et RS inversées à entrée Enable
modifier
Il est possible de modifier les bascules JK, RS et RS inversées, pour faire permettre d' « activer » ou d' « éteindre » les entrées R et S à volonté. En faisant cela, les entrées R et S ne fonctionnent que si l'on autorise la bascule à prendre en compte ses entrées.
Pour cela, il suffit de rajouter une entrée E à notre circuit. Suivant la valeur de cette entrée, l'écriture dans la bascule sera autorisée ou interdite. Si l'entrée E vaut zéro, alors tout ce qui se passe sur les entrées RS ou JK ne fera rien : la bascule conservera le bit mémorisé, sans le changer. Par contre, si l'entrée E vaut 1, alors les entrées RS ou JK feront ce qu'il faut et la bascule fonctionnera comme une bascule RS/JK normale.
La porte C, une bascule spéciale
modifier
Enfin, nous allons voir la porte C, une bascule particulière qui sera utilisée quand nous verrons les circuits et les bus asynchrones. Elle a deux entrées A et B, comme les bascules RS et les bascules D, mais seulement une sortie. Quand les deux entrées sont identiques, la sortie de la bascule correspond à la valeur des entrées (cette valeur est mémorisée). Quand les deux entrées différent, la sortie correspond au bit mémorisé.
| Entrée A | Entrée B | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | Bit mémorisé par la bascule |
| 1 | 0 | Bit mémorisé par la bascule |
| 1 | 1 | 1 |
L'implémentation des bascules avec des portes logiques
modifierLe principe qui se cache derrière toutes ces bascules est le même. Elles sont organisées autour d'un circuit dont on boucle la sortie sur son entrée. Cela veut dire que sa sortie est connectée à une de ses entrées, les autres entrées étant utilisées pour commander la bascule. Nous allons distinguer l'entrée bouclée et la ou les entrées de commande.

Le circuit doit avoir une particularité bien précise : si l'entrée de commande est à la bonne valeur (0 sur certaines bascules, 1 sur d'autres), l'entrée bouclée est recopiée sur la sortie à l'identique. On dit que le circuit a des entrées potentiellement idempotentes. Ainsi, tant que l'entrée de commande est à la bonne valeur, la bascule sera dans un état stable où la sortie et l'entrée de commande restons à la valeur mémorisée. Le circuit en question peut être une porte logique centrale, qui peut être une porte ET, OU, XOR, NAND, NOR, NXOR, ou un multiplexeur.

Toujours est-il qu'un circuit séquentiel contient toujours au moins une entrée reliée sur une sortie, contrairement aux circuits combinatoires, qui ne contiennent jamais la moindre boucle !
La bascule D fabriquée avec un multiplexeur
modifierLe cas le plus simple de circuit bouclé est la bascule D conçue à partir d'un multiplexeur. L'idée est très simple. Quand l'entrée Enable est à 0, la sortie du circuit est bouclée sur l'entrée : le bit mémorisé, qui était présent sur la sortie, est alors renvoyé en entrée, formant une boucle. Cette boucle reproduit en permanence le bit mémorisé. Par contre, quand l'entrée Enable vaut 1, la sortie du multiplexeur est reliée à l'entrée D. Ainsi, ce bit est alors renvoyé sur l'autre entrée : les deux entrées du multiplexeur valent le bit envoyé en entrée, mémorisant le bit dans la bascule.

Un défaut de cette implémentation est qu'elle ne fournit par la sortie , avec le bit inversée. Pour cela, il est possible d'ajouter une porte NON au circuit précédent.


Pour rappel, un multiplexeur peut s'implémenter de différentes manières, comme nous l'avons vu dans le chapitre sur les circuits de sélection. Il est possible de l'implémenter en utilisant seulement des portes logiques, ou alors en utilisant des portes à transmission. Les deux possibilités sont illustrées ci-contre.
Pour un multiplexeur fabriqué avec des portes logiques uniquement, boucler sa sortie sur son entrée ne pose aucun problème particulier. Mais un problème survient quand on veut fabriquer une bascule D avec de tels multiplexeurs. Le problème est qu'une porte à transmission est électriquement équivalente à un simple interrupteur, ce qui réduit le circuit à une boucle entre un interrupteur et un fil. Le courant qui circule dans le fil et l'interrupteur se dissipe rapidement du fait de la résistance du fil et disparait en quelques micro- ou millisecondes. Il n'y a pas de porte logique alimentée en courant/tension qui peut régénérer le signal électrique.
La solution est de rajouter des portes logiques dans la boucle. La solution la plus simple et la plus évidente, est de rajouter une porte OUI, la porte logique qui recopie son entrée sur sa sortie et dont l'utilité n'était pas évidente. Et la manière la plus simple de fabriquer une porte OUI est d'utiliser deux portes NON qui se suivent, ce qui donne le circuit ci-dessous. Cela garantit que la boucle est alimentée en courant/tension quand elle est fermée. Son contenu ne s'efface pas avec le temps, mais est automatiquement régénéré par les portes NON. L'ensemble sera stable tant que la boucle est fermée.

L'avantage du circuit précédent est qu'il est plus économe en portes logiques que les autres bascules, même si ce n'est pas évident. Disons que son implémentation utilise moins de transistors, bien qu'on devra en reparler dans un chapitre ultérieur. Un autre avantage est que ce circuit permet d'avoir les deux sorties Q : la sortie Q inversée est prise en sortie de la première porte NON. Une variante du circuit précédent est utilisée dans les mémoires dites SRAM, qui sont utilisées pour les registres du processeur ou ses mémoires caches.
Les bascules D avec entrées de Set/Reset
modifier
Certaines bascules D ont une entrée R, qui met à zéro le bit mémorisé dans la bascule quand l'entrée R est à 1. Pour cela, elles ajoutent un circuit de mise à zéro, que nous avons déjà vu dans le chapitre sur les opérations bit à bit. Pour rappel, il s'agit d'un circuit qui prend un bit d'entrée, en plus du bit d'entrée R, et fournit la sortie adéquate. Le bit de sortie est soit égal au bit d'entrée si R = 0, soit égal à 0 si R = 1. e porte ET couplée à une porte NON, comme illustré ci-contre. Ce circuit de mise à zéro est placé après la seconde porte NON, et sa sortie est bouclée sur l'entrée du circuit. Le circuit obtenu est le suivant :

Le circuit peut se simplement fortement en fusionnant les trois portes situées entre les deux sorties Q, à savoir la porte ET et les deux portes NON qui la précédent. La loi de De Morgan nous dit que l'ensemble est équivalent à une porte NOR, ce qui donne le circuit suivant :

La bascule RS fabriquée avec une porte OU et une porte ET
modifierUn autre exemple est la forme la plus basique de bascule RS : la bascule RS de type ET-OU. Dans celle-ci, on trouve entre trois portes : une porte ET, une porte OU, et éventuellement une porte NON. Un exemple de porte RS de ce type est le suivant, d'autres manières de connecter le tout qui donnent le même résultat. On peut par exemple se passer d'inverseur, ou inverser l'ordre des portes logiques ET et OU. L'essentiel est la boucle indiquée en vert, qui fait que le bit de sortie est recopié sur les entrées bouclées des deux portes, l'ensemble formant une boucle qui relie la sortie à elle-même.

Son fonctionnement est assez simple à expliquer. La porte ET a deux entrées, dont une est bouclée et l'autre est une entrée de commande. Les deux portes recopient leur entrée en sortie si on place ce qu'il faut sur l'entrée de commande. Par contre, toute autre valeur modifie le bit inséré dans la bascule.
- Si on place un 0 sur l'entrée de commande de la porte OU, elle recopiera l'entrée bouclée sur sa sortie. Par contre, y mettre un 1 donnera un 1 en sortie, peu importe le contenu de l'entrée bouclée. En clair, l'entrée de commande de la porte OU sert d'entrée S à la bascule.
- La porte ET recopie l'entrée bouclée, mais seulement si on place un 1 sur l'entrée de commande. Si on place un 0, elle aura une sortie égale à 0, peu importe l'entrée bouclée. En clair, l'entrée de commande de la porte ET est l'inverse de ce qu'on attend de l'entrée R à la bascule RS. Pour obtenir une véritable entrée R, il est possible d'ajouter une porte NON sur l'entrée /R, sur l'entrée de la porte ET. En faisant cela, on obtient une vraie bascule RS.
Si on essaye de concevoir le circuit, on se retrouve alors face à un choix : l'ordre dans lequel mettre les portes ET et OU. Les deux portes ET et OU peuvent être mises dans n'importe quel ordre : soit on met la porte ET avant la porte OU, soit on fait l'inverse. La seule différence sera ce qu'il se passe quand on active les deux entrées à la fois. Si la porte ET est située après la porte OU, l'entrée Reset sera prioritaire sur l'entrée Set quand elles sont toutes les deux à 1. Et inversement, si la porte OU est située après, ce sera le signal Set qui sera prioritaire. Voici ci-dessous les tables de vérité correspondantes pour chaque circuit.
| Entrée Reset | Entrée Set | Sortie Q | Circuit |
|---|---|---|---|
| 0 | 0 | Bit mémorisé par la bascule | 
|
| 1 | 0 | 0 | |
| X (0 ou 1) | 1 | 1 |
| Entrée Reset | Entrée Set | Sortie Q | Circuit |
|---|---|---|---|
| 0 | 0 | Bit mémorisé par la bascule | 
|
| 0 | 1 | 0 | |
| 1 | X (0 ou 1) | 1 |
Une autre manière de voir les choses est que ce circuit possède deux sorties Q équivalentes, situées aux deux points entre les portes OU et ET. Cette façon de voir les choses sera très utile dans ce qui va suivre.
Les bascules RS à NOR et à NAND
modifierLe circuit précédent a bien une sortie Q, mais pas de sortie /Q. Pour la rajouter, il suffit simplement d'ajouter une porte NON sur la sortie Q. Mais faire ainsi ne permet pas de profiter de certaines simplifications bien appréciables. Il est en effet possible de se débarrasser des deux portes NON, celle en amont de la porte ET, et de celle sur la sortie /Q. Pour cela, nous allons procéder d'une autre manière. Au lieu d'ajouter une seule porte NON, nous allons ajouter deux portes, en amont de la porte OU. En faisant, le circuit devient celui-ci :

On peut alors regrouper des portes logiques consécutives. Premièrement, on peut regrouper la porte OU avec la porte NON immédiatement à sa suite. Mais on peut aussi regrouper la porte ET et les deux portes NON restantes. En effet, nous avons vu dans le chapitre sur les circuits combinatoires que cette combinaison de portes est équivalente à une porte NOR. Le circuit devient donc :

Le résultat est ce qu'on appelle une bascule RS à NOR, qui tire son nom du fait qu'elle est fabriquée exclusivement avec des portes logiques NOR. En réorganisant le circuit, on trouve ceci :

Il est possible de faire la même manipulation, mais cette fois-ci sur une bascule RS inversée, de type ET-OU encore une fois. La bascule RS inversée est identique à la bascule ET-OU précédente, si ce n'est que la porte NON est placée sur l'entrée R et non sur l'entrée S. En clair, elle est sur une entrée de la porte OU et non sur la porte ET. Le résultat est une bascule RS à NAND, qui est une bascule RS inversée à deux sorties (Q et /Q), composée intégralement de portes NAND.

Les bascules peuvent se fabriquer à partir d'autres bascules
modifierIl y a quelques chapitres, nous avons vu qu'il est possible de créer une porte logique en combinant d'autres portes logiques. Et bien sachez qu'il est possible de faire la même chose pour des bascules. On peut par exemple fabriquer une bascule RS à partir d'une bascule D, et réciproquement. Ou encore, on peut fabriquer une bascule D à partir d'une bascule JK, et inversement. Les possibilités sont nombreuses. Et pour cela, il suffit juste d'ajouter un circuit combinatoire qui traduit les entrées de la bascule voulue vers les entrées de la bascule utilisée.
Le passage d'une bascule RS à une bascule RS inversée (et inversement)
modifierIl est possible de créér une bascule RS normale à partir d'une bascule RS inversée en inversant simplement les entrées R et S avec une porte NON. Et inversement, le passage d'une bascule RS normale à une bascule RS inversée se fait de la même manière. Il est possible de faire cela avec une bascule RS à portes NOR ou NAND, mais ainsi qu'avec une bascule RS à ET-OU.

Il s'agit d'une méthode simple, qui a la particularité de garder le caractère dominant/non-dominant des entrées. Rappelez-vous que pour des bascules RS à NOR ou RS à NAND, il y a une combinaison d'entrée qui est interdite. Mettez à 1 les deux entrées sur une RS à NOR, et le résultat sera indéterminé, pareil si vous mettez les deux entrées à 0 sur une bascule RS à NAND. Il faut dire qu'une telle combinaison demande de mettre à la bascule à la fois à zéro (signal R) et à 1 (entrée S). De telles bascules sont dites à entrées non-dominantes. Avec une bascule RS de type ET-OU, on n'a pas ce problème : suivant la bascule, on aura l'entrée R qui sera prioritaire, ou l'entrée S (suivant l'ordre des portes logiques : le ET avant le OU ou inversement). On dit alors que l'entrée R est dominante dans le premier cas, que l'entrée S est dominante dans le second. Et bien en mettant deux portes NON en entrée d'une bascule RS inversée, la bascule RS finale gardera le caractère dominant/non-dominant de ses entrées.
Cependant, il est possible de partir d'une bascule RS inversée/normale non-dominante, et d'en faire une bascule RS normale/inversée à entrée R ou S dominante. Pour cela, au lieu d'ajouter deux portes NON en entrée du circuit, on ajoute un petit circuit spécialement conçu. Ce circuit de conversion traduit les signaux d’entrée R et S en signaux /R et /S, (ou inversement). Prenons l'exemple d'une bascule RS normale à entrée R prioritaire, fabriquée à partir d'une bascule RS à NAND (inversée à entrée non-dominantes). La table de vérité du circuit de conversion des entrées est la suivante. Rappelez-vous que l'on veut que l'entrée R soit prioritaire. Ce qui veut dire que si R est à 1, alors on garantit que le signal /R est actif et que /S est inactif. On a donc :
| R | S | |||
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 1 |
L'entrée n'est autre que l'inverse de l'entrée R, ce qui fait qu'une simple porte NON suffit.
L'entrée a pour équation logique :
Le tout donne le circuit suivant :

L'implémentation des bascules RS avec une entrée Enable
modifier
Dans la section sur l'interface d'une bascule, nous avons vu l'entrée Enable, qui active ou désactive l'écriture dans une bascule. Elle est toujours présente sur les bascules D, mais facultative sur les bascules RS. Les bascules précédentes ne disposent pas de l'entrée Enable, sauf dans le cas de la bascule D. Elles sont donc conceptuellement plus simples que celles qui disposent d'une entrée Enable. Et vous l'avez peut-être senti venir, mais il est possible de modifier les bascules sans entrée Enable, pour leur ajouter cette entrée. Notamment, il est possible de modifier une bascules RS normale pour lui ajouter une entrée Enable. Pour cela, il suffit d'ajouter un circuit avant les entrées R et S, qui inactivera celles-ci si l'entrée E vaut zéro. La table de vérité de ce circuit est identique à celle d'une simple porte ET.
Le circuit obtenu en utilisant une bascule RS à NOR est celui-ci :

Et le circuit obtenu avec une bascule à portes NAND est le suivant. Le circuit est simple à comprendre : on part d'une porte RS inversée à NAND, on ajoute deux portes NON pour en faire une porte RS normale, puis on ajoute les deux portes ET pour l'entrée Enable. Ensuite, on simplifie le circuit en fusionnant les portes ET avec les portes NON, ce qui donne des portes NAND. Le tout donne le circuit simplifié suivant :

Les bascules D conçues à partir de bascules RS à entrée Enable
modifierOn peut construire une bascule D à partir d'une simple bascule RS ou RS inversée. Il suffit d'ajouter un circuit qui déduise quoi mettre sur les entrées R et S suivant la valeur sur D. Mais en réfléchissant un peu, on se rend compte qu'il est préférable d'utiliser une bascule RS à entrée Enable. En effet, l'entrée Enable de la bascule D et de la bascule RS sont la même, elles ont exactement le même comportement et la même utilité. Dans ce cas, il suffit de prendre une bascule RS à entrée Enable et d'ajouter un circuit qui convertit l'entrée D en Entrées R et S.

Pour une bascule RS normale, on peut remarquer que l'entrée R est toujours égale à l'inverse de D, alors que S est toujours strictement égale à D. Il suffit d'ajouter une porte NON avant l'entrée R d'une bascule RS à entrée Enable, pour obtenir une bascule D. On peut faire cela à la fois avec des bascules RS à NOR ou à NAND.


Il est possible d'améliorer légèrement le circuit précédent, afin de retirer la porte NON, en changeant le câblage du circuit. En effet, la porte NON inverse l'entrée D tout le temps, quelle que soit la valeur de l'entrée Enable. Mais on n'en a besoin que lorsque l'entrée Enable est à 1. On peut donc remplacer la porte NON par une porte qui sort un 0 quand l'entrée D et l'entrée Enable sont à 1, mais qui sort un 1 sinon. Il s'agit ni plus ni moins qu'une porte NAND, et le circuit précédent la contient déjà : c'est celle en haut à gauche. On peut donc prendre sa sortie pour l'envoyer au bon endroit, ce qui donne le circuit suivant :

Il est aussi possible de fabriquer une bascule D avec une bascule RS à ET/OU. Le circuit obtenu est alors identique au circuit obtenu avec un multiplexeur basé sur des portes logiques.
Les bascules JK conçues à partir de bascules RS
modifierIl est possible de construire une bascule JK à partir d'une bascule RS. Ce qui n'est pas étonnant, vu que les bascules RS et JK sont très ressemblantes. Il suffit d'ajouter un circuit qui déduise quoi mettre sur les entrées R et S suivant la valeur sur les entrées J et K. Le circuit en question est composé de deux portes ET, une par entrée.

Il est possible de faire la même chose avec une bascule RS à entrée Enable, qui donne une bascule JK à entrée Enable.

Les bascules sont rarement utilisées seules. Elles sont combinées avec des circuits combinatoires pour former des circuits qui possèdent une capacité de mémorisation, appelés circuits séquentiels. L'ensemble des informations mémorisées dans un circuit séquentiel, le contenu de ses bascules, forme ce qu'on appelle l'état du circuit, aussi appelé la mémoire du circuit séquentiel. Un circuit séquentiel peut ainsi être découpé en deux morceaux : des bascules qui stockent l'état du circuit, et des circuits combinatoires pour mettre à jour l'état du circuit et sa sortie. Suivant la méthode utilisée pour déterminer la sortie, on peut classer les circuits séquentiels en deux catégories :
- les automates de Moore, où la sortie ne dépend que de l'état mémorisé ;
- et les automates de Mealy, où la sortie dépend de l'état du circuit et de ses entrées.
- Ces derniers ont tendance à utiliser moins de portes logiques que les automates de Moore.

Concevoir des circuits séquentiels demande d'utiliser un formalisme assez complexe et des outils comme des machines à état finis (finite state machine). Mais nous ne parlerons pas de cela dans ce cours, car nous n'aurons heureusement pas à les utiliser.
La majorité des circuits séquentiels possèdent plusieurs bascules, dont certaines doivent être synchronisées entre elles. Sauf qu'un léger détail vient mettre son grain de sel : tous les circuits combinatoires ne vont pas à la même vitesse ! Si on change l'entrée d'un circuit combinatoire, cela se répercutera sur ses sorties. Mais toutes les sorties ne sont pas mises en même temps et certaines sorties seront mises à jour avant les autres ! Cela ne pose pas de problèmes avec un circuit combinatoire, mais ce n'est pas le cas si une boucle est impliquée, comme dans les circuits séquentiels. Si les sorties sont renvoyées sur les entrées, alors le résultat sur l'entrée sera un mix entre certaines sorties en avance et certaines sorties non-mises à jour. Le circuit combinatoire donnera alors un résultat erroné en sortie. Certes, la présence de l'entrée Enable permet de limiter ce problème, mais rien ne garantit qu'elle soit mise à jour au bon moment. En conséquence, les bascules ne sont pas mises à jour en même temps, ce qui pose quelques problèmes relativement fâcheux si aucune mesure n'est prise.
Le temps de propagation
modifierPour commencer, il nous faut expliquer pourquoi tous les circuits combinatoires ne vont pas à la même vitesse. Tout circuit, quel qu'il soit, va mettre un petit peu de temps avant de réagir. Ce temps mis par le circuit pour propager un changement sur les entrées vers la sortie s'appelle le temps de propagation. Pour faire simple, c'est le temps que met un circuit à faire ce qu'on lui demande : plus ce temps de propagation est élevé, plus le circuit est lent. Ce temps de propagation dépend de pas mal de paramètres, aussi je ne vais citer que les principaux.
Le temps de propagation des portes logiques
modifierUne porte logique n'est pas un système parfait et reste soumis aux lois de la physique. Notamment, il n'a pas une évolution instantanée et met toujours un petit peu de temps avant de changer d'état. Quand un bit à l'entrée d'une porte logique change, elle met du temps avant de changer sa sortie. Ce temps de réaction pour propager un changement fait sur les entrées vers la sortie s'appelle le temps de propagation de la porte logique. Pour être plus précis, il existe deux temps de propagation : un temps pour passer la sortie de 0 à 1, et un temps pour la passer de 1 à 0. Les électroniciens utilisent souvent la moyenne entre ces deux temps de propagation, et la nomment le retard de propagation, noté .

Le chemin critique
modifier
Si le temps de propagation de chaque porte logique a son importance, il faut aussi tenir compte de la manière dont elles sont reliées. La relation entre "temps de propagation d'un circuit" et "temps de propagation de ses portes" n'est pas simple. Deux paramètres vont venir jouer les trouble-fêtes : le chemin critique et la sortance des portes logiques. Commençons par voir le chemin critique, qui n'est autre que le nombre maximal de portes logiques entre une entrée et une sortie de notre circuit. Pour donner un exemple, nous allons prendre le schéma ci-contre. Pour ce circuit, le chemin critique est dessiné en rouge. En suivant ce chemin, on va traverser trois portes logiques, contre deux ou une dans les autres chemins.
Le temps de propagation total, lié au chemin critique, se calcule à partie de plusieurs paramètres. Premièrement, il faut déterminer quel est le temps de propagation pour chaque porte logique du circuit. En effet, chaque porte logique met un certain temps avant de fournir son résultat en sortie : quand les entrées sont modifiées, il faut un peu de temps pour que sa sortie change. Ensuite, pour chaque porte, il faut ajouter le temps de propagation des portes qui précédent. Si plusieurs portes sont reliées sur les entrées, on prend le temps le plus élevé. Enfin, il faut identifier le chemin critique, le plus long : le temps de propagation de ce chemin est le temps qui donne le tempo maximal du circuit.
 |
 |
 |
La sortance des portes logiques
modifierPassons maintenant au second paramètre lié à l'interconnexion entre portes logiques : la sortance. Dans les circuits complexes, il n'est pas rare que la sortie d'une porte logique soit reliée à plusieurs entrées (d'autre portes logiques). Le nombre d'entrées connectées à une sortie est appelé la sortance de la sortie. Il se trouve que plus on connecte de portes logiques sur une sortie, (plus sa sortance est élevée), plus il faudra du temps pour que la tension à l'entrée de ces portes passe de 1 à 0 (ou inversement). La raison en est que la porte logique fournit un courant fixe sur sa sortie, qui charge les entrées en tension électrique. Un courant positif assez fort charge les entrées à 1, alors qu'un courant nul ne charge pas les entrées qui retombent à 0. Avec plusieurs entrées, la répartition est approximativement équitable et chaque entrée reçoit seulement une partie du courant de sortie. Elles mettent plus de temps à se remplir de charges, ce qui fait que la tension met plus de temps à monter jusqu'à 1.

Le temps de latence des fils
modifierEnfin, il faut tenir compte du temps de propagation dans les fils, celui mis par notre tension pour se propager dans les fils qui relient les portes logiques entre elles. Ce temps perdu dans les fils devient de plus en plus important au cours du temps, les transistors et portes logiques devenant de plus en plus rapides à force de les miniaturiser. Par exemple, si vous comptez créer un circuit avec des entrées de 256 à 512 bits, il vaut mieux le modifier pour minimiser le temps perdu dans les interconnexions que de diminuer le chemin critique.
Les circuits synchrones et asynchrones
modifierSur les circuits purement combinatoires, le temps de propagation n'est que rarement un souci, à moins de rencontrer des soucis de métastabilité assez compliqués. Par contre, le temps de propagation doit être pris en compte quand on crée un circuit séquentiel : sans ça on ne sait pas quand mettre à jour les bascules du circuit. Si on le fait trop tôt, le circuit combinatoire peut sauter des états : il se peut parfaitement qu'on change le bit placé sur l'entrée avant qu'il ne soit mémorisé. De plus, les différents circuits d'un composant électronique n'ont pas tous le même temps de propagation, et ceux-ci vont fonctionner à des vitesses différentes. Si l'on ne fait rien, on peut se retrouver avec des dysfonctionnements : par exemple, un circuit lent peut rater deux ou trois nombres envoyés par un composant un peu trop rapide.
Pour éviter les ennuis dus à l'existence de ce temps de propagation, il existe deux grandes solutions, qui permettent de faire la différence entre circuits asynchrones et synchrones. Dans les circuits synchrones, les bascules sont mises à jour en même temps. A l'opposé, les circuits asynchrones préviennent les bascules quand ils veulent la mettre à jour. Quand le circuit combinatoire et les bascules sont tous les deux prêts, on autorise l'écriture dans les bascules.
Les circuits asynchrones ne sont presque pas utilisés dans la quasi-totalité des ordinateurs modernes, qui sont des circuits synchrones. Nous ne verrons pas beaucoup de circuits asynchrones dans la suite du cours. Il faut dire que la grosse majorité des processeurs, mémoires et périphériques, sont des composants synchrones. La seule exception que nous verrons dans ce cours sont les anciennes mémoires DRAM asynchrones, qui sont aujourd'hui obsolètes, mais ont été utilisées dans les anciens PCs. Aussi, nous allons nous concentrer sur les circuits synchrones dans ce qui suit.
Le signal d'horloge des circuits synchrones
modifierLes circuits synchrones mettent à jour leurs bascules à intervalles réguliers. La durée entre deux mises à jour est constante et doit être plus grande que le temps de propagation le plus long du circuit : on se cale donc sur le circuit combinatoire le plus lent. Les concepteurs d'un circuit doivent estimer le pire temps de propagation possible pour le circuit et ajouter une marge de sûreté.
Pour mettre à jour les circuits à intervalles réguliers, le signal d'autorisation d'écriture est une tension qui varie de façon cyclique : on parle alors de signal d'horloge. Le temps que met la tension pour effectuer un cycle est ce qu'on appelle la période. Le nombre de périodes par seconde est appelé la fréquence. Elle se mesure en hertz. On voit sur ce schéma que la tension ne peut pas varier instantanément : elle met un certain temps pour passer de 0 à 1 et de 1 à 0. On appelle cela un front. Le passage de 0 à 1 est appelé un front montant et le passage de 1 à 0 un front descendant.

Un point important est que le signal d'horloge passe régulièrement de 0 à 1. Dans le cas idéal, 50% de la période est à l'état 1 et les 50% restants à l'état 0. On a alors un signal carré. Mais il arrive que le temps passé à l'état 1 ne soit pas forcément le même que le temps passé à 0. Par exemple, le signal peut passer 10% de la période à l'état 1 et 90% du temps à l'état 0. C'est assez rare, mais possible et même parfois utile. Le signal n'est alors pas appelé un signal carré, mais un signal rectangulaire. Le signal d'horloge est donc à 1 durant un certain pourcentage de la période. Ce pourcentage est appelé le rapport cyclique (duty cycle).

En faisant cela, le circuit mettra ses sorties à jour lors d'un front montant (ou descendant) sur son entrée d'horloge. Entre deux fronts montants (ou descendants), le circuit ne réagit pas aux variations des entrées. Rappelons que seuls les circuits séquentiels doivent être synchronisés ainsi, les circuits combinatoires étant épargnés par les problématiques de synchronisation. Pour que les circuits séquentiels soient cadencés par une horloge, les bascules du circuit sont modifiées de manière à réagir aux fronts montants et/ou aux fronts descendants, ce qui fait que la mise à jour de l'état interne du circuit est synchronisée sur l'horloge. Évidemment, l’horloge est envoyée au circuit via une entrée spéciale : l'entrée d'horloge. L'horloge est ensuite distribuée à l'intérieur du composant, jusqu'aux bascules, par un ensemble de connexions qui relient l'entrée d'horloge aux bascules.

La fréquence influence la performance d'un circuit
modifierEn théorie, plus un composant utilise une fréquence élevée, plus il est rapide. C'est assez intuitif : plus un composant peut changer d'état un grand nombre de fois par seconde, plus, il peut faire de calculs, et plus il est performant. Mais attention : un processeur de 4 gigahertz peut être bien plus rapide qu'un processeur de 20 gigahertz, pour des raisons techniques qu'on verra plus tard dans ce cours. Si dans les grandes lignes, une fréquence plus élevée signifie une performance plus élevée, ce n'est qu'une règle heuristique assez imparfaite.
Un autre point important est que plus la fréquence d'un composant est élevée, plus il chauffe et consomme d'énergie. Nous ne pouvons pas expliquer pourquoi pour le moment, mais sachez que nous détaillerons cela dans le chapitre sur les tendances technologiques. Disons pour simplifier que plus la fréquence d'un composant est élevée, plus il change d'état fréquemment par seconde, et que chaque changement d'état consomme de l'énergie. Sur les circuits CMOS modernes, la consommation d'énergie est proportionnelle à la fréquence. Ne vous étonnez donc pas que les circuits qui fonctionnent à haute fréquence, comme le processeur, chauffent plus que les circuits de basse fréquence. S'il y a un radiateur et un ventilateur sur un processeur, c'est en partie à cause de ça.
Dans un ordinateur moderne, chaque composant a sa propre horloge, qui peut être plus ou moins rapide que les autres. Par exemple, le processeur fonctionne avec une horloge différente de l'horloge de la mémoire RAM ou des périphériques. La présence de plusieurs horloges vient du fait que certains composants sont plus lents que d'autres. Plutôt que de caler tous les composants d'un ordinateur sur le plus lent en utilisant une seule horloge, il vaut mieux utiliser une horloge différente pour chacun. Les mises à jour des registres sont synchronisées à l'intérieur d'un composant (dans un processeur, ou une mémoire), alors que les composants eux-mêmes synchronisent leurs communications avec d'autres mécanismes. Ces multiples signaux d'horloge dérivent d'une horloge de base qui est « transformée » en plusieurs horloges, grâce à des montages électroniques spécialisés (des PLL ou des montages à portes logiques un peu particuliers).
Les bascules synchrones
modifierUtiliser une horloge demande cependant d'adapter les circuits vus précédemment, les bascules devant être modifiées. En effet, les bascules précédentes sont mises à jour quand un signal d'autorisation est mis à 1. Mais avec un signal d'horloge, les bascules doivent être mises à jour lors d'un front, montant ou descendant, peu importe. Pour cela, les bascules ont une entrée d'autorisation d'écriture modifiée, qui réagit au signal d'horloge. Les bascules commandées par une horloge sont appelées des bascules synchrones.
Les bascules synchrones peuvent mettre à jour leur contenu soit lors d'un front montant, soit d'un front descendant, soit les deux, soit lorsque la tension d'horloge est à 1. Suivant le cas, le symbole utilisé pour représenter l'entrée d'horloge est différent, comme illustré ci-dessous.
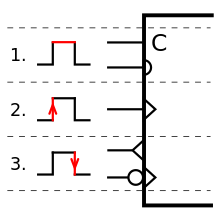
- Notons qu'en anglais, le terme bascule se dit flip-flop ou latch. De nos jours, le terme latch étant utilisé pour les bascules non-synchrones, alors que le terme flip-flop est utilisé pour désigner les bascules synchrones.
Les types de bascules synchrones
modifierIl existe plusieurs types de bascules synchrones, qu'on peut classer en fonction de leurs entrées-sorties.

La plus simple est la bascule D synchrone est une bascule D modifiée de manière à mettre à jour son contenu sur un front (montant). Celle-ci possède deux entrées : une entrée D sur laquelle on envoie la donnée à mémoriser (entrée d'écriture), et une autre pour l'horloge. Elle contient entre une et deux sorties : une pour la donnée mémorisée (sortie de lecture) et éventuellement une autre pour son opposé. Son fonctionnement est simple : son contenu est mis à jour avec ce qu'il y a sur l'entrée D, mais seulement lors d'un front (montant ou descendant suivant la bascule). Plus rares, certaines bascules D contiennent des entrées R et S pour les mettre à zéro ou à 1. La plupart des bascules D ont une entrée R pour les remettre à zéro, tandis que l'entrée S est absente, celle-ci étant peu utile.
| Entrée CLK | Entrée D | Sortie Q |
|---|---|---|
| Front montant (ou descendant, suivant la bascule) | 0 | 0 |
| 1 | 1 | |
| Pas de front montant | 0 ou 1 | Pas de changement |

Il existe aussi des versions synchrones des bascules RS à entrée Enable. Sur celles-ci, l'entrée Enable est juste remplacée par une entrée pour l’horloge. On les appelle des bascules RS synchrones.
| Entrée CLK | Entrée R | Entrée S | Sortie Q |
|---|---|---|---|
| Front montant (ou descendant, suivant la bascule) | 0 | 0 | Pas de changement |
| 0 | 1 | Mise à 1 | |
| 1 | 0 | Mise à 0 | |
| 1 | 1 | Indéterminé. | |
| Pas de front montant | 0 ou 1 | 0 ou 1 | Pas de changement |

Les bascules JK ont aussi leur version synchrone, les bascules JK synchrones.
| Entrée CLK | Entrée R | Entrée S | Sortie Q |
|---|---|---|---|
| Front montant (ou descendant, suivant la bascule) | 0 | 0 | Pas de changement |
| 0 | 1 | Mise à 1 | |
| 1 | 0 | Mise à 0 | |
| 1 | 1 | Inversion du bit mémorisé | |
| Pas de front montant | 0 ou 1 | 0 ou 1 | Pas de changement |

La bascule T est une bascule qui n'existe que comme bascule synchrone. Elle possède deux entrées : une entrée d'horloge et une entrée nommée T. Cette bascule inverse son contenu quand l'entrée T est à 1, mais à condition qu'il y ait un front sur le signal d'horloge. En clair, l'inversion a lieu quand il y a à la fois un front et un 1 sur l'entrée T. Si l'entrée T est maintenu à 1 pendant longtemps, cette bascule inverse son contenu à chaque cycle d'horloge. À ce propos, l'entrée T tire son nom du mot anglais Toggle, qui veut dite inverser.
| Entrée CLK | Entrée T | Sortie Q |
|---|---|---|
| Front montant (ou descendant, suivant la bascule) | 0 | Pas de changement |
| 1 | Inversion du contenu de la bascule | |
| Pas de front montant | 0 ou 1 | Pas de changement |

- Cette bascule est utilisée pour fabriquer des compteurs, des circuits dans lesquels des bits doivent régulièrement être inversées.

La bascule T simplifiée est une bascule T dont l'entrée T a été retiré. Cette bascule change d'état à chaque cycle d'horloge, sans besoin d'autorisation de la part d'une entrée T.
| Entrée CLK | Sortie Q |
|---|---|
| Front montant (ou descendant, suivant la bascule) | Inversion du bit mémorisé |
| Pas de front montant | Pas de changement |
L'intérieur d'une bascule synchrone
modifierPour fabriquer une bascule synchrone, les solutions sont nombreuses et dépendent de si l'on parle d'une bascule D ou d'une bascule RS. Néanmoins, une méthode assez courante, et assez simple, est de partir d'une bascule non-synchrone, puis de la modifier pour la rendre synchrone. Les bascules les plus indiquées pour cela sont les bascules avec une entrée Enable : il suffit de transformer l’entrée Enable en entrée d'horloge. Évidemment, cela demande de faire quelques modifications. Il ne suffit pas d'envoyer le signal d'horloge sur l'entrée Enable pour que cela marche.
La méthode la plus simple consiste à placer deux bascules D l'une à la suite de l'autre. De plus, l'entrée Enable de la seconde bascule est précédée d'une porte NON. Avec cette méthode, la première bascule est mise à jour quand l’horloge est à 0, la seconde étant mise à jour avec le contenu de la première quand l'horloge est à 1. Dans ces conditions, la sortie finale de la bascule est mise à jour après un front montant.

On peut faire exactement la même chose avec deux bascules asynchrones RS l'une à la suite de l'autre.


Une autre méthode associe trois bascules RS normales, les deux premières formant une couche d'entrée qui commande la troisième bascule. Ces deux bascules d'entrée vont en quelque sorte traiter le signal à envoyer à la troisième bascule. Quand le signal d'horloge est à 0, les deux bascules d'entrée fournissent un 1 sur leur sortie : la troisième bascule reste donc dans son état précédent, sans aucune modification. Quand l'horloge passe à 1 (front montant), seule une des deux bascules va fournir un 1 en sortie, l'autre voyant sa sortie passer à 0. La bascule en question dépend de la valeur de D : un 0 sur l'entrée D force l'entrée R de la troisième bascule, un 1 forçant l'entrée S. Dit autrement, le contenu de la troisième bascule est mis à jour. Quand l'entrée d'horloge passe à 1, les bascules se figent toutes dans leur état précédent. Ainsi, la troisième bascule reste commandée par les deux bascules précédentes, qui maintiennent son contenu (les entrées R et S restent à leur valeur obtenue lors du front montant).
Fabriquer des bascules synchrones à partir d'autres bascules synchrones
modifierUne bascule JK synchrone se fabrique facilement à partir d'une bascule RS synchrones, ce qui n'est pas étonnant quand on sait que leur comportement est presque identique, la seule différence étant ce qui se passe quand les entrées RS sont toutes les deux à 1. Il suffit, comme pour une bascule JK asynchrone, d'ajouter quelques circuits pour convertir les entrées JK en entrées RS.

La bascule D synchrone peut se fabriquer partir d'une bascule JK ou RS synchrone. Il suffit alors d'ajouter un circuit combinatoire pour traduire les entrées D et E en entrées RS ou JK.

|
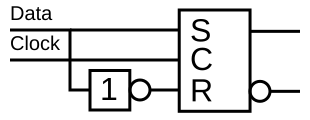
|
La bascule T simplifiée est la version la plus simple de bascule T, celle qui n'a pas d'entrée T et se contente d'inverser son contenu à chaque cycle d'horloge. La fabriquer est assez simple : il suffit de prendre une bascule D synchrone et de relier sa sortie /Q à son entrée D. On peut aussi faire la même chose avec une bascule JK synchrone ou une bascule RS synchrone.

|

|

|
Une bascule T normale peut s’implémenter une bascule T simplifiée, une bascule RS synchrone ou une bascule JK synchrone. Pour le circuit basé sur une bascule T simplifiée, l'idée est de faire un ET entre l'entrée T et le signal d'horloge, ce ET garantissant que le signal d’horloge est mis à 0 si l'entrée T est à zéro.

|

|

|
La distribution de l'horloge dans un circuit complexe
modifierL’horloge est distribuée aux bascules et autres circuits à travers un réseau de connexions électriques qu'on appelle l'arbre d'horloge. L'arbre d'horloge le plus simple, illustré dans la première image ci-dessous, relie directement l'horloge à tous les composants à cadencer.
 |
 |
Il va de soit que l'arbre d'horloge est beaucoup plus compliqué avec la logique dynamique qu'avec la logique statique. Avec la logique statique, seules les bascules doivent recevoir le signal d'horloge, avec éventuellement quelques rares circuits annexes. Mais avec la logique dynamique, toutes les portes logiques doivent recevoir le signal d'horloge, ce qui rend la distribution de l'hrologe beaucoup plus compliquée. C'est un point qui fait que la logique dynamique est assez peu utilisée, et souvent limitée à quelques portions bien précise d'un processeur.
Les défauts inhérents aux arbres d’horloge
modifierUn problème avec cette approche est la sortance de l'horloge. Cette dernière est connectée à trop de composants, ce qui la ralentit. Pour éviter tout problème, on peut ajouter des buffers, de petits répéteurs de signal. S'ils sont bien placés, ils réduisent la sortance nécessaire et empêchent que le signal de l'horloge s'atténue en parcourant les fils.
Un autre problème très fréquent sur les circuits à haute performance est qu'une bonne partie de la consommation d'énergie a lieu dans l'arbre d'horloge. Nous en reparlerons dans le chapitre sur la consommation énergétique des ordinateurs, mais il est intéressant de mettre quelques chiffres sur ce phénomène. Entre 20 à 30% de la consommation énergétique des processeurs modernes a lieu dans l'arbre d'horloge. En comparaison, les circuits asynchrones se passent de cette consommation d'énergie, sans compter que leurs mécanismes de synchronisations sont moins gourmands en courant. Ils sont donc beaucoup plus économes en énergie et chauffent moins. Malheureusement, leur difficulté de conception les rend peu courants.
Le décalage d’horloge (clock skew)
modifier
Un problème courant sur les circuits à haute fréquence est que les fils qui transmettent l’horloge ont chacun des délais de transmission différents. La raison principale à cela est qu'ils n'ont pas la même longueur, ce qui fait que l'électricité met plus de temps à traverser les quelques micromètres de différence entre fils. En conséquence, les composants sont temporellement décalés les uns d'avec les autres, même si ce n'est que légèrement. Ce phénomène est appelé le décalage d'horloge, traduction du terme clock skew utilisé en langue anglaise. Il ne pose pas de problème à faible fréquence et/ou pour des fils assez courts, mais c'est autre chose pour les circuits à haute fréquence. Pour éviter les effets néfastes du clock skew sur les circuits haute-fréquence, on doit concevoir l'arbre d'horloge avec des techniques assez complexes.
Par exemple, on peut jouer sur la forme de l'arbre d'horloge. Dans les schémas du dessus, l'arbre d'horloge part d'un côté du processeur, de là où se trouve la broche pour l'horloge. En faisant cela, un côté du processeur recevra l'horloge avant l'autre, entraînant l'apparition d'un délai entre la gauche du processeur et sa droite. Pour éviter cela, on peut faire partir l'horloge du centre du processeur. Le fil de l'horloge part de la broche d'horloge, va jusqu’au centre du processeur, puis se ramifie de plus en plus en direction des composants. En faisant cela, on garantit que les délais sont équilibrés entre les deux côtés du processeur. Cependant, il existera quand même un délai entre les composants proches du centre et ceux sur les bords du processeur. Mais le délai maximal est minimisé. Entre un délai proportionnel à la largeur du processeur, et un délai proportionnel à la distance maximale centre-bord (environ la moitié de la diagonale), le second est plus faible.
Il arrive que le clock skew soit utilisé volontairement pour compenser d'autres délais de transmission. Pour comprendre pourquoi, imaginons que deux composants soient reliés l'une avec l'autre, le premier envoyant ses données au second. Il y a évidemment un petit délai de transmission entre les deux. Mais sans clock skew, les deux composants recevront l'horloge en même temps : le receveur captera un front montant de l'horloge avant les données de l'émetteur. En théorie, on devrait cadencer l'horloge de manière à ce que ce délai inter-composants ne pose pas de problème. Mais cela n'est pas forcément la meilleure solution si on veut fabriquer un circuit à haute fréquence. Pour éviter cela, on peut ajouter un clock skew, qui retardera l’horloge du receveur. Si le clock skew est supérieur ou égal au temps de transmission inter-composants, alors le receveur réceptionnera bien le signal de l'horloge après les données envoyées par l'émetteur. On peut ainsi conserver un fonctionnement à haute fréquence, sans que les délais de transmission de données ne posent problème. Cette technique porte le nom barbare de source-synchronous clocking.

Les domaines d'horloge
modifierIl existe des composants électroniques qui sont divisés en plusieurs morceaux cadencés à des fréquences différentes. De tels composants sont très fréquents et nous en verrons quelques autres dans la suite du cours. Et pour parler de ces composants, il est très utile d'introduire la notion de domaine d'horloge.
Un domaine d'horloge est l'ensemble des registres qui sont reliés au même signal d'horloge, associé aux circuits combinatoires associés. Il n'incorpore pas l'arbre d'horloge ni même le circuit de génération du signal d'horloge, mais c'est là un détail. La plupart des composants électroniques ont un seul domaine d'horloge, ce qui veut dire que tout le circuit est cadencé à une fréquence unique, la même pour toute la puce. D'autres ont plusieurs domaines d'horloge qui vont à des fréquences distinctes. Les raisons à cela sont multiples, mais la principale est que autant certains circuits ont besoin d'être performants et donc d'avoir une haute fréquence, d'autres peuvent très bien faire leur travail à une fréquence plus faible. L'usage de plusieurs domaines d'horloge permet à une portion critique de la puce d'être très rapide, tandis que le reste de la puce va à une fréquence inférieure. Une autre raison est l’interfaçage entre deux composants allant à des vitesses différentes, par exemple pour faire communiquer un processeur avec un périphérique.
Il arrive que deux domaines d'horloge doivent communiquer ensemble et s'échanger des données, et l'on parle alors de clock domain crossing. Et cela pose de nombreux problèmes, du fait de la différence de fréquence. Les deux domaines d'horloge ne sont pas synchronisés, n'ont pas la même fréquence, la même phase, rien ne colle. Dans les explications qui suivent, on va prendre l'exemple de l'échange d'un bit entre deux domaines d'horloge, qui va d'un domaine d'horloge source vers un domaine d'horloge de destination. Dans ce cas, on peut passer par l'intermédiaire d'une bascule inséré entre les deux domaines d'horloge, bascule cadencée à la fréquence du domaine d'horloge source.
Mais pour l'échange d'un nombre, les choses sont plus compliquées et insérer un registre entre les deux domaines d'horloge ne marche pas. En effet, lors d'un changement de valeur du nombre à transmettre, tous les bits du nombre n'arrivent pas au même moment dans le registre. Il est possible que le domaine d'horloge de destination voit un état transitoire, où seule une partie des bits a été mise à jour. Le résultat est que le domaine d'horloge de destination utilisera une valeur transitoire faussée, causa tout un tas de problèmes. Pour éviter cela, les nombres transmis entre deux domaines d'horloge sont encodés en code Gray, dans lequel les états transitoires n'existent pas. Pour rappel, entre deux nombres consécutifs en code Gray, seul un bit change.
Dans les chapitres précédents, nous avons vu comment mémoriser un bit, dans une bascule. Mais les bascules en elles-mêmes sont rarement utiles seules, car les données à mémoriser font généralement plusieurs bits, pas un seul. Stocker plusieurs bits est la raison d'être des registres, des composants qui mémorisent des plusieurs bits, que l'on peut modifier et/ou récupérer plus tard. Il existe plusieurs types de registres, et nous allons faire la distinction entre les registres simples et les registres à décalage. Les registres simples sont capables de mémoriser un nombre, de taille fixe, rien de plus. Les registres à décalage sont des registres simples améliorés, capables de faire quelques petites opérations sur leur contenu.
Les registres simples
modifierLes registres simples sont capables de mémoriser un nombre, codé sur une quantité fixe de bits. On peut à tout moment récupérer le nombre mémorisé dans le registre : on dit alors qu'on effectue une lecture. On peut aussi mettre à jour le nombre mémorisé dans le registre, le remplacer par un autre : on dit qu'on effectue une écriture. Les seules opérations possibles sur ces registres sont la lecture (récupérer le nombre mémorisé dans le registre) et l'écriture (mettre à jour le nombre mémorisé dans le registre, le remplacer par un autre).
L'interface d'un registre simple
modifier
Niveau entrées et sorties, les registres possèdent des entrées-sorties pour les données mémorisées, mais aussi des entrées-sorties de commande. Les entrées-sorties pour les données permettent de lire le contenu du registre ou d'y écrire. Les entrées de commande permettent de configurer le registre pour lui ordonner de faire une écriture, pour le remettre à zéro, ou toute autre opération.
Les entrées de données sont utilisées pour l'écriture, alors que les sorties de données servent pour la lecture. Le nombre mémorisé dans le registre est disponible sur les sorties du registre. Pour utiliser les entrées d'écriture, on envoie le nombre à mémoriser (celui qui remplacera le contenu du registre) sur les entrées d'écriture et on configure les entrées de commande adéquates.
Les entrées de commande varient suivant le registre, mais on trouve au moins une entrée Enable, qui a le même rôle que pour une bascule, à savoir autoriser une écriture. Si l'entrée Enable est à 1, le registre mémorise ce qu'il y a sur l'entrée de donnée. Mais si l'entrée Enable est à 0, le registre n'est pas mis à jour : on peut mettre n'importe quelle valeur sur les entrées, le registre n'en tiendra pas compte et ne remplacera pas son contenu par ce qu'il y a sur l'entrée. Pour résumer, l'entrée Enable sert donc à indiquer au registre si son contenu doit être mis à jour, quand une écriture a lieu.
D'autres entrées de commandes sont parfois présentes, la plus commune étant une entrée permettant de remettre à zéro le registre. La présence d'un 1 sur cette entrée remet à zéro le contenu du registre, à savoir que celui-ci contient la valeur zéro.
Enfin, il faut distinguer les registres synchrones des registres asynchrones. Les registres synchrones sont reliés au signal d’horloge. Pour cela, ils disposent d'une entrée d'horloge sur laquelle on envoie le signal d'horloge. Ils ne sont mis à jour que si on présente un front montant sur l'entrée d'horloge. Les registres asynchrones ne sont pas reliés au signal d'horloge et sont mis à jour quand on envoie ce qu'il faut sur leur entré Enable, rien de plus.
L'intérieur d'un registre simple
modifierUn registre est composé de plusieurs bascules D qui sont toutes mises à jour en même temps. Cela vaut aussi bien pour les registres asynchrones que les registres synchrones. Pour cela, toutes les entrées E des bascules sont reliées à l'entrée de commande Enable. De plus, les registre synchrones envoient le signal d'horloge sur toutes les bascules. Avec un registre synchrone, toutes les bascules sont des bascules synchrones, qui ont toutes une entrée d'horloge, relié au signal d'horloge.

Les registres à décalage
modifierLes registres à décalage sont des registres dont le contenu est décalé d'un cran vers la gauche ou la droite sur commande. Nous aurons à les réutiliser plus tard dans ce cours, notamment dans la section sur les circuits de génération de nombres aléatoires, ou dans certains circuits liés au cache. Les registres à décalage sont presque tous synchrones et ce chapitre ne parlera que ce ces derniers. L'animation suivante illustre le fonctionnement d'un registre à décalage qui décale son contenu d'un cran vers la droite à chaque cycle d'horloge.

La classification des registres
modifierOn peut classer les registres selon le caractère de l'entrée et de la sortie, qui peut être parallèle (entrée de plusieurs bits) ou série (entrée d'un seul bit).
- Sur les registres simples, les entrées et sorties pour les données sont toujours parallèles. Pour un registre de N bits, il y a une entrée d'écriture de N bits et une sortie de N bits. C'est la raison pour laquelle ils sont appelés des registres à entrées et sorties parallèles.
- Sur les registres à entrée et sortie série, on peut mettre à jour un bit à la fois, de même qu'on ne peut en récupérer qu'un à la fois. Ces registres servent essentiellement à mettre en attente des bits tout en gardant leur ordre : un bit envoyé en entrée ressortira sur la sortie après plusieurs commandes de mise à jour sur l'entrée Enable.
- Les registres à décalage à entrée série et sortie parallèle sont similaires aux précédents : on peut ajouter un nouveau bit en commandant l'entrée Enable et les anciens bits sont alors décalés d'un cran. Par contre, on peut récupérer (lire) tous les bits en une seule fois. Ils permettent notamment de reconstituer un nombre qui est envoyé bit par bit sur un fil (un bus série).
- Enfin, il reste les registres à entrée parallèle et sortie série. Ces registres sont utiles quand on veut transmettre un nombre sur un fil : on peut ainsi envoyer les bits un par un.

Pour résumer, on distingue quatre types de registres (à décalage ou non), qui portent les noms de PIPO, PISO, SIPO et SISO. Les noms peuvent sembler barbares, mais il y a une logique derrière ces termes.La lettre P est pour parallèle, la lettre S est pour série. La lettre I signifie Input, ce qui veut dire entrée en anglais, la lettre O est pour Output, la sortie en anglais.
| Entrée parallèle | Entrée série | |
|---|---|---|
| Sortie parallèle | PIPO (registre simple) | SIPO |
| Sortie série | PISO | SISO |
L'intérieur d'un registre à décalage
modifierTous les registres sont conçus en plaçant plusieurs bascules les unes à la suite des autres, que ce soit pour les registres simples ou les registres à décalage. La seule différence tient dans la manière dont les bascules sont reliées. Toutes les bascules sont reliées à l'entrée d'horloge, l'entrée Enable, l'entrée Reset, ou aux autres entrées de commandes. Mais c'est une autre paire de manche pour les entrées/sorties de données.
Dans un registre simple, les bascules sont indépendantes et ne sont pas reliées entre elles.

À l'inverse, dans les registres à décalage, il existe des connexions entre bascules. Plus précisément, les bascules sont reliées les unes à la suite des autres, elles forment une chaîne de bascules reliées deux à deux. Et les connexions entre bascules sont les mêmes que l'on parle d'un registre à décalage de type SIPO, PISO ou SISO.

Outre le fait que les bascules sont reliées de la même manière, les autres connexions sont les mêmes dans tous les registres. L'entrée d'horloge (non-représentée dans les schémas qui vont suivre) est envoyée à toutes les bascules. Même chose pour l'entrée Enable, qui est reliée aux entrées E de toutes les bascules. La différence entre ces registres tient dans les endroits où se trouvent les entrées et les sorties du registre.
Une utilisation des registres : les mémoires SRAM
modifierMaintenant que nous avons les registres, il est temps d'en montrer une utilisation assez intéressante. Nous allons combiner les registres avec des multiplexeurs/démultiplexeurs pour former une mémoire adressable. Plus précisément, nous allons voir les mémoires de type SRAM, qui peuvent être vu comme un rassemblement de plusieurs registres. Mais ces registres ne sont pas assemblés pour obtenir un registre plus gros : par exemple, on peut fabriquer un registre de 32 bits à partir de 2 registres de 16 bits, ou de 4 registres de 8 bits. Ce n'est pas ce qui est fait sur les mémoires adressables, où les registres sont regroupés de manière à ce qu'il soit possible de sélectionner le registre qu'on veut consulter ou modifier.
Pour préciser le registre à sélectionner, chacun d'entre eux se voit attribuer un nombre : l'adresse. On peut comparer une adresse à un numéro de téléphone (ou à une adresse d'appartement) : chacun de vos correspondants a un numéro de téléphone et vous savez que pour appeler telle personne, vous devez composer tel numéro. Les adresses mémoires en sont l'équivalent pour les registres d'une mémoire adressable. Il existe des mémoires qui ne fonctionnent pas sur ce principe, mais passons : ce sera pour la suite.

L'interface d'une mémoire SRAM
modifier
Niveau entrées et sorties, une mémoire SRAM contient souvent des entrées-sorties dédiées aux transferts de données et plusieurs entrées de commande.
Les entrées de commande permettent de configurer la mémoire pour effectuer une lecture ou écriture, la mettre en veille, ou autre. Parmi les entrées de commande, on trouve une entrée de plusieurs bits, sur laquelle on peut envoyer l'adresse, appelée l'entrée d'adressage. On trouve aussi une entrée R/W d'un bit, qui permet de préciser si on veut faire une lecture ou une écriture. On trouve aussi parfois une entrée Enable Ou Chip Select, qui indique si la RAM est activée ou mise en veille, qui ressemble à l'entrée Enable des bascules.
Pour les données, tout dépend de la mémoire SRAM considérée. Sur certaines mémoires, on trouve une sortie sur laquelle on peut récupérer le registre sélectionné (on dit qu'on lit le registre) et une entrée sur laquelle on peut envoyer une donnée destinée à être écrite dans le registre sélectionné (on dit qu'on écrit le registre). On a donc une sortie pour la lecture et une entrée pour l'écriture. Mais sur d'autres mémoires SRAM, l'entrée et la sortie sont fusionnées en une seule entrée-sortie.
L'intérieur d'une mémoire RAM
modifierUne telle mémoire peut se fabriquer assez simplement : il suffit d'un ou de plusieurs multiplexeurs et de registres. Quand on présente l'adresse sur l'entrée de sélection du multiplexeur, celui-ci va connecter le registre demandé à la sortie (ou à l'entrée).

Les mémoire mortes et mémoires vives
modifierLes mémoires SRAM vues plus haut sont fabriquées avec des registres, eux-mêmes fabriqués avec des bascules, elles-mêmes fabriquées avec des portes logiques et/ou des transistors. Elles sont très utilisées, surtout dans les processeurs. Les mémoires sont très diverses et les mémoires SRAM ne sont qu'un type de mémoires parmi tant d'autres.
Les mémoires SRAM font elles-mêmes partie de la catégorie des mémoires vives, aussi appelées mémoires RAM (bien que ce soit un abus de langage, comme on le verra dans plusieurs chapitres). De telles mémoires sont des mémoires électroniques, qui sont adressables, dans lesquelles on peut lire et écrire. Nous verrons les différents types de RAM dans les chapitres sur les mémoires, aussi nous allons mettre cela de côté pour le moment.
Outre les mémoires RAM, il existe des mémoires qui sont elles aussi électroniques, adressables, mais dans lesquelles on ne peut pas écrire : ce sont les mémoires ROM. En général, les mémoires ROM conservent leur contenu quand on coupe l’alimentation électrique. Si on éteint l'ordinateur, le contenu de la ROM n'est pas perdu, il reste le même. C'est l'exact inverse de ce qu'on a avec les registres, mémoires SRAM, bascules et autres : tout est effacé quand on coupe le courant. Les mémoires RAM sont dites volatiles, alors que les mémoires ROM sont dites non-volatiles.
Les mémoires ROM
modifierIl existe deux types de mémoires ROM : les ROM non-programmables et les ROM programmables. La différence est que les premières sont fournies telles quelle et qu'on ne peut pas changer leur contenu, alors que ce n'est pas le cas pour les secondes.
Les ROM programmables sont des ROM dans lesquelles on ne peut évidemment pas écrire, mais qui permettent cependant de réécrire intégralement leur contenu : on dit qu'on reprogramme la ROM. Insistons sur la différence entre reprogrammation et écriture : l'écriture permet de modifier un byte sélectionné/adressé, alors que la reprogrammation efface toute la mémoire et la réécrit en totalité. Ce terme de programmation vient du fait que les mémoires ROM sont souvent utilisées pour stocker des programmes sur certains ordinateurs assez simples.
Les mémoires non-programmables sont aussi appelées des mask ROM. Elles sont utilisées dans quelques applications particulières, pour lesquelles on n'a pas besoin de changer leur contenu. Par exemple, elles étaient utilisées sur les vieilles consoles de jeux, pour stocker le jeu vidéo dans les cartouches. Elles servent aussi pour les firmware divers et variés, comme le firmware d'une imprimante ou d'une clé USB. De telles mémoires seront utiles dans les chapitres qui vont suivre. La raison en est que tout circuit combinatoire peut être remplacé par une mémoire adressable ! Imaginons que l'on souhaite créer un circuit combinatoire qui pour toute entrée A fournisse la sortie B. Celui-ci est équivalent à une ROM dont la lecture de l'adresse A renvoie B sur la sortie. Cette logique est notamment utilisée dans certains circuits programmables, les FPGA, comme on le verra plus tard.
L'implémentation des mémoires ROM
modifierLes mémoires ROM sont conçues, sur le même principe que les mémoires SRAM : on combine des registres avec des multiplexeurs. Il y a cependant des différences importantes, liées au fait que les écritures sont interdites. Et il y a une grosse différence suivant que la mémoire soit reprogrammable ou non.
Si la mémoire est reprogrammable, la différence principale est que les registres sont conçus de manière à ne pas être effacés quand on coupe le courant. Ils ne sont pas fabriqués avec des bascules, mais avec d'autres circuits plus complexes, à base de transistors à grille flottante. Les bascules sont remplacés par un équivalent qui se comporte de la même manière, sauf qu'on ne peut pas changer leur contenu facilement (interdiction des écritures), et que leur contenu ne s'efface pas quand on coupe le courant. Il peut y avoir d'autres différences, mais nous verrons cela dans le chapitre dédié aux mémoires ROM.
Quant aux mask ROM, leur implémentation est beaucoup plus simple. Ils sont conçus sur le même principe que les SRAM. Sauf que vu que l'écriture et la reprogrammation sont interdites, on peut retirer les démultiplexeurs utilisés pour les écritures (et la reprogrammation). Quand aux registres, ils sont remplacés en connectant directement la tension d'alimentation ou la masse sur les entrées des multiplexeurs de lecture. Là où on veut mettre un 0, on connecte la masse. Là où on veut mettre un 1, on connecte la tension d'alimentation. Le circuit obtenu se simplifie alors et peut se remplacer par un circuit composé d'un décodeur connecté à un paquet de portes OU.

L'implémentation d'une mask ROM est en réalité plus complexe sur certains points, notamment l'implémentation des portes OU, qui sont en réalité des OU câblés comme vu dans le chapitre sur les circuits imprimés. Mais nous reverrons cela dans quelques chapitres. L'important est que vous reteniez ce qu'est une mémoire ROM, qui n'est qu'un cas particulier de circuit combinatoire. Nous aurons à utiliser des mémoires ROM dans les chapitres suivants, à quelques endroits bien précis.
Les compteurs/décompteurs sont des circuits électroniques qui mémorisent un nombre qu'ils mettent à jour régulièrement. Pour donner un exemple d'utilisation, imaginez un circuit qui compte le nombre de voitures dans un parking dans la journée. Pour cela, vous allez prendre deux circuits qui détectent respectivement l'entrée ou la sortie d'une voiture, et un compteur. Le compteur est initialisé à 0 quand le parking est vide, puis est incrémenté à chaque entrée de voiture, décrémenté à chaque sortie. A chaque instant, le compteur contient le nombre de voitures dans le parking. C'est là un exemple d'un compteur, mais les exemples où on a besoin d'un circuit pour compter quelque chose sont nombreux.

L'incrémentation ou décrémentation d'un compteur augmente ou diminue le compteur d'une quantité fixe, appelée le pas du compteur. Suivant la valeur du pas, on fait la différence entre les compteurs d'un côté et les décompteurs de l'autre. Comme leur nom l'indique, les compteurs comptent alors que les décompteurs décomptent. Les compteurs augmentent le contenu du compteur à chaque mise à jour, alors que les décompteurs le diminuent. Dit autrement, le pas d'un compteur est positif, alors que le pas d'un décompteur est négatif. Les compteurs-décompteurs peuvent faire les deux, suivant ce qu'on leur demande.
Les compteurs/décompteurs : généralités
modifierLes compteurs et décompteurs sont très variés et ils se distinguent sur un grand nombre de points.
La plupart des compteurs utilisent un pas constant, qui est fixé à la création du compteur, ce qui simplifie la conception du circuit. Par exemple, les compteurs incrémenteurs/décrémenteurs ont un pas fixe de 1, à savoir que le contenu de leur registre est incrémenté de 1 à chaque cycle d'horloge ou demande d'incrémentation. D'autres ont un pas variable, à savoir qu'il change à chaque incrémentation/décrémentation. Cela peut aussi servir à compter quelque chose qui varie de manière non-régulière. Par exemple, imaginez un circuit qui compte combien de voitures sont rentrées sur une autoroute par un péage bien précis. Plusieurs voitures peuvent rentrer sur le péage durant la même minute, presque en même temps. Pour cela, il suffit de prendre un compteur à pas variable, qui est incrémenté du nombre de voiture rentrées sur l'autoroute lors de la dernière période de temps. Évidemment, de tels compteurs à pas variables ont une entrée supplémentaire sur laquelle on peut envoyer le pas du compteur.
Suivant le compteur, la représentation du nombre mémorisé change : certains utilisent le binaire traditionnel, d'autres le BCD, d'autre le code Gray, etc. Mais tous les compteurs que nous allons voir seront des compteurs/décompteurs binaires, à savoir que les nombres qu'ils utilisent sont codés sur bits. Au passage, le nombre de bits du compteur est appelé la taille du compteur, par analogie avec les registres.
Vu que la taille d'un compteur est limitée, il cesse de compter au-delà d'une valeur maximale. La plupart des compteurs comptent de 0 à , avec la taille du compteur. D'autres compteurs ne comptent pas jusque-là : leur limite est plus basse que . Par exemple, certains compteurs ne comptent que jusqu'à 10, 150, etc. Ils sont appelés des compteurs modulo. Prenons un compteur modulo 6, par exemple : il compte de 0 à 5, et est remis immédiatement à zéro quand il atteint 6. Il compte donc comme suit : 0, 1, 2, 3, 4, 5, 0, 1, 2, ...
Outre la valeur de la limite du compteur, il est aussi intéressant de se pencher sur ce qui se passe quand le compteur atteint cette limite. Certains restent bloqués sur cette valeur maximale tant qu'on ne les remet pas à zéro "manuellement" : ce sont des compteurs à saturation. D'autres recommencent à compter naturellement à partir de zéro : ce sont des compteurs modulaires.
L'interface d'un compteur/décompteur
modifierCompteurs et décompteurs sont presque tous des circuits synchrones, à savoir cadencés par une horloge. Du moins, c'est le cas des compteurs/décompteurs que nous allons voir dans ce chapitre, par souci de simplicité. Un compteur/décompteur est donc relié à une entrée d'horloge.
De plus, certains compteurs ont une entrée Enable qui active/désactive le comptage. Le compteur s'incrémente/décrémente seulement si l'entrée Enable est à 1, mais ne fait rien si elle est à 0. Les compteurs les plus simples sont incrémentés/décrémentés à chaque cycle d'horloge et n'ont pas d'entrée Enable, mais les compteurs plus complexes en ont une. Ce faisant, le compteur/décompteur est incrémenté seulement si deux conditions sont réunies : un front montant sur le signal d'horloge, et une entrée Enable à 1. Dans les schémas qui vont suivre, nous ferons mention soit au signal d'horloge, soit à l'entrée Enable. Si on fait référence à l'entrée Enable, il est sous-entendu que les bascules du registre sont cadencées par une horloge, qui leur dit quand s'actualiser.
En outre, les compteurs ont souvent une entrée Reset qui permet de les remettre à zéro.
Sur les compteurs/décompteurs, il y a une entrée qui décide s'il faut compter ou décompter. Typiquement, elle est à 1 s'il faut compter et 0 s'il faut décompter.
 |
 |
 |
Un compteur/décompteur peut parfois être initialisé avec la valeur de notre choix. Pour cela, ils possèdent une entrée d'initialisation sur laquelle on peut placer le nombre initial, couplée à une entrée Reset qui indique si le compteur doit être réinitialisé ou non. Certains compteurs/décompteurs spécifiques n'ont pas d'entrée d'initialisation, mais seulement une entrée de reset, mais il s'agit là d'utilisations assez particulières où le compteur ne peut qu'être réinitialisé à une valeur par défaut. Pour les compteurs/décompteurs, il faut aussi rajouter une entrée qui précise s'il faut compter ou décompter.
Le circuit d'un compteur : généralités
modifierUn compteur/décompteur peut être vu comme une sorte de registre (ils peuvent stocker un nombre), mais qu'on aurait amélioré de manière à le rendre capable de compter/décompter. Tous les compteurs/décompteurs utilisent un registre pour mémoriser le nombre, ainsi que des circuits combinatoires pour calculer la prochaine valeur du compteur. Ce circuit combinatoire est le plus souvent, mais pas toujours, un circuit capable de réaliser des additions (compteur), des soustractions (décompteurs), voire les deux (compteur-décompteur). Plus rarement, il s'agit de circuits conçus sur mesure, dans le cas où le pas du compteur est fié une bonne fois pour toutes.

Comme dit plus haut, certains compteurs ont une valeur maximale qui est plus faible que la valeur maximale du registre. Par exemple, on peut imaginer un compteur qui compte de 0 à 9 : celui-ci est construit à partir d'un registre de 4 bits qui peut donc compter de 0 à 15 ! Ces compteurs sont construits à partir d'un compteur modulo, auquel on rajoute un circuit combinatoire. Ce dernier détecte le dépassement de la valeur maximale et remet à zéro le registre quand c'est nécessaire, via l'entrée de Remise à zéro (entrée Reset).

L'incrémenteur/décrémenteur
modifierCertains compteurs, aussi appelés incrémenteurs comptent de un en un. Les décompteurs analogues sont appelés des décrementeurs. Nous allons voir comment créer ceux-ci dans ce qui va suivre. Il faut savoir qu'il existe deux méthodes pour créer des incrémenteurs/décrémenteurs. La première donne ce qu'on appelle des incrémenteurs asynchrones, et l'autre des incrémenteurs synchrones. Nous allons commencer par voir comment fabriquer un incrémenteur asynchrone, avant de passer aux incrémenteurs synchrones.
L'incrémenteur/décrémenteur asynchrone
modifierPour fabriquer un incrémenteur asynchrone, la première méthode, il suffit de regarder la séquence des premiers entiers, puis de prendre des paires de colonnes adjacentes :
- 000 ;
- 001 ;
- 010 ;
- 011 ;
- 100 ;
- 101 ;
- 110 ;
- 111.
Pour la colonne la plus à droite (celle des bits de poids faible), on remarque que celle-ci inverse son contenu à chaque cycle d'horloge. Pour les colonnes suivantes, le bit sur une colonne change quand le bit de la colonne précédente passe de 1 à 0, en clair, lorsqu'on a un front descendant sur la colonne précédente. Maintenant que l'on sait cela, on peut facilement créer un compteur avec quelques bascules. On peut les créer avec des bascules T, D, JK, et bien d'autres. Nous allons d'abord voir ceux fabriqués avec des bascules T, plus simples, puis ceux fabriqués avec des bascules D.
Les incrémenteurs/décrémenteurs asynchrones à base de bascules T
modifierPour rappel, les bascules T inversent leur contenu à chaque cycle d'horloge. Par simplicité, nous allons utiliser des bascules avec une sortie qui fournit l'inverse du bit stocké.
La première colonne inverse son contenu à chaque cycle, elle correspond donc à une bascule T simplifiée reliée directement à l'horloge. Les autres colonnes s'inversent quand survient un front descendant sur la colonne précédente. Le circuit qui correspond est illustré ci-dessous, avec des bascules T activées sur front descendant. Attention, cependant : la bascule la plus à gauche stocke le bit de poids FAIBLE, pas celui de poids fort. En fait, le nombre binaire est ici stocké de gauche à droite et non de droite à gauche ! Cela sera pareil dans tous les schémas qui suivront.

Il est aussi possible d'utiliser des bascules T actives sur front montant. En effet, notons qu'un front descendant sur la sortie Q correspond à un front montant sur la sortie /Q. En clair, il suffit de relier la sortie /Q d'une colonne sur l'entrée d'horloge de la suivante. Le circuit est donc le suivant :

Un décrémenteur est strictement identique à un incrémenteur auquel on a inversé tous les bits. On peut donc réutiliser le compteur du dessus, à part que les sorties du compteur sont reliées aux sorties Q des bascules.

Il est possible de fusionner un incrémenteur et un décrémenteur asynchrone, de manière à créer un circuit qui puisse soit incrémenter, soit décrémenter le compteur. Le choix de l'opération est réalisé par un bit d'entrée, qui vaut 1 pour une incrémentation et 0 pour une décrémentation. L'idée est que les entrées des bascules sont combinées avec ce bit, pour donner les entrées compatibles avec l'opération demandée.

L'incrémenteur asynchrone à base de bascules D
modifierIl est aussi possible d'utiliser des bascules D pour créer un compteur comme les deux précédents. En effet, une bascule T simplifiée est identique à une bascule D dont on boucle la sortie /Q sur l'entrée de données.

Cette implémentation peut être modifiée pour facilement réinitialiser le compteur à une valeur non-nulle. Pour cela, il faut ajouter une entrée au compteur, sur laquelle on présente la valeur d’initialisation. Chaque bit de cette entrée est reliée à un multiplexeur, qui choisir quel bit mémoriser dans la bascule : celui fournit par la mise à jour du compteur, ou celui présenté sur l'entrée d'initialisation. On obtient le circuit décrit dans le schéma qui suit. Quand l'entrée Reset est activée, les multiplexeurs connectent les bascules aux bits sur l'entrée d'initialisation. Dans le cas contraire, le compteur fonctionne normalement, les multiplexeurs connectant l'entrée de chaque bascule à sa sortie.

L'incrémenteur/décrémenteur synchrone
modifierPassons maintenant à l'incrémenteur synchrone. Pour le fabriquer, on repart de la séquence des premiers entiers. Dans ce qui va suivre, nous allons créer un circuit qui compte de 1 en 1, sans utiliser d'additionneur. Pour comprendre comment créer un tel compteur, nous allons reprendre la séquence d'un compteur, déjà vue dans le premier extrait :
- 000
- 001
- 010
- 011
- 100
- 101
- 110
- 111
On peut remarquer quelque chose dans ce tableau : peu importe la colonne, un bit s'inversera au prochain cycle d’horloge quand tous les bits des colonnes précédentes valent 1. Et c'est vrai quelle que soit la taille du compteur ou sa valeur ! Ainsi, prenons le cas où le compteur vaut 110111 :
- les deux premiers 1 sont respectivement précédés par la séquence 10111 et 0111 : vu qu'il y a un zéro dans ces séquences, ils ne s'inverseront pas au cycle suivant ;
- le bit qui vaut zéro est précédé de la séquence de bit 111 : il s'inversera au cycle suivant ;
- le troisième 1 en partant de la gauche est précédé de la séquence de bits 11 : il s'inversera aussi ;
- même raisonnement pour le quatrième 1 en partant de la gauche ;
- 1 le plus à droite correspond au bit de poids faible, qui s'inverse tous les cycles.
Pour résumer, un bit s'inverse (à la prochaine mise à jour) quand tous les bits des colonnes précédentes valent 1. Pour implanter cela en circuit, on a besoin d'ajouter un circuit qui détermine si les bits des colonnes précédentes sont à 1, qui n'est autre qu'un simple ET entre les bits en question. On pourrait croire que chaque bascule est précédée par une porte ET à plusieurs entrées qui fait un ET avec toutes les colonnes précédentes. Mais en réalité, il y a moyen d'utiliser des portes plus simples, avec une banale porte ET à deux entrées pour chaque bascule. Le résultat est indiqué ci-dessous.

L’implémentation de circuit avec des bascules D est légèrement plus complexe. Il faut ajouter un circuit qui prend en entrée le contenu de la bascule et un bit qui indique s'il faut inverser ou pas. En écrivant sa table de vérité, on s’aperçoit qu'il s'agit d'un simple XOR.

On peut appliquer la même logique pour un décrémenteur. Avec ce circuit, un bit s'inverse lorsque tous les bits précédents sont à zéro. En utilisant le même raisonnement que celui utilisé pour concevoir un incrémenteur, on obtient un circuit presque identique, si ce n'est que les sorties des bascules doivent être inversées avant d'être envoyée à la porte XOR qui suit.
La gestion des débordements d'entiers des incrémenteurs/décrémenteurs
modifierPour rappel, tout compteur a une valeur maximale au-delà de laquelle il ne peut pas compter. Pour un compteur modulo N, le compteur compte de 0 à N-1. Pour les compteurs non-modulo, ils peuvent compter de 0 à , pour un compteur de n bits. Tout nombre en dehors de cet intervalle ne peut pas être représenté. Si le résultat d'un calcul sort de cet intervalle, il ne peut pas être représenté par l'ordinateur et il se produit ce qu'on appelle un débordement d'entier. Les débordements d'entiers surviennent quand on incrémente une valeur au-delà de la valeur maximale du compteur, ce qui est loin d'être rare.
La gestion des débordements peut se faire de deux manières différentes, mais celle qui est la plus utilisée sur les compteurs est tout simplement de réinitialiser le compteur quand on dépasse la valeur maximale. Pour les compteurs non-modulo, il n'y a pas besoin de faire quoique ce soit, car ils sont réinitialisés automatiquement. Prenez un compteur contenant la valeur maximale 111....1111, incrémentez-le, et vous obtiendrez 000...0000 automatiquement, sans rien faire. Par contre, pour les compteurs modulo, c'est une autre paire de manche. La réinitialisation ne se fait pas automatiquement, et on doit ajouter des circuits pour réinitialiser le compteur, et pour détecter quand le réinitialiser.
Les incrémenteurs/décrémenteurs précédents ne peuvent pas être réinitialisés. Pour que cela soit possible, il faut d'abord rajouter une entrée qui commande la réinitialisation du compteur : mise à 1 pour réinitialiser le compteur, à 0 sinon. Ensuite, il faut que les bascules du compteur aient une entrée de réinitialisation Reset, qui les force à se remettre à zéro. Il suffit alors de faire comme avec n'importe quel registre réinitialisable : connecter ensemble les entrées Reset des bascules et relier le tout à l'entrée de réinitialisation du compteur.

Maintenant que l'on a de quoi les réinitialiser, on ajoute un comparateur qui détecte quand la valeur maximale est atteinte, afin de commander l'entrée de réinitialisation. Prenons un compteur modulo 6, par exemple, ce qui veut dire qu'il compte de 0 à 5, et est remis immédiatement à zéro quand il atteint 6. Il compte donc comme suit : 0, 1, 2, 3, 4, 5, 0, 1, 2, ... Le circuit comparateur vérifie si la valeur maximale 6 est atteinte et qui met à 1 l'entrée Reset si c'est le cas. Un tel circuit est juste un comparateur avec une constante, que vous savez déjà fabriquer à cet endroit du cours. Un exemple est illustré ci-dessous.

Il peut être utile de prévenir quand un compteur a débordé. Cela a des applications assez intéressantes, qu'on verra dans les chapitres suivants, notamment pour ce qui est des diviseurs de fréquence et des timers. Pour cela, on ajoute une sortie au compteur, qui est mise à 1 quand le compteur déborde. Pour les compteurs modulo, la sortie n'est autre que la sortie du comparateur. Et on peut généraliser pour n'importe quel N. Mais les choses sont plus compliquées pour les compteurs non-modulo, qui comptent de 0 au , pour lesquels on doit ajouter un circuit détecte quand un débordement d'entier a lieu. Pour cela, il y a plusieurs solutions. La plus simple est d'ajouter un comparateur qui vérifie si le compteur est à 0, signe qu'il vient d'être réinitialisé et a donc débordé. L'autre solution est d'ajouter une bascule à la toute fin de l'incrémenteur : cette bascule est mise à 1 en cas de débordement. Il suffit alors d'ajouter un circuit qui compare la valeur de cette bascule avec sa valeur du cycle précédent, et le tour est joué.
Les compteurs basés sur des registres à décalage
modifierCertains compteurs sont basés sur un registre à décalage. Pour simplifier les explications, nous allons les classer suivant le type de registre à décalage utilisé. Pour rappel, un registre à décalage dispose d'une entrée et d'une sortie. L'entrée peut être de deux types : soit une entrée série qui prend 1 bit, soit une entrée parallèle qui prend un nombre. Il en est de même pour la sortie, qui peut être série ou parallèle, à savoir qu'elle peut fournir en sortie soit un bit unique, soit un nombre complet. En combinant les deux, cela donne quatre possibilités qui portent les noms de registres à décalage PIPO, PISO, SIPO et SISO (P pour parallèle, S pour série, I pourInput, O pour Output).
| Entrée parallèle | Entrée série | |
|---|---|---|
| Sortie parallèle | (registre simple) | SIPO |
| Sortie série | PISO | SISO |
Les registres PIPO sont en réalité des registres simples, pas des registres à décalage, donc on les omets dans de qui suit. Les compteurs déterministes peuvent se fabriquer avec les trois types restants de registres à décalage, ce qui donne trois types de compteurs déterministes. Malheureusement, ces types ne portent pas de noms proprement dit. À la rigueur, les compteurs déterministes basés sur un registre SISO sont appelés des compteurs en anneau, et encore cette dénomination est légèrement impropre.
À l'exception de certains compteurs one-hot qui seront vu juste après, ces compteurs sont des compteurs à rétroaction. Un terme bien barbare pour dire que l'on boucle leur sortie sur leur entrée, parfois en insérant un circuit combinatoire entre les deux. Les compteurs à rétroaction sont particuliers dans le sens où on n'a pas à changer leur valeur en cours de fonctionnement : on peut les réinitialiser, mais pas insérer une valeur dans le compteur. La raison est qu'ils sont utilisés pour une fonction bien précise : dérouler une suite de nombres bien précise, prédéterminée lors de la création du compteur. Par exemple, on peut créer un compteur qui sort la suite de nombres 4,7,6,1,0,3,2,5 en boucle, quel qu’en soit l'utilité. Cela peut servir pour fabriquer des suites de nombres pseudo-aléatoires, ce qui est de loin leur utilisation principale, comme on le verra dans un chapitre spécialement dédié aux circuits générateurs d'aléatoire. Mais certaines de leurs utilisations sont parfois surprenantes.
- Un bon exemple de cela est leur utilisation dans l'Intel 8008, le tout premier microprocesseur 8 bits commercialisé, où ce genre de compteurs étaient utilisés pour le pointeur de pile, pour économiser quelques portes logiques. Ces compteurs implémentaient la séquence suivante : 000, 001, 010, 101, 011, 111, 110, 100. Pour les connaisseurs qui veulent en savoir plus, voici un article de blog sur le sujet : Analyzing the vintage 8008 processor from die photos: its unusual counters.
Les compteurs en anneau et de Johnson (SISO)
modifierLes compteurs basés sur des registres à décalage SISO sont aussi appelés des compteurs en anneau. Ils sont appelés ainsi car, généralement, on boucle la sortie du registre sur son entrée, ce qui veut dire que le bit sortant du registre est renvoyé sur son entrée. Pour les compteurs fabriqués avec un registre SISO (entrée et sortie de 1 bit), le bit entrant dans le registre à décalage est calculé à partir du bit sortant. Et il n'y a pas 36 façons de faire ce calcul : soit le bit sortant est laissé tel quel, soit il est inversé, pas d'autre possibilité. La première possibilité, où le bit entrant est égal au bit sortant, donne un compteur en anneau, vu plus haut. La seconde possibilité, où le bit sortant est inversé avant d'être envoyé sur l'entrée du registre à décalage, donne un compteur de Johnson. Les deux sont très différents, et ne fonctionnent pas du tout pareil.
Les compteurs en anneau : les compteurs one-hot
modifierLes compteurs one-hot sont appelés ainsi, car ils permettent de compter dans une représentation des nombres appelée la représentation one-hot. Dans une telle représentation, un bit est à 1 pendant que les autres sont à 0. es entiers sont codés de la manière suivante : le nombre N est encodé en mettant le énième bit à 1, avec la condition que l'on commence à compteur à partir de zéro. Il est important de remarquer que dans cette représentation, le zéro est n'est PAS codé en mettant tous les bits à 0. La valeur 0000...0000 n'encode aucune valeur, c'est une valeur interdite. A la place, le zéro est codé en mettant le bit de poids faible à 1. Pour N bits, on peut encoder seulement N valeurs.
| Décimal | Binaire | One-hot |
|---|---|---|
| 0 | 000 | 00000001 |
| 1 | 001 | 00000010 |
| 2 | 010 | 00000100 |
| 3 | 011 | 00001000 |
| 4 | 100 | 00010000 |
| 5 | 101 | 00100000 |
| 6 | 110 | 01000000 |
| 7 | 111 | 10000000 |
Un compteur en représentation one-hot contient un nombre codé de cette manière, qui est incrémenté ou décrémenté si besoin. Pour donner un exemple, la séquence d'un compteur en anneau de 4 bits est :
- 0001 ;
- 0010 ;
- 0100;
- 1000.
Incrémenter ou décrémenter le compteur demande alors de faire un simple décalage, ce qui fait que le compteur est un simple registre à décalage et non pas un compteur combiné à un incrémenteur/décrémenteur compliqué. L'économie en circuits d'incrémentation n'est pas négligeable. De plus, faire des comparaisons avec ce type de compteur est très simple : le compteur contient la valeur N si le énième bit est à 1. Pas besoin d'utiliser de circuit comparateur, juste de lire un bit. Mais les économies en termes de circuits (incrémenteur et comparateur) sont cependant contrebalancée par le fait que le compteur demande plus de bascules. Imaginons que l'on veut un compteur qui compte jusqu'à une valeur N arbitraire : un compteur en binaire normal utilisera environ bascules, alors qu'un compteur one-hot demande N bascules. Mais si N est assez petit, l'économie de bascules est assez faible, alors que l'économie de circuits logiques l'est beaucoup plus. De plus, il n'y a pas qu'une économie de circuit : le compteur est plus rapide.
- Si vous ne mettez que des 0 dans un compteur en anneau, il restera bloqué pour toujours. En effet, décaler une suite de 0 donnera la même suite de 0.
En théorie, un simple registre à décalage peut faire office de compteur one-hot, mais son comportement est alors invalide en cas de débordement. Un débordement met la valeur du registre à décalage à zéro, ce qui n'est pas l'effet recherché. On peut en théorie rajouter des circuits combinatoires annexes pour gérer le débordement, mais il y a encore plus simple : boucler la sortie du registre sur son entrée. Le résultat donne donc un type particulier de compteurs one-hot, appelé les compteurs en anneau sont des registres à décalage dont le bit sortant est renvoyé sur l'entrée. En faisant cela, on garantit que le registre revient à zéro, zéro étant codé avec un 1 dans le bit de poids faible. En cas de débordement, le registre est mis à zéro par le débordement, mais le bit sortant vaut 1 et ce 1 sortant est envoyé sur l'entrée pour y être inséré dans le bit de poids faible.

Il y a peu d'applications qui utilisent des compteurs en anneau. Ils étaient autrefois utilisés dans les tous premiers ordinateurs, notamment ceux qui géraient une représentation des nombres spécifique appelée la Bi-quinary coded decimal. Ils étaient aussi utilisés comme diviseurs de fréquence, comme on le verra dans le chapitre suivant. De nos jours, de tels compteurs sont utilisés dans les séquenceurs de processeurs, mais aussi dans les séquenceurs de certains périphériques, ou dans les circuits séquentiels simples qui se résument à des machines à états. Ils sont alors utilisés car très rapides, parfaitement adaptés au stockage de petites valeur, et surtout : ils n'ont pas besoin de circuit comparateur pour connaitre la valeur stockée dedans. Nous n'allons pas rentrer dans le détail de leurs utilisations car nous en reparlerons dans la suite du cours.
Les compteurs de Johnson : les compteurs unaires
modifierSur les compteurs de Johnson, le bit sortant est inversé avant d'être bouclé sur l'entrée.

La séquence d'un compteur de Johnson de 4 bits est :
- 1000 ;
- 1100 ;
- 1110 ;
- 1111 ;
- 0111 ;
- 0011 ;
- 0001 ;
- 0000.
Vous remarquerez peut-être que lorsque l'on passe d'une valeur à la suivante, seul un bit change d'état. Sachant cela, vous ferez peut-être le parallèle avec le code Gray vu dans les tout premiers chapitres, mais cela n'a rien à voir. Les valeurs d'un compteur Johnson ne suivent pas un code Gray classique, ni même une variante de celui-ci. Les compteurs qui comptent en code Gray sont foncièrement différents des compteurs Johnson.
Une application des compteurs de Johnson, assez surprenante, est la fabrication d'un signal sinusoïdal. En combinant un compteur de Johnson, quelques résistances, et des circuits annexes, on peut facilement fabriquer un circuit qui émet un signal presque sinusoïdal (avec un effet d'escalier pas négligeable, mais bref). Les oscillateurs sinusoïdaux numériques les plus simples qui soient sont conçus ainsi. Quant aux compteurs en anneau, ils sont utilisés en lieu et place des compteurs normaux dans des circuits qui portent le nom de séquenceurs ou de machines à états, afin d'économiser quelques circuits. Mais nous en reparlerons dans le chapitre sur l'unité du contrôle du processeur.
Les registres à décalage à rétroaction de type SIPO/PISO
modifierD'autres compteurs sont fabriqués en prenant un registre à décalage SIPO ou PISO dont on boucle l'entrée sur la sortie. Pour être plus précis, il y a très souvent un circuit combinatoire qui s'intercale entre la sortie et l'entrée. Son rôle est de calculer ce qu'il faut mettre sur l'entrée, en fonction de la sortie.
Les registres à décalage à rétroaction linéaire
modifierÉtudions en premier lieu le cas des registres à décalage à rétroaction linéaire. Le terme anglais pour de tels registres est Linear Feedback Shift Register, ce qui s’abrège en LFSR. Nous utiliserons cette abréviation dans ce qui suit pour simplifier grandement l'écriture. Les LFSR sont appelés ainsi pour plusieurs raisons. Déjà, registre à décalage implique qu'ils sont fabriqués avec un registre à décalage, et plus précisément des registres à décalage SIPO. A rétroaction indique que l'on boucle la sortie sur l'entrée. Linéaire indique que l'entrée du registre à décalage s'obtient par une combinaison linéaire de la sortie. Le terme combinaison linéaire signifie que l'on multiplie les bits de l'entrée par 0 ou 1, avant d'additionner le résultat. Vu que nous sommes en binaire, les constantes en question valent 0 ou 1. Voici un exemple de formule qui colle avec ce cahier des charges :
Une première simplification est possible : supprimer les multiplications par 0. Ce faisant, les bits associés ne sont tout simplement pas pris en compte dans le calcul d'addition. Tout se passe comme suit l'on ne tenait compte que de certains bits du LFSR, pas des autres. On a alors des opérations du genre :
Dans ce calcul, on ne garde qu'un seul bit du résultat, vu que l'entrée du registre à décalage ne fait qu'un bit. Par simplicité, on ne garde que le bit de poids faible. Or, il s'avère que cela simplifie grandement les calculs, car cela nous dispense de gérer les retenues. Et nous verrons dans quelques chapitres qu'additionner deux bits en binaire, sans tenir compte des retenues, revient à faire une simple opération XOR. On peut donc remplacer les additions par des XOR.
Le résultat est ce que l'on appelle un LFSR de Fibonacci, ou encore un LFSR classique, qui celui qui colle le mieux avec la définition.

Les registres à décalage à rétroaction de Gallois sont un peu l'inverse des LFSR vus juste avant. Au lieu d'utiliser un registre à décalage SIPO, on utilise un registre à décalage PISO. Pour faire la différence, nous appellerons ces derniers les LFSR PISO, et les premiers LFSR SIPO. Avec les LFSR PISO, on prend le bit sortant et on en déduit plusieurs bits à partir d'un circuit combinatoire, qui sont chacun insérés dans le registre à décalage à un endroit bien précis. Bien sûr, la fonction qui calcule des différents bits à partir du bit d'entrée conserve les mêmes propriétés que celle utilisée pour les LFSR : elle se calcule avec uniquement des portes XOR. Leur avantage est qu'ils sont plus rapides, sans avoir les inconvénients des autres LFSR. Ils sont plus rapides car il n'y a qu'une seule porte logique entre la sortie et une entrée du registre à décalage, contre potentiellement plusieurs avec les LFSR SIPO.

Les variantes des registres à décalage à rétroaction linéaire
modifierIl existe une variante des LFSR, qui modifie légèrement son fonctionnement. Il s'agit des registres à décalages à rétroaction affine.
Pour les LFSR SIPO, la fonction qui calcule le bit de résultat n'est pas linéaire, mais se calcule par une formule comme la suivante. Notez le +1 à la fin de la formule : c'est la seule différence.
Le résultat obtenu est l'inverse de celui obtenu avec le LFSR précédent. Un tel circuit est donc composé de portes NXOR, comparé à son comparse linéaire, composé à partir de portes XOR. Petite remarque : si je prends un registre à rétroaction linéaire et un registre à rétroaction affine avec les mêmes coefficients sur les mêmes bits, le résultat du premier sera égal à l'inverse de l'autre. Notons que tout comme les LFSR qui ne peuvent pas mémoriser un 0, de tels registres à décalage à rétroaction ne peuvent pas avoir la valeur maximale stockable dans le registre. Cette valeur gèle le registre à cette valeur, dans le sens où le résultat au cycle suivant sera identique. Mais cela ne pose pas de problèmes pour l'initialisation du compteur.
Pour les LFSR PISO, il existe aussi une variante affine, où les portes XOR sont remplacées par des portes NXOR.
Il existe enfin des compteurs de ce type qui ne sont pas des LFSR, même en incluant les compteurs de Gallois et autres. Ce sont des compteurs basés sur des registres à décalage où le circuit combinatoire inséré entre l'entrée et la sortie n'est pas basé sur des portes XOR ou NXOR. Ils sont cependant plus compliqués à concevoir, mais ils ont beaucoup d'avantages.
La période d'un compteur à rétroaction
modifierUn compteur à rétroaction est déterministe : pour le même résultat en entrée, il donnera toujours le même résultat en sortie. De plus, ce registre ne peut contenir qu'un nombre fini de valeurs, ce qui fait qu'il finira donc par repasser par une valeur qu'il aura déjà parcourue. Une fois qu'il repassera par cette valeur, son fonctionnement se reproduira à l'identique comparé à son passage antérieur. Lors de son fonctionnement, le compteur finira par repasser par une valeur parcourue auparavant et il bouclera. Il parcourt un nombre N de valeurs à chaque cycle, ce nombre étant appelé la période du compteur.
Le cas le plus simple est celui des compteurs en anneau, suivi par les compteurs Johnson. Les deux compteurs ont des périodes très différentes. Un compteur en anneau de N bits peut prendre N valeurs différentes, qui ont toutes un seul bit à 1. À l'opposé, un compteur Johnson peut prendre deux fois plus de valeurs. Pour nous en rendre compte, comparons la séquence de nombre déroulé par chaque compteur. Pour 5 bits, les séquences sont illustrées ci-dessous, dans les deux animations.


La période des registres à décalage à rétroaction linéaire dépend fortement de la fonction utilisée pour calculer le bit de sortie, des bits choisis, etc. Dans le meilleur des cas, le registre à décalage à rétroaction passera par presque toutes les valeurs que le registre peut prendre. Si je dis presque toutes, c'est simplement qu'une valeur n'est pas possible : suivant le registre, le zéro ou sa valeur maximale sont interdits. Si un registre à rétroaction linéaire passe par zéro, il y reste bloqué définitivement. La raison à cela est simple : un XOR sur des zéros donnera toujours 0. Le même raisonnement peut être tenu pour les registres à rétroaction affine, sauf que cette fois-ci, c'est la valeur maximale stockable dans le registre qui est fautive. Tout le chalenge consiste donc à trouver quels sont les registres à rétroaction dont la période est maximale : ceux dont la période vaut . Qu'on se rassure, quelle que soit la longueur du registre, il en existe au moins un : cela se prouve mathématiquement, même si nous ne vous donnerons pas la démonstration.
L'initialisation d'un compteur à rétroaction
modifierSur la quasi-totalité des compteurs et registres vu dans ce chapitre et les précédents, le compteur peut être initialisé à une valeur arbitraire. De plus, les débordements d'entiers sont possibles. Mais sur une bonne partie des compteurs à rétroaction, rien de tout cela n'est possible. Rappelons que les compteurs à rétroaction déroulent une suite de nombres bien précise, déterminée lors de la création du compteur. Donc, ça ne servirait à rien de charger une valeur arbitraire dans ces compteurs, du fait de leur fonctionnement. De plus, leur fonctionnement est périodique, ce qui fait que de tels compteurs ne peuvent pas déborder. En conséquence, un compteur à rétroaction ne peut pas être initialisé à une valeur arbitraire, mais seulement réinitialisé à une valeur de base qui est toujours la même.
Et ce qui est de l'initialisation, tous les compteurs basés sur un registre à décalage ne sont pas égaux. Pour résumer, deux cas sont possibles : soit le compteur peut être initialisé avec zéro sans que cela pose problème, soit ce n'est pas le cas. Les deux cas donnent des résultats différents. Autant le premier cas fait que l'on fait comme avec tous les autres registres, autant le second cas est inédit et demande des solutions particulières, qui sont les mêmes que le compteur oit en anneau, un LFSR, ou autre.
Le premier cas est celui où le compteur peut être initialisé avec zéro sans que cela ne pose problème. C'est le cas sur les compteurs de Johnson, mais aussi sur les registres à décalage à rétroaction non-linéaire. Sur de tels compteurs, la réinitialisation se fait comme pour n'importe quel registre/compteur. A savoir que les entrées de reset des bascules sont toutes connectées ensemble, au même signal de reset.

Dans le second cas, on ne peut pas l'initialiser avec uniquement des 0, comme les autres registres, et la méthode précédente ne fonctionne pas. C'est le cas sur les compteurs en anneau, et sur les LFSR. Sur les compteurs en anneau, lors de la réinitialisation, il faut faire en sorte que toutes les bascules soient réinitialisées, sauf une qui est mise à 1. Pour cela, il faut utiliser des bascules, avec une entrée pour les reset et une autre pour les mettre à 1. Le signal de reset est envoyée normalement sur toutes les bascules, sauf pour la première. La première bascule est configurée de manière à ce que le signal de reset la mette à 1, en envoyant le signal de reset directement sur l'entrée S (Set) qui met la bascule à 1 quand elle est activée. Cela garantit que le registre est réinitialisé avec un zéro codé en one-hot.

Une autre solution est de mettre un multiplexeur juste avant l'entrée du registre à décalage. Cette solution marché bien dans le sens où elle permet d'initialiser le registre avec une valeur arbitraire, qui est insérée dans le registre en plusieurs cycles. Elle fonctionne sur les registres en anneau, mais aussi sur les LFSR. Pour les LFSR, le multiplexeur est connecté soit au bit calculé par les portes XOR, soit par une entrée servant uniquement de l'initialisation.

Les compteurs en code Gray
modifierIl existe des compteurs qui comptent en code Gray. Pour rappel, le code Gray permet de coder des nombres d'une manière un peu différente du binaire normal. Son avantage principal est que lorsqu'on incrémente ou décrémente un nombre, seul un bit change ! Ils ont beaucoup d'avantages, qui sont tous liés à cette propriété.
L'absence d'états transitoires douteux
modifierLe premier l'absence d'état transitoires douteux. En binaire normal, lorsqu'on passe d'un nombre au suivant, plusieurs bits changent. La moyenne est d'environ deux bits, avec beaucoup de transitions de 1 bit, mais aussi quelques-unes qui en changent beaucoup plus. Le problème est que tous les bits modifiés ne le sont pas en même temps. Typiquement, les bits de poids faibles sont modifiés avant les autres.
Évidemment, à la fin du calcul, on obtient le résultat final, correct. Mais pendant le temps de calcul, le compteur peut se retrouver dans un état transitoire, où certains bits ont été modifiés mais pas les autres. Et c'est parfois un problème si le contenu de ce compteur est relié à des circuits assez rapides, qui peuvent, mais ne doivent pas voir cet état transitoire sous peine de dysfonctionner. L'usage de compteurs en code Gray permet d'éviter ce problème : vu que seul un bit est modifié lors d'une incrémentation/décrémentation, les états transitoires n'existent tout simplement pas.
Un exemple typique, évoqué dans les chapitres précédents, est l'échange d'informations entre deux domaines d'horloge. Pour rappel, il arrive que deux portions d'un circuit imprimé aillent à des fréquences différences : on dit que le circuit à plusieurs domaines d'horloge. Mais il faut échanger des informations entre ces deux portions, et divers problèmes surviennent alors. Un domaine d'horloge sera plus rapide que l'autre, et il pourra voir les états transitoires invisible pour le circuit. Et par voir, on veut dire qu'il les prendra pour des états valides, et cela fera dysfonctionner le circuit. Pour éviter cela, diverses techniques de croisement de domaines d'horloge existent. Et les compteurs Gray en font partie : si un domaine d'horloge utilise la valeur d'un compteur de l'autre, mieux vaut que ce compteur soit un compteur Gray. Et cette situation est assez fréquente !
La consommation énergétique du compteur Gray
modifierUn autre point est que la consommation d'énergie de ces compteurs est bien plus réduite qu'avec un compteur normal. Rappelons que pour fonctionner, les circuits électroniques consomment un peu d'électricité. Un compteur ne fait pas exception. Et la majeure partie de cette consommation sert à changer l'état des portes logiques. Faire passer un bit de 0 à 1 ou de 1 à 0 consomme beaucoup plus d'énergie que de laisser un bit inchangé. Ce qui fait que quand un compteur est incrémenté ou décrémenté, cela consomme un peu d'énergie électrique. Et les conséquences de cela sont nombreuses.
Premièrement, plus on change de bits, plus la consommation est forte. Or, comme on l'a dit plus haut, la moyenne pour un compteur binaire normal est de 2 bits changés par incrémentation/décrémentation, contre un seul pour un compteur Gray. Un compteur Gray consomme donc deux fois moins d'énergie. En soi, cela n'est pas grand-chose, un compteur consomme généralement peu. Mais l'avantage est que cela va avoir des effets en cascade sur les circuits qui suivent ce compteur. Si l'entrée de ces circuits ne change que d'un seul bit, alors leur état changera moins que si c'était deux bits. Les circuits qui suivent vont donc moins consommer.
Un autre avantage en matière de consommation énergétique est lié justement au point précédent, sur les transitions d'état douteux. Les circuits connectés au compteur vont voir ces transitions d'état douteux : ils vont réagir à ces entrées de transition et modifier leur état interne en réaction. Bien sur, l'état final correct fera de même, ce qui effacera ces états transitoires intermédiaires. Mais chaque état intermédiaire transitoire correspondra à un changement d'état, donc à une consommation d'énergie. En supprimant ces états transitoires, on réduit fortement la consommation d'énergie du circuit. Cela vaut pour le compteur Gray lui-même, mais aussi sur tous les circuits qui ont ce compteur comme entrée !
Les compteurs servent à créer divers circuits fortement liés la gestion de la fréquence, ainsi qu'à la mesure du temps. L'idée derrière ces circuits est tout simplement de compter les cycles d'horloge. Vu qu'un compteur/décompteur est cadencé par le signal d'horloge, on peut l'incrémenter ou le décrémenter à chaque cycle d'horloge, ce qui lui fait compter les cycles d'horloge. Compter les cycles d'horloge a plusieurs utilités. On peut s'en servir pour mesurer des durées, ou pour diviser une fréquence. Dans ce qui va suivre, nous allosn voire deux types de circuits : les diviseurs de fréquence, et les timers.
Les diviseurs de fréquence
modifierLes diviseurs de fréquence sont des circuits qui prennent en entrée un signal d'horloge et fournissent en sortie un autre signal d'horloge de fréquence plus faible. Plus précisément, la fréquence de sortie est 2, 3, 4, ou 18 fois plus faible que la fréquence d'entrée. La fréquence est donc divisée par un nombre N, qui dépend du diviseur de fréquence. Il existe des diviseurs de fréquence qui divisent la fréquence par 2, d'autres par 4, d'autres par 13, etc.
Leur implémentation est simple : il suffit d'un compteur auquel on rajoute une sortie. Pour être plus précis, il faut utiliser un compteur modulo. Pour rappel, le compteur modulo est un compteur qui est remis à zéro quand il atteint une valeur limite. Pour un diviseur de fréquence par N, il faut plus précisément un compteur modulo par N. Tous les N cycles, le compteur déborde, à savoir qu'il dépasse sa valeur maximale et est remis à zéro. Une sortie du compteur indique si le compteur déborde : elle est mise à 1 lors d'un débordement et reste à 0 sinon. L'idée est de compter le nombre de cycles d'horloges, et de mettre à 1 la sortie quand le compteur déborde.
Par exemple, pour diviser une fréquence par 8, on prend un compteur 3 bits. A chaque fois que le compteur déborde et est réinitialisé, on envoie un 1 en sortie. Le résultat est un signal qui est à 1 tous les 8 cycles d'horloge, à savoir un signal de fréquence 8 fois inférieure. La même idée marche avec un diviseur de fréquence par 6, sauf que l'on doit alors utiliser un compteur modulo par 6, ce qui veut dire qu'il compte de 0 à 5 comme suit : 0, 1, 2, 3, 4, 5, 0, 1, 2, ... Le compteur déborde tous les 6 cycles d’horloge, ce qui fait que sa sortie de débordement est à 1 tous les 6 cycles, ce qui est demandé.
Si n'importe quel compteur fait l'affaire, il est cependant utile d'utiliser les compteurs les plus adaptés à la tâche. Pour faire un diviseur de fréquence, on utilise rarement un compteur complet, mais souvent des compteurs plus simples, comme un circuit incrémenteur ou des compteurs en anneau.
Les diviseurs de fréquence basés sur des compteurs en anneau
modifierIl est rare que l'on doive diviser une fréquence par 50 ou par 100, par exemple. Un diviseur de fréquence divise une fréquence par N, avec N très petit. Or, les compteurs one-hot, aussi appelés compteurs en anneau, sont particulièrement adaptés pour compter jusqu'à des valeurs assez faibles : 6, 10, 12, 25, etc. Il est donc naturel d'utiliser un compteur en anneau dans un diviseur de fréquence.
Pour diviser une fréquence par N, il suffit de prendre un compteur en anneau qui compte de 0 à N-1 (inclut). Le signal de sortie est mis à 1 et/ou inversé quand le compteur est remis à zéro, c'est à dire quand son bit de poids faible est à 1. Une méthode alternative consiste à regarder au contraire le bit de poids fort : le compteur atteint N quand ce bit est à 1, ce qui fait qu'il a compté jusqu'à N. En clair, la sortie est obtenue en regardant la valeur du bit de poids faible/fort, sans même utiliser de comparateur. Pas besoin de comparateur, donc.
Et au-delà de ça, le circuit obtenu est beaucoup plus simple qu’avec un compteur normal. Et c'est la raison pour laquelle les diviseurs de fréquence sont souvent conçus en utilisant des compteurs one-hot. Plus on divise une fréquence par un N très petit, plus les compteurs auront d'avantages : très simples, demandent peu de portes logiques, sont très rapides, prennent peu de place, permettent de se passer de circuit comparateur.
Les diviseurs de fréquence basés sur des incrémenteurs à bascule T
modifierIl est aussi possible de concevoir des diviseurs de fréquence en utilisant un banal incrémenteur. Si l'incrémenteur est un incrémenteur non-modulo, on se retrouve avec un diviseur de fréquence qui divise la fréquence d'entrée par une puissance de deux. Pour comprendre comment les fabriquer, nous allons étudier le cas le plus simple : celui qui divise par 2 la fréquence d'entrée. Et bien sachez qu'il s'agit d'une simple bascule T. En effet, regardons ce qui se passe quand on envoie un signal constamment à 1 sur son entrée T. Dans ce cas, la bascule s'inversera une fois par chaque cycle d'horloge. Un cycle d'horloge sur la sortie correspond au temps passé entre deux inversions.

Pour créer un diviseur de fréquence par 4, il suffit d'enchainer deux fois le circuit précédent. La sortie de la première bascule T doit être envoyée sur l'entrée T de la seconde bascule. Et pour créer un diviseur de fréquence par 8, il suffit d'enchainer trois fois le circuit précédent. Et ainsi de suite. Au final, un diviseur de fréquence qui divise la fréquence d'entrée par 2^N est un enchainement de N bascules T, qui n'est autre qu'un circuit incrémenteur. La sortie d'un tel diviseur de fréquence se situe en sortie de la dernière bascule.

On peut en profiter pour créer un circuit à plusieurs sorties, en mettant une sortie par bascule. Le circuit, illustré ci-dessous, fournit donc plusieurs fréquences de sortie : une à la moitié de la fréquence initiale, une autre au quart de la fréquence d'entrée, une autre au huitième, etc.

Les timers
modifierLes timers, aussi appelés Programmable interval timer, sont des circuits capables de compter des durées. Leur fonctionnement est assez simple : on leur envoie un certain nombre de cycles d'horloge en entrée, et ils émettent un signal quand ce nombre de cycles est écoulé. Le signal en question est disponible sur une sortie de 1 bit, et correspond tout simplement au fait que cette sortie est mise à 1, pendant un cycle d'horloge. Ils permettent de compter des durées, exprimées en cycles d'horloge. On peut aussi générer un signal qui surviendra après 50 cycles d'horloge, ou après 100 cycles d'horloge, etc.
Les timers sont composés d'un compteur/décompteur cadencé par un signal d'horloge. Le compteur initialisé à 0, puis est incrémenté à chaque signal d'horloge, jusqu’à atteinte d'une valeur limite où il génère un signal. Pour un décompteur, c'est la même chose, sauf que le décompteur est initialisé à sa valeur limite et est décrémenté à chaque cycle, et envoie un signal quand il atteint 0. Les timers basés sur des décompteurs sont nettement plus simples que les autres, ce qui fait qu'ils sont plus utilisés. Pour que les timers soient configurables, on doit pouvoir préciser combien de cycles il faut (dé-)compter avant d'émettre un signal. On peut ainsi préciser s'il faut émettre le signal après 32 cycles d'horloge, après les 50 cycles, tous les 129 cycles, etc. Pour cela, il suffit de préciser le nombre de cycles à compter/décompter en entrée et d'initialiser le compteur/décompteur avec.
Les timers matériels peuvent compter de deux manières différentes, appelées mode une fois et mode périodique. Concrètement, le mode périodique divise la fréquence d'entrée, alors que le mode une fois compte durant une durée fixe avant de s'arrêter.
- En mode une fois, le timer s'arrête une fois qu'il a atteint la limite configurée. On doit le réinitialiser manuellement, par l'intermédiaire du logiciel, pour l'utiliser une nouvelle fois. Cela permet de compter une certaine durée, exprimée en nombre de cycles d'horloge.
- En mode périodique, le timer se réinitialise automatiquement avec la valeur de départ, ce qui fait qu'il reboucle à l'infini. En clair, le timer se comporte comme un diviseur de fréquence. Si le compteur est réglé de manière à émettre un signal tous les 9 cycles d'horloge, la fréquence de sortie sera de 9 fois moins celle de la fréquence d'entrée du compteur.
Un ordinateur est rempli de timers divers. Dans ce qui va suivre, nous allons voir les principaux timers, qui sont actuellement intégrés dans les PC modernes. Ils se trouvent sur la carte mère ou dans le processeur, tout dépend du timer.
Le watchdog timer
modifierLe watchdog timer est un timer spécifique dont le but est d'éteindre ou de redémarrer automatiquement l'ordinateur si jamais celui-ci ne répond plus ou plante. Tous les ordinateurs n'ont pas ce genre de timer, et beaucoup de PC s'en passent. Mais ce timer est très fréquent dans les architectures embarquées. Le watchdog timer est un compteur:décompteur) qui doit être réinitialisé régulièrement. S'il n'est pas réinitialisé, le watchdog timer déborde (revient à 0 ou atteint 0) et envoie un signal qui redémarre le système. le système est conçu pour réinitialiser le watchdog timer régulièrement, ce qui signifie que le système n'est pas censé redémarrer. Si jamais le système dysfonctionne gravement, le système ne pourra pas réinitialiser le watchdog timer et le système est redémarré automatiquement ou mis en arrêt.

Le Time Stamp Counter des processeurs x86
modifierTous les processeurs des PC actuels sont des processeurs dits x86. Nous ne pouvons pas expliquer ce que cela signifie pour le moment, retenez juste ce terme. Sachez que tous les processeurs x86 contiennent un compteur de 64 bits, appelé le Time Stamp Counter, qui mémorise le nombre de cycles d'horloge qu'a effectué le processeur depuis son démarrage. Les programmes peuvent accéder à ce registre assez facilement, ce qui est utile pour faire des mesures ou comparer les performances de deux applications. Il permet de compter combien de cycles d'horloge met un morceau de code à s’exécuter, combien de cycles prend une instruction à s’exécuter, etc. Les processeurs non-x86 ont un registre équivalent, que ce soit les processeurs ARM ou d'autres.
Malheureusement, ce compteur est tombé en désuétude pour tout un tas de raisons. La principale est que les processeurs actuels ont une fréquence variable. Nous expliquerons cela plus en détail dans quelques chapitres, mais les processeurs actuels font varier leur fréquence suivant les besoins. Ils augmentent leur fréquence quand on leur demande de faire beaucoup de calculs, et se mettent en mode basse(fréquence pour économiser de l'énergie si on ne leur demande pas grand chose. Avec une fréquence variable, le Time Stamp Counter perd complétement en fiabilité. Intel a tenté de corriger ce défaut en incrémentant ce registre à une fréquence constante, différente de celle du processeur, ce qui est encore le cas sur les processeurs Intel actuels. Le comportement est un peu différent sur les processeurs AMD, mais il compte par cycle d'horloge, avec des mécanismes de synchronisation assez complexes pour corriger l'effet de la fréquence variable.
L'horloge temps réel
modifierL'horloge temps réel est un timer qui génère une fréquence de 1024 Hz, soit près d'un Kilohertz. Dans ce qui suit, nous la noterons RTC, ce qui est l'acronyme du terme anglais Real Time Clock. La RTC prend en entrée un signal d'horloge de 32KHz, généré par un oscillateur à Quartz, et fournit en sortie un signal de fréquence 32 fois plus faible, c'est à dire de 1 KHz. Pour cela, elle est réglée en mode répétitif et son décompteur interne est initialisé à 32. La RTC génère donc un signal toutes les millisecondes, qui est envoyé au processeur. On peut, en théorie, changer la fréquence de la RTC, mais c'est rarement une bonne idée.
En théorie, la RTC permet de compter des durées assez courtes, comme le ping (le temps de latence d'un réseau, pour simplifier), le temps de rafraichissement de l'écran, ou bien d'autres choses. Mais dans les faits, les systèmes d'exploitation modernes ne l'utilisent pas pour ça. L'horloge temps réel est trop imprécise et sa fréquence n'aide pas. En effet, 1024 Hz est proche de 1000, mais pas assez pour faire des mesures à la missliseconde près, chose qui est nécessaire pour mesurer le ping ou d'autres choses utiles.
A la place, l'ordinateur l'utiliser pour compter les secondes, afin que l'ordinateur soit toujours à l'heure. Vous savez déjà que l'ordinateur sait quelle heure il est (vous pouvez regarder le bureau de Windows dans le coin inférieur droite de votre écran pour vous en convaincre) et il peut le faire avec une précision de l'ordre de la seconde. Mais pour savoir quel jour, heure, minute et seconde il est, l'ordinateur doit faire deux choses : mémoriser la date exacte à la seconde près, et avoir la capacité de compter le temps qui s'écoule, seconde par seconde. Pour cela, un ordinateur contient une CMOS RAM qui mémorise la date, et la RTC.
Le Programmable Interval Timer : l'Intel 8253
modifier
L'Intel 8253 est un timer programmable qui était autrefois intégré dans les cartes mères des ordinateurs personnels de type PC. Les premiers processeurs x86 étaient souvent secondés avec un Intel 8253 soudé à la carte mère. Il fût suivi par l'Intel 8254, qui en était une légère amélioration. S'il n'est plus présent dans un boitier de la carte mère, on trouve toujours un circuit semblable au 8253 à l'intérieur du chipset de la carte mère, voire à l'intérieur du processeur, pour des raisons de compatibilité. Sur les PC, il est cadencé par une horloge maitre, générée par un oscillateur à Quartz, dont la fréquence est de 32 768 Hertz, soit 2^15 cycles d'horloge par seconde. La fréquence générée par un compteur va donc de 18,2 Hz à environ 500 KHz. Il était utilisé pour dériver un grand nombre de fréquences utilisées dans l'ordinateur. Par exemple, le second compteur était utilisé par défaut pour le rafraichissement de la mémoire (D)RAM, mais il était souvent reprogrammé pour servir à générer des fréquences spécifiques par le BIOS ou la carte graphique.
L'intérieur de l'Intel 8253 est illustré ci-dessous. Nous allons expliquer l'ensemble de ce schéma, rassurez-vous, mais les explications seront plus simples à comprendre si vous survolez ce schéma en premier lieu.

L'Intel 8253 contient trois compteurs de 16 bits, numérotés de 0 à 2. Chaque compteur possède deux entrées et une sortie : l'entrée CLOCK est celle de l'horloge de 32 MHz, l'entrée GATE active ou désactive le compteur, la sortie fournit le signal voulu et/ou la fréquence de sortie.
L'Intel 8253 lui-même possède plusieurs entrées et sorties. En premier lieu, on voit un port de 8 bits connecté aux trois compteurs, qui permet à l'Intel 8253 de communiquer avec le reste de l'ordinateur. La communication se fait dans les deux sens : soit de l'ordinateur vers les compteurs, soit des compteurs vers l'ordinateur. Dans le sens ordinateur -> compteurs, cela permet à l'ordinateur de programmer les compteurs, de les initialiser. Dans l'autre sens, cela permet de récupérer le contenu des compteurs, même si ce n'est pas très utilisé.
Ensuite, on trouve un registre de 8 bits, le Control Word register qui mémorise la configuration de l'Intel 8253. Le contenu de ce registre détermine le mode de fonctionnement du compteur, de combien doit compter le compteur et bien d'autres choses. Pour programmer les trois compteurs, il faut écrire un mot de 8 bits dans le Control Word register. La configuration de l'Intel 8253 fournie en sur le port de 8 bits pendant un cycle d'horloge, puis est mémorisée dans ce registre et reste pour les cycles suivants.
Mais l'écriture a lieu à condition que les 5 entrées de configuration soit bien réglées. Les 5 entrées de configuration sont les suivantes :
- Deux bits A0 et A1 pour sélectionner le compteur voulu avec son numéro, ou le control word register.
- Un bit RD à mettre à 0 pour que l'ordinateur récupère le compteur sélectionné ou le control word register sur le port de 8 bits.
- Un bit WR à mettre à 0 pour que l'ordinateur modifie le compteur sélectionné ou le control word register, en envoyant le nombre pour l'initialisation sur le port de 8 bits.
- Un bit CS qui active ou désactive l'Intel 8253 et permet de l'allumer ou de l’éteindre.
Pour écrire dans le Control Word register, il faut mettre le bit CS à 0 (on active l'Intel 8253), mettre à 1 le bit RD et à 0 le bit WR (on indique qu'on fait une écriture), et sélectionner le Control Word register en mettant les deux bits A0 et A1 à 1. Pour écrire dans un compteur, il faut faire la même chose, sauf que les bits A0 et A1 doivent être configurés de manière à donner le numéro du compteur voulu. LA lecture s'effectue elle aussi de la même manière, mais il faut inverser les bits RD et WR.
Le High Precision Event Timer (HPET)
modifierDe nos jours, l'horloge temps réel et l'Intel 8253/8254 tendent à être remplacé par un autre timer, le High Precision Event Timer (HPET). Il s'agit d'un compteur de 64 bits, dont la fréquence est d'au moins 10 MHz. Il s'agit bien d'un compteur et non d'un décompteur. Il est couplé à plusieurs comparateurs, qui vérifient chacun une valeur limite, une valeur à laquelle générer un signal. La valeur limite peut être programmée, ce qui fait que chaque comparateur est associé à un registre pour mémoriser la valeur limite. Il doit y avoir au moins trois comparateurs, mais le nombre peut monter jusqu’à 256. Chaque comparateur doit pouvoir fonctionner en mode une fois, et au moins un comparateur doit pouvoir fonctionner en mode périodique.

Il faut noter que les systèmes d'exploitation conçus avant le HPET ne peuvent pas l'utiliser, pour des raisons techniques de compatibilité matérielle. C'est le cas de Windows XP avant le Service Pack 3. C'est la raison pour laquelle les cartes mères possèdent encore un PIT et une RTC, ou au moins qu'elles émulent RTC et PIT dans leurs circuits. D'ailleurs, pour économiser des circuits, les cartes mères modernes émulent le PIT et la RTC avec le HPET. Le HPET est configuré de manière à ce que le premier comparateur fournisse une fréquence de 1024 Hz, comme la RTC, et les 3 comparateurs suivants remplacent l'Intel 8253.
Le HPET gère de nombreux modes de fonctionnement : ses comparateurs peuvent être configuré en mode une fois ou périodique, on peut lui demander d'émuler la RTC et le PIT, etc. Aussi, il contient aussi de nombreux registres de configuration. En tout, on trouve 3 registres de configuration. à Cela, il faut ajouter trois registres pour configurer chaque comparateur indépendamment les uns des autres. Notons qu'il est aussi possible de lire ou écrire dans le compteur de 64 bits, mais ce n'est pas recommandé.
Les circuits de calcul et de comparaison
modifierDans ce chapitre, nous allons voir les décalages et les rotations. Nous allons voir ce que sont ces opérations, avant de voir les circuits associés. Précisons que dans les ordinateurs modernes, décalages et rotations sont prises en charge par un circuit, le barrel shifter, qui est capable d'effectuer aussi bien des rotations que des décalages. Il en existe de nombreux types, mais nous allons voir les barrel shifters basés sur des multiplexeurs. Mais expliquons d'abord les différentes opérations de décalage et de rotation.
Les opérations de décalage
modifierLes décalages décalent un nombre de un ou plusieurs rangs vers la gauche, ou la droite. Le nombre à décaler est envoyé sur une entrée du circuit, de même que le nombre de rangs l'est sur une autre. Le circuit fournit le nombre décalé sur sa sortie. Il existe plusieurs opérations de décalage différentes et on peut les classer en plusieurs types. Dans les grandes lignes, on distingue les rotations, les décalages logiques et les décalages arithmétiques. Elles se distinguent sur plusieurs points, les principaux étant les suivants :
- ce qu'on fait des bits qui sortent du nombre lors du décalage ;
- comment on remplit les vides qui apparaissent lors du décalage ;
- la manière dont est géré le signe du nombre décalé.

Pour comprendre les deux premiers points, prenons l'exemple d'un nombre de 8 bits, comme ci-contre. L'exemple montre le décalage de 01011101 de deux rangs. On obtient 010111 : les deux bits de poids forts sont vides et les deux bits de fin (01) sortent du nombre. Et cela vaut pour tout décalage : d'un côté le décalage fait sortir des bits du nombre, de l'autre certains bits sont inconnus ce qui laisse des vides dans le nombre. Le nombre de bits sortants et de vides est strictement égal au nombre de rangs de décalage : si on décale de n rangs, alors cela laissera n vides et fera sortir n bits. Pour un décalage de n rangs, les vides sont dans les n bits de poids fort pour un décalage à droite et dans les n bits de poids faibles pour un décalage à gauche. Et les n bits sortant sont à l'opposé : bits de poids faible pour un décalage à droite et bits de poids fort pour un décalage à gauche. Ces deux points, la gestion des vides et des bits sortants, sont assez liés.
Le différents types de décalages
modifierEn premier lieu, parlons de ce qu'on fait des bits qui sortent du nombre lors du décalage. Que fait-on de ces bits ?
La première solution est de les faire rentrer de l'autre côté, de les remettre au début du nombre décalé. L'opération en question est alors appelée une rotation. Il existe des rotations à droite et à gauche.
| MSB : bit de poids fort
(Most Significant Bit)
(Least Significant Bit) |
 |
 |
L'autre solution est d'oublier les bits sortants. L’opération est alors appelée un décalage, qui peut être soit un décalage logique, soit un décalage arithmétique. Le fait que l'on oublie les bits sortants fait que les vides ne sont pas remplis et qu'il faut trouver de quoi les combler. Et c'est là qu'on peut faire la distinction entre décalages logiques et arithmétiques.
Avec un décalage logique, les vides sont remplis par des zéros, aussi bien pour un décalage à gauche et un décalage à droite.
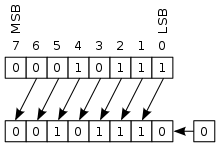 |
 |

Avec un décalage arithmétique, la situation est différente pour un décalage à gauche et à droite. Le principe des décalages arithmétique est qu'ils conservent le bit de signe du nombre décalé (qui est supposé être signé), contrairement aux autres décalages. La situation est cependant quelque peu compliquée et tout dépend de l'implémentation exacte du décalage, tous les ordinateurs ne faisant pas la même chose.
Il n'y a pas d’ambigüité pour les décalages à droite, qui sont tous réalisés de la même manière sur toutes les architectures. Pour un décalage à droite, les vides dans les vides de poids forts sont remplis par le bit de signe. Ce remplissage est une sorte d'extension de signe, ce qui fait que la conservation du signe est automatique.

Pour un décalage à gauche, les choses sont plus compliquées. Les bits de poids faible vides sont remplis par des zéros, comme pour un décalage logique. Mais pour ce qui est de la conservation du bit de signe, c'est plus compliqué. On a deux écoles : la première ne conserve pas le bit de signe, la seconde le fait. Dans le premier cas, le décalage est identique à un décalage logique à gauche. Dans le second cas, le bit de signe n'est pas concerné par le décalage.
L'interprétation mathématique des décalages
modifierL'utilité principale des opérations de décalage est qu'elles permettent de faire simplement des multiplications ou divisions par une puissance de 2. Un décalage logique/arithmétique correspond à une multiplication ou division entière par 2^n : multiplication pour les décalages à gauche, division pour les décalages à droite. Les décalages logiques fonctionnent pour les entiers non signés, alors que les décalages arithmétiques fonctionnent sur les entiers signés. Le fait est qu'un décalage logique ne donne pas le bon résultat avec un entier signé, la raison étant qu'il ne préserve pas le bit de signe. À l'inverse, le décalage arithmétique conserve le bit de signe, du moins pour les décalages à droite, ce qui le rend adapté pour les entiers signés. Les décalages arithmétiques à droite permettent donc de faire des divisions par 2^n sur des nombres signés.

Les arrondis lors des décalages
modifierLes décalages à droite entraînent l'apparition d'arrondis. Lorsqu'on effectue un décalage à droite, certains bits vont sortir du résultat et être perdus. L’équivalent en décimal est que les chiffres après la virgule sont perdus, ce qui arrondit le résultat. Mais cet arrondi dépend de la représentation des nombres utilisé. Pour comprendre pourquoi, il faut faire un rapide rappel sur les types d'arrondis en décimal.
En décimal, on peut arrondir de deux manières : soit on arrondit à l'entier au-dessus, soit on arrondi à l'entier au-dessous. Par exemple, prenons la division 29/4, qui a pour résultat 7.25. Cela donne 7 dans le premier cas et 8 dans le second. Pour un résultat négatif, c'est la même chose, mais le fait que le signe soit inversé change la donne. Par exemple, prenons le résultat de -29 / 4, soit -7.25. On peut l'arrondir soit à -7, soit à -8. En combinant les deux cas négatifs avec les deux cas positifs, on se trouve face à quatre possibilités :
- l'arrondi vers la plus basse valeur absolue (vers zéro), qui donne respectivement 7 et -7 dans l'exemple précédent.
- l'arrondi vers la plus basse valeur (vers moins l'infini), qui donne -8 et 7 dans l'exemple précédent ;
- l'arrondi vers la plus haute valeur (vers plus l'infini), qui donne -7 et 8 dans l'exemple précédent ;
- l'arrondi vers la plus haute valeur absolue (vers l'infini), qui donne 8 et -8 dans l'exemple précédent.
En binaire, c'est la même chose. Par exemple, 11100,1010 peut s'arrondir en 11100 ou en 11101, suivant qu'on arrondisse vers le bas ou vers le haut, et la même chose est possible pour les nombres négatifs. Précisons que ces arrondis n'ont lieu que si le résultat du décalage n'est pas exact. Pour un décalage d'un rang, à savoir une division par deux, seuls les nombres impairs donnent un arrondi, pas les nombres pairs. De manière générale, pour un décalage de n rangs, les nombres divisibles par 2^n ne donnent pas d'arrondi, alors que les autres si.
Lors d'un décalage, les bits sortants sont simplement éliminés. On pourrait croire que cela signifie que l'arrondi se fait vers zéro (vers la valeur inférieure). C'est bien le cas pour les nombres positifs, mais pas pour les nombres négatifs pour lesquels le résultat dépend de la représentation. Pour les décalages logiques, peu importe la représentation, l'arrondi se fait vers zéro (vu que tous les nombres sont traités comme positifs). Mais pour les décalages arithmétiques, c'est autre chose. En complément à 1, l'arrondi se fait bien vers zéro : les nombres positifs sont arrondis à la valeur inférieure et les nombres négatifs à la valeur supérieure. Par contre, en complément à deux, les nombres positifs et nombres négatifs sont arrondis à la valeur inférieure. En clair, l'arrondi se fait vers moins l'infini. Ce qui peut causer quelques problèmes si l'on ne fait pas attention, le résultat du décalage et d'une division pouvant varier à cause des règles d'arrondis.
Les débordements d'entiers lors des décalages
modifierOutre les arrondis, les décalages peuvent causer ce qu'on appelle des débordements d'entier. Ce terme barbare recouvre toutes les situations où le résultat d'un calcul devient trop gros pour être codé. Pour donner un exemple, prenons une situation équivalente mais en décimal. On suppose que l'on manipule des données codées sur 5 chiffres décimaux, pas plus. Si on prend le nombre 4512, le décalage à gauche d'un cran donne 45120, qui tient sur 5 chiffres : on n'a pas de débordement. Mais si je prends le nombre 97426, un décalage à gauche d'un cran donne 974260, ce qui ne tient pas dans 5 chiffres : on a un débordement d’entier. Celui-ci se traduit par le fait qu'un chiffre non-nul sorte du nombre. La même chose a lieu en binaire, avec les décalages à gauche. Un débordement d'entier en binaire se traduit par le fait qu'au moins un bit non-nul sorte à gauche.
La manière habituelle de gérer les débordements d'entiers est simplement de ne rien faire, mais de prévenir qu'un débordement a eu lieu. Pour cela, le circuit qui effectue le décalage a une sortie qui indique qu'un débordement a eu lieu lors du décalage. Cette sortie fournit un simple bit qui vaut 1 en cas de débordements et 0 sinon (ou l'inverse). Une autre solution est de corriger le débordement, mais si cela est fait pour les opérations arithmétiques, cela n'est pas fait pour les décalages.
Toujours est-il que déterminer l’occurrence d'un débordement n'est pas compliqué. Pour les décalages logiques, il suffit de prendre les bits sortants et de vérifier qu'un au moins d'entre eux vaut 1. Une simple porte OU sur les bits sortants fait l'affaire. Pour les décalages arithmétiques, il faut aussi tenir compte de la présence du bit de signe. La valeur des bits sortants dépend du signe positif ou négatif du nombre. Si le nombre décalé est positif, seuls des zéros doivent sortir, la présence d'un 1 indiquant un débordement d'entier. Pour un nombre négatif, c'est l'inverse : seuls des 1 doivent sortir (du fait des règles d'extension de signe), alors que l’occurrence d'un zéro trahit un débordement d'entier. Pour résumer le tout, les bits sortants sont censés être égaux au bit de signe, un débordement a eu lieu dans le cas contraire. L’occurrence d'un débordement se détermine en décomposant le décalage en une succession de décalages de 1 bit. Si un seul de ces décalages de 1 rang altère le bit de signe (change sa valeur), alors on a un débordement.
Il est possible de déterminer l’occurrence d'un débordement en analysant l'opérande, sans même avoir à faire le décalage. Pour un décalage vers la gauche de rangs, on sait que les bits sortants sont les bits de poids fort de l'opérande. En clair, on peut déterminer si un débordement a lieu en sélectionnant seulement les bits de poids fort de l'opérande. Pour cela, on peut simplement prendre l'opérande et lui appliquer un masque adéquat. Par exemple, prenons le cas d'un débordement pour un décalage logique, qui a lieu si au moins un bit sortant est à 1. Il suffit de prendre l'opérande, conserver les rangs bits de poids fort et mettre les autres à zéro, puis faire un ET entre les bits du résultat. La même logique prévaut pour les décalages arithmétiques, même s'il faut faire quelques adaptations.

Toujours est-il que le calcul des débordements peut se faire en parallèle du décalage, ce qui est utile. Précisons que le masque se calcule dans un circuit à part, qui ressemble beaucoup à un encodeur. Le masque calculé peut être utilisé sur certains circuits de décalages, pour transformer des rotations en décalage logiques, par exemple. Mais nous verrons cela plus tard.
Les décaleurs et rotateurs élémentaires
modifier
Pour commencer, nous allons voir deux types de circuits : les décaleurs qui effectuent un décalage (logique ou arithmétique, peu importe) et les rotateurs qui effectuent une rotation. Les deux circuits sont conceptuellement séparés, même s’ils se ressemblent. Faire la distinction sera utile dans la suite du cours. Leur interface est la même pour tous les décaleurs et rotateurs élémentaires. On doit fournir l'opérande à décaler et le nombre de rangs qu'on veut décaler en entrée, et on récupère l'opérande décalé en sortie.
Nous allons d'abord voir comment créer un circuit capable de décaler un nombre (vers la droite ou la gauche, peu importe) d'un nombre de rangs variable : on pourra décaler notre nombre de 2 rangs, de 3 rangs, de 4 rangs, etc. Il faudra préciser le nombre de rangs sur une entrée. On peut faire une remarque simple : décaler de 6 rangs, c'est équivalent à décaler de 4 rangs et redécaler le tout de 2 rangs. Même chose pour 7 rangs : cela consiste à décaler de 4 rangs, redécaler de 2 rangs et enfin redécaler d'un rang. En suivant notre idée jusqu'au bout, on se rend compte qu'on peut créer un décaleur à partir de décaleurs plus simples, reliés en cascade, qu'on active ou désactive suivant le nombre de rangs. L'idée est de prendre des décaleurs élémentaires qui décalent par 1, 2, 4, 8, etc ; bref : par une puissance de 2. La raison à cela est que le nombre de rangs par lequel on va devoir décaler est un nombre codé en binaire, qui s'écrit donc sous la forme d'une somme de puissances de deux. Chaque bit du nombre de rang servira à actionner le décaleur qui déplace d'un nombre égal à sa valeur (la puissance de deux qui correspond en binaire).

La même logique s'applique pour les rotateurs, la seule différence étant qu'il faut remplacer les décaleurs par 1, 2, 4, 8, etc ; par des rotateurs par 1, 2, 4, 8, etc.
Reste à savoir comment créer ces décaleurs qu'on peut activer ou désactiver à la demande. Surtout que le circuit n'est pas le même selon que l'on parle d'un décalage logique, d'un décalage arithmétique ou d'une rotation. Néanmoins, tous les circuits de décalage/rotation sont fabriqués avec des multiplexeurs à deux entrées et une sortie.
Le circuit décaleur logique
modifierCommençons par étudier le cas du décalage logique. On va prendre comme exemple un décaleur par 4 à droite, mais ce que je vais dire peut être adapté pour créer des décaleurs par 1, par 2, par 8, etc. La sortie vaudra soit le nombre tel qu'il est passé en entrée (le décaleur est inactif), soit le nombre décalé de 4 rangs. Ainsi, si je prends un nombre A, composé des bits a7, a6, a5, a4, a3, a2, a1, a0 ; (cités dans l'ordre), le résultat sera :
- soit le nombre composé des chiffres a7, a6, a5, a4, a3, a2, a1, a0 (on n'effectue pas de décalage) ;
- soit le nombre composé des chiffres 0, 0, 0, 0, a7, a6, a5, a4 (on effectue un décalage par 4).
Chaque bit de sortie peut prendre deux valeurs, qui valent soit zéro, soit un bit du nombre d'entrée. On peut donc utiliser un multiplexeur pour choisir quel bit envoyer sur la sortie. Par exemple, pour le choix du bit de poids fort du résultat, celui-ci vaut soit a7, soit 0 : il suffit d’utiliser un multiplexeur prenant le bit a7 sur son entrée 1, et un 0 sur son entrée 0. Il suffit de faire la même chose pour tous les autres bits, et le tour est joué.

En utilisant des décaleurs basiques par 4, 2 et 1 bit, on obtient le circuit suivant :

Le circuit décaleur arithmétique
modifierLes décalages arithmétiques sont basés sur le même principe, à une différence près : on n'envoie pas un zéro dans les bits de poids fort, mais le bit de signe (le bit de poids fort du nombre d'entrée). Un décaleur arithmétique ressemble beaucoup à un décaleur logique, la seule différence étant que c'est le bit de poids fort qui est relié aux entrées des multiplexeurs, là où il y avait un zéro avec le décaleur logique. Par exemple, reprenons un nombre A, composé des bits a7, a6, a5, a4, a3, a2, a1, a0 ; (cités dans l'ordre). La sortie d'un décaleur arithmétique par 4 sera :
- soit le nombre composé des chiffres a7, a6, a5, a4, a3, a2, a1, a0 (on n'effectue pas de décalage) ;
- soit le nombre composé des chiffres a7, a7, a7, a7, a7, a6, a5, a4 (on effectue un décalage arithmétique par 4).

En combinant des décaleurs basiques par 4, 2 et 1 bits, on obtient le circuit suivant :

Le circuit rotateur
modifierLes rotations sont elles aussi basées sur le même principe, sauf que ce sont les bits de poids faible qu'on injecte dans les bits de poids forts, au lieu d'un zéro ou du bit de signe. Le circuit est donc le même, sauf que les connexions ne sont pas identiques. Là où il y avait un zéro sur les entrées des multiplexeurs, on doit envoyer le bon bit de poids faible. Par exemple, reprenons un nombre A, composé des bits a7, a6, a5, a4, a3, a2, a1, a0 ; (cités dans l'ordre). La sortie d'un rotateur arithmétique par 4 sera :
- soit le nombre composé des chiffres a7, a6, a5, a4, a3, a2, a1, a0 (on n'effectue pas de décalage) ;
- soit le nombre composé des chiffres a3, a2, a1, a0, a7, a6, a5, a4 (on effectue un décalage arithmétique par 4).
Les barell shifters unidirectionnels
modifier
Dans ce qui précède, on a appris à créer un circuit qui fait des décalages logiques, un autre pour les décalages arithmétiques et un autre pour les rotations. Il nous reste à voir les décaleurs-rotateurs, aussi appelés des barrel shifters, qui sont capables de faire à la fois des décalages et des rotations. Certains décaleur-rotateurs sont capables de faire des rotations et des décalages logiques, d'autres savent aussi réaliser les décalages arithmétiques en plus. Un tel circuit a la même interface qu'un décaleur, sauf qu'on rajoute une entrée qui précise quelle opération faire. Cette entrée indique s'il faut faire un décalage logique, un décalage arithmétique ou une rotation.
Précisons dès maintenant qu'il faut faire la différence entre un barrel shifter unidirectionnel et un barrel shifter bidirectionnel. La différence entre les deux tient dans le sens possible des décalages. Le barrel shifter unidirectionnel ne peut faire que des décalages à gauche ou que des décalages à droite, mais pas les deux. À l'inverse, un barrel shifter bidirectionnel peut faire des décalages à droite et à gauche, suivant ce qu'on lui demande. Dans ce qui va suivre, nous allons nous concentrer sur les barrel shifters qui font des décalages/rotations vers la droite. Les explications seront valides aussi pour des décalages/rotations à gauche, avec quelques petites modifications triviales. Mais nous ne verrons pas comment fabriquer des barrel shifters bidirectionnels. En effet, de tels barrel shifters sont plus compliqués à fabriquer et sont de plus basés sur un barrel shifter unidirectionnel.
Il existe trois grandes méthodes pour fabriquer un décaleur-rotateur.
- La manière la plus naïve est de prendre un décaleur logique, un décaleur arithmétique et un rotateur, et de prendre le résultat adéquat suivant l’opération voulue. Le choix du bon résultat est effectué par une couche de multiplexeur adaptée. Mais cette solution est inutilement gourmande en multiplexeurs. Après tout, les trois circuits se ressemblent et partagent une même structure.
- Une autre solution, bien plus économe en multiplexeurs, élimine ces redondances en fusionnant les trois circuits en un seul. Elle part d'un circuit qui effectue des décalages logiques, auquel on ajoute des multiplexeurs pour le rendre capable de faire aussi les décalages arithmétiques et les rotations.
- La dernière méthode part d'un rotateur et on lui ajoute de quoi faire des décalages logiques.
Le décaleur-rotateur à base de multiplexeurs
modifierAvec la seconde méthode, on part d'un circuit qui effectue des décalages logiques, auquel on ajoute des multiplexeurs pour le rendre capable de faire aussi les décalages arithmétiques et les rotations. Ces nouveaux multiplexeurs ne font que choisir les bits à envoyer sur les entrées des décaleurs. Par exemple, prenons un décalage/rotation par 4 crans. La seule différence entre décalage logique, arithmétique et rotation est ce qu'on met sur les 4 bits de poids fort : un 0 pour un décalage logique, le bit de poids fort pour un décalage arithmétique et les 4 bits de poids faible pour une rotation. Pour choisir entre ces trois valeurs, il suffit de rajouter des multiplexeurs.
La prise en charge des rotations
modifierNous allons d'abord ajouter des multiplexeurs pour prendre en charge les rotations, un peu de la même manière qu'on modifie un décaleur logique pour lui faire faire aussi des décalages arithmétiques. Pour cela, prenons un décaleur par 4 et étudions les 4 bits de poids fort. Suivant le type de décalage, on doit envoyer soit un zéro, soit le bit de poids faible adéquat sur certaines entrées. Ce choix peut être réalisé par un multiplexeur, tant qu'il est commandé correctement. En clair, il suffit d'ajouter un ou plusieurs multiplexeurs pour chaque décaleur élémentaire par 1, 2, 4, etc. Ces multiplexeurs choisissent quoi envoyer sur l'entrée de l'ancienne couche : soit un 0 (décalage logique), soit le bit de poids faible (rotation). Notons qu'on doit utiliser un multiplexeur par entrée, contrairement au décaleur complet. La raison est qu'un décalage arithmétique envoie toujours le même bit dans les entrées de poids fort, alors qu'une rotation envoie un bit différent sur chaque entrée de poids fort, ce qui demande un multiplexeur par entrée.

La prise en charge des décalages arithmétiques
modifierIl est possible d'étendre le décaleur logique pour lui permettre de faire des décalages arithmétiques. Pour cela, même recette que dans le cas précédent. Encore une fois, suivant le type de décalage, on doit envoyer soit un zéro, soit le bit de poids fort sur certaines entrées. Il est possible d'utiliser un seul multiplexeur dans ce cas précis, car on envoie le même bit sur les entrées de poids fort.

En combinant des décaleurs basiques par 4, 2 et 1 bits, on obtient un circuit qui fait tous les types de décalages. Pas étonnant que ce circuit soit nommé un décaleur complet. Notons qu'on peut se contenter d'un seul mutiplexeur pour tout le barrel shifter, en utilisant le câblage astucieusement. Après tout, le choix entre 0 ou bit de poids fort est le même pour toutes les entrées concernées. Autant ne le faire qu'une seule fois et connecter toutes les entrées concernées au multiplexeur.

Le barrel shifter complet
modifierEn utilisant les deux modifications en même temps, on se retrouve avec un barrel-shifter complet, capable de faire des décalages et rotations sur 4 bits.

Les mask barrel shifters
modifierIl est temps de voir la dernière manière possible pour fabriquer un décaleur-rotateur. Celle-ci se base sur les masques, vus au chapitre précédent. L'idée est de faire une rotation et de corriger le résultat si c'est un décalage qui est demandé. La correction à effectuer dépend du type de décalage demandé, suivant qu'il soit logique ou arithmétique. Le circuit complet est organisé comme illustré ci-dessous.
Pour un décalage logique, il suffit de mettre les n bits de poids fort à zéro pour un décalage de n bits vers la droite (inversement, les n bits de poids faible pour un décalage vers la gauche). Et pour mettre des bits de poids fort à zéro sous une certaine condition, on doit utiliser un masque, comme vu précédemment. Le masque en question est le même que celui calculé pour le bit de débordement d'entier. Le masque est calculé par un circuit dédié, avant d'être appliqué au résultat du rotateur. Le circuit de calcul du masque est un encodeur modifié, qu'on peut concevoir avec les techniques des chapitres précédents.
Le circuit d'application du masque est composé d'une couche de portes ET et d'une couche de multiplexeurs. La couche de portes ET applique le masque sur le résultat du rotateur. Les multiplexeurs choisissent entre le résultat du rotateur et le résultat avec masque appliqué. Les multiplexeurs sont commandés par un bit de commande qui indique s'il faut faire un décalage ou une rotation.

Les barrel shifters bidirectionnels (à double sens de décalage/rotation)
modifierLe circuit précédent est capable d'effectuer des décalages et rotations, mais seulement vers la droite. On peut évidemment concevoir un circuit similaire capable de faire des décalages/rotations vers la gauche, mais il est intéressant d'essayer de créer un circuit capable de faire les deux. Un tel circuit est appelé un barrel shifter bidirectionnel. Notons qu'on doit obligatoirement fournir un bit qui indique dans quelle direction faire le décalage. Précédemment, nous avons vu qu'il existe deux méthodes pour créer un barrel shifter. La première se base sur un décaleur auquel on ajoute de quoi faire les rotations, alors que l'autre se base sur l'application d'un masque en sortie d'un rotateur. Dans ce qui va suivre, nous allons voir comment ces deux types de circuits peuvent être rendus bidirectionnels.

Les barrel shifters bidirectionnels basé sur des multiplexeurs
modifierCommençons par voir comment rendre bidirectionnel un barrel shifter basé sur des multiplexeurs. Pour rappel, ces derniers sont basés sur un décaleur qu'on rend capable de faire des rotations en ajoutant des multiplexeurs.
Une première solution est d'utiliser des barrel shifters bidirectionnels série, série signifiant que les deux sens sont calculés en série, l'un après l'autre. Ils sont composés de décaleurs qui sont capables de faire des décalages/rotations vers la gauche et vers la droite. De tels décaleurs peuvent se concevoir de diverses façons, mais la plus simple se base sur le principe qui veut qu'un décaleur est composé de décaleurs de 1, 2, 4, 8 bits, etc. Chaque décaleur est en double : une version qui décale vers la gauche, et une autre qui décale vers la droite. Lors d'un décalage vers la droite, les décaleurs élémentaire à gauche sont désactivés alors que les décaleurs vers la droite sont actifs (et réciproquement lors d'un décalage à gauche). Le bit qui indique la direction du décalage est envoyé à chaque décaleur et lui indique s'il doit décaler ou non.

Une autre solution, bien plus simple, est de prendre un décaleur/rotateur vers la gauche et un autre vers la droite, et de prendre la sortie adéquate en fonction de l'opération demandée. Le choix du résultat se fait encore une fois avec une couche de multiplexeurs. Le résultat est ce qu'on appelle un barrel shifter bidirectionnel parallèle, parallèle signifiant que les deux sens sont calculés en parallèle, en même temps. Notons que cette solution ressemble beaucoup à la précédente. À vrai dire, si on prend la première solution et qu'on regroupe ensemble les décaleur/rotateurs allant dans la même direction, on retombe sur un circuit presque identique à un barrel shifter bidirectionnel parallèle.
Les deux techniques précédentes utilisent beaucoup de portes logiques et il est possible de faire bien plus efficace. L'idée est simplement d'inverser l'ordre des bits avant de faire le décalage ou la rotation, puis de remettre le résultat dans l'ordre. Par exemple, pour faire un décalage à gauche, on inverse les bits du nombre à décaler, on fait un décalage à droite, puis on remet les bits dans l'ordre originel, et voilà ! Pour cela, il suffit de prendre un décaleur/rotateur à droite, et d'ajouter deux circuits qui inversent l'ordre des bits : un avant le décaleur/rotateur, un après. Ce circuit d'inversion est une simple couche de multiplexeurs. Le résultat est ce qu'on appelle un barrel shifter bidirectionnel à inversion de bits.

Le décaleur-rotateur bidirectionnel basé sur des masques
modifierDans cette section, nous allons voir concevoir un rotateur bidirectionnel avec des masques. Pour cela, il faut juste créer un rotateur bidirectionnel et utiliser des masques pour obtenir des décalages.
Le rotateur bidirectionnel
modifierPour créer le rotateur bidirectionnel, nous allons devoir étudier ce qui se passe quand on enchaine deux rotations successives. N'allons pas par quatre chemins : l'enchainement de deux rotations successives donne un résultat qui aurait pu être obtenu en ne faisant qu'une seule rotation. Le résultat issu de la succession de deux rotations est identique à celui d'une rotation équivalente. Et on peut calculer le nombre de rangs de la rotation équivalente à partir des rangs des deux rotations initiales. Pour cela, il suffit d'additionner les rangs en question. Par exemple, faire une rotation à droite par 5 rangs suivie d'une rotation à droite de 8 rangs est équivalent à faire une rotation à droite de 5+8 rangs, soit 13 rangs.
La logique est la même quand on enchaine des rotations à droite et à gauche. Il suffit de compter les rangs d'une rotation en les comptant positifs pour une rotation à droite et négatifs pour une rotation à gauche. Par exemple, une rotation de -5 rangs sera une rotation à gauche de 5 rangs, alors qu'une rotation de 10 rangs sera une rotation à droite de 10 rangs. On pourrait faire l'inverse, mais prenons cette convention pour l'explication qui suit. Toujours est-il qu'avec cette convention, l'addition des rangs donne le bon résultat pour la rotation équivalente. Par exemple, si je fais une rotation à droite de 15 rangs et une rotation à gauche de 6 rangs, le résultat sera une rotation de 15-6 rangs : c'est équivalent à une rotation à droite de 9 rangs.
Faisons dès maintenant remarquer quelque chose d'important. Prenons un nombre de n bits. Avec un peu de logique et quelques expériences, on remarque facilement qu'une rotation par ne fait rien, dans le sens où les bits reviennent à leur place initiale. Une rotation par est donc égale à pas de rotation du tout, ce qui est équivalent à faire une rotation par zéro rangs. Ce détail sera utilisé par la suite. Pour le moment, il nous permet de gérer le cas où l'addition de deux rangs donne un résultat supérieur à . Par exemple, prenons une rotation par 56 rangs pour un nombre de 9 bits. La division nous dit que 56 = 9*6 + 2. En clair, faire un décalage par 56 rangs est équivalent à faire 6 rotations totales par 9, suivie d'une rotation par 2 rangs. Les rotations par 9 ne comptant pas, cela revient en fait à faire une rotation par 2 rangs. Le même raisonnement fonctionne dans le cas général, et revient à faire ce qu'on appelle l'addition modulo n. C'est à dire qu'une fois le résultat de l'addition connu, on le divise par et l'on garde le reste de la division. Avec cette méthode, le nombre de rangs de la rotation équivalente est compris entre 0 et .
- Les additions modulo n seront notées comme suit : .
Armé de ces explications, on peut maintenant expliquer comment fonctionne le rotateur bidirectionnel. L'idée derrière ce circuit est de remplacer une rotation à droite par une rotation équivalente. Dans ce qui suit, nous utiliserons la notation suivante : est le nombre de rangs de la rotation équivalente, la taille du nombre à décaler et le nombre de rangs du décalage initial. En soi, ce n'est pas compliqué de trouver une rotation équivalente : une rotation à droite de rangs est équivalente à une rotation de rangs, à une rotation de rangs, et de manière générale à toute rotation de rangs. La raison est que les rotations par n ne comptent pas, elles sont éliminées par la division par . Mais les propriétés des calculs modulo n font que cela marche aussi quand on retranche n. Les bizarreries de l'arithmétique modulaire font que, quand on fait les additions modulo n, on peut remplacer tout nombre positif r par sans changer les résultats. Pour résumer, on a :
L'équation précédente dit qu'il suffit d'ajouter ou de retrancher n autant de fois qu'on veut au nombre de rangs initial, pour obtenir le nombre de rangs équivalent. Mais tous les cas possibles ne nous intéressent pas. En effet, on sait que le nombre de rangs de la rotation équivalente est compris entre 0 et . Le résultat que l'on recherche doit donc être compris entre 0 et . Et seul un cas respecte cette contrainte : celui où l'on retranche n une seule fois. On a alors :
L'équation nous dit qu'il est possible de remplacer une rotation à droite par une rotation à gauche équivalente. Par exemple, sur 8 bits et pour une rotation à droite de 6 bits, on a . En clair, la rotation équivalente est ici une rotation à gauche de 2 crans. Vous pouvez essayer avec d'autres exemples, vous trouverez la même chose. Par exemple, sur 16 bits, une rotation à gauche de 3 rangs est équivalente à une rotation à droite de 13 rangs.
Le calcul ci-dessus peut être simplifié en utilisant quelques astuces. Sur la plupart des ordinateurs, n est égal à 8, 16, 32, 64, ou toute autre nombre de la forme . Les cas où n vaut 3, 7, 14 ou autres sont tellement rares que l'on peut les considérer comme anecdotiques. De plus, est compris entre 0 et . On peut donc coder le rang sur un nombre bien précis de bits, tel que n est la valeur haute de débordement (en clair, n-1 est la plus grande valeur codable, n entraine un débordement d'entier). Grâce à cela, on peut coder le nombre de rangs en complément à un ou en complément à deux. Rappelons que ces deux représentations des nombres utilisent l'arithmétique modulaire, c'est à dire que l'addition et la soustraction se font modulo n, et que leur principe est de représenter tout n négatif par un n positif équivalent. Ainsi, tout négatif est codé par un positif équivalent. Et dans ces représentations, on a obligatoirement . En appliquant cette formule dans l'équation précédente, on a :
Reprenons l'exemple d'une rotation à gauche de 2 crans pour un nombre de 8 bits, ce qui est équivalent à une rotation de 6 crans à droite: on a bien 6 = -2 en complément à deux. Reste à faire le calcul ci-dessus par le circuit de rotation.
En complément à un, le calcul de l'opposé d'un nombre consiste simplement à inverser les bits de . En conséquence, le circuit est plus simple en complément à un. Le calcul du nombre de rangs demande juste un inverseur commandable, qu'on sait fabriquer depuis quelques chapitres.

En complément à deux, le calcul est le suivant :
On pourrait utiliser un circuit pour faire l'addition, mais il y a une autre manière plus simple de faire. L'idée est simplement de prendre le circuit en complément à un et d'y ajouter de quoi corriger le résultat final. En clair, on fait le calcul comme en complément à un, mais la rotation effectuée ne sera pas équivalente, du fait du +1 dans le calcul. Ce +1 indique simplement qu'il faut décaler le résultat obtenu d'un cran supplémentaire. Pour cela, on ajoute un rotateur d'un cran à la fin du circuit.

Le circuit final
modifierOn peut transformer ce circuit en décaleur-rotateur en appliquant la méthode vue plus haut, à savoir en appliquant un masque en sortie du rotateur. Le circuit obtenu est le suivant :

Tout circuit de calcul peut être conçu par les méthodes vues dans les chapitres précédents. Mais les circuits de calcul actuels manipulent des nombres de 32 ou 64 bits, ce qui demanderait des tables de vérité démesurément grandes : plus de 4 milliards de lignes en 32 bits ! Il faut donc ruser, pour créer des circuits économes en portes logiques.
Dans ce chapitre, nous allons voir les circuits capables de faire une addition ou une soustraction, ainsi que quelques circuits spécialisés, comme les additionneurs multi-opérande. Précisons cependant que les constructeurs de processeurs, ainsi que des chercheurs en arithmétique des ordinateurs, travaillent d'arrache-pied pour trouver des moyens de rendre ces circuits de calcul plus rapides et plus économes en énergie. Autant vous dire que les circuits que vous allez voir sont vraiment des circuit qui font pâle figure comparé à ce que l'on peut trouver dans un vrai processeur commercial !
Les circuits pour additionner 2 ou 3 bits
modifierPour rappel, l'addition se fait en binaire de la même manière qu'en décimal. On additionne les chiffres/bits colonne par colonne, une éventuelle retenue est propagée à la colonne d'à côté. La soustraction fonctionne sur le même principe, sur le même modèle qu'en décimal.

En clair, additionner deux nombres demande de savoir additionner 2 bits et une retenue sur chaque colonne, et de propager les retenues d'une colonne à l'autre. La propagation des retenues est quelque chose de simple en apparence, mais qui est sujet à des optimisations extraordinairement nombreuses. Aussi, pour simplifier l'exposition, nous allons voir comment gérer une colonne avant de voir comment sont propagées les retenues. Le fait que les additionneurs soient organisés de manière à séparer les deux nous aidera grandement. En effet, tout additionneur est composé d'additionneurs plus simples, capables d'additionner deux ou trois bits suivant la situation. Ceux-ci gèrent ce qui se passe sur une colonne.
Le demi-additionneur
modifierUn additionneur deux bits implémente la table d'addition, qui est très simple en binaire. Jugez plutôt :
- 0 + 0 = 0, retenue = 0 ;
- 0 + 1 = 1, retenue = 0 ;
- 1 + 0 = 1, retenue = 0 ;
- 1 + 1 = 0, retenue = 1.
Un circuit capable d'additionner deux bits est donc simple à construire avec les techniques vues dans les premiers chapitres. On voit immédiatement que la colonne des retenues donne une porte ET, alors que celle du bit de somme est calculé par un XOR. Le circuit obtenu est appelé un demi-additionneur. Le voici :
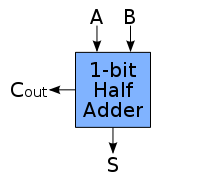 |
 |
L'additionneur complet
modifier
Si on effectue une addition en colonne, on doit additionner les deux bits sur la colonne, mais aussi additionner une éventuelle retenue. Il faut donc créer un circuit qui additionne trois bits : deux bits de données, plus une retenue. Ce circuit qui additionne trois bits est appelé un additionneur complet. Voici sa table de vérité :
| Retenue entrante | Opérande 1 | Opérande 2 | Retenue sortante | Résultat | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
Il est possible d'utiliser un tableau de Karnaugh pour traduire la table de vérité, mais elle donne un résultat légèrement sous-optimal. D'autres méthodes donnent des résultats plus compréhensibles.
L'additionneur complet conçu avec deux demi-additionneurs
modifierLa solution la plus simple consiste à enchaîner deux demi-additionneurs : un qui additionne les deux bits de données, et un second qui additionne la retenue au résultat. La retenue finale se calcule en combinant les sorties de retenue des deux demi-additionneurs, avec une porte OU. Pour vous en convaincre, établissez la table de vérité de ce circuit, vous verrez que ça marche.

|

|
Avec ce circuit, la somme est calculée avec deux portes XOR l'une à la suite de l'autre. La retenue sortante, quant à elle, est calculée avec un circuit à quatre portes logiques. Les autres versions de l'additionneur complet que nous allons voir sont des dérivés de ce circuit, auquel on a appliqué quelques simplifications. Les simplifications portent surtout sur le circuit de calcul de la retenue. En effet, le calcul de la somme n'est pas simplifié, car on ne peut pas vraiment simplifier deux portes XOR qui se suivent simplement. Par contre, le calcul de la retenue sortante est un cas particulier d'un calcul qui revient souvent en électronique, comme nous allons le voir dans la section suivante.
L'additionneur complet basé sur une porte à majorité
modifierIl est possible de calculer la retenue sortante assez simplement, mais à condition de remarquer quelque chose. La retenue sortante vaut 1 seulement si une condition particulière est respectée : au moins 2 des 3 bits d'entrée doivent être à 1. Dit autrement, plus de la moitié des bits d'entrées doivent être à 1. Or,n il existe une porte logique qui fonctionne comme cela : elle met sa sortie à 1 si plus de moitié des entrées vaut 1, et sort un 0 sinon. Cette porte logique complexe s'appelle une porte à majorité. On obtient donc un additionneur en combinant deux portes XOR pour calculer la somme, et une porte à majorité pour la retenue sortante.

L'additionneur complet basé sur un multiplexeur
modifierIl est aussi possible de fabriquer un additionneur complet en remplaçant la porte à majorité par un multiplexeur. Le câblage du circuit est cependant totalement différent.
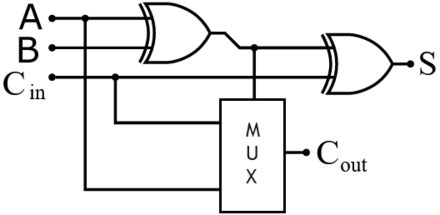
Il faut noter qu'il est possible d'implémenter n'importe quel circuit avec uniquement des multiplexeurs, et un additionneur complet ne fait pas exception. Voici une implémentation possible :

L'additionneur complet basé sur la propagation et la génération de retenue
modifierUne autre solution calcule la retenue finale d'une autre manière, en combinant le résultat de deux circuits séparés. Le premier vérifie si l'addition génère une retenue, l'autre si la retenue en entrée est propagée en sortie.
- Une retenue est dite générée si l'addition donne une retenue, quelle que soit la retenue envoyée en entrée (sous-entendu, même si celle-ci vaut 0). Cela arrive quand les bits additionnés valent tous deux 1 : la retenue sera alors de 1, seul le bit du résultat changera. On peut donc calculer si une retenue est générée en faisant un ET entre les deux bits d'entrée.
- Une retenue est propagée si la retenue en sortie est égale à la retenue en entrée. En clair, la retenue n'existe que si on envoie une retenue en entrée. Dans ce cas, la retenue finale vaut 1 quand un seul des deux bits d'entrée vaut 1, et vaut 0 sinon. En clair, on peut déterminer si une retenue est propagée en faisant un XOR entre les deux bits d'entrée.
Vous remarquerez que les signaux P et G sont calculés par le premier demi-additionneur.
Ces deux circuits fournissent deux signaux : un signal G qui indique si une retenue est générée, et un signal P qui indique si une retenue est propagée. En combinant les deux, on peut calculer la retenue finale. Elle vaut 1 soit quand la retenue est générée, soit quand la retenue d'entrée vaut 1 et qu'elle est propagée. Dans les autres cas, elle vaut zéro. La traduction en équation logique dit qu'il suffit de faire un ET entre la retenue d'entrée et le bit P, puis de faire un OU avec le bit G. Le circuit obtenu est strictement identique au circuit précédent.

L'additionneur en Manchester carry chain est une modification de l'additionneur précédent, où les portes logiques en orange dans le schéma précédent sont remplacées par un circuit à base de portes à transmission. L'idée est que la retenue de sortie vaut : soit la retenue générée, soit la retenue à propager. Il suffit donc d'ajouter deux portes à transmission : une pour connecter la retenue générée sur la sortie, une autre pour propager/connecter la retenue d'entrée sur la sortie. L'activation de chaque porte à transmission est assez simple : il dépend du signal de propagation généré par la porte XOR en vert. La première porte à transmission est activée quand il est à 1, désactivée pour un 0, l'autre porte fait l'exact inverse. Une simple porte NON suffit.
Mais l'usage de portes à transmission a quelques défauts. Le principal est que, vu que la retenue d'entrée est envoyée sur la sortie à travers des interrupteurs, la tension sur la retenue de sortie est plus faible que la tension de la retenue d'entrée. Ce qui pose des problèmes quand on doit enchainer plusieurs additionneurs de ce type, mais laissons cela pour plus tard. Il existe une version de cet additionneur en logique dynamique, où les transistors sont utilisés comme des condensateurs et sont préchargés avant de faire leurs calculs, mais nous n'en parlerons pas ici.

Il existe des additionneurs qui fournissent les signaux P et G en plus du résultat et de la retenue sortante. Mais il en existe qui ne calculent pas la retenue finale. Par contre, ils calculent les signaux P et G qui disent si l'addition de deux bits génère une retenue, ou si elle propage une retenue provenant d'une colonne précédente. Ils fournissent ces deux signaux sur deux sorties P et G pour indiquer s'il y a propagation et génération de retenue. Un tel additionneur est appelé un additionneur P/G (P/G pour propagation/génération). Ils seront très utiles pour créer des circuits additionneurs comme on le verra plus bas.

|

|
L'additionneur complet basé sur une modification de la retenue sortante
modifierDans les circuits précédents, la retenue sortante et le bit du résultat sont calculés séparément, même si quelques portes logiques sont partagées entre les deux. Une autre méthode, utilisée dans l'unité de calcul de l'Intel 4004 et de l'Intel 8008, fonctionnait autrement. Avec elle, la retenue sortante et calculée en premier, puis on détermine le bit du résultat à partir de la retenue sortante. En effet, le bit du résultat est l'inverse de la retenue sortante, sauf dans deux cas : les trois bits d'entrée sont à 0, où ils sont tous à 1. Dans les deux cas d'exception, le bit du résultat vaut 0, quelque soit la retenue sortante. L'implémentation de cette idée en circuit est assez simple.
Au circuit de calcul de la retenue sortante, il faut ajouter deux circuits, un pour vérifie si tous les bits additionner valent 0, l'autre s'ils valent tous 1. Leur sortie vaut 1 si c'est le cas. Le premier est une simple porte ET, l'autre une porte NOR. Ensuite, on combine le résultat des trois circuits précédents pour obtenir le résultat final. Si un seul des trois circuits a sa sortie à 1, alors la sortie finale doit être à 0. Elle est à 1 sinon. C'est donc une porte NOR qu'il faut utiliser. Le circuit final est donc celui-ci.

- Notons qu'on peut encore optimiser le circuit en fusionnant les deux portes NOR entre elles, mais c'est là un détail.
A ce stade, vous êtes certainement étonné qu'un tel circuit ait pu être utilisé. Il utilise beaucoup plus de portes logiques que le circuit précédent, a une profondeur logique supérieure : il n'a rien d'avantageux. Sauf qu'il était utilisé sur d'anciens processeurs, qui utilisaient des techniques de fabrication différentes de celles actuellement utilisées. Les processeurs de l'époque utilisaient la technologie TTL, et non la technologie CMOS des processeurs modernes. Et avec la technologie TTL, il est possible d'implémenter les portes logiques ET/OU/NON que nous avons évoqué rapidement dans le chapitre sur les portes logiques ! Un additionneur complet construit ainsi ne prenait que deux portes logiques : une pour le calcul de la retenue sortante, une autre pour le reste du circuit.
Les autres implémentations
modifier
Les implémentations précédentes utilisent des portes logiques, ce qui est simple et facile à comprendre, mais pas forcément le top du top en termes de performances. Mais les additionneurs des processeurs modernes sont nettement plus optimisés que ça. Et pour cela, ils sont optimisés directement au niveau des transistors. Cela permet de les rendre plus rapides, notamment au niveau du calcul de la retenue. Là où l'addition des deux bits d'opérande se doit d'être rapide, le calcul de la retenue doit absolument être le plus rapide possible, c'est crucial pour les circuits qui vont suivre. Outre les optimisations en termes de rapidité, une implémentation à base de transistors peut économiser des transistors. Tout dépend de l'objectif visé, certains circuit optimisant à fond pour la vitesse, d'autres pour le nombre de transistors, d'autres font un compromis entre les deux. Les circuits de ce genre sont très nombreux, trop pour qu'on puisse les citer.
L'addition non signée
modifierVoyons maintenant un circuit capable d'additionner deux nombres entiers: l'additionneur. Dans la version qu'on va voir, ce circuit manipulera des nombres strictement positifs (et donc les nombres codés en complètement à deux, ou en complément à un).
L'additionneur série
modifierAvec un additionneur complet, il est possible d'additionner deux nombres bit par bit. Dit autrement, on peut effectuer l'addition colonne par colonne. Cela demande de coupler l'additionneur avec plusieurs registres à décalages. Les opérandes vont être placées chacune dans un registre à décalage, afin de passer à chaque cycle d'un bit au suivant, d'une colonne à la suivante. Même chose pour le résultat. La retenue de l'addition est stockée dans une bascule de 1 bit, en attente du prochain cycle d'horloge. Un tel additionneur est appelé un additionneur série.

Bien que très simple et économe en transistors, cet additionneur est cependant peu performant. Le temps de calcul est proportionnel à la taille des opérandes. Par exemple, additionner deux nombres de 32 bits prendra deux fois plus de temps que l'addition de deux nombres de 16 bits. L'addition étant une opération fréquente, il vaut mieux utiliser d'autres méthodes d'addition, plus rapides. C'est pour cela que la totalité des autres additionneurs préfère utiliser plus de circuits, quitte à gagner quelque peu en rapidité.
L'additionneur à propagation de retenue
modifierL'additionneur à propagation de retenue pose l'addition comme en décimal, en additionnant les bits colonne par colonne avec une éventuelle retenue. Évidemment, on commence par les bits les plus à droite, comme en décimal. Il suffit ainsi de câbler des additionneurs complets les uns à la suite des autres.

Notons la présence de la retenue sortante, qui est utilisée pour détecter les débordements d'entier, ainsi que pour d'autres opérations. Le bit de retenue final est souvent stocké dans un registre spécial du processeur (généralement appelé carry flag).
Notez aussi, sur le schéma précédent, la présence de l’entrée de retenue sur l'additionneur. L'additionneur le plus à droite est bien un additionneur complet, et non un demi-additionneur,c e qui fait qui l'additionneur a une entrée de retenue. Tous les additionneurs ont une entrée de retenue de ce type. Elle est très utile pour l'implémentation de certaines opérations comme l'inversion de signe, la soustraction, l'incrémentation, etc. Certains processeurs sont capables de faire une opération appelée ADC, ADDC ou autre nom signifiant Addition with Carry, qui permet de faire le calcul A + B + Retenue (la retenue en question est la retenue sortante de l'addition précédente, stockée dans le registre carry flag). Son utilité principale est de permettre des additions d'entiers plus grands que ceux supportés par le processeur. Par exemple, cela permet de faire des additions d'entiers 32 bits sur un processeur 16 bits.

Ce circuit utilise plus de portes logiques que l'additionneur série, mais est un peu plus rapide. Il utilise très peu de portes logiques et est assez économe en transistors, ce qui fait qu'il était utilisé sur les tous premiers processeurs 8 et 16 bits. Un défaut de ce circuit est que le calcul des retenues s'effectue en série, l'une après l'autre. En effet, chaque additionneur doit attendre que la retenue de l'addition précédente soit disponible pour donner son résultat. Les retenues doivent se propager à travers le circuit, du premier additionneur jusqu'au dernier. On garde donc un défaut de l'additionneur série, à savoir : le fait que le temps de calcul est proportionnel à la taille des opérandes. Pour éviter cela, les autres additionneurs utilisent diverses solutions : soit calculer les retenues en parallèle, soit éliminer certaines opérations inutiles quand c'est possible.
Une solution est d'utiliser des additionneurs complets de type Manchester carry chain, qui propagent la retenue très rapidement. Néanmoins, l'additionneur de type Manchester carry chain fonctionne en pass transistor logic, avec tous les défauts que cela implique quand on en enchaine plusieurs. L'entrée de retenue est directement connectée sur la sortie de retenue, sans passage par une porte logique. Donc, la tension d'entrée est envoyée directement sur la sortie, sans amplification ou régénération. Si on enchaine plusieurs additionneurs complets de ce type, la tension diminue à chaque passage dans un additionneur complet. En conséquence, on peut difficilement enchainer plus de 4 à 8 additionneurs de type Manchester carry chain à la suite.
Il reste alors à trouver d'autres solutions pour résoudre ce problème de la propagation de retenue. Pour cela, il existe globalement plusieurs solutions, qui donnent quatre types d'additionneurs. Pour résumer ces solutions, en voici une liste rapide :
- Détecter quand le résultat est disponible, plutôt que d'attendre suffisamment pour couvrir le pire des cas.
- Limiter la propagation des retenues sur un petit nombre de bits et concevoir l'additionneur avec cette contrainte.
- Accélérer le calcul de la retenue avec des techniques d'anticipation de retenue.
- Utiliser des représentations binaires qui permettent de se passer de la propagation de retenue.
Les trois premières méthodes donnent, respectivement, les additionneurs à saut de retenue, à sélection de retenue, et à anticipation de retenue. Nous allons les voir dans les sections suivantes. La quatrième méthode sera vue dans le chapitre suivant, qui abordera l'addition multiopérande.
Les accélérations de la propagation de retenue
modifierLa propagation de la retenue est lente, mais il existe de nombreux moyens de la rendre plus rapide. Dans cette section, nous allons voir quelques additionneurs qui visent à accélérer la propagation de la retenue, mais en gardant la base de l'additionneur de propagation de retenue.

Avant de poursuivre, partons du principe que l'additionneur est conçu en assemblant des additionneurs à plus simples, qui additionnent environ 4 à 5 bits, parfois plus, parfois moins. Ces additionneurs simples seront nommés blocs dans ce qui suit, et l'un d'entre eux est illustré ci-contre. Chaque bloc prend en entrée les deux opérandes à additionner, mais aussi une retenue d'entrée. Il fournit en sortie non seulement le résultat de l'addition, codé sur 4/5 bits, mais aussi une retenue sortante.
En enchaînant plusieurs blocs les uns à la suite des autres, la retenue est propagée d'un bloc au suivant. La retenue sortante d'un bloc est connectée sur l'entrée de retenue du bloc suivant. L'enjeu est, pour un bloc, de calculer les retenues rapidement, plus rapidement qu'un additionneur à propagation de retenue. Le calcul de l'addition dans un bloc n'a pas besoin d'être accéléré, on garde des additionneurs à propagation de retenue.
Les blocs sont tous identiques dans le cas le plus simple, mais il est possible d'utiliser des blocs de taille variable. Par exemple, le premier bloc peut avoir des opérandes de 6 bits, le second des opérandes de 7 bits, etc. Faire ainsi permet de gagner un petit peu en performances, si la taille de chaque bloc est bien choisie. La raison est une question de temps de propagation des retenues. La retenue met plus de temps à se propager à travers 8 blocs qu'à travers 4, ce qui prend plus de temps qu'à travers 2 blocs, etc. En tenir compte fait que la taille des blocs tend à augmenter ou diminuer quand on se rapproche des bits de poids fort.
Le calcul parallèle de la retenue
modifier
L'optimisation la plus évidente est de calculer la retenue sortante en parallèle de l'addition. Chaque bloc contient, à côté de l'additionneur à propagation de retenue, on trouve un circuit qui calcule la retenue sortante. Il existe de nombreuses manières de calculer la retenue sortante. La plus simple consiste à établir la table de vérité de l'entrée de retenue, puis d'utiliser les techniques du chapitre sur les circuits combinatoire. Cela marche si les blocs sont de petite taille, mais elle devient difficile si le bloc a des opérandes de 2/3 bits ou plus. Mais des techniques alternatives existent.
Un exemple est celui de l'additionneur CMOS 4008, un additionneur de 4 bit. Il est intéressant de voir comment fonctionne ce circuit. Aussi, voici son implémentation. Le circuit est décomposé en trois sections. Une première couche de demi-additionneurs, le circuit de calcul de la retenue sortante, le reste du circuit qui finit l'addition. Le reste du circuit fait que le calcul de l'addition se fait en propageant la retenue, ce qui en fait un additionneur à propagation de retenue. Le circuit de calcul de la retenue sortante prend les résultats des demi-additionneurs, et les utilise pour calculer la retenue sortante. C'est là une constante de tous les circuits qui vont suivre.

Le point important à comprendre est que les demi-additionneurs génèrent les signaux P et G, qui disent si l'additionneur propage ou génère une retenue. Ces signaux sont alors combinés pour déterminer la retenue sortante. La méthode de combinaison des signaux P et G dépend fortement de l'additionneur utilisé. La méthode utilisée sur le 4008 utilise à la fois les signaux P et G, ce qui fait que c'est un hybride entre un additionneur à propagation de retenue, et un additionneur à anticipation de retenue qui sera vu dans la suite du chapitre. Mais il existe des techniques alternatives pour calculer la retenue sortante. La plus simple d'entre elle n'utilise que les signaux de propagation P, sans les signaux de génération. Et nous allons les voir immédiatement.
L'additionneur à saut de retenue
modifierL'additionneur à saut de retenue (carry-skip adder) est un additionneur dont le temps de calcul est variable, qui dépend des nombres à additionner. Le calcul prendra quelques cycles d'horloges avec certains opérandes, tandis qu'il sera aussi long qu'avec un additionneur à propagation de retenue avec d'autres. Il n'améliore pas le pire des cas, dans lequel la retenue doit être propagée du début à la fin, du bit de poids faible au bit de poids fort. Dans tous les autres cas, le circuit détecte quand le résultat de l'addition est disponible, quand la retenue a fini de se propager. Il permet d'avoir le résultat en avance, plutôt que d'attendre suffisamment pour couvrir le pire des cas.
L'additionneur à saut de retenue peut, sous certaines conditions, sauter complètement la propagation de la retenue dans le bloc. L'idée est de savoir si, dans le bloc, une retenue est générée par l'addition, ou simplement propagée. Dans le second cas, le bloc ne fait que propager la retenue entrante, sans en générer. La retenue entrante est simplement recopiée sur la retenue sortante. La propagation de retenue dans le bloc est alors skippée (mais elle a quand même lieu). Si une retenue est générée dans le bloc, on envoie cette retenue sur la retenue sortante. Le choix entre les deux est le fait s'un multiplexeur.

Toute la difficulté est de savoir comment commander le multiplexeur. Pour cela, on doit savoir si le circuit propage une retenue ou non. Le bloc propage une retenue si chaque additionneur complet propage la retenue. Les additionneurs complets doivent donc fournir le résultat, mais aussi indiquer s'ils propagent la retenue d'entrée ou non. Le signal de commande du multiplexeur est généré assez simplement : il vaut 1 si tous les additionneurs complets du bloc propagent la retenue précédente. C'est donc un vulgaire ET entre tous ces signaux.

L'additionneur à saut de retenue est construit en assemblant plusieurs blocs de ce type.

L'additionneur à sélection de retenue
modifierL'additionneur à sélection de retenue découper les opérandes en blocs, qui sont additionnés indépendamment. L'addition se fait en deux versions : une avec la retenue du bloc précédent valant zéro, et une autre version avec la retenue du bloc précédent valant 1. Il suffira alors de choisir le bon résultat avec un multiplexeur, une fois cette retenue connue. On gagne ainsi du temps en calculant à l'avance les valeurs de certains bits du résultat, sans connaître la valeur de la retenue. Petit détail : sur certains additionneurs à sélection de retenue, les blocs de base n'ont pas la même taille. Cela permet de tenir compte des temps de propagation des retenues entre les blocs.

Dans les exemples du dessus, chaque sous-additionneur étaient des additionneurs à propagation de retenue. Mais ce n'est pas une obligation, et tout autre type d’additionneur peut être utilisé. Par exemple, on peut faire en sorte que les sous-additionneurs soient eux-mêmes des additionneurs à sélection de retenue, et poursuivre ainsi de suite, récursivement. On obtient alors un additionneur à somme conditionnelle, plus rapide que l'additionneur à sélection de retenue, mais qui utilise beaucoup plus de portes logiques.
Les additionneurs à anticipation de retenue
modifierLes additionneurs à anticipation de retenue accélèrent le calcul des retenues en les calculant sans les propager. Au lieu de calculer les retenues une par une, ils calculent toutes les retenues en parallèle, à partir de la valeur de tout ou partie des bits précédents. Une fois les retenues pré-calculées, il suffit de les additionner avec les deux bits adéquats, pour obtenir le résultat.

Ces additionneurs sont composés de deux parties :
- un circuit qui pré-calcule la valeur de la retenue d'un étage ;
- et d'un circuit qui additionne les deux bits et la retenue pré-calculée : il s'agit d'une couche d'additionneurs complets simplifiés, qui ne fournissent pas de retenue.

Le circuit qui détermine la valeur de la retenue est lui-même composé de deux grandes parties, qui ont chacune leur utilité. La première partie réutilise des additionneurs qui donnent les signaux de propagation et génération de retenue. L'additionneur commence donc à prendre forme, et est composé de trois parties :
- un circuit qui crée les signaux P et G ;
- un circuit qui déduit la retenue à partir des signaux P et G adéquats ;
- et une couche d'additionneurs qui additionnent chacun deux bits et une retenue.

Il ne nous reste plus qu'à voir comment fabriquer le circuit qui reste. Pour cela, il faut remarquer que la retenue est égale :
- à 1 si l'addition des deux bits génère une retenue ;
- à 1 si l'addition des deux bits propage une retenue ;
- à zéro sinon.
Ainsi, l'addition des bits de rangs i va produire une retenue Ci, qui est égale à Gi+(Pi·Ci−1). Si on utilisait cette formule sans trop réfléchir, on retomberait sur un additionneur à propagation de retenue inutilement compliqué. L'astuce des additionneurs à anticipation de retenue consiste à remplacer le terme Ci−1 par sa valeur calculée avant. Par exemple, je prends un additionneur 4 bits. Je dispose de deux nombres A et B, contenant chacun 4 bits : A3, A2, A1, et A0 pour le nombre A, et B3, B2, B1, et B0 pour le nombre B. Si j'effectue les remplacements, j'obtiens les formules suivantes :
- C1 = G0 + ( P0 · C0 ) ;
- C2 = G1 + ( P1 · G0 ) + ( P1 · P0 · C0 ) ;
- C3 = G2 + ( P2 · G1 ) + ( P2 · P1 · G0 ) + ( P2 · P1 · P0 · C0 ) ;
- C4 = G3 + ( P3 · G2 ) + ( P3 · P2 · G1 ) + ( P3 · P2 · P1 · G0 ) + ( P3 · P2 · P1 · P0 · C0 ).
Ces formules nous permettent de déduire la valeur d'une retenue directement : il reste alors à créer un circuit qui implémente ces formules, et le tour est joué. On peut même simplifier le tout en fusionnant les deux couches d'additionneurs.

Ces additionneurs sont plus rapides que les additionneurs à propagation de retenue. Ceci dit, utiliser un additionneur à anticipation de retenue sur des nombres très grands (16/32bits) utiliserait trop de portes logiques. Pour éviter tout problème, nos additionneurs à anticipation de retenue sont souvent découpés en blocs, avec soit une anticipation de retenue entre les blocs et une propagation de retenue dans les blocs, soit l'inverse.

L'additionneur à calcul parallèle de préfixes
modifierLes additionneurs à calcul parallèle de préfixes sont des additionneurs à anticipation de retenue quelque peu améliorés, pour gagner en performances. Ceux-ci sont toujours découpés en trois couches :
- un circuit qui crée les signaux P et G ;
- un circuit qui déduit la retenue à partir des signaux P et G adéquats ;
- et une couche d'additionneurs qui additionnent chacun deux bits et une retenue.
Simplement, ils vont concevoir le circuit de calcul des retenues différemment. Avec eux, le calcul Gi + (Pi · Ci−1) va être modifié pour prendre en entrée non pas la retenue Ci−1, mais les signaux Gi−1 et Pi−1. Dans ce qui va suivre, nous allons noter ce petit calcul o. On peut ainsi écrire que :
- Ci = ((((Gi , Pi) o (Gi−1 , Pi−1) ) o (Gi−2 , Pi−2 )) o (Gi−3 , Pi−3)) …
Si on utilisait cette formule sans trop réfléchir, on retomberait sur un additionneur à propagation de retenue inutilement compliqué. Le truc, c'est que o est associatif, et que cela peut permettre de créer pas mal d'optimisations : il suffit de réorganiser les parenthèses. Cette réorganisation peut se faire de diverses manières qui donnent des additionneurs différents. Les diverses réorganisations donnent l'additionneur de Ladner-Fisher, l'additionneur de Brent-Kung, l'additionneur de Kogge-Stone, ou tout design hybride. L'additionneur de Brent-Kung est le plus lent de tous les additionneurs cités, mais c'est celui qui utilise le moins de portes logiques. L'additionneur de Ladner-Fisher est théoriquement le plus rapide de tous, mais aussi celui qui utilise le plus de portes logiques. Les autres sont des intermédiaires.
 |
 |
L'addition signée et la soustraction
modifierAprès avoir vu l'addition, il est logique de passer à la soustraction, les deux opérations étant très proches. Si on sait câbler une addition entre entiers positifs, câbler une soustraction n'est pas très compliqué. De plus, la soustraction permet de faire des additions de nombres signés.
Le soustracteur pour opérandes entiers
modifierPour soustraire deux nombres entiers, on peut adapter l'algorithme de soustraction utilisé en décimal, celui que vous avez appris à l'école. Celui-ci ressemble fortement à l'algorithme d'addition : on soustrait les bits de même poids, et on propage éventuellement une retenue sur la colonne suivante. La retenue est soustraite, et non ajoutée. La table de soustraction nous dit quel est le résultat de la soustraction de deux bits. La voici :
- 0 - 0 = 0 ;
- 0 - 1 = 1 et une retenue ;
- 1 - 0 = 1 ;
- 1 - 1 = 0.

La table de soustraction peut servir de table de vérité pour construire un circuit qui soustrait deux bits. Celui-ci est appelé un demi-soustracteur.

Celui-ci peut être complété afin de prendre en compte une éventuelle retenue, ce qui donne un soustracteur complet. On remarque que le soustracteur complet et composé de deux demi-soustracteurs placés en série. Le calcul de la retenue se fait en combinant les deux retenues des demi-soustracteurs avec une porte OU.

Celui-ci permet de créer des soustracteurs sur le même patron que pour les additionneurs. On peut ainsi créer un soustracteur série, un soustracteur à propagation de retenue, et ainsi de suite.
L'additionneur-soustracteur pour opérandes codées en complément à deux
modifierÉtudions maintenant le cas de la soustraction en complément à deux, dans l'objectif de créer un circuit soustracteur. Vous savez sûrement que a−b et a+(−b) sont deux expressions équivalentes. Et en complément à deux, − b = not(b) + 1. Dit autrement, a − b = a + not(b) + 1. On pourrait se dire qu'il faut deux additionneurs pour faire le calcul, mais la majorité des additionneurs possède une entrée de retenue pour incrémenter le résultat de l'addition. Un soustracteur en complément à deux est donc simplement composé d'un additionneur et d'un inverseur.

Il est possible de créer un circuit capable d'effectuer soit une addition, soit une soustraction : il suffit de remplacer l'inverseur par un inverseur commandable, qui peut être désactivé. On a vu comment créer un tel inverseur commandable dans le chapitre sur les circuits combinatoires. On peut remarquer que l'entrée de retenue et l'entrée de commande de l'inverseur sont activées en même temps : on peut fusionner les deux signaux en un seul.

Une implémentation alternative est la suivante. Elle remplace l'inverseur commandable par un multiplexeur.

L'additionneur-soustracteur pour opérandes codées en signe-magnitude
modifierPassons maintenant aux nombres codés en signe-valeur absolue.
Étudions tout d'abord un circuit d'addition de deux opérandes en signe-magnitude, les deux opérandes étant notée A et B. Suivant les signes des deux opérandes, on a quatre cas possibles : A + B, A − B (B négatif), −A + B (A négatif) et −A − B (A et B négatifs). On remarque que B − A est égal à − (A − B), et − A − B vaut − (A + B). Ainsi, le circuit n'a besoin que de calculer A + B et A − B : il peut les inverser pour obtenir − A − B ou B − A. A + B et A − B peuvent se calculer avec un additionneur-soustracteur. Il suffit de lui ajouter un inverseur commandable pour obtenir le circuit d'addition finale. On peut transformer ce circuit en additionneur-soustracteur en signe-valeur absolue, mais le circuit combinatoire devient plus complexe.

Toute la difficulté tient dans le calcul du bit de signe du résultat, quand interviennent des soustractions. Autant l'addition de deux nombres de même signe ne pose aucun problème, autant l'addition de nombres de signes différents ou les soustractions posent problème. Suivant que ou que , le signe du résultat ne sera pas le même. Intuitivement, on se dit qu'il faut ajouter des comparateurs pour déterminer le signe du résultat. Diverses optimisations permettent cependant de limiter la casse et d'utiliser moins de circuits que prévu. Mais rien d'extraordinaire.
L'additionneur-soustracteur pour opérandes codées en représentation par excès
modifierPassons maintenant aux nombres codés en représentation par excès. On pourrait croire que ces nombres s'additionnent comme des nombres non-signés, mais ce serait oublier la présence du biais, qui pose problème. Dans les cas de nombres signés gérés avec un biais, voyons ce que donne l'addition de deux nombres :
Or, le résultat correct serait :
En effectuant l'addition telle quelle, le biais est compté deux fois. On doit donc le soustraire après l'addition pour obtenir le résultat correct.
Même chose pour la soustraction qui donne ceci :
Or, le résultat correct serait :
Il faut rajouter le biais pour obtenir l'exposant correct.
On a donc besoin de deux additionneurs/soustracteurs : un pour additionner/soustraire les représentations binaires des opérandes, et un autre pour ajouter/retirer le biais en trop/manquant.
L'incrémenteur
modifierMaintenant, nous allons voir un circuit capable d'incrémenter un nombre, appelé l'incrémenteur. Les circuits incrémenteurs étaient très utilisés sur les premiers processeurs 8 bits, comme le Z-80, le 6502, les premiers processeurs x86 comme le 8008, le 8086, le 8085, et bien d'autres. Il s'agit d'un circuit assez simple, mais qu'il peut être intéressant d'étudier.
Le circuit incrémenteur se construit sur la même base qu'un additionneur, qu'on simplifie. En effet, incrémenter un nombre A revient à calculer A + 1. En clair, l'opération effectuée est la suivante :
+ 0 0 0 0 0 0 0 1 ------------------------------
Le calcul alors très simple : il suffit d'additionner 1 au bit de poids faible, sur la colonne la plus à droite, et propager les retenues pour les autres colonnes. En clair, on n'additionne que deux bits à chaque colonne : un 1 sur celle tout à droite, la retenue de la colonne précédente pour les autres. En clair : un incrémenteur est juste un additionneur normal, dont on a remplacé les additionneurs complets par des demi-additionneurs. Le 1 le plus à droite est injecté sur l'entrée de retenue entrante de l'additionneur. Et cela marche avec tous les types d'additionneurs, que ce soit des additionneurs à propagation de retenue, à anticipation de retenue, etc.
L'incrémenteur à propagation de retenue
modifierUn incrémenteur à propagation de retenue est donc constitué de demi-additionneurs enchaînés les uns à la suite des autres. Le circuit incrémenteur basique est équivalent à un additionneur à propagation de retenue, mais où on aurait remplacé tous les additionneurs complets par des demi-additionneurs. L'entrée de retenue entrante est forcément mise à 1, sans quoi l'incrémentation n'a pas lieu.

L'incrémenteur à propagation de retenue était utilisé sur le processeur Intel 8085, avec cependant une optimisation très intéressante. Pour la comprendre, rappelons que les portes logiques sont construites à partir de transistors. Les portes les plus simples à implémenter avec des transistors CMOS et TTL sont les portes NON, NAND et NOR. Le demi-additionneur est donc construit comme ci-dessous

Les ingénieurs ont tenté de se débarrasser de la porte NON, et ont réussit à s'en débarrasser pour une colonne sur deux. L'idée est de prendre les demi-additionneurs deux par deux, par paires. On peut alors regrouper les portes logiques comme ceci :

Les trois portes sont fusionnées, de manière à donner une porte NOR couplée à une porte NON.

- On peut optimiser le tout en fusionnant la porte XOR avec la porte NON pour le calcul de la somme, la porte XOR étant une porte composite. Mais nous n'en parlerons pas plus que ça ici.
Le résultat est que la propagation de la retenue est plus rapide. Au lieu de passer par une porte NAND et une porte NON, il traverse une seule porte : une porte NAND pour les colonnes paires, une porte NOR pour les colonnes impaires. Avec cette optimisation, la retenue se propage presque deux fois plus vite. Mine de rien, cette optimisation économisait des portes logiques et rendait le circuit deux fois plus rapide.
Les incrémenteurs plus complexes sont rares
modifierPour résumer, ce circuit ne paye pas de mine, mais il était largement suffisant sur les premiers microprocesseurs. Ils utilisaient généralement un incrémenteur capable de traiter des nombres de 8 bits, guère plus. Ces processeurs étaient très peu puissants, et fonctionnaient à une fréquence très faible. Ainsi, ils n'avaient pas besoin d'utiliser de circuits plus complexes pour incrémenter un nombre, et se contentaient d'un incrémenteur à propagation de retenues.
Il existe cependant des processeurs qui utilisaient des incrémenteurs complexes, avec anticipation de retenues, voir du carry skip. Par exemple, le processeur Z-80 de Zilog utilisait un incrémenteur pour des nombres de 16 bits, ce qui demandait des performances assez élevées. Et cet incrémenteur utilisait à la fois anticipation de retenues et carry skip. Pour ceux qui veulent en savoir plus sur cet incrémenteur, voici un lien sur le sujet :
L'additionneur BCD
modifierMaintenant, voyons un additionneur qui additionne deux entiers au format BCD. Pour cela, nous allons devoir passer par deux étapes. La première est de créer un circuit capable d'additionneur deux chiffres BCD. Ensuite, nous allons voir comment enchaîner ces circuits pour créer un additionneur BCD complet.
L'additionneur BCD qui fait l'opération chiffre par chiffre
modifierNous allons commencer par voir un additionneur qui additionne deux chiffres en BCD. Il fournit un résultat sur 4 bits et une retenue qui est mise à 1 si le résultat dépasse 10 (la limite d'un chiffre BCD). L'additionneur BCD se base sur un additionneur normal, pour des entiers codés en binaire, auquel on ajoute des circuits pour gérer le format BCD. Les deux chiffres sont codés sur 4 bits et sont additionnés en binaire par un additionneur des plus normal, similaire à ceux vus plus haut. Le résultat est alors un entier codé en binaire, sur 5 bits, qu'on cherche à corriger/convertir pour obtenir un chiffre BCD.
Pour corriger le résultat, une idée intuitive serait de prendre le résultat et de faire une division par 10. Le quotient donne la retenue, alors que le reste est le résultat, le chiffre BCD . Mais faire ainsi prendrait beaucoup de circuits, ce qui ne vaut pas le coup. Il existe une autre méthode beaucoup plus simple.
Une autre méthode détecte si le résultat est égal ou supérieur à 10, ce qui correspond à un "débordement" (on dépasse les limites d'un chiffre BCD). Si le résultat est plus petit que 10, il n'y a rien à faire : le résultat est bon et la retenue est de zéro. Par contre, si le résultat vaut 10 ou plus, il faut corriger le résultat et générer une retenue à 1.
Il faut donc ajouter un circuit qui détecte si le résultat est supérieur à 9. La retenue s'obtient facilement : le circuit qui détecte si le résultat est supérieur à 9 donne directement la retenue. Ce circuit peut se fabriquer simplement à partir de sa table de vérité, ou en utilisant les techniques que nous verrons dans un chapitre ultérieur sur les comparateurs. La solution la plus simple est clairement d'utiliser la table de vérité, ce qui est très simple, assez pour être laissé en exercice au lecteur.
Pour comprendre comment corriger le résultat, établissons une table de vérité qui associe le résultat et le résultat corrigé. L'entrée vaut au minimum 10 et au maximum 9 + 9 = 18. On considère la sortie comme un tout, la retenue étant un 5ème bit, le bit de poids fort.
| Entrée | Retenue | Résultat corrigé (sans retenue) | interprétation de la sortie en binaire (retenue inclue) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | (10) | 1 | 0000 | (16) | |
| 0 | 1 | 0 | 1 | 1 | (11) | 1 | 0001 | (17) | |
| 0 | 1 | 1 | 0 | 0 | (12) | 1 | 0010 | (18) | |
| 0 | 1 | 1 | 0 | 1 | (13) | 1 | 0011 | (19) | |
| 0 | 1 | 1 | 1 | 0 | (14) | 1 | 0100 | (20) | |
| 0 | 1 | 1 | 1 | 1 | (15) | 1 | 0101 | (21) | |
| 1 | 0 | 0 | 0 | 0 | (16) | 1 | 0110 | (22) | |
| 1 | 0 | 0 | 0 | 1 | (17) | 1 | 0111 | (23) | |
| 1 | 0 | 0 | 1 | 0 | (18) | 1 | 1000 | (24) | |
En analysant le tableau, on voit que pour corriger le résultat, il suffit d'ajouter 6. La raison est que le résultat déborde d'un nibble à 16 en binaire, mais à 10 en décimal : il suffit d'ajouter la différence entre les deux, à savoir 6, et le débordement binaire fait son travail. Donc, la correction après une addition est très simple : si le résultat dépasse 9, on ajoute 6.
On peut maintenant implémenter l'additionneur BCD au complet, en combinant le comparateur de débordement, le circuit de correction, et l'additionneur. La première solution calcule deux versions du résultat : la version corrigée, la version normale. Le choxi entre les deux est réalisée par un multiplexeur, commandé par le comparateur.

L'autre solution utilise un circuit commandable qui soit additionne 6, soit ne fait rien. Le choix entre les deux est commandé par un bit de commande dédié, calculé par le comparateur.

Une version assez compliquée du circuit final est illustrée ci-dessous. Le circuit commandable est un additionneur, précédé d'un circuit comparateur qui détecte si le résultat est supérieur à 9. Si c'est le cas, ce circuit génère l'opérande 6, et l'envoie en entrée de l'additionneur. Le circuit est simple à concevoir, mais gaspille beaucoup de circuit. Idéalement, il vaudrait mieux utiliser un circuit combinatoire d'addition avec une constante conçu pour.

Pour obtenir un additionneur BCD complet, il suffit d’enchaîner les additionneurs précédents, comme on le ferait avec les additionneurs complets dans un additionneur à propagation de retenue. La seule chose importante est que le circuit précédent est altéré de manière à ce qu'on puisse prendre en compte la retenue. Pour cela, rien de plus simple : il suffit d'utiliser l'entrée de retenue de l'additionneur binaire.
Au final, l'additionneur BCD est beaucoup plus compliqué qu'un additionneur normal. Il rajoute des circuits à un additionneur normal, à savoir un circuit pour détecter si chaque chiffre binaire est >9, un petit additionneur pour ajouter 6 et un multiplexeur. De plus, il est difficile d'appliquer les optimisations disponibles sur les additionneurs non-BCD. Notamment, les circuits d'anticipation de retenue sont totalement à refaire et le résultat est relativement compliqué. c'est ce qui explique pourquoi le BCD a progressivement été abandonné au profit du binaire simple.
L'additionneur BCD par ajustement décimal
modifierL'additionneur BCD précédent effectuait son travail chiffre BCD par chiffre BCD. Il additionne et corrige le résultat un chiffre BCD après l'autre, en commençant par le chiffre BCD de poids faible. Mais il existe des additionneurs BCD qui font autrement. L'idée est d’additionner les deux opérandes avec une addition binaire normale, puis de corriger le résultat. Le tout se fait donc en deux étapes : l'addition, puis la correction du résultat. Les deux étapes traitent des opérandes complètes, de 8, 16, voire 32 bits, et non des chiffres BCD seuls.
Une telle technique était utilisée dans le processeur Intel 8085, et de manière générale sur les premiers processeurs x86. Sur ce processeur, les deux étapes d'addition et de correction du résultat étaient séparées dans deux opérations distinctes. Il n'y avait pas d'opération d'addition BCD proprement dit, seulement une addition binaire normale. Par contre, l'addition était secondée par une opération dite d'ajustement décimal qui transformait un nombre binaire en nombre codé en BCD. Effectuer une addition BCD demandait donc de faire deux opérations à la suite : une addition binaire simple, suivie par l'opération d'ajustement décimal. Cela permettait de gérer des nombres entiers en binaire usuel et des entiers BCD sans avoir deux instructions d'addition séparées pour les deux, sans compter que cela simplifiait aussi les circuits d'addition. L'opération d'ajustement décimal lisait l'opérande à manipuler dans un registre (l’accumulateur), et mémorisait le résultat dans ce même registre. Elle prenait une opérande de 8 bits, soit deux chiffres BCD, et fournissait un résultat de la même taille. Elle avait son propre circuit, assez simple, que nous allons voir dans ce qui suit.
L'ajustement décimal s'effectue en ajoutant une constante bien précise à l'opérande à convertir en BCD. L'idée est que la constante est découpée en morceaux de 4 bits, correspondant chacun à un chiffre BCD de l'opérande, chaque morceau contenant soit un 0, soit 6. Cela permet d'ajouter soit 0, soit, à chaque chiffre BCD, et donc de le corriger. La propagation des retenues d'un chiffre à l'autre est effectuée automatiquement par l'addition binaire de la constante. La constante est calculée en deux étapes, sur un principe similaire à celui vu dans l'additionneur précédent. D'abord, on découpe l'opérande en nibbles et on vérifie si chaque nibble est supérieur ou égal à 10. Ensuite, la seconde étape rend les résultats de ces comparaisons et détermine la valeur de chaque nibble de la constante finale. Par exemple, si je prends l'opérande 1001 1110, le nibble de poids faible déborde, alors que celui de poids fort non. La constante sera donc 0000 0110 : 0x06. Inversement, si le nibble de poids fort déborde et pas celui de poids faible, la constante sera alors 0x60. Et la constante est de 0x66 si les deux nibbles débordent, de 0x00 si aucun ne déborde.
Le circuit d’ajustement décimal est donc composé de trois étapes : deux étapes pour calculer la constante, et un circuit d'addition pour additionner cette constante au nombre de départ. La première étape découpe l'opérande en morceaux de 4 bits, en chiffres BCD, et vérifie si chacun d'entre eux vaut 10 ou plus. La seconde étape prend les résultats de la première étape, et les combine pour calculer la constante. Enfin, on trouve l'addition finale, qui était réalisée par un circuit d'addition utilisé à la fois pour l'ajustement décimal et l'addition binaire. La différence entre une addition normale et une opération d'ajustement décimal tient dans le fait que les deux premières étapes sont désactivées dans une addition normale.

Les débordements d'entier lors d'une addition/soustraction
modifierLes instructions arithmétiques et quelques autres manipulent des entiers de taille fixe, qui ne peuvent prendre leurs valeurs que dans un intervalle. Pour les nombres positifs, un ordinateur qui code ses entiers sur n bits pourra coder tous les entiers allant de 0 à . Tout nombre en dehors de cet intervalle ne peut pas être représenté. Dans le cas où l'ordinateur gère les nombres négatifs, l'intervalle est différent. Dans le cas général, l'ordinateur peut coder les valeurs comprises de à . Si le résultat d'un calcul sort de cet intervalle, il ne peut pas être représenté par l'ordinateur et il se produit ce qu'on appelle un débordement d'entier.
La valeur haute de débordement désigne la première valeur qui est trop grande pour être représentée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 0 et 7, la valeur haute de débordement est égale à 8. On peut aussi définir la valeur basse de débordement, qui est la première valeur trop petite pour être codée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 8 et 250, la valeur basse de débordement est égale à 7. Pour les nombres entiers, la valeur haute de débordement vaut , alors que la valeur basse vaut (avec et respectivement la plus grande et la plus petite valeur codable par l'ordinateur).
La correction des débordements d'entier : l'arithmétique saturée
modifierQuand un débordement d'entier survient, tous les circuits de calcul ne procèdent pas de la même manière. Dans les grandes lignes, il y a deux réactions possibles : soit on corrige automatiquement le résultat du débordement, soit on ne fait rien et on se contente de détecter le débordement.
Si le débordement n'est pas corrigé automatiquement par le circuit, celui-ci ne conserve que les bits de poids faibles du résultat. Les bits en trop sont simplement ignorés. On dit qu'on utilise l'arithmétique modulaire. Le problème avec ce genre d'arithmétique, c'est qu'une opération entre deux grands nombres peut donner un résultat très petit. Par exemple, si je dispose de registres 4 bits et que je souhaite faire l'addition 1111 + 0010 (ce qui donne 15 + 2), le résultat est censé être 10001 (17), ce qui est un résultat plus grand que la taille d'un registre. En conservant les 4 bits de poids faible, j’obtiens 0001 (1). En clair, un résultat très grand est transformé en un résultat très petit. Cela peut poser problèmes si on travaille uniquement avec des nombres positifs, mais c'est aussi utilisé pour coder des nombres en complément à deux. En clair, faire ainsi est parfois une bonne idée, parfois non.
D'autres circuits utilisent ce qu'on appelle l'arithmétique saturée : si un résultat est trop grand au point de générer un débordement, on arrondi le résultat au plus grand entier supporté par le circuit. Les circuits capables de calculer en arithmétique saturée sont un peu tout petit peu plus complexes que leurs collègues qui ne travaillent pas en arithmétique saturée, vu qu'il faut rajouter des circuits pour corriger le résultat en cas de débordement. Il suffit généralement de rajouter un circuit de saturation, qui prend en entrée le résultat en fournit en sortie une version saturée en cas de débordement. Ce circuit de saturation met la valeur maximale en sortie si un débordement survient, mais se contente de recopier le résultat du calcul sur sa sortie s'il n'y a pas de débordement. Typiquement, il est composé d'une ou de deux couches de multiplexeurs, qui sélectionnent quelle valeur mettre sur la sortie : soit le résultat du calcul, soit le plus grand nombre entier géré par le processeur, soit le plus petit (pour les nombres négatifs/soustractions).
L'arithmétique saturée est surtout utilisée pour les additions et soustractions, mais c'est plus rare pour les multiplications/divisions. Une des raisons est que le résultat d'une addition/soustraction prend un bit de plus que le résultat, là où les multiplications doublent le nombre de bits. Cette large différence se traduit par une grande différence pour les résultats qui débordent. Quand une addition déborde, le résultat réel est proche de la valeur maximale codable. mais quand une multiplication déborde, le résultat peut parfois valoir 200 à 60000 fois plus que la valeur maximale codable. Les calculs avec une valeur saturée/corrigée sont donc crédibles pour une suite d'additions, mais pas pour une suite de multiplications. Raison pour laquelle l'arithmétique saturée est utilisée pour les additions/soustractions, là où on préfère corriger les multiplications/divisions par des méthodes logicielles.
La détection des débordements d'entier
modifierEt quand un débordement d'entier a eu lieu, il vaut mieux que le circuit prévienne ! Pour cela, les circuits de calculs ont une sortie nommée Overflow, dont la valeur indique si le calcul a donné un débordement d'entier ou non. Reste que détecter un débordement ne se fait pas de la même manière selon que l'on parle d'un additionneur non-signé, d'un additionneur signé, d'un multiplieur non-signé, etc.
Les opérations sur des nombres non-signés
modifierPour le cas des nombres positifs, la détection des débordements dépend assez peu de l'opération. L'idée générale est que le circuit de calcul calcule tous les bits du résultat, quitte à dépasser ce qui est supporté par l'ordinateur. Par exemple, un additionneur 32 bits fournit un résultat sur 33 bits, un multiplieur 32 bits fournit des résultats sur 64 bits, etc. Le circuit de calcul a donc des bits qui sont en trop et doivent être oubliés. Un débordement a lieu quand ces bits oubliés sont pertinents, à savoir quand au moins l'un d'eux est à 1. Par exemple, une addition sur 32 bits déborde quand le 33ème bit est à 1, une multiplication sur 32 bits déborde quand un des 32 bits de poids fort est à 1, etc.
Pour les additionneurs non-signés, la sortie Overflow n'est autre que la retenue finale, celle fournie par le dernier additionneur complet. De plus, le seul type de débordement possible est un débordement par le haut, où le résultat dépasse la valeur maximale. Le circuit de saturation est alors très simple. Il consiste au pire en une seule couche de multiplexeurs. Une solution encore plus simple consiste à utiliser le circuit de mise à la valeur maximale vu dans le chapitre sur les opérations bits à bits.

Les opérations signées
modifierPour les additionneurs non-signés, la gestion des débordements d'entiers dépend fortement de la représentation signée. Dans les grandes lignes, rien ne change avec les représentations en signe-magnitude et par excès, dont les débordements sont gérés de la même manière que pour les nombres positifs. Par contre, il n'en est pas de même pour le complément à deux. Si vous vous rappelez le chapitre 1, j'ai clairement dit que les calculs sur des nombres en complètement à deux utilisent les règles de l'arithmétique modulaire : les calculs sont faits avec un nombre de bits fixé une fois pour toute. Si un résultat dépasse ce nombre de bits fixé, on ne conserve pas les bits en trop. C'est une condition nécessaire pour pouvoir faire nos calculs. À priori, on peut donc penser que dans ces conditions, les débordements d'entiers sont une chose parfaitement normale, qui nous permet d'avoir des résultats corrects. Néanmoins, certains débordements d'entiers peuvent survenir malgré tout et produire des bugs assez ennuyeux.
Si l'on tient en compte les règles du complément à deux, on sait que le bit de poids fort (le plus à gauche) permet de déterminer si le nombre est positif ou négatif : il indique le signe du nombre. Tout se passe comme si les entiers en complément à deux étaient codés sur un bit de moins, et avaient leur longueur amputé du bit de poids fort. Si le résultat d'un calcul a besoin d'un bit de plus que cette longueur, amputée du bit de poids fort, le bit de poids fort sera écrasé; donnant un débordements d'entiers. Il existe une règle simple qui permet de détecter ces débordements d'entiers. L'addition (ou la multiplication) de deux nombres positifs ne peut pas être un nombre négatif : on additionne deux nombres dont le bit de signe est à 0 et que le bit de signe du résultat est à 1, on est certain d'être en face d'un débordements d'entiers. Même chose pour deux nombres négatif : le résultat de l'addition ne peut pas être positif. On peut résumer cela en une phrase : si deux nombres de même signe sont ajoutés, un débordement a lieu quand le bit du signe du résultat a le signe opposé. On peut préciser que cette règle s'applique aussi pour les nombres codés en complément à 1, pour les mêmes raisons que pour le codage en complément à deux. Cette règle est aussi valable pour d'autres opérations, comme les multiplications.
Modifier les circuits d'au-dessus pour qu'ils détectent les débordements en complément à deux est simple comme bonjour : il suffit créer un petit circuit combinatoire qui prenne en entrée les bits de signe des opérandes et du résultat, et qui fasse le calcul de l'indicateur de débordements. Si l'on rédige sa table de vérité, on doit se retrouver avec la table suivante :
| Entrées | Sortie |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 0 |
| 011 | 0 |
| 100 | 0 |
| 101 | 0 |
| 110 | 1 |
| 111 | 0 |
L'équation de ce circuit est la suivante, avec et les signes des deux opérandes, et la retenue de la colonne précédente :
En simplifiant, on obtient alors :
Or, il se trouve que est tout simplement la retenue en sortie du dernier additionneur, que nous noterons . On trouve donc :
Il suffit donc de faire un XOR entre la dernière retenue et la précédente pour obtenir le bit de débordement.
Pour le moment, nous savons faire des additions, des soustractions, des décalages et rotations, ainsi que des opérations bit à bit. Chaque opération est réalisée par un circuit séparé. Cependant, il est possible de les fusionner en un seul circuit appelé une unité de calcul arithmétique et logique, abrévié ALU (Arithmetic and Logical Unit). Comme son nom l'indique, elle effectue des opérations arithmétiques et des opérations logiques (bit à bit). Tous les processeurs contiennent une ALU très similaire à celle qu'on va voit dans ce qui suit. La plupart des ALUs ne gèrent donc pas les opérations compliquées, comme les multiplications ou les divisions, de même que les décalages et rotation, et vous comprendrez pourquoi dans ce qui suit.
L'interface d'une unité de calcul et sa conception
modifierL'interface d'une ALU est assez simple. Il y a évidemment les entrées pour les opérandes et la sortie pour le résultat, mais aussi une entrée de commande qui permet de choisir l'instruction à effectuer. Sur cette entrée, on place une suite de bits qui précise l'instruction à effectuer. La suite de bit est très variable d'une ALU à l'autre. Elle peut être très structuré, chaque bit configurant une portion de l'ALU, ou être totalement arbitraire. La suite de bit peut être vu est aussi appelée l'opcode, ce qui est un diminution de code opération.
De plus, l'ALU a des sorties pour la retenue de sortie, les bits qui indiquent que le calcul a entrainé un débordement d'entier, etc. Ces bits sont appelés des flags, ou indicateurs. Les plus fréquents sont la retenue de sortie, un bit qui est à 1 si un débordement d'entier a eu lieu, un bit qui est à 1 si un débordement d'entier a eu lieu pour une addition signée (débordement en complètement à deux), un bit qui indique si le résultat est zéro, et quelques autres. Les flags sont calculés avec les circuits vus dans le chapitre précédent, dans la section sur la détection des débordements d'entiers.

Le bit-slicing
modifierAvant l'invention des premiers microprocesseurs, les processeurs étaient fournis en pièces détachées qu'il fallait relier entre elles. Le processeur était composé de plusieurs circuits intégrés, placés sur la même carte mère et connectés ensemble par des fils métalliques. Et l'ALU était un de ces circuits intégrés.
Les ALUs en pièces détachée de l'épique étaient assez simples et géraient 2, 4, 8 bits, rarement 16 bits. Mais il était possible d'assembler plusieurs ALU pour créer des ALU plus grandes. Par exemple, on pouvait combiner plusieurs ALU 4 bits afin de créer une unité de calcul 8 bits, 12 bits, 16 bits, etc. Par exemple, l'ALU des processeurs AMD Am2900 est une ALU de 16 bits composée de plusieurs sous-ALU de 4 bits. Cette technique qui consiste à créer des unités de calcul plus grosses à partir d’unités de calcul plus élémentaires s'appelle en jargon technique du bit slicing.
Le bit slicing est utilisé pour des ALU capables de gérer les opérations bit à bit, l'addition, la soustraction, mais guère plus. Les ALU en bit-slice qui gére les multiplications existent, mais sont rares. La raison est qu'il n'est pas facile d'implémenter une multiplication entre deux nombres de 16 bits avec deux multiplieurs de 4 bits (idem pour la division). Alors que c'est plus simple pour l'addition et la soustraction : il suffit de transmettre la retenue d'une ALU à la suivante. Bien sûr, les performances seront alors nettement moindres qu'avec des additionneurs modernes, à anticipation de retenue, mais ce n'était pas un problème pour l'époque.
L'implémentation des opérations bit à bit avec une ALU bit-slice est très simple, la seule complexité est l'addition. Si on combine deux ALU de 4 bits, la première calcule l'addition des 4 bits de poids faible, alors que le second calcule l'addition des 4 bits de poids fort. Mais il faut propager la retenue de l'addition des 4 bits de poids faible à la seconde ALU. Pour cela, l'ALU doit transmettre un bit de retenue sortant à l'ALU suivante, qui doit elle accepter celui-ci sur une entrée. Rappelons qu'une addition en binaire s'effectue comme en décimal : on additionne les bits colonne par colonne pour obtenir le bit de résultat, et il arrive qu'une retenue soit propagée à la colonne suivante.
Pour cela, l'ALU doit avoir une interface compatible : il faut qu'elle ait une entrée de retenue, et une sortie pour la retenue sortante. La retenue passée en entrée est automatiquement prise en compte lors d'une addition par l'ALU. Comme nous l'avons vu dans le chapitre dédié aux circuits de calculs, ajouter une entrée de retenue ne coute rien et est très simple à implémenter en à peine quelques portes logiques.
L'intérieur d'une unité de calcul
modifierLes unités de calcul les plus simples contiennent un circuit différent pour chaque opération possible. L’entrée de sélection commande des multiplexeurs pour sélectionner le bon circuit.

D'autres envoient les opérandes à tous les circuits en même temps, et activent ou désactivent chaque sous-circuit suivant les besoins. Chaque circuit possède ainsi une entrée de commande, dont la valeur est déduite par un circuit combinatoire à partir de l'entrée de sélection d'instruction de l'ALU (généralement un décodeur). Nous allons voir plusieurs exemples d'unités de calcul configurable dans ce chapitre. Pour le moment, sachez qu'un simple additionneur-soustracteur est un circuit configurable de ce genre.

Les ALU sérielles
modifierLes ALU sérielles effectuent leurs calculs 1 bit à la fois, bit par bit. Le circuit est alors très simple : il contient un circuit de calcul très simple, de 1 bit, couplé à trois registres à décalage : un par opérande, un pour le résultat. Le circuit de calcul prend trois bits en entrées et fournit un résultat d'un bit en sortie, avec éventuellement une retenue en sortie. Une bascule est ajoutée au circuit, pour propager les retenues des additions/soustractions, elle ne sert pas pour les opérations bit à bit.

Les ALU sérielles ne payent pas de mine, mais elles étaient très utilisées autrefois, sur les tout premiers processeurs. Les ordinateurs antérieurs aux années 50 utilisaient des ALU de ce genre. L'avantage de ces ALU est qu'elles peuvent gérer des opérandes de grande taille, avec plus d'une trentaine de bits, sans trop de problèmes. Il suffit de prévoir des registres à décalage suffisamment longs, ce qui est tout sauf un problème. Par contre, elles sont assez lentes pour faire leur calcul, vu que les calculs se font bit par bit. Elles sont d'autant plus lentes que les opérandes sont longs.
Les ALU entières basées sur un additionneur-soustracteur
modifierIl est possible d'obtenir une ALU entière simple en modifiant un additionneur-soustracteur simple. Pour rappel, un additionneur soustracteur est fait en combinant un additionneur avec un inverseur commandable.

Il est possible de modifier l'additionneur, mais aussi les circuits situés juste avant. L'idée est d'ajouter un circuit commandable de mise à zéro la seconde entrée d'opérande. Il est aussi possible de commander l'entrée de retenue entrante de l'additionneur séparément, via sa propre entrée.

Les opérations que peut faire cette ALU sont assez nombreuses. Déjà, elle supporte l'addition et la soustraction, quand la seconde opérande n'est pas inversée. En inversant la seconde opérande, on peut gérer deux opérations. La première est l'identité (on recopie l'opérande d'entrée sur la sortie), qui se fait en désactivant l'inverseur. En activant l'inverseur, on a l'opération d'inversion NOT, à savoir que les bits de l'opérande sont inversés. En jouant sur l'entrée de retenue, on peut aussi émuler d'autres opérations, comme l'incrémentation. Les 8 opérations possibles sont les suivantes :
| Reset | Invert | Retenue entrante | Sortie de l'ALU | |
|---|---|---|---|---|
| 0 | 0 | 0 | A + B | |
| 0 | 0 | 1 | A + B + 1 | |
| 0 | 1 | 0 | A + = A - B - 1 | |
| 0 | 1 | 1 | A + + 1 = A - B | |
| 1 | 0 | 0 | B | |
| 1 | 0 | 1 | B + 1 | |
| 1 | 1 | 0 | ||
| 1 | 1 | 1 | + 1 |
Les ALU basées sur un additionneur, avec manipulation des retenues
modifierMaintenant que nous avons vu ce qu'il est possible de faire en modifiant ce qu'il y a avant l'additionneur, nous allons modifier l'additionneur lui-même.
L'implémentation du XOR/NXOR
modifierDans cette section, nous allons nous intéresser à un circuit qui effectue un XOR en plus de l'addition. Le choix d'utiliser à la fois une addition et un XOR peut sembler bizarre, mais s'explique par le fait qu'une opération XOR est identique à une addition binaire dont on ne tiendrait pas compte des retenues.
Pour rappel, un additionneur complet additionne trois bits, en faisant deux XOR :
Si on met la retenue entrante à zéro, on a :
En clair, en manipulant les entrées de retenue des additionneurs complets, on peut avoir un XOR à partir de l'addition. Pour cela, on ajoute un circuit de masquage, comme vu dans le chapitre sur les opérations bit à bit, pour mettre les entrées à 0, on a le circuit ci-dessous. Le choix de l'opération est le fait d'une entrée de commande, mise à 0 pour un XOR et à 1 pour l'addition. Cette méthode marche avec tous les additionneurs, mais elle est plus simple à implémenter avec les additionneurs à anticipation de retenue.

Si un XOR est équivalent à une addition où les retenues sont mises à 0, on peut se demander ce qu'il se passe quand on les met à 1. Dans ce cas, pour chaque additionneur complet, le bit du résultat est :
Sachant que , on se rend compte que le circuit calcule le NXOR des deux entrées.
En clair, en masquant les retenues entrantes, on peut transformer une addition en XOR ou en NXOR. Il suffit d'insérer des circuits de masquage avant les entrées de retenue. Le circuit de masquage soit recopie le bit d'entrée (pour l'addition), soit force les entrées de retenue à 0, soit les force à 1. Et on a déjà vu le circuit adéquat dans le chapitre sur les opérations bit à bit, à savoir la porte 1 bit universelle. Pour rappel, c'est un circuit avec deux bits de commandes, qui prend un bit en entrée et fournit sur la sortie : soit 0, soit 1, soit le bit d'entrée, soit son inverse. Il suffit donc d'ajouter une porte universelle 1 bit juste avant l'entrée de retenue entrante, et le tour est joué !

L'implémentation du ET/OU avec une addition, en utilisant les retenues sortantes
modifierMaintenant, faisons la même chose, mais regardons les retenues de sortie.
| Retenue entrante | Opérande 1 | Opérande 2 | Retenue sortante | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
On remarque deux choses :
- si la retenue d'entrée est à 0, la retenue de sortie est un ET entre les deux bits d'opérandes.
- si on met la retenue entrante à 1, alors la retenue sortante sera un OU entre les deux bits d'opérandes
Pour implémenter le circuit, il faut connecter la sortie soit aux bits de résultat, soit aux entrées de retenue. Dans le circuit précédent, si la couche d'additionneurs finale est une couche d'additionneurs complets, on peut extraire le ET et le OU des deux opérandes. Un simple MUX placé à la suite permet de choisir si l'on regarde les bits du résultat ou la "retenue sortante" de ces additionneurs complets.

L'implémentation du NOT avec une addition, en manipulant retenues et opérandes
modifierIl est enfin possible d'implémenter l'opération NOT avec seulement un additionneur, pas besoin qu'il soit un additionneur-soustracteur. En effet, on obtient le NOT d'une opérande, via deux manières légèrement différentes.
Un additionneur complet peut se comporter comme une porte NOT à condition que l'une des entrées soit à 0 et l'autre à 1. La raison à cela est que l'additionneur complet fait un double XOR : le bit à inverser est XORé avec 0, ce qui le recopie, puis avec 1, ce qui l'inverse. Peu importe l'ordre, vu que le XOR est commutatif et associatif.
Cela donne deux possibilités : soit on met le second opérande à 0 et les retenues à 1, soit on fait l'inverse. Le résultat est disponible sur les bits de résultat. Pour cela, la solution consiste à ajouter un circuit qui met à 0 la seconde opérande, on a déjà le circuit pour manipuler les retenues. Mais cette solution est rarement utilisée, vu que la majorité des ALU utilise un additionneur-soustracteur, qui permet d'implémenter l'opération NOT facilement, tout en permettant d'implémenter aussi la soustraction, pour un cout en porte logique mineur et des performances quasiment identiques.
Les ALU basées sur des ALU 1 bit
modifierLes ALU précédentes sont basées sur des additionneurs auxquels on a rajouté des circuits. Mais les additionneurs complets eux-même n'ont pas été modifiés. Les ALU que l'on va voir dans ce qui suit fonctionnent sur un principe différent. Au lieu d'ajouter des circuits autour des additionneurs complets, elles modifient les additionneurs complets de manière à ce qu'il puisse faire des opérations logiques ET/OU/XOR/NXOR. Ils deviennent alors de véritables ALU de 1 bit, qui sont assemblées pour donner des ALU entières.
En plus d'assembler des ALU 1 bit, il faut aussi gérer les retenues, et les différentes manières de faire ressemblent beaucoup à ce qui se fait avec les additionneurs. Par exemple, on peut relier chaque ALU 1 bit comme dans un additionneur à propagation de retenue, où chaque ALU 1 bit envoie sa retenue sortante sur l'entrée de retenue de l'ALU 1 bit suivante. Une autre possibilité est d'utiliser un circuit de calcul des retenues, comme pour un additionneur à anticipation de retenue.

L'exemple de l'ALU du processeur 8086 d'Intel
modifierVoyons maintenant l'exemple du processeur 8086 d'Intel, un des tout premier de la marque. L'additionneur de cette ALU est un additionneur à propagation de retenue, avec une Manchester Carry Chain pour accélérer la propagation des retenues. Pour rappel, un additionneur Manchester carry chain génère en interne deux signaux : un signal de propagation de retenue et un signal de génération de retenue. Les deux sont combinés avec la retenue entrante pour calculer le résultat et la retenue de sortie, la combinaison se faisant avec un circuit basé sur des portes à transmission. Les deux signaux sont déterminés par une unique porte logique, qui prend en entrée les deux bits d'opérande : une porte logique détermine si l'addition génère une retenue, un autre si elle propage la retenue d'entrée sur la colonne suivante. Un tel additionneur est illustré ci-dessous, pour rappel.

Sur le 8086, ces deux portes sont remplacées par une porte logique universelle commandable 2 bit, à savoir un circuit qui peut remplacer toutes les portes logiques 2 bit existantes. Comme vu dans le chapitre sur les opérations bit à bit, cette porte universelle est un simple multiplexeur configuré convenablement. En conséquence, le signal de propagation et de génération de retenue sont configurables et on peut les utiliser pour calculer autre chose. Par exemple, la première porte XOR peut être remplacée par une porte ET, OU, NOR, FALSE (elle donne toujours zéro en sortie), OUI (recopie un bit d'entrée sur la sortie), etc.

La gestion des additions et soustractions est alors triviale. Il suffit de configurer les deux portes universelles de manière à obtenir le circuit d'un additionneur complet ou d'un soustracteur complet.
Lors des opérations bit à bit et des décalages, les deux signaux sont configurés de manière à ce qu'au moins l'un d'entre elle ait sa sortie mise à 0. C'est-à-dire que l'une des deux portes universelles sera configurée de manière à devenir une porte FALSE. En faisant cela, la porte XOR aura une entrée à 0, ce qui fait qu'elle recopiera l'autre entrée sur sa sortie. Elle se comportera comme une porte OUi pour l'autre entrée, celle pas mise à 0.
Pour les opérations logiques, l'une des portes universelle est configurée de manière à avoir la porte logique voulue, l'autre est mise à 0, la porte XOR recopie l'entrée de la première. La porte logique mise à 0 est celle qui génère les retenues. La porte qui calcule le signal de propagation de la retenue, celle qui additionne les deux bits d'opérande, est alors configurée pour donner la porte voulue : soit un ET, soit un OU, soit un XOR, soit...

L'ALU du 8086 supporte aussi les décalages d'un rang vers la gauche, qui sont équivalents à une multiplication par deux. L'opérande décalée est envoyé sur les entrées A de chaque additionneur complet. Pour effectuer, ils utilisent une solution très simple : chaque additionneur envoie le bit de l'opérande sur la sortie de retenue. De plus, les entrées d'opérandes ne sont pas additionnées. Pour résumer, il faut que le signal de propagation de retenue soit mis à zéro, alors que le signal de génération de retenue soit égal au bit d'entrée de l'opérande. Les deux portes logiques universelles sont alors configurées pour : la porte de propagation se comporte comme une porte FALSE, l'autre comme une porte OUI qui recopie l'entrée A.

En somme, l'ALU fait son travail en configurant les deux portes universelles. Pour configurer les portes, l'ALU contient un petit circuit combinatoire qui traduit l'opcode en signaux envoyés aux portes universelles.
Pour ceux qui veulent en savoir plus sur les circuits de calcul de l'Intel 8086, voici un lien :
L'exemple de l'ALU du processeur Intel x86 8008
modifierL'ALU du processeur Intel x86 8008 est une ALU 8 bits (les opérandes sont de 8 bits), qui implémente 4 opérations : l'addition, ET, OU, XOR. L'addition est réalisée par un circuit d'anticipation de retenue, chose assez rare sur les processeurs de l'époque. Il n'était pas possible de placer beaucoup de transistors sur les puces de l'époque, ce qui fait que les concepteurs de processeurs tournaient à l'économie et privilégiaient des additionneurs à propagation de retenue.
Comme beaucoup d'ALU des processeurs assez anciens, elle est construite en assemblant plusieurs ALU de 1 bits, chacune étant un additionneur complet amélioré. L'ALU de 1 bit utilise des additionneurs complets implémentés avec le circuit suivant :

L'additionneur précédent est modifié pour gérer les trois opérations XOR, ET, OU. Pour gérer le XOR, il suffit de mettre la retenue d'entrée à 0, ce qui est réalisé avec une vulgaire porte ET pour chaque additionneur complet, placée en aval de l'entrée de retenue. Pour gérer les deux autres opérations logiques, le circuit ne suit pas la logique précédente et n'utilise pas de multiplexeur. Le résultat du ET/OU est bien disponible sur la sortie de résultat, non sur la sortie de retenue. A la place, le circuit utilise la porte ET et la porte OU de l'additionneur complet, et désactive la porte inutile. Pour un ET/OU, le circuit met à zéro la retenue entrante. De plus, elle met aussi à zéro la retenue sortante, sans quoi le circuit donne des résultats invalides.
Dans les faits, l'implémentation exacte était légèrement plus complexe, vu que ce circuit était conçu à partir de portes TTL AND-OR-NAND, qui regroupe une porte ET, une porte OU et une porte NAND en une seule. Pour ceux qui veulent en savoir plus sur les circuits de calcul de l'Intel 8008, voici un lien qui pourrait vous intéresser :
L'exemple de l'unité de calcul 74181
modifierAfin d'illustrer ce qui a été dit plus haut, nous allons étudier un exemple d'unité de calcul : l'unité de calcul 74181, très souvent utilisée dans les autres cours d'architecture des ordinateurs pour son aspect pédagogique indéniable. Il s'agit d'une unité de calcul commercialisée dans les années 60, à une époque où le microprocesseur n'existait pas. Les processeurs de l'époque étaient conçus à partir de pièces détachées assemblées et connectées les unes aux autres. Les pièces détachées en question étaient des boitiers qui contenaient des registres, l'unité de calcul, des compteurs, des PLA, qu'on assemblait sur une carte électronique pour faire le processeur. L'unité 74181 était une des toutes premières unités de calcul fournie dans un boitier, là où il fallait auparavant fabriquer une ALU à partir de circuits plus simples comme des additionneurs ou des circuits d’opérations bit à bit.
Le 74181 était une unité de calcul de 4 bits, ce qui veut dire qu'il était capable de faire des opérations arithmétiques sur des nombres entiers codés sur 4 bits. Il prenait en entrée deux nombres de 4 bits, et fournissait un résultat de 4 bits. Il était possible de faire du bit-slicing, à savoir de combiner plusieurs 74181 afin de créer une unité de calcul 8 bits, 12 bits, 16 bits, etc. Le 74181 était spécifiquement conçu pour, car il gérait un bit de retenue en entrée et fournissait une sortie pour la retenue du résultat.
Les opérations gérées par l'ALU 74181
modifierLes opérations de base du 74181 comprennent l'addition et 16 opérations dites bit à bit. Il peut fonctionner selon deux modes. Dans le premier mode, il effectue une opération bit à bit seule. Dans le second mode, il effectue une opération bit à bit entre les deux nombres d'entrée A et B, additionne le nombre A au résultat, et additionne la retenue d'entrée. Pour résumer, il effectue une opération bit à bit et une addition facultative. En tout, le 74181 était capable de réaliser 32 opérations différentes : les 16 opérations bit à bit seules (le maximum d'opérations de ce type possibles entre deux bits), et 16 autres opérations obtenues en combinant les 16 opérations bit à bit avec une addition.
Le fait de faire une opération bit à bit avant l'addition permet d'émuler une soustraction. Rappelons qu'une soustraction entre deux nombres A et B s'obtient en inversant les bits de B, en additionnant et en ajoutant 1. Or, il existe une opération bit à bit qui inverse tous les bits d'un nombre et celle-ci est supportée par le 74181. Ajouter 1 se fait en envoyant une retenue égale à 1 sur l'entrée de retenue.

L'entrée de sélection de l'instruction fait 5 bits, ce qui colle parfaitement avec les 32 instructions possibles. Les 5 bits en question sont séparés en deux : un groupe de 4 bits qui précise l'opération bit à bit, et un bit isolé qui indique s'il faut faire l'addition ou non. L'opération bit à bit à effectuer, est précisée par 4 bits d'entrée notés s0, s1, s2 et s3. L'activation de l'addition se fait par un bit d'entrée, le bit M, qui précise s'il faut faire ou non l'addition.
L'implémentation de l'ALU 74181
modifierLe 74181 comprend 75 portes logiques, du moins en théorie. Ce nombre est à relativiser, car l’implémentation utilisait des optimisations qui fusionnaient plusieurs portes entre elles. Elle utilisait notamment des portes AND-OR-NOT, identique à une porte ET suivie d'une porte NOR.
L'implémentation de ce circuit est, sur le papier, très simple. On prend un additionneur à anticipation de retenue, et chaque additionneur complet est précédé par une porte logique universelle 2 bit, réalisée avec un multiplexeur, qui implémente les 16 opérations logiques. Le circuit est cependant très optimisé, dans le sens où l'additionneur complet est fusionné avec la porte logique universelle. Comme sur le 8086, on modifie la manière dont les signaux de propagation et de génération de retenue sont calculés. Sauf qu'ici, on n'utilise qu'une seule porte logique universelle, très modifiée.
Le 74181 est composé de circuits assez semblables à une porte logique universelle de 2 bits, sauf qu'elle fournit deux sorties : un signal de propagation de retenue, un signal de génération de retenue. Pour comprendre comment il fonctionne, le mieux est d'établir sa table de vérité. On part du principe que le circuit a deux entrées A et B, et calcule A + f(A,B), avec f(A,B) une opération bit à bit.
| A | B | A PLUS f(a,b) | P | G | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0+f(0,0) | f(0,0) | 0 | ||
| 0 | 1 | 0+f(0,1) | f(0,0) | 0 | ||
| 1 | 0 | 1+f(1,0) | 1 | f(1,0) | ||
| 1 | 1 | 1+f(1,1) | 1 | f(1,1) |
Sur le 74181, il faut imaginer que le circuit qui calcule f(A,B) est une porte universelle commandable 2 bits, réalisée avec un multiplexeur. Les bits du résultat sont envoyés sur les 4 entrées du multiplexeur, et le multiplexeur choisit le bon bit à partir des entrées A et B (qui sont envoyés sur son entrée de commande. Les 4 entrées du multiplexeur sont notées S0, S1, S2 et S3. On a alors :
| A | B | A PLUS f(a,b) | P | G | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0+f(0,0) | S1 | 0 | ||
| 0 | 1 | 0+f(0,1) | S0 | 0 | ||
| 1 | 0 | 1+f(1,0) | 1 | S2 | ||
| 1 | 1 | 1+f(1,1) | 1 | S3 |
Le circuit pour faire cela est le suivant :

Le schéma du circuit est reproduit ci-dessous. Un oeil entrainé peut voir du premier coup d’œil que l'additionneur utilisé est un additionneur à anticipation de retenue modifié. La première couche dans le schéma ci-dessous correspond au circuit qui calcule les signaux P et G. La seconde couche est composée du reste de l'additionneur, à savoir du circuit qui combine les signaux de propagation et de génération des retenues finales.

Pour ceux qui veulent en savoir plus sur cette unité de calcul et n'ont pas peur de lire une analyse des transistors TTL de la puce, voici deux articles très intéressant sur cette ALU :
- Inside the vintage 74181 ALU chip: how it works and why it's so strange
- Inside the 74181 ALU chip: die photos and reverse engineering
L'implémentation naïve, avec des multiplexeurs
modifierPour obtenir une ALU, vous avez peut-être pensé à la solution ci-dessous. L'idée est d'utiliser un circuit par opération et de choisir le résultat adéquat avec des multiplexeurs. Le multiplexeur est évidemment commandé par l'entrée de commande, il reçoit l'opcode. Un exemple avec une ALU de 2 bits est conné ci-dessous.

Mais cette solution peut être mélangée avec les solutions précédentes. Par exemple, il est possible de mélanger cette idée avec une ALU basée sur un additionner-soustracteur. Pour obtenir un additionneur-soustracteur, on doit placer un inverseur commandable avant l'additionneur, en aval d'un opérande. L'idée est de relier l'inverseur commandable non seulement à l'additionneur, mais aussi aux portes ET/OU/XOR. Cela permet de faire les opérations NOR/NAND/NXOR, gratuitement, juste en changeant le câblage du circuit. Il est aussi possible d'ajouter un circuit pour mettre à zéro l'éoprande non inversée, comme vu plus haut. Le résultat est celui vu plus haut.


Dans ce chapitre, nous allons voir les circuits pour additionner entre eux plus de deux nombres en même temps. Additiuonneur plus de deux opérandes est appelé une addition multiopérande, terme que nous utiliserons dans la suite de ce cours. C'est une opération assez utilisée, qui est notamment à la base de la multiplication binaire, qui sera vue au chapitre suivant. Mais elle est aussi utilisée pour d'autres opérations, comme certaines opérations vectorielles utilisées dans le rendu 3D (et les moteurs de jeux vidéo).
Il existe de nombreux types de circuits capables d'effectuer une addition multiopérande. Ce sont tous des additionneurs normaux modifiés. L'interface de ces additionneurs est la même que celle des additionneurs normaux, sauf qu'ils disposent de plusieurs entrées pour les opérandes. L'un d'entre eux est illustré ci-contre, pour l'addition de trois opérandes de 4 bits. Il est préférable de voir les circuits d'addition multiopérande séparémment des circuits pour la multiplication, pour diverses raisons pédagogiques, ce qui est fait dans ce cours.
Les implémentations naïves, non-optimisées
modifierA cet instant du cours, nous ne disposons que d'additionneurs 2-opérandes, à savoir qu'ils additionnent deux nombres. Pour créer un additionneur multiopérandes, l'intuition nous dit de combiner plusieurs additionneurs 2-opérandes. Et c'est en effet une solution, qui peut se mettre en œuvre de deux manières.

La première solution utilise des additionneurs en série, placés l'un après l'autre. La seconde solution effectue certaines additions en parallèle d'autres : on obtient alors un additionneur parallèle. Avec la seconde solution, le résultat est alors connu plus tôt, car il y a moins d'additionneurs à traverser en partant des opérandes pour arriver au résultat. Dans les deux cas, on utilise presque autant d'additionneurs que d'opérandes (un additionneur en moins, pour être précis).
Les additionneurs utilisés peuvent être n'importe quel type d'additionneurs. Pour donner un exemple d'additionneurs en série, nous allons prendre un additionneur 4-opérandes (qui additionne 8 opérandes différentes). Par exemple, si on utilise des additionneurs à propagation de retenue, le circuit d'un additionneur 4 bits est celui-ci :

Bizarrement, l'usage d'additionneurs à propagation de retenue donne de bonnes performances, tout en économisant beaucoup de portes logiques.
L'addition carry save
modifierLe problème de l'addition, qu'elle soit multiopérande ou non, est la propagation des retenues. La propagation des retenues prend du temps, le reste d'un additionneur étant simplement composé de portes XOR. Mais il se trouve qu'il est possible d'additionner un nombre arbitraire d'opérandes et de ne propager les retenues qu'une seule fois ! Pour cela, on additionne les opérandes entre elles avec une addition carry-save, une addition qui ne propage pas les retenues.
L'addition carry save de trois opérandes
modifierL'addition carry-save fournit deux résultats : un résultat obtenu en effectuant l'addition sans tenir compte des retenues, et un autre composé uniquement des retenues. Pour que cela soit plus concret, nous allons étudier le cas où l'on additionne trois opérandes entre elles. Par exemple, 1000 + 1010 + 1110 donne 1010 pour les retenues, et 1100 pour la somme sans retenue. L'addition se fait comme en binaire normal, colonne par colonne, sauf que les retenues ne sont pas propagées.

Une fois le résultat en carry-save obtenu, il faut le convertir en résultat final. Pour cela, il faut faire une addition normale, avec les retenues placées sur la bonne colonne (les retenues sont ajoutées sur la colonne suivante). L'additionneur carry save est donc suivi par un additionneur normal. L'avantage de cette organisation se comprend quand on compare la même organisation sans carry save. Sans carry save, on devrait utiliser deux additionneurs normaux. Avec, on utilise un additionneur normal et un additionneur carry save plus simple et plus rapide.
L'adder compressor 3:2
modifierReste à voir comment faire l'addition en carry save. Notez que les calculs se font indépendamment, colonne par colonne. Cela vient du fait que la table d'addition en binaire, pour 3 bits, le permet :
- 0 + 0 + 0 = 0, retenue = 0 ;
- 0 + 0 + 1 = 1, retenue = 0 ;
- 0 + 1 + 0 = 1, retenue = 0 ;
- 0 + 1 + 1 = 0, retenue = 1 ;
- 1 + 0 + 0 = 1, retenue = 0 ;
- 1 + 0 + 1 = 0, retenue = 1 ;
- 1 + 1 + 0 = 0, retenue = 1 ;
- 1 + 1 + 1 = 1, retenue = 1.
La seule contrainte est de pouvoir additionner trois bits. Il se trouve que l'on a déjà un circuit capable de le faire : l'additionneur complet ! Un circuit d'addition de trois opérandes en carry save est donc composé de plusieurs additionneurs complets indépendants, chacun additionnant le contenu d'une colonne. Le tout est illustré ci-dessous.

Les additionneurs carry save en général
modifierLes additionneurs carry save additionnent plusieurs opérandes et fournissent un résultat en carry save. Faire une addition multiopérande demande donc : d'additionner les opérandes en carry save, puis de convertir le résultat carry save en résultat final. Le tout demande juste un additionneur carry save et un additionneur normal. L'avantage est que l'additionneur carry save économise beaucoup de portes logiques et est aussi plus rapide.

Les additionneurs carry save sériels
modifierDans le cas le plus fréquent, un additionneur carry save se conçoit en combinant des additionneurs carry save 3-opérandes. La manière la plus simple est d'enchainer les additionneurs 3-opérandes les uns à la suite des autres, comme illustré ci-dessous.

Prenez garde : les retenues sont décalées d'un rang pour être additionnées. En conséquence, le circuit ressemble à ceci :

Mais cette méthode est généralement peu efficace, et on préfére utiliser une organisation parallèle, en arbre, avec des additions faites en parallèle. Les deux méthodes les plus connues donnent les additionneurs en arbres de Wallace, ou en arbres Dadda.
Les arbres de Wallace
modifierLes arbres les plus simples à construire sont les arbres de Wallace. Le principe est d'ajouter des couches d'additionneurs carry-save, et de capturer un maximum de nombres lors de l'ajout de chaque couche. On commence par additionner un maximum de nombres avec des additionneurs carry-save. Pour additionner n nombres, on commence par utiliser n/3 additionneurs carry-save. Si jamais n n'est pas divisible par 3, on laisse tranquille les 1 ou 2 nombres restants. On se retrouve ainsi avec une couche d'additionneurs carry-save. On répète cette étape sur les sorties des additionneurs ainsi ajoutés : on rajoute une nouvelle couche. Il suffit de répéter cette étape jusqu'à ce qu'il ne reste plus que deux résultats : on se retrouve avec une couche finale composée d'un seul additionneur carry-save. Là, on rajoute un additionneur normal, pour additionner retenues et sommes.

Les arbres de Dadda
modifierLes arbres de Dadda sont plus difficiles à comprendre. Contrairement à l'arbre de Wallace qui cherche à réduire la hauteur de l'arbre le plus vite possible, l'arbre de Dadda cherche à diminuer le nombre d'additionneurs carry-save utilisés. Pour cela, l'arbre de Dadda se base sur un principe mathématique simple : un additionneur carry-save peut additionner trois nombres, pas plus. Cela implique que l'utilisation d'un arbre de Wallace gaspille des additionneurs si on additionne n nombres, avec n non multiple de trois.
L'arbre de Dadda résout ce problème d'une manière simple :
- si n est multiple de trois, on ajoute une couche complète d'additionneurs carry-save ;
- si n n'est pas multiple de trois, on ajoute seulement 1 ou 2 additionneur carry-save : le but est de faire en sorte que la couche suivante fournisse un nombre d'opérandes multiple de trois.
Et on répète cette étape d'ajout de couche jusqu'à ce qu'il ne reste plus que deux résultats : on se retrouve avec une couche finale composée d'un seul additionneur carry-save. Là, on rajoute un additionneur normal, pour additionner retenues et sommes.

Les adders compressors
modifierDans les circuits précédents, il n'est pas rare d'enchainer plusieurs additionneurs complets l'un à la suite des autres. Mais il est possible de les regrouper par 2 ou 3, ce qui permet de faire des simplifications. Les regroupements en question sont appelés des adder compressors. Ils prennent en entrée plusieurs bits, provenant d'opérandes différents, et les additionnent. Le résultat est évidemment en carry save, ce qui fait qu'il est codé sur deux bits : un bit de retenue, un bit de résultat.
Les mal-nommés adders compressors 4:2
modifierLe résultat de la fusion de deux additionneurs complets donne un mal nommé "adder compressor 4:2". Ils disposent de 5 entrées et fournissent 3 sorties. Plus précisément, ils prennent en entrée 4 bits pour les 4 opérandes et un bit pour la retenue d'entrée. Pour la sortie, ils fournissent 3 sorties : le bit de retenue du résultat final, les deux retenues des additions intermédiaires.
La manière la plus simple de les fabriquer est d'utiliser deux additionneurs complets l'un à la suite de l'autre. Le premier additionne trois bits d'opérande et fournit un résultat et des retenues, le résultat est ensuite additionné avec les deux opérandes restantes. Au final, on se retrouve avec deux retenues, et un résultat.

Il est cependant possible d'améliorer le circuit pour le rendre légèrement plus rapide. Le problème du circuit précédent est que les portes XOR sont enchainées l'une après l'autre, alors que l'on peut faire comme suit :

L'additionneur multiopérande itératif
modifierL'additionneur multiopérande itératif additionne les opérandes une par une, le résultat temporaire étant stocké dans le registre. Il porte le nom d'additionneur (multi-opérande) itératif. Il est composé d'un additionneur couplé à un registre, le tout entouré de circuits de contrôle (non-représentés dans les schémas suivants). Le circuit de contrôle est, dans le cas le plus simple, un simple compteur initialisé avec le nombre d'opérandes à additionner. Le registre est appelé le registre accumulateur, ce qui trahit bien son rôle dans le circuit.

L'avantage de ce circuit est que le nombre d'opérandes à additionner est variable. Par exemple, prenons un additionneur itératif qui permet d'additionner maximum 127 opérandes (le compteur des circuits de contrôle est de 7 bits). Dans ce cas, qui peut le plus peut le moins : il peut additionner seulement 16 opérandes, seulement 7, seulement 20, etc. Et le résultat est alors connu plus vite : moins on a d'opérandes à additionner, moins le circuit fera d'additions. Par exemple, l'addition de 7 opérandes demandera seulement 6 additions, pas une de plus ou de moins. Les autres circuits que nous verrons dans ce chapitre sont moins flexibles. Ils additionnent toujours le même nombre d'opérandes, ce qui n'est pas un problème dans les cas où ils sont utilisés. Rien n'empêche de mettre certaines opérandes à 0, ce qui permet de faire moins, de faire des calculs avec moins d'opérandes.
Les additionneurs itératifs hydrides
modifierL'additionneur multiopérande itératif peut s'implémenter avec des additionneurs carry save. Par exemple, un additionneur itératif peut utiliser un additionneur carry save et un registre pour additionner les opérandes, avant d'envoyer le résultat final à un additionneur normal pour calculer le résultat final. Le circuit obtenu est un L'additionneur multiopérande hybride, mi-itératif, mi carry save.

Un cas particulier d'addition multi-opérande : le calcul de population count
modifierVoyons maintenant un cas très particulier d'addition multi-opérande : le calcul de la population count d'un nombre, aussi appelée poids de Hamming. Il s'agit d'un calcul qui prend en entrée un nombre, une opérande tout ce qu'il y a de plus normale, codée sur plusieurs bits. La population count calcule le nombre de bits de l'opérande qui sont à 1. C'est donc une addition multi-opérande, sauf que l'on additionne des bits individuels.
Elle est très utilisée quand il faut manipuler la représentation binaire d'un nombre, ou quand on manipule des tableaux de bits. Les deux cas sont peu fréquents en-dehors des codes très bas niveau, mais tout programmeur a déjà eu l'occasion d'en manipuler. C'est une opération très courante dans les algorithmes de correction d'erreur, utilisés dans les transmissions réseaux, que nous verrons dans quelques chapitres. Elle est aussi utilisée pour le codage/décodage vidéo/audio, quand il faut crypter/décrypter des données, etc. Les réseaux de neurones artificiels, notamment ceux utilisés dans l'intelligence artificielle, font aussi usage de cette opération.
Elle peut se calculer de beaucoup de manières différentes. La plus simple s'obtient avec le raisonnement est alors le suivant : si on découpe un nombre en deux parties, la population count du nombre est la somme des population count de chaque partie. Il est possible d'appliquer ce raisonnement de manière récursive sur chaque morceau, jusqu'à réduire chaque morceau 1 bit. Or, la population count d'un bit est égale au bit lui-même, par définition. On en déduit qu'il suffit d'utiliser une série d'additionneurs enchainés en arbre, comme illustré ci-dessous.

Le circuit est alors composé de plusieurs couches d'additionneurs différents. La première couche additionne deux bits entre eux, elle est donc composée uniquement de demi-additionneurs. La seconde couche est composée d'additionneurs qui prennent des opérandes de deux bits (le résultat des demi-additionneurs), la couche suivante est faite d'additionneurs pour opérandes de 3 bits, etc.

Il est naturellement possible d'utiliser des additionneurs carry save pour économiser des circuits.

Nous allons maintenant aborder un circuit appelé le multiplieur, qui multiplie deux opérandes. La multiplication se fait en binaire de la même façon qu'on a appris à le faire en primaire, si ce n'est que la table de multiplication est vraiment très simple en binaire, jugez plutôt !
- 0 × 0 = 0.
- 0 × 1 = 0.
- 1 × 0 = 0.
- 1 × 1 = 1.
Pour commencer, petite précision de vocabulaire : une multiplication s'effectue sur deux nombres, le multiplicande et le multiplicateur. Une multiplication génère des résultats temporaires, chacun provenant de la multiplication du multiplicande par un chiffre du multiplicateur : ces résultats temporaires sont appelés des produits partiels. Multiplier deux nombres en binaire demande de générer les produits partiels, de les décaler, avant de les additionner.
La génération des produits partiels est assez simple. Sur le principe, la table de multiplication binaire est un simple ET logique. Générer un produit partiel demande donc, à minima, de faire un ET entre un bit du multiplicateur et le multiplicande. Le circuit pour cela est trivial.
La seconde étape est ensuite de décaler le résultat du ET pour tenir compte du poids du bit choisit. En effet, regarder le schéma de droite qui montre comment faire une multiplication en binaire. Vous voyez que c'est comme en décimal : chaque ligne correspond à un produit partiel, et chaque produit partiel est décalé d'un cran par rapport au précédent. Il faut donc ajouter de quoi faire ce décalage. Intuitivement, on se dit qu'il faut ajouter des circuits décaleurs, un pour chaque bit du multiplicateur. Ce ne sera pas toujours le cas, mais il y en aura parfois besoin.
La multiplication non-signée
modifierNous allons d'abord commencer par les multiplieurs qui font de la multiplication non-signée. La multiplication de deux nombres signés est en effet un peu particulière et demande des techniques particulières, là où la multiplication non-signée est beaucoup plus simple.
Les multiplieurs non-itératifs
modifierUne première solution calcule tous les produits partiels en parallèle, en même temps, avant de les additionner avec un additionneur multi-opérandes non-itératif, composé d'additionneurs carry-save. C'est une solution simple, qui utilise beaucoup de circuits, mais est très rapide. C'est la solution utilisée dans les processeurs haute performance moderne, dans presque tous les processeurs grand public, depuis plusieurs décennies.

Notons que la génération des produits partiels se passe de circuits décaleur, elle se contente d'utiliser un paquet de portes ET. Le câblage permet de câbler les sorties des portes ET aux bonnes entrées de l'additionneur, ce qui permet de se passer de circuits décaleurs.
Les multiplieurs itératifs
modifierLes multiplieurs les plus simples génèrent les produits partiels les uns après les autres, et les additionnent au fur et à mesure. Le multiplicateur et le multiplicande sont mémorisés dans des registres. Le reste du circuit est composé d'un circuit de génération des produits partiels, suivi d'un additionneur multiopérande itératif. La multiplication est finie quand tous les bits du multiplicateur ont étés traités (ce qui peut se détermine avec un compteur).

Rappelons que l'additionneur multiopérande itératif est composé d'un additionneur normal, à deux opérandes, couplé à un registre appelé le registre accumulateur. Il mémorise le résultat temporaire de l'addition des produits partiels. A la fin de la multiplication, une fois tous les produits partiels additionnés, il contient le résultat.

Il existe plusieurs multiplieurs itératifs, qui différent par la façon dont ils génèrent le produit partiel. Dans tous les cas, la multiplication multiplie un bit du multiplicateur par le multiplicande. La différence tient dans le sens de parcours : certains traitent les bits du multiplicateur de droite à gauche, les autres dans le sens inverse. Dans le premier cas, le multiplieur subit un décalage à droite et il est traité de droite à gauche, des bits de poids faible vers les bits de poids fort. Dans le second cas, il subit un décalage à gauche et est traité de gauche à droite, des bits de poids fort vers les bits de poids faible.
Pour cela, on stocke le multiplieur dans un registre à décalage, ce qui fait qu'un bit sort à chaque cycle. Et c'est ce bit qui sort du registre à décalage qui est utilisé pour générer le produit partiel. Voici comment se déroule une multiplication avec un multiplieur qui fait le calcul de droite à gauche, qui commence par les bits de poids faible du multiplicateur :

Il faut noter que le contenu du registre accumulateur est aussi décalé d'un cran vers la gauche ou la droite à chaque cycle, pour tenir compte du poids des bits multipliés. Pour comprendre pourquoi, rappelez-vous que dans une multiplication, en décimal ou binaire, les produits partiels ne sont pas alignés sur une même colonne : ils sont décalés d'un cran par rapport au précédent. Vu qu'on additionne les produits partiels un par un, on doit donc faire un décalage d'un cran entre chaque addition. En théorie, le décalage doit être réalisé à la génération des produits partiels, par un circuit décaleur. Mais cette solution demande d'utiliser des produits partiels qui sont deux fois plus longs que le multiplicande/multiplicateur.
Une solution alternative, beaucoup plus simple, effectue ce décalage directement dans le registre accumulateur. En effet, chaque produit partiel est décalé d'un cran vers la gauche par rapport au précédent, d'un cran vers la droite par rapport au précédent. On peut donc faire le décalage entre chaque addition. Le registre accumulateur est donc un registre à décalage ! Ce qui n'est pas le cas sur un additionneur multiopérande itératif normal. Avec cette technique, les produits partiels générés ont la même taille que le multiplicateur, le même nombre de bits. On économise pas mal de circuit : pas besoin de circuits décaleur, moins d'entrées sur l'additionneur.
Le sens de décalage du multiplicateur et du registre accumulateur sont identiques. Si on effectue la multiplication de droite à gauche, en commençant par les bits de poids faible, alors le registre accumulateur est aussi décalé vers la droite. Cela permet au produit partiel suivant d'être placé un cran à gauche du précédent. A l'inverse, si on effectue la multiplication en commençant par les bits de poids fort, alors on décale le registre accumulateur vers la gauche, histoire de placer un produit partiel à la droite du précédent.
Les deux solutions ne sont pas strictement équivalentes, car la seconde à un avantage. Prenons un multiplicateur de N bits. Avec une multiplication qui commence par les bits de poids fort, l'addition donne un résultat sur 2N bits, la totalité d'entre eux étant utiles. En allant dans l'autre sens, l'addition donne un résultat qui a N bits effectifs, à savoir que le reste sont systèmatiquement à zéro et sont en réalité pris en charge par le décalage de l'accumulateur. Commencer par les bits de poids faible permet d'utiliser des produits partiels sur n bits, donc d'utiliser un additionneur sur N bits. Les produits partiels aussi sont de N bits. Le registre accumulateur reste de 2N bits, mais seuls les N bits de poids fort sont utilisés dans l'addition.

Il est même possible de ruser encore plus : on peut se passer du registre pour le multiplicateur. Il suffit d'initialiser les bits de poids faible du registre accumulateur avec le multiplicateur au démarrage de la multiplication. Le bit du multiplicateur choisi pour le calcul du produit partiel est simplement le bit de poids faible du résultat.

Les optimisations liées aux opérandes
modifierles circuits plus incorporent certaines optimisations, notamment concernant le sens de parcours du multiplieur, afin de rendre les calculs plus rapides. Mais d'autres optimisations permettent de gagner encore plus en performance, mais qui dépendent de la valeur des opérandes. Avec ces optimisations, la multiplication sera plus ou moins rapide suivant l'opérande : certaines opérandes donneront une multiplication en 32 cycles, d'autres en 12 cycles, d'autres en 20, etc. L'idée est de zapper certains cycles où on sait que le multiplicande sera multiplié par zéro, ce qui arrive quand le bit du multiplieur vaut 0. En théorie, on pourrait faire cela à chaque cycle, mais cela n'a pas d'intérêt, car contourner l'additionneur n'a pas grand intérêt. Mais on peut cependant faire quelques optimisations.
La première optimisation consiste à terminer l'opération une fois que tous les calculs nécessaires ont été faits, c'est à dire une fois que le multiplieur décalé atteint 0. Dans ce cas, on a multiplié tous les bits à 1 du multiplieur, tous les produits partiels restants valent 0, pas besoin de les calculer. L'optimisation ne marche cependant que si on commence les calculs à partir du bit de poids faible du multiplieur. Si on commence par les bits de poids fort, il faudra faire plusieurs décalages pour obtenir le bon résultat. Par exemple, si les N bits de poids faible su multiplieurs valent 0, alors il faudra décaler le résultat dans le registre accumulateur de N rangs vers la gauche.
Voyons maintenant une autre optimisation, qui va de pair avec l'optimisation précédente. Prenons d'abord une multiplication qui part du bit de poids fort, et décale le multiplieur vers la gauche. Elle fonctionne sur les opérandes dont les N bits de poids fort sont à 0. L'idée est de commencer la multiplication pour le premier bit du multiplieur à 1, et de zapper les 0 précédents en décalant le multiplier. Ce faisant, on utilise un circuit qui effectue l'opération adéquate, à savoir l'opération de count leading zeros, puis décale le multiplieur de ce nombre, ainsi que le reste partiel. La même optimisation s'applique si on commence la multiplication à partir du bit de poids faible, il faut alors effectuer l'opération count trailing zeros pour savoir de combien décaler.

Si on décale le multiplieur vers la droite, on ne doit gérer les 0 que dans les bits de poids fort. Pour gérer les bits de poids faible à 0, il suffit de tester si l'opérande est zéro, à savoir appliquer l'optimisation précédente. Les deux optimisations sont complémentaires, elles sont deux faces d'une même pièce.
Les multiplieurs en base 4, 8, 16
modifierAvec les multiplieurs itératifs précédents, la multiplication se fait produit partiel par produit partiel. On ne tient compte que d'un seul bit du multiplieur, qui est multiplié avec le multiplicande, ce qui génère un produit partiel. À l'inverse, avec les multiplieurs basés sur un additionneur multiopérande non-itératif, on génère tous les produits partiels en même temps, pour les additionner tous en même temps (ou presque). Il existe cependant des multiplieurs intermédiaires, qui génèrent et additionnent plusieurs produits partiels à la fois, tout en restant des multiplieurs itératifs.
L'idée est qu'au lieu de faire la multiplication bit par bit pour le multiplicande, on prend deux bits du multiplicande, ou trois ou quatre. Concrètement, on génère deux, trois, quatre produits partiels en même temps et on les additionne d'un seul coup au résultat temporaire dans le registre. On parle alors de multiplieurs en base 4, 8, ou 16. Le multiplieur en base 4 génère deux produits partiels à la fois, celui en base 8 en génère 3, celui en base 16 en génère 4, etc.
Il existe plusieurs manières de fabriquer un multiplieur en base 4, 8, 16, etc. La première, la plus simple, utilise un multiplieur hybride, qui mélange un multiplieur itératif et un autre non-itératif. La seconde, plus complexe, modifie le circuit d'un multiplieur itératif en rajoutant des circuits annexes.
Les multiplieurs hybrides
modifierUne solution, assez évidente, mélange l'usage d'additionneurs carry save et multiplieur itératif. L'idée est simple : on génère plusieurs produits partiels à la fois, on les additionne avec le registre accumulateur avec un additionneur multiopérande normal. En clair, on rajoute des circuits de génération des produits partiels et on remplace l'additionner normal par un additionneur multiopérande. Voici ce que cela donne quand on prend deux produits partiels à la fois :

La seule difficulté est de prendre en compte les décalages entre produits partiels. Déjà, dans l'exemple avec deux produits partiels, vu qu'on traite deux bits à la fois, on doit décaler le registre accumulateur de deux rangs. De plus, les deux bits du multiplieur utilisés n'ont pas le même poids. Un des produits partiel doit être décalé d'un rang par rapport à l'autre. En théorie, on devrait user d'un circuit décaleur, mais on peut s'en passer avec des bidouilles de câblage. La même chose a lieu quand on génère trois produits partiels à la fois : l'un n'est pas décalé, le suivant l'est d'un rang, l'autre de trois rangs. Et ainsi de suite avec quatre produits partiels simultanés. Rien d'insurmontable en soi, cela ne fait que marginalement complexifier le circuit.
Il est possible d'optimiser le circuit en changeant son organisation. L'idée est de faire les additions de produits partiels en carry save uniquement, sans passer par un résultat temporaire en binaire. Pour cela, il faut déplacer l'additionneur normal après le registre. De plus, le registre accumulateur mémorise le résultat temporaire en carry save. Il est donc dupliqué, avec un registre pour les retenues, et l'autre pour la somme. Une fois que tous les produits partiels ont été additionnés, on traduit le résultat temporaire en carry save en binaire normal, avec l'additionneur normal.

Le design précédent peut être amélioré en tenant compte d'un détail portant sur le registre accumulateur. Il s'agit d'un registre synchrone, commandé par un signal d’horloge non-représenté dans les schémas précédents. Une implémentation de ce registre utilise des bascules dites master-slave, composées de deux bascules D non-synchrones à entrée Enable qui se suivent, comme nous l'avions vu dans le chapitre sur les circuits synchrones. Le registre synchrone est donc composé de deux registres non-synchrones qui se suivent. Avec ce type de registres, il est possible de modifier le multiplieur précédent de manière à doubler le nombre de produits partiels additionnés à chaque cycle d'horloge. L'idée est très simple : on insère un second additionneur carry save entre les deux registres ! On obtient alors un multiplieur multibeat.

Les multiplieurs itératifs en base 4, 8, 16
modifierLa méthode précédente utilise un multiplieur hybride. Mais il est aussi possible d'utiliser un multiplieur itératif normal, et de le modifier pour en faire un multiplieur en base 4, 8, 16, etc. Les méthodes pour cela sont moins intuitives, plus complexes, mais sont cependant intéressantes à étudier. Elles ne sont pas utilisées, car elles utilisent plus de circuits ou sont moins performantes.
Leur idée est d'additionner les produits partiels entre eux avant de les additionner au registre accumulateur. Le problème est que l'on ne va pas rajouter un second additionner dans le circuit, aussi diverses méthodes permettent de ruser. La ruse consiste à précalculer tous les produits partiels possibles et de les stocker dans des registres. Le choix du produit partiel à envoyer à l'additionneur se fait avec un MUX commandé par un paquet de 2, 3, 4 bits du multiplieur.
Prenons l'exemple le plus simple : celui d'un multiplieur en base 4, qui demande d’additionner deux produits partiels à la fois, de traiter l'opérande multiplieur par paquets de deux bits. Dans ce cas, la somme des produits partiels vaut : O, A, 2A, 3A. Et c'est cette somme qu'il faut additionner au contenu du registre accumulateur. Les quatre sommes possibles sont toujours les mêmes, et on peut les précalculer et les mémoriser dans des registres dédiés. On peut choisir la bonne somme en fonction des deux bits du multiplieur

Il est cependant possible de ruser afin d'éliminer certains registres. Par exemple, pas besoin d'un registre pour le 0 : juste d'un circuit de mise à zéro, comme dans n'importe quel circuit de génération de produit partiel. Pareil pour le registre contenant le double du multiplicande : un simple décalage suffit pour le calculer à la volée (une simple bidouille de câblage permet de se passer de circuit décaleur). Seuls restent les registres pour le multiplicande et son triple. Il est généré par l'additionneur normal, en fin de circuit, au tout début de l'addition.
La solution marche aussi quand on veut générer trois produits partiels à la fois, ou quatre, ou cinq, mais deviennent rapidement inutiles. Par exemple, pour générer trois produits partiels à la fois, il faut calculer 0, A, 2A, 3A, 5A et 7A, et calculer le reste à partir de cela. Mais le jeu n'en vaut pas la chandelle. Certes, calculer trois produits partiels à la fois divise par trois le nombre d'additions, sauf que générer à l'avance les produits partiels rajoute quelques additions. Ce qu'on gagne d'un côté, on le perd de l'autre.
Les multiplieurs diviser pour régner
modifierIl existe enfin un tout dernier type de multiplieurs : les multiplieurs diviser pour régner. Pour comprendre le principe, nous allons prendre un multiplieur qui multiplie deux nombres de 32 bits. Les deux opérandes A et B peuvent être décomposées en deux morceaux de 16 bits, qu'il suffit de multiplier entre eux pour obtenir les produits partiels voulus : une seule multiplication 32 bits se transforme en quatre multiplications d'opérandes de 16 bits. En clair, ces multiplieurs sont composés de multiplieurs qui travaillent sur des opérandes plus petites, associés à des additionneurs.
La multiplication de nombres signés
modifierTous les circuits qu'on a vus plus haut sont capables de multiplier des nombres entiers positifs, mais on peut les adapter pour qu'ils fassent des calculs sur des entiers signés. Et la manière de faire la multiplication dépend de la représentation utilisée. Les nombres en signe-magnitude ne se multiplient pas de la même manière que ceux en complément à deux ou en représentation par excès. Dans ce qui va suivre, nous allons voir ce qu'il en est pour la représentation signe-magnitude et pour le complément à deux. La représentation par excès est volontairement mise de côté, car ce cas est assez compliqué à gérer et qu'il n'existe pas de solutions simples à ce problème. Cela explique le peu d'utilisation de cette représentation, qui est limitée aux cas où l'on sait qu'on ne fera que des additions/multiplications, le cas de l'exposant des nombres flottants en étant un cas particulier.
Multiplier les valeurs absolues et convertir
modifierUne première solution pour multiplier des entiers signés est simple : on prend les valeurs absolues des opérandes, on multiplie, et on inverse le résultat si besoin. Mathématiquement, la valeur absolue du résultat est le produit des valeurs absolues des opérandes. Quant au signe, on apprend dans les petites classes le tableau suivant. On s’aperçoit qu'on doit inverser le résultat si et seulement si une seule opérande est négative, pas les deux.
| Signe du multiplicande | Signe du multiplieur | Signe du résultat |
|---|---|---|
| + | + | + |
| - | + | - |
| + | - | - |
| - | - | + |
Pour les entiers en signe-valeur absolue, le calcul est très simple, vu que la valeur absolue et le signe sont séparés. Il suffit de calculer le bit de signe à part, et multiplier les valeurs absolues. En traduisant le tableau d'avant en binaire, avec la convention + = 0 et - = 1, on trouve la table de vérité d'une porte XOR. Pour résumer, il suffit de multiplier les valeurs absolues et de faire un vulgaire XOR entre les bits de signe.

Pour les entiers en complément à deux, cette solution n'est pas utilisée. Prendre les valeurs absolues demande d'utiliser deux incrémenteurs et deux inverseurs, sans compter qu'il faut en rajouter un de plus pour inverser le résultat. Le cout en circuits serait un peu gros, sans compter qu'on peut faire autrement.
Les multiplieurs itératifs signés en complément à deux
modifierPour la représentation en complément à deux, les multiplieurs non-signés vus plus haut fonctionnent parfaitement quand les deux opérandes ont le même signe, mais pas quand un des deux opérandes est négatif.
Avec un multiplicande négatif, le produit partiel est censé être négatif. Les multiplieurs vus plus haut peuvent gérer la situation so on utilise une extension de signe sur les produits partiels. Pour cela, il faut faire en sorte que le décalage du résultat soit un décalage arithmétique. Cette technique marche très bien que on utilise un multiplieur qui travaille de droite à gauche, avec des décalages à droite.
Pour traiter les multiplicateurs négatifs, le produit partiel correspondant au bit de poids fort doit être soustrait. L'explication du pourquoi est assez dure à comprendre, aussi je vous épargne les détails, mais c'est lié au fait que ce bit a une valeur négative. L'additionneur doit donc être remplacé par un additionneur-soustracteur.

Les multiplieurs de Booth
modifierIl existe une autre façon, nettement plus élégante, inventée par un chercheur en cristallographie du nom de Booth : l'algorithme de Booth. Le principe de cet algorithme est que des suites de bits à 1 consécutives dans l'écriture binaire d'un nombre entier peuvent donner lieu à des simplifications. Si vous vous rappelez, les nombres de la forme 01111…111 sont des nombres qui valent 2n − 1. Donc, X × (2^n − 1) = (X × 2^n) − X. Cela se calcule avec un décalage (multiplication par 2^n) et une soustraction. Ce principe peut s'appliquer aux suites de 1 consécutifs dans un nombre entier, avec quelques modifications. Prenons un nombre composé d'une suite de 1 qui commence au n-ième bit, et qui termine au X-ième bit : celle-ci forme un nombre qui vaut 2^n − 2^n−x. Par exemple, 0011 1100 = 0011 1111 − 0000 0011, ce qui donne (2^7 − 1) − (2^2 − 1). Au lieu de faire des séries d'additions de produits partiels et de décalages, on peut remplacer le tout par des décalages et des soustractions.
C'est le principe qui se cache derrière l’algorithme de Booth : il regarde le bit du multiplicateur à traiter et celui qui précède, pour déterminer s'il faut soustraire, additionner, ou ne rien faire. Si les deux bits valent zéro, alors pas besoin de soustraire : le produit partiel vaut zéro. Si les deux bits valent 1, alors c'est que l'on est au beau milieu d'une suite de 1 consécutifs, et qu'il n'y a pas besoin de soustraire. Par contre, si ces deux bits valent 01 ou 10, alors on est au bord d'une suite de 1 consécutifs, et l'on doit soustraire ou additionner. Si les deux bits valent 10 alors c'est qu'on est au début d'une suite de 1 consécutifs : on doit soustraire le multiplicande multiplié par 2^n-x. Si les deux bits valent 01, alors on est à la fin d'une suite de bits, et on doit additionner le multiplicande multiplié par 2^n. On peut remarquer que si le registre utilisé pour le résultat décale vers la droite, il n'y a pas besoin de faire la multiplication par la puissance de deux : se contenter d’additionner ou de soustraire le multiplicande suffit.
Reste qu'il y a un problème pour le bit de poids faible : quel est le bit précédent ? Pour cela, le multiplicateur est stocké dans un registre qui contient un bit de plus qu'il n'en faut. On remarque que pour obtenir un bon résultat, ce bit précédent doit mis à 0. Le multiplicateur est placé dans les bits de poids fort, tandis que le bit de poids faible est mis à zéro. Cet algorithme gère les signes convenablement. Le cas où le multiplicande est négatif est géré par le fait que le registre du résultat subit un décalage arithmétique vers la droite à chaque cycle. La gestion du multiplicateur négatif est plus complexe à comprendre mathématiquement, mais je peux vous certifier que cet algorithme gère convenablement ce cas.
Les division signée et non-signée
modifierLa division en binaire se fait de la même manière qu'en décimal : avec une série de soustractions. L'opération implique un dividende, qui est divisé par un diviseur pour obtenir un quotient et un reste.
Implémenter la division sous la forme de circuit est quelque peu compliqué. La difficulté est simplement que chaque étape de la division dépend de la précédente ! Cela réduit les possibilités d'optimisation. Il est très difficile d'utiliser des soustracteurs multiopérande non-itératifs pour créer un circuit diviseur. Pas de problème pour la multiplication, où utiliser un paquet d'additionneurs en parallèle marche bien. La division ne permet pas de faire de genre de choses facilement. C'est possible, mais le cout en circuits est prohibitif.
Les techniques que nous allons voir en premier lieu calculent le quotient bit par bit, elles font une soustraction à la fois. Il est possible de calculer le quotient non pas bit par bit, mais par groupe de deux, trois, quatre bits, voire plus encore. Mais les circuits deviennent alors très compliqués. Dans tous les cas, cela revient à utiliser des diviseurs itératifs, sur le même modèle que les multiplicateurs itératifs, sauf que l’addition est remplacée par une soustraction. Nous commencer par les trois techniques les plus simples pour cela : l'implémentation naïve, la division avec restauration, et sans restauration.
L'implémentation itérative naïve
modifier
En binaire, l'opération de division est la même qu'en décimal, si on omet que la table de soustraction est beaucoup plus simple. La seule différence est qu'en binaire, à chaque étape, on doit soit soustraire zéro, soit soustraire le diviseur, rien d'autre. Mais pour le reste, tout se passe de la même manière qu'en décimal. À chaque étape, on prend le reste partiel, le résultat de la soustraction précédente, et on abaisse le bit adéquat, exactement comme en décimal.
Sur le principe, général, un diviseur ressemble à ce qui est indiqué dans le schéma ci-dessous. On trouve en tout quatre registres : un pour le dividende, un pour le diviseur, un pour le quotient, et un registre accumulateur dans lequel se trouve le "reste partiel" (ce qui reste une fois qu'on a soustrait le diviseur dans chaque étape).
À chaque étape de la division, on effectue une soustraction, ce qui demande un circuit soustracteur. On soustrait soit le diviseur, soit zéro. Le choix entre les deux est réalisé par un multiplexeur, ou encore mieux : par un circuit de mise à zéro sélectif.
Abaisser le bit suivant demande un peu plus de réflexion. Le bit abaissé appartient au dividende, et on abaisse les bits en progressant du bit de poids fort vers le bit de poids faible. Pour faire cela, le dividende est placé dans un registre à décalage, qui se décale d'un rang vers la gauche à chaque itération. Le bit sortant du registre n'est autre que le bit abaissé. Il suffit alors de le concaténer au reste partiel, avec une petite ruse de câblage, et d'envoyer le tout en opérande du soustracteur. Rien de bien compliqué, il faut juste envoyer le bit abaissé sur l'entrée de poids faible du soustracteur, et de câbler le reste pareil à côté, ce qui décale le tout d'un rang automatiquement, sans qu'on ait besoin de circuit décaleur pour le reste partiel.
Reste ensuite à déterminer le quotient, ce qui est fait par un circuit spécialisé relié au diviseur et au dividende. Au passage, déterminer le bit du quotient permet au passage de savoir si on doit soustraire le diviseur ou non (soustraire zéro). Ce circuit n'est pas relié qu'au registre pour le quotient, mais aussi au multiplexeur mentionné précédemment. Toute la difficulté tient dans la détermination du quotient. En soi, elle est très simple : il suffit de comparer le dividende et le diviseur. Si le dividende est supérieur au diviseur, alors on peut soustraire. S'il est inférieur, on ne soustrait pas, et on passe à l'étape suivante. Si les deux sont égaux, on soustrait.

L’optimisation de ce circuit la plus intéressante est la mise à l'échelle les opérandes. L'idée est juste de commencer la division au bon moment, en ne faisant pas certaines étapes dont on sait qu'elles vont fournir un zéro sur le quotient. L'idée marche sur les dividendes dont les n bits de poids fort sont à zéro. L'idée est de zapper ces n bits, en décalant le dividende de n rangs au début de la division, vu qu'on sait que ces bits donneront des zéros pour le quotient et pas de reste partiel. Il faut aussi décaler le quotient de n rangs, en insérant des 0 à chaque rang décalé.
L'implémentation itérative sans redondance du soustracteur
modifierUn défaut du circuit précédent est qu'il y a une duplication de circuit cachée. En effet, le circuit de détermination du quotient est un comparateur. Mais un comparateur peut s'implémenter par un circuit soustracteur ! Pour vérifier si un opérande est supérieur, égale ou inférieur à une seconde opérande, il suffit de les soustraire entre elles et de regarder le signe du résultat. On a donc deux circuits soustracteurs cachés dans ce circuit : un pour déterminer le quotient, un autre pour faire la soustraction. Mais il y a moyen de ruser pour éliminer cette redondance.
De plus, retirer cette duplication ne rend pas le circuit plus lent. En n'utilisant qu'un seul soustracteur, on fera la comparaison et la soustraction dans le même soustracteur, l'une après l'autre. Mais avec le circuit ci-dessous, c'est la même chose : on effectue la comparaison pour sélectionner le bon opérande, avant de faire la soustraction. Dans les deux cas, c'est globalement la même chose.
Si on retire la redondance mentionnée dans la section précédente, le circuit reste globalement le même, à un détail près. Chaque étape demande de comparer reste partiel et diviseur pour déterminer le bit du quotient et l'opérande à soustraire, puis faire la soustraction. La comparaison se fait avec une soustraction, et le bit de signe du résultat est utilisé pour déterminer le signe de l'opérande. Chaque étape est donc découpée en deux sous-étapes consécutives : la comparaison et la soustraction. La manière la plus simple pour cela est de faire en sorte que le circuit fasse chaque étape en deux cycles d'horloges : un dédié à la comparaison, un autre dédié à la soustraction proprement dit.
Le circuit doit donc fonctionner en deux temps, et la meilleure manière pour cela est de lui faire faire une étape de la division en deux cycles d'horloges. Certains circuits vont fonctionner lors du premier cycle, d'autres lors du second. Lors du premier cycle, le bit du quotient est déterminé, le multiplexeur est configuré pour pointer vers le diviseur, et le registre du quotient est décalé. Les autres circuits ne fonctionnent pas. Le résultat de la soustraction n'est pas pris en compte, il n'est pas enregistré dans le registre du reste partiel. Lors du second cycle, c'est l'inverse : le multiplexeur est configuré par le bit calculé à l'étape précédente, le résultat de la soustraction est enregistré dans le registre accumulateur, et le registre du dividende est décalé.

On pourrait croire que le circuit de division obtenu est plus lent, vu qu'il a besoin de deux cycles d'horloge pour faire son travail. Mais la réalité est que ce n'est pas forcément le cas. En réalité, on peut très bien doubler la fréquence de l'horloge uniquement dans le circuit de division, qui fonctionne deux fois plus vite que les circuits alentours, y compris ceux auquel il est relié. Par exemple, si le circuit de division est intégré dans un processeur, le processeur ira à une certaine fréquence, mais le circuit de division ira deux fois plus vite. Mine de rien, cette solution a été utilisée dans de nombreux designs commerciaux, et notamment sur le processeur HP PA7100.
La division avec restauration
modifier
Un point important pour que l’algorithme précédent fonctionne est que le résultat fournit par le soustracteur ne soit pas pris en compte lors de l'étape de comparaison. Plus haut, la solution retenue était de ne pas l'enregistrer dans le registre du reste partiel. Il s'agit là de la solution la plus simple, mais il existe une solution alternative plus complexe, qui autorise l'enregistrement du reste partiel faussé dans le registre accumulateur, mais effectue une correction pour restaurer le reste partiel tel qu'il était avant la comparaison. C'est le principe de la division avec restauration que nous allons voir dans ce qui suit.
Développons la division avec restauration par un exemple illustré ci-contre. Nous allons cherche à diviser 1000 1100 1111 (2255 en décimal) par 0111 (7 en décimal). Pour commencer, nous allons commencer par sélectionner le bit de poids fort du dividende (le nombre qu'on veut diviser par le diviseur), et soustraire le diviseur à ce bit, pour voir le signe du résultat. Si le résultat de cette soustraction est négatif, alors le diviseur est plus grand que ce qu'on a sélectionné dans notre dividende. On place alors un zéro dans le quotient. On restaure alors le reste partiel antérieur, en ajoutant le diviseur retranché à tort. Ensuite, on abaisse le bit juste à côté du bit qu'on vient de tester, et on recommence. À chaque étape, on restaure le reste partiel si le résultat de la soustraction est négatif, on ne fait rien s'il est positif ou nul.
L'algorithme de division se déroule assez simplement. Tout d'abord, on initialise les registres, avec le registre du reste partiel qui est initialisé avec le dividende. Ensuite, on soustrait le diviseur de ce "reste" et on stocke le résultat dans le registre qui stocke le reste. Deux cas de figure se présentent alors : le reste partiel est négatif ou positif. Dans les deux cas, on réussit trouver le signe du reste partiel en regardant simplement le bit de signe du résultat. Reste à savoir quoi faire.
- Le résultat est négatif : cela signifie que le reste est plus petit que le diviseur et qu'on n’aurait pas dû soustraire. Vu que notre soustraction a été effectuée par erreur, on doit remettre le reste tel qu'il était. Ce qui est fait en effectuant une addition. Il faut aussi mettre le bit de poids faible du quotient à zéro et le décaler d'un rang vers la gauche.
- Le résultat est positif : dans ce cas, on met le bit de poids faible du quotient à 1 avant de le décaler, sans compter qu'il faut décaler le reste partiel pour mettre le diviseur à la bonne place (sous le reste partiel) lors des soustractions.
Et on continue ainsi de suite jusqu'à ce que le reste partiel soit inférieur au diviseur. L'algorithme utilise en tout, pour des nombres de N bits, 2N+1 additions/soustractions maximum.
Le seul changement est la restauration du reste partiel. Restaurer le dividende initial demande d'ajouter le diviseur qu'on vient de soustraire. L'algorithme ressemble au précédent, sauf que l'on a plus besoin du multiplexeur, le diviseur est toujours utilisé comme opérande du soustracteur. Sauf que le soustracteur est remplacé par un additionneur-soustracteur. Le circuit de détermination du bit du quotient commande non seulement l'additionneur/soustracteur. Il est beaucoup plus simple que le comparateur d'avant.

La division sans restauration
modifierLa méthode précédente a toutefois un léger défaut : on a besoin de remettre le reste partiel comme il faut lorsqu'on a soustrait le diviseur décalé alors qu'on aurait pas du et que le résultat obtenu est négatif. La division sans restauration se passe de cette restauration du reste partiel et continue de calculer avec ce reste faux,. Par contre, elle effectue une phase de correction lors du cycle suivant. De plus, il faut corriger le quotient obtenu pour obtenir le quotient adéquat, pareil pour le reste.
Mettons que l'on souhaite soustraire le diviseur du reste partiel, mais que le résultat soit négatif. Au lieu de restaurer le reste partiel initial, on continue, en effectuant une correction au cycle suivant. Il y a donc deux cycles d'horloge à analyser. Au premier, on a le reste partiel R, dont on soustrait le diviseur D décalé de n rangs :
Si le résultat est positif, on continue la division normalement, le cycle suivant implique une soustraction normale, il n'y a rien à faire. Mais si le résultat est négatif, une division normale restaure R, puis poursuit la soustraction. Lors du second cycle, le reste partiel est décalé d'un rang vers la gauche, ce qui donne :
Maintenant, regardons ce qui se passe avec une division sans restauration. On fait la soustraction, on a R - D, qui est négatif. On décale vers la gauche, et on soustrait de nouveau D au second cycle :
Le résultat est incorrect, il faut le corriger pour obtenir le bon résultat. Pour cela, on calcule l'erreur, la différence entre les deux équations précédentes :
La correction demande donc juste de faire une addition du diviseur au cycle suivant.
Un autre point à prendre en compte est l'interprétation des bits du quotient. Avec la division avec restauration, le bit du quotient s’interprète comme suit : 0 signifie que l'on a pas soustrait le diviseur décalé par le poids du bit, 1 signifie qu'on a soustrait. Avec la division sans restauration, l'interprétation est différente : 0 signifie que l'on a additionné le diviseur décalé par le poids du bit, 1 signifie qu'on a soustrait. La différence signifie qu'il faut convertir le quotient de l'un vers l'autre pour obtenir le bon quotient. Pour cela, il faut inverser les bits du quotient, multiplier le résultat par deux et ajouter 1.
- Inverser les bits du quotient peut se faire à la volée, lors du calcul, alors que les deux opérations finales se font à la toute fin du calcul, lors du dernier cycle.
Enfin, il faut tenir compte d'un cas particulier : le cas où le reste final est invalide. Cela arrive si on arrive à la fin du calcul, au dernier cycle, et que l'on effectue une soustraction mais que l'on aurait pas dû soustraire. Dans ce cas, on se retrouve avec un reste négatif. Dans ce cas, on est censé poursuivre le calcul encore un cycle pour corriger le résultat, en additionnant le diviseur. Le circuit diviseur doit détecter la situation et effectuer un cycle supplémentaire.
Pour résumer, la division sans restauration :
- Continue le calcul en cas de reste partiel incorrect, sauf qu'au cycle suivant, on additionne le diviseur au lieu de soustraire ;
- Inverser les bits du quotient, multiplier le résultat par deux et ajouter 1.
- Corrige le reste avec l'addition du diviseur si celui-ci devient négatif au dernier cycle.
Les diviseurs améliorés
modifierOn peut améliorer toutes les méthodes précédentes en ne traitant pas notre dividende bit par bit, mais en le manipulant par groupe de deux, trois, quatre bits, voire plus encore. Mais les circuits deviennent alors très compliqués. Sur certains processeurs, le résultat de la division par un groupe 2,3,4,... bits est accéléré par une petite mémoire qui précalcule certains résultats utiles. Bien sûr, il faut faire attention quand on remplit cette mémoire, sous peine d'obtenir des résultats erronés. Et si vous croyez que les constructeurs de processeurs n'ont jamais fait cette erreur, sachez qu'Intel en a fait les frais sur le Pentium 1. L'unité en charge des divisions flottantes utilisait un algorithme similaire à celui vu au-dessus (les mantisses des nombres flottants étaient divisées ainsi), et la mémoire qui permettait de calculer les bits du quotient contenait quelques valeurs fausses. Résultat : certaines divisions donnaient des résultats incorrects ! C'est de là que vient le fameux "Pentium FDIV bug".
Il est possible de modifier les circuits diviseurs pour remplacer l'additionneur-soustracteur par un équivalent qui fait les calculs en carry save. Les calculs sont alors drastiquement accélérés. Mais le circuit devient alors beaucoup plus complexe. Le calcul du quotient, qui demande un comparateur, est difficile du fait de l'usage de la représentation carry save.
De nos jours, les diviseurs utilisent une version améliorée de la division sans restauration, appelé l'algorithme de division SRT. C'est cette méthode qui est utilisée dans les processeurs pour la division entière ou la division flottante.
Maintenant, nous allons voir dans les grandes lignes comment fonctionnent les circuits capables de calculer avec des nombres flottants. Nous allons aborder les calculs en virgule flottante, mais aussi les calculs avec les flottants à virgule fixe et les nombres flottants logarithmiques. La raison à cela est que certaines opérations impossibles avec des entiers deviennent possibles avec des nombres à virgule fixe. C'est le cas du calcul des fonctions trigonométriques, par exemple. Et leur calcul en virgule flottante ou en virgule fixe est relativement similaire.
Il est possible de créer des circuits qui effectuent des opérations trigonométriques, mais ceux-ci sont peu utilisés dans les ordinateurs actuels. La raison est que les calculs trigonométriques sont assez rares et ne sont réellement utilisés que dans les jeux vidéos (pour les calculs des moteurs physique et graphique), dans les applications graphiques de rendu 3D et dans les applications de calcul scientifique. Ils sont par contre plus courants dans les systèmes embarqués, bien que leur utilisation reste quand même assez peu fréquente. Malgré leur rareté, il est intéressant de voir comment sont conçus ces circuits de calcul trigonométrique en virgule fixe.
L'usage d'une mémoire à interpolation
modifierDans cette section, nous allons voir qu'il est possible de faire des calculs avec l'aide d'une mémoire de précalcul. Avec cette technique, le calcul est pris en charge non pas par un circuit dédié, mais par une ROM ou une RAM qui contient les résultats des calculs possibles. L'opérande du calcul sert d'adresse mémoire, et le mot mémoire associé à cette adresse contient le résultat du calcul demandé. Cette technique peut s'appliquer pour n'importe quelle opération. La raison est que tout circuit combinatoire existant peut être remplacé par une mémoire ROM.

La technique marche très bien pour les calculs qui n'ont qu'une seule opérande. Par exemple, les calculs trigonométriques, le logarithme, l'exponentielle, la racine carrée, ce genre de calculs. On peut adapter cette technique pour les calculs à deux opérandes ou plus : il suffit de les concaténer pour obtenir une opérande unique.
Cependant, si on utilisait cette technique telle qu'elle, la mémoire ROM/RAM serait trop importante pour être implémentée. Rien qu'avec des nombres à virgule fixe de plus de 16 bits, il faudrait une mémoire de 2^16 cases mémoire, chacune faisant 16 bits, soit 128 kiloctets, et ce pour une seule opération. Ne parlons même pas du cas avec des nombres de 32 ou 64 bits ! Pour cela, on va donc devoir ruser pour réduire la taille de cette ROM.
Mais qui dit réduire la taille de la ROM signifie que certains résultats ne seront pas connus. Il y aura forcément des opérandes pour lesquelles la ROM n'aura pas mémorisé le résultat et pour lesquels la mémoire de précalcul seule ne peut rien faire. La solution sera alors de calculer ces résultats à partir d'autres résultats connus et mémorisés dans la mémoire ROM. La mémoire ROM n'a donc pas besoin de stocker tous les résultats et peu se contenter de ne mémoriser que les résultats essentiels, ceux qui permettent de calculer tous les autres. On doit distinguer deux types d'opérandes : celles dont le résultat est stocké dans la ROM, celles dont le résultat est calculé à partir des précédentes. Les opérandes dont le résultat est en ROM seront appelées des opérandes précalculés dans ce qui suit, alors que les autres seront appelées les opérandes non-précalculés.
Une première optimisation : les identités trigonométriques
modifierLa première manière de ruser est d'utiliser les identités trigonométriques pour calculer les résultats non-précalculés.
Par exemple, on sait que , ce qui permet d'éliminer la moitié des valeurs stocker dans la ROM. On a juste à utiliser des inverseurs commandables commandés par le bit de signe pour faire le calcul de à partir de celui de .
De même, l'identité permet de calculer des cosinus à partir de sinus déjà connus, ce qui élimine le besoin d'utiliser une mémoire séparée pour les cosinus.
Enfin, l'identité permet de calculer la moitié des sinus quand l'autre est connue.
Et on peut penser à utiliser d'autres identités trigonométriques, mais pas les trois précédentes sont déjà assez intéressantes. Le problème est qu'on ne peut pas envoyer les opérandes non-précalculés. À la place, on doit transformer l'opérande non-précalculées pour obtenir un opérande précalculé, géré par la mémoire ROM. Il faut donc des circuits qui se chargent de détecter ces opérandes , de les transformer en opérandes reconnus par la ROM, puis de corriger la donnée lue en ROM pour obtenir le résultat adéquat. Les circuits en question dépendent de l'identité trigonométrique utilisée, aussi on ne peut pas faire de généralités sur le sujet.
Une seconde optimisation : l'interpolation linéaire
modifier
La seconde ruse n'utilise pas d'identités trigonométriques qui donnent un résultat exact, mais calcule une approximation du résultat, sauf pour les opérandes précalculés. L'idée est de prendre les deux (ou trois, ou quatre, peu importe) résultats précalculés les plus proches du résultat voulu, et de les utiliser pour faire une approximation.
L'approximation du résultat se calcule en faisant une interpolation linéaire, à savoir une moyenne pondérée des deux résultats les plus proches. Par exemple, si on connaît le résultat pour sin(45°) et pour sin(50°), alors on peut calculer sin(47,5°), sin(47°), sin(45,5°), sin(46,5°) ou encore sin(46°) en faisant une moyenne pondérée des deux résultats. Une telle approximation est largement suffisante pour beaucoup d'applications.
Le circuit qui permet de faire cela est appelée une mémoire à interpolation. Le schéma de principe du circuit est illustré ci-contre, alors que le schéma détaillé est illustré ci-dessous.

L'algorithme CORDIC
modifierSur du matériel peu puissant, les fonctions trigonométriques peuvent être calculées avec l'algorithme CORDIC. Celui-ci est notamment très utilisé dans les calculatrices modernes, qui possèdent un circuit séquentiel ou un logiciel pour exécuter cet algorithme. Cet algorithme fonctionne par approximations successives, chaque itération de l'algorithme permettant de s’approcher du résultat final. Il utilise les mathématiques du cercle trigonométrique (qui sont considérées acquises dans ce qui suit). Cet algorithme représente un angle par un vecteur unitaire dans le cercle trigonométrique, plus précisément par l'angle que forme le vecteur avec l'axe des abscisses. Le cosinus et le sinus de l'angle sont tout simplement les coordonnées x et y du vecteur, par définition. En travaillant donc directement avec les coordonnées du vecteur, l'algorithme peut connaître à chaque itération le cosinus et le sinus de l'angle. Dit autrement, pour un vecteur de coordonnées (x,y) et d'ange , on a :

L'algorithme CORDIC part d'un principe simple : il va décomposer un angle en angles plus petits, dont il connaît le cosinus et le sinus. Ces angles sont choisis de manière à avoir une propriété assez particulière : leur tangente est une puissance de deux. Ainsi, par définition de la tangente, on a : . Vous aurez deviné que cette propriété se marie bien avec le codage binaire et permet de simplifier fortement les calculs. Nous verrons plus en détail pourquoi dans ce qui suit. Toujours est-il que nous pouvons dire que les angles qui respectent cette propriété sont les suivants : 45°, 26.565°, 14.036°, 7,125°, ... , 0.0009°, 0.0004°, etc.
L'algorithme part d'un angle de 0°, qu'il met à jour à chaque itération, de manière à se rapprocher de plus en plus du résultat. Plus précisément, cet algorithme ajoute ou retranche un angle précédemment cité à chaque itération. Typiquement, on commence par faire une rotation de 45°, puis une rotation de 26.565°, puis de 14.036°, et ainsi de suite jusqu’à tomber sur l'angle qu'on souhaite. À chaque itération, on vérifie si la valeur de l'angle obtenue est égale inférieure ou supérieure à l'angle voulu. Si l'angle obtenu est supérieur, la prochaine itération retranchera l'angle précalculé suivant. Si l'angle obtenu est inférieur, on ajoute l'angle précalculé. Et enfin, si les deux sont égaux, on se contente de prendre les coordonnées x et y du vecteur, pour obtenir le cosinus et le sinus de l'angle voulu.

Du principe aux calculs
modifierCette rotation peut se calculer assez simplement. Pour un vecteur de coordonnées , la rotation doit donner un nouveau vecteur de coordonnées . Pour une rotation d'angle , on peut calculer le second vecteur à partir du premier en multipliant par une matrice assez spéciale (nous ne ferons pas de rappels sur la multiplication matricielle ou les vecteurs dans ce cours). Voici cette matrice :
Une première idée serait de pré-calculer les valeurs des cosinus et sinus, vu que les angles utilisés sont connus. Mais ce pré-calcul demanderait une mémoire assez imposante, aussi il faut trouver autre chose. Une première étape est de simplifier la matrice. En factorisant le terme , la multiplication devient celle-ci (les signes +/- dépendent de si on retranche ou ajoute l'angle) :
Encore une fois, la technique du précalcul serait utilisable, mais demanderait une mémoire trop importante. Rappelons maintenant que la tangente de chaque angle est une puissance de deux. Ainsi, la multiplication par devient un simple décalage ! Autant dire que les calculs deviennent alors nettement plus simples. L'équation précédente se simplifie alors en :
Le terme sera noté , ce qui donne :
Il faut noter que la constante peut être omise dans le calcul, tant qu'on effectue la multiplication à la toute fin de l'algorithme. À la fin de l'algorithme, on devra calculer le produit de tous les et y multiplier le résultat. Or, le produit de tous les est une constante, approximativement égale à 0,60725. Cette omission donne :
Le tout se simplifie en :
On peut alors simplifier les multiplications pour les transformer en décalages, ce qui donne :
Les circuits CORDIC
modifierAinsi, une rotation demande juste de décaler x et y et d'ajouter le tout aux valeurs avant décalage d'une certaine manière. Voici le circuit qui dérive de la matrice précédente. Ce circuit prend les coordonnées du vecteur et lui ajoute/retranche un angle précis. On obtient ainsi le circuit de base de CORDIC.

Pour effectuer plusieurs itérations, il est possible de procéder de deux manières. La plus évidente est d'ajouter un compteur et des circuits à la brique de base, afin qu'elle puisse enchainer les itérations les unes après les autres.

La seconde méthode est d'utiliser autant de briques de base pour chaque itération.

Les nombres flottants IEEE754
modifierIl est temps de voir comment créer des circuits de calculs qui manipulent des nombres flottants au format IEEE754. Rappelons que la norme IEEE754 précise le comportement de 5 opérations: l'addition, la soustraction, la multiplication et la division. Paradoxalement, les multiplications, divisions et racines carrées sont relativement simples à calculer avec des nombres flottants, là où l'addition et la soustraction sont plus complexes. Dans ce qui va suivre, nous allons d'abord parler des procédés d'arrondis des résultats, applicables à toutes les opérations, avant de poursuivre par l'étude des opérations simples (multiplications, divisions, racines carrées), avant de terminer avec les opérations compliquées (addition et soustraction).
La normalisation et les arrondis flottants
modifier
Calculer sur des nombres flottants peut sembler trivial, mais les mathématiques ne sont pas vraiment d'accord avec cela. En effet, le résultat d'un calcul avec des flottants n'est pas forcément un flottant valide. Il doit subir quelques transformations pour être un nombre flottant : il doit souvent être arrondi, mais il doit aussi passer par d'autres étapes dites de normalisation.
La prénormalisation
modifierLa prénormalisation gère le bit implicite. Lorsqu'un circuit de calcul fournit son résultat, celui-ci n'a pas forcément son bit implicite à 1. On est obligé de décaler la mantisse du résultat de façon à ce que ce soit le cas. Pour savoir de combien de rangs il faut décaler, il faut compter le nombre de zéros situés avant le 1 de poids fort, avec un circuit spécialisé. Ce circuit permet aussi de détecter si la mantisse vaut zéro.
Mais si on décale notre résultat de n rangs, cela signifie qu'on le multiplie par 2 à la puissance n. Il faut donc corriger l'exposant du résultat pour compenser le décalage de la mantisse. Il suffit pour cela de lui soustraire n, le nombre de rangs dont on a décalé la mantisse.

La normalisation
modifierUne fois ce résultat calculé, il faut faire un arrondi du résultat avec un circuit de normalisation. L'arrondi se base sur les bits de poids faible situés juste à gauche et à droite de la virgule., ce qui demande d'analyser une dizaine de bits tout au plus. Une fois les bits de poids faible à gauche de la virgule sont remplacé, les bits à droite sont éliminés. L'arrondi peut être réalisé par un circuit combinatoire, mais le faible nombre de bits d'entrée rend possible d'utiliser une mémoire ROM. Ce qui est réalisé dans quelques unités flottantes.

Malheureusement, il arrive que ces arrondis décalent la position du bit implicite d'un rang, ce qui se résout avec un décalage si cela arrive. Le circuit de normalisation contient donc de quoi détecter ces débordements et un décaleur. Bien évidemment, l'exposant doit alors lui aussi être corrigé en cas de décalage de la mantisse.

résumé
modifierLe circuit complet, qui effectue à la fois normalisation et arrondis est le suivant :
La multiplication flottante
modifierPrenons deux nombres flottants de mantisses et et les exposants et . Leur multiplication donne :
On regroupe les termes :
On simplifie la puissance :
En clair, multiplier deux flottants revient à multiplier les mantisses et additionner les exposants.
Il faut cependant penser à plusieurs choses pas forcément évidentes.
- Premièrement, il faut ajouter les bits implicites aux mantisses avant de les multiplier. Sans cela, la mantisse résultat sera tout simplement fausse.
- Deuxièmement, il faut se rappeler que les exposants sont encodés en représentation par excès, ce qui fait que l'additionneur-soustracteur utilisé est un additionneur-soustracteur spécifiques à cette représentation.
- Enfin, il ne faut pas oublier de rajouter les étapes de normalisation et d'arrondis.
La division flottante
modifierLa division fonctionne sur le même principe que la multiplication, si ce n'est que les calculs sont quelque peu différents : les exposants sont soustraits et que les mantisses sont divisées.
Pour le démontrer, prenons deux flottants et et divisons le premier par le second. On a alors :
On applique les règles sur les fractions :
On simplifie la puissance de 2 :
On voit que les mantisses sont divisées entre elles, tandis que les exposants sont soustraits.
La racine carrée flottante
modifierLe calcul de la racine carrée d'un flottant est relativement simple. Par définition, la racine carrée d'un flottant vaut :
La racine d'un produit est le produit des racines :
Vu que , on a :
On voit qu'il suffit de calculer la racine carrée de la mantisse et de diviser l'exposant par deux (ou le décaler d'un rang vers la droite ce qui est équivalent). Voici le circuit que cela doit donner :

L'addition et la soustraction flottante
modifierLa somme de deux flottants n'est simplifiable que quand les exposants sont égaux : dans ce cas, il suffit d'additionner les mantisses. Il faut donc mettre les deux flottants au même exposant, l'exposant choisi étant souvent le plus grand exposant des deux flottants. Convertir le nombre dont l'exposant est le plus petit demande de décaler la mantisse vers la droite, d'un nombre de rangs égal à la différence entre les deux exposants. Pour comprendre pourquoi, il faut se souvenir que décaler vers la droite diminuer l'exposant du nombre de rangs. Pour faire ce décalage, on utilise un décaleur et un circuit qui échange les deux opérandes (histoire d'envoyer le plus petit exposant dans le décaleur). Ce circuit d'échange est piloté par un comparateur qui détermine quel est le nombre avec le plus petit exposant. Nous verrons comment fabriquer un tel comparateur dans le chapitre suivant sur les comparateurs.

Suivant les signes, il faudra additionner ou soustraire les opérandes.

Voici le circuit complet :

Les fonctions trigonométriques
modifierL'implémentation des fonctions trigonométriques est quelque peu complexe, du moins pour ce qui est de créer des circuits de calcul du sinus, cosinus, tangente, etc. S'il est possible d'utiliser une mémoire à interpolation, la majorité des processeurs actuels réalise ce calcul à partir d'une suite d'additions et de multiplications, qui donne le même résultat. Cette suite peut être implémentée via le logiciel, un petit bout de programme s'occupant de faire les calculs. Il est aussi possible, bien que nettement plus rare, d'implémenter ce bout de logiciel directement sous la forme de circuits : la boucle de calcul est remplacée par un circuit séquentiel. Mais il faut avouer que cette solution n'est pas pratique et que faire les calculs au niveau logiciel est nettement plus simple, tout aussi performant (et oui !) et moins coûteux. La tactique habituelle consiste à utiliser une approximation de Taylor, largement suffisante pour calculer la majorité des fonctions trigonométriques.
Les flottants logarithmiques
modifierMaintenant, nous allons fabriquer une unité de calcul pour les flottants logarithmiques. Nous avions vu les flottants logarithmiques dans le chapitre Le codage des nombres, dans la section sur les flottants logarithmiques. Pour résumer rapidement, ce sont des flottants qui codent uniquement un bit de signe et un exposant, mais sans la mantisse (qui vaut implicitement 1). L'exposant stocké n'est autre que le logarithme en base 2 du nombre codé, d'où le nom donné à ces flottants. Au passage, l'exposant est stocké dans une représentation à virgule fixe.
Nous avions dit dans le chapitre sur le codage des nombres que l'utilité de cette représentation est de simplifier certains calculs, comme les multiplications, divisions, puissances, etc. Eh bien, vous allez rapidement comprendre pourquoi dans cette section. Nous allons commencer par voir les deux opérations de base : la multiplication et la division. Celles-ci sont en effet extrêmement simples dans cet encodage, bien plus que l'addition et la soustraction. C'est d'ailleurs la raison d'être de cet encodage : simplifier fortement les calculs multiplicatifs, quitte à perdre en performance sur les additions/soustractions.
La multiplication et la division de deux flottants logarithmiques
modifierPour commencer, il faut se souvenir d'un théorème de mathématique sur les logarithmes : le logarithme d'un produit est égal à la somme des logarithmes. Dans ces conditions, une multiplication entre deux flottants logarithmiques se transforme en une simple addition d'exposants.
Le même raisonnement peut être tenu pour la division. Dans les calculs précédents, il suffit de se rappeler que diviser par , c'est multiplier par . Or, il faut se rappeler que . On obtient alors, en combinant ces deux expressions :
La division s'est transformée en simple soustraction. Dans ces conditions, une unité de calcul logarithmique devant effectuer des multiplications et des divisions est constituée d'un simple additionneur/soustracteur et de quelques (ou plusieurs, ça marche aussi) circuits pour corriger le tout.
L'addition et la soustraction de deux flottants logarithmiques
modifierPour l'addition et la soustraction, la situation est beaucoup plus corsée, vu qu'il n'y a pas vraiment de formule mathématique pour simplifier le logarithme d'une somme. Dans ces conditions, la seule solution est d'utiliser une mémoire de précalcul, comme vu au début du chapitre. Et encore une fois, il est possible de réduire la taille de mémoire ROM de précalcul en utilisant des identités mathématiques. L'idée est de transformer l'addition en une opération plus simple, qui peut se pré-calculer plus facilement.
Pour cela, partons de la formule suivante, qui pose l'équivalence des termes suivants :
Vu que le logarithme d'un produit est égal à la somme des logarithmes, on a :
Pour rappel, les représentations de x et y en flottant logarithmique sont égales à et . En notant ces dernières et , on a :
Par définition, et . En injectant dans l'équation précédente, on obtient :
On simplifie la puissance de deux :
On a donc :
- , avec f la fonction adéquate.
Pour la soustraction, on a la même chose, sauf que les signes changent, ce qui donne :
- , avec g une fonction différente de f.
On vient donc de trouver la formule qui permet de faire le calcul, le seul obstacle étant la fonction f et la fonction g. Heureusement, le terme de droite peut se pré-calculer facilement, ce qui donne une table beaucoup plus petite qu'avec l'idée initiale. Dans ces conditions, l'addition se traduit en :
- un circuit qui additionne/soustrait les deux opérandes ;
- une table qui prend le résultat de l'additionneur/soustracteur et fournit le terme de droite ;
- et un autre additionneur pour le résultat.
Résumé
modifierPour implémenter les quatre opérations, on a donc besoin :
- de deux additionneurs/soustracteur et d'un diviseur pour l'addition/soustraction ;
- de deux autres additionneurs/soustracteur pour la multiplication et la division ;
- et d'une ROM.
Il est bon de noter qu'il est tout à fait possible de mutualiser les additionneurs pour la multiplication et l'addition. En rajoutant quelques multiplexeurs, on peut faire en sorte que le circuit puisse se configurer pour que les additionneurs servent soit pour la multiplication, soit pour l'addition. On économise en peu de circuits.

Les comparateurs sont des circuits qui permettent de comparer deux nombres, à savoir s'ils sont égaux, si l'un est supérieur à l'autre, ou inférieur, ou différent, etc. Dans ce qui va suivre, nous allons voir quatre types de comparateurs. Le premier type de circuit vérifie si un nombre est nul ou différent de zéro. Le second vérifie si deux nombres sont égaux, tandis que le troisième vérifie s'ils sont différent. Enfin, le quatrième vérifie si un nombre est supérieur ou inférieur à un autre. Il faut signaler que nous avons déjà vu comment vérifier qu'un nombre est égal à une constante dans le chapitre sur les circuits combinatoires, aussi nous ne reviendrons pas dessus.
Le comparateur de 1 bit
modifier
Maintenant, nous allons voir comment vérifier si deux bits sont égaux/différents, si le premier est inférieur au second ou supérieur. Le but est de créer un circuit qui prend en entrée deux bits A et B, et fournit en sortie quatre bits :
- qui vaut 1 si le bit A est supérieur à B et 0 sinon ;
- qui vaut 1 si le bit A est inférieur à B et 0 sinon ;
- qui vaut 1 si le bit A est égal à B et 0 sinon ;
- qui vaut 1 si le bit A est différent de B et 0 sinon.
Peut-être avez-vous remarqué l'absence de sortie qui indique si ou . Mais ces deux sorties peuvent se calculer en combinant la sortie avec les sorties et . De plu, vous pouvez remarquer que les deux dernières entrées sont l'inverse l'une de l'autre, ce qui n'est pas le cas des deux premières. Nous allons d'abord voir comment calculer les deux premières sorties, à savoir et . La raison à cela est que les deux autres sorties peuvent se calculer à partir de celles-ci.
Le comparateur de supériorité/infériorité stricte
modifierEn premier lieu, nous allons voir comment vérifier qu'un bit A est strictement supérieur ou inférieur à un bit B. Pour cela, le mieux est d'établir la table de vérité des deux comparaisons. La table de vérité est la suivante :
| Entrée A | Entrée B | Sortie < | Sortie > |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 |
On obtient les équations suivantes :
- Sortie > :
- Sortie < :
On voit que quand les deux bits sont égaux, alors les deux sorties sont à zéro.
Le comparateur d'inégalité 1 bit
modifierLa seconde étape est de concevoir un petit circuit qui vérifie si deux bits sont différents, inégaux. Pour cela, on peut combiner les deux signaux précédents. En effet, on sait que si A et B sont différents, alors soit A>B, soit A<B. En conséquence, on a juste à combiner les deux signaux vus précédemment avec une porte OU.

Ce circuit devrait vous dire quelque chose. Pour ceux qui n'ont pas déjà remarqué, le mieux est d'établir la table de vérité du circuit, ce qui donne :
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
On voit rapidement qu'il s'agit d'une porte XOR.
Le comparateur d'égalité 1 bit
modifierEnfin, nous allons concevoir un petit circuit qui vérifie si deux bits sont égaux. La logique veut que l'égalité est l'inverse de l'inégalité, ce qui fait qu'il suffirait d'ajouter une porte NON en sortie du circuit. Le circuit précédent est alors facile à adapter : il suffit de remplacer la porte OU par une porte NOR. Et si le comparateur d'inégalité 1 bit était une porte XOR, on devine rapidement que le comparateur d'égalité 1 bit est quant à lui une porte NXOR. Ce qui se vérifie quand on regarde la table de vérité du comparateur :
| A | B | A=B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
L'interprétation de ce circuit est assez simple. Par définition, deux nombres sont égaux si les deux conditions et sont fausses. C’est pour cela que le circuit calcule d'abord les deux signaux et , puis qu'il les combine avec une porte NOR.
Le circuit complet
modifierFort de ces résultats, nous pouvons fabriquer un comparateur de 1 bit. Celui-ci prend deux bits en entrée, et fournit trois bits en sortie : un pour l'égalité, un autre pour la supériorité et un autre pour l'infériorité. Voici le circuit au complet (sans le bit de différence). On pourrait rajouter le bit de différence assez simplement, en ajoutant une porte OU en sortie des signaux et , mais nous le ferons pas pour ne pas surcharger inutilement les schémas.
 |
 |
Il est aussi possible de reformuler le schéma précédent pour supprimer une redondance invisible dans le circuit, au niveau de la porte NXOR qui calcule le bit d'égalité. À la place, il est possible de prendre les signaux et et de les combiner avec une porte NOR. Ou encore mieux : on utilise une porte OU et une porte NON, la sortie de la porte OU donnant directement le bit d'inégalité, celle de la porte NON donnant le bit d'égalité.

Les comparateurs spécialisés
modifierDans cette section, nous allons voir des comparateurs assez simples, plus simples que les autres, qui ont une structure similaire. Ils sont composés d'une couche de comparateurs de 1 bits, suivi par une porte logique à plusieurs entrées. La porte logique combine les résultats de ces comparaisons individuelles et en déduit le bit de sortie. Les comparateurs que nous allons voir sont : un comparateur d'égalité qui vérifie si deux nombres sont égaux, et un comparateur qui vérifie si une opérande vaut zéro.
Le comparateur avec zéro
modifierLe circuit que nous allons maintenant aborder ne compare pas deux nombres, mais vérifie si l'opérande d'entrée est nulle. Il fonctionne sur un principe simple : un nombre est nul si tous ses bits valent 0. La quasi-totalité des représentation binaire utilisent la valeur 0000...0000 pour encoder le zéro. Les entiers non-signés et en complément à deux sont dans ce cas, c'est la même chose en complément à un ou en signe-magnitude si on omet le bit de signe. La seule exception est la représentation one-hot, et encore !
La solution la plus simple pour créer ce circuit est d'utiliser une porte NOR à plusieurs entrées. Par définition, la sortie d'une NOR vaut zéro si un seul bit de l'entrée est à 1 et 0 sinon, ce qui répond au cahier des charges.

Il existe une autre possibilité strictement équivalente, qui inverse l'entrée avant de vérifier si tous les bits valent 1. Si l'entrée est nulle, tous les bits inversés valent tous 1, alors qu'une entrée non-nulle donnera au moins un bit à 0. Le circuit est donc conçu avec des portes NON pour inverser tous les bits, suivies d'une porte ET à plusieurs entrées qui vérifie si tous les bits sont à 1.

- Notons qu'en peut passer d'un circuit à l'autre en utilisant les lois de de Morgan.
Le comparateur d'égalité
modifierPassons maintenant à un circuit qui compare deux nombres et vérifie s'ils sont identiques/différents. Les deux sont l'inverse l'un de l'autre, aussi nous allons nous concentrer sur le comparateur d'égalité. Intuitivement, on se dit que deux nombres sont égaux s'ils ont la même représentation en binaire, ils sont différents sinon. Mais cela ne marche pas dans les autres représentations pour les entiers signés. La raison est la présence de deux zéros : un zéro positif et un zéro négatif. Mais nous laissons ces représentations de côté pour le moment.
Le circuit qui vérifie si deux nombres sont égaux est très simple : il prend les bits de même poids des deux opérandes (ceux à la même position, sur la même colonne) et vérifie qu'ils sont égaux. Le circuit est donc composé d'une première couche de portes NXOR qui vérifie l'égalité des paires de bits, suivie par une porte logique qui combine les résultats des porte NXOR. La logique dit que la sortie vaut 1 si tous les bits de sortie des NXOR valent 1. La seconde couche est donc, par définition, une porte ET à plusieurs entrées.

Une autre manière de concevoir ce circuit inverse la logique précédente. Au lieu de tester si les paires de bits sont égales, on va tester si elles sont différentes. La moindre différence entre deux bits entraîne l'inégalité. Pour tester la différence de deux bits, une porte XOR suffit. Le fait qu'une seule paire soit différente suffit à rendre les deux nombres inégaux. Dit autrement, si une porte XOR sort un 1, alors la sortie du comparateur d'égalité doit être de 0 : c'est le fonctionnement d'une porte NOR.
Voici une autre interprétation de ce circuit : le circuit compare un circuit XOR et un comparateur avec zéro. Il faut savoir que lorsqu'on XOR un nombre avec lui-même, le résultat est zéro. Et c'est le seul moyen d'obtenir un zéro comme résultat d'un XOR. Donc, les deux nombres sont XOR et un comparateur vérifie si le résultat vaut zéro. Le circuit final est donc un paquet de portes XOR, et un comparateur avec zéro.
Notons qu'on peut passer d'un circuit à l'autre en utilisant la loi de de Morgan
- Le circuit qui vérifie si deux nombres sont différents peut être construit à partir du circuit précédent et d'inverser son résultat avec une porte NON. Le résultat est que l'on change la porte ET finale du premier circuit par une porte NAND, la porte NOR du second circuit par une porte OU.
Les comparateurs pour entiers non-signés
modifier
Dans ce qui va suivre, nous allons créer un circuit qui est capable de vérifier l'égalité, la supériorité ou l'infériorité de deux nombres. Celui-ci prend deux nombres en entrée, et fournit trois bits : un pour l'égalité des deux nombres, un autre pour préciser que le premier est supérieur au second, et un autre pour préciser que le premier est inférieur au second.
Il existe deux méthodes pour créer des comparateurs : une basée sur une soustraction, l'autre sur des comparaisons bit par bit. Dans cette section, nous allons nous concentrer sur le second type, les comparateurs basés sur une soustraction étant vu à la fin du chapitre. De plus, nous allons nous concentrer sur des comparateurs qui testent deux opérandes non-signées (nulles ou positives, mais pas négatives).
Les comparateurs sériels
modifierLa manière la plus simple est de faire la comparaison bit par bit avec un circuit séquentiel. Pour cela, on doit utiliser deux registres à décalage pour les opérandes. Les bits sortants à chaque cycle sont les bits de même poids et ils sont comparés par un comparateur 1 bit. Le résultat de la comparaison est mémorisé dans une bascule de quelques bits, qui mémorise le résultat temporaire de la comparaison. A chaque cycle, le comparateur de 1 bit fournit son résultat, qu'il faut combiner avec celui dans la bascule, ce qui permet de combiner les résultats temporaire avec les résultats de la colonne en cours de traitement. Et c'est une chose que le comparateur 1 bit précédent ne sait pas faire. Pour cela, nous allons devoir créer un circuit, nommé le comparateur complet.

Dans ce qui va suivre, la comparaison va s'effectuer en partant du bit de poids faible et se fera de gauche à droite, chose qui a son importance pour ce qui va suivre. Quel que soit le sens de parcours, on sait comment calculer le bit d'égalité : celui-ci est égal à un ET entre le bit d'égalité fournit en entrée, et le résultat de la comparaison A = B. Pour les bits de supériorité et d'infériorité, les choses changent : la colonne en cours de traitement supplante l'autre colonne. Dit autrement, les bits de poids fort donnent le résultat de la comparaison. Pour déterminer comment calculer ces bits, le mieux est encore d'établir la table de vérité du circuit pour ces deux bits. Nous allons postuler que les bits A > B et A < B ne peuvent être à 1 en même temps : il s'agit de supériorité et d'infériorité stricte. Voici la table de vérité :
| Entrée > | Entrée < | A > B | A < B | Sortie > | Sortie < | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | X | X | |
| 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | X | X | |
| 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 1 | X | X | |
| 1 | 1 | 0 | 0 | X | X | |
| 1 | 1 | 0 | 1 | X | X | |
| 1 | 1 | 1 | 0 | X | X | |
| 1 | 1 | 1 | 1 | X | X |
Les équations logiques obtenues sont donc les suivantes :
- Sortie (=) :
- Sortie (>) :
- Sortie (<) :
Il est possible de simplifier le circuit de manière à ce qu'il ne fasse pas la comparaison d'égalité, qui se déduit des deux autres comparaisons. Si les deux sorties < et > sont à 0, alors les deux bits sont égaux. Si on avait utilisé des sorties >= et <=, il aurait fallu que les deux bits soient à 1 pour montrer une égalité.
On peut aussi fabriquer un comparateur d'égalité sériel. Nous aurons à utiliser ce circuit plusieurs fois dans la suite du cours, notamment dans le chapitre sur les mémoires associatives. Le circuit est strictement identique au précédent, si ce n'est que l'on retire les portes pour les comparaisons non-voulues, et que la bascule n'a besoin que de mémoriser un seul bit. La comparaison d'égalité est réalisée par une porte NXOR, et le résultat est combiné avec le contenu de la bascule avec une porte ET.

Les comparateurs parallèles
modifierIl est possible de dérouler le circuit précédent, de la même manière que l'on peut dérouler un additionneur sériel pour obtenir un additionneur à propagation de retenue. L'idée est de traiter les bits les uns après les autres, chacun avec un comparateur complet par colonne. Les comparateurs sont connectés de manière à traiter les opérandes dans un sens bien précis : soit des bits de poids faible vers ceux de poids fort, soit dans le sens inverse. Tout dépend du comparateur. Un tel circuit n'a pas l'air très optimisé et ne paye pas de mine, mais il a déjà été utilisé dans des processeurs commerciaux. Par exemple, c'est ce circuit qui était utilisé dans le processeur HP Nanoprocessor, un des tout premiers microprocesseurs.

Un inconvénient de cette méthode est que le résultat est lent à calculer, car on doit traiter les opérande colonne par colonne, comme pour les additionneurs. Sur ces derniers, il fallait propager une retenue de colonne en colonne, mais diverses optimisations permettaient d'optimiser le tout, soit en accélérant la propagation de la retenue, soit en l’anticipant, soit en faisant les calculs de retenue en parallèle, etc. Pour les comparateurs, ce n'est pas une retenue qui se déplace, mais des résultats temporaires. Sauf qu'il n'y a pas de moyen simple pour faire comme avec les additionneurs/soustracteurs et d'anticiper ou calculer en parallèle ces résultats temporaires.
Les comparateurs combinés
modifierIl est possible de combiner plusieurs comparateurs simples pour traiter des nombres assez longs. Par exemple, on peut enchainer 2 comparateurs série 4 bits pour obtenir un comparateur série 8 bits. Pour cela, il y a deux grandes solutions : soit on enchaine les comparateurs en série, soit on les fait travailler en parallèle.
La première méthode place les comparateurs en série, c'est à dire que le second comparateur prend le résultat du premier pour faire son travail. Le second comparateur doit avoir trois entrées nommées <, > et =, qui fournissent le résultat du comparateur précédent. On peut faire la même chose avec plus de 2 comparateurs, l'essentiel étant que les comparateurs se suivent.

Une autre solution est de faire les comparaisons en parallèle et de combiner les bits de résultats des différents comparateurs avec un dernier comparateur. Le calcul de la comparaison est alors légèrement plus rapide qu'avec les autres méthodes, mais le circuit devient plus compliqué à concevoir.

Les comparateurs pour nombres signés
modifierComparer deux nombres signés n'est pas la même chose que comparer deux nombres non-signés. Autant la comparaison d'égalité et de différence est strictement identique, autant les comparaisons de supériorité et d'infériorité ne le sont pas. Les comparateurs pour nombres signés sont naturellement différents des comparateurs vus précédemment. On verra plus tard qu'il en est de même avec les comparateurs pour nombres flottants. Il fut aussi faire attention : la comparaison ne s'effectue pas de la même manière selon que les nombres à comparer sont codés en signe-magnitude, en complément à deux, ou dans une autre représentation. Dans ce qui va suivre, nous allons aborder la comparaison en signe-magnitude et en complément à deux, mais pas les autres représentations.
Le comparateur signe-magnitude
modifierUn comparateur en signe-magnitude n'est pas trop différent d'un comparateur normal. Effectuer une comparaison entre deux nombres en signe-magnitude demande de comparer les valeurs absolues, ainsi que comparer les signes. Une fois cela fait, il faut combiner les résultats de ces deux comparaisons en un seul résultat.

Comment comparer les signes ?
modifierComparer les signes est relativement simple : le circuit n'ayant que deux bits à comparer, celui-ci est naturellement simple à concevoir. On pourrait penser que l'on peut réutiliser le comparateur 1 bit vu précédemment dans ce chapitre, mais cela ne marcherait pas ! En effet, un nombre positif a un bit de signe nul alors qu'un nombre négatif a un bit de signe égal à 1 : les résultats sont inversés. Un bon moyen de s'en rendre compte est d'écrire la table de vérité de ce circuit, selon les signes des nombres à comparer. Nous allons supposer que ces deux nombres sont appelés A et B.
| Bit de signe de A | Bit de signe de B | Sortie = | Sortie < | Sortie > |
|---|---|---|---|---|
| 0 (+) | 0 (+) | 1 | 0 | 0 |
| 1 (-) | 0 (+) | 0 | 0 | 1 |
| 0 (+) | 1 (-) | 0 | 1 | 0 |
| 1 (-) | 1 (-) | 1 | 0 | 0 |
On obtient les équations suivantes :
- Sortie = :
- Sortie < :
- Sortie > :
On peut remarquer que si le bit d'égalité est identique au comparateur 1 bit vu plus haut, les bits de supériorité et l'infériorité sont inversés, échangés. On peut donc réutiliser le comparateur à 1 bit, mais en intervertissant les deux sorties de supériorité et d'infériorité.
Comment combiner les résultats ?
modifierUne fois qu'on a le résultat de la comparaison des signes, on doit combiner ce résultat avec le résultat de la comparaison des valeurs absolues. Pour cela, on doit rajouter un circuit à la suite des deux comparateurs. On pourrait penser qu'il suffit d'établir la table de vérité de ce comparateur, mais il faut faire attention au cas où les deux opérandes sont nulles : dans ce cas, peut importe les signes, les deux opérandes sont égales. Pour le moment, mettons ce fait de côté et établissons la table de vérité du circuit. Dans tous les cas, la comparaison des bits de signe prend le pas sur la comparaison des valeurs absolues. Par exemple, 2 est supérieur à -255, bien que ce ne soit pas le cas pour les valeurs absolues. Ce fait n'est que l'expression du fait qu'un nombre positif est systématiquement supérieur à un négatif, de même qu'un négatif est systématiquement inférieur à un positif. Ce n'est que quand les deux bits de signes sont égaux que la comparaison des valeurs absolue est à prendre en compte. Cela devrait donner les équations suivantes. On note les résultats de la comparaison des bits de signe comme suit : , alors que les résultats de la comparaison des valeurs absolues sont notés : .
- pour le résultat d'égalité ;
- pour l’infériorité ;
- pour la supériorité.
Néanmoins, il faut prendre en compte le cas où les deux opérandes sont nulles, ce qui complique un petit peu les équations Pour cela, il fat rajouter une sortie au comparateur de valeurs absolues, qui indique si les deux nombres valent tous deux zéro. Notons cette sortie . Les équations deviennent :
- pour l'égalité ;
- pour l’infériorité ;
- pour la supériorité.
Les comparateurs en complément à un et en complément à deux
modifierLa comparaison en complément à un ou à deux peut s'implémenter comme en signe-magnitude : on compare les valeurs absolues, puis les signes, avant de déterminer le résultat. Reste à calculer les valeurs absolues, ce qui est loin d'être simple.

En complément à 1, il suffit d'inverser tous les bits si le bit de signe est de 1. E, complément à deux, il faut faire pareil, puis incrémenter le résultat.

Les comparateurs basés sur un soustracteur
modifierLes comparateurs présents dans les ordinateurs modernes fonctionnent sur un principe totalement différents. Ils soustraient les deux opérandes et étudient le résultat. Le résultat peut avoir quatre propriétés intéressantes lors d'une comparaison : si le résultat est nul ou non, son bit de signe, s'il génère une retenue sortante (débordement entier non-signé) et s'il génère un débordement entier en complément à deux. Ces quatre propriétés sont extraites du résultat, et empaquetées dans 4 bits, appelés les 4 bits intermédiaires. En effectuant quelques opérations sur ces 4 bits intermédiaires, on peut déterminer toutes les conditions possibles : si la première opérande est supérieure à l'autre, si elle est égale, si elle est supérieure ou égale, etc. Le circuit est donc composé de trois sous-circuits : le soustracteur, un circuit qui calcule les 4 bits intermédiaires, puis un autre qui calcule la ou les conditions voulues.
L'avantage de ce circuit est qu'il est plus rapide que les autres comparateurs. Rappelons que les comparateurs parallèles testent les opérandes colonne par colonne, et qu'on a pas de moyens simples pour éviter cela. Avec un soustracteur, on peut utiliser des techniques d'anticipation de retenue pour accélérer les calculs. Les calculs sont donc faits en parallèle, et non colonne par colonne, ce qui est beaucoup plus rapide, surtout quand les opérandes sont un peu longues. Ce qui fait que tous les processeurs modernes utilisent le circuit suivant pour faire des comparaisons. Il faut dire qu'il n'a que des avantages : plus rapide, il utilise un peu plus de portes logiques mais cela reste parfaitement supportable, il permet de générer des bits intermédiaires utiles que les autres comparateurs peinent à fournir, etc. De plus, il peut comparer aussi bien des entiers codés en complément à deux que des entiers non-signés, là où les comparateurs précédents ne le permettaient pas.
La génération des conditions
modifierLa génération des 4 bits intermédiaire est simple et demande peu de calculs. Déterminer si le résultat est nul demande juste d'utiliser un comparateur avec zéro, qui prend en entrée le résultat de la soustraction. La génération des bits de débordement a été vue dans le chapitre sur les circuits d'addition et de soustraction, aussi pas besoin de revenir dessus. Par contre, il est intéressant de voir comment les 4 bits intermédiaires sont utilisés pour générer les conditions voulues.
Déjà, les deux opérandes sont égales si le résultat de leur soustraction est nul, et elles sont différentes sinon. Le bit qui indique si le résultat est nul ou non indique si les deux opérandes ont égales ou différentes. Cela fait déjà deux conditions de faites. De plus, l'égalité et la différence se calculent de la même manière en complément à deux et avec des entiers non-signés.
Pour ce qui est de savoir quelle opérande est supérieure ou inférieure à l'autre, cela dépend de si on analyse deux entiers non-signés ou deux entiers en complément à deux.
- Avec des entiers non-signés, il faut regarder si la soustraction génère une retenue sortante, un débordement entier non-signé. Si c'est le cas, alors la première opérande est inférieure à la seconde. Si ce n'est pas le cas, alors la première opérande est supérieure ou égale à la seconde.
- Pour la comparaison en complément à deux on se dit intuitivement qu'il faut regarder le signe du résultat. L'intuition nous dit que la première opérande est inférieure à l'autre si le résultat est négatif, qu'elle est supérieure ou nulle s'il est positif. Sauf que cela ne marche pas exactement comme cela : il faut aussi regarder si le calcul entraine un débordement d'entier en complément à deux. La règle est que le résultat est négatif si on a un débordement d'entier en complément à deux OU que le bit de signe est à 1. Une seule des deux conditions doit être respectée : le résultat est positif sinon. On doit donc faire un XOR entre le bit de débordement et le bit de signe. Le bit sortant de la porte XOR indique que le résultat de la soustraction est négatif, et donc que la première opérande est inférieure à la seconde.

Avec ces deux informations, égalité et supériorité, on peut déterminer toutes les autres. Dans ce qui va suivre, nous allons partir du principe que le soustracteur est suivi par des circuits qui calculent les bits suivants :
- un bit S qui n'est autre que le bit de signe en complément à deux ;
- un bit Z qui indique si le résultat est nul ou non (1 pour un résultat nul, 0 sinon) ;
- un bit C qui n'est autre que la retenue sortante (1 pour un débordement d'entier non-signé, 0 sinon) ;
- un bit D qui indique un débordement d'entier signé (1 pour un débordement d'entier signé, 0 sinon).
| Condition testée | Calcul | |
|---|---|---|
| A == B | Z = 1 | |
| A != B | Z = 0 | |
| Opérandes non-signées | ||
| A < B | C = 1 | |
| A >= B | C = 0 | |
| A <= B | C OU Z = 1 | |
| A > B | C ET Z = 0 | |
| Opérandes en complément à deux | ||
| A < B | S XOR D = 1 | |
| A >= B | S XOR D = 0 | |
| A <= B | (S XOR D) OU Z = 1 | |
| A > B | (S XOR D) ET Z = 0 | |
Le comparateur-soustracteur total
modifierIl est possible de raffiner ce circuit, de manière à pouvoir choisir la condition en sortie du circuit. L'idée est que le circuit possède une seule sortie, sur laquelle on a le résultat de la condition choisie. Le circuit possède une entrée sur laquelle on envoie un nombre, qui permet de choisir la condition à tester. Par exemple, on peut vouloir vérifier si deux nombres sont égaux. Dans ce cas, on configure le circuit en envoyant sur l'entrée de sélection le nombre qui correspond au test d'égalité. Le circuit fait alors le test, et fournit le résultat sur la sortie de 1 bit. Ce circuit se construit simplement à partir du circuit précédent, en ajoutant un multiplexeur. Concrètement, on prend un soustracteur, on ajoute des circuits pour calculer les bits intermédiaires, puis on ajoute des portes pour calculer les différentes conditions, et enfin, on ajoute un multiplexeur.

Nous réutiliserons ce circuit bien plus tard dans ce cours, dans les chapitres sur les branchements. Mais ne vous inquiétez pas, dans ces chapitres, nous ferons des rappels sur les bits intermédiaires, la manière dont sont calculées les conditions et globalement sur tout ce qui a été dit dans cette section. Pas besoin de mémoriser par coeur les équations de la section précédente, tout ce qui compte est que vous ayez retenu le principe général.
De nombreuses situations demandent de générer des nombres totalement aléatoires. C'est très utile dans des applications cryptographiques, statistiques, mathématiques, dans les jeux vidéos, et j'en passe. Ces applications sont le plus souvent logicielles, et cette génération de nombres aléatoire s'effectue avec divers algorithmes plus ou moins efficaces. L'aléatoire dans les jeux vidéos en est un bon exemple : pas besoin d'un aléatoire de qualité, un simple algorithme logiciels suffit. Mais dans certaines situations, il arrive que l'on veuille créer ces nombres aléatoires de manière matérielle. Cela peut servir pour sélectionner une ligne de cache à remplacer lors d'un défaut de cache, pour implémenter des circuits cryptographiques, pour calculer la durée d'émission sur un bus Ethernet à la suite d'une collision, et j'en passe. Mais comment créer une suite de nombres aléatoires avec des circuits ? C'est le but de ce tutoriel de vous expliquer comment !
Les registres à décalage à rétroaction
modifierLa première solution consiste à utiliser des registres à décalages à rétroaction, aussi appelés Feedback Shift Registers, abréviés LSFR. Ce genre de circuit donne un résultat assez proche de l'aléatoire, mais on peut cependant remarquer qu'il ne s'agit pas de vrai aléatoire. En effet, un tel circuit est déterministe : pour le même résultat en entrée, il donnera toujours le même résultat en sortie. De plus, ce registre ne peut contenir qu'un nombre fini de valeurs, ce qui fait qu'il finira donc par repasser par une valeur qu'il aura déjà parcourue. Lors de son fonctionnement, le compteur finira donc par repasser par une valeur qu'il aura déjà parcourue, vu que le nombre de valeurs possibles est fini. Une fois qu'il repassera par cette valeur, son fonctionnement se reproduira à l'identique comparé à son passage antérieur. Un LSFR ne produit donc pas de « vrai » aléatoire, vu que la sortie d'un tel registre finit par faire des cycles. Ceci dit, si la période d'un cycle est assez grande, son contenu semblera varier de manière totalement aléatoire, tant qu'on ne regarde pas durant longtemps. Il s'agit d'une approximation de l'aléatoire particulièrement bonne.

Si les LSFR sont très intéressants, diverses techniques permettent d'améliorer le fonctionnement de ces registres à décalages à rétroaction. Par exemple, on peut décider d'utiliser des LSFR plus compliqués, non linéaires. La fonction appliquée au bit sur l'entrée est alors plus complexe, mais le jeu en vaut la chandelle. Une variante de cette technique consiste à prendre la totalité des bits d'un registre à décalage à rétroaction linéaire (ou affine), et à envoyer ces bits dans un circuit non-linéaire. La différence, c'est que dans ce cas, tous les bits du registre sont pris en compte. Cependant, les techniques les plus efficaces consistent à combiner plusieurs LSFR pour obtenir une meilleure approximation de l'aléatoire. Avec cette technique, plusieurs registres à décalages à rétroaction sont reliés à un circuit combinatoire non-linéaire. Ce circuit prendra en entrée un (ou plusieurs) bit de chaque registre à décalage à rétroaction, et combinera ces bits pour fournir un bit de sortie. Un circuit conçu avec ce genre de méthode va fournir un bit à la fois. Les bits en sortie de ce circuit seront alors accumulés dans un registre à décalage normal, pour former un nombre aléatoire.
Problème : ces circuits ne sont pas totalement fiables : ils peuvent produire plus de bits à 0 que de bits à 1, et des corrections sont nécessaires pour éviter cela. Pour cela, ces circuits de production de nombres aléatoires sont souvent couplés à des circuits qui corrigent le flux de bits accumulé dans le registre pour l'aléatoiriser. Une solution consiste à simplement prendre plusieurs de ces circuits, et d'appliquer un XOR sur les bits fournis par ces circuits : on obtient alors un bit un peu moins biaisé, qu'on peut envoyer dans notre registre à décalage. Pratiquement, des circuits avec trop de bits en entrées sont difficilement concevables.
Pour rendre le tout encore plus aléatoire, il est possible de cadencer nos registres à décalage à rétroaction linéaire à des fréquences différentes. Ainsi, le résultat fourni par notre circuit combinatoire est encore plus aléatoire. Cette technique est utilisée dans les générateurs stop-and-go, alternative step, et à shrinking. Dans le premier, on utilise trois registres à décalages à rétroaction linéaire. Le bit fourni par le premier va servir à choisir lequel de deux restants sera utilisé. Dans le générateur stop-and-go, on utilise deux registres à décalage à rétroaction. Le premier est relié à l'entrée d'horloge du second. Le bit de sortie du second est utilisé comme résultat. Une technique similaire était utilisée dans les processeurs VIA C3, pour l'implémentation de leurs instructions cryptographiques. Dans le shrinking generator, deux registres à décalage à rétroaction sont cadencés à des vitesses différentes. Si le bit de sortie du premier vaut 1, alors le bit de sortie du second est utilisé comme résultat. Par contre, si le bit de sortie du premier vaut 0, aucun bit n'est fourni en sortie, et le bit de sortie du second registre est oublié.
L'aléatoire généré par l'horloge
modifierOn vient de voir que les registres à décalage à rétroaction ne permettent pas d'obtenir du vrai aléatoire, compte tenu de leur comportement totalement déterministe. Pour obtenir un aléatoire un peu plus crédible, il est possible d'utiliser d'autres moyens qui ne sont pas aussi déterministes et surtout qui ne sont pas cycliques. Parmi ces moyens, certains d'entre eux utilisent le signal d'horloge. Par exemple, une technique très simple utilise un compteur incrémenté à chaque cycle d'horloge. Si on a besoin d'un nombre aléatoire, il suffit de lire le contenu de ce registre et de l'utiliser directement comme nombre aléatoire. Si le délai entre deux demandes est irrégulier, le résultat semblera bien aléatoire. Mais il s'agit là d'une technique assez peu fiable dans le monde réel et seules quelques applications bien spécifiques se satisfont de cette méthode.
Une solution un peu plus fiable utilise ce qu'on appelle la dérive de l'horloge. Il faut savoir qu'un signal d'horloge n'est jamais vraiment très précis. Une horloge censée tourner à 1 Ghz ne tournera pas en permanence à 1Ghz exactement, mais verra sa fréquence varier de quelques Hz ou Khz de manière irrégulière. Ces variations peuvent venir de variations aléatoires de température, des variations de tension, des perturbations électromagnétiques, ou à des phénomènes assez compliqués qui peuvent se produire dans tout circuit électrique (comme le shot noise). L'idée consiste à prendre au moins deux horloges et d'utiliser la dérive des horloges pour les désynchroniser.
On peut par exemple prendre deux horloges : une horloge lente et une horloge rapide, dont la fréquence est un multiple de l'autre. Par exemple, on peut choisir une fréquence de 1 Mhz et une autre de 100 Hz : la fréquence la plus grande est égale à 10000 fois l'autre. La dérive d'horloge fera alors son œuvre : les deux horloges se désynchroniseront en permanence, et cette désynchronisation peut être utilisée pour produire des nombres aléatoires. Par exemple, on peut compter le nombre de cycles d'horloge produit par l'horloge rapide durant une période de l'horloge lente. Si ce nombre est pair, on produit un bit aléatoire qui vaut 1 sur la sortie du circuit. Pour information, c'est exactement cette technique qui était utilisée dans l'Intel 82802 Firmware Hub.
L'aléatoire généré par la tension d'alimentation
modifierIl existe d'autres solutions matérielles. Dans les solutions électroniques, il arrive souvent qu'on utilise le bruit thermique présent dans tous les circuits électroniques de l'univers. Tous nos circuits sont soumis à de microscopiques variations de température, dues à l'agitation thermique des atomes. Plus la température est élevée, plus les atomes qui composent les fils de nos circuits s'agitent. Vu que les particules d'un métal contiennent des charges électriques, ces vibrations font naître des variations de tensions assez infimes. Il suffit d'amplifier ces variations pour obtenir un résultat capable de représenter un zéro ou un 1. C'est sur ce principe que fonctionne le circuit présent dans les processeurs Intel modernes. Comme vous le savez peut-être déjà, les processeurs Intel Haswell contiennent un circuit capable de générer des nombres aléatoires. Ces processeurs incorporent des instructions capables de fournir des nombres aléatoires, instructions utilisant le fameux circuit que je viens de mentionner.
Dans ce chapitre, nous allons voir un dernier type de circuits, qui font les conversion entre de l'analogique et du numérique. Il en existe deux types . Le circuit qui convertit un signal analogique en signal numérique cela est un CAN (convertisseur analogique-numérique). Le circuit qui fait la conversion inverse est un CNA (convertisseur numérique-analogique).

Les CNA sont utilisés dans les cartes son, et ils étaient utilisés dans les anciennes cartes graphiques. Par exemple, il y a un CAN intégré à la carte son, qui sert à convertir le signal provenant d'un microphone en un signal numérique utilisable par la carte son. Il existe aussi un CNA, qui cette fois convertit le signal provenant de la carte son en signal analogique à destination des haut-parleurs. Mais nous reverrons cela dans quelques chapitres.

Les anciennes cartes graphiques incorporaient aussi un CNA dans l'interface avec l'écran. Les anciens écrans CRT avaient des entrées analogiques, connues sous le nom de connecteur VGA. C'est le fameux connecteur bleu typique des anciens écrans, mais qui est aussi présent sur la plupart des nouveaux modèles. Pour s'interfacer à l'entrée VGA, la carte graphique incorporait un circuit CNA pour transformer les données numériques des pixels en signaux analogiques à envoyer sur l'entrée VGA. De nos jours, la plupart des écrans ont des entrées numériques, et la conversion numérique-analogique est réalisée dans l'écran lui-même.
Le convertisseur numérique-analogique
modifierLes CNA sont plus simples à étudier que les CAN, ce qui fait que nous allons les voir en premier. Les CNA convertissent un nombre en binaire codé sur bits en tension analogique. la tension de sortie est comprise dans un intervalle, qui va du 0 volts à une tension maximale . Un 0 binaire sera convertie en une tension de 0 volts, tandis que la valeur binaire est codée avec la tension maximale. Tout nombre entre les deux est compris entre la tension maximale et minimale. Le lien entre nombre binaire et tension de sortie varie pas mal selon le CNA, mais la plupart sont des convertisseurs dits linéaires.


On peut expliquer leur fonctionnement de deux manières différentes. Une première manière de voir un CAN linéaire est de regarder l'association entre tension de sortie et nombre binaire. L'intervalle de la tension de sortie est découpé en sous-intervalles de même taille, chacun d'entre eux se voyant attribuer un nombre binaire. Des sous-intervalles consécutifs codent des intervalles consécutifs, le premier codant un 0 et le dernier la valeur maximale .
La taille de chaque sous-intervalle est appelé le quantum de tension et vaut . Il s'agit de la différence de tension minimale que l'on obtient en changeant l'entrée. En clair, la différence de tension en sortie entre deux nombres binaires consécutifs, est toujours la même, égale au quantum de tension. Par exemple, supposons qu'un 5 et un 6 en binaire donneront des tensions différentes de 1 volt. Alors ce sera la même différence de tension entre un 10 binaire et un 11, entre un 1000 et 1001, etc. La seconde manière de les voir est de considérer que la tension de sortie est proportionnelle au nombre à convertir, le coefficient de proportionnalité n'étant autre que le quantum de tension.

Les CNA uniformes (non-pondérés)
modifierLe CNA peut être construit de diverses manières, qui utilisent toutes des composants analogiques nommés résistances et amplificateurs analogiques, que vous avez certainement vu en cours de collège ou de lycée.
Le premier type utilise autant de générateurs de tension qu'il y a de valeurs possibles en sortie. En clair, ce CNA possède générateurs de tension (en comptant la masse et la tension d'alimentation). L'idée est de connecter le générateur qui fournit la tension de sortie et de déconnecter les autres. Chaque connexion/déconnexion se fait par l'intermédiaire d'un interrupteur commandable, à savoir une porte à transmission et/ou un transistor. Pour faire le lien entre chaque porte à transmission et la valeur binaire, on utilise un décodeur. Il suffit de relier chaque sortie du décodeur (qui correspond à une entrée unique) au transistor (la tension) qui correspond.

Les CNA pondérés en binaire
modifierIl est maintenant temps de passer aux CNA pondérés. L'idée qui se cache derrière les circuits que nous allons voir est très simple. Partons d'un nombre binaire de bits . Si le bit correspond à un quantum de tension , alors la tension correspondant au bit est de , celle de est de , etc. Une fois chaque bit convertit en tension, il suffit d'additionner les tension obtenues pour obtenir la tension finale. Toute la difficulté est de convertir chaque bit en tension, puis d'additionner le tout. C’est surtout l'addition des tensions qui pose problème, ce qui fait que la plupart des circuits convertit les bits en courants, plus faciles à additionner, avant de convertir le résultat final en tension. Dans ce qui va suivre, nous allons voir deux circuits : les CNA pondérés à résistances équilibrées et non-équilibrées.

|
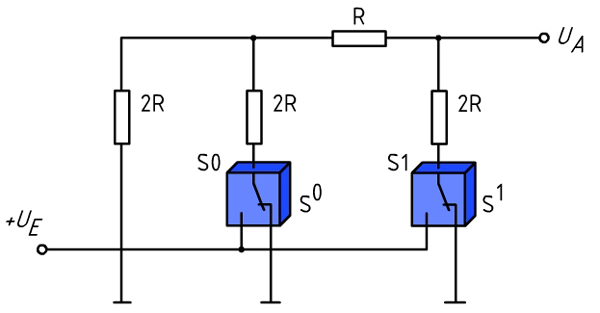
|
Le CNA à résistances non-équilibrées
modifierLe circuit suivant utilise des résistances pour convertir un bit en un courant proportionnel à sa valeur. Rappelons que chaque bit est codé par une tension égale à la tension d'alimentation (pour un 1) ou un 0 volt (pour un 0). Cette tension est convertie en courant par un interrupteur, une tension et une résistance. Le courant est obtenu en faisant passer une tension à travers une résistance, l'interrupteur ouvrant ou fermant le circuit selon le bit à coder. Quand le bit est de zéro, l'interrupteur s'ouvre, et le courant ne passe pas : il vaut 0. Quand le bit est à 1, l'interrupteur se ferme et le courant est alors mis à sa valeur de conversion. La valeur de la résistance permet de multiplier chaque bit par son poids (par 1, 2, 4, , 16, ...) : c'est pour cela qu'il y a des résistances de valeur R, 2R, 4R, 8R, etc. Les courants en sortie de chaque résistance sont ensuite additionnés par le reste du circuit, avant d'être transformé en une tension proportionnelle.

Le CNA à résistances équilibrées
modifierLe circuit précédent a pour défaut d'utiliser des résistances de valeurs fort différentes : R, 2R, 4R, etc. Mais la valeur d'une résistance est rarement très fiable, surtout quand on commence à utiliser des résistances assez fortes. Chaque résistance a une petit marge d'erreur, qui fait que sa résistance véritable n'est pas tout à fait égale à sa valeur idéale. Avec des résistances fort variées, les marges d'erreurs s'accumulent et influencent le fonctionnement du circuit. Si on veut un circuit réellement fiable, il vaut mieux utiliser des résistances qui ont des marges d'erreur similaires. Et qui dit marges d'erreur similaire dit résistances de valeur similaires. Pas question d'utiliser une résistance de valeur R avec une autre de valeur 16R ou 32R. Pour éviter cela, on doit modifier le circuit précédent de manière à utiliser des résistances de même valeur ou presque. Cela donne le circuit suivant.

Le convertisseur analogique-numérique
modifierLes convertisseurs analogique-numérique convertissent une tension en un nombre binaire codé sur bits. Comme pour les CNA, la tension d'entrée peut prendre toutes les valeurs dans un intervalle de tension allant de 0 à une tension maximale. L'intervalle de tension est découpé en sous-intervalles de même taille, chacun se voyant attribuer un nombre binaire. Si la tension d'entrée tombe dans un de ces intervalle, le nombre binaire en sortie est celui qui correspond à cet intervalle. Des intervalles consécutifs correspondent à des nombres binaires consécutifs, le premier intervalle codant un 0 et le dernier le nombre . En clair, le nombre binaire est plus ou moins proportionnel à la tension d'entrée. La taille de chaque intervalle est appelé le quantum de tension, comme pour les CNA.
La conversion d'un signal analogique se fait en plusieurs étapes. La toute première consiste à mesurer régulièrement le signal analogique, pour déterminer sa valeur. Il est en effet impossible de faire la conversion au fil de l'eau, en temps réel. À la place, on doit échantillonner à intervalle réguliers la tension, pour ensuite la convertir. La seconde étape consiste à convertir celle-ci en un signal numérique, un signal discret. Enfin, ce dernier est convertit en binaire. Ces trois étapes portent le nom d’échantillonnage, la quantification et le codage.
 |
 |
L'échantillonnage
modifierL’échantillonnage mesure régulièrement le signal analogique, afin de fournir un flux de valeurs à convertir en numérique. Il a lieu régulièrement, ce qui signifie que le temps entre deux mesures est le même. Ce temps entre deux mesures est appelée la période d'échantillonnage, notée . Le nombre de fois que la tension est mesurée par seconde s'appelle la fréquence d'échantillonnage. Elle n'est autre que l'inverse de la période d’échantillonnage : . Plus celle-ci est élevée, plus la conversion sera de bonne qualité et fidèle au signal original. Les deux schémas ci-dessous montrent ce qui se passe quand on augmente la fréquence d’échantillonnage : le signal à gauche est échantillonné à faible fréquence, alors que le second l'est à une fréquence plus haute.
 |
 |
L’échantillonnage est réalisé par un circuit appelé l’échantillonneur-bloqueur. L'échantillonneur-bloqueur le plus simple ressemble au circuit du schéma ci-dessous. Les triangles de ce schéma sont ce qu'on appelle des amplificateurs opérationnels, mais on n'a pas vraiment à s'en préoccuper. Dans ce montage, ils servent juste à isoler le condensateur du reste du circuit, en ne laissant passer les tensions que dans un sens. L'entrée C est reliée à un signal d'horloge qui ouvre ou ferme l'interrupteur à fréquence régulière. La tension va remplir le condensateur quand l'interrupteur se ferme. Une fois le condensateur remplit, l'interrupteur est déconnecté isolant le condensateur de la tension d'entrée. Celui-ci mémorisera alors la tension d'entrée jusqu'au prochain échantillonnage.

La quantification et le codage
modifierLe signal échantillonné est ensuite convertit en un signal numérique, codé sur plusieurs bits. Le nombre de bits du résultat est ce qu'on appelle la résolution du CAN. Plus celle-ci est important,e plus le signal codé sera fidèle au signal d'origine. La précision du CAN sera plus importante avec une résolution importante. Malgré tout, un signal analogique ne peut pas être traduit en numérique sans pertes, l'infinité de valeurs d'un intervalle de tension ne pouvant être codé sur un nombre fini de bits. La tension envoyée va ainsi être arrondie à une tension qui peut être traduite en un entier sans problème. Cette perte de précision va donner lieu à de petites imprécisions qui forment ce qu'on appelle le bruit de quantification. Plus le nombre de bits utilisé pour encoder la valeur numérique est élevée, plus ce bruit est faible.

Le CAN Flash
modifierUn CAN peut être construit de diverses manières, à partir de composants nommés résistances et amplificateurs analogiques. Par exemple, voici à quoi ressemble un CAN Flash, le type de CAN le plus performant. C'est aussi le plus simple à comprendre, bizarrement. Pour comprendre comment celui-ci fonctionne, précisons que le CAN code la tension analogique sur bits, soit des valeurs comprises entre 0 et . Chaque nombre binaire est associée à la tension d'entrée qui correspond. L'idée est de comparer la tension avec toutes les valeurs de tension correspondantes. On utilise pour cela un comparateur pour chaque tension, qui fournit un résultat codé sur un bit : ce dernier vaut 1 si la tension d'entrée est supérieure à la valeur, 0 sinon. Les résultats de chaque comparateur sont combinés entre eux pour déterminer la tension la plus grande qui est proche du résultat. La combinaison des résultats est réalisée avec un encodeur à priorité. Les résultats des comparateurs sont envoyés sur l'entrée adéquate de l'encodeur, qui convertit aussi cette tension en nombre binaire.

Ce circuit, bien que très simple, a cependant de nombreux défauts. Le principal est qu'il prend beaucoup de place : les comparateurs de tension sont des dispositifs encombrants, sans compter l'encodeur. Mais le défaut principal est le nombre de comparateurs à utiliser. Sachant qu'il en faut un par valeur, on doit utiliser comparateurs pour un CAN de bits. En clair, le nombre de comparateurs à utiliser croît exponentiellement avec le nombre de bits. En conséquence, les CAN Flash ne sont utilisables que pour de petits convertisseurs, limités à quelques bits. Mais il existe des CAN construits autrement qui n'ont pas ce genre de problèmes.
Le CAN simple rampe
modifierLe CAN simple rampe est un CAN construit avec un compteur, un générateur de tension, un comparateur de tension et un signal d'horloge. L'idée derrière ce circuit est assez simple : au lieu de faire toutes les comparaisons en parallèle, comme avec un CAN Flash, celles-ci sont faites une par une, une tension après l'autre. Ce faisant, on n'a besoin que d'un seul comparateur de tension. Les tensions sont générées successivement par un générateur de rampe, à savoir un circuit qui crée une tension qui croit linéairement. La tension en sortie du générateur de rampe commence à 0, puis monte régulièrement jusqu’à une valeur maximale. Celle-ci est alors comparée à la tension d'entrée. Tant que la tension générée est plus faible, la sortie du comparateur est à 0. Quand la tension en sortie du générateur de rampe dépasse à la tension d'entrée, le comparateur renvoie un 1.
Tout ce système permet de faire les comparaisons de tension, mais il n'est alors plus possible d'utiliser un encodeur pour faire la traduction (tension -> nombre binaire). L'encodeur est remplacé par un autre circuit, qui n'est autre que le compteur. Le compteur est initialisé à 0, mais est incrémenté régulièrement, ce qui fait qu'il balaye toutes les valeurs que peut prendre la sortie numérique. L'idée est que le compteur et la tension du générateur de rampe se suivent : quand l'un augmente, l'autre augmente dans la même proportion. Ainsi, la valeur dans le compteur correspondra systématiquement à la tension de sortie du générateur. Pour cela, on synchronise les deux circuits avec un signal d'horloge. À chaque cycle, le compteur est incrémenté, tandis que le générateur augmente d'un quantum de tension. Ce faisant, quand le comparateur renverra un 0, on saura que la tension d'entrée est égale à celle du générateur. Au même cycle d'horloge, le compteur contient la valeur binaire qui lui correspond. Il suffit alors d’arrêter le compteur et de recopier son contenu sur la sortie.

Ce CAN a l'avantage de prendre bien moins de place que son prédécesseur, sans compter qu'il utilise très peu de circuits. Pas besoin de beaucoup de comparateurs de tension, ni d'un encodeur très compliqué : quelques circuits très simples et peu encombrants suffisent. Ce qui est un avantage certain pour les CAN avec beaucoup de bits. Mais ce CAN a cependant des défauts assez importants. Le défaut principal de ce CAN est qu'il est très lent. Déjà, la conversion est plus rapide pour les tensions faibles, mais très lente pour les grosses tensions, vu qu'il faut balayer les tensions unes par unes. On gagne en place ce qu'on perd en vitesse.
Le CAN delta
modifierLe CAN delta peut être vu comme une amélioration du circuit précédent. Il est lui aussi organisé autour d'un compteur, initialisé à 0, qui est incrémenté jusqu'à tomber sur la valeur de sortie. Encore une fois, ce compteur contient un nombre binaire et celui-ci est associé à une tension équivalente. Sauf que cette fois-ci, la tension équivalente n'est pas générée par un générateur synchronisé avec le compteur, mais directement à partir du compteur lui-même. Le compteur relié à un CNA, qui génère la tension équivalente. La tension équivalente est alors comparée avec la tension d'entrée, et le comparateur commande l'incrémentation du compteur, comme dans le circuit précédent.

Le CAN par approximations successives
modifierLe CAN par approximations successives effectue une comparaison par étapes, en suivant une procédure dite de dichotomie. Chaque étape correspond à un cycle d'horloge du CAN, qui met donc plusieurs cycles d'horloges pour faire une conversion. Le CAN essaye d'encadrer la tension dans un intervalle, est divisé en deux à chaque étape. L'intervalle à la première étape est de [0 , Tension maximale en entrée ], puis il se réduit progressivement, jusqu'à atteindre un encadrement suffisant, compatible avec la résolution du CAN. À chaque étape, le CAN découpe l'intervalle en deux parties égales, séparées au niveau d'une tension médiane. Il compare l'entrée à la tension médiane et en déduit un bit du résultat, qui est ajouté dans un registre à décalage.
Pour comprendre le concept, prenons l’exemple d'un CAN qui prend en entrée une tension comprise entre 0 et 5 Volts.
- Lors de la première étape, le CAN vérifie si la tension d'entrée est supérieure/inférieure à 2,5 V.
- Lors de la seconde étape, il vérifie si la tension d'entrée est supérieure/inférieure 3,75 V ou de 1,25 Volts, selon le résultat de l'étape précédente : 1,25 V si l'entrée est inférieure à 2,5 V, 3,75 V si elle est supérieure.
- Et on procède sur le même schéma, jusqu’à la dernière étape.
Pour faire son travail, ce CAN comprend un comparateur, un registre et un CNA. Le comparateur est utilisé pour comparer la tension d'entrée avec la tension médiane. Le registre à décalage sert à accumuler les bits calculés à chaque étape, dans le bon ordre. En réfléchissant un petit peu, on devine que les bits sont calculés en partant du bit de poids fort vers le bit de poids faible : le bit de poids fort est calculé dans la première étape, le bit de poids faible lors de la dernière, .... Le CNA sert à générer la tension médiane de chaque étape, à partir de la valeur du registre. L'ensemble est organisé comme illustré dans le schéma ci-dessous.

Voici une animation du CAN à approximation succesive en fonctionnement :

Les circuits intégrés
modifierDans le chapitre précédent, nous avons abordé les portes logiques. Dans ce chapitre, nous allons voir qu'elles sont fabriquées avec des composants électroniques que l'on appelle des transistors. Ces derniers sont reliés entre eux pour former des circuits plus ou moins compliqués. Pour donner un exemple, sachez que les derniers modèles de processeurs peuvent utiliser près d'un milliard de transistors.
Les transistors MOS
modifier
Les transistors possèdent trois broches, des pattes métalliques sur lesquelles on connecte des fils électriques. On peut appliquer une tension électrique sur ces broches, qui peut représenter soit 0 soit 1. Sur ces trois broches, il y en a deux entre lesquelles circule un courant, et une troisième qui commande le courant. Le transistor s'utilise le plus souvent comme un interrupteur commandé par sa troisième broche. Le courant qui traverse les deux premières broches passe ou ne passe pas selon ce qu'on met sur la troisième.
Il existe plusieurs types de transistors, mais les deux principaux sont les transistors bipolaires et les transistors MOS. De nos jours, les transistors utilisés dans les ordinateurs sont tous des transistors MOS. Les raisons à cela sont multiples, mais les plus importantes sont les suivantes. Premièrement, les transistors bipolaires sont plus difficiles à fabriquer et sont donc plus chers. Deuxièmement, ils consomment bien plus de courant que les transistors MOS. Et enfin, les transistors bipolaires sont plus gros, ce qui n'aide pas à miniaturiser les puces électroniques. Tout cela fait que les transistors bipolaires sont aujourd'hui tombés en désuétude et ne sont utilisés que dans une minorité de circuits.
Les types de transistors MOS : PMOS et NMOS
modifierSur un transistor MOS, chaque broche a un nom, nom qui est indiqué sur le schéma ci-dessous.On distingue ainsi le drain, la source et la grille On l'utilise le plus souvent comme un interrupteur commandé par sa grille. Appliquez la tension adéquate et la liaison entre la source et le drain se comportera comme un interrupteur fermé. Mettez la grille à une autre valeur et cette liaison se comportera comme un interrupteur ouvert.
Il existe deux types de transistors CMOS, qui diffèrent entre autres par le bit qu'il faut mettre sur la grille pour les ouvrir/fermer :
- les transistors NMOS qui s'ouvrent lorsqu'on envoie un zéro sur la grille et se ferment si la grille est à un ;
- et les PMOS qui se ferment lorsque la grille est à zéro, et s'ouvrent si la grille est à un.

Voici les symboles de chaque transistor.
 |
 |
 |
L'anatomie d'un transistor MOS
modifierÀ l'intérieur du transistor, on trouve simplement une plaque en métal reliée à la grille appelée l'armature, un bout de semi-conducteur entre la source et le drain, et un morceau d'isolant entre les deux. Pour rappel, un semi-conducteur est un matériau qui se comporte soit comme un isolant, soit comme un conducteur, selon les conditions auxquelles on le soumet. Dans un transistor, son rôle est de laisser passer le courant, ou de ne pas le transmettre, quand il faut. C'est grâce à ce semi-conducteur que le transistor peut fonctionner en interrupteur : interrupteur fermé quand le semi-conducteur conduit, ouvert quand il bloque le courant. La commande de la résistance du semi-conducteur (le fait qu'il laisse passer ou non le courant) est réalisée par la grille, comme nous allons le voir ci-dessous.

Suivant la tension que l'on place sur la grille, celle-ci va se remplir avec des charges négatives ou positives. Cela va entrainer une modification de la répartition des charges dans le semi-conducteur, ce qui modulera la résistance du conducteur. Prenons par exemple le cas d'un transistor NMOS et étudions ce qui se passe selon la tension placée sur la grille. Si on met un zéro, la grille sera vide de charges et le semi-conducteur se comportera comme un isolant : le courant ne passera pas. En clair, le transistor sera équivalent à un interrupteur ouvert. Si on met un 1 sur la grille, celle-ci va se remplir de charges. Le semi-conducteur va réagir et se mettre à conduire le courant. En clair, le transistor se comporte comme un interrupteur fermé.
 |
 |
La tension de seuil d'un transistor
modifierLe fonctionnement d'un transistor est légèrement plus complexe que ce qui a été dit auparavant. Mais pour rester assez simple, disons que son fonctionnement exact dépend de trois paramètres : la tension d'alimentation, le courant entre drain et source, et un nouveau paramètre appelé la tension de seuil.
Appliquons une tension sur la grille d'un transistor NMOS. Si la tension de grille reste sous un certain seuil, le transistor se comporte comme un interrupteur fermé. Le seuil de tension est appelé, très simplement, la tension de seuil. Au-delà de la tension de seuil, le transistor se comporte comme un interrupteur ouvert, il laisse passer le courant. La valeur exacte du courant dépend de la tension entre drain et source, soit la tension d'alimentation. Elle aussi dépend de la différence entre tension de grille et de seuil, à savoir .
Le paragraphe qui va suivre n'est pas très important, pas plus que le schéma. Tout ce qu'il faut comprendre est que la tension de seuil est une tension minimale pour ouvrir le transistor. Si la tension d'alimentation est trop faible, plus faible que cette tension de seuil, alors le transistor ne peut pas fonctionner. Ce détail reviendra plus tard dans ce cours, quand nous parlerons de la consommation d'énergie des circuits électroniques. LE fait qu'on ne peut pas baisser la tension sous la tension de seuil est un léger problème en termes de consommation énergétique.
Dans les cas que nous allons voir dans ce cours, la tension d'alimentation est plus grande que . Le courant est alors maximal, il est proportionnel à . Le transistor ne fonctionne alors pas comme un amplificateur, le courant reste le même. Si la tension d'alimentation est plus petite que , le transistor est en régime linéaire : le courant de sortie est proportionnel à , ainsi qu'à la tension d'alimentation. Le transistor fonctionne alors comme un amplificateur de courant, dont l'intensité de l'amplification est commandée par la tension.

La technologie CMOS
modifierLes portes logiques que nous venons de voir sont actuellement fabriquées en utilisant des transistors. Il existe de nombreuses manières pour concevoir des circuits à base de transistors, qui portent les noms de DTL, RTL, TLL, CMOS et bien d'autres. Les techniques anciennes concevaient des portes logiques en utilisant des diodes, des transistors bipolaires et des résistances. Mais elles sont aujourd'hui tombées en désuétudes dans les circuits de haute performance. De nos jours, on n'utilise que des logiques MOS (Metal Oxyde Silicium), qui utilisent des transistors MOS vus plus haut dans ce chapitre, parfois couplés à des résistances. On distingue :
- La logique NMOS, qui utilise des transistors NMOS associés à des résistances.
- La logique PMOS, qui utilise des transistors PMOS associés à des résistances.
- La logique CMOS, qui utilise des transistors PMOS et NMOS, sans résistances.
Dans cette section, nous allons montrer comment fabriquer des portes logiques en utilisant la technologie CMOS. Avec celle-ci, chaque porte logique est fabriquée à la fois avec des transistors NMOS et des transistors PMOS. On peut la voir comme un mélange entre la technologie PMOS et NMOS. Tout circuit CMOS est divisé en deux parties : une intégralement composée de transistors PMOS et une autre de transistors NMOS. Chacune relie la sortie du circuit soit à la masse, soit à la tension d'alimentation.

La première partie relie la tension d'alimentation à la sortie, mais uniquement quand la sortie doit être à 1. Si la sortie doit être à 1, des transistors PMOS vont se fermer et connecter tension et sortie. Dans le cas contraire, des transistors s'ouvrent et cela déconnecte la liaison entre sortie et tension d'alimentation. L'autre partie du circuit fonctionne de la même manière que la partie de PMOS, sauf qu'elle relie la sortie à la masse et qu'elle se ferme quand la sortie doit être mise à 0

Dans ce qui va suivre, nous allons étudier la porte NON, la porte NAND et la porte NOR. La porte de base de la technologie CMOS est la porte NON, les portes NAND et NOR ne sont que des versions altérées de la porte NON qui ajoutent des entrées et quelques transistors. Les autres portes, comme la porte ET et la porte OU, sont construites à partir de ces portes. Nous parlerons aussi de la porte XOR, qui est un peu particulière.
La porte NON
modifierCette porte est fabriquée avec seulement deux transistors, comme indiqué ci-dessous.

Si on met un 1 en entrée de ce circuit, le transistor du haut va fonctionner comme un interrupteur ouvert, et celui du bas comme un interrupteur fermé : la sortie est reliée au zéro volt, et vaut donc 0. Inversement, si on met un 0 en entrée de ce petit montage électronique, le transistor du bas va fonctionner comme un interrupteur ouvert, et celui du haut comme un interrupteur fermé : la sortie est reliée à la tension d'alimentation, et vaut donc 1.

Les portes logiques à deux entrées
modifierPassons maintenant aux portes logiques à deux entrées. Pour celles-ci, on devra utiliser plus de transistors, au moins deux par entrée. Il existe plusieurs manières de relier deux transistors, mais celle qui va nous intéresser en premier lieu est la suivante : deux transistors en série, c'est-à-dire l'un à la suite de l'autre. On peut mettre deux transistors PMOS en série ou deux transistors NMOS en série. Il y aura un transistor PMOS par entrée, un NMOS par entrée. Étudions plus en détail les deux cas.
On rappelle que les transistors se ferment si l'entrée vaut 0 pour des transistors PMOS, 1 pour des NMOS. Prenons deux transistors PMOS en série, chacun associé à son entrée. Pour que la connexion se fasse entre tension d'alimentation et sortie, il faudra que les deux transistors se ferment, ce qui demande que les deux entrées soient à 0. C'est la seule possibilité, et cela laisse de côté le cas où une seule entrée est à 0, ainsi que le cas où les deux entrées sont à 1. Pour gérer ces trois cas, il suffit d'inverser une entrée, voire les deux, avec des portes logiques NON.
Avec les transistors NMOS, c'est la même chose. Avec deux transistors NMOS, la connexion est fermée quand les deux entrées sont à 1. On peut gérer les autres cas avec des portes NON. Le tout est illustré ci-dessous.

Mine de rien, avec ces 8 montages de base, on peut créer n'importe quelle porte logique à deux entrées. Nous allons notamment voir dans la section suivante comment faire une porte XOR avec. Il suffit de prendre les 4 montages adéquats par les 8 précédents pour obtenir la porte logique voulue. Rappelons que d'après les règles du CMOS, les deux transistors PMOS se placent entre la tension d'alimentation et la sortie, et servent à mettre la sortie à 1. Pour les deux transistors NMOS, ils sont reliés à la masse et mettent la sortie à 0. Pour mieux comprendre, prenons l'exemple d'une porte XOR.
Un exemple d'application avec la porte XOR
modifierIl est possible de créer une porte XOR en combinant d'autres portes logiques, mais la méthode que je vais expliquer donne un résultat plus économe en circuit, sans compter que la méthode en question marche pour toute porte logique à deux entrées. L'idée est très simple : on prend la table de vérité de la porte logique, et on associe deux transistors en série pour chaque ligne. Regardons d'abord la table de vérité ligne par ligne :
| Entrée 1 | Entrée 2 | Sortie |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La première ligne a ses deux entrées à 0 et sort un 0. La sortie est à 0, ce qui signifie qu'il faut regarder sur la ligne des transistors NMOS, qui connectent la sortie à la masse. Le montage qui se ferme quand les deux entrées sont à 0 est celui tout en bas à droite du tableau précédent, à savoir deux transistors NMOS avec deux portes NON.
Les deux lignes du milieu ont une entrée à 0 et une à 1, et leur sortie à 1. La sortie à 1 signifie qu'il faut regarder sur la ligne des transistors PMOS, qui connectent la tension d'alimentation à la sortie. Les deux montages avec deux entrées différentes sont les deux situés au milieu, avec deux transistors PMOS et une porte logique.
La dernière ligne a ses deux entrées à 1 et sort un 0. La sortie est à 0, ce qui signifie qu'il faut regarder sur la ligne des transistors NMOS, qui connectent la sortie à la masse. Le montage qui se ferme quand les deux entrées sont à 1 est celui tout en bas à gauche du tableau précédent, à savoir deux transistors NMOS seuls.
En combinant ces quatre montages, on trouve le circuit suivant. Notons qu'il n'y a que deux portes NON marquées en vert et bleu : on a juste besoin d'inverser la première entrée et la seconde, pas besoin de portes en plus. Les portes NOn sont en quelque sorte partagées entre les transistors PMOS et NMOS.

Si les deux entrées sont à 1, alors les deux transistors en bas à gauche vont se fermer et connecter la sortie au 0 volt, les trois autres groupes ayant au moins un transistor ouvert. Si les deux entrées sont à 0, alors les deux transistors en bas à droite vont se fermer et connecter la sortie au 0 volt, les autres quadrants ayant au moins un transistor ouvert. Et pareil quand les deux bits sont différents : un des deux quadrants aura ses deux transistors fermés, alors que les autres auront au moins un transistor ouvert, ce qui connecte la sortie à la tension d'alimentation.
On peut construire la porte NXOR sur la même logique. Et toutes les portes logiques peuvent se construire avec cette méthode. Le nombre de transistors est alors le même : on utilise 12 transistors au total : 4 paires de transistors en série, 4 transistors en plus pour les portes NON. Que ce soit pour la porte XOR ou NXOR, on économise beaucoup de transistors comparés à la solution naïve, qui consiste à utiliser plusieurs portes NON/ET/OU. Si on ne peut pas faire mieux dans le cas de la porte XOR/NXOR, sachez cependant que les autres portes construites avec cette méthode utilisent plus de transistors que nécessaire. De nombreuses simplifications sont possibles, comme on le verra plus bas.
Les portes NAND et NOR
modifierPour simplifier une porte NOR/NAND en CMOS, on doit câbler les transistors d'une certaine façon. On retrouve des transistors en série (l'un après l'autre, sur le même fil), mais on trouve aussi des transistors en parallèle (sur des fils différents). Le tout est illustré ci-dessous. Les transistors en série ferment la connexion quand toutes les entrées sont à 1 (NMOS) ou 0 (PMOS). A l'inverse, pour les transistors en parallèle, il faut qu'une seule entrée soit à la bonne valeur pour que la connexion se fasse. L'usage de transistors PMOS/NMOS en parallèle permet de faire de nombreuses simplifications.

Une porte NOR met sa sortie à 1 si toutes les entrées sont à 0, à 0 si une seule entrée vaut 1. Pour reformuler, il faut connecter la sortie à la tension d'alimentation si toutes les entrées sont à 0, ce qui demande d'utiliser des transistors PMOS en série. Le second cas (une seule entrée à 1) peut théoriquement se faire en combinant plusieurs transistors en séries : deux NMOS en série pour le cas avec les deux entrées à 1, deux pour le cas où la première entrée est à 1 et l'autre à 0, etc. Mais on peut faire autrement et directement utiliser deux transistors en parallèle. Il y a alors deux cas : soit la première entrée vaut 1, soit l'autre vaut 1. On place alors un transistor NMOS pour chaque possibilité, là encore entre la masse et la sortie.
Le circuit obtenu est donc celui obtenu dans le premier schéma. Le même raisonnement pour une porte NAND donne le second schéma.
 |
 |
Leur fonctionnement s'explique assez bien si on regarde ce qu'il se passe en fonction des entrées. Suivant la valeur de chaque entrée, les transistors vont se fermer ou s'ouvrir, ce qui va connecter la sortie soit à la tension d'alimentation, soit à la masse.
Voici ce que cela donne pour une porte NAND :

Voici ce que cela donne pour une porte NOR :

Les autres portes logiques : ET/OU/XOR/NXOR
modifierEn logique CMOS, les portes logiques ET et OU sont construites en prenant une porte NAND/NOR et en mettant une porte NON sur sa sortie. Il est théoriquement possible d'utiliser uniquement des transistors en série et en parallèle, mais cette solution utilise plus de transistors.
 |
 |
Avec ces portes, il est possible de créer d'autres portes. Par exemple, on peut construire une porte XOR avec seulement 10 transistors, et non 12 avec la méthode de base.

Les portes logiques à trois entrées ou plus
modifierTout ce qui a été dit plus haut sur les transistors en série et en parallèle vaut aussi pour les portes logiques à trois entrées ou plus. Il est possible de créer des portes logiques à 3 entrées avec uniquement des paquets de 3 transistors en série, mais c'est rarement une bonne idée. La quasi-totalité de ces portes gagnent à utiliser des transistors en parallèle.
Les portes NAND/NOR/ET/OU à plusieurs entrées
modifierLes portes NOR/NAND à plusieurs entrées sont construites comme les portes ET et OU à deux entrées, mais en rajoutant des transistors. Il y a autant de transistors en série que d'entrée, pareil pour les transistors en parallèle. Leur fonctionnement est similaire à leurs cousines à deux entrées. Les portes ET et OU à plusieurs entrées sont construites à partie de NAND/NOR suivies d'une porte NON.
 |
 |
En théorie, on pourrait créer des portes avec un nombre arbitraire d'entrées avec cette méthode. Cependant, au-delà d'un certain nombre de transistors en série/parallèle, les performances s'effondrent rapidement. Le circuit devient alors trop lent, sans compter que des problèmes purement électriques surviennent. En pratique, difficile de dépasser la dizaine d'entrées. Dans ce cas, les portes sont construites en assemblant plusieurs portes NAND/NOR ensemble. Et faire ainsi marche nettement mieux pour fabriquer des portes ET/OU que pour des portes NAND/NOR.
On s'attend à ce qu'une porte ET/OU avec beaucoup d'entrées soit construite en combinant plusieurs portes ET/OU. Il existe cependant une alternative qui se marie nettement mieux avec la logique CMOS. Rappelons qu'en logique CMOS, les portes NAND et NOR sont les portes à plusieurs entrées les plus simples à fabriquer. L'idée est alors de combiner des portes NAND/NOR pour créer une porte ET/OU.
Voici la comparaison entre les deux solutions pour une porte ET :
 |
 |
Voici la comparaison entre les deux solutions pour une porte OU :
 |
 |
D'autres portes mélangent transistors en série et en parallèle d'une manière différente. Les portes ET-OU-NON et OU-ET-NON en sont un bon exemple.
Les portes ET-OU-NON et OU-ET-NON
modifierIl est possible de créer des portes ET-OU-NON et OU-ET-NON assez simplement en CMOS. La solution la plus simple est de combiner des portes ET et une porte NOR, mais il est possible de faire beaucoup plus simple, comme indiqué dans le schéma ci-dessous.

Le schéma ci-contre montre l'implémentation d'une porte OU-ET-NON, où l'on fait un OU entre les trois premières entrées, avant de faire un ET avec la quatrième, puis un NON sur le résultat. On voit qu'on arrive à se débrouiller avec seulement quatre transistors, ce qui est une sacrée économie comparé à une implémentation naïve avec trois portes logiques.
Le schéma suivant compare l'implémentation d'une porte ET-OU-NON de type 2-1, à savoir qu'elle fait un ET entre les deux premières entrées, puis un NOR entre le résultat du ET et la troisième entrée. L'implémentation à droite du schéma avec une porte ET et une porte NOR prend 10 transistors. L'implémentation la plus simple, à gauche du schéma, prend seulement 6 transistors.

La pass transistor logic
modifierLa pass transistor logic est une forme particulière de technologie CMOS, une version non-conventionnelle. Avec le CMOS normal, la porte de base est la porte NON. En modifiant celle-ci, on arrive à fabriquer des portes NAND, NOR, puis les autres portes logiques. Les transistors sont conçus de manière à connecter la sortie, soit la tension d'alimentation, soit la masse. Avec la pass transistor logic, le montage de base est un circuit interrupteur, qui connecte l'entrée directement sur la sortie. Le circuit interrupteur n'est autre que les portes à transmission vues il y a quelques chapitres.
La pass transistor logic a été utilisée dans des processeurs commerciaux, comme dans l'ARM1, le premier processeur ARM. Sur l'ARM1, les concepteurs ont décidé d'implémenter certains circuits avec des multiplexeurs. La raison n'est pas une question de performance ou d'économie de transistors, juste que c'était plus pratique à fabriquer, sachant que le processeur était le premier CPU ARM de l'entreprise.
Dans la suite du cours, nous verrons quelques circuits qui utilisent cette technologie, mais ils seront rares. Nous l'utiliserons quand nous parlerons des additionneurs, ou les multiplexeurs, guère plus. Mais il est sympathique de savoir que cette technologie existe.
La porte à transmission
modifierLe circuit de base est une porte à transmission, à savoir une porte logique qui agit comme une sorte d'interrupteur, qui s'ouvre ou se ferme suivant ce qu'on met sur l'entrée de commande. Le circuit peut soit connecter l'entrée et la sortie, soit déconnecter la sortie de l'entrée. Le choix entre les deux dépend de l’entrée de commande.
Intuitivement, on se dit qu'une transistor fonctionne déjà comme un interrupteur, mais une porte à transmission est construit avec deux transistors. La raison la plus intuitive est que la logique CMOS fait que tout transistor PMOS doit être associé à un transistor NMOS et réciproquement. Mais une autre raison, plus importante, est que les transistors NMOS et PMOS ne sont pas des interrupteurs parfaits. Les NMOS laissent passer les 0, mais laissent mal passer les 1 : la tension en sortie, pour un 1, est atténuée. Et c'est l'inverse pour les PMOS, qui laissent bien passer les 1 mais fournissent une tension de sortie peut adéquate pour les 0. Donc, deux transistors permettent d'obtenir une tension de sortie convenable. Le montage de base est le suivant :

Vous remarquerez que le circuit est fondamentalement différent des circuits précédents. Les précédents connectaient la sortie soit à la tension d'alimentation, soit à la masse. Ici, la sortie est connectée sur l'entrée, rien de plus. Il n'y a pas d'alimentation électrique ni de contact à la masse. Retenez ce point, il sera important par la suite.
Les deux entrées A et /A sont l'inverse l'une de l'autre, ce qui fait qu'il faut en théorie rajouter une porte NON CMOS normale, pour obtenir le circuit complet. Mais dans les faits, on arrive souvent à s'en passer. Ce qui fait que la porte à transmission est définie comme étant le circuit à deux transistors précédents.
Les multiplexeurs 2 vers 1 en pass transistor logic
modifierDans les chapitres précédents, nous avions vu que les portes à transmission sont assez peu utilisées. Nous ne nous en sommes servies que dans de rares cas, mais l'un d'entre eux va nous intéresser : les multiplexeurs et les démultiplexeurs. Pour rappel, il est assez simple de fabriquer un multiplexeur 2 vers 1 en utilisant des portes à transmission. L'idée est de relier chaque entrée à la sortie par l'intermédiaire d'une porte à transmission. Quand l'une sera ouverte, l'autre sera fermée. Le résultat n'utilise que deux portes à transmission et une porte NON. Voici le circuit qui en découle :

En utilisant les portes à transmission CMOS vues plus haut, on obtient le circuit suivant :

La pass transistor logic utilise des multiplexeurs 2 vers 1
modifierLa pass transistor logic permet d'implémenter des multiplexeurs assez facilement, en combinant des portes NON avec des portes à transmission. Et la pass transistor logic en profite pour implémenter les portes logiques d'une manière assez étonnante : les portes logiques sont basées sur un multiplexeur 2 vers 1 amélioré ! Un multiplexeur 2 vers 1 peut être utilisé pour implémenter de nombreux circuits différents. Par exemple, il peut être utilisé pour implémenter des portes logiques, tout dépend de ce qu'on met sur ses entrées.
L'idée est d'émuler une porte logique à deux entrées avec un multiplexeur 2 vers 1. Et intuitivement, vous vous dites que les deux entrées de la porte logique correspondent aux deux entrées de donnée du multiplexeur. Mais non, c'est une erreur ! En réalité, un bit d'entrée est envoyé sur l'entrée de commande, et l'autre bit sur une entrée de donnée du multiplexeur. Suivant ce qu'on met sur la seconde entrée du multiplexeur, on obtient une porte ET, OU, XOR, etc. Il y a quatre choix possibles : soit on envoie un 0, soit un 1, soit l'inverse du bit d'entrée, soit envoyer deux fois le bit d'entrée.

Ils peuvent aussi être utilisés pour implémenter une bascule D, (pour rappel : une petite mémoire de 1 bit), comme on l'a vu dans les chapitres sur les bascules. Il suffit pour cela de boucler la sortie d'un multiplexeur sur une entrée, en ajoutant deux portes NON dans la boucle pour régénérer le signal électrique.

La porte XOR en pass transistor logic
modifierIl est facile d'implémenter une porte XOR avec un multiplexeur 2 vers 1. Pour rappel, une porte XOR est une sorte d'inverseur commandable, à savoir un circuit prend un bit d'entrée A, et l'inverse ou non suivant la valeur d'un bit de commande B. Un tel circuit commandable n'est autre qu'une porte logique XOR, qui XOR A et B. Et cela nous dit comment implémenter une porte XOR avec un multiplexeur : il suffit de prendre un multiplexeur qui choisit sa sortie parmi deux entrées : A et ! Pour deux bits A et B, l'un est envoyé sur l'entrée de commande, l'autre bit est envoyée sur les deux entrées (le bit sur une entrée, son inverse sur l'autre). Le circuit obtenu, sans les portes NON, est celui-ci :

La version précédente est une porte XOR où les signaux d'entrée sont doublés : on a le bit d'entrée original, et son inverse. C'est quelque chose de fréquent dans les circuits en pass transistor logic, où les signaux/bits sont doublés. Mais il est possible de créer des versions normales, sans duplication des bits d'entrée. La solution la plus simple de rajouter deux portes NON, pour inverser les deux entrées. Le circuit passe donc de 4 à 8 transistors, ce qui reste peu. Mais on peut ruser, ce qui donne le circuit ci-dessous. Comme vous pouvez les voir, il mélange porte à transmission et portes NON CMOS normales.

Dans les deux cas, l'économie en transistors est drastique comparé au CMOS normal. Plus haut, nous avons illustré plusieurs versions possibles d'une porte XOR en CMOS normal, toutes de 12 transistors. Ici, on va de 6 transistors maximum, à seulement 4 ou 5 pour les versions plus simples. Le gain est clairement significatif, suffisamment pour que les circuits avec beaucoup de portes XOR gagnent à être implémentés avec la pass transistor logic.
Quelques processeurs implémentaient leurs portes XOR en pass transistor logic, alors que les autres portes étaient en CMOS normal. Un exemple est le mythique processeur Z80.
Les avantages et défauts de la pass transistor logic
modifierUne porte logique en logique CMOS connecte directement sa sortie sur la tension d'alimentation ou la masse. Mais dans une porte logique en pass transistor logic, il n'y a ni tension d'alimentation, ni masse (O Volts). La sortie d'une porte à transmission est alimentée par la tension d'entrée. Et vu que les transistors ne sont pas parfaits, on a toujours une petite perte de tension en sortie d'une porte à transmission.
Le résultat est que si on enchaine les portes à transmission, la tension de sortie a tendance à diminuer, et ce d'autant plus vite qu'on a enchainé de portes à transmission. Il faut souvent rajouter des portes OUI pour restaurer les tensions adéquates, à divers endroits du circuit. La pass transistor logic mélange donc porte OUI/NON CMOS normales avec des portes à transmission. Afin de faire des économies de circuit, on utilise parfois une seule porte NON CMOS comme amplificateur, ce qui fait que de nombreux signaux sont inversés dans les circuits, sans que cela ne change grand chose si le circuit est bien conçu.
Par contre, ce défaut entraine aussi des avantages. Notamment, la consommation d'énergie est fortement diminuée. Seules les portes amplificatrices, les portes NON CMOS, sont alimentées en tension/courant. Le reste des circuits n'est pas alimenté, car il n'y a pas de connexion à la tension d'alimentation et la masse. De même, la pass transistor logic utilise généralement moins de transistors pour implémenter une porte logique, et un circuit électronique en général. L'exemple avec la porte XOR est assez parlant : on passe de 12 à 6 transistors par porte XOR. Des circuits riches en portes XOR, comme les circuits additionneurs, gagnent beaucoup à utiliser des portes à transmission.
Les technologies PMOS et NMOS
modifierDans ce qui va suivre, nous allons voir la technologie NMOS et POMS. Pour simplifier, la technologie NMOS est équivalente aux circuits CMOS, sauf que les transistors PMOS sont remplacés par une résistance. Pareil avec la technologie PMOS, sauf que c'est les transistors NMOS qui sont remplacés par une résistance. Les deux technologies étaient utilisées avant l'invention de la technologie CMOS, quand on ne savait pas comment faire pour avoir à la fois des transistors PMOS et NMOS sur la même puce électronique, mais sont aujourd'hui révolues. Nous en parlons ici, car nous évoquerons quelques circuits en PMOS/NMOS dans le chapitre sur les cellules mémoire, mais vous pouvez considérer que cette section est facultative.
Le fonctionnement des logiques NMOS et PMOS
modifierAvec la technologie NMOS, les portes logiques sont fabriqués avec des transistors NMOS intercalés avec une résistance.

Leur fonctionnement est assez facile à expliquer. Quand la sortie doit être à 1, tous les transistors sont ouverts. La sortie est connectée à la tension d'alimentation et déconnectée de la masse, ce qui fait qu'elle est mise à 1. La résistance est là pour éviter que le courant qui arrive dans la sortie soit trop fort. Quand au moins un transistor NMOS qui se ferme, il connecte l'alimentation à la masse, les choses changent. Les lois compliquées de l'électricité nous disent alors que la sortie est connectée à la masse, elle est donc mise à 0.

Les circuits PMOS sont construits d'une manière assez similaire aux circuits CMOS, si ce n'est que les transistors NMOS sont remplacés par une résistance qui relie ici la masse à la sortie. Rien d'étonnant à cela, les deux types de transistors, PMOS et NMOS, ayant un fonctionnement inverse.
Les portes logiques en NMOS et PMOS
modifierQue ce soit en logique PMOS ou NMOS, les portes de base sont les portes NON, NAND et NOR. Les autres portes sont fabriquées en combinant des portes de base. Voici les circuits obtenus en NMOS et PMOS:
| NMOS | ||||
|---|---|---|---|---|

|

|
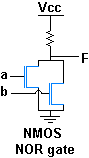
|

|

|
| PMOS | ||||

|

|

|
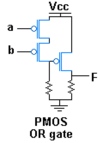
| |
Les portes logiques de base en NMOS
modifierLe circuit d'une porte NON en technologie NMOS est illustré ci-dessous. Le principe de ce circuit est similaire au CMOS, avec quelques petites différences. Si on envoie un 0 sur la grille du transistor, il s'ouvre et connecte la sortie à la tension d'alimentation à travers la résistance. À l'inverse, quand on met un 1 sur la grille, le transistor se ferme et la sortie est reliée à la masse, donc mise à 0. Le résultat est bien un circuit inverseur.

|
La porte NOR est similaire à la porte NON, si ce n'est qu'il y a maintenant deux transistors en parallèle. Si l'une des grilles est mise à 1, son transistor se fermera et la sortie sera mise à 0. Par contre, quand les deux entrées sont à 0, les transistors sont tous les deux ouverts, et la sortie est mise à 1. Le comportement obtenu est bien celui d'une porte NOR.

|

|
La porte NAND fonctionne sur un principe similaire au précédent, si ce n'est qu'il faut que les deux grilles soient à zéro pour obtenir une sortie à 1. Pour mettre la sortie à 0 quand seulement les deux transistors sont ouverts, il suffit de les mettre en série, comme dans le schéma ci-dessous. Le circuit obtenu est bien une porte NAND.
 |
 |
Les avantages et inconvénients des technologies CMOS, PMOS et NMOS
modifierLa technologie PMOS et NMOS ne sont pas totalement équivalentes, niveau performances. Ces technologies se distinguent sur plusieurs points : la vitesse des transistors et leur consommation énergétique.
La vitesse des circuits NMOS/PMOS/CMOS dépend des transistors eux-mêmes. Les transistors PMOS sont plus lents que les transistors NMOS, ce qui fait que les circuits NMOS sont plus rapides que les circuits PMOS. Les circuits CMOS ont une vitesse intermédiaire, car ils contiennent à la fois des transistors NMOS et PMOS.
Pour la consommation électrique, les résistances sont plus goumandes que les transistors. En PMOS et NMOS, la résistance est traversée par du courant en permanence, peu importe l'état des transistors. Et résistance traversée par du courant signifie consommation d'énergie, dissipée sous forme de chaleur par la résistance. Il s'agit d'une perte sèche d'énergie, une consommation d'énergie inutile. En CMOS, l'absence de résistance fait que la consommation d'énergie est liée aux transistors, et celle-ci est beaucoup plus faible que pour une résistance.
Les transistors PMOS sont plus simples à fabriquer que les NMOS, ils sont plus simples à sortir d'usine. Les premiers processeurs étaient fabriqués en logique PMOS, plus simple à fabriquer. Puis, une fois la fabrication des circuits NMOS maitrisée, les processeurs sont tous passés en logique NMOS du fait de sa rapidité. La logique CMOS a mis du temps à remplacer les logiques PMOS et NMOS, car il a fallu maitriser les techniques pour mettre à la fois des transistors NMOS et PMOS sur la même puce. Les premières puces électroniques étaient fabriquées en PMOS ou en NMOS, parce qu'on n’avait pas le choix. Mais une fois la technologie CMOS maitrisée, elle s'est imposée en raison de deux gros avantages : une meilleure fiabilité (une meilleure tolérance au bruit électrique), et une consommation électrique plus faible.
La logique dynamique MOS
modifierLa logique dynamique permet de créer des portes logiques ou des bascules d'une manière assez intéressante. Et aussi étonnant que cela puisse paraître, le signal d’horloge est alors utilisé pour fabriquer des circuits combinatoires !
Un transistor MOS peut servir de condensateur
modifierLes technologies CMOS conventionnelles mettent la sortie d'une porte logique à 0/1 en la connectant à la tension d'alimentation ou à la masse. La logique pass transistor transfère la tension et le courant de l'entrée vers la sortie. Dans les deux cas, la sortie est connectée directement ou indirectement à la tension d'alimentation quand on veut lui faire sortie un 1. Avec la logique dynamique, ce n'est pas le cas. La sortie est maintenue à 0 ou à 1 en utilisant un réservoir d'électron qui remplace la tension d'alimentation.
En électronique, il existe un composant qui sert de réservoir à électricité : il s'agit du condensateur. On peut le charger en électricité, ou le vider pour fournir un courant durant une petite durée de temps. Par convention, un condensateur stocke un 1 s'il est rempli, un 0 s'il est vide. L'intérieur d'un condensateur est formé de deux couches de métal conducteur, séparées par un isolant électrique. Les deux plaques de conducteur sont appelées les armatures du condensateur. C'est sur celles-ci que les charges électriques s'accumulent lors de la charge/décharge d'un condensateur. L'isolant empêche la fuite des charges d'une armature à l'autre, ce qui permet au condensateur de fonctionner comme un réservoir, et non comme un simple fil.
Il est possible de fabriquer un pseudo-condensateur avec un transistor MOS. En effet, tout transistor MOS a un pseudo-condensateur caché entre la grille et la liaison source-drain. Pour comprendre ce qui se passe dans ce transistor de mémorisation, il faut savoir ce qu'il y a dans un transistor CMOS. À l'intérieur, on trouve une plaque en métal appelée l'armature, un bout de semi-conducteur entre la source et le drain, et un morceau d'isolant entre les deux. L'ensemble forme donc un condensateur, certes imparfait, qui porte le nom de capacité parasite du transistor. Suivant la tension qu'on envoie sur la grille, l'armature va se remplir d’électrons ou se vider, ce qui permet de stocker un bit : une grille pleine compte pour un 1, une grille vide compte pour un 0.

L'utilisation de transistors MOS comme condensateur n'est pas spécifique à la logique dynamique. Certains mémoires RAM le font, comme nous le verrons dans le chapitre sur les cellules mémoires. Aussi, il est intéressant d'en parler maintenant, histoire de préparer le terrain. D'ailleurs, les mémoires RAM sont remplies de logique dynamique.
L'utilisation des pseudo-condensateurs en logique dynamique
modifierUn circuit conçu en logique dynamique contient un transistor est utilisé comme condensateur. Il s’insère entre la tension d'alimentation et la sortie du circuit. Son rôle est simple : lorsqu'on utilise la sortie, le condensateur se vide, ce qui place la sortie à 1. le reste du temps, le condensateur est relié à la tension d'alimentation et se charge. Un circuit en logique dynamique effectue son travail en deux phases : une phase d'inactivité où il remplit ses condensateurs, et une phase où sa sortie fonctionne. Les deux phases sont appelées la phase de précharge et la phase d'évaluation. La succession de ces deux phases est réalisée par le signal d'horloge : la première pahse a lieu quand le signal d'horloge est à 1, l'autre quand il est à 0.
Une porte NAND en logique dynamique CMOS
modifierVoici un exemple de porte NAND en logique dynamique MOS. La porte est alors réalisée avec des transistors NMOS et PMOS, le circuit ressemble à ce qu'on a en logique NMOS. En bas, on trouve les transistors NMOS pour relier la sortie au 0 volt. Mais au-dessus, on trouve un transistor CMOS qui remplace la résistance. Le fonctionnement du circuit est simple. Quand l'entrée clock est à 1, le condensateur se charge, les deux transistors NMOS sont déconnectés de la masse et le circuit est inactif. Puis, quand clock passe à 0, Le transistor PMOS se comporte en circuit ouvert, ce qui déconnecte la tension d'alimentation. Et son pseudo-condensateur se vide, ce qui fournit une tension d'alimentation de remplacement temporaire. Le transistor NMOS du bas se ferme, ce qui fait que les deux transistors A et B décident de si la sortie est connectée au 0 volt ou non. Si c'est le cas, le pseudo-condensateur se vide dans le 0 volt et la sortie est à 0. Sinon, le pseudo-condensateur se vide dans la sortie, ce qui la met à 1.

Une bascule D en logique dynamique CMOS
modifierIl est possible de créer une bascule D en utilisant la logique dynamique. L'idée est de prendre une bascule D normale, mais d'ajouter un fonctionnement en deux étapes en ajoutant des transistors/interrupteurs. Pour rappel, une bascule D normale est composée de deux inverseurs reliés l'un à l'autre en formant une boucle, avec un multiplexeur pour permettre les écritures dans la boucle.


Le circuit final ajoute deux transistors entre les inverseurs tête-bêche. Les transistors en question sont reliés à l'horloge, l'un étant ouvert quand l'autre est fermé. Grâce à eux, le bit mémorisé circule d'un inverseur à l'autre : il est dans le premier inverseur quand le signal d'horloge est à 1, dans l'autre inverseur quand il est à 0 (en fait son inverse, comme vous l'aurez compris). Le tout est illustré ci-contre. Cette implémentation a été utilisée autrefois, notamment dans le processeur Intel 8086.

Il existe une variante très utilisée, qui permet de remplacer le multiplexeur par un circuit légèrement plus simple. Avec elle, on a deux entrées pour commander la bascule, et non une seule entrée Enable. L'entrée Enable autorise les écriture, l'entrée Hold ferme la boucle qui relie la sortie du second inverseur au premier. Chaque entrée est associé à un transistor/interrupteur. Le transistor sur lequel on envoie l'entrée Enable se ferme uniquement lors des écritures et reste fermé sinon. A l'inverse, le transistor relié au signal Hold est fermé en permanence, sauf lors des écritures. En clair, les deux signaux sont l'inverse l'un de l'autre. Il permet de fermer le circuit, de bien relier les deux inverseurs en tête-bêche, sauf lors des écritures. On envoie donc l'inverse de l'entrée Enable sur ce transistor.

Une manière de comprendre le circuit précédent est de le comparer à celui avec le multiplexeur. Le multiplexeur est composé d'une porte NON et de deux transistors. Il se trouve que les deux transistors en question sont placés au même endroit que les transistors connectés aux signaux Hold et Enable. En prenant retirant la porte NON du multiplexeur, on se retrouve avec le circuit. Au lieu de prendre un Signal Enable qui commande les deux transistors, ce qui demande d'ajouter une porte NON vu que les deux transistors doivent faire l'inverse l'un de l'autre, on se contente d'envoyer deux signaux séparés pour commander chaque transistor indépendamment.
Avantages et inconvénients
modifierLes circuits en logique dynamique sont opposés aux circuits en logique statique, ces derniers étant les circuits CMOS, PMOS, NMOS ou TTL vu jusqu'à présent. Les circuits dynamiques et statiques ont des différences notables, ainsi que des avantages et inconvénients divers. Si on devait résumer :
- la logique dynamique utilise généralement un peu plus de transistors qu'un circuit CMOS normal ;
- la logique dynamique est souvent très rapide par rapport à la concurrence, car elle n'utilise que des transistors NMOS, plus rapides ;
- la consommation d'énergie est généralement supérieure comparé au CMOS.
Un désavantage de la logique dynamique est qu'elle utilise plus de transistors. On économise certes des transistors MOS, mais il faut rajouter les transistors pour déconnecter les transistors NMOS de la masse (0 volt). Le second surcompense le premier.
Un autre désavantage est que le signal d'horloge ne doit pas tomber en-dessous d'une fréquence minimale. Avec une logique statique, on a une fréquence maximale, mais pas de fréquence minimale. Avec un circuit statique peut réduire la fréquence d'un circuit pour économiser de l'énergie, pour améliorer sa stabilité, et de nombreux processeurs modernes ne s'en privent pas. On peut même stopper le signal d'horloge et figer le circuit, ce qui permet de le mettre en veille, d'en stopper le fonctionnement, etc. Impossible avec la logique dynamique, qui demande de ne pas tomber sous la fréquence minimale. Cela a un impact sur la consommation d'énergie, sans compter que cela se marie assez mal avec certaines applications. Un processeur moderne ne peut pas être totalement fabriqué en logique dynamique, car il a besoin d'être mis en veille et qu'il a besoin de varier sa fréquence en fonction des besoins.
La logique TTL : un apercu rapide
modifierTous ce que nous avons vu depuis le début de ce chapitre porte sur les transistors MOS et les technologies associées. Mais les transistors MOS n'ont pas été les premiers inventés. Ils ont été précédés par les transistors bipolaires. Nous ne parlerons pas en détail du fonctionnement d'un transistor bipolaire, car celui-ci est extraordinairement compliqué. Cependant, nous devons parler rapidement de la logique TTL, qui permet de fabriquer des portes logiques avec ces transistors bipolaires. Là encore, rassurez-vous, nous n'allons pas voir comment fabriquer des portes logiques en logique TTL, cela serait trop compliqué, sans compter que le but n'est pas de faire un cours d'électronique. Mais nous devons fait quelques remarques et donner quelques explications superficielles.
La raison à cela est double. La première raison est que certains circuits présents dans les mémoires RAM sont fabriqués avec des transistors bipolaires. C'est notamment le cas des amplificateurs de lecture ou d'autres circuits de ce genre. De tels circuits ne peuvent pas être implémentés facilement avec des transistors CMOS et nous expliquerons rapidement pourquoi dans ce qui suit. La seconde raison est que ce cours parlera occasionnellement de circuits anciens et qu'il faut quelques bases sur le TTL pour en parler.
Dans la suite du cours, nous verrons occasionnellement quelques circuits anciens, pour la raison suivante : ils sont très simples, très pédagogiques, et permettent d'expliquer simplement certains concepts du cours. Rien de mieux que d'étudier des circuits réels pour donner un peu de chair à des explications abstraites. Par exemple, pour expliquer comment fabriquer une unité logique de calcul bit à bit, je pourrais utiliser l'exemple du Motorola MC14500B, un processeur 1 bit qui est justement une unité logique sous stéroïdes. Ou encore, dans le chapitre sur les circuits additionneurs, je parlerais du circuit additionneur présent dans l'Intel 8008 et dans l'Intel 4004, les deux premiers microprocesseurs commerciaux. Malheureusement, malgré leurs aspects pédagogiques indéniables, ces circuits ont le défaut d'être des circuits TTL. Ce qui est intuitif : les circuits les plus simples ont été inventés en premier et utilisent du TTL plus ancien. Beaucoup de ces circuits ont été inventés avant même que le CMOS ou même les transistors MOS existent. D'où le fait que nous devons faire quelques explications mineures sur le TTL.
Les transistors bipolaires
modifierLes transistors bipolaires ressemblent beaucoup aux transistors MOS. Les transistors bipolaires ont trois broches, appelées le collecteur, la base et l'émetteur. Notez que ces trois termes sont différents de ceux utilisés pour les transistors MOS, où on parle de la grille, du drain et de la source.
Là encore, comme pour les transistors PMOS et NMOS, il existe deux types de transistors bipolaires : les NPN et les PNP. Là encore, il est possible de fabriquer une puce en utilisant seulement des NPN, seulement des PNP, ou en mixant les deux. Mais les ressemblances s'arrêtent là. La différence entre PNP et NPN tient dans la manière dont les courants entrent ou sortent du transistor. La flèche des symboles ci-dessous indique si le courant rentre ou sort par l'émetteur : il rentre pour un PNP, sort pour un NPN. Dans la suite du cours, nous n'utiliserons que des transistors NPN, les plus couramment utilisés.
 |
 |
Plus haut nous avons dit que les transistors CMOS sont des interrupteurs. La réalité est que tout transistor peut être utilisé de deux manières : soit comme interrupteur, soit comme amplificateur de tension/courant. Pour simplifier, le transistor bipolaire NPN prend en entrée un courant sur sa base et fournit un courant amplifié sur l'émetteur. Pour s'en servir comme amplificateur, il faut fournir une source de courant sur le collecteur. Le fonctionnement exact est cependant plus compliqué.

Les transistors bipolaires sont de bons amplificateurs, mais de piètres interrupteurs. A l'inverse, les transistors CMOS sont généralement de bons interrupteurs, mais de moyens amplificateurs. Pour des circuits numériques, la fonction d'interrupteur est clairement plus adaptée, car elle-même binaire (un transistor est fermé ou ouvert : deux choix possibles). Aussi, les circuits modernes privilégient des transistors CMOS aux transistors bipolaires. A l'inverse, la fonction d'amplification est adaptée aux circuits analogiques.
C'est pour ça que nous rencontrerons les transistors bipolaires soit dans des portions de l'ordinateur qui sont au contact de circuits analogiques. Pensez par exemple aux cartes sons ou au vieux écrans cathodiques, qui gèrent des signaux analogiques (le son pour la carte son, les signaux vidéo analogique pour les vieux écrans). On les croisera aussi dans les mémoires DRAM, dont la conception est un mix entre circuits analogiques et numériques. Nous les croiserons aussi dans de vieux circuits antérieurs aux transistors MOS. Les anciens circuits faisaient avec les transistors bipolaires car ils n'avaient pas le choix, mais ils ont été partiellement remplacés dès l'apparition des transistors CMOS.
Les portes logiques complexes en TTL
modifierLe détail le plus important qui nous concernera dans la suite du cours est le suivant : on peut créer des portes logiques exceptionnellement complexes en TTL. Pour comprendre pourquoi, sachez qu'il existe des transistors bipolaires qui possèdent plusieurs émetteurs. Ils sont très utilisés pour fabriquer des portes logiques à plusieurs entrées. Les émetteurs correspondent alors à des entrées de la porte logique. Ainsi, une porte logique à plusieurs entrées se fait non pas en ajoutant des transistors, comme c'est le cas avec les transistors MOS, mais en ajoutant un émetteur sur un transistor. Cela permet à une porte NAND à trois entrées de n'utiliser que deux transistors bipolaires, au lieu de quatre transistors MOS.

De plus, là où les logiques PMOS/NMOS/CMOS permettent de fabriquer les portes de base que nous avons précédemment, elles ne peuvent pas faire plus. Au pire, on peut implémenter des portes ET/OU/NAND/NOR à plusieurs entrées, mais pas plus. En TTL, on peut parfaitement créer des portes de type ET/OU/NON ou OU/ET/NON, avec seulement quatre transistors. Par exemple, une porte ET/OU/NON de type 2-2 entrées (pour rappel, qui effectue un ET par paire d’entrée puis fait un NOR entre le résultat des deux ET) est bien implémenté en une seule porte logique, pas en enchainant deux ou trois portes à la suite.

Les désavantages et avantages des circuits TTL
modifierPour résumer, le TTL à l'avantage de pouvoir fabriquer des portes logiques avec peu de transistors comparé au CMOS, surtout pour les portes logiques complexes. Et autant vous dire que les concepteurs de puce électroniques ne se gênaient pas pour utiliser ces portes complexes, capables de fusionner 3 à 5 portes en une seule : les économies de transistors étaient conséquentes.
Et pourtant, les circuits TTL étaient beaucoup plus gros que leurs équivalents CMOS. La raison est qu'un transistor bipolaire prend beaucoup de place : il est environ 10 fois plus gros qu'un transistor MOS. Autant dire que les économies réalisées avec des portes logiques complexes ne faisaient que compenser la taille énorme des transistors bipolaires. Et encore, cette compensation n'était que partielle, ce qui fait que les circuits PMOS/NMOS/CMOS se miniaturisent beaucoup plus facilement. Un avantage pour le transistor MOS !
De plus, les schémas précédents montrent que les portes logiques en TTL utilisent une résistance, elle aussi difficile à miniaturiser. Et cette résistance est parcourue en permanence par un courant, ce qui fait qu'elle consomme de l'énergie et chauffe. C'est la même chose en logique NMOS et PMOS, ce qui explique leur forte consommation d'énergie. Les circuits TTL ont donc le même problème.

Un autre défaut est lié à la une tension d'alimentation. Les circuits TTL utilisent une tension d'alimentation de 5 volts, alors que les circuits CMOS ont une tension d'alimentation beaucoup plus variable. Les circuits CMOS vont de 3 volts à 18 volts pour les circuits commerciaux, avec des tensions de 1 à 3 volts pour les circuits optimisés. Les circuits CMOS sont généralement bien optimisés et utilisent une tension d'alimentation plus basse que les circuits TTL, ce qui fait qu'ils consomment moins d'énergie et de courant.
De plus, rappelons que coder un zéro demande que la tension soit sous un seuil, alors que coder un 1 demande qu'elle dépasse un autre seuil, avec une petite marge de sécurité entre les deux. Les seuils en question sont indiqués dans le diagramme ci-dessous. Il s'agit des seuils VIH et VIL. On voit que sur les circuits TTL, la marge de sécurité est plus faible qu'avec les circuits CMOS. De plus, les marges sont bien équilibrées en CMOS, à savoir que la marge de sécurité est en plein milieu entre la tension max et le zéro volt. Avec le TTL normal, la marge de sécurité est très proche du zéro volt. Un 1 est codé par une tension entre 2 et 5 volts en TTL ! Une version améliorée du TTL, le LVTTL, corrige ce défaut. Elle baisse la tension d'alimentation à 3,3 Volts, mais elle demande des efforts de fabrication conséquents.

De nos jours, les portes logiques et/ou transistors sont rassemblés dans des circuits intégrés. Les circuits intégrés modernes regroupent un grand nombre de transistors qui sont reliés entre eux par des interconnexions métalliques. Par exemple, les derniers modèles de processeurs peuvent utiliser près d'un milliard de transistors. Cette orgie de transistors permet d'ajouter des fonctionnalités aux composants électroniques. C'est notamment ce qui permet aux processeurs récents d'intégrer plusieurs cœurs, une carte graphique, etc.
Les circuits intégrés : généralités
modifier
Les circuits intégrés se présentent le plus souvent sous la forme de boitiers rectangulaires, comme illustré ci-contre. D'autres ont des boitiers de forme carrées, comme ceux que l'on peut trouver sur les barrettes de mémoire RAM, ou à l'intérieur des clés USB/ disques SSD. Enfin, certains circuits intégrés un peu à part ont des formes bien différentes, comme les processeurs ou les mémoires RAM. Quoiqu'il en soit, il est intéressant de voir l'interface d'un circuit intégré et ce qu'il y a à l'intérieur.
L'interface d'un circuit intégré
modifierLes circuits intégrés ont, comme les portes logiques, des broches métalliques sur lesquelles on envoie des tensions. Quelques broches vont recevoir la tension d'alimentation (broche VCC), d'autres vont être reliées à la masse (broche GND), et surtout : les broches restantes vont porter des bits de données ou de contrôle. Ces dernières peuvent se classer en trois types : les entrées, sorties et entrée-sorties. Les entrées sont celles sur lesquelles on place des bits à envoyer au circuit imprimé, les sorties sont là où le circuit imprimé envoie des informations vers l'extérieur, les entrées-sorties servent alternativement de sortie ou d'entrée.
La plupart des circuits actuels, processeurs et mémoires, comprennent un grand nombre de broches : plusieurs centaines ! Si on prend l'exemple du processeur MC68000, un vieux processeur inventé en 1979 présent dans les calculatrices TI-89 et TI-92, celui-ci contient 68000 transistors (d'où son nom : MC68000). Il s'agit d'un vieux processeur complètement obsolète et particulièrement simple. Et pourtant, celui-ci contient pas mal de broches : 37 au total ! Pour comparer, sachez que les processeurs actuels utilisent entre 700 et 1300 broches d'entrée et de sortie. À ce jeu là, notre pauvre petit MC68000 passe pour un gringalet !
Pour être plus précis, le nombre de broches (entrées et sorties) d'un processeur dépend du socket de la carte mère. Par exemple, un socket LGA775 est conçu pour les processeurs comportant 775 broches d'entrée et de sortie, tandis qu'un socket AM2 est conçu pour des processeurs de 640 broches. Certains sockets peuvent carrément utiliser 2000 broches (c'est le cas du socket G34 utilisé pour certains processeurs AMD Opteron). Pour la mémoire, le nombre de broches dépend du format utilisé pour la barrette de mémoire (il existe trois formats différents), ainsi que du type de mémoire. Certaines mémoires obsolètes (les mémoires FPM-RAM et EDO-RAM) se contentaient de 30 broches, tandis que la mémoire DDR2 utilise entre 204 et 244 broches.
L'intérieur d'un circuit intégré et sa fabrication
modifierAprès avoir vu les boitiers d'un circuit imprimé et leurs broches, voyons maintenant ce qu'il y a dans le circuit imprimé. Si vous découpez le boitier d'un circuit imprimé, vous allez voir que le boitier en plastique entoure une sorte de carré/rectangle de couleur grisâtre, appelé le die du circuit imprimé, ou encore la puce électronique. Le die est un bloc de matériau semi-conducteur. C'est là où se trouvent les transistors et les interconnexions entre eux. Les broches métalliques sont connectées à des endroits bien précis du die. Le die est très petit, quelques millimètres de côté, guère plus. Il est très variable d'un circuit intégré à l'autre et il est difficile de faire des généralités dessus.


Les dies sont fabriqués à partir de silicium, à l'exception de quelques die fabriqués avec du gernanium, peu utilisés et encore en cours de recherche. Le silicium a des propriétés semiconductrices très intéressantes, qui font que c'est le matériau le plus utilisé dans l'industrie actuellement. La fabrication d'un circuit électronique moderne part d'un lingot de silicium pur, qui a une forme cylindrique. Un tel lingot est illustré ci-contre. Le lingot est découpé en tranches circulaires sur lesquelles on vient graver le die. Les tranches circulaires sont appelées des wafers.


Avant d'expliquer ce qui arrive aux wafers pour qu'on vienne graver des dies dessus, précisons que la forme des waffer n'est pas très compatible avec celle des dies. Un wafer est circulaire, un die est carré/rectangulaire. L’incompatibilité se manifeste sur les bords du wafer, qui sont gâchés car on ne peut pas y mettre de die, comme indiqué dans le schéma ci-contre. Il y a donc un léger gâchis en silicium, qu'il est préférable de réduire au plus possible.
De plus, les dies gravés ne sont pas tous fonctionnels. Il n'est pas rare que certains ne fonctionnent pas à cause d'un défaut de gravure. Il faut dire que graver des transistors de quelques nanomètres de diamètre est un procédé très compliqué qui ne peut pas marcher à tous les coups. Il suffit d'un grain de poussière mal placé pour qu'un die soit irrémédiablement perdu. Lors de la fabrication, il y a un certain pourcentage moyen de dies gravés sur un wafer qui sont défectueux. Le nombre de dies fonctionnels sur le nombre total de dies gravés est appelé le Yield. Idéalement, il faudrait que le yield soit le plus élevé possible.
Pour augmenter le yield et réduire les pertes aux bords du wafer, il y a une solution qui marche pour les deux problèmes : utiliser des dies très petits, le plus petit possible. Plus les dies sont petits, plus la perte sur les bords du wafer sera faible. Mais réduire le die signifie réduire la taille du circuit intégré, et donc son nombre de transistors. Il semblerait qu'il y a donc un compromis à faire : soit avoir des circuits bourrés de transistors mais avec un yield bas, ou avoir un yield élevé pour des circuits simples. Mais il y a une solution pour obtenir le meilleur des deux mondes.

Les chiplets et circuits imprimés en 3D
modifierIl existe des boitiers qui regroupent plusieurs boitiers et/ou plusieurs dies, plusieurs puces électroniques. Ils sont appelés des circuits intégrés Multi-chip Module (MCM). Les puces électroniques d'un MCM sont appelées des chiplets, pour les différencier des autres dies. L'idée est qu'il vaut mieux combiner plusieurs dies simples que d'utiliser un gros die bien complexe.

Les circuits imprimés en 3D sont une sous-classe de circuits imprimés MCM conçus en empilant plusieurs circuits plats l'un au-dessus de l'autre, dans le même boitier. Ils sont composés de plusieurs couches, chacune contenant des transistors MOS, empilées les unes au-dessus des autres. Les différentes couches sont connectées entre elles par des fils métalliques qui traversent les différentes couches, au nom à coucher dehors : Through-silicon via (TSV), Cu-Cu connections, etc. Le nom de la technique en anglais est 3DS die stacking.
Le 3DS die stacking regroupe un grand nombre de technologies différentes, qui partagent la même idée de base, mais dont l'implémentation est fortement différente. Mais les différences sont difficiles à expliquer ici, car la fabrication de circuits imprimés est un domaine complexe, faisant intervenir physique des matériaux et ingénierie.
Les avantages du 3DS die stacking est qu'on peut mettre plus de circuits dans un même boitier, en l'utilisant en hauteur plutôt qu'en largeur. Par contre, la dissipation de la chaleur est plus compliquée. Un circuit électronique chauffe beaucoup et il faut dissiper cette chaleur. L'idéal pour dissiper la chaleur est d'avoir une surface plane, avec un volume faible. Plus le rapport surface/volume d'un circuit à semi-conducteur est élevé, mieux c'est pour dissiper la chaleur, physique de la dissipation thermique oblige. Et empiler des couches augmente le volume sans trop augmenter la surface. D'où le fait que la gestion de la température est plus compliquée.
Le 3DS die stacking est surtout utilisé sur les mémoires, bien moins sur les autres types de circuits. Elle est surtout utilisée pour les mémoires FLASH, mais quelques mémoires RAM en utilisent. Pour les mémoires RAM proprement dit, deux standards incompatibles s'opposent. D'un côté la technologie High Bandwidth Memory, de l'autre la technologie Hybrid Memory Cube.

L'avantage de cette technique pour les mémoires est qu'elle permet une plus grande capacité, à savoir qu'elles ont plus de gibioctets. De plus, elle ne nuit pas aux performances de la mémoire. En effet, la performance des mémoires/circuits dépend un peu de la longueur des interconnexions : plus elles sont longues, plus le temps pour lire/écrire une donnée est important. Et il vaut mieux avoir de courtes interconnexions en hauteur, que de longues interconnexions sur une surface.
Il y a quelques processeurs dont la mémoire cache utilise le 3DS die stacking, on peut notamment citer les processeurs AMD de microarchitecture Zen 3, Zen 4 et Zen 5. Le premier processeur disposant d'une mémoire cache en 3D a été le R7 5800X3D. Il succédait aux anciens processeurs de microarchitecture Zen 3, qui disposaient d'un cache L3 de 32 mébioctets. Le 5800X3D ajoutait 64 mébioctets, ce qui fait au total 96 mébioctets de mémoire cache L3. Et surtout : la rapidité du cache était la même sur le 5800X3D et les anciens Zen 3. À peine quelques cycles d'horloge de plus pour un cache dont le temps d'accès se mesure en 50-100 cycles d'horloge.
La miniaturisation des circuits intégrés et la loi de Moore
modifierEn 1965, le cofondateur de la société Intel, spécialisée dans la conception de mémoires et de processeurs, a affirmé que la quantité de transistors présents dans un circuit intégré doublait tous les 18 mois : c'est la première loi de Moore. En 1975, il réévalua cette affirmation : ce n'est pas tous les 18 mois que le nombre de transistors d'un circuit intégré double, mais tous les 2 ans. Elle est respectée sur la plupart des circuits intégrés, mais surtout par les processeurs et les cartes graphiques, les mémoires RAM et ROM, bref : tout ce qui est majoritairement constitué de transistors.

La miniaturisation des transistors
modifierL'augmentation du nombre de transistors n'aurait pas été possible sans la miniaturisation, à savoir le fait de rendre les transistors plus petits. Il faut savoir que les circuits imprimés sont fabriqués à partir d'une plaque de silicium pur, un wafer, sur laquelle on vient graver le circuit imprimé. On ne peut pas empiler deux transistors l'un sur l'autre, du moins pas facilement. Il y a bien des technologiques pour faire ça, mais elles sont complexes et nous les omettons ici. Les transistors sont donc répartis sur une surface plane, qui a une forme approximativement rectangulaire et qui a une certaine aire. L'aire en question est la même pour tous les processeurs, qui font tous la même taille, leur circuits imprimés sont les mêmes.
Les transistors sont des structures en 3D, mais ils sont posés sur une surface en 2D. En clair, on n'empile pas les transistors les uns sur les autres, on les mets les uns à côté des autres. Leur épaisseur peut se réduire avec le temps, mais cela n'a pas d'importance pour la loi de Moore. Par contre, ils ont souvent une largeur et une longueur qui sont très proches, et qui diminuent avec l'évolution des technologies de fabrication. Pour simplifier, la taille des transistors est aussi appelée la finesse de gravure. Elle s'exprime le plus souvent en nanomètres.
Doubler le nombre de transistors signifie qu'on peut mettre deux fois plus de transistors sur une même surface. Pour le dire autrement, la surface occupée par un transistor a été divisée par deux. On s'attendrait à ce que leur taille soit divisée par deux tous les 2 ans, comme le dit la loi de Moore. Mais c’est là une erreur de raisonnement.
Rappelez-vous que la taille d'un processeur reste la même, ils gardent la même surface carrée d'un modèle à l'autre. Si on divise la taille des transistors par deux, l'aire prise par un transistor sur cette surface carrée sera divisée par 4, donc on pourra en mettre 4 fois plus. Incompatible avec la loi de Moore ! En réalité, diviser une surface carrée/rectangulaire par deux demande de diviser la largeur et la longueur par . Ainsi, la finesse de gravure est divisée par , environ 1,4, tous les deux ans. Une autre manière de le dire est que la finesse de gravure est multipliée par 0,7 tous les deux ans, soit une diminution de 30 % tous les deux ans. En clair, la taille des transistors décroit de manière exponentielle avec le temps !

La fin de la loi de Moore
modifierNéanmoins, la loi de Moore n'est pas vraiment une loi gravée dans le marbre. Si celle-ci a été respectée jusqu'à présent, c'est avant tout grâce aux efforts des fabricants de processeurs, qui ont tenté de la respecter pour des raisons commerciales. Vendre des processeurs toujours plus puissants, avec de plus en plus de transistors est en effet gage de progression technologique autant que de nouvelles ventes.
Il arrivera un moment où les transistors ne pourront plus être miniaturisés, et ce moment approche ! Quand on songe qu'en 2016 certains transistors ont une taille proche d'une vingtaine ou d'une trentaine d'atomes, on se doute que la loi de Moore n'en a plus pour très longtemps. Et la progression de la miniaturisation commence déjà à montrer des signes de faiblesses. Le 23 mars 2016, Intel a annoncé que pour ses prochains processeurs, le doublement du nombre de transistors n'aurait plus lieu tous les deux ans, mais tous les deux ans et demi. Cet acte de décès de la loi de Moore n'a semble-t-il pas fait grand bruit, et les conséquences ne se sont pas encore faites sentir dans l'industrie. Au niveau technique, on peut facilement prédire que la course au nombre de cœurs a ses jours comptés.
On estime que la limite en terme de finesse de gravure sera proche des 5 à 7 nanomètres : à cette échelle, le comportement des électrons suit les lois de la physique quantique et leur mouvement devient aléatoire, perturbant fortement le fonctionnement des transistors au point de les rendre inutilisables. Et cette limite est proche : des finesses de gravure de 10 nanomètres sont déjà disponibles chez certaines fondeurs comme TSMC. Autant dire que si la loi de Moore est respectée, la limite des 5 nanomètres sera atteinte dans quelques années, à peu-près vers l'année 2020. Ainsi, nous pourrons vivre la fin d'une ère technologique, et en voir les conséquences. Les conséquences économiques sur le secteur du matériel promettent d'être assez drastiques, que ce soit en terme de concurrence ou en terme de réduction de l'innovation.
Quant cette limite sera atteinte, l'industrie sera face à une impasse. Le nombre de cœurs ou la micro-architecture des processeurs ne pourra plus profiter d'une augmentation du nombre de transistors. Et les recherches en terme d'amélioration des micro-architectures de processeurs sont au point mort depuis quelques années. La majeure partie des optimisations matérielles récemment introduites dans les processeurs sont en effet connues depuis fort longtemps (par exemple, le premier processeur superscalaire à exécution dans le désordre date des années 1960), et ne sont améliorables qu'à la marge. Quelques équipes de recherche travaillent cependant sur des architectures capables de révolutionner l'informatique. Le calcul quantique ou les réseaux de neurones matériels sont une première piste, mais qui ne donneront certainement de résultats que dans des marchés de niche. Pas de quoi rendre un processeur de PC plus rapide.
L'invention du microprocesseur
modifierLe processeur est le circuit de l'ordinateur qui effectue des calculs sur des nombres codés en binaire, c’est la pièce maitresse de l'ordinateur. C'est un circuit assez complexe, qui utilise beaucoup de transistors. Avant les années 1970, il n'était pas possible de produire un processeur en un seul morceau. Impossible de mettre un processeur dans un seul boitier, les processeurs étaient fournis en pièces détachées qu'il fallait relier entre elles. Un exemple de processeur conçu en kit est la série des Intel 3000. Elle regroupe plusieurs circuits séparés : l'Intel 3001 est le séquenceur, l'Intel 3002 est le chemin de données (ALU et registres), le 3003 est un circuit d'anticipation de retenue censé être combiné avec l'ALU, le 3212 est une mémoire tampon, le 3214 est une unité de gestion des interruptions, les 3216/3226 sont des interfaces de bus mémoire. On pourrait aussi citer la famille de circuits intégrés AMD Am2900.
L'intel 4004 : le premier microprocesseur
modifierPar la suite, les progrès de la miniaturisation ont permis de mettre un processeur entier dans un seul circuit intégré. C'est ainsi que sont nés les microprocesseurs, à savoir des processeurs qui tiennent tout entier sur une seule puce de silicium. Les tout premiers microprocesseurs étaient des processeurs à application militaire, comme le processeur du F-14 CADC ou celui de l'Air data computer.
Le tout premier microprocesseur commercialisé au grand public est le 4004 d'Intel, sorti en 1971. L'intel 4004 comprenait environ 2300 transistors, avait une fréquence de 740 MHz, pouvait faire 46 opérations différentes, et manipulait des entiers de 4 bits. De plus, le processeur manipulait des entiers en BCD, ce qui fait qu'il pouvait manipuler un chiffre BCD à la fois (un chiffre BCD est codé sur 4 bits). Il était au départ un processeur de commande, prévu pour être intégré dans la calculatrice Busicom calculator 141-P, mais il fut utilisé pour d'autres applications quelque temps plus tard. Son successeur, l'Intel 4040, garda ces caractéristiques et n'apportait que quelques améliorations mineures : plus de registres, plus d'opérations, etc.
Le 4004 était commercialisé dans un boitier DIP simple, fort différent des boitiers et sockets des processeurs actuels. Le boitier du 4004 avait seulement 16 broches, ce qui était permis par le fait qu'il s'agissait d'un processeur 4 bits. On trouve 4 broches pour échanger des données avec le reste de l'ordinateur, 5 broches pour communiquer avec la mémoire (4 broches d'adresse, une pour indiquer s'il faut faire une lecture ou écriture), le reste est composé de broches pour la tension d'alimentation VDD, la masse VSS et pour le signal d'horloge (celui qui décide de la fréquence).
 |
 |
Immédiatement après le 4004, les premiers microprocesseurs 8 bits furent commercialisés. Le 4004 fut suivi par le 8008 et quelques autres processeurs 8 bits extrêmement connus, comme le 8080 d'Intel, le 68000 de Motorola, le 6502 ou le Z80. Ces processeurs utilisaient là encore des boitiers similaires au 4004, mais avec plus de broches, vu qu'ils étaient passés de 4 à 8 bits. Par exemple, le 8008 utilisait 18 broches, le 8080 était une version améliorée du 8008 avec 40 broches. Le 8086 fut le premier processeur 16 bits.
Le passage des boitiers aux slots et sockets
modifierLa forme des processeurs a changé au cours du temps. Ils sont devenus plats et carrés. Les raisons qui expliquent la forme des boitiers des processeurs actuels sont assez nombreuses. La première est que les techniques de fabrications des puces électroniques actuelles font qu'il est plus simple d'avoir un circuit planaire, relativement peu épais. De plus, la forme carrée s'explique par la fabrication des puces de silicium, où un cristal de silicium est coupé en tranches, elles-mêmes découpées en puces carrées identiques, ce qui facilite la conception. Un autre avantage de cette forme est que la dissipation de la chaleur est meilleure. Les processeurs actuels sont devenus plus puissants que ceux d'antan, mais au prix d'une dissipation thermique augmentée. Dissiper cette chaleur est devenu un vrai défi sur les processeurs actuels, et la forme des microprocesseurs actuels aide à cela, couplé à des radiateurs et ventilateurs.
Un autre changement tient dans la manière dont le processeur est relié à la carte mère. Les premiers processeurs 8 et 16 bits étaient soudés à la carte mère. Les retirer demandait de les dé-souder, ce qui n'était pas très pratique, mais ne posait pas vraiment de problèmes à l'époque. Il faut noter que certains processeurs assez anciens étaient placés sur des cartes intégrées, elles-mêmes connectées à la carte mère par un slot d'extension, similaire à celui des cartes graphiques.


De nos jours, les processeurs n'utilisent plus les boitiers soudés d'antan. Les processeurs sont clipsés dans un connecteur spécial sur la carte mère, appelé le socket. Grâce à ce système, il est plus simple d'ajouter ou de retirer un processeur de la carte mère. L'upgrade d'un processeur est ainsi fortement facilitée. Les broches sont composées de billes ou de pins métalliques qui font contact avec le connecteur.
 |
 |
L'invention des processeurs multicœurs
modifierAvec l'avancée des processus de fabrication, il est devenu possible de mettre plusieurs processeurs sur une même puce de silicium, et c'est ainsi que sont nés les processeurs multicœurs. Pour simplifier, les processeurs multicœurs regroupent plusieurs processeurs, soit sur une même puce de silicium, soit dans un même boitier. Les processeurs en question sont appelés des cœurs. Il arrive donc qu'un processeur multicœurs ait en réalité 8 cœurs/processeurs sur la même puce, ou 4, ou 2, parfois 16, 32, 64, rarement plus. Les processeurs multicœurs contenant 2 processeurs sont aujourd'hui obsolète, la norme est entre 4 et 16.
Les fabricants ont généralement plusieurs modèles d'un même processeur : un modèle entrée de gamme peu cher et peu performant, un modèle haut de gamme très cher et performant, et un modèle milieu de gamme aux prix et performances entre les deux précédents. Et ces trois modèles n'ont pas le même nombre de cœurs. Et bien sachez qu'en réalité, tous ces processeurs sortent de la même usine et sont fabriqués de la même manière, avec le même nombre de cœurs. Par exemple, imaginez qu'un modèle entrée de gamme ait 4 cœurs , le milieu de gamme 8 cœurs, et le haut de gamme en ait 16. Et bien ils sont fabriqués à partir d'un modèle haut de gamme à 16 cœurs, dont on désactive certains cœurs pour obtenir les modèles bas et milieu de gamme.
Après leur fabrication, les processeurs subissent des tests pour vérifier si le processeur fonctionne normalement. Et il arrive qu'un cœur soit défectueux et ne fonctionne pas, mais que les autres fonctionnent parfaitement. Par exemple, si on prend un processeur à 8 cœurs , il se peut que deux d'entre eux ne fonctionne pas et les 6 autres soient fonctionnels. Dans ce cas, on en fait un modèle milieu ou entrée de gamme en désactivant les cœurs défectueux. La désactivation est généralement matérielle, en coupant des fils pour déconnecter les cœurs défectueux.
La révolution des chiplets
modifierLes processeurs multicœurs modernes utilisent la technique des chiplets. Pour donner un exemple, prenons celui du processeur POWER 5, autrefois utilisé sur d'anciens ordinateurs Macintosh. Chaque coeur avait son propre boitier rien que pour lui. Il en a existé deux versions. La première était dite double cœur, à savoir qu'elle intégrait deux processeurs dans la même puce. Le seconde version étiat quadruple coeur, avec 4 processeurs dans un même boitier, avec 4 dies. La dernière version est illustrée ci-dessous. On voit qu'il y a quatre boitier rouges, un par coeur, et quatre autres en vert qui correspondent à de la mémoire cache (le cache L3).

Un autre exemple est celui des processeurs AMD récents, d'architectures Zen 2/3/4/5. Ils incorporent deux puces dans le même boitier : une puce qui contient les processeurs, les cœurs, et une autre pour les interconnexions avec le reste de l'ordinateur. La puce pour les interconnexions gère l'interface avec la mémoire RAM, les bus PCI-Express pour la carte graphique, et quelques autres. Les deux puces n'ont pas la même finesse de gravure, ni les mêmes performances.

Certains processeurs AMD Epyc avaient plusieurs chiplets pour les processeurs/coeurs, combinés avec un chiplet pour les interconnexions. L'image ci-dessous montre un processeur AMD Epyc 7702, avec un chiplet central pour les interconnexions, et les chiplets autour qui contiennent chacun 4 cœurs.


La conception d'un circuit intégré
modifier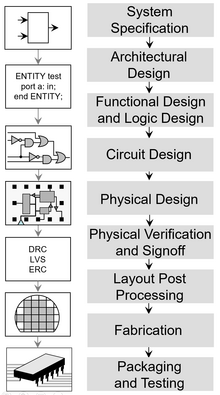
La conception d'un circuit intégré se fait en une série d'étapes assez complexes, dont certaines sont aidées par ordinateur. Inutile de voir dire que concevoir un circuit intégré est généralement assez complexe et demande des compétences très variées. Concevoir une puce électronique doit se faire à plusieurs niveaux d'abstraction, que nous allons détailler dans ce qui suit. Nous allons grandement simplifier le tout en donnant une description assez sommaire.
La conception logique
modifierLa première étape est de créer une sorte de cahier des charge, de spécification qui décrit comment fonctionne le circuit. La spécification décrit son architecture externe, à savoir comment le circuit se comporte. Elle décrit comment le circuit réagit quand on envoie telle donnée sur telle entrée, qu'est-ce qu'on retrouve sur ses sorties si... , etc. Pour un circuit combinatoire, cela revient à écrire sa table de vérité. Mais il va de soit que pour des circuits complexes, la spécification est beaucoup plus complexe.
La seconde étape est d'implémenter le circuit en utilisant les circuits de base, à savoir les circuits vus dans les chapitres précédents. Le circuit intégré est conçu en combinant registres, bascules, portes logiques, décodeurs, multiplexeurs, additionneurs et autres circuits basiques. La conception se fait en utilisant un langage de description matérielle, qui a des ressemblances superficielles avec un langage de programmation.
Le résultat est une description du circuit assez haut niveau, appelée le Register-transfer level (RTL), qui combine registres, portes logiques et autres circuits combinatoires basiques. Les circuits de base utilisés lors de cette étape sont appelés des cellules standard. La RTL ressemble aux schémas vus dans les chapitres précédents, et ce n'est pas un hasard : de tels schémas sont des RTL simples de circuits eux-mêmes simples.
La conception physique
modifier
La troisième étape traduit la RTL en un plan à appliquer sur le die physique, à graver dessus. Elle traduit les portes logiques en montages à base de transistors, comme vu dans le chapitre précédents. Les autres cellules standards sont elles aussi directement traduites en un montage à base de transistors, conçu à l'avance par des ingénieurs spécialisé, qui est potentiellement optimisé qu'un montage à base de portes logiques.
Les cellules sont placées sur la puce par un algorithme, qui cherche à optimiser l'usage du die. Les interconnexions métalliques entre transistors sont ajoutées, de même que le signal d'horloge, la masse et la tension d'alimentation. L'arbre d'horloge est généré à cette étape, de même que l'arbre qui transmet la tension d'alimentation aux portes logiques. Le résultat est une sorte de description physique du die.

Les circuits intégrés sont connectés au monde extérieur, par l'intermédiaire de leurs broches. Broches qui peuvent servir d'entrée ou de sortie. Nous allons étudier les sorties des circuits intégrés, car il y a des choses importantes à dire dessus. Dans ce chapitre, nous allons voir qu'il existe trois types de sorties différentes. L'intérêt est qu'interconnecter des circuits intégrés entre eux demande de savoir comment ces sorties fonctionnent. Nous détaillerons les interconnexions dans les chapitres sur les bus et les liaisons point à point, où les acquis du présent chapitre seront réutilisés. De plus, la section sur le OU câblé à la fin du chapitre sera utile dans le chapitre sur les mémoires ROM.
Les trois types de sorties : totem-pole, trois états et à drain ouvert
modifierLes sorties des circuits intégrés peuvent se classer en plusieurs types, selon leur fonctionnement. Pour les sorties basées sur des transistors, on distingue principalement les sorties totem-pole, les sorties à drain ouvert et les sorties trois-état. Et les trois donnent des bus très différents.
Les sorties totem-pole sont les plus communes pour les circuits CMOS. Ce sont des sorties qui sont connectées à deux transistors : un qui relie la sortie à la masse, et un autre qui la relie à la tension d'alimentation. En technologie CMOS, elles sont équivalentes à des sorties connectées à une porte logique. Elles sont toujours connectées soit à la masse, soit à la tension d'alimentation.
Les sorties trois-état peuvent prendre trois états, comme leur nom l'indique. Soit elles sont connectées à la masse, soit elles sont reliées à la tension d'alimentation, soit elles ne sont connectées ni à l'une ni à l'autre. Si les deux premiers cas correspondent à un 0 et à un 1, l'état déconnecté ne correspond à aucun des deux. Il s'agit d'un état utilisé quand on souhaite déconnecter ou connecter à la demande certains composants dans un circuit.

Les sorties à drain/collecteur ouvert sont soit connectées à la masse, soit connectées à rien. La sortie peut être mise à 0 par le circuit intégré, mais elle ne peut pas être mise à 1 sans intervention extérieure. Pour utiliser une sortie à drain ouvert, il faut relier la sortie à la tension d'alimentation à travers une résistance, appelée résistance de rappel. Il existe aussi une variante, où la sortie peut être mise à 1 par le circuit intégré, ou être déconnectée, mais ne peut pas être mise à 0 sans intervention extérieure. Ici on connecte la sortie à la masse, et non à la tension d'alimentation.

Les sorties à drain ouvert et les sorties trois-états sont très utilisés quand il s'agit de connecter plusieurs circuits intégrés entre eux. Vous comprendrez en quoi ces sorties sont utiles quand nous parlerons des mémoires et des bus de communication, et nous en reparlerons longuement dans le chapitre sur les bus électroniques. Nous verrons que de nombreux bus exigent que les circuits branchés dessus aient des entrées-sorties trois-états, ou en drain/collecteur ouvert.
Transformer une sortie totem-pole en sortie trois états
modifierIl est possible de fabriquer une sortie trois-états à partir d'une sortie totem-pole normale. Pour cela, il faut placer une porte logique modifiée juste avant la sortie totem-pole. Cette porte logique est une porte OUI améliorée appelée tampon trois-état. Elle possède une entrée de donnée, une entrée de commande, et une sortie : suivant ce qui est mis sur l'entrée de commande, la sortie est soit en état de haute impédance (déconnectée du bus), soit dans l'état normal (0 ou 1).
| Commande | Entrée | Sortie |
|---|---|---|
| 0 | 0 | Haute impédance/Déconnexion |
| 0 | 1 | Haute impédance/Déconnexion |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Pour simplifier, on peut voir ceux-ci comme des interrupteurs :
- si on envoie un 0 sur l'entrée de commande, ces circuits trois états se comportent comme un interrupteur ouvert ;
- si on envoie un 1 sur l'entrée de commande, ces circuits trois états se comportent comme une porte OUI.

Les tampons trois-états ressemblent aux portes à transmission, à un détail près : ce sont des composants actifs, qui régénèrent le signal d'entrée. Là où les portes à transmission sont électriquement équivalentes à un interrupteur, ce n'est pas le cas des tampons trois-états. Les tampons trois-états sont reliés à la tension d'alimentation et à la masse, ils amplifient un peu le signal d'entrée si besoin.
Un tampon trois-état est parfois implémenté avec le circuit ci-dessous. Son fonctionnement est simple à expliquer. Si le bit de commande vaut 0, la sortie des deux portes vaut 0 et les deux transistors sont ouverts. Si le bit de commande vaut 1, les deux sorties des portes ET sont l'inverse l'une de l'autre. Si le bit d'entrée est à 1, le transistor du haut se ferme et met un 1 en sortie, alors que le transistor du bas s'ouvre. Si le bit d'entrée est à 0, c'est l'inverse, la sortie est reliée à la masse et sort un 0. Si le bit de commande est à 0, la sortie des deux portes sort un 0, les deux transistors se ferment.

Transformer une sortie totem-pole en sortie à collecteur ouvert
modifierIl est possible de fabriquer une sortie à collecteur ouvert à partir d'une sortie totem-pole normale. Pour cela, il faut placer un transistor en aval de la sortie normale. Les sorties à drain ouvert utilisent un transistor MOS, les sorties à collecteur ouvert utilisent un transistor bipolaire au lieu d'un transistor MOS. Le tout est illustré ci-dessous.
La sortie est mise à 0 ou 1 selon que le transistor est ouvert ou fermé. Si le transistor est ouvert, la sortie est connectée à la tension d'alimentation, ce qui fait que la sortie est à 1. Si le transistor est fermé, la tension d'alimentation est reliée à la masse, la tension d'alimentation est alors aux bornes de la résistance, et la sortie est donc au niveau de la masse : elle est à 0.

Pour la variante où la sortie est soit à 1 ou déconnectée, on peut procéder de la même manière, en plaçant un transistor en aval de la sortie. Mais il est aussi possible d'utiliser un autre composant que le transistor : une diode. Une diode est un composant qui ne laisse passer le courant que dans un sens : de l'entrée vers la sortie, mais pas dans l'autre sens. La diode est dite bloquée quand elle ne laisse pas passer le courant, passante quand le courant passe. La diode est passante si on met une tension suffisante sur l'entrée, bloquée sinon. En clair, la diode recopie un 1 présenté sur l'entrée, mais déconnecte la sortie quand on présente un 0 sur l'entrée.
Le ET câblé et le OU câblé avec des sorties à drain ouvert
modifierLes sorties à drain ouvert ont une particularité assez sympathique, qui permet d'implémenter une porte ET simplement en croisant des fils. Il suffit de connecter ces sorties au même fil et de relier celui-ci à la tension d'alimentation à travers une résistance. On obtient alors un ET câblé, qui fait un ET entre plusieurs sorties d'un circuit intégré. Il est illustré ci-dessous.
La tension d'alimentation est reliée au fil à travers une résistance, ce qui permet d'imposer un 1 sur la sortie, à condition que les sorties en collecteur ouvert soient coopératives. Si toutes les sorties sont à 1, elles sont déconnectées, et la sortie est connectée à la résistance de rappel : le circuit sort un 1. Par contre, si une seule sortie sort un 0, elle connectera la tension d'alimentation à la masse et mettra la sortie à 0. C'est le comportement attendu d'une porte ET.

Pour comprendre comment cela fonctionne, rappelons qu'une sortie en collecteur ouvert est connectée à un transistor relié à la masse. En explicitant ce transistor dans les schémas du dessus, on obtient le schéma ci-dessous. Vous remarquerez qu'il ressemble très fortement au schéma d'une porte logique NOR en technologie NMOS, même le transistor NMOS est remplacé par un transistor bipolaire.

Le OU câblé fonctionne sur le même principe, avec cependant deux grosses différences. Premièrement, les sorties en collecteur ouvert doivent soit imposer un 1 sur la sortie, soit la déconnecter. C'est le fonctionnement inverse à celui vu précédemment. Deuxièmement, la résistance est reliée à la masse, ce qui permet d'imposer un 0 sur la sortie si les sorties en collecteur ouvert soient coopératives. Si toutes les sorties sont à 0, elles sont déconnectées, et la sortie est connectée à masse à travers la résistance de rappel : le circuit sort un 0. Par contre, si une seule sortie sort un 1, elle impose le 1 sur la sortie. C'est le comportement attendu d'un OU.

En théorie, beaucoup de circuits peuvent se simplifier en utilisant des OU/ET câblés. C'en est au point où de nombreux circuits que nous allons voir dans la suite de ce cours pourraient se simplifier grâce à ces montages. Mais ils sont peu utilisés en pratique, surtout sur les circuits CMOS.
Les multiplexeurs fabriqués avec un OU câblé
modifierUn exemple d'utilisation est la fabrication de multiplexeurs. Pour rappel, un multiplexeur est composé d'un décodeur combiné à une couche de portes ET suivies par une porte OU à plusieurs entrées.


Sur les vieux circuits et avec les vielles technologies de fabrication, il était intéressant de remplacer la porte OU finale par une porte OU câblée. Utiliser un ou câblé permettait aussi de remplacer les portes ET par des portes à transmission, plus simples.
Un OU câblé peut se faire de plusieurs manières, mais la plus commune demande que les sorties des portes logiques ET soient de type collecteur ouvert, à savoir qu'elles fournissent seulement un 1, et déconnectent leur sortie quand elles doivent sortir un 0 (ou inversement). De plus, il faut relier le fil soit à la masse (à la tension d'alimentation) à travers une résistance. Le circuit illustré ci-dessous utilise une méthode similaire. Le OU câblé est en réalité un circuit équivalent à une porte NAND réalisée avec un ET câblé. Le ET câblé est plus simple à fabriquer, mais le circuit utilise une porte logique en plus.
L'architecture d'un ordinateur
modifierDans les chapitres précédents, nous avons vu comment représenter de l'information, la traiter et la mémoriser avec des circuits. Mais un ordinateur n'est pas qu'un amoncellement de circuits et est organisé d'une manière bien précise. Il est structuré autour de trois circuits principaux :
- les entrées/sorties, qui permettent à l'ordinateur de communiquer avec l'extérieur ;
- une mémoire qui mémorise les données à manipuler ;
- un processeur, qui manipule l'information et donne un résultat.

Pour faire simple, le processeur est un circuit qui s'occupe de faire des calculs et de traiter des informations. La mémoire s'occupe purement de la mémorisation des informations. Les entrées-sorties permettent au processeur et à la mémoire de communiquer avec l'extérieur et d'échanger des informations avec des périphériques. Tout ce qui n'appartient pas à la liste du dessus est obligatoirement connecté sur les ports d'entrée-sortie et est appelé périphérique. Ces composants communiquent via un bus, un ensemble de fils électriques qui relie les différents éléments d'un ordinateur.

La mémoire
modifierLa mémoire est le composant qui mémorise des informations, des données. Dans la majorité des cas, la mémoire est découpée en plusieurs bytes, des blocs de mémoire qui contiennent chacun un nombre fini et constant de bits. Le plus souvent, ces bytes sont composés de plusieurs groupes de 8 bits, appelés des octets. Mais certaines mémoires assez anciennes utilisaient des cases mémoires contenant 1, 2, 3, 4, 7, 18, 36 bits. Si les notions de byte et d'octet sont très différentes, la confusion est souvent faite et elle le sera dans ce cours.
La capacité mémoire
modifierBien évidemment, une mémoire ne peut stocker qu'une quantité finie de données. Et à ce petit jeu, certaines mémoires s'en sortent mieux que d'autres et peuvent stocker beaucoup plus de données que les autres. La capacité d'une mémoire correspond à la quantité d'informations que celle-ci peut mémoriser. Plus précisément, il s'agit du nombre maximal de bits qu'une mémoire peut contenir.
Le fait que les mémoires aient presque toutes des bytes faisant un ou plusieurs octets nous arrange pour compter la capacité d'une mémoire. Au lieu de compter cette capacité en bits, on préfère mesurer la capacité d'une mémoire en donnant le nombre d'octets que celle-ci peut contenir. Mais les mémoires des PC font plusieurs millions ou milliards d'octets. Pour se faciliter la tâche, on utilise des préfixes pour désigner les différentes capacités mémoires. Vous connaissez sûrement ces préfixes : kibioctets, mébioctets et gibioctets, notés respectivement Kio, Mio et Gio.
| Préfixe | Capacité mémoire en octets | Puissance de deux |
|---|---|---|
| Kio | 1024 | 210 octets |
| Mio | 1 048 576 | 220 octets |
| Gio | 1 073 741 824 | 230 octets |
On peut se demander pourquoi utiliser des puissances de 1024, et ne pas utiliser des puissances un peu plus communes ? Dans la majorité des situations, les électroniciens préfèrent manipuler des puissances de deux pour se faciliter la vie. Par convention, on utilise souvent des puissances de 1024, qui est la puissance de deux la plus proche de 1000. Or, dans le langage courant, kilo, méga et giga sont des multiples de 1000. Quand vous vous pesez sur votre balance et que celle-ci vous indique 58 kilogrammes, cela veut dire que vous pesez 58 000 grammes. De même, un kilomètre est égal à 1000 mètres, et non 1024 mètres.
Autrefois, on utilisait les termes kilo, méga et giga à la place de nos kibi, mebi et gibi, par abus de langage. Mais peu de personnes sont au courant de l'existence de ces nouvelles unités, et celles-ci sont rarement utilisées. Et cette confusion permet aux fabricants de disques durs de nous « arnaquer » : Ceux-ci donnent la capacité des disques durs qu'ils vendent en kilo, mega ou giga octets : l’acheteur croit implicitement avoir une capacité exprimée en kibi, mebi ou gibi octets, et se retrouve avec un disque dur qui contient moins de mémoire que prévu.
Lecture et écriture : mémoires ROM et RWM
modifierPour simplifier grandement, on peut grossièrement classer les mémoires en deux types : les Read Only Memory et les Read Write Memory, aussi appelées mémoires ROM et mémoires RWM. Pour les mémoires ROM, on ne peut pas modifier leur contenu. On peut y récupérer une donnée ou une instruction : on dit qu'on y accède en lecture. Mais on ne peut pas modifier les données qu'elles contiennent. Quant aux mémoires RWM, on peut y accéder en lecture (récupérer une donnée stockée en mémoire), mais aussi en écriture : on peut stocker une donnée dans la mémoire, ou modifier une donnée existante. Tout ordinateur contient au moins une mémoire ROM et une mémoire RWM (souvent une RAM). La mémoire ROM stocke un programme, alors que la mémoire RWM sert essentiellement pour maintenir des résultats de calculs.
Tout ordinateur contient au minimum une ROM et une RWM (souvent une mémoire RAM), les deux n'ont pas exactement le même rôle. Idéalement, les mémoires ROM stockent des programmes à exécuter et sont lues directement par le processeur. La mémoire ROM stocke aussi les constantes, à savoir des données qui peuvent être lues mais ne sont jamais accédées en écriture durant l'exécution du programme. Elles ne sont donc jamais modifiées et gardent la même valeur quoi qu'il se passe lors de l'exécution du programme.
Pour les mémoires RWM, nous allons nous concentrer sur une mémoire électronique appelée la mémoire RAM. Il s'agit d'une mémoire qui stocke temporairement des données que le processeur doit manipuler (on dit qu'elle est volatile). Elle sert donc essentiellement pour maintenir des résultats de calculs, contenir temporairement des programmes à exécuter, etc. Elle est censée mémoriser des données temporaires, nécessaires pour que le programme en mémoire ROM fonctionne. Elle mémorise alors les variables du programme à exécuter, qui sont des données que le programme va manipuler. Pour les systèmes les plus simples, la mémoire RWM ne sert à rien de plus.

L'adressage
modifierSur une mémoire RAM ou ROM, on ne peut lire ou écrire qu'un byte, qu'un registre à la fois : une lecture ou écriture ne peut lire ou modifier qu'un seul byte. Techniquement, le processeur doit préciser à quel byte il veut accéder à chaque lecture/écriture. Pour cela, chaque byte se voit attribuer un nombre binaire unique, l'adresse, qui va permettre de le sélectionner et de l'identifier celle-ci parmi toutes les autres. En fait, on peut comparer une adresse à un numéro de téléphone (ou à une adresse d'appartement) : chacun de vos correspondants a un numéro de téléphone et vous savez que pour appeler telle personne, vous devez composer tel numéro. Les adresses mémoires en sont l'équivalent pour les bytes.
Une autre explication est que l'adresse donne la position dans la mémoire d'une donnée.

Il existe des mémoires qui ne fonctionnent pas sur ce principe, mais passons : ce sera pour la suite.
Le processeur
modifierDans les ordinateurs, l'unité de traitement porte le nom de processeur, ou encore de Central Processing Unit, abrévié en CPU. Un processeur est un circuit qui s'occupe de faire des calculs et de manipuler l'information provenant des entrées-sorties ou récupérée dans la mémoire. Tout ordinateur contient au moins un processeur. Je dis au moins un, car un ordinateur peut avoir plusieurs processeurs.
Le processeur effectue des instructions, dont des calculs
modifierTout processeur est conçu pour effectuer un nombre limité d'opérations bien précises, comme des calculs, des échanges de données avec la mémoire, etc. Ces opérations sont appelées des instructions. Elles se classent en quelques grands types très simples. Les instructions arithmétiques font des calculs, comme l'addition, la soustractions, la multiplication, la division. Les instructions de test comparent deux nombres entre eux et agissent en fonction. Les instructions d'accès mémoire échangent des données entre la mémoire et le processeur. Et il y en d'autres.
L'important est de retenir qu'un processeur fait beaucoup de calculs. La plupart des processeurs actuels supportent au minimum l'addition, la soustraction et la multiplication. Quelques processeurs ne gèrent pas la division, qui est une opération très gourmande en circuit, peu utilisée, très lente. Il arrive que des processeurs très peu performants ne gèrent pas la multiplication, mais c'est assez rare. Les autres instructions ne sont pas très intuitives, aussi passons-les sous silence pour le moment, nous n'aurons besoin de les comprendre que dans la section du cours sur le processeur.
Un processeur contient des registres et communique avec la mémoire
modifierUn processeur contient des circuits de calcul, des circuits annexes pour gérer les instructions, mais aussi des registres. Pour rappel, ce sont de petites mémoires très rapides et de faible capacité, capables de mémoriser un nombre, ou du moins une petite suite de quelques bits. Tout processeur contient des registres pour fonctionner, leur utilité dépendant du registre considéré. Les registres du processeur peuvent servir à plein de choses : stocker des données afin de les manipuler plus facilement, stocker l'adresse de la prochaine instruction, stocker l'adresse d'une donnée à aller chercher en mémoire, etc.
Les registres les plus simples à comprendre contiennent les opérandes et les résultats des opérations de calcul, appelons-les registres de données. La capacité des registres de données dépend fortement du processeur, et elle détermine la taille des données manipulée par le processeur. Par exemple, un processeur avec des registres de données de 8 bits ne peut pas gérer des données plus grandes qu'un octet, sauf en trichant de manière logicielle. De même, un processeur ayant des registres de 32 bits ne peut pas gérer des opérandes de plus de 32 bits, idem pour les résultats ce qui fait que les débordements d'entiers apparaissent quand un résultat dépasse les 32 bits.
Au tout début de l'informatique, il n'était pas rare de voir des registres de 3, 4, voire 8 bits. Par la suite, la taille de ces registres a augmenté, passant rapidement de 16 à 32 bits, voire 48 bits sur certaines processeurs spécialisés. De nos jours, les processeurs des PC utilisent des registres de 64 bits, même s'il existe toujours des processeurs de faible performance avec des registres relativement petits, de 8 à 16 bits.
Notons qu'un processeur incorpore souvent des instructions pour copier des données provenant de la mémoire RAM dans un registre, et des instructions qui font l'inverse (d'un registre vers la mémoire). Sans cela, les registres seraient un peu difficiles à utiliser. Les instructions en question sont appelées LOAD (copie RAM vers registre) et STORE (copie registre vers RAM). Les échanges de données entre RAM et registres sont fréquents, les instructions LOAD et STORE sont tout aussi importante que les instructions de calcul. Tout cela pour dire qu'il ne faut pas confondre instruction avec opération mathématique, la notion d'instruction est plus large. Mais cela sera certainement plus claire quand on verra l'ensemble des instructions que peut gérer un processeur, dans un chapitre dédié.
Mais les registres de données ce ne sont pas les seuls. Pour pouvoir fonctionner, tout processeur doit mémoriser un certain nombre d’informations nécessaires à son fonctionnement : il faut qu'il se souvienne à quel instruction du programme il en est, qu'il connaisse la position en mémoire des données à manipuler, etc. Et ces informations sont mémorisées dans des registres spécialisés, appelés des registres de contrôle.
La plupart ont des noms assez barbares (registre d'état, program counter) et nous ne pouvons pas en parler à ce moment du cours car nous n'en savons pas assez sur le fonctionnement d'un processeur pour expliquer à quoi ils servent. Il y a cependant une exception, un registre particulier présent sur presque tous les ordinateurs existants au monde, qu'il est important de voir maintenant : le program counter.
Le processeur exécute un programme, une suite d'opérations
modifierTout processeur est conçu pour exécuter une suite d'instructions dans l'ordre demandé, cette suite s'appelant un programme. Ce que fait le processeur est défini par la suite d'instructions qu'il exécute, par le programme qu'on lui demande de faire. La totalité des logiciels présents sur un ordinateur sont des programmes comme les autres. Un programme est stocké dans la mémoire de l'ordinateur, comme les données : sous la forme de suites de bits. C'est ainsi que l'ordinateur est rendu programmable : modifier le contenu de la mémoire permet de changer le programme exécuté. Mine de rien, cette idée de stocker le programme en mémoire est ce qui a fait que l’informatique est ce qu'elle est aujourd’hui. C'est la définition même d'ordinateur : appareil programmable qui stocke son programme dans une mémoire modifiable.
Les instructions sont exécutées dans un ordre bien précis, les unes après les autres. L'ordre en question est décidé par le programmeur. Sur la grosse majorité des ordinateurs, les instructions sont placées les unes à la suite des autres dans l'ordre où elles doivent être exécutées. Un programme informatique n'est donc qu'une vulgaire suite d'instructions stockée quelque part dans la mémoire de l'ordinateur.
| Adresse | Instruction |
|---|---|
| 0 | Copier le contenu de l'adresse 0F05 dans le registre numéro 5 |
| 1 | Charger le contenu de l'adresse 0555 dans le registre numéro 4 |
| 2 | Additionner ces deux nombres |
| 3 | Charger le contenu de l'adresse 0555 |
| 4 | Faire en XOR avec le résultat antérieur |
| ... | ... |
| 5464 | Instruction d'arrêt |
Pour exécuter une suite d'instructions dans le bon ordre, le processeur détermine à chaque cycle quelle est la prochaine instruction à exécuter. Le processeur mémorise l'adresse de la prochaine instruction dans un registre spécialisé appelé Program Counter. Cette adresse qui permet de localiser la prochaine instruction en mémoire. Cette adresse ne sort pas de nulle part : on peut la déduire de l'adresse de l'instruction en cours d’exécution assez simplement. Il suffit de prendre l'adresse de l'instruction en cours, et en ajoutant la longueur de l'instruction (le nombre de case mémoire qu'elle occupe). En clair, il suffit d'incrémenter le program counter de la longueur de l'instruction.
Mais sur d'autres processeurs, chaque instruction précise l'adresse de la suivante. Ces processeurs n'ont pas besoin de calculer une adresse qui leur est fournie sur un plateau d'argent. Sur de tels processeurs, chaque instruction précise quelle est la prochaine instruction, directement dans la suite de bit représentant l'instruction en mémoire. Sur des processeurs aussi bizarres, pas besoin de stocker les instructions en mémoire dans l'ordre dans lesquelles elles sont censées être exécutées. Mais ces processeurs sont très très rares et peuvent être considérés comme des exceptions à la règle.
Un ordinateur peut avoir plusieurs processeurs
modifierLa plupart des ordinateurs n'ont qu'un seul processeur, ce qui fait qu'on désigne avec le terme d'ordinateurs mono-processeur. Mais il a existé (et existe encore) des ordinateurs multi-processeurs, avec plusieurs processeurs sur la même carte mère. L'idée était de gagner en performance : deux processeurs permettent de faire deux fois plus de calcul qu'un seul, quatre permettent d'en faire quatre fois plus, etc. C'est très courant sur les supercalculateurs, des ordinateurs très puissants conçus pour du calcul industriel ou scientifique, mais aussi sur les serveurs ! Dans le cas le plus courant, ils utilisent plusieurs processeurs identiques : on utilise deux processeurs Core i3 de même modèle, ou quatre Pentium 3, etc.
Pour utiliser plusieurs processeurs, les programmes doivent être adaptés. Pour cela, il y a plusieurs possibilités :
- Une première possibilité, assez intuitive, est d’exécuter des programmes différents sur des processeurs différents. Par exemple, on exécute le navigateur web sur un processeur, le lecteur vidéo sur un autre, etc.
- La seconde option est de créer des programmes spéciaux, qui utilisent plusieurs processeurs. Ils répartissent les calculs à faire sur les différents processeurs. Un exemple est la lecture d'une vidéo sur le web : un processeur peut télécharger la vidéo pendant le visionnage et bufferiser celle-ci, un autre processeur peut décoder la vidéo, un autre décoder l'audio. De tels programmes restent des suites d'instructions, mais ils sont plus complexes que les programmes normaux, aussi nous les passons sous silence.
- La troisième option est d’exécuter le même programme sur les différents processeurs, mais chaque processeur traite son propre ensemble de données. Par exemple, pour un programme de rendu 3D, quatre processeurs peuvent s'occuper chacun d'une portion de l'image.

De nos jours, les ordinateurs grand public les plus utilisés sont dans un cas intermédiaire, ils ne sont ni mono-, ni multi-processeur. Ils n'ont qu'un seul processeur, dans le sens où si on ouvre l'ordinateur et qu'on regarde la carte mère, il n'y a qu'un seul processeur. Mais ce processeur est en réalité assez similaire à un regroupement de plusieurs processeurs dans le même boitier. Il s'agit de processeurs multicœurs, qui contiennent plusieurs cœurs, chaque cœur pouvant exécuter un programme tout seul.
La différence entre cœur et processeur est assez difficile à saisir, mais pour simplifier : un cœur est l'ensemble des circuits nécessaires pour exécuter un programme. Chaque cœur dispose de toute la machinerie électronique pour exécuter un programme, à savoir des circuits aux noms barbares comme : un séquenceur d'instruction, des registres, une unité de calcul. Par contre, certains circuits d'un processeur ne sont présents qu'en un seul exemplaire dans un processeur multicœur, comme les circuits de communication avec la mémoire ou les circuits d’interfaçage avec la carte mère.
Suivant le nombre de cœurs présents dans notre processeur, celui-ci sera appelé un processeur double-cœur (deux cœurs), quadruple-cœur (4 cœurs), octuple-cœur (8 cœurs), etc. Un processeur double-cœur est équivalent à avoir deux processeurs dans l'ordinateur, un processeur quadruple-cœur est équivalent à avoir quatre processeurs dans l'ordinateur, etc. Ces processeurs sont devenus la norme dans les ordinateurs grand public et les logiciels et systèmes d'exploitation se sont adaptés.
Les coprocesseurs
modifierQuelques ordinateurs assez anciens disposaient de coprocesseurs, des processeurs qui complémentaient un processeur principal. Les ordinateurs de ce type avaient un processeur principal, le CPU, qui était secondé par un ou plusieurs coprocesseurs. En théorie, le coprocesseur exécute des calculs que le CPU n'est pas capable de faire. Il y a cependant quelques exceptions, où les coprocesseurs effectuent des calculs que le CPU est capable de faire. Mais passons cela sous silence pour le moment et voyons à quoi peuvent servir ces coprocesseurs.
Les coprocesseurs arithmétiques sont de loin les plus simples à comprendre. Ils permettent de faire certains calculs que le processeur ne peut pas faire. Les plus connus d'entre eux étaient utilisés pour implémenter les calculs en virgule flottante; à une époque où les CPU de l'époque ne géraient que des calculs entiers (en binaire ou en BCD). Sans ce coprocesseur, les calculs flottants étaient émulés en logiciel, par des fonctions et libraires spécialisées, très lentes. Un exemple est le coprocesseur flottant x87, complémentaire des premiers processeurs Intel x86. Il y a eu la même chose sur les processeurs Motorola 68000, avec deux coprocesseurs flottants appelés les Motorola 68881 et les Motorola 68882. Certaines applications conçues pour le coprocesseur étaient capables d'en tirer profit : des logiciels de conception assistée par ordinateur, par exemple. Ils sont aujourd'hui tombés en désuétude, depuis que les CPU sont devenus capables de faire des calculs sur des nombres flottants.
Un autre exemple de coprocesseur est celui utilisé sur la console de jeu Nintendo DS. La console utilisait deux processeurs, un ARM9 et un ARM7, qui ne pouvaient pas faire de division entière. Il s'agit pourtant d'opérations importantes dans le cas du rendu 3D, ce qui fait que les concepteurs de la console ont rajouté un coprocesseur spécialisé dans les divisions entières et les racines carrées. Le coprocesseur était adressable directement par le processeur, comme peuvent l'être la RAM ou les périphériques.
Les coprocesseurs les plus connus, au-delà des coprocesseurs arithmétiques, sont les coprocesseurs pour le rendu 2D/3D et les coprocesseurs sonores. Ils ont eu leur heure de gloire sur les anciennes consoles de jeux vidéo, comme La Nintendo 64, la Playstation et autres consoles de cette génération ou antérieure. Pour donner un exemple, on peut citer la console Neo-géo, qui disposait de deux processeurs travaillant en parallèle : un processeur principal, et un co-processeur sonore. Le processeur principa était un Motorola 68000, alors que le co-processeur sonore était un processeur Z80.
Enfin, il faut aussi citer les coprocesseurs pour l'accès aux périphériques. L'accès aux périphériques est quelque chose sur lequel nous passerons plusieurs chapitres dans ce cours. Mais sachez que l'accès aux périphériques peut demander pas mal de puissance de calculs. Le CPU principal peut faire ce genre de calculs par lui-même, mais il n'est pas rare qu'un coprocesseur soit dédié à l'accès aux périphériques.
Un exemple assez récent est celui, là encore, de la Nintendo 3DS. Elle disposait d'un processeur principal de type ARM9, du coprocesseur pour les divisions, et d'un second processeur ARM7. L'ARM 7 était le seul à communiquer avec les périphériques et les entrées-sorties. Il était utilisé presque exclusivement pour cela, ainsi que pour l'émulation de la console GBA. Il est donc utilisé comme coprocesseur d'I/O, mais n'est pas que ça.

Maintenant que nous venons de voir différents types de coprocesseurs, passons maintenant aux généralités sur ceux-ci. Le CPU peut soit exécuter des programmes en parallèle du coprocesseur, soit se mettre en pause en attendant que le coprocesseur finisse son travail. Dans l'exemple des coprocesseurs arithmétiques, le processeur principal passe la main au coprocesseur et attend sagement qu'i finisse son travail. Les deux processeurs se passent donc la main pour exécuter un programme unique. On parle alors de coprocesseurs fortement couplés. Pour les autres coprocesseurs, le CPU et le coprocesseur travaillent en parallèle et exécutent des programmes différents. On a un programme qui s’exécute sur le coprocesseur, un autre qui s’exécute sur le CPU. On parle alors de coprocesseurs faiblement couplés. C'est le cas pour les coprocesseurs d'accès au périphérique, pour ceux de rendu 2D/3D, etc.
Dans les deux cas, les programmes doivent être codés de manière à tirer parti du coprocesseur. Sans aide de la part du logiciel, le coprocesseur est inutilisable. Et c'est un défaut qui a été responsable de la disparition des coprocesseurs dans les ordinateurs grand public. La présence du coprocesseur étant optionnelle, les programmeurs devaient en tenir compte. La solution la plus simple était de fournir deux versions du logiciel : une sans usage du coprocesseur, et une autre qui en fait usage, plus rapide. Une autre solution est de recourir à l'émulation logicielle des instructions du coprocesseur en son absence. Dans les deux cas, c'était beaucoup de complications pour pas grand-chose. Aussi, les fonctions des coprocesseurs ont aujourd'hui été intégrées dans les processeurs modernes, ce qui les rendait redondants.
À l'inverse, le hardware d'une console est toujours le même d'un modèle à l'autre, contrairement à la forte variabilité des composants sur PC. Les programmeurs n'hésitaient pas à utiliser le coprocesseur, qui était là avec certitude, ils n'avaient pas à créer deux versions de leurs jeux vidéo, ni à émuler un coprocesseur absent, etc. Ajoutons que les concepteurs de consoles n'hésitent pas à utiliser des processeurs grand public dans leurs consoles, quitte à les compléter par des coprocesseurs. Au lieu de créer un processeur sur mesure, autant prendre un processeur déjà existant et le compléter avec un coprocesseur pour être plus puissant que la concurrence. Ce qui explique que les coprocesseurs graphiques et sonores ont eu leur heure de gloire sur les anciennes consoles de jeux vidéo.
Les entrées-sorties
modifierTous les circuits vus précédemment sont des circuits qui se chargent de traiter des données codées en binaire. Ceci dit, les données ne sortent pas de n'importe où : l'ordinateur contient des composants électroniques qui se chargent de traduire des informations venant de l’extérieur en nombres. Ces composants sont ce qu'on appelle des entrées. Par exemple, le clavier est une entrée : l'électronique du clavier attribue un nombre entier (scancode) à une touche, nombre qui sera communiqué à l’ordinateur lors de l'appui d'une touche. Pareil pour la souris : quand vous bougez la souris, celle-ci envoie des informations sur la position ou le mouvement du curseur, informations qui sont codées sous la forme de nombres. La carte son évoquée il y a quelques chapitres est bien sûr une entrée : elle est capable d'enregistrer un son, et de le restituer sous la forme de nombres.
S’il y a des entrées, on trouve aussi des sorties, des composants électroniques qui transforment des nombres présents dans l'ordinateur en quelque chose d'utile. Ces sorties effectuent la traduction inverse de celle faite par les entrées : si les entrées convertissent une information en nombre, les sorties font l'inverse : là où les entrées encodent, les sorties décodent. Par exemple, un écran LCD est un circuit de sortie : il reçoit des informations, et les transforme en image affichée à l'écran. Même chose pour une imprimante : elle reçoit des documents texte encodés sous forme de nombres, et permet de les imprimer sur du papier. Et la carte son est aussi une sortie, vu qu'elle transforme les sons d'un fichier audio en tensions destinées à un haut-parleur : c'est à la fois une entrée, et une sortie.
Dans ce qui va suivre, nous allons parfois parler de périphériques au lieu d'entrées-sorties. Les deux termes ne sont pas synonymes. En théorie, les périphériques, sont les composants connectés sur l'unité centrale. Exemple : les claviers, souris, webcam, imprimantes, écrans, clés USB, disques durs externes, les câbles Ethernet de la Box internet, etc. les entrées-sorties incluent les périphériques, mais aussi d'autres composants comme les cartes d'extensions ou des composants installés sur la carte mère. Les cartes d'extension sont les composants qui se connectent sur la carte mère via un connecteur, comme les cartes son ou les cartes graphiques. D'autres composants sont soudés à la carte mère mais sont techniquement des entrées-sorties : les cartes sons soudées sur les cartes mères actuelles, par exemple. Mais par simplicité, nous parlerons de périphériques au lieu d'entrées-sorties.
L'interface avec le reste de l'ordinateur
modifierLes entrées-sorties sont très diverses, fonctionnent très différemment les unes des autres. Mais du point de vue du reste de l'ordinateur, les choses sont relativement standardisées. Du point de vue du processeur, les entrées-sorties sont juste des paquets de registres ! Tous les périphériques, toutes les entrées-sorties contiennent des registres d’interfaçage, qui permettent de faire l'intermédiaire entre le périphérique et le reste de l'ordinateur. Le périphérique est conçu pour réagir automatiquement quand on écrit dans ces registres.

Les registres d’interfaçage sont assez variés. Les plus évidents sont les registres de données, qui permettent l'échange de données entre le processeur et les périphériques. Pour échanger des données avec le périphérique, le processeur a juste à lire ou écrire dans ces registres de données. On trouve généralement un registre de lecture et un registre d'écriture, mais il se peut que les deux soient fusionnés en un seul registre d’interfaçage de données. Si le processeur veut envoyer une donnée à un périphérique, il a juste à écrire dans ces registres. Inversement, s'il veut lire une donnée, il a juste à lire le registre adéquat.
Mais le processeur ne fait pas que transmettre des données au périphérique. Le processeur lui envoie aussi des « commandes », des valeurs numériques auxquelles le périphérique répond en effectuant un ensemble d'actions préprogrammées. En clair, ce sont l'équivalent des instructions du processeur, mais pour le périphérique. Par exemple, les commandes envoyées à une carte graphique peuvent être : affiche l'image présente à cette adresse mémoire, calcule le rendu 3D à partir des données présentes dans ta mémoire, etc. Pour recevoir les commandes, le périphérique contient des registres de commande qui mémorisent les commandes envoyées par le processeur. Quand le processeur veut envoyer une commande au périphérique, il écrit la commande en question dans ce ou ces registres.
Enfin, beaucoup de périphériques ont un registre d'état, lisible par le processeur, qui contient des informations sur l'état du périphérique. Ils servent notamment à indiquer au processeur que le périphérique est disponible, qu'il est en train d’exécuter une commande, qu'il est occupé, qu'il y a un problème, qu'il y a une erreur de configuration, etc.
Les adresses des registres d’interfaçage
modifierLes registres des périphériques sont identifiés par des adresses mémoires. Et les adresses sont conçues de façon à ce que les adresses des différents périphériques ne se marchent pas sur les pieds. Chaque périphérique, chaque registre, chaque contrôleur a sa propre adresse. D'ordinaire, certains bits de l'adresse indiquent quel contrôleur de périphérique est le destinataire, d'autres indiquent quel est le périphérique de destination, les restants indiquant le registre de destination.
Il existe deux organisations possible pour les adresses des registres d’interfaçages. La première possibilité est de séparer les adresses pour les registres d’interfaçage et les adresses pour la mémoire. Le processeur doit avoir des instructions séparées pour gérer les périphériques et adresser la mémoire. Il a des instructions de lecture/écriture pour lire/écrire en mémoire, et d'autres pour lire/écrire les registres d’interfaçage. Sans cela, le processeur ne saurait pas si une adresse est destinée à un périphérique ou à la mémoire.

L'autre méthode mélange les adresses mémoire et des entrées-sorties. Si on prend par exemple un processeur de 16 bits, où les adresses font 16 bits, alors les 65536 adresses possibles seront découpées en deux portions : une partie ira adresser la RAM/ROM, l'autre les périphériques. On parle alors d'entrées-sorties mappées en mémoire. L'avantage est que le processeur n'a pas besoin d'avoir des instructions séparées pour les deux.

Le pilote de périphérique
modifierUtiliser un périphérique se résume donc à lire ou écrire les valeurs adéquates dans les registres d’interfaçage. Les registres en question ont une adresse, similaire à l'adresse mémoire des RAM/ROM. Les adresses en question ne sont pas forcément mélangées, la relation entre adresses mémoire et adresses de périphériques est compliquée et sera vue dans la suite du chapitre. Communiquer avec un périphérique est similaire à ce qu'on a avec les mémoires, c'est simple : lire ou écrire dans des registres.
Le problème est que le système d'exploitation ne connaît pas toujours le fonctionnement d'un périphérique : il faut installer un programme qui va s'exécuter quand on souhaite communiquer avec le périphérique, et qui s'occupera de tout ce qui est nécessaire pour le transfert des données, l'adressage du périphérique, etc. Ce petit programme est appelé un driver ou pilote de périphérique. La « programmation » périphérique est très simple : il suffit de savoir quoi mettre dans les registres, et c'est le pilote qui s'en charge.
Le bus de communication
modifierLe processeur est relié à la mémoire ainsi qu'aux entrées-sorties par un ou plusieurs bus de communication. Ce bus n'est rien d'autre qu'un ensemble de fils électriques sur lesquels on envoie des zéros ou des uns. Tout ordinateur contient au moins un bus, qui relie le processeur, la mémoire, les entrées et les sorties ; et leur permet d’échanger des données ou des instructions.
Les bus d'adresse, de données et de commande
modifierPour permettre au processeur (ou aux périphériques) de communiquer avec la mémoire, il y a trois prérequis qu'un bus doit respecter : pouvoir sélectionner la case mémoire (ou l'entrée-sortie) dont on a besoin, préciser à la mémoire s'il s'agit d'une lecture ou d'une écriture, et enfin pouvoir transférer la donnée. Pour cela, on doit donc avoir trois bus spécialisés, bien distincts, qu'on nommera le bus de commande, le bus d'adresse, et le bus de donnée.
- Le bus de données est un ensemble de fils par lequel s'échangent les données entre les composants.
- Le bus de commande permet au processeur de configurer la mémoire et les entrées-sorties.
- Le bus d'adresse, facultatif, permet au processeur de sélectionner l'entrée, la sortie ou la portion de mémoire avec qui il veut échanger des données.
Chaque composant possède des entrées séparées pour le bus d'adresse, le bus de commande et le bus de données. Par exemple, une mémoire RAM possédera des entrées sur lesquelles brancher le bus d'adresse, d'autres sur lesquelles brancher le bus de commande, et des broches d'entrée-sortie pour le bus de données.

Tous les ordinateurs ne sont pas organisés de la même manière, pour ce qui est de leurs bus. Dans les grandes lignes, on peut distinguer deux possibilités : soit l'ordinateur a un seul bus, soit il en a plusieurs.
Les bus systèmes
modifierSi l'ordinateur dispose d'un bus unique, celui-ci est appelé le bus système, aussi appelé backplane bus. Il s'agissait de l'organisation utilisée sur les tout premiers ordinateurs, pour sa simplicité. Elle était parfaitement adaptée aux anciens composants, qui allaient tous à la même vitesse. De nos jours, les ordinateurs à haute performance ne l'utilisent plus trop, mais elle est encore utilisée sur certains systèmes embarqués, en informatique industrielle dans des systèmes très peu puissants.

De tels bus avaient pour avantage que la communication entre composant était simple. Le processeur peut communiquer directement avec la mémoire et les périphériques, les périphériques peuvent communiquer avec la mémoire, etc. Il n'y a pas de limitations quant aux échanges de données.
Un autre avantage est que le processeur ne doit gérer qu'un seul bus, ce qui utilise peu de broches. Le fait de partager le bus entre mémoire et entrées-sorties fait qu'on économise des fils, des broches sur le processeur, et d'autres ressources. Le câblage est plus simple, la fabrication aussi. Et cela a d'autres avantages, notamment au niveau du processeur, qui n'a pas besoin de gérer deux bus séparés, mais un seul.
Mais ils ont aussi des désavantages. Par exemple, il faut gérer les accès au bus de manière à ce que le processeur et les entrées-sorties ne se marchent pas sur les pieds, en essayant d'utiliser le bus en même temps. De tels conflits d'accès au bus système sont fréquents et ils réduisent la performance, comme on le verra dans le chapitre sur les bus. De plus, un bus système a le fâcheux désavantage de relier des composants allant à des vitesses très différentes : il arrivait fréquemment qu'un composant rapide doive attendre qu'un composant lent libère le bus. Le processeur était le composant le plus touché par ces temps d'attente.
Un bus système contient un bus d'adresse, de données et de commande. Le bus d'adresse ne sert pas que pour l'accès à la mémoire RAM/ROM, mais aussi pour l'accès aux entrées-sorties. En théorie, un bus système se marie bien avec des entrées-sorties mappées en mémoire. Il y a moyen d'implémenter un système d'adresse séparés avec, mais c'est pas l'idéal.

Les bus spécialisés
modifierPour éliminer ces problèmes, beaucoup d'ordinateurs disposent de plusieurs bus, plus ou moins spécialisés. Nous verrons des exemples de tels systèmes à la fin du chapitre. Pour le moment, citons un exemple assez courant : le cas où on a un bus séparé pour la mémoire, et un autre séparé pour les entrées-sorties. Le bus spécialisé pour la mémoire est appelé le bus mémoire, l'autre bus n'a pas de nom précis, mais nous l’appellerons le bus d'entrées-sorties. Une telle organisation implique d'avoir des adresses séparées pour les registres d’interfaçage et la mémoire. Pas d'entrée-sortie mappée en mémoire !

Les avantages de tels bus sont nombreux. Par exemple, le processeur peut accéder à la mémoire pendant qu'il attend qu'un périphérique lui réponde sans trop de problèmes. De plus, l'on a pas à gérer les conflits d'accès au bus entre la mémoire et les périphériques. Mais surtout, les bus peuvent être adaptés et simplifiés. Par exemple, le bus pour les entrées-sorties peut se passer de bus d'adresse, avoir un bus de commande différent de celui de la mémoire, avoir des bus de données de taille différentes, etc. Il est ainsi possible d'avoir un bus mémoire capable de lire/écrire 16 bits à la fois, alors que la communication avec les entrées-sorties se fait octet par octet ! Plutôt que d'avoir un seul bus qui s'adapte aux mémoires et entrées-sorties, on a des bus spécialisés.
L'avantage principal de cette adaptation est que la mémoire et les périphériques ne vont pas à la même vitesse du tout. Il est alors possible d'avoir un bus mémoire ultra-rapide et qui fonctionne à haute fréquence, pendant que le bus pour les entrées-sorties est un bus plus simple, moins rapide. Au lieu d'avoir un bus système moyen en vitesse, on a deux bus qui vont chacun à la vitesse adéquate.
Mais il y a d'autres défauts. Par exemple, il faut câbler deux bus distincts sur le processeur. Le nombre de broches nécessaires augmente drastiquement. Et cela peut poser problème si le processeur n'a pas beaucoup de broches à la base. Aussi, les processeurs avec peu de broches utilisent de préférence un bus système, plus simple à câbler, bien que moins performant. Un autre problème est que les entrées-sorties ne peuvent pas communiquer avec la mémoire directement, elles doivent passer par l'intermédiaire du processeur. De tels échanges ne sont pas forcément nécessaires, mais les performances s'en ressentent s’ils le sont.
Les bus avec répartiteur
modifierIl existe une méthode intermédiaire, qui garde deux bus séparés pour la mémoire et les entrées-sorties, mais élimine les problèmes de brochage sur le processeur. L'idée est d'intercaler, entre le processeur et les deux bus, un circuit répartiteur. Il récupère tous les accès et distribue ceux-ci soit sur le bus mémoire, soit sur le bus des périphériques. Le ou les répartiteurs s'appellent aussi le chipset de la carte mère.
C'était ce qui était fait à l'époque des premiers Pentium. À l'époque, la puce de gestion du bus PCI faisait office de répartiteur. Elle mémorisait des plages mémoires entières, certaines étant attribuées à la RAM, les autres aux périphériques mappés en mémoire. Elles utilisaient ces plages pour faire la répartition.

Niveau adresses des registres d'interfacage, il est possible d'avoir soit des adresses unifiées avec les adresses mémoire, soit des adresses séparées.
Les architectures Harvard et Von Neumann
modifierUn point important d'un ordinateur est la séparation entre données et instructions. Dans ce qui va suivre, nous allons faire la distinction entre la mémoire programme, qui stocke les programmes à exécuter, et la mémoire travail qui mémorise des variables nécessaires au fonctionnement des programmes. Nous avons vu plus haut que les données sont censées être placées en mémoire RAM, alors que les instructions sont placées en mémoire ROM. En fait, les choses sont plus compliquées. Il y a des architectures où cette séparation est nette et sans bavures. Mais d'autres ne respectent pas cette séparation à dessin. Cela permet de faire la différence entre les architectures Harvard où la séparation entre données et instructions est stricte, des architectures Von Neumann où données et instructions sont traitées de la même façon par le processeur.
Sur les architectures Harvard, la mémoire ROM est une mémoire programme, alors que la mémoire RWM est une mémoire travail. À l’opposé, les architectures Von Neumann permettent de copier des programmes et de les exécuter dans la RAM. La mémoire RWM sert alors en partie de mémoire programme, en partie de mémoire travail. Par exemple, on pourrait imaginer le cas où le programme est stocké sous forme compressée dans la mémoire ROM, et est décompressé pour être exécuté en mémoire RWM. Le programme de décompression est lui aussi stocké en mémoire ROM et est exécuté au lancement de l’ordinateur. Cette méthode permet d'utiliser une mémoire ROM très petite et très lente, tout en ayant un programme rapide (si la mémoire RWM est rapide). Mais un cas d'utilisation bien plus familier est celui de votre ordinateur personnel, comme nous le verrons plus bas.

L'architecture Harvard
modifierAvec l'architecture Harvard, la mémoire ROM et la mémoire RAM sont reliées au processeur par deux bus séparés. L'avantage de cette architecture est qu'elle permet de charger une instruction et une donnée simultanément : une instruction chargée sur le bus relié à la mémoire programme, et une donnée chargée sur le bus relié à la mémoire de données.

Sur ces architectures, le processeur voit bien deux mémoires séparées avec leur lot d'adresses distinctes.

Sur ces architectures, le processeur sait faire la distinction entre programme et données. Les données sont stockées dans la mémoire RAM, le programme est stocké dans la mémoire ROM. Les deux sont séparés, accédés par le processeur sur des bus séparés, et c'est ce qui permet de faire la différence entre les deux. Il est impossible que le processeur exécute des données ou modifie le programme. Du moins, tant que la mémoire qui stocke le programme est bien une ROM.
L'architecture Von Neumann
modifierAvec l'architecture Von Neumann, mémoire ROM et mémoire RAM sont reliées au processeur par un bus unique. Quand une adresse est envoyée sur le bus, les deux mémoires vont la recevoir mais une seule va répondre.

Avec l'architecture Von Neumann, tout se passe comme si les deux mémoires étaient fusionnées en une seule mémoire. Une adresse correspond soit à la mémoire RAM, soit à la mémoire ROM, mais pas aux deux.

Une particularité de ces architectures est qu'il est impossible de distinguer programme et données, sauf en ajoutant des techniques de protection mémoire avancées. La raison est qu'il est impossible de faire la différence entre donnée et instruction, vu que rien ne ressemble plus à une suite de bits qu'une autre suite de bits. Et c'est à l'origine d'un des avantages majeur de l'architecture Von Neumann : il est possible que des programmes soient recopiés dans la mémoire RWM et exécutés dans celle-ci. Un cas d'utilisation familier est celui de votre ordinateur personnel. Le système d'exploitation et les autres logiciels sont copiés en mémoire RAM à chaque fois que vous les lancez.
L'impossibilité de séparer données et instructions a beau être l'avantage majeur des architectures Von Neumann, elle est aussi à l'origine de problèmes assez fâcheux. Il est parfaitement possible que le processeur charge et exécute des données, qu'il prend par erreur pour des instructions. C'est le cas quand le programme exécuté est bugué, le cas le plus courant étant l'exploitation de ces bugs par les pirates informatiques. Il arrive que des pirates informatiques vous fournissent des données corrompues, destinées à être accédées par un programme bugué. Les données corrompues contiennent en fait un virus ou un programme malveillant, caché dans les données. Le bug en question permet justement à ces données d'être exécutées, ce qui exécute le virus. En clair, exécuter des données demande que le processeur ne fasse pas ce qui est demandé ou que le programme exécuté soit bugué. Pour éviter cela, le système d'exploitation fournit des mécanismes de protection pour éviter cela. Par exemple, il peut marquer certaines zones de la mémoire comme non-exécutable, c’est-à-dire que le système d'exploitation interdit d’exécution de quoi que ce soit qui est dans cette zone.
Il existe cependant des cas très rares où un programme informatique est volontairement codé pour exécuter des données. Par exemple, cela permet de créer des programmes qui modifient leurs propres instructions : cela s'appelle du code auto-modifiant. Ce genre de choses servait autrefois à écrire certains programmes sur des ordinateurs rudimentaires, pour gérer des tableaux et autres fonctionnalités de base utilisées par les programmeurs. Au tout début de l'informatique, où les adresses à lire/écrire devaient être écrites en dur dans le programme, dans les instructions exécutées. Pour gérer certaines fonctionnalités des langages de programmation qui ont besoin d'adresses modifiables, comme les tableaux, on devait recopier le programme dans la mémoire RWM et corriger les adresses au besoin. De nos jours, ces techniques peuvent être utilisées occasionnellement pour compresser un programme, le cacher et le rendre indétectable dans la mémoire (les virus informatiques utilisent beaucoup ce genre de procédés). Mais passons !
L'architecture Harvard modifiée
modifierLes architectures Von Neumann et Harvard sont des cas purs, qui sont encore très utilisés dans des microcontrôleurs ou des DSP (processeurs de traitement de signal). Mais quelques architectures ne suivent pas à la lettre les critères des architectures Harvard et Von Neumann et mélangent les deux, et sont des sortes d'intermédiaires entre les deux. De telles architectures sont appelées des architectures Harvard modifiée. Pour rappel, les architectures Harvard et Von neumman se distinguent sur deux points :
- Les adresses pour la mémoire ROM (le programme) et la mémoire RAM (les données) sont séparées sur les architectures Harvard, partagées sur l’architecture Von Neumann.
- L'accès aux données et instructions se font par des voies séparées sur l'architecture Harvard, sur le même bus avec l'architecture Von Neumann.
Les deux points sont certes reliés, mais on peut cependant les décorréler. On peut par exemple imaginer une architecture où les adresses sont partagées, mais où les voies d'accès aux instructions et aux données sont séparées. On peut aussi imaginer le cas où les voies d'accès aux données et instructions sont les mêmes, mais les adresses différentes.
Prenons le premier cas, où les adresses sont partagées, mais où les voies d'accès aux instructions et aux données sont séparées. C'est le cas sur les ordinateurs personnels modernes, où programmes et données sont stockés dans la même mémoire comme dans l'architecture Von Neumann. Cependant, les voies d'accès aux instructions et aux données ne sont pas les mêmes au-delà d'un certain point. La séparation se fait au niveau de la mémoire intégrée dans le processeur, la fameuse mémoire cache dont nous parlerons dans le prochain chapitre. Aussi, nous repartons les explications sur ces architectures dans le chapitre suivant, nous n’avons pas le choix que de faire ainsi.
Le deuxième type d'architecture Harvard modifiée est celle où les voies d'accès aux données et instructions sont les mêmes, mais les adresses différentes. Concrètement, cela ne signifie pas qu'il n'y a qu'un seul bus, mais que des mécanismes sont prévus pour que les deux bus d’instruction et de données interagissent et échangent des informations. Et là, on en trouve deux types.
Le cas le plus simple d'architecture Harvard modifiée est une architecture Harvard, où le processeur peut lire des données constantes depuis la mémoire ROM. Vu que les adresses des données et des instructions sont séparées, le processeur doit disposer d'une instruction pour lire les données en mémoire RWM, et d'une instruction pour lire des données en mémoire ROM. Ce n'est pas le cas sur les architectures Harvard, où la lecture des données en ROM est interdite, ni sur les architectures Von Neumann, où la lecture des données se fait avec une unique instruction qui peut lire n'importe quelle adresse aussi bien en ROM qu'en RAM. Une autre possibilité est que le processeur copie ces données constantes depuis la mémoire ROM dans la mémoire RAM, au lancement du programme, avec des instructions adaptées.
D'autres architectures font l’inverse. Là où les architectures précédentes pouvaient lire des données en ROM et en RWM, mais chargent leurs instructions depuis la ROM seulement, d'autres architectures font l'inverse. Il leur est possible d’exécuter des instructions peut importe qu'elles viennent de la ROM ou de la RAM. Par contre, quand les instructions sont exécutées depuis la mémoire RAM, les performances s'en ressentent, car on ne peut plus accéder à une donnée en même temps qu'on charge une instruction.
Étude de quelques exemples d'architectures
modifierL'architecture de base vue plus haut est une architecture assez simple. Tous les ordinateurs modernes, mais aussi dans les smartphones, les consoles de jeu et autres, utilisent cependant une version grandement modifiée et améliorée. Les ordinateurs modernes utilisent un grand nombre de périphériques, ont des systèmes d'exploitation sur des disques durs/SSD, il y a un grand nombre de mémoires différentes, etc. Seuls les systèmes assez anciens, ainsi que les systèmes embarqués ou d'informatique industrielle, se contentent de cette architecture de base.
L'architecture de la console de jeu NES
modifierDans cette section, nous allons étudier l'exemple de la console de Jeu Famicom, et allons voir que même des systèmes assez simples et anciens apportent des modifications à l'architecture de base. La console de base a une architecture très simple, avec seulement un CPU, de la RAM, et quelques entrées-sorties. Malgré tout, on trouve des détails assez intéressants. L'architecture de la NES est illustrée ci-dessous.

On voit qu'elle est centrée sur un processeur Ricoh 2A03, similaire au processeur 6502, un ancien processeur autrefois très utilisé et très populaire. Ce processeur est associé à 2 KB de mémoire RAM et à une mémoire ROM. La mémoire ROM se trouve dans la cartouche de jeu, et non dans la console : Le programme du jeu est dans la cartouche, dans cette ROM. On trouve aussi une RAM dans la cartouche, qui est utilisée pour les sauvegardes, et qui est adressée par le processeur directement. Première variation par rapport à l'architecture de base : on a plusieurs RAM, une généraliste et une autre pour les sauvegardes.
Les entrées-sorties sont au nombre de deux : une carte son et une carte vidéo. La carte son est le composant qui s'occupe de commander les haut-parleurs et de gérer tout ce qui a rapport au son. La carte graphique est le composant qui es t en charge de calculer les graphismes, tout ce qui s'affiche à l'écran. La carte graphique est connectée à 2 KB de RAM, séparée de la RAM normale, via un bus séparé. De plus, la carte graphique est connectée via un autre bus à une ROM/RAM qui contient les sprites et textures du jeu, qui est dans la cartouche. Sur cette console, les cartes son et graphique ne sont PAS des co-processeurs. Elles ne sont pas programmables, ce sont des circuits électroniques fixes, non-programmables. C'est totalement différent de ce qu'on a sur les consoles modernes, aussi le préciser est important.
L'organisation des bus est assez simple, bien qu'elle se démarque de l'architecture de base avec un bus système : on ne trouve pas un seul bus de communication, mais plusieurs. Déjà, il s'agit d'une architecture Harvard, car la ROM et la RAM utilisent des bus différents. De plus, on a un bus qui connecte le processeur aux autres entrées-sorties, séparé des bus pour les mémoires. Ce bus est relié à la carte graphique et la carte sonore. Mais il n'est pas le seul bus dédié aux périphériques : les manettes sont connectées directement sur le processeur, via un bus dédié !
L'architecture de la SNES
modifierL'architecture de la SNES est plus complexe que pour la NES. L'architecture est illustrée ci-dessous. La RAM a augmenté en taille et passe à 128 KB. Pareil pour la RAM de la carte vidéo, qui passe à 64 KB. On remarque un changement complet au niveau des bus : il n'y a plus qu'un seul bus sur lequel tout est connecté : ROM, RAM, entrées-sorties, etc. La seule exception est pour les manettes, qui sont encore connectées directement sur le processeur, via un bus séparé. La console a donc un bus système, mais qui est malgré tout complété par un bus pour les manettes, chose assez originale.
Un autre changement est que la carte graphique est maintenant composée de deux circuits séparés. Encore une fois, il ne s'agit pas de coprocesseurs, mais de circuits non-programmables. Par contre, la carte son est remplacée par deux coprocesseurs audio ! De plus, les deux processeurs sont connectés à une mémoire RAM dédiée de 64 KB, comme pour la carte graphique. L'un est un processeur 8 bits (le DSP), l'autre est un processeur 16 bits.

Un point très intéressant : certains jeux intégraient des coprocesseurs dans leurs cartouches de jeu ! Par exemple, les cartouches de Starfox et de Super Mario 2 contenait un coprocesseur Super FX, qui gérait des calculs de rendu 2D/3D. Le Cx4 faisait plus ou moins la même chose, il était spécialisé dans les calculs trigonométriques, et diverses opérations de rendu 2D/3D. En tout, il y a environ 16 coprocesseurs d'utiliser et on en trouve facilement la liste sur le net. La console était conçue pour, des pins sur les ports cartouches étaient prévues pour des fonctionnalités de cartouche annexes, dont ces coprocesseurs. Ces pins connectaient le coprocesseur au bus des entrées-sorties. Les coprocesseurs des cartouches de NES avaient souvent de la mémoire rien que pour eux, qui était intégrée dans la cartouche.
Les system on chip et microcontrôleurs
modifierParfois, on décide de regrouper la mémoire, les bus, le CPU et les ports d'entrée-sortie dans un seul circuit intégré, un seul boitier. L'ensemble forme alors ce qu'on appelle un System on Chip (système sur une puce), abrévié en SoC. Le nom est assez explicite : un SoC comprend un système informatique complet sur une seule puce de silicium, microprocesseurs, mémoires et périphériques inclus. Ils incorporent aussi des timers, des compteurs, et autres circuits très utiles.
Le terme SoC regroupe des circuits imprimés assez variés, aux usages foncièrement différents et à la conception distincte. Les plus simples d’entre eux sont des microcontrôleurs, qui sont utilisés pour des applications à base performance. Les plus complexes sont utilisés pour des applications qui demandent plus de puissance, nous les appellerons SoC haute performance. La relation entre SoC et microcontrôleurs est assez compliquée à expliquer, la terminologie n'est pas clairement établie. Il existe quelques cours/livres qui séparent les deux, d'autres qui pensent que les deux sont très liés. Dans ce cours, nous allons partir du principe que tous les systèmes qui regroupent processeur, mémoire et quelques périphériques/entrées-sorties sont des SoC. Les microcontrôleurs sont donc un cas particulier de SoC, en suivant cette définition.
Les microcontrôleurs
modifierUn exemple d'intégration assez similaire aux SoC est le cas des microcontrôleurs, des composants utilisés dans l'embarqué ou d'informatique industrielle. Leur nom trahit leur rôle. Ils sont utilisés pour contrôler de l'électroménager, des chaines de fabrication dans une usine, des applications robotiques, les alarmes domestiques, les voitures. De manière générale, on les trouve dans tous les systèmes dits embarqués et/ou temps réel. Ils ont besoin de s'interconnecter à un grand nombre de composants et intègrent pour cela un grand nombre d'entrée-sorties. Les microcontrôleurs sont généralement peu puissants, et doivent consommer peu d'énergie/électricité.

Un microcontrôleur tend à intégrer des entrées-sorties assez spécifiques, qu'on ne retrouve pas dans les SoC destinés au grand public. Un microcontrôleur est typiquement relié à un paquet de senseurs et son rôle est de commander des moteurs ou d'autres composants. Et les entrées-sorties intégrées sont adaptées à cette tâche. Par exemple, ils tendent à intégrer de nombreux convertisseurs numériques-analogiques pour gérer des senseurs. Ils intègrent aussi des circuits de génération de signaux PWM spécialisés pour commander des moteurs, le processeur peut gérer des calculs trigonométriques (utiles pour commander la rotation d'un moteur),etc.

Fait amusant, on en trouve dans certains périphériques informatiques. Par exemple, les anciens disques durs intégraient un microcontrôleur qui contrôlait plusieurs moteurs/ Les moteurs pour faire tourner les plateaux magnétiques et les moteurs pour déplacer les têtes de lecture/écriture étaient commandés par ce microcontrôleur. Comme autre exemple, les claviers d'ordinateurs intègrent un microcontrôleur connecté aux touches, qui détecte quand les touches sont appuyées et qui communique avec l'ordinateur. Nous détaillerons ces deux exemples dans les chapitres dédiés aux périphériques et aux disques durs, tout deviendra plus clair à ce moment là. La majorité des périphériques ou des composants internes à un ordinateur contiennent des microcontrôleurs.
Les SoC haute performance
modifierLes SoC les plus performants sont actuellement utilisés dans les téléphones mobiles, tablettes, Netbook, smartphones, ou tout appareil informatique grand public qui ne doit pas prendre beaucoup de place. La petite taille de ces appareils fait qu'ils gagnent à regrouper toute leur électronique dans un circuit imprimé unique. Mais les contraintes font qu'ils doivent être assez puissants. Ils incorporent des processeurs assez puissants, surtout ceux des smartphones. C'est absolument nécessaire pour faire tourner le système d'exploitation du téléphone et les applications installées dessus.
Niveau entrées-sorties, ils incorporent souvent des interfaces WIFI et cellulaires (4G/5G), des ports USB, des ports audio, et même des cartes graphiques pour les plus puissants d'entre eux. Les SoC incorporent des cartes graphiques pour gérer tout ce qui a trait à l'écran LCD/OLED, mais aussi pour gérer la caméra, voire le visionnage de vidéo (avec des décodeurs/encodeurs matériel). Par exemple, les SoC Tegra de NVIDIA incorporent une carte graphique, avec des interfaces HDMI et VGA, avec des décodeurs vidéo matériel H.264 & VC-1 gérant le 720p. Pour résumer, les périphériques sont adaptés à leur utilisation et sont donc foncièrement différents de ceux des microcontrôleurs.

Un point important est que les processeurs d'un SoC haute performance sont... performants. Il sont le plus souvent des processeurs de marque ARM, qui sont différents de ceux utilisés dans les PC fixe/portables grand public qui sont eux de type x86. Nous verrons dans quelques chapitres en quoi consistent ces différences, quand nous parlerons des jeux d'instruction du processeur. Autrefois réservé au monde des PCs, les processeurs multicœurs deviennent de plus en plus fréquents pour les SoC de haute performance. Il n'est pas rare qu'un SoC incorpore plusieurs cœurs. Il arrive même qu'ils soient foncièrement différents, avec plusieurs cœurs d'architecture différente.
La frontière entre SoC haute performance et microcontrôleur est de plus en plus floue. De nombreux appareils du quotidien intègrent des SoC haute performance, d'autres des microcontrôleurs. Par exemple, les lecteurs CD/DVD/BR et certains trackers GPS intègrent un SoC ou des processeurs dont la performance est assez pêchue. A l'opposé, les systèmes domotiques intègrent souvent des microcontrôleurs simples. Malgré tout, les deux cas d'utilisation font que le SoC/microcontrôleur est connecté à un grand nombre d'entrées-sorties très divers, comme des capteurs, des écrans, des LEDs, etc.

Sur la plupart des systèmes embarqués ou des tous premiers ordinateurs, on n'a que deux mémoires : une mémoire RAM et une mémoire ROM, comme indiqué dans le chapitre précédent. Mais ces systèmes sont très simples et peuvent se permettre d'implémenter l'architecture de base sans devoir y ajouter quoi que ce soit. Ce n'est pas le cas sur les ordinateurs plus puissants.
Un ordinateur moderne ne contient pas qu'une seule mémoire, mais plusieurs. Entre le disque dur, la mémoire RAM, les différentes mémoires cache, et autres, il y a de quoi se perdre. Et de plus, toutes ces mémoires ont des caractéristiques, voire des fonctionnements totalement différents. Certaines mémoires seront très rapides, d'autres auront une grande capacité mémoire (elles pourront conserver beaucoup de données), certaines s'effacent quand on coupe le courant et d'autres non.
La raison à cela est que plus une mémoire peut contenir de données, plus elle est lente. On doit faire le choix entre une mémoire de faible capacité et très performante, ou une mémoire très performante mais très petite. Les cas intermédiaires, avec une capacité et des performances intermédiaires, existent aussi. Le fait est que si l'on souhaitait utiliser une seule grosse mémoire dans notre ordinateur, celle-ci serait trop lente et l'ordinateur serait inutilisable. Pour résoudre ce problème, il suffit d'utiliser plusieurs mémoires de taille et de vitesse différentes, qu'on utilise suivant les besoins. Des mémoires très rapides de faible capacité seconderont des mémoires lentes de capacité importante.
Finalement, l'architecture d'un ordinateur moderne diffère de l'architecture de base par la présence d'une grande quantité de mémoires, organisées sous la forme d'une hiérarchie qui va des mémoires très rapides mais très petites à des mémoires de forte capacité très lentes. Le reste de l’architecture ne change pas trop par rapport à l'architecture de base : on a toujours un processeur, des entrées-sorties, un bus de communication, et tout ce qui s'en suit. Les mémoires d'un ordinateur moderne sont les suivantes :
| Type de mémoire | Temps d'accès | Capacité | Relation avec la mémoire primaire/secondaire |
|---|---|---|---|
| Registres | 1 nanosecondes | Entre 1 et 512 bits | Mémoire incorporée dans le processeur |
| Caches | 10 - 100 nanosecondes | Kibi- ou mébi-octets | Mémoire incorporée dans le processeur, sauf pour d'anciens processeurs |
| Mémoire RAM | 1 microsecondes | Gibioctets | Mémoire primaire |
| Mémoires de masse (Disque dur, disque SSD, autres) | 1 millisecondes | Dizaines à centaines de gibioctets | Mémoire secondaire |
Précisons cependant que le compromis capacité-performance n'est pertinent que quand on compare des mémoires avec des capacités très différentes, avec au moins un ordre de grandeur de différence. Entre un ordinateur avec 16 gibioctets de RAM et un autre avec 64 gibioctets, les différences de performances sont marginales. Par contre, la différence entre un cache de quelques mébioctets et une RAM de plusieurs gibioctets, la différence est très importante. Ce qui fait que l'ensemble des mémoires de l'ordinateur est organisé en plusieurs niveaux, avec des registres ultra-rapides, des caches intermédiaires, une mémoire RAM un peu lente, et des mémoires de masse très lentes.
La distinction entre mémoire primaire et secondaire
modifierLa première amélioration de l'architecture de base consiste à rajouter un niveau de mémoire. Il n'y a alors que deux niveaux de mémoire : les mémoires primaires directement accessibles par le processeur, et la mémoire secondaire accessible comme les autres périphériques. La mémoire primaire, correspond aux mémoire RAM et ROM de l'ordinateur, dans laquelle se trouvent les programmes en cours d’exécution et les données qu'ils manipulent. Les mémoires secondaires correspondent aux disques durs, disques SSD, clés USB et autres. Ce sont des périphériques connectés sur la carte mère ou via un connecteur externe.

Les mémoires secondaires sont généralement confondues avec les mémoires de masse, des mémoires de grande capacité qui servent à stocker de grosses quantités de données. De plus, elles conservent des données qui ne doivent pas être effacés et sont donc des mémoire de stockage permanent (on dit qu'il s'agit de mémoires non-volatiles). Concrètement, elles conservent leurs données mêmes quand l'ordinateur est éteint et ce pendant plusieurs années, voir décennies. Les disques durs, mais aussi les CD/DVD et autres clés USB sont des mémoires de masse.
Du fait de leur grande capacité, les mémoires de masse sont très lentes. Leur lenteur pachydermique fait qu'elles n'ont pas besoin de communiquer directement avec le processeur, ce qui fait qu'il est plus pratique d'en faire de véritables périphériques, plutôt que de les souder/connecter sur la carte mère. C'est la raison pour laquelle mémoires de masse et mémoires secondaires sont souvent confondues.
Les mémoires de masse se classent en plusieurs types : les mémoires secondaires proprement dit, les mémoires tertiaires et les mémoires quaternaires. Toutes sont traitées comme des périphériques par le processeur, la différence étant dans l’accessibilité.
- Une mémoire secondaire a beau être un périphérique, elle est située dans l'ordinateur, connectée à la carte mère. Elle s'allume et s'éteint en même temps que l'ordinateur et est accessible tant que l'ordinateur est allumé. Les disques durs et disques SSD sont dans ce cas.
- Une mémoire tertiaire est un véritable périphérique, dans le sens où on peut l'enlever ou l'insérer dans un connecteur externe à loisir. Par exemple, les clés USB, les CD/DVD ou les disquettes sont dans ce cas. Une mémoire tertiaire est donc rendue accessible par une manipulation humaine, qui connecte la mémoire à l'ordinateur. Le système d'exploitation doit alors effectuer une opération de montage (connexion du périphérique à l’ordinateur) ou de démontage (retrait du périphérique).
- Quant aux mémoires quaternaires, elles sont accessibles via le réseau, comme les disques durs montés en cloud.
Les technologies de fabrication des mémoires secondaires sont à part
modifierLes mémoires de masse sont par nature des mémoires non-volatiles, à savoir qui ne s'effacent pas quand on coupe l'alimentation électrique, à l'opposé des mémoires RAM qui elles s'effacent quand on coupe le courant. Et ce fait nous dit quelque chose de très important : les mémoires de masse ne sont pas fabriquées de la même manière que les mémoires volatiles.
Les mémoires volatiles sont presque toutes électroniques, à quelques exceptions qui appartiennent à l'histoire de l'informatique. Elles sont fabriquées avec des transistors, que ce soit des transistors CMOS ou bipolaire. Et quand on cesse de l'alimenter en courant, les transistors repasse en état inactif, de repos, qui est soit fermé ou ouvert. Ils ne mémorisent pas l'état qu'ils avaient avant qu'on coupe le courant. On ne peut donc pas fabriquer de mémoire non-volatile avec des transistors ! Et ce genre de chose vaut pour les ancêtres du transistors, comme les thrysistors, les triodes, les tubes à vide et autres : ils permettaient de fabriquer des mémoires volatiles, mais rien d'autres.
- Les mémoires ROM ne sont pas concernées par ce problème vu que ce sont de simples circuits combinatoires, qui n'ont pas besoin d'avoir de capacité de mémorisation proprement dit. Elles sont donc non-volatiles, mais le fait qu'on ne puisse pas modifier leur contenu rend la solution aisée.
Aussi, pour fabriquer des mémoires de masse, on doit utiliser des technologies différentes, on ne peut pas utiliser de transistors CMOS ou bipolaire normaux. Et le moins qu'on puisse dire est que les technologies des mémoires de masse sont très nombreuses, absolument tous les supports de mémorisation possibles ont été essayés et commercialisés. L'évolution des technologies de fabrication est difficile à résumer pour les mémoires de masse. Mais dans les grandes lignes, on peut distinguer quatre grandes technologies.
La solution la plus ancienne était d'utiliser un support papier, avec les cartes perforées. Mais cette solution a rapidement été remplacée par l'usage de d'un support de mémorisation magnétique, à savoir que chaque bit était attribué à un petit morceau de matériau magnétique. Le matériau magnétique peut être magnétisé dans deux sens N-S ou S-N, ce qui permet d'encoder un bit. C'est ainsi que sont nées les toutes premières mémoire de masse magnétique : les bandes magnétiques (similaires à celles utilisées dans les cassettes audio), les tambours magnétiques, les mémoires à tore de ferrite, et quelques autres. Par la suite, sont apparues les disquettes et les disques durs.
Par la suite, les CD-ROM, puis les DVD sont apparus sur le marchés. Ils sont regroupés sous le terme de mémoires optiques, car leur fonctionnement utilise les propriétés optiques du support de mémorisation, on les lit en faisant passer un laser très fin dessus. Ils n'ont cependant pas remplacé les disques durs, leur usage était tout autre. En effet, les mémoires optiques ne peuvent pas être effacées et réécrites. Sauf dans le cas des CD/DVD réincriptibles, mais on ne peut les effacer qu'un nombre limité de fois, mettons une dizaine. De plus, il faut les effacer intégralement avant de réécrire complétement leur contenu. Cette limitation fait qu'ils n'étaient pas utilisés pour mémoriser le système d'exploitation ou les programmes installés.
Toutes ces mémoires sont totalement obsolètes de nos jours, à l'exception des disques durs magnétiques. Et encore ces derniers tendent à disparaitre. Les mémoires de masse actuelles sont toutes... électroniques ! J'ai dit plus haut qu'il n'était pas possible de fabriquer des mémoires de masse/secondaires avec des transistors CMOS, je n'ai pas mentit. Les mémoires électronique actuelle sont des mémoires FLASH, qui sont fabriquées avec des transistors CMOS à grille flottante. Leur fonctionnement est différent des transistors CMOS normaux, ils ont une capacité de mémorisation que les transistors CMOS normaux n'ont pas. Par contre, leur procédé de fabrication est différent, ils ne sont pas fabriqués dans les mêmes usines que les transistors CMOS normaux.
Le démarrage de l'ordinateur à partir d'une mémoire secondaire
modifierL'ajout de deux niveaux de mémoire pose quelques problèmes pour le démarrage de l'ordinateur : comment charger les programmes depuis un périphérique ?
Les tout premiers ordinateurs pouvaient démarrer directement depuis un périphérique. Ils étaient conçus pour cela, directement au niveau de leurs circuits. Ils pouvaient automatiquement lire un programme depuis une carte perforée ou une mémoire magnétique, et le copier en mémoire RAM. Par exemple, l'IBM 1401 lisait les 80 premiers caractères d'une carte perforée et les copiait en mémoire, avant de démarrer le programme copié. Si un programme faisait plus de 80 caractères, les 80 premiers caractères contenaient un programme spécialisé, appelé le chargeur d’amorçage, qui s'occupait de charger le reste. Sur l'ordinateur Burroughs B1700, le démarrage exécutait automatiquement le programme stocké sur une cassette audio, instruction par instruction.
Les processeurs "récents" ne savent pas démarrer directement depuis un périphérique. À la place, ils contiennent une mémoire ROM utilisée pour le démarrage, qui contient un programme qui charge les programmes depuis le disque dur. Rappelons que la mémoire ROM est accessible directement par le processeur.
Sur les premiers ordinateurs avec une mémoire secondaire, le programme à exécuter était en mémoire ROM et la mémoire secondaire ne servait que de stockage pour les données. Le système d'exploitation était dans la mémoire ROM, ce qui fait que l'ordinateur pouvait démarrer même sans mémoire secondaire. La mémoire secondaire était utilisée pour stocker données comme programmes à exécuter. Les programmes à utiliser étaient placés sur des disquettes, des cassettes audio, ou tout autre support de stockage. Les premiers ordinateurs personnels, comme les Amiga, Atari et Commodore, étaient de ce type.
Par la suite, le système d'exploitation aussi a été déporté sur la mémoire secondaire, à savoir qu'il est installé sur le disque dur, voire un SSD. Un cas d'utilisation familier est celui de votre ordinateur personnel. Le système d'exploitation et les logiciels que vous utilisez au quotidien sont mémorisés sur le disque dur. Mais vu qu'aucun ordinateur ne démarre directement depuis le disque dur ou une clé USB, il y a forcément une mémoire ROM dans un ordinateur moderne, qui n'est autre que le BIOS sur les ordinateurs anciens, l'UEFI sur les ordinateurs récents. Elle est utilisée lors du démarrage de l'ordinateur pour le configurer à l'allumage et démarrer son système d'exploitation. La ROM en question ne sert donc qu'au démarrage de l'ordinateur, avant que le système d'exploitation prenne la relève. L'avantage, c'est qu'on peut modifier le contenu du disque dû assez facilement, tandis que ce n'est pas vraiment facile de modifier le contenu d'une ROM (et encore, quand c'est possible). On peut ainsi facilement installer ou supprimer des programmes, en rajouter, en modifier, les mettre à jour sans que cela ne pose problème.
Le fait de mettre les programmes et le système d'exploitation sur des mémoires secondaire a quelques conséquences. La principale est que le système d'exploitation et les autres logiciels sont copiés en mémoire RAM à chaque fois que vous les lancez. Impossible de faire autrement pour les exécuter. Les systèmes de ce genre sont donc des architectures de type Von Neumann ou de type Harvard modifiée, qui permettent au processeur d’exécuter du code depuis la RAM. Vu que le programme s’exécute en mémoire RAM, l'ordinateur n'a aucun moyen de séparer données et instructions, ce qui amène son lot de problèmes, comme nous l'avons dit au chapitre précédent.

L'ajout des mémoires caches et des local stores
modifierLa hiérarchie mémoire d'un ordinateur moderne est une variante de la hiérarchie à deux niveaux de la section précédente (primaire et secondaire) à laquelle on a rajouté une ou plusieurs mémoires caches. Le rajout de ces niveaux supplémentaires est une question de performance. Les processeurs anciens pouvaient se passer de mémoires caches. Mais au fil du temps, les processeurs ont gagné en performances plus rapidement que la mémoire RAM et les processeurs ont incorporé des mémoires caches pour compenser la différence de vitesse entre processeur et mémoire RAM.
Plus haut, on a vu que les mémoires secondaires ne sont pas fabriqués avec le même processeur que les mémoires volatiles/RAM. Il en est de même avec les mémoires caches, ce qui explique la différence de performance entre RAM et cache. Les caches sont plus rapides, non seulement car ils sont plus petits, mais aussi car ils ne sont pas fabriqués comme des mémoires RAM. Les mémoires RAM actuelles sont des mémoires dites DRAM, alors que les caches sont fabriqués avec des mémoires dites SRAM. La différence sera expliquée dans quelques chapitres, retenez simplement que les procédés de fabrication sont différents. La SRAM est rapide, mais a une faible capacité, la DRAM est lente et de forte capacité. La raison est que 1 bit de SRAM prend beaucoup de place et utilise beaucoup de circuits, alors que les DRAM sont plus économes en circuits et en espace.
Les caches peuvent ou non être intégrés au processeur. Il a existé des caches séparés du processeur, connectés sur la carte mère. Mais de nos jours, les caches sont incorporés au processeur, pour des raisons de performance. Les caches devant être très rapides, de l'ordre de la nanoseconde, il fallait réduire drastiquement la distance entre le processeur et ces mémoires. Cela n'a l'air de rien, mais l'électricité met quelques dizaines ou centaines de nanosecondes pour parcourir les connexions entre le processeur et le cache, si le cache est en dehors du processeur. En intégrant les caches dans le processeur, on s'assure que le temps d'accès est minimal, la mémoire étant la plus proche possible des circuits de calcul.

Les caches et local stores
modifier
Le niveau intermédiaire entre les registres et la mémoire principale regroupe deux types distincts de mémoires : les mémoires caches (du moins, certains caches) et les local stores.
Dans la majorité des cas, la mémoire intercalée entre les registres et la mémoire RAM/ROM est ce qu'on appelle une mémoire cache. De nos jours, ce cache est intégré dans le processeur, mais il a existé des caches qui s'installaient sur un port dédié de la carte mère, du temps du Pentium 1 et 2. Aussi bizarre que cela puisse paraître, elle n'est jamais adressable ! Le contenu du cache est géré par un circuit spécialisé et le programmeur ne peut pas gérer directement ce cache.
Le cache contient une copie de certaines données présentes en RAM et cette copie est accessible bien plus rapidement, le cache étant beaucoup plus rapide que la RAM. Tout accès mémoire provenant du processeur est intercepté par le cache, qui vérifie si une copie de la donnée demandée est présente ou non dans le cache. Si c'est le cas, on accède à la copie le cache : on a un succès de cache (cache hit). Sinon, c'est un défaut de cache (cache miss) : on est obligé d’accéder à la RAM et/ou de charger la donnée de la RAM dans le cache. Tout s'éclairera dans le chapitre dédié aux mémoires caches.
Sur certains processeurs, les mémoires caches sont remplacées par des mémoires RAM appelées des local stores. Ce sont des mémoires RAM, identiques à la mémoire RAM principale, mais qui sont plus petites et plus rapides. Contrairement aux mémoires caches, il s'agit de mémoires adressables, ce qui fait qu'elles ne sont plus gérées automatiquement par le processeur : c'est le programme en cours d'exécution qui prend en charge les transferts de données entre local store et mémoire RAM. Ces local stores consomment moins d'énergie que les caches à taille équivalente : en effet, ceux-ci n'ont pas besoin de circuits compliqués pour les gérer automatiquement, contrairement aux caches. Côté inconvénients, ces local stores peuvent entraîner des problèmes de compatibilité : un programme conçu pour fonctionner avec des local stores ne fonctionnera pas sur un ordinateur qui en est dépourvu.
Les principes de localité spatiale et temporelle
modifierUtiliser au mieux la hiérarchie mémoire demande placer les données accédées souvent, ou qui ont de bonnes chances d'être accédées dans le futur, dans la mémoire la plus rapide possible. Le tout est de faire en sorte de placer les données intelligemment, et les répartir correctement dans cette hiérarchie des mémoires. Ce placement se base sur deux principes qu'on appelle les principes de localité spatiale et temporelle :
- un programme a tendance à réutiliser les instructions et données accédées dans le passé : c'est la localité temporelle ;
- et un programme qui s'exécute sur un processeur a tendance à utiliser des instructions et des données consécutives, qui sont proches, c'est la localité spatiale.
Pour donner un exemple, les instructions d'un programme sont placées en mémoire dans l’ordre dans lequel on les exécute : la prochaine instruction à exécuter est souvent placée juste après l'instruction en cours (sauf avec les branchements). La localité spatiale est donc respectée tant qu'on a pas de branchements qui renvoient assez loin dans la mémoire (appels de sous-programmes). De même, les boucles (des fonctionnalités des langages de programmation qui permettent d’exécuter en boucle un morceau de code tant qu'une condition est remplie) sont un bon exemple de localité temporelle. Les instructions de la boucle sont exécutées plusieurs fois de suite et doivent être lues depuis la mémoire à chaque fois.
On peut exploiter ces deux principes pour placer les données dans la bonne mémoire. Par exemple, si on a accédé à une donnée récemment, il vaut mieux la copier dans une mémoire plus rapide, histoire d'y accéder rapidement les prochaines fois : on profite de la localité temporelle. On peut aussi profiter de la localité spatiale : si on accède à une donnée, autant précharger aussi les données juste à côté, au cas où elles seraient accédées. Ce placement des données dans la bonne mémoire peut être géré par le matériel de notre ordinateur, mais aussi par le programmeur.
Une bonne utilisation des principes de localité par les programmeurs
modifierDe nos jours, le temps que passe le processeur à attendre la mémoire principale devient de plus en plus un problème au fil du temps, et gérer correctement la hiérarchie mémoire est une nécessité, particulièrement sur les processeurs multi-cœurs. Il faut dire que la différence de vitesse entre processeur et mémoire est très importante : alors qu'une simple addition ou multiplication va prendre entre 1 et 5 cycles d'horloge, une lecture en mémoire RAM fera plus dans les 400-1000 cycles d'horloge. Les processeurs modernes utilisent des techniques avancées pour masquer ce temps de latence, qui reviennent à exécuter des instructions pendant ce temps d'attente, mais elles ont leurs limites.
Bien évidement, optimiser au maximum la conception de la mémoire et de ses circuits dédiés améliorera légèrement la situation, mais n'en attendez pas des miracles. Il faut dire qu'il n'y a pas vraiment de solution facile à implémenter. Par exemple, changer la taille d'une mémoire pour contenir plus de données aura un effet désastreux sur son temps d'accès qui peut se traduire par une baisse de performance. Par exemple, les processeurs Nehalem d'Intel ont vus leurs performances dans les jeux vidéos baisser de 2 à 3 % malgré de nombreuses améliorations architecturales très évoluées : la latence du cache L1 avait augmentée de 2 cycles d'horloge, réduisant à néant de nombreux efforts d'optimisations architecturales.
Une bonne utilisation de la hiérarchie mémoire repose en réalité sur le programmeur qui doit prendre en compte les principes de localités vus plus haut dès la conception de ses programmes. La façon dont est conçue un programme joue énormément sur sa localité spatiale et temporelle. Un programmeur peut parfaitement tenir compte du cache lorsqu'il programme, et ce aussi bien au niveau :
- de son algorithme : on peut citer l'existence des algorithmes cache oblivious ;
- du choix de ses structures de données : un tableau est une structure de donnée respectant le principe de localité spatiale, tandis qu'une liste chaînée ou un arbre n'en sont pas (bien qu'on puisse les implémenter de façon à limiter la casse);
- ou de son code source : par exemple, le sens de parcours d'un tableau multidimensionnel peut faire une grosse différence.
Cela permet des gains très intéressants pouvant se mesurer avec des nombres à deux ou trois chiffres. Je vous recommande, si vous êtes programmeur, de vous renseigner le plus possible sur les optimisations de code ou algorithmiques qui concernent le cache : il vous suffira de chercher sur Google. Quoi qu’il en soit, il est quasiment impossible de prétendre concevoir des programmes optimisés sans tenir compte de la hiérarchie mémoire. Et cette contrainte va se faire de plus en plus forte quand on devra passer aux architectures multicœurs.
Dans ce chapitre, nous allons définir ce qui fait qu'un ordinateur est plus rapide qu'un autre. En clair, nous allons étudier la performance d'un ordinateur. C'est loin d'être une chose triviale : de nombreux paramètres font qu'un ordinateur sera plus rapide qu'un autre. De plus, la performance ne signifie pas la même chose selon le composant dont on parle. La performance d'un processeur n'est ainsi pas comparable à la performance d'une mémoire ou d'un périphérique.
La performance du processeur
modifierConcevoir un processeur n'est pas une chose facile et en concevoir un qui soit rapide l'est encore moins, surtout de nos jours. Pour comprendre ce qui fait la rapidité d'un processeur, nous allons devoir déterminer ce qui fait qu'un programme lancé sur notre processeur va prendre plus ou moins de temps pour s’exécuter.
Le temps d’exécution d'une instruction : CPI et fréquence
modifierLe temps que met un programme pour s’exécuter est le produit :
- du nombre moyen d'instructions exécutées par le programme ;
- de la durée moyenne d'une instruction, en seconde.
- , avec N le nombre moyen d'instruction du programme et la durée moyenne d'une instruction.
Le nombre moyen d'instructions exécuté par un programme s'appelle l'Instruction path length, ou encore longueur du chemin d'instruction en français. Si on utilise le nombre moyen d’instructions, c'est car il n'est pas forcément le même d'une exécution à l'autre. Par exemple, certaines sections de code ne sont exécutées que si une condition bien spécifique est remplie, d'autres sont répétées en boucle, etc. Tout cela deviendra plus clair quand nous aborderons les instructions et les structures de contrôle, dans un chapitre dédié.
Le temps d’exécution d'une instruction peut s'exprimer en secondes, mais on peut aussi l'exprimer en nombre de cycles d'horloge. Par exemple, sur les processeurs modernes, une addition va prendre un cycle d'horloge, une multiplication entre 1 et 2 cycles, etc. Cela dépend du processeur, de l'opération, et d'autres paramètres assez compliqués. Mais on peut calculer un nombre moyen de cycle d'horloge par opération : le CPI (Cycle Per Instruction). Le temps d’exécution moyen d'une instruction dépend alors :
- du nombre moyen de cycles d'horloge nécessaires pour exécuter une instruction, qu'on notera CPI (ce qui est l'abréviation de Cycle Per Instruction) ;
- et de la durée d'un cycle d'horloge, notée P (P pour période).
Quand on sait que la durée d'un cycle d'horloge n'est autre que l'inverse de la fréquence on peut reformuler en :
- , avec f la fréquence.
La puissance de calcul : IPC et fréquence
modifierOn peut rendre compte de la puissance du processeur par une seconde approche. Au lieu de faire intervenir le temps mis pour exécuter une instruction, on peut utiliser la puissance de calcul, à savoir le nombre de calculs que l'ordinateur peut faire par seconde. En toute rigueur, cette puissance de calcul se mesure en nombre d'instructions par secondes, une unité qui porte le nom de IPS. En pratique, la puissance de calcul se mesure en MIPS : Million Instructions Per Second, (million de calculs par seconde en français). Plus un processeur a un MIPS élevé, plus il sera rapide : un processeur avec un faible MIPS mettra plus de temps à faire une même quantité de calcul qu'un processeur avec un fort MIPS. Le MIPS est surtout utilisé comme estimation de la puissance de calcul sur des nombres entiers. Mais il existe cependant une mesure annexe, utilisée pour la puissance de calcul sur les nombres flottants : le FLOPS, à savoir le nombre d'opérations flottantes par seconde.
Par définition, le nombre d'instruction par secondes se calcule en prenant le nombre d'instruction exécutée, et en divisant par le temps d’exécution, ce qui donne :
- , avec le temps moyen d’exécution d'une instruction.
Sachant que l'on a vu plus haut que , on peut faire le remplacement :
Pour simplifier les calculs, on peut remarquer que l'inverse du CPI n'est autre que le nombre de calculs qui sont effectués par cycle d'horloge. Celui-ci porte le doux nom d'IPC (Instruction Per Cycle). Celui-ci a plus de sens sur les processeurs actuels, qui peuvent effectuer plusieurs calculs en même temps, dans des circuits différents (des unités de calcul différentes, pour être précis). Sur ces ordinateurs, l'IPC est supérieur à 1. En remplaçant l'inverse du CPI par l'IPC, on a alors :
L'équation nous dit quelque chose d'assez intuitif : plus la fréquence du processeur est élevée, plus il est puissant. Cependant, des processeurs de même fréquence ont souvent des IPC différents, ce qui fait que la relation entre fréquence et puissance de calcul dépend fortement du processeur. On ne peut donc pas comparer deux processeurs sur la seule base de leur fréquence. Et si la fréquence est généralement une information qui est mentionnée lors de l'achat d'un processeur, l'IPC ne l'est pas. La raison vient du fait que la mesure de l'IPC n'est pas normalisée car l'IPC varie énormément suivant les opérations, le programme, diverses optimisations matérielles, etc.
On vient de voir que le temps d’exécution d'un programme est décrit par la formule suivante :
- , avec f la fréquence.
Les équations précédentes nous disent qu'il existe trois moyens pour accélérer un programme :
- diminuer le nombre d'instructions à exécuter ;
- diminuer le CPI (nombre de cycles par instruction) ou augmenter l'IPC ;
- augmenter la fréquence.
Diminuer le nombre d'instructions à exécuter dépend surtout du programmeur ou des compilateurs, et la conception du processeur n'a actuellement que peu d'impact à l'heure actuelle. Les deux autres solutions sont fortement impactées par la loi de Moore, et nous en parlerons au chapitre suivant.
La performance d'une mémoire
modifierToutes les mémoires ne sont pas faites de la même façon et les différences entre mémoires sont nombreuses. Dans cette partie, on va passer en revue les différences les plus importantes. La rapidité d'une mémoire se mesure grâce à deux paramètres : le temps de latence et son débit binaire.
- Le temps de latence correspond au temps qu'il faut pour effectuer une lecture ou une écriture : plus il est bas, plus la mémoire est rapide.
- Le débit mémoire correspond à la quantité d'informations qui peut être récupéré ou enregistré en une seconde dans la mémoire : plus il est élevé, plus la mémoire est rapide
Le temps d’accès d'une mémoire
modifierLa vitesse d'une mémoire correspond au temps qu'il faut pour récupérer une information dans la mémoire, ou pour y effectuer un enregistrement. Lors d'une lecture/écriture, il faut attendre un certain temps que la mémoire finisse de lire ou d'écrire la donnée : ce délai est appelé le temps d'accès, ou aussi temps de latence. Plus celui-ci est bas, plus la mémoire est rapide. Il se mesure en secondes, millisecondes, microsecondes pour les mémoires les plus rapides. Généralement, le temps de latence dépend de temps de latences plus élémentaires, qui sont appelés les timings mémoires.
Cependant, tous les accès à la mémoire ne sont pas égaux en termes de temps d'accès. Généralement, lire une donnée ne prend pas le même temps que l'écrire. Dit autrement, le temps d'accès en lecture est souvent inférieur au temps d'accès en écriture. Il faut dire qu'il est beaucoup plus fréquent de lire dans une mémoire qu'y écrire, et les fabricants préfèrent donc réduire le temps d'accès en lecture.
Voici les temps d'accès moyens en lecture de chaque type de mémoire :
- Registres : 1 nanoseconde (10-9)
- Caches : 10 - 100 nanosecondes (10-9)
- Mémoire RAM : 1 microseconde (10-6)
- Mémoires de masse : 1 milliseconde (10-3)
Le débit d'une mémoire
modifierEnfin, toutes les mémoires n'ont pas le même débit binaire. Le débit binaire d'une mémoire est la quantité de données qu'on peut lire ou écrire par seconde. Il se mesure en octets par seconde ou en bits par seconde. Évidemment, plus ce débit est élevé, plus la mémoire sera rapide.
Il ne faut pas confondre le débit et le temps d'accès. Pour faire une analogie avec les réseaux, le débit binaire peut être vu comme la bande passante, alors que le temps d'accès serait similaire au ping. Il est parfaitement possible d'avoir un ping élevé avec une connexion qui télécharge très vite, et inversement. Pour la mémoire, c'est similaire. D'ailleurs, le débit binaire est parfois improprement appelé bande passante.
Le temps de balayage
modifierLe temps de balayage d'une mémoire est le temps mis pour parcourir/accéder à toute la mémoire. Concrètement, il est défini en divisant la capacité de la mémoire par son débit binaire. Le résultat s'exprime en secondes. Le temps de balayage est en soi une mesure peu utilisée, sauf dans quelques applications spécifiques. C'est le temps nécessaire pour lire ou réécrire tout le contenu de la mémoire. On peut le voir comme une mesure du compromis réalisé entre la capacité de la mémoire et sa rapidité : une mémoire aura un temps de balayage d'autant plus important qu'elle est lente à capacité identique, ou qu'elle a une grande capacité à débit identique. Généralement un temps de balayage faible signifie que la mémoire est rapide par rapport à sa capacité.
Comme dit plus haut, le temps d'accès est différent pour les lectures et les écritures, et il en est de même pour le débit binaire. En conséquence, le temps de balayage n'est pas le même si le balayage se fait en lecture ou en écriture. On doit donc distinguer le temps de balayage en lecture qui est le temps mis pour lire la totalité de la mémoire, et le temps de balayage en écriture qui est le temps mis pour écrire une donnée dans toute la mémoire. Généralement, on balaye une mémoire en lecture quand on veut recherche une donnée bien précise dedans. Par contre, le balayage en écriture correspond surtout aux cas où on veut réinitialiser la mémoire, la remplir tout son contenu avec des zéros afin de la remettre au même état qu'à son démarrage.
Un exemple de balayage en écriture est celui d'une réinitialisation de la mémoire, à savoir remplacer le contenu de chaque case mémoire par un 0. Le temps nécessaire pour réinitialiser la mémoire n'est autre que le temps de balayage en écriture. En soi, les opérations de réinitialisation de la mémoire sont plutôt rares. Certains vieux ordinateurs effaçaient la mémoire à l'allumage, et encore pas systématiquement, mais ce n'est plus le cas de nos jours. Un cas plus familier est celui du formatage complet du disque dur. Si vous voulez formater un disque dur ou une clé USB ou tout autre support de stockage, le système d'exploitation va vous donner deux choix : le formatage rapide et le formatage complet. Le formatage rapide n'efface pas les fichiers sur le disque dur, mais utilise des stratagèmes pour que le système d'exploitation ne puisse plus savoir où ils sont sur le support de stockage. Les fichiers peuvent d'ailleurs être récupérés avec des logiciels spécialisés trouvables assez facilement. Par contre, le formatage complet efface la totalité du disque dur et effectue bel et bien une réinitialisation. Le temps mis pour formater le disque dur n'est autre que le temps de balayage en écriture.
Un autre cas de réinitialisation de la mémoire est celui de l'effacement du framebuffer sur les très vielles cartes graphiques. Sur les vielles cartes graphiques, la mémoire vidéo ne servait qu'à stocker des images calculées par le processeur. Le processeur calculait l'image à afficher et l'écrivait dans la mémoire vidéo, appelée framebuffer. Puis, l'image était envoyée à l'écran quand celui-ci était libre, la carte graphique gérant l'affichage. L'écran affichait généralement 60 images par secondes, et le processeur devait calculer une image en moins de 1/60ème de seconde. Mais si le processeur mettait plus de temps, l'image dans le framebuffer était un mélange de l'ancienne image et des parties de la nouvelle image déjà calculées par le processeur. L'écran affichait donc une image bizarre durant 1/60ème de seconde, ce qui donnait des légers bugs graphiques très brefs, mais visibles. Pour éviter cela, le framebuffer était effacé entre chaque image calculée par le processeur. Au lieu d'afficher un bug graphique, l'écran affichait alors une image blanche en cas de lenteur du processeur. Cette solution était possible, car les mémoires de l'époque avaient un temps de balayage en écriture assez faible. De nos jours, cette solution n'est plus utilisée, car la mémoire vidéo stocke d'autres données que l'image à afficher à l'écran, et ces données ne doivent pas être effacées.
Le temps de balayage en lecture est surtout pertinent dans les cas où on recherche une donnée précise dans la mémoire. L'exemple le plus frappant est celui des antivirus, qui recherchent si une certaine suite de donnée est présente en mémoire RAM. Les antivirus scannent régulièrement la RAM à la recherche du code binaire de virus, et doivent donc balayer la RAM et appliquer des algorithmes assez complexes sur les données lues. Bref, le temps de balayage donne le temps nécessaire pour scanner la RAM, si on oublie le temps de calcul. Tous les exemples précédents demandent de scanner la RAM à la recherche d'une donnée précise, et le temps de balayage donne une borne inférieure à ce temps de recherche. Cet exemple n'est peut-être pas très réaliste, mais il deviendra plus clair dans le chapitre sur les mémoires associatives, un type de mémoire particulier conçu justement pour réduire le temps de balayage en lecture au strict minimum.
Enfin, on peut aussi citer le cas où l'on souhaite vérifier le contenu de la mémoire, pour vérifier si tous les bytes fonctionnent bien. Il arrive que les mémoires RAM aient des pannes : certains bytes tombent en panne après quelques années d'utilisation, et deviennent inaccessibles. Lorsque cela arrive, tout se passe bien tant que les bytes défectueux ne sont pas lus ou écrits. Mais quand cela arrive, les lectures renvoient des données incorrectes. Les conséquences peuvent être très variables, mais cela cause généralement des bugs assez importants, voire des écrans ou de beaux plantages. De nombreux cas d'instabilité système sont liés à ces bytes défectueux. Il est possible de vérifier l'intégrité de la mémoire avec des logiciels spécialisés, qui vérifient chaque byte de la mémoire un par un. Les systèmes d'exploitation modernes incorporent un logiciel de ce genre, comme Windows qui en a un d'intégré. Le BIOS ou l'UEFI de votre ordinateur a de bonnes chances d'intégrer un logiciel de ce genre. Ces logiciels de diagnostic mémoire balayent la mémoire byte par byte, case mémoire par case mémoire, et effectuent divers traitements dessus. Dans le cas le plus simple, ils écrivent une donnée dans chaque byte, avant de le lire : si la donnée lue et écrite ne sont pas la même, le byte est défectueux. Mais d'autres traitements sont possibles. Toujours est-il que ces utilitaires balayent la mémoire, généralement plusieurs fois. Le temps de balayage donne alors une idée du temps que mettront ces logiciels de diagnostic pour s’exécuter.
La performance d'un bus
modifierLa performance d'un bus est quelque chose de complexe à décrire. Mais le critère principal est le débit binaire. Le débit binaire est la quantité de données que le bus peut transmettre d'un composant à un autre, par seconde. Il se mesure en octets par seconde ou en bits par seconde. Les bus haute performance sont capables de transmettre un grand nombre de données par seconde, alors que ceux de basse performance ne peuvent échanger qu'un petit nombre de données sur le bus.
Le débit binaire d'un bus est influencé par deux autres paramètres : sa largeur et sa fréquence. La fréquence du bus est assez simple à comprendre : le bus est cadencé par une horloge, qui a une certaine fréquence. A chaque cycle, il transfère plusieurs bits à la fois. Le nombre de bits transmis en même temps est appelé la largeur du bus. Par exemple, un bus d'une largeur de 16 bits peut transférer deux octets par cycle d'horloge. La largeur du bus correspond au nombre de fils utilisés pour transférer les données. Si un bus peut transférer 8 bits par cycle, cela signifie que ce bus dispose de 8 fils, un par bit, chaque fil peut transmettre un bit par cycle. Le débit binaire est le produit de la largeur du bus par sa fréquence.
Les limites de la performance des applications : le roofline model
modifierPlus haut, nous avons parlé des performances du processeur et de la mémoire de manière isolée. Dans les faits, les programmes qui s'exécutent sur un processeur utilisent les deux, et à des degrés divers. Il y a un continuum entre des programmes qui accèdent beaucoup à la mémoire et font peu de calculs, et les programmes opposé qui font beaucoup de calculs mais accèdent peu à la RAM. Un programme très gourmand en calculs profitera d'un processeur rapide, même si la mémoire RAM est lente. Et inversement, un programme qui accède beaucoup à la mémoire a besoin d'une mémoire RAM rapide, même si le processeur ne suit pas.
- Dans le même genre, les personnes afficionados de jeux vidéos ont sans doute entendu parler du bottleneck CPU/GPU pour désigner les jeux vidéo dont le framerate est limité soit le CPU ou par la carte graphique. La performance est alors la responsabilité partagée du processeur et de la carte graphique, mais l'un des deux sera le facteur limitant.
Pour quantifier ce genre de compromis, Samuel Williams, Andrew Waterman, et David Patterson, ont inventé le roffline model, initialement été décrit dans cet article scientifique :
Nous allons décrire ce modèle dans ce chapitre. Il est souvent vu dans les chapitres sur les architectures parallèles dans les rares cours d'architecture des ordinateur qui en font mention, mais il s'agit bel et bien d'un modèle qui marche sur les architectures à un seul cœur/processeur.
Le modèle de base
modifierLe modèle introduit le concept d'intensité calculatoire. Il s'agit du nombre d'opérations réalisées pour un octet lu/écrit depuis la mémoire RAM. Elle varie suivant le programme considéré, tous les programmes n'ont pas la même intensité calculatoire. En clair, il s'agit du nombre d’opérations réalisé par un programme, divisé par le débit binaire mémoire. Le débit binaire utilisé est celui de la mémoire RAM, pas des caches, car la mémoire est supposée partagée.
A forte intensité calculatoire, on fait beaucoup de calculs comparé aux accès mémoires. On demande donc plus au processeur qu'à la mémoire. A basse intensité calculatoire, on accède beaucoup à la mémoire et on fait peu d'opérations. La mémoire est donc le facteur limitant. Globalement, au-delà d'une certaine intensité calculatoire, c'est le processeur qui sera limitant (et inversement, ce sera la mémoire). Il existe un point d'équilibre où la mémoire et la performance des CPU sont tous deux des facteurs limitants, le système est parfaitement équilibré.
Le roofline donne la performance totale, qui est limitée par le débit de la mémoire, par la performance maximale des CPUs parallèles exprimée en MIPS/FLOPS, et par l'intensité calculatoire. Le modèle est un simple diagramme en deux dimensions, avec l'intensité calculatoire en abscisse, et la performance en ordonnée. Plus l'intensité calculatoire augmente, plus les performances augmentent, à débit binaire égal. La mémoire est alors le facteur limitant, et on fait alors plus de calcul à débit binaire égal. Mais au-delà d'une intensité calculatoire bien précise, le débit binaire n'est plus le facteur limitant, mais c'est le processeur qui limite les performances. On a atteint un plateau dépendant des CPUs.

Les calculs qui permettent d'obtenir la courbe du modèle
modifierPour obtenir la courbe, rien de plus simple. Le modèle part du principe qu'il y a une puissance de calcul maximale indépassable, exprimée en FLOPS ou en MIPS. Il s'agit de la limite maximale obtenable en ne tenant compte que du processeur, pas du débit de la mémoire. Elle correspond à la portion plate de la courbe. Notons la puissance de calcul maximale permise par le CPU .
Maintenant, la performance est aussi limitée par le débit binaire de la mémoire. Si l'on a un débit binaire de , alors la performance maximale se calcule en multipliant ce débit binaire par l'intensité calculatoire. Ce dernier est un nombre de calculs par octet lu/écrit, on multiplie par le nombre total d'octets lus/écrits : on a bien une puissance de calcul. En notant le résultat, on a :
- , avec I l'intensité calculatoire et le débit binaire.
La puissance réelle dépend des deux limites. Elle ne peut pas dépasser la performance max permise par le CPU, pas plus qu'elle ne peut dépasser celle permise par le débit de la RAM. En clair, la performance maximale possible est la plus petite valeur entre les deux :

Les limites du modèle
modifierIl faut préciser que le modèle donne une limite maximale pour la performance. Dans les faits, les applications ne l'atteindront pas. Elle auront une performance inférieure à la limite maximale, pour une intensité arithmétique donnée. La performance réelle sera parfois très proche, parfois très éloignée de la performance maximale.

Les raisons à cela sont multiples. La première est tout simplement que le processeur n'utilise pas son plein potentiel, sans que ce soit lié à la mémoire ou aux caches. Par exemple, il n'arrive pas à alimenter ses circuits de calculs pour des raisons diverses et variées. Le plafond est alors plus bas qu'il n'y parait et quelques optimisations logicielles permettent de faire remonter le plafond effectif.

Il est aussi possible que le programme considéré n'utilise pas bien le débit binaire de la mémoire, une partie est gâchée par des accès mémoire inutiles. Diverses optimisations logicielles ou matérielles permettent alors de se rapprocher du maximum théorique dans la portion limitée par la mémoire. Sans ces optimisations, la courbe a une pente décalée vers la droite, car le programme fait moins d'accès mémoire pour une intensité arithmétique inchangée.

Notons que le débit binaire considéré dans le modèle est celui de la mémoire RAM. L'usage de mémoires caches change la donne d'une manière assez originale. Une mauvaise utilisation des caches fait que l'intensité arithmétique stagnera à un niveau maximal. En clair, cela se traduit par des barrières verticales sur le diagramme, que le programme ne pourra pas dépasser. Le programme restera à gauche, dans la partie limitée par la barrière. Et celle-ci est systématiquement dans la portion gauche de la courbe, celle limitée par la mémoire.

Pour résumer, le modèle peut aider les programmeurs à savoir quoi optimiser, s'ils savent faire des mesures adéquates sur un grand nombre de hardware différents. Mais il nous dit plusieurs choses importantes : un programme peut être limité soit par le CPU, soit par le débit binaire de la mémoire, soit par une mauvaise utilisation des caches. Par un programme ne se comportera de la même manière qu'un autre, les compromis seront différents du fait d'intensité arithmétiques différentes. Et suivant la machine, un même programme se comportera très différemment. Il y a donc une grande variabilité des performances d'un programme et d'une machine à l'autre.
De plus, les programmeurs doivent faire face à des compromis lorsqu'ils optimisent. Par exemple, optimiser l'intensité arithmétique en améliorant l'utilisation des mémoires caches ou en réduisant les accès mémoire a du sens, mais seulement si la performance est limitée par la mémoire. Mais une telle optimisation ne servira à rien si le facteur limitant est la performance du processeur. Dans le passé, c'était surtout la performance des mémoire et du processeur qui étaient limitante. Mais de nos jours, le problème tient surtout dans les caches et la bonne utilisation de la hiérarchie mémoire, du moins pour une majorité de programmes. Les situations sont assez variables, mais les grandes lignes du hardware actuel sont là : les processeurs sont des monstres de puissance théorique, les mémoires RAM ont un débit absolument énorme, mais on se heurte aux barrières liées aux mémoires caches.
Il va de soi que les nouveaux processeurs sont plus puissants que les anciens, pareil pour les mémoires. La raison à cela vient des optimisations apportées par les concepteurs de processeurs. La plupart de ces optimisations ne sont cependant possibles qu'avec la miniaturisation des transistors, qui leur permet d'aller plus vite. Et cela se voit dans les données empiriques. Il est intéressant de regarder comment les mémoires et processeurs ont évolué dans le temps.
Pour les processeurs, la loi de Moore a des conséquences qui sont assez peu évidentes. Certes, on peut mettre plus de transistors dans un processeur, mais en quoi cela se traduira par de meilleures performances ? Pour comprendre l'influence qu'à eu la loi de Moore sur les processeurs modernes, regardons ce graphique, qui montre les relations entre nombre de transistors, fréquence du processeur, performance d'un seul cœur, nombre de cœurs, et consommation énergétique.

Globalement, on voit que le nombre de transistors augmente de façon exponentielle : doubler tous les X années donne une courbe exponentielle, d'où l'échelle semi-logarithmique du graphique. Mais pour le reste, quelque chose s'est passé en 2005 : les courbes n'ont pas la même pente avant et après 2005. Que ce soit la fréquence, la performance d'un seul cœur, la consommation électrique, tout. Et le nombre de cœurs explose au même moment. Tout cela fait penser que toutes ces caractéristiques étaient liées entre elles et augmentaient exponentiellement, mais il y a un après 2005. Reste à expliquer pourquoi, ce qui est le sujet de ce chapitre, sans compter qu'on détaillera tout ce qui a trait à la consommation énergétique.
La miniaturisation des transistors est la cause des tendances technologiques
modifierAvant toute chose, nous devons faire quelques rappels sur les transistors MOS, sans lesquels les explications qui vont suivre seront compliquées. Un transistor MOSFET a de nombreuses caractéristiques : ses dimensions, mais aussi d'autres paramètres plus intéressants. Par exemple, il est intéressant de regarder la consommation d'énergie d'un transistor, à savoir combien de watts ils utilise pour faire ce qu'on lui demande. Pour cela, il faudra parler rapidement de certaines de ses caractéristiques comme sa capacité électrique. Rien de bien compliqué, rassurez-vous.
Les caractéristiques d'un transistor : finesse de gravure, capacité, etc
modifier
Un transistor MOS est composé de deux morceaux de conducteurs (l'armature de la grille et la liaison drain-source) séparés par un isolant. Les dimensions d'un transistors sont au nombre de deux : la distance entre source et drain, la distance entre grille et semi-conducteur. Les deux sont regroupées sous le terme de finesse de gravure, bien que cela soit un terme impropre.
Nous avons dit plus haut qu'un transistor MOS est composé de deux (semi-)conducteurs séparés par un isolant. Tout cela ressemble beaucoup à un autre composant électronique appelé le condensateur, qui sert de réservoir à électricité. On peut le charger en électricité, ou le vider pour fournir un courant durant une petite durée de temps. L'intérieur d'un condensateur est formé de deux couches de métal conducteur, séparées par un isolant électrique. Les charge s'accumulent dans les couche de métal quand on charge le condensateur en électricité. L'intérieur d'un transistor MOS est donc similaire à celui d'un condensateur, si ce n'est qu'une couche métallique est remplacée par un morceau de semi-conducteur. Tout cela fait qu'un transistor MOS incorpore un pseudo-condensateur caché entre la grille et la liaison source-drain, qui porte le nom de capacité parasite du transistor.
Tout condensateur possède une caractéristique importante : sa capacité électrique. Il s'agit simplement de la quantité d'électrons/charges qu'il peut contenir en fonction de la tension. Il faut savoir que la quantité de charge contenue dans un condensateur est proportionnelle à la tension, la capacité est le coefficient de proportionnalité entre les deux. Tout cela est sans doute plus clair avec une équation :
- , avec Q la quantité de charges contenues dans le condensateur, U la tension, et C la capacité.

La capacité d'un transistor MOS a une influence directe sur la fréquence à laquelle il peut fonctionner. Pour changer l'état d'un transistor MOS, il faut soit charger la grille, soit la décharger. Et pour remplir le transistor, il faut fournir une charge égale à celle donnée par l'équation précédente.
Si on met ce processus en équations, on s’aperçoit qu'on se trouve avec des charges ou décharges exponentielles. Mais par simplicité, on considère que le temps de charge/décharge d'un condensateur est proportionnel à sa capacité (pour être précis, proportionnel au produit 5 RC, avec R la résistance des fils). Tout ce qu'il faut retenir est que plus la capacité est faible, plus le transistor est rapide et plus il peut fonctionner à haute fréquence.
Les lois de Dennard, ce qui se cache derrière la loi de Moore
modifierLa loi de Moore est le résultat d'une tendance technologique bien précise : les dimensions d'un transistors se réduisent avec les progrès de la miniaturisation. Elles sont réduites de 30% tous les deux ans. Pour le dire autrement, elles sont multipliées par 0.7 tous les deux ans.
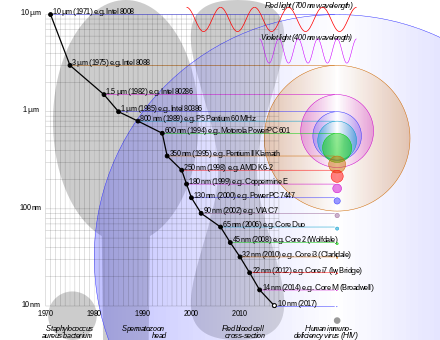
Les processeurs sont des composants qui ont actuellement une forme carrée, les transistors sont tous placés sur un plan et ne sont pas empilés les uns sur les autres. Ils occupent donc une certaine aire sur la surface du processeur. Si la taille des transistors est réduite de 30% tous les 2 ans, l'aire que prend un transistor sur la puce est quand à elle divisée par 30% * 30% 50%. En conséquence, on peut mettre deux fois plus de transistors sur la même puce électronique : on retrouve la loi de Moore.
Cela a aussi des conséquences sur la tension d'alimentation nécessaire pour faire fonctionner le transistor. Sans rentrer dans les détails, la tension est elle aussi proportionnelle aux dimensions du transistor. La raison technique, que vous comprendrez si vous avez eu des cours d'électricité avancés durant votre scolarité, est que le champ électrique ne change pas dans le transistor, et que la tension est le produit du champ électrique par la distance. Là encore, la tension d'alimentation est réduite de 30% tous les deux ans.

La miniaturisation a une influence directe sur la capacité électrique du transistor. Pour comprendre pourquoi, il faut savoir que le condensateur formé par la grille, l'isolant et le morceau de semi-conducteur est ce que l'on appelle un condensateur plan. La capacité de ce type de condensateur dépend de la surface de la plaque de métal (la grille), du matériau utilisé comme isolant et de la distance entre la grille et le semi-conducteur. On peut calculer cette capacité comme suit, avec A la surface de la grille, e un paramètre qui dépend de l'isolant utilisé et d la distance entre le semi-conducteur et la grille (l'épaisseur de l'isolant, quoi).
Le coefficient e (la permittivité électrique) reste le même d'une génération de processeur à l'autre, même si les fabricants ont réussit à le faire baisser un peu grâce à matériaux particuliers. Mais laissons cela de côté : dans les faits, seuls les coefficients S et d vont nous intéresser. Si la finesse de gravure diminue de 30%, la distance d diminue du même ordre, la surface A diminue du carré de 30%, c’est-à-dire qu'elle sera approximativement divisée par 2. La capacité totale sera donc divisée par 30% tous les deux ans.
Réduire la capacité des transistors a un impact indirect très fort sur la fréquence à laquelle on peut faire fonctionner le transistor. En effet, la période de l'horloge correspond grosso modo au temps qu'il faut pour remplir ou vider l'armature de la grille, et on sait que le temps de charge/décharge d'un condensateur est approximativement proportionnel à sa capacité. La capacité et le temps de charge/décharge est donc réduit de 30% tous les deux ans. La fréquence étant inversement proportionnelle au temps de remplissage du condensateur, elle est donc augmentée de 1/0.7 = 40%.
Tout ce qu'on vient de dire plus a été formalisé sous le nom de lois de Dennard, du nom de l'ingénieur qui a réussi à démontrer ces équations à partir des lois de la physique des semi-conducteurs. Une réduction de la finesse de gravure impacte plusieurs paramètres : le nombre de transistors d'une puce électronique, sa tension d'alimentation, sa fréquence, et quelques autres paramètres qu'on détaillera plus bas comme la capacité d'un transistor ou ses courants de fuite.
| Paramètre | Coefficient multiplicateur (tous les deux ans) | Variation en pourcentage |
|---|---|---|
| Finesse de gravure | 0.7 | - 30% |
| Aire occupée par un transistor | 0.5 | - 50% |
| Nombre de transistors par unité de surface | 2 | + 100% |
| Tension d'alimentation | 0.7 | - 30% |
| Capacité d'un transistor | 0.7 | - 30% |
| Fréquence | (1/0.7) = 1.4 | + 40% |
La fin des lois de Dennard
modifierLes lois de Dennard ont cessé de s'appliquer aux alentours de 2005/2006. Les dimensions d'un transistors sont toujours réduites de 30% tous les deux ans, la loi de Moore est encore valable, mais pour ce qui est de la fréquence et de la tension d'alimentation, c'est autre chose. Les raisons à cela sont multiples, et il faut revenir au fonctionnement d'un transistor MOS pour comprendre pourquoi.
Un MOSFET est composé d'une grille métallique, d'une couche de semi-conducteur, et d'un isolant entre les deux. L'isolant empêche la fuite des charges de la grille vers le semi-conducteur. Mais avec la miniaturisation, la couche d'isolant ne fait guère plus de quelques dizaines atomes d'épaisseur et laisse passer un peu de courant : on parle de courants de fuite. Plus cette couche d'isolant est petite, plus le courant de fuite sera fort. En clair, une diminution de la finesse de gravure a tendance à augmenter les courants de fuite.
Les courants de fuite dépendent d'une tension appelée tension de seuil. Il s'agit de la tension minimale pour avoir un courant passant entre la source et le drain. Sous cette tension, le transistor se comporte comme un interrupteur fermé, peut importe ce qu'on met sur la grille. Au-dessus de cette tension, le courant se met à passer entre source et drain, il se comporte comme un interrupteur ouvert. Le courant est d'autant plus fort que la tension sur la grille dépasse la tension de seuil. On ne peut pas faire fonctionner un transistor si la tension d'alimentation (entre source et drain) est inférieure à la tension de seuil. C'est pour cela que ces dernières années, la tension d'alimentation des processeurs est restée plus ou moins stable, à une valeur proche de la tension de seuil (1 volt, environ). Et l'incapacité à réduire cette tension a eu des conséquences fâcheuses.
Nous verrons plus bas que la consommation d'énergie d'un processeur dépend de sa fréquence et de sa tension. Les lois de Dennard nous disent que Si la seconde baisse, on peut augmenter la première sans changer drastiquement la consommation énergétique. Mais si la tension d'alimentation stagne, alors la fréquence doit faire de même. Vu que les concepteurs de processeurs ne pouvaient pas diminuer la fréquence pour garder une consommation soutenable, et ont donc préféré augmenter le nombre de cœurs. L'augmentation de consommation énergétique ne découle que de l'augmentation du nombre de transistors et des diminutions de capacité. Et la diminution de 30 % tous les deux ans de la capacité ne compense plus le doublement du nombre de transistors : la consommation énergétique augmente ainsi de 40 % tous les deux ans. Bilan : la performance par watt stagne. Et ce n'est pas près de s'arranger tant que les tensions de seuil restent ce qu'elles sont.
L'explication est convaincante, mais nous détaillerons celle-ci plus bas, avec les vraies équations qui donnent la consommation d'énergie d'un processeur. Nous en profiterons aussi pour voir quelles sont les technologies utilisées pour réduire cette consommation d'énergie, les deux étant intrinsèquement liés.
La consommation d'un circuit électronique CMOS
modifierTout ordinateur consomme une certaine quantité de courant pour fonctionner, et donc une certaine quantité d'énergie. On peut dire la même chose de tout circuit électronique, que ce soit une mémoire, un processeur, ou quoique ce soit d'autre d'électronique. Il se trouve que cette énergie finit par être dissipée sous forme de chaleur : plus un composant consomme d'énergie, plus il chauffe. La chaleur dissipée est mesurée par ce qu'on appelle l'enveloppe thermique, ou TDP (Thermal Design Power), mesurée en Watts.
Pour donner un exemple, le TDP d'un processeur tourne autour des 50 watts, parfois plus sur les modèles plus anciens. De telles valeurs signifient que les processeurs actuels chauffent beaucoup. Pourtant, ce n'est pas la faute des fabricants de processeurs qui essaient de diminuer la consommation d'énergie de nos CPU au maximum. Malgré cela, les processeurs voient leur consommation énergétique augmenter toujours plus : l'époque où l'on refroidissait les processeurs avec un simple radiateur est révolue. Place aux gros ventilateurs super puissants, placés sur un radiateur.
La consommation d'un circuit électronique CMOS
modifierPour comprendre pourquoi, on doit parler de ce qui fait qu'un circuit électronique consomme de l'énergie. Une partie de la consommation d'énergie d'un circuit vient du fait qu'il consomme de l'énergie en changeant d'état. On appelle cette perte la consommation dynamique. A l’opposé, la consommation statique vient du fait que les circuits ne sont pas des dispositifs parfaits et qu'ils laissent fuiter un peu de courant.
Pour commencer, rappelons qu'un transistor MOS est composé de deux morceaux de conducteurs (l'armature de la grille et la liaison drain-source) séparés par un isolant. L'isolant empêche la fuite des charges de la grille vers la liaison source-drain. Charger ou décharger un condensateur demande de l'énergie. Les lois de la physique nous disent que la quantité d'énergie que peut stocker un condensateur est égale au produit ci-dessous, avec C la capacité du condensateur et U la tension d'alimentation. Il s'agit de l'énergie qu'il faut fournir quand on charge ou décharger un condensateur/MOSFET.
L'énergie est dissipée quand les transistors changent d'état, il dissipe une quantité de chaleur proportionnelle au carré de la tension d'alimentation. Or, la fréquence définit le nombre maximal de changements d'état qu'un transistor peut subir en une seconde : pour une fréquence de 50 hertz, un transistor peut changer d'état 50 fois par seconde maximum. Après, il s'agit d'une borne maximale : il se peut qu'un transistor ne change pas d'état à chaque cycle. Sur les architectures modernes, la probabilité de transition 0 ⇔ 1 étant d'environ 10%-30%. Et si les bits gardent la même valeur, alors il n'y a pas de dissipation de puissance. Mais on peut faire l'approximation suivante : le nombre de changement d'état par seconde d'un transistor est proportionnel à la fréquence. L'énergie dissipée en une seconde (la puissance P) par un transistor est approximée par l'équation suivante :
On peut alors multiplier par le nombre de transistors d'une puce électronique, ce qui donne :
Cette équation nous donne la consommation dynamique, à savoir celle liée à l'activité du processeur/circuit. De plus, l'équation précédente permet de comprendre comment la consommation dynamique a évolué grâce à la loi de Moore. Pour cela, regardons comment chaque variable a évolué et faisons les comptes :
- le nombre de transistors fait *2 tous les deux ans ;
- la capacité est réduite de 30% tous les deux ans ;
- la tension d'alimentation est réduite de 30% tous les deux ans ;
- la fréquence augmente de 40% tous les deux ans.
L'augmentation du nombre de transistors est parfaitement compensé par la baisse de la tension d'alimentation : multiplication par deux d'un côté, divisé par 2 (30% au carré) de l'autre. Idem avec la capacité et la fréquence : la capacité est multipliée par 0.7 tous les deux ans, la fréquence est multipliée par 1.4 de l'autre, et . En clair, la consommation dynamique d'un processeur ne change pas dans le temps, du moins tant que les lois de Dennard sont valides. Ce qui n'est plus le cas depuis 2005.
Tout ce qui est dit plus haut part du principe que le transistor MOS est un dispositif parfait. Dans les faits, ce n'est pas le cas. En effet, la couche d'isolant entre la grille et le semi-conducteur est très petite. Avec la miniaturisation, la couche d'isolant ne fait guère plus de quelques dizaines atomes d'épaisseur et laisse passer un peu de courant : on parle de courants de fuite. La consommation d'énergie qui résulte de ce courant de fuite est la consommation statique. Elle s'appelle statique car elle a lieu même si les transistors ne changent pas d'état.
La diminution de la finesse de gravure a tendance à augmenter les courants de fuite. Elle diminue la consommation dynamique, mais augmente la consommation statique. Vu que les processeurs anciens avaient une consommation statique ridiculement basse et une consommation dynamique normale, doubler la première et diviser par deux la seconde donnait un sacré gain au total.
Quantifier la consommation statique est assez compliqué, et les équations deviennent généralement très complexes. Mais une simplification nous dit que les courants de fuite dépendent de la tension de seuil. Une équation très simplifiée est la suivante :
- , avec la tension de seuil, et K une constante.
La consommation statique est le produit des courants de fuite et de la tension d'alimentation, avec d'autres facteurs de proportionnalités qui ne nous intéressent pas ici.
- , avec U la tension d'alimentation.
La loi de Kommey
modifierAvant 2005, la réduction de la finesse de gravure permettait de diminuer la consommation d'énergie, tout en augmentant la puissance de calcul. Mais depuis, la consommation statique a fini par rattraper la consommation dynamique. Et cela a une conséquence assez importante. L'efficacité énergétique des processeurs n'a pas cessé d'augmenter au cours du temps : pour le même travail, les processeurs chauffent moins. Globalement, le nombre de Watts nécessaires pour effectuer une instruction a diminué de manière exponentielle avec les progrès de la miniaturisation.

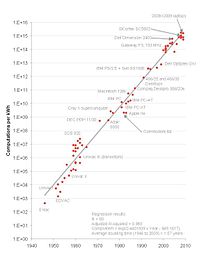
Il est aussi intéressant d'étudier la performance par watts, à savoir le nombre de Millions d'instructions par secondes pour chaque watt/kilowatt dépensé pour faire le calcul. Avant l'année 2005, la quantité de calcul que peut effectuer le processeur en dépensant un watt double tous les 1,57 ans. Cette observation porte le nom de loi de Kommey. Mais depuis 2005, on est passé à une puissance de calcul par watt qui double tous les 2,6 ans. Il y a donc eu un ralentissement dans l'efficacité énergétique des processeurs.
Le dark silicon et le mur du TDP
modifierMalgré les nombreuses améliorations de la performance par watt dans le temps, les processeurs actuels chauffent beaucoup et sont contraints par les limites thermiques. Et ces limites thermiques se marient assez mal avec le grand nombre de transistors présents sur les processeurs modernes. Dans un futur proche, il est possible que les contraintes thermiques limitent le nombre de transistors actifs à un instant donné. Pour le dire autrement, il serait impossible d'utiliser plus de 50% des transistors d'un CPU en même temps, ou encore seulement 30%, etc. Ce genre de scénarios ont reçu le nom d'"utilization wall" dans la communauté académique.
Il y aurait donc un certain pourcentage du processeur qui ne pourrait pas être activée en raison des performances thermiques, portion qui porte le nom de dark silicon. Mais le dark silicon n'est pas du circuit inutile. Il faut bien comprendre que ce dark silicon n'est pas une portion précise de la puce. Par exemple, imaginons que 50% d'un processeur soit du dark silicon : cela ne veut pas dire que 50% du CPU ne sert à rien, mais que les deux moitié du processeur se passent le flambeau régulièrement, ils sont utilisés à tour de rôle.
En soi, le fait que tous les transistors ne soient pas actifs en même temps n'est pas un problème. Les processeurs modernes n'utilisent pas tous leurs circuits en même temps, et certains restent en pause tant qu'on ne les utilise pas. Par exemple, sur un processeur multicœurs, il arrive que certains cœurs ne soient pas utilisés, et restent en veille, voire soient totalement éteints. Par exemple, sur un processeur octo-coeurs, si seuls 4 cœurs sur les 8 sont utilisés, alors 50% du processeur est techniquement en veille.
L'existence du dark silicon implique cependant qu'il faut construire les processeurs en tenant compte de sa présence, du fait que les contrainte thermiques empêchent d'utiliser une portion significative des transistors à un instant t. Pour cela, l'idée en vogue actuellement est celle des architectures hétérogènes, qui regroupent des processeurs très différents les uns des autres sur la même puce, avec chacun leur spécialisation.
Le premier cas existe déjà à l'heure actuelle. Il s'agit de processeurs qui regroupent deux types de cœurs : des cœurs optimisés pour la performance, et des cœurs optimisés pour la performance. Un exemple est celui des processeurs Intel de 12ème génération et plus, qui mélangent des P-core et des E-core, les premiers étant des coeurs très performants mais gourmands en énergie, les autres étant économes en énergie et moins performants. Les noms complets des coeurs trahissent le tout : Efficiency core et Performance core. L'utilité des E-core est d'exécuter des programmes peu gourmands, généralement des tâches d'arrière-plan. Les processeurs ARM de type BIG.little faisaient la même chose, mais avec un cœur de chaque type.
Le second cas est celui des processeurs regroupant un ou plusieurs cœurs normaux, généralistes, complétés par plusieurs accélérateurs spécialisés dans des tâches précises. Par exemple, on peut imaginer que le processeur incorpore un circuit spécialisé dans les calculs cryptographiques, un circuit spécialisé dans le traitement d'image, un autre dans le traitement de signal, un autre pour accélérer certains calculs liés à l'IA, etc. De tels circuits permettent des gains de performance dans des tâches très précises, qui ne se mélangent pas. Par exemple, si on lance un vidéo, le circuit de traitement d'image/vidéo sera activé, mais l'accélérateur cryptographique et l'accélération d'IA seront désactivés.
En soi, le fait d'adapter l'architecture des ordinateurs pour répondre à des contraintes thermiques n'est pas nouvelle. Nous verrons plus bas que l'apparition des processeurs multicœurs dans les années 2000 est une réponse à des contraintes technologiques assez strictes concernant la température, par exemple. La fin de la loi de Dennard a grandement réduit l'amélioration de performance par watt des processeurs à un seul cœur, rendant les processeurs multicœurs plus intéressants. Mais expliquer pourquoi demande d'expliquer pas mal de choses sur la performance d'un processeur simple cœur et comment celle-ci évolue avec la loi de Moore.
L'évolution de la performance des processeurs
modifierLes processeurs ont gagné en performance avec le temps. Les raisons à cela sont doubles, mais liées aux lois de Dennard. La première raison est la hausse de la fréquence. C'était une source importante avant 2005, avant que les lois de Dennard cessent de fonctionner. L'autre raison, est la loi de Moore. Mettre plus de transistors permet de nombreuses optimisations importantes, comme utiliser des circuits plus rapide,s mais plus gourmands en circuits. Voyons les deux raisons l'une après l'autre.
La fréquence des processeurs a augmenté
modifierLes processeurs et mémoires ont vu leur fréquence augmenter au fil du temps. Pour donner un ordre de grandeur, le premier microprocesseur avait une fréquence de 740 kilohertz (740 000 hertz), alors que les processeurs actuels montent jusqu'à plusieurs gigahertz : plusieurs milliards de fronts par secondes ! L'augmentation a été exponentielle, mais plus faible que le nombre de transistors. Les nouveaux processeurs ont augmenté en fréquence, grâce à l'amélioration de la finesse de gravure. On est maintenant à environ 3 GHz à mi-2020.
Plus haut, on a dit que la fréquence augmentait de 40% tous les deux ans, tant que la loi de Dennard restait valide, avant 2005. En réalité, cette augmentation de 40% n'est qu'une approximation : la fréquence effective d'un processeur dépend fortement de sa conception (de la longueur du pipeline, notamment). Pour mettre en avant l'influence de la conception du processeur, il est intéressant de calculer une fréquence relative, à savoir la fréquence à finesse de gravure égale. Elle est difficile à calculer, mais on peut l'utiliser pour comparer des processeurs entre eux, à condition de prendre la fréquence d'un processeur de référence.
Quelques observations montrent qu'elle a subi pas mal de variation d'un processeur à l'autre. La raison est que diverses techniques de conception permettent de gagner en fréquence facilement, la plus importante étant le pipeline. Augmenter la fréquence relative était une approche qui a eu son heure de gloire, mais qui a perdu de sa superbe. Avant les années 2000, augmenter la fréquence permettait de gagner en performance assez facilement. De plus, la fréquence était un argument marketing assez saillant, et l'augmenter faisait bien sur le papier. Aussi, les fréquences ont progressivement augmenté, et ont continué dans ce sens, jusqu’à atteindre une limite haute avec le Pentium 4 d'Intel.

Le Pentium 4 était une véritable bête en termes de fréquence pour l'époque : 1,5 GHz, contre à peine 1Ghz pour les autres processeurs de l'époque. La fréquence avait été doublée par rapport au Pentium 3 et ses 733 MHz. Et cette fréquence était juste la fréquence de base du processeur, certains circuits allaient plus vite, d'autres moins vite. Par exemple, l'unité de calcul intégrée dans le processeur allait deux fois plus vite, avec une fréquence de 3 GHz ! Et à l'inverse, certaines portions du processeur allaient au quart de cette fréquence, à 750 MHz. Bref, le Pentium 4 gérait plusieurs fréquences différentes : certaines portions importantes pour la performance allaient très vite, d'autres allaient à une vitesse intermédiaire pour faciliter leur conception, d'autres allaient encore moins vite, car elles n'avaient pas besoin d'être très rapides.
Le processeur était spécialement conçu pour fonctionner à très haute fréquence, grâce à diverses techniques qu'on abordera dans les chapitres suivants (pipeline très long, autres). Mais tout cela avait un cout : le processeur chauffait beaucoup ! Et c'était un défaut majeur. De plus, les techniques utilisées pour faire fonctionner le Pentium 4 à haute fréquence (le superpipeline) avaient beaucoup de défauts. Défauts compensés partiellement par des techniques innovantes pour l'époque, comme son replay system qu'on abordera dans un chapitre à part, mais sans grand succès. Les versions ultérieures du Pentium 4 avaient une fréquence plus base, mais avec un processeur complétement repensé, avec un résultat tout aussi performant. Ces versions chauffaient quand même beaucoup et les contraintes thermiques étaient un vrai problème.
En conséquence, la course à la fréquence s'est arrêtée avec ce processeur pour Intel, et l'industrie a suivi. La raison principale est que l'augmentation en fréquence des processeurs modernes est de plus en plus contrainte par la dissipation de chaleur et la consommation d'énergie. Et cette contrainte s'est manifestée en 2005, après la sortie du processeur Pentium 4. Le point d'inflexion en 2005, à partir duquel la fréquence a cessée d'augmenter drastiquement, s'explique en grande partie par cette contrainte. Les premiers processeurs étaient refroidis par un simple radiateur, alors que les processeurs modernes demandent un radiateur, un ventilateur et une pâte thermique de qualité pour dissiper leur chaleur. Pour limiter la catastrophe, les fabricants de processeurs doivent limiter la fréquence de leurs processeurs. Une autre raison est que la fréquence dépend des transistors, mais aussi de la rapidité du courant dans les interconnexions (les fils) qui relient les transistors, celles-ci devenant de plus en plus un facteur limitant pour la fréquence.
La performance à fréquence égale a augmenté : la loi de Pollack
modifierSi la miniaturisation permet d'augmenter la fréquence, elle permet aussi d'améliorer la performance à fréquence égale. Rappelons que la performance à fréquence égale se mesure avec deux critères équivalents : l'IPC et le CPI. Le CPI est le nombre de cycles moyen pour exécuter une instruction. L'IPC est son inverse, à savoir le nombre d'instruction exécutable en un seul cycle. Les deu sont l'inverse l'un de l'autre. La loi de Pollack dit que l'augmentation de l'IPC d'un processeur est approximativement proportionnelle à la racine carrée du nombre de transistors ajoutés : si on double le nombre de transistors, la performance est multipliée par la racine carrée de 2.
On peut expliquer cette loi de Pollack assez simplement. Il faut savoir que les processeurs modernes peuvent exécuter plusieurs instructions en même temps (on parle d’exécution superscalaire), et peuvent même changer l'ordre des instructions pour gagner en performances (on parle d’exécution dans le désordre). Pour cela, les instructions sont préchargées dans une mémoire tampon de taille fixe, interne au processeur, avant d'être exécutée en parallèle dans divers circuits de calcul. Cependant, le processeur doit gérer les situations où une instruction a besoin du résultat d'une autre pour s'exécuter : si cela arrive, on ne peut exécuter les instructions en parallèle. Pour détecter une telle dépendance, chaque instruction doit être comparée à toutes les autres, pour savoir quelle instruction a besoin des résultats d'une autre. Avec N instructions, vu que chacune d'entre elles doit être comparée à toutes les autres, ce qui demande N^2 comparaisons.
En doublant le nombre de transistors, on peut donc doubler le nombre de comparateurs, ce qui signifie que l'on peut multiplier le nombre d'instructions exécutables en parallèle par la racine carrée de deux. En utilisant la loi de Moore, on en déduit qu'on gagne approximativement 40% d'IPC tous les deux ans, à ajouter aux 40 % d'augmentation de fréquence. En clair, la performance d'un processeur augmente de 40% grâce à la loi de Pollack, et de 40% par l'augmentation de fréquence. On a donc une augmentation de 80% tous les deux ans, donc une multiplication par 1,8 tous les deux ans, soit moins que la hausse de transistors.
On peut cependant contourner la loi de Pollack, qui ne vaut que pour un seul processeur. Mais en utilisant plusieurs processeurs, la performance est la somme des performances individuelles de chacun d'entre eux. C'est pour cela que les processeurs actuels sont doubles, voire quadruple cœurs : ce sont simplement des circuits imprimés qui contiennent deux, quatre, voire 8 processeurs différents, placés sur la même puce. Chaque cœur correspond à un processeur. En faisant ainsi, doubler le nombre de transistors permet de doubler le nombre de cœurs et donc de doubler la performance, ce qui est mieux qu'une amélioration de 40%.
L'évolution de la performance des mémoires
modifierAprès avoir vu le processeur, voyons comment la loi de Moore a impacté l'évolution des mémoires. Beaucoup de cours d'architecture des ordinateurs se contentent de voir l'impact de la loi de Moore sur le processeur, mais mettent de côté les mémoires. Et il y a une bonne raison à cela. Le fait est que les ordinateurs modernes ont une hiérarchie mémoire très complexe, avec beaucoup de mémoires différentes. Et les technologies utilisées pour ces mémoires sont très diverses, elles n'utilisent pas toutes des transistors MOS, la loi de Moore ne s'applique pas à toutes les mémoires.
Déjà, évacuons le cas des mémoires magnétiques (disques durs, disquettes) et des mémoires optiques (CD/DVD), qui ne sont pas fabriquées avec des transistors MOS et ne suivent donc pas la loi de Moore. Et de plus, elles sont en voie de disparition, elles ne sont plus vraiment utilisées de nos jours. Il ne reste que les mémoires à semi-conducteurs qui utilisent des transistors MOS, mais pas que. Seules ces dernières sont concernées par la loi de Moore, mais certaines plus que d'autres. Mais toutes les mémoires ont vu leur prix baisser en même temps que leur capacité a augmenté dans le temps, que ce soit à cause de la loi de Moore pour les mémoires à semi-conducteurs, l'amélioration exponentielle des technologies de stockage magnétique pour les disques durs.

L'impact de la loi de Moore dépend de la mémoire considérée et de sa place dans la hiérarchie mémoire. Les mémoires intégrées au processeur, comme le cache ou les registres, sont des mémoires SRAM/ROM fabriquées intégralement avec des transistors MOS, et donc soumises à la loi de Moore. Leurs performances et leur capacité suivent l'évolution du processeur qui les intègre, leur fréquence augmente au même rythme que celle du processeur, etc. Aussi on peut considérer qu'on en a déjà parlé plus haut. Reste à voir les autres niveaux de la hiérarchie mémoire, à savoir la mémoire RAM principale, la mémoire ROM et les mémoires de masse. Dans les grandes lignes, on peut distinguer deux technologies principales : les mémoires DRAM et les mémoires FLASH.
Les mémoires FLASH ont suivi la loi de Moore
modifierLes mémoires FLASH sont utilisées dans les mémoires de masse, comme les clés USB, les disques durs de type SSD, les cartes mémoires, et autres. Le passage à la mémoire FLASH a fait qu'elles sont plus rapides que les anciennes mémoires magnétiques, pour une capacité légèrement inférieure. Les mémoires FLASH sont aussi utilisées comme mémoire ROM principale ! Par exemple, les PC actuels utilisent de la mémoire FLASH pour stocker le firmware/BIOS/UEFI. De même, les systèmes embarqués qui ont besoin d'un firmware rapide utilisent généralement de la mémoire FLASH, pas de la mémoire ROM proprement dite (on verra dans quelques chapitres que la mémoire FLASH est un sous-type de mémoire ROM, mais laissons cela à plus tard).
Elles sont basées sur des transistors MOS modifiés, appelés transistors à grille flottante. Un transistor à grille flottante peut être vu comme une sorte de mélange entre transistor et condensateur, à savoir qu'il dispose d'une grille améliorée, dont le caractère de condensateur est utilisé pour mémoriser une tension, donc un bit. Un transistor à grille flottante est utilisé pour mémoriser un bit sur les mémoires dites SLC, deux bits sur les mémoires dites MLC, trois bits sur les mémoires TLC, quatre sur les mémoires QLC. Non, ce n'est pas une erreur, c'est quelque chose de permis grâce aux technologies de fabrication d'une mémoire FLASH, nous détaillerons cela dans le chapitre sur les mémoires FLASH.
Vu que les mémoires FLASH sont basées sur des transistors MOS modifiés, vous ne serez pas trop étonnés d’apprendre que la loi de Moore s'applique à la mémoire FLASH. La taille des transistors à grille flottante suit la loi de Moore : elle diminue de 30% tous les deux ans.

La conséquence est que l'aire occupée par un transistor à grille flottante est divisée par deux tous les deux ans. Le résultat est que la capacité des mémoires FLASH augmente de 50 à 60% par an, ce qui fait un doublement de leur capacité tous les deux ans.

Les mémoires RAM ne sont pas concernées par la loi de Moore
modifier
Les mémoires DRAM sont utilisées pour la mémoire principale de l'ordinateur, la fameuse mémoire RAM. A l'intérieur des mémoires DRAM actuelles, chaque bit est mémorisé en utilisant un transistor MOS et un condensateur (un réservoir à électron). Leur capacité et leur performance dépend aussi bien de la miniaturisation du transistor que de celle du condensateur. Elles sont donc partiellement concernées par la loi de Moore.
Pour ce qui est de la capacité, les DRAM suivent la loi de Moore d'une manière approximative. La raison est que gagner en capacité demande de réduire la taille des cellules mémoire, donc du transistors et du condensateur à l'intérieur. La miniaturisation des transistors suit la loi de Moore, mais la réduction de la taille du condensateur ne la suit pas. Dans le passé, la capacité des DRAM augmentait légèrement plus vite que la loi de Moore, avec un quadruplement tous les trois ans (4 ans pour la loi de Moore), mais tout a considérablement ralentit avec le temps.

Niveau performances, la loi de Moore ne s'applique tout simplement pas. La raison à cela est que la performance des DRAM est dominée par la performance du condensateur, pas par celle du transistor. Miniaturiser des transistors permet de les rendre plus rapides, mais le condensateur ne suit pas vraiment. Aussi, les performances des mémoires DRAM stagnent.
Rappelons que la performance d'une mémoire RAM/ROM dépend de deux paramètres : son débit binaire, et son temps d'accès. Il est intéressant de comparer comment les deux ont évolué. Pour les mémoires RAM, le débit binaire a augmenté rapidement, alors que le temps d'accès a baissé doucement. Les estimations varient d'une étude à l'autre, mais disent que le temps d'accès des mémoires se réduit d'environ 10% par an, alors que le débit binaire a lui augmenté d'environ 30 à 60% par an. Une règle approximative est que le débit binaire a grandi d'au moins le carré de l'amélioration du temps d'accès.
L'évolution de la fréquence des mémoires DRAM et de la fréquence du bus mémoire
modifierPour comprendre pourquoi temps d'accès et débit binaire n'ont pas évolué simultanément, il faut regarder du côté de la fréquence de la mémoire RAM. Les mémoires modernes sont cadencées avec un signal d'horloge, ce qui fait qu'il faut tenir compte de la fréquence de la mémoire. Le débit et les temps d'accès dépendent fortement de la fréquence de la mémoire. Plus la fréquence est élevée, plus les temps d'accès sont faibles, plus le débit est important.
Le calcul du débit binaire d'une mémoire est simplement le produit entre fréquence et largeur du bus mémoire. Il se trouve que la largeur du bus de données n'a pas beaucoup augmenté avec le temps. Les premières barrettes de mémoire datée des années 80, les barrettes SIMM, avaient un bus de données de 8 bits pour la version 30 broches, 32 bits pour la version 72 broches. Le bus mémoire était déjà très important. Dans les années 2000, la démocratisation des barrettes mémoires DIMM a permis au bus de données d'atteindre 64 bits, valeur à laquelle il est resté actuellement. Il est difficile d'augmenter la largeur du bus, ca cela demanderait d'ajouter des broches sur des barrettes et des connecteurs déjà bien chargées. L'augmentation du débit binaire ne peut venir que de l'augmentation de la fréquence.
Les premières mémoires utilisées dans les PCs étaient asynchrones, à savoir qu'elles n'avaient pas de fréquence ! Elles se passaient de fréquence d'horloge, et le processeur se débrouillait avec. Il s'agissait des premières mémoires DRAM d'Intel, les mémoires EDO, Fast-page RAM et autres, que nous verrons dans quelques chapitres. Elles étaient utilisées entre les années 70 et 90, où elles étaient le type de mémoire dominant. Elles étaient assez rapides pour le processeur, mémoire et processeur avaient des performances comparables.
Dans les années 1990, la SDRAM est apparue. La terme SDRAM regroupe les premières mémoires RAM synchrones, cadencées par un signal d'horloge. La fréquence des SDRAM était de 66, 100, 133 et 150 MHz. Les RAM à 66 MHz sont apparues en premier, suivies par les SDRAM à 100MHz et puis par les 133 MHz, celles de 150 MHz étaient plus rares. Lors de cette période, la relation entre fréquence, temps d'accès et débit binaire était assez claire. Le temps d'accès est proportionnel à la fréquence, à peu de choses près. Le temps d'accès est de quelques cycles d'horloge, bien qu'il dépende des barrettes de mémoire utilisées. Le débit est le produit entre fréquence et largeur du bus. Donc plus la fréquence est grande, meilleures sont les performances globales. Et la fréquence de la mémoire et celle du bus mémoire étaient identiques.
Depuis les années 2000, les mémoires RAM utilisent des techniques de Double data rate ou de Quad data rate qui permettent d'atteindre de hautes fréquences en trichant. La triche vient du fait que la fréquence de la mémoire n'est plus égale à la fréquence du bus mémoire depuis les années 2000. Nous verrons cela en détail dans le chapitre sur le bus mémoire. Pour le moment, nous allons nous contenter de dire que l'idée derrière cette différence de fréquence est d'augmenter le débit binaire des mémoires, mais sans changer leur fréquence interne.
| Année | Type de mémoire | Fréquence de la mémoire (haut de gamme) | Fréquence du bus | Coefficient multiplicateur entre les deux fréquences |
|---|---|---|---|---|
| 1998 | DDR 1 | 100 - 200 MHz | 200 - 400 MHz | 2 |
| 2003 | DDR 2 | 100 - 266 MHz | 400 - 1066 MHz | 4 |
| 2007 | DDR 3 | 100 - 266 MHz | 800 - 2133 MHz | 8 |
| 2014 | DDR 4 | 200 - 400 MHz | 1600 - 3200 MHz | 8 |
| 2020 | DDR 5 | 200 - 450 MHz | 3200 - 7200 MHz | 8 à 16 |
Le débit binaire est proportionnel à la fréquence du bus mémoire, alors que les temps d'accès sont proportionnel à la fréquence de la mémoire. La fréquence de la mémoire n'a pas beaucoup augmentée et reste très faible, les temps d'accès ont donc fait de même. Par contre, le débit binaire est lui très élevé, car dépendant de la fréquence du bus mémoire, qui a beaucoup augmenté. Au final, les mémoires modernes ont donc un gros débit, mais un temps de latence très élevé.
La comparaison avec l'évolution des processeurs : le memory wall
modifierLa performance du processeur et de la mémoire doivent idéalement être comparables. Rien ne sert d'avoir un processeur puisant si la mémoire ne suit pas. A quoi bon avoir un processeur ultra-puissant s'il passe 80% de son temps à attendre des données en provenance de la mémoire ? Si la performance des mémoires RAM stagne, alors que les processeurs gagnent en performance de manière exponentielle, on fait face à un problème.
Pour nous rendre compte du problème, il faut comparer la performance du processeur avec celle de la mémoire. Et c'est loin d'être facile, car les indicateurs de performance pour le processeur et la mémoire sont fondamentalement différents. La performance d'une mémoire dépend de son débit binaire et de son temps d'accès, la performance du processeur dépend de son CPI et de sa fréquence. Mais on peut comparer la vitesse à laquelle ces indicateurs grandissent. Pour donner un chiffre assez parlant, quelques estimations estiment que le temps d'accès de la mémoire, exprimé en cycles d'horloge du processeur, double tous les 2,6 ans.
Une autre possibilité est comparer la fréquence des processeurs et des mémoires, pour voir si la fréquence de la mémoire a suivi celle du processeur. On s'attendrait à une augmentation de 40% de la fréquence des mémoires tous les deux ans, comme c'est le cas pour les processeurs. Mais la fréquence des mémoires n'a pas grandit au même rythme et a été beaucoup plus faible que pour les processeurs. Faisons un historique rapide.
Lors de l'époque des mémoires asynchrones, mémoire et processeur avaient des performances comparables. Les accès mémoire se faisaient globalement en un cycle d'horloge, éventuellement deux ou trois cycles, rarement plus. Bien qu'asynchrone, on peut considérer qu'elles allaient à la même fréquence que le processeur, mais cela ne servait à rien de parler de fréquence de la mémoire ou de fréquence du bus mémoire.
Pour la période des mémoires SDRAM, le tableau ci-dessous fait une comparaison des fréquences processeur-mémoire. La comparaison avec les processeurs était assez simple, car la fréquence du bus mémoire et la fréquence de la mémoire sont identiques. On voit que la fréquence de la mémoire est déjà loin derrière la fréquence du processeur, elle est 3 à 5 fois plus faible.
| Année | Fréquence du processeur (haut de gamme) | Fréquence de la mémoire (haut de gamme) |
|---|---|---|
| 1993 | Intel Pentium : 60 à 300 MHz | 66 Mhz |
| 1996-1997 |
|
100 MHz |
| 1999 |
|
133 MHz |
Avec l'invention des mémoires DDR, la comparaison est rendue plus compliquée par la dissociation entre fréquence du bus et fréquence de la mémoire. La comparaison est la suivante :
| Année | Type de mémoire | Fréquence de la mémoire (haut de gamme) | Fréquence du bus | Fréquence du processeur (haut de gamme) |
|---|---|---|---|---|
| 1998 | DDR 1 | 100 - 200 MHz | 200 - 400 MHz | 200 - 1000 MHz |
| 2003 | DDR 2 | 100 - 266 MHz | 400 - 1066 MHz | 700 - 1500 MHz |
| 2007 | DDR 3 | 100 - 266 MHz | 800 - 2133 MHz | 1500 - 3000 MHz |
| 2014 | DDR 4 | 200 - 400 MHz | 1600 - 3200 MHz | 1600 - 4200 MHz |
| 2020 | DDR 5 | 200 - 450 MHz | 3200 - 7200 MHz | 1700 - 4500 MHz |
Le constat est assez clair : le processeur est plus rapide que la mémoire, et l'écart se creuse de plus en plus avec le temps. Il s'agit d'un problème assez important, qui dicte l'organisation des ordinateurs modernes. Les mémoires sont actuellement très lentes comparé au processeur. On parle souvent de memory wall, pour décrire ce problème, nous utiliserons le terme mur de la mémoire. Pour cela, diverses solutions existent. Et la plus importante d'entre elle est l'usage d'une hiérarchie mémoire.
Les solutions contre le mur de la mémoire : hiérarchie mémoire et RAM computationnelle
modifierLe mur de la mémoire est un problème avec lequel les architectures modernes doivent composer. Le mur de la mémoire a deux origines. La première est que processeur et mémoire sont strictement séparés et que tout traitement doit lire des opérandes en mémoire, pour ensuite écrire des résultats en mémoire RAM. La seconde est que les transferts entre processeurs et mémoire sont assez lents, ce qui fait que l'idéal est de réduire ces transferts le plus possible.
La solution la plus souvent retenue est l'usage de mémoires caches intégrées au processeur, pour réduire le trafic entre DRAM et CPU. Les mémoires caches ne sont pas des DRAM, ce qui permet de contourner le problème du mur de la mémoire, causé par la technologie de fabrication des DRAM. Les caches sont des mémoires à semi-conducteur fabriquées avec des transistors CMOS, ce qui fait que leurs performances augmentent au même rythme que le processeur. Elles sont intégrées dans le processeur, même s'il a existé des mémoires caches connectées sur la carte mère.
Mais une autre solution consiste à faire l'inverse, à savoir ajouter des capacités de calcul dans la mémoire RAM. L'idée est de faire les calculs dans la mémoire directement : pas besoin de transférer les opérandes du calcul de la mémoire vers le CPU, ni de transférer les résultats du CPU vers la RAM. L'idée est alors de déléguer certains calculs à la DRAM, voire carrément de fusionner le CPU et la DRAM ! On parle alors de in-memory processing, que nous traduirons par le terme quelque peu bâtard de RAM computationnelle.
Cependant, l'implémentation d'une RAM computationnelle pose quelques problèmes d'ordre pratique. Le premier est au niveau de la technologie utilisée pour les transistors. Comme on vient de le voir, les technologies utilisées pour fabriquer la mémoire sont très différentes de celles utilisées pour fabriquer des circuits logiques, les circuits d'un processeur. Les processeurs utilisent des transistors CMOS normaux, les mémoires FLASH des transistors MOS à grille flottante, les DRAM utilisent un mélange de transistors MOS et de condensateurs. Et au niveau des procédés de fabrication, de gravure des puce, de photolithographie, de la technique des semi-conducteurs, les trois procédés sont totalement différents. Aussi, fusionner DRAM et CPU pose des problèmes de fabrication assez complexes.
Notons que ce problème n'a pas lieu avec la mémoire utilisée pour les registres et les caches, car elle est fabriquée avec des transistors. Nous avons vu il y a quelques chapitres comment créer des registres à partir de transistors et de portes logiques, ce qui utilise le même procédé technologique que pour les CPU. Les mémoires caches utilisent des cellules de mémoire SRAM fabriquées uniquement avec des transistors CMOS, comme nous le verrons dans quelques chapitres. Registres et SRAM sont donc fabriqués avec le même procédé technologique que les processeurs, ce qui fait que l'intégration de registres/caches dans le processeur est assez simple. Ce n'est pas le cas pour la fusion DRAM/CPU.
La majorité des architectures à RAM computationnelle ont été des échecs commerciaux. La raison est qu'il s'agit d'architectures un peu particulières, qui sont formellement des architectures dites à parallélisme de données, assez difficiles à exploiter. La tentative la plus connue était le projet IRAM de l'université de Berkeley. L'idée était de fusionner un processeur et une mémoire sur la même puce, les deux étant intégrés dans le même circuit. Démarré en 1996, il a été abandonnée en 2004.
Le chapitre précédent nous a appris que la consommation d'un processeur dépend de sa fréquence et de sa tension d'alimentation, la tension d'alimentation ayant un effet largement supérieur à celui de la fréquence. Diminuer la tension ou la fréquence permettent de diminuer la consommation énergétique. De plus, la diminution de tension a un effet plus marqué que la diminution de la fréquence. La plupart des processeurs calibrent leur tension et leur fréquence de manière à avoir le meilleur compromis possible entre performance et consommation électrique.
Pour réduire la consommation énergétique, les ingénieurs ont inventé diverses techniques assez intéressantes. Globalement, elles se classent en deux catégories, suivant la méthode utilisée pour réduire la consommation d'énergie. Les premières consistent à tout simplement mettre en veille les circuits inutilisés du processeur, ou du moins à faire en sorte qu'ils ne consomment pas d'énergie. La seconde technique, plus complexe, adapte la tension et la fréquence en fonction des besoins.
Éviter la consommation des circuits inutilisés
modifierSi on prend un exemple pour une maison, ne pas éclairer et/ou chauffer une pièce inutilisée évite des gaspillages. Eh bien des économies du même genre sont possibles dans un circuit imprimé. Un bon moyen de réduire la consommation électrique est simplement de couper les circuits inutilisés. Par couper, on veut dire soit ne plus les alimenter en énergie, soit les déconnecter de l'horloge. Par chance, un circuit intégré complexe est constitué de plusieurs sous-circuits distincts, aux fonctions bien délimitées. Et il est rare que tous soient utilisés en même temps. Pour économiser de l'énergie, on peut tout simplement déconnecter les sous-circuits inutilisés, temporairement.
Le Power Gating et le Clock Gating
modifier
Une première solution consiste à ne pas dépenser d'énergie inutilement, ne pas alimenter ce qui ne fonctionne pas, ce qui est en pause ou inutilisé, afin qu'ils ne consomment plus de courant : on parle de power gating. Elle s'implémente en utilisant des Power Gates qui déconnectent les circuits de la tension d'alimentation quand ceux-ci sont inutilisés. Cette technique est très efficace, surtout pour couper l'alimentation du cache du processeur. Cette technique réduit la consommation statique des circuits, mais pas leur consommation dynamique, par définition.
Une autre solution consiste à jouer sur la manière dont l'horloge est distribuée dans le processeur. On estime qu'une grande partie des pertes ont lieu dans l'arbre d'horloge (l'ensemble de fils qui distribuent l'horloge aux bascules), approximativement 20 à 30% (mais tout dépend du processeur). La raison est que l'horloge change d'état à chaque cycle, même si les circuits cadencés par l'horloge sont inutilisés, et que la dissipation thermique a lieu quand un bit change de valeur. S'il est possible de limiter la casse en utilisant des bascules spécialement conçues pour consommer peu, il est aussi possible de déconnecter les circuits inutilisés de l'horloge : on appelle cela le Clock Gating.

Pour implémenter cette technique, on est obligé de découper le processeur en plusieurs morceaux, reliés à l'horloge. Un morceau forme un tout du point de vue de l'horloge : on pourra tous le déconnecter de l'horloge d'un coup, entièrement. Pour implémenter le Clock Gating, on dispose entre l'arbre d'horloge et le circuit, une Clock Gate, un circuit qui inhibe l'horloge au besoin. Comme on le voit sur le schéma du dessus, ces Clock Gates sont commandées par un bit, qui ouvre ou ferme la Clock Gate Ce dernier est relié à la fameuse unité de gestion de l'énergie intégrée dans le processeur qui se charge de le commander.
Une clock gate est, dans le cas le plus simple, une vulgaire porte logique tout ce qu'il y a de plus banale. Ce peut être une porte OU ou encore une porte ET. La seule différence entre les deux est la valeur du signal d'horloge quand celle-ci est figée : soit elle est figée à 1 avec une porte OU, soit elle est figée à 0 avec une porte ET. Le bit à envoyer sur l'entrée de contrôle n'est pas le même : il faut envoyer un 1 avec une porte OU pour figer l'horloge, un 0 avec une porte ET.


Il est aussi possible de complexifier le circuit en ajoutant une bascule pour mémoriser le signal de contrôle avant la porte logique.

L'évaluation gardée
modifierL'évaluation gardée est une technique assez proche du clock gating et du power gating, dans l'esprit. Elle s'applique dans le cas d'un circuit dont les sorties sont utiles sous certaines conditions, mais inutiles dans d'autres. Un tel circuit peut en théorie utiliser une clock ou power gate pour l'éteindre quand on ne l'utilise pas. Mais le temps de réaction d'une clock/power gate n'est pas compatible avec un circuit à l'utilisation rapidement changeante.
Une solution alternative active ou désactive le circuit avec un signal de commande, relié à un registre d'entrée. Chose très importante : le registre est à entrée Enable. Concrètement, si l'entrée Enable est activée, l'entrée est recopiée sur la sortie, le registre est alors transparent et tout se passe comme s'il n'était pas là. Mais quand le signal Enable passe à 0, alors l'ancienne valeur de l'entrée est mémorisée dans le registre. Si le circuit est utilisé, l'entrée Enable est à 1 et le circuit fonctionne normalement. Mais si on veut désactiver le circuit, on met l'entrée à 0 : le circuit est figé avec l'ancienne valeur de l'entrée.
L'intérêt est que cela fige le circuit dans l'état dans lequel il était. N'oublions pas que ce qui consomme de l'énergie, c'est de faire changer d'état les transistors ! Si on éteignait ou remettait le circuit à zéro, cela demanderait un petit peu d'énergie pour faire la transition. Ici, au lieu d'éteindre le circuit, on fige ce qu'il y a sur l'entrée, et donc l'état des transistors dans tout le circuit ! Pas de transition pour éteindre le circuit, sauf peut-être un petit peu dans le registre.

Le défaut est que le circuit fournit sur sa sortie un résultat, qu'il faut ignorer. Mais heureusement, il arrive que la sortie d'un circuit ne soit tout simplement pas prise en compte. Le cas le plus simple est celui où le circuit est suivi par un multiplexeur. Dans ce cas, si la sortie du circuit n'est pas choisie par le multiplexeur et qu'on peut le savoir à l'avance, le circuit peut être figé par évaluation gardée. Un exemple est celui des processeurs, qui disposent de plusieurs circuits de calculs : des circuits de calcul spécialisés dans les additions/soustraction, d'autres dans les multiplications, d'autres dans les opérations logiques, et autres ; qui sont suivies par un multiplexeur pour choisir le résultat adéquat. Suivant le calcul à effectuer, qui est connu à l'avance, on sait quel circuit de calcul choisir et comment configurer le multiplexeur.
Les techniques basées sur la relation entre tension et fréquence
modifierUn point important est fréquence et tension d'alimentation sont liées. Il est possible de démontrer que la fréquence d'un circuit imprimé dépend de la tension d'alimentation et suit une relation approximative qui ressemble à ceci :
- , avec U la tension d'alimentation et une tension minimale appelée la tension de seuil en-dessous de laquelle les transistors ne fonctionnent plus correctement.
L'équation précédente se reformule en :
La conséquence immédiate est que baisser la fréquence permet de faire baisser l'autre. Et inversement, faire baisser la tension implique de faire baisser la fréquence, sans quoi les transistors ne peuvent plus suivre.
La distribution de fréquences et de tensions d'alimentations multiples
modifierUne première solution prend en compte le fait que certaines portions du processeur sont naturellement plus rapides que d'autres. La technique a été utilisée sur certains processeurs multicoeurs, où certains coeurs sont naturellement cadencés à une fréquence inférieur. De tels processeurs regroupent des cœurs puissants à haute fréquence et des cœurs basse-consommation à basse fréquence. C'est le cas sur certaines puces ARM et sur les processeurs Intel Core de 12e génération, de micro-architecture "Alder Lake".
Mais ce principe peut aussi s'appliquer à l'intérieur d'un coeur, qu'il soit de haute ou basse performance. Il est en effet possible de faire fonctionner certaines portions du processeur à une fréquence plus basse que le reste. Autant les circuits de calculs doivent fonctionner à la fréquence maximale, autant un processeur intègre des circuits annexes assez divers, sans rapport avec ses capacités de calcul et qui peuvent fonctionner au ralenti. Par exemple, les circuits de gestion de l'énergie n'ont pas à fonctionner à la fréquence maximale, tout comme les timers (des circuits qui permettent de compter les secondes, intégrés dans les processeurs et utilisés pour des décomptes logiciels).
Pour cela, les concepteurs de CPU font fonctionner ces circuits à une fréquence plus basse que la normale. Ils ont juste à ajouter des circuits diviseurs de fréquence dans l'arbre d'horloge. Le processeur est divisé en domaines d'horloge séparés, chacun allant à sa propre fréquence. Les circuits sont répartis dans chaque domaine d’horloge suivant ses besoins. Nous avions abordé les domaines d'horloge dans le chapitre sur les circuits synchrones et asynchrones, dans la dernière section nommée "La distribution de l'horloge dans un circuit complexe".
Vu que les circuits en question fonctionnent à une fréquence inférieure à ce qu'ils peuvent, on peut baisser leur tension d'alimentation juste ce qu'il faut pour les faire aller à la bonne vitesse. Pour ce faire, on doit utiliser plusieurs tensions d'alimentation pour un seul processeur. Ainsi, certaines portions du processeur seront alimentées par une tension plus faible, tandis que d'autres seront alimentées par des tensions plus élevées. La distribution de la tension d'alimentation dans le processeur est alors un peu plus complexe, mais rien d'insurmontable. Pour obtenir une tension quelconque, il suffit de partir de la tension d'alimentation et de la faire passer dans un régulateur de tension, qui fournit la tension voulue en sortie. Les concepteurs de CPU ont juste besoin d'ajouter plusieurs régulateurs de tension, qui fournissent les diverses tensions nécessaires, et de relier chaque circuit avec le bon régulateur.
Le Dynamic Voltage Scaling et le Frequency Scaling
modifierLes fabricants de CPU ont eu l'idée de faire varier la tension et la fréquence en fonction de ce que l'on demande au processeur. Rien ne sert d'avoir un processeur qui tourne à 200 gigahertz pendant que l'on regarde ses mails. Par contre, avoir un processeur à cette fréquence peut être utile lorsque l'on joue à un jeu vidéo dernier cri. Dans ce cas, pourquoi ne pas adapter la fréquence suivant l'utilisation qui est faite du processeur ? C'est l'idée qui est derrière le Dynamic Frequency Scaling, aussi appelé DFS.
Il est possible de réduire la tension d'alimentation, si on réduit la fréquence en même temps. La technologie consistant à diminuer la tension d'alimentation suivant les besoins s'appelle le Dynamic Voltage Scaling, de son petit nom : DVS. Elle donne des gains bien plus importants que le DFS, vu que la consommation dynamique dépend du carré de la tension d'alimentation.
Le seul problème avec cette technique est la tension de seuil, qui dépend de la physique des transistors et qui est relativement constante, proche de 0,4 Volts. Plus la tension d'alimentation des processeurs diminue, plus elle se rapproche de la tension de seuil. En soi, pas de problème pour ce qui est de la fréquence maximale, qui reste globalement la même du fait de l'impact de la loi de Moore. Par contre, le DVS est limité par la tension de seuil. Comparons par exemple une tension de 2 volts et de 1 Volt. Avec 2 volts, on a une marge de 1,6 V que le DVS peut utiliser. Mais avec une tension d'alimentation de 1 Volt, il ne reste qu'une marge de 0,6 V à exploiter pour le DVS. La réduction de consommation liée au DVS est donc de plus en plus limité avec le temps, avce la réduction naturelle de la tension d'alimentation.
La configuration de la fréquence et de la tension peut se faire de plusieurs manières. Une méthode simple est une configuration logicielle. Le processeur contient de DVFS un registre dans lequel le système d'exploitation écrit les valeurs de configuration nécessaire. L'OS ne peut pas choisir directement la fréquence et le voltage, mais il peut choisir un niveau de DFVS, un numéro qui correspond à un couple tension-fréquence précis. De nos jours, cette solution n'est plus trop utilisée, le réglage étant le fait du processeur lui-même. Tous les processeurs modernes incorporent un sous-processeur qui est spécialisé dans la régulation de la tension et de la fréquence, qui monitore l'utilisation du processeur, de ses circuits, sa température, et qui décide du couple tension-fréquence en fonction de.
Sur les processeurs multicoeurs, la régulation du couple tension-fréquence se fait cœur par cœur, avec cependant une régulation globale. Il est possible d'éteindre les cœurs non-utilisés, de faire tourner les cœurs peu utilisés à basse fréquence, pendant que les cœurs très utilisés sont à fréquence maximale. De nos jours, la fréquence maximale n'est atteinte que dans ces circonstances bien précises : il faut que seul un cœur soit actif, et les autres en veille ou très peu occupés. Si tous les cœurs sont très occupé, la fréquence des cœurs atteint un plateau inférieur à la fréquence maximale. Mais si un seul cœur est utilisé, alors il ira à la fréquence maximale. La raison tient dans les limitations thermique, et au problème du dark silicon.
La régulation tension-fréquence doit aussi tenir compte des domaines d'horloge. Dans le cas le plus simple, la réduction de la fréquence est la même pour chaque domaine d'horloge, de même que la réduction de la tension. Elle ne tient pas vraiment compte des domaines d'horloge, du moins dans le sens où la régulation est globale, même si chaque domaine d'horloge voit sa fréquence impactée. Mais il est aussi possible de réguler le couple tension-fréquence indépendamment pour chaque domaine d'horloge, afin de gérer plus finement la réduction de fréquence. Il est même possible de vérifier l'utilisation de chaque domaine d'horloge, et de régler leur fréquence suivant s'ils font beaucoup de calculs ou pas.
Les bus et liaisons point à point
modifierTout ordinateur contient au minimum un bus, qui sert à connecter processeur, mémoire et entrées-sorties. Mais c'est là le cas le plus simple : rien n’empêche un ordinateur d'avoir plusieurs bus. c'est le cas sur les architectures Harvard, qui ont un bus séparé pour la mémoire RAM et la mémoire ROM. Comme autre possibilité, on pourrait avoir un bus entre processeur et mémoires, et un autre bus qui connecte le processeur aux entrées-sorties. Bref, les possibiliés sont multiples. Dans un ordinateur de type PC, les composants sont placés sur un circuit imprimé (la carte mère), sur lequel on vient connecter les différents composants d'un ordinateur et qui les relie via divers bus. Si je dis "par divers bus", c'est parce qu'il n'y a pas qu'un seul bus dans un ordinateur, mais plusieurs : un bus pour communiquer avec le disque dur, un bus pour la carte graphique, un pour le processeur, un pour la mémoire, etc. De ce fait, un PC moderne contient un nombre impressionnant de bus, jugez plutôt :
- les bus USB ;
- le bus PCI Express, utilisé pour communiquer avec des cartes graphiques ou des cartes son ;
- le bus S-ATA et ses variantes eSATA, eSATAp, ATAoE, utilisés pour communiquer avec le disque dur ;
- le bus Low Pin Count, qui permet d'accéder au clavier, aux souris, au lecteur de disquette, et aux ports parallèle et série ;
- le SMBUS, qui est utilisé pour communiquer avec les ventilateurs, les sondes de température et les sondes de tension présentes un peu partout dans notre ordinateur ;
- l'Intel QuickPath Interconnect et l'HyperTransport, qui relient les processeurs récents au reste de l'ordinateur ;
Et c'est oublier tous les bus aujourd'hui défunts, mais qui étaient utilisés sur les anciens PC. Comme exemples, on pourrait citer :
- le bus ISA et le bus PCI (l'ancêtre du PCI Express), autrefois utilisés pour les cartes d'extension ;
- le bus AGP, autrefois utilisé pour les cartes graphiques ;
- les bus P-ATA et SCSI, pour les disque durs ;
- le bus MIDI, qui servait pour les cartes son ;
- le fameux RS-232 utilisé dans les ports série ;
- enfin, le bus IEEE-1284 utilisé pour le port parallèle.
Et à ces bus reliés aux périphériques, il faudrait rajouter le bus mémoire qui connecte processeur et mémoire, le bus système et bien d'autres. La longue liste précédente sous-entend qu'il existe de nombreuses différences entre les bus. Et c'est le cas : ces différents bus sont très différents les uns des autres.
Les bus dédiés et multiplexés
modifierCommençons par parler de la distinction entre les bus (et plus précisément les bus dits multiplexés) et les liaisons point à point (aussi appelées bus dédiés).
- Petite précision de vocabulaire : Le composant qui envoie une donnée sur un bus est appelé un émetteur, alors que ceux reçoivent les données sont appelés récepteurs.
Les liaisons point à point (bus dédiés)
modifierLes bus dédiés se contentent de connecter deux composants entre eux. Un autre terme, beaucoup utilisé dans le domaine des réseaux informatiques, est celui de liaisons point-à-point. Pour en donner un exemple, le câble réseau qui relie votre ordinateur à votre box internet est une liaison point à point. Mais le terme est plus large que cela et regroupe tout ce qui connecte deux équipements informatiques/électroniques entre eux, et qui permet l'échange de données. Par exemple, le câble qui relie votre ordinateur à votre imprimante est lui aussi une liaison point à point, au même titre que les liaisons USB sur votre ordinateur. De même, certaines liaisons point à point relient des composants à l'intérieur d'un ordinateur, comme le processeur et certains capteurs de températures.
Les liaisons point à point sont classés en trois types, suivant les récepteurs et les émetteurs.
| Type de bus | Description |
|---|---|
| Simplex | Les informations ne vont que dans un sens : un composant est l'émetteur et l'autre reste à tout jamais récepteur. |
| Half-duplex | Il est possible d'être émetteur ou récepteur, suivant la situation. Par contre, impossible d'être en même temps émetteur et récepteur. |
| Full-duplex | Il est possible d'être à la fois récepteur et émetteur. |
| Liaison simplex | Liaison half-duplex | Liaison full-duplex |
|---|---|---|

|

|

|
Les bus full duplex sont créés en regroupant deux bus simplex ensemble : un pour l'émission et un pour la réception. Mais certains bus full-duplex, assez rares au demeurant, n'utilisent pas cette technique et se contentent d'un seul bus bidirectionnel.
Les bus multiplexés
modifierLes liaisons point à point, ou bus dédiés, sont à opposer aux bus proprement dit, aussi appelés bus multiplexés. Ces derniers ne sont pas limités à deux composants et peuvent interconnecter un grand nombre de circuits électroniques. Par exemple, un bus peut interconnecter la mémoire RAM, le processeur et quelques entrées-sorties entre eux. Et cela fait qu'il existe quelques différences entre un bus et une liaison point à point.

Avec un bus, l'émetteur envoie ses données à tous les autres composants reliés aux bus, à tous les récepteurs. Sur tous ces récepteurs, il se peut que seul l'un d'entre eux soit le destinataire de la donnée : les autres vont alors l'ignorer, seul le destinataire la traite. Cependant, il se peut qu'il y ait plusieurs récepteurs comme destinataires : dans ce cas, les destinataires vont tous recevoir la donnée et la traiter. Les bus permettent donc de faire des envois de données à plusieurs composants en une seule fois.

La fréquence du bus et son caractère synchrone/asynchrone
modifierOn peut faire la différence entre bus synchrone et asynchrone, la différence se faisant selon l'usage ou non d'une horloge. La méthode de synchronisation des composants et des communications sur le bus peut ainsi utiliser une horloge, ou la remplacer par des mécanismes autres.
Les bus synchrones
modifierLa grande majorité des bus actuellement utilisés sont synchronisés sur un signal d'horloge : ce sont les bus synchrones. Avec ces bus, le temps de transmission d'une donnée est fixé une fois pour toute. Le composant sait combien de cycles d'horloge durent une lecture ou une écriture. Sur certains bus, le contenu du bus n'est pas mis à jour à chaque front montant, ou à chaque front descendant, mais aux deux : fronts montant et descendant. De tels bus sont appelés des bus double data rate. Cela permet de transférer deux données sur le bus (une à chaque front) en un seul cycle d'horloge : le débit binaire est doublé sans toucher à la fréquence du bus.

Les bus asynchrones
modifierUne minorité de bus se passent complètement de signal d'horloge, et ont un protocole conçu pour : ce sont les bus asynchrones. Les bus asynchrones utilisent des protocoles de communication spécialisés. Les bus asynchrones permettent à deux circuits/composants de se synchroniser, l'un des deux étant un émetteur, l'autre étant un récepteur. Pour se synchroniser, l’émetteur indique au récepteur qu'il lui a envoyé une donnée, généralement grâce à un bit dédié sur le bus, souvent appelé le bit REQ. Le récepteur réceptionne alors la donnée et indique qu'il a pris en compte les données envoyées en envoyant un bit ACK. Cette synchronisation se fait grâce à des fils spécialisés du bus de commande, qui transmettent des bits particuliers.

De tels bus sont donc très adaptés pour transmettre des informations sur de longues distances (plusieurs centimètres ou plus). La raison est qu'à haute fréquence, le signal d'horloge met un certain temps pour se propager à travers le fil d'horloge, ce qui induit un léger décalage entre les composants. Plus on augmente la longueur des fils, plus ces décalages deviendront ennuyeux. Plus on augmente la fréquence, plus la période est dominée par le temps de propagation de l'horloge dans le fil. Les bus asynchrones n'ont pas ce genre de problèmes.
La largeur du bus
modifier
La plupart des bus peuvent échanger plusieurs bits en même temps et sont appelés bus parallèles. Mais il existe des bus qui ne peuvent échanger qu'un bit à la fois : ce sont des bus série.
Les bus série
modifierOn pourrait croire qu'un bus série ne contient qu'un seul fil pour transmettre les données, mais il existe des contrexemples. Généralement, c'est le signe que le bus n'utilise pas un codage NRZ, mais une autre forme de codage un peu plus complexe. Par exemple, le bus USB utilise deux fils D+ et D- pour transmettre un bit. Pour faire simple, lorsque le fil D+ est à sa tension maximale, l'autre est à zéro (et réciproquement).
La transmission et la réception sur un bus série demande de faire une conversion entre les données, qui sont codées sur plusieurs bits, et le flux série à envoyer sur le bus. Cela s'effectue généralement en utilisant des registres à décalage, commandés par des circuits de contrôle.

Les bus parallèles
modifierPassons maintenant aux bus parallèles. Pour information, si le contenu d'un bus de largeur de bits est mis à jour fois par secondes, alors son débit binaire est de . Mais contrairement à ce qu'on pourrait croire, les bus parallèles ne sont pas plus rapides que les bus série. Sur les bus synchrones, la fréquence est bien meilleure pour les bus série que pour les bus parallèles. La fréquence plus élevée l'emporte sur la largeur plus faible, ce qui surcompense le fait qu’un bus série ne peut envoyer qu'un bit à la fois. Le même problème se pose pour les bus asynchrones : le temps entre deux transmissions est plus grand sur les bus parallèles, alors qu'un bus série n'a pas ce genre de problèmes.
Il existe plusieurs raisons à cela, qui proviennent de phénomènes électriques assez subtils. Premièrement, les fils d'un bus ne sont pas identiques électriquement : leur longueur et leur résistance changent très légèrement d'un fil à l'autre. En conséquence, un bit va se propager à des vitesses différentes suivant le fil. On est obligé de se caler sur le fil le plus lent pour éviter des problèmes à la réception. En second lieu, il y a le phénomène de crosstalk. Lorsque la tension à l'intérieur du fil varie (quand le fil passe de 0 à 1 ou inversement), le fil va émettre des ondes électromagnétiques qui perturbent les fils d'à côté. Il faut attendre que la perturbation électromagnétique se soit atténuée pour lire les bits, ce qui limite le nombre de changements d'état du bus par seconde.
Avant de passer aux liaisons point à point et aux bus, nous allons voir comment un bit est codé sur un bus. Vous pensez certainement que l'encodage des bits est le même sur un bus que dans un processeur ou une mémoire. Mais ce n'est pas le cas. Il existe des encodages spécifiques pour les bus.
Les codes en ligne : le codage des bits sur une ligne de transmission
modifierIl existe des méthodes relativement nombreuses pour coder un bit de données pour le transmettre sur un bus : ces méthodes sont appelées des codages en ligne. Toutes codent celui-ci avec une tension, qui peut prendre un état haut (tension forte) ou un état bas (tension faible, le plus souvent proche de 0 volts). Outre le codage des données, il faut prendre aussi en compte le codage des commandes. En effet, certains bus série utilisent des fils dédiés pour la transmission des bits de données et de commande. Cela permet d'éviter d'utiliser trop de fils pour un même procédé.
Les codages non-différentiels
modifierPour commencer, nous allons voir les codages qui permettent de transférer un bit sur un seul fil (nous verrons que d'autres font autrement, mais laissons cela à plus tard). Il en existe de toutes sortes, qui se distinguent par des caractéristiques électriques qui sont à l’avantage ou au désavantage de l'un ou l'autre suivant la situation : meilleur spectre de bande passante, composante continue nulle/non-nulle, etc. Les plus courants sont les suivants :
- Le codage NRZ-L utilise l'état haut pour coder un 1 et l'état bas pour le zéro (ou l'inverse).
- Le codage RZ est similaire au codage NRZ, si ce n'est que la tension retourne systématiquement à l'état bas après la moitié d'un cycle d'horloge. Celui-ci permet une meilleure synchronisation avec le signal d'horloge, notamment dans les environnements bruités.
- Le codage NRZ-M fonctionne différemment : un état haut signifie que le bit envoyé est l'inverse du précédent, tandis que l'état bas indique que le bit envoyé est identique au précédent.
- Le codage NRZ-S est identique au codage NRZ-M si ce n'est que l'état haut et bas sont inversés.
- Avec le codage Manchester, aussi appelé codage biphasé, un 1 est codé par un front descendant, alors qu'un 0 est codé par un front montant (ou l'inverse, dans certaines variantes).

Faisons une petite remarque sur le codage de Manchester : il s'obtient en faisant un XOR entre l'horloge et le flux de bits à envoyer (codé en NRZ-L). Les bits y sont donc codés par des fronts montants ou descendants, et l'absence de front est censé être une valeur invalide. Si je dis censé, c'est que de telles valeurs invalides peuvent avoir leur utilité, comme nous le verrons dans le chapitre sur la couche liaison. Elles peuvent en effet servir pour coder autre chose que des bits, comme des bits de synchronisation entre émetteur et récepteur, qui ne doivent pas être confondus avec des bits de données. Mais laissons cela à plus tard.

Les codages différentiels
modifierPour plus de fiabilité, il est possible d'utiliser deux fils pour envoyer un bit (sur un bus série). Ces deux fils ont un contenu qui est inversé électriquement : le premier utilise une tension positive pour l'état haut et le second une tension négative. Ce faisant, on utilise la différence de tension pour coder le bit. Un tel codage est appelé un codage différentiel.
Ce codage permet une meilleure résistance aux perturbations électromagnétiques, aux parasites et autres formes de bruits qui peuvent modifier les bits transmis. L'intérêt d'un tel montage est que les perturbations électromagnétiques vont modifier la tension dans les deux fils, la variation induite étant identique dans chaque fil. La différence de tension entre les deux fils ne sera donc pas influencée par la perturbation.
- Évidemment, chaque codage a son propre version différentielle, à savoir avec deux fils de transmission.
Ce type de codage est, par exemple, utilisé sur le protocole USB. Sur ce protocole, deux fils sont utilisés pour transmettre un bit, via codage différentiel. Dans chaque fil, le bit est codé par un codage NRZ-I.

Les codes redondants
modifierD'autres bus encodent un bit sur plusieurs fils, mais sans pour autant utiliser de codage différentiel. Il s'agit des codes redondants, dans le sens où ils dupliquent de l'information, ils dupliquent des bits. L'intérêt est là encore de rendre le bus plus fiable, d'éliminer les erreurs de transmission.
La méthode la plus simple est la suivante : le bit est envoyé à l'identique sur deux fils. Si jamais les deux bits sont différents à l'arrivée, alors il y a un problème. Une autre méthode encode un 1 avec deux bits identiques, et un 0 avec deux bits différents, comme illustré ci-dessous. Mais ce genre de redondance est rarement utilisé, vu qu'on lui préfère des systèmes de détection/correction d'erreur comme un bit de parité.
Les codes redondants sont aussi utilisés pour faire communiquer entre eux des composants asynchrones, à savoir deux composants qui ne ne sont pas synchronisés par l'intermédiaire d'une horloge. Il s'agit d'ailleurs de leur utilisation principale. Vu que les composants ne sont pas synchronisés par une horloge, il se peut que certains bits arrivent avant les autres lors de la transmission d'une donnée sur une liaison parallèle. L'usage d'un code redondant permet de savoir quels bits sont valides et ceux pas encore transmis. Nous détaillerons cela à la fin de ce chapitre.
L'ordre d'envoi des bits sur une liaison série
modifierSur une liaison ou un bus série, les bits sont envoyés uns par uns. L'intuition nous dit que l'on peut procéder de deux manières : soit on envoie la donnée en commençant par le bit de poids faible, soit on commence par le bit de poids fort. Les deux méthodes sont valables et tout n'est au final qu'une question de convention. Les deux méthodes sont appelées LSB0 et MSB0. Avec la convention LSB0, le bit de poids faible est envoyé en premier, puis on parcourt la donnée de gauche à droite, jusqu’à atteindre le bit de poids fort. Avec la convention MSB0, c'est l'inverse ; on commence par le bit de poids fort, on parcours la donnée de gauche à droite, jusqu'à arriver au bit de poids faible.
Exemple sur un octet (groupe de 8 bits) :
Les encodages de bus
modifierLes encodages de bus encodent des données pour les envoyer sur un bus. Ils s'appliquent aux bus parallèles, à savoir ceux qui transmettent plusieurs bits en même temps sur des fils séparés. Un de leurs nombreux objectifs est de réduire la consommation d'énergie des bus parallèles. La consommation d'énergie dépend en effet de deux choses : de l'énergie utilisée pour faire passer un fil de 0 à 1 (ou de 1 à 0), et du nombre de fois qu'il faut inverser un bit par secondes. Le premier paramètre est fixé une fois pour toute, mais le second ne l'est pas et peut être modifié par des encodages spécifiques.
Le retour du code Gray
modifierUne première idée serait d'utiliser des encodages qui minimisent le passage d'un 0 à un 1 et inversement. Dans les premiers chapitres du cours, nous avions parlé du code Gray, qui est spécifiquement conçu dans cet optique. Rappelons qu'avec des entiers codés en code de Gray, deux entiers consécutifs ne différent que d'un seul bit. Ainsi, quand on passe d'un entier au suivant, seul un bit change de valeur. Une telle propriété est très utile pour les compteurs, mais pas vraiment pour les bus : on envoie rarement des données consécutives sur un bus.
Il y a cependant un contre-exemple assez flagrant : le bus mémoire ! En effet, les processeurs ont tendance à accéder à des données consécutives quand ils font des lectures/écritures successives. Nous verrons pourquoi dans les chapitres sur le processeurs, mais sachez que c'est lié au fait que les programmeurs utilisent beaucoup les tableaux, une structure de données qui regroupe des données dans des adresses consécutives. Les programmeurs parcourent ces tableaux dans le sens croissant/décroissant des adresses, c'est une opération très fréquente. Une autre raison est que les transferts entre RAM et mémoire cache se font par paquets de grande taille, environ 64 octets, voire plus, qui sont composés d'adresses consécutives. De ce fait, utiliser le code Gray pour encoder les adresses sur un bus mémoire est l'idéal.
Maintenant, cela demande d'ajouter des circuits pour convertir un nombre du binaire vers le code Gray et inversement. Et il faut que l'économie d'énergie liée au code Gray ne soit pas supprimée par l'énergie consommée par ces circuits. Heureusement, de tels circuits sont basés sur des portes XOR. Jugez plutôt. On voit que pour convertir un nombre du binaire vers le code Gray, il suffit de faire un XOR entre chaque bit et le suivant. Pour faire la conversion inverse, c'est la même chose, sauf qu'on fait un XOR entre le bit à convertir et le précédent.
 |
 |
L'encodage à adressage séquentiel
modifierPlus haut, on a dit que l'on peut profiter du fait que des accès mémoire consécutifs se font à des adresses consécutives. L'utilisation du code Gray est une première solution, mais il y a une autre solution équivalente. L'idée est d'ajouter un fil sur le bus mémoire, qui indique si l'adresse envoyée est la suivante. Le fil, nommé INC, indique qu'il faut incrémenter l'adresse envoyée juste avant sur le bus. Si on envoie l'adresse suivante, alors on met ce fil à 1, mais on n'envoie pas l'adresse suivante sur le bus mémoire. Si l'adresse envoyée est totalement différente, ce fil reste à 0 et l'adresse est effectivemen envoyée sur le bus mémoire. On parle de Sequential addressing ou encore de T0 codes.
La mémoire de l'autre côté du bus doit incorporer quelques circuits pour gérer un tel encodage. Premièrement, il faut stocker l'adresse reçue dans un registre à chaque accès mémoire. De plus, il faut aussi ajouter un circuit incrémenteur qui incrémente l'adresse si le fil INC est mis à 1. Le registre et l'incrémenteur sont placés juste entre le bus et le reste de la mémoire, il ne faut rien de plus, si ce n'est quelques multiplexeurs.
Le codage à inversion de bus
modifierLe codage à inversion de bus (bus inversion encoding, BIE) est un codage généraliste qui s'applique à tous les bus, pas seulement au bus mémoire. L'idée est que pour transmettre une donnée, on peut transmettre soit la donnée telle quelle, soit son complément obtenu en inversant tous les bits. Pour minimiser le nombre de bits qui changent entre deux données consécutives envoyées sur le bus, l'idée est de comparer quelle est le cas qui change le plus de bits.
Par exemple, imaginons que j'envoie la donnée 0000 1111 suivie de la donnée 1110 1000. Les deux données n'ont que deux bits de commun, 6 de différents. Par contre, si je prends le complément de 1110 1000, j'obtiens 0001 0111. Il y a maintenant 6 bits de commun et 2 de différents. Envoyer la donnée inversée est donc plus efficace : moins de bits sont à changer. Mais cela ne marche pas toujours : parfois, ne pas inverser la donnée est une meilleure idée. Par exemple, si j'envoie la donnée 0000 1111 suivie de la donnée 0001 1110, inverse les bits donnera un plus mauvais résultat.
Pour implémenter cette technique, le récepteur doit savoir si la donnée a été inversée avant d'être envoyée. Pour cela, on rajoute un fil/bit sur le bus qui indique si la donnée a été inversée ou non. Le bit associé, appelé le bit INV, vaut 1 pour une donnée inversée, 0 sinon.

L'implémentation de ce code est assez simple, du côté du récepteur : il suffit d'ajouter un inverseur commandable dans le récepteur, qui est commandé par le bit INV du bus. Et pour rappel, un inverseur commandable est un circuit qui fait un XOR avec le bit reçu.

Du côté de l'émetteur, il faut ajouter là aussi un inverseur commandable, mais sa commande est plus compliquée. Le circuit doit détecter s'il est rentable ou non d'inverser la donnée. Pour cela, il faut ajouter un registre pour contenir la donnée envoyé juste avant. La donnée à envoyer est comparé à ce registre, pour déterminer quels sont les bits différents, en faisant un XOR entre les deux. Le résultat passe ensuite dans un circuit qui détermine s'il vaut mieux inverser ou non, qui commande un inverseur commandable.

Déterminer s'il faut inverser ou non la donnée est assez simple. On détermine les bits différents avec une porte XOR. Puis, on les compte avec un circuit de population count. Si le résultat est supérieur à la moitié des bits, alors il est bénéfique d'inverser. En effet prenons deux entiers de taille N. S'il y a X bits de différence entre eux, alors si l'on inverse l'un des deux, on aura N-X bits de différents. Il est possible de remplacer le circuit de population count par un circuit de vote à majorité, qui détermine quel est le bit majoritaire. S'il y a plus de 1 dans le résultat du XOR, cela signifie que l'on a plus de bits différents que de bits identiques, on dépasse la moitié (et inversement si on a plus de 0).
Le cout en circuits de cette technique est relativement faible, mais elle est assez efficace. Elle permet des économies qui sont au maximum de 50%, soit une division par deux de la consommation électrique du bus. Elle est plus proche de 10% dans des cas réalistes, pour un cout en circuit proche de plusieurs centaines de portes logiques pour des entiers 32/64 bits. De plus, la technique réduit la consommation dynamique du bus, celle liée aux changements d'état du bus, il reste une consommation statique qui a lieu en permanence, même si les bits du bus restent identiques.
Des calculs théoriques, couplés à des observations empiriques, montrent que la technique marche assez bien pour les petits bus, de 8/16 bits. Mis pour des bus de 32/64 bits, la technique n'offre que peu d'avantages. Une solution est alors d'appliquer la méthode sur chaque octet du bus indépendamment des autres. Par exemple, pour un bus de 64 bits, on peut utiliser 8 signaux INV, un par octet. Ou encore, on peut l'utiliser pour des blocs de 16 bits, ce qui donne 4 signaux INV pour 64 bits, un par bloc de 16 bits. On parle alors de Partitioned inversion encoding. La technique marche bien pour les bus mémoire, car c'est surtout les octets de poids faible qui changent souvent.
Les encodages sur les liaisons point à point asynchrones
modifierAvant de passer à la suite, nous allons voir comment sont encodées les données sur les bus asynchrones. Les liaisons point à point asynchrones permettent à deux circuits/composants de se communiquer sans utiliser de signal d'horloge. L'absence de signal d'horloge fait qu'il faut trouver d'autres méthodes de synchronisation entre composants. Et les méthodes en question se basent sur l'ajout de plusieurs bits ACK et REQ sur le bus.
Dans ce qui suit, on se concentrera sur les liaisons point à point asynchrones unidirectionnelles, on avec un composant émetteur qui envoie des données/commandes à un récepteur. Pour se synchroniser, l’émetteur indique au récepteur qu'il lui a envoyé une donnée. Le récepteur réceptionne alors la donnée et indique qu'il a pris en compte les données envoyées. Cette synchronisation se fait grâce à des fils spécialisés du bus de commande, qui transmettent des bits particuliers.

Les liaisons asynchrones doivent résoudre deux problèmes : comment synchroniser émetteur et récepteur, comment transmettre les données. Les deux problèmes sont résolus de manière différentes. Le premier problème implique d'ajouter des fils au bus de commande, qui remplacent le signal d'horloge. Le second problème est résolu en jouant sur l'encodage des données. Voyons les deux problèmes séparément.
La synchronisation des composants sur une liaison asynchrone
modifierLa synchronisation entre deux composants asynchrones utilise deux fils : REQ et ACK (des mots anglais request =demande et acknowledg(e)ment =accusé de réception). Le fil REQ indique au récepteur que l'émetteur lui a envoyé une donnée, tandis que le fil ACK indique que le récepteur a fini son travail et a accepté la donnée entrante.
Plus rarement, un seul fil est utilisé à la fois pour la requête et l'acquittement, ce qui limite le nombre de fils. Un 1 sur ce fil signifie qu'une requête est en attente (le second composant est occupé), tandis qu'un 0 indique que le second composant est libre. Ce fil est manipulé aussi bien par l'émetteur que par le récepteur. L'émetteur met ce fil à 1 pour envoyer une donnée, le récepteur le remet à 0 une fois qu'il est libre.

Si l'on utilise deux fils séparés, le codage des requêtes et acquittements peut se faire de plusieurs manières. Deux d'entre elles sont très utilisées et sont souvent introduites dans les cours sur les circuits asynchrones. Elles portent les noms de protocole à 4 phases et protocole à 2 phases. Elles ne sont cependant pas les seules et beaucoup de protocoles asynchrones utilisent des méthodes alternatives, mais ces deux méthodes sont très pédagogiques, d'où le fait qu'on les introduise ici.

Avec le protocole à 4 phases, les requêtes d'acquittement sont codées par un bit et/ou un front montant. Les signaux REQ/ACK sont mis à 1 en cas de requête/acquittement et repassent 0 s'il n'y en a pas. Le protocole assure que les deux signaux sont remis à zéro à la fin d'une transmission, ce qui est très important pour le fonctionnement du protocole. Lorsque l'émetteur envoie une donnée au récepteur, il fait passer le fil REQ de 0 à 1. Cela dit au récepteur : « attention, j'ai besoin que tu me fasses quelque chose ». Le récepteur réagit au front montant et/ou au bit REQ et fait ce qu'on lui a demandé. Une fois qu'il a terminé, il positionne le fil ACK à 1 histoire de dire : j'ai terminé ! les deux signaux reviennent ensuite à 0, avant de pouvoir démarrer une nouvelle transaction.
Avec le protocole à deux phases, tout changement des signaux REQ et ACK indique une nouvelle transmission, peu importe que le signal passe de 0 à 1 ou de 1 à 0. En clair, les signaux sont codés par des fronts montants et descendants, et non par le niveau des bits ou par un front unique. Il n'y a donc pas de retour à 0 des signaux REQ et ACK à la fin d'une transmission. Une transmission a lieu entre deux fronts de même nature, deux fronts montants ou deux fronts descendants.
Le tout est illustré ci-contre. On voit que le protocole à 4 phases demande 4 fronts pour une transmission : un front montant sur REQ pour le mettre à 1, un autre sur ACk pour indiquer l'acquittement, et deux fronts descendants pour remettre les deux signaux à 0. Avec le protocole à 2 phases, on n'a que deux fronts : deux fronts montants pour la première transmission, deux fronts descendants pour la suivante. D'où le nom des deux protocoles : 4 et 2 phases.
La transmission des données sur une liaison asynchrone
modifierLa transmission des données/requêtes peut se faire de deux manières différentes, qui portent les noms de Bundled Encoding et de Multi-Rail Encoding. La première est la plus intuitive, car elle correspond à l'encodage des bits que nous utilisons depuis le début de ce cours, alors que la seconde est inédite à ce point du cours.

Le Bundled Encoding utilise un fil par bit de données à transmettre. De telles liaisons sont souvent utilisées dans les composants asynchrones, à savoir les processeurs, mémoires et autres circuits asynchrones. Les circuits asynchrones sont composés de sous-circuits séparés, qui communiquent avec des liaisons asynchrones, qui utilisent le Bundled Encoding. Les circuits construits ainsi sont souvent appelés des micro-pipelines.
Le Bundled Encoding a quelques défauts, le principal étant la sensibilité aux délais. Pour faire simple, la conception du circuit doit prendre en compte le temps de propagation dans les fils : il faut garantir que le signal REQ arrive au second circuit après les données, ce qui est loin d'être trivial. Pour éviter cela, d'autres circuits utilisent plusieurs fils pour coder un seul bit, ce qui donne un codage multiple-rails.
Le cas le plus simple utilise deux fils par bit, ce qui lui vaut le nom de codage dual-rail.

Il en existe plusieurs sous-types, qui différent selon ce qu'on envoie sur les deux fils qui codent un bit.
- Certains circuits asynchrones utilisent un signal REQ par bit, d'où la présence de deux fils par bit : un pour le bit de données, et l'autre pour le signal REQ.
- D'autres codent un bit de données sur deux bits, certaines valeurs indiquant un bit invalide.

On a vu dans le chapitre précédent qu'il faut distinguer les liaisons point à point des bus de communication. Dans ce chapitre, nous allons voir tout ce qui a trait aux liaisons point à point, à savoir comment les données sont transmises sur de telles liaisons, comment l'émetteur et le récepteur s'interfacent, etc. Gardez cependant à l'esprit que tout ce qui sera dit dans ce chapitre vaut aussi bien pour les liaisons point à point que pour les bus de communication. En effet, les liaisons point à point font face aux même problèmes que les bus de communication, si ce n'est la gestion de l'arbitrage.
Deux composants électroniques communiquent entre eux en s'envoyant des trames, des paquets de bits où chaque information nécessaire à la transmission est à une place précise. Le codage des trames indique comment interpréter les données transmises. Le but est que le récepteur puisse extraire des informations utiles du flux de bits transmis : quelle est l'adresse du récepteur, quand la transmission se termine-t-elle, et bien d'autres. Les transmissions sur un bus sont standardisées de manière à rendre l'interprétation du flux de bit claire et sans ambiguïté.
Le terme trame est parfois réservé au cas où le paquet est envoyé en plusieurs fois. Le cas le plus classique est celui des bus série : la trame est envoyée bit par bit, donc en plusieurs fois. Le récepteur accumule les bits dans un registre à décalage, jusqu'à avoir une trame complète. Sur un bus parallèle, il peut y avoir des trames, si les données à transmettre sont plus grandes que la largeur du bus. Tout ce qui sera dit dans ce chapitre vaut pour les trames au sens ! paquet de données envoyé en plusieurs fois.
La taille d'une trame
modifierLa taille d'une trame est soit fixe, soit variable. Par fixe, on veut dire que toutes les trames ont la même taille, le même nombre de bits. Une taille de trame fixe rend l'interprétation du contenu des trames très simple. On sait où sont les données, elles sont tout le temps au même endroit, le format est identique dans toutes les trames. Mais il arrive que le bus gère des trames de taille variable.
Par exemple, prenons l'exemple d'un bus mémoire série, à savoir que la mémoire est reliée à l'extérieur via un bus série (certaines mémoires FLASH sont comme ça). Un accès mémoire doit préciser deux choses : s'il s'agit d'une lecture ou d'une écriture, quelle est l'adresse à lire/écrire, et éventuellement la donnée à écrire. Une trame pour le bus mémoire contient donc : un bit R/W, une adresse, et éventuellement une donnée. La trame pour la lecture n'a pas besoin de préciser de données à écrire, ce qui fait qu'elle contient moins de données, elle est plus courte. Pour une mémoire à accès série, reliée à un bus série, cela fait que la transmission de la trame est plus rapide pour une lecture que pour une écriture.
Sur un bus parallèle, la taille de la trame pose quelques problèmes. Dans le cas idéal, la taille de la trame est un multiple de la taille d'un mot, un multiple de la largeur du bus. Une trame contient N mots, avec N entier. Mais si ce n'est pas le cas, alors on fait face à un problème. Par exemple, imaginons que l'on doive envoyer une trame 2,5 fois plus grande qu'un mot. Dans ce cas, on envoie la trame dans trois mot, le dernier sera juste à moitié remplit. Il faut alors rajouter des bits/octets de bourrage pour remplir un mot.
Le codage des trames : début et de la fin de transmission
modifierLe transfert d'une trame est soumis à de nombreuses contraintes, qui rendent le codage de la trame plus ou moins simple. Le cas le plus simple sont ceux où la trame a une taille inférieur ou égale à la largeur du bus, ce qui permet de l'envoyer en une seule fois, d'un seul coup. Cela simplifie fortement le codage de la trame, vu qu'il n'y a pas besoin de coder la longueur de la trame ou de préciser le début et la fin de la transmission. Mais ce cas est rare et n'apparait que sur certains bus parallèles conçus pour. Sur les autres bus parallèles, plus courants, une trame est envoyée morceau par morceau, chaque morceau ayant la même taille que le bus. Sur les bus série, les trames sont transmises bit par bit grâce à des circuits spécialisés. La trame est mémorisée dans un registre à décalage, qui envoie celle-ci bit par bit sur sa sortie (reliée au bus).
Il arrive qu'une liaison point à point soit inutilisée durant un certain temps, sans données transmises. Émetteur et récepteur doivent donc déterminer quand la liaison est inutilisée afin de ne pas confondre l'état de repos avec une transmission de données. Une transmission est un flux de bits qui a un début et une fin : le codage des trames doit indiquer quand commence une transmission et quand elle se termine. Le récepteur ne reçoit en effet qu'un flux de bits, et doit détecter le début et la fin des trames. Ce processus de segmentation d'un flux de bits en trames n’est cependant pas simple et l'émetteur doit fatalement ajouter des bits pour coder le début et la fin de la trame.
Ajouter un bit sur le bus de commande
modifierPour cela, on peut ajouter un bit au bus de commande, qui indique si le bus est en train de transmettre une trame ou s'il est inactif. Cette méthode est très utilisée sur les bus mémoire, à savoir le bus qui relie le processeur à une mémoire. Il faut dire que de tels bus sont généralement assez simples et ne demandent pas un codage en trame digne de ce nom. Les commandes sont envoyées à la mémoire en une fois, parfois en deux fois, guère plus. Mais il y a moyen de se passer de ce genre d'artifice avec des méthodes plus ingénieuses, qui sont utilisées sur des bus plus complexes, destinés aux entrées-sorties.
Inactiver la liaison à la fin de l'envoi d'une trame
modifierUne première solution est de laisser la liaison complètement inactive durant un certain temps, entre l'envoi de deux trames. La liaison reste à 0 Volts durant un temps fixe à la fin de l'émission d'une trame. Les composants détectent alors ce temps mort et en déduisent que l'envoi de la trame est terminée. Malheureusement, cette méthode pose quelques problèmes.
- Premièrement, elle réduit les performances. Une bonne partie du débit binaire de la liaison passe dans les temps morts de fin de trame, lorsque la liaison est inactivée.
- Deuxièmement, certaines trames contiennent de longues suites de 0, qui peuvent être confondues avec une liaison inactive.
Dans ce cas, le protocole de couche liaison peut résoudre le problème en ajoutant des bits à 1, dans les données de la trame, pour couper le flux de 0. Ces bits sont identifiés comme tel par l'émetteur, qui reconnait les séquences de bits problématiques.
Les octets START et STOP
modifierDe nos jours, la quasi-totalité des protocoles utilisent la même technique : ils placent un octet spécial (ou une suite d'octet) au début de la trame, et un autre octet spécial pour la fin de la trame. Ces octets de synchronisation, respectivement nommés START et STOP, sont standardisés par le protocole.
Problème : il se peut qu'un octet de la trame soit identique à un octet START ou STOP. Pour éviter tout problème, ces pseudo-octets START/STOP sont précédés par un octet d'échappement, lui aussi standardisé, qui indique qu'ils ne sont pas à prendre en compte. Les vrais octets START et STOP ne sont pas précédés de cet octet d'échappement et sont pris en compte, là où les pseudo-START/STOP sont ignorés car précédés de l'octet d'échappement. Cette méthode impose au récepteur d'analyser les trames, pour détecter les octets d'échappements et interpréter correctement le flux de bits reçu. Mais cette méthode a l'avantage de gérer des trames de longueur arbitrairement grandes, sans vraiment de limites.

Une autre solution consiste à remplacer l'octet/bit STOP par la longueur de la trame. Immédiatement à la suite de l'octet/bit START, l'émetteur va envoyer la longueur de la trame en octet ou en bits. Cette information permettra au récepteur de savoir quand la trame se termine. Cette technique permet de se passer totalement des octets d'échappement : on sait que les octets START dans une trame sont des données et il n'y a pas d'octet STOP à échapper. Le récepteur a juste à compter les octets qu'il reçoit et 'a pas à détecter d'octets d'échappements. Avec cette approche, la longueur des trames est bornée par le nombre de bits utilisés pour coder la longueur. Dit autrement, elle ne permet pas de trames aussi grandes que possibles.

Dans le cas où les trames ont une taille fixe, à savoir que leur nombre d'octet ne varie pas selon la trame, les deux techniques précédentes sont inutiles. Il suffit d'utiliser un octet/bit de START, les récepteurs ayant juste à compter les octets envoyés à sa suite. Pas besoin de STOP ou de coder la longueur de la trame.
Les bits de START/STOP
modifierIl arrive plus rarement que les octets de START/STOP soient remplacés par des bits spéciaux ou une séquence particulière de fronts montants/descendants.
Une possibilité est d'utiliser les propriétés certains codages, comme le codage de Manchester. Dans celui-ci, un bit valide est représenté par un front montant ou descendant, qui survient au beau milieu d'une période. L'absence de fronts durant une période est censé être une valeur invalide, mais les concepteurs de certains bus ont décidé de l'utiliser comme bit de START ou STOP. Cela donne du sens aux deux possibilités suivantes : la tension reste constante durant une période complète, soit à l'état haut, soit à l'état bas. Cela permet de coder deux valeurs supplémentaires : une où la tension reste à l'état haut, et une autre où la tension reste à l'état bas. La première valeur sert de bit de START, alors que l'autre sert de bit de STOP. Cette méthode est presque identique aux octets de START et de STOP, sauf qu'elle a un énorme avantage en comparaison : elle n'a pas besoin d'octet d'échappement dans la trame, pas plus que d'indiquer la longueur de la trame.
Un autre exemple est celui des bus RS-232, RS-485 et I²C, où les bits de START et STOP sont codés par des fronts sur les bus de données et de commande.
Le codage des trames : les bits d'ECC
modifierLorsqu'une trame est envoyée, il se peut qu'elle n'arrive pas à destination correctement. Des parasites peuvent déformer la trame et/ou en modifier des bits au point de la rendre inexploitable. Dans ces conditions, il faut systématiquement que l'émetteur et le récepteur détectent l'erreur : ils doivent savoir que la trame n'a pas été transmise ou qu'elle est erronée.
Pour cela, il existe diverses méthodes de détection et de correction d'erreur, que nous avons abordées en partie dans les premiers chapitres du cours. On en distingue deux classes : celles qui ne font que détecter l'erreur, et celles qui permettent de la corriger. Tous les codes correcteurs et détecteurs d'erreur ajoutent tous des bits de correction/détection d'erreur aux données de base, aussi appelés des bits d'ECC. Ils servent à détecter et éventuellement corriger toute erreur de transmission/stockage. Plus le nombre de bits ajoutés est important, plus la fiabilité des données sera importante.
Les bits d'ECC sont générés lors de l'envoi de la donnée sur la liaison point à point. Dans ce qui suit, on part du principe que l'on utilise une liaison série, la donnée est envoyée sur le bus bit par bit. La conversion parallèle-série est faite en utilisant un registre à décalage. La sortie du registre à décalage donne le bit envoyé sur le bus.
Le générateur/checker de parité
modifierDans le cas le plus simple, on se contente d'un simple bit de parité. C'est par exemple ce qui est fait sur les bus ATA qui relient le disque dur à la carte mère, mais aussi sur les premières mémoires RAM des PC. Lors de l'envoi d'une donnée, le bit de parité est généré par un circuit appelé le générateur de parité sériel. Comme son nom l'indique, il calcule le bit de parité bit par bit, avec une bascule et une porte XOR. Rappelons que le bit de parité se calcule en faisant un XOR entre tous les bits du nombre à envoyer.
Le registre à décalage est initialisé avec le nombre dont on veut calculer la parité. La bascule est initialisée à zéro et son but est de conserver le bit de parité calculé à chaque étape. À chaque cycle, un bit de ce nombre sort du registre à décalage et est envoyé en entrée de la porte XOR. La porte XOR fait un XOR entre ce bit et le bit de parité stocké dans la bascule, ce qui donne un bit de parité temporaire. Ce dernier est mémorisé dans la bascule pour être utilisé au prochain cycle. Le bit de parité final est disponible quand tous les bits ont été envoyés sur le bus, et la sortie du générateur de parité est alors connectée au bus pendant un cycle.

Le générateur/checker de CRC
modifierDans d'autres cas, on peut ajouter une somme de contrôle ou un code de Hamming à la trame, ce qui permet de détecter les erreurs de transmission. Mais cet usage de l'ECC est beaucoup plus rare. On trouve quelques carte mères qui gèrent l'ECC pour la communication avec la RAM, mais elles sont surtout utilisées sur les serveurs.
Pour les transmissions réseaux, le code utilisé est un code de redondance cyclique, un CRC. Les circuits de calcul de CRC sont ainsi très simples à concevoir : ce sont souvent de simples registres à décalage à rétroaction linéaire améliorés. Le registre en question a la même taille que le mot dont on veut vérifier l'intégrité. Il suffit d'insérer le mot à contrôler bit par bit dans ce registre, et le CRC est calculé au fil de l'eau, le résultat étant obtenu une fois que le mot est totalement inséré dans le registre.
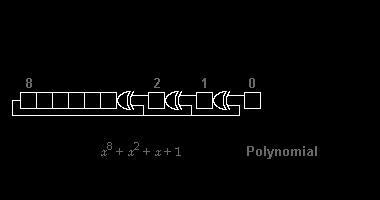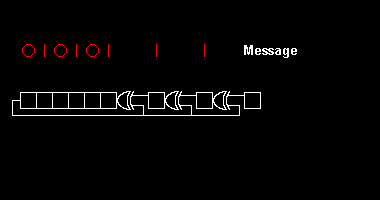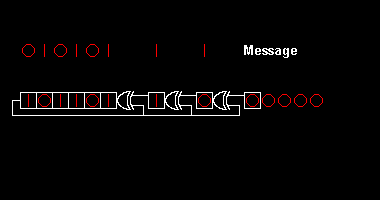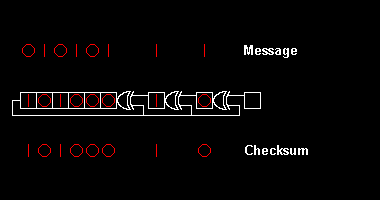
Le registre dépend du CRC à calculer, chaque CRC ayant son propre registre.

Les méthodes de retransmission
modifierLes codes de détection d'erreurs permettent parfois de corriger une erreur de transmission. Mais il arrive souvent que ce ne soit pas le cas : l'émetteur doit alors être prévenu et agir en conséquence. Pour cela, le récepteur peut envoyer une trame à l'émetteur qui signifie : la trame précédente envoyée est invalide. Cette trame est appelée un accusé de non-réception. La trame fautive est alors renvoyée au récepteur, en espérant que ce nouvel essai soit le bon. Mais cette méthode ne fonctionne pas si la trame est tellement endommagée que le récepteur ne la détecte pas.
Pour éviter ce problème, on utilise une autre solution, beaucoup plus utilisée dans le domaine du réseau. Celle-ci utilise des accusés de réception, à savoir l'inverse des accusés de non-réception. Ces accusés de réception sont envoyés à l'émetteur pour signifier que la trame est valide et a bien été reçue. Nous les noterons ACK dans ce qui suivra.
Après avoir envoyé une trame, l'émetteur va attendra un certain temps que l'ACK correspondant lui soit envoyé. Si l’émetteur ne reçoit pas d'ACK pour la trame envoyée, il considère que celle-ci n'a pas été reçue correctement et la renvoie. Pour résumer, on peut corriger et détecter les erreurs avec une technique qui mélange ACK et durée d'attente : après l'envoi d'une trame, on attend durant un temps nommé time-out que l'ACK arrive, et on renvoie la trame au bout de ce temps si non-réception. Cette technique porte un nom : on parle d'Automatic repeat request.
Le protocole Stop-and-Wait
modifierDans le cas le plus simple, les trames sont envoyées unes par unes au rythme d'une trame après chaque ACK. En clair, l'émetteur attend d'avoir reçu l'ACK de la trame précédente avant d'en envoyer une nouvelle. Parmi les méthodes de ce genre, la plus connue est le protocole Stop-and-Wait.
Cette méthode a cependant un problème pour une raison simple : les trames mettent du temps avant d'atteindre le récepteur, de même que les ACK mettent du temps à faire le chemin inverse. Une autre conséquence des temps de transmission est que l'ACK peut arriver après que le time-out (temps d'attente avant retransmission de la trame) soit écoulé. La trame est alors renvoyée une seconde fois avant que son ACK arrive. Le récepteur va alors croire que ce second envoi est en fait l'envoi d'une nouvelle trame !
Pour éviter cela, la trame contient un bit qui est inversé à chaque nouvelle trame. Si ce bit est le même dans deux trames consécutives, c'est que l'émetteur l'a renvoyée car l'ACK était en retard. Mais les temps de transmission ont un autre défaut avec cette technique : durant le temps d'aller-retour, l'émetteur ne peut pas envoyer de nouvelle trame et doit juste attendre. Le support de transmission n'est donc pas utilisé de manière optimale et de la bande passante est gâchée lors de ces temps d'attente.
Les protocoles à fenêtre glissante
modifierLes deux problèmes précédents peuvent être résolus en utilisant ce qu'on appelle une fenêtre glissante. Avec cette méthode, les trames sont envoyées les unes après les autres, sans attendre la réception des ACKs. Chaque trame est numérotée de manière à ce que l'émetteur et le récepteur puisse l’identifier. Lorsque le récepteur envoie les ACK, il précise le numéro de la trame dont il accuse la réception. Ce faisant, l'émetteur sait quelles sont les trames qui ont été reçues et celles à renvoyer (modulo les time-out de chaque trame).
On peut remarquer qu'avec cette méthode, les trames sont parfois reçues dans le désordre, alors qu'elles ont été envoyées dans l'ordre. Ce mécanisme permet donc de conserver l'ordre des données envoyées, tout en garantissant le fait que les données sont effectivement transmises sans problèmes. Avec cette méthode, l'émetteur va accumuler les trames à envoyer/déjà envoyées dans une mémoire. L'émetteur devra gérer deux choses : où se situe la première trame pour laquelle il n'a pas d'ACK, et la dernière trame envoyée. La raison est simple : la prochaine trame à envoyer est l'une de ces deux trames. Tout dépend si la première trame pour laquelle il n'a pas d'ACK est validée ou non. Si son ACK n'est pas envoyé, elle doit être renvoyée, ce qui demande de savoir quelle est cette trame. Si elle est validée, l'émetteur pourra envoyer une nouvelle trame, ce qui demande de savoir quelle est la dernière trame envoyée (mais pas encore confirmée). Le récepteur doit juste mémoriser quelle est la dernière trame qu'il a reçue. Lui aussi va devoir accumuler les trames reçues dans une mémoire, pour les remettre dans l'ordre.
Il y a quelques chapitres, nous avons vu la différence entre bus et liaison point à point : là où ces dernières ne connectent que deux composants, les bus de communication en connectent bien plus. Ce faisant, les bus de communication font face à de nouveaux problèmes, inconnus des liaisons point à point. Et ce sont ces problèmes qui font l'objet de ce chapitre. Autant le chapitre précédent valait à la fois pour les liaisons point à point et les bus, autant ce n'est pas le cas de celui-ci. Ce chapitre va parler de ce qui n'est valable que pour les bus de communication, comme leur arbitrage, la détection des collisions, etc. Tous ces problèmes ne peuvent pas survenir, par définition, sur les liaisons point à point.
L'adressage du récepteur
modifier
La trame doit naturellement être envoyée à un récepteur, seul destinataire de la trame. Sur les liaisons point à point, il n'y a pas besoin de préciser quel est le récepteur. Mais sur les bus, c'est une toute autre histoire. Tous les composants reliés aux bus sont de potentiels récepteurs et l'émetteur doit préciser à qui la trame est destinée. Pour résoudre ce problème, chaque composant se voit attribuer une adresse, il est « numéroté ». Cela fonctionne aussi pour les composants qui sont des périphériques.
L'adressage sur les bus parallèles et série
modifierSur les bus parallèles, l'adresse est généralement transmise sur des fils à part, sur un sous-bus dédié appelé le bus d'adresse. En général, les adresses sur les bus pour périphériques sont assez petites, de quelques bits dans le cas le plus fréquent, quelques octets tout au plus. Il n'y a pas besoin de plus pour adresser une centaine de composants ou plus. Les seuls bus à avoir des adresses de plusieurs octets sont les bus liés aux mémoires, ou ceux qui ont un rapport avec les réseaux informatiques.
Les bus multiplexés utilisent une astuce pour économiser des fils et des broches. Un bus multiplexé sert alternativement de bus de donnée ou d'adresse, suivant la valeur d'un bit du bus de commande. Ce dernier, le bit Adress Line Enable (ALE), précise si le contenu du bus est une adresse ou une donnée : il vaut 1 quand une adresse transite sur le bus, et 0 si le bus contient une donnée.
Un défaut de ces bus est que les transferts sont plus lents, car l'adresse et la donnée ne sont pas envoyées en même temps lors d'une écriture. Un autre problème des bus multiplexé est qu'ils ont a peu près autant de bits pour coder l'adresse que pour transporter les données. Par exemple, un bus multiplexé de 8 bits transmettra des adresses de 16 bits, mais aussi des données de 16 bits. Ils sont donc moins versatiles, mais cela pose problème sur les bus où l'on peut connecter peu de périphériques. Dans ce cas, les adresses sont très petites et l'économie de fils est donc beaucoup plus faible.
Passons maintenant aux bus série (ou certains bus parallèles particuliers). Pour arriver à destination, la trame doit indiquer l'adresse du composant de destination. Les récepteurs espionnent le bus en permanence pour détecter les trames qui leur sont destinées. Ils lisent toutes les trames envoyées sur le bus et en extraient l'adresse de destination : si celle-ci leur correspond, ils lisent le reste de la trame, ils ne la prennent pas en compte sinon.
L'adresse en question est intégrée à la trame et est placée à un endroit précis, toujours le même, pour que le récepteur puisse l'extraire. Le plus souvent, l'adresse de destination est placée au début de la trame, afin qu'elle soit envoyée au plus vite. Ainsi, les périphériques savent plus rapidement si la trame leur est destinée ou non, l'adresse étant connue le plus tôt possible.
Le décodage d'adresse
modifierLe fait d'attribuer une adresse à chaque composant est une idée simple, mais efficace. Encore faut-il la mettre en œuvre et il existe plusieurs possibilités pour cela. Implémenter l'adressage sur un bus demande à ce que chaque composant sache d'une manière ou d'une autre que c'est à lui que l'on veut parler et pas à un autre. Lorsqu'une adresse est envoyée sur le bus, seul l'émetteur et le récepteur se connectent au bus, les autres composants ne sont pas censés réagir. Et pour cela, il existe deux possibilités : soit on délègue l'adressage au composant, soit on ajoute un circuit qui active le composant adressé et désactive les autres.
Avec la première méthode, les composants branchés sur le bus monitorent en permanence ce qui est transféré sur le bus. Quand un envoi de commande a lieu, chaque composant extrait l'adresse transmise sur le bus et vérifie si c'est bien la sienne. Si c'est le cas, le composant se connecte sur le bus et les autres composants se déconnectent. En conséquence, chaque composant contient un comparateur pour cette vérification d'adresse, dont la sortie commande les circuits trois états qui relient le contrôleur au bus. Cette méthode est particulièrement pratique sur les bus où le bus d'adresse est séparé du bus de données. Si ce n'est pas le cas, le composant doit mémoriser l'adresse transmise sur le bus dans un registre, avant de faire la comparaison? Même chose sur les bus série.
La seconde solution est celle du décodage d'adresse. Elle utilise un circuit qui détermine, à partir de l'adresse, quel est le composant adressé. Seul ce composant sera activé/connecté au bus, tandis que les autres seront désactivés/déconnectés du bus. Pour implémenter la dernière solution, chaque périphérique possède une entrée CS, qui active ou désactive le composant suivant sa valeur. Le composant se déconnecte du bus si ce bit est à 0 et est connecté s'il est à 1. Pour éviter les conflits, un seul composant doit avoir son bit CS à 1. Pour cela, il faut ajouter un circuit qui prend en entrée l'adresse et qui commande les bits CS : ce circuit est un circuit de décodage partiel d'adresse.

L'interfaçage avec le bus
modifierUne fois que l'on sait quel composant a accès au bus à un instant donné, il faut trouver un moyen pour que les composants non sélectionnés par l'arbitrage ne puissent pas écrire sur le bus.
Une première solution consiste à relier les entrées/sorties des composants au bus via un multiplexeur/démultiplexeur : on est alors certain que seul un composant pourra émettre sur le bus à un moment donné. L'arbitrage du bus choisit quel composant peut émettre, et configure l'entrée de commande du multiplexeur en fonction. Les multiplexeurs et démultiplexeurs sont configurés en utilisant l'adresse du composant émetteur/récepteur.
Une autre solution consiste à connecter et déconnecter les circuits du bus selon les besoins. A un instant t, seul l'émetteur et le récepteur sont connectés au bus. Mais cela demande pouvoir déconnecter du bus les entrées/sorties qui n'envoient pas de données. Plus précisément, leurs sorties peuvent être mises dans un état de haute impédance, qui n'est ni un 0 ni un 1. Quand une sortie est en haute impédance, elle n'a pas la moindre influence sur le bus et ne peut donc pas y écrire. Tout se passe comme si elle était déconnectée du bus, et dans les faits, elle l'est souvent.
Dans le chapitre sur les circuits intégrés, nous avons vu qu'il existait trois types de sorties : les sorties totem-pole, à drain/collecteur ouvert, et trois-état. Les sorties totem-pole fournissent soit un 1, soit un zéro, et ne peuvent pas être déconnectées proprement dit. Les deux autres types de sorties en sont capables. Et nous allons les voir dans ce qui suit.
L'interfaçage avec le bus avec des circuits trois-états
modifierLe cas le plus simple est celui des sorties trois-état, qui peuvent soit fournir un 1, soit fournir un 0, soit être déconnectées. Malheureusement, les circuits intégrés normaux n'ont pas naturellement des entrées-sorties trois-état. Les portes logiques fournissent soit un 0, soit un 1, pas d'état déconnecté.

La solution retenue sur presque tous les circuits actuels est d'utiliser des tampons trois états. Pour rappel, nous avions vu ce circuit dans le chapitre sur les circuits intégrés, mais un rappel ne fera clairement pas de mal. Un tampon trois-états peut être vu comme une porte OUI modifiée, qui peut déconnecter sa sortie de son entrée. Un tampon trois-état possède une entrée de donnée, une entrée de commande, et une sortie : suivant ce qui est mis sur l'entrée de commande, la sortie est soit en état de haute impédance (déconnectée du bus), soit égale à l'entrée.
| Commande | Entrée | Sortie |
|---|---|---|
| 0 | 0 | Haute impédance/Déconnexion |
| 0 | 1 | Haute impédance/Déconnexion |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

On peut utiliser ces tampons trois états pour permettre à un composant d'émettre ou de recevoir des données sur un bus. Par exemple, on peut utiliser ces tampons pour autoriser les émissions sur le bus, le composant étant déconnecté (haute impédance) s'il n'a rien à émettre. Le composant a accès au bus en écriture seule. L'exemple typique est celui d'une mémoire ROM reliée à un bus de données.

Une autre possibilité est de permettre à un composant de recevoir des données sur le bus. Le composant peut alors surveiller le bus et regarder si des données lui sont transmises, ou se déconnecter du bus. Le composant a alors accès au bus en lecture seule.

Évidemment, on peut autoriser lectures et écritures : le composant peut alors aussi bien émettre que recevoir des données sur le bus quand il s'y connecte. On doit alors utiliser deux circuits trois états, un pour l'émission/écriture et un autre pour la réception/lecture. Comme exemple, on pourrait citer les mémoires RAM, qui sont reliées au bus mémoire par des circuits de ce genre. Dans ce cas, les circuits trois états doivent être commandés par le bit CS (Chip Select) qui connecte ou déconnecte la mémoire du bus, mais aussi par le bit R/W (Read/Write) qui décide du sens de transfert. Pour faire la traduction entre ces deux bits et les bits à placer sur l'entrée de commande des circuits trois états, on utilise un petit circuit combinatoire assez simple.

L'interfaçage avec le bus avec des circuits à drain/collecteur ouvert
modifierLes sorties à drain/collecteur ouvert sont plus limitées et ne peuvent prendre que deux états. Dans le cas le plus fréquent, la sortie est soit déconnectée, soit mise à 0 par le circuit intégré, mais elle ne peut pas être mise à 1 sans intervention extérieure. Pour compenser cela, le bus est relié à la tension d'alimentation à travers une résistance, appelée résistance de rappel. Cela garantit que le bus est naturellement à l'état 1, du moins tant que les sorties des composants sont déconnectées. Au repos, quand les composants n’envoient rien sur le bus, les sorties des composants sont déconnectées et les résistances de rappel mettent le bus à 1. Mais quand un seul composant met sa sortie à 0, cela force le bus à passer à 0.

Pour le dire autrement, on peut voir le contenu du bus comme un ET des bits envoyés sur les sorties des composants connectés au bus. Ce détail aura son importance par la suite. Le contenu du fil peut être lu sans altérer l'état électrique du bus/fil.
Avec cette méthode, le nombre de composants que l'on peut placer sur le bus est surtout limité par les spécifications électriques du bus, notamment sa capacité. Mais cela a l'avantage que le bus est compatible avec des technologies de fabrication totalement différentes, qu'il s'agisse de composants TTL, CMOS ou autres. En effet, la tension d'alimentation des composants TTL n'est pas la même que celle des composants CMOS. Utiliser des entrées-sorties à drain ouvert fait que l'on peut choisir la tension d'alimentation que l'on veut, et donc que l'on peut choisir entre TTL et CMOS. Par contre, on ne peut pas connecter composants TTL et CMOS avec des tensions d'alimentation différentes sur un même bus.
Il est possible de mélanger sorties à drain/collecteur ouvert, avec des entrées "trois-états" (des entrées qui peuvent soit permettre une lecture du bus, soit être déconnectées). C'est par exemple le cas sur les microprocesseurs 8051.

L'arbitrage du bus
modifier
Sur certains bus, il arrive que plusieurs composants tentent d'envoyer une donnée sur le bus en même temps : c'est un conflit d'accès au bus. Cette situation arrive sur de nombreux types de bus, qu'ils soient multiplexés ou non. Sur les bus multiplexés, qui relient plus de deux composants, cette situation est fréquente du fait du nombre de récepteurs/émetteurs potentiels. Mais cela peut aussi arriver sur certains bus dédiés, les bus half-duplex étant des exemples particuliers : il se peut que les deux composants veuillent être émetteurs en même temps, ou récepteurs.
Quoi qu’il en soit, ces conflits d'accès posent problème si un composant cherche à envoyer un 1 et l'autre un 0 : tout ce que l’on reçoit à l'autre bout du fil est une espèce de mélange incohérent des deux. Pour résoudre ce problème, il faut répartir l'accès au bus pour n'avoir qu'un émetteur à la fois. On doit choisir un émetteur parmi les candidats. Ce choix sera effectué différemment suivant le protocole du bus et son organisation, mais ce choix n’est pas gratuit. Certains composants devront attendre leur tour pour avoir accès au bus. Les concepteurs de bus ont inventé des méthodes pour gérer ces conflits d’accès, et choisir le plus efficacement possible l’émetteur : on parle d'arbitrage du bus.
Les méthodes d'arbitrage (algorithmes)
modifierIl existe plusieurs méthodes d'arbitrages, qui peuvent se classer en différents types, selon leur fonctionnement.
Pour donner un exemple d'algorithme d'arbitrage, parlons de l'arbitrage par multiplexage temporel. Celui-ci peut se résumer en une phrase : chacun son tour ! Chaque composant a accès au bus à tour de rôle, durant un temps fixe. Cette méthode fort simple convient si les différents composants ont des besoins approximativement équilibrés. Mais elle n'est pas adaptée quand certains composants effectuent beaucoup de transactions que les autres. Les composants gourmands manqueront de débit, alors que les autres monopoliseront le bus pour ne presque rien en faire. Une solution est d'autoriser à un composant de libérer le bus prématurément, s'il n'en a pas besoin. Ce faisant, les composants qui n'utilisent pas beaucoup le bus laisseront la place aux composants plus gourmands.
Une autre méthode est celle de l'arbitrage par requête, qui se résume à un simple « premier arrivé, premier servi » ! L'idée est que tout composant peut réserver le bus si celui-ci est libre, mais doit attendre si le bus est déjà réservé. Pour savoir si le bus est réservé, il existe deux méthodes :
- soit chaque composant peut vérifier à tout moment si le bus est libre ou non (aucun composant n'écrit dessus) ;
- soit on rajoute un bit qui indique si le bus est libre ou occupé : le bit busy.
Certains protocoles permettent de libérer le bus de force pour laisser la place à un autre composant : on parle alors de bus mastering. Sur certains bus, certains composants sont prioritaires, et les circuits chargés de l'arbitrage libèrent le bus de force si un composant plus prioritaire veut utiliser le bus. Bref, les méthodes d'arbitrage sont nombreuses.
Arbitrage centralisé ou décentralisé
modifierUne autre classification nous dit si un composant gère le bus, ou si cet arbitrage est délégué aux composants qui accèdent au bus.
- Dans l'arbitrage centralisé, un circuit spécialisé s'occupe de l'arbitrage du bus.
- Dans l'arbitrage distribué, chaque composant se débrouille de concert avec tous les autres pour éviter les conflits d’accès au bus : chaque composant décide seul d'émettre ou pas, suivant l'état du bus.
- Notons qu'un même algorithme peut être implémenté soit de manière centralisée, soit de manière décentralisée.
Pour donner un exemple d'arbitrage centralisé, nous allons aborder l'arbitrage par daisy chain. Il s'agit d'un algorithme centralisé, dans lequel tout composant a une priorité fixe. Dans celui-ci, tous les composants sont reliés à un arbitre, qui dit si l'accès au bus est autorisé.
Les composants sont reliés à l'arbitre via deux fils : un fil nommé Request qui part des composants et arrive dans l'arbitre, et un fil Grant qui part de l'arbitre et parcours les composants un par un. Le fil Request transmet à l'arbitre une demande d'accès au bus. Le composant qui veut accéder au bus va placer un sur ce fil 1 quand il veut accéder au bus. Le fil Grant permet à l'arbitre de signaler qu'un des composants pourra avoir accès au bus. Le fil est unique Request est partagé entre tous les composants (cela remplace l'utilisation d'une porte OU). Par contre, le fil Grant relie l'arbitre au premier composant, puis le premier composant au second, le second au troisième, etc. Tous les composants sont reliés en guirlande par ce fil Grant.
Par défaut, l'arbitre envoie un 1 quand il accepte un nouvel accès au bus (et un 0 quand il veut bloquer tout nouvel accès). Quand un composant ne veut pas accéder au bus, il transmet le bit reçu sur ce fil tel quel, sans le modifier. Mais s'il veut accéder au bus, il mettra un zéro sur ce fil : les composants précédents verront ainsi un 1 sur le fil, mais les suivants verront un zéro (interdiction d'accès). Ainsi, les composants les plus près du bus, dans l'ordre de la guirlande, seront prioritaires sur les autres.

L'arbitrage sur les bus à collecteur ouvert
modifierLes bus à collecteur ouvert ont un avantage pour ce qui est de l'arbitrage : ils permettent de détecter les collisions assez simplement. En effet, le contenu du bus est égal à un ET entre toutes les sorties reliées au bus. Si tous les composants veulent laisser le bus à 1 à un instant t, le bus sera à 1 : s'il y a collision, elle n'est pas grave car tous les composants envoient la même chose. Pareil s'ils veulent tous mettre le bus à 0 : le bus sera à 0 et la collision n'aura aucun impact. Par contre, si une sortie veut mettre le bus à 0 et un autre veut le laisser à 1, alors le bus sera mis à 0.
La détection des collisions est alors évidente. Les composants qui émettent quelque chose sur le bus vérifient si le bus a bien la valeur qu'ils envoient dessus. Si les deux concordent, on ne sait pas il y a collision et il y a de bonnes chances que ce ne soit pas le cas, alors on continue la transmission. Mais si un composant envoie un 1 et que le bus est à 0, cela signifie qu'un autre composant a mis le bus à 0 et qu'il y a une collision. Le composant qui a détecté la collision cesse immédiatement la transmission et laisse la place au composant qui a mis le bus à 0, il le laisse finir la transmission entamée.
Dans ce qui va suivre, nous allons étudier quelques bus relativement connus, autrefois très utilisés dans les ordinateurs. La plupart de ces bus sont très simples : il n'est pas question d'étudier les bus les plus en vogue à l'heure actuelle, du fait de leur complexité. Nous allons surtout étudier les bus série, les bus parallèles étant plus rares.
Un exemple de liaison point-à-point série : le port série RS-232
modifierLe port RS-232 est une liaison point à point de type série, utilisée justement sur les ports série qu'on trouvait à l'arrière de nos PC. Celui-ci était autrefois utilisé pour les imprimantes, scanners et autres périphériques du même genre, et est encore utilisé comme interface avec certaines cartes électroniques. Il existe des cartes d'extension permettant d'avoir un port série sur un PC qui n'en a pas, se branchant sur un autre type de port (USB en général).
Le câblage de la liaison série RS-232
modifierLe RS-232 est une liaison point à point de type full duplex, ce qui veut dire qu'elle est bidirectionnelle. Les données sont transmises dans les deux sens entre deux composants. Si la liaison est bidirectionnelle, les deux composants ont cependant des rôles asymétriques, ce qui est assez original. Un des deux composants est appelé le Data Terminal Equipment (DTE), alors que l'autre est appelé le Data Circuit-terminating Equipment (DCE). Les connecteurs pour ces deux composants sont légèrement différents. Mais mettons cela de côté pour le moment. En raison, de son caractère bidirectionnel, on devine que la liaison RS-232 est composée de deux fils de transmission de données, qui vont dans des sens opposés. À ces deux fils, il faut ajouter la masse, qui est commune entre les deux composants.

Certains périphériques RS-232 n'avaient pas besoin d'une liaison bidirectionnelle et ne câblaient pas le second fil de données, et se contentaient d'un fil et de la masse. À l'inverse, d'autres composants ajoutaient d'autres fils, définis par le standard RS-232, pour implémenter un protocole de communication complexe. C'était notamment le cas sur les vieux modems connectés sur le ports série. Généralement, 9 fils étaient utilisés, ce qui donnait un connecteur à 9 broches de type DE-9.

La trame RS-232
modifierLe bus RS-232 est un bus série asynchrone. Une transmission sur ce bus se résume à l'échange d'un octet de donnée. La trame complète se décompose en un bit de start, l'octet de données à transmettre, un bit de parité, et un bit de stop. Le bit de start est systématiquement un bit qui vaut 0, tandis que le bit de stop vaut systématiquement 1.

L'envoi et la réception des trames sur ce bus se fait simplement en utilisant un composant nommé UART composé de registres à décalages qui envoient ou réceptionnent les données bit par bit sur le bus. Les données envoyées sont placées dans un registre à décalage, dont le bit de sortie est connecté directement sur le bus série. La réception se fait de la même manière : le bus est connecté à l'entrée d'un registre à décalage. Quelques circuits annexes s'occupent du calcul de la parité et de la détection des bits de start et de stop.
Un exemple de bus série : le bus I²c
modifierNous allons maintenant voir le fameux bus I²c. Il s'agit d'un bus série, qui utilise deux fils pour le transport des données et de l'horloge, nommés respectivement SDA (Serial Data Line) et SCL (Serial Clock Line). Chaque composant compatible I²c a donc deux broches, une pour le fil SDA et une autre pour le fil SCL.
La spécification électrique
modifierLes composants I²c ont des entrées et sorties qui sont dites à drain ouvert. Pour rappel, cela veut dire qu'une broche peut mettre le fil à 0 ou le laisser à son état de repos, mais ne peut pas décider de mettre le fil à 1. Pour compenser, les fils sont connectés à la tension d'alimentation à travers une résistance, ce qui garantit que l'état de repos soit à 1.
- Pour le dire autrement, on peut voir le contenu du bus comme un ET des bits envoyés sur les sorties des composants connectés au bus. Ce détail aura son importance par la suite. Le contenu du fil peut être lu sans altérer l'état électrique du bus/fil.

En faisant cela, le nombre de composants que l'on peut placer sur le bus est surtout limité par les spécifications électriques du bus, notamment sa capacité. Mais cela a l'avantage que le bus est compatible avec des technologies de fabrication totalement différentes, qu'il s'agisse de composants TTL, CMOS ou autres. En effet, la tension d'alimentation des composants TTL n'est pas la même que celle des composants CMOS. Utiliser des entrées-sorties à drain ouvert fait que la spécification du bus I²c ne spécifie pas la tension d'alimentation du bus, mais la laisse au choix du concepteur. En clair, on peut connecter plusieurs composants TTL sur un même bus, ou plusieurs composants CMOS sur le même bus, mais on ne peut pas connecter composants TTL et CMOS avec des tensions d'alimentation différentes sur un même bus. La compatibilité est donc présente, même si elle n'est pas parfaite.
L'adressage sur le bus I²c
modifierChaque composant connecté à un bus I²c a une adresse unique, qui sert à l’identifier. Les mémoires I²c ne font pas exception. Les adresses I²c sont codées sur 7 bits, ce qui donne un nombre de 128 adresses distinctes. Certaines adresses sont cependant réservées et ne peuvent pas être attribuées à un composant. C'est le cas des adresses allant de 0000 0000 à 0000 0111 et des adresses allant de 1111 1100 à 1111 1111, ce qui fait 8 + 4 = 12 adresses réservées. Les adresses impaires sont des adresses de lecture, alors que les adresses paires sont des adresses d'écriture. En tout, cela fait donc 128 - 12 = 116 adresses possibles, dont 2 par composant, ce qui fait 58 composants maximum.
Le codage des trames sur un bus I²c
modifierLe codage d'une trame I²c est assez simple. La trame de données est organisée comme suit : un bit de START, suivi de l'octet à transmettre, suivi par un bit d'ACK/NACK, et enfin d'un bit de STOP. Le bit d'ACK/NACK indique si le récepteur a bien reçu la donnée sans erreurs. Là où les bits START, STOP et de données sont émis par l'émetteur, le bit ACK/NACK est émis par le récepteur.
Vous êtes peut-être étonné par la notion de bit START et STOP et vous demandez comment ils sont codés. La réponse est assez simple quand on se rappelle que les fils SDA et SCL sont mis à 1 à l'état de repos. L'horloge n'est active que lors du transfert effectif des données, et reste à 1 sinon. Si SDA et SCL sont à 1, cela signifie qu'aucun composant ne veut utiliser le bus. Le début d'une transmission demande donc qu'au moins un des fils passe à 0. Un transfert de données commence avec un bit START, qui est codé par une mise à 0 de l'horloge avant le fil de donnée, et se termine avec un bit STOP, qui correspond aux conditions inverses.

|

|

|
Les données sont maintenues tant que l’horloge est à 1. Dit autrement, le signal de donnée ne montre aucun front entre deux fronts de l'horloge. Retenez bien cette remarque, car elle n'est valide que pour la transmission d'un bit de données (et les bits d'ACK/NACK). Les bits START et STOP correspondent à une violation de cette règle qui veut qu'il y ait absence de front sur le signal de données entre deux fronts d'horloge.

|

|
Pour résumer, une transmission I²c est schématisée ci-dessous. Sur ce schéma, S représente le marqueur de début de transmission (start), puis chaque période en bleue est celle ou la ligne de donnée peut changer d'état pour le prochain bit de données à transmettre durant la période verte qui suit notée B1, B2... jusqu'à la période finale notée P marquant la fin de transmission (stop).

Une trame transmet soit une donnée, soit une adresse. Généralement, la trame transmet un octet, qu'il s'agisse d'un octet de données ou un octet d'adresse. Pour une adresse, l'octet transmis contient une adresse de 7 bits et un bit R/W. Une lecture/écriture est composée de au moins deux transmissions : d'abord on transmet l'adresse, puis la donnée est transmise ensuite. Si je viens de dire "au moins deux transmissions", c'est parce qu'il est possible de lire/écrire des données de 16 ou 32 bits, en plusieurs fois. Dans ce cas, on envoie l'adresse avec la première transmission, puis on envoie/réceptionne plusieurs octets les uns à la suite des autres, avec une transmission par octet. Il est aussi possible d'envoyer une adresse en plusieurs fois,c e qui est très utilisé pour les mémoires I²c : la première adresse envoyée permet de sélectionner la mémoire, l'adresse suivante identifie le byte voulu dans la mémoire.

La synchronisation sur le bus I²c
modifierIl arrive que des composants lents soient connectés à un bus I²c, comme des mémoires EEPROM. Ils mettent typiquement un grand nombre de cycles avant de faire ce qu'on leur demande, ce qui donne un temps d'attente particulièrement long. Dans ce cas, les transferts de ou vers ces composants doivent être synchronisés d'une manière ou d'une autre. Pour cela, le bus I²c permet de mettre en pause une transmission tant que le composant lent n'a pas répondu, en allongeant la durée du bit d'ACK.
Un périphérique normal répondrait à une transmission comme on l'a vu plus haut, avec un bit ACK. Pour cela, le récepteur met la ligne SDA à 0 pendant que l'horloge SCL est à 1. L'idée est qu'un récepteur lent peut temporairement maintenir la ligne SCL à 0 pendant toute la durée d'attente. Dans ce cas, l'émetteur attend un nouveau front sur l'horloge avant de faire quoi que ce soit. L'horloge est inhibée, le bus I²c est mis en pause. Quand le récepteur lent a terminé, il relâche la ligne d'horloge SDL, et envoie un ACK normal. Cette méthode est utilisée par beaucoup de mémoires EEPROM I²c. Évidemment, cela réduit les performances et la perte est d'autant plus grande que les temps d'attente sont longs.
L’arbitrage sur le bus I²c
modifierLe bit START est impliqué dans l'arbitrage du bus : dès que le signal SDA est mis à 0 par un émetteur, les autres composants savent qu'une transmission a commencé et qu'il faut attendre.
Il est malgré tout possible que deux composants émettent chacun une donnée en même temps, car ils émettent un bit START à peu près en même temps. Dans ce cas, l'arbitrage du bus utilise intelligemment le fait que les entrées-sorties sont à drain ouvert. Nous avions dit que le bus est à 1 au repos, mais qu'il est mis à 0 dès qu'au moins un composant veut envoyer un 0. Pour le dire autrement, on peut voir le contenu du bus comme un ET des bits envoyés sur les sorties des composants connectés au bus. Ce détail est utilisé pour l'arbitrage.
Si deux émetteurs envoient chacun une donnée, le bus accepte cette double transmission. Tant que les bits transmis sont identiques, cela ne pose pas de problème : le bus est à 1 si les deux composants veulent envoyer un 1 en même temps, idem pour un 0. Par contre, si un composant veut envoyer un 1 et l'autre un 0, le bus est mis à 0 du fait des sorties à drain ouvert. Le truc est que les émetteurs vérifient si les bits transmis sur le bus correspondent aux bits envoyés. Si l'émetteur émet un 1 et voit un 0 sur le bus, il comprend qu'il y a une collision et cesse sa transmission pour laisser la place à l'autre émetteur. Il retentera une nouvelle transmission plus tard.
Un exemple de bus parallèle : le bus PCI
modifier
Le bus PCI est un bus autrefois très utilisé dans les ordinateurs personnels, qui a eu son heure de gloire entre les années 90 et 2010. Il était utilisé pour la plupart des cartes d'extension, à savoir les cartes son, les cartes graphiques et d'autres cartes du genre. Il remplace le bus ISA, un ancien bus devenu obsolète dans les ordinateurs personnels.
- Les lecteurs aguerris qui veulent une description détaillée du bus PCI peuvent lire le livre nommé "PCI Bus Demystified".
Les performances théoriques du bus PCI
modifierLe bus ISA avait une largeur de seulement 16 bits et une fréquence de 8 MHz, ce qui était suffisant lors de son adoption, mais était devenu trop limitant dès les années 90. Le bus PCI avait de meilleures performances : un bus de 32 bits et une fréquence de 33 MHz dans sa première version, ce qui faisait un débit maximum de 133 mébioctets par secondes. Des extensions faisaient passer le bus de données de 32 à 64 bits, augmentaient la fréquence à 66/133 MHz, ou alors ajoutaient des fonctionnalités. Les versions 64 bits du bus PCI avaient généralement une fréquence plus élevée, de 66 MHz pour le PCI version 2.3, de 133 MHz pour le PCI-X.
La tension d'alimentation : deux normes
modifierIl existait aussi une version 3,3 volts et une version 5 volts du bus PCI, la tension faisant référence à la tension utilisée pour alimenter le bus. L'intérêt était de mieux s'adapter aux circuits imprimés de l'époque : certains fonctionnaient en logique TTL à 5 volts, d'autres avec une logique différente en 3,3 volts. La logique ici mentionnée est la manière dont sont construits les transistors et portes logiques. Concrètement, le fait qu'il s'agisse de deux logiques différentes change tout au niveau électrique. La norme du bus PCI en 3,3 volts est fondamentalement différente de celle en 5 volts, pour tout ce qui touche aux spécifications électriques (et elles sont nombreuses). Une carte conçue pour le 3,3 volts ne pourra pas marcher sur un bus PCI 5 volts, et inversement. Il existe cependant des cartes universelles capables de fonctionner avec l'une ou l'autre des tensions d'alimentation, mais elles sont rares. Pour éviter tout problème, les versions 3,3 et 5 volts du bus PCI utilisaient des connecteurs légèrement différents, de même que les versions 32 et 64 bits.

L'arbitrage du bus PCI
modifierLe bus PCI utilise un arbitrage centralisé, avec un arbitre qui commande plusieurs composants maîtres. Chaque composant maitre peut envoyer des données sur le bus, ce qui en fait des émetteurs-récepteurs, contrairement aux composants esclaves qui sont toujours récepteurs. Chaque maître a deux broches spécialisées dans l'arbitrage : un fil REQ (Request) pour demander l'accès au bus à l'arbitre, et un fil GNT (Grant) pour recevoir l'autorisation d'accès de la part de l'arbitre de bus. Les deux signaux sont actifs à l'état bas, à zéro. Un seul signal GNT peut être actif à la fois, ce qui fait qu'un seul composant a accès au bus à un instant donné.
L'arbitrage PCI gère deux niveaux de priorité pour l'arbitrage. Les composants du premier niveau sont prioritaires sur les autres pour l'arbitrage. En cas d'accès simultané, le composant de niveau 1 aura accès au bus alors que ceux de niveau 2 devront attendre. En général, les cartes graphiques sont de niveau 1, alors que les cartes réseau, son et SCSI sont dans le niveau 2.
Un composant ne peut pas monopoliser le bus en permanence, mais doit laisser la place aux autres après un certain temps. Une fois que l'émetteur a reçu l'accès au bus et démarré une transmission avec le récepteur, il a droit à un certain temps avant de devoir laisser la place à un autre composant. Le temps en question est déterminé par un timer, un compteur qui est décrémenté à chaque cycle d'horloge. Au démarrage de la transaction, ce compteur est initialisé avec le nombre de cycle maximal, au-delà duquel l'émetteur doit laisser le bus. Si le compteur atteint 0, que d'autres composants veulent accéder au bus, et que l'émetteur ait terminé sa transmission, la transmission est arrêtée de force. Le composant peut certes redemander l'accès au bus, mais elle ne lui sera pas accordée car d'autres composants veulent accéder au bus.
Il est possible que, quand aucune transaction n'a lieu, le bus soit attribué à un composant maître choisit par défaut. On appelle cela le bus parking. Cela garantit qu'il y a toujours un composant qui a son signal REQ actif, il ne peut pas avoir de situation où aucun composant PCI n'a accès au bus. Quand un autre composant veut avoir accès au bus, l'autre composant est choisit, sauf si une transmission est en cours. L'avantage est que le composant maître choisit par défaut n'a pas besoin de demander l'accès au bus au cas où il veut faire une transmission, ce qui économise quelques cycles d'horloge. L'arbitre du bus doit cependant être configuré pour. Le réglage par défaut du bus PCI est que le maître choisi par défaut est le dernier composant à avoir émis une donnée sur le bus.
L'adressage et le bus PCI
modifierLe bus PCI est multiplexé, ce qui signifie que les mêmes fils sont utilisés pour transmettre successivement adresse ou données. Les adresses ont la même taille que le bus de données : 32 bits ou 64 bits, suivant la version du bus. On trouve aussi un bit de parité, transmis en même temps que les données et adresses. Notons que les composants 32 bits pouvaient utiliser des adresses 64 bits sur un bus PCI : il leur suffit d'envoyer ou de recevoir les adresses en deux fois : les 32 bits de poids faible d'abord, les 32 bits de poids fort ensuite. Fait important, le PCI ne confond pas les adresses des périphériques et de la mémoire RAM. Il existe trois espaces d'adressage distincts : un pour la mémoire RAM, un pour les périphériques, et un pour la configuration qui est utilisé au démarrage de l'ordinateur pour détecter et configurer les périphériques branchés sur le bus.
Le bus de commande possède 4 fils/broches sur lesquelles on peut transmettre une commande à un périphérique. Il existe une commande de lecture et une commande d'écriture pour chaque espace d'adressage. On a donc une commande de lecture pour les adresses en RAM, une commande de lecture pour les adresses de périphériques, une autre pour les adresses de configuration, idem pour les commandes d'écritures. Il existe aussi des commandes pour les adresses en RAM assez spéciales, qui permettent de faire du préchargement, de charger des données à l'avance. Ces commandes permettent de faire une lecture, mais préviennent le contrôleur PCI que les données suivantes seront accédées par la suite et qu'il vaut mieux les précharger à l'avance.
Les commandes en question sont transmises en même temps que les adresses. Lors de la transmission d'une donnée, les 4 broches sont utilisées pour indiquer quels octets du bus sont valides et quels sont ceux qui doivent être ignorés.
| Bits de commande | Nom de la commande | Signification |
|---|---|---|
| 0000 | Interrupt Acknowledge | Commande liée aux interruptions |
| 0001 | Special Cycle | Envoie une commande/donnée à tous les périphériques PCI |
| 0010 | I/O Read | Lecture dans l'espace d’adressage des périphériques |
| 0011 | I/O Write | Écriture dans l'espace d’adressage des périphériques |
| 0100 | Reserved | |
| 0101 | Reserved | |
| 0110 | Memory Read | Lecture dans l'espace d’adressage de la RAM |
| 0111 | Memory Write | Écriture dans l'espace d’adressage de la RAM |
| 1000 | Reserved | |
| 1010 | Reserved | |
| 1011 | Configuration Read | Lecture dans l'espace d’adressage de configuration |
| 1011 | Configuration Write | Écriture dans l'espace d’adressage de configuration |
| 1100 | Memory Read Multiple | Lecture dans l'espace d’adressage de la RAM, avec préchargement |
| 1101 | Dual-Address Cycle | Lecture de 64 bits, sur un bus PCI de 32 bits |
| 1110 | Memory Read Line | Lecture dans l'espace d’adressage de la RAM, avec préchargement |
| 1111 | Memory Write and Invalidate | Écriture dans l'espace d’adressage de la RAM, avec préchargement |
Plusieurs fils optionnels ajoutent des interruptions matérielles (IRQ), une fonctionnalité que nous verrons d'ici quelques chapitres. Pour le moment, sachez juste qu'il y a quatre fils dédiés aux interruptions, qui portent les noms INTA, INTB, INTC et INTD. En théorie, un composant peut utiliser les quatre fils d'interruptions s'il le veut, mais la pratique est différente. Tous les composants PCI, sauf en quelques rares exceptions, utilisent une seule sortie d'interruption pour leurs interruptions. Sachant qu'il y a généralement quatre ports PCI dans un ordinateur, le câblage des interruptions est simplifié, avec un fil par composant. Lorsqu'une interruption est levée par un périphérique, le composant qui répond aux interruption, typiquement le processeur, répond alors par une commande Interrupt Acknowledge.
Le protocole de transmission sur le bus PCI
modifierEn tout, 6 fils commandent les transactions sur le bus. On a notamment un fil FRAME qui est maintenu à 0 pendant le transfert d'une trame. Le fil STOP fait l'inverse : il permet à un périphérique de stopper une transaction dont il est le récepteur. Les deux signaux IRDY et TRDY permettent à l'émetteur et le récepteur de se mettre d'accord pour démarrer une transmission. Le signal IRDY (Initiator Ready) est mis à 1 par le maître quand il veut démarrer une transmission, le signal TRDY (Target Ready) est la réponse que le récepteur envoie pour indiquer qu'il est près à démarrer la transmission. Le signal DEVSEL est mis à zéro quand le récepteur d'une transaction a détecté son adresse sur le bus, ce qui lui permt d'indiquer qu'il a bien compris qu'il était le récepteur d'une transaction.
- Pour la commande Special Cycle, qui envoie une donnée à tous les périphériques PCI en même temps, les signaux IRDY, TRDY et DEVSEL ne sont pas utilisés. Ces signaux n'ont pas de sens dans une situation où il y a plusieurs récepteurs. Seul le signal FRAME est utilisé, ainsi que le bus de données.
Une transaction en lecture procède comme suit :
- En premier lieu, l'émetteur acquiert l'accès au bus et son signal GNT est mis à 0.
- Ensuite, il fait passer le fil FRAME à 0, qui pour indiquer le début d'une transaction, et envoie l'adresse et la commande adéquate.
- Au cycle suivant, le récepteur met le signal IRDY à 0, pour indiquer qu'il est près pour recevoir la donnée lue.
- Dans un délai de 3 cycles d'horloge maximum, le récepteur doit avoir reçu l'adresse et le précise en mettant le signal DEVSEL à 0.
- Le récepteur place la donnée lue sur le bus, et met le signal TRDY à 0.
- Le signal TRDY remonte à 1 une fois la donnée lue. En cas de lecture en rafale, à savoir plusieurs lectures consécutives à des adresses consécutives, on reprend à l'étape précédente pour transmettre une nouvelle donnée.
- Puis tous les signaux du bus repassent à 1 et le bus revient à son état initial, le signal GNT est réattribué à un autre composant.
Le Plug And Play
modifierOutre sa performance, le bus PCI était plus simple d'utilisation. La configuration des périphériques ISA était laborieuse. Il fallait configurer des jumpers ou des interrupteurs sur chaque périphérique impliqué, afin de configurer le DMA, les interruptions et d'autres paramètres cruciaux pour le fonctionnement du bus. La moindre erreur était source de problèmes assez importants. Autant ce genre de chose était acceptable pour des professionnels ou des power users, autant le grand public n'avait ni les compétences ni l'envie de faire cela. Le bus PCI était lui beaucoup plus facile d'accès, car il intégrait la fonctionnalité Plug And Play, qui fait que chaque périphérique est configuré automatiquement lors de l'allumage de l'ordinateur.
Les mémoires
modifierMémoire. Ce mot signifie dans le langage courant le fait de se rappeler quelque chose, de pouvoir s'en souvenir. La mémoire d'un ordinateur fait exactement la même chose (le nom de mémoire n'a pas été donné par hasard) mais pour un ordinateur. Son rôle est de retenir des données stockées sous la forme de suites de bits, afin qu'on puisse les récupérer si nécessaire et les traiter.
Il existe différents types de mémoires, au point que tous les citer demanderait un chapitre entier. Il faut avouer qu'entre les DRAM, SRAM, eDRAM, SDRAM, DDR-SDRAM, SGRAM, LPDDR, QDRSRAM, EDO-RAM, XDR-DRAM, RDRAM, GDDR, HBM, ReRAM, QRAM, CAM, VRAM, ROM, EEPROM, EPROM, Flash, et bien d'autres, il y a de quoi se perdre. Dans ce chapitre, nous allons parler des caractéristiques basiques qui permettent de classer les mémoires. Nous allons voir différents critères qui permettent de classer assez simplement les mémoires, sans évidemment rentrer dans les détails les plus techniques. Nous allons aussi voir les classifications basiques des mémoires.
La technologie utilisée pour le support de mémorisation
modifierLa première distinction que nous allons faire est la différence entre mémoire électronique, magnétique, optique et mécanique. Cette distinction n'est pas souvent évoquée dans les cours sur les mémoires, car elle est assez évidente et que l'on ne peut pas dire grand chose dessus. Mais elle a cependant son importance et elle mérite qu'on en parle.
Cette distinction porte sur la manière dont sont mémorisées les données. En effet, une mémoire informatique contient forcément des circuits électroniques, qui servent pour interfacer la mémoire avec le reste de l'ordinateur, pour contrôler la mémoire, et bien d'autres choses. Par contre, cela n'implique pas que le stockage des données se fasse forcément de manière électronique. Il faut bien distinguer le support de mémorisation, c'est à dire la portion de la mémoire qui mémorise effectivement des données, et le reste des circuits de la mémoire. Cette distinction sera décrite dans les prochains chapitres, mais elle est très importante.
Les mémoires à semi-conducteurs
modifierLe support de mémorisation peut être un support électronique, comme sur les registres ou les mémoires ROM/RAM/SSD et autres. Les mémoires en question sont appelées des mémoires à semi-conducteurs. Le codage des données n'est pas différent de celui observé dans les registres, à savoir que les bits sont codées par une tension électrique. Elles sont presque toutes fabriquées avec des transistors MOS/CMOS, peu importe qu'il s'agisse des mémoires RAM ou ROM. La seule exception est celle des mémoires EEPROM et des mémoires FLASH, qui sont fabriquées avec des transistors à grille flottante, qui sont des transistors MOS modifiés. L'essentiel est que les mémoires à semi-conducteurs sont fabriquées à partir de transistors MOS et de portes logiques, comme les circuits vus dans les premiers chapitres du cours.
La loi de Moore influence directement la capacité des mémoires à semi-conducteurs. Une mémoire à semi-conducteurs est composée de cellules mémoires qui mémorisent chacune 1 bit (parfois plusieurs bits, comme sur les mémoires FLASH). Chaque cellule est elle-même composées d'un ou de plusieurs transistors MOS reliés entre eux. Plus la finesse de gravure est petite, plus des transistors l'est aussi et plus la taille d'une cellule mémoire l'est aussi. Quand le nombre de transistors d'une mémoire double, le nombre de cellules mémoire double, et donc la capacité double. D'après la loi de Moore, cela arrive tous les deux ans, ce qui est bien ce qu'on observe pour les mémoires SRAM, ROM, EEPROM et bien d'autres. Les performances de ces mémoires ont aussi suivi, encore que les mémoires DRAM stagnent pour des raisons qu'on expliquera dans quelques chapitres.
La quasi-totalité des mémoires actuelles utilisent un support électronique, les exceptions étant rares. Il faut dire que les mémoires électroniques ont l'avantage d'être généralement assez rapides, avec un débit binaire élevé et un temps d'accès faible. Mais en contrepartie, elles ont tendance à avoir une faible capacité comparé aux autres technologies. En conséquence, les mémoires électroniques ont surtout été utilisées dans le passé pour les niveaux élevés de la hiérarchie mémoire, mais pas comme mémoire de masse. Ce n'est qu'avec l'avancée des techniques de miniaturisation que les mémoires électroniques ont pu obtenir des capacités suffisantes pour servir de mémoire de masse. Là où les anciennes mémoires de masse étaient des mémoires magnétiques ou optiques, comme les disques durs ou les DVD/CD, la tendance actuelle est aux remplacement de celles-ci par des supports électroniques, comme les clés USB ou les disques SSD.
Les anciennes technologies de mémoire
modifier
Les mémoires magnétiques, assez anciennes, utilisaient un support de mémorisation magnétique, dont l'aimantation permet de coder un 0 ou un 1. Le support magnétique est généralement un plateau dont la surface est aimantée et aimantable, comme sur les disques durs et disquettes, ou une bande magnétique similaire à celle des vielles cassettes audio. Elles avaient des performances inférieures aux mémoires électroniques, mais une meilleure capacité, d'où leur utilisation en tant que mémoire de masse. Un autre de leur avantage est qu'elles ont une durée de vie assez importante, liée au support de mémorisation. On peut aimanter, ré-aimanter, désaimanter le support de mémorisation un très très grand nombre de fois sans que cela endommage le support de mémorisation. Le support de mémorisation magnétique tient donc dans le temps, bien plus que les supports de mémorisation électronique dont le nombre d'accès avant cassure est généralement limité. Malheureusement, les mémoires magnétiques contiennent des circuits électroniques faillibles, ce qui fait qu'elles ne sont pas éternelles.

Enfin, n’oublions pas les mémoires optiques comme les CD ou les DVD, dont le support de mémorisation est une surface réfléchissante. Elles sont composées d'une couche de plastique dans laquelle on fait des creux, creux qui sont utilisés pour coder des bits. Elles ont l'avantage d'avoir une bonne capacité, même si les temps d'accès et les débits sont minables. Elles ont une capacité et des performances plus faibles que celles des disques durs magnétiques, mais souvent meilleure que les autres formes de mémoire magnétique. Cette capacité intermédiaire est un avantage sur les mémoires magnétiques, hors disque dur. Leur inconvénient majeur est qu'elles s’abîment facilement. Toute personne ayant déjà eu des CD/DVD sait à quel point ils se rayent facilement et à quel point ces rayures peuvent tout simplement rendre le disque inutilisable.
Enfin, il faut mentionner les mémoires mécaniques, basées sur un support physique. L'exemple le plus connu est celui des cartes perforées, et d'autres mémoires similaires basées sur du papier. Mais il existe d'autres types de mémoire basées sur un support électro-acoustique comme les lignes à délai, des techniques de stockage basées sur de l'ADN ou des polymères, et bien d'autres. L'imagination des ingénieurs en terme de supports de stockage n'est plus à démontrer et leur créativité a donné des mémoires étonnantes.
Les mémoires ROM et RWM
modifier
Une seconde différence concerne la façon dont on peut accéder aux informations stockées dans la mémoire. Celle-ci permet de faire la différence entre les mémoires ROM et les mémoires RWM. Dans une mémoire ROM, on peut seulement récupérer les informations dans la première, mais pas les modifier individuellement. À l'inverse, les mémoires RWM permettent de récupérer les données, mais aussi de les modifier individuellement.
Les mémoires ROM
modifierAvec les mémoires ROM, on peut récupérer les informations dans la mémoire, mais pas les modifier : la mémoire est dite accessible en lecture, mais pas en écriture. Si on ne peut pas modifier les données d'une ROM, certaines permettent cependant de réécrire intégralement leur contenu : on dit qu'on reprogramme la ROM. Insistons sur la différence entre reprogrammation et écriture : l'écriture permet de modifier un byte bien précis, alors que la reprogrammation efface toute la mémoire et la réécrit en totalité. De plus, la reprogrammation est généralement beaucoup plus lente qu'une écriture, sans compter qu'il est plus fréquent d'écrire dans une mémoire que la reprogrammer. Ce terme de programmation vient du fait que les mémoires ROM sont souvent utilisées pour stocker des programmes sur certains ordinateurs assez simples.
Les mémoires ROM sont souvent des mémoires électroniques, même si les exceptions sont loin d'être rares. On peut classer les mémoires ROM électroniques en plusieurs types :
- les mask ROM sont fournies déjà programmées et ne peuvent pas être reprogrammées ;
- les mémoires PROM sont fournies intégralement vierges, et on peut les programmer une seule fois ;
- les mémoires RPROM sont reprogrammables, ce qui signifie qu'on peut les effacer pour les programmer plusieurs fois ;
- les mémoires EPROM s'effacent avec des rayons UV et peuvent être reprogrammées plusieurs fois de suite ;
- certaines RPROM peuvent être effacées par des moyens électriques : ce sont les mémoires EEPROM.
- Les mémoires Flash sont un cas particulier d'EEPROM, selon la définition utilisée plus haut.
Les mémoires de type mask ROM sont utilisées dans quelques applications particulières. Par exemple, elles étaient utilisées sur les vieilles consoles de jeux, pour stocker le jeu vidéo dans les cartouches. Elles servent aussi pour les firmware divers et variés, comme le firmware d'une imprimante ou d'une clé USB. Par contre, le BIOS d'un PC (qui est techniquement un firmware) est stocké dans une mémoire EEPROM, ce qui explique qu'on peut le mettre à jour (on dit qu'on flashe le BIOS).
Les mémoires mask ROM sont intégralement construites en utilisant des transistors MOS normaux, ce qui fait que leurs performances est censée suivre la loi de Moore. Mais dans les faits, ce n'est pas vraiment le cas pour une raison simple : on n'a pas besoin de mémoires ROM ultra-rapides, ni de ROM à grosse capacité. Les ROM sont aujourd'hui presque exclusivement utilisées pour les firmware des systèmes embarqués à faible performance, ce qui contraint les besoins. Pas besoin d'avoir des ROM ultra-rapides pour stocker ce firmware.
Les mémoires PROM, RPROM, EPROM et EEPROM sont elles fabriqués autrement, généralement en utilisant des transistors MOS modifiés appelés transistors à grille flottante. Nous verrons ce que sont ces transistors dans quelques chapitres, mais nous pouvons d'or et déjà dire que leur fabrication n'est pas si différente des transistors MOS normaux. En conséquence, la loi de Moore s'applique, ce qui fait que la capacité de ces mémoires doubles environ tous les deux ans. Les performances s'améliorent aussi avec le temps, mais à un rythme moindre.
Il existe des mémoires ROM qui ne sont pas électroniques. Par exemple, prenez le cas des CD-ROM : une fois gravés, on ne peut plus modifier leur contenu. Cela en fait naturellement des mémoires ROM. D'ailleurs, c'est pour cela qu'on les appelle des CD-ROM : Compact Disk Read Only Memory ! Même chose pour les DVD-ROM ou les Blue-Ray.
Les mémoires RWM
modifierSur les mémoires RWM, on peut récupérer les informations dans la mémoire et les modifier : la mémoire est dite accessible en lecture et en écriture. Attention aux abus de langage : le terme mémoire RWM est souvent confondu dans le langage commun avec les mémoires RAM. Les mémoires RAM sont un cas particulier de mémoire RWM. La définition souvent retenue est qu'une mémoire RAM est une mémoire RWM dont le temps d'accès est approximativement le même pour chaque byte, contrairement aux autres mémoires RWM comme les disques durs ou les disques optiques où le temps d'accès dépend de la position de la donnée. Mais nous verrons dans la suite du cours que cette définition est quelques peu trompeuse et qu'elle omet des éléments importants. Un point important est que les mémoires RAM sont des mémoires électroniques : les mémoires RWM magnétiques, optiques ou mécaniques ne sont pas considérées comme des mémoires RAM.
Précisons que la définition des mémoires RWM contient quelques subtilités assez contre-intuitives. Par exemple, prenez les CD et DVD. Ceux qui ne sont pas réinscriptibles sont naturellement des mémoires ROM, comme l'a dit plus haut. Mais qu'en est-il des CD/DVD réinscriptibles ? On pourrait croire que ce sont des mémoires RWM, car on peut modifier leur contenu sans avoir formellement à les reprogrammer. Mais en fait non, ce n'en sont pas. Là encore, on retrouve la distinction entre écriture et reprogrammation des mémoires ROM. Pouvoir effacer totalement une mémoire pour y réinscrire de nouvelles données ensuite n'en fait pas une mémoire RWM. Il faut que l'écriture puisse être localisée, qu'on puisse modifier des données sans avoir à réécrire toute la mémoire. La capacité de modifier les données des mémoires RWM doit porter sur des données individuelles, sur des morceaux de données bien précis.
Une classification des mémoires suivant la possibilité de lecture/écriture/reprogrammation
modifierPour résumer, les mémoires peuvent être lues, écrites, ou reprogrammées. La distinction entre lecture et écriture permet de distinguer les mémoires ROM et RWM. Mais la distinction entre écriture et reprogrammation rend les choses plus compliquées. S'il fallait faire une classification des mémoires en fonction des opérations possibles en lecture et modification, cela donnerait quelque chose comme ceci :
- Les mémoires ROM (Read Only Memory) sont accessibles en lecture uniquement, mais ne peuvent pas être écrites ou reprogrammées. Les mémoires mask ROM ainsi que les CD-ROM sont de ce type.
- Les mémoires de type WOM (Write Once Memory), aussi appelées mémoires à programmation unique, sont des mémoires fournies vierges, que l'on peut reprogrammer une seule fois. Les mémoires PROM et les CD/DVD vierges inscriptibles une seule fois, sont de ce type.
- Les mémoires PROM, aussi appelées mémoires reprogrammables peuvent être lues, mais aussi reprogrammées plusieurs fois, voire autant de fois que possible. Les mémoires EPROM et EEPROM, ainsi que les CD/DVD réinscirptibles sont dans ce cas.
- Les mémoires RWM (Read Write Memory) peuvent être lues et écrites, la reprogrammation étant parfois possible sur certaines mémoires, bien que peu utile.
Notons que la technologie utilisée influence le caractère RWM/ROM/WOM/PROM d'une mémoire. Les mémoires magnétiques sont presque systématiquement de type RWM. En effet, un support magnétisable peut être démagnétisé facilement, ce qui les rend reprogrammables. On peut aussi changer son aimantation localement, et donc changer les bits mémorisés, ce qui les rend faciles à utiliser en écriture. Les mémoires électroniques peuvent être aussi bien de type ROM, ROM, WOM que RWM. Les mémoires optiques ne peuvent pas être des mémoires RWM, et ce sont les seules. En effet, les mémoires optiques sont composées d'une couche de plastique dans laquelle on fait des creux, creux qui sont utilisés pour coder des bits. Une fois la surface plastique altérée, on ne peut pas la remettre dans l'état initiale. Cela explique que les CD-ROM et DVD-ROM sont donc des mémoires de type ROM. les CD et DVD vierges sont vierges, mais on peut les programmer en faisant des trous dedans, ce qui en fait des mémoires de type WOM. Les CD/DVD réinscriptibles ont plusieurs couches de plastiques, ce qui permet de les reprogrammer plusieurs fois. La reprogrammation demande juste d'enlever une couche de plastique, ce qui est facile quand on sait faire des trous dans cette couche pour écrire des bits. On peut alors entamer la couche d'en-dessous.
Le tableau suivant montre le lien entre la technologie de fabrication et les autres caractères.
| Mémoire RWM/ROM | |
|---|---|
| Mémoires électroniques | ROM, WOM, reprogrammables ou RWM. |
| Mémoires magnétiques | RWM |
| Mémoires optiques | ROM, WOM ou reprogrammable |
Les mémoires volatiles et non-volatiles
modifierLorsque vous éteignez votre ordinateur, le système d'exploitation et les programmes que vous avez installés ne s'effacent pas, contrairement au document Word que vous avez oublié de sauvegarder. Les programmes et le système d'exploitation sont placés sur une mémoire qui ne s'efface pas quand on coupe le courant, contrairement à votre document Word non-sauvegardé. Cette observation nous permet de classer les mémoires en deux types : les mémoires non-volatiles conservent leurs informations quand on coupe le courant, alors que les mémoires volatiles les perdent.
Les mémoires volatiles
modifierLes mémoire volatiles sont presque toutes des mémoires électroniques. Comme exemple de mémoires volatiles, on peut citer la mémoire principale, aussi appelée mémoire RAM, les registres du processeur, la mémoire cache et bien d'autres. Globalement, toutes les mémoires qui ne sont pas soit des mémoires ROM/PROM/..., soit des mémoires de masse (des mémoires non-volatiles capables de conserver de grandes quantités de données, comme les disques durs ou les clés USB) sont des mémoires volatiles. La raison à cela est simplement liée à la hiérarchie mémoire : là où les mémoires ROM et les mémoires de masse conservent des données permanentes, les autres mémoires servent juste à accélérer les temps d'accès en stockant des données temporaires ou des copies des données persistantes.
Typiquement, si on omet quelques mémoires historiques aujourd'hui obsolètes, les mémoires volatiles sont toutes des mémoires RAM ou associées. Il existe cependant des projets de mémoires RAM (donc des mémoires RWM électroniques) destinées à être non-volatiles. C'est le cas de la FeRAM, la ReRAM, la CBRAM, la FeFET memory, la Nano-RAM, l'Electrochemical RAM et de bien d'autres encore. Mais ce sont encore des projets en cours de développement, la recherche poursuivant lentement son cours. Elles ne sont pas prêtes d'arriver dans les ordinateurs grand publics de si tôt. Pour le moment, la correspondance entre mémoires RAM et mémoires volatile tient bien la route.
Les mémoires SRAM et DRAM
modifierParmi les mémoires volatiles, on peut distinguer les mémoires statiques et les mémoires dynamiques. La différence entre les deux est la suivante. Les données d'une mémoire statique ne s'effacent pas tant qu'elles sont alimentées en courant. Pour les mémoires dynamiques, les données s'effacent en quelques millièmes ou centièmes de secondes si l'on n'y touche pas. Sur les mémoires volatiles dynamiques, il faut réécrire chaque bit de la mémoire régulièrement, ou après chaque lecture, pour éviter qu'il ne s'efface. On dit qu'on doit effectuer régulièrement un rafraîchissement mémoire. Le rafraîchissement prend du temps, et a tendance à légèrement diminuer la rapidité des mémoires dynamiques. Mais en contrepartie, les mémoires dynamiques ont une meilleure capacité, car leurs bits prennent moins de place, utilisent moins de transistors.
Les RAM statiques sont appelées des SRAM (Static RAM), alors que les RAM dynamiques sont appelées des DRAM (Dynamic RAM). Les SRAM et DRAM ne sont pas fabriquées de la même manière : transistors uniquement pour la première, transistors et condensateurs (des réservoirs à électrons) pour l'autre. Les SRAM ont des performances excellentes, mais leur capacité laisse à désirer, alors que c'est l'inverse pour la DRAM. Aussi, leur usage ne sont pas les mêmes.
Leur usage dépend de si l'on parle de systèmes embarqués/industriels ou des PC pour utilisateur particulier/professionnel. La SRAM est surtout utilisée dans les microcontrôleurs ou les systèmes assez simples, pour lesquels le rafraichissement mémoire poserait plus de problèmes que nécessaires. Les microcontrôleurs ou systèmes embarqués n'utilisent généralement pas de mémoire DRAM. Dans les PC actuels, la SRAM est intégrée dans le processeur et se trouve dans le cache du processeur, éventuellement pour les local store. A l'opposé, la DRAM est utilisée pour fabriquer des barrettes de mémoire, pour la RAM principale.
La différence entre les deux est que la SRAM est utilisée comme mémoire à l'intérieur d'un circuit imprimé, qui regroupe mémoire, processeur, et éventuellement d'autres circuits. Par contre, la DRAM est placée dans un circuit à part, séparé du processeur, dans son propre boitier rien qu'à elle, voire dans des barrettes de mémoire. Et la raison à cela est assez simple : la SRAM utilise les mêmes technologies de fabrication CMOS que les autres circuits imprimés, alors que la DRAM requiert des condensateurs et donc des techniques de fabrication distinctes.
Les eDRAM et pseudo-SRAM
modifierIl existe cependant une exception : la eDRAM, pour embedded DRAM, qui est intégrée dans le même circuit intégré, le même boitier, la même puce que d'autres composants. Tout le défi est de mettre des condensateurs sur une puce en silicium, dans un circuit intégré, alors que les techniques de fabrication des processeurs font que ce n'est pas facile. Généralement, elle est placée dans la même puce qu'un processeur, afin de servir de mémoire cache ou de local store.
L'eDRAM a été utilisée sur certains processeurs comme mémoire cache (cache L4, le plus proche de la mémoire sur ces puces). Elle a aussi été utilisée dans des consoles de jeu vidéo, pour la carte graphique des consoles suivantes : la PlayStation 2, la PlayStation Portable, la GameCube, la Wii, la Wii U, et la XBOX 360. Sur ces consoles, la RAM de la carte graphique était intégrée avec le processeur graphique dans le même circuit. La fameuse mémoire vidéo et le GPU n'étaient qu'une seule et même puce électronique, un seul circuit intégré.
Il existe des mémoires qui sont des intermédiaires entre les mémoires SRAM et DRAM. Il s'agit des mémoires pseudo-statiques, qui sont techniquement des mémoires DRAM, utilisant des transistors et des condensateurs, mais qui gèrent leur rafraichissement mémoire toutes seules. Sur les DRAM normales, le rafraichissement mémoire est effectué par le processeur ou par le contrôleur mémoire sur la carte mère. Il envoie régulièrement des commandes de rafraichissement à la mémoire, qui rafraichissent une ou plusieurs adresses à la fois. Mais sur les mémoires pseudo-statiques, le rafraichissement se fait automatiquement sans intervention extérieure. Des circuits intégrés à la mémoire pseudo-statiques font le rafraichissement automatiquement.
Les mémoires non-volatiles
modifierLes mémoires de masse, à savoir celles destinées à conserver un grand nombre de données sur une longue durée, sont presque toutes des mémoires non-volatiles. Il faut dire qu'on attend d'elles de conserver des données sur un temps très long, y compris quand l'ordinateur s’éteint. Personne ne s'attend à ce qu'un disque dur ou SSD s'efface quand on éteint l'ordinateur. Ainsi, les mémoires suivantes sont des mémoires non-volatiles : les clés USB, les disques SSD, les disques durs, les disquettes, les disques optiques comme les CD-ROM et les DVD-ROM, de vielles mémoires comme les bandes magnétiques ou les rubans perforés, etc. Comme on le voit, les mémoires non-volatiles peuvent être des mémoires magnétiques (disques durs, disquettes, bandes magnétiques), électroniques (clés USB, disques SSD), optiques (CD, DVD) ou autres. Vous remarquerez que certaines de ces mémoires sont de type RWM (disques SSD, clés USB), alors que d'autres sont de type ROM (les CD/DVD non-réinscriptibles).
Il faut cependant noter qu'il existe quelques exceptions, où des mémoires RAM sont rendues non-volatiles et utilisées pour du stockage de long terme. Nous ne parlons pas ici des projets de mémoires RAM non-volatiles comme la FeRAM ou la CBRAM, évoqués plus haut. Nous parlons de cas où la mémoire volatile est couplée à un système qui empêche toute perte de données. Un exemple de mémoire de masse volatile est celui des nvSRAM et des BBSRAM. Ce sont des mémoires RAM, donc volatiles, de petite taille, qui sont rendues non-volatiles par divers stratagèmes.
- Sur les BBSRAM (Battery Backed SRAM), la mémoire SRAM est couplée à une petite batterie/pile/super-condensateur qui l'alimente en permanence, ce qui lui empêche d'oublier des données. La batterie est généralement inclue dans le même boîtier que la mémoire SRAM. Ce sont des composants qui consomment peu de courants et qui peuvent tenir des années en étant alimentés par une simple pile bouton. Vous en avez une dans votre ordinateur, appelée la CMOS RAM, qui mémorise les paramètres du BIOS, la date, l'heure et divers autres informations.
- Contrairement aux BBSRAM, les nvRAM (non-volatile RAM) n'ont pas de circuit d'alimentation qui prend le relai en cas de coupure de l’alimentation électrique. À la place, elles contiennent une mémoire non-volatile RWM dans laquelle les données sont sauvegardées régulièrement ou en cas de coupure de alimentation. Typiquement, la SRAM est couplée à une petite mémoire FLASH (la mémoire des clés USB et des SSD) dans laquelle on sauvegarde les données quand le courant est coupé. Si la tension d'alimentation descend en dessous d'un certain seuil critique, la sauvegarde dans l'EEPROM démarre automatiquement. Pendant la sauvegarde, la mémoire est alimentée durant quelques secondes par un condensateur de secours qui sert de batterie temporaire.

Les ordinateurs personnels de type PC contiennent tous une mémoire nvRAM ou BBSRAM, appelée la CMOS RAM. Elle mémorise des paramètres de configuration basique (les paramètres du BIOS). Les paramètres en question permettent de configurer le matériel lors de l'allumage, de stocker l'heure et la date et quelques autres paramètres du genre. Les BBSRAM ont aussi été utilisées dans les cartouches de jeux vidéo, pour stocker les sauvegardes. C'est le cas sur les cartouches de jeux vidéo NES ou d'anciennes consoles de cette époque, qui contenaient une puce de sauvegarde interne à la cartouche. La puce de sauvegarde n'était autre qu'une BBSRAM dans laquelle le processeur de la console allait écrire les données de sauvegarde. Les données de sauvegarde n'étaient pas effacée quand on retirait la cartouche de la console grâce à une petit pile bouton qui alimentait la BBSRAM. Si vous ouvrez une cartouche de ce type, vous verrez la pile assez facilement. Il y avait la même chose sur les cartouches de GameBoy ou de GBA, et la pile était parfois visible sur certaines cartouches transparentes (c'était notamment le cas sur la cartouche de Pokemon Cristal).

Un autre exemple de mémoire non-volatile fabriquée à partir de mémoires RAM est celui des RAM drive matériels, des disques durs composés de barrettes de RAM connectées à une carte électronique et une batterie. La carte électronique fait l'interface entre le connecteur du disque dur et les barrettes de mémoire, afin de simuler un disque dur à partir des barrettes de RAM. Les barrettes sont alimentées par une batterie, afin qu'elles ne s'effacent pas. Ces RAM drive sont plus rapides que les disques durs normaux, mais ont le défaut de consommer beaucoup plus d'électricité et d'avoir une faible capacité mémoire. Ils sont peu utilisés, car très cher et peu utiles au quotidien.
Le lien avec la technologie de fabrication et les autres critères
modifierLa technologie de fabrication influence le caractère volatile ou non d'une mémoire. Prenons par exemple le cas des mémoires magnétiques. L'aimantation du support magnétique est persistante, ce qui veut dire qu'il est rare qu'un support aimanté perde son aimantation avec le temps. Le support de mémorisation ne s'efface pas spontanément et lui faire perdre son aimantation demande soit de lui appliquer un champ magnétique adapté, soit de le chauffer à de très fortes températures. Il n'est donc pas surprenant que toutes les mémoires magnétiques soient non-volatiles. Pareil pour les mémoires optiques : le plastique qui les compose ne se dégrade pas rapidement, ce qui lui permet de conserver des informations sur le long-terme. Mais pour les mémoires électroniques, ce n'est pas étonnant que des mémoires qui marche à l'électricité s'effacent quand on coupe le courant. On s'attend donc à ce que les mémoires électroniques soient volatiles, sauf pour les mémoires ROM/PROM/EPROM/EEPORM qui sont rendues non-volatiles par une conception adaptée.
| Mémoire non-volatile/volatile | |
|---|---|
| Mémoires électroniques | Volatile ou non-volatile |
| Mémoires magnétiques | Non-volatiles |
| Mémoires optiques | Non-volatiles |
Le lien entre caractère volatile/non-volatile et le caractère RWM/ROM est lui plus compliqué. Toutes les mémoires volatiles sont des mémoires de type RWM, le caractère volatile impliquant d'une manière ou d'une autre que la mémoire est de type RWM ou au minimum reprogrammable. Après tout, si une mémoire s'efface quand on l'éteint, c'est signe qu'on doit écrire des données utiles demande au prochain allumage pour qu'elle serve à quelque chose. Par contre, la réciproque n'est pas vraie : il existe des mémoires RWM non-volatiles, comme les disque SSD ou les disques dur. Inversement, si on ne peut pas reprogrammer ou écrire dans une mémoire, c'est signe qu'elle ne peut pas s'effacer : les mémoires de type ROM, WOM ou reprogrammables, sont forcément non-volatiles. On a donc :
- mémoire ROM/WOM => mémoire non-volatile
- mémoire volatile => mémoire RWM et/ou reprogrammable.
Le tableau suivant résume les liens entre le caractère volatile/non-volatile d'une mémoire et son caractère ROM/RWM. La liste des mémoires n'est pas exhaustive.
| Mémoire non-volatile | Mémoire volatile | |
|---|---|---|
| Mémoire RWM |
|
|
| Mémoire reprogrammable |
|
Théoriquement possible, mais pas utilisé en pratique |
| Mémoire WOM |
|
Impossible |
| Mémoire ROM |
|
L'adressage et les accès mémoire
modifierLes mémoires se différencient aussi par la méthode d'accès aux données mémorisées.
Les mémoires adressables
modifierLes mémoires actuelles utilisent l'adressage : chaque case mémoire se voit attribuer un numéro, l'adresse, qui va permettre de la sélectionner et de l'identifier parmi toutes les autres. On peut comparer une adresse à un numéro de téléphone (ou à une adresse d'appartement) : chacun de vos correspondants a un numéro de téléphone et vous savez que pour appeler telle personne, vous devez composer tel numéro. Les adresses mémoires en sont l'équivalent pour les cases mémoires. Ces mémoires adressables peuvent se classer en deux types : les mémoires à accès aléatoire, et les mémoires adressables par contenu.

Les mémoires à accès aléatoire sont des mémoires adressables, sur lesquelles on doit préciser l'adresse de la donnée à lire ou modifier. Certaines d'entre elles sont des mémoires électroniques non-volatiles de type ROM, d'autres sont des mémoires volatiles RWM, et d'autres sont des mémoires RWM non-volatiles. Comme exemple, les disques durs de type SSD sont des mémoires adressables. La mémoire principale, la fameuse mémoire RAM est aussi une mémoire adressable. D'ailleurs, le terme de mémoire RAM (Random Access Memory) désigne des mémoires qui sont à la fois adressables, de type RWM et surtout volatiles.
Les mémoires associatives fonctionnent comme une mémoire à accès aléatoire, mais dans le sens inverse. Au lieu d'envoyer l'adresse pour accéder à la donnée, on va envoyer la donnée pour récupérer son adresse : à la réception de la donnée, la mémoire va déterminer quelle case mémoire contient cette donnée et renverra l'adresse de cette case mémoire. Cela peut paraître bizarre, mais ces mémoires sont assez utiles dans certains cas de haute volée. Dès que l'on a besoin de rechercher rapidement des informations dans un ensemble de données, ou de savoir si une donnée est présente dans un ensemble, ces mémoires sont reines. Certains circuits internes au processeur ont besoin de mémoires qui fonctionnent sur ce principe. Mais laissons cela à plus tard.
Les mémoires caches
modifierSur les mémoires caches, chaque donnée se voit attribuer un identifiant, qu'on appelle le tag. Une mémoire à correspondance stocke non seulement la donnée, mais aussi l'identifiant qui lui est attribué : cela permet ainsi de mettre à jour l'identifiant, de le modifier, etc. En somme, le Tag remplace l'adresse, tout en étant plus souple. La mémoire cache stocke donc des couples tag-donnée. À chaque accès mémoire, on envoie le tag de la donnée voulue pour sélectionner la donnée.

Les mémoires séquentielles
modifierSur d'anciennes mémoires, comme les bandes magnétiques, on était obligé d'accéder aux données dans un ordre prédéfini. On parcourait la mémoire dans l'ordre, en commençant par la première donnée : c'est l'accès séquentiel. Pour lire ou écrire une donnée, il fallait visiter toutes les cases mémoires dans l'ordre croissant avant de tomber sur la donnée recherchée. Et impossible de revenir en arrière ! Et ces mémoires sont loin d'être les seules. Les CD-ROM et les DVD/Blue-Ray sont dans le même cas, dans une certaine mesure. Les mémoires de ce type sont appelées des mémoires séquentielles. Ce sont des mémoires spécialisées qui ne fonctionnent pas avec des adresses et qui ne permettent d’accéder aux données que dans un ordre bien précis, qui contraint l'accès en lecture ou en écriture.

Il existe plusieurs types de mémoires séquentielles, qui se différencient par l'ordre dans lequel les données sont lues ou écrites, ou encore par leur caractère électronique, magnétique ou optique. Dans ce qui va suivre, nous allons nous restreindre aux mémoires séquentielles qui sont volatiles, la totalité étant électroniques. Si on omet les registres à décalage, les mémoires séquentielles électroniques sont toutes soit des mémoires FIFO, soit des mémoires LIFO. Ces deux types de mémoire conservent les données triées dans l'ordre d'écriture (l'ordre d'arrivée). La différence est qu'une lecture dans une mémoire FIFO renvoie la donnée la plus ancienne, alors qu'elle renverra la donnée la plus récente pour une mémoire LIFO, celle ajoutée en dernier dans la mémoire. Dans les deux cas, la lecture sera destructrice : la donnée lue est effacée.
On peut voir les mémoires FIFO comme des files d'attente, des mémoires qui permettent de mettre en attente des données tant qu'un composant n'est pas prêt. Seules deux opérations sont possibles sur de telles mémoires : mettre en attente une donnée (enqueue, en anglais) et lire la donnée la plus ancienne (dequeue, en anglais).

De même, on peut voir les mémoires LIFO comme des piles de données : toute écriture empilera une donnée au sommet de cette mémoire LIFO (on dit qu'on push la donnée), alors qu'une lecture enlèvera la donnée au sommet de la pile (on dit qu'on pop la donnée).

Les mémoires synchrones et asynchrones
modifierLes toutes premières mémoires électroniques étaient des mémoires asynchrones, non-synchronisées avec le processeur via une horloge. Avec elles, le processeur devait attendre que la mémoire réponde et devait maintenir adresse et données pendant ce temps. Pour éviter cela, les concepteurs de mémoire ont synchronisé les échanges entre processeur et mémoire avec un signal d'horloge : les mémoires synchrones sont nées. L'utilisation d'une horloge a l'avantage d'imposer des temps d'accès fixes. Un accès mémoire prend un nombre déterminé (2, 3, 5, etc) de cycles d'horloge et le processeur peut faire ce qu'il veut dans son coin durant ce temps.
Il existe plusieurs types de mémoires synchrones. Les premières sont tout simplement des mémoires naturellement synchrones. Elles sont construites avec des bascules D synchrones, ce qui fait que le support de mémorisation est lui-même synchrone. Mais cela ne concerne que quelques mémoires SRAM bien spécifiques, d'une utilisation très limitée. De nos jours, cela ne concerne que les registres du processeurs ou quelques mémoires tampons bien spécifiques utilisées dans les processeurs modernes.
Le second type de mémoire synchrone prend une mémoire asynchrone et ajoute des registres sur ses entrées/sorties. Instinctivement, on se dit qu'il suffit de mettre des registres sur les entrées associées au bus d'adresse/commande, et sur les entrées-sorties du bus de données. Mais faire ainsi a des conséquences pas évidentes, au niveau du nombre de cycles utilisés pour les lectures et écritures. Nous détaillerons tout cela dans le chapitre sur les mémoires SRAM synchrones, ainsi que dans le chapitre sur les DRAM.
Le lien entre les différents types de mémoires
modifierLe tableau suivant montre le lien entre la technologie de fabrication et les autres caractères.
| Mémoire non-volatile/volatile | Mémoire RWM/ROM | Méthode d'accès | |
|---|---|---|---|
| Mémoires électroniques | Volatile ou non-volatile | ROM, WOM, reprogrammables ou RWM | Adressables, séquentielles, autres |
| Mémoires magnétiques | Non-volatiles | RWM | Séquentielles, adressables pour les disques durs et disquettes |
| Mémoires optiques | Non-volatiles | ROM, WOM ou reprogrammable | Séquentielles |
Une mémoire communique avec d'autres composants : le processeur, les entrées-sorties, et peut-être d'autres. Pour cela, la mémoire est reliée à un ou plusieurs bus, des ensembles de fils qui permettent de la connecter aux autres composants. Suivant la mémoire et sa place dans la hiérarchie mémoire, le bus sera plus ou moins spécialisé. Par exemple, la mémoire principale est reliée au processeur et aux entrées-sorties via le bus système. Pour les autres mémoires, la logique est la même, si ce n'est que la mémoire est reliée à d'autres composants électroniques : une unité de calcul pour les registres, par exemple.
Dans tous les cas, le bus connecté à la mémoire est composé de deux ensembles de fils : le bus de données et le bus de commande. Le bus de données permet les transferts de données avec la mémoire, alors que le bus de commande prend en charge tout le reste. Nous allons commencer par voir le bus de données avant le bus de commandes, vu que son abord est plus simple. Le bus de commande est un ensemble d'entrées, là où ce n'est pas forcément le cas pour le bus de données. Le bus de données est soit une sortie (sur les mémoires ROM), soit une entrée-sortie (sur les mémoires RAM), les exceptions étant rares.
Le bus de commande et d'adresse
modifier
Le bus de commande transmet des commandes mémoire, des ordres auxquels la mémoire va devoir réagir pour faire ce qu'on lui demande. Dans les grandes lignes, chaque commande contient des bits qui ont une fonction fixée lors de la conception de la mémoire. Et les bits utilisés sont rarement les mêmes d'une mémoire à l'autre. Dans ce qui suit, nous verrons quelques bits qui reviennent régulièrement dans les bus de commande les plus communs, mais sachez qu'ils sont en réalité facultatifs. Le bus de commande dépend énormément du bus utilisé ou de la mémoire. Certains bus de commande se contentent d'un seul bit, d'autres en ont une dizaine, et d'autres en ont une petite centaine.
Comme on le verra plus bas, les mémoires adressables ont généralement des broches dédiées aux adresses, qui sont connectées au bus d'adresse. Mais les autres mémoires s'en passent et il arrive que certaines mémoires adressables arrivent à s'en passer. Pour résumer, le bus d'adresse est facultatif, seules certaines mémoires en ayant réellement un. On peut d'ailleurs voir le bus d'adresse comme une sous-partie du bus de commandes.
Les bits Chip Select et Output Enable
modifierLa majorité des mémoires possède deux broches/bits qui servent à l'activer ou la désactiver : le bit CS (Chip Select). Lorsque ce bit est à 1, toutes les autres broches sont désactivées, qu'elles appartiennent au bus de données ou de commande. On verra dans quelques chapitres l'utilité de ce bit. Pour le moment, on peut dire qu'il permet d'éteindre une mémoire (temporairement) inutilisée. L'économie d'énergie qui en découle est souvent intéressante.
Tout aussi fréquent, le bit OE (Output Enable) désactive les broches du bus de données, laissant cependant le bus de commande fonctionner. Ce bit déconnecte la mémoire du bus de données, stoppant les transferts. Il a une utilité similaire au bit CE, avec cependant quelques différences. Ce bit ne va pas éteindre la mémoire, mais juste stopper les transmissions. L'économie d'énergie est donc plus faible. Cependant, déconnecter la mémoire est beaucoup plus rapide que de l'éteindre. On verra dans quelques chapitres l'utilité de ce bit. Grossièrement, il permet de déconnecter une mémoire quand un composant prioritaire souhaite communiquer sur le bus, en même temps que la mémoire.
L'entrée d'horloge ou de synchronisation
modifierCertaines mémoires assez anciennes n'étaient pas synchronisées par un signal d'horloge, mais par d'autres procédés : on les appelle des mémoires asynchrones. Les bus de commande de ces mémoires devaient transmettre les informations de synchronisation, sous la forme de bits de synchronisation.
D'autres mémoires sont cadencées par un signal d'horloge : elles portent le nom de mémoires synchrones. Ces mémoires ont un bus de commande beaucoup plus simple, qui n'a qu'une seule broche de synchronisation. Celle-ci reçoit le signal d'horloge, d'où le nom d'entrée d'horloge qui lui est donné.
Les bits de lecture/écriture
modifierLe bus de commande doit préciser à la mémoire s'il faut effectuer une lecture ou une écriture. Pour cela, le bus envoie sur le bus de commande un bit appelé bit R/W, qui indique s'il faut faire une lecture ou une écriture. Il est souvent admis par convention que R/W à 1 correspond à une lecture, tandis que R/W vaut 0 pour les écritures. Ce bit de commande est évidemment inutile sur les mémoires ROM, vu qu'elles ne peuvent effectuer que des lectures. Notons que les mémoires qui ont un bit R/W ont souvent un bit OE, bien que ce ne soit pas systématique. En effet, une mémoire n'a pas toujours une lecture ou écriture à effectuer et il faut préciser à la mémoire qu'elle n'a rien à faire, ce que le bit OE peut faire.
| Bit OE | Bit R/W | Opération demandée à la mémoire |
|---|---|---|
| 0 | 0 | NOP (pas d'opération) |
| 0 | 1 | NOP (pas d'opération) |
| 1 | 0 | Écriture |
| 1 | 1 | Lecture |
Une autre solution est d'utiliser un bit pour indiquer qu'on veut faire une lecture, et un autre bit pour indiquer qu'on veut démarrer une écriture. On pourrait croire que c'est un gâchis, mais c'est en réalité assez pertinent. L'avantage est que la combinaison des deux bits permet de coder quatre valeurs : 00, 01, 10 et 11. En tout, on a donc une valeur pour la lecture, une pour l'écriture, et deux autres valeurs. La logique veut qu'une de ces valeur, le plus souvent 00, indique l'absence de lecture et d'écriture. Cela permet de fusionner le bit R/W avec le bit OE. Au lieu de mettre un bit OE à 0 quand la mémoire n'est pas utilisée, on a juste à mettre le bit de lecture et le bit d'écriture à 0 pour indiquer à la mémoire qu'elle n'a rien à faire. La valeur restante peut être utilisée pour autre chose, ce qui est utile sur les mémoires qui gèrent d'autres opérations que la lecture et l'écriture. Par exemple, les mémoires EPROM et EEPROM gèrent aussi l'effacement et il faut pouvoir le préciser.
| Bit de lecture | Bit d'écriture | Opération demandée à la mémoire |
|---|---|---|
| 0 | 0 | NOP (pas d'opération) |
| 0 | 1 | Ecriture |
| 1 | 0 | Lecture |
| 1 | 1 | Interdit, ou alors code pour une autre opération (reprogrammation, effacement, NOP sur certaines mémoires) |
Le bus d'adresse (facultatif)
modifierToutes les mémoires adressables sont naturellement connectées au bus. La transmission de l'adresse à la mémoire peut se faire de plusieurs manières. La plus simple utilise un bus dédié pour envoyer les adresses à la mémoire, séparé du bus de données et du bus de commande. Le bus en question est appelé le bus d'adresse.

Mais d'autres mémoires font autrement et fusionnent le bus d'adresse et de données. Le bus de commande existe toujours, il est secondé par un autre bus qui sert à transmettre données et adresses, mais pas en même temps. De tels bus sont appelés soit des bus multiplexés, soit des bus à transmission par paquet. Les deux méthodes sont légèrement différentes, comme on le verra dans ce qui suit.
Les bus d'adresse multiplexés
modifierAvec un bus d'adresse dédié, il existe quelques astuces pour économiser des fils. La première astuce est d'envoyer l'adresse en plusieurs fois. Sur beaucoup de mémoires, l'adresse est envoyée en deux fois. Les bits de poids fort sont envoyés avant les bits de poids faible. On peut ainsi envoyer une adresse de 32 bits sur un bus d'adresse de 16 bits, par exemple. Le bus d'adresse contient alors environ moitié moins de fils que la normale. Cette technique est appelée un bus d'adresse multiplexé.
Elle est surtout utilisée sur les mémoires de grande capacité, pour lesquelles les adresses sont très grandes. Songez qu'il faut 32 fils d'adresse pour une mémoire de 4 gibioctet, ce qui est déjà assez peu pour la mémoire principale d'un ordinateur personnel. Et câbler 32 fils est déjà un sacré défi en soi, là où 16 bits d'adresse est déjà largement plus supportable. Aussi, la mémoire RAM d'un ordinateur utilise systématiquement un envoi de l'adresse en deux fois. Les SRAM étant de petite capacité, elles n'utilisent que rarement un bus d'adresse multiplexé. Inversement, les DRAM utilisent souvent un bus d'adresse multiplexé du fait de leur grande capacité.
| Type de la mémoire | Bus d'adresse normal ou multiplexé |
|---|---|
| ROM/PROM/EPROM/EEPROM | Bus d'adresse normal (envoi de l'adresse en une seule fois) |
| SRAM | Bus d'adresse normal |
| DRAM | Bus d'adresse multiplexé (envoi de l'adresse en deux fois) |
Les bus multiplexés
modifierUne autre astuce est celle des bus multiplexés, à ne pas confondre avec les bus précédents où seule l'adresse est multiplexée. Un bus multiplexé sert alternativement de bus de donnée ou d'adresse. Ces bus rajoutent un bit sur le bus de commande, qui précise si le contenu du bus est une adresse ou une donnée. Ce bit Adresse Line Enable, aussi appelé bit ALE, vaut 1 quand une adresse transite sur le bus, et 0 si le bus contient une donnée (ou l'inverse !).

Un bus multiplexé est plus lent pour les écritures : l'adresse et la donnée à écrire ne peuvent pas être envoyées en même temps. Par contre, les lectures ne posent pas de problèmes, vu que l'envoi de l'adresse et la lecture proprement dite ne sont pas simultanées. Heureusement, les lectures en mémoire sont bien plus courantes que les écritures, ce qui fait que la perte de performance due à l'utilisation d'un bus multiplexé est souvent supportable.
Un autre problème des bus multiplexé est qu'ils ont a peu-près autant de bits pour coder l'adresse que pour transporter les données. Par exemple, un bus multiplexé de 8 bits transmettra des adresses de 8 bits, mais aussi des données de 8 bits. Cela entraine un couplage entre la taille des données et la taille de la capacité de la mémoire. Cela peut être compensé avec un bus d'adresse multiplexé, les deux techniques pouvant être combinées sans problèmes. Dans ce cas, les transferts avec la mémoire se font en plusieurs fois : l'adresse est transmise en plusieurs fois, la donnée récupérée/écrite ensuite.
Les bus à commutation de paquet
modifierDes mémoires DRAM assez rares ont exploré un bus mémoire particulier : avoir un bus peu large mais de haute fréquence, sur lequel on envoie les commandes/données en plusieurs fois. Elles sont regroupées sous le nom de mémoires à commutation par paquets. Elles utilisent des bus spéciaux, où les commandes/adresses/données sont transmises par paquets, par trames, en plusieurs fois. Le processeur envoie des paquets de commandes, les mémoires répondent avec des paquets de données ou des accusés de réception. Toutes les barrettes de mémoire doivent vérifier toutes les transmissions et déterminer si elles sont concernées en analysant l'adresse transmise dans la trame. En théorie, ce qu'on a dit sur le codage des trames dans le chapitre sur le bus devrait s'appliquer à de telles mémoires. En pratique, les protocoles de transmission sur le bus mémoire sont simplifiés, pour gérer le fonctionnement à haute fréquence.
Les mémoires à commutation par paquets sont peu nombreuses. Les plus connues sont les mémoires conçues par la société Rambus, à savoir la RDRAM (Rambus DRAM) et ses deux successeurs XDR RAM et XDR RAM 2. La Synchronous-link DRAM (SLDRAM) est un format concurrent conçu par un consortium de plusieurs concepteurs de mémoire.
Un premier exemple est celui des mémoires RDRAM, où le bus permettait de transmettre soit des commandes (adresse inclue), soit des données, avec un multiplexage total. Le processeur envoie un paquet contenant commandes et adresse à la mémoire, qui répond avec un paquet d'acquittement. Lors d'une lecture, le paquet d'acquittement contient la donnée lue. Lors d'une écriture, le paquet d'acquittement est réduit au strict minimum. Le bus de commandes est réduit au strict minimum, à savoir l'horloge et quelques bits absolument essentiels, les bits RW est transmis dans un paquet et n'ont pas de ligne dédiée, pareil pour le bit OE.
Pour donner un autre exemple, parlons rapidement des mémoires SLDRAM. Elles utilisaient un bus de commande de 11 bits, qui était utilisé pour transmettre des commandes de 40 bits, transmises en quatre cycles d'horloge consécutifs. Le bus de données était de 18 bits, mais les transferts de donnée se faisaient par paquets de 4 à 8 octets (32-65 bits). Pour résumer, données et commandes sont chacunes transmises en plusieurs cycles consécutifs, sur un bus de commande/données plus court que les données/commandes elle-mêmes.
Le bus de données et les mémoires multiports
modifierLe bus de données transmet un nombre fixe de bits. Dans la plupart des cas, le bus de données peut transmettre un byte à chaque transmission (à chaque cycle d'horloge). Un bus qui permet cela est appelé un bus parallèle. Quelques mémoires sont cependant connectées à un bus qui ne peut transmettre qu'un seul bit à la fois. Un tel bus est appelé un bus série. Les mémoires avec un bus série ne sont pas forcément adressables bit par bit. Elles permettent de lire ou écrire par bytes complets, mais ceux-ci sont transmis bits par bits sur le bus de données. La conversion entre byte et flux de bits sur le bus est réalisée par un simple registre à décalage. On pourrait croire que de telles mémoires séries sont rares, mais ce n'est pas le cas : les mémoires Flash, très utilisées dans les clés USB ou les disques durs SSD sont des mémoires séries.

Le sens de transmission sur le bus
modifierLe bus de données est généralement un bus bidirectionnel, rarement unidirectionnel (pour les mask ROM qui ne gèrent que la lecture). Sur la plupart des mémoires, le bus de données est bidirectionnel et sert aussi bien pour les lectures que pour les écritures.

Sur d'autres mémoires, on trouve deux bus de données : un dédié aux lectures et un autre pour les écritures. Le bus de commande est alors assez compliqué, dans le sens où il y a deux bus d'adresses : un qui commande l'entrée d'écriture et un pour la sortie de lecture. Le bus d'adresse est donc dupliqué et d'autres bits du bus de commande le sont aussi, mais les signaux d'horloge et le bit CS ne sont pas dupliqués. En théorie, il n'y a pas besoin de bit R/W, qui est remplacé par deux bits : un qui indique qu'on veut faire une écriture sur le bus dédié, un autre pour indiquer qu'on veut faire une lecture sur l'autre bus. L’avantage d'utiliser un bus de lecture séparé du bus d'écriture est que cela permet d'effectuer une lecture en même temps qu'une écriture. Cependant, cet avantage signifie que la conception interne de la mémoire est naturellement plus compliquée. Par exemple, la mémoire doit gérer le cas où la donnée lue est identique à celle écrite en même temps. L'augmentation du nombre de broches est aussi un désavantage.

Les mémoires multiport
modifierLe cas précédent, avec deux bus séparés, est un cas particulier de mémoire multiport. Celles-ci sont reliées non pas à un, mais à plusieurs bus de données. Évidemment, le bus de commande d'une telle mémoire est adapté à la présence de plusieurs bus de données. La plupart des bits du bus de commande sont dupliqués, avec un bit par bus de données. c'est le cas pour les bits R/W, les bits d'adresse, le bit OE, etc. Par contre, d'autres entrées du bus de commande ne sont pas dupliquées : c'est le cas du bit CS, de l'entrée d'horloge, etc. Les entrées de commandes associés à chaque bus de données, ainsi que les broches du bus de données, sont regroupées dans ce qu'on appelle un port.

Les mémoires multiport permettent de transférer plusieurs données à la fois, une par port. Le débit est sont donc supérieur à celui des mémoires mono-port. De plus, chaque port peut être relié à des composants différents, ce qui permet de partager une mémoire entre plusieurs composants.
Dans l'exemple de la section précédente, on a un port pour les lectures et un autre pour les écritures. Chaque port est donc spécialisé soit dans les lectures, soit dans les écritures. D'autres mémoires suivent ce principe et ont deux/trois ports de lecture et un d'écriture, d'autres trois ports de lecture et deux d'écriture, bref : les combinaisons possibles sont légion. Mais d'autres mémoires ont des ports bidirectionnels, capables d'effectuer soit une lecture, soit une écriture. On peut imaginer une mémoire avec 5 ports, chacun faisant lecture et écriture.
L'interface d'une mémoire ne correspond pas forcément à celle du bus mémoire
modifierEn théorie, une mémoire est utilisé avec un bus qui utilise la même interface. Par exemple, une mémoire multiport est utilisée avec un bus lui-même multiport, avec des fils séparés pour les lectures et les écritures. De même, un bus multipléxé est utilisé avec une mémoire multiplexé. Mais dans certains cas, ce n'est pas le cas.
La raison à de telles configurations tient dans un fait simple : le processeur doit économiser des broches, alors que les mémoires sont épargnée par cette économie. Il faut dire qu'un processeur a besoin de beaucoup plus de broches qu'une mémoire pour faire son travail, vu que l'interface d'une mémoire est plus simple que celle du processeur. Les processeurs doivent donc utiliser pas mal de ruses pour économiser des broches, comme un usage de bus multiplexés, de bus d'adresse multiplexé, etc. A l'inverse, les mémoires peuvent parfaitement s'en passer. Les mémoires de faible capacité sont souvent sans bus multiplexés, alors que les processeurs à bas cout avec bus multiplexés sont plus fréquents.
Les bus et mémoires multiplexés
modifierIl est possible d'utiliser un bus multiplexé avec une mémoire qui ne l'est pas. La raison est que le processeur que l'on utilise un bus multiplexé pour économiser des broches, mais que la mémoire n'a pas besoin de faire de telles économies. Cela arrive si l'on prend un processeur et une mémoire à bas prix. Les mémoires multiplexées ont tendance à être plus rares et plus chères, alors que c'est l'inverse pour les processeurs.
Un exemple est donné dans le schéma ci-dessous. On voit que le processeur et une mémoire EEPROM sont reliées à un bus multiplexé très simple. Le processeur possède un bus multiplexé, alors que la mémoire a un bus d'adresse séparé du bus de données. Dans cet exemple, le processeur ne peut faire que des lectures, vu que la mémoire est une mémoire EEPROM, mais la solution marche bien dans le cas où la mémoire est une RAM. L'interface entre bus multiplexé et mémoire qui ne l'est pas se résume à deux choses : l'ajoput d'un registre en amont de l'entrée d'adresse de la mémoire, et une commande adéquate de l'entrée OE.
Pour faire une lecture, le processeur procède en deux étapes, comme sur un bus multiplexé normale : l'envoi de l'adresse, puis la lecture de la donnée.
- Lors de l'envoi de l'adresse, l'adresse est mémorisée dans le registre, la broche ALE étant reliée à l'entrée Enable du registre. De plus, on doit déconnecter la mémoire du bus de donnée pour éviter un conflit entre l'envoi de la donnée par la mémoire et l'envoi de l'adresse par le processeur. Pour cela, on utilise l'entrée OE (Output Enable).
- La lecture de la donnée consiste à mettre ALE à 0, et à récupérer la donnée sur le bus. Pendant cette étape, le registre maintient l'adresse sur le bus d'adresse. Le bit OE est configuré de manière à activer la sortie de données.

Le bus mémoire des PC modernes est très important pour les performances. Les processeurs sont de plus en plus exigeants et la vitesse de la mémoire commence à être de plus en plus limitante pour leurs performances. La solution la plus évidente est d'augmenter la fréquence des mémoires et/ou de diminuer leur temps d'accès. Mais c'est que c'est plus facile à dire qu'à faire ! Les mémoires actuelles ne peut pas vraiment être rendu plus rapides, compte tenu des contraintes techniques actuelles. La solution actuellement retenue est d'augmenter le débit de la mémoire. Et pour cela, la performance du bus mémoire est primordiale.
Le débit binaire des mémoires actuelles dépend beaucoup de la performance du bus mémoire. La performance d'un bus dépend de son débit binaire, qui lui-même est le produit de sa fréquence et de sa largeur. Diverses technologies tentent d'augmenter le débit binaire du bus mémoire, que ce soit en augmentant sa largeur ou sa fréquence. La largeur du bus mémoire est quelque peu limitée par le fait qu'il faut câbler des fils sur la carte mère et ajouter des broches sur les barrettes de mémoire. Les deux possibilités sont déjà utilisées à fond, les bus actuels ayant plusieurs centaines de fils/broches.
Les bus mémoire à multiples canaux
modifierPour commencer, mettons de côté la fréquence, et intéressons-nous à la largeur du bus mémoire. Les PC actuels ont des bus d’une largeur de 64 bits minimum, avec cependant possibilité de passer à 128, 192, voire 256 bits ! C'est ce qui se cache derrière les technologies dual-channel, triple-channel ou quad-channel.
Le bus mémoire a une taille de 64 bits par barrette de mémoire, avec quelques contraintes de configuration. Le dual-channel permet de connecter deux barrettes de 64 bits, à un bus de 128 bits. Ainsi, on lit/écrit 64 bits de poids faible depuis la première barrette, puis les 64 bits de poids fort depuis la seconde barrette. Le triple-channel fait de même avec trois barrettes de mémoire, le quad-channel avec quatre barrettes de mémoire. Ces techniques augmentent la largeur du bus, donc influencent le débit binaire, mais n'ont pas d'effet sur le temps de latence de la mémoire. Et ce ne sont pas les seules techniques dans ce genre.

Pour en profiter, il faut placer les barrettes mémoire d'une certaine manière sur la carte mère. Typiquement, une carte mère dual channel a deux slots mémoires, voire quatre. Quand il y en a deux, tout va bien, il suffit de placer une barrette dans chaque slot. Mais dans le cas où la carte mère en a quatre, les slots sont d'une couleur différent pour indiquer comment les placer. Il faut placer les barrettes dans les slots de la même couleur pour profiter du dual channel.
Le préchargement des mémoires Dual et Quad data rate
modifierAccroître plus la largeur du bus a trop de désavantages : il faudrait câbler beaucoup trop de fils. Une autre solution est d'augmenter la fréquence du bus, mais cela demande alors d'augmenter la fréquence de la mémoire, qui ne suit pas. Mais il existe une solution alternative, qui est une sorte de mélange des deux techniques. Cette technique s'appelle le préchargement, prefetching en anglais. Elle donne naissance aux mémoires mémoires Dual Data Rate, aussi appelées mémoires DDR. Il s'agit de mémoires SDRAM améliorées, avec une interface avec la mémoire légèrement bidouillée.
Les mémoires sans préchargement
modifierLes mémoires sans préchargement sont appelées des mémoires SDR (Single Data Rate). Avec elles, le plan mémoire et le bus vont à la même fréquence et ils ont la même largeur (le nombre de bits transmit en une fois). Par exemple, si le bus mémoire a une largeur de 64 bits et une fréquence de 100 MHz, alors le plan mémoire fait de même.

Toute augmentation de la fréquence et/ou de la largeur du bus se répercute sur le plan mémoire et réciproquement. Problème, le plan mémoire est difficile à faire fonctionner à haute fréquence, mais peut avoir une largeur assez importante sans problèmes. Pour le bus, c'est l'inverse : le faire fonctionner à haute fréquence est possible, bien que cela requière un travail d'ingénierie assez conséquent, alors qu'en augmenter la largeur poserait de sérieux problèmes.
Les mémoires avec préchargement
modifierL'idée du préchargement est un compromis idéal entre les deux contraintes précédentes : on augmente la largeur du plan mémoire sans en augmenter la fréquence, mais on fait l'inverse pour le bus. En faisant cela, le plan mémoire a une fréquence inférieure à celle du bus, mais a une largeur plus importante qui compense exactement la différence de fréquence. Si le plan mémoire a une largeur de N fois celle du bus, le bus a une fréquence N plus élevée pour compenser.
Sur les mémoires DDR (Double Data Rate), le plan mémoire est deux fois plus large que le bus, mais a une fréquence deux fois plus faible. Les données lues ou écrites dans le plan mémoire sont envoyées en deux fois sur le bus, ce qui est compensé par le fait qu'il soit deux fois plus rapide. Ceci dit, il faut trouver un moyen pour découper un mot mémoire de 128 bits en deux blocs de 64, à envoyer sur le bus dans le bon ordre. Cela se fait dans l'interface avec le bus, grâce à une sorte de mémoire tampon un peu spéciale, dans laquelle on accumule les 128 bits lus ou à écrire.

- Sur les mémoires DDR dans les ordinateurs personnels, seul un signal d'horloge est utilisé, que ce soit pour le bus, le plan mémoire, ou le contrôleur. Seulement, le bus et les contrôleurs mémoire réagissent à la fois sur les fronts montants et sur les fronts descendants de l'horloge. Le plan mémoire, lui, ne réagit qu'aux fronts montants.
Il existe aussi des mémoires quad data rate, pour lesquelles la fréquence du bus est quatre fois celle du plan mémoire. Évidemment, la mémoire peut alors lire ou écrire 4 fois plus de données par cycle que ce que le bus peut supporter.

Vous remarquerez que le préchargement se marie extrêmement bien avec le mode rafale.
Le préchargement augmente donc le débit théorique maximal. Sur les mémoires sans préchargement, le débit théorique maximal se calcule en multipliant la largeur du bus de données par sa fréquence. Par exemple, une mémoire SDRAM fonctionnant à 133 Mhz et qui utilise un bus de 8 octets, aura un débit de 8 * 133 * 1024 * 1024 octets par seconde, ce qui fait environ du 1 giga-octets par secondes. Pour les mémoires DDR, il faut multiplier la largeur du bus mémoire par la fréquence, et multiplier le tout par deux pour obtenir le débit maximal théorique. En reprenant notre exemple d'une mémoire DDR fonctionnant à 200 Mhz et utilisée en simple channel utilisera un bus de 8 octets, ce qui donnera un débit de 8 * 200 * 1024 * 1024 octets par seconde, ce qui fait environ du 2.1 gigaoctets par secondes.
Les bus mémoire à base de liaisons point à point : les barrettes FB-DIMM
modifierDans le cas le plus fréquent, toutes les barrettes d'un PC sont reliées au même bus mémoire, comme indiqué dans le schéma ci-dessous. Le bus mémoire est un bus parallèle, avec tous les défauts que ca implique quand on travaille à haute fréquence. Diverses contraintes électriques assez compliquées à expliquer font que les bus parallèles ont du mal à fonctionner à haute fréquence, la stabilité de transmission du signal est altérée.


Les barrettes mémoire FB-DIMM contournent le problème en utilisant plusieurs liaisons point à point. Il y a deux choses à comprendre. La première est que chaque barrette est connectée à la suivante par une liaison point à point, comme indiqué ci-dessous. Il n'y a pas de bus sur lequel on connecte toutes les barrettes, mais une série de plusieurs liaisons point à point. Les commandes/données passent d'une barrette à l'autre jusqu'à destination. Par exemple, une commande SDRAM part du contrôleur mémoire, passe d'une barrette à l'autre, avant d'arriver à la barrette de destination. Même chose pour les données lues depuis les DRAM, qui partent de la barrette, passent d'une barrette à la suivante, jusqu’à arriver au contrôleur mémoire.
Ensuite, les liaisons point à point sont au nombre de deux par barrette : une pour la lecture (northbound channel), l'autre pour l'écriture (southbound channel). Chaque barrette est reliée aux liaisons point à point par un circuit de contrôle qui fait l'interface. Le circuit de contrôle s'appelle l'Advanced Memory Buffer, il vérifie si chaque transmission est destinée à la barrette, et envoie la commande/donnée à la barrette suivante si ce n'est pas le cas.

L'avantage de cette organisation est que l'on peut facilement brancher beaucoup de barrettes mémoire sur la carte mère. Avec un bus parallèle, il est difficile de mettre plus de 4 barrettes mémoire. Plus on insère de barrettes de mémoire, plus la stabilité du signal transmis avec un bus parallèle se dégrade. Cela ne pose pas de problème quand on rajoute des barrettes sur la carte mère, car elles sont conçues pour que le signal reste exploitable même si tous les slots mémoire sont remplis. Mais cela fait qu'on a rarement plus de 4 slots mémoire par carte mère. Avec des barrettes FB-DIMM, on peut monter facilement à 8 ou 16 barrettes.
La micro-architecture d'une mémoire adressable
modifierDe nos jours, ces cellules mémoires sont fabriquées avec des composants électroniques et il nous faudra impérativement passer par une petite étude de ces composants pour comprendre comment fonctionnent nos mémoires. Dans les grandes lignes, les mémoires RAM et ROM actuelles sont toutes composées de cellules mémoires, des circuits capables de retenir un bit. En prenant plein de ces cellules et en ajoutant quelques circuits électroniques pour gérer le tout, on obtient une mémoire. Dans ce chapitre, nous allons apprendre à créer nos propres bits de mémoire à partir de composants élémentaires : des transistors et des condensateurs.
L'interface d'une cellule mémoire (généralités)
modifierLes cellules mémoires se présentent avec une interface simple, limitée à quelques broches. Et cette interface varie grandement selon la mémoire : elle n'est pas la même selon qu'on parle d'une DRAM ou d'une SRAM, avec quelques variantes selon les sous-types de DRAM et de SRAM. Là où les DRAM se limitent souvent à deux broches, les SRAM peuvent aller jusqu'à quatre. Nous reparlerons dans la suite des interfaces pour chaque type (voire sous-type) de mémoire. Pour le moment, nous allons commencer par voir le cas général. Dans les grandes lignes, on peut grouper les broches d'une cellule mémoire en plusieurs types :
- Les broches de données, sur lesquelles on va lire ou écrire un bit.
- Les broches de commande, sur lesquelles on envoie des ordres de lecture/écriture.
- D'autres broches, comme la broche pour le signal d'horloge ou les broches pour l’alimentation électrique et la masse.
Les broches de données
modifierConcernant les broches de données, il y a plusieurs possibilités qui comprennent une, deux ou trois broches.
- Dans le cas le plus simple, la cellule mémoire n'a qu'une seule broche d'entrée-sortie, sur laquelle on peut écrire ou lire un bit. On parle alors de cellule mémoire simple port.
- Les cellules mémoires plus compliquées ont une sortie de lecture, sur laquelle on peut lire le bit stocké dans la cellule, et une entrée d'écriture, sur laquelle on place le bit à stocker dans la cellule. Dans ce cas, on parle de cellule mémoire double port.
- Sur les cellules mémoires différentielles, la cellule mémoire dispose de deux broches d’entrée-sortie, dites différentielles, c'est à dire que le bit présent sur la seconde broche est l'inverse de la première. L'utilité de ces deux broches inversées n'est pas évidente, mais elle deviendra évidente dans le chapitre sur le plan mémoire.

Les cellules mémoires simple port se trouvent dans les DRAM modernes, comme nous le verrons plus bas dans la section sur les 1T-DRAM.
Les cellules mémoire double port sont présentes dans les SRAM et les DRAM anciennes. Quelques vieilles DRAM, nommées 2T et 3T-DRAM, étaient de ce type. Quand aux cellules SRAM double port, elles sont plus rares, mais on en trouve dans les mémoires SRAM multiport avec un port d'écriture séparé du port de lecture. Après tout, les bascules elles-mêmes ont un "port" d'écriture et un de lecture, ce qui se marie bien avec ce genre de mémoire multiport.
Quand aux cellules mémoires différentielles, toutes les SRAM modernes sont de ce type.
Les broches de commande
modifierPour les broches de commande, il y a deux possibilités : soit la cellule reçoit un bit Enable couplé à un bit R/W, soit elle possède deux bits qui autorisent respectivement les lectures et écriture.
- La forme la plus simple est une broche de sélection qui autorise/interdit les communications avec la cellule mémoire. Cette broche de sélection connecte ou déconnecte les autres broches du reste de la mémoire. Elle est couplée, dans le cas des mémoires RAM, à une broche R/W, sur laquelle on vient placer le fameux bit R/W, qui dit s'il faut faire une lecture ou une écriture.
- Encore une fois, elle peut être scindée en une broche d'autorisation de lecture et une broche d'autorisation d'écriture, sur laquelle on place le bit R/W (ou son inverse) pour autoriser/interdire les écritures.

Il est possible de passer d'une interface à l'autre assez simplement, grâce à un petit circuit à ajouter à la cellule mémoire. Cela est utile pour faciliter la conception du contrôleur mémoire. Celui-ci peut en effet générer assez simplement le signa Enable, à envoyer sur la broche de sélection. Quant au bit R/W, il est fournit directement à la mémoire, via le bus de commande. L'interface avec les broches Enable et R/W est donc la plus facile à utiliser. Mais si on regarde l'intérieur de certaines cellules mémoire (celles de SRAM, notamment), on s’aperçoit que leur organisation interne se marie très bien avec la seconde interface, celle avec une broche d'autorisation de lecture et une pour autoriser les écritures. Il faut donc faire la conversion de la seconde interface vers la première.
Pour cela, on ajoute un petit circuit qui convertit les bits Enable et R/W en signaux d'autorisation de lecture/écriture. On peut établir la table de vérité de ce circuit assez simplement. Déjà, les deux bits d'autorisation ne sont à 1 que si le signal de sélection est à 1 : s'il est à 0, la cellule mémoire doit être totalement déconnectée du bus. Ensuite, la valeur de ces deux bits sont l'inverse l'une de l'autre : soit on fait une lecture, soit on fait une écriture, mais pas les deux en même temps. Pour finir, on peut utiliser la valeur de R/W pour savoir lequel des deux bit est à mettre à 1. On a donc le circuit suivant.

Les cellules de SRAM
modifierAvant toute chose, faisons un petit point terminologique. Techniquement, les cellules mémoire d'une SRAM peuvent se fabriquer de deux manières différentes. La toute première utilise tout simplement une bascule D, la seconde utilise utilise un montage de plusieurs transistors. Le terme cellule de SRAM (SRAM cell) désigne uniquement la seconde possibilité. Il faut ainsi faire la distinction entre une bascule D fabriquée avec des portes logiques, et une cellule de SRAM fabriquée directement avec des transistors. La distinction est assez subtile et pas intuitive : le terme cellule de SRAM fait référence à une méthode de fabrication de la cellule mémoire, pas à la mémoire qui l'utilise. Il est possible de créer une mémoire SRAM en utilisant des bascules D ou des cellules de SRAM, les deux sont possibles. Il s'agit là d'une distinction qui ne sera pas faite pour les autres cellules mémoire.
Nous ne reviendrons pas sur les bascules D, pour ne pas faire de redite des chapitres précédents. Par contre, nous allons étudier les cellules de SRAM. Les cellules de SRAM ont bien évoluées depuis les toutes premières versions jusqu’au SRAM actuelles. Les SRAM modernes arrivent à se débrouiller avec un nombre de transistors qui se compte sur les doigts d'une main. Les variantes les plus légères se contentent de 4 transistors, les intermédiaires de 6, et les plus grosses de 8 transistors. En comparaison, les bascules D sont composées de 10 à 20 transistors.
La différence de nombre de transistors fait que les mémoires SRAM ont une meilleure densité, à savoir que l'on peut mettre plus de cellules SRAM sur une même surface. En général, moins la cellule contient de transistors, moins elle prend de place et plus la RAM aura une grande capacité mémoire. Par contre, cela se fait au détriment des performances. Ainsi, une SRAM fabriquée avec des bascules D sera très rapide, mais aura une faible capacité. Une SRAM fabriquée avec des cellules de SRAM aura une meilleure capacité, mais des performances moindres. En conséquence, les bascules D sont surtout utilisées pour les registres du processeur, alors que les cellules de SRAM sont utilisées pour les mémoires caches.
L'interface d'une cellule SRAM varie beaucoup suivant la cellule utilisée, mais nous allons parler des trois cas les plus courants, à savoir les SRAM double port, simple port et différentielles.
Les cellules de SRAM différentielles de type 6T-SRAM et 4T-SRAM
modifierLes cellules SRAM différentielles n'ont pas une seule broche d'entrée-sortie, mais deux. Les deux broches sont dites différentielles, c'est à dire que le bit présent sur la seconde entrée est l'inverse du premier. Elles sont souvent notées et . L'utilité de ces deux broches inversées n'est pas évidente, mais elle deviendra évidente dans le chapitre sur le plan mémoire.
Dans les chapitres du début du cours, nous avions vu qu'une bascule D est composée de deux inverseurs reliés l'un à l'autre de manière à former une boucle, avec des circuits annexes associés (un multiplexeur, notamment). Les cellules de SRAM utilisent elles aussi une boucle avec deux portes NON, mais ajoutent à peine quelques transistors autour, le strict minimum pour que le circuit fonctionne. Les deux broches d'entrée-sortie de la cellule sont directement connectées aux entrées des inverseurs, à travers deux transistors de contrôle, comme montré ci-dessous. Le tout ressemble au circuit précédent, sauf qu'on aurait retiré le multiplexeur.

Le circuit se comporte différemment entre les lectures et écritures. Lors d'une écriture, les broches servent d'entrée, et elles ont la priorité car le courant envoyé sur ces entrées est plus important que le courant qui circule dans la boucle. De plus, les transistors de contrôle sont plus gros et ont une amplification plus importante que les transistors des inverseurs. Si on veut écrire un 1 dans la cellule SRAM, la broche BL aura la priorité sur la sortie de l'inverseur et la bascule mémorisera bien un 1. Lors de l'écriture d'un 0, ce sera cette fois-ci l'entrée qui aura un courant plus élevé que la sortie de l'autre inverseur, et la cellule mémorisera bien un 0, mais qui sera injecté par l'autre entrée. Lors d'une lecture, les broches n'ont aucun courant d'entrée, ce qui fait que les inverseurs fourniront un courant plus fort que celui présent sur la broche. Le contenu de la bascule est cette fois-ci envoyé dans la broche d'entrée-sortie.
Un problème de cette cellule est que les portes logiques fournissent peu de courant, ce qui est gênant lors d'une lecture. Mais expliquer en quoi cela est un problème ne peut pas se faire pour le moment, il vous faudra attendre le chapitre suivant. Toujours est-il que la faiblesse de la sortie des inverseurs est compensée en-dehors de la cellule SRAM, par des circuits spécialisés d'une mémoire, que nous verrons dans le chapitre suivant. Il s'agit de l'amplificateur de lecture, ainsi que des circuits de précharge, qui sont partagés entre toutes les cellules mémoires. N'en disons pas plus pour le moment.
Il existe plusieurs types de cellules différentielles de SRAM, qui se distinguent par la technologie utilisée : bipolaire, CMOS, PMOS, NMOS, etc. Chaque type a ses avantages et inconvénients : certaines fonctionnent plus vite, d'autres prennent moins de place, d'autres consomment moins de courant, etc. La différence tient dans la manière dont ont conçus les portes NON dans la cellule.
La cellule en technologie CMOS, dite 6T-SRAM
modifierLes deux inverseurs peuvent être conçus en utilisant la technologie CMOS, bipolaire, NMOS ou PMOS. Dans le cas de la technologie CMOS, chaque inverseur est réalisé avec deux transistors, un PMOS et un NMOS, comme nous l'avons vu dans le chapitre sur les portes logiques. La cellule mémoire obtenue est alors une cellule à 6 transistor : 2 pour l'autorisation des lectures et écritures et 4 pour la cellule de mémorisation proprement dite (les inverseurs tête-bêche).

Ce montage a divers avantages, le principal étant sa très faible consommation électrique. Mais son grand nombre de transistors fait que chaque cellule prend beaucoup de place. On ne peut donc pas l'utiliser pour construire des mémoires de grande capacité.
La cellule en technologie MOS, NMOS ou PMOS, dite 4T-SRAM
modifierEn technologie MOS, ainsi qu'en technologie PMOS et NMOS, chaque porte logique est créée avec un transistor et une résistance. La cellule contient alors, au total, quatre transistors et deux résistances. Le circuit obtenu avec la technologie MOS est illustré ci-dessous.

Il est possible de remplacer la résistance par un transistor MOS câblé d'une manière précise, avec un montage dit en résistance variable. Ce montage fait que le transistor MOS se comporte comme une source de courant, équivalente au courant qui traverse la résistance.

D'autres cellules retirent les résistances de charge, histoire de gagner un peu de place. La réduction de taille de la cellule mémoire est assez intéressante, mais se fait au prix d'une plus grande complexité de la cellule. L'alimentation VDD doit être fournie à l'extérieur de la cellule mémoire, qui doit être alimentée à travers les transistors d'accès. Ceux-ci sont ouverts en-dehors des lectures et écritures, une tension devant être fournie sur leur source/drain, par l'extérieur de la cellule.

La cellule en technologie bipolaire
modifierLes cellules de SRAM en version bipolaire sont de loin les plus rapides, mais leur consommation électrique est bien plus élevée. C'est pour cette raison que les RAM actuelles sont toutes réalisées avec une technologie MOS ou CMOS. Presque aucune mémoire n'est réalisée en technologie bipolaire à l'heure actuelle.
Dans le cas le plus simple, qui utilise le moins de composants, la commande du transistor a lieu au niveau des émetteurs des transistors, qui sont reliés ensemble.

Il est possible d'améliorer le montage en ajoutant deux diodes, une en parallèle de chaque résistance. Cela permet d'augmenter le courant dispensé par la cellule mémoire lors d'une lecture ou écriture. Cela a son utilité, comme on le verra dans le prochain chapitre (pour anticiper : cela rend plus rapide la charge/décharge de la ligne de bit, sans système de précharge). Mais cela demande d'inverser les connexions dans la cellule mémoire. Le circuit obtenu est le suivant.

Les cellules SRAM double port
modifierIl existe des cellules SRAM double port, avec deux entrées d'écriture et une sortie spécifique pour la lecture. Elles sont similaires aux cellules précédentes, sauf qu'on a rajouté deux transistors pour la lecture. Cela fait en tout 8 transistor, d'om le nom de 8T-SRAM donné à ce type de cellules mémoires. Le circuit précédent à six transistors est utilisé tel quel pour l'écriture. Si on utilise deux transistors pour le port de lecture, c'est pour une raison assez simple. Le premier transistor sert à connecter la sortie de l'inverseur à la ligne de bit (le fil sur lequel on récupère le bit), quand on sélectionne la cellule mémoire. Le second transistor, quant à lui est facultatif. Il est utilisé pour amplifier le signal de sortie de l'inverseur, pour l'envoyer sur la ligne de bit, pour des raisons que nous verrons au prochain chapitre.

Les cellules de DRAM
modifierComme pour les SRAM, les DRAM sont composées d'un circuit qui mémorise un bit, entouré par des transistors pour autoriser les lectures et écritures. La différence avec les SRAM tient dans le circuit utilisé pour mémoriser un bit. Contrairement aux mémoires SRAM, les mémoires DRAM ne sont pas fabriquées avec des portes logiques. À la place, elles utilisent un composant électronique qui sert de "réservoir" à électrons. Un réservoir remplit code un 1, alors qu'un réservoir vide code un 0.
La nature du réservoir dépend cependant de la version de la cellule de mémoire DRAM utilisée. Car oui, il existe plusieurs types de cellules de DRAM, qui utilisent des composants réservoir différents. Étudier les versions plus récentes, actuellement utilisées dans les mémoires DRAM modernes, est bien plus facile que de comprendre les versions plus anciennes. Aussi, nous allons commencer par le cas le plus simple : les cellules de DRAM dites 1T-DRAM. Nous verrons ensuite les cellules de type 3T-DRAM, plus complexes et plus anciennes.
Les DRAM à base de condensateurs : 1T-DRAM
modifier
Les DRAM actuelles n'utilisent qu'un seul transistor, associé à un autre composant électronique nommé condensateur. Ce condensateur est un réservoir à électrons : on peut le remplir d’électrons ou le vider en mettant une tension sur ses entrées. Il stocke un 1 s'il est rempli, un 0 s'il est vide. C'est donc lui qui sert de circuit de mémorisation. On peut naturellement remplir ou vider un condensateur (on dit qu'on le charge ou qu'on le décharge), ce qui permet d'écrire un bit à l'intérieur.
À côté du condensateur, on ajoute un transistor qui va autoriser l'écriture ou la lecture dans notre condensateur. Tant que le transistor se comporte comme un interrupteur ouvert, le condensateur est isolé du reste du circuit : pas d'écriture ou de lecture possible. Il faut l'ouvrir pour lire ou écrire dans le condensateur.
La cellule de DRAM a donc deux broches : une broche de données connectée indirectement au condensateur à travers le transistor MOS, une broche de commande connectée à la grille du transistor MOS. La broche de commande est connectée à un fil appelé la word line ou ligne de mot, la broche de données est connectée à un fil appelé la bitline ou ligne de bit. Retenez bien ces termes, nous les utiliserons beaucoup dans ce qui suit.

Le condensateur est connecté au transistor MOS d'un côté, à la masse (le 0 volts) de l'autre. Du moins, c'était le cas avant, les DRAM actuelles ne connectent pas le condensateur à la masse, mais à une tension égale à la moitié de la tension d'alimentation, pour des raisons qu'on expliquera plus tard. Le condensateur stocke alors un 1 quand la tension est positive, un 0 quand elle est négative.
Le rafraichissement mémoire
modifierL'intérieur d'un condensateur n'est pas très compliqué : il est formé de deux couches de métal conducteur, séparées par un isolant électrique. Les deux plaques de conducteur sont appelées les armatures du condensateur. C'est sur celles-ci que les charges électriques s'accumulent lors de la charge/décharge d'un condensateur. L'isolant empêche la fuite des charges d'une armature à l'autre, ce qui permet au condensateur de fonctionner comme un réservoir, et non comme un simple fil.
Mais sur les DRAM actuelles, les condensateurs sont tellement miniaturisés qu'ils en deviennent de vraies passoires. Il possède toujours quelques défauts et des imperfections qui font que l'isolant n'est jamais totalement étanche : des électrons passent de temps en temps d'une armature à l'autre et quittent le condensateur. En clair, le bit contenu dans la cellule de mémoire DRAM s'efface. Ce qui explique qu'on doive rafraîchir régulièrement les mémoires DRAM de ce type.
La lecture et l'écriture d'une cellule de 1T-DRAM
modifierLe circuit précédent a deux broches : une broches de données et une broche de contrôle. La broche de données est celle sur laquelle on récupère un bit lors d'une lecture, mais aussi sur laquelle on envoie le bit lors d'une écriture. Elle est connectée à la ligne de bit. La broche de commande sert à connecter le condensateur au bus de données lors d'une lecture ou écriture, elle est connectée à la ligne de mot.
Lors d'une écriture, la broche de données est mise à 0 ou 1. Si elle est mise à 0, le condensateur va se vider intégralement dans le fil et restera à zéro une fois vidé. Si l'entrée-sortie est mise à 1, le condensateur se remplit, s'il n'est pas déjà remplit. Au final, un 1 sera stocké dedans.
Lors d'une lecture, le condensateur est connecté sur la broche de données et se vide entièrement dedans. Il faut le récrire après chaque lecture sous peine de perdre le contenu de la cellule de DRAM. Il s'agit d'une forme de rafraichissement mémoire, dans le sens où on doit rafraichir le contenu de la cellule mémoire après chaque lecture.
Pire : le condensateur se vide sur le bus, mais cela ne suffit pas à créer une tension de plus de quelques millivolts dans celui-ci. Pas de quoi envoyer un 1 sur le bus ! Mais il y a une solution : amplifier la tension de quelques millivolts induite par la vidange du condensateur sur le bus, avec un circuit adapté. Les circuits de rafraichissement sur lecture et celui d'amplification sont souvent fusionnés en un seul circuit qui fait les deux, comme on le verra plus tard.
La conception du condensateur
modifierUne DRAM peut stocker plus de bits pour la même surface qu'une SRAM : un transistor couplé à un condensateur prend moins de place que 6 transistors. Un autre avantage est que les deux peuvent s'empiler l'un au-dessus de l'autre ce qu'on ne peut pas faire avec des transistors CMOS, ce qui améliore encore la densité des DRAM par rapport aux autres mémoires.
Au tout début, le transistor et le condensateur étaient placés l'un à côté de l'autre, sur le même plan. Le condensateur était alors appelé un condensateur planaire. Mais depuis les années 80, le condensateur et le transistor sont placés l'un au-dessus de l'autre, ou l'un en-dessous de l'autre. Si le condensateur est placé au-dessus du transistor, on parle de condensateur empilés (stacked capacitor). Mais si le condensateur est placé en-dessous du transistor, on parle de condensateur enterré (trench capacitor).
La taille d'une cellule de DRAM est souvent mesurée en utilisant une mesure appelée le . F est approximativement égal à la finesse de gravure, mais prenez garde à ne pas faire de comparaison avec la finesse de gravure des transistors CMOS. L'aire est l'unité de base pour comparer la taille des cellules DRAM, qui est un multiple de , et vaut donc : . Il existe trois types de DRAM en fonction de la place prise par la cellule de DRAM : les DRAM où la taille de la cellule mémoire est de 8 fois celle d'une unité de base, les DRAM où c'est seulement 6 fois, et les DRAM où c'est seulement 4 fois.
L'arrangement le plus simple est l'arrangement 4F2. Avec lui, les cellules de DRAM sont carrées. Il ne s'agit pas de l'arrangement le plus utilisé, car les cellules mémoires ne sont pas assez denses pour le moment. Le tout est illustré ci-dessous. La cellule de DRAM est le carré orange, les lignes de bits sont en vert et les lignes de mot en jaune. On voit que le transistor est situé au-dessus, que le transistor est composé des structures 6, 7 et 8 (source, grille et drain), avec une connexion directe à la ligne de mot sur la grille en 7. La ligne de bit est située tout en-dessous, elle est connectée au drain (le numéro 8).

L'arrangement actuel est cependant différent, car les cellules de DRAM ne sont pas carrées, mais rectangulaires. Dans larrangement 8F2, les cellules de DRAM sont deux fois plus longues que larges. Le tout donne ce qui est illustré dans le schéma suivant, où la cellule de DRAM est le rectangle orange, les lignes de bits sont en vert et les lignes de mot en jaune. La forme rectangulaire de la cellule de DRAM impose de placer les lignes de bit et de mot d'une manière bien précise. On s'attendrait que à ce que les lignes de mot soient deux fois plus éloignées que les lignes de bits (ou l'inverse), mais ce n'est pas le cas ! La distance est la même entre toutes les cellules. Pour cela, les cellules de DRAM ne sont pas alignées, mais décalées d'une ligne à l'autre.

Larrangement 6F2 utilise des cellules de mémoire 1.5 fois plus longues que large. Il est utilisé depuis les années 2010.
Les DRAM à base de transistors : 3T-DRAM et 2D-DRAM
modifierLes premières mémoires DRAM fabriquées commercialement n'utilisaient pas un condensateur comme réservoir à électrons, mais un transistor. Pour rappel, tout transistor MOS a un pseudo-condensateur caché entre la grille et la liaison source-drain. Pour comprendre ce qui se passe dans ce transistor de mémorisation, il savoir ce qu'il y a dans un transistor CMOS. À l'intérieur, on trouve une plaque en métal appelée l'armature, un bout de semi-conducteur entre la source et le drain, et un morceau d'isolant entre les deux. L'ensemble forme donc un condensateur, certes imparfait, qui porte le nom de capacité parasite du transistor. Suivant la tension qu'on envoie sur la grille, l'armature va se remplir d’électrons ou se vider, ce qui permet de stocker un bit : une grille pleine compte pour un 1, une grille vide compte pour un 0.

L'armature n'est pas parfaite et elle se vide régulièrement, d'où le fait que la mémoire obtenue soit une DRAM. Comme avec les autres DRAM, le bit stocké dans la capacité parasite doit être rafraîchit régulièrement. Avec cette organisation, lire un bit ne le détruit pas : on peut relire plusieurs fois un bit sans que celui-ci ne soit effacé. C'est une qualité que les DRAM modernes n'ont pas.
3T-DRAM
modifierLes premières DRAM de ce type utilisaient 3 transistors, d'où leur nom de 3T-DRAM. Le bit est mémorisé dans celui du milieu, indiqué en bleu sur le schéma suivant, les deux autres transistors servant pour les lectures et écritures.

Cette organisation donne donc, dans le cas le plus simple, une cellule avec quatre broches : deux broches de commandes, une pour la lecture et une pour l'écriture, ainsi qu'une entrée d'écriture et une sortie de lecture. Mais il est possible de fusionner certaines broches à une seule. Par exemple, on peut fusionner la broche de lecture avec celle d'écriture. De toute façon, les broches de commande diront si c'est une lecture ou une écriture qui doit être faite. De même, il est possible de fusionner les signaux de lecture et d'écriture, afin de faciliter le rafraîchissement de la mémoire. Avec une telle cellule, et en utilisant un contrôleur mémoire spécialement conçu, toute lecture réécrit automatiquement la cellule avec son contenu. Pour résumer, quatre cellules différentes sont possibles, selon qu'on fusionne ou non les broches de données et/ou les broches de commande. Ces quatre possibilités sont illustrées ci-dessous.

2T-DRAM
modifierUne amélioration des 3T-DRAM permet d'éliminer un transistor. Plus précisément, l'idée est de fusionner le transistor qui stocke le bit et celui qui connecte la cellule à la bitline de lecture. Le tout donne une DRAM fabriquée avec seulement deux transistors, d'où leur nom de 2T-DRAM. La cellule 2T-DRAM est illustrée ci-dessous.

Les cellules des mémoires EPROM, EEPROM et Flash
modifierDans le chapitre sur les généralités des mémoires, nous avons vu les différents types de ROM : ROM proprement dite (mask ROM), PROM, EPROM, EEPROM, et mémoire Flash. Ces différents types ne fonctionnent évidement pas de la même manière, non seulement au niveau du contrôleur mémoire, mais aussi des cellules mémoires. Les cellules mémoires des mask ROM et PROM sont un peu à part, dans le sens où elles n'ont pas vraiment de cellule mémoire proprement dit. C'est ce qui fait que le fonctionnement des mémoires PROM et ROM seront vues plus tard, dans un chapitre dédié. Dans ce qui va suivre, nous n'allons voir que les mémoires de type EPROM et leurs dérivés (EEPROM, Flash). Toutes fonctionnent avec le même type de cellule mémoire, les différences étant assez mineures.
Les transistors à grille flottante
modifierLes mémoires EPROM, EEPROM et Flash sont fabriquées avec des transistors à grille flottante (un par cellule mémoire). On peut les voir comme une sorte de mélange entre transistor et condensateur. Un transistor MOS normal est composé d'une grille métallique et d'une tranche de semi-conducteur, séparés par un isolant, ce qui en fait un mini-condensateur. Un transistor à grille flottante, quant à lui, possède deux armatures et deux couches d'isolant. La seconde armature est celle qui sert de condensateur, celle qui stocke un bit : il suffit de la remplir d’électrons pour stocker un 1, et la vider pour stocker un 0. La première armature sert de grille de contrôle, de signal qui autorise ou interdit le remplissage de la seconde armature.

Pour effacer une EPROM, on doit soumettre la mémoire à des ultra-violets : ceux-ci vont donner suffisamment d'énergie aux électrons coincés dans l'armature pour qu'ils puissent s'échapper. Pour les EEPROM et les mémoires Flash, ce remplissage ou vidage se fait en faisant passer des électrons entre la grille et le drain, et en plaçant une tension sur la grille : les électrons passeront alors dans l'armature à travers l'isolant.
Les différents types de cellules EEPROM/Flash : SLC/MLC/TLC/QLC
modifierSur la plupart des EEPROM, un transistor à grille flottante sert à mémoriser un bit. La tension contenue dans la seconde armature est alors divisée en deux intervalles : un pour le zéro, et un autre pour le un. De telles mémoires sont appelées des mémoires SLC (Single Level Cell). Mais d'autres EEPROM utilisent plus de deux intervalles, ce qui permet de stocker plusieurs bits par transistor : les mémoires MLC (Multi Level Cell) stockent 2 bits par cellules, les mémoires TLC (Triple Level Cell) stockent 3 bits, les mémoires QLC (Quad Level Cell) en stockent 4, etc.

Évidemment, utiliser un transistor pour stocker plusieurs bits aide beaucoup les mémoires non-SLC à obtenir une grande capacité, mais cela se fait au détriment des performances et de la durabilité de la cellule mémoire. Typiquement, plus une cellule de mémoire FLASH contient de bits, moins elle est performante en lecture et écriture, et plus elle tolère un faible nombre d'écritures/lectures avant de rendre l'âme. Pour les performances, cela s'explique par le fait que la lecture et l'écriture doivent être plus précises sur les mémoires MLC/TLC/QLC, elles doivent distinguer des niveaux de tensions assez proches, là où l'écart entre un 0 et un 1 est assez important sur les mémoires SLC.
La lecture et l'écriture des cellules des mémoires EEPROM
modifierSur les EEPROM, la reprogrammation et l'effacement de ces cellules demande de placer les bonnes tensions sur la grille, le drain et la source. Le procédé exact est en soit très simple, mais comprendre ce qui se passe exactement est une autre paire de manches. Les phénomènes qui se produisent dans le transistor à grille flottante lors d'une écriture ou d'un effacement sont très compliqués et font intervenir de sombres histoires de mécanique quantique. C’est la raison pour laquelle nous ne pouvons pas vraiment en dire plus.
 |
 |
Avec le chapitre précédent, on sait que les RAM et ROM contiennent des cellules mémoires, qui mémorisent chacune un bit. On pourrait croire que cela suffit à créer une mémoire, mais il n'en est rien. Il faut aussi des circuits pour gérer l'adressage, le sens de transfert (lecture ou écriture), et bien d'autres choses. Schématiquement, on peut subdiviser toute mémoire en plusieurs circuits principaux.
- La mémorisation des informations est prise en charge par le plan mémoire. Il est composé d'un regroupement de cellules mémoires, auxquelles on a ajouté quelques fils pour communiquer avec le bus.
- La gestion de l'adressage et de la communication avec le bus sont assurées par un circuit spécialisé : le contrôleur mémoire, composé d'un décodeur et de circuits de contrôle.
- L'interface avec le bus relie le plan mémoire au bus de données. C'est le plus souvent ici qu'est géré le sens de transfert des données, ainsi que tout ce qui se rapporte aux lectures et écritures.

Nous allons étudier le plan mémoire dans ce chapitre, le contrôleur mémoire et l'interface avec le bus seront vu dans les deux chapitres suivants. Cela peut paraitre bizarre de dédier un chapitre complet au plan mémoire, mais il y a de quoi. Celui-ci n'est pas qu'un simple amoncellement de cellules mémoire et de connexions vaguement organisées. On y trouve aussi des circuits électroniques aux noms barbares : amplificateur de tension, égaliseur de ligne de bit, circuits de pré-charge, etc. L'organisation des fils dans le plan mémoire est aussi intéressante à étudier, celle-ci étant bien plus complexe qu'on peut le croire.
Les fils et signaux reliés aux cellules
modifierLe plan mémoire est surtout composé de fils, sur lesquels on connecte des cellules mémoires. Rappelons que les cellules mémoires se présentent avec une interface simple, qui contient des broches pour le transfert des données et d'autres broches pour les commandes de lecture/écriture. Reste à voir comment toutes ses broches sont reliées aux différents bus et au contrôleur mémoire. Ce qui va nous amener à parler des lignes de bit et des signaux de sélection de ligne. Il faut préciser que la distinction entre broches de commande et de données est ici très importante : les broches de données sont connectées indirectement au bus, alors que les broches de commande sont reliées au contrôleur mémoire. Aussi, nous allons devoir parler des deux types de broches dans des sections séparées.
La connexion des broches de données : les lignes de bit
modifierAfin de simplifier l'exposé, nous allons étudier une mémoire série dont le byte est de 1 bit. Une telle mémoire est dite bit-adressable, c’est-à-dire que chaque bit de la mémoire a sa propre adresse. Nous étudierons le cas d'une mémoire quelconque plus loin, et ce pour une raison : on peut construire une mémoire quelconque en améliorant le plan mémoire d'une mémoire bit-adressable, d'une manière assez simple qui plus est. Parler de ces dernières est donc un bon marche-pied pour aboutir au cas général.
Le cas d'une mémoire bit-adressable
modifierUne mémoire bit-adressable est de loin celle qui a le plan mémoire le plus rudimentaire. Quand on sélectionne un bit, avec son adresse, son contenu va se retrouver sur le bus de données. Dit autrement, la cellule mémoire va se connecter sur ce fils pour y placer son contenu. On devine donc comment est organisé le plan mémoire : il est composé d'un fil directement relié au bus de donnée, sur lequel les cellules mémoire se connectent si besoin. Le plan mémoire se résume donc à un ensemble de cellules mémoires dont l'entrée/sortie est connectée à un unique fil. Ce fil s'appelle la ligne de bit (bitline en anglais). Une telle organisation se marie très bien avec les cellules de DRAM, qui disposent d'une unique broche d'entrée-sortie, par laquelle se font à la fois les lectures et écritures.

Il est possible d'utiliser une organisation avec deux lignes de bits, où la moitié des cellules est connectée à la première ligne, l'autre moitié à la seconde, avec une alternance entre cellules consécutives. Cela permet d'avoir moins de cellules mémoires connectées sur le même fil, ce qui améliore certains paramètres électriques des lignes de bit. Cette organisation porte le nom de ligne de bit repliée.

Pour ce qui est des cellules mémoire double port, les choses sont un petit peu compliquées. Normalement, les cellules mémoire double port demandent d'utiliser deux lignes de bit : une pour le port de lecture, une autre pour le port d'écriture. Le tout est illustré ci-dessous. Mais certaines mémoires font autrement et utilisent des cellules mémoires double port avec des lignes de bit unique ou repliées. Dans ce cas, l'entrée et la sortie de la cellule mémoire sont connectées à la ligne de bit, et la lecture ou l'écriture sont contrôlés par l'entrée Enable de la cellule mémoire (qui autorise ou interdit les écritures).

En réalité, peu de mémoires suivent actuellement des lignes de bit normales. Les mémoires assez évoluées utilisent deux lignes de bit par colonne ! La première transmet le bit lu et l'autre son inverse. La mémoire utilise la différence de tension entre ces deux fils pour représenter le bit lu ou à écrire. Un tel codage est appelé un codage différentiel. L'utilité d'un tel codage assez difficile à expliquer sans faire intervenir des connaissances en électricité, mais tout est une histoire de fiabilité et de résistance aux parasites électriques.
De telles lignes de bits différentielles sont le plus souvent associées à des cellules mémoires elles aussi différentielles, notamment les cellules de SRAM abordées au chapitre précédent. Mais elles se marient très mal avec les cellules de SRAM non-différentielles, ainsi qu'avec les cellules mémoire de DRAM, qui n'ont qu'une seule broche d'entrée-sortie non-différentielle. Mais quelques astuces permettent d'utiliser des lignes de bit différentielles sur ces mémoires. La plus connue est de loin l'utilisation de cellules factices (dummy cells), des cellules mémoires vides placées aux bouts des lignes de bit. Lors d'une lecture, ces cellules vides se remplissent avec l'inverse du bit à lire. La ligne de bit inverse (celle qui contient l'inverse du bit) est alors remplie avec le contenu de la cellule factice, ce qui donne bien un signal différentiel. Le bit inversé est fournit par une porte logique qui inverse la tension fournie par la cellule mémoire. Cette tension remplis alors la cellule factice, avec l'inverse du bit lu.

Certaines mémoires ont amélioré les lignes de bit différentielles en interchangeant leur place à chaque cellule mémoire. La ligne de bit change donc de côté à chaque passage d'une cellule mémoire. Cette organisation porte le nom de lignes de bit croisées.

Le cas d'une mémoire quelconque (avec byte > 1)
modifierAprès avoir vu le cas des mémoires bit-adressables, il est temps d'étudier les mémoires quelconques, celles où un byte contient plus que 1 bit. Surprenamment, ces mémoires peuvent être conçues en utilisant plusieurs mémoires bit-adressables. Par exemple, prenons une mémoire dont le byte fait deux bits (ce qui est rare, convenons-en). On peut l'émuler à partir de deux mémoires de 1 bit : la première stocke le bit de poids faible de chaque byte, alors que l'autre stock le bit de poids fort. Et on peut élargir le raisonnement pour des bytes de 3, 4, 8, 16 bits, et autres. Par exemple, pour une mémoire dont le byte fait 64 bits, il suffit de mettre en parallèle 64 mémoires de 1 bit.
Mais cette technique n'est pas appliquée à la lettre, car il y a moyen d'optimiser le tout. En effet, on ne va pas mettre effectivement plusieurs mémoires bit-adressables en parallèle, car seuls les plans mémoires doivent être dupliqués. Si on utilisait effectivement plusieurs mémoires, chacune aurait son propre plan mémoire, mais aussi son propre contrôleur mémoire, ses propres circuits de communication avec le bus, etc. Or, ces circuits sont en fait redondants dans le cas qui nous intéresse.
Prenons le cas du contrôleur mémoire, qui reçoit l'adresse à lire/écrire et qui envoie les signaux de commande au plan mémoire. Avec N mémoires en parallèle, N contrôleurs mémoire recevront l'adresse et généreront les N mêmes signaux, qui seront envoyés à N plans mémoire distincts. Au lieu de cela, il est préférable d'utiliser un seul contrôleur mémoire, mais de dupliquer les signaux de commande en autant N exemplaires (autant qu'il y a de plan mémoire). Et c'est ainsi que sont conçues les mémoires quelconques : pour un byte de N bits, il faut prendre N plans mémoires de 1 bit. Cela demande donc d'utiliser N lignes de bits, reliée convenablement aux cellules mémoires. Le résultat est un rectangle de cellules mémoires, où chaque colonne est traversée par une ligne de bit. Chaque ligne du tableau/rectangle, correspond à un byte, c'est-à-dire une case mémoire.
Là encore, chaque colonne peut utiliser des lignes de bits différentielles ou croisées.

La connexion des broches de commande : le transistor et le signal de sélection
modifierÉvidemment, les cellules mémoires ne doivent pas envoyer leur contenu sur la ligne de bit en permanence. En réalité, chaque cellule est connectée sur la ligne de bit selon les besoins. Les cellules correspondant au mot adressé se connectent sur la ligne de bit, alors que les autres ne doivent pas le faire. La connexion des cellules mémoire à la ligne de bit est réalisée par un interrupteur commandable, c’est-à-dire par un transistor appelé transistor de sélection. Quand la cellule mémoire est sélectionnée, le transistor se ferme, ce qui connecte la cellule mémoire à la ligne de bit. À l'inverse, quand une cellule mémoire n'est pas sélectionnée, le transistor de sélection se comporte comme un interrupteur ouvert : la cellule mémoire est déconnectée du bus.
La commande du transistor de sélection est effectuée par le contrôleur mémoire. Pour chaque ligne de bit, le contrôleur mémoire n'ouvre qu'un seul transistor à la fois (celui qui correspond à l'adresse voulue) et ferme tous les autres. La correspondance entre un transistor de sélection et l'adresse est réalisée dans le contrôleur mémoire, par des moyens que nous étudierons dans les prochains chapitres. Toujours est-il que le contrôleur mémoire génère, pour chaque octet, un bit qui dit si celui-ci est adressé ou non. Ce bit est appelé le signal de sélection. Le signal de sélection est envoyé à toutes les cellules mémoire qui correspondent au byte adressé. Vu que tous les bits d'un byte sont lus ou écrits en même temps, toutes les cellules correspondantes doivent être connectées à la ligne de bit en même temps, et donc tous les transistors de sélection associés doivent se fermer en même temps. En clair, le signal de sélection est partagé par toutes les cellules d'un même mot mémoire.

Le cas des lignes de bit simples et repliées
modifierVoyons comment les bitlines simples sont reliées aux cellules mémoires. Les mémoires 1T-DRAM n'ont qu'une seule broche entrée/sortie, sur laquelle on effectue à la fois les lectures et les écritures. Cela se marie très bien avec des bitlines simples, mais ça les rend incompatibles avec des bitlines différentielles. Le cas des DRAM à bitlines simples, avec une seule sortie, un seul transistor de sélection, est illustré ci-dessous.

La connexion des transistors de sélection pour des lignes de bit repliée n’est pas très différente de celle des lignes de bit simple. Elle est illustrée ci-dessous.

Le cas des lignes de bit différentielles
modifierLe cas des mémoires SRAM est de loin le plus simple à comprendre. Celles-ci utilisent toutes (ou presque) des bitlines différentielles, chose qui se marie très bien avec l'interface des cellules SRAM. Rappelons que celles-ci possèdent deux broches d'entrée-sortie pour les données : une broche Q sur laquelle on peut lire ou écrire un bit, et une broche complémentaire sur laquelle on envoie/récupère l'inverse du bit lu/écrit. À chaque broche correspond un transistor de sélection différent, qui sont intégrés dans la cellule de mémoire SRAM.

Le cas des cellules mémoires double port
modifierAprès avoir vu les cellules mémoire "normales" plus haut, il est temps de passer aux cellules mémoire de type double port (celles avec une sortie pour les lectures et une entrée pour les écritures). Elles contiennent deux transistors : un pour l'entrée d'écriture et un pour la sortie de lecture. Le contrôleur mémoire est relié directement aux transistors de sélection. Il doit générer à la fois les signaux d'autorisation de lecture que ceux pour l'écriture. Ces deux signaux peuvent être déduit du bit de sélection et du bit R/W, comme vu dans le chapitre précédent.

Sur les mémoires double port, le transistor de lecture est connecté à la ligne de bit de lecture, alors que celui pour l'écriture est relié à la ligne de bit d'écriture.

Pour les mémoires simple port, les deux transistors sont reliés à la même ligne de bit. Ils vont s'ouvrir ou se fermer selon les besoins, sous commande du contrôleur mémoire.

Les lignes de bit ont une capacité parasite qui pose de nombreux problèmes
modifier
Les lignes de bit ne sont pas des fils parfaits : non seulement ils ont une résistance électrique, mais ils se comportent aussi comme des condensateurs (dans une certaine mesure). Nous n'expliquerons pas dans la physique de ce phénomène, mais allons simplement admettre qu'un fil électrique se modélise bien en mettant une résistance R en série avec un condensateur : le circuit obtenu est un circuit RC. Le condensateur est appelé la capacité parasite de la ligne de bit.
Sur les mémoires DRAM, la capacité parasite est plus grande que la capacité de la cellule de DRAM. Une cellule de DRAM a une capacité de l'ordre de la dizaine de picoFarads, le condensateur stocke quelques millions d'électrons. La ligne de bit a une capacité parasite qui est au moins d'un ordre de grandeur plus grand. Pour les anciennes DRAMA de 16 Kibioctets, la capacité parasite était 3 à 6 fois plus grande. Pour les premières mémoires de 64 Kibioctets, elle est passée à 8-10 fois plus grande. Les mémoires modernes ont un ratio différent, mais qui est fortement influencé par un paquet d'optimisations, qu'on verra dans la suite.
La capacité parasite atténue le signal fournit par la cellule de DRAM/SRAM
modifierImaginons maintenant que l'on lise une cellule de DRAM. Lors d'une lecture, la cellule est connectée sur la ligne de bit et se vide dedans. Les électrons stockés dans la cellule se dispersent dans la ligne de bit, ce qui donne une certaine tension dans la ligne de bit. Et c'est cette tension qui code pour le 1/0 lu. Le truc, c'est que la tension de sortie dépend non seulement de la cellule de DRAM, mais aussi de la capacité parasite de la ligne de bit.
Pour rappel, la cellule DRAM stocke une certaine quantité d'électron, une certaine quantité de charges électriques, qui vaut : . Lors d'une lecture, la charge est répartie dans la la ligne de bit et la cellule DRAM. La tension de sortie se calcule approximativement en prenant la charge Q et en divisant par la capacité totale, ligne de bit inclue. La capacité totale de l'ensemble est la somme de la capacité de la cellule et de la capacité parasite : , ce qui donne :
Ce que l'équation dit, c'est que la tension stockée dans la cellule et la tension en sortie de la ligne de bit ne sont ps égales. La tension de la ligne de bit est bien plus faible, elle est grandement atténuée. Le rapport est généralement proche de 10, voire 50, ce qui fait qu'une tension de 5 volts dans la cellule DRAM se transforme en une tension de moins d'un Volt en sortie. Le seul moyen pour corriger ce problème est d'amplifier la tension de sortie. Le même problème a lieu pour les mémoires SRAM, bien que d'une manière un peu différente.
La solution pour cela est d'amplifier le signal présent sur la ligne de bit, afin d'obtenir un 0/1 valide en sortie. Divers optimisations visent aussi à réduire la capacité parasite de la ligne de bit.
La capacité parasite ralentit les lectures
modifierPlus haut, on a dit qu'une ligne de bit se modélise bien en mettant une résistance R en série avec une capacité parasite : le circuit obtenu est un circuit RC. Lorsque l'on change la tension en entrée d'un tel montage, la tension de sortie met un certain temps avant d'atteindre la valeur d'entrée. Ce qui est illustré dans les deux schémas ci-dessous, pour la charge (passage de 0 à 1) et la décharge (passage de 1 à 0). La variation est d'ailleurs exponentielle.

|

|

|
On estime qu'il faut un temps égal , avec R la valeur de la résistance et C celle du condensateur. En clair : la ligne de bit met un certain temps avant que la tension atteigne celle qui correspond au bit lu ou à écrire.
Pour résumer, selon la longueur des lignes de bits, la tension va prendre plus ou moins de temps pour s'établir dans la ligne de bit, ce qui impacte directement les performances de la mémoire. Diverses techniques ont étés inventées pour résoudre ce problème, la plus importante étant l'utilisation d'un circuit dit de pré-charge, que nous allons étudier vers la fin du chapitre.
L'amplificateur de tension
modifierPlus haut on a vu que la lecture d'une cellule de DRAM génère une tension très faible dans la ligne de bit, insuffisante pour coder un 1. La lecture crée à peine une tension de quelques millivolts dans la ligne de bit, pas plus. Mais il y a une solution : amplifier la tension de quelques millivolts induite par la vidange du condensateur sur le bus. Pour cela, il faut donc placer un dispositif capable d'amplifier cette tension, bien nommé amplificateur de lecture.

L’amplificateur utilisé n'est pas le même avec des lignes de bit simples et des lignes de bit différentielles. Dans le cas différentiel, l'amplificateur doit faire la différence entre les tensions sur les deux lignes de bit et traduire cela en un niveau logique. C'est l'amplificateur lui-même qui fait la conversion entre codage différentiel (sur deux lignes de bit) et codage binaire. Pour le distinguer des autres amplificateurs, il porte le nom d'amplificateur différentiel. L'amplificateur différentiel possède deux entrées, une pour chaque ligne de bit, et une sortie. Dans ce qui va suivre, les entrées seront notées et , la sortie sera notée . L’amplificateur différentiel fait la différence entre ces deux entrées et amplifie celle-ci. En clair :
Il faut noter qu'un amplificateur différentiel peut fonctionner aussi bien avec des lignes de bit différentielles qu'avec des lignes de bit simples. Avec des lignes de bit simples, il suffit de placer l'autre entrée à la masse, au 0 Volts, et de n'utiliser qu'une seule sortie.
Il existe de nombreuses manières de concevoir un amplificateur différentiel, mais nous n'allons aborder que les circuits les plus simples. Dans les grandes lignes, il existe deux types d'amplificateurs de lecture : ceux basés sur des bascules et ceux basés sur une paire différentielle. Bizarrement, vous verrez que les deux ont une certaine ressemblance avec les cellules de SRAM ! Il faut dire qu'une porte NON, fabriquée avec des transistors, est en réalité un petit amplificateur spécialisé, chose qui tient au fonctionnement de son circuit.
L'amplificateur de lecture à paire différentielle
modifierLe premier type d'amplificateur que nous allons voir est fabriqué à partir de transistors bipolaires. Pour rappel, un transistor bipolaire contient deux entrées, la base et l'émetteur, et une sortie appelée le collecteur. Il prend en entrée un courant sur sa base et fournit un courant amplifié sur l'émetteur. Pour cela, il faut fournir une source de courant sur le collecteur, obtenue en faisant une tension aux bornes d'une résistance.

La paire différentielle est composée de deux amplificateurs de ce type, reliés à un générateur de courant. La résistance est placée entre la tension d'alimentation et le transistor, alors que le générateur de courant est placé entre le transistor et la tension basse (la masse, ou l'opposé de la tension d'alimentation, selon le montage). Le circuit ci-contre illustre le circuit de la paire différentielle.

Précisons que la résistance mentionnée précédemment peut être remplacée par n'importe quel autre circuit, l'essentiel étant qu'il fournisse un courant pour alimenter l'émetteur. Il en est de même que le générateur de courant. Dans le cas le plus simple, une simple résistance suffit pour les deux. Mais ce n'est pas cette solution qui est utilisée dans les mémoires actuelles. En effet, intégrer des résistances est compliqué dans les circuits à semi-conducteurs modernes, et les mémoires RAM en sont. Aussi, les résistances sont généralement remplacées par des circuits équivalents, qui ont le même rôle ou qui peuvent remplacer une résistance dans le montage voulu.
Les deux résistances du haut sont remplacées chacunes par un miroir de courant, à savoir un circuit qui crée un courant constant sur une sortie et le recopie sur une seconde sortie. Il existe plusieurs manières de créer un tel miroir de courant avec des transistors MOS/CMOS, la plus simple étant illustrée ci-dessous (le miroir de courant est dans l'encadré bleu). On pourrait aborder le fonctionnement d'un tel circuit, pourquoi il fonctionne, mais nous n'en parlerons pas ici. Cela relèverait plus d'un cours d'électronique analogique, et demanderait de connaître en détail le fonctionnement d'un transistor, les équations associées, etc. L'avantage est que le miroir de courant fournit le même courant aux deux bitlines, il égalise les courants dans les deux bitlines.

L'amplificateur de lecture à verrou
modifierLe second type d'amplificateur de lecture est l'amplificateur à verrou. Il amplifie une différence de tension entre les deux lignes de bit d'une colonne différentielle. Les deux colonnes doivent être préchargées à Vdd/2, à savoir la moitié de la tension d'alimentation. La raison à cela deviendra évidente dans les explications qui vont suivre. Toujours est-il que ce circuit a besoin qu'un circuit dit de précharge s'occupe de placer la tension adéquate sur les lignes de bit, avant toute lecture ou écriture. Nous reparlerons de ce circuit de précharge dans les sections suivantes, vers la fin de ce chapitre. Cela peu paraître peu pédagogique, mais à notre décharge, sachez que le circuit de précharge et l'amplificateur de lecture sont intimement liés. Il est difficile de parler de l'un sans parler de l'autre et réciproquement. Pour le moment, tout ce que vous avez à retenir est qu'avant toute lecture, les lignes de bit sont chargées à Vdd/2, ce qui permet à l'amplificateur à verrou de fonctionner correctement.
Le circuit de l'amplificateur de lecture à verrou
modifierL'amplificateur à verrou est composé de deux portes NON reliées tête-bêche, comme dans une cellule de SRAM. Chaque ligne de bit est reliée à l'autre à travers une porte NON. Sauf que cette fois-ci, il n'y a pas toujours de transistors de sélection, ou alors ceux-ci sont placés autrement.

Le circuit complet est illustré ci-dessous, de même qu'une version plus détaillée avec des transistors CMOS. Du fait de son câblage, l'amplificateur à verrou a pour particularité d'avoir des broches d'entrées qui se confondent avec celles de sortie : l'entrée et la sortie pour une ligne de bit sont fusionnées en une seule broche. L'utilisation d'inverseurs explique intuitivement pourquoi il faut précharger les lignes de bit à Vdd/2 : cela place la tension dans la zone de sécurité des deux inverseurs, là où la tension ne correspond ni à un 0, ni à un 1. Le fonctionnement du circuit dépend donc du fonctionnement des transistors, qui servent alors d'amplificateurs.

On peut noter que cet amplificateur est parfois fabriqué avec des transistors bipolaires, qui consomment beaucoup de courant. Mais même avec des transistors MOS, il est préférable de réduire la consommation électrique du circuit, quand bien même ceux-ci consomment peu. Pour cela, on peut désactiver l’amplificateur quand on ne l'utilise pas. Pour cela, on entoure l'amplificateur avec des transistors qui le débranchent, le déconnectent si besoin.

Le fonctionnement de l'amplificateur à verrou
modifierExpliquer en détail le fonctionnement de l'amplificateur à verrou demanderait de faire de l'électronique assez poussée. Il nous faudrait détailler le fonctionnement d'un transistor quand il est utilisé en tant qu'amplificateur, donner des équations, et bien d'autres joyeusetés. À la place, je vais donner une explication très simplifiée, que certains pourraient considérer comme fausse (ce qui est vrai, dans une certaine mesure).
Avant toute chose, précisons que les seuils pour coder un 0 ou un 1 ne sont pas les mêmes entre l’entrée d'une porte NON et sa sortie. Ils sont beaucoup plus resserrés sur l'entrée, la marge de sécurité entre 1 et 0 étant plus faible. Un signal qui ne correspondrait pas à un 0 ou un 1 en sortie peut l'être en entrée.
Le fonctionnement du circuit ne peut s'expliquer correctement qu'à partir du rapport entre tension à l'entrée et tension de sortie d'une porte NON. Le schéma ci-dessous illustre cette relation. On voit que la porte logique amplifie le signal d'entrée en plus de l'inverser. Pour caricaturer, on peut décomposer cette caractéristique en trois parties : deux zones dites de saturation et une zone d'amplification. Dans la zone de saturation, la tension est approximativement égale à la tension maximale ou minimale, ce qui fait qu'elle code pour un 0 ou un 1. Entre ces deux zones extrêmes, la tension de sortie dépend linéairement de la tension d'entrée (si on omet l'inversion).

Quand on place deux portes NON l'une à la suite de l'autre, le résultat est un circuit amplificateur, dont la caractéristique est illustrée dans le second schéma. On voit que l'amplificateur amplifie la différence de tension entre VDD/2 et la tension d'entrée (sur la ligne de bit).

Si on regarde le circuit complet, on s’aperçoit que chaque ligne de bit est bouclée sur elle-même, à travers cet amplificateur. Cela fait boucler la sortie de l'amplificateur sur son entrée : la tension de base est alors amplifiée une fois, puis encore amplifiée, et ainsi de suite. Au final, les seuls points stables du montage sont la tension maximale ou la tension minimale, soit un 0 ou un 1, ou la tension VDD/2.
Ceci étant dit, on peut enfin comprendre le fonctionnement complet du circuit d'amplification. Commençons l'explication par la situation initiale : la ligne de bit est préchargée à VDD/2, et la cellule mémoire est déconnectée des lignes de bit. La ligne de bit est préchargée à VDD/2, l'amplificateur a sa sortie comme son entrée égales à VDD/2 et le circuit est parfaitement stable. Ensuite, la cellule mémoire à lire est connectée à la ligne de bit et la tension va passer au-dessous ou au-dessus de VDD/2. Nous allons supposer que celle-ci contenait un 1, ce qui fait que sa connexion entraîne une montée de la tension de la ligne de bit. La tension ne va cependant pas monter de beaucoup, mais seulement de quelques millivolts. Cette différence de tension va être amplifiée par les deux portes logiques, ce qui amplifie la différence de tension. Et rebelote : cette différence amplifiée est ré-amplifiée par le montage, et ainsi de suite jusqu’à ce que le circuit se stabilise soit à 0 soit à 1.

L'organisation du plan mémoire
modifierIl est important de réduire la capacité parasite et la résistance de la ligne de bit. Il se trouve que les deux sont proportionnelles à sa longueur : plus la ligne de bit est longue, plus sa résistance R sera élevée, plus sa capacité parasite le sera aussi. Réduire la taille des lignes de bit est donc une bonne solution. Les petites mémoires, avec peu de cellules sur une colonne, ont des lignes de bit plus petites et sont donc plus rapides. Cela explique en partie pourquoi les temps d'accès des mémoires varient selon la capacité, chose que nous avons abordé il y a quelques chapitres. De même, à capacité égale, il vaut mieux utiliser des bytes large, pour réduire la taille des colonnes. Mais d'autres optimisations du plan mémoire permettent d'obtenir des lignes de bit plus petites, à capacité et largeur de byte inchangée.
La technique du wire partitionning
modifierL première technique visant à réduire la longueur des lignes de bit s'appelle le wire partitionning. Elle consiste à couper une longue ligne de bits en plusieurs lignes de bits, reliées entre elles par des répéteurs, des circuits qui régénèrent la tension. La ligne de bits est donc découpée en segments, et la tension est recopiée d'un segment à l'autre.
Ainsi, si une cellule mémoire est reliée à un segment, la tension augmente dans ce fil assez rapidement, vu que le segment est très court. Et pendant ce temps, la tension se propage au segment suivant par l'intermédiaire du répéteur, la tension augmente rapidement vu que ce segment aussi est court. Et ainsi de suite, la tension se propage d'un segment à un autre.
L'avantage principal est que si l'on coupe une ligne de bit en N segments, le temps mis pour qu'un bit se propage sur une ligne de bit est divisé par N², le carré de N. Mais il y a un désavantage : la consommation d’électricité est plus importante. Les répéteurs consomment beaucoup de courant, sans compter que le fait que la tension monte plus vite a aussi un impact significatif. Il est possible de démontrer que la consommation d'énergie augmente exponentiellement avec N.
Pour éviter cela, l'idée est de désactiver les parties de la ligne de bit qui ne sont pas nécessaires pour effectuer une lecture. Pour cela, les répéteurs sont remplacés par des tampons trois-états, ce qui permet de déconnecter un segment. La mémoire a juste à désactiver les segments de la ligne de bit qui sont situés au-delà de la cellule mémoire à lire/écrire, et de n'activer que ceux qui sont entre la cellule mémoire et le bus de données.

Nous verrons que cette technique n'est pas utilisée que sur les mémoires RAM, mais est aussi utilisée sur les mémoires associatives, ou sur certaines mémoires caches. Nous en reparlerons aussi dans le chapitre sur les processeurs à exécution dans le désordre, qui incorporent des pseudo-mémoires spécialisées qui font grand usage de cette technique.
L'agencement en colonne de donnée ouvertes
modifierLa première optimisation consiste à placer l'amplificateur de lecture au milieu du plan mémoire, et non au bout. En faisant ainsi, on doit couper la ligne de bit en deux, chaque moitié étant placée d'un côté ou de l'autre de l’amplificateur. La colonne contient ainsi deux lignes de bits séparées, chacune ayant une longueur réduite de moitié. Mais cette organisation complexifie l'amplificateur au milieu de la mémoire. Et le nombre de fils qui doivent passer par le milieu de la RAM est important, rendant le câblage compliqué. De plus, les perturbations électromagnétiques ne touchent pas de la même manière chaque côté de la mémoire et l'amplificateur peut donner des résultats problématiques à cause d'elles.
L'amplificateur de lecture est un amplificateur différentiel. Lors de l'accès à une cellule mémoire, la cellule sélectionnée se trouve sur une moitié de la ligne de bit. La ligne de bit en question est comparée à l'autre moitié de la ligne de bit, sur laquelle aucune cellule ne sera connectée. Cette organisation est dite en ligne de bits ouvertes.

Pour donner un exemple, voici l'intérieur d'une mémoire DRAM de 16 kibioctets, d'origine soviétique. La ligne du milieu regroupe l'amplificateur de lecture et le multiplexeur des colonnes.

Il est aussi possible de répartir les amplificateurs de tension autrement. On peut mélanger les organisations en colonne de données ouvertes et "normales", en mettant les amplificateurs à la fois au milieu de la RAM et sur les bords. Une moitié des amplificateurs est placée au milieu du plan mémoire, l'autre moitié est placée sur les bords. On alterne les lignes de bits connectée entre amplificateurs selon qu’ils sont sur les bords ou au milieu. L'organisation est illustrée ci-dessous.

Pour donner un exemple, voici l'intérieur d'une mémoire DRAM de 1 mébioctet, de marque Sanyo. Les deux lignes sont les amplificateur de lecture. On voit qu'ils sont situés de manière à réduire au maximum la longueur des lignes de bit.

La pré-charge des lignes de bit
modifier
Pour réduire le temps de lecture/écriture, une autre solution, beaucoup plus ingénieuse, ne demande pas de modifier la longueur des lignes de bit. À la place, on rend leur charge plus rapide en les pré-chargeant. Sans pré-charge, la ligne de bit est à 0 Volts avant la lecture et la lecture altère cette tension, que ce soit pour la laisser à 0 (lecture d'un 0), ou pour la faire monter à la tension maximale Vdd (lecture d'un 1). Le temps de réaction de la ligne de bit dépend alors du temps qu'il faut pour la faire monter à Vdd. Avec la pré-charge, la ligne de bit est chargée avant la lecture, de manière à la mettre à la moitié de Vdd. La lecture du bit fera descendre celle-ci à 0 (lecture d'un 0) ou la faire grimper à Vdd (lecture d'un 1). Le temps de charge ou de décharge est alors beaucoup plus faible, vu qu'on part du milieu.
- Il faut noter que la pré-charge à Vdd/2 est un cas certes simple à comprendre, mais qui n'a pas valeur de généralité. Certaines mémoires pré-chargent leurs lignes de bit à une autre valeur, qui peut être Vdd, à 60% de celui-ci, ou une autre valeur. En fait, tout dépend de la technologie utilisée. Par exemple, Les mémoires de type CMOS pré-chargent à Vdd/2, alors que les mémoires TTL, NMOS ou PMOS pré-chargent à une autre valeur (le plus souvent Vdd).
On peut penser qu'il faudra deux fois moins de temps, mais la réalité est plus complexe (regardez les graphes de charge/décharge situés plus haut). De plus, il faut ajouter le temps mis pour précharger la ligne de bit, qui est à ajouter au temps de lecture proprement dit. Sur la plupart des mémoires, la pré-charge n'est pas problématique. Il faut dire qu'il est rare que la mémoire soit accédé en permanence et il y a toujours quelques temps morts pour pré-charger la ligne de bit. On verra que c'est notamment le cas sur les mémoires DRAM synchrones modernes, comme les SDRAM et les mémoires DDR. Mais passons...
Les circuits de précharge
modifierLa pré-charge d'une ligne de bit se fait assez facilement : il suffit de connecter la ligne de bit à une source de tension qui a la valeur adéquate. Par exemple, une mémoire qui se pré-charge à Vdd a juste à relier la ligne de bit à la tension d'alimentation. Mais attention : cette connexion doit disparaître quand on lit ou écrit un bit dans les cellules mémoire. Sans cela, le bit envoyé sur la ligne de bit sera perturbé par la tension ajoutée. Il faut donc déconnecter la ligne de bit de la source d'alimentation lors d'une lecture écriture. On devine rapidement que le circuit de pré-charge est composé d'un simple interrupteur commandable, placé entre la tension d'alimentation (Vdd ou Vdd/2) et la ligne de bit. Le contrôleur mémoire commande cet interrupteur pour précharger la ligne de bit ou stopper la pré-charge lors d'un accès mémoire. Si un seul transistor suffit pour les lignes de bit simples, deux sont nécessaires pour les lignes de bit différentielles ou croisées. Ils doivent être ouvert et fermés en même temps, ce qui fait qu'ils sont commandés par un même signal.

L'égaliseur de tension
modifierPour les lignes de bit différentielles et croisées, il se peut que les deux lignes de bit complémentaires n'aient pas tout à fait la même tension suite à la pré-charge. Pour éviter cela, il est préférable d'ajouter un circuit d'égalisation qui égalise la tension sur les deux lignes. Celui-ci est assez simple : c'est un interrupteur commandable qui connecte les deux lignes de bit lors de la pré-charge. Là encore, un simple transistor suffit. L'égalisation et la pré-charge ayant lieu en même temps, ce transistor est commandé par le même signal que celui qui active le circuit de précharge. Le circuit complet, qui fait à la fois pré-charge et égalisation des tensions, est représenté ci-dessous.

La gestion de l'adressage et de la communication avec le bus sont assurées par un circuit spécialisé : le contrôleur mémoire. Une mémoire adressable est ainsi composée :
- d'un plan mémoire ;
- du contrôleur mémoire, composé d'un décodeur et de circuits de contrôle ;
- et des connexions avec le bus.

Nous avons vu le fonctionnement du plan mémoire dans les chapitres précédents. Les circuits qui font l'interface entre le bus et la mémoire ne sont pas différents des circuits qui relient n'importe quel composant électronique à un bus, aussi ceux-ci seront vus dans le chapitre sur les bus. Bref, il est maintenant temps de voir comment fonctionne un contrôleur mémoire. Je parlerai du fonctionnement des mémoires multiports dans le chapitre suivant.
Les mémoires à adressage linéaire
modifierPour commencer, nous allons voir les mémoires à adressage linéaire. Sur ces mémoires, le plan mémoire est un tableau rectangulaire de cellules mémoires, et toutes les cellules mémoires d'une ligne appartiennent à une même case mémoire. Les cellules mémoire d'une même colonne sont connectées à la même bitline. Avec cette organisation, la cellule mémoire stockant le énième bit du contenu d'une case mémoire (le bit de poids i) est reliée au énième fil du bus. Rappelons que chaque ligne est reliée à un signal de sélection de ligne Row Line, qui permet de connecter les cellules mémoires du byte adressé à la bitline.

Le rôle du contrôleur mémoire est de déduire quelle entrée Row Line mettre à un à partir de l'adresse envoyée sur le bus d'adresse. Pour cela, le contrôleur mémoire doit répondre à plusieurs contraintes :
- il reçoit des adresses codées sur n bits : ce contrôleur a donc n entrées ;
- l'adresse de n bits peut adresser 2n bytes : notre contrôleur mémoire doit donc posséder 2^n sorties ;
- la sortie numéro N est reliée au N-iéme signal Row Line (et donc à la N-iéme case mémoire) ;
- on ne doit sélectionner qu'une seule case mémoire à la fois : une seule sortie devra être placée à 1 ;
- et enfin, deux adresses différentes devront sélectionner des cases mémoires différentes : la sortie de notre contrôleur qui sera mise à 1 sera différente pour deux adresses différentes placées sur son entrée.
Le seul composant électronique qui répond à ce cahier des charges est le décodeur, ce qui fait que le contrôleur mémoire se résume à un simple décodeur, avec quelques circuits pour gérer le sens de transfert (lecture ou écriture), et la détection/correction d'erreur. Ce genre d'organisation s'appelle l'adressage linéaire.

Les mémoires à adressage ligne-colonne
modifierSur des mémoires ayant une grande capacité, l'adressage linéaire n'est plus vraiment pratique. Si le nombre de sorties est trop grand, utiliser un seul décodeur utilise trop de portes logiques et a un temps de propagation au fraises, ce qui le rend impraticable. Pour éviter cela, certaines mémoires organisent leur plan mémoire autrement, sous la forme d'un tableau découpé en lignes et en colonnes, avec une case mémoire à l'intersection entre une colonne et une ligne. Ce type de mémoire s'appelle des mémoires à adressage ligne-colonne, ou encore des mémoires à adressage bidimensionnel.

Adresser la mémoire demande de sélectionner la ligne voulue, et de sélectionner la colonne à l'intérieur de la ligne. Pour cela, chaque ligne a un numéro, une adresse de ligne, et il en est de même pour les colonnes qui sont adressées par un numéro de colonne, une adresse de colonne. L'adresse mémoire complète n'est autre que la concaténation de l'adresse de ligne avec l'adresse de colonne. L'avantage est que l'adresse mémoire peut être envoyée en deux fois à la mémoire : on envoie d'abord la ligne, puis la colonne. Ce n'est cependant pas systématique, et on peut parfaitement envoyer adresse de ligne et de colonne en même temps, en une seule adresse. Envoyer l'adresse en deux fois permet d'économiser des fils sur le bus d'adresse, mais nécessite de mémoriser l'adresse de ligne dans un registre. Lorsque l'on envoie l'adresse de la colonne sur le bus d'adresse, la mémoire doit avoir mémorisé l'adresse de ligne envoyée au cycle précédent. Pour cela, la mémoire incorpore deux registres pour mémoriser la ligne et la colonne. Il faut aussi ajouter de quoi aiguiller le contenu du bus d'adresse vers le bon registre, en utilisant un démultiplexeur.

Du point de vue du contrôleur mémoire, sélectionner une ligne est facile : on utilise un décodeur. Mais la méthode utilisée pour sélectionner la colonne dépend de la mémoire utilisée. On peut utiliser un multiplexeur ou un décodeur, suivant l'organisation interne de la mémoire. L'avantage est qu'utiliser deux décodeurs assez petits prend moins de circuits qu'un seul gros décodeur. Idem pour l'usage d'un décodeur assez petit avec un multiplexeur lui-même petit, comparé à un seul gros décodeur.
Les avantages de cette organisation sont nombreux : possibilité de décoder une ligne en même temps qu'une colonne, possibilité d'envoyer l'adresse en deux fois, consommation moindre de portes logiques, etc.
Les mémoires à tampon de ligne
modifierLes mémoires à ligne-colonne les plus simples à comprendre sont les mémoires à tampon de ligne, aussi appelées mémoires à Row Buffer. Sur celles-ci, l'accès à une ligne copie celle-ci dans un registre interne, appelé le tampon de ligne (en anglais, Row Buffer). Puis, un circuit, généralement un multiplexeur, sélectionne la colonne adéquate dans ce tampon de ligne.

Une telle mémoire est composée de trois composants : une mémoire qui mémorise les lignes, et un multiplexeur qui sélectionne la colonne, avec un tampon de ligne entre les deux. Avant le tampon de ligne, se trouve une mémoire normale, à adressage linéaire, dont chaque case mémoire est une ligne. Dit autrement, une mémoire à tampon de ligne émule une mémoire de N bytes à partir d'une mémoire contenant B fois moins de bytes, mais dont chacun des bytes seront B fois plus gros.

Le tampon de ligne s'intercale entre la mémoire à adressage linéaire et la sélection des colonnes. Chaque accès lit ou écrit un « super-byte » de la mémoire interne, et le copie dans le tampon de ligne? Puis, un multiplexeur sélectionner le byte dans celui-ci.

Les avantages de cette organisation sont nombreux. Le plus simple à comprendre est que le rafraichissement est beaucoup plus rapide et plus simple. Rafraichir la mémoire se fait ligne par ligne, et non byte par byte. Autre avantage : en concevant correctement la mémoire, il est possible d'améliorer les performances lors de l'accès à des données proches en mémoire. Par contre, cette organisation consomme beaucoup d'énergie. Il faut dire que pour chaque lecture d'un byte dans notre mémoire, on doit charger une ligne complète dans le tampon de ligne.
L'avantage principal est que l'accès à des données proches, localisées sur la même ligne, est fortement accéléré sur ces mémoires. Quand une ligne est chargée dans le tampon de ligne, elle reste dans ce tampon durant plusieurs accès consécutifs. Et les accès ultérieurs peuvent utiliser cette possibilité. Nous allons supposer qu'une ligne a été copiée dans le tampon de ligne, lors d'un accès précédent. Deux cas sont alors possibles.
- Premier cas : on accède à une donnée située dans une ligne différente : c'est un défaut de tampon de ligne. Dans ce cas, il faut vider le tampon de ligne, en plus de sélectionner la ligne adéquate et la colonne. L'accès mémoire n'est alors pas différent de ce qu'on aurait sur une mémoire sans tampon de ligne, avec cependant un temps d'accès un peu plus élevé.
- Second cas : la donnée à lire/écrire est dans la ligne chargée dans le tampon de ligne. Ce genre de situation s'appelle un succès de tampon de ligne. Dans ce cas, la ligne entière a été recopiée dans le tampon de ligne et on n'a pas à la sélectionner : on doit juste changer de colonne. Le temps nécessaire pour accéder à notre donnée est donc égal au temps nécessaire pour sélectionner une colonne, auquel il faut parfois ajouter le temps nécessaire entre deux sélections de deux colonnes différentes.
Les accès consécutifs à une même ligne sont assez fréquents. Ils surviennent lorsque l'on doit accéder à des données proches les unes des autres en mémoire, ce qui est très fréquent. La majorité des programmes informatiques accèdent à des données proches en mémoire : c'est le principe de localité spatiale vu dans les chapitres précédents. Les mémoires à tampon de ligne profitent au maximum de cet effet de localité spatiale, ce qui leur donne un boost de performance assez important. Dans les faits, la mémoire RAM de votre ordinateur personnel est une mémoire à tampon de ligne. Toutes les mémoires RAM des ordinateurs grand public sont des mémoires à tampon de ligne, et ce depuis plusieurs décennies.
L'adressage par coïncidence
modifierAvec l'adressage par coïncidence, la sélection de la ligne se fait comme pour toutes les autres mémoire : grâce à un signal row line qui est envoyé à toutes les cases mémoire d'une même ligne. Les mémoires à adressages par coïncidence font la même chose mais pour les colonnes. Toutes les cases mémoires d'une colonne sont reliées à un autre fil, le column line. Une case mémoire est sélectionnée quand ces row lines et la column line sont tous les deux mis à 1 : il suffit d'envoyer ces deux signaux aux entrées d'une porte ET pour obtenir le signal d'autorisation de lecture/écriture pour une cellule. On utilise donc deux décodeurs : un pour sélectionner la ligne et un autre pour sélectionner la colonne.

L'avantage de cette organisation est que l'on a pas à recopier une ligne complète dans un tampon de ligne pour faire un accès mémoire. Mais c'est aussi un défaut car cela ne permet pas de profiter des diverses optimisations pour des accès à une même ligne. Ce qui explique que ces mémoires ne sont presque pas utilisées de nos jours, du moins pas dans les ordinateurs personnels.
Les mémoires à adresse tridimensionnel : les mémoires par blocs
modifierl'adressage par coïncidence peut être amélioré en rajoutant un troisième niveau de subdivision : chaque ligne est découpée en sous-lignes, qui contiennent plusieurs colonnes. On obtient alors des mémoires par blocs, ou divided word line structures. Chaque ligne est donc découpée en N lignes, numérotées de 0 à N-1. Les sous-lignes qui ont le même numéro sont en quelque sorte alignées verticalement, et sont reliées aux mêmes bitlines : celles-ci forment ce qu'on appelle un bloc. Chacun de ces blocs contient un plan mémoire, un multiplexeur, et éventuellement des amplificateurs de lecture et des circuits d'écriture.

Tous les blocs de la mémoire sont reliés au décodeur d'adresse de ligne. Mais malgré tout, on ne peut pas accéder à plusieurs blocs à la fois : seul un bloc est actif lors d'une lecture ou d'une écriture. Pour cela, un circuit de sélection du bloc se charge d'activer ou de désactiver les blocs inutilisés lors d'une lecture ou écriture. L'adresse d'une sous-ligne bien précise se fait par coïncidence entre une ligne, et un bloc.

La ligne complète est activée par un signal wordline, généré par un décodeur de ligne. Les blocs sont activés individuellement par un signal nommé blocline, produit par un décodeur de bloc : ce décodeur prend en entrée l'adresse de bloc, et génère le signal blocline pour chaque bloc. Ensuite, une fois la sous-ligne activée, il faut encore sélectionner la colonne à l'intérieur de la sous-ligne sélectionnée, ce qui demande un troisième décodeur. L'adresse mémoire est évidemment coupée en trois : une adresse de ligne, une adresse de sous-ligne, et une adresse de colonne.
Annexe : l'attaque rowhammer
modifierVous connaissez maintenant comment fonctionnent les cellules mémoires et le plan mémoire, ce qui fait que vous avez les armes nécessaires pour aborder des sujets assez originaux. Profitons-en pour aborder une faille de sécurité présente dans la plupart des mémoires DRAM actuelles : l'attaque row hammer. Vous avez bien entendu : il s'agit d'une faille de sécurité matérielle, qui implique les mémoires RAM, qui plus est. Voilà qui est bien étrange. D'ordinaire, quand on parle de sécurité informatique, on parle surtout de failles logicielles ou de problèmes d'interface chaise-clavier. La plupart des attaques informatiques sont des attaques d’ingénierie sociale où on profite de failles humaines pour obtenir un mot de passe ou toute autre information confidentielle, suivies par les failles logicielles, les virus, malwares et autres méthodes purement logicielles. Mais certaines failles de sécurités sont purement matérielles et profitent de bugs présents dans le matériel pour fonctionner. Car oui, les processeurs, mémoires, bus et périphériques peuvent avoir des bugs matériels qui sont généralement bénins, mais que des virus, logiciels ou autres malware peuvent exploiter pour commettre leur méfaits.

L'attaque row hammer, aussi appelée attaque par martèlement de mémoire, utilise un bug de conception des mémoires DRAM. Le bug en question tient dans le fait que les cellules mémoires ne sont pas parfaites et que leur charge électrique tend à fuir. Ces fuites de courant se dispersent autour de la cellule mémoire et tendent à affecter les cellules mémoires voisines. En temps normal, cela ne pose aucun problème : les fuites sont petites et l'interaction électrique est limitée. Cependant, des hackers ont réussit à exploiter ce comportement pour modifier le contenu d'une cellule mémoire sans y accèder. En accédant d'une manière bien précise à une ligne de la mémoire, on peut garantir que les fuites de courant deviennent signifiantes, suffisamment pour recopier le contenu d'une ligne mémoire dans les lignes mémoires voisines. Pour cela, il faut accéder un très grand nombre de fois à la cellule mémoire en question, ce qui explique pourquoi cette attaque s'appelle le martèlement de mémoire. Une autre méthode, plus fiable, est d’accéder à deux lignes de mémoires, qui prennent en sandwich la ligne mémoire à altérer. On accède successivement à la première, puis la seconde, avant de reprendre au début, et cela un très grand nombre de fois par secondes.
Modifier plusieurs bytes sans y accéder, mais en accédant à leurs voisins est une faille exploitable par les pirates informatiques. L'intérêt est de contourner les protections mémoires liées au système d'exploitation. Sur les systèmes d'exploitation modernes, chaque programme se voit attribuer certaines portions de la mémoire, auxquelles il est le seul à pouvoir accéder. Des mécanismes de protection mémoire intégré dans le processeur permettent d'isoler la mémoire de chaque programme, comme nous le verrons dans le chapitre sur la mémoire virtuelle. Mais avec row hammer, les accès à un byte attribué à un programme peuvent déborder sur les bytes d'un autre programme, avec des conséquences assez variables. Par exemple, un virus présent en mémoire pourrait interagir avec le byte qui mémorise un mot de passe ou une clé de sécurité RSA, ou toute donnée confidentielle. Il pourrait récupérer cette information, ou alors la modifier pour la remplacer par une valeur connue et l'attaquant.
La faille row hammer est d'autant plus simple que la physique des cellules mémoire est médiocre. Les progrès de la miniaturisation rendent cette attaque de plus en plus facilement exploitable, les fuites étant d'autant plus importantes que les cellules mémoires sont petites. Mais exploiter cette attaque est compliqué, car il faut savoir à quelle adresse se situe a donnée à altérer, sans compter qu'il faut avoir des informations sur l'adresse des cellules voisines. Rappelons que la répartition physique des adresses/bytes dépend de comment la mémoire est organisée en interne, avec des banques, rangées et autres. Deux adresses consécutives ne sont pas forcément voisines sur la barrette de mémoire et l relation entre deux adresses de cellules mémoires voisines n'est pas connue avec certitude tant elle varie d'un système mémoire à l'autre.
Les solutions pour mitiger l'attaque row hammer sont assez limitées. Une première solution est d'utiliser les techniques de correction et de détection d'erreur comme l'ECC, mais là l'effet est limité. Une autre solution est de rafraichir la mémoire plus fréquemment, mais cela a un effet assez limité, sans compter que cela a un impact sur les performance et la consommation d'énergie de la RAM. Les concepteurs de matériel ont dû inventer des techniques spécialisées, comme le pseudo target row refresh d'Intel ou le target row refresh des mémoires LPDDR4. Ces techniques consistent, pour simplifier, à détecter quand une ligne mémoire est accédée très souvent, à rafraichir les lignes de mémoire voisines assez régulièrement. L'effet sur les performances est limité, mais cela demande d'intégrer cette technique dans le contrôleur mémoire externe/interne.
Les mémoires vues au chapitre précédent sont les mémoires les plus simples qui soient. Mais ces mémoires peuvent se voir ajouter quelques améliorations pas franchement négligeables, afin d'augmenter leur rapidité, ou de diminuer leur consommation énergétique. Dans ce chapitre, nous allons voir quelles sont ces améliorations les plus courantes.
L'accès en rafale
modifierL'accès en rafale est un accès mémoire qui permet de lire ou écrire plusieurs adresses consécutives en envoyant une seule adresse, en un seul accès mémoire. On envoie la première adresse et la mémoire s'occupe de lire/écrire les adresses suivantes les unes après les autres, automatiquement. L'accès en rafale fait que l'on n'a pas à envoyer plusieurs adresses, mais une seule, ce qui libère le processeur durant quelques cycles et lui économise du travail. Un accès de ce type est appelé un accès en rafale, ou encore une rafale.

Le nombre d'adresses consécutives lues lors d'une rafale est généralement fixé une fois pour toutes et toutes les rafales ont la même taille. Par exemple, sur les mémoires asynchrones EDO-RAM, les rafales lisent/écrivent 4 octets consécutifs automatiquement, au rythme d'un par cycle d’horloge. D'autres mémoires gèrent plusieurs tailles pré-fixées, que l'on peut choisir au besoin. Par exemple, on peut choisir entre une rafale de 4 octets consécutifs, 8 octets consécutifs, ou 16 octets consécutifs. C'est le cas sur les mémoires SDRAM, où on peut choisir s'il faut lire 1, 2, 4, ou 8 octets en rafale.
L'accès en rafale séquentiel, linéaire et entrelacé
modifierIl existe plusieurs types d'accès en rafale : l'accès entrelacé, l'accès linéaire et l'accès séquentiel.
Le mode séquentiel est le mode rafale normal : on accède à des octets consécutifs les uns après les autres. Peu importe l'adresse à laquelle on commence, on lit les N adresses suivantes lors de l'accès en rafale. Sur certaines mémoires, la rafale peut commencer n'importe où. Mais sur d'autres, le mode séquentiel est parfois restreint et ne peut démarrer qu'à certaines adresses bien précises. Par exemple, pour une mémoire dont le mot mémoire fait 4 octets bits, avec une rafale de 8 mots, on ne peut démarrer les rafales qu'à des adresses multiples de 8 * 4 = 64 octets. Il s'agit d'une contrainte dite d'alignement de rafale. Pour le dire autrement, la mémoire est découpées en blocs qui font la même taille qu'une rafale, et une rafale ne peut transmettre qu'on bloc complet en partant du début.
Le mode linéaire est un petit peu plus compliqué. Il lit un bloc de taille fixe, qui est aligné en mémoire, comme expliqué dans le paragraphe précédent. Mais il peut commencer l'accès en rafale n'importe où dans le bloc, tout en lisant/écrivant la totalité du bloc. Par exemple, prenons une rafale de 8 octets, dont les bytes ont les adresses 0, 1, 2, 3, 4, 5, 6, et 7. Un accès séquentiel aligné doit commencer à l'adresse 0. Mais une rafale en mode linéaire peut très bien commencer par lire ou écrire au byte 3, par exemple. Dans ce cas, on commence par lire le byte numéroté 3, puis le 4, le 5, le 6 et le 7. Puis, l'accès reprend au bloc 0, avant d'accèder aux blocs 1, 2 et 3. En clair, la mémoire est découpée en bloc de 8 bytes consécutifs et l'accès lit un bloc complet. Si la première adresse lue commence à la première adresse du bloc, l'accès est identique à l'accès séquentiel. Mais si l'adresse de départ de la rafale est dans le bloc, la lecture commence à cette adresse, puis reprend au début du bloc une fois arrivé au bout.
Le mode entrelacé utilise un ordre différent. Avec ce mode de rafale, le contrôleur mémoire effectue un XOR bit à bit entre un compteur (incrémenté à chaque accès) et l'adresse de départ pour calculer la prochaine adresse de la rafale.
Pour comprendre un petit peu mieux ces notions, nous allons prendre l'exemple du mode rafale sur les processeurs x86 présents dans nos ordinateurs actuels. Sur ces processeurs, le mode rafale permet des rafales de 4 octets, alignés sur en mémoire. Les rafales peuvent se faire en mode linéaire ou entrelacé, mais il n'y a pas de mode séquentiel. Vu que les rafales se font en 4 octets dans ces deux modes, la rafale gère les deux derniers bits de l'adresse, qui sont modifiés automatiquement par la rafale. Dans ce qui suit, nous allons indiquer les deux bits de poids faible et montrer comment ils évoluent lors d'une rafale. Le reste de l'adresse ne sera pas montré, car il pourrait être n'importe quoi.
Voici ce que cela donne en mode linéaire :
| 1er accès | 2nd accès | 3ème accès | 4ème accès | |
|---|---|---|---|---|
| Exemple 1 | 00 | 01 | 10 | 11 |
| Exemple 2 | 01 | 10 | 11 | 00 |
| Exemple 3 | 10 | 11 | 00 | 01 |
| Exemple 4 | 11 | 00 | 01 | 10 |
Voici ce que cela donne en mode entrelacé :
| 1er accès | 2nd accès | 3ème accès | 4ème accès | |
|---|---|---|---|---|
| Exemple 1 | 00 | 01 | 10 | 11 |
| Exemple 2 | 01 | 00 | 11 | 10 |
| Exemple 3 | 10 | 11 | 00 | 01 |
| Exemple 4 | 11 | 10 | 01 | 00 |
L'implémentation des accès en rafale
modifierAu niveau de la microarchitecture, l'accès en rafale s'implémente en ajoutant un compteur dans la mémoire. L'adresse de départ est mémorisée dans un registre en aval de la mémoire. Pour gérer les accès en rafale séquentiels, il suffit que le registre qui stocke l'adresse mémoire à lire/écrire soit transformé en compteur.
Pour les accès en rafale linéaire, le compteur est séparé de ce registre. Ce compteur est initialisé à 0 lors de la transmission d'une adresse, mais est incrémenté à chaque cycle sinon. L'adresse à lire/écrire à chaque cycle se calcule en additionnant l'adresse de départ, mémorisée dans le registre, au contenu du compteur. Pour les accès en rafale entrelacés, c'est la même chose, sauf que l'opération effectuée entre l'adresse de départ et le compteur n'est pas une addition, mais une opération XOR bit à bit.

Les banques et rangées
modifierSur certaines puces mémoires, un seul boitier peut contenir plusieurs mémoires indépendantes regroupées pour former une mémoire unique plus grosse. Chaque sous-mémoire indépendante est appelée une banque, ou encore un banc mémoire. La mémoire obtenue par combinaison de plusieurs banques est appelée une mémoire multi-banques. Cette technique peut servir à améliorer les performances, la consommation d'énergie, et j'en passe. Par exemple, cela permet de faciliter le rafraichissement d'une mémoire DRAM : on peut rafraichir chaque sous-mémoire en parallèle, indépendamment des autres. Mais cette technique est principalement utilisée pour doubler le nombre d'adresses, doubler la taille d'un mot mémoire, ou faire les deux.

L'arrangement horizontal
modifierL'arrangement horizontal utilise plusieurs banques pour augmenter la taille d'un mot mémoire sans changer le nombre d'adresses. Chaque banc mémoire contient une partie du mot mémoire final. Avec cette organisation, on accède à tous les bancs en parallèle à chaque accès, avec la même adresse.

Pour l'exemple, les barrettes de mémoires SDRAM ou DDR-RAM des PC actuels possèdent un mot mémoire de 64 bits, mais sont en réalité composées de 8 sous-mémoires ayant un mot mémoire de 8 bits. Cela permet de répartir la production de chaleur sur la barrette : la production de chaleur est répartie entre plusieurs puces, au lieu d'être concentrée dans la puce en cours d'accès.
L'arrangement vertical
modifierL'arrangement vertical rassemble plusieurs boitiers de mémoires pour augmenter la capacité sans changer la taille d'un mot mémoire. On utilisera un boitier pour une partie de la mémoire, un autre boitier pour une autre, et ainsi de suite. Toutes les banques sont reliées au bus de données, qui a la même largeur que les sorties des banques. Une partie de l'adresse est utilisée pour choisir à quelle banque envoyer les bits restants de l'adresse. Les autres banques sont désactivées. Mais un arrangement vertical peut se mettre en œuvre de plusieurs manières différentes.
La première méthode consiste à connecter la bonne banque et déconnecter toutes les autres. Pour cela, on utilise la broche CS, qui connecte ou déconnecte la mémoire du bus. Cette broche est commandée par un décodeur, qui prend les bits de poids forts de l'adresse en entrée.

Une autre solution est d'ajouter un multiplexeur/démultiplexeur en sortie des banques et de commander celui-ci convenablement avec les bits de poids forts. Le multiplexeur sert pur les lectures, le démultiplexeur pour les écritures.

Sans la technique dite de l'entrelacement, qu'on verra dans la section suivante, on utilise les bits de poids forts pour sélectionner la banque, ce qui fait que les adresses sont réparties comme illustré dans le schéma ci-dessous. Un défaut de cette organisation est que, si on souhaite lire/écrire deux mots mémoires consécutifs, on devra attendre que l'accès au premier mot soit fini avant de pouvoir accéder au suivant (vu que ceux-ci sont dans la même banque).

Si on mélange l'arrangement vertical et l'arrangement horizontal, on obtient ce que l'on appelle une rangée. Sur ces mémoires, les adresses sont découpées en trois morceaux, un pour sélectionner la rangée, un autre la banque, puis la ligne et la colonne.
L'entrelacement (interleaving)
modifierLa technique de l'entrelacement utilise un arrangement vertical assez spécifique, afin de gagner en performance. Avec une mémoire sans entrelacement, on doit attendre qu'un accès mémoire soit fini avant d'en démarrer un autre. Avec l'entrelacement, on peut réaliser un accès mémoire sans attendre que les précédents soient finis. L'idée est d’accéder à plusieurs banques en parallèles. Pendant qu'une banque est occupée par un accès mémoire, on en démarre un nouveau dans une autre banque, et ainsi de suite jusqu’à avoir épuisé toutes les banques libres. L'organisation en question se marie bien avec l'accès en rafale, si des bytes consécutifs sont placés dans des banques séparées.

Précisons que le temps d'accès mémoire ne change pas beaucoup avec l'entrelacement. Par contre, on peut faire plus d'accès mémoire simultanés. Cela implique que la fréquence de la mémoire augmente avec l'entrelacement. Au lieu d'avoir un cycle d'horloge assez long, capable de couvrir un accès mémoire entier, le cycle d'horloge est plus court. On peut démarrer un accès mémoire par cycle d'horloge, mais l'accès en lui-même prend plusieurs cycles. Le nombre de cycles d'un accès mémoire augmente, non pas car l'accès mémoire est plus lent, mais car la fréquence est plus élevée. D'un seul cycle par accès mémoire, on passe à autant de cycles qu'il y a de banques.
Les mémoires à entrelacement ont un débit supérieur aux mémoires qui ne l'utilisent pas, essentiellement car la fréquence a augmentée. Rappelons que le débit binaire d'une mémoire est le produit de sa fréquence par la largeur du bus. L'entrelacement est une technique qui augmente le débit en augmentant la fréquence du bus mémoire, sans pour autant changer les temps d'accès de chaque banque. Tout se passe comment si la fréquence de chaque banque restait la même, mais que l'entrelacement trichait en augmentant la fréquence du bus mémoire et en compensant la différence par des accès parallèles à des banques distinctes.
L'entrelacement basique
modifierSans entrelacement, les accès séquentiels se font dans la même banque, ce qui les rend assez lents. Mais il est possible d'accélérer les accès à des bytes consécutifs en rusant quelque peu. L'idée est que des accès consécutifs se fassent dans des banques différentes, et donc que des bytes consécutifs soient localisés dans des banques différentes. Les mémoires qui fonctionnent sur ce principe sont appelées des mémoires à entrelacement simple.

Pour cela, il suffit de prendre une mémoire à arrangement vertical, avec un petit changement : il faut utiliser les bits de poids faible pour sélectionner la banque, et les bits de poids fort pour le Byte.

En faisant cela, on peut accéder à un plusieurs bytes consécutifs assez rapidement. Cela rend les accès en rafale plus rapide. Pour cela, deux méthodes sont possibles.
- La première méthode utilise un accès en parallèle aux banques, d'où son nom d'accès entrelacé parallèle. Sans entrelacement, on doit accéder à chaque banque l'une après l'autre, en lisant chaque byte l'un après l'autre. Avec l’entrelacement parallèle, on lit plusieurs bytes consécutifs en même temps, en accédant à toutes les banques en même temps, avant d'envoyer chaque byte l'un après l'autre sur le bus (ce qui demande juste de configurer le multiplexeur). Un tel accès est dit en rafale : on envoie une adresse, puis on récupère plusieurs bytes consécutifs à partir de cette adresse initiale.
- Une autre méthode démarre un nouvel accès mémoire à chaque cycle d'horloge, pour lire des bytes consécutifs un par un, mais chaque accès se fera dans une banque différente. En faisant cela, on n’a pas à attendre que la première banque ait fini sa lecture/écriture avant de démarrer la lecture/écriture suivante. Il s'agit d'une forme de pipelining, qui fait que l'accès à des bytes consécutifs est rendu plus rapide.
Les mémoires à entrelacement par décalage
modifierLes mémoires à entrelacement simple ont un petit problème : sur une mémoire à N banques, des accès dont les adresses sont séparées par N mots mémoires vont tous tomber dans la même banque et seront donc impossibles à pipeliner. Pour résoudre ce problème, il faut répartir les mots mémoires dans la mémoire autrement. Dans les explications qui vont suivre, la variable N représente le nombre de banques, qui sont numérotées de 0 à N-1.
Pour obtenir cette organisation, on va découper notre mémoire en blocs de N adresses. On commence par organiser les N premières adresses comme une mémoire entrelacée simple : l'adresse 0 correspond à la banque 0, l'adresse 1 à la banque 1, etc. Pour le bloc suivant, nous allons décaler d'une adresse, et continuer à remplir le bloc comme avant. Une fois la fin du bloc atteinte, on finit de remplir le bloc en repartant du début du bloc. Et on poursuit l’assignation des adresses en décalant d'un cran en plus à chaque bloc. Ainsi, chaque bloc verra ses adresses décalées d'un cran en plus comparé au bloc précédent. Si jamais le décalage dépasse la fin d'un bloc, alors on reprend au début.

En faisant cela, on remarque que les banques situées à N adresses d'intervalle sont différentes. Dans l'exemple du dessus, nous avons ajouté un décalage de 1 à chaque nouveau bloc à remplir. Mais on aurait tout aussi bien pu prendre un décalage de 2, 3, etc. Dans tous les cas, on obtient un entrelacement par décalage. Ce décalage est appelé le pas d'entrelacement, noté P. Le calcul de l'adresse à envoyer à la banque, ainsi que la banque à sélectionner se fait en utilisant les formules suivantes :
- adresse à envoyer à la banque = adresse totale / N ;
- numéro de la banque = (adresse + décalage) modulo N, avec décalage = (adresse totale * P) mod N.
Avec cet entrelacement par décalage, on peut prouver que la bande passante maximale est atteinte si le nombre de banques est un nombre premier. Seulement, utiliser un nombre de banques premier peut créer des trous dans la mémoire, des mots mémoires inadressables. Pour éviter cela, il faut faire en sorte que N et la taille d'une banque soient premiers entre eux : ils ne doivent pas avoir de diviseur commun. Dans ce cas, les formules se simplifient :
- adresse à envoyer à la banque = adresse totale / taille de la banque ;
- numéro de la banque = adresse modulo N.
L'entrelacement pseudo-aléatoire
modifierUne dernière méthode de répartition consiste à répartir les adresses dans les banques de manière pseudo-aléatoire. La première solution consiste à permuter des bits entre ces champs : des bits qui étaient dans le champ de sélection de ligne vont être placés dans le champ pour la colonne, et vice-versa. Pour ce faire, on peut utiliser des permutations : il suffit d'échanger des bits de place avant de couper l'adresse en deux morceaux : un pour la sélection de la banque, et un autre pour la sélection de l'adresse dans la banque. Cette permutation est fixe, et ne change pas suivant l'adresse. D'autres inversent les bits dans les champs : le dernier bit devient le premier, l'avant-dernier devient le second, etc. Autre solution : couper l'adresse en morceaux, faire un XOR bit à bit entre certains morceaux, et les remplacer par le résultat du XOR bit à bit. Il existe aussi d'autres techniques qui donnent le numéro de banque à partir d'un polynôme modulo N, appliqué sur l'adresse.
Les mémoires multiports
modifierLes mémoires multiports sont reliées non pas à un, mais à plusieurs bus. Chaque bus est connecté sur la mémoire sur ce qu'on appelle un port. Ces mémoires permettent de transférer plusieurs données à la fois, une par port. Le débit est sont donc supérieur à celui des mémoires mono-port. De plus, chaque port peut être relié à des composants différents, ce qui permet de partager une mémoire entre plusieurs composants. Comme autre exemple, certaines mémoires multiports ont un bus sur lequel on ne peut que lire une donnée, et un autre sur lequel on ne peut qu'écrire.

Le multiports idéal
modifierUne première solution consiste à créer une mémoire qui soit vraiment multiports. Avec une mémoire multiports, tout est dupliqué sauf les cellules mémoire. La méthode utilisée dépend de si la cellule mémoire est fabriquée avec une bascule, ou avec une cellule SRAM. Elle dépend aussi de l'interface de la bascule.
Les mémoires multiport les plus simples sont les mémoires double port, avec un port de lecture et un d'écriture. Il suffit de prendre des cellules à double port, avec un port de lecture et un d'écriture. Il suffit de connecter la sortie de lecture à un multiplexeur, et l'entrée d'écriture à un démultiplexeur.

On peut améliorer la méthode précédente pour augmenter le nombre de ports de lecture assez facilement : il suffit de connecter plusieurs multiplexeurs.

Les choses sont plus compliquées avec les cellules mémoires à une seule broche d'entrée-sortie, ou à celles connectées à une ligne de bit. Dans les mémoires vues précédemment, chaque cellule mémoire est reliée à bitline via un transistor, lui-même commandé par le décodeur. Chaque port a sa propre bitline dédiée, ce qui donne N bitlines pour une mémoire à N ports. Évidemment, cela demande d'ajouter des transistors de sélection, pour la connexion et la déconnexion. De plus, ces transistors sont dorénavant commandés par des décodeurs différents : un par port. Et on a autant de duplications que l'on a de ports : N ports signifie tout multiplier par N. Autant dire que ce n'est pas l'idéal en termes de consommation énergétique !
Cette solution pose toutefois un problème : que se passe-t-il lorsque des ports différents écrivent simultanément dans la même cellule mémoire ? Eh bien tout dépend de la mémoire : certaines donnent des résultats plus ou moins aléatoires et ne sont pas conçues pour gérer de tels accès, d'autres mettent en attente un des ports lors de l'accès en écriture. Sur ces dernières, il faut évidemment rajouter des circuits pour détecter les accès concurrents et éviter que deux ports se marchent sur les pieds.
Le multiports à état partagé
modifierCertaines mémoires ont besoin d'avoir un très grand nombre de ports de lecture. Pour cela, on peut utiliser une mémoire multiports à état dupliqué. Au lieu d'utiliser une seule mémoire de 20 ports de lecture, le mieux est d'utiliser 4 mémoires qui ont chacune 5 ports de lecture. Toutefois, ces quatre mémoires possèdent exactement le même contenu, chacune d'entre elles étant une copie des autres : toute donnée écrite dans une des mémoires l'est aussi dans les autres. Comme cela, on est certain qu'une donnée écrite lors d'un cycle pourra être lue au cycle suivant, quel que soit le port, et quelles que soient les conditions.

Le multiports externe
modifierD'autres mémoires multiports sont fabriquées à partir d'une mémoire à un seul port, couplée à des circuits pour faire l'interface avec chaque port.

Une première méthode pour concevoir ainsi une mémoire multiports est d'augmenter la fréquence de la mémoire mono-port sans toucher à celle du bus. À chaque cycle d'horloge interne, un port a accès au plan mémoire.
La seconde méthode est basée sur des stream buffers. Elle fonctionne bien avec des accès à des adresses consécutives. Dans ces conditions, on peut tricher en lisant ou en écrivant plusieurs blocs à la fois dans la mémoire interne mono-port : la mémoire interne a un port très large, capable de lire ou d'écrire une grande quantité de données d'un seul coup. Mais ces données ne pourront pas être envoyées sur les ports de lecture ou reçues via les ports d'écritures, nettement moins larges. Pour la lecture, il faut obligatoirement utiliser un circuit qui découpe les mots mémoires lus depuis la mémoire interne en données de la taille des ports de lecture, et qui envoie ces données une par une. Et c'est la même chose pour les ports d'écriture, si ce n'est que les données doivent être fusionnées pour obtenir un mot mémoire complet de la RAM interne.
Pour cela, chaque port se voit attribuer une mémoire qui met en attente les données lues ou à écrire dans la mémoire interne : le stream buffer. Si le transfert de données entre RAM interne et stream buffer ne prend qu'un seul cycle, ce n'est pas le cas pour les échanges entre ports de lecture et écriture et stream buffer : si le mot mémoire de la RAM interne est n fois plus gros que la largeur d'un port de lecture/écriture, il faudra envoyer le mot mémoire en n fois, ce qui donne n^cycles. Ainsi, pendant qu'un port accèdera à la mémoire interne, les autres ports seront occupés à lire le contenu de leurs stream buffers. Ces stream buffers sont gérés par des circuits annexes, pour éviter que deux stream buffers accèdent en même temps dans la mémoire interne.

La troisième méthode remplace les stream buffers par des caches, et utilise une mémoire interne qui ne permet pas de lire ou d'écrire plusieurs mots mémoires d'un coup. Ainsi, un port pourra lire le contenu de la mémoire interne pendant que les autres ports seront occupés à lire ou écrire dans leurs caches.

La méthode précédente peut être améliorée, en utilisant non pas une seule mémoire monoport en interne, mais plusieurs banques monoports. Dans ce cas, il n'y a pas besoin d'utiliser de mémoires caches ou de stream buffers : chaque port peut accéder à une banque tant que les autres ports n'y touchent pas. Évidemment, si deux ports veulent lire ou écrire dans la même banque, un choix devra être fait et un des deux ports devra être mis en attente.

Les mémoires à détection et correction d'erreur
modifierLa performance et la capacité ne sont pas les deux seules caractéristiques importantes des mémoires. On attend d'elles qu'elles soient fiables, qu'elles stockent des données sans erreur. Si on stocke un 0 dans une cellule mémoire, on ne souhaite pas qu'une lecture ultérieure renvoie un 1 ou une valeur illisible. Malheureusement, ce n'est pas toujours le cas et quelques erreurs mineures peuvent survenir. Les erreurs en question se traduisent le plus souvent par l'inversion d'un bit : un bit censé être à 0 passe à 1, ou inversement. Pour donner un exemple, on peut citer l'incident du 18 mai 2003 dans la petite ville belge de Schaerbeek. Lors d'une élection, la machine à voter électronique enregistra un écart de 4096 voix entre le dépouillement traditionnel et le dépouillement électronique. La faute à un rayon cosmique, qui avait modifié l'état d'un bit de la mémoire de la machine à voter.
La majorité de ces inversions de bits proviennent de l'interaction de particules à haute énergie avec le circuit. Les plus importantes sont les rayons cosmiques, des particules à haute énergie produites dans la haute atmosphère et qui traversent celle-ci à haute vitesse. Les secondes plus importantes sont les rayons alpha, provenant de la radioactivité naturelle qu'on trouve un peu partout. Et, ironie du sort, ces rayons alpha proviennent souvent du métal présent dans la puce elle-même ou de son packaging !
Les techniques pour détecter et corriger ces erreurs sont nombreuses, comme nous l'avions vu dans le chapitre dédié sur les circuits de correction d'erreur. Mais elles ne sont pas appliquées de manière systématique, seulement quand ça en vaut la peine. Pour ce qui est du processeur, les techniques sont très rarement utilisées et sont réservées à l'automobile, l'aviation, le spatial, etc. Pour les mémoires les techniques sont déjà plus fréquentes sur les ordinateurs personnels, bien que vous n'en ayez pas vraiment conscience.
La première raison à cela est que les mémoires sont plus sujettes aux erreurs. Historiquement, du fait de leur conception, les mémoires sont plus sensibles à l'action des rayons cosmiques ou des particules alpha. Leur plus grande densité, le fait qu'elles stockent des bits sur de longues périodes de temps, leur processus de fabrication différent, tout cela les rend plus fragiles. La seconde raison est qu'il existe des techniques assez simples et pratiques pour rendre les mémoires tolérantes aux erreurs, qui ne s'appliquent pas pour le processeur ou les autres circuits. Il s'agit ni plus ni moins que l'usage de codes ECC, que nous avions abordé au début du cours dans un chapitre dédié, mais que nous allons rapidement réexpliquer dans ce qui suit.
Les mémoires ECC
modifierLes codes de détection et de correction d'erreur ajoutent des bits de correction/détection d'erreur aux données mémorisées. A chaque byte, on rajoute quelques bits calculés à partir des données du byte, qui servent à détecter et éventuellement corriger une erreur. Plus le nombre de bits ajoutés est important, plus la fiabilité des données sera importante. Ils sont généralement assez simples à mettre en œuvre, pour un cout modéré en circuit et en performance.
Il existe différents codes de ce type. Le plus simple est le bit de parité mémoire, qui ajoute un bit au byte mémorisé, de manière à ce que le nombre de bits à 1 soit pair. En clair, si on compte les bits à 1 dans le byte, bit de parité inclus, alors le résultat est pair. Cela permet de détecter qu'une erreur a eu lieu, qu'un bit a été inversé, mais on ne peut pas corriger l'erreur. Un bit de parité indique qu'un bit a été modifié, mais on ne sait pas lequel.
Lorsqu'on lisait un byte dans la mémoire, le contrôleur mémoire calculait le bit de parité du byte lu. Le résultat était alors comparé au bit de parité stocké dans le byte. Si les deux concordent, on suppose qu'il n'y a pas eu d'erreurs. C'est possible qu'il y en ait eu, comme une double erreur qui inverse deux bits à la fois, mais de telles erreurs ne se voient pas avec un bit de parité. Par contre, si les deux bits de parité sont différents, alors on sait qu'il y a eu une erreur. Par contre, vu qu'on ne sait pas quel bit a été inversé, on sait que la donnée du byte est corrompue, sans pouvoir récupérer la donnée originale. Aussi, quand l'ordinateur détectait une erreur, il n'avait pas d'autre choix que de stopper l'ordinateur et d'afficher un écran bleu dans le pire des cas.
Les mémoires DRAM d'avant les années 1990 utilisaient systématiquement un bit de parité par byte, par octet. Les mémoires de l'époque étaient assez peu fiables, du fait de processus de fabrication pas encore perfectionnés, et l'usage d'un bit de parité permettait de compenser cela. Les tous premiers ordinateurs mémorisaient les bits de parité dans une mémoire séparée, adressée en parallèle de la mémoire principale. Mais depuis l'arrivée des barrettes de mémoire, les bits de parité sont stockés dans les byte eux-même, sur la barrette de mémoire. Depuis les années 1990, l'usage d'un bit de parité est tombé en désuétude avec l'amélioration de la fiabilité intrinsèque des DRAM.

Les mémoires ECC utilisent un code plus puissant qu'un simple bit de parité. Le code en question permet non seulement de détecter qu'un bit a été inversé, mais permettent aussi de déterminer lequel. Le code en question ajoute au minimum deux bits par byte. Nous avions vu quelques codes de ce genre dans le chapitre sur les circuits de correction d'erreur, nous ne ferons pas de rappels, qui seraient de toute façon inutiles dans ce chapitre. La majorité des codes utilisés sur les mémoires ECC permettent de corriger l'inversion d'un bit. De plus, ils permettent de détecter les situations où deux bits ont été inversés (deux erreurs simultanés) mais sans les corriger. Mais le cout en circuits est plus conséquent : il y a environ 4 bits d'ECC par octet.
Là encore, la détection/correction d'erreur est le fait de circuits spécialisés qui calculent les bits d'ECC à partir du byte lu, et comparent le tout aux bits d'ECC mémorisés dans la RAM. Les circuits d'ECC se situent généralement dans le contrôleur mémoire, mais se peut qu'ils soient intégrés dans la barrette mémoire. La différence entre les deux est une question de compatibilité. S'ils sont intégrés dans la barrette mémoire, la gestion de l'ECC est complétement transparente et est compatible avec n'importe quelle carte mère, peu importe le contrôleur mémoire utilisé. Par contre, si elle est le fait du contrôleur mémoire, alors il peut y avoir des problèmes de compatibilité. Une barrette non-ECC fonctionnera toujours, mais ce n'est pas le cas des barrettes ECC. Le contrôleur mémoire doit gérer l'ECC et être couplé à des barrettes ECC pour que le tout fonctionne. Si on branche une mémoire ECC sur un contrôleur mémoire qui ne gère pas l'ECC, l'ordinateur ne démarre même pas. Notons que de nos jours, le contrôleur mémoire est intégré dans le processeur : c'est ce dernier qui gère l'ECC.
L'usage de l'ECC sur les ordinateurs personnels est assez complexe à expliquer. Précisons d'abord qu'il est rare de trouver des mémoires ECC dans les ordinateurs personnels, alors qu'elles sont systématiquement présentes sur les serveurs. Par contre, les mémoires cache d'un processeur de PC utilisent systématiquement l'ECC. En effet, si les DRAM sont sensibles aux erreurs, mais que les SRAM le sont tout aussi ! Les caches aussi peuvent subir des erreurs, et ce d'autant plus que le processeur est miniaturisé. Et pour cela, les caches des CPU actuels incorporent soit des bits de parité, soit de la SRAM ECC. Tout dépend du niveau de cache, comme on le verra dans le chapitre sur le cache.
Le memory scrubbing
modifierLa plupart des erreurs ne changent qu'un seul bit dans un byte, mais le problème est que ces erreurs s'accumulent. Entre deux accès à un byte, il se peut que plusieurs erreurs se soient accumulées, ce qui dépasse les capacités de correction de l'ECC. Dans ce cas, il existe une solution appelée le memory scrubbing, qui permet de résoudre le problème au prix d'un certain cout en performance.
L'idée est de vérifier chaque byte régulièrement, pour éviter que les erreurs s'accumulent. Par exemple, on peut vérifier chaque byte toutes les N millisecondes, et corriger une éventuelle erreur lors de cette vérification. En faisant des vérifications régulières, on garantir que les erreurs n'ont pas le temps de s'accumuler, sauf en cas de malchance avec des erreurs très proches dans le temps. Et évidemment, le memory scrubbing a un cout en performance, car cela fait des accès en plus. Des accès qui sont de plus timés à des instants bien précis qui ne sont pas forcément les plus adéquats.
Précisons qu'il ne s'agit pas d'un rafraichissement mémoire, même si ça a un effet similaire. Disons que lors de chaque "pseudo-rafraichissement", le byte est purgé de ses erreurs, pas rafraichit. D'ailleurs, les mémoires SRAM peuvent incorporer du memory scrubbing, et de nombreuses mémoires cache ne s'en privent pas, comme on le verra dans le chapitre sur le cache. Cependant, sur les mémoires DRAM, le memory scrubbing peut se faire en même temps que le rafraichissement mémoire, afin de fortement limiter son cout en performance.
Le memory scrubbing peut compléter soit l'ECC, soit un bit de parité. Imaginons par exemple qu'on le combine avec un bit de parité. Le bit de parité permet de détecter qu'une erreur a eu lieu. Mais si deux erreurs ont lieu, le bit de parité ne pourra pas détecter la double erreur. Le bit de parité indiquera que la donnée est valide. Pour éviter cela, on utilise le memory scrubbing pour éviter que deux erreurs consécutives s'accumulent, permettant de détecter un problème dès la première erreur. On n'attend pas de lire la donnée invalide pour vérifier le bit de parité.
Le même raisonnement a lieu avec l'ECC, avec quelques différences. Au lieu d'attendre que deux erreurs aient lieu, ce que l'ECC peut détecter, mais pas corriger, on effectue des vérifications régulières. Si une vérification tombe entre deux erreurs, elle corrigera la première erreur avant que la seconde survienne. Au final, on a une mémoire non-corrompue : l'ECC corrige la première erreur, puis la suivante, au lieu de laisser deux erreurs s'accumuler et d'avoir un résultat détectable mais pas corrigeable.
Les mémoires à tampon de ligne optimisées
modifierDans cette section, nous allons voir les optimisations rendues possibles sur les mémoires à tampon de ligne. Ce sont techniquement des mémoires à tampon de ligne. Pour rappel, elles sont organisées en lignes et colonnes. Elles sont composées d'une mémoire dont les bytes sont des lignes, d'un tampon de ligne pour mémoriser la ligne en cours de traitement, et d'un multiplexeur/démultiplexeur pour lire/écrire les mots mémoires adressés dans la ligne.

L'implémentation du mode rafale
modifierDiverses optimisations se basent sur la présence du tampon de ligne. L'implémentation du mode rafale est par exemple grandement facilitée sur ces mémoires. Une rafale permet de lire le contenu d'une ligne d'un seul bloc, idem pour les écritures. Pour une lecture, la ligne est copiée dans le tampon de ligne, puis la rafale démarre. Les mot mémoires à lire sont alors lus dans le tampon de ligne directement, un par un. Il suffit de configurer le multiplexeur pour passer d'une adresse à la suivante. Le compteur de rafale est relié au multiplexeur, sur son entrée, et est incrémenté à chaque cycle d'horloge du bus mémoire.
Il en est de même pour l'écriture, sauf qu'il y a une étape en plus. La ligne à écrire est copiée dans le tampon de ligne, puis l'écriture en rafale a lieu dans le tampon de ligne, mot mémoire par mot mémoire, et la ligne est ensuite recopiée du tampon de ligne vers la mémoire. Vous vous demandez sans doute pourquoi copier la ligne dans le tampon de ligne avant d'écrire dedans. La réponse est que la rafale ne fait pas forcément la taille d'une ligne. Par exemple, si une ligne fait 126 octets et que la rafale en seulement 8, il faut tenir compte des octets non-modifiés dans la ligne. Sachant qu'il n'y a pas de copie partielle du tampon de ligne dans la mémoire RAM, recopier la ligne pour la modifier est la meilleure solution.
Un défaut de cette implémentation est qu'une rafale ne put pas être à cheval sur deux lignes, sauf si la RAM incorpore des optimisations complémentaires. Les rafales doivent être alignées de manière à rentrer dans une ligne complète. Pour rendre l'alignement plus facile, la taille des lignes doit être un multiple de la longueur de la rafale. De plus, les rafales doivent être alignées, que ce soit en mode séquentiel ou linéaire. Par exemple, si une rafale lit/écrit 4 octets, alors les lignes doivent faire 8 * N octets. De plus, les rafales doivent commencer à une adresse multiple de 8 octets * 4 adresses consécutives = 32 octets. Pour le dire autrement, la rafale voit la mémoire comme des blocs qui peuvent être transmis en rafale. Mais impossible de lancer une rafale au beau milieu d'un bloc, sauf à utiliser le mode rafale linéaire pour revenir au début du bloc quand on atteint la fin.
Les mémoires à cache de ligne intégré
modifierQuelques modèles de RAM à tampon de ligne ont ajouté un cache qui mémorise les dernières lignes ouvertes, ce qui permet d'améliorer les performances. Les RAM en question sont les EDRAM (enhanced DRAM), ESDRAM (enhanced synchronous DRAM), Virtual Channel Memory RAM, et CDRAM (Cached DRAM). Elles demandaient pour certaines une modification de l'interface, avec des commandes pour copier le tampon de ligne dans le cache, en plus des traditionnelles commandes de lecture/écriture. L'idée était d'avoir plusieurs lignes ouvertes en même temps, ce qui améliorait les performances dans certains scénarios.

Les optimisations des copies en mémoire
modifierUne telle organisation en tampon de ligne permet d'implémenter facilement les accès en rafale, mais aussi d'autres opérations. L'une d'entre elle est la copie de données en mémoire. Il n'est pas rare que le processeur copie des blocs de données d'une adresse vers une autre. Par exemple, pour copier 12 kibioctets qui commencent à l'adresse X, vers un autre bloc de même taille, mais qui commence à l'adresse M. En théorie, la copie se fait mot mémoire par mot mémoire, mais la technologie row clone permet de faire la copie ligne par ligne.
L'idée est de lire une ligne, de la stocker dans le tampon de ligne, puis de l'écrire à la destination voulue. Pas de passage par le bus de données, les données ne sortent pas de la mémoire. L'avantage est que la copie des données est beaucoup plus rapide. De plus, elle consomme nettement moins d'énergie, car il n'y a pas de transmission sur le bus mémoire, sans compter qu'on n'a pas d'utilisation des multiplexeurs/démultiplexeurs.
L'implémentation demande d'ajouter des registres dans la mémoire pour mémoriser les adresses de départ/destination, mais surtout d'ajouter des commandes sur le bus mémoire pour déclencher ce genre de copie. Il faut ajouter une commande de copie, qui désigne la ligne originelle et la ligne de destination, des numéros de lignes doivent être transmis dans la commande et mémorisés par la mémoire, etc.
L'implémentation est plus compliquée sur les mémoires multi-banques, car il faut prévoir de quoi copier des données d'une banque à l'autre. L'optimisation précédente ne fonctionne alors pas du tout, mais on gagne quand même un peu en performance et en consommation d'énergie, vu qu'il n'y a pas de transmission sur le bus mémoire avec toutes les lenteurs que cela implique.
Les mémoires primaires
modifier
Dans les chapitres précédents, nous avons vu ce qu'il y a à l'intérieur des diverses mémoires. Nous avons abordé des généralités qui valent aussi bien pour des mémoires ROM, RAM, de masse, ou autres. Et il va de soi qu'après avoir vu les généralités, nous allons passer sur les spécificités de chaque type de mémoire. Nous allons d'abord étudier les mémoires ROM, pour une raison simple : l'intérieur de ces mémoires est très simple. Il faut dire qu'il s'agit de mémoires de faible capacité, dont les besoins en termes de performance sont souvent assez frustres, les seules ROM à haute performance étant les mémoires Flash. En conséquence, elles intègrent peu d'optimisations qui complexifient leur micro-architecture.
Rappelons qu'il existe plusieurs types de mémoires ROM :
- les mémoires ROM sont fournies déjà programmées et ne peuvent pas être reprogrammées ;
- les mémoires PROM sont fournies intégralement vierges, et on peut les programmer une seule fois ;
- les mémoires RPROM sont reprogrammables, ce qui signifie qu'on peut les effacer pour les programmer plusieurs fois ;
- les mémoires EPROM s'effacent avec des rayons UV et peuvent être reprogrammées plusieurs fois de suite ;
- certaines EPROM peuvent être effacées par des moyens électriques : ce sont les mémoires EEPROM et les mémoires Flash.
Toutes ces mémoires ROM ont un contrôleur mémoire limité à son plus simple appareil : un simple décodeur pour gérer les adresses. Les circuits d'interface avec la mémoire sont aussi très simples et se limitent le plus souvent à un petit circuit combinatoire. Le plan mémoire est des plus classiques et ce chapitre ne l'abordera pas, pour ne pas répéter ce qui a été vu dans les chapitres précédents. Seuls les cellules mémoires se démarquent un petit peu, celles-ci étant assez spécifiques sur les mémoires ROM. Les cellules mémoires ROM varient grandement selon le type de mémoire, ce qui explique les différences entre types de ROM.
Les mémoires ROM
modifierLes mémoires ROM les plus simples sont de loin les Mask ROM, qui sont fournies avec leur contenu directement intégré dans la ROM lors de sa fabrication. Ces mémoires ROM sont accessibles uniquement en lecture, mais pas en écriture, sans compter qu'elles ne sont pas reprogrammables. Il est possible de les fabriquer avec plusieurs méthodes différentes, que nous n'allons pas toutes présenter. La plus simple est de loin de prendre une mémoire FROM et de la programmer avec les données voulues. Et c'est d'ailleurs ainsi que procèdent certains fabricants. Mais cette méthode n'est pas très intéressante : le constructeur ne produit alors pas vraiment une "vraie" Mask ROM. À la place, nous allons vous parler des autres méthodes, plus intéressantes à étudier et aussi plus économes en circuits.
Les Mask ROM sont fabriquées en combinant un décodeur avec un OU câblé
modifierLes ROM sont techniquement des circuits combinatoires : leur sortie (la donnée lue) ne dépend que de l'entrée (l'adresse). Et en conséquence, pour chaque mémoire ROM, il existe un circuit combinatoire équivalent. Prenons un circuit qui, pour chaque entrée , renvoie le résultat : celui-ci est équivalent à une ROM dont le byte d'adresse contient la donnée . Et réciproquement : une telle ROM est équivalente au circuit précédent. En clair, on peut créer un circuit combinatoire quelconque en utilisant une ROM, ce qui est très utilisé dans certains circuits que nous verrons dans quelques chapitres. Cependant, cela ne signifie pas que chaque circuit combinatoire soit une mémoire ROM : une vraie ROM contient un plan mémoire, un décodeur, de même que les circuits d'interface avec le bus, des bitlines, et j'en passe.
Il existe une sorte d'intermédiaire entre une ROM véritable et un circuit combinatoire optimisé. Rappelons que tout circuit combinatoire est composé de trois couches de portes logiques : une couche de portes NON, une autre de portes ET, et une dernière couche de portes OU. Les deux couches de portes NON et ET calculent des minterms, et la couche de porte OU effectue un OU entre ces minterms. On peut remplacer les deux premières couches par un décodeur, comme nous l'avions vu dans le chapitre sur les circuits de sélection. En effet, par définition, un décodeur est un circuit qui fournit tous les minterms que l'on peut obtenir à partir de l'entrée. Il reste à faire un OU entre les sorties adéquates du décodeur pour obtenir le circuit voulu.
Un tel circuit commence à ressembler à une mémoire, bien que ce soit encore imparfait. On trouve bien un décodeur, comme dans toute mémoire, mais le plan mémoire n'existe pas vraiment car les portes OU ne sont pas des cellules mémoires en elles-mêmes. Néanmoins, ce circuit sert de base aux véritables mémoires ROM, qui s'obtient à partir du circuit précédent.


Les mémoires ROM sont conçues en remplaçant les portes OU par un OU câblé (wired OR). Pour rappel, le OU câblé est une technique qui permet d'obtenir un équivalent d'une porte OU en reliant les sorties à un même fil. Mais elle demande que le décodeur utilise des sorties à drain/collecteur ouvert, c'est-à-dire des sorties qui peuvent soit sortir un 1, soit être déconnectées, mais ne peuvent pas fournir un 0 (ou inversement). Le OU câblé connecte au même fil les sorties dont on souhaite faire un OU. Si toutes ces sorties sont à 0, alors tous les circuits sont déconnectés et la sortie est connectée à la masse à travers la résistance : elle est à 0. Mais si une seule entrée est à 1, alors le 1 d'entrée est recopié sur le fil, ce qui met la sortie à 1.
Certains portes logiques TTL ont des sorties à collecteur ouvert de ce type et on peut fabriquer un décodeur avec, mais elles sont rares. Aussi, il vaut mieux utiliser un décodeur normal et transformer ses sorties en sorties à drain/collecteur ouvert. Pour cela, il suffit d'ajouter un petit circuit en aval d'une sortie normale. Il existe deux manières pour cela : la première utilise une diode, la seconde utilise un transistor.
Les ROM à diodes
modifierLes ROM à diodes sont des mémoires ROM fabriquées en combinant un décodeur avec des diodes pour obtenir un décodeur à sorties à collecteur ouvert. Le OU câblé ressemble donc à ceci, en tenant compte des diodes. Les entrées A et B sont les sorties normales du décodeur, ce ne sont pas des sorties à collecteur ouvert !
 |
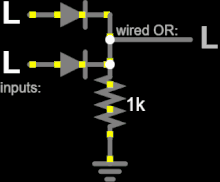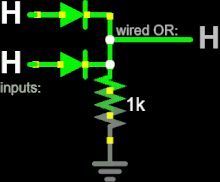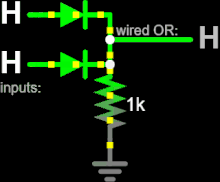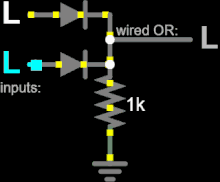 |
L'intérieur d'une mémoire à diode ressemble à ceci :

Les ROM à transistors MOS
modifierLes ROM de type MOS fonctionnent comme les ROM à diodes, si ce n'est que les diodes sont remplacées par des transistors MOS. On peut utiliser aussi bien des transistors NMOS que PMOS, ce qui donne des circuits très différents. Avec des transistors PMOS, les diodes sont simplement remplacées par des transistors, et le reste du circuit ne change pas. Le transistor PMOS se ferme quand on met un 1 sur sa base, et s'ouvre si on lui envoie un 0. Il se comporte alors un peu comme une diode, d'où le fait que le remplacement se fait à l'identique.
Regardons ce qui se passe quand on veut lire dans une ROM à transistors PMOS. Les cellules mémoire qui contiennent un 1 sont représentées par un simple fil, les autres ont un transistor. Si la cellule mémoire n'est pas sélectionnée, le décodeur envoie un 0 sur la grille du transistor, qui reste fermé. Il se comporte comme un fil.

Si la cellule est sélectionnée, le décodeur envoie un 1 sur la grille du transistor, qui s'ouvre. La bitline est déconnectée de la tension d'alimentation, et est reliée à la masse à travers une résistance : la bitline est mise à 0.

Si un transistor NMOS qui est utilisé, le circuit est en quelque sorte inversé. Rappelons qu'un transistor NMOS se ferme quand on met un 0 sur sa base, et s'ouvre si on lui envoie un 1. En conséquence, les sorties du décodeur sont ici réellement à collecteur ouvert, à savoir qu'elles sont à 0 ou déconnectées. C'est l'inverse de ce qu'on a avec une diode. Les conséquences sont multiples. Déjà, la résistance de rappel est connectée à la tension d'alimentation et non à la masse. De plus, là où on aurait mis une diode dans une ROM à diode, on ne met pas de transistor MOS. Et inversement, on place un transistor MOS là où on ne met pas de diodes.
Les mémoires PROM et autres circuits logiques programmables
modifierLes mémoires ROM et circuits combinatoires sont tous créés de la même manière : une couche de portes NON, suivi d'une couche de portes ET, suivie par une couche de portes OU. La seule différence tient dans la manière dont ces couches sont interconnectées, ainsi que dans le nombre de portes logiques. Et cela nous donne un indice sur la manière de créer des circuits programmables, dont les mémoires PROM ne sont qu'un sous-ensemble.
Les PROM sont regroupées avec d'autres circuits similaires, mais qui ne sont techniquement pas des mémoires. Ces derniers portent les doux noms de Programmable Logic Device (PLD). Il s'agit de circuits qui comprennent un grand nombre de portes logiques, dont un peu programmer les interconnexions. La programmation peut être définitive ou non, ce qui donne différents types de PLD :
- les PLD simples, dont la programmation est définitive, comme sur une PROM ;
- les EPLD dont la programmation est réversible après exposition aux UV comme sur les EPROM ;
- les EEPLD dont la programmation est effaçable électriquement, comme sur les EEPROM.
Les PLD programmables une seule fois
modifierPour le moment, nous allons uniquement parler des PLD dont la configuration est permanente. Une fois qu'on a configuré ce genre de PLD, le circuit ne peut pas être reprogrammé. Ils servent à créer n’importe quel circuit combinatoire, voire séquentiel pour les plus complexes. Leur intérêt est assez similaire à celui des PROM, comparé aux mask ROM : ils sont plus simples à utiliser. Au lieu de créer un circuit combinatoire sur mesure en interconnectant des portes logiques, autant prendre un PLD et le configurer comme on le souhaite.
Tous sont fabriqués sur le même modèle, qui est décrit dans ce qui suit. En premier lieu, on trouve une couche de portes NON, reliée aux entrées. En sortie de celle-ci, on trouve les entrées ou leur inverse. On trouve aussi une couche de portes ET et une couche de portes OU. Mais surtout : on trouve des circuits d'interconnexion qui permettent soit de relier les entrées aux portes ET, soit les sorties des portes ET aux entrées des portes OU. Les deux sont appelés respectivement la matrice ET, et la matrice OU.

Les interconnexions sont programmables une fois, on verra comment elles sont faites plus bas. Pour l'expliquer rapidement, les deux matrices contiennent des circuits permettent de connecter/déconnecter une entrée à une sortie, qui sont représentés par des petits ronds dans le schéma ci-dessous. Pour les PLD simples, ces connecteurs sont des fusibles qui sont grillés si on met une tension trop importantes.
Par défaut, toutes les interconnexions possibles sont présentes. Pour la matrice ET, cela signifie que toutes les entrées sont reliées à chaque porte ET, que tous les minterms sont présents. Pour la matrice OU, cela veut dire que chaque porte ET sont reliées à toutes les portes OU. Lors de la programmation, on va conserver seulement une partie des interconnexions, le reste étant éliminé.

La plupart des PLD récents ajoutent un registre sur leur sortie. Pour cela, en aval de chaque porte OU, on trouve une bascule D qui mémorise la sortie du circuit PLD. Le PLD est un circuit imprimé, qui a une sortie pour chaque porte OU, mais cette sortie n'est pas toujours connectée directement à la sortie de la bascule. La raison est qu'on trouve un MUX qui permet de choisir si on veut récupérer soit le contenu de la bascule, soit la sortie directe de la porte OU. La plupart des PLD ajoutent aussi la possibilité de prendre l'inverse de chaque sortie. Le tout est configuré par quelques bits d'entrée.

La classification des PLD est assez complexe, mais on peut en distinguer trois sous-types principaux :
- Les PLA (Programmable logic array) : les deux matrices ET et OU sont programmables.
- Les PAL (Programmable Array Logic) : la matrice ET est programmable, mais pas la matrice OU.
- Les PROM : la matrice OU est programmable, mais pas la matrice ET.
| Matrice ET non-programmable | Matrice ET programmable | |
|---|---|---|
| Matrice OU non-programmable | Circuit combinatoire | PAL |
| Matrice OU programmable | PROM | PLA |
Les mémoires PROM
modifier
Avec une mémoire PROM, la matrice ET est fixée une fois pour toute. L'ensemble matrice ET + portes ET + portes NON forme un simple décodeur, aux sorties à collecteur ouvert. La couche de portes OU peut faite de portes OU câblées, mais ce n'est pas systématique.
L'intérieur d'une mémoire FROM est similaire à celui d'une mémoire ROM simple, sauf que les diodes/transistors (ou leur absence) sont remplacées par un autre dispositif. Précisément, chaque cellule mémoire est composé d'une sorte d'interrupteur qu'on ne peut configurer qu'une seule fois. Celui est localisé à l'intersection d'une bitline et d'un signal row line, et connecte ces deux fils. Lors de la programmation, ce connecteur est soit grillé (ce qui déconnecte les deux fils), soit laissé intact. Pour faire un parallèle avec une ROM à diode, ce connecteur fonctionne comme une diode quand il est laissé intact, mais comme l'absence de diode quand il est grillé.
Suivant la mémoire, ce connecteur peut être un transistor, ou un fusible. Dans le premier cas, chaque transistor fonctionne soit comme un interrupteur ouvert, soit comme un interrupteur fermé. Un 1 correspond à un transistor laissé intact, qui fonctionne comme un interrupteur ouvert. Par contre, un 0 correspond à un transistor grillé, qui se comporte comme un interrupteur fermé. Dans le cas avec les fusibles, chaque bit est stocké en utilisant un fusible : un 1 est codé par un fusible intact, et le zéro par un fusible grillé. Une fois le fusible claqué, on ne peut pas revenir en arrière : la mémoire est programmée définitivement.
Programmer une PROM consiste à faire claquer certains fusibles/transistors en les soumettant à une tension très élevée. Pour cela, le contrôleur mémoire balaye chaque ligne une par une, ce qui permet de programmer la ROM ligne par ligne, byte par byte. Lorsqu'une ligne est sélectionnée, on place une tension très importante sur les bitlines voulues. Les fusibles de la ligne connectés à ces bitlines sont alors grillés, ce qui les met à 0. Les autres bitlines sont soumises à une tension normale, ce qui est insuffisant pour griller les fusibles. En choisissant bien les bitlines en surtension pour chaque ligne, on arrive à programmer la mémoire FROM comme souhaité.
Les mémoires EPROM et EEPROM
modifierLes mémoires EPROM et EEPROM, y compris la mémoire Flash, sont fabriquées avec des transistors à grille flottante, que nous avons déjà abordés il y a quelques chapitres. Je vous renvoie au chapitre sur les cellules mémoire pour plus d'informations à ce sujet. La grille de ces transistors est connectée à la row line, ce qui permet de commander leur ouverture, le drain et la source sont connectés à une bitline.
Les mémoires EPROM
modifier
Avant de pouvoir (re-)programmer une mémoire EPROM ou EEPROM, il faut effacer son contenu. Sur les EPROM, l'effacement se fait en exposant les transistors à grille flottante à des ultraviolets. Divers phénomènes physiques vont alors décharger les transistors, mettant l'ensemble de la mémoire à 0.
Pour pouvoir exposer le plan mémoire aux UV, toutes les mémoires EPROM ont une petite fenêtre transparente, qui expose le plan mémoire. Il suffit d'éclairer cette fenêtre aux UV pour effacer la mémoire. Pour éviter un effacement accidentel de la mémoire, cette fenêtre est d'ordinaire recouverte par un film plastique qui ne laisse pas passer les UV.
Les mémoires EEPROM et Flash
modifierLes mémoires Flash et les mémoires EEPROM se ressemblent beaucoup, suffisamment pour que la différence entre les deux est assez subtile. Pour simplifier, on peut dire que les EEPROM effectuent les effacements/écritures byte par byte, alors que les Flash les font par paquets de plusieurs bytes. Là où on peut effacer/programmer un byte individuel sur une EEPROM, ce n'est pas possible sur une mémoire Flash. Sur une mémoire Flash, on est obligé d'effacer/programmer un bloc entier de la mémoire, le bloc faisant plus de 512 bytes. C’est une simplification, qui cache le fait que la distinction entre EEPROM et Flash n'est pas très claire. Dans les faits, on considère que le terme EEPROM est à réserver aux mémoires dont les unités d'effacement/programmation sont petites (elles ne font que quelques bytes, pas plus), alors que les Flash ont des unités beaucoup plus larges.
Les différences entre EEPROM, Flash NOR et Flash NAND
modifierDans ce cours, nous ferons la distinction entre EEPROM et Flash sur le critère suivant : l'effacement peut se faire byte par byte sur une EEPROM, alors qu'il se fait par blocs entiers sur une Flash. Quant à la reprogrammation, tout dépend du type de mémoire. Sur les EEPROM, elle a forcément lieu byte par byte, comme l'effacement. Mais sur les mémoires Flash, elle peut se faire soit byte par byte, soit par paquets de plusieurs centaines de bytes. Cela permet de distinguer deux sous-types de mémoires Flash : les mémoires Flash de type NOR et les Flash de type NAND. Nous verrons ci-dessous d'où proviennent ces termes, mais laissons cela de côté pour le moment. Sur les Flash de type NOR, on doit effacer la mémoire par blocs, mais on peut reprogrammer les bytes uns par uns, indépendamment les uns des autres. Par contre, sur les Flash de type NAND, effacement et reprogrammation se font par paquets de plusieurs centaines de bytes. Pire : les blocs pour l'effacement n'ont pas la même taille que pour la reprogrammation : environ 512 à 8192 octets pour la reprogrammation, plus de 64 kibioctets pour l'effacement. Par exemple, il est possible de lire un octet individuel, d'écrire par paquets de 512 octets et d'effacer des paquets de 4096 octets. Sur les Flash NAND, l'unité d'effacement s'appelle un bloc (comme pour les Flash NOR), alors que l'unité de reprogrammation s'appelle une page mémoire.

| Reprogrammation Byte par byte | Reprogrammation par blocs entiers | |
|---|---|---|
| Effacement Byte par byte | EEPROM | N'existe pas |
| Effacement par blocs entiers | Flash de type NOR | Flash de type NAND |
Les avantages et inconvénients de chaque type d'EEPROM
modifierEn termes d’avantages et d'inconvénients, les différents types de Flash sont assez distincts. Les Flash NOR ont meilleur un temps de lecture que les Flash NAND, alors que c'est l'inverse pour la reprogrammation et l'effacement. Pour faire simple, l'écriture est assez lente sur les Flash NOR. En termes de capacité mémoire, les Flash NAND ont l'avantage, ce qui les rend mieux adaptées pour du stockage de masse. Leur conception réduit de loin le nombre d'interconnexions internes, ce qui augmente fortement la densité de ces mémoires.
Les différents types de Flash/EEPROM sont utilisées dans des scénarios très différents. Les Flash NAND sont idéales pour des accès séquentiels, comme on en trouve dans des accès à des fichiers. Par contre, les EEPROM et les Flash de type NOR sont idéales pour des accès aléatoires. En conséquence, les Flash NAND sont idéales comme mémoire de masse, alors que les Flash NOR/EEPROM sont idéales pour stocker des programmes de petite taille, comme des Firmware ou des BIOS. C'est la raison pour laquelle les Flash NAND sont utilisées dans les disques de type SSD, alors que les autres sont utilisées comme de petites mémoires mortes.
La micro-architecture des mémoires FLASH simples
modifierLes mémoires Flash sont fabriquées avec des transistors à grille flottante, comme pour les mémoires EEPROM. Du point de vue de la micro-architecture, il n'y a pas de différence notable entre EEPROM et mémoire Flash. La seule exception tient dans le plan mémoire et notamment dans la manière dont les cellules mémoires sont reliées aux bitlines (les fils sur lesquels on connecte les cellules mémoires pour lire et écrire dedans). Mais la manière utilisée n'est pas la même entre les Flash NAND et les Flash NOR.
Le tout est illustré dans le schéma qui suit, dans lequel on voit que chaque cellule d'une Flash NOR est connectée à la bitline directement, alors que les Flash NAND placent les cellules en série. De ce fait, les Flash NAND ont beaucoup moins de fils et de connexions, ce qui dégage de la place. Pas étonnant que ces dernières aient une densité mémoire plus importante que pour les Flash NOR (on peut mettre plus de cellules mémoire par unité de surface). Cette différence n'a strictement rien à voir avec ce qui a été dit plus haut. Peu importe que chaque cellule soit connectée à la bitline ou que les transistors soient en série, on peut toujours lire et reprogrammer chaque cellule indépendamment des autres.
 |
 |
Les toutes premières mémoires SRAM étaient des mémoires asynchrones, non-cadencées par une horloge. Avec elles, le processeur devait attendre que la mémoire réponde et devait maintenir adresse et données pendant ce temps. Pour éviter cela, les concepteurs de mémoire ont synchronisé les échanges entre processeur et mémoire avec un signal d'horloge : les mémoires synchrones sont nées. L'utilisation d'une horloge a l'avantage d'imposer des temps d'accès fixes. Un accès mémoire prend un nombre déterminé (2, 3, 5, etc) de cycles d'horloge et le processeur peut faire ce qu'il veut dans son coin durant ce temps.
Fabriquer une mémoire synchrone demande de rajouter des registres sur les entrées/sorties d'une mémoire asynchrone. Instinctivement, on se dit qu'il suffit de mettre des registres sur les entrées associées au bus d'adresse/commande, et sur les entrées-sorties du bus de données. Mais faire ainsi a des conséquences pas évidentes, au niveau du nombre de cycles utilisés pour les lectures et écritures. Aussi, nous allons procéder par étapes, en ajoutant des registres d'abord pour mémoriser l'adresse, puis les données à écrire, puis sur toutes les entrées-sorties. Ces trois cas correspondent à des mémoires qui existent vraiment, les trois modèles ont été commercialisé et utilisés.
Pour simplifier les explications, nous allons prendre le cas d'une mémoire avec un port de lecture séparé du port d'écriture. On peut alors ajouter des registres sur le bus d'adresse/commande, sur le port de lecture et sur le port d'écriture. Il est possible de faire la même chose sur une mémoire avec un port unique de lecture/écriture, mais laissons cela de côté pour le moment.
Les SRAM synchrones à tampon d'adresse
modifierLe premier type de SRAM synchrone que nous allons étudier est celui des SRAM synchrones à tampon d’adresse. Leur nom est assez clair et dit bien comment ces SRAM sont rendues synchrones. L'adresse et les signaux de commande sont mémorisés dans des registres, mais pas les données. Elle partent d'un modèle asynchrone, sur lequel on ajoute des registres pour les entrées d'adresse et de commande, mais pas pour les ports de lecture/écriture, pas pour le bus de données.

Grâce à l'ajout du registre d'adresse, le processeur n'a pas à maintenir l'adresse en entrée de la SRAM durant toute la durée d'un accès mémoire : le registre s'en charge. Le diagramme suivant montre ce qu'il se passe pendant une lecture, avec l'ajout d'un registre sur l'adresse uniquement. On voit que sur la SRAM asynchrone, l'adresse doit être maintenue durant toute la durée du cycle d'horloge mémoire, c'est à dire durant une dizaine de cycles d'horloge du processeur. Mais sur la SRAM synchrone, l'adresse est envoyée en début du cycle seulement, l'adresse est écrite dans le registre lors d'un cycle processeur, puis maintenue par le registre pour les autres cycles processeur.

L'écriture se passe comme sur les SRAM asynchrones, si ce n'est que l'adresse n'a pas à être maintenue. La donnée à écrire doit être maintenue pendant toute la durée de l'écriture, même si elle dure plusieurs cycles d'horloge processeur. Le processeur envoie la donnée à écrire en même temps que l'adresse, mais peut se déconnecter du bus d'adresse précocement. Les SRAM de ce style ont des lectures rapides, mais des écritures plus lentes.

Avec cette organisation, les lectures et écritures ont le même nombre de cycles. La présentation de l'adresse se fait au premier cycle, la lecture/écriture proprement dite est effectuée au cycle suivant. Pour une lecture, on a le premier cycle pour la présentation de l'adresse, et le second cycle où la donnée est disponible sur le bus de données. Pour l'écriture, c'est pareil, sauf que la donnée à écrire peut être présentée dès le premier cycle, mais elle n'est terminée qu'à la fin du second cycle. De telles mémoires synchrones sont de loin les plus simples. Les toutes premières SRAM synchrones étaient de ce type, la première d'entre elle étant la HM-6508.
Les SRAM synchrones à tapon d'écriture
modifierLes SRAM synchrones à tampon d'écriture reprennent la structure précédente, et y ajoutent d'un registre sur le port d'écriture. Pour les SRAM avec un seul port, le registre sert de tampon pour les données à écrire, mais il est contourné pour les lectures, qui ne passent pas par ce registre. Un exemple de SRAM de ce type est la HM-6504, qui disposait d'un port de lecture séparé du port d'écriture. Un autre exemple est celui de la HM-6561, qui elle n'a qu'un seul port utilisé à la fois pour la lecture et l'écriture, mais qui dispose bien d'un registre utilisé uniquement pour les écritures. Lors des lectures, ce registre est contourné et n'est pas utilisé.

Les écritures anticipées
modifierL'ajout d'un registre pour les écritures permet de faire la même chose que pour les adresses, mais pour les données à écrire. La donnée à écrire est envoyée en même temps que l'adresse et le processeur n'a plus rien à faire au cycle suivant. On dit que l'on réalise une écriture anticipée. Les lectures comme les écritures sont plus rapides que sur les SRAM à tampon d'adresse, du moins en apparence.

Du point de vue du processeur, les écritures ne prennent plus qu'un seul cycle : celui où on présente l'adresse et la donnée à écrire. Mais en réalité, la durée d'une écriture n'a pas changée, c'est juste que la SRAM effectue l'écriture au second cycle, comme dans les SRAM précédentes. Simplement, la SRAM effectue l'écriture elle-même, sans que le processeur ait besoin de maintenir la donnée à écrire sur le bus de données. Pour le processeur, les écritures prennent un cycle et les lectures deux, alors que la SRAM considère que les deux se font en deux cycles. Et cela a des conséquences.
Les écritures tardives
modifierLes écritures anticipées ne posent pas de problèmes quand on effectue des écritures consécutives, mais elle pose problème quand on enchaine les lectures et écritures. Pour comprendre pourquoi, prenons le cas simple où une lecture est suivie d'une écriture, séparées par un seul cycle d'horloge. Au premier cycle d'horloge, le processeur présente l'adresse à lire à la SRAM. Au second cycle, la donnée lue sera disponible, mais le processeur va aussi présenter l'adresse et la donnée à écrire. Autant cela ne pose pas de problème si la SRAM a un port de lecture séparé de celui d'écriture, autant lire une donnée et écrire la suivante en même temps n'est pas possible avec un seul bus de données.
Pour éviter cela, on peut utiliser des écritures tardives, où la donnée à écrire est présentée un cycle d'horloge après la présentation de l'adresse d'écriture. L'intérêt des écritures tardives est qu'elles garantissent que l'écriture se fasse en deux cycles, tout comme les lectures. Ce faisant, dans une succession de lectures/écritures, il n'y a pas de différences de durée entre lectures et écritures, donc les problèmes disparaissent.

Évidemment, il y a des situations où il est possible d'effectuer des écritures anticipées sans problèmes, notamment quand la SRAM a des cycles inutilisées. Les SRAM synchrones gèrent à la fois les écritures anticipées et les écritures tardives, sauf pour quelques exceptions. Quelques bits de commande permettent de choisir s'il faut faire une écriture tardive ou anticipée, ce qui permet au processeur et/ou au contrôleur de mémoire externe de faire le choix le plus adéquat. Le choix se fait suivant les accès mémoire à réaliser, suivant qu'il y ait ou non alternance entre lectures et écritures, et bien d'autres paramètres.
Les SRAM synchrones pipelinées
modifierLes SRAM précédentes, à tampon d'adresse et à tampon d'écriture, sont regroupées dans la catégorie des SRAM à flot direct, pour lesquelles la donnée lue ne subit pas de mémorisation dans un registre de sortie. L'avantage est que les lectures sont plus rapides, elles ne prennent qu'un seul cycle. On écrit l'adresse à lire lors d'un cycle, la donnée est disponible au cycle suivant.
Elles sont opposées aux SRAM synchrones pipelinées, qui ont un registre tampon pour les lectures, pour les données lues depuis la RAM. Avec elles, la donnée sortante est mémorisée dans un registre commandé par un front d'horloge, afin d'augmenter la fréquence de la SRAM et son débit.

Avec une SRAM à pipeline, il faut ajouter un cycle supplémentaire pour lire la donnée. Sur une SRAM à flot direct (non-pipelinée), l'adresse de lecture est envoyée lors du premier cycle, la donnée lue est présentée au cycle suivant. Avec un registre sur le port de lecture, le processeur écrit l'adresse dans le registre lors du premier cycle, la mémoire récupère la donnée lue et l'enregistre dans le registre de sortie lors du second cycle, la donnée est disponible pour le processeur lors du troisième cycle. Au final, la donnée lue est disponible deux cycles après la présentation de l'adresse.
Mais quel est l'avantage des SRAM à pipeline, dans ce cas ? Et bien il vient du fait qu'elles peuvent fonctionner à une fréquence supérieure et effectuer plusieurs accès mémoire en même temps.
Le pipeline de base à trois étages
modifierPour comprendre pourquoi les SRAM à pipeline fonctionnent à une fréquence plus élevée, il faut étudier comment s'effectue une lecture.
Sur une SRAM à flot direct, on doit attendre que l'accès mémoire précédent soit terminé avant d'en lancer un autre. Si on effectue plusieurs lectures successives, voici ce que cela donne :

Sur une SRAM à pipeline, l'accès en lecture se fait en trois étapes : on envoie l'adresse lors d'un premier cycle, effectue la lecture durant le cycle suivant, et récupère la donnée sur le bus un cycle plus tard. Les trois étapes sont complétement séparées, temporellement et surtout : physiquement. La première implique les registres et bus d'adresse et de commande, la seconde la SRAM asynchrone, la troisième le registre de sortie et le bus de données.
La conséquence est qu'on peut lancer une nouvelle lecture à chaque cycle d'horloge. Et ce n'est pas incompatible avec le fait qu'une lecture prenne 3 cycles d'horloge. Les différentes lectures successives seront à des étapes différentes et s’exécuteront en même temps. Pendant que l'on lit le registre de sortie pour la première lecture, la seconde lecture accède à la SRAM asynchrone, et la troisième lecture prépare l'adresse à écrire dans le registre d'adresse/commande. Le résultat est que l'on peut effectuer plusieurs lectures en même temps. On lance un nouvel accès mémoire à chaque cycle d'horloge, même si une lecture prend trois cycles. Le résultat est que l'on peut effectuer trois lectures en même temps, comme montré dans le schéma plus haut.

Un point sur lequel il faut insister est qu'avec un pipeline, une lecture prend globalement le même temps en secondes, comparé à une SRAM à flot direct. Il y a une petite différence liée au fait que les registres ont un temps de propagation non-nul, mais laissons cela de côté pour le moment. Si la lecture prend trois cycles, ce n'est pas parce que les lectures deviennent sensiblement plus lentes, mais parce que la fréquence augmente. Au lieu d'avoir un cycle horloge long, capable de couvrir une lecture complète, un cycle d'horloge avec pipeline correspond à une seule étape de la lecture, environ un tiers. Les SRAM à pipeline fonctionnent à plus haute fréquence, ce qui donne un débit binaire plus élevé, pour des temps d'accès identiques.
Notons que ce pipeline ne vaut que pour les lectures. Les écritures sont dans un cas un peu différent, avec une différence entre les écritures anticipées et tardives. les écritures anticipées sont toujours possibles et une succession d'écriture n'a pas d'organisation en pipeline nette. La données à écrire et l'adresse sont envoyées en même temps, à raison d’une par cycle. Mais l'écriture effective a lieu au cycle suivant. En clair, une écriture se fait en deux étapes, pas trois ! Il y a bien un pipeline, mais il est plus court : deux étapes au lieu de deux, ce qui fait que l'on ne peut faire que deux écritures simultanées. Pendant que l'une écrit dans les registres, l'autre effectue l'écriture dans la SRAM asynchrone. Et ce pose évidemment quelques problèmes, comme on va le voir dans la section suivante.
Notons que le principe a des conséquences assez similaires à celles de l'entrelacement. On peut effectuer plusieurs accès en parallèle, la fréquence augmente, le débit binaire est améliorée, mais les temps d'accès restent les mêmes. Les deux techniques peuvent d'ailleurs se combiner, bien que ce soit assez rare.
Les conflits d'accès liés au pipeline
modifierPlus haut, pour les SRAM sans pipeline, nous avions vu qu'il est possible qu'il y ait des conflits d'accès où une donnée lue est envoyée sur le bus en même temps qu'une donnée à écrire. Ces conflits, qui ont lieu lors d'alternances entre lectures et écritures, sont appelés des retournements de bus. La solution pour les SRAM sans pipeline était de retarder la présentation de la donnée à écrire, ce qui donne des écritures tardives.
Sur les SRAM à pipeline, un problème similaire à lieu. Il est causé par le fait que les écritures prennent entre un et deux cycles et les lectures trois. Et cela se marie mal avec l'organisation en pipeline qui permet des accès mémoires simultanés. Par exemple, imaginons qu'une écriture ait lieu deux cycles après une lecture. Dans ce cas, la lecture utilise le bus de données à son troisième cycle, l'écriture utilise le bus de données à son premier cycle, le décalage de deux cycles entre les deux fait qu'il y a conflit : l’écriture et la lecture veulent utiliser le bus en même temps. Le même problème peut survenir quand on utilise des écritures tardives, même si les timings ne sont pas les mêmes.

Une solution est d'utiliser un port de lecture séparé du port d'écriture. Les conflits d'alternance entre lectures et écritures disparaissent. La seule exception est le cas où une lecture tente de lire une donnée en même temps qu'elle est écrite. La solution est de lire la donnée directement depuis le registre d'écriture. Pour cela, il faut ajouter un comparateur qui vérifie si les deux adresses consécutives sont identiques, et qui commande le bus de données pour le connecter au registre d'écriture.
Sur les mémoires simple port, il existe plusieurs solutions pour gérer ce cas. La plus simple consiste à retarder l'écriture d'un cycle en cas de conflit potentiel. Le contrôleur mémoire externe à la SRAM doit détecter de potentiels conflits et retarder les écritures problématiques d'un cycle quand c'est nécessaire. Une autre solution utilise les écritures tardives, à savoir des écritures où la donnée à écrire est envoyée un cycle après l'adresse. Mais il faut adapter le retard pour le faire correspondre au temps des lectures. Vu que la lecture prend trois cycles sur une SRAM à pipeline, il faut retarder l'écriture de deux cycles d'horloge, et non d'un seul. Cette technique s'appelle l'écriture doublement tardive.
Les écritures doublement tardives posent le même problème que les écritures tardives. Il se peut qu'une lecture accède à une adresse écrite au cycle précédent ou dans les deux cycles précédents. La lecture lira alors une donnée pas encore mise à jour par l'écriture. Pour éviter cela, il faut soit mettre en attente la lecture, soit renvoyer le contenu du registre d'écriture sur le bus de donnée au bon timing. Dans les deux cas, il faut ajouter deux comparateurs : un qui compare l'adresse à lire avec l'adresse précédente, et un qui compare avec l'adresse d'il y a deux cycles.
Les SRAM synchrones registre-à-verrou
modifierAvec les mémoires registre à verrou, il y a un registre pour la donnée lue, mais ce registre est un registre commandé par un signal Enable et non par un front d'horloge. Le registre commandé par un signal Enable est en quelque sorte transparent. L'usage d'un registre de ce type fait qu'on peut maintenir la donnée lue durant plusieurs cycles sur le bus mémoire. De plus, on n’a pas à rajouter un cycle d'horloge pour chaque lecture, mais cela fait qu'on se prive de l'avantage des mémoires pipelinées.

Les mémoires RAM dynamiques sont opposées aux mémoires RAM statiques. Les RAM statiques sont les plus intuitives à comprendre : elles conservent leurs données tant qu'on ne les modifient pas, ou tant que l’alimentation électrique est maintenue. Les RAM dynamiques ont pour défaut que les données s'effacent après un certain temps, en quelques millièmes ou centièmes de secondes si l'on n'y touche pas. En conséquence, il faut réécrire chaque bit de la mémoire régulièrement pour éviter qu'il ne s'efface. On dit qu'on doit effectuer régulièrement un rafraîchissement mémoire.
La mémoire principale de l'ordinateur, la fameuse mémoire RAM, est actuellement une mémoire dynamique sur tous les PC actuels. Le rafraîchissement prend du temps, et a tendance à légèrement diminuer la rapidité des mémoires dynamiques. Mais en contrepartie, les mémoires dynamiques ont une meilleure capacité, car leurs bits prennent moins de place, utilisent moins de transistors.
L'interface des DRAM et le contrôleur mémoire
modifierUn point important est que les DRAM modernes ne sont pas connectées directement au processeur, mais le sont par l'intermédiaire d'un contrôleur mémoire externe. Le contrôleur mémoire sert d'intermédiaire, d'interface entre la DRAM et le processeur. Il ne faut pas le confondre avec le contrôleur mémoire interne, placé dans la mémoire RAM, et qui contient notamment le décodeur. Les deux sont totalement différents, bien que leur nom soit similaire.
Le contrôleur mémoire est reliée au CPU par un bus, et est connecté aux barrettes ou boitiers de DRAM via le bus mémoire proprement dit. Les anciens contrôleurs mémoire étaient des composants séparés du processeur, du chipset ou du reste de la carte mère. Par exemple, les composants Intel 8202, Intel 8203 et Intel 8207 étaient des contrôleurs mémoire pour DRAM qui étaient vendus dans des boitiers DIP et étaient soudés sur la carte mère. Par la suite, ils ont été intégré au chipset de la carte mère pendant les décennies 90-2000. Après les années 2000, ils ont été intégrés dans les processeurs.
Le contrôleur mémoire externe
modifierLe contrôleur mémoire gère le bus mémoire et tout ce qui est envoyé dessus. Il envoie des commandes aux barrettes de mémoire, commandes qui peuvent être des lectures, des écritures, ou des demandes de rafraichissement, parfois d'autres commandes. La mémoire répond à ces commandes par l'action adéquate : lire la donnée et la placer sur le bus de données pour une commande de lecture, par exemple.
Il est possible de connecter plusieurs barrettes sur le même bus mémoire, ou alors celles-ci sont connectées au contrôleur mémoire avec un bus par barrette/boitier. C'est ce qui permet de placer plusieurs barrettes de mémoire sur la même carte mère : toutes les barrettes sont connectées au contrôleur mémoire DRAM d'une manière ou d'une autre. Notons que le contrôleur mémoire est presque toujours un circuit synchrone, cadencé par une horloge, comme le processeur. Et ce peu importe que les mémoires DRAM soient elles-mêmes synchrones ou au contraire asynchrones (sans horloge).
Le rôle du contrôleur mémoire varie grandement suivant le contrôleur en question, ainsi que selon le type de DRAM. Par exemple, les contrôleurs mémoires des toutes premières DRAM ne géraient pas du tout le rafraichissement mémoire, qui était géré par le processeur. Par exemple, le processeur Zilog Z80 implémentait des compteurs pour gérer le rafraichissement mémoire. D'autres processeurs avaient des interruptions dédiées pour gérer le rafraichissement mémoire. Mais les contrôleurs mémoires modernes gèrent le rafraichissement mémoire de manière automatique.
Le bus d'adresse des DRAM est multiplexé
modifierUn point important pour le contrôleur mémoire est de transformer les adresses mémoires fournies par le processeur, en adresses utilisables par la DRAM. Car les DRAM ont une interface assez spécifique. Les DRAM ont ce qui s'appelle un bus d'adresse multiplexé. Avec de tels bus, l'adresse est envoyée en deux fois. Les bits de poids fort sont envoyés avant les bits de poids faible. On peut ainsi envoyer une adresse de 32 bits sur un bus d'adresse de 16 bits, par exemple. Le bus d'adresse contient alors environ moitié moins de fils que la normale.
Pour rappel, l'avantage de cette méthode est qu'elle permet de limiter le nombre de fils du bus d'adresse, ce qui très intéressant sur les mémoires de grande capacité. Les mémoires DRAM étant utilisées comme mémoire principale d'un ordinateur, elles devaient avoir une grande capacité. Cependant, avoir un petit nombre de broches sur les barrettes de mémoire est clairement important, ce qui impose d'utiliser des stratagèmes. Envoyer l'adresse en deux fois répond parfaitement à ce problème : cela permet d'avoir des adresses larges et donc des mémoires de forte capacité, avec une performance acceptable et peu de fils sur le bus d'adresse.
Les bus multiplexés se marient bien avec le fait que les DRAM sont des mémoires à adressage par coïncidence ou à tampon de ligne. Sur ces mémoires, l'adresse est découpée en deux : une adresse haute pour sélectionner la ligne, et une adresse basse qui sélectionne la colonne. L'adresse est envoyée en deux fois : la ligne, puis la colonne. Pour savoir si une donnée envoyée sur le bus d'adresse est une adresse de ligne ou de colonne, le bus de commande de ces mémoires contenait deux fils bien particuliers : les RAS et le CAS. Pour simplifier, le signal RAS permettait de sélectionner une ligne, et le signal CAS permettait de sélectionner une colonne.

Si on a deux bits RAS et CAS, c'est parce que la mémoire prend en compte les signaux RAS et CAS quand ils passent de 1 à 0. C'est à ce moment là que la ligne ou colonne dont l'adresse est sur le bus sera sélectionnée. Tant que des signaux sont à zéro, la ligne ou colonne reste sélectionnée : on peut changer l'adresse sur le bus, cela ne désélectionnera pas la ligne ou la colonne et la valeur présente lors du front descendant est conservée.

Le rafraichissement mémoire
modifierLa spécificité des DRAM est qu'elles doivent être rafraichies régulièrement, sans quoi leurs cellules perdent leurs données. Le rafraichissement est basiquement une lecture camouflée. Elle lit les cellules mémoires, mais n'envoie pas le contenu lu sur le bus de données. Rappelons que la lecture sur une DRAM est destructive, à savoir qu'elle vide la cellule mémoire, mais que le système d'amplification de lecture régénère le contenu de la cellule automatiquement. La cellule est donc rafraichie automatiquement lors d'une lecture.
Les DRAM à rafraichissement externe et pseudo-statiques
modifierSur la quasi-totalité des DRAM, modernes comme anciennes, le rafraichissement est géré par le processeur ou le contrôleur mémoire. Le rafraichissement est déclenché par une commande de rafraichissement, provenant du processeur ou du contrôleur mémoire. Une commande de rafraichissement est un troisième type d'accès mémoire, séparé de la lecture ou de l'écriture, qui n’existe que sur les DRAM de ce type.
Une commande de rafraichissement ordonne de rafraichir une adresse, parfois une ligne complète. Dans le premier cas, le rafraichissement se fait adresse par adresse, on doit préciser l'adresse à chaque fois. Le second cas est spécifique aux mémoires à tampon de ligne, organisées en lignes et colonnes. La lecture d'une ligne la rafraichit automatiquement, ce qui fait qu'il suffit de d'adresser une ligne, pas besoin de préciser la colonne. Les commandes sont donc plus courtes.
Enfin, un dernier cas permet d'envoyer des commandes de rafraichissement vides, qui ne précisent ni adresse ni numéro de ligne. Pour cela, la mémoire contient un compteur, qui pointe sur la prochaine ligne à rafraichir, qui est incrémenté à chaque commande de rafraichissement. Une commande de rafraichissement indique à la mémoire d'utiliser l'adresse dans ce compteur pour savoir quelle adresse/ligne rafraichir.

Il existe des mémoires qui sont des intermédiaires entre les mémoires SRAM et DRAM. Il s'agit des mémoires pseudo-statiques, qui sont techniquement des mémoires DRAM, utilisant des transistors et des condensateurs, mais qui gèrent leur rafraichissement mémoire toutes seules. Le rafraichissement mémoire est alors totalement automatique, ni le processeur, ni le contrôleur mémoire ne devant s'en charger. Le rafraichissement est purement le fait des circuits de la mémoire RAM et devient une simple opération de maintenance interne, gérée par la RAM elle-même.
L'impact du rafraichissement sur les performances
modifierLe rafraichissement mémoire a un impact sur les performances. L'envoi des commandes de rafraichissement entre des lectures/écritures fait qu'une partie du débit binaire de la mémoire est gâché. De même, ces commandes doivent être envoyées à des timings bien précis, et peuvent entrer en conflit avec des lectures ou écritures simultanées.
L'envoi des commandes de rafraichissement peuvent se faire de deux manières : soit on les envoie toutes en même temps, soit on les disperse le plus possible. Le premier cas est un rafraichissement en rafale, le second un rafraichissement étalé. Le rafraichissement en rafale n'est pas utilisé dans les PC, car il bloque la mémoire pendant un temps assez long. Le rafraichissement étalé est étalé dans le temps, ce qui permet des accès mémoire entre chaque rafraichissement de ligne/adresse. Les PC gagnent en performance avec le rafraichissement étalé. Mais les anciennes consoles de jeu gagnaient parfois à utiliser eu rafraichissement en rafale. En effet, la mémoire était souvent effacée entre l'affichage de deux images, pour éviter certains problèmes dont on ne parlera pas ici. Le rafraichissement de la mémoire était effectué à ce moment là : l'effacement rafraichissait la mémoire.
Le temps mis pour rafraichir la mémoire est le temps mis pour parcourir toute la mémoire. Il s'agit du temps de balayage vu dans le chapitre sur les performances d'un ordinateur. Concrètement, il est défini en divisant la capacité de la mémoire par son débit binaire. C'est le temps nécessaire pour lire ou réécrire tout le contenu de la mémoire. Cependant, il faut signaler que l'usage de banques mémoire change la donne. Il est en effet possible de rafraichir des banques indépendantes en même temps, ce qui divise le temps de rafraichissement par le nombre de banques.
Les mémoires asynchrones à RAS/CAS : FPM et EDO-RAM
modifierAvant l'invention des mémoires SDRAM et DDR, il exista un grand nombre de mémoires différentes, les plus connues étant les mémoires fast page mode et EDO-RAM. Ces mémoires n'étaient pas synchronisées par un signal d'horloge, c'était des mémoires asynchrones. Quand ces mémoires ont été créées, cela ne posait aucun problème : les accès mémoire étaient très rapides et le processeur était certain que la mémoire aurait déjà fini sa lecture ou écriture au cycle suivant. Les mémoires asynchrones les plus connues étaient les mémoires FPM et mémoires EDO.
Les mémoires FPM
modifierLes mémoires FPM (Fast Page Mode) possédaient une petite amélioration, qui rendait l'adressage plus simple. Avec elles, il n'y a pas besoin de préciser deux fois la ligne si celle-ci ne changeait pas lors de deux accès consécutifs : on pouvait garder la ligne sélectionnée durant plusieurs accès. Par contre, il faut quand même préciser les adresses de colonnes à chaque changement d'adresse. Il existe une petite différence entre les mémoire FPM proprement dit et les mémoires Fast-Page Mode. Sur les premières, le signal CAS est censé passer à 0 avant qu'on fournisse l'adresse de colonne. Avec les Fast-Page Mode, l'adresse de colonne pouvait être fournie avant que l'on configure le signal CAS. Cela faisait gagner un petit peu de temps, en réduisant quelque peu le temps d'accès total.

Avec les mémoires en mode quartet, il est possible de lire quatre octets consécutifs sans avoir à préciser la ligne ou la colonne à chaque accès. On envoie l'adresse de ligne et l'adresse de colonne pour le premier accès, mais les accès suivants sont fait automatiquement. La seule contrainte est que l'on doit générer un front descendant sur le signal CAS pour passer à l'adresse suivante. Vous aurez noté la ressemblance avec le mode rafale vu il y a quelques chapitres, mais il y a une différence notable : le mode rafale vrai n'aurait pas besoin qu'on précise quand passer à l'adresse suivante avec le signal CAS.

Les mémoires FPM à colonne statique se passent même du signal CAS. Le changement de l'adresse de colonne est détecté automatiquement par la mémoire et suffit pour passer à la colonne suivante. Dans ces conditions, un délai supplémentaire a fait son apparition : le temps minimum entre deux sélections de deux colonnes différentes, appelé tCAS-to-CAS.

Les mémoires EDO-RAM
modifierL'EDO-RAM a été inventée quelques années après la mémoire FPM. Elle a été déclinée en deux versions : la EDO simple, et la EDO en rafale.
L'EDO simple ajoutait une capacité de pipelining limitée aux mémoires FPM. L'implémentation n'est pas différente des mémoires FPM, si ce n'est qu'il y a un registre ajouté sur la sortie de donnée pour les lectures, un peu comme sur les mémoires SRAM synchrones. La donnée pouvait être maintenue sur le bus de données durant un certain temps, même après la remontée du signal CAS. Le registre de sortie maintenait la donnée lu tant que le signal RAS restait à 0, et tant qu'un nouveau signal CAS n'a pas été envoyé. Faire remonter le signal CAS à 1 n'invalidait pas la donnée en sortie.
La conséquence est qu'on pouvait démarrer un nouvel accès alors que la donnée de l'accès précédent était encore présent sur le bus de données. Le pipeline obtenu avait deux étages : un où on présentait l'adresse et sélectionnait la colonne, un autre où la donnée était lue depuis le registre de sortie. Les mémoires EDO étaient donc plus rapides.

Les EDO en rafale effectuent les accès à 4 octets consécutifs automatiquement : il suffit d'adresser le premier octet à lire. Les 4 octets étaient envoyés sur le bus les uns après les autres, au rythme d'un par cycle d’horloge : ce genre d'accès mémoire s'appelle un accès en rafale.

Implémenter cette technique nécessite d'ajouter un compteur, capable de faire passer d'une colonne à une autre quand on lui demande, et quelques circuits annexes pour commander le tout.

Le rafraichissement mémoire
modifierLes mémoires FPM et EDO doivent être rafraichies régulièrement. Au début, le rafraichissement se faisait ligne par ligne. Le rafraichissement avait lieu quand le RAS passait à l'état haut, alors que le CAS restait à l'état bas. Le processeur, ou le contrôleur mémoire, sélectionnait la ligne à rafraichir en fournissant son adresse mémoire. D'où le nom de rafraichissement par adresse qui est donné à cette méthode de commande du rafraichissement mémoire.
Divers processeurs implémentaient de quoi faciliter le rafraichissement par adresse. Par exemple, le Zilog Z80 contenait un compteur de ligne, un registre qui contenait le numéro de la prochaine ligne à rafraichir. Il était incrémenté à chaque rafraichissement mémoire, automatiquement, par le processeur lui-même. Un timer interne permettait de savoir quand rafraichir la mémoire : quand ce timer atteignait 0, une commande de rafraichissement était envoyée à la mémoire, et le timer était reset.

Par la suite, certaines mémoires ont implémenté un compteur interne d'adresse, pour déterminer la prochaine adresse à rafraichir sans la préciser sur le bus d'adresse. Le déclenchement du rafraichissement se faisait toujours par une commande externe, provenant du contrôleur mémoire ou du processeur. Cette commande faisait passer le CAS à 0 avant le RAS. Cette méthode de rafraichissement se nomme rafraichissement interne.

On peut noter qu'il est possible de déclencher plusieurs rafraichissements à la suite en laissant le signal CAS dans le même état. Ce genre de choses pouvait avoir lieu après une lecture : on pouvait profiter du fait que le CAS soit mis à zéro par la lecture ou l'écriture pour ensuite effectuer des rafraichissements en touchant au signal RAS. Dans cette situation, la donnée lue était maintenue sur la sortie durant les différents rafraichissements.

Les mémoires SDRAM
modifierDans les années 90, les mémoires asynchrones ont laissé la place aux mémoires SDRAM, qui sont synchronisées avec le bus par une horloge. L'utilisation d'une horloge a comme avantage des temps d'accès fixes : le processeur sait qu'un accès mémoire prendra un nombre déterminé de cycles d'horloge et peut faire ce qu'il veut dans son coin durant ce temps. Avec les mémoires asynchrones, le processeur ne pouvait pas prévoir quand la donnée serait disponible et ne faisait rien tant que la mémoire n'avait pas répondu : il exécutait ce qu'on appelle des wait states en attendant que la mémoire ait fini.
Les mémoires SDRAM sont standardisées par un organisme international, le JEDEC. Le standard SDRAM impose des spécifications électriques bien précise pour les barrettes de mémoire et le bus mémoire, décrit le protocole utilisé pour communiquer avec les barrettes de mémoire, et bien d'autres choses encore. LE standard autorise l'utilisation de 2 à 8 banques dans chaque barrette de SDRAM, autorise une forme de pipeline (une commande peut démarrer avant que la précédente termine), les barrettes mémoires utilisent de l'entrelacement. Les SDRAM ont été déclinées en versions de performances différentes, décrites dans le tableau ci-dessous :
| Nom standard | Fréquence | Bande passante |
|---|---|---|
| PC66 | 66 mhz | 528 Mio/s |
| PC66 | 100 mhz | 800 Mio/s |
| PC66 | 133 mhz | 1064 Mio/s |
| PC66 | 150 mhz | 1200 Mio/s |
Le mode rafale
modifierLes SDRAM gèrent à la fois l'accès entrelacé et l'accès linéaire. Nous avions vu ces deux types d'accès dans le chapitre sur les mémoires évoluées, mais faisons un bref rappel. Le mode linéaire est le mode rafale normal : un compteur est incrémenté à chaque cycle et son contenu est additionné à l'adresse de départ. Le mode entrelacé utilise un ordre différent. Avec ce mode de rafale, le contrôleur mémoire effectue un XOR bit à bit entre un compteur (incrémenté à chaque accès) et l'adresse de départ pour calculer la prochaine adresse de la rafale.
Sur les SDRAM, les paramètres qui ont trait au mode rafale sont modifiables, programmables. Déjà, on peut configurer la mémoire pour effectuer au choix des accès sans rafale ou des accès en rafale. Ensuite, on peut décider s'il faut faire un accès en mode linéaire ou entrelacé. Il y a aussi la possibilité de configurer le nombre d'octets consécutifs à lire ou écrire en mode rafale. On peut ainsi accéder à 1, 2, 4, ou 8 octets en une seule fois, alors que les EDO ne permettaient que des accès à 4 octets consécutifs.
Les délais mémoires
modifierIl faut un certain temps pour sélectionner une ligne ou une colonne, sans compter qu'une SDRAM doit gérer d'autres temps d'attente plus ou moins bien connus : ces temps d'attente sont appelés des délais mémoires. La façon de mesurer ces délais varie : sur les mémoires FPM et EDO, on les mesure en unités de temps (secondes, millisecondes, micro-secondes, etc.), tandis qu'on les mesure en cycles d'horloge sur les mémoires SDRAM.
| Timing | Description |
|---|---|
| tRAS | Temps mis pour sélectionner une ligne. |
| tCAS | Temps mis pour sélectionner une colonne. |
| tRP | Temps mis pour réinitialiser le tampon de ligne et décharger la ligne. |
| tRCD | Temps entre la fin de la sélection d'une ligne, et le moment où l'on peut commencer à sélectionner la colonne. |
| tWTR | Temps entre une lecture et une écriture consécutives. |
| tCAS-to-CAS | Temps minimum entre deux sélections de deux colonnes différentes. |
Les délais/timings mémoire ne sont pas les mêmes suivant la barrette de mémoire que vous achetez. Certaines mémoires sont ainsi conçues pour avoir des timings assez bas et sont donc plus rapides, et surtout : beaucoup plus chères que les autres. Le gain en performances dépend beaucoup du processeur utilisé et est assez minime comparé au prix de ces barrettes. Les circuits de notre ordinateur chargés de communiquer avec la mémoire (ceux placés soit sur la carte mère, soit dans le processeur), doivent connaitre ces timings et ne pas se tromper : sans ça, l’ordinateur ne fonctionne pas.
Le registre de mode du contrôleur mémoire
modifierLes mémoires SDRAM sont connectées à un bus mémoire spécifique, qui lui-même est commandé par un contrôleur mémoire externe. Et ce contrôleur mémoire est partiellement configurable pour les SDRAM. La configuration en question permet de gérer diverses options du mode rafale, comme le tableau ci-dessous le montre bien.
Le contrôleur mémoire interne de la SDRAM mémorise ces informations dans un registre de 10 bits, le registre de mode. Il contient un bit qui permet de préciser s'il faut effectuer des accès normaux ou des accès en rafale, ainsi qu'un autre bit pour configurer le type de rafale (normale, entrelacée). Il mémorise aussi le nombre d'octets consécutifs à lire ou écrire. Voici à quoi correspondent les 10 bits de ce registre :
| Bit n°9 | Type d'accès : en rafale ou normal |
|---|---|
| Bit n°8 et 7 | Doivent valoir 00, sont réservés pour une utilisation ultérieur dans de futurs standards. |
| Bit n°6, 5, et 4 | Latence CAS |
| Bit n°3 | Type de rafale : linéaire ou entrelacée |
| Bit n°2, 3, et 0 | Longueur de la rafale : indique le nombre d'octets à lire/écrire lors d'une rafale. |
Les commandes SDRAM
modifierLe bus de commandes d'une SDRAM contient évidemment un signal d'horloge, pour cadencer la mémoire, mais pas que. En tout, 18 fils permettent d'envoyer des commandes à la mémoire, commandes qui vont effectuer une lecture, une écriture, ou autre chose dans le genre. Les commandes en question sont des demandes de lecture, d'écriture, de préchargement et autres. Elles sont codées par une valeur bien précise qui est envoyée sur les 18 fils du bus de commande. Ces commandes sont nommées READ, READA, WRITE, WRITEA, PRECHARGE, ACT, ...
| Bit CS | Bit RAS | Bit CAS | Bit WE | Bits de sélection de banque (2 bits) | Bit du bas d'adresse A10 | Reste du bus d'adresse | Nom de la commande : Description |
|---|---|---|---|---|---|---|---|
| 1 | X | Absence de commandes. | |||||
| 0 | 1 | 1 | 1 | X | No Operation : Pas d'opération | ||
| 0 | 1 | 1 | 0 | X | Burst Terminante : Arrêt d'un accès en rafale en cours. | ||
| 0 | 1 | 0 | 1 | Adresse de la banque | 0 | Adresse de la colonne | READ : lire une donnée depuis la ligne active. |
| 0 | 1 | 0 | 1 | Adresse de la banque | 1 | Adresse de la colonne | READA : lire une donnée depuis la ligne active, avec rafraichissement automatique de la ligne. |
| 0 | 1 | 0 | 0 | Adresse de la banque | 0 | Adresse de la colonne | WRITE : écrire une donnée depuis la ligne active. |
| 0 | 1 | 0 | 0 | Adresse de la banque | 1 | Adresse de la colonne | WRITEA : écrire une donnée depuis la ligne active, avec rafraichissement automatique de la ligne. |
| 0 | 0 | 1 | 1 | Adresse de la banque | Adresse de la ligne | ACT : charge une ligne dans le tampon de ligne. | |
| 0 | 0 | 1 | 0 | Adresse de la banque | 0 | X | PRECHARGE : précharge le tampon de ligne dans la banque voulue. |
| 0 | 0 | 1 | 0 | Adresse de la X | 1 | X | PRECHARGE ALL : précharge le tampon de ligne dans toutes les banques. |
| 0 | 0 | 0 | 1 | X | Auto refresh : Demande de rafraichissement, gérée par la SDRAM. | ||
| 0 | 0 | 0 | 0 | 00 | Nouveau contenu du registre de mode | LOAD MODE REGISTER : configure le registre de mode. | |
Les commandes READ et WRITE ne peuvent se faire qu'une fois que la banque a été activée par une commande ACT. Une fois la banque activée par une commande ACT, il est possible d'envoyer plusieurs commandes READ ou WRITE successives. Ces lectures ou écritures accèderont à la même ligne, mais à des colonnes différentes. Le commandes ACT se font à partir de l'état de repos, l'état où toutes les banques sont préchargées. Par contre, les commandes MODE REGISTER SET et AUTO REFRESH ne peuvent se faire que si toutes les banques sont désactivées.
Le fonctionnement simplifié d'une SDRAM peut se résumer dans ce diagramme :

Les mémoires DDR
modifierLes mémoires SDRAM récentes sont des mémoires de type dual data rate, ce qui fait qu'elles portent le nom de mémoires DDR. Pour rappel, les mémoires dual data rate ont un plan mémoire deux fois plus large que le bus mémoire, avec un bus mémoire allant à une fréquence double. Par double, on veut dire que les transferts sur le bus mémoire ont lieu sur les fronts montants et descendants de l'horloge. Il y a donc deux transferts de données sur le bus pour chaque cycle d'horloge, ce qui permet de doubler le débit sans toucher à la fréquence du plan mémoire lui-même.
Les mémoires DDR sont standardisées par un organisme international, le JEDEC, et ont été déclinées en plusieurs générations : DDR1, DDR2, DDR3, et DDR4. La différence entre ces modèles sont très nombreuses, mais les plus évidentes sont la fréquence de la mémoire et du bus mémoire. D'autres différences mineures existent entre les SDRAM et les mémoires DDR.
Par exemple, la tension d'alimentation des mémoires DDR est plus faible que pour les SDRAM. ET elle a diminué dans le temps, d'une génération de DDR à l'autre. Avec les mémoires DDR2,la tension d'alimentation est passée de 2,5/2,6 Volts à 1,8 Volts. Avec les mémoires DDR3, la tension d'alimentation est notamment passée à 1,5 Volts.
Les performances des mémoires DDR
modifierLes mémoires SDRAM ont évolué dans le temps, mais leur temps d'accès/fréquence n'a pas beaucoup changé. Il valait environ 10 nanosecondes pour les SDRAM, approximativement 5 ns pour la DDR-400, il a peu évolué pendant la génération DDR et DDR3, avant d'augmenter pendant les générations DDR4 et de stagner à nouveau pour la génération DDR5. L'usage du DDR, puis du QDR, visait à augmenter les performances malgré la stagnation des temps d'accès. En conséquence, la fréquence du bus a augmenté plus vite que celle des puces mémoire pour compenser.
| Année | Type de mémoire | Fréquence de la mémoire (haut de gamme) | Fréquence du bus | Coefficient multiplicateur entre les deux fréquences |
|---|---|---|---|---|
| 1998 | DDR 1 | 100 - 200 MHz | 200 - 400 MHz | 2 |
| 2003 | DDR 2 | 100 - 266 MHz | 400 - 1066 MHz | 4 |
| 2007 | DDR 3 | 100 - 266 MHz | 800 - 2133 MHz | 8 |
| 2014 | DDR 4 | 200 - 400 MHz | 1600 - 3200 MHz | 8 |
| 2020 | DDR 5 | 200 - 450 MHz | 3200 - 7200 MHz | 8 à 16 |
Une conséquence est que la latence CAS, exprimée en nombre de cycles, a augmenté avec le temps. Si vous comparez des mémoires DDR2 avec une DDR4, par exemple, vous allez voir que la latence CAS est plus élevée pour la DDR4. Mais c'est parce que la latence est exprimée en nombre de cycles d'horloge, et que la fréquence a augmentée. En comparant les temps d'accès exprimés en secondes, on voit une amélioration.
Les commandes des mémoires DDR
modifierLes commandes des mémoires DDR sont globalement les mêmes que celles des mémoires SDRAM, vues plus haut. Les modifications entre SDRAM, DDR1, DDR2, DDR3, DDR4, et DDR5 sont assez mineures. Les seules différences sont l'addition de bits pour la transmission des adresses, des bits en plus pour la sélection des banques, un registre de mode un peu plus grand (13 bits sur la DDR 2, au lieu de 10 sur les SDRAM). En clair, une simple augmentation quantitative.
Avant la DDR4, les modifications des commandes sont mineures. La DDR2 supprime la commande Burst Terminate, la DDR3 et la DDR4 utilisent le bit A12 pour préciser s'il faut faire une rafale complète, ou une rafale de moitié moins de données. Mais avec la DDR4, les choses changent, notamment au niveau de la commande ACT. Avec l'augmentation de la capacité des barrettes mémoires, la taille des adresses est devenue trop importante. Il a donc fallu rajouter des bits d'adresses. Mais pour éviter d'avoir à rajouter des broches sur des barrettes déjà bien fournies, les concepteurs du standard DDR4 ont décidé de ruser. Lors d'une commande ACT, les bits RAS, CAS et WE sont utilisés comme bits d'adresse, alors qu'ils ont leur signification normale pour les autres commandes. Pour éviter toute confusion, un nouveau bit ACT est ajouté pour indiquer la présence d'une commande ACT : il est à 1 pour une commande ACT, 0 pour les autres commandes.
| Bit CS | Bit ACT | Bit RAS | Bit CAS | Bit WE | Bits de sélection de banque (2 bits) | Bit du bas d'adresse A10 | Reste du bus d'adresse | Nom de la commande : Description |
|---|---|---|---|---|---|---|---|---|
| 1 | X | Absence de commandes. | ||||||
| 0 | 0 | 1 | 1 | 1 | X | No Operation : Pas d'opération | ||
| 0 | 0 | 1 | 1 | 0 | X | Burst Terminante : Arrêt d'un accès en rafale en cours. | ||
| 0 | 0 | 1 | 0 | 1 | Adresse de la banque | 0 | Adresse de la colonne | READ : lire une donnée depuis la ligne active. |
| 0 | 0 | 1 | 0 | 1 | Adresse de la banque | 1 | Adresse de la colonne | READA : lire une donnée depuis la ligne active, avec rafraichissement automatique de la ligne. |
| 0 | 0 | 1 | 0 | 0 | Adresse de la banque | 0 | Adresse de la colonne | WRITE : écrire une donnée depuis la ligne active. |
| 0 | 0 | 1 | 0 | 0 | Adresse de la banque | 1 | Adresse de la colonne | WRITEA : écrire une donnée depuis la ligne active, avec rafraichissement automatique de la ligne. |
| 0 | 1 | Adresse de la ligne (bits de poids forts) | Adresse de la banque | Adresse de la ligne (bits de poids faible) | ACT : charge une ligne dans le tampon de ligne. | |||
| 0 | 0 | 0 | 1 | 0 | Adresse de la banque | 0 | X | PRECHARGE : précharge le tampon de ligne dans la banque voulue. |
| 0 | 0 | 0 | 1 | 0 | Adresse de la X | 1 | X | PRECHARGE ALL : précharge le tampon de ligne' dans toutes les banques. |
| 0 | 0 | 0 | 0 | 1 | X | Auto refresh : Demande de rafraichissement, gérée par la SDRAM. | ||
| 0 | 0 | 0 | 0 | 0 | 00 | Nouveau contenu du registre de mode | LOAD MODE REGISTER : configure le registre de mode. | |
Les VRAM des cartes vidéo
modifierLes cartes graphiques ont des besoins légèrement différents des DRAM des processeurs, ce qui fait qu'il existe des mémoires DRAM qui leur sont dédiées. Elles sont appelés des Graphics RAM (GRAM). La plupart incorporent des fonctionnalités utiles uniquement pour les mémoires vidéos, comme des fonctionnalités de masquage (appliquer un masque aux données lue ou à écrire), ou le remplissage d'un bloc de mémoire avec une donnée unique.
Les anciennes cartes graphiques et les anciennes consoles utilisaient de la DRAM normale, faute de mieux. La première GRAM utilisée était la NEC μPD481850, qui a été utilisée sur la console de jeu PlayStation, à partir de son modèle SCPH-5000. D'autres modèles de GRAM ont rapidement suivi. Les anciennes consoles de jeu, mais aussi des cartes graphiquesn utilisaient des GRAM spécifiques.
Les mémoires vidéo double port
modifierSur les premières consoles de jeu et les premières cartes graphiques, le framebuffer était mémorisé dans une mémoire vidéo spécialisée appelée une mémoire vidéo double port. Le premier port était connecté au processeur ou à la carte graphique, alors que le second port était connecté à un écran CRT. Aussi, nous appellerons ces deux port le port CPU/GPU et l'autre sera appelé le port CRT. Le premier port était utilisé pour enregistrer l'image à calculer et faire les calculs, alors que le second port était utilisé pour envoyer à l'écran l'image à afficher. Le port CPU/GPU est tout ce qu'il y a de plus normal : on peut lire ou écrire des données, en précisant l'adresse mémoire de la donnée, rien de compliqué. Le port CRT est assez original : il permet d'envoyer un paquet de données bit par bit.
De telles mémoires étaient des mémoires à tampon de ligne, dont le support de mémorisation était organisé en ligne et colonnes. Une ligne à l'intérieur de la mémoire correspond à une ligne de pixel à l'écran, ce qui se marie bien avec le fait que les anciens écrans CRT affichaient les images ligne par ligne. L'envoi d'une ligne à l'écran se fait bit par bit, sur un câble assez simple comme un câble VGA ou autre. Le second port permettait de faire cela automatiquement, en permettant de lire une ligne bit par bit, les bits étant envoyés l'un après l'autre automatiquement.
Pour cela, les mémoires vidéo double port incorporaient un tampon de ligne spécialisé pour le port lié à l'écran. Ce tampon de ligne n'était autre qu'un registre à décalage, contrairement au tampon de ligne normal. Lors de l'accès au second port, la carte graphique fournissait un numéro de ligne et la ligne était chargée dans le tampon de ligne associé à l'écran. La carte graphique envoyait un signal d'horloge de même fréquence que l'écran, qui commandait le tampon de ligne à décalage : un bit sortait à chaque cycle d'écran et les bits étaient envoyé dans le bon ordre.
Les mémoires SGRAM et GDDR
modifierDe nos jours, les cartes graphiques n'utilisent plus de mémoires double port, mais des mémoires simple port. Les mémoires graphiques actuelles sont des SDRAM modifiées pour fonctionner en tant que Graphic RAM. Les plus connues sont les mémoires GDDR, pour graphics double data rate, utilisées presque exclusivement sur les cartes graphiques. Il en existe plusieurs types pendant que j'écris ce tutoriel : GDDR, GDDR2, GDDR3, GDDR4, et GDDR5. Mais attention, il y a des différences avec les DDR normales. Par exemple, les GDDR ont une fréquence plus élevée que les DDR normales, avec des temps d'accès plus élevés (sauf pour le tCAS). De plus, elles sont capables de laisser ouvertes deux lignes en même temps. Par contre, ce sont des mémoires simple port.
Les mémoires SLDRAM, RDRAM et associées
modifierLes mémoires précédentes sont généralement associées à des bus larges. Les mémoires SDRAM et DDR modernes ont des bus de données de 64 bits de large, avec des d'adresse et de commande de largeur similaire. Le nombre de fils du bus mémoire dépasse facilement la centaine de fils, avec autant de broches sur les barrettes de mémoire. Largeur de ces bus pose de problèmes problèmes électriques, dont la résolution n'est pas triviale. En conséquence, la fréquence du bus mémoire est généralement moins performantes comparé à ce qu'on aurait avec un bus moins large.
Mais d'autres mémoires DRAM ont exploré une solution alternative : avoir un bus peu large mais de haute fréquence, sur lequel on envoie les commandes/données en plusieurs fois. Elles sont regroupées sous le nom de DRAM à commutation par paquets. Elles utilisent des bus spéciaux, où les commandes/adresses/données sont transmises par paquets, par trames, en plusieurs fois. En théorie, ce qu'on a dit sur le codage des trames dans le chapitre sur le bus devrait s'appliquer à de telles mémoires. En pratique, les protocoles de transmission sur le bus mémoire sont simplifiés, pour gérer le fonctionnement à haute fréquence. Le processeur envoie des paquets de commandes, les mémoires répondent avec des paquets de données ou des accusés de réception.
Les mémoires à commutation par paquets sont peu nombreuses. Les plus connues sont les mémoires conçues par la société Rambus, à savoir la RDRAM (Rambus DRAM) et ses deux successeurs XDR RAM et XDR RAM 2. La Synchronous-link DRAM (SLDRAM) est un format concurrent conçu par un consortium de plusieurs concepteurs de mémoire.
La SLDRAM (Synchronous-link DRAM)
modifierLes mémoires SLDRAM avaient un bus de données de 64 bits allant à 200-400 Hz, avec technologie DDR, ce qui était dans la norme de l'époque pour la fréquence (début des années 2000). Elle utilisait un bus de commande de 11 bits, qui était utilisé pour transmettre des commandes de 40 bits, transmises en quatre cycles d'horloge consécutifs (en réalité, quatre fronts d'horloge donc deux cycles en DDR). Le bus de données était de 18 bits, mais les transferts de donnée se faisaient par paquets de 4 à 8 octets (32-65 bits). Pour résumer, données et commandes sont chacunes transmises en plusieurs cycles consécutifs, sur un bus de commande/données plus court que les données/commandes elle-mêmes.
Là où les SDRAM sélectionnent la bonne barrette grâce à des signaux de commande dédiés, ce n'est pas le cas avec la SLDRAM. A la place, chaque barrette de mémoire reçoit un identifiant, un numéro codé sur 7-8 bits. Les commandes de lecture/écriture précisent l'identifiant dans la commande. Toutes les barrettes reçoivent la commande, elles vérifient si l'identifiant de la commande est le leur, et elles la prennent en compte seulement si c'est le cas.
Voici le format d'une commande SLDRAM. Elle contient l'adresse, qui regroupe le numéro de banque, le numéro de ligne et le numéro de colonne. On trouve aussi un code commande qui indique s'il faut faire une lecture ou une écriture, et qui configure l'accès mémoire. Il configure notamment le mode rafale, en indiquant s'il faut lire/écrire 4 ou 8 octets. Enfin, il indique s'il faut fermer la ligne accédée une fois l'accès terminé, ou s'il faut la laisser ouverte. Le code commande peut aussi préciser que la commande est un rafraichissement ou non, effectuer des opérations de configuration, etc. L'identifiant de barrette mémoire est envoyé en premier, histoire que les barrettes sachent précocement si l'accès les concerne ou non.
| FLAG | CA9 | CA8 | CA7 | CA6 | CA5 | CA4 | CA3 | CA2 | CA1 | CA0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Identifiant de barrette mémoire | Code de commande | ||||||||
| 0 | Code de commande | Banque | Ligne | |||||||
| 0 | Ligne | 0 | ||||||||
| 0 | 0 | 0 | 0 | Colonne | ||||||
Les mémoires Rambus
modifierLes mémoires conçues par la société Rambus regroupent la RDRAM (Rambus DRAM) et ses deux successeurs XDR RAM et XDR RAM 2.
Les toutes premières étaient les mémoires RDRAM, où le bus permettait de transmettre soit des commandes (adresse inclue), soit des données, avec un multiplexage total. Le processeur envoie un paquet contenant commandes et adresse à la mémoire, qui répond avec un paquet d'acquittement. Lors d'une lecture, le paquet d'acquittement contient la donnée lue. Lors d'une écriture, le paquet d'acquittement est réduit au strict minimum. Le bus de commandes est réduit au strict minimum, à savoir l'horloge et quelques bits absolument essentiels, les bits RW est transmis dans un paquet et n'ont pas de ligne dédiée, pareil pour le bit OE. Toutes les barrettes de mémoire doivent vérifier toutes les transmissions et déterminer si elles sont concernées en analysant l'adresse transmise dans la trame.
Elles ont été utilisées dans des PC ou d'anciennes consoles de jeu. Par exemple, la Nintendo 64 incorporait 4 mébioctets de mémoire RDRAM en tant que mémoire principale. La RDRAM de la Nintendo 64 était cadencée à 500 MHz, utilisait un bus de 9 bits, et avait un débit binaire maximal théorique de 500 MB/s. La Playstation 2 contenait quant à elle 32 mébioctets de RDRAM en dual-channel, pour un débit binaire de 3.2 Gibioctets par seconde. Les processeurs Pentium 3 pouvaient être associés à de la RDRAM sur certaines mères. Les Pentium 4 étaient eux aussi associés à la de RDRAM, mais les cartes mères ne géraient que ce genre de mémoire. La Playstation 3 contenait quant à elle de la XDR RAM.
Les barrettes de mémoire DRAM
modifier
Dans les PC, les mémoires prennent la forme de barrettes mémoires. Les barrettes de mémoire se fixent à la carte mère sur un connecteur standardisé, appelé slot mémoire. Le dessin ci-contre montre une barrette de mémoire, celui-ci ci-dessous est celui d'un slot mémoire.

Le format des barrettes de mémoire
modifierSur le schéma de droite, on remarque facilement les boitiers de DRAM, rectangulaires, de couleur sombre. Chaque barrette combine ces puces de manière à additionner leurs capacités : on peut ainsi créer une mémoire de 8 gibioctets à partir de 8 puces d'un gibioctet, par exemple. Ils sont soudés sur un PCB en plastique vert sur lequel sont gravés des connexions métalliques. Certaines barrettes ont des puces mémoire d'un seul côté alors que d'autres en ont sur les deux faces. Cela permet de distinguer les barrettes SIMM et DIMM.
- Les barrettes SIMM ont des puces sur une seule face de la barrette. Elles étaient utilisées pour les mémoires FPM et EDO-RAM.
- Les barrettes DIMM ont des puces sur les deux côtés. Elles sont utilisées sur les SDRAM et les DDR.
 |
 |
Les trucs dorés situés en bas des barrettes de mémoire sont des broches qui connectent la barrette au bus mémoire. Les barrettes des mémoires FPM/EDO/SDRAM/DDR n'ont pas le même nombre de broches, pour des raisons de compatibilité.
| Type de barrette | Type de mémoire | Nombre de broches |
|---|---|---|
| SIMM | FPM/EDO | 30 |
| 72 | ||
| DIMM | SDRAM | 168 |
| DDR | 184 | |
| DDR2 | 214, 240 ou 244, suivant la barrette ou la carte mère. | |
| DDR3 | 204 ou 240, suivant la barrette ou la carte mère. |
Enfin, les barrettes n'ont pas le même format, car il n'y a pas beaucoup de place à l'intérieur d'un PC portable, ce qui demande de diminuer la taille des barrettes. Les barrettes SO-DIMM, pour ordinateurs portables, sont différentes des barrettes DIMM normales des DDR/SDRAM.
 |
 |
Les barrettes de Rambus ont parfois été appelées des barrettes RB-DIMM, mais ce sont en réalité des DIMM comme les autres. La différence principale est que la position des broches n'était pas la même que celle des formats DIMM normaux, sans compter que le connecteur Rambus n'était pas compatible avec les connecteurs SDR/DDR normaux.
Les interconnexions à l'intérieur d'une barrette de mémoire
modifierLes boîtiers de DRAM noirs sont connectés au bus par le biais de connexions métalliques. Toutes les puces sont connectées aux bus d'adresse et de commande, ce qui permet d'envoyer la même adresse/commande à toutes les puces en même temps. La manière dont ces puces sont reliées au bus de commande dépend selon la mémoire utilisée.
Les DDR1 et 2 utilisent ce qu'on appelle une topologie en T, illustrée ci-dessous. On voit que le bus de commande forme une sorte d'arbre, dont chaque extrémité est connectée à une puce. La topologie en T permet d'égaliser le délai de transmission des commandes à travers le bus : la commande transmise arrive en même temps sur toutes les puces. Mais elle a de nombreux défauts, à savoir qu'elle fonctionne mal à haute fréquence et qu'elle est aussi difficile à router parce que les nombreuses connexions posent problèmes.

En comparaison, les DDR3 utilisent une topologie fly-by, où les puces sont connectées en série sur le bus de commande/adresse. La topologie fly-by n'a pas les problèmes de la topologie en T : elle est simple à router et fonctionne très bien à haute fréquence.

Les barrettes tamponnées (à registres)
modifierCertaines barrettes intègrent un registre tampon, qui fait l'interface entre le bus et la barrette de RAM. L'utilité est d'améliorer la transmission du signal sur le bus mémoire. Sans ce registre, les signaux électriques doivent traverser le bus, puis traverser les connexions à l'intérieur de la barrette, jusqu'aux puces de mémoire. Avec un registre tampon, les signaux traversent le bus, sont mémorisés dans le registre et c'est tout. Le registre envoie les commandes/données jusqu'aux puces mémoire, mais le signal a été régénéré par le registre. Le signal transmis est donc de meilleure qualité, ce qui augmente la fiabilité du système mémoire. Le défaut est que la présence de ce registre fait que les barrettes ont un temps de latence est plus important que celui des barrettes normales, du fait de la latence du registre.
Les barrettes de ce genre sont appelées des barrettes RIMM. Il en existe deux types :
- Avec les barrettes RDIMM, le registre fait l'interface pour le bus d'adresse et le bus de commande, mais pas pour le bus de données.
- Avec les barrettes LRDIMM (Load Reduced DIMMs), le registre fait tampon pour tous les bus, y compris le bus de données.

Le Serial Presence Detect
modifier
Toute barrette de mémoire assez récente contient une petite mémoire ROM qui stocke les différentes informations sur la mémoire : délais mémoire, capacité, marque, etc. Cette mémoire s'appelle le Serial Presence Detect, aussi communément appelé le SPD. Ce SPD contient non seulement les timings de la mémoire RAM, mais aussi diverses informations, comme le numéro de série de la barrette, sa marque, et diverses informations. Le SPD est lu au démarrage de l'ordinateur par le BIOS, afin de pourvoir configurer ce qu'il faut.
Le contenu de ce fameux SPD est standardisé par un organisme nommé le JEDEC, qui s'est chargé de standardiser le contenu de cette mémoire, ainsi que les fréquences, timings, tensions et autres paramètres des mémoires SDRAM et DDR. Pour les curieux, vous pouvez lire la page wikipédia sur le SPD, qui donne son contenu pour les mémoires SDR et DDR : Serial Presence Detect.
Les mémoires ROM ou SRAM ont généralement une interface simple, à laquelle le processeur peut s'interfacer directement. Mais pour d'autres mémoires, notamment les DRAM, ce n'est pas le cas. C'est le cas sur les mémoires où les adresses sont multiplexées, sur les DRAM qui nécessitent un rafraichissement, et bien d'autres. Pour les mémoires multiplexées, connecter le processeur directement sur ces mémoires n'est pas possible : le bus d'adresse du processeur et celui de la mémoire ne collent pas. Pour le rafraichissement, on pourrait le déléguer au processeur, mais cela imposerait des contraintes assez fortes qui sont loin d'être idéales. Et il y a bien d'autres raisons qui font que le processeur ne peut pas s'interfacer facilement avec certaines mémoires. Imaginez par exemple, les mémoires à bus de donnée série, où les données sont communiquées bit par bit.
Bref, pour gérer ces problèmes intrinsèques aux mémoires DRAM et à quelques autres modèles, les mémoires ne sont pas connectées directement au processeur. À la place, on ajoute un composant entre le processeur et la mémoire : le contrôleur mémoire externe. Celui-ci est placé sur la carte mère ou dans le processeur, et ne doit pas être confondu avec le contrôleur mémoire intégré dans la mémoire. Ce chapitre va voir quels sont les rôles du contrôleur mémoire, son interface et ce qu'il y a à l'intérieur.
Le contrôleur mémoire externe est relié au CPU par un bus, et est connecté aux barrettes ou boitiers de DRAM via le bus mémoire proprement dit. Les anciens contrôleurs mémoire étaient des composants séparés du processeur, du chipset ou du reste de la carte mère. Par exemple, les composants Intel 8202, Intel 8203 et Intel 8207 étaient des contrôleurs mémoire pour DRAM qui étaient vendus dans des boitiers DIP et étaient soudés sur la carte mère. Par la suite, ils ont été intégré au chipset de la carte mère pendant les décennies 90-2000. Après les années 2000, ils ont été intégrés dans les processeurs.
Les rôles et l'interface du contrôleur mémoire
modifierL'interface du contrôleur mémoire, à savoir ses broches d'entrées/sorties et leur signification, est généralement très simple. Il se connecte au processeur et à la mémoire, ce qui fait qu'il a deux ports : un qui a la même interface mémoire que le processeur, un autre qui a la même interface que la mémoire. Cela trahit d'ailleurs son rôle principal, qui est de transformer les requêtes de lecture/écriture provenant du processeur en une suite de commandes acceptée par la mémoire.
En effet, les requêtes du processeur ne sont pas forcément compatibles avec les entrées de la mémoire. Un accès mémoire typique venant du processeur contient juste une adresse à lire/écrire, le bit R/W qui indique s'il faut faire une lecture ou une écriture, et éventuellement une donnée à écrire. Mais, nous avons vu que les accès mémoires sur une DRAM sont multiplexés : on envoie l'adresse en deux fois : la ligne d'abord, puis la colonne. De plus, il faut générer les signaux RAS, CAS et bien d'autres. Le tout est illustré ci-dessous.

La traduction d'adresse
modifierNotons que cette fonction d’interfaçage implique beaucoup de choses, la première étant que les adresses du processeur sont traduites en adresses compatibles avec la mémoire. Sur les mémoires DRAM, cela signifie que l'adresse est découpée en une adresse de ligne et une adresse de colonne, envoyées l'une après l'autre. Mais ce n'est pas la seule opération de conversion possible. Il y a aussi le cas où le bus d'adresse et le bus de données sont fusionnés. Nous avions vu cela dans le chapitre sur l'interface des mémoires. Dans ce cas, on peut envoyer soit une adresse, soit lire/écrire une donnée sur le bus, mais on ne peut pas faire les deux en même temps. Un bit ALE indique si le bus est utilisé en tant que bus d'adresse ou bus de données. Le contrôleur mémoire gère cette situation, en fixant le bit ALE et en envoyant séparément adresse et donnée pour les écritures.
Une autre possibilité est la gestion de l'entrelacement, qui intervertit certains bits de l'adresse lors des accès mémoires. Rappelons qu'avec l'entrelacement, des adresses consécutives sont placées dans des mémoires séparées, ce qui demande de jouer avec les bits d'adresse, chose qui est dévolue à l'étape de traduction d'adresse du contrôleur mémoire.
Une autre possibilité est le cas où les adresses du processeur n'ont pas la même taille que les adresses du bus mémoire, le contrôleur peut se charger de tronquer les adresses mémoires pour les faire rentrer dans le bus d'adresse. Cela arrive quand la mémoire a des mots mémoires plus longs que le byte du processeur. Prenons l'exemple où le processeur gère des bytes de 1 octet, alors que la mémoire a des mots mémoires de 4 octets. Lors d'une lecture, le contrôleur mémoire va lire des blocs de 4 octets et récupérera l'octet demandé par le processeur. En conséquence, la lecture dans la mémoire utilise une adresse différente, plus courte que celle du processeur : il faut tronquer les bits de poids faible lors de la lecture, mais les utiliser lors de la sélection de l'octet.
Les séquencement des commandes mémoires
modifierUne demande de lecture/écriture faite par le processeur se fait en plusieurs étapes sur une mémoire SDRAM. Il faut d'abord précharger le tampon de ligne avec une commande PRECHARGE, puis envoyer une commande ACT qui fixe l'adresse de ligne, et enfin envoyer une commande READ/WRITE. Et encore, ce cas est simple : il y a des opérations mémoires qui sont beaucoup plus compliquées. Et outre l'ordre d'envoi des commandes pour chaque requête, il faut aussi tenir compte des timings mémoire, à savoir le fait que ces commandes doivent être séparées par des temps d'attentes bien précis. Par exemple, sur certaines mémoires, il faut attendre 2 cycles entre une commande ACT et une commande READ, il faut attendre 6 cycles avant deux commandes WRITE consécutives, etc.
Chaque requête du processeur correspond donc à une séquence de commandes envoyées à des timings bien précis. Le contrôleur mémoire s'occupe de faire cette traduction des requêtes en commandes si besoin. Notons que cette traduction demande deux choses : traduire une requête processeur en une série de commandes à faire dans un ordre bien précis, et la gestion des timings. Les deux sont parfois effectués par des circuits séparés, comme nous le verrons plus bas.
Le rafraichissement mémoire
modifierN'oublions pas non plus la gestion du rafraichissement mémoire, qui est dévolue au contrôleur mémoire ! Il pourrait être réalisé par le processeur, mais ce ne serait pas pratique. Il faudrait que le processeur lui-même incorpore un compteur dédié pour le rafraichissement des lignes, et qu'il dispose de la circuiterie pour envoyer un signal de rafraichissement à intervalles réguliers. Et le processeur devrait régulièrement s'interrompre pour s'occuper du rafraichissement, ce qui perturberait l’exécution des programmes en cours d'une manière assez subtile, mais pas assez pour ne pas poser de problèmes. Pour éviter cela, on préfère déléguer le rafraichissement au contrôleur mémoire externe.
La traduction des signaux et l’horloge
modifierA cela, il faut ajouter l'interface électrique et la gestion de l'horloge.
Rappelons que la mémoire ne va pas à la même fréquence que le processeur et qu'il y a donc une adaptation à faire. Soit le contrôleur mémoire génère la fréquence qui commande la mémoire, soit il prend en entrée une fréquence de base qu'il multiplie pour obtenir la fréquence désirée. Les deux solutions sont presque équivalentes, si ce n'est que les circuits impliqués ne sont pas les mêmes. Dans le premier cas, le contrôleur doit embarquer un circuit oscillateur, qui génère la fréquence demandée. Dans l'autre cas, un simple multiplieur/diviseur de fréquence suffit et c'est généralement une PLL qui est utilisée pour cela. Il va de soi qu'un générateur de fréquence est beaucoup plus complexe qu'une simple PLL.
Un autre point est que la mémoire peut avoir une interface série, à savoir que les données sont transmises bit par bit. Dans ce cas, les mots mémoire sont transférés bit par bit à la mémoire ou vers le processeur. La traduction d'un mot mémoire de N bits en une transmission bit par bit est réalisée par cette interface électrique. Un simple registre à décalage suffit dans les cas les plus simples.
Enfin, n'oublions pas l’interfaçage électrique, qui traduit les signaux du processeur en signaux compatibles avec la mémoire. Il est en effet très fréquent que la mémoire et le processeur n'utilisent pas les mêmes tensions pour coder un bit, ce qui fait qu'elles ne sont pas compatibles. Dans ce cas, le contrôleur mémoire fait la conversion.
Les autres fonctions (résumé)
modifierPour résumer, le contrôleur mémoire externe gère au minimum la traduction des accès mémoires en suite de commandes (ACT, sélection de ligne, etc.), le rafraîchissement mémoire, ainsi que l’interfaçage électrique. Mais il peut aussi incorporer diverses optimisations pour rendre la mémoire plus rapide. Par exemple, c'est lui qui s'occupe de l'entrelacement. Il gère aussi le séquencement des accès mémoires et peut parfois réorganiser les accès mémoires pour mieux utiliser les capacités de pipelining d'une mémoire synchrone, ou pour mieux utiliser les accès en rafale. Évidemment, cette réorganisation ne se voit pas du côté du processeur, car le contrôleur remet les accès dans l'ordre. Si les commandes mémoires sont envoyées dans un ordre différent de celui du processeur, le contrôleur mémoire fait en sorte que cela ne se voit pas. Notamment, il reçoit les données lues depuis la mémoire et les remet dans l'ordre de lecture demandé par le processeur. Mais nous reparlerons de ces capacités d'ordonnancement plus bas.
L'architecture du contrôleur
modifierDans les grandes lignes, on peut découper le contrôleur mémoire externe en deux grands ensembles : un gestionnaire mémoire et une interface physique. Cette dernière s'occupe, comme dit haut, de la traduction des tensions entre processeur et mémoire, ainsi que de la génération de l'horloge. Si la mémoire est une mémoire série, elle contient un registre à décalage pour transformer un mot mémoire de N bits en signal série transmis bit par bit. Elle s'occupe aussi de la correction et de la détection d'erreur si la mémoire gère cette fonctionnalité. En clair, elle gère tout ce qui a trait à la transmission des bits, au niveau électronique voire électrique.
Le séquenceur mémoire gère tout le reste. L'interface électrique est presque toujours présente, alors que le séquenceur peut parfois être réduit à peu de chagrin sur certaines mémoires. le gestionnaire mémoire est découpé en deux : un circuit qui s'occupe de la gestion des commandes mémoires proprement dit, et un circuit qui s'occupe des échanges de données avec le processeur. Ce dernier prévient le processeur quand une donnée lue est disponible et lui fournit la donnée avec, il prévient le processeur quand une écriture est terminée, etc.

Le séquenceur mémoire
modifierLe rôle principal du contrôleur est la traduction des requêtes processeurs en une suite de commandes mémoire. Pour faire cette traduction, il y a plusieurs méthodes. Dans le cas le plus simple, le contrôleur mémoire contient un circuit séquentiel appelé une machine à état fini, aussi appelée séquenceur, qui s'occupe de cette traduction. Il s'occupe à la fois de la traduction des requêtes en suite de commande et des timings d'envoi des commandes à la mémoire. Mais cette organisation marche assez mal avec la gestion du rafraichissement. Aussi, il est parfois préférable de séparer la traduction des requêtes en suite de commandes, et la gestion des timings d'envoi de ces commandes à la mémoire. S'il y a séparation, le séquenceur est alors séparé en deux : un circuit de traduction et un circuit d’ordonnancement des commandes. Ce dernier reçoit les commandes du circuit de traduction, les mets en attente et les envoie à la mémoire quand les timings le permettent.
Notons que cela implique une fonction de mise en attente des commandes. Les raisons à cela sont multiples. Le cas le plus simple est celui des requêtes processeur qui correspondent à plusieurs commandes. Prenons l'exemple d'une requête de lecture se traduit en une série de deux commandes : ACT et READ. La commande ACT peut être envoyée directement à la mémoire si elle est libre, mais la commande READ doit être envoyée deux cycles plus tard. Cette dernière doit donc être mise en attente durant deux cycles. Et on pourrait aussi citer le cas où plusieurs requêtes processeur arrivent très vite, plus vite que la mémoire ne peut les traiter. Si des requêtes arrivent avant que la mémoire n'ait pu terminer la précédente, elles doivent être mises en attente.
Notons que pour les mémoires SDRAM et DDR, ce circuit décide s'il faut ajouter ou non des commandes PRECHARGE. Certains accès demandent des commandes PRECHARGE alors que d'autres peuvent s'en passer. C'est aussi lui qui détecte les accès en rafale et envoie les commandes adaptées. Notons que quand on accède à des données consécutives, on a juste à changer l'adresse de la colonne : pas besoin d'envoyer de commande ACT pour changer de ligne. C'est le séquenceur mémoire qui se charge de cela, et qui détecte les accès en rafale et/ou les accès à des données consécutives. Nous en parlerons plus en détail dans la suite du chapitre, dans la section sur la politique de gestion du tampon de ligne.
Le circuit de gestion du rafraichissement et le circuit d'arbitrage
modifierLa gestion du rafraichissement est souvent séparée de la gestion des commandes de lecture/écriture, et est effectuée dans un circuit dédié, même si ce n'est pas une obligation. Si les deux sont séparés, le circuit de gestion des commandes et le circuit de rafraichissement sont secondés par un circuit d'arbitrage, qui décide qui a la priorité. Ainsi, cela permet que les commandes de rafraichissement et les commandes mémoires ne se marchent pas sur les pieds. Notamment quand une commande mémoire et une commande de rafraichissement sont envoyées en même temps, la commande de rafraichissement a la priorité.
Le circuit d'arbitrage est aussi utilisé quand la mémoire est connectée à plusieurs composants, plusieurs processeurs notamment. Dans ce cas, les commandes des deux processeurs ont tendance à se marcher sur les pieds et le circuit d'arbitrage doit répartir le bus mémoire entre les deux processeurs. Il doit gérer de manière la plus neutre possible les commandes des deux processeurs, de manière à empêcher qu'un processeur monopolise le bus pour lui tout seul.
L'architecture complète du contrôleur mémoire externe
modifierEn clair, le contrôleur mémoire contient notamment un circuit de traduction des requêtes processeur en commandes mémoire, suivi par une FIFO pour mettre en attente les commandes mémoires, un module de rafraichissement, ainsi qu'un circuit d'arbitrage (qui décide quelle requête envoyer à la mémoire). Ajoutons à cela des FIFO pour mettre en attente les données lues ou à écrire, afin qu'elles soient synchronisées par les commandes mémoires correspondantes. Si une commande mémoire est mise en attente, alors les données qui vont avec le sont aussi. Ces FIFOS sont couplées à quelques circuits annexes, le tout formant le circuit d'échange de données avec le processeur, dans le gestionnaire mémoire, vu dans les schémas plus haut.

Le contrôleur mémoire externe est schématiquement composé de quatre modules séparés.
- Le module d'interface avec le processeur gère la traduction d’adresse ;
- Le module de génération des commandes traduit les accès mémoires en une suite de commandes ACT, READ, PRECHARGE, etc.
- Le module d’ordonnancement des commandes contrôle le rafraîchissement, l'arbitrage entre commandes/rafraichissement et les timings des commandes mémoires.
- Le module d'interface physique se charge de la conversion de tension, de la génération d’horloge et de la détection et la correction des erreurs.
Si la mémoire (et donc le contrôleur) est partagée entre plusieurs processeurs, certains circuits sont dupliqués. Dans le pire des cas, tout ce qui précède le circuit d'arbitrage, circuit de rafraichissement mis à part, est dupliqué en autant d’exemplaires qu'il y a de processeurs.
La politique de gestion du tampon de ligne
modifierLe séquenceur mémoire décide quand envoyer les commandes PRECHARGE, qui pré-chargent les bitlines et vident le tampon de ligne. Il peut gérer cet envoi des commandes PRECHARGE de diverses manières nommées respectivement politique de la page fermée, politique de la page ouverte et politique hybride.
La politique de la page fermée
modifierDans le premier cas, le contrôleur ferme systématiquement toute ligne ouverte par un accès mémoire : chaque accès est suivi d'une commande PRECHARGE. Cette méthode est adaptée à des accès aléatoires, mais est peu performante pour les accès à des adresses consécutives. On appelle cette méthode la close page autoprecharge, ou encore politique de la page fermée.
La politique de la page ouverte
modifierAvec des accès consécutifs, les données ont de fortes chances d'être placées sur la même ligne. Fermer celle-ci pour la réactiver au cycle suivant est évident contreproductif. Il vaut mieux garder la ligne active et ne la fermer que lors d'un accès à une autre ligne. Cette politique porte le nom d'open page autoprecharge, ou encore politique de la page ouverte.
Lors d'un accès, la commande à envoyer peut faire face à deux situations : soit la nouvelle requête accède à la ligne ouverte, soit elle accède à une autre ligne.
- Dans le premier cas, on doit juste changer de colonne : c'est un succès de tampon de ligne. Le temps nécessaire pour accéder à la donnée est donc égal au temps nécessaire pour sélectionner une colonne avec une commande READ, WRITE, WRITA, READA. On observe donc un gain signifiant comparé à la politique de la page fermée dans ce cas précis.
- Dans le second cas, c'est un défaut de tampon de ligne et il faut procéder comme avec la politique de la page fermée, à savoir vider le tampon de ligne avec une commande PRECHARGE, sélectionner la ligne avec une commande ACT, avant de sélectionner la colonne avec une commande READ, WRITE, WRITA, READA.
Détecter un succès/défaut de tampon de ligne n'est pas très compliqué. Le séquenceur mémoire a juste à se souvenir des lignes et banques actives avec une petite mémoire : la table des banques. Pour détecter un succès ou un défaut, le contrôleur doit simplement extraire la ligne de l'adresse à lire ou écrire, et vérifier si celle-ci est ouverte : c'est un succès si c'est le cas, un défaut sinon.
Les politiques dynamiques
modifierPour gagner en performances et diminuer la consommation énergétique de la mémoire, il existe des techniques hybrides qui alternent entre la politique de la page fermée et la politique de la page ouverte en fonction des besoins.
La plus simple décide s'il faut maintenir ouverte la ligne en regardant les accès mémoire en attente dans le contrôleur. La politique de ce type la plus simple laisse la ligne ouverte si au moins un accès en attente y accède. Une autre politique laisse la ligne ouverte, sauf si un accès en attente accède à une ligne différente de la même banque. Avec l'algorithme FR-FCFS (First Ready, First-Come First-Service), les accès mémoires qui accèdent à une ligne ouverte sont exécutés en priorité, et les autres sont mis en attente. Dans le cas où aucun accès mémoire ne lit une ligne ouverte, le contrôleur prend l'accès le plus ancien, celui qui attend depuis le plus longtemps comparé aux autres.
Pour implémenter ces techniques, le contrôleur compare la ligne ouverte dans le tampon de ligne et les lignes des accès en attente. Ces techniques demandent de mémoriser la ligne ouverte, pour chaque banque, dans une mémoire RAM : la table des banques, aussi appelée bank status memory. Le contrôleur extrait les numéros de banque et de ligne des accès en attente pour adresser la table des banques, le résultat étant comparé avec le numéro de ligne de l'accès.

Les politiques prédictives
modifierLes techniques prédictives prédisent s'il faut fermer ou laisser ouvertes les pages ouvertes.
La méthode la plus simple consiste à laisser ouverte chaque ligne durant un temps prédéterminé avant de la fermer.
Une autre solution consiste à effectuer ou non la pré-charge en fonction du type d'accès mémoire effectué par le dernier accès. On peut très bien décider de laisser la ligne ouverte si l'accès mémoire précédent était une rafale, et fermer sinon.
Une autre solution consiste à mémoriser les N derniers accès et en déduire s'il faut fermer ou non la prochaine ligne. On peut mémoriser si l'accès en question a causé la fermeture d'une ligne avec un bit. Mémoriser les N derniers accès demande d'utiliser un simple registre à décalage, un registre couplé à un décaleur par 1. Pour chaque valeur de ce registre, il faut prédire si le prochain accès demandera une ouverture ou une fermeture.
- Une première solution consiste à faire la moyenne des bits à 1 dans ce registre : si plus de la moitié des bits est à 1, on laisse la ligne ouverte et on ferme sinon.
- Pour améliorer l'algorithme, on peut faire en sorte que les bits des accès mémoires les plus récents aient plus de poids dans le calcul de la moyenne. Mais rien de transcendant.
- Une autre technique consiste à détecter les cycles d'ouverture et de fermeture de page potentiels. Pour cela, le contrôleur mémoire associe un compteur pour chaque valeur du registre. En cas de fermeture du tampon de ligne, ce compteur est décrémenté, alors qu'une non-fermeture va l'incrémenter : suivant la valeur de ce compteur, on sait si l'accès a plus de chance de fermer une page ou non.
Le ré-ordonnancement des commandes mémoires
modifierLe contrôleur mémoire peut optimiser l'utilisation de la mémoire en changeant l'ordre des requêtes mémoires pour regrouper les accès à la même ligne/banque. Ce ré-ordonnancement marche très bien avec la politique à page ouverte ou les techniques assimilées. Elles ne servent à rien si le séquenceur utilise une politique de la page fermée. L'idée est de profiter du fait qu'une page est restée ouverte pour effectuer un maximum d'accès dans cette ligne avant de la fermer. Les commandes sont réorganisés de manière à regrouper les accès dans la même ligne, afin qu'ils soient consécutifs s'ils ne l'étaient pas avant ré-ordonnancement.
Pour réordonnancer les accès mémoire, le séquenceur vérifie si il y a des dépendances entre les accès mémoire. Les dépendances en question n'apparaissent que si les accès se font à une même adresse. Si tous les accès mémoire se font à des adresses différentes, il n'y a pas de dépendances et ont peut, en théorie, faire les accès dans n'importe quel ordre. Le tout est juste que le séquenceur remette les données lues dans l'ordre demandé par le processeur et communique ces données lues dans cet ordre au processeur. Les dépendances apparaissent quand des accès mémoire se font à une même adresse. le cas réellement bloquant, qui empêche toute ré-ordonnancement, est le cas où une lecture lit une donnée écrite par une écriture précédente. Dans ce cas, la lecture doit avoir lieu après l'écriture.
Une première solution consiste à regrouper plusieurs accès à des données successives en un seul accès en rafale. Le séquenceur analyse les commandes mises en attente et détecte si plusieurs commandes consécutives se font à des adresses consécutives. Si c'est le cas, il fusionne ces commandes en une lecture/écriture en rafale. Une telle optimisation est appelée la combinaison de lecture pour les lectures, et la combinaison d'écriture pour les écritures. Cette méthode d'optimisation ne fait que fusionner des lectures consécutives ou des écritures consécutives, mais ne fait pas de ré-ordonnancement proprement dit. Une variante améliorée combine cette fusion avec du ré-ordonnancement.
Une seconde solution consiste à effectuer les lectures en priorité, quitte à mettre en attente les écritures. Il suffit d'utiliser des files d'attente séparées pour les lectures et écritures. Si une lecture accède à une donnée pas encore écrite dans la mémoire (car mise en attente), la donnée est lue directement dans la file d'attente des écritures. Cela demande de comparer toute adresse à lire avec celles des écritures en attente : la file d'attente est donc une mémoire associative. Cette solution a pour avantage de faciliter l'implémentation de la technique précédente. Séparer les lectures et écritures facilite la fusion des lectures en mode rafale, idem pour les écritures.

Une autre solution répartit les accès mémoire sur plusieurs banques en parallèle. Ainsi, on commence par servir la première requête de la banque 0, puis la première requête de la banque 1, et ainsi de suite. Cela demande de trier les requêtes de lecture ou d'écriture suivant la banque de destination, ce qui demande une file d'attente pour chaque banque.

Les mémoires exotiques
modifierLes mémoires associatives ont un fonctionnement totalement opposé aux mémoires adressables normales : au lieu d'envoyer l'adresse pour accéder à la donnée, on envoie la donnée pour récupérer son adresse. On les appelle aussi des mémoires adressables par contenu, ou encore Content-adressed Memory (CAM) en anglais. Dans ce qui suit, nous utiliserons parfois l'abréviation CAM pour désigner les mémoires associatives.
Les mémoires associatives semblent assez bizarres au premier abord. Quand on y réfléchit, à quoi cela peut-il bien servir de récupérer l'adresse d'une donnée ? La réponse est que les mémoires associatives ont été conçues pour répondre à une problématique assez connue des programmeurs : la recherche d'une donnée dans un ensemble. Généralement, les données manipulées par un programme sont regroupées dans des structures de données organisées : tableaux, listes, graphes, sets, tables de hachage, arbres, etc. Et il arrive fréquemment que l'on recherche une donnée bien précise dedans. Certaines structures de données sont conçues pour accélérer cette recherche, ce qui donne des gains de performance bienvenus, mais au prix d'une complexité de programmation non-négligeable. Les mémoires associatives sont une solution matérielle alternative bien plus rapide. Le processeur envoie la donnée recherchée à la mémoire associative, et celle-ci répond avec son adresse en quelques cycles d'horloge de la mémoire.
Les mémoires associatives dépassent rarement quelques mébioctets et nous n'avons pas encore de mémoire associative capable de mémoriser un gibioctet de mémoire. Leur faible capacité fait qu'elles sont utilisées dans certaines applications bien précises, où les structures de données sont petites. La contrainte de la taille des données fait que ces situations sont très rares. Un cas d'utilisation basique est celui des routeurs, des équipements réseaux qui servent d'intermédiaire de transmission. Chaque routeur contient une table CAM et une table de routage, qui sont souvent implémentées avec des mémoires associatives. Nous en reparlerons dans le chapitre sur le matériel réseau. Elles sont normalement utilisées en supplément d'une mémoire RAM principale. Il arrive plus rarement que la mémoire associative soit utilisée comme mémoire principale. Mais cette situation est assez rare car les mémoires associatives ont souvent une faible capacité.
L'interface des mémoires associatives
modifierUne mémoire associative prend en entrée une donnée et renvoie son adresse. Le bus de donnée est donc accessible en lecture/écriture, comme sur une mémoire normale. Par contre, son bus d'adresse est accessible en lecture et en écriture, c'est une entrée/sortie. L'usage du bus d'adresse comme entrée est similaire à celui d'une mémoire normale : il faut bien écrire des données dans la mémoire associative, ce qui demande de l'adresser comme une mémoire normale. Par contre, le fonctionnement normal de la mémoire associative, à savoir récupérer l'adresse d'une donnée, demande d'utiliser le bus d'adresse comme une sortie, de lire l'adresse dessus.

Lorsque l'on recherche une donnée dans une mémoire CAM, il se peut que la donnée demandée ne soit pas présente en mémoire. La mémoire CAM doit donc préciser si elle a trouvé la donnée recherchée avec un signal dédié. Un autre problème survient quand la donnée est présente en plusieurs exemplaires en mémoire : la mémoire renvoie alors le premier exemplaire rencontré (celui dont l'adresse est la plus petite). D'autres mémoires renvoient aussi les autres exemplaires, qui sont envoyées une par une au processeur.

Notons que tout ce qui a été dit dans les deux paragraphes précédent ne vaut que pour le port de lecture de la mémoire. Les mémoires associatives ont généralement un autre port, qui est un port d'écriture, qui fonctionne comme pour une mémoire normale. Après tout, les donnée présentes dans la mémoire associatives viennent bien de quelque part. Elles sont écrites dans la mémoire associative par le processeur, en passant par ce port d'écriture. Sur ce port, on envoie l'adresse et la donnée à écrire, en même temps ou l'une après l'autre, comme pour une mémoire RAM. Le port d'écriture est géré comme pour une mémoire RAM : la mémoire associative contient un décodeur d'adresse, connecté aux cellules mémoires, et tout ce qu'il faut pour fabriquer une mémoire RAM normale, excepté que le port de lecture est retiré. Cela fait partie des raisons pour lesquelles les mémoires associatives sont plus chères et ont une capacité moindre : elles contiennent plus de circuits à capacité égale. On doit ajouter les circuits qui rendent la mémoire associative, en plus des circuits d'une RAM quasi-normale pour le port d'écriture.
La microarchitecture des mémoires associatives
modifierSi on omet tout ce qui a rapport au port d'écriture, l'intérieur d'une mémoire associative est organisée autour de deux fonctions : vérifier la présence d'une donnée dans chaque case mémoire (effectuer une comparaison, donc), et déterminer l'adresse d'une case mémoire sélectionnée.
La donnée à rechercher dans la mémoire est envoyée à toutes les cases mémoires simultanément et toutes les comparaisons sont effectuées en parallèle.

Une fois la case mémoire qui contient la donnée identifiée, il faut déduire son adresse. Si vous regardez bien, le problème qui est posé est l'exact inverse de celui qu'on trouve dans une mémoire adressable : on n'a pas l'adresse, mais les signaux sont là. La traduction va donc devoir se faire par un circuit assez semblable au décodeur : l'encodeur. Dans le cas où la donnée est présente en plusieurs exemplaires dans la mémoire, la solution la plus simple est d'en sélectionner un seul, généralement celui qui a l'adresse la plus petite (ou la plus grande). Pour cela, l'encodeur doit subir quelques modifications et devenir un encodeur à priorité.

Les cellules CAM des mémoires associatives
modifierAvec une mémoire associative normale, la comparaison réalisée par chaque case mémoire est une comparaison d'égalité stricte : on vérifie que la donnée en entrée correspond exactement à la donnée dans la case mémoire. Cela demande de comparer chaque bit d'entrée avec le bit correspondant mémorisé, avant de combiner les résultats de ces comparaisons. Pour faciliter la compréhension, nous allons considérer que la comparaison est intégrée directement dans la cellule mémoire. En clair, chaque cellule d'une CAM compare le bit d'entrée avec son contenu et fournit un résultat de 1 bit : il vaut 1 si les deux sont identiques, 0 sinon. L'interface d'une cellule mémoire associative contient donc deux entrées et une sortie : une sortie pour le résultat de la comparaison, une entrée pour le bit d'entrée, et une entrée write enable qui dit s'il faut faire la comparaison avec le bit d'entrée ou écrire le bit d'entrée dans la cellule. Une cellule mémoire de ce genre sera appelée une cellule CAM dans ce qui suit.

Les cellules CAM avec une porte NXOR/XOR
modifierLa comparaison de deux bits est un problème des plus simples. Rappelons que nous avions vu dans le chapitre sur les comparateurs qu'un comparateur qui vérifie l"égalité de deux bits n'est autre qu'une porte NXOR. Ce faisant, dans leur implémentation la plus naïve, chaque cellule CAM incorpore une porte NXOR pour comparer le bit d'entrée avec le bit mémorisé. Une cellule CAM ressemble donc à ceci :

Pour limiter le nombre de portes logiques utilisées pour le comparateur, les circuits de comparaison sont fusionnés avec les cellules mémoires. Concrètement, la porte NXOR est fusionnée avec la cellule mémoire, en bidouillant le circuit directement au niveau des transistors. Et cela peut se faire de deux manières, la première donnant les cellules CAM de type NOR et la seconde les cellules mémoire de type NAND. Les cellules CAM de type NOR sont de loin les plus performantes mais consomment beaucoup d'énergie, alors que c'est l'inverse pour les cellules CAM de type NAND.
- Précisons que cette distinction entre cellules mémoire de type NOR et NAND n'a rien à voir avec les mémoires FLASH de type NOR et NAND.


Les cellules CAM de type NAND
modifierAvec les cellules CAM de type NAND, le câblage est le suivant :

Voici comment elle fonctionne :

Les cellules CAM de type NOR
modifierUne cellule CAM de type NOR ressemble à ceci :

Pour comprendre son fonctionnement, il suffit de se rappeler que les transistors se ferment quand on place un 1 sur la grille. De plus, le signal trouvé est mis à 1 par un stratagème technique si les transistors du circuit ne le connectent pas à la masse. Ce qui donne ceci :

Les performances des cellules de mémoire CAM
modifierComme vous pouvez le constater plus haut, les cellules CAM contiennent beaucoup de transistors, surtout quand on les compare avec des cellules de SRAM, voire de DRAM. Une cellule de CAM NOR contient 4 transistors, plus une cellule de SRAM (la bascule D), ce qui fait 10 transistors au total. Une cellule de CAM NAND en contient 2, plus la bascule D/cellule de SRAM, ce qui fait 8 au total. Quelques optimisations diverses permettent d'économiser 1 ou 2 transistors, mais guère plus, ce qui donne entre 6 et 9 transistors dans le meilleur des cas.

En comparaison, une cellule de mémoire SRAM contient 6 transistors en tout, pour une cellule double port, transistor de sélection inclut. Cela ne fait que 1 à 3 transistors de plus, mais cela réduit la densité des mémoires CAM par rapport aux mémoires SRAM d'un facteur qui va de 10 à 50%. Les mémoires CAM ont donc une capacité généralement assez faible, plus faible que celle des SRAM qui n'est déjà pas terrible. Ne faisons même pas la comparaison avec les mémoires DRAM, qui elles ont une densité près de 10 fois meilleures dans le pire des cas. Autant dire que les mémoires CAM sont chères et que l'on ne peut pas en mettre beaucoup dans un ordinateur. C'est sans doute la raison pour laquelle leur utilisation est des plus réduites, limitée à quelques routeurs/switchs et quelques autres circuits assez rares.
La combinaison des résultats des comparaisons pour un mot mémoire
modifierLes cellules CAM comparent le bit stocké avec le bit d'entrée, ce qui donne un résultat de comparaison pour un bit. Les résultats des comparaisons sont alors combinés ensemble, pour donner un signal "trouve/non-trouvé" qui indique si le mot mémoire correspond au mot envoyé en entrée. Dans le cas le plus simple, on utilise une porte ET à plusieurs entrées pour combiner les résultats. Mais il s'agit là d'un circuit assez naïf et diverses techniques permettent de combiner les résultats comparaisons de 1 bit sans elle. Cela permet d'économiser des circuits, mais aussi de gagner en performances et/ou en consommation d'énergie. Il existe deux grandes méthodes pour cela.
Avec la première méthode, le signal en question est déterminé avec le circuit donné ci-dessous. Le transistor du dessus s'ouvre durant un moment afin de précharger le fil qui transportera le signal. Le signal sera relié au zéro volt si une seule cellule CAM a une sortie à zéro. Dans le cas contraire, le fil aura été préchargé avec une tension correspondant à un 1 sur la sortie et y restera durant tout le temps nécessaires : on aura un 1 en sortie.

La seconde méthode relie les cellules CAM d'un mot mémoire ensemble comme indiqué dans le schéma ci-dessous. Chaque cellule mémoire a un résultat de comparaison inversé : il vaut 0 quand le bit de la cellule CAM est identique au bit d'entrée, et vaut 1 sinon. Si toutes les cellules CAM correspondent aux bits d'entrée, le signal final sera mis à la masse (à zéro). Et inversement, il suffit qu'une seule cellule CAM ouvre son transistor pour que le signal soit relié à la tension d'alimentation. En somme, le signal obtenu vaut zéro si jamais la donnée d'entrée et le mot mémoire sont identiques, et 1 sinon.

En théorie, les deux méthodes peuvent s'utiliser indifféremment avec les cellules NOR ou NAND, mais elles ont des avantages et inconvénients similaires à celles des cellules NOR et NAND. La première méthode a de bonnes performances et une consommation d'énergie importante, comme les cellules NOR, ce qui fait qu'elle est utilisée avec elles. L'autre a une bonne consommation d'énergie mais de mauvaises performances, au même titre que les cellules NAND, ce qui fait qu'elle est utilisée avec elles. Il existe cependant des CAM hybrides, pour lesquelles on a des cellules NOR avec un agencement NAND, ou l'inverse.
Les mémoires associatives avec opérations de masquage intégrées
modifierLes mémoires associatives vues précédemment sont les plus simples possibles, dans le sens où elles ne font que vérifier l'égalité de la donnée d'entrée pour chaque case mémoire. Mais d'autres mémoires associatives sont plus complexes et permettent d'effectuer facilement des opérations de masquage facilement. Nous avons vu les opérations de masquage dans le chapitre sur les opérations bit à bit, mais un petit rappel ne fait pas de mal. Le masquage permet d'ignorer certains bits lors de la comparaison, de sélectionner seulement certains bits sur lesquels la comparaison sera effectuée. L'utilité du masquage sur les mémoires associatives n'est pas évidente, mais on peut cependant dire qu'il est très utilisé sur les routeurs, notamment pour leur table de routage.
Pour implémenter le masquage, il existe trois méthodes distinctes : celle des CAM avec un masque fournit en entrée, les CAM avec masquage intégré, et les CAM ternaires. Les deux méthodes se ressemblent beaucoup, mais il y a quelques différences qui permettent de séparer les deux types.
Les CAM avec masquage fournit en entrée
modifierSur les CAM avec masquage fournit en entrée, les bits sélectionnés pour la comparaison sont précisés par un masque, un nombre de la même taille que les cases mémoires. Le masque est envoyé à la mémoire via un second bus, séparé du bus de données. Le masque est alors appliqué à toutes les cases mémoires. Notons que si le contenu d'une cellule n'est pas à prendre en compte, alors le résultat de l'application du masque doit être un 1 : sans cela, la porte ET à plusieurs entrées (ou son remplacement) ne donnerait pas le bon résultat. Pour implémenter ce comportement, il suffit de rajouter un circuit qui prend en entrée : le bit du masque et le résultat de la comparaison. On peut établir la table de vérité du circuit en question et appliquer les méthodes vues dans le chapitre sur les circuits combinatoires, mais le résultat sera dépend du format du masque. En effet, deux méthodes sont possibles pour gérer un masque.
- Avec la première, les bits à ignorer sont indiqués par un 0 alors que les bits sélectionnés sont indiqués par des 1.
- Avec la seconde méthode, c'est l'inverse : les bits à ignorer sont indiqués par des 1 et les autres par des 0.
La seconde méthode donne un circuit légèrement plus simple, où l'application du masque demande de faire un OU logique entre le bit du masque et la cellule mémoire associée. Il suffit donc de rajouter une porte OU à chaque cellule mémoire, entre la bascule D et la porte NXOR. Une autre manière de voir les choses est de rajouter un circuit de masquage à chaque case mémoire, qui s'intercale entre les cellules mémoires et le circuit qui combine les résultats de comparaison de 1 bit. Ce circuit est constitué d'une couche de portes OU, ou de tout autre circuit compatible avec le format du masque utilisé.

Les CAM avec masquage intégré
modifierSur d'autres mémoires associatives plus complexes, chaque case mémoire mémorise son propre masque attitré. Il n'y a alors pas de masque envoyé à toutes les cases mémoires en même temps, mais un masque par case mémoire. L'interface de la mémoire CAM change alors quelque peu, car il faut pouvoir indiquer si l'on souhaite écrire soit une donnée, soit un masque dans une case mémoire. Cette méthode peut s'implémenter de deux manière équivalentes. La première est que chaque case mémoire contient en réalité deux registres, deux cases mémoires : un pour la case mémoire proprement dit, et un autre pour le masque. Ces deux registres sont connectés au circuit de masquage, puis au circuit qui combine les résultats de comparaison de 1 bit. Une autre manière équivalente demande d'utiliser deux bits de SRAM par cellules mémoires : un qui code la valeur 0 ou 1, et un pour le bit du masque associé. Le bit qui indique si la valeur stockée est X est prioritaire sur l'autre. En clair, chaque case mémoire stocke son propre masque.

Il est cependant possible d'optimiser le tout pour réduire les circuits de comparaison, en travaillant directement au niveau des transistors. On peut notamment s'inspirer des méthodes vues pour les cellules CAM normales, avec une organisation de type NAND ou NOR. Une telle cellule demande 2 bascules SRAM, ce qui fait 2 × 6 = 12 transistors. Il faut aussi ajouter les circuits de comparaison, ce qui rajoute 4 à 6 transistors. Un défaut de cette approche est qu'elle augmente la taille de la cellule mémoire, ce qui réduit donc la densité de la mémoire. La capacité de la mémoire CAM s'en ressent, car les cellules CAM sont très grosses et prennent beaucoup de transistors. Les cellules CAM de ce type les plus optimisées utilisent entre 16 et 20 transistors par cellules, ce qui est énorme comparé aux 6 transistors d'une cellule SRAM, déjà assez imposante. Autant dire que les mémoires de ce type sont des plus rares.

Les CAM ternaires
modifierUne alternative aux opérations de masquage proprement dit est d'utiliser des mémoires associatives ternaires. Pour bien les comprendre, il faut les comparer avec les mémoires associatives normales. Avec une mémoire associative normale, chaque cellule mémoire stocke un bit, qui vaut 0 et 1, mais ne peut pas prendre d'autres valeurs. Avec une mémoire associative ternaire, chaque cellule mémoire stocke non pas un bit, mais un trit, c’est-à-dire une valeur qui peut prendre trois valeurs : 0, 1 ou une troisième valeur nommée X. Sur les mémoires associatives ternaires, cette valeur est utilisée pour signaler que l'on se moque de la valeur réelle du trit, ce qui lui vaut le nom de valeur "don't care". Et c'est cette valeur X qui permet de faciliter l'implémentation des opérations de masquage. Lorsque l'on compare un bit avec cette valeur X, le résultat sera toujours 1 (vrai). Par exemple, si on compare la valeur 0101 0010 1010 avec la valeur 01XX XXX0 1010, le résultat sera vrai : les deux sont considérés comme identiques dans la comparaison. Pareil si on compare la valeur 0100 0000 1010 avec la valeur 01XX XXX0 1010 ou 0111 1110 1010 avec la valeur 01XX XXX0 1010.
Formellement, ces mémoires associatives ternaires ne sont pas différentes des mémoires associatives avec un masque intégré dans chaque case mémoire. La différence est au niveau de l'interface : l'interface d'une CAM ternaire est plus complexe et ne fait pas la distinction entre donnée stockée et masque. À l'opposé, les CAM avec masque intégré permettent de spécifier séparément le masque de la donnée pour chaque case mémoire. Mais au niveau du fonctionnement interne, les deux types de CAM se ressemblent beaucoup. D'ailleurs, les CAM ternaires sont souvent implémentées par une CAM avec masque intégré, avec un bit de masque pour chaque cellule mémoire, à laquelle on rajoute quelques circuits annexes pour l'interface. Mais il existe des mémoires associatives ternaires pour lesquelles le stockage du bit de donnée et du masque se font sans utiliser deux cellules mémoires. Elles sont plus rares, plus chères, mais elles existent.
Les mémoires associatives bit-sérielles
modifierLes circuits comparateurs des mémoires associatives sont gourmands et utilisent beaucoup de circuits. Les optimisations vues plus haut limitent quelque peu la casse, sans trop nuire aux performances, mais elles ne sont pas une panacée. Mais il existe une solution qui permet de drastiquement économiser sur les circuits de comparaison, qu détriment des performances. L'idée est que la comparaison entre donnée d'entrée et case mémoire se fasse un bit après l'autre, plutôt que tous les bits en même temps. Pour prendre un exemple, prenons une mémoire dont les cases mémoires font 16 bits. Les techniques précédentes comparaient les 16 bits de la case mémoire avec les 16 bits de l'entrée en même temps, en parallèle, avant de combiner les comparaisons pour obtenir un résultat. L'optimisation est de faire les 16 comparaisons bit à bit non pas en même temps, mais l'une après l'autre, et de combiner les résultats autrement.
Avec cette méthode, la comparaison bit à bit est effectuée par un comparateur d'égalité sériel, un circuit que nous avions vu dans le chapitre sur les comparateurs, qui vérifie l'égalité de deux nombres bits par bit. Rappelons que ce circuit ne fait pas que comparer deux bits : il mémorise le résultat des comparaisons précédentes et le combine avec la comparaison en cours. Il fait donc à la fois la comparaison bit à bit et la combinaison des résultats. Pour cela, il intègre une bascule qui mémorise le résultat de la comparaison des bits précédents. L'avantage est que les circuits de comparaison sont beaucoup plus simples. Le comparateur parallèle utilise beaucoup de transistors, alors qu'un comparateur sériel utilise au maximum une bascule et deux portes logiques, moins s'il est optimisé. Au final, l'économie en portes logiques et en consommation électrique est drastique et peut être utilisée pour augmenter la capacité de la mémoire associative. Par contre, le traitement bit par bit fait qu'on met plus de temps pour faire la comparaison, ce qui réduit les performances.
Un tel traitement des bits en série s'oppose à une comparaison des bits en parallèle des mémoires précédentes. Ce qui fait que les mémoires de ce type sont appelées des mémoires bit-sérielles. L'idée est simple, mais il reste à l'implémenter. Pour cela, il existe deux grandes solutions, la première utilisant des registres à décalage, l'autre avec un système qui balaye les colonnes de la mémoire une par une.
Les mémoires bit-sérielles basées sur des registres à décalage
modifierL'implémentation la plus simple à comprendre est celle qui utilise des registres à décalage, mais elle a le défaut d'utiliser beaucoup de circuits, comparé aux alternatives. Avec cette implémentation, chaque byte, chaque case mémoire, est stockée dans un registre à décalage, et il en est de même pour le mot d'entrée à comparer. Ainsi, à chaque cycle, les deux bits à comparer sortent de ces deux registres à décalage. La comparaison bit à bit est effectuée par un comparateur d'égalité sériel. Le bit qui sort de la case mémoire est envoyé au comparateur sériel, mais il est aussi réinjecté dans le registre à décalage, afin que la case mémoire ne perde pas son contenu. L'idée est que le contenu de la case mémoire fasse une boucle avant de revenir à son état initial : on applique une opération de rotation dessus.

Pour donner un exemple, je vais prendre l'exemple d'un Byte qui contient la valeur 1100, et une donnée d'entrée qui vaut 0100. À chaque cycle d’horloge, le processeur associatif compare un bit de l'entrée avec le bit de même poids dans la case mémoire. La comparaison est le fait d'un circuit comparateur sériel (vu dans le chapitre sur les circuits comparateurs). Le résultat de la comparaison est disponible dans la bascule de 1 bit une fois la comparaison terminée. La bascule est reliée à la sortie sur laquelle on envoie le signal Trouvé / Non-trouvé.

Les mémoires bit-sérielles basées sur un système de sélection des colonnes
modifierL’implémentation précédente a quelques défauts, liés à l'usage de registres à décalage. Le fait de devoir déplacer des bits d'une bascule à l'autre n'est pas anodin : cela n'est pas immédiat, sans compter que ça consomme du courant. Autant ce n'est pas du tout un problème d'utiliser un registre à décalage pour le mot d'entrée, autant en utiliser un par case mémoire est déjà plus problématique. Aussi, d'autres mémoires associatives ont corrigé ce problème avec un subterfuge assez intéressant, inspiré du fonctionnement des mémoires RAM.
Vous vous rappelez que les mémoires RAM les plus simples sont organisées en lignes et en colonnes : chaque ligne est une case mémoire, un bit se trouve à l'intersection d'une ligne et d'une colonne. Les mémoires CAM ne sont pas différentes de ce point de vue. L'idée est de n'activer qu'une seule colonne à la fois, du moins pour ce qui est des comparaisons. L'activation de la colonne connecte toutes les cellules CAM de la colonne au comparateur sériel, mais déconnecte les autres. En conséquence, les bits situés sur une même colonne sont envoyés au comparateur en même temps, alors que les autres sont ignorés. Un système de balayage des colonnes active chaque colonne l'une après l'autre, il passe d'une colonne à l'autre de manière cyclique. Ce faisant, le résultat est le même qu'avec l'implémentation avec des registres à décalage, mais sans avoir à déplacer les bits. La consommation d'énergie est donc réduite, sans compter que l'implémentation est légèrement plus rapide.
Les mémoires associatives word-sérielles
modifierles mémoires associatives word-sérielles sont des mémoires associatives qui sont conçues totalement différemment des précédentes. Elles sont conçues à partir d'une mémoire RAM, à laquelle on rajoute des circuits pour simuler une mémoire réellement associative. Là où les mémoires réellement associatives comparent la donnée d'entrée avec toutes les cases mémoires en parallèle, les mémoires associatives word-sérielles comparent avec chaque case mémoire une par une. Les circuits qui entourent la mémoire balayent la mémoire, en partant de l'adresse la plus basse, puis en passant d'une adresse à l'autre. Les circuits en question sont composés d'un comparateur, d'un compteur, et de quelques circuits annexes. Le compteur calcule les adresses à lire à chaque cycle d'horloge, la mémoire RAM est adressée par ce compteur, le comparateur récupère la donnée lue et effectue la comparaison. Dès qu'un match est trouvé, la mémoire associative renvoie le contenu du compteur, qui contient l'adresse du byte adéquat.

Les avantages et inconvénients des mémoires associatives word-sérielles
modifierIl est possible que la mémoire s'arrête au premier match trouvé, mais elle peut aussi continuer et balayer toute la mémoire afin de trouver toutes les cases mémoires qui correspondent à l'entrée, tout dépend de comment la logique de contrôle est conçue. L'avantage de balayer toute la mémoire est que l'on peut savoir si une donnée est présente en plusieurs exemplaires dans la mémoire, et localiser chaque exemplaire. À chaque cycle, la mémoire indique si elle a trouvé un match et quel est l'adresse associée. Le processeur a juste à récupérer les adresses transmises quand un match est trouvé, il récupérera les adresses de chaque exemplaire au fur et à mesure que la mémoire est balayée. En comparaison, les autres mémoires associatives utilisent un encodeur à priorité qui choisit un seule exemplaire de la donnée recherchée.
Un autre avantage de telles architectures est qu'elles utilisent peu de circuits, sans compter qu'elles sont simples à fabriquer. Elles sont économes en circuits essentiellement en raison du faible nombre de comparateurs utilisés. Elles n'utilisent qu'un seul comparateur non-sériel, là où les autres mémoires associatives utilisent un comparateur par case mémoire (comparateur parallèle ou sériel, là n'est pas le propos). Vu le grand nombre de cases mémoires que contient une mémoire réellement associative, l'avantage est aux mémoires associatives word-sérielles.
Par contre, cette économie de circuits se fait au détriment des performances. Le fait que chaque case mémoire soit comparée l’une après l'autre, en série, est clairement un désavantage. Le temps mis pour balayer la mémoire est très long et cette solution n'est praticable que pour des mémoires très petites, dont le temps de balayage est faible. De plus, balayer une mémoire est quelque chose que les ordinateurs normaux savent faire avec un morceau de code adapté. N'importe quel programmeur du dimanche peut coder une boucle qui traverse un tableau ou une autre structure de donnée pour y vérifier la présence d'un élément. Implémenter cette boucle en matériel n'a pas grand intérêt et le gain en performance est généralement mineur. Autant dire que les mémoires associatives word-sérielles sont très rares et n'ont pas vraiment d'utilité.
Les mémoires associatives sérielles par blocs
modifierIl est cependant possible de faire un compromis entre performance et économie de circuit/énergie avec les mémoires associatives word-sérielles. L'idée est d'utiliser plusieurs mémoires RAM internes, au lieu d'une seule, qui sont accédées en parallèle. Ainsi, au lieu de comparer chaque case mémoire une par une, on peut en comparer plusieurs à la fois : autant qu'il y a de mémoires internes. L'idée n'est pas sans rappeler l'organisation en banques et rangées des mémoires RAM modernes. En faisant cela, la comparaison sera plus rapide, mais au prix d'une consommation d'énergie et de circuits plus importante. Les mémoires ainsi créées sont appelées des mémoires associatives sérielles par blocs.

Les mémoires associatives sont assez peu utilisées, surtout les mémoires associatives word-sérielles. Cependant, les mémoires caches leur ressemblent beaucoup et une bonne partie de ce que nous venons de voir sera très utile quand nous verrons les mémoires caches. Si les informations de ce chapitre ne pourrons pas être réutilisées à l'identique, il s'agit cependant d'une introduction particulièrement propédeutique. Vous verrez que les mémoires réellement associative ressemblent beaucoup aux mémoires caches de type totalement associative, que les mémoires associatives word-sérielles ressemblent beaucoup aux caches directement adressés, et que les mémoires associatives word-sérielles optimisées avec plusieurs banques ressemblent beaucoup aux mémoires caches à plusieurs voies. Mais laissons cela de côté pour le moment, les mémoires caches étant abordées dans un chapitre à la fin de ce cours, et passons au prochain chapitre.
Les mémoires FIFO et LIFO conservent les données triées dans l'ordre d'écriture (l'ordre d'arrivée). La différence est qu'une lecture dans une mémoire FIFO renvoie la donnée la plus ancienne, alors que pour une mémoire LIFO, elle renverra la donnée la plus récente, celle ajoutée en dernier dans la mémoire. Dans les deux cas, la lecture sera destructrice : la donnée lue est effacée. Di autrement, une mémoire FIFO renvoie des données dans leur ordre d'arrivée, alors qu'une LIFO renvoie les données dans l'ordre inverse.

On peut voir les mémoires FIFO comme des files d'attente, des mémoires qui permettent de mettre en attente des données tant qu'un composant n'est pas prêt. Seules deux opérations sont possibles sur de telles mémoires : mettre en attente une donnée (enqueue, en anglais) et lire la donnée la plus ancienne (dequeue, en anglais).

De même, on peut voir les mémoires LIFO comme des piles de données : toute écriture empilera une donnée au sommet de cette mémoire LIFO (on dit qu'on push la donnée), alors qu'une lecture enlèvera la donnée au sommet de la pile (on dit qu'on pop la donnée).

L'utilité des mémoires LFIO et FIFO
modifierEn soi, les mémoires LIFO sont assez rares. Les seules utilisations connues sont liées à la pile d'appel du processeur, que nous verrons d'ici une dizaine de chapitres. Il existe quelques processeurs qui placent cette pile d'appel dans une mémoire LIFO séparée, mais ce n'est pas le cas sur la quasi-totalité des processeurs récents. Il a existé quelques processeurs qui intégraient le sommet de la pile d'appel dans une mémoire LIFO intégrée au processeur, mais ce n'est plus d'actualité. Il en existe dans les unités de prédiction de branchement des processeurs modernes, pour la prédiction des retour de fonction, mais c'est un sujet que nous aborderons dans la fin du cours.
Les mémoires FIFO sont beaucoup plus utiles. Elles sont surtout utilisées pour mettre en attente des données ou commandes, tout en conservant leur ordre d'arrivée. Si on utilise une mémoire FIFO dans cet optique, elle prend le nom de mémoire tampon. L'utilisation principale des mémoires tampons est l’interfaçage de deux composants de vitesse différentes qui doivent communiquer entre eux. Le composant rapide émet des commandes à destination du composant lent, mais le fait à un rythme discontinu, par rafales entrecoupées de "moments de silence". Lors d’une rafale, le composant lent met en attente les commandes dans la mémoire FIFO et il les consomme progressivement lors des moments de silence.
On retrouve des mémoires tampons dans beaucoup de matériel électronique : dans les disques durs, des les lecteurs de CD/DVD, dans les processeurs, dans les cartes réseau, etc. Prenons par exemple le cas d'un disque dur : il reçoit régulièrement, de la part du processeur, des commandes de lecture écriture et les données associées. Mais le disque dur étant un périphérique assez lent, il doit mettre en attente les commandes/données réceptionnées avant de pouvoir les traiter. Et cette mise en attente doit conserver l'ordre d'arrivée des commandes, sans quoi on ne lirait pas les données demandés dans le bon ordre. Pour cela, les commandes sont stockées dans une mémoire FIFO et sont consommées au fur et à mesure. On trouve le même genre de logique dans les cartes réseau, qui reçoivent des paquets de données à un rythme discontinu, qu'elles doivent parfois mettre en attente tant que la carte réseau n'a pas terminé de gérer le paquet précédent.
L'interface d'une mémoire FIFO/LIFO
modifierLes mémoires FIFO/LIFO possèdent un bus de commande assez simple, sans bus d'adresse vu que ces mémoires ne sont pas adressables. Il contient les bits CS et OE, le signal d'horloge et quelques bits de commande annexes comme un bit R/W.
La mémoire FIFO/LIFO doit indiquer quand celle-ci est pleine, à savoir qu'elle ne peut plus accepter de nouvelle donnée en écriture. Elle doit aussi indiquer quand elle est vide, ce qui signifie qu'il n'y a pas possibilité de lire son contenu. Pour cela, la mémoire possède deux sorties nommées FULL et EMPTY. Ces deux bits indiquent respectivement si la mémoire est pleine ou vide, quand ils sont à 1.
Les mémoires FIFO/LIFO les plus simples n'ont qu'un seul port qui sert à la fois pour la lecture et l'écriture, mais elles sont cependant rares. Dans les faits, les mémoires FIFO sont presque toujours des mémoires double ports, avec un port pour la lecture et un autre pour les écritures. Du fait de la présence de deux ports dédiés, le bit R/W est souvent séparé en deux bits distincts : un bit Write Enable sur le port d'écriture, qui indique qu'une écriture est demandée, et un bit Read Enable sur le port de lecture qui indique qu'une lecture est demandée. La séparation du bit R/W en deux bits séparés pour chaque port s'expliquera dans les paragraphes suivants.
Les mémoires FIFO/LIFO sont souvent des mémoires synchrones, les implémentations asynchrones étant plus rares. Elles ont donc au moins une entrée pour le signal d'horloge. Point important, de nombreuses mémoires FIFO ont une fréquence pour la lecture qui est distincte de la fréquence pour l'écriture. En conséquence, elles reçoivent deux signaux d'horloge sur deux entrées séparées : un pour la lecture et un pour l'écriture. La présence de deux fréquences s'explique par le fait que les mémoires FIFO servent à interfacer deux composants qui ont des vitesses différentes, comme un disque dur et un processeur, un périphérique et un chipset de carte mère, etc. D'ailleurs, c'est ce qui explique que le bit R/W soit scindé en deux bits, un par port : les deux ports n'allant pas à la même vitesse, ils ne peuvent pas partager un même bit d'entrée sans que cela ne pose problème.
L'interface la plus classique pour une mémoire FIFO/LIFO est illustrée ci-dessous. On voit la présence d'un port d'écriture séparé du port de lecture, et la présence de deux signaux d'horloge distincts pour chaque port.

Les mémoires LIFO
modifierLes mémoires LIFO peuvent se concevoir en utilisant une mémoire RAM, couplée à un registre. Les données y sont écrites à des adresses successives : on commence par remplir la RAM à l'adresse 0, puis on poursuit adresse après adresse, ce qui garantit que la donnée la plus récente soit au sommet de la pile. Tout ce qu'il y a à faire est de mémoriser l'adresse de la donnée la plus récente, dans un registre appelé le pointeur de pile. Cette adresse donne directement la position de la donnée au sommet de la pile, celle à lire lors d'une lecture. Le pointeur de pile est incrémenté à chaque écriture, pour pointer sur l'adresse de la nouvelle donnée. De même, il est décrémenté à chaque lecture, vu que les lectures sont destructrices (elles effacent la donnée lue).
La gestion des bits EMPTY et FULL est relativement simple : il suffit de comparer le pointeur de pile avec l'adresse minimale et maximale. Si le pointeur de pile et l'adresse maximale sont égaux, cela signifie que toutes les cases mémoires sont remplies : la mémoire est pleine. Quand le pointeur de pile pointe sur l'adresse minimale (0), la mémoire est vide.

Il est aussi possible, bien que plus compliqué, de créer des LIFO à partir de registres. Pour cela, il suffit d'enchainer des registres les uns à la suite des autres. Les données peuvent passer d'un registre à son suivant, ou d'un registre aux précédents. Toutes les lectures ou écritures ont lieu dans le même registre, celui qui contient le sommet de la pile. Quand on écrit une donnée, celle-ci est placée dans ce registre de sommet de pile. Pour éviter de perdre des données, celles-ci sont déplacées de leur registre actuel au précédent. Toutes les données sont donc décalées d'un registres, avant l'écriture de la donnée au sommet de pile. Lors d'une lecture, le sommet de la pile est effacé. Pour cela, toutes les données sont avancées d'un registre, en passant du registre actuel au suivant. Les échanges de données entre registres sont gérés par divers circuits d’interfaçage, commandés par un gigantesque circuit combinatoire (le contrôleur mémoire).

Les mémoires FIFO
modifierLes FIFO de taille fixe
modifierLes mémoires FIFO les plus simples ont une taille fixe, à savoir qu'elles contiennent toujours le même nombre de données mises en attente. Elles peuvent se fabriquer en enchainant des registres.

Il est aussi possible de fabriquer une FIFO en utilisant plusieurs registres à décalages. Chaque registre à décalage contient un bit pour chaque byte mis en attente. Le circuit en question est décrit dans le schéma ci-dessous.

Les FIFO de taille variable
modifierLa plupart des applications requièrent des FIFOs qui mémorisent un nombre variable de données. De telles FIFO de taille variable peuvent se fabriquer à partir d'une mémoire RAM en y ajoutant deux compteurs/registres et quelques circuits annexes. Les deux compteurs mémorisent l'adresse de la donnée la plus ancienne, ainsi que l'adresse de la plus récente, à savoir l'adresse à laquelle écrire la prochaine donnée à enqueue, et l'adresse de lecture pour la prochaine donnée à dequeue. Quand une donnée est retirée, l'adresse la plus récente est décrémentée, pour pointer sur la prochaine donnée. Quand une donnée est ajoutée, l'adresse la plus ancienne est incrémentée pour pointer sur la bonne donnée.

Petit détail : quand on ajoute des instructions dans la mémoire, il se peut que l'on arrive au bout, à l'adresse maximale, même s'il reste de la place à cause des retraits de données. La prochaine entrée à être remplie sera celle numérotée 0, et on poursuivra ainsi de suite. Une telle situation est illustrée ci-dessous.

La gestion des bits EMPTY et FULL se fait par comparaison des deux compteurs. S'ils sont égaux, c'est que la pile est soit vide, soit pleine. On peut faire la différence selon la dernière opération : la pile est vide si c'est une lecture et pleine si c'est une écriture. Une simple bascule suffit pour mémoriser le type de la dernière opération. Un simple circuit combinatoire contenant un comparateur permet alors de gérer les flags simplement.

L'implémentation des deux compteurs
modifierL'implémentation d'une mémoire FIFO demande donc d'utiliser deux compteurs. Vous vous attendez à ce que ces deux compteurs soient des compteurs binaires normaux, pas quelque chose d'exotique. Mais dans les faits, il est parfaitement possible d'utiliser des compteurs en anneau, ou des registres à décalage à rétroaction linéaire, ou des compteurs modulo comme compteurs dans une FIFO.
Premièrement, rien n'impose que les compteurs comptent de 1 en 1. Dans les faits, la séquence comptée peut être arbitraire : tout ce qui compte est qu'elle est la même entre les deux compteurs, pour vérifier si la RAM est pleine ou vide. Et cela amène à une optimisation assez simple : on peut utiliser des registres à décalage à rétroaction linéaire (LFSR ), au lieu de compteurs binaires usuels. Le résultat fonctionnera de la même façon vu de l'extérieur : on aura une FIFO qui fonctionne normalement, sans problèmes particuliers. Certes, la mémoire RAM ne sera pas remplie en partant de l'adresse 0, puis en remplissant la mémoire en sautant d'une adresse à sa voisine. A la place, les données seront ajoutées dans un ordre différent, mais qui ne change globalement pas grand chose. Les raisons de faire ainsi sont que les compteurs à base de LFSR est qu'ils sont plus simples à concevoir, moins gourmands en circuits et plus rapides. Le seul défaut est que les LFSR ne peuvent en effet pas contenir la valeur 0, ce qui fait qu'une adresse est gâchée. Mais sur les FIFOs assez grosses, le gain en vitesse et l'économie de circuits liée au compteur vaut la peine de gâcher une adresse.
Deuxièmement, rien n'impose que le compteur contienne une valeur codée en binaire. L'encodage de la valeur en binaire est cependant nécessaire pour adresser la mémoire RAM, mais il suffit d'ajouter un circuit pour traduire le contenu du compteur en binaire usuel pour cela. Sur les FIFO avec un port de lecture et un port d'écriture cadencés à des fréquences différentes, on utilise deux compteurs qui encodent des entiers en code Gray. La raison à cela est que les deux compteurs sont respectivement dans le port de lecture et dans le port d'écriture, et sont donc cadencés à deux fréquences différentes. Et la différence de fréquence entre compteurs peut causer des soucis pour calculer les bits EMPTY et FULL. Pour le dire autrement, la FIFO contient deux domaines d'horloge qui doivent communiquer entre eux pour calculer les bits EMPTY et FULL. C'est un cas de clock domain crossing tel que vu dans le chapitre sur le signal d'horloge, et la solution est alors celle évoquée dans ce chapitre : utiliser le code Gray.
Lors de l'incrémentation d'un compteur, tous les bits ne sont pas modifiés en même temps : les bits de poids faible sont typiquement modifiés avant les autres. Évidemment, à la fin de l'incrémentation, on obtient le résultat final, correct. Mais pendant le temps de calcul, le compteur peut se retrouver dans un état transitoire, où certains bits ont été modifiés mais pas les autres. Or, le comparateur qui s'occupe de déterminer les bits EMPTY et FULL est cadencé de manière à être au moins aussi rapide que le plus rapide des deux compteurs. Le comparateur est donc plus rapide que le compteur le plus lent et peut "voir" cet état transitoire. Il se peut que le comparateur compare le contenu du compteur le plus rapide avec l'état transitoire de l'autre, ce qui donnera un résultat temporairement faux. L'usage de compteurs en code Gray permet d'éviter ce problème : vu que seul un bit est modifié lors d'une incrémentation/décrémentation, les états transitoires n'existent tout simplement pas.
Le processeur
modifierL'architecture externe
modifierCe chapitre va aborder le langage machine, à savoir un standard qui définit les instructions du processeur, le nombre de registres, etc. Dans ce chapitre, on considérera que le processeur est une boîte noire au fonctionnement interne inconnu. Nous verrons le fonctionnement interne d'un processeur dans quelques chapitres. Les concepts que nous allons aborder ne sont rien d'autre que les bases nécessaires pour apprendre l'assembleur. Nous allons surtout parler des instructions du processeur. Pour simplifier, on peut classer les instructions en quatre grands types :
- les échanges de données entre mémoires ;
- les calculs et autres opérations arithmétiques ;
- les instructions de comparaison ;
- les instructions de branchement.
À côté de ceux-ci, on peut trouver d'autres types d'instructions plus exotiques, pour gérer du texte, pour modifier la consommation en électricité de l'ordinateur, pour chiffrer ou de déchiffrer des données de taille fixe, générer des nombres aléatoires, etc. Dans ce chapitre, nous allons voir un aperçu assez large des instructions qui existent. Nous n'allons pas nous limiter aux instructions les plus importantes, mais nous allons aussi parler d'instructions assez exotiques, soit présentes uniquement sur d'anciens ordinateurs, soit très rares, soit franchement tordues. Et certaines de ces instructions exotiques sont assez impressionnantes et risquent de vous surprendre !
Les instructions arithmétiques
modifierTout ordinateur gère des instructions qui font des calculs arithmétiques simples. Une opération mathématique ne se fait pas de la même manière suivant la représentation utilisée pour coder ces nombres : on ne manipule pas de la même façon des nombres signés, des nombres codés en complément à 1, des flottants simple précision, des flottants double précision, etc. Tout dépend du type de la donnée, à savoir est-ce un flottant, un entier codé en BCD, etc.
Dans le cas le plus simple, le processeur dispose d'une instruction par type à manipuler : une instruction de multiplication pour les flottants, une autre pour les entiers codés en complément à deux, etc. Sur d'autres machines assez anciennes, on stockait le type de la donnée dans la mémoire. Chaque nombre manipulé par le processeur incorporait un tag, une petite suite de bits qui permettait de préciser son type. Le processeur ne possédait pas d'instructions en plusieurs exemplaires pour faire la même chose, et utilisait le tag pour déduire comment faire ses calculs. Par exemple, ces processeurs n'avaient qu'une seule instruction d'addition, qui pouvait traiter indifféremment flottants, nombres entiers codés en BCD, en complément à deux, etc. Le traitement effectué par cette instruction dépendait du tag incorporé dans la donnée. Des processeurs de ce type s'appellent des architectures à tags, ou tagged architectures.
Les instructions entières
modifierLes instructions arithmétiques sont les plus courantes et comprennent au minimum l'addition, la soustraction, la multiplication, éventuellement la division, parfois les opérations plus complexes comme la racine carrée. La division est une opération très complexe et particulièrement lente, bien plus qu'une addition ou une multiplication. Pour information, sur les processeurs actuels, la division est 20 à 80 fois plus lente qu'une addition/soustraction, et presque 7 à 26 fois plus lente qu'une multiplication. Mais on a de la chance : c'est aussi une opération assez rare.
Les tous premiers ordinateurs pouvaient manipuler des données de taille arbitraire. Alors certes, ces processeurs n'utilisaient pas vraiment les encodages de nombres qu'on a vus au premier chapitre. À la place, ils stockaient leurs nombres dans des chaines de caractères ou des tableaux encodés en BCD. De nos jours, les ordinateurs utilisent des entiers de taille fixe. La taille des données à manipuler peut dépendre de l'instruction. Ainsi, un processeur peut avoir des instructions pour traiter des nombres entiers de 8 bits, et d'autres instructions pour traiter des nombres entiers de 32 bits, par exemple.
La ou les instructions d'addition entière
modifierUn processeur implémente au minimum une opération d'addition, même s'il existe de rares exemples de processeurs qui s'en passent. Mieux : certains processeurs implémentent plusieurs instructions d'addition, qui se distinguent par de subtiles différences.
La première différence est la gestion des débordements, qui est parfois gérée en ayant deux instructions d'addition : une pour les additions de nombres signés et une autre pour les nombres non-signés. L’additionneur utilisé pour ces deux instructions est le même, l'addition elle-même ne change pas, mais les débordements d'entiers ne sont pas gérés de la même manière. Comme on le verra plus tard, certains processeurs disposent d'un registre de débordement, de 1 bit, qui indique si une instruction arithmétique a généré un débordement d'entier ou non. Il est mis à 1 en cas de débordement, mais reste à 0 sinon. Ce bit de débordement est mis à jour à chaque addition/multiplication/soustraction. Et les débordements d'entiers sont différents selon que l'addition est signée ou non, d'où l'existence des deux instructions dédiées. D'autres processeurs s'en sortent autrement, en ayant deux bits de débordement : un si le résultat est signé, l'autre pour les résultats non-signés. Mais nous reparlerons de cela plus tard.
Une autre possibilité, présente sur les vieux processeurs, tient dans la gestion de la retenue. A l'époque, les processeurs ne pouvaient gérer que des nombres de 4 à 8 bits, guère plus. Pourtant, la plupart des applications logicielles demandait d'utiliser des entiers de 16 bits. Les opérations comme l'addition ou la soustraction étaient alors réalisées en plusieurs fois. Par exemple, on additionnait les 8 bits de poids faible, puis les 8 bits de poids fort. Dans un cas pareil, il fallait aussi gérer la retenue dans l'addition des 8 bits de poids fort.
Pour cela, la retenue en question était mémorisée dans un registre de 1 bit dédié, semblable au registre de débordement, appelé le bit de retenue. De plus, les processeurs incorporaient une instruction d'addition qui additionnait les deux opérandes avec la retenue en question, instruction souvent appelée ADDC (ADD with Carry). Niveau circuits, cela ne changeait pas grand chose, tous les additionneurs ayant une entrée pour la retenue (qui est utilisée pour implémenter la soustraction, rappelez-vous). L'implémentation de l'instruction ADDC était très simple, n'utilisait presque pas de circuits, et rendait de fiers services aux programmeurs de l'époque. Nous parlons là des vieux processeurs 4 et 8, mais certains processeurs 16, 32, voire 64 bits, sont capables d'effectuer ce genre d'opération, même si ils sont rares.
- Il existe parfois des instructions pour mettre le bit de retenue à 0 ou à 1. C'est le cas sur l'architecture x86. Mais son utilité est marginale, car toutes les instructions arithmétiques modifient le bit de retenue.
La même chose a lieu pour la soustraction, qui demande qu'une "retenue" soit propagée d'une colonne à l'autre (bien que la "retenue" soit utilisée différemment : elle n'est pas additionnée, mais soustraite du résultat de la colonne). Pour cela, les processeurs implémentent l'opération SUBC (Substract with Carry). Et pour mettre en œuvre cette opération, ils ont deux options. La première est d'ajouter un bit pour la "retenue" de la soustraction. Pour une soustraction qui calcule a-b, elle vaut 0 si a>=b et 1 si a<b. Elle est utilisée telle qu'elle par le circuit qui effectue la soustraction, généralement un soustracteur. L'autre option est d'utiliser le but de retenue de l'addition, sans rien modifier. Pour comprendre pourquoi, rappelons que la soustraction est implémentée en complément à deux par le calcul suivant :
Il s'agit d'une addition, qui a donc une retenue lors d'un débordement. On peut alors réutiliser le bit de retenue de l'addition pour la soustraction, en modifiant quelque peu la soustraction à effectuer. Pour comprendre comment faire la modification, précisons tout d'abord que les règles du complément à deux nous disent qu'on a un débordement quand a>=b. Passons maintenant à l'étude d'un exemple théorique : le cas où on veut soustraire deux nombres de 16 bits avec deux opérations SUBC qui travaillent sur 8 bits. Appelons les deux opérandes A et B, et les 8 bits de poids forts de ces opérandes, et et leurs 8 bits de poids faible. Voyons ce qui se passe suivant que la retenue soit de 0 ou 1.
- Si la retenue de l'addition est de 1, on a , ce qui veut dire que la seconde soustraction doit calculer .
- A l'inverse, si la retenue de l'addition est de 0, on a . Cela veut dire que si on posait la soustraction, alors une retenue devrait être propagée à la colonne suivante, ce qui veut dire que la seconde soustraction doit calculer .
Récapitulons dans un tableau.
| Retenue | Opération à effectuer pour la seconde soustraction |
|---|---|
| 0 | |
| 1 |
On voit que ce qu'il faut ajouter à est égal à la retenue. L'opération SUBC fait donc le calcul suivant :
La plupart des processeurs 8 et 16 bits avaient deux instructions de soustraction séparées : une sans gestion de la retenue, une avec. Mais certains processeurs comme le 6502 n'avaient qu'une seule instruction de soustraction : celle qui tient compte de la retenue ! Il n'y avait pas de soustraction normale. Pour éviter tout problème, les programmeurs devaient faire attention. Ils disposaient d'une instruction mettre à 0 ou à 1 le bit de retenue pour éviter tout problème, qu'ils utilisaient avant toute soustraction simple.
Les instructions de multiplication et de division entière
modifierIl faut savoir que la division est une opération très lourde pour le processeur : une instruction de division dédiée met au mieux une dizaine de cycles d'horloge pour fournir un résultat, parfois plus de 50 à 70 cycles d’horloge. Heureusement, les divisions les plus courantes sont des divisions par une constante : un programme devant manipuler des nombres décimaux aura tendance à effectuer des divisions par 10, un programme manipulant des durées pourra faire des divisions par 60 (gestion des minutes/secondes) ou 24 (gestion des heures). Or, diverses astuces permettent de les remplacer par des suites d'instructions plus simples, qui donnent le même résultat (l'usage de décalages, la multiplication par un entier réciproque, etc). En-dehors de ce cas, l'usage des divisions est assez rare. Sachant cela, certains processeurs ne possèdent pas d'instruction de division, car les gains de performance seraient modérés et le coût en transistors élevé. D'autres processeurs implémentent toutefois la division dans une instruction machine, avec un circuit dédié, mais c'est signe que le coût en transistors n'est pas un problème pour le concepteur de la puce.
Par contre, l'opération de multiplication entière est très courante, presque tous les processeurs modernes en ont une. Les multiplications sont plus fréquentes dans le code des programmes, sans compter que c'est une opération pas trop lourde à implémenter en circuit. Il en existe parfois plusieurs versions sur un même processeur. Ces différentes versions servent à résoudre un problème quant à la taille du résultat d'une multiplication. En effet, la multiplication de deux opérandes de bits donne un résultat de , ce qui ne tient donc pas dans un registre. Pour résoudre ce problème, il existe plusieurs solutions.
Dans sa version la plus simple, l'instruction de multiplication se contente de garder les bits de poids faible, ce qui peut entraîner l'apparition de débordements d'entiers.
Une autre solution est de calculer soit les bits de poids fort, soit les bits de poids faible, le choix étant laissé au programmeur. Des processeurs disposent de deux instructions de multiplication : une instruction pour calculer les bits de poids fort du résultat et une autre pour les bits de poids faible. Certains processeurs disposent d'une instruction de multiplication configurable, qui permet de choisir quels bits conserver : poids fort ou poids faible.
Une autre version mémorise le résultat dans deux registres : un pour les bits de poids faible et un autre pour les bits de poids fort. Il faut noter que certains processeurs disposent de registres spécialisés pour cela. Par spécialisés, on veut dire qu'ils sont séparés des autres registres. Les autres registres, appelés les registres généraux, mémorisent n'importe quelle opérande entière et sont utilisables pour toutes les opérations. Mais la multiplication mémorise son résultat dans deux registres à part, qu'on nommera HO et LO. Seule l'instruction de multiplication peut écrire un résultat dans ces deux registres, avec HO pour les bits de poids fort, et LO pour les bits de poids faibles. Par contre, n'importe quelle instruction peut les lire, pour récupérer une opérande dans ces deux registres.
Les instructions sur les entiers BCD
modifierEnfin, il faut citer les instructions BCD, qui agissent sur des opérandes codées en BCD. Devenues très rares avec la disparition du BCD dans l'informatique grand-public, elles étaient quasiment essentielles sur les tous premiers processeurs 8 bits.
Au tout début de l'informatique, il a existé des processeurs qui travaillaient uniquement en BCD, appelés des processeurs décimaux. Ils avaient uniquement des instructions BCD, pas d'instruction sur des opérandes codées en binaire. Ils étaient assez courants entre les années 60 et 70, même s'ils ne représentent pas la majorité des architectures de l'époque. Il y avait une vraie séparation entre processeurs décimaux et processeurs binaires, sans intermédiaires notables. Le grand avantage des processeurs décimaux est leur très bonne performance dans les tâches de bureautique, de comptabilité, et autres. Les processeurs de l'époque recevaient des entiers codés en BCD de la part des entrées-sorties, et devaient les traiter. Les processeurs binaires devaient faire des conversion BCD-binaire pour communiquer avec les entrées-sorties, mais pas les processeurs décimaux. Le gain en performance pouvait être substantiel dans certaines applications.
Par la suite, dans les années 80, l'augmentation des performances a favorisé les processeurs binaires. Faire des conversions binaires-BCD n'était plus un problème, les conversions étaient suffisamment rapides. Par contre, faire les calculs en BCD était plus lent que faire les calculs en binaire, ce qui fait que le compromis technologique de l'époque favorisaient le binaire. Mais pour obtenir le meilleur des deux mondes, les processeurs binaires ont ajouté un support du BCD. C'était l'époque des architectures 8 bits, puis 16 bits. Intuitivement, on se dit que, les processeurs de l'époque des 8 bits avaient leurs instructions de calcul en double : une instruction pour les calculs entier et une autre pour les calculs BCD. Mais d'autres processeurs faisaient autrement.
A l'époque des processeurs 8-16 bits, certains processeurs ne géraient pas d'instructions BCD proprement dit, mais géraient quand même les calculs en BCD grâce à des instructions spéciales. Concrètement, il n'y avait pas d'instruction d'addition ou de soustraction spécifique pour le BCD. Les programmeurs utilisaient une instruction d'addition ou de soustraction normale, celle utilisée sur les nombres binaires normaux. Le résultat de l'opération n'était évidemment pas le bon, mais il était possible de corriger ce résultat pour obtenir le bon résultat codé en BCD. Les processeurs de l'époque disposaient d'une instruction pour, souvent appelée Decimal Adjust After Addition.
Avant d'aller plus loin, nous devons préciser que les processeurs 8 bits de l'époque pouvaient gérer deux formats de BCD. Le premier est le format Packed, où deux chiffres sont mémorisé dans un octet. Le premier nibble (4bits) mémorise un chiffre BCD, le second nibble mémorise le second. Il s'agit d'un format qui remplit au maximum les bits de l'octet avec des données utiles. L'autre format, appelé Unpacked, ne mémorise qu'un seul chiffre BCD dans un octet. Le chiffre est quasi- tout le temps dans le nibble de poids faible. Il se trouve que la manière de corriger le résultat d'une opération n'est pas la même suivant que le nombre est codé en BCD packed et unpacked.
Pour commencer, étudions le cas des nombres BCD unpacked, plus simples à comprendre. Lors d'une addition, il se peut que le résultat ne soit pas représentable en BCD unpacked. Par exemple, si je fais le calcul 5 + 8, le résultat sera 13 : il tient dans un nibble en décimal, mais pas en BCD ! Cette situation survient quand le résultat d'une addition de deux entiers BCD unpacked dépasse 9, la limite de débordement en BCD unpacked. Nous avons vu dans le chapitre sur les circuits d'addition que la correction est alors toute simple : si le résultat dépasse 9, on ajoute 6. De plus, on doit prévenir que le résultat a débordé et ne tient pas sur un nibble en BCD. Pour cela, on ajoute un bit spécialisé, appelé le half carry flag, indicateur de demi-retenue en français, qui joue le même rôle que le bit de débordement, mais pour le BCD unpacked. Sur les processeurs x86, tout cela est réalisé par une instruction appelée ASCII adjust after addition.
- Pour la soustraction, il faut faire la même chose, sauf qu'il faut soustraire 6, pas l'ajouter. Et il y a aussi une instruction pour cela : ASCII adjust after substraction.
Pour les nombres BCD packed, la procédure est globalement la même, sauf qu'il faut traiter les deux nibbles : on ajoute 6 si le nibble de poids faible dépasse 9, puis on fait la même chose avec le nibble de poids fort. Le bit half carry flag n'est pas mis à jour et est tout simplement ignoré. Notons qu'on modifie d'abord le nibble de poids faible, avant de traiter celui de poids fort. En effet, si on corrige celui de poids faible, la retenue obtenue en ajoutant 6 se propage au nibble suivant, ce qui fait que ce dernier peut voir sa valeur augmenter. Une fois cela fait, le bit de retenue est mis à 1. La procédure est différente, vu qu'il faut traiter deux nibles au lieu d'un, et que le bit half-carry est ignoré au profit du bit de retenue normal'. D'où l'existence d'une instruction séparée pour l'addition des nombres BCD packed, appelée Décimal adjust after addition sur les processeurs x86.
Les processeurs modernes ne supportent plus le BCD, car il est très peu utilisé. Les processeurs ARM et MIPS ont toujours fait sans instructions BCD. Les processeurs x86 des PC désactivent les instructions BCD en mode 64 bits, mais conservent des opérations BCD en mode 32 bits, pour des raisons de compatibilité. Le support du codage BCD est surtout quelque chose qu'on trouve sur les anciens processeurs.
Les instructions flottantes
modifierAvant les années 60, les processeurs n'était pas encore capables de faire de calculs avec des nombres flottants. Les calculs flottants étaient émulés soit par une bibliothèque logicielle, soit par le système d'exploitation. Pour améliorer les performances, les concepteurs de processeurs ont conçus des coprocesseurs arithmétiques, des processeurs secondaires spécialisés dans les calculs flottants, qui complémentaient le processeur principal, et avaient leur propre emplacement sur la carte mère. Par la suite, les concepteurs de processeurs ont incorporé des instructions de calculs sur des nombres flottants, rendant le coprocesseur inutile.
Les processeurs modernes disposent d'instructions de calculs sur des nombres flottants, qui sont standardisées. Le standard IEEE 754 standardise aussi quelques instructions sur les flottants : les quatre opérations arithmétiques de base, les comparaisons et la racine carrée. Certains processeurs vont plus loin et implémentent aussi d'autres instructions sur les flottants qui ne sont pas supportées par la norme IEEE 754. Par exemple, certaines fonctions mathématiques telles que sinus, cosinus, tangente, arctangente et d'autres. Le seul problème, c'est que ces instructions peuvent mener à des erreurs de calcul incompatibles avec la norme IEEE 754. Heureusement, les compilateurs peuvent mitiger ces désagréments.
Il faut néanmoins préciser que le support de la norme IEEE 754 n'est pas une obligation : certains processeurs ne la supportent que partiellement. Par exemple, certains processeurs ne supportent que les flottants simple précision, mais pas les double précision (ou inversement). Exemple : les premiers processeurs Intel ne géraient que les flottants double précision étendue. D'autres processeurs ne gèrent pas les underflow, overflow, les NaN, les infinis, ou même les flottants dénormaux. Précisons que même lorsque la gestion des dénormaux est implémentée en hardware (comme c'est le cas sur certains processeurs AMD), celle-ci reste malgré tout très lente.
Si les exceptions ne sont pas supportées, le processeur peut être configuré de façon à soit ignorer les exceptions en fournissant un résultat, soit déclencher une exception matérielle (à ne pas confondre avec les exceptions de la norme). Le choix du mode d'arrondi ou la gestion des exceptions flottantes se fait en configurant un registre dédié, intégré dans le processeur.
Plus rarement, il arrive que certains processeurs gèrent des formats de flottants spéciaux qui ne font pas partie de la norme IEEE 754. Par exemple, certains processeurs utilisent des formats de flottants différents de la norme IEEE 754, avec par exemple des flottants codés sur 8 ou 16 bits, qui sont très utiles pour les applications qui * se contentent très bien d'un résultat approché.
Les instructions logiques
modifierÀ côté des instructions de calcul, on trouve des instructions logiques qui travaillent sur des bits ou des groupes de bits. Les opérations bit à bit ont déjà été vues dans les premiers chapitres, ceux sur l'électronique. Pour rappel, les plus courantes sont :
- La négation, ou encore le NON bit à bit, inverse tous les bits d'un nombre : les 1 deviennent des 0 et les 0 deviennent des 1.
- Le ET bit à bit, qui agit sur deux nombres : il va prendre les bits qui sont à la même place et va effectuer un ET (l’opération effectuée par la porte logique ET). Exemple : 1100·1010=1000.
- Les instructions similaires avec le OU ou le XOR.
Mais d'autres instructions sont intéressantes à étudier.
Les instructions de décalage et de rotation
modifierLes instructions de décalage décalent tous les bits d'un nombre vers la gauche ou la droite. Pour rappel, il existe plusieurs types de décalages : les rotations, les décalages logiques, et les décalages arithmétiques. Nous avions déjà vu ces trois opérations dans le chapitre sur les circuits de décalage et de rotation, ce qui fait que nous allons simplement faire un rappel dans le tableau suivant. Pour résumer, voici la différence entre les trois opérations :
Pour rappel, les décalages de n rangs sont équivalents à une multiplication/division par 2^n. Un décalage à gauche est une multiplication par 2^n, alors qu'un décalage à droite est une division par 2^n. Les décalages logiques effectuent la multiplication/division pour un nombre non-signé (positif), alors que les décalages arithmétiques sont utilisés pour les nombres signés. Précisons cependant que pour ce qui est des décalages à droite, les décalages logiques et arithmétiques n'arrondissent pas le résultat de la même manière. Les décalages logiques à droite arrondissent vers zéro, alors que les décalages arithmétiques arrondissent vers la valeur inférieure (vers moins l'infini). De plus, les décalages à gauche entraînent des débordements d'entiers qui ne se gèrent pas de la même manière entre décalage logique et décalage arithmétique.
La plupart des processeurs stockent le bit sortant dans un registre, généralement le registre qui stocke le bit de retenue des additions qui est réutilisé pour cette optique. Ils possèdent aussi une variante des instructions de décalage où le bit de retenue est utilisé pour remplir le bit libéré au lieu de mettre un zéro. Cela permet d'enchaîner les décalages sur un nombre de bits plus grand que celui supporté par les instructions en procédant par morceaux. Par exemple, pour un processeur supportant les décalages sur 8 et 16 bits, il peut enchaîner deux décalages de 16 bits pour décaler un nombre de 32 bits ; ou bien un décalage de 8 bits et un autre de 16 bits pour décaler un nombre de 24 bits.

Ils existe une variante des instructions de rotation où le bit de retenue est utilisé. Un bon exemple est celui des instructions LRCY (Left Rotate Through Carry) et RRCY (Right Rotate Through Carry). La première est un décalage/rotation à gauche, l'autre est un décalage/rotation à droite. Les deux décalent un registre de 16 bits, mais on pourrait imaginer la même chose avec des registres de taille différente. Lors du décalage, le bit sortant est mémorisé dans le registre de retenue, alors que le bit de retenue précédent est lui envoyé dans le vide laissé par le décalage. Tout se passe comme s'il s'agissait d'une rotation, sauf que le nombre décalé/rotaté est composé du registre concaténé au bit de retenue, le bit de retenue étant le bit de poids fort pour un décalage à gauche, de poids faible pour un décalage à droite.
Le cas particuliers des processeurs ARM
modifierSur les processeurs ARM, il n'y a pas d'instruction de décalage à proprement parler, ni de rotations. Par contre, les décalages sont fusionnés avec la plupart des opérations arithmétiques ! Toute opération arithmétique prend deux registres d'opérandes et un registre de destination, ainsi qu'un décalage facultatif. Le décalage est appliqué sur la seconde opérande automatiquement, sans avoir à faire une instruction séparée.
A l'intérieur de l'instruction, deux bits précisent quel type de décalage effectuer (logique à droite, arithmétique à droite, à gauche, rotation à droite). Le nombre de rangs dont il faut décaler est soit encodé directement dans l'instruction sur 5-6 bits, soit précisé dans un registre.
Toutes les instructions ne permettent pas de faire un décalage automatique. Seules les opérations simples peuvent le faire, à savoir les additions, soustractions, copies d'un registre à un autre, les opérations logiques, et quelques autres. Et cela se marie très bien avec le fait qu'on applique le décalage sur la seconde opérande fait qu'il se marie très bien avec les calculs d'adresse. En effet, quand un programmeur manipule une structure de données, notamment un tableau, il arrive souvent qu'il fasse des calculs d'adresse cachés. La majeure partie de ces calculs d'adresse sont de la forme : adresse de base + (indice * taille de la donnée). Vu que les données ont très souvent une taille qui est une puissance de deux, le second terme se calcule en décalant l'indice, le calcul total demande une simple addition avec une opérande décalée, ce qui prend une seule instruction sur les processeur ARM.
Les instructions de manipulation de bits
modifierD'autres opérations effectuent des calculs non pas bit à bit (on traite en parallèle les bits sur la même colonne), mais qui manipulent les bits à l'intérieur d'un nombre. les plus simples d'entre elles comptent sur les bits.
Une instruction très commune de ce type est l'instruction population count, qui compte le nombre de bits d'un nombre qui sont à 1. Par exemple, pour le nombre 0100 1100 (sur 8 bits), la population count est de 3. Il s'agit d'une instruction utile dans les codes correcteurs d'erreur, très utilisés pour tout et n'importe quoi (trames réseau, sommes de contrôle des secteurs des disques dur, et bien d'autres). De plus, elle permet de calculer facilement le bit de parité d'un nombre, ce qui est utile pour les codes de détection d'erreur. En soi, l'instruction est facultative et l'implémenter est un choix qui n'est pas trivial. Mais cette instruction est très simple à implémenter en circuits, sans compter que son implémentation utilise assez peu de transistors. Le circuit de calcul est ridiculement simple, utilise peu de transistors.
Les processeurs gèrent aussi assez souvent des instructions pour compter les zéros ou les uns après le bit de poids fort/faible. Pour rappel, voici les quatre possibilités :
- Count Trailing Zeros donne le nombre de zéros situés à droite du 1 de poids faible.
- Count Leading Zeros donne le nombre de zéros situés à gauche du 1 de poids fort.
- Count Trailing Ones donnent le nombre de 1 situés à gauche du 0 de poids fort.
- Count Leading Ones donne le nombre de 1 situés à droite du 0 de poids faible.

Comme vous le voyez sur le schéma du dessus, ces quatre opérations de comptage sont liées à quatre autres opérations. Ces dernières donnent la position du 0 ou du 1 de poids faible/fort :
- Find First Set, donne la position du 1 de poids faible.
- Find highest set donne la position du 1 de poids fort.
- Find First Zero donne la position du 0 de poids faible.
- Find Highest Zero donne la position du 0 de poids fort.
Il est rare que des processeurs s’implémentent toutes ces opérations. En effet, le résultat de certaines opérations se calcule à partir des autres. Pour donner un exemple, les processeurs x86 modernes incorporent une extension, appelée Bit manipulation instructions sets (BMI sets), qui ajoute quelques instructions de ce type. Pour le moment, seules les instructions Count Trailing Zeros et Count Leading Zeros sont supportées.
Et il existe bien d'autres instructions de ce type. On peut citer, par exemple, l'instruction BLSI, qui ne garde que le 1 de poids faible et met à zéro tous les autres bits. L'instruction BLSR quant à elle, met à 0 ce 1 de poids faible. Et il y en a bien d'autres, qui impliquent le 1 de poids fort, le 0 de poids faible, le 1 de poids faible, etc.
Les instructions d'extension de registres
modifierCertains processeurs sont capables de gérer des données de taille diverses. Ils peuvent par exemple gérer des données codées sur 16 bits ou sur 32 bits comme c'est le cas sur certains processeurs anciens. Comme autre exemple, les processeurs x86 modernes peuvent gérer des données de 8, 16 et 32 bits. Pour cela, ils disposent généralement de registres de taille différentes, certains font 8 bits, d'autres 16, d'autres 32, etc. Dans ce cas, il est courant que l'on ait à faire des conversions vers un nombre de taille plus grande. Par exemple, convertir un nombre de 8 bits en un nombre de 16 bits, ou un nombre de 8 bits en 32 bits. Les processeurs de ce type incorporent des instructions pour ce faire, qui s'appellent les instructions d'extension de nombres.
La seule difficulté de ces instructions tient à la manière dont on remplit les bits de poids forts. Par exemple, si l'on passe de 8 bits à 16 bits, les 8 bits de poids forts sont inconnus. Pareil si on passe de 16 bits à 32 bits : quelle doit être la valeur des 16 bits de poids fort ? Intuitivement, on se dit qu'il suffit de les remplir par des zéros. Faire ainsi marche très bien, mais à condition que le nombre soit un nombre positif ou nul. Mais dans le cas d'un nombre négatif, cela ne marche pas (le résultat n'est pas bon). Pour les nombres codés en complément à deux, il faut remplir les bits manquants par le bit de signe, le bit de poids fort. On a donc deux choix : soit on remplit les bits manquants par des 0, ou par le bit de poids fort. Globalement, les deux choix possibles correspondent à deux instructions : une pour les nombres non-signés et une autre pour les nombres codés en complément à deux. On parle respectivement d'instruction de zero extension et instruction d'extension de signe.
Formellement, les instructions d'extension de nombre sont des copies entre registres : le contenu d'un registre est copié dans un autre plus grand. L'extension de signe est couplée avec cette copie, les deux étant effectués en une instruction. Du moins, c'est le cas sur la plupart des processeurs. On pourrait imaginer séparer les deux en deux instructions séparées, une instruction MOV (qui copie un registre dans un autre, comme on le verra plus bas) et une instruction d'extension de signe/zéro. Dans ce cas, l'instruction d'extension de signe/zéro prend un registre de grande taille et étend la donnée dans ce registre. Par exemple, pour une extension de signe de 16 à 32 bits, l'instruction prendrait un registre de 32 bits, ne considérerait que les 16 bits de poids faible et effectuerait l'extension de signe/zéro à partir de ces derniers. En soi, l'extension avec des zéros est un simple masque, réalisable avec des opérations bit à bit et cette instruction n'a pas besoin d'être implémentée. Par contre, les instructions d'extension de signe sont elles très utiles.
De plus, une instruction d'extension de signe séparée a l'avantage d'être utilisable même sur des architecture avec des registres de taille identique. Mais quel intérêt, me direz-vous ? Il faut savoir que certaines langages de programmation permettent de travailler sur des entiers dont on peut préciser la taille. Un même programme peut ainsi manipuler des entiers de 16 bits et de 32 bits, ou des entiers de 8, d'autres de 16, d'autres de 32, et d'autres de 64. L'intérêt n'est as évident, mais un bon exemple est celui de la rétrocompatibilité entre programmes. Par exemple, un programme 64 bits qui utilise une librairie 32 bits, ou un programme codé en 64 bits qui émule une console 16 bits. Ou encore, la communication entre un programme codé en 16 bits avec un capteur qui mesure des données de 8 bits. Bref, les possibilités sont nombreuses. Imaginons que tout se passe dans des registres de 32 bits. Le processeur peut incorporer des instructions de calcul sur 16 bits, en plus des instructions 32 bits. Dans ce cas, l'extension de signe sert à faire des conversions entre entiers de taille différentes.
Les instructions de permutation d'octets
modifierLes instructions de byte swap, aussi appelée instructions de permutation d'octets, échangent de place les octets d'un nombre. Leur implémentation varie grandement selon la taille des entiers. Le cas le plus simple est celui des instructions qui travaillent sur des entiers de 16 bits, soit deux octets. Il n'y a alors qu'une seule solution pour échanger les octets : l'octet de poids fort devient l'octet de poids faible et réciproquement. Les deux octets échangent leur place.
Pour les nombres de 32 bits, soit 4 octets, il y a plusieurs possibilités. La première inverse l'ordre des octets dans le nombre : on échange l'octet de poids faible et de poids fort, mais on échange aussi les deux octets restant entre eux. Une autre solution découpe l'entier en deux morceaux de 16 bits : l'un avec les deux octets de poids fort, l'autre avec les deux octets de poids faible. Les octets sont inversés dans ces blocs de 16 bitzs, mais on n'effectue pas d'autres échanges. On peut aussi échanger les deux morceaux de 16 bits, mais sans changer l'ordre des octets dans les blocs.

L'utilité de ces instructions n'est pas évidente au premier abord, mais elle sert beaucoup dans les opérations de conversion de données. Tout cela devrait devenir plus clair dans le chapitre sur le boutisme.
Les instructions d'accès mémoire
modifierLes instructions d’accès mémoire permettent de copier ou d'échanger des données entre le processeur et la RAM. On peut ainsi copier le contenu d'un registre en mémoire, charger une donnée de la RAM dans un registre, initialiser un registre à une valeur bien précise, etc. Il en existe plusieurs, les plus connues étant les suivantes : LOAD, STORE et MOV. D'autres processeurs utilisent une instruction d'accès mémoire généraliste, plus complexe.
Les instructions d'accès à la RAM : LOAD et STORE
modifierLes instructions LOAD et STORE sont deux instructions qui permettent d'échanger des données entre la mémoire RAM et les registres. Elles copient le contenu d'un registre dans la mémoire, ou au contraire une portion de mémoire RAM dans un registre.
- L'instruction LOAD est une instruction de lecture : elle copie le contenu d'un ou plusieurs mots mémoire consécutifs dans un registre. Le contenu du registre est remplacé par le contenu des mots mémoire de la mémoire RAM.
- L'instruction STORE fait l'inverse : elle copie le contenu d'un registre dans un ou plusieurs mots mémoire consécutifs en mémoire RAM.

|

|
D'autres instructions d'accès mémoire plus complexes existent. Pour en donner un exemple, citons les instructions de transferts par bloc sur les premiers processeurs ARM. Ces instructions permettent de copier plusieurs registres en mémoire RAM, en une seule instruction. Sur l'ARM1, il y a 16 registres en tout. Les instructions de transfert de bloc peuvent sélectionner n'importe quel sous-ensemble de ces 16 registres, pour les copier en mémoire : on peut sélectionner tous les registres, une partie des registres (5 registres sur 16, ou 7, ou 8, ...), voire aucun registre.
Les instructions de transfert entre registres : MOV et XCHG
modifierL'instruction MOV copie le contenu d'un registre dans un autre sans passer par la mémoire. C'est donc un échange de données entre registres, qui n'implique en rien la mémoire RAM, mais MOV est quand même considérée comme une instruction d'accès mémoire. Les données sont copiées d'un registre source vers un registre de destination. Le contenu du registre source est conservé, alors que le contenu du registre de destination est écrasé (il est remplacé par la valeur copiée). Cette instruction est utile pour gérer les registres, notamment sur les architectures avec peu de registres et/ou sur les architectures avec des registres spécialisés.

Mais quelques rares architectures ne disposent pas d'instruction MOV, qui n'est formellement pas nécessaire, même si bien utile. En effet, on peut émuler une instruction MOV avec des instructions logiques utilisées convenablement. L'idée est de faire une opération dont le résultat est l'opérande envoyée, et d'enregistrer le résultat dans le registre de destination. Par exemple, on peut faire un OU entre le registre opérande et 0 : le résultat sera l'opérande. Idem avec un ET et la valeur adéquate. Ou encore, on peut imaginer faire un ET/OU entre un registre et lui-même : le résultat est égal au contenu du registre opérande.
Quelques processeurs assez rares ont des instructions pour échanger le contenu de deux registres. Par exemple, on peut citer l'instruction XCHG sur les processeurs x86 des PC anciens et actuels. Elle permet d'échanger le contenu de deux registres, quel qu'ils soient, il n'y a pas de restrictions sur le registre source et sur le registre de destination. Mais d'autres processeurs ont des restrictions sur les registres source et destination. Par exemple, le processeur Z80 a des instructions d'échanges assez restrictives, comme on le verra dans quelques chapitres.
Sur les processeurs ARM, l'instruction MOV fait partie des instructions qui permettent d'effectuer un décalage sur la seconde opérande. Il s'agit en réalité de décalages/rotations décalées, qui sont fusionnées avec une instruction MOV. L'instruction MOV des processeurs ARM fait soit un MOV normal, soit un décalage.
Les instructions d'accès mémoire complexes
modifierSur certains processeurs, il n'y a pas d'instruction LOAD ou STORE. A la place, on trouve une instruction d'accès mémoire généraliste. Elle est notamment capable de faire une lecture, une écriture, ou une copie entre registres, et parfois une copie d'une adresse mémoire vers une autre. Les trois premières opérations sont presque toujours supportées, mais la copie d'une adresse mémoire vers une autre est beaucoup plus rare.
Sur les processeurs x86, l'instruction généraliste s'appelle l'instruction MOV, mais elle gère la lecture en RAM, l'écriture en RAM, la copie d'un registre vers un autre, l'écriture d'une constante dans un registre ou une adresse. Par contre, elle ne gère pas la copie d'une adresse mémoire vers une autre. Le choix entre les opérations possibles dépend de l'ordre des opérandes et de leurs nature. L'instruction mémoire généraliste utilise deux opérandes, et leur ordre compte. Typiquement, la première opérande désigne la source et l'autre la destination. Par exemple, si les deux opérandes sont des registres, alors le premier registre est copié dans le second. Si la première opérande est un registre, et l'autre une adresse, alors c'est une écriture. Inversez l'adresse et le registre et c'est une lecture.
Pour les transferts entre deux adresses, il existe d'autres instructions mémoires spécialisées. Elles sont connues sous le nom d'instructions de chaines de caractère, bien qu'elles travaillent en réalité plus sur des tableaux ou des zones de mémoire. Fait intéressant, ces instructions mémoires peuvent être répétée automatiquement plusieurs fois, en leur ajoutant un préfixe. Pour cela, le nombre de répétitions doit être stocké dans le registre ECX, qui est décrémenté à chaque exécution de l'instruction. Une fois que ce registre atteint 0, l'instruction n'est plus répété et on passe à l'instruction suivante. En clair, l'instruction décrémente automatiquement ce registre à chaque éxecution et s'arrête quand il atteint zéro.
Pour les échanges entre deux adresses mémoire, les processeurs x86 fournissent une instruction dédiée, appelée MOVS. Pour cela, on doit préciser l'adresse de la source et l'adresse de destination dans deux registres spécifiques. Elle peut être répétée plusieurs fois avec l'ajout du préfixe REP. L'instruction avec préfixe, REPMOVS, permet donc de copier un bloc de mémoire dans un autre, de copier n adresses consécutives ! Les deux registres pour l'adresse source et destination sont modifiés à chaque exécution de l'instruction, afin de pointer vers le mot mémoire suivant. Par modifiés, je veux dire qu'ils peuvent être tous les deux soit incrémentés, soit décrémentés. Cela permet de parcourir la mémoire dans l'ordre montant (adresses croissantes) ou descendant (adresses décroissantes). La direction de parcours de la mémoire est spécifiée dans un bit incorporé dans le processeur, qui vaut 0 (décrémentation) ou 1 (incrémentation). Il peut être altéré par des instructions dédiées, de manière à être mis à 1 ou 0.
D'autres instructions d'accès mémoire peuvent être préfixées avec REP. Par exemple, l'instruction STOS, qui copie le contenu du registre EAX dans une adresse. On peut exécuter cette instruction une fois, ou la répéter plusieurs fois avec le préfixe REP. Là encore, on doit préciser l'adresse à laquelle écrire dans un registre spécifié, puis le nombre de répétitions dans le registre ECX. Là encore, le nombre de répétitions est décrémenté à chaque exécution, alors que l'adresse est incrémentée/décrémentée. L'instruction REPSTOS est très utile pour mettre à zéro une zone de mémoire, ou pour initialiser un tableau avec des données préétablies.
D'autres instructions mémoires effectuent des opérations à l'utilité moins évidente. Sur certains processeurs, on trouve notamment des instructions pour vider la mémoire cache de son contenu, pour la réinitialiser. L'utilité ne vous est pas évidente, mais cela peut servir dans certains scénarios, notamment sur les architectures avec plusieurs processeurs pour synchroniser ces derniers. Cela sert aussi pour le système d'exploitation, qui doit remettre à zéro certains caches (comme la TLB qu'on verra dans le chapitre sur la mémoire virtuelle) quand on exécute plusieurs programmes en même temps.
Les instructions de contrôle (branchements et tests)
modifierUn processeur serait sacrément inflexible s'il ne faisait qu'exécuter des instructions dans l'ordre. Certains processeurs ne savent pas faire autre chose, comme le Harvard Mark I, et il est difficile, voire impossible, de coder certains programmes sur de tels ordinateurs. Mais rassurez-vous : il existe de quoi permettre au processeur de faire des choses plus évoluées. Pour rendre notre ordinateur "plus intelligent", on peut par exemple souhaiter que celui-ci n'exécute une suite d'instructions que si une certaine condition est remplie. Ou faire mieux : on peut demander à notre ordinateur de répéter une suite d'instructions tant qu'une condition bien définie est respectée. Diverses structures de contrôle de ce type ont donc étés inventées.
Voici les plus utilisées et les plus courantes : ce sont celles qui reviennent de façon récurrente dans un grand nombre de langages de programmation actuels. Concevoir un programme (dans certains langages de programmation), c'est simplement créer une suite d'instructions, et utiliser ces fameuses structures de contrôle pour l'organiser. D'ailleurs, ceux qui savent déjà programmer auront reconnu ces fameuses structures de contrôle. On peut bien sur en inventer d’autres, en spécialisant certaines structures de contrôle à des cas un peu plus particuliers ou en combinant plusieurs de ces structures de contrôles de base, mais cela dépasse le cadre de ce cours : on ne va pas vous apprendre à programmer.
| Nom de la structure de contrôle | Description |
|---|---|
| SI...ALORS | Exécute une suite d'instructions si une condition est respectée |
| SI...ALORS...SINON | Exécute une suite d'instructions si une condition est respectée ou exécute une autre suite d'instructions si elle ne l'est pas. |
| Boucle WHILE...DO | Répète une suite d'instructions tant qu'une condition est respectée. |
| Boucle DO...WHILE aussi appelée REPEAT UNTIL | Répète une suite d'instructions tant qu'une condition est respectée. La différence, c'est que la boucle DO...WHILE exécute au moins une fois cette suite d'instructions. |
| Boucle FOR | Répète un nombre fixé de fois une suite d'instructions. |
Les conditions à respecter pour qu'une structure de contrôle fasse son office sont généralement très simples. Elles se calculent le plus souvent en comparant deux opérandes (des adresses, ou des nombres entiers ou à virgule flottante). Elles correspondent le plus souvent aux comparaisons suivantes :
- A == B (est-ce que A est égal à B ?) ;
- A != B (est-ce que A est différent de B ?) ;
- A > B (est-ce que A est supérieur à B ?) ;
- A < B (est-ce que A est inférieur à B ?) ;
- A >= B (est-ce que A est supérieur ou égal à B ?) ;
- A <= B (est-ce que A est inférieur ou égal à B ?).
Pour implémenter ces structures de contrôle, on a besoin d'une instruction qui saute en avant ou en arrière dans le programme, suivant le résultat d'une condition. Par exemple, un SI...ALORS zappera une suite d'instruction si une condition n'est pas respectée, ce qui demande de sauter après cette suite d’instruction cas échéant. Répéter une suite d'instruction demande juste de revenir en arrière et de redémarrer l’exécution du programme au début de la suite d'instruction. Nous verrons comment sont implémentées les structures de contrôle plus bas, mais toujours est-il que cela implique de faire des sauts dans le programme. Faire un saut en avant ou en arrière dans le programme est assez simple : il suffit de modifier la valeur stockée dans le program counter, ce qui permet de sauter directement à une instruction et de poursuivre l'exécution à partir de celle-ci. Et un tel saut est réalisé par des instructions spécialisées. Dans ce qui va suivre, nous allons appeler instructions de branchement les instructions qui sautent à un autre endroit du programme. Ce n'est pas la terminologie la plus adaptée, mais elle conviendra pour les explications.
L'implémentation des structures de contrôle demande donc de calculer une condition, puis de faire un saut. Mais il faut savoir que l'implémentation demande parfois de faire un saut, sans avoir à tester de condition. Dans ce cas, l'instruction qui fait un saut sans faire de test de condition est elle aussi une instruction de branchement. Cela nous amène à faire la différence entre un branchement conditionnel et non-conditionnel. La différence entre les deux est simple. Une instruction de branchement conditionnel effectue deux opérations : un test qui vérifie si la condition adéquate est respectée, et un saut dans le programme aussi appelé branchement. Une instruction de branchement inconditionnelle ne teste pas de condition et ne fait qu'un saut dans le programme.
Les structures de contrôle
modifierLe IF permet d’exécuter une suite d'instructions si et seulement si une certaine condition est remplie.

Le IF...ELSE sert à effectuer une suite d'instructions différente selon que la condition est respectée ou non : c'est un SI…ALORS contenant un second cas. Une boucle consiste à répéter une suite d'instructions machine tant qu'une condition est valide (ou fausse).

Les boucles sont une variante du IF dont le branchement renvoie le processeur sur une instruction précédente. Commençons par la boucle DO…WHILE : la suite d'instructions est exécutée au moins une fois, et est répétée tant qu'une certaine condition est vérifiée. Pour cela, la suite d'instructions à exécuter est placée avant les instructions de test et de branchement, le branchement permettant de répéter la suite d'instructions si la condition est remplie. Si jamais la condition testée est fausse, on passe tout simplement à la suite du programme.

Une boucle WHILE…DO est identique à une boucle DO…WHILE à un détail près : la suite d'instructions de la boucle n'a pas forcément besoin d'être exécutée au moins une fois. On peut donc adapter une boucle DO…WHILE pour en faire une boucle WHILE…DO : il suffit de tester si la boucle doit être exécutée au moins une fois avec un IF, et exécuter une boucle DO…WHILE équivalente si c'est le cas.

Les branchements conditionnels et leur implémentation
modifierIl existe de nombreuses manières de mettre en œuvre les branchements conditionnels et tous les processeurs ne font pas de la même manière. Sur la plupart des processeurs, les branchements conditionnels sont séparés en deux instructions : une instruction de test qui vérifie si la condition voulue est respectée, et une instruction de saut conditionnelle. D'autres processeurs effectuent le test et le saut en une seule instruction machine.

- Plus surprenant, sur quelques rares processeurs, le program counter est un registre qui peut être modifié comme tous les autres. Cela permet de remplacer les branchements par une simple écriture dans le program counter, avec une instruction MOV. Un bon exemple est le processeur ARM1, un des tout premiers processeur ARM. Cette dernière solution n'est presque jamais utilisée, mais elle reste surprenante !
Dans les faits, la solution la plus simple est clairement d'implémenter le tout avec une seule instruction. Mais beaucoup de processeurs anciens utilisent la première méthode, celle qui sépare le branchement conditionnel en deux instructions. Le branchement prend le résultat de l'instruction de test et décide s'il faut passer à l'instruction suivante ou sauter à une autre adresse. Il faut donc mémoriser le résultat de l'instruction de test dans un registre spécialisé, afin qu'il soit disponible pour l'instruction de branchement. L'usage d'un registre intermédiaire pour mémoriser le résultat de l'instruction de test demande d'ajouter un registre au processeur. De plus, le résultat de l'instruction de test varie grandement suivant le processeur, suivant la manière dont on répartit les responsabilités entre test et branchements.
Il existe, dans les grandes lignes, deux techniques pour séparer test et branchement conditionnel. La première impose une séparation stricte entre calcul de la condition et saut : l'instruction de test calcule la condition, le branchement fait ou non le saut dans le programme suivant le résultat de la condition. On a alors une instruction de test proprement dit, qui vérifie si une condition est valide et fournit un résultat sur 1 bit. Nous appellerons ces dernières des comparaisons, car de telles instruction effectuent réellement une comparaison. La seconde méthode procède autrement, avec un calcul de la condition qui est réalisé en partie par l'instruction de test, en partie par le branchement. Cela peut paraitre surprenant, mais il y a de bonnes raisons à cette séparation peu intuitive. La raison est que l'instruction de test est une soustraction déguisée, qui fournit un résultat de plusieurs bits, qui est ensuite utilisé pour calculer la condition voulue par le branchement. l'instruction de test ne fait pas une comparaison proprement dit, mais leur résultat permet de déterminer le résultat d'une comparaison avec quelques manipulations simples.
Les instructions de test proprement dit
modifierLes premières sont réellement des instructions de test, qui effectuent une comparaison et disent si deux nombres sont égaux, différents, lequel est supérieur, inférieur, etc. En clair, elles implémentent directement les comparaisons vues précédemment. Au total, on s'attend à ce que les 6 comparaisons précédentes soient implémentées avec 6 instructions de test différentes : une pour l'égalité, une pour la différence, une autre pour la supériorité stricte, etc. Mais certaines de ces comparaisons sont en deux versions : une qui compare des entiers non-signés, et une autre pour les entiers signés. La raison est que comparer deux nombres entiers ne se fait pas de la même manière selon que les opérandes soient signées ou non. Nous avions vu cela dans le chapitre sur les comparateurs, mais un petit rappel ne fait pas de mal. Pour comparer deux entiers signés, il faut tenir compte de leurs signes, et le circuit utilisé n'est pas le même. Cela a des conséquences au niveau des instructions du processeur, ce qui impose d'avoir des opérations séparées pour les entiers signés et non-signés.
Dans les faits, les processeurs actuels utilisent le complément à deux pour les entiers signés, ce qui fait que les comparaisons d'égalité ou de différence A == B et A != B ne sont présentes qu'en un seul exemplaire. En complément à deux, l'égalité se détermine avec la même règle que pour les entiers non-signés : deux nombres sont égaux s'ils ont la même représentation binaire, ils sont différents sinon. Ce ne serait pas le cas avec les entiers en signe-magnitude ou en complément à un, du fait de la présence de deux zéros : un zéro positif et un zéro négatif. Les circuits de comparaison d'égalité et de différence seraient alors légèrement différents pour les entiers signés ou non. Au total, en complément à deux, on trouve donc 10 comparaisons usuelles, vu que les comparaisons de supériorité/infériorité sont en double.
Le résultat d'une comparaison est un bit, qui dit si la condition testée est vraie ou fausse. Dans la majorité des cas, ce bit vaut 1 si la comparaison est vérifiée, et 0 sinon. Une fois que l'instruction a fait son travail, il reste à stocker son résultat quelque part. Pour cela, le processeur utilise un ou plusieurs registres à prédicats, des registres de 1 bit qui peuvent stocker n'importe quel résultat de comparaison. Une comparaison peut enregistrer son résultat dans n'importe quel registre à prédicats : elle a juste à préciser lequel avec son nom de registre.
Les registres à prédicats sont utiles pour accumuler les résultats de plusieurs comparaisons et les combiner par la suite. Par exemple, cela permet d'émuler une instruction qui teste si A >= B à partir de deux instructions qui calculent respectivement A > B et A == B. Pour cela, certains processeurs incorporent des instructions pour faire des opérations logiques sur les registres à prédicats. Ces opérations permettent de faire un ET, OU, XOR entre deux registres à prédicats et de stocker le résultat dans un registre à prédicat quelconque.
D'autres instructions permettent de lire le résultat d'un registre à prédicat, de calculer une condition, de combiner son résultat avec la valeur lue et d'altérer le registre à prédicat sélectionné. Par exemple, sur l'architecture IA-64, il existe une instruction cmp.eq.or, qui calcule une condition, lit un registre à prédicat fait un OU logique entre le registre lu et le résultat de la condition, et enregistre le tout dans un autre registre à prédicat. De telles instructions facilitent grandement le codage de certaines fonctions, qui demandent que plusieurs conditions soient vérifiées pour exécuter un morceau de code.
Les instructions de test qui sont des soustractions déguisées
modifierLe second type d'instruction de test ne calcule pas ces conditions directement, mais elle fournit un résultat de quelques bits qui permet de les calculer avec quelques manipulations simples. Sur ces processeurs, il n'y a qu'une seule instruction de comparaison, qui est une soustraction déguisée. Le résultat de la soustraction n'est pas sauvegardé dans un registre et est simplement perdu. C'est le cas sur certains processeurs ARM ou sur les processeurs x86. Par exemple, un processeur x86 possède une instruction CMP qui n'est qu'une soustraction déguisée dans un opcode différent.
Le résultat de cette soustraction déguisée est un résultat portant sur 4 bits, qui donne des informations sur le résultat de la soustraction. Le premier bit, appelé bit null, indique si le résultat est nul ou non. Le second bit indique le signe du résultat, s'il est positif ou négatif. Enfin, deux autres bits précisent si la soustraction a donné lieu à un débordement d'entier. Il y a deux bits, car on vérifie deux types de débordement : un débordement non-signé (une retenue sortante de l'additionneur), et le débordement signé (débordement en complément à deux). Pour mémoriser le résultat d'une soustraction déguisée, le processeur incorpore un registre d'état. Le registre d'état stocke des bits qui ont chacun une signification prédéterminée lors de la conception du processeur et il sert à beaucoup de choses. Dans le cas qui nous intéresse, le registre d'état mémorise les résultats de l'instruction de test : les deux bit de débordement, le bit qui précise que le résultat d'une instruction vaut zéro, le bit de retenue pour le bit de signe.
La condition en elle-même est réalisée par le branchement. L'instruction de branchement fait donc deux choses : calculer la condition à partir du registre d'état, et effectuer le saut si la condition est valide. Le calcul des conditions se fait à partir des 4 bits de résultat. Le bit null permet de savoir si les deux opérandes sont égales ou non : si le résultat d'une soustraction est nul, cela implique que les deux opérandes sont égales. Le bit de signe permet de déterminer si le première opérande est supérieur ou inférieure à la seconde : le résultat de la soustraction est positif si A >= B, négatif sinon. Les bits de débordements permettent de faire la différence entre infériorité stricte ou non. Tout cela sera expliqué plus en détail dans le paragraphe suivant.

La conséquence est qu'il y a autant d'instructions de branchements que de conditions possibles. Aussi, on a une instruction de test, mais environ une dizaine d'instructions de branchements. C'est l'inverse de ce qu'on a avec des instructions de test proprement dites, où on a autant d'instructions de test que de conditions, mais un seul branchement. Un bon exemple est celui des processeurs x86. Le registre d'état des CPU x86 contient 5 bits appelés OF, SF, ZF, CF et PF : ZF indique que le résultat de la soustraction vaut 0, SF indique son signe, CF est le bit de retenue et de débordement non-signé, OF le bit de débordement signé, et PF le bit qui donne la parité du résultat. Il existe plusieurs branchements, certains testant un seul bit du registre d'état, et d'autres une combinaison de plusieurs bits.
| Instruction de branchement | Bit du registre d'état testé | Condition testée si on compare deux nombres A et B avec une instruction de test |
|---|---|---|
| JS (Jump if Sign) | SF = 1 | Le résultat est négatif |
| JNS (Jump if not Sign) | SF = 0 | Le résultat est positif |
| JO (Jump if Overflow) | OF = 1 | Le calcul arithmétique précédent a généré un débordement signé |
| JNO (Jump if Not Overflow) | OF = 0 | Le calcul arithmétique précédent n'a pas généré de débordement signé |
| JNE (Jump if Not equal) | ZF = 1 | Les deux nombres A et B sont égaux |
| JE (Jump if Equal) | ZF = 0 | Les deux nombres A et B sont différents |
| JB (Jump if below) | CF = 1 | A < B, avec A et B non-signés |
| JAE (Jump if Above or Equal) | CF = 0 | A >= B, avec A et B non-signés |
| (JBE) Jump if below or equal | CF OU ZF = 1 | A >= B si A et B sont non-signés |
| JA (Jump if above) | CF ET ZF = 0 | A > B si A et B sont non-signés |
| JL (Jump if less) | SF != OF | si A < B, si A et B sont signés |
| JGE (Jump if Greater or Equal) | SF = OF | si A >= B, si A et B sont signés |
| JLE (Jump if less or equal) | (SF != OF) OU ZF = 1 | si A <= B, si A et B sont signés |
| JGE (Jump if Greater) | (SF = OF) ET (NOT ZF) = 1 | si A > B, si A et B sont signés |
Les instructions à prédicat
modifierLes instructions à prédicat sont des instructions qui ne font quelque chose que si une condition est respectée, et se comportent comme un NOP (une instruction qui ne fait rien) sinon. Elles lisent le résultat d'une comparaison, dans le registre d'état ou un registre à prédicat, et s’exécutent ou non suivant sa valeur. En théorie, les instructions à prédicats sont des instructions en plus des instructions normales, pas à prédicat. L'instruction à prédicat la plus représentative, présente sur de nombreux processeurs, est l'instruction CMOV, qui copie un registre dans un autre si une condition est remplie. Elle permet de faire certaines opérations assez simples, comme calculer la valeur absolue d'un nombre, le maximum de deux nombres, etc.
Mais sur certains processeurs, assez rares, toutes les instructions sont des instructions à prédicat : on parle de prédication totale. Cela peut paraitre étranger, vu que certaines instructions ne sont pas dans une structure de contrôle et doivent toujours s’exécuter, peu importe les conditions testées avant. Mais rassurez-vous, sur les processeurs à prédication totale, il y a toujours un moyen pour spécifier que certaines instructions doivent toujours s’exécuter, de manière inconditionnelle. Par exemple, sur les processeurs d'architecture HP IA-64, un des registre à prédicat, le tout premier, contient la valeur 1 et ne peut pas être modifié. Si on veut une instruction inconditionnelle, il suffit qu'elle précise que le registre à prédicat à lire est ce registre.
Sur les processeurs disposant d'instructions à prédicats, les instructions de test s'adaptent sur plusieurs points. L'un d'entre eux est que les instructions de test utilisent souvent des registres à prédicats. L'utilité principale des instructions à prédicats est d'éliminer les branchements, qui posent des problèmes sur les architectures modernes pour des raisons que nous verrons dans les derniers chapitres de ce cours. Toujours est-il que l'usage d'un registre d'état se marierait un petit peu mal avec cet objectif. Avec des registres à prédicats, on peut ajouter des instructions pour faire un ET, un OU ou un XOR entre registres à prédicats, comme dit plus haut. Cela permet de tester des combinaisons de conditions, voire des conditions complexes, sans faire appel au moindre branchement. Et ces conditions complexes ne sont pas rares, ce qui rend l'usage de registres à prédicats très utiles avec les instructions à prédicats. Les processeurs avec un registre d'état n'ont généralement que de la prédication partielle, le plus souvent limitée à une seule instruction CMOV. Alors que qui dit prédication totale dit systématiquement registres à prédicats.
Une autre adaptation est que les instructions de test tendent à fournir deux résultats : le résultat de la condition, et le résultat de la condition inverse. Les deux résultats sont l'inverse l'un de l'autre : si le premier vaut 1, l'autre vaut 0 (et réciproquement). Les deux résultats sont naturellement fournis dans deux registres à prédicats distincts. L'utilité de cette adaptation est que les instructions à prédicats servent à implémenter des structures de contrôle SI...ALORS simples, qui ont deux morceaux de code : un qui s’exécute si une condition est remplie, l'autre si elle ne l'est pas. pour le dire autrement, le premier morceau de code s’exécute quand la condition est remplie, l'autre quand la condition inverse est remplie. On comprend donc mieux l'utilité pour les isntructions de test de fournir deux résultats, l'un étant l'inverse de l'autre.
L'instruction SKIP
modifierL'instruction SKIP permet de zapper l'instruction suivante si une condition testée est fausse. Il en existe deux versions. La première est fusionnée avec l'instruction de test. La condition est calculée par l'instruction SKIP, qui décide s'il faut sauter l'instruction suivante. Dans un autre cas, l'instruction SKIP est précédée d'une instruction de test, récupère son résultat dans un registre de prédicat ou dans le registre d'état, et effectue le saut. On peut la voir comme une forme particulière de branchement conditionnel, qui brancherait deux instructions plus loin.
Son utilité n'est pas évidente, mais on peut classer ses utilisations en trois catégories. La première permet d'émuler une instruction de branchement conditionnel en combinant une instruction SKIP avec un branchement inconditionnel. Le branchement inconditionnel est skippé si la condition est remplie/fausse, mais éxecuté dans le cas contraire : c'est le comportement d'un branchement conditionnel. Une autre utilisation permet d'émuler une instruction à prédicat en faisant précéder une instruction normale par une instruction SKIP. Enfin, elles servent à implémenter des structures de controle IF à condition que le code du IF se résume à une vulgaire instruction. C'est assez rare, mais certains calculs comme la valeur absolue ou le calcul du minimum peuvent se calculer ainsi.

Vous pourriez imaginer des versions améliorées de l'instruction, qui permettent de zapper plusieurs instructions, mais de telles instructions ne sont autres que des instructions de branchement conditionnelles spécifiques, comme nous le verrons dans le chapitre sur les modes d'adressage.
Les méta-instructions REPEAT et EXECUTE
modifierEnfin, il faut aussi citer les méta-instructions, des instructions qui agissent sur l’exécution d'autres instructions. Il en existe deux : REPEAT et EXECUTE. Elles servent techniquement à manipuler le flot de contrôle d'un programme, et ont quelques ressemblances avec les branchements ou les boucles. Elles sont extrêmement rares et on ne les trouve que sur des anciens processeurs (généralement micro-codés), ou sur certaines processeurs spécialisés dans le traitement de signal appelés des DSP, qui feront l'objet d'un chapitre à eux seuls.
L’instruction REPEAT et le Zero-overhead looping
modifierLa première est la méta-instruction REPEAT, qui permet de simplifier l'implémentation des boucles. Dans sa version la plus simple, elle fait en sorte que l'instruction qui la suit soit répétée plusieurs fois. Le nombre de répétition est soit un nombre fixe, toujours le même, soit l'instruction se répète tant qu'une condition n'est pas remplie. Les deux situations ne se rencontrent pas sur les mêmes processeurs. Par exemple, l'UNIVAC 1103 possède une instruction REPEAT très simple, qui répète l'instruction cible un nombre fixe de fois, mais ne gère pas les conditions.
Le GE-600/Honeywell 6000 series incorpore trois instructions REPEAT de ce type. La première répète l'instruction suivante soit un nombre fixe de fois, soit quand une condition est remplie. La seconde répète les deux instructions suivantes, l'une après l'autre. Enfin, la dernière répète l'instruction suivante jusqu'à : soit qu'une condition soit remplie, soit qu'une adresse bien précise soit atteinte. Elle servait sans doute à implémenter le parcours d'une liste chainée pour trouver un item bien précis.
Une version améliorée de l'instruction REPEAT permet de répéter un bloc de plusieurs instructions, ce qui permet d'implémenter une boucle en une seule instruction. On parle d'ailleurs de Zero-overhead looping. Elles sont fréquentes sur certains processeurs de traitement de signal, qui doivent exécuter fréquemment des boucles. Typiquement, elles permettent d'implémenter des boucles FOR dont le nombre d’exécution est fixe, ou du moins stocké dans un registres. La répétition de la boucle est contrôlée par un registre de boucle, qui mémorise le nombre de répétitions, et qui est décrémenté à chaque itération.
- Les instructions REP mentionnées plus haut, ne sont PAS des exemples d'instruction REPEAT. Le préfixe REP des processeurs x86 est une instruction qui se répète elle-même. Mais l'instruction REPEAT force la répétition de l'instruction suivante ! Elle agit sur une autre instruction, d'où son caractère de méta-instruction.
L'instruction EXECUTE
modifierLa méta-instruction EXECUTE fournit l'adresse d'une instruction cible, qui est exécutée en lieu et place de l'instruction EXECUTE. Quand le processeur exécute l'instruction EXECUTE, il prend l'adresse cible, charge l'instruction dans l'adresse cible, et l’exécute à la place de l'instruction EXECUTE. Il est possible de comprendre l'instruction EXECUTE comme un branchement spécial. Tout se passe comme si l'instruction EXECUTE effectuait un branchement vers l'instruction cible, mais que le processeur ne poursuivait pas l’exécution à la suite de l’instruction cible, et revenait à la suite de l'instruction cible.
Il y a souvent des contraintes sur l'instruction cible, qui est pointée par l'adresse cible. Généralement, il n'est pas possible que l'instruction cible soit elle-même une autre instruction EXECUTE. De même, beaucoup de processeurs interdisent que l’instruction cible soit un branchement. Mais d'autres processeurs n'ont pas ces contraintes et autorisent à utiliser des branchements pour l'instruction cible.
L'utilité d'une telle instruction est tout sauf évidente. Elle servait pourtant à beaucoup de choses sur les processeurs où elle était implémentée. Précisons qu'elle était surtout présente sur des vieux ordinateurs, dans les années 50-60, et quelques processeurs des années 70. Elle a disparu dès les années 80 et n'est présentée que par souci d'exhaustivité et intérêt historique pour les curieux. Cette précision permet de comprendre que cette instruction servait pour résoudre des problèmes qui sont actuellement résolus autrement.
L'adresse cible peut être soit intégrée dans l'instruction, soit dans un registre. Dans le second cas, l'adresse peut être incrémentée ou modifiée afin que l'instruction EXECUTE change de cible à chaque exécution. Tout se passe comme si le registre contenant l'adresse cible servait à émuler un program counter. En mettant une instruction EXECUTE dans une boucle et en complétant le tout avec du code annexe, on peut exécuter du code extérieur sans modifier le véritable program counter. L'utilité est de faciliter l'implémentation des logiciels debuggers, des émulateurs, ou d'autres programmes dans le même genre.
Les autres utilisations sont assez nombreuses, mais aussi difficiles à expliquer pour qui n'a pas de connaissances poussées en programmation. La première utilité est l'implémentation de certaines fonctionnalités des langages de programmation évolués, à savoir le late binding, les fonctions virtuelles, et quelques autres. Elle facilite aussi l'implémentation des compilateurs à la volée, en permettant d’exécuter du code produit à volée sans faire tiquer les mécanismes de protection mémoire implémentés dans le processeur. Elle permet d'émuler du code automodifiant pour les logiciels qui gagnaient autrefois à l'utiliser. Et il y en a d'autres.
Les instructions exotiques
modifierPour résumer, les instructions les plus courantes sont les suivantes :
| Instruction | Utilité |
|---|---|
| Instructions arithmétiques | Ces instructions font simplement des calculs sur des nombres. On peut citer par exemple :
|
| Instructions logiques | Elles travaillent sur des bits ou des groupes de bits. On peut citer :
|
| Instructions de test et de contrôle (branchements) | Elles permettent de contrôler la façon dont notre programme s’exécute sur notre ordinateur. Elles permettent notamment de choisir la prochaine instruction à exécuter, histoire de répéter des suites d'instructions, de ne pas exécuter des blocs d'instructions dans certains cas, et bien d'autres choses. |
| Instructions d’accès mémoire | Elles permettent d'échanger des données entre le processeur et la mémoire, ou encore permettent de gérer la mémoire et son adressage. Les deux les plus courantes sont les suivantes :
|
En plus de ces instructions, beaucoup de processeurs ajoutent d'autres instructions. La plupart sont utilisées par le système d'exploitation pour configurer certaines fonctionnalités importante : la protection mémoire, la mémoire virtuelle, les modes de compatibilité du processeur, la gestion de l'alimentation, l'arrêt ou la mise en veille, etc.
On peut aussi trouver des instructions spécialisées dans les calculs cryptographiques : certaines instructions permettent de chiffrer ou de déchiffrer des données de taille fixe. De même, certains processeurs ont une instruction permettant de générer des nombres aléatoires. Et on peut trouver bien d'autres exemples...
Mais d'autres sont franchement exotiques. Par exemple, certains processeurs sont capables d'effectuer des instructions sur du texte directement. Pour stocker du texte, la technique la plus simple utilise une suite de lettres, stockées les unes à la suite des autres dans la mémoire, dans l'ordre dans lesquelles elles sont placées dans le texte. Quelques ordinateurs disposent d'instructions pour traiter ces suites de lettres. D'ailleurs, n'importe quel PC x86 actuel dispose de telles instructions, bien qu'elles ne soient pas utilisées car paradoxalement trop lente comparé aux solutions logicielles ! Cela peut paraître surprenant, mais il y a une explication assez simple qui sera compréhensible dans quelques chapitres (les instructions en question sont microcodées).
Dans ce chapitre, nous allons étudier une fonctionnalité du processeur appelée la pile d'appel. Son rôle est de simuler une mémoire de type FIFO, mais à l'intérieur d'une mémoire RAM. Sans elle, certaines fonctionnalités de nos langages de programmation actuels n'existeraient pas ! Pour les connaisseurs, cela signifierait qu'on ne pourrait pas utiliser de fonctions réentrantes ou de fonctions récursives.
La pile d'appel
modifierLa pile d'appel est une portion de mémoire qui simule une mémoire FIFO. On peut ajouter ou retirer une donnée de la pile d'appel, mais la donnée retirée est systématiquement la plus récente, la dernière qui fut ajoutée. La pile d'appel est souvent une partie de la mémoire RAM, mais c'est parfois une mémoire séparée. Certains processeurs sauvegardent une copie de la pile dans des registres cachés au lieu de tout mémoriser en RAM. Cette technique permet d'améliorer les performances, une partie de la pile étant mémorisée dans des registres rapides et non dans une mémoire RAM lente.
Les cadres de pile
modifierLes données sont organisées d'une certaine façon à l'intérieur. Les données sont regroupées dans la pile dans ce qu'on appelle des cadres de pile, des espèces de blocs de mémoire de taille fixe ou variable suivant le processeur.

Le contenu d'un cadre de pile varie fortement suivant le processeur. Certains processeurs se contentent d'y placer une adresse mémoire par cadre de pile. D'autres y placent plusieurs entiers ou adresses bien précises, avec une organisation fixe et immuable, ce qui donne des cadres de pile de taille fixe. Mais d'autres ont des cadres de pile de taille variable, ce qui permet aux logiciels d'y mettre ce qu'ils veulent. Les cadres de taille fixe sont surtout utilisées sur les processeurs anciens, alors que les piles d'appel programmables sont utilisées sur les processeurs modernes.
L'ordre des cadres de pile : une structure de type LIFO
modifierLes cadres sont créés un par uns et sont placés les uns à la suite des autres dans la mémoire. C'est une première contrainte : on ne peut pas créer de cadres n'importe où dans la mémoire. On peut comparer l'organisation des cadres à une pile d'assiette : on peut parfaitement rajouter une assiette au sommet de la pile d'assiette, ou enlever celle qui est au sommet, mais on ne peut pas toucher aux autres assiettes. Sur la pile de notre ordinateur, c'est la même chose : on ne peut accéder qu'à la donnée située au sommet de la pile. Comme pour une pile d'assiette, on peut rajouter ou enlever le cadre au sommet de la pile, mais pas toucher aux cadres en dessous, ni les manipuler.
Le nombre de manipulations possibles sur cette pile se résume donc à trois manipulations de base qu'on peut combiner pour créer des manipulations plus complexes. On peut ainsi :
- détruire le cadre de pile au sommet de la pile, et supprimer tout son contenu de la mémoire : on dépile.
- créer un cadre de pile immédiatement après le dernier cadre de pile existante : on empile.
- utiliser les données stockées dans le cadre de pile au sommet de la pile.

Si vous regardez bien, vous remarquerez que la donnée au sommet de la pile est la dernière donnée à avoir été ajoutée (empilée) sur la pile. Ce sera aussi la prochaine donnée à être dépilée (si on n'empile pas de données au-dessus). Ainsi, on sait que dans cette pile, les données sont dépilées dans l'ordre inverse d'empilement. Ainsi, la donnée au sommet de la pile est celle qui a été ajoutée le plus récemment.
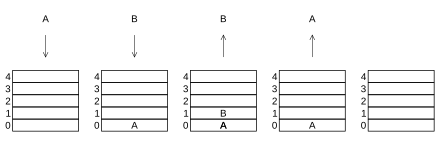
Au fait, la pile peut contenir un nombre maximal de cadres, ce qui peut poser certains problèmes. Si l'on souhaite utiliser plus de cadres de pile que possible, il se produit un débordement de pile. En clair, l'ordinateur plante !
La délimitation des cadres de pile
modifierPour gérer ces piles, on a besoin de sauvegarder deux choses : l'adresse à laquelle commence le cadre de pile en mémoire, et de quoi connaître l'adresse de fin. Le registre qui indique où est le sommet de la pile, quelle est son adresse, est appelé le pointeur de sommet, ou encore le Stack Pointer (SP). À ce registre, on peut rajouter un registre qui sert à donner l'adresse de début du cadre de pile : le Frame Pointer (FP), ou pointeur de contexte.
Pour localiser une donnée dans un cadre de pile, on utilise sa position par rapport au début ou la fin du cadre de pile. On peut donc calculer l'adresse de la donnée en additionnant cette position avec le contenu du pointeur de pile.
Certains processeurs possèdent deux registres spécialisés qui servent respectivement de pointeur de contexte et de pointeur de pile : on ne peut pas les utiliser pour autre chose. Si ce n'est pas le cas, on est obligé de stocker ces informations dans deux registres normaux, et se débrouiller avec les registres restants.

D'autres processeurs arrivent à se passer de Frame Pointer. Ceux-ci n'utilisent pas de registres pour stocker l'adresse de la base du cadre, mais préfèrent calculer cette adresse à partir de l'adresse de fin du cadre et de sa longueur. Cette longueur peut être stockée directement dans certaines instructions censées manipuler la pile : si chaque cadre a toujours la même taille, cette solution est clairement la meilleure. Cette solution est idéale si le cadre de pile a toujours la même taille. Mais il arrive que les cadres aient une taille qui ne soit pas constante : dans ce cas, on a deux solutions : soit stocker cette taille dans un registre, soit la stocker dans les instructions qui manipulent la pile, soit utiliser du code automodifiant.
Les fonctions et procédures logicielles
modifierLa pile est très utilisée pour faciliter l'implémentation des fonctions, des fonctionnalités très communes des langages de programmation. Pour comprendre ce que sont ces fonctions, il faut faire quelques rappels.
Un programme contient souvent des suites d'instructions présentes en plusieurs exemplaires, qui servent souvent à effectuer une tâche bien précise : calculer un résultat bien précis, communiquer avec un périphérique, écrire un fichier sur le disque dur, ou autre chose encore. Sans utiliser de sous-programmes, ces suites d'instructions sont présentes en plusieurs exemplaires dans le programme. Le programmeur doit donc recopier à chaque fois ces suites d'instructions, ce qui ne lui facilite pas la tâche (sauf en utilisant l’ancêtre des sous-programmes : les macros). De plus, ces suites d'instructions sont présentes plusieurs fois dans le programme et elles prennent de la place inutilement ! Dans les langages de programmation modernes, il est possible de ne conserver qu'un seul exemplaire en mémoire et l'utiliser au besoin. L'exemplaire en question est ce qu'on appelle une fonction, ou encore un sous-programme. C'est au programmeur de « sélectionner » ces suites d'instructions et d'en faire des fonctions.
Les langages de programmation actuels ont des fonctionnalités liées aux fonctions, qui simplifient bien la vie des programmeurs.
- En premier lieu, la fonction peut calculer un ou plusieurs résultats, qui sont récupérés par le programme principal et seront utilisés dans divers calculs. Ces résultats sont appelés des valeurs de retour. Généralement, c'est le programmeur qui décide de conserver une donnée et d'en faire une valeur de retour. Celui-ci peut avoir besoin de conserver le résultat d'un calcul pour pouvoir l'utiliser plus tard, par exemple. Ce résultat dépend fortement du sous-programme, et peut être n'importe quelle donnée : nombre entier, nombre flottant, tableau, objet, ou pire encore.
- En second lieu, il est possible de communiquer des valeurs à une fonction : ce sont des arguments ou paramètres. On peut communiquer ces valeurs de deux manières, soit en en fournissant une copie, soit en fournissant leur adresse.
- Enfin, une fonction peut calculer des données temporaires, souvent appelées des variables locales. Ces variables locales sont des données accessibles par le code de la fonction mais invisibles pour tout autre code. La variable locale est dite déclarée dans le code de la fonction, mais inaccessible ailleurs. Les variables locales sont opposées aux variables globales, qui sont accessibles dans tout le programme, par toute fonction. L'usage des variables globales est déconseillé, mais on en a parfois besoin.
Les instructions d'appel et de retour de fonction
modifierPour exécuter une fonction, il faut exécuter un branchement dont l'adresse de destination est celle de la fonction : on dit qu'on appelle la fonction. Toute fonction se termine aussi par un branchement, qui permet au processeur de revenir là où il en était avant d'appeler la fonction.

Lors de l'appel d'une fonction, outre le branchement, il est parfois nécessaire d'effectuer d'autres opérations dont on ne peut pas encore parler à ce stade. Sur beaucoup de processeurs, ces opérations sont effectuées par le programme. Le branchement qui appelle le sous-programme est précédé par d'autres instructions qui s'en occupent. Mais sur d'autres processeurs, ces opérations et le branchement d'appel sont fusionnés en une seule instruction d'appel de fonction.

De même, outre le branchement, d'autres opérations sont parfois nécessaires pour que le retour de la fonction se passe normalement. Là encore, certains processeurs disposent d'une instruction de retour de fonction dédiée, alors que d'autres non. Ces derniers émulent l'instruction de retour avec un branchement complété par d'autres instructions.
La sauvegarde de l'adresse de retour
modifierLe programme doit donc reprendre à l'instruction qui est juste après le branchement d'appel de fonction, l'adresse de celle-ci étant appelée l'adresse de retour. Mais vu qu'une fonction apparaît plusieurs fois dans notre programme, il y a plusieurs possibilités de retour, qui dépend de où est appelé la fonction. Mais alors, comment savoir à quelle instruction reprendre l'exécution de notre programme, une fois notre sous-programme terminé ? La seule solution est de sauvegarder l'adresse de retour lorsqu'on appelle la fonction ! Une fois le sous-programme fini, faut reprendre l’exécution de notre programme principal là où il s'était arrêté pour laisser la place au sous-programme. Pour cela, il suffit de charger l'adresse de retour dans un registre et d’exécuter un branchement inconditionnel vers cette adresse de retour.
La sauvegarde de l'adresse de retour est effectuée soit par l'instruction d'appel de fonction, soit par une instruction de branchement spéciale. L'instruction de branchement spéciale est souvent appelée branch and link, elle effectue un branchement et mémorise l'adresse de retour dans un registre. L'instruction d'appel de fonction fait cela, mais aussi d'autres choses (voir plus bas).
Pour la restauration de l'adresse de retour dans le program counter, c'est la même chose. Sur certains processeurs, il faut charger l'adresse de retour dans un registre et utiliser un branchement inconditionnel vers cette adresse. Le branchement inconditionnel en question est un branchement inconditionnel indirect. Sur d'autres, l’instruction de retour de fonction fait cela automatiquement. C'est un branchement inconditionnel, mais l'adresse de retour est adressée implicitement.
La sauvegarde des registres
modifierLorsqu'un sous-programme s'exécute, il va utiliser certains registres qui sont souvent déjà utilisés par le programme principal. Pour éviter d'écraser le contenu des registres, on doit donc conserver une copie de ceux-ci dans la pile, une sauvegarde de ceux-ci. Une fois que le sous-programme a fini de s'exécuter, il remet les registres dans leur état original en chargeant la sauvegarde dans les registres adéquats. Ce qui fait que lorsqu'un sous-programme a fini son exécution, tous les registres du processeur reviennent à leur ancienne valeur : celle qu'ils avaient avant que le sous-programme ne s'exécute. Rien n'est effacé !
Cette sauvegarde peut être effectuées automatiquement par l'instruction d'appel de fonction, mais c'est plutôt rare. La plupart du temps, elle est effectuée registre par registre par le logiciel, un petit morceau de code se chargeant de sauvegarder les registres. Plus rarement, certains processeurs ont une instruction pour sauvegarder les registres du processeur. C'est le cas sur les processeurs ARM1, qui ont une instruction pour sauvegarder n'importe quel sous-ensemble des registres du processeur. On peut par exemple choisir de sauvegarder le premier et le troisième registre en RAM, sans toucher aux autres. Le processeur se charge alors automatiquement de sauvegarder les registres uns par un en mémoire, bien que cela ne prenne qu'une seule instruction pour le programmeur.
- L'implémentation matérielle de cette instruction est décrite dans les deux articles suivants :
- Counting bits in hardware: reverse engineering the silicon in the ARM1 processor
- More ARM1 processor reverse engineering: the priority encoder
L'usage de la pile d'appel par les fonctions
modifierIl n'est pas rare qu'un programme imbrique des fonctions, c'est à dire qu'une fonction peut appeler une autre fonction, qui elle-même en appelle une autre, et ainsi de suite. Pour exécuter plusieurs fonctions imbriquées les unes dans les autres, la totalité des langages de programmation actuels utilise la ou les pile d'appel du processeur. C'est d'ailleurs ce qui lui vaut son nom : elle sert pour les appels de fonction, ce qui fait qu'elle s'appelle pile d'appel (de fonctions). Le principe est simple : lorsqu'on appelle une fonction, on crée un cadre de pile qui va stocker toutes les informations nécessaires pour que l'appel de fonction se passe comme prévu : l'adresse de retour, les arguments/paramètres, la copie de sauvegarde des registres du processeur, les variables locales, etc. Une autre méthode utilise une pile séparée pour les appels de retour, une autre pour les arguments, etc. Mais passons, voyons maintenant comment cela fonctionne.
La pile d'adresse de retour
modifierEn premier lieu, on doit sauvegarder plusieurs adresses de retour, les unes à la suite des autres dans l'ordre d'appel des fonctions.Ainsi, si une fonction F1 appelle une fonction F2, puis une fonction F3, les adresses de retour doivent se trouver dans le même ordre. De plus, quand une fonction se termine, l'adresse de retour est utilisée et doit être supprimée. On voit bien que ce comportement correspond à une pile. Si on stocke les adresses de retour dans une pile, l'adresse de retour à utiliser est située au sommet de la pile. La pile d'appel sert donc pour les fonctions imbriquées et est une pile d'adresses de retour pour les fonctions. Il est primordial que les adresses de retour soient stockées dans le bon ordre, pour que le programme reprenne au bon endroit.
Sur certains processeurs, la pile d'appel gère les adresses de retour et tout le reste des données. Mais sur d'autres, la pile d'appel est découpée en plusieurs piles séparées : la pile d'adresses de retour et une seconde pile appelée la pile de données. Cette séparation a des avantages et des inconvénients. Les avantages sont que la gestion des données est plus simple pour le programmeur, bien qu'elle manque de flexibilité. Un autre avantage est que certaines techniques de sécurité sont plus faciles à implémenter avec une pile d'appel séparée, comme on le verra plus bas. Par contre, la séparation a divers désavantages. Le principal est que les deux piles séparées sont potentiellement éloignées en mémoire, ce qui ne respecte pas très bien le principe de localité spatiale. Les performances sont alors réduites sur les processeurs avec une mémoire cache.
Si une fonction retourne et que l'adresse de retour n'est pas la bonne, le programme ne fonctionne pas comme prévu et cela peut donner des plantages ou tout autre conséquence fâcheuse. Diverses attaques informatiques cherchent justement à modifier l'adresse de retour d'une fonction pour exécuter du code malicieux. L'attaque demande d'insérer un morceau de code malicieux dans un programme (par exemple, un virus) et de l’exécuter lors d'un retour de fonction. Pour cela, l'assaillant trouve un moyen de modifier l'adresse de retour d'une fonction mal codée, puis en détourne le retour pour que le processeur ne reprenne pas là où il le devrait, mais reprenne l’exécution sur le virus/code malicieux. Le code malicieux est programmé pour que, une fois son travail accompli, le programme reprenne là où il devait une fois la fonction détournée terminée.
Il existe diverses techniques pour éviter cela et certaines de ces techniques se basent sur des procédés matériels, intégrés dans le processeur. Le premier de ces procédé est l'usage d'une shadow stack, une pile fantôme. Celle-ci est une simple copie de la pile d'appel, mémorisée en mémoire ou dans le processeur, qui est utilisée pour vérifier que les retours de fonction se passent bien. Sauf que là où la pile d'appel a des cadres volumineux, la pile fantôme ne mémorise que les adresses de retour. L'avantage est que ces attaques consistent généralement à injecter des données volumineuses dans un cadre de pile, afin de déborder d'un cadre de pile, voire de déborder de la mémoire allouée à la pile. Autant c'est possible avec les cadres de la pile d'appel, autant ce n'est pas possible avec la pile fantôme, vu qu'on n'y insère pas ces données. De plus, les deux piles d'appel sont éloignées en mémoire, ce qui fait que toute modification de l'une a peu de chances de se répercuter sur l'autre. Notons que les failles de sécurité de ce type sont plus compliquées si la pile d'adresse de retour est séparée de la pile d'appel, mais que ce n'est pas le cas sur les PC actuels.
La pile d'appel fantôme peut être gérée soit au niveau logiciel, par le langage de programmation ou le système d'exploitation, mais aussi directement en matériel. C'est le cas sur les processeurs x86 récents, depuis l'intégration par Intel de la technologie Control-flow Enforcement Technology. Il s'agit d'une pile fantôme gérée directement par le processeur. Quand le processeur exécute une instruction de retour de fonction RET, il vérifie automatiquement que l'adresse de retour est la même dans la pile d'appel et la pile fantôme. Si il y a une différence, il stoppe l’exécution du programme et prévient le système d'exploitation (pour ceux qui a ont déjà lu le chapitre sur les interruptions : il démarre une exception matérielle spécialisée appelée Control Flow Protection Fault.
Les autres piles/données du cadre d'appel
modifierOutre l'adresse de retour, il faut aussi sauvegarder les registres du processeur avant l'appel de la fonction. Là encore, les registres à sauvegarder sont mémorisés dans une pile, pour les mêmes raisons. Là encore, on peut sauvegarder ces registres dans une pile d'appel unique, ou dans une pile de sauvegarde des registres séparée.
La transmission des arguments à une fonction peut se faire en les copiant soit dans la pile, soit dans les registres. Dans le cas d'un passage par les registres, les registres qui contiennent les paramètres ne sont pas sauvegardés lors de l'appel de la fonction. Généralement, le passage par la pile est très utilisé sur les processeurs avec peu de registres, alors que les processeurs avec beaucoup de registres privilégient le passage par les registres. Si on utilise le passage par les registres, il faut que le nombre de registres soit suffisant. La plupart des fonctions ayant peu d'arguments, cela ne pose que rarement problème. Mais si une fonction a plus d'arguments que de registres, ou que la fonction utilise beaucoup de variables locales, les arguments en trop doivent être passés par la pile.
On a le même genre de compromis à faire avec la valeur de retour d'une fonction, qui peut être conservée soit dans les registres, soit dans la pile d'appel. Il est théoriquement possible de la stocker dans un registre, mais il faut faire attention à ce qu'elle ne soit pas écrasée lors de la restauration des registres. Mais cela ne marche que si la valeur de retour tient dans un registre : un registre contenant 64 bits pourra difficilement contenir une valeur de retour de 5 kilo-octets. Une autre solution consiste à stocker ces valeurs de retour dans la pile d'appel, plus rarement dans une pile des valeurs de retour dédiée (à condition que ces valeurs de retour aient toutes une taille fixe, ce qui n'est pas possible avec certains langages de programmation).
Pour gérer les variables locales, il est possible de réserver une portion de la mémoire statique pour chaque, dédiée au stockage de ces variables locales, mais cela gère mal le cas où une fonction s'appelle elle-même (fonctions récursives). Une autre solution est de réserver un cadre de pile pour les variables locales. Cela demande cependant d'avoir des cadres de pile de taille variable, ce que le processeur et/ou le langage de programmation doit gérer nativement. Le processeur dispose de modes d'adressages spécialisés pour adresser les variables automatiques d'un cadre de pile. Ces derniers ajoutent une constante au pointeur de pile.
Pour résumer, les processeurs processeurs possèdent soit une pile pour tout, soit plusieurs piles spécialisées. La plupart des processeurs ne possèdent qu'une seule pile à la fois pour les adresses de retour, les variables locales, les paramètres, et le reste. La pile utilise alors des cadres de pile de taille variable, dans lesquels on peut ranger plusieurs données. Les variables locales sont souvent regroupées, de même que les arguments, le reste étant placé à une position bien précise dans le cadre de pile.

Les interruptions sont des fonctionnalités du processeur qui ressemblent beaucoup aux appels de fonctions, mais avec quelques petites différences. Les interruptions, comme leur nom l'indique, interrompent temporairement l’exécution d'un programme pour effectuer un sous-programme nommé routine d'interruption. Lorsqu'un processeur exécute une interruption, celui-ci :
- arrête l'exécution du programme en cours et sauvegarde l'état du processeur (registres et program counter) ;
- exécute la routine d'interruption ;
- restaure l'état du programme sauvegardé afin de reprendre l'exécution de son programme là ou il en était.

L'appel d'une routine d'interruption est très similaire à un appel de fonction et implique les mêmes chose : sauvegarder les registres du processeur, l'adresse de retour, etc. Tout ce qui a été dit pour les fonctions marche aussi pour les interruptions. La différence est que la routine d'interruption appartient au système d'exploitation ou à un pilote de périphérique, mais pas au programme en cours d'exécution.
Les interruptions sont classées en trois types distincts, aux utilisations très différentes : les exceptions matérielles, les interruptions matérielles et les interruptions logicielles. Les deux premières sont des interruptions générés par un évènement extérieur au programme, alors que les interruptions logicielles sont déclenchées quand le programme éxecute une instruction précise pour s'interrompre lui-même, afin d'éxecuter du code appartenant au système d'exploitation ou à un pilote de périphérique.
Les interruptions et les exceptions matérielles
modifierLes exceptions matérielles et les interruptions matérielles permettent de réagir à un événement extérieur : communication avec le matériel, erreur fatale d’exécution d'un programme. Le programme en cours d'exécution est alors stoppé pour réagir, avant d'en reprendre l'exécution. Elles sont initiés par un évènement extérieur au programme, contrairement aux interruptions logicielles.
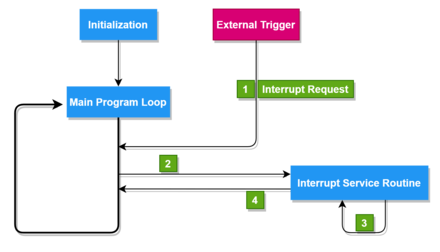
Les exceptions matérielles
modifierUne exception matérielle est une interruption déclenchée par un évènement interne au processeur, par exemple une erreur d'adressage, une division par zéro... Le processeur intègre des circuits qui détectent l'évènement déclencheur, ainsi que des circuits pour déclencher l'exception matérielle. Prenons l'exemple d'une exception déclenchée par une division par zéro : le processeur doit détecter les divisions par zéro. Lorsqu'une exception matérielle survient, la routine exécutée corrige l'erreur qui a été la cause de l'exception matérielle, et prévient le système d'exploitation si elle n'y arrive pas. Elle peut aussi faire planter l'ordinateur, si l'erreur est grave, ce qui se traduit généralement par un écran bleu soudain.
Pour donner un exemple d'utilisation, sachez qu'il existe une exception matérielle qui se déclenche quand on souhaite exécuter une instruction non-reconnue par le processeur. Rappelons que les instructions sont codées par des suites de bits en mémoire, codées sur quelques octets. Mais cela ne signifie pas que toutes les suites de bits correspondent à des instructions : certaines suites ne correspondent pas à des instructions et ne sont pas reconnues par le processeur. Dans ce cas, le chargement dans le processeur d'une telle suite de bit déclenche une exception matérielle "Instruction non-reconnue".
Et cela a été utilisé pour émuler des instructions sur les nombres flottants sur des processeurs qui ne les géraient pas. Autrefois, à savoir il y a une quarantaine d'années, les processeurs n'étaient capables d'utiliser que des nombres entiers et aucune instruction machine ne pouvait manipuler de nombres flottants. On devait alors émuler les calculs flottants par une suite d'instructions machine effectuées sur des entiers. Cette émulation était effectuée soit par une bibliothèque logicielle, soit par le système d'exploitation par le biais d'exceptions matérielles. Pour cela, on modifiait la routine de l'exception "Instruction non-reconnue" de manière à ce qu'elle reconnaisse les suites de bits correspondant à des instructions flottantes et exécute une suite d'instruction entière équivalente.
Les interruptions matérielles
modifierLes interruptions matérielles, aussi appelées IRQ, sont des interruptions déclenchées par un périphérique. La routine d'interruption est alors fournie par le pilote du périphérique. Du moins, c'est comme ça sur le matériel moderne, les anciens PC utilisaient des routines d'interruption fournies par le BIOS. Ce sont celles qui vont nous intéresser dans le chapitre sur la communication avec les périphériques, mais nous n'en parlerons pas dans le détail avant quelques chapitres.
Un exemple d'utilisation des interruptions matérielles la gestion de certains périphériques. Par exemple, quand vous tapez sur votre clavier, celui-ci émet une interruption à chaque appui/relevée de touche. Ainsi, le processeur est prévenu quand une touche est appuyée, le système d'exploitation qu'il doit regarder quelle touche est appuyée, etc.
Un autre exemple est la gestion des timers. Par exemple, imaginons que vous voyiez à un jeu vidéo, et qu'il vous reste 2 minutes 45 secondes pour sortir d'un laboratoire de recherche avant que l'auto-destruction ne s'active. La durée de 2 minutes 45 est programmée dans un timer, un circuit compteur qui permet de compter une durée. Le jeu vidéo programme le timer pour qu'il compte durant 2 minutes 45 secondes, puis attend que ce dernier ait finit de compter. Une fois la durée atteinte, le timer déclenche une interruption, pour stopper l'exécution du jeu vidéo. La routine d'interruption prévient le système d'exploitation que le timer a fini de compter, le jeu vidéo est alors prévenu, et fait ce qu'il a à faire.
Un autre exemple, qui n'est plus d'actualité, est le rafraichissement mémoire des DRAM sur quelques anciens ordinateurs. Dans l'ancien temps, le rafraichissement mémoire était géré par le processeur, pas par le contrôleur mémoire. La plupart des processeurs intégraient des optimisations pour gérer le rafraichissement mémoire par eux-même, sans recourir à des interruptions. Mais quelques ordinateurs ont tenté de relier des processeurs très simples à une mémoire DRAM, directement, alors que les processeurs n'avaient aucune optimisation du rafraichissement mémoire. La gestion du rafraichissement était alors gérée via des interruptions : tous les x millisecondes, un timer déclenchait une interruption de rafraichissement mémoire, qui rafraichissait la mémoire ou une adresse précise. Cette solution était très peu performante.
Les interruptions logicielles
modifierLes interruptions logicielles sont différentes des deux précédentes dans le sens où elles ne sont pas déclenchées par un évènement extérieur. A la place, elles sont déclenchées par un programme en cours d'exécution, via une instruction d'interruption. On peut les voir comme des appels de fonction un peu particuliers, si ce n'est que la routine d'interruption exécutée n'est pas fournie par le programme exécuté, mais par le système d'exploitation, un pilote de périphérique ou le BIOS. Le code éxecuté ne fait pas partie du programme éxecuté, mais en est extérieur, et cela change beaucoup de choses.
Sur les PC anciens, le BIOS fournissait les routines de base et le système d'exploitation se contentait d’exécuter les routines fournies par le BIOS. Mais de nos jours, les routines d'interruptions du BIOS sont utilisées lors du démarrage de l'ordinateur, mais ne sont plus utilisées une fois le système d'exploitation lancé. Le système d'exploitation fournit ses propres routines et n'a pas plus besoin des routines du BIOS.
Les interruptions du BIOS et des autres firmwares
modifierLe BIOS fournit des routines d'interruption pour gérer les périphériques et matériels les plus courants. Ce n'est pas pour rien que « BIOS » est l'abréviation de Basic Input Output System, ce qui signifie « programme basique d'entrée-sortie ». Ces routines sont standardisées de façon à assurer la compatibilité des programmes sur tous les BIOS existants. Ce standard, malgré sa simplicité, était extrêmement puissant. Il était possible de créer un OS complet en utilisant juste des appels de routine du BIOS. Par exemple, le DOS, ancêtre de Windows, utilisait exclusivement les routines du BIOS !
Certaines routines peuvent notamment effectuer plusieurs traitements : par exemple, la routine qui permet de communiquer avec le disque dur peut aussi bien lire un secteur, l'écrire, etc. Pour spécifier le traitement à effectuer, on doit placer une certaine valeur dans le registre AH du processeur : la routine est programmée pour déduire le traitement à effectuer uniquement à partir de la valeur du registre AH. Mais certaines routines ne font pas grand-chose : par exemple, l'interruption 0x12h ne fait que lire la taille de la mémoire conventionnelle, qui est mémorisée à un endroit bien précis en mémoire RAM.
Voici une description assez succincte de ces routines. Vous remarquerez que je n'ai pas vraiment détaillé ce que font ces interruptions, ni comment les utiliser. Il faut dire que de nos jours, ce n'est pas franchement utile. Mais si vous voulez en savoir plus, je vous invite à lire la liste des interruptions du BIOS de Ralf Brown, disponible via ce lien : Liste des interruptions du BIOS, établie par Ralf Brown.
| Adresse de la routine dans le vecteur d'interruption | Description succinte |
|---|---|
| 10h | Si aucune ROM vidéo n'est détectée, le BIOS peut quand même communiquer directement avec la carte graphique grâce à cette routine. Elle a plusieurs fonctions différentes et peut tout aussi bien envoyer un caractère à l'écran que renvoyer la position du curseur. |
| 13h | Cette routine du BIOS permet de lire ou d'écrire sur le disque dur ou sur une disquette. Plus précisément, cette routine lui sert à lire les premiers octets d'un disque dur afin de pouvoir charger le système d'exploitation. Elle était aussi utilisée par les systèmes d'exploitation du style MS-DOS pour lire ou écrire sur le disque dur. |
| 14h | La routine 14h était utilisée pour communiquer avec le port série RS232 de notre ordinateur. |
| 15h | La routine 15h a des fonctions diverses et variées, toutes plus ou moins rattachées à la gestion du matériel. Le BIOS était autrefois en charge de la gestion de l'alimentation de notre ordinateur : il se chargeait de la mise en veille, de réduire la fréquence du processeur, d'éteindre les périphériques inutilisés. Pour cela, la routine 15h était utilisée. Ses fonctions de gestion de l'énergie étaient encore utilisées jusqu'à la création de Windows 95. De nos jours, avec l'arrivée de la norme ACPI, le système d'exploitation gère tout seul la gestion de l'énergie de notre ordinateur et cette routine est donc obsolète. À toute règle, il faut une exception : cette routine est utilisée par certains systèmes d'exploitation modernes à leur démarrage afin d'obtenir une description correcte et précise de l'organisation de la mémoire de l'ordinateur. Pour cela, nos OS configurent cette routine en plaçant la valeur 0x0000e820 dans le registre EAX. |
| 16h | La routine 16h permet de gérer le clavier et de le configurer. Cette routine est utilisée tant que le système d'exploitation n'a pas démarré, c'est pour cela que vous pouvez utiliser le clavier pour naviguer dans l'écran de configuration de votre BIOS. En revanche, aucune routine standard ne permet la communication avec la souris : il est impossible d'utiliser la souris dans la plupart des BIOS. Certains BIOS possèdent malgré tout des routines capables de gérer la souris, mais ils sont très rares. |
| 17h | Cette routine permet de communiquer avec une imprimante sur le port parallèle de l'ordinateur. Comme les autres, on la configure avec le registre AH. |
| 19h | Cette routine est celle qui s'occupe du démarrage du système d'exploitation. Elle sert donc à lancer le système d'exploitation lors du démarrage d'un ordinateur, mais elle sert aussi en cas de redémarrage. |
Les routines du BIOS étaient parfois recopiées dans la mémoire RAM afin de rendre leur exécution plus rapide. Certaines options du BIOS, souvent nommées BIOS memory shadowing, permettent justement d'autoriser ou d'interdire cette copie du BIOS dans la RAM.
Les appels systèmes des systèmes d'exploitation
modifierTout OS fournit un ensemble de routines d'interruptions spécifiques qui servent à manipuler la mémoire, gérer des fichiers, etc. Les interruptions en question sont appelées des appels système. Par exemple, linux fournit les appels systèmes open, read, write et close pour manipuler des fichiers, ou encore les appels brk, sbrk, pour allouer et désallouer de la mémoire. Évidemment, ceux-ci ne sont pas les seuls : linux fournit environ 380 appels systèmes distincts.
Les appels systèmes permettent aux programmes d'exécuter des interruptions pré-programmées, mais ne peuvent pas demander n'importe quoi au système d'exploitation. La communication entre OS et programmes est donc standardisée, limitée par une interface, ce qui limite les problèmes de sécurité et simplifie la programmation des applications.
Les appels systèmes sont un concept des systèmes d'exploitation, qui peuvent se mettre en œuvre de plusieurs manières. On peut les implémenter avec des interruptions logicielles, des instructions de commutation en mode noyau, éventuellement d'autres. Assimiler interruptions logicielles et appels systèmes est en soi une erreur, mais même si les deux sont très liés.
L'espace noyau et l'espace utilisateur : systèmes d'exploitation et virtualisation
modifier
La différence entre une interruption et un appel de fonction est notable sur les systèmes d'exploitation modernes, où le système d'exploitation a des privilèges que les autres programmes n'ont pas. Rappelons que le système d'exploitation sert d'intermédiaire entre les autres logiciels et le matériel. Les programmes ne sont pas censés accéder d'eux-mêmes au matériel, pour des raisons de portabilité et de sécurité. Ils ne peuvent pas accéder directement au disque dur, au clavier, à la carte son, etc. À la place, ils demandent au système d'exploitation de le faire à leur place et de leur transmettre les résultats. Il y a donc une séparation stricte entre :
- les programmes systèmes qui gèrent la mémoire et les périphériques ;
- les programmes applicatifs ou applications, qui délèguent la gestion de la mémoire et des périphériques aux programmes systèmes.
Pour simplifier, l'ensemble des programmes système porte le nom de noyau du système d'exploitation. Mais la séparation entre les deux types de programmes est garantie pas le matériel ! En effet, sans intervention du matériel, rien n’empêche à un programma applicatif de lire ou d'écrire dans les registres des périphériques, par exemple. Mais les processeurs incorporent des mécanismes de protection pour empêcher cela.
Les niveaux de privilèges
modifier
Pour forcer la séparation entre OS et programmes, les processeurs modernes intègrent des sécurités qui portent le nom de niveaux de privilèges, ou encore d'anneaux mémoires. Tous les processeurs des PC modernes (x86 64 bits) gèrent seulement deux niveaux de privilèges : un mode noyau pour le système d'exploitation et un mode utilisateur pour les applications. Tout est autorisé en mode noyau, alors le mode utilisateur a de nombreuses restrictions quant à l'accès au matériel et la mémoire. Un programme en mode utilisateur ne peut pas accéder aux périphériques, ni gérer certaines portions protégées de la mémoire. C'est un mécanisme qui force à déléguer la gestion du matériel au système d'exploitation.
- Au passage, tout l'OS n'est pas en mode noyau, seule une petite partie l'est, à savoir le noyau du système d’exploitation.
Si le mode noyau n'a aucune contraintes quant à l'accès à la mémoire, l'espace utilisateur restreint l'accès à la mémoire par divers mécanismes dits de protection mémoire. Un programme en mode utilisateur se voit attribuer une certaine portion de la mémoire RAM, et ne peut accéder qu'à celle-ci. En clair, les programmes sont isolés les uns des autres : un programme ne peut pas aller lire ou écrire dans la mémoire d'un autre, les programmes ne se marchent pas sur les pieds, les bugs d'un programme ne débordent pas sur les autres programmes, etc.
De plus, le mode utilisateur n'a pas accès à certaines instructions importantes, appelées des instructions privilégiées, qui ne s'exécutent qu'en espace noyau. Elles regroupent les instructions pour accéder aux entrées-sorties et celles pour configurer le processeur. On peut considérer qu'il s'agit d'instructions que seul l'O.S peut utiliser. À côté, on trouve des instructions non-privilégiées qui peuvent s’exécuter aussi bien en mode noyau qu'en mode utilisateur. Si un programme tente d'exécuter une instruction privilégiée en espace utilisateur, le processeur considère qu'une erreur a eu lieu et lance une exception matérielle.
Les anneaux mémoire/niveaux de privilèges étaient initialement gérés par des mécanismes purement logiciels, mais sont actuellement gérés par le processeur. Le processeur contient un registre qui précise si le programme en cours est en espace noyau ou en espace utilisateur. À chaque accès mémoire ou exécution d'instruction, le processeur vérifie si le niveau de privilège permet l'opération demandée. Lorsqu'un programme effectue une instruction interdite en mode utilisateur, une exception matérielle est levée. Généralement, le programme est arrêté sauvagement et un message d'erreur est affiché.

Sur certains processeurs, on trouve des niveaux de privilèges intermédiaires entre l'espace noyau et l'espace utilisateur. Les processeurs x86 des PC 32 bits contiennent 4 niveaux de privilèges. Le système Honeywell 6180 en possédait 8. À l'origine, ceux-ci ont été inventés pour faciliter la programmation des pilotes de périphériques. Mais force est de constater que ceux-ci ne sont pas vraiment utilisés, seuls les espaces noyau et utilisateur étant pertinents.
Les appels systèmes
modifierLes programmes systèmes sont en réalité des routines d'interruptions, fournies par l'OS ou les pilotes de périphérique. Les applications peuvent appeler à la demande ces routines via une interruption logicielle : ils effectuent ce qu'on appelle un appel système. Sur les PC anciens, le BIOS fournissait les routines d'interruption et le système d'exploitation se contentait d’exécuter les routines fournies par le BIOS. Mais de nos jours, le système d'exploitation fournit ses propres routines qui sont utilisées à la place de celles du BIOS.
Tout OS fournit un ensemble d'appels systèmes de base, qui servent à manipuler la mémoire, gérer des fichiers, etc. Par exemple, linux fournit les appels systèmes open, read, write et close pour manipuler des fichiers, les appels brk, sbrk, pour allouer et désallouer de la mémoire, etc. Évidemment, ceux-ci ne sont pas les seuls : linux fournit environ 380 appels systèmes distincts. Ceux-ci sont souvent encapsulés dans des librairies et peuvent s'utiliser comme de simples fonctions.
Les appels systèmes sont des interruptions, et non des appels de fonction, alors que ces derniers pourraient pourtant faire l'affaire. La raison est qu'un appel système branche vers un programme système en espace noyau, alors que le programme qui lance l'appel système est en espace utilisateur. Même sans accès aux périphériques, le passage en mode noyau est nécessaire pour passer outre la protection mémoire. La routine de l'appel système est dans une portion de mémoire réservée à l'OS, auquel le programme exécutant n'a pas accès en espace utilisateur. Il en est de même pour certaines structures de données du système d'exploitation, accessibles seulement dans l'espace noyau. Or, les appels de fonction et branchements ne permettent pas de passer de l'espace utilisateur à l'espace noyau, alors que les interruptions le font automatiquement.
Les interruptions basculent en mode noyau
modifierToute interruption bascule automatiquement le processeur dans l'espace noyau. C'est une nécessité pour les interruptions logicielles, afin de passer d'un programme en espace utilisateur à une routine qui est en espace noyau. Les interruptions matérielles doivent aussi faire la transition en espace noyau, car l'accès au matériel n'étant possible qu'en mode noyau.
Le passage en mode noyau n'est cependant pas gratuit, de même que l'interruption qui lui est associée. Ainsi, les interruptions sont généralement considérées comme lentes, très lentes. Elles sont beaucoup plus lentes que les appels de fonction normaux, qui sont beaucoup plus simples. Les raisons à cela sont multiples, mais la principale est la suivante : les mémoires caches doivent être vidés lors des transferts entre mode noyau et mode utilisateur. Alors attention : diverses optimisations font que seuls certains caches spécialisés dont nous n'avons pas encore parlé, comme les TLB, doivent être vidés. Mais malgré tout, cela prend beaucoup de temps.
Divers processeurs incorporent des techniques pour rendre les appels systèmes plus rapides, en remplaçant les interruptions logicielles par des instructions spécialisées (SYSCALL/SYSRET et SYSENTER/SYSEXIT d'AMD et Intel). D'autres techniques similaires tentent de faire la même chose, à savoir changer le niveau de privilège sans utiliser d'interruptions : les call gate d’Intel, les Supervisor Call instruction des IBM 360, etc.
L'implémentation des interruptions
modifierToutes les interruptions, qu'elles soient logicielles ou matérielles, ne s'implémentent pas exactement de la même manière. Mais certaines choses sont communes à toutes les interruptions et à toutes leurs mises en œuvre. Par exemple, on s'attend à ce que la majeure partie des processeurs qui supportent les interruptions disposent des fonctionnalités que nous allons voir dans ce qui suit, à savoir : un vecteur d'interruption, une pile dédiée aux interruptions, la possibilité de désactiver les interruptions, etc. Elles ne sont pas tout le temps présentes, mais leur absence est plus une exception que la régle.
Le vecteur d'interruption
modifierVu le grand nombre d'interruptions logicielles/appels système, on se doute bien qu'il y a a peu-près autant de routines d'interruptions différentes. Et celles-ci sont placées à des endroits différents en mémoire RAM. Une solution simple serait de placer chaque routine d'interruption systématiquement au même endroit en mémoire. Les appels systèmes se résumeraient alors à des appels de fonctions basiques, avec un branchement inconditionnel vers l'adresse de la routine, connue à l'avance. Mais elle n'est pas très pratique, surtout quand on ne connait pas à l'avance l'emplacement des pilotes de périphériques en mémoire. Autant on peut prévoir tout cela à l'avance pour les routines du système d'exploitation, autant on ne peut pas le faire pour les routines des pilotes de périphériques dont on ne connait pas à l'avance ni le nombre, ni la taille, ni la fonction. De plus, sur les systèmes modernes, les adresses des routines peuvent changer lors de l'exécution des programmes pour de sombres raisons impliquant de la mémoire virtuelle et que nous verrons dans les chapitres à la fin de ce wikilivre.
Pour résoudre ce problème, les systèmes d'exploitation modernes font autrement. Ils numérotent les interruptions, à savoir qu'ils leur attribuent un numéro en commençant par 0. Un PC X86 moderne gére 256 interruptions, numérotées de 0 à 255. Un appel système ne précise pas l'adresse vers laquelle faire un branchement, mais précise le numéro de l'interruption à exécuter. Le système d'exploitation s'occupe ensuite de retrouver l'adresse de la routine à partir du numéro de l'interruption. Pour cela, ils dispersent un petit peu les routines dans la mémoire, mais mémorisent l'emplacement de chaque routine. Pour cela, le système d'exploitation utilise un tableau qui contient les adresses de chaque routine : la case numéro X du tableau contient l'adresse de l'interruption numéro X. Ce tableau s'appelle le vecteur d'interruption.
- Pour ceux qui connaissent la programmation, le vecteur d'interruption est un tableau de pointeurs sur fonction, les fonctions étant les routines à exécuter.
Il faut préciser que le vecteur d'interruption mémorise les adresses pour toutes les routines, sans exceptions. Non seulement il mémorise celles des appels systèmes, mais aussi les routines des exceptions matérielles, ainsi que les routines des interruptions matérielles. Sur les PC modernes, le vecteur d'interruption est stocké dans les 1024 premiers octets de la mémoire. Il gére 256 interruptions, et les 32 premières sont réservées aux exceptions matérielles.
Une interruption logicielle se déroule donc comme suit : le programme exécute une instruction d'interruption et précise le numéro de l'interruption logicielle à exécuter, puis l'OS utilise le numéro pour lire dans le vecteur d'interruption, ce qui permet de récupérer l'adresse de la routine adéquate, et effectue un branchement vers celle-ci. Avec cette méthode, l'adresse de la routine n'a pas à être précisée à l'avance, lors de la conception de l'OS, et elle peut même changer lors de l'exécution d'un programme !
Le fait que les interruptions soient désignées non pas par une adresse, mais par un numéro explique pourquoi un appel système n'est pas qu'un simple appel de fonction. Il y a un niveau d'indirection en plus. C'est une des raisons qui fait qu'il est préférable d'avoir une instruction spécifique pour le processeur, séparée de l'instruction d'appel de fonction normale.
La conversion d'un numéro d'interruption en adresse peut se faire au niveau matériel ou logiciel. S'il est fait au niveau matériel, le processeur lit l'adresse automatiquement dans le vecteur d'interruption. Avec la solution logicielle, on délègue ce choix au système d'exploitation. Dans ce cas, le processeur contient un registre qui stocke le numéro de l'interruption, ou du moins de quoi déterminer la cause de l'interruption : est-ce le disque dur qui fait des siennes, une erreur de calcul dans l'ALU, une touche appuyée sur le clavier, etc.
Le vecteur d'interruption peut être mis à jour, ce qui permet de remplacer à la volée les routines d'interruptions utilisées. Il suffit de remplacer les adresses des routines à mettre à jour par les adresses des routines adéquates. On dit qu'on déroute ou qu'on détourne le vecteur d'interruption. Tous les systèmes d'exploitation modernes le font après le démarrage de l'ordinateur, pour remplacer les interruptions du BIOS par les interruptions fournies par le système d'exploitation et les pilotes. Cette mise à jour est effectuée par le système d'exploitation, une fois que le BIOS lui a laissé les commandes.
La pile dédiée aux interruptions
modifierLa plupart des systèmes d'exploitation utilisent une pile d'appel dédiée, séparée, pour les interruptions. Les raisons à cela sont multiples. La principale est que sur les systèmes d'exploitation capables de gérer plusieurs programmes en même temps, c'est une solution assez évidente. Chaque programme a sa propre pile d'appel, séparée des autres. Et la routine d'interruption est un programme comme un autre, qui doit donc avoir sa propre pile d'appel.
Désactiver les interruptions
modifierIl faut noter qu'il est possible de désactiver temporairement l’exécution des interruptions, quelle qu’en soit la raison. C'est beaucoup utilisé sur les systèmes multiprocesseurs, afin d'éviter des problèmes lors de lecture/écriture d'une donnée manipulée par plusieurs processeurs. Mais nous verrons cela dans le chapitre adéquat, quand nous parlerons des systèmes multicœurs/multi-processeurs.
C'est aussi utilisé dans certains systèmes dit temps réels, où les concepteurs ont besoin de garanties assez fortes pour le temps d’exécution. Dans ces systèmes, chaque morceau de code doit s’exécuter en un temps définit à l'avance, qu'il ne doit pas dépasser. Pour garantir cela, certaines portions de code ne doivent pas être interrompues par des interruptions. Par exemple, prenons le cas d'une portion de code devant s’exécuter en moins de 300 millisecondes. Imaginons aussi que le code en question prend 200 ms sans interruption. Ce code peut parfaitement dépasser son temps attitré si plusieurs interruptions surviennent avec un timing problématique : il suffit que plus de 2 interruptions de 50 ms surviennent pendant que le code s’exécute. Désactiver les interruptions pendant le temps d’exécution du code permet d'éviter cela.
Un programmeur (ou un compilateur) qui souhaite programmer en langage machine peut manipuler les registres intégrés dans le processeur. À ce stade, il faut faire une petite remarque : tous les registres d'un processeur ne sont pas forcément manipulables par le programmeur. Il existe ainsi deux types de registres : les registres architecturaux, manipulables par des instructions, et les registres internes aux processeurs. Ces derniers servent à simplifier la conception du processeur ou mettre en œuvre des optimisations de performance. Dans ce qui suit, nous allons parler uniquement des registres architecturaux.
Les registres de contrôle
modifierDans cette section, nous allons voir les registres de contrôle, des registres qui permettent au processeur de fonctionner correctement, qui sont distincts des registres qui stockent des données. Les registres pour les données seront vus dans la section suivantes. Et ces derniers mémorisent des informations comme des entiers, des adresses, des flottants, manipulés par un programme. Les registres de contrôle sont différents. Ils mémorisent soit des adresses importantes (program counter), soit des bits isolés qui permettent de rendre compte de l'état du processeur.
Les registres de contrôle familiers
modifierLes registres de contrôle les plus importants vous seront certainement familiers. Le premier est le Program Counter, qui mémorise l'adresse de l’instruction en cours ou de la prochaine instruction (le choix entre les deux dépend du processeur). Les seconds sont les registres pour gérer la pile d'appel (le Stack Pointer et le Frame Pointer). De tels registres sont bel et bien des registres architecturaux, ce ne sont pas des registres internes.
La raison est qu'ils sont manipulés par certaines instructions, implicitement ou explicitement, ce ne sont pas des registres utilisés à des fins d'optimisation ou de simplicité d'implémentation. Par exemple, les registres pour la pile sont implicitement modifiés par les instructions PUSH et POP, ou toute autre instruction de gestion de la pile. Soit pour lire leur contenu afin d'adresser des données dans la pile, soit en écriture pour empiler/dépiler des données. Idem pour le program counter qui est altéré par les instructions de branchement !
Nous avons parlé de ces registres dans les chapitres précédents, ce qui fait que nous n'allons pas revenir dessus. Par contre, nous n’avons pas encore vu le registre de contrôle par excellence : le registre d'état.
Le registre d'état
modifierLe registre d'état contient au minimum des bits qui indiquent le résultat d'une instruction de test. Il contient aussi d'autres bits, mais dont l'interprétation dépend du jeu d'instruction. Il arrive que le registre d'état soit mis à jour non seulement par les instructions de test, mais aussi par les instructions arithmétiques. Par exemple, si le résultat d'une opération arithmétique entraine un débordement d'entier, le registre d'état mémorisera ce débordement. Dans le chapitre précédent, nous avions vu que les débordements sont mémorisés par le processeur dans un bit dédié, appelé le bit de débordement. Et bien ce dernier est un bit du registre d'état. Il en est de même pour le bit de retenue vu dans le chapitre précédent, qui mémorise la retenue effectuée par une opération arithmétique comme une addition, une soustraction ou un décalage. En général, le registre d'état contient les bits suivants :
- le bit d'overflow, qui est mis à 1 lors d'un débordement d'entiers ;
- le bit de retenue, qui indique si une addition/soustraction a donné une retenue ;
- le bit null précise que le résultat d'une instruction est nul (vaut zéro) ;
- le bit de signe, qui permet de dire si le résultat d'une instruction est un nombre négatif ou positif.
Le bit de débordement est parfois présent en double : un bit pour les débordements pour les nombres non-signés, et un autre pour les nombres signés (en complément à deux). En effet, la manière de détecter les débordements n'est pas la même pour des nombres strictement positifs et pour des nombres en complément à deux. Certains processeurs s'en sortent avec un seul bit de débordement, en utilisant deux instructions d'addition : une pour les nombres signés, une autre pour les nombres non-signés. Mais d'autres processeurs utilisent une seule instruction d'addition pour les deux, qui met à jour deux bits de débordements : l'un qui détecte les débordements au cas où les deux opérandes sont signés, l'autre si les opérandes sont non-signées. Sur les processeurs ARM, c'est la seconde solution qui a été choisie. N'oublions pas les bits de débordement pour les entiers BCD, à savoir le bit de retenue et le bit half-carry, dont nous avions parlé au chapitre précédent.
- Le registre d'état n'est pas présent sur toutes les architectures, notamment sur les jeux d'instruction modernes, mais beaucoup d'architectures anciennes en ont un.
Sur certains processeurs, comme l'ARM1, chaque instruction arithmétique existe en deux versions : une qui met à jour le registre d'état, une autre qui ne le fait pas. L'utilité de cet arrangement n'est pas évident, mais il permet à certaines instructions arithmétiques de ne pas altérer le registre d'état, ce qui permet de conserver son contenu pendant un certain temps.
Le fait que le registre d'état est mis à jour par les instructions arithmétiques permet d'éviter de faire certains tests gratuitement. Par exemple, imaginons un morceau de code qui doit vérifier si deux entiers A et B sont égaux, avant de faire plusieurs opérations sur la différence entre les deux (A-B). Le code le plus basique pour cela fait la comparaison entre les deux entiers avec une instruction de test, effectue un branchement, puis fait la soustraction pour obtenir la différence, puis les calculs adéquats. Mais si la soustraction met à jour le registre d'état, on peut simplement faire la soustraction, faire un branchement qui teste le bit null du registre d'état, puis faire les calculs. Une petite économie toujours bonne à prendre.
Il faut noter que certaines instructions sont spécifiquement conçues pour altérer uniquement le registre d'état. Par exemple, sur les processeurs x86, certaines instructions ont pour but de mettre le bit de retenue à 0 ou à 1. Il existe en tout trois instructions capables de manipuler le bit de retenue : l'instruction CLC (CLear Carry) le met à 0, l'instruction STC (SeT Carry) le met à 1, l'instruction CMC (CompleMent Carry) l'inverse (passe de 0 à 1 ou de 1 à 0). Ces instructions sont utilisées de concert avec les instructions d'addition ADDC (ADD with Carry) et SUBC (SUB with Carry), qui effectuent le calcul A + B + Retenue et A - B - Retenue, et qui sont utilisées pour additionner/soustraire des opérandes plus grandes que les registres. Nous avions vu ces instructions dans le chapitre sur les instructions machines, aussi je ne reviens pas dessus.
Les registres pour les données
modifierLes registres architecturaux se distinguent par le type de données que peuvent contenir leurs registres. Des processeurs ont des registres banalisés qui peuvent contenir tout type de données, tandis que d'autres ont des registres spécialisés pour chaque type de données. Les deux solutions ont des avantages et inconvénients différents. Elles sont toutefois complémentaires et non exclusives. Certains processeurs ont des registres généraux complémentés avec des registres spécialisés, pour des raisons de facilité.
Les registres spécialisés
modifierLes registres spécialisés ont une utilité bien précise et leur fonction est fixée une bonne fois pour toutes. Un registre spécialisé est conçu pour stocker soit des nombres entiers, des flottants, des adresses, etc; mais pas autre chose. Pour ce qui est des registres de données les plus courants, en voici la liste.
- Les registres entiers sont spécialement conçus pour stocker des nombres entiers.
- Les registres flottants sont spécialement conçus pour stocker des nombres flottants.
- Les registres de constante contiennent des constantes assez souvent utilisées. Par exemple, certains processeurs possèdent des registres initialisés à zéro pour accélérer la comparaison avec zéro ou l'initialisation d'une variable à zéro. On peut aussi citer certains registres flottants qui stockent des nombres comme \pi, ou e pour faciliter l'implémentation des calculs trigonométriques).
- Les registres d'indice servent à calculer des adresses, afin de manipuler rapidement des données complexes comme les tableaux. Nous en parlerons rapidement dans le chapitre sur les modes d'adressage.
Les registres généraux
modifierFournir des registres très spécialisés n'est pas très flexible. Prenons un exemple : j'ai un processeur disposant d'un Program Counter, de 4 registres entiers, de 4 registres d'Index pour calculer des adresses, et de 4 registres flottants. Si jamais j’exécute un morceau de programme qui manipule beaucoup de nombres entiers, mais qui ne manipule pas d'adresses ou de nombre flottants, j'utiliserais juste les 4 registres entiers. Une partie des registres du processeur sera inutilisé : tous les registres flottants et d'Index. Le problème vient juste du fait que ces registres ont une fonction bien fixée.
En réfléchissant, un registre est un registre, et il ne fait que stocker une suite de bits. Il peut tout stocker : adresses, flottants, entiers, etc. Pour plus de flexibilité, certains processeurs ne fournissent pas de registres spécialisés comme des registres entiers ou flottants, mais fournissent à la place des registres généraux utilisables pour tout et n'importe quoi. Ce sont des registres qui n'ont pas d'utilité particulière et qui peuvent stocker toute sorte d’information codée en binaire. Pour reprendre l'exemple du dessus, un processeur avec des registres généraux fournira un Program Counter et 12 registres généraux, qu'on peut utiliser sans vraiment de restrictions. On pourra s'en servir pour stocker 12 entiers, 10 entiers et 2 flottants, 7 adresses et 5 entiers, etc. Ce qui sera plus flexible et permettra de mieux utiliser les registres.
Les méthodes hybrides
modifierLe choix entre registres spécialisés et registres généraux est une question de pragmatisme. Il existe bien des processeurs qui ne le sont pas et où tous les registres sont des registres généraux, même le Program Counter. Sur ces processeurs, on peut parfaitement lire ou écrire dans le Program Counter sans trop de problèmes. Ainsi, au lieu d'effectuer des branchements sur le Program Counter, on peut simplement utiliser une instruction qui ira écrire l'adresse à laquelle brancher dans le registre. On peut même faire des calculs sur le contenu du Program Counter : cela n'a pas toujours de sens, mais cela permet parfois d'implémenter facilement certains types de branchements avec des instructions arithmétiques usuelles.
D'autres processeurs font des choix moins extrême mais tout aussi discutables. Par exemple, l'ARM1 fusionne le registre d'état et le program counter en un seul registre de 32 bits... La raison à cela est que ce processeur manipule des manipule entiers et adresses de 32 bits, ce qui fait que ses registres font 32 bits, le le program counter ne fait pas exception. Mais le program counter n'a besoin que de 26 bits pour fonctionner. Il reste donc 32-26=6 bits à utiliser pour autre chose. De plus, les instructions de ce processeur font exactement 32 bits, pas un de plus ni de moins, et elles sont alignées en mémoire. Donc, les 2 bits de poids faibles du program counter sont inutilisés. Au total, cela fait 8 bits inutilisés. Et ils ont été réutilisés pour mémoriser les bits du registre d'état.
Mais le cas précédent est rare, très rare. Dans la réalité, les processeurs utilisent souvent une espèce de mélange entre les deux solutions. Généralement, une bonne partie des registres du processeur sont des registres généraux, à part quelques registres spécialisés, accessibles seulement à travers quelques instructions bien choisies. Sur les processeurs modernes, l'usage de registres spécialisés est tombé en désuétude, sauf évidemment pour le program counter. Les registres d'indice ont disparus, les registres pour gérer la pile aussi, le registre d'état est en voie de disparition car il se marie mal avec les optimisations modernes que nous verrons dans quelques chapitres (pipeline, exécution dans le désordre, renommage de registres).
L'adressage des registres architecturaux
modifierOutre leur taille, les registres du processeur se distinguent aussi par la manière dont on peut les adresser, les sélectionner. Les registres du processeur peuvent être adressés par trois méthodes différentes. À chaque méthode correspond un mode d'adressage différent. Les modes d'adressage des registres sont les modes d'adressages absolu (par adresse), inhérent (à nom de registre) et/ou implicite.
Les registres nommés
modifierDans le premier cas, chaque registre se voit attribuer une référence, une sorte d'identifiant qui permettra de le sélectionner parmi tous les autres. C'est un peu la même chose que pour la mémoire RAM : chaque byte de la mémoire RAM se voit attribuer une adresse. Pour les registres, c'est un peu la même chose : ils se voient attribuer quelque chose d'équivalent à une adresse, une sorte d'identifiant qui permettra de sélectionner un registre pour y accéder.
L'identifiant en question est ce qu'on appelle un nom de registre ou encore un numéro de registre. Ce nom n'est rien d'autre qu'une suite de bits attribuée à chaque registre, chaque registre se voyant attribuer une suite de bits différente. Celle-ci sera intégrée à toutes les instructions devant manipuler ce registre, afin de sélectionner celui-ci. Le numéro/nom de registre permet d'identifier le registre que l'on veut, mais ne sort jamais du processeur, il ne se retrouve jamais sur le bus d'adresse. Les registres ne sont donc pas identifiés par une adresse mémoire.

Les registres adressés
modifierMais il existe une autre solution, assez peu utilisée. Sur certains processeurs assez rares, on peut adresser les registres via une adresse mémoire. Il est vrai que c'est assez rare, et qu'à part quelques vielles architectures ou quelques microcontrôleurs, je n'ai pas d'exemples à donner. Mais c'est tout à fait possible ! C'est le cas du PDP-10.

Les registres adressés implicitement
modifierLes registres de contrôle n'ont pas forcément besoin d'avoir un nom. Par exemple, la gestion de la pile se fait alors via des instructions Push et Pop qui sont les seules à pouvoir manipuler ces registres. Toute manipulation des registres de pile se faisant grâce à ces instructions, on n'a pas besoin de leur fournir un numéro/nom de registre pour les sélectionner. C'est aussi le cas du Program Counter : à part sur certains processeurs vraiment très rares, on ne peut modifier son contenu qu'en utilisant des instructions de branchements. Idem pour le registre d'état, manipulé obligatoirement par les instructions de comparaisons et de test, et certaines opérations arithmétiques.
Dans ces cas bien précis, on n'a pas besoin de préciser le ou les registres à manipuler : le processeur sait déjà quels registres manipuler et comment, de façon implicite. Le seul moyen de manipuler ces registres est de passer par une instruction appropriée, qui fera ce qu'il faut. Les registres adressés implicitement sont presque toujours des registres de contrôle, beaucoup plus rarement des registres de données. Mais précisons encore une fois que sur certains processeurs, le registre d'état et/ou le Program Counter sont adressables, pareil pour les registres de pile. Inversement, il arrive que certains registres de données puissent être adressés implicitement, notamment certains registres impliqués dans la gestion des adresses mémoire.
La taille des registres architecturaux
modifierVous avez certainement déjà entendu parler de processeurs 32 ou 64 bits. Derrière cette appellation qu'on retrouve souvent dans la presse ou comme argument commercial se cache un concept simple. Il s'agit de la quantité de bits qui peuvent être stockés dans les registres principaux. Les registres principaux en question dépendent de l'architecture. Sur les architectures avec des registres généraux, la taille des registres est celle des registres généraux. Sur les autres architectures, la taille mentionnée est généralement celle des nombres entiers mais les autres registres peuvent avoir une taille totalement différente. Sur les processeurs x86, un registre pour les nombres entiers contient environ 64 bits tandis qu'un registre pour nombres flottants contient entre 80 et 256 bits (suivant les registres utilisés).
Aujourd'hui, les processeurs utilisent presque tous des registres dont la taille est une puissance de 2 : 8, 16, 32, 64, 128, 256, voire 512 bits. L'usage de registres qui ne sont pas des puissances de 2 posent quelques problèmes techniques en termes d’adressage, comme on le verra dans le chapitre sur l'alignement et le boutisme. Mais ca n'a pas toujours été le cas.
Aux tout début de l'informatique, les processeurs utilisaient tous l'encodage BCD, ce qui fait qu'ils codaient leurs chiffres surs 5/6/7 bits. La taille des registres était donc un multiple de 4/5/6. Les registres de 36 bits étaient assez courants. Certaines machines utilisaient des registres de 3, 7, 13, 17, 23, 36 et 48 bits ; mais elles sont aujourd'hui tombées en désuétude.
On peut aussi citer les processeurs dédiés au traitement de signal audio, que l'on trouve dans les chaînes HIFI, les décodeurs TNT, les lecteurs DVD, etc. Ceux-ci utilisent des registres de 24 bits, car l'information audio est souvent codée par des nombres de 24 bits.
Le nombre de bits que peut contenir un registre est parfois différent de la largeur du bus de données (c'est à dire du nombre de bits qui peuvent transiter en même temps sur le bus de données). Exemple : sur les processeurs x86-32 bits, un registre stockant un entier fait 32 bits alors que le bus de données peut contenir 64 bits en même temps. La raison à cela est la présence d'un cache entre la mémoire et le CPU.
Le système d'aliasing de registres sur les processeurs x86
modifierSur les processeurs x86, on trouve des registres de taille différentes. Certains registres sont de 8 bits, d'autres de 16, d'autres de 32, et on a même des registres de 64 bits depuis plus d'une décennie. Limitons-nous pour le moment aux registres 8 et 16 bits, sur lesquels il y a beaucoup de choses à dire. Les premiers processeurs x86 étaient des processeurs 16 bits, mais ils s’inspiraient grandement des processeurs 8008 qui étaient des processeurs 8 bits. Le 8086 et le 8088 étaient en effet des versions améliorées et grandement remaniées des premiers 8008 d'Intel. En théorie, la rétrocompatibilité n'était pas garantie, dans le sens où les jeux d'instruction étaient différents entre le 8086 et le 8008. Mais Intel avait prévu quelques améliorations pour rendre la transition plus facile. Et l'une d'entre elle concerne directement le passage des registres de 8 à 16 bits.
Les registres 16 bits étaient découpés en deux portions de 8 bits, chacune adressable séparément. On pouvait adresser un registre de 16, ou alors adresser seulement les 8 bits de poids fort ou les 8 bits de poids faible. Ces octets étaient considérés comme des registres à part entière. Du moins, c'est le cas pour 4 registres de données, nommés AX, BX, CX et DX. le registre AX fait 16 bits, l'octet de poids fort est adressable comme un registre à part entière nommé AH, alors que l'octet de poids faible est aussi un registre nommé AL (H pour High et L pour Low). idem avec les registres BX, BH et BL, les registres CX, CH et CL, ou encore les registres DX, DH, DL. Pour ces registres, on a un système d'alias de registres, qui permet d'adresser certaines portions d'un registre comme un registre à part entière. Les registres AH, AL, BH, BL, ..., ont tous un nom de registre et peuvent être utilisés dans des opérations arithmétiques, logiques ou autres. Dans ce cas, les opérations ne modifient que l'octet sélectionné, pas le reste du registre. Une même opération peut donc agir sur 16 ou 8 bits suivant le registre sélectionné. Les autres registres ne sont pas concernés par ce découpage, que ce soit les registres de données, d'adresse ou autres.
Au départ, l'architecture x86 avait des registres de 16 bits. Puis, par la suite, l'architecture a étendu ses registres à 32 et enfin 64 bits. Mais cela s'est ressentit au niveau des registres, où le système d'alias a été étendu. Les registres 32 bits ont le même système d'alias, mais légèrement modifié. Sur un registre 32 bits, les 16 bits de poids faible sont adressables séparément, mais pas les 16 bits de poids fort. La raison est que les registres 16 bits originaux, présents sur les processeurs x86 16 bits, ont été étendus à 32 bits. Les 16 originaux sont toujours adressables comme avant, avec le même nom de registre que sur les anciens modèles. par contre, le registre étendu a un nouveau nom de registre. Pour rendre tout cela plus clair, voyons l'exemple du registre EAX des processeurs 64 bits. C'est un registre 32 bits, dont les 16 bits de poids faible sont tout simplement le registre AX vu plus haut, ce dernier pouvant être subdivisé en AH et AL. La même chose a lieu pour les registres EBX, ECX et EDX. Chose étonnante, presque tous les registres ont étés étendus ainsi, même le program counter, les registres liés à la pile et quelques autres, notamment pour adresser plus de mémoire.

Lors du passage au 64 bits, les registres 32 bits ont étés étendus de la même manière, et les registres étendus à 64 bits ont reçu un nom de registre supplémentaire, RAX, RBX, RCX ou RDX. Le passage à 64 bits s'est accompagné de l'ajout de 4 nouveaux registres.
Un point intéressant est qu'Intel a beaucoup utilisé ce système d'alias pour éviter d'avoir à réellement ajouter certains registres. Dans le chapitre sur les architectures à parallélisme de données, nous verrons plusieurs cas assez impressionnants de cela. Pour le moment, bornons-nous à citer les exemples les plus frappants, sans rentrer dans les détails, et parlons du MMX, du SSE et de l'AVX.
Le MMX est une extension du x86, à savoir l'ajout d'instructions particulières au jeu d’instruction x86 de base. Cette extension ajoutait 8 registres appelés MM0, MM1, MM2, MM3, MM4, MM5, MM6 et MM7, d'une taille de 64 bits, qui ne pouvaient contenir que des nombres entiers. En théorie, on s'attendrait à ce que ces registres soient des registres séparés. Mais Intel utilisa le système d'alias pour éviter d'avoir à rajouter des registres. À la place, il étendit les registres flottants déjà existants, eux-même ajoutés par l'extension x87, qui définit 8 registres flottants de 80 bits. Chaque registre MMX correspondait aux 64 bits de poids faible d'un des 8 registres flottants de la x87 ! Cela posa pas mal de problèmes pour les programmeurs qui voulaient utiliser l'extension MMX. Il était impossible d'utiliser à la fois le MMX et les flottants x87...

Par la suite, Intel ajouta une nouvelle extension appelée le SSE, qui ajoutait plusieurs registres de 128 bits, les XMM registers illustrés ci-contre. Le SSE fût décliné en plusieurs versions, appelées SSE1, SSE2, SSE3, SS4 et ainsi de suite, chacune rajoutant de nouvelles instructions. Puis, Intel ajouta une nouvelle extension, l'AVX. L'AVX complète le SSE et ses extensions, en rajoutant quelques instructions, et surtout en permettant de traiter des données de 256 bits. Et cette dernière ajoute 16 registres d'une taille de 256 bits, nommés de YMM0 à YMM15 et dédiés aux instructions AVX. Et c'est là que le système dalias a encore frappé. Les registres AVX sont partagés avec les registres SSE : les 128 bits de poids faible des registres YMM ne sont autres que les registres XMM. Puis, arriva l'AVX-515 qui ajouta 32 registres de 512 bits, et des instructions capables de les manipuler, d'où son nom. Là encore, les 256 bits de poids faible de ces registres correspondent aux registres de l'AVX précédent. Du moins, pour les premiers 16 registres, vu qu'il n'y a que 16 registres de l'AVX normal.
Pour résumer, ce système permet d'éviter d'ajouter des registres de plus grande taille, en étendant des registres existants pour en augmenter la taille. Ce n'était peut-être pas sa fonction première, du moins sur les processeurs Intel, mais c’est ainsi qu'il a été utilisé à l'excès par Intel. En soi, la technique est intéressante et permet certainement des économies de circuits dignes de ce nom. La longévité des architectures x86 a fait que cette technique a beaucoup été utilisée, l'architecture ayant été étendue deux fois : lors du passage de 16 à 32 bits, puis de 32 à 64 bits. Le système d'extension a aussi été la source de plusieurs usage de l'aliasing de registres. Mais les autres architectures n'implémentent pas vraiment ce système. De plus, ce système marche assez mal avec les processeurs modernes, dont la conception interne se marie mal avec laliasing de registres, pour des raisons que nous verrons plus tard dans ce cours (cela rend plus difficile le renommage de registres et la détection des dépendances entre instructions).
Le pseudo-aliasing des registres sur le processeur Z80
modifierLe processeur Z80 est très inspiré des premiers processeurs Intel, mais avec un jeu d'instruction légèrement différent. Il a un système de pseudo-aliasing de registres. Formellement, ce n'est pas un système d'alias, mais un système où les registres sont regroupés lors de certaines opérations.
Le Z80 est un processeur 8 bits, qui contient plusieurs registres généraux de 8 bits nommés A, B, C, D, E, F, H, L. Les registres A et F correspondent à l'accumulateur et aux registres d'état, ils ne sont pas concernés par ce qui va suivre. La quasi-totalité des opérations arithmétiques ne manipule que ces registres de 8 bits, mais l'opération d'incrémentation est un peu à part.
Le Z80 supporte 3 paires de registres aliasés. Chaque paire contient deux registres de 8 bits, mais une paire est considérée comme un registre unique de 16 bits pour certaines opérations. Les registres 16 bits sont la paire BC, la paire DE et la paire HL. Le registre BC de 16 bits est composé du registre B de 8 bits et du registre C de 8 bits, et ainsi de suite pour les paires DE et HL. Le système de paires de registres permet d'effectuer une opération d'incrémentation sur une paire complète. Les paires sont concrètement utilisées seulement pour l'incrémentation, avec une instruction spécialisée, qui incrémente le registre de 16 bit d'une paire.
Cela peut paraître étrange, mais c'est en réalité un petit plus qui se marie bien avec le reste de l'architecture. Le Z80 gère des adresses de 16 bits, ce qui signifie que les registres dédiés aux adresses sont de 16 bits. Et cela concerne son pointeur de pile et son program counter, qui sont de 16 bits tous les deux. Aussi, pour mettre à jour le pointeur de pile et le program counter, le processeur incorpore un incrémenteur de 16 bits. Les concepteurs du processeur ont sans doute cherché à rentabiliser cet incrémenteur et lui ont permis d'incrémenter des registres de données. Pour cela, il fallait regrouper les registres de 8 bits par paire de deux, ce qui rendait l’implémentation matérielle la plus simple possible.
Les optimisations liées aux registres architecturaux
modifierAfin d'améliorer les performances, les concepteurs des processeurs ont optimisé les registres architecturaux au mieux. Leur nombre, leur taille, leur adressage : tout est optimisé sur les jeux d'instruction dignes de ce nom. Et sur certains processeurs, on trouve des optimisations assez spéciales, qui visent à dupliquer les registres architecturaux sans que cela se voie dans le jeu d'instruction. Pour le dire autrement, un registre architectural correspond à plusieurs registres physiques dans le processeur.
Les registres dédiés aux interruptions
modifierSur certains processeurs, les registres généraux sont dupliqués en deux ensembles identiques. Le premier ensemble est utilisé pour exécuter les programmes normaux, alors que le second ensemble est dédié aux interruptions. Mais les noms de registres sont identiques dans les deux ensembles.
Prenons l'exemple du processeur Z80 pour simplifier les explications. Comme dit plus haut, ce processeur a beaucoup de registres et tous ne sont pas dupliqués. Les registres pour la pile ne sont pas dupliqués, le program counter non plus. Par contre, les autres registres, qui contiennent des données, sont dupliqués. Il s'agit des registres nommés A (accumulateur), le registre d'état F et les registres généraux B, C, D, E, H, L, ainsi que les registres temporaires W et Z. L'ensemble de registres pour interruption dispose lui aussi de registres nommés A, F et les registres généraux B, C, D, E, H, L, mais il s'agit de registres différents. Pour éviter les confusions, ils sont notés A', F', B', C', D', E', H', L', mais les noms de registres sont en réalité identiques. Le processeur ne confond pas les deux, car il sait s'il est dans une interruption ou non.
Les deux ensembles de registres sont censés être isolés, il n'est pas censé y avoir d'échanges de données entre les deux. Mais le Z80 permettait d'échanger des données entre les deux ensembles de registres. Dans le détail, une instruction permettait d'échanger le contenu d'une paire de registres avec la même paire dans l'autre ensemble. En clair, on peut échanger les registres BC avec BC', DE avec DE′, et HL avec HL′. Par contre, il est impossible d'échanger le registre A avec A', et F avec F'. Le résultat est que les programmeurs utilisaient l'autre ensemble de registres comme registres pour les programmes, même s'ils n'étaient pas prévus pour.
Ce système permet de simplifier grandement la gestion des interruptions matérielles. Lors d'une interruption sur un processeur sans ce système, l'interruption doit sauvegarder les registres qu'elle manipule, qui sont potentiellement utilisés par le programme qu'elle interrompt. Avec ce système, il n'y a pas besoin de sauvegarder les registres lors d'une interruption, car les registres utilisés par le programme et l'interruption ne sont en réalité pas les mêmes. Les interruptions sont alors plus rapides.
Notons qu'avec ce système, seuls les registres adressables par le programmeur sont dupliqués. Les registres comme le pointeur de pile ou le program counter ne sont pas dupliqués, car ils n'ont pas à l'être. Et attention : certains registres doivent être sauvegardés par l'interruption. Notamment, l'adresse de retour, qui permet de reprendre l'exécution du programme interrompu au bon endroit. Elle est réalisée automatiquement par le processeur.
Le fenêtrage de registres
modifierLe fenêtrage de registres est une amélioration de la technique précédente, qui est adaptée non pas aux interruptions, mais aux appels de fonction/sous-programmes. Là encore, lors de l'appel d'une fonction, on doit sauvegarder les registres du processeur sur la pile, avant qu'ils soient utilisés par la fonction. Plus un processeur a de registres architecturaux, plus leur sauvegarde prend du temps. Et là encore, on peut dupliquer les registres pour éviter cette sauvegarde. Pour limiter le temps de sauvegarde des registres, certains processeurs utilisent le fenêtrage de registres, une technique qui permet d'intégrer cette pile de registre directement dans les registres du processeur.
Le fenêtrage de registres de taille fixe
modifierLa technique de fenêtrage de registres la plus simple duplique chaque registre architectural en plusieurs exemplaires qui portent le même nom. Chaque ensemble de registres architecturaux forme une fenêtre de registre, qui contient autant de registres qu'il y a de registres architecturaux.
Lorsqu'une fonction s’exécute, elle se réserve une fenêtre inutilisée, et peut utiliser les registres de la fenêtre comme bon lui semble : une fonction manipule le registre architectural de la fenêtre réservée, mais pas les registres avec le même nom dans les autres fenêtres. Ainsi, pas besoin de sauvegarder les registres de cette fenêtre, vu qu'ils étaient vides de toute donnée. S'il ne reste pas de fenêtre inutilisée, on est obligé de sauvegarder les registres d'une fenêtre dans la pile.

Les interruptions peuvent aussi utiliser le fenêtrage de registres. Lorsqu'une interruption se déclenche, elle se voit allouer sa propre fenêtre de registres.
Le fenêtrage de registres de taille variable
modifierL'implémentation précédente a des fenêtres de taille fixe, qui sont toutes isolées les unes des autres. C'était le fenêtrage de registre implémenté sur le processeur Berkeley RISC, et quelques autres processeurs. Des techniques similaires permettent cependant d'avoir des fenêtres de taille variable !
Avec des fenêtres de registre de taille variable, chaque fonction peut réserver un nombre de registres différent des autres fonctions. Une fonction peut réserver 5 registres, une autre 8, une autre 6, etc. Par contre, il y a une taille maximale. Les registres du processeur se comportent alors comme une pile de registres. Un exemple est celui du processeur AMD 29000, qui implémente des fenêtres de taille variable, chaque fenêtre pouvant aller de 1 à 8 registres. C'était la même chose sur les processeurs Itanium.
Il faut noter que les processeurs Itanium et AMD 29000 n'utilisaient le fenêtrage de registres que sur une partie des registres généraux. Par exemple, l'AMD 29000 disposait de 196 registres, soit 64 + 128. Les registres sont séparés en deux groupes : un de 64, un autre de 128. Les 128 registres sont ceux avec le fenêtrage de registres, à savoir qu'ils forment une pile de registres utilisée pour les appels de fonction. Les 64 registres restants sont des registres généraux normaux, où le fenêtrage de registre ne s'applique pas, et qui est accessible par toute fonction. Cette distinction entre pile de registres (avec fenêtrage) et registres globaux (sans fenêtrage) existe aussi sur l'Itanium, qui avait 32 registres globaux et 96 registres avec fenêtrage.
Le renommage de registre
modifierLes processeurs récents utilisent des techniques de renommage de registre, que l'on ne peut pas aborder pour le moment (par manque de concepts importants). Mais d'autres techniques similaires sur le principe sont possibles, comme le fenêtrage de registres.
Pour rappel, les programmes informatiques exécutés par le processeur sont placés en mémoire RAM, au même titre que les données qu'ils manipulent. En clair, les instructions sont stockées dans la mémoire sous la forme de suites de bits, tout comme les données. La seule différence est que les instructions sont chargées via le program counter, alors que les données sont lues ou écrites par des instructions d'accès mémoire. En théorie, il est impossible de faire la différence entre donnée et instruction, vu que rien ne ressemble plus à une suite de bits qu'une autre suite de bits. Mais il est très rare que le processeur charge et exécute des données, qu'il prend par erreur pour des instructions. Cela demanderait en effet que le program counter ne fasse pas ce qui est demandé, ou que le programme exécuté soit bugué, voire qu'il soit conçu pour.
Toujours est-il qu'une instruction est codée sur plusieurs bits. Le nombre de bits utilisé pour coder une instruction est appelée la taille de l'instruction. Sur certains processeurs, la taille d'une instruction est fixe, c’est-à-dire qu'elle est la même pour toutes les instructions. Mais sur d'autres processeurs, les instructions n'ont pas toutes la même taille, ils gèrent des instructions de longueur variable. Un exemple de jeu d’instruction à longueur variable est le x86 des pc actuels, où une instruction peut faire entre 1 et 15 octets. L'encodage de ces instructions est tellement compliqué qu'il prendrait à lui seul plusieurs chapitres !
Les instructions de longueur variable permettent d'économiser un peu de mémoire : avoir des instructions qui font entre 1 et 3 octets est plus avantageux que de tout mettre sur 3 octets. Mais en contrepartie le chargement de l'instruction suivante par le processeur est rendu plus compliqué. Le processeur doit en effet identifier la longueur de l'instruction courante pour savoir où est la suivante. À l'opposé, des instructions de taille fixe gâchent un peu de mémoire, mais permettent au processeur de calculer plus facilement l’adresse de l'instruction suivante et de la charger plus facilement.
Il existe des processeurs qui sont un peu entre les deux, avec des instructions de taille fixe, mais qui ne font pas toutes la même taille. Un exemple est jeu d'instruction RISC-V, où il existe des instructions "normales" de 32 bits et des instructions "compressées" de 16 bits. Le processeur charge un mot de 32 bits, ce qui fait qu'il peut lire entre une et deux instructions à la fois. Au tout début de l'instruction, un bit est mis à 0 ou 1 selon que l'instruction soit longue ou courte. Le reste de l'instruction varie suivant sa longueur. Les instructions de 32 bits sont des instructions à trois adresses : elles indiquent deux opérandes et la destination du résultat. Les instructions de 16 bits n'ont que deux opérandes. Cela expliquent qu'elles soient plus courtes : deux opérandes prennent moins de place que trois.
L'opcode et l'encodage des modes d'adressage
modifierUne instruction n'est pas encodée n'importe comment et la suite de bits associée a une certaine structure. Quelques bits de l’instruction indiquent quelle est l'opération à effectuer : est-ce une instruction d'addition, de soustraction, un branchement inconditionnel, un appel de fonction, une lecture en mémoire, etc. Cette portion de mémoire s'appelle l'opcode. Pour la même instruction, l'opcode peut être différent suivant le processeur, ce qui est source d'incompatibilités. Par exemple, les opcodes de l'instruction d'addition ne sont pas les mêmes sur les processeurs x86 (ceux de nos PC) et les anciens macintosh, ou encore les microcontrôleurs. Ce qui fait qu'un opcode de processeur x86 n'aura pas d'équivalent sur un autre processeur, ou correspondra à une instruction totalement différente. De manière générale, on peut dire qu'il existe autant d'opcode que d'instructions pour un processeur. Évidemment, qui dit beaucoup d'opcodes dit processeur plus complexe : les circuits de gestion des opcodes sont naturellement plus complexes quand ces opcodes sont nombreuses. Pour l'anecdote, certains processeurs n'utilisent qu'une seule et unique instruction, et qui peuvent se passer d'opcodes.
Il arrive que certaines instructions soient composées d'un opcode, sans rien d'autre : elles ont alors une représentation en binaire qui est unique. Mais certaines instructions ajoutent une partie variable, pour préciser la localisation des données à manipuler. Une instruction peut alors fournir au processeur ce qu'on appelle une référence, à savoir quelque chose qui permet de localiser une donnée dans la mémoire. Cette référence pourra ainsi préciser plus ou moins explicitement dans quel registre, à quelle adresse mémoire, à quel endroit sur le disque dur, se situe la donnée à manipuler. Elles indiquent où se situent les opérandes d'un calcul, où stocker son résultat, où se situe la donnée à lire ou écrire, à quel l'endroit brancher. Il faut préciser que toutes les références n'ont pas la même taille : une adresse utilisera plus de bits qu'un nom de registres, par exemple (il y a moins de registres que d'adresses). Par exemple, une instruction de calcul dont les deux références sont des adresse mémoire prendra plus de place qu'un calcul qui manipule deux registres.
Reste à savoir quelle est la nature de la référence : est-ce une adresse, un nombre, un nom de registre ? Chaque manière d’interpréter la partie variable s'appellent un mode d'adressage. Pour résumer, un mode d'adressage indique au processeur que telle référence est une adresse, un registre, autre chose. Il est possible qu'une instruction précise plusieurs références, qui sont chacune soit une adresse, soit une donnée, soit un registre. Par exemple, une addition manipule deux opérandes, ce qui demande d'utiliser une opérande pour chaque (dans le pire des cas). Les instructions manipulant plusieurs références peuvent parfois utiliser un mode d'adressage différent pour chaque. Comme nous allons le voir, certaines instructions supportent certains modes d'adressage et pas d'autres. Généralement, les instructions d'accès mémoire possèdent plus de modes d'adressage que les autres, encore que cela dépende du processeur (chose que nous détaillerons dans le chapitre suivant).
Il existe deux méthodes pour préciser le mode d'adressage utilisé par l'instruction. Dans le premier cas, l'instruction ne gère qu'un mode d'adressage par opérande. Par exemple, toutes les instructions arithmétiques ne peuvent manipuler que des registres. Dans un cas pareil, pas besoin de préciser le mode d'adressage, qui est déduit automatiquement via l'opcode: on parle de mode d'adressage implicite. Dans certains cas, il se peut que plusieurs instructions existent pour faire la même chose, mais avec des modes d'adressages différents.

Dans le second cas, les instructions gèrent plusieurs modes d'adressage par opérande. Par exemple, une instruction d'addition peut additionner soit deux registres, soit un registre et une adresse, soit un registre et une constante. Dans un cas pareil, l'instruction doit préciser le mode d'adressage utilisé, au moyen de quelques bits intercalés entre l'opcode et les opérandes. On parle de mode d'adressage explicite. Sur certains processeurs, chaque instruction peut utiliser tous les modes d'adressage supportés par le processeur : on dit que le processeur est orthogonal.

Les modes d'adressages pour les données
modifierPour comprendre un peu mieux ce qu'est un mode d'adressage, nous allons voir les modes d'adressage les plus simples qui soient. Ils sont supportés par la majorité des processeurs existants, à quelques détails près que nous élaborerons dans le chapitre suivant. Il s'agit des modes d'adressage directs, qui permettent de localiser directement une donnée dans la mémoire ou dans les registres. Ils précisent dans quel registre, à quelle adresse mémoire se trouve une donnée.
L'adressage implicite
modifierAvec l'adressage implicite, la partie variable n'existe pas ! Il peut y avoir plusieurs raisons à cela. Il se peut que l'instruction n'ait pas besoin de données : une instruction de mise en veille de l'ordinateur, par exemple. Ensuite, certaines instructions n'ont pas besoin qu'on leur donne la localisation des données d'entrée et « savent » où sont les données. Comme exemple, on pourrait citer une instruction qui met tous les bits du registre d'état à zéro. Pareil pour les instructions manipulant la pile : on sait d'avance dans quels registres sont stockées l'adresse de la base ou du sommet de la pile.
L'adressage inhérent (à registre)
modifierAvec le mode d'adressage inhérent, la partie variable va identifier un registre qui contient la donnée voulue. Ce mode d'adressage demande d'attribuer un numéro de registre à chaque registre, parfois appelé abusivement un nom de registre. Pour rappel, ce dernier est un numéro attribué à chaque registre, utilisé pour préciser à quel registre le processeur doit accéder. On parle aussi d'adressage à registre, pour simplifier.

L'adressage immédiat
modifierAvec l'adressage immédiat, la partie variable est une constante : un nombre entier, un caractère, un nombre flottant, etc. Avec ce mode d'adressage, la donnée est placée dans la partie variable et est chargée en même temps que l'instruction.

Les constantes en adressage immédiat sont souvent codées sur 8 ou 16 bits. Aller au-delà serait inutile vu que la quasi-totalité des constantes manipulées par des opérations arithmétiques sont très petites et tiennent dans un ou deux octets. La plupart du temps, les constantes sont des entiers signés, c'est à dire qui peuvent être positifs, nuls ou négatifs. Au vu de la différence de taille entre la constante et les registres, les constantes subissent une opération d'extension de signe avant d'être utilisées.
Pour rappel, l'extension de signe convertit un entier en un entier plus grand, codé sur plus de bits, tout en préservant son signe et sa valeur. L'extension de signe des nombres positifs consiste à remplir les bits de poids fort avec des 0 jusqu’à arriver à la taille voulue : c'est la même chose qu'en décimal, où rajouter des zéros à gauche d'un nombre positif ne changera pas sa valeur. Pour les nombres négatifs, il faut remplir les bits à gauche du nombre à convertir avec des 1, jusqu'à obtenir le bon nombre de bits : par exemple, 1000 0000 (-128 codé sur 8 bits) donnera 1111 1111 1000 000 après extension de signe sur 16 bits. L'extension de signe d'un nombre codé en complément à 2 se résume donc en une phrase : il faut recopier le bit de poids fort de notre nombre à convertir à gauche de celui-ci jusqu’à atteindre le nombre de bits voulu.
L'adressage absolu
modifierPassons maintenant à l'adressage absolu, aussi appelé adressage direct. Avec lui, la partie variable est l'adresse de la donnée à laquelle accéder. Cela permet de lire une donnée directement depuis la mémoire RAM/ROM. Le terme "adressage par adresse" est aussi utilisé. Un défaut de ce mode d'adressage est que l'adresse en question a une taille assez importante, elle augmente drastiquement la taille de l'instruction. Les instructions sont donc soit très longues, sans optimisations.

Pour raccourcir les instructions, il est possible de ne pas mettre des adresses complètes, mais de retirer les bits de poids forts. L'adressage absolu ne peut alors lire qu'une partie de la mémoire RAM. Il est aussi possible de ne pas encoder les bits de poids faible pour des questions d'alignement mémoire. Les processeurs RISC modernes gèrent parfois le mode d'adressage absolu, ils encodent des adresses sur 16-20 bits pour des processeurs 32 bits. Un exemple plus ancien est le cas de l’ordinateur Data General Nova. Son processeur était un processeur 16 bits, capable d'adresser 64 kibioctets. Il gérait plusieurs modes d'adressages, dont un mode d'adressage absolu avec des adresses codées sur 8 bits. En conséquence, il était impossible d’accéder à plus de 256 octets avec l'adressage absolu, il fallait utiliser d'autres modes d'adressage pour cela. Il s'agit d'un cas extrême.
Une solution un peu différente des précédentes utilise des adresses de taille variable, et donc des instructions de taille variable. Un exemple est celui du mode zero page des processeurs Motorola, notamment des Motorola 6800 et des MOS Technology 6502. Sur ces processeurs, il y avait deux types d'adressages absolus. Le premier mode utilisait des adresses complètes de 16 bits, capables d'adresser toute la mémoire, tout l'espace d'adressage. Le second mode utilisait des adresses de 8 bits, et ne permettait que d'adresser les premiers 256 octets de la mémoire. L'instruction était alors plus courte : avec un opcode de 8bits et des adresses de 8 bits, elle rentrait dans 16 bits, contre 24 avec des adresses de 16 bits. Un autre avantage était que l'accès à ces 256 octets était plus rapide d'un cycle d'horloge, ce qui fait qu'ils étaient monopolisés par le système d'exploitation et les programmes utilisateurs, mais ce n'est pas lié au mode d'adressage absolu proprement dit.
Les modes d'adressage indirects pour les pointeurs
modifierLes modes d'adressages précédents sont appelés les modes d'adressage directs car ils fournissent directement une référence vers la donnée, en précisant dans quel registre ou adresse mémoire se trouve la donnée. Les modes d'adressage qui vont suivre ne sont pas dans ce cas, ils permettent de localiser une donnée de manière indirecte, en passant par un intermédiaire. D'où leurs noms de modes d'adressage indirects. L'intermédiaire en question est ce qui s'appelle un pointeur. Il s'agit de fonctionnalités de certains langages de programmation dits bas-niveau (proches du matériel), dont le C. Les pointeurs sont des variables dont le contenu est une adresse mémoire. En clair, les modes d'adressage indirects ne disent pas où se trouve la donnée, mais où se trouve l'adresse de la donnée, un pointeur vers celle-ci.
Pour rendre le tout plus intuitif, sachez qu'on a déjà rencontré un cas de ce genre. En effet, les registres de pile sont déjà en soi une forme d'adressage indirect : ils mémorisent une adresse mémoire, pas une donnée ! D'ailleurs, ce n'est pas pour rien que le registre pointeur de pile s'appelle ainsi ! Le pointeur de pile indique la position du sommet de la pile en mémoire RAM, il stocke l'adresse de la donnée au sommet de la pile, c'est un pointeur vers le sommet de la pile. Et ce pointeur de pile est stocké dans un registre, adressé implicitement ou explicitement.
L'utilité des pointeurs : les structures de données
modifierLes pointeurs ont une définition très simple, mais beaucoup d'étudiants la trouve très abstraite et ne voient pas à quoi ces pointeurs peuvent servir. Pour résumer rapidement, les pointeurs sont utilisées pour manipuler/créér des structures de données, à savoir des regroupements structurées de données plus simples, peu importe le langage de programmation utilisé. Manipuler des tableaux, des listes chainées, des arbres, ou tout autre structure de donnée un peu complexe, se fait à grand coup de pointeurs. C'est explicite dans des langages comme le C, mais implicite dans les langages haut-niveau. C'est surtout le cas dans les structures de données où les données sont dispersées dans la mémoire, comme les listes chaînées, les arbres, et toute structure éparse. Localiser les données en question dans la mémoire demande d'utiliser des pointeurs qui pointent vers ces données, qui donnent leur adresse.

Les structures de données les plus simples sont appelées "structures" ou enregistrements. Elles regroupent plusieurs données simples, comme des entiers, des adresses, des flottants, des caractères, etc. Par exemple, on peut regrouper deux entiers et un flottant dans une structure, qui regroupe les deux. Les données de la structure sont placées les unes à la suite des autres dans la RAM, à partir d'une adresse de début. Localiser une donnée dans la structure demande simplement de connaitre à combien de byte se situe la donnée par rapport à l'adresse de début. Une simple addition permet de calculer cette adresse, et des modes d'adressage permettent de faire ce calcul implicitement.
Un autre type de structure de donnée très utilisée est les tableaux, des structures de données où plusieurs données de même types sont placées les unes à la suite des autres en mémoire. Par exemple, on peut placer 105 entiers les uns à la suite des autres en mémoire. Toute donnée dans le tableau se voit attribuer un indice, un nombre entier qui indique la position de la donnée dans le tableau. Attention : les indices commencent à zéro, et non à 1, ce qui fait que la première donnée du tableau porte l'indice 0 ! L'indice dit si on veut la première donnée (indice 0), la deuxième (indice 1), la troisième (indice 2), etc.

Le tableau commence à une adresse appelée l'adresse de base, qui est mémorisée dans un pointeur. Localiser un entier dans le tableau demande de faire des calculs avec le pointeur et l'indice. Intuitivement, on se dit qu'il suffit d'additionner le pointeur avec l'indice. Mais ce serait oublier qu'il faut tenir compte de la taille de la donnée. Le calcul de l'adresse d'une donnée dans le tableau se fait en multipliant l'indice par la taille de la donnée, puis en additionnant le pointeur. De nombreux modes d'adressage permettent de faire ce calcul directement, comme nous allons le voir.
L'adressage indirect à registre pour les pointeurs
modifierLes modes d'adressage indirects sont des variantes des modes d'adressages directs. Par exemple, le mode d'adressage inhérent indique le registre qui contient la donnée, sa version indirecte indique le registre qui contient le pointeur, qui pointe vers une donnée en RAM/ROM. Idem avec le mode d'adressage absolu : sa version directe fournit l'adresse de la donnée, sa version indirecte fournit l'adresse du pointeur.
Par contre, il n'est pas possible de prendre tous les modes d'adressage précédents, et d'en faire des modes d'adressage indirects. L'adressage implicite reste de l'adressage implicite, peu importe qu'il adresse une donnée ou un pointeur (comme le pointeur de pile). Quand à l'adressage immédiat, il n'a pas d'équivalent indirect, même si on peut interpréter l'adressage absolu comme tel. Pour résumer, un pointeur peut être soit dans un registre, soit en mémoire RAM, ce qui donne deux classes de modes d'adressages indirect : à registre et mémoire. Nous allons d'abord voir l'adressage indirect à registre, ainsi que ses nombreuses variantes.
Avec l'adressage indirect à registre, le pointeur est stockée dans un registre. Le registre en question contient donc un l'adresse de la donnée à lire/écrire, celle qui pointe vers la donnée à lire/écrire. Lors de l'exécution de l'instruction, le pointeur dans le registre est envoyé sur le bus d'adresse, et la donnée est récupérée sur le bus de données.
Ici, la partie variable de l'instruction identifie un registre contenant l'adresse de la donnée voulue. La différence avec le mode d'adressage inhérent vient de ce qu'on fait de ce nom de registre : avec le mode d'adressage inhérent, le registre indiqué dans l'instruction contiendra la donnée à manipuler, alors qu'avec le mode d'adressage indirect à registre, le registre contiendra l'adresse de la donnée.

L'adressage indirect à registre gère les pointeurs nativement, mais pas plus. Il faut encore faire des calculs d'adresse pour gérer les tableaux ou les enregistrements, et ces calculs sont réalisés par des instructions de calcul normales. Le mode d'adressage indirect à registre ne gére pas de calculs d'adresse en lui-même. Et les modes d'adressages qui vont suivre intègrent ce mode de calcul directement dans le mode d'adressage ! Avec eux, le processeur fait le calcul d'adresse de lui-même, sans recourir à des instructions spécialisées. Sans ces modes d'adressage, utiliser des tableaux demande d'utiliser du code automodifiant ou d'autres méthodes qui relèvent de la sorcellerie.
Pour faciliter ces parcours de tableaux, il existe des variantes de l'adressage précédent, qui incrémentent ou décrémentent automatiquement le pointeur à chaque lecture/écriture. Il s'agit des modes d'adressages indirect avec auto-incrément (register indirect autoincrement) et indirect avec auto-décrément (register indirect autodecrement). Avec eux, le contenu du registre est incrémenté/décrémenté d'une valeur fixe automatiquement. Cela permet de passer directement à l’élément suivant ou précédent dans un tableau.

En théorie, il y a une différence entre les deux modes d'adressages. Avec l'adressage indirect avec auto-incrément, l'incrémentation se fait APRES l'envoi de l'adresse, après la lecture/écriture. On effectue l'accès mémoire avec le pointeur, avant d'incrémenter le pointeurs. Par contre, pour l'adresse indirect avec auto-décrément, on décrémente le pointeur AVANT de faire l'accès mémoire. Les deux comportements semblent incohérents, mais ils sont en réalité très intuitifs quand on sait comment se fait le parcours d'un tableau.
Le parcours d'un tableau du début vers la fin commence à l'adresse de base du tableau, celle de son premier élément. Aussi, si on place l'adresse de base du tableau dans un pointeur, on accède à l'adresse, puis ensuite on incrémente le tout. Pour le parcours en sens inverse, on commence à l'adresse de fin du tableau, celle à laquelle on quitte le tableau. Ce n'est pas l'adresse du dernier élément, mais l'adresse qui se situe immédiatement après. Pour obtenir l'adresse du dernier élément, on doit soustraire la taille de l'élément à l'adresse initiale. En clair, on décrémente l'adresse avant d'y accéder.

Les deux modes d'adressage posent des problèmes avec les exceptions matérielles. Le problème vient du fait que l'accès mémoire peut générer une exception matérielle, comme un problème de mémoire virtuelle ou autres. Dans ce cas, l'exception matérielle est gérée par une routine d'interruption, puis la routine se termine et l'instruction cause est ré-exécutée. Mais la ré-exécution doit tenir compte du fait que le pointeur initial a été incrémenté/décrémentée, et qu'il faut donc le faire revenir à sa valeur initiale. Quelques machines ont eu des problèmes d'implémentation de ce genre, notamment le DEC VAX et le Motorola 68000.
Les modes d'adressage indirects indicés pour les tableaux
modifierLe mode d'adressage base + indice est utilisé lors de l'accès à un tableau, quand on veut lire/écrire un élément de ce tableau. L'adressage base + indice, fournit à la fois l'adresse de base du tableau et l'indice de l’élément voulu. Les deux sont dans un registre, ce qui fait que ce mode d'adressage précise deux numéros/noms de registre. En clair, indice et pointeur sont localisés via adressage inhérent (à registre). Le calcul de l'adresse est effectué automatiquement par le processeur.

Il existe une variante qui permet de vérifier qu'on ne « déborde » pas du tableau, qu'on ne calcule pas une adresse en dehors du tableau, à cause d'un indice erroné, par exemple. Accéder à l’élément 25 d'un tableau de seulement 5 éléments n'a pas de sens et est souvent signe d'une erreur. Pour cela, l'instruction peut prendre deux opérandes supplémentaires (qui peuvent être constants ou placés dans deux registres). L'instruction BOUND sur le jeu d'instruction x86 en est un exemple. Si cette variante n'est pas supportée, on doit faire ces vérifications à la main.
Le mode d'adressage absolu indexé (indexed absolute, ou encore base+offset) est une variante de l'adressage précédent, qui est spécialisée pour les tableaux dont l'adresse de base est fixée une fois pour toute, elle est connue à la compilation. Les tableaux de ce genre sont assez rares : ils correspondent aux tableaux de taille fixe, déclarée dans la mémoire statique. L'adresse de base du tableau est alors précisée via une adresse mémoire et non un nom de registre. En clair, l'adresse de base est précisée par adressage absolu, alors que l'indice est précisé par adressage inhérent. À partir de ces deux données, l'adresse de l’élément du tableau est calculée, envoyée sur le bus d'adresse, et l’élément est récupéré.

Les deux modes d'adressage précédents sont appelés des modes d'adressage indicés, car ils gèrent automatiquement l'indice. Ils existent en deux variantes, assez similaires. La première variante ne tient pas compte de la taille de la donnée. L'adresse de base est additionnée avec l'indice, rien de plus. Le programme doit donc incrémenter/décrémenter l'indice en tenant compte de la taille de la donnée. Par exemple, pour un tableau d'entiers de 4 octets chacun, l'indice doit être incrémenté/décrémenté par pas de 4. Pour éviter ce genre de choses, la seconde variante se charge automatiquement de gérer la taille de la donnée. Le programme doit donc incrémenter/décrémenter les indices normalement, par pas de 1, l'indice est automatiquement multiplié par la taille de la donnée. Cette dernière est généralement encodée dans l'instruction, qui gère des tailles de données basiques 1, 2, 4, 8 octets, guère plus.
Pour les deux modes d'adressage précédent, l'indice est généralement mémorisé dans un registre général, éventuellement un registre entier. Mais il a existé des processeurs qui utilisaient des registres d'indice spécialisés dans les indices de tableaux. Les processeurs en question sont des processeurs assez anciens, la technique n'est plus utilisée de nos jours.
Les modes d'adressage indirect à décalage pour les enregistrements
modifierAprès avoir vu les modes d'adressage pour les tableaux, nous allons voir des modes d'adressage spécialisés dans les enregistrements, aussi appelées structures en langage C. Elles regroupent plusieurs données, généralement une petite dizaine d'entiers/flottants/adresses. Mais le processeur ne peut pas manipuler ces enregistrements : il est obligé de manipuler les données élémentaires qui le constituent une par une. Pour cela, il doit calculer leur adresse, et les modes d'adressage qui vont suivre permettent de le faire automatiquement.
Une donnée a une place prédéterminée dans un enregistrement : elle est donc a une distance fixe du début de celui-ci. En clair, l'adresse d'un élément d'un enregistrement se calcule en ajoutant une constante à l'adresse de départ de l'enregistrement. Et c'est ce que fait le mode d'adressage base + décalage. Il spécifie un registre et une constante. Le registre contient l'adresse du début de l'enregistrement, un pointeur vers l'enregistrement.

D'autres processeurs vont encore plus loin : ils sont capables de gérer des tableaux d'enregistrements ! Ce genre de prouesse est possible grâce au mode d'adressage base + indice + décalage. Il calcule l'adresse du début de la structure avec le mode d'adressage base + indice avant d'ajouter une constante pour repérer la donnée dans la structure. Et le tout, en un seul mode d'adressage.
Les modes d'adressage pseudo-absolus pour adresser plus de mémoire
modifierUne variante de l'adressage base + décalage a été utilisée sur d'anciennes architectures Motorola pour permettre d'adresser plus de mémoire. La variante en question visait à améliorer l'adressage absolu, qui intègre l'adresse à lire/écrire dans l'instruction elle-même. L'adresse en question est généralement très courte et n'encode que les bits de poids faible de l'adresse, ce qui ne permet que d'adresser une partie de la mémoire de manière absolue, là où les autres instructions ne sont pas limitées. Pour contourner ce problème, plusieurs modes d'adressages ont été inventées. Tous incorporent une adresse dans l'instruction, mais combinent cette adresse avec un registre adressé implicitement, ce qui en fait des adressages mi-indirects, mi-absolus. Nous regrouperons ces modes d'adressages sous le terme de modes d'adressages pseudo-absolus, terme de mon invention.
La première idée met les bits de poids fort de l'adresse dans un registre spécialement dédié pour. L'adresse finale est obtenue en concaténant ce registre avec l'adresse mémoire intégrée dans l’instruction. Le registre est appelé le registre de page. Un exemple est celui des premiers processeurs Motorola. Le registre de page 8 bits, l'adresse finale de 16 bits était obtenue en concaténant le registre de page avec les 8 bits fournit par adressage absolu. Le résultat est que la mémoire était découpée en blocs de 256 consécutifs, chacun pouvant servir de fenêtre de 256 octets.
Un autre exemple est celui du HP 2100, qui avait un registre de page de 5 bits et qui encodait 10 bits d'adresse dans ses instructions. Ses instructions d'accès mémoire disposaient d'un bit qui choisit quel mode d'adressage utiliser. S'il était à 0, l'adressage absolu était utilisé, le registre de page n'était pas utilisé. Mais s'il était à 1, le registre de page était utilisé pour calculer l'adresse.
Formellement, ce mode d'adressage a des ressemblances avec la commutation de banques, une technique qu'on verra dans les chapitres sur l'espace d'adressage et la mémoire virtuelle. Mais ce n'en est pas du tout : le registre de page est utilisé uniquement pour les accès mémoire avec le mode d'adressage base + décalage, mais pas pour les autres accès mémoire, qui gèrent des adresses complètes. Notons que l'usage d'un registre de page dédié fait que celui-ci est adressé implicitement.
Une évolution de l'adressage précédent est le mode page direct. Avec lui, le registre de page est étendu et contient une adresse mémoire complète. L'adresse finale n'est pas obtenue par concaténation, mais en additionnant le registre de page avec l'adresse fournie par adressage absolu. Un exemple est celui des premiers processeurs Motorola, qui géraient des adresses courtes de 8 bits. L'adresse courte de 8 bits correspondait non pas aux 256 premiers octets de la mémoire, mais à une fenêtre de 256 octets déplaçable en mémoire. La position de la fenêtre de 256 octets était spécifiée par le registre de page de 16 bits, qui précisait l'adresse du début de la fenêtre, celle de sa première donnée.
Il s'agit donc formellement d'adressage base + décalage, à un détail près : il n'y a qu'un seul registre de base. Le fait que ce registre de base soit unique fait qu'il est adressé implicitement, on n'a pas à encoder le numéro/noms de registre dans l'instruction. Le registre de base est utilisé uniquement pour l'adressage absolu, pas pour les autres accès mémoire. S'il y a des ressemblances avec la segmentation, une technique de mémoire virtuelle qu'on abordera dans quelques chapitres, ce n'en est pas vu que le registre de base est utilisé seulement pour un mode d'adressage bien précis.
Les modes d'adressage indirect mémoire
modifierLes modes d'adressage précédents mémorisent les pointeurs dans des registres, mais il existe quelques modes d'adressage qui font autrement. Ils existaient autrefois sur quelques vieux ordinateurs se débrouillaient sans registres pour les données/adresses. Avec de tels modes d'adressages, les pointeurs sont stockés en mémoire, d'où leur nom de modes d'adressage indirects mémoire.
Le plus simple d'entre eux est le mode d'adressage absolu indirect . L'instruction incorpore une adresse mémoire, mais ce n'est pas l'adresse de la donnée voulue : c'est l'adresse du pointeur qui pointe vers la donnée. Un tel mode d'adressage était utilisée sur de vieux processeurs, il était assez répandu, comparé à ses variantes. Un exemple est le cas des instructions LOAD et STORE des ordinateurs Data General Nova. Les deux isntructions existaient en deux versions, distinguées par un bit d'indirection. Si ce bit est à 0 dans l'opcode, alors l'instruction utilise le mode d'adressage absolu normal : l'adresse intégrée dans l'instruction est celle de la donnée. Mais s'il est à 1, alors l'adresse intégrée dans l'instruction est celle du pointeur.
Sur le même modèle que l’adressage indirect à registre, il a existé des modes d'adressage absolus indirects avec auto-incrément/auto-décrément. L'instruction incorpore alors l'adresse du pointeur. A chaque exécution de l'instruction, le pointeur est incrémenté ou décrémenté automatiquement. Les deux exemples les plus connus sont le PDP-8 et le Data General Nova, les autres exemples sont très rares. Sur le PDP-8, les adresses 8 à 15 avaient un comportement spécial. Quand on y accédait via adressage mémoire indirect, leur contenu était automatiquement incrémenté. Le Data General Nova avait la même chose, mais pour ses adresses 16 à 31 : les adresses 16 à 24 étaient incrémentées, celles de 25 à 31 étaient décrémentées.
Il faut noter que les modes d'adressages indicés et à décalage peuvent être rendus indirects. Par exemple, on peut imaginer un mode d'adressage indirect Base + indice. Avec lui, la somme adresse de base + indice calcule l'adresse du pointeur et non l'adresse de la donnée, ce qui rajoute un accès mémoire pour accéder à la donnée finale. Un tel mode d'adressage serait utile pour gérer des tableaux de pointeurs. En fait, tous les modes d'adressage précédents peuvent être modifiés de manière à ce que la donnée lue/écrite soit traitée comme un pointeur. Il y a donc un grand nombre de modes d'adressages indirects mémoire !
D'autres architectures supportaient des modes d'adressages indirects récursifs. l'idée était simple : le mode d'adressage identifie un mot mémoire, qui peut être soit une donnée soit un pointeur. Le pointeur peut lui aussi pointer vers une donnée ou un pointeur, qui lui-même... Une véritable chaine de pointeurs pouvait être supportée avec une seule instruction. Pour cela, chaque mot mémoire avait un bit d'indirection qui disait si son contenu était un pointeur ou une donnée. Des exemples d'ordinateurs supportant un tel mode d'adressage sont le DEC PDP-10, les IBM 1620, le Data General Nova, l'HP 2100 series, and le NAR 2. Le PDP-10 gérait même l'usage de registres d'indice à chaque étape d'accès à un pointeur.
Les modes d'adressage pour les branchements
modifierLes modes d'adressage des branchements permettent de donner l'adresse de destination du branchement, l'adresse vers laquelle le processeur reprend son exécution si le branchement est pris. Les instructions de branchement peuvent avoir plusieurs modes d'adressages : implicite, direct, relatif ou indirect. Suivant le mode d'adressage, l'adresse de destination est soit dans l'instruction elle-même (adressage direct), soit dans un registre du processeur (branchement indirect), soit calculée à l’exécution (relatif), soit précisée de manière implicite (retour de fonction, adresse sur la pile).
Les branchements directs
modifierAvec un branchement direct, l'opérande est simplement l'adresse de l'instruction à laquelle on souhaite reprendre.

Les branchements relatifs
modifierLes branchements relatifs permettent de localiser la destination d'un branchement par rapport à l'instruction en cours. Cela permet de dire « le branchement est 50 instructions plus loin ». Avec eux, l'opérande est un nombre qu'il faut ajouter au registre d'adresse d'instruction pour tomber sur l'adresse voulue. On appelle ce nombre un décalage (offset).

Les branchements indirects
modifierAvec les branchements indirects, l'adresse vers laquelle on souhaite brancher peut varier au cours de l’exécution du programme. Ces branchements sont souvent camouflés dans des fonctionnalités un peu plus complexes des langages de programmation (pointeurs sur fonction, chargement dynamique de bibliothèque, structure de contrôle switch, et ainsi de suite). Avec ces branchements, l'adresse vers laquelle on veut brancher est stockée dans un registre.

Les branchements implicites
modifierLes branchements implicites se limitent aux instructions de retour de fonction, où l'adresse de destination est située au sommet de la pile d'appel.
L'instruction SKIP est équivalente à un branchement relatif dont le décalage est de 2. Il n'est pas précisé dans l'instruction, mais est implicite.
Les modes d'adressage pour les conditions/tests
modifierPour rappel, les instructions à prédicats et les branchements s’exécutent si une certaine condition est remplie. Pour rappel, on peut faire face à deux cas. Dans le premier, le branchement et l'instruction de test sont fusionnés en une seule instruction. Dans le second, la condition en question est calculée par une instruction de test séparée du branchement. Dans les deux cas, on doit préciser quelle est la condition qu'on veut vérifier. Cela peut se faire de différentes manières, mais la principale est de numéroter les différentes conditions et d'incorporer celles-ci dans l'instruction de test ou le branchement. Un second problème survient quand on a une instruction de test séparée du branchement. Le résultat de l'instruction de test est mémorisé soit dans un registre de prédicat (un registre de 1 bit qui mémorise le résultat d'une instruction de test), soit dans le registre d'état. Les instructions à prédicats et les branchements doivent alors préciser où se trouve le résultat de la condition adéquate, ce qui demande d'utiliser un mode d'adressage spécialisé.
Pour résumer peut faire face à trois possibilités :
- soit le branchement et le test sont fusionnés et l'adressage est implicite ;
- soit l'instruction de branchement doit préciser le registre à prédicat adéquat ;
- soit l'instruction de branchement doit préciser le bon bit dans le registre d'état.
L'adressage des registres à prédicats
modifierLa première possibilité est celle où les instructions de test écrivent leur résultat dans un registre à prédicat, qui est ensuite lu par le branchement. De tels processeurs ont généralement plusieurs registres à prédicats, chacun étant identifié par un nom de registre spécialisé. Les noms de registres pour les registres à prédicats sont séparés des noms des registres généraux/entiers/autres. Par exemple, on peut avoir des noms de registre à prédicats codés sur 4 bits (16 registres à prédicats), alors que les noms pour les autres registres sont codés sur 8 bits (256 registres généraux).
La distinction entre les deux se fait sur deux points : leur place dans l'instruction, et le fait que seuls certaines instructions utilisent les registres à prédicats. Typiquement, les noms de registre à prédicats sont utilisés uniquement par les instructions de test et les branchements. Ils sont utilisés comme registre de destination pour les instructions de test, et comme registre source (à lire) pour les branchements et instructions à prédicats. De plus, ils sont placés à des endroits très précis dans l'instruction, ce qui fait que le décodeur sait identifier facilement les noms de registres à prédicats des noms des autres registres.
L'adressage du registre d'état
modifierLa seconde possibilité est rencontrée sur les processeurs avec un registre d'état. Sur ces derniers, le registre d'état ne contient pas directement le résultat de la condition, mais celle-ci doit être calculée par le branchement ou l'instruction à prédicat. Et il faut alors préciser quels sont le ou les bits nécessaires pour connaitre le résultat de la condition. En conséquence, cela ne sert à rien de numéroter les bits du registre d'état comme on le ferais avec les registres à prédicats. A la place, l'instruction précise la condition à tester, que ce soit l'instruction de test ou le branchement. Et cela peut être fait de manière implicite ou explicite.
La première possibilité est d'indiquer explicitement la condition à tester dans l'instruction. Pour cela, les différentes conditions possibles sont numérotées, et ce numéro est incorporé dans l'instruction de branchement. L'instruction de branchement contient donc un opcode, une adresse de destination ou une référence vers celle-ci, puis un numéro qui indique quelle condition tester. Un exemple assez intéressant est l'ARM1, le tout premier processeur de marque ARM. Sur l'ARM1, le registre d'état est mis à jour par une opération de comparaison, qui est en fait une soustraction déguisée. L'opération de comparaison soustrait deux opérandes A et B, met à jour le registre d'état en fonction du résultat, mais n'enregistre pas ce résultat dans un registre et s'en débarrasse. Le registre d'état est un registre contenant 4 bits appelés N, Z, C et V : Z indique que le résultat de la soustraction vaut 0, N indique qu'il est négatif, C indique que le calcul a donné un débordement d'entier non-signé, et V indique qu'un débordement d'entier signé. Avec ces 4 bits, on peut obtenir 16 conditions possibles, certaines indiquant que les deux nombres sont égaux, différents, que l'un est supérieur à l'autre, inférieur, supérieur ou égal, etc. L'instruction précise laquelle de ces 16 conditions est nécessaire : l'instruction s’exécute si la condition est remplie, ne s’exécute pas sinon. Voici les 16 conditions possibles :
| Code fournit par l’instruction | Test sur le registre d'état | Interprétation |
|---|---|---|
| 0000 | Z = 1 | Les deux nombres A et B sont égaux |
| 0001 | Z = 0 | Les deux nombres A et B sont différents |
| 0010 | C = 1 | Le calcul arithmétique précédent a généré un débordement non-signé |
| 0011 | C = 0 | Le calcul arithmétique précédent n'a pas généré un débordement non-signé |
| 0100 | N = 1 | Le résultat est négatif |
| 0101 | N = 0 | Le résultat est positif |
| 0110 | V = 1 | Le calcul arithmétique précédent a généré un débordement signé |
| 0111 | V = 0 | Le calcul arithmétique précédent n'a pas généré de débordement signé |
| 1000 | C = 1 et Z = 0 | A > B si A et B sont non-signés |
| 1001 | C = 0 ou Z = 1 | A <= B si A et B sont non-signés |
| 1010 | N = V | A >= B si on calcule A - B |
| 1011 | N != V | A < B si on calcule A - B |
| 1100 | Z = 0 et ( N = V ) | A > B si on calcule A - B |
| 1101 | Z = 1 ou ( N = 1 et V = 0 ) ou ( N = 0 et V = 1 ) | A <= B si on calcule A - B |
| 1110 | L'instruction s’exécute toujours (pas de prédication). | |
| 1111 | L'instruction ne s’exécute jamais (NOP). | |
La seconde possibilité est celle de l'adressage implicite du registre d'état. C'est le cas sur les processeurs x86, où il y a plusieurs instructions de branchements, chacune calculant une condition à partir des bits du registre d'état. Le registre d'état est similaire à celui de l'ARM1 vu plus haut. Le registre d'état des CPU x86 contient 5 bits : ZF indique que le résultat de la soustraction vaut 0, SF indique son signe, CF est le bit de retenue et de débordement non-signé, OF le bit de débordement signé, et PF le bit qui donne la parité du résultat. Il existe plusieurs branchements, certains testant un seul bit du registre d'état, d'autres une combinaison de plusieurs bits.
| Instruction de branchement | Bit du registre d'état testé | Condition testée si on compare deux nombres A et B avec une instruction de test |
|---|---|---|
| JS (Jump if Sign) | N = 1 | Le résultat est négatif |
| JNS (Jump if not Sign) | N = 0 | Le résultat est positif |
| JO (Jump if Overflow) | SF = 1 ou | Le calcul arithmétique précédent a généré un débordement signé |
| JNO (Jump if Not Overflow) | SF = 0 | Le calcul arithmétique précédent n'a pas généré de débordement signé |
| JNE (Jump if Not equal) | Z = 1 | Les deux nombres A et B sont égaux |
| JE (Jump if Equal) | Z = 0 | Les deux nombres A et B sont différents |
| JB (Jump if below) | C = 1 | A < B, avec A et B non-signés |
| JAE (Jump if Above or Equal) | C = 0 | A >= B, avec A et B non-signés |
| (JBE) Jump if below or equal | C = 1 ou Z = 0 | A >= B si A et B sont non-signés |
| JA (Jump if above) | C = 0 et Z = 0 | A > B si A et B sont non-signés |
| JL (Jump if less) | SF != OF | si A < BA et B sont signés |
| JGE (Jump if Greater or Equal) | SF = OF | si A >= BA et B sont signés |
| JLE (Jump if less or equal) | SF != OF OU ZF = 1 | si A <= BA et B sont signés |
| JGE (Jump if Greater) | SF = OF OU ZF = 0 | si A > B et B sont signés |
Les instructions d'un processeur dépendent fortement du processeur utilisé. La liste de toutes les instructions qu'un processeur peut exécuter s'appelle son jeu d'instructions. Celui-ci définit les instructions supportées, ainsi que la manière dont elles sont encodées en mémoire. Le jeu d'instruction des PC actuels est le x86, un jeu d'instructions particulièrement ancien, apparu en 1978. Les anciens macintoshs (la génération de macintosh produits entre 1994 et 2006) utilisaient un jeu d'instruction différent : le PowerPC (depuis 2006, les macintoshs utilisent un processeur X86). Mais les architectures x86 et Power PC ne sont pas les seules au monde : il existe d'autres types d'architectures qui sont très utilisées dans le monde de l’informatique embarquée et dans tout ce qui est tablettes et téléphones portables derniers cris. On peut citer notamment les architectures ARM, MIPS et SPARC. Pour résumer, il existe différents jeux d'instructions, que l'on peut classer suivant divers critères.
L'adressage des opérandes : les 5 architectures canoniques
modifierLa première classification que nous allons voir est basée sur l'adressage des opérandes par les instructions arithmétiques. Les accès mémoire et branchements ne sont pas impliqués dans cette classification. La raison à cela est que les branchements ont des modes d'adressages dédiés, idem pour les accès mémoire. Tel n'est pas le cas des instructions de calculs, qui ont souvent un nombre plus limité de modes d'adressage, du moins sur la plupart des architectures, qui limitent les modes d'adressages pour les opérandes afin de simplifier le processeur. Dans les grandes lignes, on trouve cinq catégories principales : les architectures mémoire-mémoire, les architectures à registres, les architectures LOAD-STORE, les architectures à accumulateur, les architectures à pile. Il s'agit de ce que je vais appeler les cinq architectures canoniques.
Les architectures à registres et LOAD-STORE
modifier
Les architectures à registres peuvent stocker temporairement des données dans des registres généraux ou spécialisés. La présence de registre améliore grandement les performances comparé aux autres architectures. Le gain en performance est d'autant plus important que la mémoire est lente par rapport au processeur. Aussi, à part quelques architectures assez anciennes, toutes les architectures sont des architectures à registres. Cependant, les processeurs de ce type gèrent de nombreux modes d'adressages, et peuvent lire leurs opérandes soit depuis les registres, soit depuis la mémoire.
Une architecture à registre gère le cas où les deux opérandes sont dans des registres. Mais elle gère aussi au minimum un autre cas : celui où une opérande est lue en mémoire RAM/ROM, alors que l'autre est dans les registres. Les instructions de ce type sont appelées des instructions load-op. Les processeurs pouvant lire les deux opérandes depuis la mémoire sont rares. Par exemple, sur les processeurs x86, impossible d'avoir les deux opérandes lues depuis la mémoire. Il existe quelques rares processeurs qui permettent d'écrire le résultat d'une instruction directement en mémoire, sans passer par les registres. Et il peut y avoir des restrictions.
Les architectures LOAD-STORE se distinguent des architectures à registres sur un détail : les instructions arithmétiques et logiques ne peuvent pas lire leurs opérandes en mémoire, seules les instructions d'accès mémoire le peuvent. Leurs opérandes sont systématiquement dans les registres, il n'y a pas d'instructions load-op. En conséquence, les instructions de calcul ne peuvent prendre que des noms de registres ou des constantes comme opérandes : cela n'autorise que les modes d'adressage immédiat et à registre.

Les architectures mémoire-mémoire
modifier
Les toutes premières machines n'avaient pas de registres pour les données et ne faisaient que manipuler la mémoire RAM ou ROM : on parle d'architectures mémoire-mémoire. Dans ces architectures, il n'y a pas de registres généraux : les instructions n'accèdent qu'à la mémoire principale. Malgré l'absence de registres pour les données, le program counter existe toujours, de même que le registre d'état et le pointeur de pile.
Le défaut des architectures mémoire-mémoire est qu'elles font beaucoup d'accès mémoire, du fait de l'absence de registres. Aussi, la performance dépendait grandement de la performance de la mémoire RAM. En conséquence, les processeurs de ce type étaient couplés à une mémoire assez rapide pour servir ce grand nombre d'accès mémoire. Au début de l'informatique, le processeur et la mémoire RAM avaient des performances similaires. Mais depuis que la mémoire est devenue très lente comparé au processeur, ce genre d'architectures est tombé en désuétude.
Un autre défaut de ces processeurs est que leurs instructions de calcul effectuent plusieurs accès mémoire. Prenons une instruction dyadique, à savoir qu'elle lit deux opérandes et calcule un résultat unique. Elle demande de faire trois accès mémoire : deux pour charger les opérandes, une pour enregistrer le résultat. Et il faut séquencer ces accès mémoire, à savoir faire deux lectures consécutives à deux adresses différentes pour charger les opérandes, pour ensuite écrire le résultat en mémoire. Ce séquençage des accès mémoire pour une seule instruction est assez complexe, demande de concevoir le séquenceur pour, et demande d'ajouter des registres internes au processeur qui sont cachés du programmeur.
Un cas intéressant d'architecture de ce genre est celle du processeur AT&T Hobbit. L'origine de ce processeur se trouve dans un projet de processeur abandonné par AT&T. Le processeur en question, la C-machine, était un processeur spécifiquement conçus pour le langage de programmation C. Et pour coller le plus possible à ce langage, le processeur n'utilisait pas de registres, seulement des adresses mémoires. Et vu que les programmes codés en C manipulent beaucoup la pile d'appel, le processeur avait une architecture mémoire-mémoire complétée par un cache de pile. Pour résumer, la pile d'appel est en mémoire, mais le sommet de la pile est stocké dans une mémoire LIFO intégrée au processeur. Le cache de pile contient 64 données de 4 octets chacun. En soi, il s'agit bien d'un cache, le processeur accède à la pile d'appel en mémoire RAM, mais ces accès sont interceptés par le cache de pile et c'est lui qui fournit la donnée demandée s'il la contient.
L'usage d'un cache de pile est assez spécifique aux architectures mémoire-mémoire, ainsi que pour les architectures à pile qu'on verra plus bas, même s'il doit exister quelques exceptions. La raison est que les architectures avec des registres utilisent des registres en lieu et place de ce cache de pile. De plus, les processeurs avec des registres utilisent généralement des mémoires caches générales, qui peuvent stocker n'importe quel type de données, et ne sont pas spécialisés pour la pile d'appel.
Les architectures à accumulateur
modifierLes architectures à accumulateur sont des architectures intermédiaires entre architectures à registre et architecture mémoire-mémoire. Elles visent à corriger un défaut des architectures mémoire-mémoire, en ajoutant un registre architectural unique. Plus haut, on a vu qu'une opération dyadique demande de faire trois accès mémoire : deux pour charger les opérandes, une pour enregistrer le résultat. Et cela demande d'ajouter de quoi séquencer ces accès mémoire, et d'ajouter des registres dans le processeur pour mémoriser les opérandes. Les architectures à accumulateur résolvent ce problème en ajoutant un registre unique, visible par le programmeur, afin d'éliminer des accès mémoire. Grâce à lui, une instruction dyadique ne fait qu'un seul accès mémoire, pas trois.

Elles incorporent un unique registre, appelé l'accumulateur, qui mémorise un opérande. Si l'instruction manipule plusieurs opérandes, les opérandes qui ne sont pas dans l'accumulateur sont lus depuis la mémoire RAM. De plus, le résultat d'une instruction est automatiquement mémorisé dans l'accumulateur. Grâce à ce registre, un opérande est lu depuis l'accumulateur, le résultat est stocké dans l'accumulateur, le seul accès mémoire à réaliser est celui pour la seconde opérande (si elle est nécessaire). Le nombre d'accès mémoire est donc grandement réduit pour les instructions dyadiques, les plus fréquentes.
Historiquement, les premières architectures à accumulateur ne contenaient aucun autre registre que l'accumulateur. L'accumulateur est adressé grâce au mode d'adressage implicite, de même que le résultat de l'opération. Par contre, les autres opérandes sont localisés avec d'autres modes d'adressage, et lues en mémoire RAM. Le résultat ainsi qu'un des opérandes sont adressés de façon implicite car dans l'accumulateur, seule la seconde opérande étant adressée directement.
Les architectures à pile
modifier
Les dernières architectures que nous allons voir sont les machines à pile, des jeux d'instructions où les opérandes sont organisés avec une pile semblable à la pile d'appel. De tels processeurs gèrent nativement une pile semblable à la pile d'appel, sauf qu'elle mémorise les opérandes des calculs et leur résultat. La pile est placée en mémoire RAM, on peut copier des opérandes dans la pile ou en retirer grâce à des instructions PUSH et POP qu'on analysera sous peu. Une instruction de calcul prend les opérandes qui sont au sommet de la pile. L'instruction dépile automatiquement les opérandes qu'elle utilise et empile son résultat.
Les opérandes sont ajoutés ou retirés de la pile grâce à deux instructions nommées PUSH et POP.
- L'instruction PUSH permet d'empiler une donnée. Elle prend l'adresse de la donnée à empiler, charge la donnée, et met à jour le pointeur de pile.
- L'instruction POP dépile la donnée au sommet de la pile, la stocke à l'adresse indiquée dans l'instruction, et met à jour le pointeur de pile.


Un défaut lié à l'absence des registres est qu'il est impossible de réutiliser une donnée chargée dans la pile. Vu qu'une instruction dépile ses opérandes, on ne peut pas les réutiliser. Ceci dit, certaines instructions ont été inventées pour limiter la casse : on peut notamment citer l'instruction DUP, qui copie le sommet de la pile en deux exemplaires. On peut aussi citer l'instruction SWAP, qui échange deux données dans la pile. La solution a pour défaut que ces instructions sont des opérations à faire en plus, comparé aux autres architectures. Les autres classes d'architectures n'ont pas à copier des données dans une pile, les empiler, et les déplacer avant de les manipuler.


Les instructions de calcul manipulent les opérandes qui sont au sommet de la pile. Les opérandes sont retirés de la pile par l'instruction et le résultat est placé au sommet de la pile. C'est du moins le cas sur les machines à pile dites "pures", mais d'autres architectures permettent de préciser la position dans la pile des opérandes à utiliser. Une instruction peut donc indiquer qu'elle veut utiliser les opérandes situés 2, 3 ou 5 cases sous le sommet de la pile. Si les opérandes sélectionnés ne sont pas toujours retirés de la pile (tout dépend de l'architecture), le résultat est lui toujours placé au sommet de la pile. Ces jeux d'instruction n'utilisent pas la pile comme une mémoire LIFO, ce qui lui vaut le nom d'architecture à pseudo-pile.
Les machines à pile que je viens de décrire ne peuvent manipuler que des données sur la pile. Toutefois, des machines à pile plus évoluées ajoutent des modes d'adressages pour que la seconde opérande soit lue non pas depuis la pile, mais soit adressées explicitement en mémoire RAM, avec une adresse mémoire ou un mode d’adressage de type base+index. Notons que le résultat est stocké au sommet de la pile malgré tout. Les instructions pouvant adresser explicitement une ou plusieurs opérandes sont en plus des instructions normales qui lisent leurs opérandes sur la pile.
L'implémentation d'une architecture à pile est assez complexe, mais elle a l'avantage de ne pas utiliser beaucoup de registres. À part un program counter, une architecture à pile se contente d'un registre pointeur de pile, qui indique l'adresse du sommet de la pile en RAM. Il va de soi que pour simplifier la conception du processeur, celui-ci peut contenir des registres internes pour stocker temporairement les opérandes des calculs, mais ces registres ne sont pas accessibles au programmeur, ce ne sont pas des registres architecturaux.
Pour de meilleures performances, tout ou partie de la pile est stockée directement dans le processeur, pour gagner en performance. En général, le sommet de la pile est stockée dans une mémoire tampon de type LIFO. Si jamais la LIFO en question est totalement remplie, le processeur peut gérer la situation de plusieurs manières. Avec la première, les données au bas de la pile débordent en mémoire RAM. Si la LIFO est déjà pleine au moment d'un PUSH, l'opérande au fond de la pile est alors envoyé en mémoire RAM. Reste qu'implémenter la gestion du débordement de la pile pile est quelque peu complexe. Une autre solution est de déléguer les débordements au logiciel. Un PUSH dans pune pile pleine déclenche une exception matérielle, dont la routine gère la situation.
Une autre solution remplace la LIFO par un cache de pile, qui mémorise les données au sommet de la pile. Il s'agit réellement d'un cache, dans le sens où il contient une copie du sommet de la pile d'appel, qui est aussi en RAM. La pile est donc en RAM, totalement, et seuls les portions utilisées de la pile sont maintenues dans le processeur. La gestion du débordement se fait en utilisant le remplacement des lignes de cache naturellement incorporé dans tout cache digne de ce nom.

La présence/absence de registres impacte le jeu d'instruction
modifierPour comprendre pourquoi les architectures à registre et LOAD-STORE dominent actuellement, il faut les comparer aux autres architectures canoniques. Et la différence principale concerne le nombre de registres. De ce point de vue, on peut distinguer trois classes d'architectures : celles sans registres de données, les architectures à accumulateur, et les architectures à registres.
| Classe d'architecture | Nombre de registres pour les données |
|---|---|
| Architecture mémoire-mémoire | Aucun. |
| Architecture à pile/à file | |
| Architecture à accumulateur | Un registre appelé l'accumulateur. |
| Architecture à registres | Plusieurs registres dits généraux et/ou spécialisés. |
| Architecture LOAD-STORE |
La présence de registres réduit grandement le nombre d'accès mémoire à effectuer, ce qui améliore grandement la performance. Du moins, à condition que la mémoire soit moins rapide que le processeur, ce qui n'a pas toujours été le cas. Au début de l'informatique, mémoire et processeur étaient tout aussi rapides, ce qui fait que les architectures à registre ou LOAD-STORE n'avait pas d'avantage évident en termes de performances. Mais cela ne signifie pas qu'elles n'avaient ni avantages, ni inconvénients. La présence/absence des registres de données a de nombreuses conséquences assez intéressantes à étudier, bien au-delà des performances. Elle impacte le support des procédures, des interruptions, mais aussi la gestion des pointeurs/tableaux, ainsi que le support de certaines instructions mémoire.
La rapidité des interruptions/appels de fonction
modifierL'absence de registre a des avantages pour la gestion des procédures. Pas besoin de sauvegarder les registres du processeur à chaque appel de fonction, ni de les restaurer à la fin. La gestion de la pile est ainsi grandement simplifiée : pas de sauvegarde/restauration des registres signifie pas besoin d'instructions pour échanger des données entre registres et cadres de pile. Les programmes avec beaucoup d'appels de fonction économisent ainsi beaucoup d’instructions, ils étaient plus petits. L'avantage est d'autant plus important que les procédures/fonctions sont petites (une large partie des instructions est alors dédiée à la sauvegarde/restauration des registres) et nombreuses.
En conséquence, les architectures mémoire-mémoire et les architectures à pile ont un avantage pour ce qui est des appels de fonction. L'avantage concerne aussi les interruptions, qui sont des appels de fonction comme les autres. Ce qui fait que les architectures sans registres de données sont parfois utilisés comme processeurs pour gérer les entrées-sorties, vu que ces processeurs doivent fréquemment gérer des interruptions matérielles. Ils sont aussi très adaptés pour des processeurs faible performance dans l'embarqué, dans des cas d'utilisation où les interruptions matérielles sont fréquentes.
Les architectures à accumulateur sont aussi dans ce cas. Avec elles, il n'y a qu'un seul registre accumulateur en plus comparé aux architectures sans registres, ce qui ce qui rend la sauvegarde/restauration des registres très rapide. Et encore, dans quelques situations, l'accumulateur n'a pas à être sauvegardé. Et tout cela vaut aussi pour les interruptions. Aussi, beaucoup de processeurs embarqués à faible performance, qui doivent gérer un grand nombre d'entrées-sorties, sont des architectures à accumulateur. Leur simplicité de conception, leur facilité de programmation, leur parfaite adaptation aux interruptions fréquentes, les rend idéaux pour ce genre d'applications.
Les modes d'adressage indicés et indirects impliquent la présence de registres
modifierUn désavantage lié à l'absence des registres est lié au calcul des adresses. Par exemple, de nombreux modes d'adressage ne sont pas possibles dans registres pour les données/adresse. Prenez le mode d'adressage base + index, qui prend une adresse et y ajoute un indice, les deux étant stockés dans des registres séparés. Il n'est théoriquement pas possible sur les architectures mémoire-mémoire et les architectures à pile. De même, il n'est pas possible sur les architectures à accumulateur, vu qu'il n'y a pas assez de registres.
En clair, les modes d'adressage possibles sont très limités. Outre l'adressage implicite et l'adressage immédiat (constante inclue dans l'instruction), il ne reste que l'adressage absolu. Les modes d'adressage indirect à registre ne sont simplement pas possibles, de même que les modes d'adressage indicés (base + indice et variantes). Or, ces modes d'adressage sont très utiles pour manipuler des pointeurs et des tableaux. Sans ces modes d'adressages, l'utilisation de tableaux ou de structures de données était un véritable calvaire, qui se résolvait parfois à grand coup de code automodifiant.
Pour améliorer la situation, les processeurs à accumulateurs ont alors incorporé des registres d'indice, pour faciliter les calculs d'adresse mémoire. Les registres d'indice stockent des indices de tableaux. Les registres d'indice permettait de supporter le mode d'adressage Indexed Absolute (adresse fixe + indice variable). Les autres modes d'adressages, comme le mode d'adressage base + indice ou le mode d'adressage indirect à registre étaient difficiles à mettre en œuvre sur ce genre de machines. Il faut dire que l'on ne pouvait pas mémoriser de pointeur dans un registre d'indice.
Au départ, ces processeurs n'utilisaient qu'un seul registre d'Index qui se comportait comme un second accumulateur spécialisé dans les calculs d'adresses mémoire. Le processeur supportait de nouvelles instructions capables de lire ou d'écrire une donnée dans/depuis l'accumulateur, qui utilisaient ce registre d'Index de façon implicite. Mais avec le temps, les processeurs finirent par incorporer plusieurs de ces registres. Les instructions de lecture ou d'écriture devaient alors préciser quel registre d'indice utiliser, en précisant un nom de registre d'indice, un numéro de registre d'indice.
Un exemple est le cas du processeur Motorola 6809, un processeur à accumulateur qui contient deux registres d'indices nommés X et Y. L'accumulateur est noté D et fait 16 bits, il peut être parfois géré comme deux accumulateurs séparés A et B de 8 bits chacun. Il contenait aussi deux pointeurs de pile, l'un pour les programmes, l'autre pour le système d'exploitation, ainsi qu'un program counter. Le registre de page était utilisé pour l'adressage absolu, comme vu dans le chapitre sur les modes d'adressage.

Une autre solution est celle de l'instruction Index next instruction, que nous appellerons INI, qui a été utilisée sur des architectures comme l'Apollo Guidance Computer et quelques autres. Elle INI additionne une certaine valeur à l'instruction suivante. Par exemple, si l’instruction suivante est une instruction LOAD adresse 50, l'INI permet d'y ajouter la valeur 5, ce qui donne LOAD adresse 55. L'idée est d'émuler un adressage par indice : on utilise l'INI pour ajouter l'indice à l'instruction LOAD suivante. La valeur à ajouter est précisée via mode d'adressage absolu est lue depuis la mémoire. Un point important est que l'addition a lieu à l'intérieur du processeur, pas en mémoire RAM/ROM. Le mode d'adressage ne fait pas de code auto-modifiant, l'instruction modifiée reste la même qu'avant en mémoire RAM. Elle est altérée une fois chargée par le processeur, avant son exécution.
- Notons que cette instruction est aussi utilisée pour modifier des branchements : si l'instruction suivante est l'instruction JUMP à adresse 100, on peut la transformer en JUMP à adresse 150. Elle peut en théorie changer l'opcode d'une instruction, ce qui permet en théorie de faire des calculs différents suivant le résultat d'une condition. Mais ces cas d'utilisation étaient assez rares, ils étaient peu fréquents.
Les instructions d'accès mémoire LOAD et STORE
modifierUn point important est que toutes les architectures précédentes disposent d'instructions d'accès mémoire. Par contre, elles varient entre les 5 catégories précédentes.
Par exemple, la présence d'instruction LOAD et STORE n'est possible que sur les architectures disposant de registres, à savoir les architectures à accumulateur, à registre et LOAD-STORE. les autres architectures ont bien des instructions d'accès mémoire, mais pas d'instruction LOAD ni d'instruction STORE. Elles se contentent de quelques instructions mémoire, dont une instruction MOV pour copier une adresse dans une autre, une instruction XCHG pour échange le contenu de deux adresses, etc.
Les instructions LOAD et STORE existent bel et bien sur les architectures à accumulateur, mais n'ont pas les mêmes modes d'adressages. L'instruction LOAD copie une donnée de la RAM vers l'accumulateur, l'instruction STORE copie l'accumulateur dans une adresse. Les deux instructions n'ont pas besoin d'adresser l'accumulateur, qui est adressé de manière implicite, mais doivent préciser l'adresse dans laquelle écrire/lire.
Il faut aussi noter que les architectures LOAD-STORE sont les seules à avoir une stricte séparation entre instructions d'accès mémoire et instructions de calcul. Sur les autres architectures, la plupart des instructions peuvent aller chercher leurs opérandes en RAM, et effectuent dont des accès mémoire. Elles peuvent même en faire plusieurs si plusieurs opérandes sont en mémoire, encore que ce ne soit pas possible sur tous les jeux d'instructions. Mais avec les architectures LOAD-STORE, les accès mémoire sont circonscrits aux instructions d'accès mémoire, les instructions de calcul/branchement n’effectuent pas le moindre accès mémoire.
| Classe d'architecture | LOAD et STORE | Séparation des instructions d'accès mémoire et de calcul |
|---|---|---|
| Architecture à pile | Non | Non |
| Architecture mémoire-mémoire | ||
| Architecture à accumulateur | Oui, accumulateur adressé implicitement | |
| Architecture à registres | Oui, registres adressés explicitement | |
| Architecture LOAD-STORE | Oui |
Si on analyse le nombre d'accès mémoire par instruction de calcul, on peut déceler d'autres différences entre les 5 architectures précédentes. La pire de ce point de vue est celui des architectures sans registres, où toutes les instructions lisent leurs opérandes en mémoire, et écrivent les résultats en mémoire RAM. C'est le cas sur les architectures mémoire-mémoire, mais aussi sur les architectures à pile ! Les architectures à accumulateur sont intermédiaires : la présence de l'accumulateur fait qu'on n'a qu'un seul accès mémoire par instruction dyadique, dans le meilleur des cas. Les architectures à registre réduisent encore le nombre d'accès mémoire par instruction, allant de zéro si tous les opérandes sont dans des registres, à un peu plus si un opérande est à lire dans la RAM. Les architectures LOAD-STORE ganratissent qu'il n'y a au maximum pas d'accès mémoire par instruction.
| Classe d'architecture | Nombre d'accès mémoire minimum par opération dyadique | Nombre d'accès mémoire dans le pire des cas |
|---|---|---|
| Architecture à pile | Trois accès mémoire par opération : un par opérande, un pour le résultat | |
| Architecture mémoire-mémoire | ||
| Architecture à accumulateur | Un accès mémoire par instruction, pour lire la seconde opérande | Variable, dépend du jeu d'instruction et des modes d'adressages supportés |
| Architecture à registres | Zéro si les opérandes sont dans les registres | |
| Architecture LOAD-STORE | Zéro : les opérandes sont dans les registres | |
La densité de code
modifierAu début de l'informatique, la mémoire avait des performances similaires à celles du processeur, mais elle était de petite taille. Les programmes gagnaient à être de petite taille. Aussi, les architectures se distinguaient sur autre chose : la densité de code. La densité de code n'est ni plus ni moins que la taille des programmes. Les mémoires de l'époque étaient assez petites, aussi il était avantageux d'avoir des programmes assez petits. La taille d'un programme dépend de deux choses : le nombre d'instructions, et la taille de celles-ci. Et ces deux paramètres sont influencés par l'architecture. La taille des instructions est surtout influencée par les modes d'adressage disponibles.
Les architectures 0, 1, 2 et 3 références
modifierPour ce qui est de comparer la densité de code des cinq architectures canoniques, il est intéressant de parler de la distinction entre architectures 0, 1, 2 et 3 adresses. Elle est lié aux opérations arithmétiques dites dyadiques, à savoir qui ont deux opérandes. Les plus communes sont les additions, multiplications, soustraction, division, etc. Les instructions de test sont aussi dans ce cas, pour la plupart.
Elles ont besoin de préciser trois choses : la localisation des deux opérandes, et l'endroit où ranger le résultat. Opérandes et résultat peuvent être adressés soit explicitement, soit implicitement. Par implicitement, on veut dire avec le mode d'adressage implicite, alors que explicite signifie qu'on doit préciser un numéro/nom de registre, une adresse mémoire, ou toute autre référence pour localiser l'opérande/résultat. Et le nombre de référence par instruction dyadique varie grandement suivant l'architecture utilisée.
Notons que ce qui nous intéresse ici est le cas des instructions dyadiques uniquement. La raison est que les autres instructions ont un encodage similaire. Par exemple, toutes les instructions d'accès mémoire utilisent généralement l'adressage absolu sur les 5 architectures canoniques, ce qui demande juste une adresse mémoire et un opcode. Les instructions d'accès mémoire PUSH et POP sont dans ce cas, pareil pour les instructions LOAD et STORE des des architectures LOAD-STORE, ou pour les instructions pour copier une donnée dans l'accumulateur ou inversement pour copier l'accumulateur dans une adresse. L'encodage des branchements est lui aussi globalement le même d'une architecture à l'autre.
Les architectures à zéro référence sont les architectures à pile. Elles n'ont pas besoin de préciser la localisation de leurs opérandes, qui sont au sommet de la pile et sont adressées implicitement, sauf pour Pop et Push Et sachez que cela vaut aussi pour les architectures à pile où il est possible de préciser l'adresse mémoire d'un opérande. De telles architectures supportent des instructions où tous les opérandes sont lus depuis la pile, et d'autres avec un opérande adressé explicitement et l'autre implicitement. Mais ce sont des instructions annexes, la majorité des instructions adressant tous les opérandes implicitement.
Les architectures à une référence correspondent aux architectures à accumulateur. Les instructions dyadiques lisent un opérande depuis la mémoire, la seconde est lue depuis l'accumulateur. Seule la première est adressée explicitement, alors que l'accumulateur est adressé implicitement. Le résultat de l'opération est enregistré dans l'accumulateur, là aussi avec un adressage implicite.
Les architectures à deux et trois références regroupent toutes les autres architecture.
Les architectures à deux références adressent les opérandes explicitement, mais le résultat est adressé implicitement. Pour ce faire, le résultat d'une instruction est stocké à l'endroit indiqué par la référence du premier opérande : l'opérande sera remplacé par le résultat de l'instruction. Avec cette organisation, les instructions ne précisent que deux opérandes, pas le résultat. Mais la gestion des instructions est moins souple, vu qu'un opérande est écrasé.
Les architectures à trois références permettent de préciser le registre de destination du résultat explicitement. Ce genre d'architectures permet une meilleure utilisation des registres, mais les instructions deviennent plus longues que sur les architectures à deux références.
La taille des instructions
modifierL'intérêt de cette distinction est une question de taille des instructions. La raison est assez intuitive : il faut encoder de quoi localiser un opérande adressé explicitement, à savoir encoder une référence. Plus elles sont nombreuses à être adressées explicitement, plus il faudra ajouter de bits à une instruction pour ça, plus les instructions sont longues. Mais il faut aussi tenir compte de la taille des références. Un numéro/nom de registre est bien plus court qu'une adresse, par exemple. Aussi, le nombre d'opérandes à adresser ne fait pas tout : il faut aussi tenir compte du mode d'adressage. Voyons ce qu'il en est pour chaque type d'architecture.
Avant toute chose, précisons que nous allons mettre de côté les instructions d'accès mémoire. La raison est qu'elles ont toutes des encodages et des tailles similaires, peu importe l'architecture. Elles se font presque toutes en adressage absolu, ce qui fait qu'elles encodent au minimum une adresse. Elles peuvent aussi préciser un registre sur les architectures à registre ou LOAD-STORE, mais cela ne change pas grand chose, leur taille est relativement similaire. Nous allons nous concentrer sur la taille des instructions dyadiques, qui sont généralement des instructions de calcul arithmétique ou logique.
Les architectures à zéro référence ont les instructions dyadiques les plus courtes, car elles adressent toutes leurs opérandes implicitement. Elles sont aussi appelées architectures à zéro adresse par abus de langage. Les instructions se limitent généralement à un opcode, du moins pour les instructions de calcul et les branchements.
Les architectures à une référence utilisent une adresse mémoire pour adresser l'opérande en RAM. Elles sont aussi appelées architectures à une adresse par abus de langage. Les instructions dyadiques utilisent donc un opcode couplé à une adresse mémoire. L'adresse mémoire est généralement assez longue, plus que l'opcode.
Les autres architectures sont toutes à deux ou trois références. Par contre, la nature de ces références change d'une architecture à l'autre.
- Sur les architectures LOAD-STORE, les instructions dyadiques utilisent des numéros de registres, mais aucune adresse. Aussi, encoder les 2/3 registres adressés prend autant, voire moins de place qu'une adresse. Elles ont donc les instructions les plus courtes des trois, leur instructions sont globalement de même taille que sur les architectures à accumulateur, voire un peu moins.
- Les architectures mémoire-mémoire encodent deux/trois adresses mémoires en plus de l'opcode. Elles ont les instructions les plus longues des trois.
- Les architectures à registre sont intermédiaires entre les deux cas précédents. Leurs instructions ont la même taille que sur une architecture LOAD-STORE dans le meilleur des cas, si opérandes et résultat vont dans les registres. Pour les instructions load-op, leur taille est légérement supérieure à celle d'une architecture à accumulateur, vu qu'elles encodent une adresse et un registre. Les architectures devant encoder deux ou trois adresses sont très rares.
Si on fait le résumé, le classement en termes de longueur d'instruction est le suivant, en partant des instructions les plus courtes vers les plus longues.
- Architectures à pile ;
- Architectures LOAD-STORE ;
- Architectures à registres ;
- Architectures à accumulateur ;
- Architectures mémoire-mémoire.
Le nombre d'instructions d'un programme
modifierLes développements précédents nous parlent de la taille des instructions, mais il faut aussi tenir compte du nombre d'instructions. La taille d'un programme est en effet égale à la taille moyenne d'une instruction multipliée par le nombre d'instructions de ce programme. Et ce nombre est fortement influencé par l'architecture du processeur. Les architectures à pile et mémoire-mémoire ne sont pas égales sur ce point, pareil pour les différents types d'architectures à registre.
La raison est que tout ce que nous avons dit plus haut ne vaut que pour les instructions dyadiques. Les instructions d'accès mémoire ou les branchements ont des encodages similaires sur toutes ces architectures, elles ont la même taille sur les 5 architectures canoniques. Mais il faut savoir que les 5 architectures canoniques ne sont pas égales niveau accès mémoire. Pour faire la même chose, le nombre d'instructions mémoire ne sera pas le même sur les 5 architectures canoniques. Et le nombre d'instructions mémoire peut compenser l'effet de la taille des instructions dyadiques. Si on a des instructions dyadiques très courtes, cela peut être compensé par des un plus grand nombre d'instructions d'accès mémoire. L'étude de la densité de code demande donc de regarder comment se manifeste ce compromis pour les 5 architectures canoniques.
Les machines à pile ont un nombre d'instructions par programme est pourtant plus élevé que sur les autres architectures, en grande aprtie à cause des instructions mémoire. Une bonne partie des instructions sont des instructions Pop et Push. De plus, les programmes utilisent souvent des instructions pour dupliquer/copier des données dans la pile, chose qui n'est pas nécessaire sur les autres architectures. La situation est légèrement améliorée sur les architectures à pile supportent des instructions qui permettent de préciser l'adresse d'un opérande, voire des deux. Mais pas de quoi sensiblement changer la donne.
Les architectures à registre ont en théorie un désavantage en termes de nombre d'instructions, lié à la gestion des procédures. Elles ont besoin de sauvegarder les registres lors d'un appel de fonction, et de les restaurer quand la fonction termine. Cela implique des échanges avec la mémoire réalisée avec des instructions LOAD-STORE. Plus les fonctions sont fréquentes et petites, plus le désavantage est important. Le nombre d'instruction augmente donc assez rapidement, mais reste en-deça de celui des architectures à pile.
Les architectures LOAD-STORE sont identiques aux architectures à registres, avec cependant un léger désavantage en plus. Pour l'illustrer, prenons un exemple où on veut faire un calcul entre un opérande un registre, un opérande en RAM, et stocker le résultat dans un registre. Comparons une architecture à registre et une architecture LOAD-STORE. Avec une architecture LOAD-STORE, l'opérande en RAM doit être copiée dans un registre avec une instruction LOAD, avant de faire des calculs dessus avec une instruction de calcul. Avec une architecture à registre, on n'a besoin que d'une seule instruction. L'instruction est plus longue, mais elle en remplace deux. Plus la situation est fréquente, plus l'avantage est pour l'architecture à registre.
Les architectures mémoire-mémoire sont celles qui ont le moins d'instructions par programme. Comme les architectures à accumulateur, elles se passent d'un paquet d'opérations nécessaires sur les autres machines. Pas besoin de sauvegarder/restaurer les registres lors d'un appel de fonction, la gestion de la pile d'appel est simplifiée. Les architectures à accumulateur sont proches des architectures mémoire-mémoire pour les mêmes raisons, avec cependant un léger désavantage : elles doivent sauvegarder l'accumulateur lors des appels de fonction, et le restaurer après. Mais le désavantage est vraiment mineur.
Pour résumer :
- Les architectures mémoire-mémoire utilisent moins d'instructions par programme que les autres, elles se contentent du strict minimum.
- Les architectures à pile utilisent en plus des instructions PUSH et POP, ainsi que d'autres instructions pour manipuler la pile.
- Les architectures à registre ajoutent des instructions de sauvegarde/restauration des registres lors d'un appel de fonction, idem pour les architectures LOAD-STORE.
- Les architectures LOAD-STORE utilisent en plus des instructions LOAD-STORE pour copier les opérandes dans les registres et écrire les résultats en RAM, mais seulement si besoin.
| Instructions d'accès mémoire hors opérandes | Instructions pour gérer les opérandes/résultats | |
|---|---|---|
| Architecture mémoire-mémoire | ||
| Architecture à pile | Instructions PUSH et POP, ainsi que d'autres instructions pour manipuler la pile. | |
| Architecture à registres | Instructions de sauvegarde/restauration des registres lors d'un appel de fonction | |
| Architecture LOAD-STORE | Instructions LOAD-STORE pour lire les opérandes et enregistrer les résultats. | |
| Architecture à accumulateur | Rares copies de l'accumulateur en mémoire RAM. |
La conclusion : la densité de code finale
modifierSi on compare les 5 types d'architectures précédentes, on s’aperçoit que c'est surtout la taille des instructions qui compte en premier lieu, suivi par le nombre d'instruction, et enfin par le caractère 0/1/2/3 opérandes. Les machines à pile ont la meilleure densité de code, suivies par les architectures à registre, puis par les architectures LOAD-STORE, puis par les architectures à accumulateur, et enfin par les architectures mémoire-mémoire.
Les architectures à pile ont des programmes avec plus d'instructions, mais cela est plus que compensé par le fait que ce sont des architectures à zéro adresse, où les instructions sont très petites. Les architectures à registre ont une bonne densité de code, bien qu'inférieure à celle des architectures à pile, du fait que de la petite taille de leurs instructions dépasse l'effet des instructions liées aux appels de fonction. Les architectures LOAD-STORE viennent en troisième position, car leurs instructions sont aussi longues que celles à registres, mais qu'elles ont le désavantage des instructions LOAD-STORE. Enfin, les architectures sans registres viennent en dernier du fait de leur encodage désastreux, qui encodent des adresses mémoires. Les architectures à accumulateur sont en quatrième position, car ce sont des architectures 1-adresse, là où les architectures mémoire-mémoire sont de type 2/3 adresses.
Les jeux d'instruction RISC vs CISC
modifierLa seconde classification que nous allons aborder se base sur le nombre d'instructions. Elle classe nos processeurs en deux catégories :
- les RISC (reduced instruction set computer), au jeu d'instruction simple ;
- et les CISC (complex instruction set computer), qui ont un jeu d'instruction étoffé.
Reste à expliquer ce que l'on veut dire quand on parler de jeu d'instruction "simple" ou "complexe".
Les différences entre CISC et RISC
modifierLa différence la plus intuitive est le nombre d'instructions supporté. Les processeurs CISC supportent beaucoup d'instructions, dont certaines assez complexes, alors que les processeurs RISC se contentent d'un petit nombre d'instructions de base assez simples. Les processeurs CISC incorporent souvent des instructions complexes, capables de remplacer des suites d'instructions simples. Par exemple, on peut implémenter des instructions pour le calcul de la division, de la racine carrée, de l'exponentielle, des puissances, des fonctions trigonométriques : cela évite d'avoir à simuler ces calculs à partir d'additions ou de multiplications. Plus fréquent, on trouvait des instructions de contrôle élaborées pour gérer les appels de fonction, simplifier l'implémentation des boucles, etc. Par contre, il n'est pas garanti que les instructions ajoutées sont plus rapides que leur équivalent logiciel, ce qui n'est pas gagné. L'avantage est surtout que le programme prend moins d'instructions pour faire la même chose, ce qui augmente la densité de code.
Une autre différence très liée à la précédente est une différence au niveau des modes d'adressages. Les processeurs CISC supportent plus de modes d'adressage que les processeurs RISC, mais ce n'est pas la différence principale. Les processeurs CISC sont techniquement des architectures à registres, alors que les processeurs RISC sont des architectures LOAD-STORE. Les processeurs CISC supportent au minimum les instructions load-op, où une opérande est lue en mémoire RAM/ROM. Plus rarement, les instructions des CPU CISC peuvent ainsi effectuer plusieurs accès mémoire par instruction, si plusieurs opérandes sont à lire en mémoire RAM.
La conséquence est la disponibilité des modes d'adressage. Sur les processeurs RISC, les instructions de calcul n'utilisent que le mode d'adressage inhérent (à registre), ce sont les instructions LOAD et STORE qui ont droit à des modes d'adressages plus ou moins élaborés (par adresse, base+index, autres). Mais sur les processeurs CISC, les modes d'adressage élaborés sont disponibles pour les instructions load-op et autres, pas seulement les instructions mémoire.
Les deux propriétés précédentes, à savoir un grand nombre d'instruction et des modes d'adressages complexes, se marient bien avec des instructions de longueur variable. Les instructions d'un processeur CISC sont de taille variable pour diverses raisons, mais la variété des modes d'adressage y est pour beaucoup. Quand une même instruction peut incorporer soit deux noms de registres, soit deux adresses, soit un nom de registre et une adresse, sa taille ne sera pas la même dans les trois cas. Les processeurs RISC ne sont pas concernés par ce problème. Les instructions de calcul n'utilisent que deux-trois modes d'adressages simples, qui demandent d'encoder des registres ou des constantes immédiates de petite taille. Les autres instructions se débrouillent avec des adresses et éventuellement un nom de registre. Le tout peut être encodé sur 32 ou 64 bits sans problèmes.
| Propriété | CISC | RISC |
|---|---|---|
| Instructions |
|
|
| Modes d'adressage |
|
|
| Registres |
|
|
Les contraintes d'implémentation sont différentes
modifierLes processeurs CISC sont naturellement plus complexes que les processeurs RISC, et cela a un impact sur leur conception. Le grand nombre d'instructions fait qu'on doit câbler beaucoup de circuit pour gérer toutes ces instructions. Non pas qu'il faille forcément beaucoup de circuits de calcul, les CISC ne gère pas tant que d'opérations complexes. Par contre, le support des nombreux modes d'adressage, des instructions de taille variable, et le grand nombre de variantes de la même opération font que les circuits de contrôle du processeur sont plus complexes, utilisent beaucoup de transistors et d'énergie. Et les transistors utilisés pour ces instructions ne sont pas disponibles pour autre chose, comme de la mémoire cache. La difficulté de conception de ces processeurs était aussi sans précédent.
Les processeurs RISC sont eux plus économes, ils ont moins d'instructions, donc moins de circuits de contrôle, et peuvent utiliser plus de transistors pour autre chose. Le autre chose est généralement du cache, mais aussi des registres. Les processeurs RISC peuvent se permettre d'utiliser beaucoup de registres, ils ont le budget en transistor pour, sans compter que la simplicité des circuits de contrôle et des connexions intra-processeur (le bus interne au CPU qu'on verra dans quelques chapitres) rendent la chose plus aisée.
Si les registres sont plus nombreux sur les architectures RISC, ce n'est pas qu'une question de budget en transistors. Une autre raison est que les architectures LOAD-STORE ont besoin de plus de registres pour faire le même travail que les architectures à registres. En effet, les processeurs CISC supportent des modes d'adressage qui permettent de lire une opérande directement depuis la mémoire, sans passer par un registre. Sur une architecture RISC LOAD-STORE, une instruction de ce genre est émulée avec une instruction LOAD et une instruction de calcul, ce qui fait que la donnée lue depuis la mémoire passe explicitement par un registre. La register pressure est donc légèrement plus importante, ce qui est compensée en ajoutant des registres.
Un petit historique de la distinction entre processeurs CISC et RISC
modifierLes jeux d'instructions CISC sont les plus anciens et étaient à la mode jusqu'à la fin des années 1980. À cette époque, on programmait rarement avec des langages de haut niveau et beaucoup de programmeurs codaient en assembleur. Avoir un jeu d'instruction complexe, avec des instructions de "haut niveau" facilitait la vie des programmeurs. Et outre ces avantages "humains", les architectures CISC avaient une meilleure densité de code, car un programme codé sur CISC utilise moins d'instructions, sans compter que celles-ci sont de longueur variable. À l'époque, la mémoire était rare et chère, l'économiser était crucial, la densité de code des CISC était parfaitement adaptée.
Mais par la suite, la mémoire est devenue moins chère et sa capacité a augmenté. De plus, les langages de haut niveau sont devenus plus fréquents au cours des années 70-80. Le contexte technologique ayant changé, les avantages des processeurs CISC étaient à réévaluer. Est-ce que les instructions complexes des processeurs CISC sont vraiment utiles ? Pour le programmeur qui écrit ses programmes en assembleur, elles le sont. Mais depuis l'invention des langages de haut niveau, la réponse dépend de l'efficacité des compilateurs. Des analyses assez anciennes, effectuées par IBM, DEC et quelques laboratoires de recherche, ont montré que les compilateurs n'utilisaient pas la totalité des instructions fournies par un processeur. Les analyses plus récentes fournissent la même conclusion : les compilateurs ou programmeurs n'utilisent pas souvent les instructions complexes, même quand elles peuvent être utiles. Autant dire que beaucoup de transistors étaient gâchés !
L'idée de créer des processeurs RISC commença à germer. Ils n'ont pas les défauts des CISC, mais n'en ont pas les avantages : la densité de code est mauvaise, en contrepartie d'un processeur plus simple à concevoir. Ils étaient plus adaptés au contexte technologique moderne. Avec des programmes provenant de compilateurs, avoir un petit nombre d'instructions aux modes d'adressages simples est plus que largement suffisant. Et ne pas implémenter beaucoup d'instructions permet de dégager un budget en transistor conséquent, qui sert à ajouter des registres ou du cache, améliorant ainsi les performances. La faible densité de code n'est pas un problème, vu que les mémoires ont une capacité suffisante, encore que ce soit à nuancer.
Mais de tels processeurs RISC, complètement opposés aux processeurs CISC, durent attendre un peu avant de percer. Par exemple, IBM décida de créer un processeur possédant un jeu d'instruction plus sobre, l'IBM 801, qui fût un véritable échec commercial. Mais la relève ne se fit pas attendre. C'est dans les années 1980 que les processeurs possédant un jeu d'instruction simple devinrent à la mode. Cette année-là, un scientifique de l'université de Berkeley décida de créer un processeur possédant un jeu d'instruction contenant seulement un nombre réduit d'instructions simples, possédant une architecture particulière. Ce processeur était assez novateur et incorporait de nombreuses améliorations qu'on retrouve encore dans nos processeurs haute performances actuels, ce qui fit son succès : les processeurs RISC étaient nés.
Durant longtemps, les CISC et les RISC eurent chacun leurs admirateurs et leurs détracteurs. Mais de nos jours, on ne peut pas dire qu'un processeur CISC sera toujours meilleur qu'un RISC ou l'inverse. Chacun a des avantages et des inconvénients, qui rendent le RISC/CISC adapté ou pas selon la situation. Par exemple, on mettra souvent un processeur RISC dans un système embarqué, devant consommer très peu.
En tout cas, la performance d'un processeur dépend assez peu du fait que le processeur soit un RISC ou un CISC, même si cela peut faire la différence en termes de simplicité de conception. Les processeurs modernes disposent de tellement de transistors qu'implémenter des instructions complexes est négligeable. Pour donner une référence, près de 50% du budget en transistor des processeurs modernes part dans le cache. Et il est estimé que le support des instructions complexes sur les processeurs x86 ne prend que 2 à 3% des transistors de la puce, ce qui est négligeable.
De plus, de nos jours, les différences entre CISC et RISC commencent à s'estomper. Les processeurs actuels sont de plus en plus difficiles à ranger dans des catégories précises. Les processeurs actuels sont conçus d'une façon plus pragmatique : au lieu de respecter à la lettre les principes du RISC et du CISC, on préfère intégrer les instructions qui fonctionnent, peu importe qu'elles viennent de processeurs purement RISC ou CISC. Les anciens processeurs RISC se sont ainsi garnis d'instructions et de modes d'adressage de plus en plus complexes et les processeurs CISC ont intégré des techniques provenant des processeurs RISC (pipeline, etc). La guerre RISC ou CISC n'a plus vraiment de sens de nos jours.
En parallèle de ces architectures CISC et RISC, qui sont en quelque sorte la base de tous les jeux d'instructions, d'autres classes de jeux d'instructions sont apparus, assez différents des jeux d’instructions RISC et CISC. On peut par exemple citer le Very Long Instruction Word, qui sera abordé dans les chapitres à la fin du tutoriel. La plupart de ces jeux d'instructions sont implantés dans des processeurs spécialisés, qu'on fabrique pour une utilisation particulière. Ce peut être pour un langage de programmation particulier, pour des applications destinées à un marché de niche comme les supercalculateurs, etc.
Les jeux d'instructions spécialisés
modifierEn parallèle de ces architectures CISC et RISC, d'autres classes de jeux d'instructions sont apparus. Ceux-ci visent des buts distincts, qui changent suivant le jeu d'instruction :
- soit ils cherchent à diminuer la taille des programmes et à économiser de la mémoire ;
- soit ils cherchent à gagner en performance, en exécutant plusieurs instructions à la fois ;
- soit ils tentent d'améliorer la sécurité des programmes et les rendent résistants aux attaques ;
- soit ils sont adaptés à certaines catégories de programmes ou de langages de programmation.
Les architectures compactes
modifierCertains chercheurs ont inventé des jeux d’instruction pour diminuer la taille des programmes. Certains processeurs disposent de deux jeux d'instructions : un compact, et un avec une faible densité de code. Il est possible de passer d'un jeu d'instructions à l'autre en plein milieu de l’exécution du programme, via une instruction spécialisée.
D'autres processeurs sont capables d’exécuter des binaires compressés (la décompression a lieu lors du chargement des instructions dans le cache).
Les architectures parallèles
modifierCertaines architectures sont conçues pour pouvoir exécuter plusieurs instructions en même temps, lors du même cycle d’horloge : elles visent le traitement de plusieurs instructions en parallèle, d'où leur nom d’architectures parallèles. Ces architectures visent la performance, et sont relativement généralistes, à quelques exceptions près. On peut, par exemple, citer les architectures very long instruction word, les architectures dataflow, les processeurs EDGE, et bien d'autres. D'autres instructions visent à exécuter une même instruction sur plusieurs données différentes : ce sont les instructions SIMD, vectorielles, et autres architectures utilisées sur les cartes graphiques actuelles. Nous verrons ces architectures plus tard dans ce tutoriel, dans les derniers chapitres.
Les Digital Signal Processors
modifierCertains jeux d'instructions sont dédiés à des types de programmes bien spécifiques, et sont peu adaptés pour des programmes généralistes. Parmi ces jeux d'instructions spécialisés, on peut citer les fameux jeux d'instructions Digital Signal Processor, aussi appelés des DSP. Nous reviendrons plus tard sur ces processeurs dans le cours, un chapitre complet leur étant dédié, ce qui fait que la description qui va suivre sera quelque peu succincte. Ces DSP sont des processeurs chargés de faire des calculs sur de la vidéo, du son, ou tout autre signal. Dès que vous avez besoin de traiter du son ou de la vidéo, vous avez un DSP quelque part, que ce soit une carte son ou une platine DVD.
Ls DSP ont un jeu d'instruction similaire aux jeux d'instructions RISC, avec quelques instructions supplémentaires spécialisées pour faire du traitement de signal. On peut par exemple citer l'instruction phare de ces DSP, l'instruction MAD, qui multiplie deux nombres et additionne un 3éme au résultat de la multiplication. De nombreux algorithmes de traitement du signal (filtres FIR, transformées de Fourier) utilisent massivement cette opération. Ces DSP possèdent aussi des instructions dédiées aux boucles, ou des instructions capables de traiter plusieurs données en parallèle (en même temps). De plus, les DSP utilisent souvent des nombres flottants assez particuliers qui n'ont rien à voir avec les nombres flottants que l'on a vu dans le premier chapitre. Certains DSP supportent des instructions capables d'effectuer plusieurs accès mémoire en un seul cycle d'horloge : ils sont reliés à plusieurs bus mémoire et sont donc capables de lire et/ou d'écrire plusieurs données simultanément. L'architecture mémoire de ces DSP est une architecture Harvard, couplée à une mémoire multi-ports. Les caches sont rares dans ces architectures, quoique parfois présents.
Les architectures dédiées à un langage de programmation
modifierCertains processeurs sont carrément conçus pour un langage de programmation en particulier. On appelle ces processeurs, conçus pour des besoins particuliers, des processeurs dédiés. Par exemple, l'ALGOL-60, le COBOL et le FORTRAN ont eu leurs architectures dédiées. Les fameux Burrough E-mode B5000/B6000/B7000 étaient spécialement conçus pour exécuter de l'ALGOL-60. Leurs cousins B2000/B3000/B4000 étaient eux conçus pour le COBOL. Le FORTH, un des premiers langages à pile de haut niveau, possède de nombreuses implémentations hardware et est un des rares langages de haut niveau à avoir été directement câblé en assembleur sur certains processeurs. Par exemple, on peut citer le processeur FC16, capable d’exécuter nativement du FORTH.
Des langages fonctionnels ont aussi eu droit à leurs processeurs dédiés. Le prolog en est un bel exemple, avec les superordinateurs de 5ème génération qui lui étaient dédié. On peut aussi citer les machines LISP, dédiés au langage LISP, qui datent des années 1970. Elles étaient capables d’exécuter certaines fonctions de base du langage directement dans leur circuits : elles possédaient notamment un garbage collector câblé dans ses circuits ainsi que des instructions machines supportant un typage déterminé à l’exécution.
Les processeurs dédiés ont eu leur heure de gloire au début de l'informatique, à une époque où les langages de haut niveau venaient d'être inventés. À cette époque, les compilateurs n'étaient pas performants et ne savaient pas bien optimiser le code machine. Les programmes compilés faisaient un mauvais usage des instructions machines, ne savaient pas bien utiliser les modes d'adressages adéquats, manipulaient assez mal les registres, etc. Il était alors rationnel, pour l'époque, de rapprocher le code machine cible et le langage de programmation de haut niveau. De nombreuses architectures dédiés ont ainsi étés inventées, avant que les concepteurs se rendent compte des défauts de cette approche. À l'heure actuelle, les algorithmes des compilateurs se sont améliorés et savent nettement mieux utiliser le matériel. Ils produisent du code machine efficace, ce qui rend les architecture dédiées bien moins intéressantes. Si on ajoute les défauts de ces architectures dédiées, par étonnant que les architectures dédiées aient presque disparues.
Les défauts en question ne sont pas nombreux, mais assez simples à comprendre. Premièrement, elles sont très rapides pour un langage de programmation en particulier, mais sont assez mauvaises pour les autres, d'où un problème de "compatibilité". Ajoutons à cela que les langages de programmation peuvent évoluer, devenir de moins en moins populaires/utilisés, ce qui rend la création d'architectures généralistes plus pertinente. Enfin, les architectures dédiées sont évidemment des processeurs CISC, pour implémenter les nombreuses fonctionnalités des langages évolués. Et les défauts des CISC sont assez rédhibitoires à l'heure actuelle.
Les implémentations matérielles de machines virtuelles
modifier
Comme vous le savez sûrement, les langages de programmation de haut niveau sont traduits en langage machine. La traduction d'un programme en un fichier exécutable est donc un processus en deux étapes : la compilation traduit le code source en langage assembleur (une représentation textuelle du langage machine), puis l'assembleur est assemblé en langage machine. Les deux étapes sont réalisées respectivement par un compilateur et un assembleur. Le compilateur ne fait pas forcément la traduction directement, la plupart des compilateurs modernes passent par un langage intermédiaire, avant d'être transformés en langage machine.
Faire ainsi a de nombreux avantages pour les concepteurs de compilateurs. Notamment, cela permet d'avoir un compilateur qui traduit le langage de haut niveau pour plusieurs jeux d’instructions différents. Par exemple, on peut plus facilement créer un compilateur qui traduit du C soit en code machine x86, soit en code machine pour un CPU ARM, soit pour un CPU POWERPC, etc. Pour cela, le compilateur est composé de deux parties : une partie commune qui traduit le C en langage intermédiaire, et plusieurs back-end qui traduisent le langage intermédiaire en code machine cible.
Le langage intermédiaire qui sert...d'intermédiaire, peut être vu comme l'assembleur d'une machine abstraite, que l'on appelle une machine virtuelle, qui n'existe pas forcément dans la réalité. Le langage intermédiaire est conçu de manière à ce que la traduction en code machine soit la plus simple possible. Et surtout, il est conçu pour pouvoir être transformé en plusieurs langages machines différents sans trop de problèmes. Par exemple, il dispose d'un nombre illimité de registres. Lors de la transformation en code machine, un algorithme d'allocation de registres se débrouille pour traduire le code intermédiaire en code qui utilise des registres ou des adresses, en insérant des instructions d'accès mémoire. Et cela permet de gérer des architectures très différentes qui n'ont pas les mêmes nombres de registres.

Mais si la majorité des langages de haut niveau sont compilés, il en existe qui sont interprétés, c'est à dire que le code source n'est pas traduit directement, mais transformé en code machine à la volée. Là encore, on trouve un langage intermédiaire appelé le bytecode . Le procédé d'interprétation est le suivant. Premièrement, le langage de haut niveau est traduit en bytecode, via un processus de pré-compilation. Puis, le bytecode est passé à un logiciel appelé l'interpréteur, qui lit une instruction à la fois dans le bytecode. L’interpréteur exécute alors une instruction équivalente sur le processeur. Si l'instruction est un peu complexe, il exécute une fonction/procédure qui fait la même chose. Pour résumer, le bytecode est ensuite traduit à la volée et exécuté instruction par instruction par un logiciel appelé l'interpréteur.

L'avantage est celui de la portabilité, à savoir qu'un même code peut tourner sur plusieurs machines différentes. Le code machine est spécifique à un jeu d’instruction, la compatibilité est donc limitée. C'est très utilisé par certains langages de programmation comme le Python ou le Java, afin d'obtenir une bonne compatibilité : on compile le Python/Java en bytecode, qui lui-même est interprété à l’exécution. Tout ordinateur sur lequel on a installé une machine virtuelle Java/Python peut alors exécuter ce bytecode.
Le bytecode est un code machine, ce qui signifie qu'il peut en théorie s'exécuter sur un processeur qui implémente le jeu d’instruction associé. Le processeur en question n'existe pas forcément, mais il est possible de décrire son jeu d'instruction en détail. Lesbytecode assez anciens sont conçus pour une machine à pile, pour diverses raisons. Premièrement, cela réduit la taille du bytecode. Deuxièmement, il existe un algorithme simple et rapide pour traduire un code écrit pour une machine à pile en un code écrit pour une machine à registre. Il fonctionne peu importe le nombre de registres, et se débrouille pas trop mal pour allouer efficacement les registres. C'est un avantage assez important pour les langages interprétés.
Si le jeu d'instruction d'un bytecode est souvent une description censée être fictive, elle n'en reste pas moins un jeu d'instruction et des caractéristiques précises. Et on peut l'implémenter en matériel ! Un premier exemple est celui des Pascal MicroEngine, des processeurs qui exécutaient directement le bytecode du langage Pascal, le fameux UCSD P-code. Un second exemple est la machine SECD, qui sert de langage intermédiaires pour certains compilateurs de langages fonctionnels. Elle a été implémentée en matériel par plusieurs équipes. La première implémentation a été créée par les chercheurs de l'université de Calgary, en 1989. Dans le même genre, quelques processeurs simples étaient capables d’exécuter directement le bytecode utilisé comme représentation intermédiaire pour le langage FORTH.
Mais le cas le plus impressionnant est celui de la machine virtuelle Java, qui est un design de processeur comme un autre, avec un jeu d'instruction simple, une architecture à pile, etc. En temps normal, le bytecode Java n'est pas exécuté directement par le processeur, mais est compilé ou interprété. Et c'est ce qui permet au bytecode Java d'être portable sur des architectures différentes. Mais certains processeurs ARM, qu'on trouve dans des système embarqués, sont une implémentation matérielle de la machine virtuelle Java. Les architectures de ce type permettent de se passer de l'étape de traduction bytecode -> langage machine, vu que leur langage machine est le bytecode Java lui-même.
L'intérêt de ce genre de stratagèmes reste cependant mince. Cela permet d’exécuter plus vite les programmes compilés en bytecode, comme des programmes Java pour la JVM Java, mais cela n'a guère plus d'intérêt.
Outre le jeu d'instruction et l'architecture interne, les processeurs différent par la façon dont ils lisent et écrivent la mémoire. On pourrait croire qu'il n'y a pas grande différence entre processeurs dans la façon dont ils gèrent la mémoire. Mais ce n'est pas le cas : des différences existent qui peuvent avoir un effet assez important. Dans ce chapitre, on va parler de l'endianess du processeur et de son alignement mémoire : on va s'intéresser à la façon dont le processeur va repartir en mémoire les octets des données qu'il manipule. Ces deux paramètres sont sûrement déjà connus de ceux qui ont une expérience de la programmation assez conséquente. Les autres apprendront ce que c'est dans ce chapitre.
La différence entre mots et bytes
modifierAvant toute chose, nous allons reparler rapidement de la différence entre un byte et un mot. Les deux termes sont généralement polysémiques, avec plusieurs sens. Aussi, définir ce qu'est un mot est assez compliqué. Voyons les différents sens de ce terme, chacun étant utile dans un contexte particulier.
Dans les chapitres précédents, nous avons parlé des mots mémoire, à savoir des blocs de mémoire dont le nombre de bits correspond à la largeur du bus mémoire. Le premier sens possible est donc la quantité de données que l'on peut transférer entre CPU et RAM en un seul cycle d'horloge. Il s'agit d'une définition basée sur les transferts réels entre processeur et mémoire. Le terme que nous avons utilisé pour cette définition est : mot mémoire. Remarquez la subtile différence entre les termes "mot" et "mot mémoire" : le second terme indique bien qu'il s'agit de quelque de lié à la mémoire, pas le premier. Les deux ne sont pas confondre, et nous allons voir pourquoi.
La définition précédente ne permet pas de définir ce qu'est un byte et un mot, vu que la distinction se fait au niveau du processeur, au niveau du jeu d'instruction. Précisément, elle intervient au niveau des instructions d'accès mémoire, éventuellement de certaines opérations de traitement de données. Dans ce qui va suivre, nous allons faire la différence entre les architectures à mot, à byte, et à chaines de caractères. Voyons dans le détail ces histoires de mots, de bytes, et autres.
Les architectures à adressage par mot
modifierAu tout début de l'informatique, sur les anciens ordinateurs datant d'avant les années 80, les processeurs géraient qu'une seule taille pour les données. Par exemple, de tels processeurs ne géraient que des données de 8 bits, pas autre chose. Les données en question était des mots. Aux tout début de l'informatique, certaines machines utilisaient des mots de 3, 4, 5, 6 7, 13, 17, 23, 36 ou 48 bits. Pour donner quelques exemples, l'ordinateur ERA 1103 utilisait des mots de 36-bits, tout comme le PDP-10, et ne gérait pas d'autre taille pour les données : c'était 36 bits pour tout le monde.
Les processeurs en question ne disposaient que d'une seule instruction de lecture/écriture, qui lisait/écrivait des mots entiers. On pouvait ainsi lire ou écrire des paquets de 3, 4, 5, 6 7, 13, 17, 23, 36 ou 48 bits. Les registres du processeur avaient généralement la même taille qu'un mot, ce qui fait que les processeurs de l'époque avaient des registres de 4, 8, 12, 24, 26, 28, 31, 36, 48, voire 60 bits.
Les mots en question sont en théorie à distinguer des mots mémoire, mais ce n'est pas souvent le cas en pratique. Les architectures à adressage par mot faisaient en sorte qu'un mot soit de la même taille qu'un mot mémoire. La mémoire était donc découpée en mots, chacun avait sa propre adresse. Par exemple, une mémoire de 64 kilo-mots contenait 65 536 mots, chacun contenant autant de bits qu'un mot. Les mots faisaient tous la même taille, qui variait suivant la mémoire ou le processeur utilisé. Chaque mot avait sa propre adresse, ce qui fait qu'on parlait d'adressage par mot. Il n'y avait qu'une seule unité d'adressage, ce qui fait que le byte et le mot étaient la même chose sur de telles architectures. La distinction entre byte et mot est apparue après, sur des ordinateurs/processeurs différents.
Les architectures à adressage par byte
modifierPar la suite, des processeurs ont permis d'adresser des données plus petites qu'un mot. Les processeurs en question disposent de plusieurs instructions de lecture/écriture, qui manipulent des blocs de mémoire de taille différente. Par exemple, il peut avoir une instruction de lecture pour lire 8 bits, une autre pour lire 16 bits, une autre 32, etc. Une autre possibilité est celle où le processeur dispose d'une instruction de lecture, qu'on peut configurer suivant qu'on veuille lire/écrire un octet, deux, quatre, huit.
Dans ce cas, on peut faire une distinction entre byte et mot : le byte est la plus petite donnée, le mot est la plus grande. Par exemple, un processeur disposant d'instruction d'accès mémoire capables de lire/écrire 8 ou 16 bits sont dans ce cas. Le byte fait alors 8 bits, le mot en fait 16. La séparation entre byte et mot peut parfois se compléter avec des tailles intermédiaires. Par exemple, prenons un processeur qui dispose d'une instruction de lecture capable de lire soit 8 bits, soit 16 bits, soit 32 bits, soit 64 bits. Dans ce cas, le byte vaut 8 bits, le mot en fait 64, les autres tailles sont des intermédiaires. Pour résumer, un mot est la plus grande unité adressable par le processeur, un byte est la plus petite.
En général, le byte fait 8 bits, un octet. Mais ça n'a pas toujours été le cas, pas mal de jeux d'instructions font exception. L'exemple le plus parlant est celui des processeurs décimaux, qui utilisaient des entiers codés en BCD mais ne géraient pas les entiers codés en binaire normal. De tels processeurs encodaient des nombres sous la forme d'une suite de chiffres décimaux, codés en BCD sur 4 bits. Ils avaient des bytes de 4 bits, voire de 5/6 bits pour les ordinateurs qui ajoutaient un bit de parité/ECC par chiffre décimal. D'autres architectures avaient un byte de 3 à 7 bits.
La taille d'un mot mémoire est de plusieurs bytes : un mot mémoire contient un nombre entier de bytes. La norme actuelle est d'utiliser des bytes d'un octet (8 bits), avec des mots contenant plusieurs octets. Le nombre d'octets dans un mot est généralement une puissance de deux pour simplifier les calculs. Cette règle souffre évidemment d'exceptions, mais l'usage de mots qui ne sont pas des puissances de 2 posent quelques problèmes techniques en termes d’adressage, comme on le verra plus bas.
Sur de telles architectures, il y a une adresse mémoire par byte, et non par mot, ce qui fait qu'on parle d'adressage par byte. Tous les ordinateurs modernes utilisent l'adressage par byte. Concrètement, sur les processeurs modernes, chaque octet de la mémoire a sa propre adresse, peu importe la taille du mot utilisé par le processeur. Par exemple, les anciens processeurs x86 32 bits et les processeurs x86 64 bits utilisent tous le même système d'adressage, où chaque octet a sa propre adresse, la seule différence est que les adresses sont plus nombreuses. Avec un adressage par mot, on aurait eu autant d'adresses qu'avant, mais les mots seraient passés de 32 à 64 bits en passant au 64 bits. Les registres font encore une fois la même taille qu'un mot, bien qu'il existe quelques rares exceptions.
Les architectures à adressage par mot de type hybrides
modifierIl a existé des architectures adressées par mot qui géraient des bytes, mais sans pour autant leur donner des adresses. Leur idée était que les transferts entre CPU et mémoire se faisaient par mots, mais les instructions de lecture/écriture pouvaient sélectionner un byte dans le mot. Une instruction d'accès mémoire devait alors préciser deux choses : l'adresse du mot à lire/écrire, et la position du byte dans le mot adressé. Par exemple, on pouvait demander à lire le mot à l'adresse 0x5F, et de récupérer uniquement le byte numéro 6.
Il s'agit d'architectures adressables par mot car l'adresse identifie un mot, pas un byte. Les bytes en question n'avaient pas d'adresses en eux-mêmes, il n'y avait pas d'adressage par byte. La sélection des bytes se faisait dans le processeur : le processeur lisait des mots entiers, avant que le hardware du processeur sélectionne automatiquement le byte voulu. D'ailleurs, aucune de ces architectures ne supportait de mode d'adressage base+index ou base+offset pour sélectionner des bytes dans un mot. Elles supportaient de tels modes d'adressage pour un mot, pas pour les bytes. Pour faire la différence, nous parlerons de pseudo-byte dans ce qui suit, pour bien préciser que ce ne sont pas de vrais bytes.
Un exemple est le PDP-6 et le PDP-10, qui avaient des instructions de lecture/écriture de ce type. Elles prenaient trois informations : l'adresse d'un mot, la position du pseudo-byte dans le mot, et enfin la taille d'un pseudo-byte ! L'adressage était donc très flexible, car on pouvait configurer la taille du pseudo-byte. Outre l'instruction de lecture LDB et celle d'écriture DPB, d'autres instructions permettaient de manipuler des pseudo-bytes. L'instruction IBP incrémentait le numéro du pseudo-byte, par exemple.
Les architectures à mot de taille variable
modifierD'autres architectures codaient leurs nombres en utilisant un nombre variable de bytes ! Dit autrement, elles avaient des mots de taille variable, d'où leur nom d'architectures à mots de taille variable. Il s'agit d'architectures qui codaient les nombres par des chaines de caractères terminées par un byte de terminaison.
La grande majorité étaient des architectures décimales, à savoir des ordinateurs qui utilisaient des nombres encodés en BCD ou dans un encodage similaire. Les nombres étaient codés en décimal, mais chaque chiffre était encodé en binaire sur quelques bits, généralement 4 à 6 bits. Les bytes stockaient chacun un caractère, qui était utilisé pour encoder soit un chiffre décimal, soit un autre symbole comme un byte de terminaison. Un caractère faisait plus de 4 bits, vu qu'il fallait au minimum coder les chiffres BCD et des symboles supplémentaires. La taille d'un caractère était généralement de 5/6 bits.
Un exemple est celui des IBM 1400 series, qui utilisaient des chaines de caractères séparées par deux bytes : un byte de wordmark au début, et un byte de record mark à la fin. Les caractères étaient des chiffres codés en BCD, chaque caractère était codé sur 6 bits. Les calculs se faisaient chiffre par chiffre, au rythme d'un chiffre utilisé comme opérande par cycle d'horloge. Le processeur passait automatiquement d'un chiffre au suivant pour chaque opérande. Chaque caractère/chiffre avait sa propre adresse, ce qui fait l'architecture est techniquement adressable par byte, alors que les mots correspondaient aux nombres de taille variable.
La comparaison entre l'adressage par mot et par byte
modifierPlus haut, nous avons vu deux types d'adressage : par mot et par byte. Avec la première, ce sont les mots qui ont des adresses. Les bytes n'existent pas forcément sur de telles architectures. Si une gestion des bytes est présente, les instructions de lecture/écriture utilisent des adresses pour les mots, couplé à la position du byte dans le mot. Les lectures/écritures se font pas mots entiers. A l'opposé, sur les architectures adressées par byte, une adresse correspond à un byte et non à un mot.
Les deux techniques font que l'usage des adresses est différent. Entre une adresse par mot et une par byte, le nombre d'adresse n'est pas le même à capacité mémoire égale. Prenons un exemple assez simple, où l'on compare deux processeurs. Les deux ont des mots mémoire de 32 bits, pour simplifier la comparaison. Le premier processeur gère des bytes de 8 bits, et chacun a sa propre adresse, ce qui fait que c'est un adressage par byte qui est utilisé. Le second ne gère pas les bytes mais seulement des mots de 32 bits, ce qui fait que c'est un adressage par mot qui est utilisé.
Dans les deux cas, la mémoire n'est pas organisée de la même manière. Prenons une mémoire de 24 octets pour l'exemple, soit 24/4 = 6 mots de 4 octets. Le premier processeur aura une adresse par byte, soit 24 adresses, et ce sera pareil pour la mémoire, qui utilisera une case mémoire par byte. Le second processeur n'aura que 6 adresses : une par mot. La mémoire a des cases mémoire qui contiennent un mot entier, soit 32 bits, 4 octets.

L'avantage de l'adressage par mot est que l'on peut adresser plus de mémoire pour un nombre d'adresses égal. Si on a un processeur qui gère des adresses de 16 bits, on peut adresser 2^16 = 65 536 adresses. Avec un mot mémoire de 4 bytes d'un octet chacun, on peut adresser : soit 65 536bytes/octets, soit 65 536mots et donc 65 536*4 octets. L'adressage par mot permet donc d'adresser plus de mémoire avec les mêmes adresses. Une autre manière de voir les choses est qu'une architecture à adressage par byte va utiliser beaucoup plus d'adresses qu'une architecture par mot, à capacité mémoire égale.
L'avantage des architectures à adressage par byte est que l'on peut plus facilement modifier des données de petite taille. Par exemple, imaginons qu'un programmeur manipule du texte, avec des caractères codés sur un octet. S'il veut remplacer les lettres majuscules par des minuscules, il doit changer chaque lettre indépendamment des autres, l'une après l'autre. Avec un adressage par mot, il doit lire un mot entier, modifier chaque octet en utilisant des opérations de masquage, puis écrire le mot final. Avec un adressage par byte, il peut lire chaque byte indépendamment, le modifier sans recourir à des opérations de masquage, puis écrire le résultat. Le tout est plus simple avec l'adressage par byte : pas besoin d'opérations de masquage !
Par contre, les architectures à adressage par byte ont de nombreux défauts. Le fait qu'un mot contienne plusieurs octets/bytes a de nombreuses conséquences, desquelles naissent les contraintes d'alignement, de boutisme et autres. Dans ce qui suit, nous allons étudier les défauts des architectures adressables par byte, et allons laisser de côté les architectures adressables par mot. La raison est que toutes les architectures modernes sont adressables par byte, les seules architectures adressables par mot étant de très vieux ordinateurs aujourd'hui disparus.
Le boutisme : une spécificité de l'adressage par byte
modifierLe premier problème lié à l'adressage par byte est lié au fait que l'on a plusieurs bytes par mot : dans quel ordre placer les bytes dans un mot ? On peut introduire le tout par une analogie avec les langues humaines : certaines s’écrivent de gauche à droite et d'autres de droite à gauche. Dans un ordinateur, c'est pareil avec les bytes/octets des mots mémoire : on peut les écrire soit de gauche à droite, soit de droite à gauche. Quand on veut parler de cet ordre d'écriture, on parle de boutisme (endianness).
Dans ce qui suit, nous allons partir du principe que le byte fait un octet, mais gardez dans un coin de votre tête que ce n'a pas toujours été le cas. Les explications qui vont suivre restent valide peu importe la taille du byte.
Les différents types de boutisme
modifierLes deux types de boutisme les plus simples sont le gros-boutisme et le petit-boutisme. Sur les processeurs gros-boutistes, la donnée est stockée des adresses les plus faibles vers les adresses plus grande. Pour rendre cela plus clair, prenons un entier qui prend plusieurs octets et qui est stocké entre deux adresses. L'octet de poids fort de l'entier est stocké dans l'adresse la plus faible, et inversement pour le poids faible qui est stocké dans l'adresse la plus grande. Sur les processeurs petit-boutistes, c'est l'inverse : l'octet de poids faible de notre donnée est stocké dans la case mémoire ayant l'adresse la plus faible. La donnée est donc stockée dans l'ordre inverse pour les octets.
Certains processeurs sont un peu plus souples : ils laissent le choix du boutisme. Sur ces processeurs, on peut configurer le boutisme en modifiant un bit dans un registre du processeur : il faut mettre ce bit à 1 pour du petit-boutiste, et à 0 pour du gros-boutiste, par exemple. Ces processeurs sont dits bi-boutistes.

|

|
Petit et gros-boutisme ont pour particularité que la taille des mots ne change pas vraiment l'organisation des octets. Peu importe la taille d'un mot, celui-ci se lit toujours de gauche à droite, ou de droite à gauche. Cela n’apparaît pas avec les techniques de boutismes plus compliquées.


Certains processeurs ont des boutismes plus compliqués, où chaque mot mémoire est découpé en plusieurs groupes d'octets. Il faut alors prendre en compte le boutisme des octets dans le groupe, mais aussi le boutisme des groupes eux-mêmes. On distingue ainsi un boutisme inter-groupe (le boutisme des groupes eux-même) et un boutisme intra-groupe (l'ordre des octets dans chaque groupe), tout deux pouvant être gros-boutiste ou petit-boutiste. Si l'ordre intra-groupe est identique à l'ordre inter-groupe, alors on retrouve du gros- ou petit-boutiste normal. Mais les choses changent si jamais l'ordre inter-groupe et intra-groupe sont différents. Dans ces conditions, on doit préciser un ordre d’inversion des mots mémoire (byte-swap), qui précise si les octets doivent être inversés dans un mot mémoire processeur, en plus de préciser si l'ordre des mots mémoire est petit- ou gros-boutiste.
Avantages, inconvénients et usage
modifierLe choix entre petit boutisme et gros boutisme est généralement une simple affaire de convention. Il n'y a pas d'avantage vraiment probant pour l'une ou l'autre de ces deux méthodes, juste quelques avantages ou inconvénients mineurs. Dans les faits, il y a autant d'architectures petit- que de gros-boutistes, la plupart des architectures récentes étant bi-boutistes. Précisons que le jeu d'instruction x86 est de type petit-boutiste.
Si on quitte le domaine des jeu d'instruction, les protocoles réseaux et les formats de fichiers imposent un boutisme particulier. Les protocoles réseaux actuels (TCP-IP) sont de type gros-boutiste, ce qui impose de convertir les données réseaux avant de les utiliser sur les PC modernes. Et au passage, si le gros-boutisme est utilisé dans les protocoles réseau, alors que le petit-boutisme est roi sur le x86, c'est pour des raisons pratiques, que nous allons aborder ci-dessous.
Le gros-boutisme est très facile à lire pour les humains. Les nombres en gros-boutistes se lisent de droite à gauche, comme il est d'usage dans les langues indo-européennes, alors que les nombres en petit boutistes se lisent dans l'ordre inverse de lecture. Pour la lecture en hexadécimal, il faut inverser l'ordre des octets, mais il faut garder l'ordre des chiffres dans chaque octet. Par exemple, le nombre 0x015665 (87 653 en décimal) se lit 0x015665 en gros-boutiste, mais 0x655601 en petit-boutiste. Et je ne vous raconte pas ce que cela donne avec un byte-swap...
Cette différence pose problème quand on doit lire des fichiers, du code machine ou des paquets réseau, avec un éditeur hexadécimal. Alors certes, la plupart des professionnels lisent directement les données en passant par des outils d'analyse qui se chargent d'afficher les nombres en gros-boutiste, voire en décimal. Un professionnel a à sa disposition du désassembleur pour le code machine, des analyseurs de paquets pour les paquets réseau, des décodeurs de fichiers pour les fichiers, des analyseurs de dump mémoire pour l'analyse de la mémoire, etc. Cependant, le gros-boutisme reste un avantage quand on utilise un éditeur hexadécimal, quel que soit l'usage. En conséquence, le gros-boutiste a été historiquement pas mal utilisé dans les protocoles réseaux et les formats de fichiers. Par contre, cet avantage de lecture a dû faire face à divers désavantages pour les architectures de processeur.
Le petit-boutisme peut avoir des avantages sur les architectures qui gèrent des données de taille intermédiaires entre le byte et le mot. C'est le cas sur le x86, où l'on peut décider de lire des données de 8, 16, 32, ou 64 bits à partir d'une adresse mémoire. Avec le petit-boutisme, on s'assure qu'une lecture charge bien la même valeur, le même nombre. Par exemple, imaginons que je stocke le nombre 0x 14 25 36 48 sur un mot mémoire, en petit-boutiste. En petit-boutiste, une opération de lecture reverra soit les 8 bits de poids faible (0x 48), soit les 16 bits de poids faible (0x 36 48), soit le nombre complet. Ce ne serait pas le cas en gros-boutiste, où les lectures reverraient respectivement 0x 14, 0x 14 25 et 0x 14 25 36 48. Avec le gros-boutisme, de telles opérations de lecture n'ont pas vraiment de sens. En soit, cet avantage est assez limité et n'est utile que pour les compilateurs et les programmeurs en assembleur.
Un autre avantage est un gain de performance pour certaines opérations. Les instructions en question sont les opérations où on doit additionner d'opérandes codées sur plusieurs octets; sur un processeur qui fait les calculs octet par octet. En clair, le processeur dispose d'instructions de calcul qui additionnent des nombres de 16, 32 ou 64 bit, voire plus. Mais à l'intérieur du processeur, les calculs sont faits octets par octets, l'unité de calcul ne pouvant qu'additionner deux nombres de 8 bits à la fois. Dans ce cas, le petit-boutisme garantit que l'addition des octets se fait dans le bon ordre, en commençant par les octets de poids faible pour progresser vers les octets de poids fort. En gros-boutisme, les choses sont beaucoup plus compliquées...
Pour résumer, les avantages et inconvénients de chaque boutisme sont mineurs. Le gain en performance est nul sur les architectures modernes, qui ont des unités de calcul capables de faire des additions multi-octets. L'usage d'opérations de lecture de taille variable est aujourd'hui tombé en désuétude, vu que cela ne sert pas à grand chose et complexifie le jeu d'instruction. Enfin, l'avantage de lecture n'est utile que dans situations tellement rares qu'on peut légitimement questionner son statut d'avantage. En bref, les différentes formes de boutisme se valent.
L'implémentation de l'adressage par byte au niveau de la mémoire RAM/ROM
modifierAvant de poursuivre, rappelons que la notion de byte est avant tout liée au jeu d'instruction, mais qu'elle ne dit rien du bus mémoire ! Il est parfaitement possible d'utiliser un bus mémoire d'une taille différente de celle du byte ou du mot. La largeur du bus mémoire, la taille d'un mot, et la taille d'un byte, ne sont pas forcément corrélées. Néanmoins, deux cas classiques sont les plus courants.
Les architectures avec une mémoire adressable par byte
modifierLe premier est celui où le bus mémoire transmet un byte à la fois. En clair, la largeur du bus mémoire est celle du byte. Le moindre accès mémoire se fait byte par byte, donc en plusieurs cycles d'horloge. Par exemple, sur un processeur 64 bits, la lecture d'un mot complet se fera octet par octet, ce qui demandera 8 cycles d'horloge, cycles d'horloge mémoire qui plus est. Ce qui explique le désavantage de cette méthode : la performance est assez mauvaise. La performance dépend de plus de la taille des données lue/écrites. On prend moins de temps à lire une donnée courte qu'une donnée longue.
L'avantage est qu'on peut lire ou écrire un mot, peu importe son adresse. Pour donner un exemple, je peux parfaitement lire une donnée de 16 bits localisée à l'adresse 4, puis lire une autre donnée de 16 bits localisée à l'adresse 5 sans aucun problème. En conséquence, il n'y a pas de contraintes d'alignements et les problèmes que nous allons aborder dans la suite n'existent pas.

Les architectures avec une mémoire adressable par mot
modifierPour éviter d'avoir des performances désastreuses, on utilise une autre solution : le bus mémoire a la largeur nécessaire pour lire un mot entier. Le processeur peut charger un mot mémoire entier dans ses registres, en un seul accès mémoire. Et pour lire des données plus petites qu'un mot mémoire, le processeur charge un mot complet, mais ignore les octets en trop.

Il y a alors confusion entre un mot au sens du jeu d'instruction, et un mot mémoire. Pour rappel, une donnée qui a la même taille que le bus de données est appelée un mot mémoire. Mais dans ce cas, l'adressage de la mémoire et du CPU ne sont pas compatibles : le processeur utilise une adresse par byte, la mémoire une adresse par mot ! Tout se passe comme si la mémoire était découpée en blocs de la taille d'un mot. La capacité de la mémoire reste inchangée, ce qui fait que le nombre d'adresses utilisables diminue : il n'y a plus besoin que d'une adresse par mot mémoire et non par octet. Il faut donc faire une sorte d'interface entre les deux.

Par convention, l'adresse d'un mot est l'adresse de son octet de poids faible. Les autres octets du mot ne sont pas adressables par la mémoire. Par exemple, si on prend un mot de 8 octets, on est certain qu'une adresse sur 8 disparaîtra. L'adresse du mot est utilisée pour communiquer avec la mémoire, mais cela ne signifie pas que l'adresse des octets est inutile au-delà du calcul de l'adresse du mot. En effet, l'accès à un octet précis demande de déterminer la position de l'octet dans le mot à partir de l'adresse du octet.
Prenons un processeur ayant des mots de 4 octets et répertorions les adresses utilisables. Le premier mot contient les octets d'adresse 0, 1, 2 et 3. L'adresse zéro est l'adresse de l'octet de poids faible et sert donc d'adresse au premier mot, les autres sont inutilisables sur le bus mémoire. Le second mot contient les adresses 4, 5, 6 et 7, l'adresse 4 est l'adresse du mot, les autres sont inutilisables. Et ainsi de suite. Si on fait une liste exhaustive des adresses valides et invalides, on remarque que seules les adresses multiples de 4 sont utilisables. Et ceux qui sont encore plus observateurs remarqueront que 4 est la taille d'un mot.
Dans l'exemple précédent, les adresses utilisables sont multiples de la taille d'un mot. Sachez que cela fonctionne quelle que soit la taille du mot. Si N est la taille d'un mot, alors seules les adresses multiples de N seront utilisables. Avec ce résultat, on peut trouver une procédure qui nous donne l'adresse d'un mot à partir de l'adresse d'un octet. Si un mot contient N bytes, alors l'adresse du mot se calcule en divisant l'adresse du byte par N. La position du byte dans le mot est quant à elle le reste de cette division. Un reste de 0 nous dit que l'octet est le premier du mot, un reste de 1 nous dit qu'il est le second, etc.

Le processeur peut donc adresser la mémoire RAM en traduisant les adresses des octets en adresses de mot. Il lui suffit de faire une division pour cela. Il conserve aussi le reste de la division dans un registre pour sélectionner l'octet une fois la lecture terminée. Un accès mémoire se fait donc comme suit : il reçoit l'adresse à lire, il calcule l'adresse du mot, effectue la lecture, reçoit le mot à lire, et utilise le reste pour sélectionner l'octet final si besoin. La dernière étape est facultative et n'est présente que si on lit une donnée plus petite qu'un mot.
La division est une opération assez complexe, mais il y a moyen de ruser. L'idée est de faire en sorte que N soit une puissance de deux. La division se traduit alors par un vulgaire décalage vers la droite, le calcul du reste pas une simple opération de masquage. C'est la raison pour laquelle les processeurs actuels utilisent des mots de 1, 2, 4, 8 octets. Sans cela, les accès mémoire seraient bien plus lents.
De plus, cela permet d'économiser des fils sur le bus d'adresse. Si la taille d'un mot est égale à , seules les adresses multiples de seront utilisables. Or, ces adresses se reconnaissent facilement : leurs n bits de poids faibles valent zéro. On n'a donc pas besoin de câbler les fils correspondant à ces bits de poids faible.
L'alignement mémoire
modifierDans la section précédente, nous avons évoqué le cas où un processeur à adressage par byte est couplé à une mémoire adressable par mot. Sur de telles architectures, des problèmes surviennent quand les lectures/écritures se font par mots entiers. Le processeur fournit l'adresse d'un byte, mais lit un mot entier à partir de ce byte. Par exemple, prenons une lecture d'un mot complet : celle-ci précise l'adresse d'un byte. Sur un CPU 64 bits, le processeur lit alors 64 bits d'un coup à partir de l'adresse du byte. Et cela peut poser quelques problèmes, dont la résolution demande de respecter des restrictions sur la place de chaque mot en mémoire, restrictions résumées sous le nom d'alignement mémoire.
L'alignement mémoire des données
modifierImaginons le cas particulier suivant : je dispose d'un processeur utilisant des mots de 4 octets. Je dispose aussi d'un programme qui doit manipuler un caractère stocké sur 1 octet, un entier de 4 octets et une donnée de deux octets. Mais un problème se pose : le programme qui manipule ces données a été programmé par quelqu'un qui n'était pas au courant de ces histoire d'alignement, et il a répartit mes données un peu n'importe comment. Supposons que cet entier soit stocké à une adresse non-multiple de 4. Par exemple :
| Adresse | Octet 4 | Octet 3 | Octet 2 | Octet 1 |
|---|---|---|---|---|
| 0x 0000 0000 | Caractère | Entier | Entier | Entier |
| 0x 0000 0004 | Entier | Donnée | Donnée | |
| 0x 0000 0008 |
La lecture ou écriture du caractère ne pose pas de problème, vu qu'il ne fait qu'un seul byte. Pour la donnée de 2 octets, c'est la même chose, car elle tient toute entière dans un mot mémoire. La lire demande de lire le mot et de masquer les octets inutiles. Mais pour l'entier, ça ne marche pas car il est à cheval sur deux mots ! On dit que l'entier n'est pas aligné en mémoire. En conséquence, impossible de le charger en une seule fois
La situation est gérée différemment suivant le processeur. Sur certains processeurs, la donnée est chargée en deux fois : c'est légèrement plus lent que la charger en une seule fois, mais ça passe. On dit que le processeur gère des accès mémoire non-alignés. D'autres processeurs ne gérent pas ce genre d'accès mémoire et les traitent comme une erreur, similaire à une division par zéro, et lève une exception matérielle. Si on est chanceux, la routine d'exception charge la donnée en deux fois. Mais sur d'autres processeurs, le programme responsable de cet accès mémoire en dehors des clous se fait sauvagement planter. Par exemple, essayez de manipuler une donnée qui n'est pas "alignée" dans un mot de 16 octets avec une instruction SSE, vous aurez droit à un joli petit crash !
Pour éviter ce genre de choses, les compilateurs utilisés pour des langages de haut niveau préfèrent rajouter des données inutiles (on dit aussi du bourrage) de façon à ce que chaque donnée soit bien alignée sur le bon nombre d'octets. En reprenant notre exemple du dessus, et en notant le bourrage X, on obtiendrait ceci :
| Adresse | Octet 4 | Octet 3 | Octet 2 | Octet 1 |
|---|---|---|---|---|
| 0x 0000 0000 | Caractère | X | X | X |
| 0x 0000 0004 | Entier | Entier | Entier | Entier |
| 0x 0000 0008 | Donnée | Donnée | X | X |
Comme vous le voyez, de la mémoire est gâchée inutilement. Et quand on sait que de la mémoire cache est gâchée ainsi, ça peut jouer un peu sur les performances. Il y a cependant des situations dans lesquelles rajouter du bourrage est une bonne chose et permet des gains en performances assez abominables (une sombre histoire de cache dans les architectures multiprocesseurs ou multi-cœurs, mais je n'en dit pas plus).
L'alignement mémoire se gère dans certains langages (comme le C, le C++ ou l'ADA), en gérant l'ordre de déclaration des variables. Essayez toujours de déclarer vos variables de façon à remplir un mot intégralement ou le plus possible. Renseignez-vous sur le bourrage, et essayez de savoir quelle est la taille des données en regardant la norme de vos langages.
L'alignement des instructions en mémoire
modifierLes instructions ont toute une certaine taille, et elles peuvent être de taille fixe (toutes les instructions font X octets), ou de taille variable (le nombre d'octets dépend de l'instruction). Dans les deux cas, le processeur peut incorporer des contraintes sur l'alignement des instructions, au même titre que les contraintes d'alignement sur les données vues précédemment.
Pour les instructions de taille fixe, les instructions sont placées à des adresses précises. Par exemple, prenons des instructions de 8 octets. La première instruction prend les 8 premiers octets de la mémoire, la seconde prend les 8 octets suivants, etc. En faisant cela, l'adresse d'une instruction est toujours un multiple de 8. Et on peut généraliser pour toute instruction de taille fixe : si elle fait X octets, son adresse est un multiple de X.
Généralement, on prend X une puissance de deux pour simplifier beaucoup de choses. Notamment, cela permet de simplifier le program counter : quelques bits de poids faible deviennent inutiles. Par exemple, si on prend des instructions de 4 octets, les adresses des instructions sont des multiples de 4, donc les deux bits de poids faible de l'adresse sont toujours 00 et ne sont pas intégrés dans le program counter. Le program counter est alors plus court de deux bits. Idem avec des instructions de 8 octets qui font économiser 3 bits, ou avec des instructions de 16 octets qui font économiser 4 bits.
Les instructions de taille variable ne sont généralement pas alignées. Sur certains processeurs, les instructions n'ont pas de contraintes d'alignement du tout. Leur chargement est donc plus compliqué et demande des méthodes précises qui seront vues dans le chapitre sur l'unité de chargement du processeur. Évidemment, le chargement d'instructions non-alignées est donc plus lent. En conséquence, même si le processeur supporte des instructions non-alignées, les compilateurs ont tendance à aligner les instructions comme les données, sur la taille d'un mot mémoire, afin de gagner en performance.
Sur d'autres processeurs, les instructions doivent être alignées. Dans le cas le plus simple, les instructions doivent être alignées sur un mot mémoire, elles doivent respecter les mêmes contraintes d'alignement que les données. Elles peuvent être plus courtes ou plus longues qu'un mot, mais elles doivent commencer à la première adresse d'un mot mémoire. D'autres architectures ont des contraintes d'alignement bizarres. Par exemple, les premiers processeurs x86 16 bits imposaient des instructions alignées sur 16 bits et cette contrainte est restée sur les processeurs 32 bits.
Que ce soit pour des instructions de taille fixe ou variables, les circuits de chargement des instructions et les circuits d'accès mémoire ne sont pas les mêmes, ce qui fait que leurs contraintes d'alignement peuvent être différentes. On peut avoir quatre possibilités : des instructions non-alignées et des données alignées, l'inverse, les deux qui sont alignées, les deux qui ne sont pas alignées. Par exemple, il se peut qu'un processeur accepte des données non-alignées, mais ne gère pas des instructions non-alignées ! Le cas le plus simple, fréquent sur les architectures RISC, est d'avoir des instructions et données alignées de la même manière. Les architectures CISC utilisent souvent des contraintes d'alignement, avec généralement des instructions de taille variables non-alignées, mais des données alignées. Les deux dernières possibilités ne sont presque jamais utilisées.
De plus, sur les processeurs où les deux sont alignés, on peut avoir un alignement différent pour les données et les instructions. Par exemple, pour un processeur qui utilise des instructions de 8 octets, mais des données de 4 octets. Les différences d'alignements posent une contrainte sur l'économie des bits sur le bus d'adresse. Il faut alors regarder ce qui se passe sur l'alignement des données. Par exemple, pour un processeur qui utilise des instructions de 8 octets, mais des données de 4 octets, on ne pourra économiser que deux bits, pour respecter l'alignement des données. Ou encore, sur un processeur avec des instructions alignées sur 8 octets, mais des données non-alignées, on ne pourra rien économiser.
Un cas particulier est celui de l'Intel iAPX 432, dont les instructions étaient non-alignées au niveau des bits ! Leur taille variable faisait que la taille des instructions n'était pas un multiple d'octets. Il était possible d'avoir des instructions larges de 23 bits, d'autres de 41 bits, ou toute autre valeur non-divisible par 8. Un octet pouvait contenir des morceaux de deux instructions, à cheval sur l'octet. Ce comportement fort peu pratique faisait que l'implémentation de l'unité d"e chargement était complexe.
Après avoir vu la théorie, nous allons étudier un cas particulier de jeu d'instruction. Précisément, nous allons étudier une extension de l'architecture x86. Pour rappel, les processeurs x86 sont ceux qui sont présents à l'intérieur des PC, à savoir tous les processeurs Intel et AMD actuels. Il s'agit d'une architecture qui a recu de nombreux ajouts au cours du temps, et qui a été fortement modifiée, tout en gardant une certaine compatibilité avec les versions plus anciennes. Ce qui a donné un jeu d’instruction particulièrement compliqué. Dans ce chapitre, nous allons étudier un de ces ajout, une extension de ce jeu d'instruction, qui a ajouté la gestion des flottants au x86. La gestion des flottants est une option qui a été rajoutée au cours de l'existence de l'architecture. Si les processeurs x86 des années 80 ne pouvaient pas faire des calculs flottants, ou alors seulement avec l'aide d'un coprocesseur, tous les processeurs x86 actuels le peuvent. L'ensemble des instructions machine x86 liées aux flottants s'appelle l'extension x87. L'extension x87 est encore utilisée par défaut sur les PC 32 bits. Par contre, avec le jeu d'instructions x86-64 bits, c'est une autre extension qui est utilisée pour les calculs flottants, l'extension SSE.
Les registres x87
modifierL'extension x87 fournit, en plus des instructions, plusieurs registres :
- 8 registres pour les opérandes flottantes ;
- 3 registres d'état pour configurer les exceptions, les arrondis, etc ;
- 1 registre utilisé pour gérer les exceptions flottantes, auquel seul le processeur a accès.
Une organisation en pseudo-pile
modifierL'extension x87 est un cas d'architecture à pile, assez spécialisée, totalement différente de la gestion des registres x86 normaux. Les 8 registres x87 sont ordonnés et numérotés de 0 à 7 : le premier registre est le registre 7, tandis que le dernier registre est le registre 0. Lorsque la FPU x87 est initialisée, ces 8 registres sont complètement vides : ils ne contiennent aucun flottant. Les registres x87 sont organisés sous la forme d'une pile de registres, similaire à une pile d'assiette, que l'on remplit dans un ordre bien précis. Lors du chargement d'une opérande de la RAM vers les registres, il n'est pas possible de décider du registre de destination. Si on veut ajouter des flottants dans nos registres, on doit les « remplir » dans un ordre de remplissage imposé : on remplit d'abord le registre 7, puis le 6, puis le 5, et ainsi de suite jusqu'au registre 0. Si on veut ajouter un flottant dans cette pile de registres, celui-ci sera stocké dans le premier registre vide dans l'ordre de remplissage indiqué au-dessus. Prenons un exemple, les 3 premiers registres sont occupés par un flottant et on veut charger un flottant supplémentaire : le 4e registre sera utilisé pour stocker ce flottant. La même chose existe pour le « déremplissage » des registres. Imaginez que vous souhaitez déplacer le contenu d'un registre dans la mémoire RAM et effacer complètement son contenu. On ne peut pas choisir n'importe quel registre pour faire cela : on est obligé de prendre le registre non vide ayant le numéro le plus grand.
 |
 |
Les instructions à une opérande (les instructions de calcul d'une tangente, d'une racine carrée et d'autres) vont dépiler le flottant au sommet de la pile. Les instructions à deux opérandes (multiplication, addition, soustraction et autres) peuvent se comporter de plusieurs manières différentes. Le cas le plus simple est celui attendu de la part d'une architecture à pile : l'instruction dépile les deux opérandes au sommet de la pile. La seconde possibilité est celle attendue de la part d'une architecture à pile à une adresse : elles dépilent le sommet de la pile et chargent l'autre opérande depuis la mémoire RAM. Le troisième cas est plus intéressant : l'instruction dépile le sommet de la pile, et charge l'autre opérande depuis n'importe quel autre registre de la pile. En somme, les registres de la pile sont adressables, du moins pour ce qui est de gérer la seconde opérande. C'est cette particularité qui vaut le nom de pseudo-pile à cette organisation à mi-chemin entre une pile et une architecture à registres.
Le registre d'état
modifierSi vous avez bonne mémoire, vous vous souvenez sûrement de ce que j'ai dit que la FPU contient 3 registres spéciaux qui ne stockent pas de flottants, mais sont malgré tout utiles. Ces 3 registres portent les noms de Control Word, Status Word et Tag Word. Le registre Tag Word indique, pour chaque registre flottant, s'il est vide ou non. Avouez que c'est pratique pour gérer la pile de registres vue au-dessus ! Ce registre contient 16 bits et pour chacun des 8 registres de données de la FPU, 2 bits sont réservés dans le registre Tag Word. Ces deux bits contiennent des informations sur le contenu du registre de données réservé.
- Si ces deux bits valent 00, le registre contient un flottant « normal » différent de zéro ;
- Si ces deux bits valent 01, le registre contient une valeur nulle : 0 ;
- Si ces deux bits valent 10, le registre contient un NAN, un infini, ou un dénormal ;
- Si ces deux bits valent 11, le registre est vide et ne contient pas de nombre flottant.
Passons maintenant au Status Word. Celui-ci fait lui aussi 16 bits et contient tout ce qu'il faut pour qu'un programme puisse comprendre la cause d'une exception.
| Bit | Utilité |
|---|---|
| TOP | Ce registre contient trois bits regroupés en un seul ensemble nommé TOP, qui stocke le numéro du premier registre vide dans l'ordre de remplissage. Idéal pour gérer notre pile de registres |
| U | Sert à détecter les underflow. Il est mis à 1 lorsqu'un underflow a lieu. |
| O | Pareil que U, mais pour les overflow : ce registre est mis à 1 lors d'un overflow |
| Z | C'est un bit qui est mis à 1 lorsque notre FPU exécute une division par zéro |
| D | Ce bit est mis à 1 lorsqu'un résultat de calcul est un dénormal ou lorsqu'une instruction doit être exécutée sur un dénormal |
| I | Bit mis à 1 lors de certaines erreurs telles que l'exécution d'une instruction de racine carrée sur un négatif ou une division du type 0/0 |
Enfin, voyons le Control Word, le petit dernier. Il fait 16 bits et contient lui aussi des bits ayant chacun une utilité précise. Beaucoup de bits de ce registre sont inutilisés et on ne va citer que les plus utiles.
| Bit | Utilité |
|---|---|
| Infinity Control | S'il vaut zéro, les infinis sont tous traités comme s'ils valaient . S'il vaut un, les infinis sont traités normalement |
| Rouding Control | C'est un ensemble de deux bits qui détermine le mode d'arrondi utilisé
|
| Precision Control | Ensemble de deux bits qui détermine la taille de la mantisse de l'arrondi du résultat d'un calcul. En effet, on peut demander à notre FPU d'arrondir le résultat de chaque calcul qu'elle effectue. Cette instruction ne touche pas à l'exposant, mais seulement à la mantisse. La valeur par défaut de ces deux bits est 11 : notre FPU utilise donc des flottants double précision étendue. Les valeurs 00 et 10 demandent au processeur d'utiliser des flottants non pris en compte par la norme IEEE 754.
|
Les instructions flottantes x87
modifierL’extension x87 comprend les instructions de base supportées par la norme IEEE 754, ainsi que quelques autres. On y retrouve les quatre instructions arithmétiques de base de la norme IEEE754 (+, -, *, /), avec quelques autres calculs supplémentaires.
Les comparaisons
modifierVoici une liste de quelques instructions de comparaisons supportées par l'extension x87 :
- FTST : compare le sommet de la pseudo-pile avec la valeur 0 ;
- FICOM : compare le contenu du sommet de la pseudo-pile avec une constante entière ;
- FCOM : compare le contenu du sommet de la pseudo-pile avec une constante flottante ;
- FCOMI : compare le contenu des deux flottants au sommet de la pseudo-pile.
Les instructions arithmétiques
modifierOn trouve aussi des instructions de calculs, qui comprennent les cinq opérations définies par la norme IEE754, mais aussi quelques instructions supplémentaires :
- l'addition : FADD ;
- la soustraction FSUB ;
- la multiplication FMUL ;
- la division FDIV ;
- la racine carrée FSQRT ;
- des instructions de calcul de la valeur absolue (FABS) ou encore de changement de signe (FCHS).
L'extension x87 implémente aussi des instructions trigonométriques et analytiques telles que :
- le cosinus : instruction FCOS ;
- le sinus : instruction FSIN ;
- la tangente : instruction FPTAN ;
- l'arc tangente : instruction FPATAN ;
- ou encore des instructions de calcul de logarithmes ou d'exponentielles.
Il va de soi que ces dernières ne sont pas supportées par la norme IEEE 754 et que tout compilateur qui souhaite être compatible avec la norme IEEE 754 ne doit pas les utiliser.
Les instructions d'accès mémoire
modifierEn plus de ces instructions de calcul, l'extension x87 fournit des instructions pour transférer des flottants entre la mémoire et les registres. Celles-ci sont des équivalents des instructions PUSH et POP qu'on trouve sur les machines à pile, à l'exception d'une instruction équivalente à l'instruction SWAP. On peut citer par exemple les instructions dans le tableau suivant. D'autres instructions chargent certaines constantes (PI, 1, 0, certains logarithmes en base 2) dans le registre au sommet de la pile de registres.
| Instruction | Ce qu'elle fait |
|---|---|
| FLD | Elle est capable de charger un nombre flottant depuis la mémoire vers notre pile de registres vue au-dessus. Cette instruction peut charger un flottant codé sur 32 bits, 64 bits ou 80 bits |
| FSTP | Déplace le contenu d'un registre vers la mémoire. Une autre instruction existe qui est capable de copier le contenu d'un registre vers la mémoire sans effacer le contenu du registre : c'est l'instruction FST |
| FXCH | Échange le contenu du dernier registre non vide dans l'ordre de remplissage (celui situé au sommet de la pile) avec un autre registre |
Le phénomène de double arrondi
modifierChacun des registres de données vus plus haut stocke un nombre flottant codé sur 80 bits. Oui, vous avez bien lu, 80 bits et non 32 ou 64 : cette FPU calcule sur des nombres flottants double précision étendue et non sur des flottants simple ou double précision, qui ne sont pas gérés par la FPU x87. On peut alors se demander comment le processeur fait pour calculer avec des flottants simple et double précision. Tout se joue lors de l'accès à la mémoire avec l'instruction FLD : celle-ci se comporte différemment suivant le flottant qu'on lui demande de charger. En effet, cette instruction peut charger depuis la mémoire un flottant simple précision, double précision ou double précision étendue. Le format du flottant qui doit être chargé est stocké directement dans l'instruction. Je m'explique : une instruction machine est stockée en mémoire sous la forme d'une suite de bits, et pour certaines instructions, des bits supplémentaires sont ajoutés. Dans notre cas, ces bits optionnels servent à indiquer à notre instruction le format du flottant qu'elle doit charger.
La FPU x87 peut charger depuis la mémoire un nombre flottant 80 bits directement dans un registre. Pour les flottants 32 et 64 bits, la FPU va devoir effectuer une conversion de notre flottant simple ou double précision en un flottant 80 bits. Tous les calculs faits par notre FPU vont donner des résultats codés sur 80 bits, et ceux-ci restent codés sur 80 bits tant que ceux-ci sont stockés dans les registres de la FPU. Par contre, dès qu'il faut enregistrer un nombre flottant en mémoire RAM, les problèmes commencent. Si le flottant en question est stocké dans la mémoire sur 32 ou 64 bits, notre processeur doit convertir le contenu du registre dans le format du flottant en mémoire, histoire de conserver le bon format de base. Cette conversion est faite automatiquement par l'instruction d'écriture en mémoire utilisée. Par contre, si notre flottant est représenté en mémoire sur 80 bits, l'écriture en mémoire est directe : pas de conversion. Et ces conversions posent problème : elles ne respectent pas la norme IEEE 754 !
Comparons un calcul effectué sur un processeur gérant nativement les formats 64 et 32 bits et ce même calcul exécuté par la x87. Dans tous les cas, les flottants seront chargés dans les registres, le calcul s'effectuera et le résultat sera enregistré en mémoire RAM. Sur un processeur qui gére nativement les formats simple et double précision, ni le chargement, ni les calculs, ni l'enregistrement ne demanderont de faire des conversions vers des flottants 80 bits. Avec la x87, les flottants 32/64 bits sont convertis en un flottant x87 80 bits lors des échanges entre la pseudo-pile et la RAM. Les calculs sont effectués sur des flottants 80 bits uniquement, sans conversions. Lors de l'enregistrement d'un flottant x87 80 bits en mémoire, celui-ci est converti dans son format de base, au flottant 32 ou 64 bits le plus proche. On se retrouve donc avec un arrondi supplémentaire, en plus des arrondis liés aux calculs : c'est le phénomène du double rounding (qui signifie double-arrondi en français). Et rien n'implique que le résultat de ces deux conversions aurait donné le même résultat que le calcul effectué sur des flottants 64 bits !

Pour citer un exemple, sachez que des failles de sécurité de PHP et de Java aujourd'hui corrigées et qui avaient fait la une de la presse informatique étaient causées par ces arrondis supplémentaires. Bien sûr, sachez que ce bogue a pu être reproduit sur de nombreux autres langages et n'était certainement pas limité au PHP ou au Java : c'est le non-respect de la norme IEE754 par notre unité de calcul x87 qui était clairement en cause.
De plus, si une série de calculs est faite sur des flottants stockés dans les registres, les résultats intermédiaires auront une précision supérieure à ce qui se serait passé avec des flottants simple ou double précision. Dans ces conditions, le résultat peut être différent de celui qu'on aurait obtenu en utilisant seulement des flottants 64 bits lors des calculs. Le pire, c'est qu'on n'a aucune solution à ce problème, pour les calculs faits avec l'extension x87.
Autre problème, lié au précédent : rares sont les calculs effectués intégralement dans les registres, et on est parfois obligé de temporairement sauvegarder en mémoire le contenu d'un registre pour laisser le registre libre pour un autre nombre flottant. C'est le programmeur ou le compilateur qui gère quand effectuer ce genre de sauvegarde et sur quels registres. Chacune de ces sauvegardes va arrondir le flottant que l'on souhaite sauvegarder. Conséquence : suivant l'ordre de ces sauvegardes, le moment auquel elles ont lieu et les flottants qui sont choisis pour être sauvegardés, le résultat ne sera pas le même ! Avec le même programme, si vous décidez de sauvegarder un flottant et votre voisin un autre, ce ne sera pas le même flottant qui sera arrondi lors de son transfert en mémoire, et le résultat des calculs sur votre ordinateur sera différent des résultats obtenus sur l'ordinateur de votre voisin. Pour limiter la casse, il existe une solution : sauvegarder tout résultat d'un calcul sur un flottant directement dans la mémoire RAM. Comme cela, on se retrouve avec des calculs effectués uniquement sur des flottants 32/64 bits ce qui supprime pas mal d'erreurs de calcul.
La mémoire virtuelle et la protection mémoire
modifierL'espace d'adressage du processeur correspond à l'ensemble des adresses utilisables par le processeur. Par exemple, si je prends un processeur 16 bits, il peut adresser en tout 2^16 = 65536 adresses et l'ensemble de ces adresses forme son espace d'adressage. L'espace d'adressage n'est pas la mémoire réellement installée : s'il n'y a pas assez de RAM installée, des adresses seront inoccupées. De plus, une partie de l'espace d'adressage peut être détourné pour communiquer avec les périphériques, comme nous le verrons plus bas. Nous verrons aussi dans ce chapitre qu'il est possible qu'un processeur ait plusieurs espaces d'adressages séparés. Et même si cela peut sembler contre-intuitif, nous allons voir que les architectures avec plusieurs espaces d'adressage sont plus simples à comprendre !
Les processeurs avec un seul espace d'adressage
modifierPour le moment, considérons le cas intuitif où on ne dispose que d'un seul espace d'adressage. Même si on omet les portions inoccupées de l'espace d'adressage, la RAM n'est pas la seule occupante de l'espace d'adressage. On y trouve aussi la mémoire ROM, les périphériques et d'autres choses encore.
Les architectures Von Neumann
modifierSi on n'a qu'un seul espace d'adressage unique, il est utilisé pour adresser non seulement la mémoire RAM, mais aussi la mémoire ROM. On est alors face à une architecture Von Neumann, où un seul espace d'adressage est découpé entre la mémoire RAM d'un côté et la mémoire ROM de l'autre. Une adresse correspond soit à la mémoire RAM, soit à la mémoire ROM, mais pas aux deux. Typiquement, la mémoire ROM est placée dans les adresses hautes, les plus élevées, alors que la RAM est placée dans les adresses basses en commençant par l'adresse 0. C'est une convention qui n'est pas toujours respectée, aussi mieux vaut éviter de la tenir pour acquise.

Les entrées-sorties mappées en mémoire
modifierSur les ordinateurs avec un seul espace d'adressage, une partie de l'espace d'adressage peut être détourné pour communiquer avec les périphériques. L'idée est que le périphérique se retrouve inclus dans l'ensemble des adresses utilisées pour manipuler la mémoire : on dit qu'il est mappé en mémoire. Les adresses mémoires associées à un périphérique sont redirigées automatiquement vers le périphérique en question. On parle alors d'entrées-sorties mappées en mémoire.

On remarque ainsi le défaut inhérent à cette technique : les adresses utilisées pour les périphériques ne sont plus disponibles pour la mémoire RAM. Dit autrement, on ne peut plus adresser autant de mémoire qu'avant. La perte peut être très légère ou très importante, en fonction des périphériques installés et de leur gourmandise en adresses mémoires.
C'est ce qui causait autrefois un problème assez connu sur les ordinateurs 32 bits, qui ne géraient que 2^32 octets = 4 gibioctets. Certaines personnes installaient 4 gigaoctets de mémoire sur leur ordinateur 32 bits et se retrouvaient avec « seulement » 3,5 à 3,8 gigaoctets de mémoire, les périphériques prenant le reste. Et mine de rien, quand on a une carte graphique avec 512 mégaoctets de mémoire intégrée, une carte son, une carte réseau PCI, des ports USB, un port parallèle, un port série, des bus PCI Express ou AGP, et un BIOS à stocker dans une EEPROM/Flash, ça part assez vite.
L'exemple des cartes graphiques modernes
modifierNotons qu'il est possible que la RAM d'un périphérique soit mappée en RAM. Et pire : il arrive que seule une partie le soit. Un exemple classique est celui des cartes graphiques. Seule une portion de la mémoire vidéo (celle de la carte 3D) est mappée en mémoire RAM. Le processeur a donc accès à une partie de la mémoire vidéo, dans laquelle il peut lire ou écrire comme bon lui semble. Le reste de la mémoire vidéo est invisible du point de vue du processeur, mais manipulable par le GPU à sa guise.
Il est possible pour le CPU de copier des données dans la portion invisible de la mémoire vidéo, mais cela se fait de manière indirecte en passant par le GPU d'abord. Il faut typiquement envoyer une commande spéciale au GPU, pour lui dire de charger une texture en mémoire vidéo, par exemple. Le GPU effectue alors une copie de la mémoire système vers la mémoire vidéo, en utilisant un contrôleur DMA intégré au GPU. Pour résumer, tout se passe comme si la mémoire partagée entre CPU et GPU était coupée en deux : une portion sur le GPU et une autre dans la RAM système.

Pour un périphérique PCI-Express, la portion de mémoire vidéo visible est configurée via des registres spécialisés, appelés les Base Address Registers (BARs). La configuration des registres précise quelle portion de mémoire vidéo est adressable par le processeur, quelle est sa taille, sa position en mémoire vidéo, etc. Avant 2008, les BAR permettaient d’accéder à seulement 256 mégaoctets, pas plus. Après 2008, la spécification du PCI-Express ajouta un support de la technologie Resizable Bar', qui permet au processeur d’accéder directement à plus de 256 mégaoctets de mémoire vidéo, voire à la totalité de la mémoire vidéo. De nombreux fabricants de cartes graphiques commencent à incorporer cette technologie, qui demande quelques changements au niveau du système d'exploitation, des pilotes de périphériques et du matériel.
La memory map d'un ordinateur avec un seul espace d'adressage
modifierOutre la mémoire RAM principale, des mémoires vidéo et même plusieurs mémoires ROM sont mappées en mémoire. Il y a un unique espace d'adressage qui contient tout ce qui est adressable : toutes les mémoires et tous les périphériques de l'ordinateur. Généralement, les adresses hautes sont réservées aux périphériques et aux mémoires ROM, alors que les adresses basses sont pour la RAM. La ROM est au sommet de l'espace d'adressage, les périphériques sont juste en-dessous, la RAM commence à l'adresse 0 et prend les adresses basses.

Notons que d'autres composants que les périphériques ou les mémoires peuvent se trouver dans l'espace d'adressage. On peut y trouver les horloges temps réels, des timers, des senseurs de température, ou d'autres composants placés sur la carte mère. Un exemple un peu original est le suivant : la console de jeu Nintendo DS incorporait une unité de calcul spécialisée dans les divisions et racines carrées, séparée du processeur, qui était justement mappée en mémoire !
Les premiers micro-ordinateurs et consoles de jeux
modifierLes vielles machines, notamment les premiers ordinateurs comme les Commodores et les Amiga et les vielles consoles de jeux, utilisaient cette méthode pour sa simplicité. Ces machines n'étaient pas comme les ordinateurs personnels, pour lesquels on a une variété de cartes graphiques ou de cartes sons différentes. Tous avaient la même configuration matérielle, le matériel était fourni tel quel, ne pouvait pas être changé ni upgradé. Toutes les commodores 64 avaient exactement le même matériel, par exemple : la même carte son, la même carte graphique, les mêmes périphériques.
Cette standardisation faisait que cela ne servait à rien de limiter l'accès au matériel. De telles machines n'avaient pas de système d'exploitation, ou bien celui-ci était rudimentaire et ne contrôlait pas vraiment l'accès au matériel. Les programmeurs avaient donc totalement accès au matériel et mapper les entrées/sorties en mémoire rendait la programmation des périphériques très simple.
-
Adressage mémoire (carte mémoire) du N5200mk2.
-
Adressage mémoire (carte mémoire) du PC-9801VM.
Les PC IBM x86
modifierUn autre exemple est celui des ordinateurs PC un peu anciens, avec des processeurs x86. A l'époque, les processeurs x86 avaient des adresses de 20 bits, ce qui fait 1 mébioctet de mémoire adressable. Le premier mébioctet de mémoire est décomposé en deux portions de mémoire : les premiers 640 kibioctets sont ce qu'on appelle la mémoire conventionnelle, alors que les octets restants forment la mémoire haute. La mémoire au-delà du premier mébioctet, la mémoire étendue, est apparue quand les processeurs x86 32 bits sont apparus.
- Les deux premiers kibioctets de la mémoire conventionnelle sont initialisés au démarrage de l'ordinateur. Ils sont utilisés pour stocker le vecteur d'interruption (on expliquera cela dans quelques chapitres) et servent aussi au BIOS. La portion réservée au BIOS, la BIOS Data Area, mémorise des informations en RAM. Elle commence à l'adresse 0040:0000h, a une taille de 255 octets, et est initialisée lors du démarrage de l'ordinateur.
- Le reste de la mémoire conventionnelle est réservée à la mémoire RAM utilisée par le système d'exploitation (MS-DOS, avant sa version 5.0) et le programme en cours d’exécution.
- Le bas de la mémoire haute est réservé pour communiquer avec les périphériques. On y trouve les BIOS des périphériques (dont celui de la carte vidéo, s'il existe) , qui sont nécessaires pour les initialiser et parfois pour communiquer avec eux. De plus, on y trouve la mémoire de la carte vidéo, et éventuellement la mémoire d'autres périphériques comme la carte son.
- Le sommet de la mémoire haute est réservé au BIOS.
- La mémoire étendue n'est pas réservée pour une utilisation précise.

Les processeurs avec plusieurs espaces d'adressages
modifierIl existe des processeurs qui sont capables de gérer plusieurs espaces d'adressage. Cela peut paraitre surprenant, mais nous avons déjà abordé un exemple dans les chapitres précédents (essayez de deviner lequel). Toujours est-il que l'on peut se demander quelle est l'utilité d'avoir plusieurs espaces d'adressage. La raison est pourtant simple, et même intuitive. Avec un seul espace d'adressage, les périphériques et la ROM sont mappés dans l'espace d'adressage. Des adresses censées être disponibles pour la RAM sont détournées vers la ROM ou les périphériques. Si très peu de RAM est installé, alors ce n'est pas un problème : des adresses inutilisées sont détournées pour des choses utiles. Mais si on veut utiliser plus de RAM, les choses se compliquent. L'idée est d'utiliser plusieurs espaces d'adressage dans lesquels on ne met pas la même chose, d'utiliser des espaces séparés pour des utilisations distinctes. On peut par exemple utiliser un espace d'adressage séparé pour la RAM, un autre pour la ROM, un autre pour les périphériques, etc. En dire plus demande de détailler plusieurs techniques qui utilisent chacune un espace d'adressage séparé.
Les architectures Harvard
modifierLe premier cas d'espace d'adressage séparé est celui des architectures Harvard. Pour rappel, avec l'architecture Harvard, on a un espace d'adressage séparé pour la RAM et la ROM. Une même adresse peut correspondre soit à la ROM, soit à la RAM : le processeur voit bien deux mémoires séparées, chacune dans son propre espace d'adressage. Les deux espaces d'adressage n'ont pas forcément la même taille : l'un peut contenir plus de mémoire/adresses que l'autre. Il est par exemple possible d'avoir un plus gros espace d'adressage pour la RAM que pour la ROM. Mais cela implique que les adresses des instructions et des données soient de taille différentes. C'est peu pratique et c'est rarement implémenté, ce qui fait que le cas le plus courant est celui où les deux espaces d'adressages ont la même taille.

L'espace d'adressage séparé pour les entrées-sorties
modifierLes entrées-sorties et périphériques peuvent avoir leur propre espace d'adressage dédié, séparé de celui utilisé pour la mémoire. Sur ce genre d'architectures, on trouve un espace d'adressage pour la mémoire RAM et la mémoire ROM, et un espace d'adressage spécialisé pour les périphériques et les entrées-sorties.

Une même adresse peut donc adresser soit une entrée-sortie, soit une case mémoire. Et pour faire la différence, le processeur doit avoir des instructions séparées pour gérer les périphériques et adresser la mémoire. Il a des instructions de lecture/écriture pour lire/écrire en mémoire, et d'autres pour lire/écrire les registres d’interfaçage. Sans cela, le processeur ne saurait pas si une adresse est destinée à un périphérique ou à la mémoire. Cela élimine aussi les problèmes avec les caches : les accès à l'espace d'adressage de la RAM passent par l'intermédiaire de la mémoire cache, alors les accès dans l'espace d'adressage des périphériques le contournent totalement.
Là encore, les deux espaces d'adressage n'ont pas forcément la même taille. Il arrive que les deux espaces d'adressage aient la même taille, le plus souvent sur des ordinateurs complexes avec beaucoup de périphériques. Mais les systèmes embarqués ont souvent des espaces d'adressage plus petits pour les périphériques que pour la ou les mémoires. L'implémentation varie grandement suivant le cas, la première méthode imposant d'avoir deux bus séparés pour les mémoires et les périphériques, l'autre permettant un certain partage du bus d'adresse. Nous reviendrons dessus plus en détail dans le chapitre sur l'adressage des périphériques.
La commutation de banques (bank switching)
modifierLe bank switching, aussi appelé commutation de banque, permet d'utiliser plusieurs espaces d'adressage sur un même processeur, sans attribuer chaque espace d'adressage pour une raison précise. L'espace d'adressage est présent en plusieurs exemplaires appelés des banques. Les banques sont numérotées, chaque numéro de banque permettant de l'identifier et de le sélectionner.
Le but de cette technique est d'augmenter la mémoire disponible pour l'ordinateur. Par exemple, supposons que j'ai besoin d'adresser une mémoire ROM de 4 kibioctets, une RAM de 8 kibioctets, et divers périphériques. Le processeur a un bus d'adresse de 12 bits, ce qui limite l'espace d'adressage à 4 kibioctets. Dans ce cas, je peux réserver 4 banques : une pour la ROM, une pour les périphériques, et deux banques qui contiennent chacune la moitié de la RAM. La simplicité et l'efficacité de cette technique font qu'elle est beaucoup utilisée dans l'informatique embarquée.

Cette technique demande d'utiliser un bus d'adresse plus grand que les adresses du processeur. L'adresse réelle se calcule en concaténant le numéro de banque avec l'adresse accédée. Le numéro de la banque actuellement en cours d'utilisation est mémorisé dans un registre appelé le registre de banque. On peut changer de banque en changeant le contenu de ce registre. Le processeur dispose souvent d'instructions spécialisées qui en sont capables.
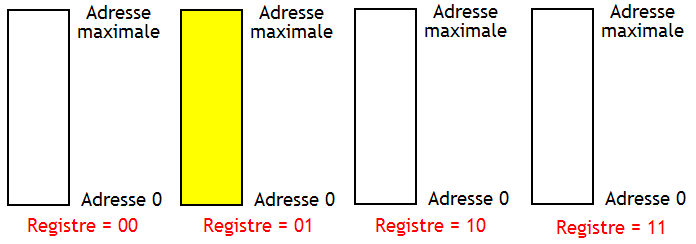
|

|
Après avoir vu qu'un processeur pouvait gérer plusieurs espaces d'adressage, nous allons voir comment les programmes gèrent les espaces d'adressage. Nous allons étudier le cas où un seul programme d'éxecute, mais aussi celui où plusieurs programmes partagent la mémoire. Nous allons voir les deux cas, l'un après l'autre. Mais avant toute chose, parlons de la protection mémoire.
La protection mémoire : généralités
modifierSans protection particulière, les programmes peuvent techniquement lire ou écrire les données des autres. Si un programme pouvait modifier les données d'un autre programme, on se retrouverait rapidement avec une situation non prévue par le programmeur, avec des conséquences qui vont d'un joli plantage à des failles de sécurité dangereuses. Il faut donc introduire des mécanismes de protection mémoire, pour isoler les programmes les uns des autres, et éviter toute modification problématique. La protection mémoire regroupe plusieurs techniques assez variées, qui ont des objectifs différents. Elles ont pour point commun de faire intervenir à des niveaux divers le système d'exploitation et le processeur.
Le premier objectif est l'isolation des processus. Elle garantit que chaque programme n'a accès qu'à certaines portions dédiées de la mémoire et rend le reste de la mémoire inaccessible en lecture et en écriture. Le système d'exploitation attribue à chaque programme une ou plusieurs portions de mémoire rien que pour lui, auquel aucun autre programme ne peut accéder. Un tel programme, isolé des autres, s'appelle un processus, d'où le nom de cet objectif. Toute tentative d'accès à une partie de la mémoire non autorisée déclenche une exception matérielle (rappelez-vous le chapitre sur les interruptions) qui est traitée par une routine du système d'exploitation. Généralement, le programme fautif est sauvagement arrêté et un message d'erreur est affiché à l'écran.
La protection de l'espace exécutable empêche d’exécuter quoique ce soit provenant de certaines zones de la mémoire. En effet, certaines portions de la mémoire sont censées contenir uniquement des données, sans aucun programme ou code exécutable. Cependant, des virus informatiques peuvent se cacher dedans et d’exécuter depuis celles-ci. Ou encore, des failles de sécurités peuvent permettre à un attaquant d'injecter du code exécutable malicieux dans des données, ce qui peut lui permettre de lire les données manipulées par un programme, prendre le contrôle de la machine, injecter des virus, ou autre. Pour éviter cela, le système d'exploitation peut marquer certaines zones mémoire comme n'étant pas exécutable. Toute tentative d’exécuter du code localisé dans ces zones entraîne la levée d'une exception ou d'une erreur et le système d'exploitation réagit en conséquence. Là encore, le processeur doit détecter les exécutions non autorisées.
D'autres méthodes de protection mémoire visent à limiter des actions dangereuses. Pour cela, le processeur et l'OS gérent des droits d'accès, qui interdisent certaines actions pour des programmes non-autorisés. Lorsqu'on exécute une opération interdite, le système d’exploitation et/ou le processeur réagissent en conséquence. La première technique de ce genre n'est autre que la séparation entre espace noyau et utilisaeur, vue dans le chapitre sur les interruptions. Mais il y en a d'autres, comme nous le verrons dans ce chapitre.
Un seul espace d'adressage, non-partagé
modifierLe cas le plus simple est celui où il n'y a pas de système d'exploitation et où un seul programme s'exécute sur l'ordinateur. Le programme a alors accès à tout l'espace d'adressage. L'usage qu'il fait du ou des espaces d'adressage dépend de si on est sur une architecture Von Neumann ou Harvard.
Sur une architecture Von Neumann, le programme et ses données sont placées dans le même espace d'adressage. Le programme organise la mémoire en plusieurs sections, dans lesquelles le programme range des données différentes. Typiquement, on trouve quatre sections, qui regroupent des données suivant leur utilisation. Voici ces trois sections :
- Le segment text contient le code machine du programme, de taille fixe.
- Le segment data contient des données de taille fixe qui occupent de la mémoire de façon permanente.
- Le segment pour la pile, de taille variable.
- le reste est appelé le tas, de taille variable.

Sur une architecture Harvard, le programme est placé dans un espace d'adressage à part du reste. Le problème, c'est que cet espace d'adressage ne contient pas que le code machine à exécuter. Il contient aussi des constantes, à savoir des données qui gardent la même valeur lors de l'exécution du programme. Elles peuvent être lues, mais pas modifiées durant l'exécution du programme. L'accès à ces constantes demande d'aller lire celles-ci dans l'autre espace d'adressage, pour les copier dans l'autre espace d'adressage. Pour cela, les architectures Harvard modifiées ajoutent des instructions pour copier les constantes d'un espace d'adressage à l'autre.


La pile et le tas sont de taille variable, ce qui veut dire qu'ils peuvent grandir ou diminuer à volonté, contrairement au reste. Entre le tas et la pile, on trouve un espace de mémoire inutilisée, qui peut être réquisitionné selon les besoins. La pile commence généralement à l'adresse la plus haute et grandit en descendant, alors que le tas grandit en remontant vers les adresses hautes. Il s'agit là d'une convention, rien de plus. Il est possible d'inverser la pile et le tas sans problème, c'est juste que cette organisation est rentrée dans les usages.
Il va de soi que cette vision de l'espace d'adressage ne tient pas compte des périphériques. C'est-à-dire que les schémas précédents partent du principe qu'on a un espace d'adressage séparé pour les périphériques. Dans le cas où les entrées-sorties sont mappées en mémoire, l'organisation est plus compliquée. Généralement, les adresses associées aux périphériques sont placées juste au-dessus de la pile, dans les adresses hautes.
La protection mémoire avec seul espace d'adressage non-partagé est très simple. On n'a pas besoin d'isolation des processus, la gestion des droits d'accès est minimale quand elle existe. Par contre, on a besoin de protection de l'espace exécutable. Sur les architectures Harvard, le code machine et les données sont dans des espaces d'adressage séparés, et le code machine est dans une ROM, la protection de l'espace exécutable est donc garantie. Sur une architecture Von Neumann, elle ne l'est pas du tout.
Un seul espace d'adressage, partagé avec le système d'exploitation
modifierMaintenant, étudions le cas où le programme partage la mémoire avec le système d'exploitation. Sur les systèmes d'exploitation les plus simples, on ne peut lancer qu'un seul programme à la fois. Le système d'exploitation réserve une portion de taille fixe réservée au système d'exploitation, alors que le reste de la mémoire est utilisé pour le reste et notamment pour le programme à exécuter. Le programme est placé à un endroit en RAM qui est toujours le même.

L'OS utilise soit les adresses basses, soit les adresses hautes
modifierD'ordinaire, le système d'exploitation est est en mémoire RAM, comme le programme à lancer. Il faut alors copier le système d'exploitation dans la RAM, depuis une mémoire de masse. Sur d'autres systèmes, le système d'exploitation est placé dans une mémoire ROM. C'est le cas si le système d'exploitation prend très peu de mémoire, comme c'est le cas sur les systèmes les plus anciens, ou encore sur certains systèmes embarqués rudimentaires. Les deux cas font généralement un usage différent de l'espace d'adressage.
Si le système d'exploitation est copié en mémoire RAM, il est généralement placé dans les premières adresses, les adresses basses. A l'inverse, un OS en mémoire ROM est généralement placé à la fin de la mémoire, dans les adresses hautes. Mais tout cela n'est qu'une convention, et les exceptions sont monnaie courante. Il existe aussi une organisation intermédiaire, où le système d'exploitation est chargé en RAM, mais utilise des mémoires ROM annexes, qui servent souvent pour accéder aux périphériques. On a alors un mélange des deux techniques précédentes : l'OS est situé au début de la mémoire, alors que les périphériques sont à la fin, et les programmes au milieu.

La protection mémoire quand l'espace d'adressage est partagé avec l'OS
modifierSur de tels systèmes, il n'y a pas besoin d'isolation des processus, juste de protection de l'espace exécutable. Protéger les données de l'OS contre une erreur ou malveillance d'un programme utilisateur est nécessaire. Notons qu'il s'agit d'une protection en écriture, pas en lecture. Le programme peut parfaitement lire les données de l'OS sans problèmes, et c'est même nécessaire pour certaines opérations courantes, comme les appels systèmes. Par contre, la protection de l'espace exécutable doit rendre impossible au programme d'écrire dans la portion mémoire du système d'exploitation.
Dans le cas où le système d'exploitation est placé dans une mémoire ROM, il n'y a pas besoin de faire grand chose. Une écriture dans une ROM n'est pas possible, ce qui fait que l'OS est protégé. Le processeur peut détecter ce genre d'accès et terminer le programme fautif, mais ce n'est pas une nécessité. Mais dans le cas où le système d'exploitation est chargé en RAM, tout change. Il devient possible pour un programme d'aller écrire dans la portion réservée à l'OS et d'écraser le code de l'OS. Chose qu'il faut absolument empêcher.
La solution la plus courante est d'interdire les écritures d'un programme de dépasser une certaine limite, en-dessous ou au-dessus de laquelle se trouve le système d’exploitation. Pour cela, le processeur incorpore un registre limite, qui contient l'adresse limite au-delà de laquelle un programme peut pas aller. Quand un programme applicatif accède à la mémoire, l'adresse à laquelle il accède est comparée au contenu du registre limite. Si cette adresse est inférieure/supérieure au registre limite, le programme cherche à accéder à une donnée placée dans la mémoire réservée au système : l’accès mémoire est interdit, une exception matérielle est levée et l'OS affiche un message d'erreur. Dans le cas contraire, l'accès mémoire est autorisé et notre programme s’exécute normalement.

Un seul espace d'adressage, partagé entre plusieurs programmes
modifierLes systèmes d’exploitation modernes implémentent la multiprogrammation, le fait de pouvoir lancer plusieurs logiciels en même temps. Et ce même si un seul processeur est présent dans l'ordinateur : les logiciels sont alors exécutés à tour de rôle. Toutefois, cela amène un paquet de problèmes qu'il faut résoudre au mieux. Les programmes s’exécutent à tour de rôle sur un même processeur, ils partagent la mémoire RAM, etc. Le partage du processeur est géré au niveau logiciel par le système d'exploitation, et il ne nous intéressera pas ici. Par contre, le partage de la RAM et demande la coopération du logiciel et du matériel, ce qui nous intéressera dans ce chapitre.
Un point important est le partage de la RAM entre les différents programmes. Le système d'exploitation répartit les différents programmes dans la mémoire RAM et chaque programme se voit attribuer un ou plusieurs blocs de mémoire. Ils sont appelés des partitions mémoire, ou encore des segments. Dans ce qui va suivre, nous allons parler de segments, pour simplifier les explications. Nous allons partir du principe qu'un programme est égal à un segment, pour simplifier les explications, mais sachez qu'un programme peut être éclaté en plusieurs segments dispersés dans la mémoire, et même être conçu pour ! Nous en reparlerons dans le chapitre sur le mémoire virtuelle.

Toutefois, cela amène un paquet de problèmes qu'il faut résoudre au mieux. Le premier problème est tout simplement de placer les segments dans des sections vides de l'espace d'adressage, mais c'est quelque chose qui est du ressort du système d'exploitation proprement dit. Par contre, cela implique qu'un segment peut être placé n'importe où en RAM et sa position en RAM change à chaque exécution. En conséquence, les adresses des branchements et des données ne sont jamais les mêmes d'une exécution à l'autre. L'usage de branchements relatifs résout en partie le problème, mais il reste à corriger les adresses des données.
Pour résoudre ce problème, le compilateur considère que le segment commence à l'adresse zéro. En clair, les programmes sont conçus sans tenir compte des autres programmes en mémoire, à savoir qu'ils sont compilés de manière à accéder à toutes les adresses disponibles à partir de l'adresse zéro, à tout l'espace d'adressage. Mais l'OS ou le processeur corrigent les adresses internes au segment, en décalant toutes les adresses du segment à partir de sa base. Cette correction est en général réalisée par l'OS, mais il existe aussi des techniques matérielles, que nous verrons dans la suite du chapitre.
Il faut aussi prendre en compte le phénomène de l'allocation mémoire. Derrière ce nom barbare, se cache quelque chose de simple : les programmes peuvent déclamer de la mémoire au système d'exploitation, pour y placer des données. Les langages de programmation bas niveau supportent des fonctions comme malloc(), qui permettent de demander un bloc de mémoire de N octets à l'OS, qui doit alors accommoder la demande. S'il n'y a pas assez de mémoire, l'appel échoue et le programme doit gérer la situation. De même, un programme peut libérer de la mémoire qu'il n'utilise plus avec des fonctions comme free(). Avec des segments, cela revient à changer la taille d'un segment, plus précisément à la fin du segment. Et tout cela est géré par le système d'exploitation, aussi on laisse cela pour plus tard.
Un dernier problème est que les programmes peuvent lire ou écrire dans le segment d'un autre. Si un programme pouvait modifier les données d'un autre programme, on se retrouverait rapidement avec une situation non prévue par le programmeur, avec des conséquences qui vont d'un joli plantage à des failles de sécurité dangereuses. Il faut donc introduire des mécanismes de protection mémoire, pour isoler les segments les uns des autres. Nous parlerons de ces mécanismes dans quelques chapitres.
Il arrive cependant que des programmes partagent une même zone de mémoire, pour échanger des données. En effet, les systèmes d'exploitation modernes gèrent nativement des systèmes de communication inter-processus, très utilisés par les programmes modernes. Les implémentations les plus simples consistent soit à partager un bout de mémoire entre processus, soit à communiquer par l’intermédiaire d'un fichier partagé. Et le partage de la mémoire entre deux processus est très simple avec un espace d'adressage unique. Il suffit de manipuler la protection mémoire pour qu'elle autorise aux deux programmes d'accéder à un même segment. Les adresses utilisées par les deux programmes sont les mêmes.
La protection mémoire avec des registres de base et limite
modifierChaque programme commence à une adresse précise et se termine à une autre. Les accès mémoire d'un programme doivent donc rester dans cet intervalle d'adresse. Pour cela, le système d'exploitation mémorise l'adresse de départ et de fin de chaque segment. Le processeur utilise ces deux adresses pour vérifier que les accès mémoire sont dans les clous. Quand il démarre un programme, le système d'exploitation charge ces deux adresses dans le processeur, dans deux registres spécialisés : le registre de base pour l'adresse du début du segment, le registre limite pour l'adresse de fin du segment.
Les deux registres servent à vérifier si un programme qui lit/écrit de la mémoire au-delà de sa partition. Le processeur vérifie pour chaque accès mémoire ne déborde pas au-delà de la partition qui lui est allouée, ce qui n'arrive que si l'adresse d'accès dépasse la valeur du registre limite. A noter que le registre de base est parfois utilisé pour la relocation matérielle, à savoir que le processeur ajoute automatiquement l'adresse de base à chaque accès mémoire. La relocation garantit que les adresses utilisées commencent à l'adresse de base, grâce au registre de base. Du moins, c'est le cas si l'addition ne déborde pas au-delà de la mémoire physique, tout débordement signifiant erreur de protection mémoire.
Les deux registres ne sont accessibles que pour le système d'exploitation et ne sont généralement accessibles qu'en espace noyau. Lorsque le processeur exécute un programme, ou reprend son exécution, il charge les limites des partitions dans ces deux registres. Ces deux registres doivent être sauvegardés en cas d'interruption, mais pas d'appel de fonction.
Les clés de protection
modifierLes premiers IBM 360 disposaient d'un mécanisme de protection mémoire assez simple. Ce mécanisme de protection attribue à chaque programme une clé de protection, qui consiste en un nombre unique de 4 bits (chaque programme a donc une clé différente de ses collègues). La mémoire est fragmentée en blocs de même taille, de 2 kibioctets. Le processeur mémorise, pour chacun de ses blocs, la clé de protection du programme qui a réservé ce bloc. À chaque accès mémoire, le processeur compare la clé de protection du programme en cours d’exécution et celle du bloc de mémoire de destination. Si les deux clés sont différentes, alors un programme a effectué un accès hors des clous et il se fait sauvagement arrêter.
Un espace d'adressage par processus : l'abstraction matérielle de processus
modifierL'usage de partitions mémoire est assez complexe, mais est encore en cours aujourd'hui, sous des formes plus ou moins élaborées. Mais de nos jours, la relocation est gérée autrement. La différence principale est que l'on a pas un espace d'adressage partagé entre plusieurs programmes. Grâce à diverses fonctionnalités du processeur, chaque programme a son propre espace d'adressage rien que pour lui ! Le fait que chaque programme ait son propre espace d'adressage ne porte pas de nom, mais on pourrait l'appeler abstraction matérielle des processus. Nous verrons comment elle est implémentée dans la section suivante, qui porte sur l'abstraction mémoire, mais nous pouvons donner quelques explications sur l'abstraction des processus.
Le noyau est mappé en mémoire
modifierLe noyau du système d'exploitation a son propre espace d'adressage, séparé des autres. C'est une sécurité qui isole le noyau et les programmes, et les force à communiquer à travers des appels systèmes. Cependant, sachez que cette isolation n'est pas parfaite, volontairement. Dans l'espace d'adressage d'un programme, les adresses hautes sont remplies avec une partie du noyau ! Le programme peut utiliser cette portion du noyau avec des appels systèmes simplifiés, qui ne sont pas des interruptions, mais des appels systèmes couplés avec un changement de niveau de privilège (passage en espace noyau nécessaire). L'idée est d'éviter des appels systèmes trop fréquents. Évidemment, ces adresses sont accessibles uniquement en lecture, pas en écriture. Pas question de modifier le noyau de l'OS ! De plus, il s'agit d'une portion du noyau dont on sait que la consultation ne pose pas de problèmes de sécurité.
L'espace d'adressage est donc séparé en deux portions : l'OS d'un côté, le programme de l'autre. On retrouve la même chose que ce qu'on avait avec un espace d'adressage unique, partagé entre un OS et un programme. La répartition des adresses entre noyau et programme varie suivant l'OS ou le processeur utilisé. Sur les PC x86 32 bits, Linux attribuait 3 gigas pour les programmes et 1 giga pour le noyau, Windows attribuait 2 gigas à chacun. Sur les systèmes 64 bits, la situation est plus complexe.

Sur les systèmes x86 64 bits, l'espace d'adressage est en théorie coupé en deux, la moitié basse pour le programme, la moitié haute pour le noyau. Sauf que les systèmes x86 64 bits actuels utilisent des adresses de 48 bits, le bus mémoire ne gère pas plus. Il manque donc 64 - 48 = 16 bits d'adresses, qui ne peuvent pas être utilisés pour adresser quoi que ce soit. L'espace d'adressage est donc de 64 bits, mais est coupé en trois parties, comme illustré ci-dessous. Les deux premières parties ont des adresses dont les 16 bits de poids fort sont identiques : soit ils sont tous à 0, soit tous à 1. Il s'agit des adresses canoniques. Les adresses canoniques basses ont leurs 16 bits de poids fort à 0, elles sont attribuées au programme. Les adresses canoniques hautes ont leurs 16 bits de poids fort à 1, elles sont attribuées au noyau. Les adresses non-canoniques ne sont pas accessibles, y accéder déclenche la levée d'une exception matérielle. Les futurs systèmes x86 devraient passer à des adresses de 57 bits.
La communication inter-processus et les threads
modifierL'abstraction des processus fait que deux programmes ne peuvent pas se marcher sur les pieds. L'isolation des processus est donc garantie. Mais un gros problème est alors celui de la communication inter-processus, à savoir faire communiquer plusieurs processus entre eux. Il arrive régulièrement que des applications doivent coopérer pour faire leur travail, et échanger des données. L'isolation des processus met des bâtons dans les roues de ce partage.
Un moyen pour est de partager une portion de mémoire, accessible aux deux processus. Par exemple, l'un peut écrire dans cette zone, l'autre peut lire dedans. Mais l'isolation des processus fait que le partage de la mémoire est plus compliqué. Imaginez que deux programmes veulent partager une même zone de mémoire, pour échanger des données. La portion de mémoire sera placée à une certaine adresse physique en mémoire RAM. Mais cette adresse ne sera pas la même pour les deux programmes, vu qu'ils sont dans deux espaces d'adressage distincts. On peut résoudre ce problème, mais avec des mécanismes assez compliqués, dépendant des techniques de "mémoire virtuelle" qu'on verra au chapitre suivant.
Une autre méthode est de regrouper plusieurs programmes dans un seul processus, afin qu'ils partagent le même morceau de mémoire. Les programmes portent alors le nom de threads. Les threads d'un même processus partagent le même espace d'adressage. Ils partagent généralement certains segments : ils se partagent le code, le tas et les données statiques. Par contre, chaque thread dispose de sa propre pile d'appel.

Les identifiants de processus intégrés au processeur
modifierPour simplifier la gestion de plusieurs processus, le processeur numérote chaque espace d'adressage. Le numéro est donc spécifique à chaque processus, ce qui fait qu'il est appelé les identifiants de processus CPU, aussi appelés identifiants d'espace d'adressage. Le processeur mémorise l'identifiant du programme en cours d'exécution dans un registre dédié. Le registre d'identifiant est modifié à chaque changement de processus, à chaque commutation de contexte.
L'identifiant de processus CPU est utilisé lors des accès mémoire, afin de ne se pas se tromper d'espace d'adressage. Il est utilisé pour les accès au cache, entre autres. Il sert à savoir si une donnée dans le cache appartient à tel ou tel processus, ce qui est utile pour la protection mémoire. Sans cela, chaque processus peut en théorie accéder à des données qui ne sont pas à lui dans le cache, en envoyant l'adresse adéquate. Nous en reparlerons dans le chapitre sur les mémoires caches.
Un défaut de cette méthode est que l'identifiant de processus est généralement codé sur une dizaine de bits, alors que le système d'exploitation utilise des identifiants de processus beaucoup plus larges, de 32 à 64 bits sur les CPU 32/64 bits. L'OS doit gérer la correspondance entre identifiants de processus CPU et ceux de l'OS. Parfois, pour cette raison, les OS n'utilisent pas toujours ce système d'identifiant de processus CPU.
Pour introduire ce chapitre, nous devons faire un rappel sur le concept d'espace d'adressage. Pour rappel, un espace d'adressage correspond à l'ensemble des adresses utilisables par le processeur. Par exemple, si je prends un processeur 16 bits, il peut adresser en tout 2^16 = 65536 adresses, l'ensemble de ces adresses forme son espace d'adressage. Intuitivement, on s'attend à ce qu'il y ait correspondance avec les adresses envoyées à la mémoire RAM. J'entends par là que l'adresse 1209 de l'espace d'adressage correspond à l'adresse 1209 en mémoire RAM. C'est là une hypothèse parfaitement raisonnable et on voit mal comment ce pourrait ne pas être le cas.
Mais sachez qu'il existe des techniques d'abstraction mémoire qui font que ce n'est pas le cas. Avec ces techniques, l'adresse 1209 de l'espace d'adressage correspond en réalité à l'adresse 9999 en mémoire RAM, voire n'est pas en RAM. L'abstraction mémoire fait que les adresses de l'espace d'adressage sont des adresses fictives, qui doivent être traduites en adresses mémoires réelles pour être utilisées. Les adresses de l'espace d'adressage portent le nom d'adresses logiques, alors que les adresses de la mémoire RAM sont appelées adresses physiques.
L'abstraction mémoire implémente de nombreuses fonctionnalités complémentaires
modifierL'utilité de l'abstraction matérielle n'est pas évidente, mais sachez qu'elle est si que tous les processeurs modernes la prennent en charge. Elle sert notamment à implémenter les techniques d'abstraction matérielle des processus vues au chapitre précédent, à savoir le fait que chaque processus a son propre espace d'adressage rien que pour lui. Mais elle sert aussi pour d'autres fonctionnalités, comme la mémoire virtuelle, que nous aborderons dans ce qui suit.
La plupart de ces fonctionnalités manipulent la relation entre adresses logiques et physique. Dans le cas le plus simple, une adresse logique correspond à une seule adresse physique. Mais beaucoup de fonctionnalités avancées ne respectent pas cette règle.
L'abstraction matérielle des processus
modifierDans le chapitre précédent, nous avions vu l'abstraction matérielle des processus, une technique qui fait que chaque programme a son propre espace d'adressage. Chaque programme a l'impression d'avoir accès à tout l'espace d'adressage, de l'adresse 0 à l'adresse maximale gérée par le processeur. Évidemment, il s'agit d'une illusion maintenue justement grâce à la traduction d'adresse. Les espaces d'adressage contiennent des adresses logiques, les adresses de la RAM sont des adresses physiques, la nécessité de l'abstraction mémoire est évidente.
Implémenter l'abstraction mémoire peut se faire de plusieurs manières. Mais dans tous les cas, il faut que la correspondance adresse logique - physique change d'un programme à l'autre. Ce qui est normal, vu que les deux processus sont placés à des endroits différents en RAM physique. La conséquence est qu'avec l'abstraction mémoire, une adresse logique correspond à plusieurs adresses physiques. Une même adresse logique dans deux processus différents correspond à deux adresses phsiques différentes, une par processus. Une adresse logique dans un processus correspondra à l'adresse physique X, la même adresse dans un autre processus correspondra à l'adresse Y.
Les adresses physiques qui partagent la même adresse logique sont alors appelées des adresses homonymes. Le choix de la bonne adresse étant réalisé par un mécanisme matériel et dépend du programme en cours. Le mécanisme pour choisir la bonne adresse dépend du processeur, mais il y en a deux grands types :
- La première consiste à utiliser l'identifiant de processus CPU, vu au chapitre précédent. C'est, pour rappel, un numéro attribué à chaque processus par le processeur. L'identifiant du processus en cours d'exécution est mémorisé dans un registre du processeur. La traduction d'adresse utilise cet identifiant, en plus de l'adresse logique, pour déterminer l'adresse physique.
- La seconde solution mémorise les correspondances adresses logiques-physique dans des tables en mémoire RAM, qui sont différentes pour chaque programme. Les tables sont accédées à chaque accès mémoire, afin de déterminer l'adresse physique.
Le partage de la mémoire entre programmes
modifierDans le chapitre précédent, nous avions vu qu'il est possible de lancer plusieurs programmes en même temps, mais que ceux-ci doivent se partager la mémoire RAM. Toutefois, cela amène un paquet de problèmes qu'il faut résoudre au mieux. Le problème principal est que les programmes ne doivent pas lire ou écrire dans les données d'un autre, sans quoi on se retrouverait rapidement avec des problèmes. Il faut donc introduire des mécanismes de protection mémoire, pour isoler les programmes les uns des autres.
Il faut cependant que la protection mémoire permette à deux programmes de partager des morceaux de mémoire, ce qui est nécessaire pour implémenter les mécanismes de communication inter-processus des systèmes d'exploitation modernes. Ce partage de mémoire est rendu très compliqué par l'abstraction mémoire, mais est parfaitement possible.
Avec le partage de mémoire, plusieurs adresses logiques correspondent à la même adresse physique. Les adresses logiques sont alors appelées des adresses synonymes. Lorsque deux processus partagent une même zone de mémoire, la zone sera mappées à des adresses logiques différentes. Tel processus verra la zone de mémoire partagée à l'adresse X, l'autre la verra à l'adresse Y. Mais il s'agira de la même portion de mémoire physique, avec une seule adresse physique.
La mémoire virtuelle : quand l'espace d'adressage est plus grand que la mémoire
modifierToutes les adresses ne sont pas forcément occupées par de la mémoire RAM, s'il n'y a pas assez de RAM installée. Par exemple, un processeur 32 bits peut adresser 4 gibioctets de RAM, même si seulement 3 gibioctets sont installés dans l'ordinateur. L'espace d'adressage contient donc 1 gigas d'adresses inutilisées, et il faut éviter ce surplus d'adresses pose problème.
Sans mémoire virtuelle, seule la mémoire réellement installée est utilisable. Si un programme utilise trop de mémoire, il est censé se rendre compte qu'il n'a pas accès à tout l'espace d'adressage. Quand il demandera au système d'exploitation de lui réserver de la mémoire, le système d'exploitation le préviendra qu'il n'y a plus de mémoire libre. Par exemple, si un programme tente d'utiliser 4 gibioctets sur un ordinateur avec 3 gibioctets de mémoire, il ne pourra pas. Pareil s'il veut utiliser 2 gibioctets de mémoire sur un ordinateur avec 4 gibioctets, mais dont 3 gibioctets sont déjà utilisés par d'autres programmes. Dans les deux cas, l'illusion tombe à plat.
Les techniques de mémoire virtuelle font que l'espace d'adressage est utilisable au complet, même s'il n'y a pas assez de mémoire installée dans l'ordinateur ou que d'autres programmes utilisent de la RAM. Par exemple, sur un processeur 32 bits, le programme aura accès à 4 gibioctets de RAM, même si d'autres programmes utilisent la RAM, même s'il n'y a que 2 gibioctets de RAM d'installés dans l'ordinateur.
Pour cela, on utilise une partie des mémoires de masse (disques durs) d'un ordinateur en remplacement de la mémoire physique manquante. Le système d'exploitation crée sur le disque dur un fichier, appelé le swapfile ou fichier de swap, qui est utilisé comme mémoire RAM supplémentaire. Il mémorise le surplus de données et de programmes qui ne peut pas être mis en mémoire RAM.

Une technique naïve de mémoire virtuelle serait la suivante. Avant de l'aborder, précisons qu'il s'agit d'une technique abordée à but pédagogique, mais qui n'est implémentée nulle part tellement elle est lente et inefficace. Un espace d'adressage de 4 gigas ne contient que 3 gigas de RAM, ce qui fait 1 giga d'adresses inutilisées. Les accès mémoire aux 3 gigas de RAM se font normalement, mais l'accès aux adresses inutilisées lève une exception matérielle "Memory Unavailable". La routine d'interruption de cette exception accède alors au swapfile et récupère les données associées à cette adresse. La mémoire virtuelle est alors émulée par le système d'exploitation.
Le défaut de cette méthode est que l'accès au giga manquant est toujours très lent, parce qu'il se fait depuis le disque dur. D'autres techniques de mémoire virtuelle logicielle font beaucoup mieux, mais nous allons les passer sous silence, vu qu'on peut faire mieux, avec l'aide du matériel.
L'idée est de charger les données dont le programme a besoin dans la RAM, et de déplacer les autres sur le disque dur. Par exemple, imaginons la situation suivante : un programme a besoin de 4 gigas de mémoire, mais ne dispose que de 2 gigas de mémoire installée. On peut imaginer découper l'espace d'adressage en 2 blocs de 2 gigas, qui sont chargés à la demande. Si le programme accède aux adresses basses, on charge les 2 gigas d'adresse basse en RAM. S'il accède aux adresses hautes, on charge les 2 gigas d'adresse haute dans la RAM après avoir copié les adresses basses sur le swapfile.
On perd du temps dans les copies de données entre RAM et swapfile, mais on gagne en performance vu que tous les accès mémoire se font en RAM. Du fait de la localité temporelle, le programme utilise les données chargées depuis le swapfile durant un bon moment avant de passer au bloc suivant. La RAM est alors utilisée comme une sorte de cache alors que les données sont placées dans une mémoire fictive représentée par l'espace d'adressage et qui correspond au disque dur.
Mais avec cette technique, la correspondance entre adresses du programme et adresses de la RAM change au cours du temps. Les adresses de la RAM correspondent d'abord aux adresses basses, puis aux adresses hautes, et ainsi de suite. On a donc besoin d'abstraction mémoire. Les correspondances entre adresse logique et physique peuvent varier avec le temps, ce qui permet de déplacer des données de la RAM vers le disque dur ou inversement. Une adresse logique peut correspondre à une adresse physique, ou bien à une donnée swappée sur le disque dur. C'est l'unité de traduction d'adresse qui se charge de faire la différence. Si une correspondance entre adresse logique et physique est trouvée, elle l'utilise pour traduire les adresses. Si aucune correspondance n'est trouvée, alors elle laisse la main au système d'exploitation pour charger la donnée en RAM. Une fois la donnée chargée en RAM, les correspondances entre adresse logique et physiques sont modifiées de manière à ce que l'adresse logique pointe vers la donnée chargée.
L'extension d'adressage
modifierUne autre fonctionnalité rendue possible par l'abstraction mémoire est l'extension d'adressage. Elle permet d'utiliser plus de mémoire que l'espace d'adressage ne le permet. Par exemple, utiliser 7 gigas de RAM sur un processeur 32 bits, dont l'espace d'adressage ne gère que 4 gigas. L'extension d'adresse est l'exact inverse de la mémoire virtuelle. La mémoire virtuelle sert quand on a moins de mémoire que d'adresses, l'extension d'adresse sert quand on a plus de mémoire que d'adresses.
Il y a quelques chapitres, nous avions vu que c'est possible via la commutation de banques. Mais l'abstraction mémoire est une méthode alternative. Que ce soit avec la commutation de banques ou avec l'abstraction mémoire, les adresses envoyées à la mémoire doivent être plus longues que les adresses gérées par le processeur. La différence est que l'abstraction mémoire étend les adresses d'une manière différente.
Une implémentation possible de l'extension d'adressage fait usage de l'abstraction matérielle des processus. Chaque processus a son propre espace d'adressage, mais ceux-ci sont placés à des endroits différents dans la mémoire physique. Par exemple, sur un ordinateur avec 16 gigas de RAM, mais un espace d'adressage de 2 gigas, on peut remplir la RAM en lançant 8 processus différents et chaque processus aura accès à un bloc de 2 gigas de RAM, pas plus, il ne peut pas dépasser cette limite. Ainsi, chaque processus est limité par son espace d'adressage, mais on remplit la mémoire avec plusieurs processus, ce qui compense. Il s'agit là de l'implémentation la plus simple, qui a en plus l'avantage d'avoir la meilleure compatibilité logicielle. De simples changements dans le système d'exploitation suffisent à l'implémenter.

Un autre implémentation donne plusieurs espaces d'adressage différents à chaque processus, et a donc accès à autant de mémoire que permis par la somme de ces espaces d'adressage. Par exemple, sur un ordinateur avec 16 gigas de RAM et un espace d'adressage de 4 gigas, un programme peut utiliser toute la RAM en utilisant 4 espaces d'adressage distincts. On passe d'un espace d'adressage à l'autre en changeant la correspondance adresse logique-physique. L'inconvénient est que la compatibilité logicielle est assez mauvaise. Modifier l'OS ne suffit pas, les programmeurs doivent impérativement concevoir leurs programmes pour qu'ils utilisent explicitement plusieurs espaces d'adressage.
Les deux implémentations font usage des adresses logiques homonymes, mais à l'intérieur d'un même processus. Pour rappel, cela veut dire qu'une adresse logique correspond à des adresses physiques différentes. Rien d'étonnant vu qu'on utilise plusieurs espaces d'adressage, comme pour l'abstraction des processus, sauf que cette fois-ci, on a plusieurs espaces d'adressage par processus. Prenons l'exemple où on a 8 gigas de RAM sur un processeur 32 bits, dont l'espace d'adressage ne gère que 4 gigas. L'idée est qu'une adresse correspondra à une adresse dans les premiers 4 gigas, ou dans les seconds 4 gigas. L'adresse logique X correspondra d'abord à une adresse physique dans les premiers 4 gigas, puis à une adresse physique dans les seconds 4 gigas.
La MMU
modifierLa traduction des adresses logiques en adresses physiques se fait par un circuit spécialisé appelé la Memory Management Unit (MMU), qui est souvent intégré directement dans l'interface mémoire. La MMU est souvent associée à une ou plusieurs mémoires caches, qui visent à accélérer la traduction d'adresses logiques en adresses physiques. En effet, nous verrons plus bas que la traduction d'adresse demande d'accéder à des tableaux, gérés par le système d'exploitation, qui sont en mémoire RAM. Aussi, les processeurs modernes incorporent des mémoires caches appelées des Translation Lookaside Buffers, ou encore TLB. Nous nous pouvons pas parler des TLB pour le moment, car nous n'avons pas encore abordé le chapitre sur les mémoires caches, mais un chapitre entier sera dédié aux TLB d'ici peu.

Les MMU intégrées au processeur
modifierD'ordinaire, la MMU est intégrée au processeur. Et elle peut l'être de deux manières. La première en fait un circuit séparé, relié au bus d'adresse. La seconde fusionne la MMU avec l'unité de calcul d'adresse. La première solution est surtout utilisée avec une technique d'abstraction mémoire appelée la pagination, alors que l'autre l'est avec une autre méthode appelée la segmentation. La raison est que la traduction d'adresse avec la segmentation est assez simple : elle demande d'additionner le contenu d'un registre avec l'adresse logique, ce qui est le genre de calcul qu'une unité de calcul d'adresse sait déjà faire. La fusion est donc assez évidente.
Pour donner un exemple, l'Intel 8086 fusionnait l'unité de calcul d'adresse et la MMU. Précisément, il utilisait un même additionneur pour incrémenter le program counter et effectuer des calculs d'adresse liés à la segmentation. Il aurait été logique d'ajouter les pointeurs de pile avec, mais ce n'était pas possible. La raison est que le pointeur de pile ne peut pas être envoyé directement sur le bus d'adresse, vu qu'il doit passer par une phase de traduction en adresse physique liée à la segmentation.

Les MMU séparées du processeur, sur la carte mère
modifierIl a existé des processeurs avec une MMU externe, soudée sur la carte mère.
Par exemple, les processeurs Motorola 68000 et 68010 pouvaient être combinés avec une MMU de type Motorola 68451. Elle supportait des versions simplifiées de la segmentation et de la pagination. Au minimum, elle ajoutait un support de la protection mémoire contre certains accès non-autorisés. La gestion de la mémoire virtuelle proprement dit n'était possible que si le processeur utilisé était un Motorola 68010, en raison de la manière dont le 68000 gérait ses accès mémoire. La MMU 68451 gérait un espace d'adressage de 16 mébioctets, découpé en maximum 32 pages/segments. On pouvait dépasser cette limite de 32 segments/pages en combinant plusieurs 68451.
Le Motorola 68851 était une MMU qui était prévue pour fonctionner de paire avec le Motorola 68020. Elle gérait la pagination pour un espace d'adressage de 32 bits.
Les processeurs suivants, les 68030, 68040, et 68060, avaient une MMU interne au processeur.
La relocation matérielle
modifierPour rappel, les systèmes d'exploitation moderne permettent de lancer plusieurs programmes en même temps et les laissent se partager la mémoire. Dans le cas le plus simple, qui n'est pas celui des OS modernes, le système d'exploitation découpe la mémoire en blocs d'adresses contiguës qui sont appelés des segments, ou encore des partitions mémoire. Les segments correspondent à un bloc de mémoire RAM. C'est-à-dire qu'un segment de 259 mébioctets sera un segment continu de 259 mébioctets dans la mémoire physique comme dans la mémoire logique. Dans ce qui suit, un segment contient un programme en cours d'exécution, comme illustré ci-dessous.

Le système d'exploitation mémorise la position de chaque segment en mémoire, ainsi que d'autres informations annexes. Le tout est regroupé dans la table de segment, un tableau dont chaque case est attribuée à un programme/segment. La table des segments est un tableau numéroté, chaque segment ayant un numéro qui précise sa position dans le tableau. Chaque case, chaque entrée, contient un descripteur de segment qui regroupe plusieurs informations sur le segment : son adresse de base, sa taille, diverses informations.
La relocation avec la relocation matérielle : le registre de base
modifierUn segment peut être placé n'importe où en RAM physique et sa position en RAM change à chaque exécution. Le programme est chargé à une adresse, celle du début du segment, qui change à chaque chargement du programme. Et toutes les adresses utilisées par le programme doivent être corrigées lors du chargement du programme, généralement par l'OS. Cette correction s'appelle la relocation, et elle consiste à ajouter l'adresse de début du segment à chaque adresse manipulée par le programme.

La relocation matérielle fait que la relocation est faite par le processeur, pas par l'OS. La relocation est intégrée dans le processeur par l'intégration d'un registre : le registre de base, aussi appelé registre de relocation. Il mémorise l'adresse à laquelle commence le segment, la première adresse du programme. Pour effectuer la relocation, le processeur ajoute automatiquement l'adresse de base à chaque accès mémoire, en allant la chercher dans le registre de relocation.

Le processeur s'occupe de la relocation des segments et le programme compilé n'en voit rien. Pour le dire autrement, les programmes manipulent des adresses logiques, qui sont traduites par le processeur en adresses physiques. La traduction se fait en ajoutant le contenu du registre de relocation à l'adresse logique. De plus, cette méthode fait que chaque programme a son propre espace d'adressage.

Le système d'exploitation mémorise les adresses de base pour chaque programme, dans la table des segments. Le registre de base est mis à jour automatiquement lors de chaque changement de segment. Pour cela, le registre de base est accessible via certaines instructions, accessibles en espace noyau, plus rarement en espace utilisateur. Le registre de segment est censé être adressé implicitement, vu qu'il est unique. Si ce n'est pas le cas, il est possible d'écrire dans ce registre de segment, qui est alors adressable.
La protection mémoire avec la relocation matérielle : le registre limite
modifierSans restrictions supplémentaires, la taille maximale d'un segment est égale à la taille complète de l'espace d'adressage. Sur les processeurs 32 bits, un segment a une taille maximale de 2^32 octets, soit 4 gibioctets. Mais il est possible de limiter la taille du segment à 2 gibioctets, 1 gibioctet, 64 Kibioctets, ou toute autre taille. La limite est définie lors de la création du segment, mais elle peut cependant évoluer au cours de l'exécution du programme, grâce à l'allocation mémoire. Le processeur vérifie à chaque accès mémoire que celui-ci se fait bien dans le segment, en comparant l'adresse accédée à l'adresse de base et l'adresse maximale, l'adresse limite.
Limiter la taille d'un segment demande soit de mémoriser sa taille, soit de mémoriser l'adresse limite (l'adresse de fin de segment, l'adresse limite à ne pas dépasser). Les deux sont possibles et marchent parfaitement, le choix entre les deux solutions est une pure question de préférence. A la rigueur, la vérification des débordements est légèrement plus rapide si on utilise l'adresse de fin du segment. Précisons que l'adresse limite est une adresse logique, le segment commence toujours à l'adresse logique zéro.
Pour cela, la table des segments doit être modifiée. Au lieu de ne contenir que l'adresse de base, elle contient soit l'adresse maximale du segment, soit la taille du segment. En clair, le descripteur de segment est enrichi avec l'adresse limite. D'autres informations peuvent être ajoutées, comme on le verra plus tard, mais cela complexifie la table des segments.
De plus, le processeur se voit ajouter un registre limite, qui mémorise soit la taille du segment, soit l'adresse limite. Les deux registres, base et limite, sont utilisés pour vérifier si un programme qui lit/écrit de la mémoire en-dehors de son segment attitré : au-delà pour le registre limite, en-deça pour le registre de base. Le processeur vérifie pour chaque accès mémoire ne déborde pas au-delà du segment qui lui est allouée, ce qui n'arrive que si l'adresse d'accès dépasse la valeur du registre limite. Pour les accès en-dessous du segment, il suffit de vérifier si l'addition de relocation déborde, tout débordement signifiant erreur de protection mémoire.
Techniquement, il y a une petite différence de vitesse entre utiliser la taille et l'adresse maximale. Vérifier les débordements avec la taille demande juste de comparer la taille avec l'adresse logique, avant relocation, ce qui peut être fait en parallèle de la relocation. Par contre, l'adresse limite est comparée à une adresse physique, ce qui demande de faire la relocation avant la vérification, ce qui prend un peu plus de temps. Mais l'impact sur les performances est des plus mineurs.

Les registres de base et limite sont altérés uniquement par le système d'exploitation et ne sont accessibles qu'en espace noyau. Lorsque le système d'exploitation charge un programme, ou reprend son exécution, il charge les adresses de début/fin du segment dans ces registres. D'ailleurs, ces deux registres doivent être sauvegardés et restaurés lors de chaque interruption. Par contre, et c'est assez évident, ils ne le sont pas lors d'un appel de fonction. Cela fait une différence de plus entre interruption et appels de fonctions.
- Il faut noter que le registre limite et le registre de base sont parfois fusionnés en un seul registre, qui contient un descripteur de segment tout entier.
Pour information, la relocation matérielle avec un registre limite a été implémentée sur plusieurs processeurs assez anciens, notamment sur les anciens supercalculateurs de marque CDC. Un exemple est le fameux CDC 6600, qui implémentait cette technique.
La mémoire virtuelle avec la relocation matérielle
modifierIl est possible d'implémenter la mémoire virtuelle avec la relocation matérielle. Pour cela, il faut swapper des segments entiers sur le disque dur. Les segments sont placés en mémoire RAM et leur taille évolue au fur et à mesure que les programmes demandent du rab de mémoire RAM. Lorsque la mémoire est pleine, ou qu'un programme demande plus de mémoire que disponible, des segments entiers sont sauvegardés dans le swapfile, pour faire de la place.
Faire ainsi de demande juste de mémoriser si un segment est en mémoire RAM ou non, ainsi que la position des segments swappés dans le swapfile. Pour cela, il faut modifier la table des segments, afin d'ajouter un bit de swap qui précise si le segment en question est swappé ou non. Lorsque le système d'exploitation veut swapper un segment, il le copie dans le swapfile et met ce bit à 1. Lorsque l'OS recharge ce segment en RAM, il remet ce bit à 0. La gestion de la position des segments dans le swapfile est le fait d'une structure de données séparée de la table des segments.
L'OS exécute chaque programme l'un après l'autre, à tour de rôle. Lorsque le tour d'un programme arrive, il consulte la table des segments pour récupérer les adresses de base et limite, mais il vérifie aussi le bit de swap. Si le bit de swap est à 0, alors l'OS se contente de charger les adresses de base et limite dans les registres adéquats. Mais sinon, il démarre une routine d'interruption qui charge le segment voulu en RAM, depuis le swapfile. C'est seulement une fois le segment chargé que l'on connait son adresse de base/limite et que le chargement des registres de relocation peut se faire.
Un défaut évident de cette méthode est que l'on swappe des programmes entiers, qui sont généralement assez imposants. Les segments font généralement plusieurs centaines de mébioctets, pour ne pas dire plusieurs gibioctets, à l'époque actuelle. Ils étaient plus petits dans l'ancien temps, mais la mémoire était alors plus lente. Toujours est-il que la copie sur le disque dur des segments est donc longue, lente, et pas vraiment compatible avec le fait que les programmes s'exécutent à tour de rôle. Et ca explique pourquoi la relocation matérielle n'est presque jamais utilisée avec de la mémoire virtuelle.
L'extension d'adressage avec la relocation matérielle
modifierPassons maintenant à la dernière fonctionnalité implémentable avec la traduction d'adresse : l'extension d'adressage. Elle permet d'utiliser plus de mémoire que ne le permet l'espace d'adressage. Par exemple, utiliser plus de 64 kibioctets de mémoire sur un processeur 16 bits. Pour cela, les adresses envoyées à la mémoire doivent être plus longues que les adresses gérées par le processeur.
L'extension des adresses se fait assez simplement avec la relocation matérielle : il suffit que le registre de base soit plus long. Prenons l'exemple d'un processeur aux adresses de 16 bits, mais qui est reliée à un bus d'adresse de 24 bits. L'espace d'adressage fait juste 64 kibioctets, mais le bus d'adresse gère 16 mébioctets de RAM. On peut utiliser les 16 mébioctets de RAM à une condition : que le registre de base fasse 24 bits, pas 16.
Un défaut de cette approche est qu'un programme ne peut pas utiliser plus de mémoire que ce que permet l'espace d'adressage. Mais par contre, on peut placer chaque programme dans des portions différentes de mémoire. Imaginons par exemple que l'on ait un processeur 16 bits, mais un bus d'adresse de 20 bits. Il est alors possible de découper la mémoire en 16 blocs de 64 kibioctets, chacun attribué à un segment/programme, qu'on sélectionne avec les 4 bits de poids fort de l'adresse. Il suffit de faire démarrer les segments au bon endroit en RAM, et cela demande juste que le registre de base le permette. C'est une sorte d'émulation de la commutation de banques.
La segmentation en mode réel des processeurs x86
modifierAvant de passer à la suite, nous allons voir la technique de segmentation de l'Intel 8086, un des tout premiers processeurs 16 bits. Il s'agissait d'une forme très simple de segmentation, sans aucune forme de protection mémoire, ni même de mémoire virtuelle, ce qui le place à part des autres formes de segmentation. Il s'agit d'une amélioration de la relocation matérielle, qui avait pour but de permettre d'utiliser plus de 64 kibioctets de mémoire, ce qui était la limite maximale sur les processeurs 16 bits de l'époque.
Par la suite, la segmentation s'améliora et ajouta un support complet de la mémoire virtuelle et de la protection mémoire. L'ancienne forme de segmentation fut alors appelé le mode réel, et la nouvelle forme de segmentation fut appelée le mode protégé. Le mode protégé rajoute la protection mémoire, en ajoutant des registres limite et une gestion des droits d'accès aux segments, absents en mode réel. De plus, il ajoute un support de la mémoire virtuelle grâce à l'utilisation d'une des segments digne de ce nom, table qui est absente en mode réel ! Mais nous ne pouvons pas parler du mode protégé à ce moment du cours, ni le voir en même temps que le mode réel, à cause d'une différence très importante : l'interprétation des adresses change complètement, comme on le verra dans la suite du cours. Les registres de segment ne mémorisent pas des adresses de base en mode protégé, la relocation se fait de manière moins directe. Nous allons voir le mode réel seul, dans cette section.
Les segments en mode réel
modifier
L'idée de la segmentation en mode réel est d'offrir à chaque programme plusieurs espaces d'adressage. Pour cela, la segmentation en mode réel sépare la pile, le tas, le code machine et les données constantes dans quatre segments distincts.
- Le segment text, qui contient le code machine du programme, de taille fixe.
- Le segment data contient des données de taille fixe qui occupent de la mémoire de façon permanente, des constantes, des variables globales, etc.
- Le segment pour la pile, de taille variable.
- le reste est appelé le tas, de taille variable.
Un point important est que sur ces processeurs, il n'y a pas de table des segments proprement dit. Chaque programme gére de lui-même les adresses de base des segments qu'il manipule. Il n'est en rien aidé par une table des segments gérée par le système d'exploitation.
Chaque segment subit la relocation indépendamment des autres. Pour cela, la meilleure solution est d'utiliser plusieurs registres de base, un par segment. Notons que cette solution ne marche que si le nombre de segments par programme est limité, à une dizaine de segments tout au plus. Les processeurs x86 utilisaient cette méthode, et n'associaient que 4 à 6 registres de segments par programme.
Les registres de segments en mode réel
modifierLes processeurs 8086 et le 286 avaient quatre registres de segment : un pour le code, un autre pour les données, et un pour la pile, le quatrième étant un registre facultatif laissé à l'appréciation du programmeur. Ils sont nommés CS (code segment), DS (data segment), SS (Stack segment), et ES (Extra segment). Le 386 rajouta deux registres, les registres FS et GS, qui sont utilisés pour les segments de données.
Les registres CS et SS sont adressés implicitement, en fonction de l'instruction exécutée. Les instructions de la pile manipulent le segment associé à la pile, le chargement des instructions se fait dans le segment de code, les instructions arithmétiques et logiques vont chercher leurs opérandes sur le tas, etc. Et donc, toutes les instructions sont chargées depuis le segment pointé par CS, les instructions de gestion de la pile (PUSH et POP) utilisent le segment pointé par SS.
Les segments DS et ES sont, eux aussi, adressés implicitement. Pour cela, les instructions LOAD/STORE sont dupliquées : il y a une instruction LOAD pour le segment DS, une autre pour le segment ES. D'autres instructions lisent leurs opérandes dans un segment par défaut, mais on peut changer ce choix par défaut en précisant le segment voulu. Un exemple est celui de l'instruction CMPSB, qui compare deux octets/bytes : le premier est chargé depuis le segment DS, le second depuis le segment ES.
Un autre exemple est celui de l'instruction MOV avec un opérande en mémoire. Elle lit l'opérande en mémoire depuis le segment DS par défaut. Il est possible de préciser le segment de destination si celui-ci n'est pas DS. Par exemple, l'instruction MOV [A], AX écrit le contenu du registre AX dans l'adresse A du segment DS. Par contre, l'instruction MOV ES:[A], copie le contenu du registre AX das l'adresse A, mais dans le segment ES.
La traduction d'adresse en mode réel
modifierLa segmentation en mode réel a pour seul but de permettre à un programme de dépasser la limite des 64 KB autorisée par les adresses de 16 bits. L'idée est que chaque segment a droit à son propre espace de 64 KB. On a ainsi 64 Kb pour le code machine, 64 KB pour la pile, 64 KB pour un segment de données, etc. Les registres de segment mémorisaient la base du segment, les adresses calculées par l'ALU étant des offsets. Ce sont tous des registres de 16 bits, mais ils ne mémorisent pas des adresses physiques de 16 bits, comme nous allons le voir.

L'Intel 8086 utilisait des adresses de 20 bits, ce qui permet d'adresser 1 mébioctet de RAM. Vous pouvez vous demander comment on peut obtenir des adresses de 20 bits alors que les registres de segments font tous 16 bits ? Cela tient à la manière dont sont calculées les adresses physiques. Le registre de segment n'est pas additionné tel quel avec le décalage : à la place, le registre de segment est décalé de 4 rangs vers la gauche. Le décalage de 4 rangs vers la gauche fait que chaque segment a une adresse qui est multiple de 16. Le fait que le décalage soit de 16 bits fait que les segments ont une taille de 64 kibioctets.
0000 0110 1110 11110000
|
Registre de segment - | 16 bits, décalé de 4 bits vers la gauche |
+ 0001 0010 0011 0100
|
Décalage/Offset | 16 bits |
0000 1000 0001 0010 0100
|
Adresse finale | 20 bits |
Le mode réel du 8086 avait une particularité : les adresses calculées ne dépassaient pas 20 bits. Si l'addition de la base du segment et de l'offset déborde, alors les bits au-delà du vingtième sont perdus. Dit autrement, le calcul de l'adresse physique utilise l'arithmétique modulaire sur le 8086.
Le 80286 en mode réel gère des adresses de base de 24 bits, soit 4 bits de plus que le 8086.Par contre, les offsets restent de 16 bits. L'additionneur du 80286 ne gère pas les débordements comme un 8086 et calcule les bits en trop, au-delà du 20ème. En conséquence, les applications peuvent utiliser plus d'un mébioctet de RAM, mais au prix d'une rétrocompatibilité imparfaite. Pour résoudre ce problème, certains fabricants de carte mère mettaient à 0 le 20ème fil du bus d'adresse, quand le programmeur leur demandait. La carte mère avait un petit interrupteur qui pouvait être activé de manière à activer ou non la mise à 0 du 20ème bit d'adresse.
Le 80386 ajouta deux registres de segment, les registres FS et GS. Les processeurs 386 gérent un mode réel similaire à celui du 286, mais émulé. Un autre mode de segmentation est ajouté avec le 386 : le mode virtual 8086. Il permet d’exécuter des programmes en mode réel, pendant que le système d'exploitation s’exécute en mode protégé. C'est une technique de virtualisation matérielle qui permet d'émuler un 8086 sur un 386. L'avantage est que la compatibilité avec les programmes anciens écrits pour le 8086 est conservée, tout en profitant de la protection mémoire.
Les processeurs x86 64 bits désactivent la segmentation en mode 64 bits.
L'implémentation de la MMU sur les processeurs x86 en mode réel
modifierL'implémentation de la MMU dépend fortement du processeur. Mais sur les processeurs qui font seulement de la segmentation en mode réel, la MMU se résume à quelques registres et des additionneurs/soustracteurs.
Un exemple est l'Intel 8086, un des tout premier processeur Intel. Le processeur était découpé en deux portions : l'interface mémoire et le reste du processeur. L'interface mémoire est appelée la Bus Interface Unit, et le reste du processeur est appelé l'Execution Unit. L'interface mémoire contenait les registres de segment, au nombre de 4, ainsi qu'un additionneur utilisé pour traduire les adresses logiques en adresses physiques. Elle contenait aussi une file d'attente où étaient préchargées les instructions.
Sur le 8086, la MMU est fusionnée avec les circuits de gestion du program counter. Les registres de segment sont regroupés avec le program counter dans un même banc de registres. Au lieu d'utiliser un additionneur séparé pour le program counter et un autre pour le calcul de l'adresse physique, un seul additionneur est utilisé pour les deux. L'idée était de partager l'additionneur, qui servait à la fois à incrémenter le program counter et pour gérer la segmentation. En somme, il n'y a pas vraiment de MMU dédiée, mais un super-circuit en charge du Fetch et de la mémoire virtuelle, ainsi que du préchargement des instructions. Nous en reparlerons au chapitre suivant.

La MMU du 286 était fusionnée avec l'unité de calcul d'adresse. Elle contient les registres de segments, un comparateur pour détecter les accès hors-segment, et plusieurs additionneurs. Il y a un additionneur pour les calculs d'adresse proprement dit, suivi d'un additionneur pour la relocation.

L'occupation de l'espace d'adressage par les segments
modifier
Vous remarquerez qu'avec des registres de segments de 16 bits, on peut gérer 65536 segments différents, chacun de 64 KB. Et cela ne rentre pas dans le mébioctet de mémoire permis avec des adresses de 20 bits. La raison est que plusieurs couples segment+offset pointent vers la même adresse. En tout, chaque adresse peut être adressée par 4096 couples segment+offset différents.
Vous remarquerez aussi qu'avec 4 registres de segment et des segments de 64 KB, on peut remplir au maximum 64 * 6 = 384 KB de RAM, soit bien moins que le mébioctet de mémoire théoriquement adressable. La raison à cela est que plusieurs processus peuvent s'exécuter sur un seul processeur, si l'OS le permet. Mais ce n'était pas le cas à l'époque, le DOS était un OS mono-programmé. La raison est tout autre, comme nous allons le voir dans ce qui suit.
La segmentation en mode réel accepte plusieurs segments par programme
modifierLes programmes peuvent parfaitement répartir leur code machine dans plusieurs segments de code, et faire de même pour les données. La limite de 64 KB par segment est en effet assez limitante, et il n'était pas rare qu'un programme ait besoin de plus juste stocker son code machine ou ses données. La seule contrainte à respecter est que tous les segments doivent être chargés en RAM, il n'y a pas de mémoire virtuelle en mode réel. La seule exception est la pile : elle est forcément dans un segment unique et ne peut pas dépasser 64 KB.
Il faut alors changer de segment à la volée, en remplaçant le segment de code/données par un autre, en modifiant les registres de segment. Pour cela, tous les registres de segment, à l'exception de CS, peuvent être altérés par une instruction d'accès mémoire. Il est possible d'écrire dedans, sans restriction particulière, soit avec une instruction MOV, soit en y copiant le sommet de la pile avec une instruction de dépilage POP. L'absence de sécurité fait que la gestion de ces registres est le fait du programmeur, qui doit redoubler de prudence pour ne pas faire n'importe quoi.
Pour le code machine, le répartir dans plusieurs segments posait des problèmes au niveau des branchements. Si la plupart des branchements sautaient vers une instruction dans le même segment, quelques rares branchements sautaient vers du code machine dans un autre segment. Intel avait prévu le coup et disposait de deux instructions de branchement différentes pour ces deux situations : les near jumps et les far jumps. Les premiers sont des branchements normaux, qui précisent juste l'adresse à laquelle brancher, qui correspond à la position de la fonction dans le segment. Les seconds branchent vers une instruction dans un autre segment, et doivent préciser deux choses : l'adresse de base du segment de destination, et la position de la destination dans le segment. Le branchement met à jour le registre CS avec l'adresse de base, avant de faire le branchement. Ces derniers étaient plus lents, car on n'avait pas à changer de segment et mettre à jour l'état du processeur.
Il y avait la même pour l'instruction d'appel de fonction, avec deux versions de cette instruction. La première version, le near call est un appel de fonction normal, la fonction appelée est dans le segment en cours. Avec la seconde version, le far call, la fonction appelée est dans un segment différent. L'instruction a là aussi besoin de deux opérandes : l'adresse de base du segment de destination, et la position de la fonction dans le segment. Un far call met à jour le registre CS avec l'adresse de base, ce qui fait que les far call sont plus lents que les near call. Il existe aussi la même chose, pour les instructions de retour de fonction, avec une instruction de retour de fonction normale et une instruction de retour qui renvoie vers un autre segment, qui sont respectivement appelées near return et far return. Là encore, il faut préciser l'adresse du segment de destination dans le second cas.
La même chose est possible pour les segments de données. Sauf que cette fois-ci, ce sont les pointeurs qui sont modifiés. pour rappel, les pointeurs sont, en programmation, des variables qui contiennent des adresses. Lors de la compilation, ces pointeurs sont placés soit dans un registre, soit dans les instructions (adressage absolu), ou autres. Ici, il existe deux types de pointeurs, appelés near pointer et far pointer. Vous l'avez deviné, les premiers sont utilisés pour localiser les données dans le segment en cours d'utilisation, alors que les seconds pointent vers une donnée dans un autre segment. Là encore, la différence est que le premier se contente de donner la position dans le segment, alors que les seconds rajoutent l'adresse de base du segment. Les premiers font 16 bits, alors que les seconds en font 32 : 16 bits pour l'adresse de base et 16 pour l'offset.
Les modèles mémoire en mode réel
modifierIl n'était pas nécessaire d'avoir 4 à 6 segments différents, un programme pouvait se débrouiller avec seulement 1 ou 2 segments. D'autres programmes faisaient l'inverse, à savoir qu'ils avaient plus de 6 segments. Suivant le nombre de segments utilisés, la configuration des registres n'était pas la même. Les configurations possibles sont appélées des modèle mémoire, et il y en a en tout 6. En voici la liste :
| Modèle mémoire | Configuration des segments | Configuration des registres | Pointeurs utilisés | Branchements utilisés |
|---|---|---|---|---|
| Tiny* | Segment unique pour tout le programme | CS=DS=SS | near uniquement | near uniquement |
| Small | Segment de donnée séparé du segment de code, pile dans le segment de données | DS=SS | near uniquement | near uniquement |
| Medium | Plusieurs segments de code unique, un seul segment de données | CS, DS et SS sont différents | near et far | near uniquement |
| Compact | Segment de code unique, plusieurs segments de données | CS, DS et SS sont différents | near uniquement | near et far |
| Large | Plusieurs segments de code, plusieurs segments de données | CS, DS et SS sont différents | near et far | near et far |
La segmentation avec une table des segments
modifierLa segmentation avec une table des segments est apparue sur des processeurs assez anciens, le tout premier étant le Burrough 5000. Elle a ensuite été utilisée sur les processeurs x86 de nos PCs, à partir du 286 d'Intel. Tout comme la segmentation en mode réel, la segmentation attribue plusieurs segments par programmes ! Sauf que le nombre de segments géré par le processeur est plus important. Et cela a des répercutions sur la manière dont la traduction d'adresse est effectuée.
Pourquoi plusieurs segments par programme ?
modifierLa taille et le nombre des segments varie grandement d'un processeur à l'autre. Certains ne supportent qu'un petit nombre de segments par processus, les segments sont alors assez gros. D'autres utilisent un grand nombre de segments, qui sont individuellement plus petits. La différence entre ces deux méthodes permet de faire la différence entre segmentation à granularité grossière et segmentation à granularité fine.
La segmentation à granularité grossière
modifierL'utilité d'avoir plusieurs segments par programme n'est pas évidente, mais elle devient évidente quand on se plonge dans le passé. Dans le passé, les programmeurs devaient faire avec une quantité de mémoire limitée et il n'était pas rare que certains programmes utilisent plus de mémoire que disponible sur la machine. Mais les programmeurs concevaient leurs programmes en fonction.
L'idée était d'implémenter un système de mémoire virtuelle, mais émulé en logiciel, appelé l'overlaying. Le programme était découpé en plusieurs morceaux, appelés des overlays. Certains blocs overlays en permanence en RAM, mais d'autres étaient soit chargés en RAM, soit stockés sur le disque dur. Le chargement des overlays ou leur sauvegarde sur le disque dur était réalisé en logiciel, par le programme lui-même. Le matériel n'intervenait pas, comme c'est le cas avec la mémoire virtuelle.

Avec la segmentation, un programme peut utiliser la technique des overlays, mais avec l'aide du matériel. Il suffit de mettre chaque overlay dans son propre segment, et laisser la segmentation faire. Les segments sont swappés en tout ou rien : on doit swapper tout un segment en entier. L'intérêt est que la gestion du swapping est grandement facilitée, vu que c'est le système d'exploitation qui s'occupe de swapper les segments sur le disque dur ou de charger des segments en RAM. Pas besoin pour le programmeur de coder quoique ce soit. Par contre, cela demande l'intervention du programmeur, qui doit découper le programme en segments/overlays de lui-même. Sans cela, la segmentation n'est pas très utile.
La segmentation à granularité fine
modifierLa segmentation à granularité fine pousse le concept encore plus loin. Avec elle, il y a idéalement un segment par entité manipulée par le programme, un segment pour chaque structure de donnée et/ou chaque objet. Par exemple, un tableau aura son propre segment, ce qui est idéal pour détecter les accès hors tableau. Pour les listes chainées, chaque élément de la liste aura son propre segment. Et ainsi de suite, chaque variable agrégée (non-primitive), chaque structure de donnée, chaque objet, chaque instance d'une classe, a son propre segment. Diverses fonctionnalités supplémentaires peuvent être ajoutées, ce qui transforme le processeur en véritable processeur orienté objet, mais passons ces détails pour le moment.
Vu que les segments correspondent à des objets manipulés par le programme, on peut deviner que leur nombre évolue au cours du temps. En effet, les programmes modernes peuvent demander au système d'exploitation du rab de mémoire pour allouer une nouvelle structure de données. Avec la segmentation à granularité fine, cela demande d'allouer un nouveau segment à chaque nouvelle allocation mémoire, à chaque création d'une nouvelle structure de données ou d'un objet. De plus, les programmes peuvent libérer de la mémoire, en supprimant les structures de données ou objets dont ils n'ont plus besoin. Avec la segmentation à granularité fine, cela revient à détruire le segment alloué pour ces objets/structures de données. Le nombre de segments est donc dynamique, il change au cours de l'exécution du programme.
La relocation avec la segmentation
modifierLa segmentation avec une table des segment utilise, comme son nom l'indique, une ou plusieurs tables des segments. Pour rappel, celle-ci est une table qui mémorise, pour chaque segment, quelles sont ses adresses de base et limite. Avec cette forme de segmentation, la table des segments doit respecter plusieurs contraintes. Premièrement, il y a plusieurs segments par programmes. Deuxièmement, le nombre de segments est variable : certains programmes se contenteront d'un seul segment, d'autres de dizaine, d'autres plusieurs centaines, etc. La solution la plus pratique est d'utiliser une table de segment par processus/programme.
La traduction d'adresse additionne l'adresse de base du segment à chaque accès mémoire. Sauf que la présence de plusieurs segments change la donne. On n'a plus une adresse de base, mais une par segment associé au programme. Il faut donc sélectionner la bonne adresse de base, le bon segment. Pour cela, les segments sont numérotés, le nombre s'appelant un indice de segment, appelé sélecteur de segment dans la terminologie Intel. Les segments sont placés dans la table des segments les uns après les autres, dans l'ordre de numérotation. La table des segments est donc un tableau de segment, et l'indice de segment n'est autre que l'indice du segment dans ce tableau.
Il n'y a pas de registre de segment proprement dit, qui mémoriserait l'adresse de base. A la place, les registres de segment mémorisent des sélecteurs de segment. De fait, tout se passe comme si les registres de relocation, qui mémorisent une adresse de base, étaient remplacés par des registres qui mémorisent des sélecteurs de segment. L'adresse manipulée par le processeur se déduit en combinant l'indice de segment qui sélectionne le segment voulu, avec un décalage (offset) qui donne la position de la donnée dans ce segment.
L'accès à la table des segments se fait automatiquement à chaque accès mémoire. La conséquence est que chaque accès mémoire demande d'en faire deux : un pour lire la table des segments, l'autre pour l'accès lui-même. Et il faut dire que les performances s'en ressentent.

Pour effectuer automatiquement l'accès à la table des segments, le processeur doit contenir un registre supplémentaire, qui contient l'adresse de la table de segment, afin de la localiser en mémoire RAM. Nous appellerons ce registre le pointeur de table. Le pointeur de table est combiné avec l'indice de segment pour adresser le descripteur de segment adéquat.

Un point important est que la table des segments n'est pas accessible pour le programme en cours d'exécution. Il ne peut pas lire le contenu de la table des segments, et encore moins la modifier. L'accès se fait seulement de manière indirecte, en faisant usage des indices de segments, mais c'est un adressage indirect. Seul le système d'exploitation peut lire ou écrire la table des segments directement.
La protection mémoire : les accès hors-segments
modifierComme avec la relocation matérielle, le processeur utilise l'adresse ou la taille limite pour vérifier si l'accès mémoire ne déborde pas en-dehors du segment en cours. Pour cela, le processeur compare l'adresse logique accédée avec l'adresse limite, ou compare la taille limite avec le décalage. L'information est lue depuis la table des segments à chaque accès.

Par contre, une nouveauté fait son apparition avec la segmentation : la gestion des droits d'accès. Chaque segment se voit attribuer un certain nombre d'autorisations d'accès qui indiquent si l'on peut lire ou écrire dedans, si celui-ci contient un programme exécutable, etc. Les autorisations pour chaque segment sont placées dans le descripteur de segment. Elles se résument généralement à trois bits, qui indiquent si le segment est accesible en lecture/écriture ou exécutable. Par exemple, il est possible d'interdire d'exécuter le contenu d'un segment, ce qui fournit une protection contre certaines failles de sécurité ou certains virus. Lorsqu'on exécute une opération interdite, le processeur lève une exception matérielle, à charge du système d'exploitation de gérer la situation.
La mémoire virtuelle avec la segmentation
modifierLa mémoire virtuelle est une fonctionnalité souvent implémentée sur les processeurs qui gèrent la segmentation, alors que les processeurs avec relocation matérielle s'en passaient. Il faut dire que l'implémentation de la mémoire virtuelle est beaucoup plus simple avec la segmentation, comparé à la relocation matérielle. Le remplacement des registres de base par des sélecteurs de segment facilite grandement l'implémentation.
Le problème de la mémoire virtuelle est que les segments peuvent être swappés sur le disque dur n'importe quand, sans que le programme soit prévu. Le swapping est réalisé par une interruption de l'OS, qui peut interrompre le programme n'importe quand. Et si un segment est swappé, le registre de base correspondant devient invalide, il point sur une adresse en RAM où le segment était, mais n'est plus. De plus, les segments peuvent être déplacés en mémoire, là encore n'importe quand et d'une manière invisible par le programme, ce qui fait que les registres de base adéquats doivent être modifiés.
Si le programme entier est swappé d'un coup, comme avec la relocation matérielle simple, cela ne pose pas de problèmes. Mais dès qu'on utilise plusieurs registres de base par programme, les choses deviennent soudainement plus compliquées. Le problème est qu'il n'y a pas de mécanismes pour choisir et invalider le registre de base adéquat quand un segment est déplacé/swappé. En théorie, on pourrait imaginer des systèmes qui résolvent le problème au niveau de l'OS, mais tous ont des problèmes qui font que l'implémentation est compliquée ou que les performances sont ridicules.
L'usage d'une table des segments accédée à chaque accès résout complètement le problème. La table des segments est accédée à chaque accès mémoire, elle sait si le segment est swappé ou non, chaque accès vérifie si le segment est en mémoire et quelle est son adresse de base. On peut changer le segment de place n'importe quand, le prochain accès récupérera des informations à jour dans la table des segments.
L'implémentation de la mémoire virtuelle avec la segmentation est simple : il suffit d'ajouter un bit dans les descripteurs de segments, qui indique si le segment est swappé ou non. Tout le reste, la gestion de ce bit, du swap, et tout ce qui est nécessaire, est délégué au système d'exploitation. Lors de chaque accès mémoire, le processeur vérifie ce bit avant de faire la traduction d'adresse, et déclenche une exception matérielle si le bit indique que le segment est swappé. L'exception matérielle est gérée par l'OS.
Le partage de segments
modifierIl est possible de partager un segment entre plusieurs applications. Cela peut servir quand plusieurs instances d'une même application sont lancés simultanément : le code n'ayant pas de raison de changer, celui-ci est partagé entre toutes les instances. Mais ce n'est là qu'un exemple.
Le partage de segment avec des tables des segments locales
modifierLa première solution pour cela est de configurer les tables de segment convenablement. Le même segment peut avoir des droits d'accès différents selon les processus. Les adresses de base/limite sont identiques, mais les tables des segments ont alors des droits d'accès différents. Mais cette méthode de partage des segments a plusieurs défauts.
Premièrement, les sélecteurs de segments ne sont pas les mêmes d'un processus à l'autre, pour un même segment. Le segment partagé peut correspondre au segment numéro 80 dans le premier processus, au segment numéro 1092 dans le second processus. Rien n'impose que les sélecteurs de segment soient les mêmes d'un processus à l'autre, pour un segment identique.
Deuxièmement, les adresses limite et de base sont dupliquées dans plusieurs tables de segments. En soi, cette redondance est un souci mineur. Mais une autre conséquence est une question de sécurité : que se passe-t-il si jamais un processus a une table des segments corrompue ? Il se peut que pour un segment identique, deux processus n'aient pas la même adresse limite, ce qui peut causer des failles de sécurité. Un processus peut alors subir un débordement de tampon, ou tout autre forme d'attaque.

Le partage de segment avec une table des segments globale
modifierUne seconde solution, complémentaire, utilise une table de segment globale, qui mémorise des segments partagés ou accessibles par tous les processus. Les défauts de la méthode précédente disparaissent avec cette technique : un segment est identifié par un sélecteur unique pour tous les processus, il n'y a pas de duplication des descripteurs de segment. Par contre, elle a plusieurs défauts.
Le défaut principal est que cette table des segments est accessible par tous les processus, impossible de ne partager ses segments qu'avec certains pas avec les autres. Un autre défaut est que les droits d'accès à un segment partagé sont identiques pour tous les processus. Impossible d'avoir un segment partagé accessible en lecture seule pour un processus, mais accessible en écriture pour un autre. Il est possible de corriger ces défauts, mais nous en parlerons dans la section sur les architectures à capacité.
L'extension d'adresse avec la segmentation
modifierL'extension d'adresse est possible avec la segmentation, de la même manière qu'avec la relocation matérielle. Il suffit juste que les adresses de base soient aussi grandes que le bus d'adresse. Mais il y a une différence avec la relocation matérielle : un même programme peut utiliser plus de mémoire qu'il n'y en a dans l'espace d'adressage. La raison est simple : il y a un espace d'adressage par segment, plusieurs segments par programme.
Pour donner un exemple, prenons un processeur 16 bits, qui peut adresser 64 kibioctets, associé à une mémoire de 4 mébioctets. Il est possible de placer le code machine dans les premiers 64k de la mémoire, la pile du programme dans les 64k suivants, le tas dans les 64k encore après, et ainsi de suite. Le programme dépasse donc les 64k de mémoire de l'espace d'adressage. Ce genre de chose est impossible avec la relocation, où un programme est limité par l'espace d'adressage.
Le mode protégé des processeurs x86
modifierL'Intel 80286, aussi appelé 286, ajouta un mode de segmentation séparé du mode réel, qui ajoute une protection mémoire à la segmentation, ce qui lui vaut le nom de mode protégé. Dans ce mode, les registres de segment ne contiennent pas des adresses de base, mais des sélecteurs de segments qui sont utilisés pour l'accès à la table des segments en mémoire RAM.
Le 286 bootait en mode réel, puis le système d'exploitation devait faire quelques manipulations pour passer en mode protégé. Le 286 était pensé pour être rétrocompatible au maximum avec le 80186. Mais les différences entre le 286 et le 8086 étaient majeures, au point que les applications devaient être réécrites intégralement pour profiter du mode protégé. Un mode de compatibilité permettait cependant aux applications destinées au 8086 de fonctionner, avec même de meilleures performances. Aussi, le mode protégé resta inutilisé sur la plupart des applications exécutées sur le 286.
Vint ensuite le processeur 80386, renommé en 386 quelques années plus tard. Sur ce processeur, les modes réel et protégé sont conservés tel quel, à une différence près : toutes les adresses passent à 32 bits, qu'il s'agisse de l'adresse physique envoyée sur le bus, de l'adresse de base du segment ou des offsets. Le processeur peut donc adresser un grand nombre de segments : 2^32, soit plus de 4 milliards. Les segments grandissent aussi et passent de 64 KB maximum à 4 gibioctets maximum. Mais surtout : le 386 ajouta le support de la pagination en plus de la segmentation. Ces modifications ont été conservées sur les processeurs 32 bits ultérieurs.
Les tables des segments des processeurs x86
modifierLes processeurs gèrent deux types de tables des segments : une table locale pour chaque processus, et une table globale partagée netre tous les processus.
La table globale est utilisée pour les segments du noyau et la mémoire partagée entre processus. Un défaut est qu'un segment partagé par la table globale est visible par tous les processus, avec les mêmes droits d'accès. Ce qui fait que cette méthode était peu utilisée en pratique. La table globale mémorise aussi des pointeurs vers les tables locales, avec un descripteur de segment par table locale.
La table locale gére les segments de son processus. Il est possible d'avoir plusieurs tables locales, mais une seule doit être active, vu que le processeur ne peut exécuter qu'un seul processus en même temps. Chaque table locale définit 8192 segments, pareil pour la table globale.
Les descripteurs de segments des processeurs x86
modifierSur les processeurs x86 32 bits, un descripteur de segment est organisé comme suit, pour les architectures 32 bits. On y trouve l'adresse de base et la taille limite, ainsi que de nombreux bits de contrôle.
Le premier groupe de bits de contrôle est l'octet en bleu à droite. Il contient :
- le bit P qui indique que l'entrée contient un descripteur valide, qu'elle n'est pas vide ;
- deux bits DPL qui indiquent le niveau de privilège du segment (noyau, utilisateur, les deux intermédiaires spécifiques au x86) ;
- un bit S qui précise si le segment est de type système (utiles pour l'OS) ou un segment de code/données.
- un champ Type qui contient les bits suivants : un bit E qui indique si le segment contient du code exécutable ou non, le bit RW qui indique s'il est en lecture seule ou non, les bits A et DC assez spécifiques.
En haut à gauche, en bleu, on trouve deux bits :
- Le bit G indique comment interpréter la taille contenue dans le descripteur : 0 si la taille est exprimée en octets, 1 si la taille est un nombre de pages de 4 kibioctets. Ce bit précise si on utilise la segmentation seule, ou combinée avec la pagination.
- Le bit DB précise si l'on utilise des segments en mode de compatibilité 16 bits ou des segments 32 bits.

Les sélecteurs de segments sur les processeurs x86
modifierLes indices de segment sont appelés des sélecteurs de segment. Ils ont une taille de 16 bits. Les 16 bits sont organisés comme suit :
- 13 bits pour le numéro du segment dans la table des segments, l'indice de segment proprement dit ;
- un bit qui précise s'il faut accéder à la table des segments globale ou locale ;
- deux bits qui indiquent le niveau de privilège de l'accès au segment (les 4 niveaux de protection, dont l'espace noyau et utilisateur).

En tout, l'indice permet de gérer 8192 segments pour la table locale et 8192 segments de la table globale.
La segmentation sur les processeurs Burrough B5000 et plus
modifierLe Burrough B5000 est un très vieil ordinateur, commercialisé à partir de l'année 1961. Ses successeurs reprennent globalement la même architecture. C'était une machine à pile, doublé d'une architecture taguée, choses très rare de nos jours. Mais ce qui va nous intéresser dans ce chapitre est que ce processeur incorporait la segmentation, avec cependant une différence de taille : un programme avait accès à un grand nombre de segments. La limite était de 1024 segments par programme ! Il va de soi que des segments plus petits favorise l'implémentation de la mémoire virtuelle, mais complexifie la relocation et le reste, comme nous allons le voir.
Le processeur gère deux types de segments : les segments de données et de procédure/fonction. Les premiers mémorisent un bloc de données, dont le contenu est laissé à l'appréciation du programmeur. Les seconds sont des segments qui contiennent chacun une procédure, une fonction. L'usage des segments est donc différent de ce qu'on a sur les processeurs x86, qui n'avaient qu'un segment unique pour l'intégralité du code machine. Un seul segment de code machine x86 est découpé en un grand nombre de segments de code sur les processeurs Burrough.
La table des segments
modifierLa table des segments contenait 1024 entrées de 48 bits chacune. Fait intéressant, chaque entrée de la table des segments pouvait mémoriser non seulement un descripteur de segment, mais aussi une valeur flottante ou d'autres types de données ! Parler de table des segments est donc quelque peu trompeur, car cette table ne gère pas que des segments, mais aussi des données. La documentation appelaiat cette table la Program Reference Table, ou PRT.
La raison de ce choix quelque peu bizarre est que les instructions ne gèrent pas d'adresses proprement dit. Tous les accès mémoire à des données en-dehors de la pile passent par la segmentation, ils précisent tous un indice de segment et un offset. Pour éviter d'allouer un segment pour chaque donnée, les concepteurs du processeur ont décidé qu'une entrée pouvait contenir directement la donnée entière à lire/écrire.
Les descripteurs de segments
modifierLa PRT supporte trois types de segments/descripteurs : les descripteurs de données, les descripteurs de programme et les descripteurs d'entrées-sorties. Les premiers décrivent des segments de données. Les seconds sont associés aux segments de procédure/fonction et sont utilisés pour les appels de fonction (qui passent, eux aussi, par la segmentation). Le dernier type de descripteurs sert pour les appels systèmes et les communications avec l'OS ou les périphériques.
Chaque entrée de la PRT contient un tag, une suite de bit qui indique le type de l'entrée : est-ce qu'elle contient un descripteur de segment, une donnée, autre. Les descripteurs contiennent aussi un bit de présence qui indique si le segment a été swappé ou non. Car oui, les segments pouvaient être swappés sur ce processeur, ce qui n'est pas étonnant vu que les segments sont plus petits sur cette architecture. Le descripteur contient aussi l'adresse de base du segment ainsi que sa taille, et diverses informations pour le retrouver sur le disque dur s'il est swappé.
- L'adresse mémorisée ne faisait que 15 bits, ce qui permettait d'adresse 32 kibi-mots, soit 192 kibioctets de mémoire. Diverses techniques d'extension d'adressage étaient disponibles pour contourner cette limitation. Outre l'usage de l'overlay, le processeur et l'OS géraient aussi des identifiants d'espace d'adressage et en fournissaient plusieurs par processus. Les processeurs Borrough suivants utilisaient des adresses plus grandes, de 20 bits, ce qui tempérait le problème.

Les architectures à capacités
modifierLes architectures à capacité utilisent la segmentation à granularité fine, mais ajoutent des mécanismes de protection mémoire assez particuliers, qui font que les architectures à capacité se démarquent du reste. Les architectures de ce type sont très rares et sont des processeurs assez anciens. Le premier d'entre eux était le Plessey System 250, qui date de 1969. Il fu suivi par le CAP computer, vendu entre les années 70 et 77. En 1978, le System/38 d'IBM a eu un petit succès commercial. En 1980, la Flex machine a aussi été vendue, mais à très peu d'examplaires, comme les autres architectures à capacité. Et enfin, en 1981, l'architecture à capacité la plus connue, l'Intel iAPX 432 a été commercialisée. Depuis, la seule architecture de ce type est en cours de développement. Il s'agit de l'architecture CHERI, dont la mise en projet date de 2014.
Le partage de la mémoire sur les architectures à capacités
modifierLe partage de segment est grandement modifié sur les architectures à capacité. Avec la segmentation normale, il y a une table de segment par processus. Les conséquences sont assez nombreuses, mais la principale est que partager un segment entre plusieurs processus est compliqué. Les défauts ont été évoqués plus haut. Les sélecteurs de segments ne sont pas les mêmes d'un processus à l'autre, pour un même segment. De plus, les adresses limite et de base sont dupliquées dans plusieurs tables de segments, et cela peut causer des problèmes de sécurité si une table des segments est modifiée et pas l'autre. Et il y a d'autres problèmes, tout aussi importants.

A l'opposé, les architectures à capacité utilisent une table des segments unique pour tous les processus. La table des segments unique sera appelée dans de ce qui suit la table des segments globale, ou encore la table globale. En conséquence, les adresses de base et limite ne sont présentes qu'en un seul exemplaire par segment, au lieu d'être dupliquées dans autant de processus que nécessaire. De plus, cela garantit que l'indice de segment est le même quelque soit le processus qui l'utilise.
Un défaut de cette approche est au niveau des droits d'accès. Avec la segmentation normale, les droits d'accès pour un segment sont censés changer d'un processus à l'autre. Par exemple, tel processus a accès en lecture seule au segment, l'autre seulement en écriture, etc. Mais ici, avec une table des segments uniques, cela ne marche plus : incorporer les droits d'accès dans la table des segments ferait que tous les processus auraient les mêmes droits d'accès au segment. Et il faut trouver une solution.
Les capacités sont des pointeurs protégés
modifierPour éviter cela, les droits d'accès sont combinés avec les sélecteurs de segments. Les sélecteurs des segments sont remplacés par des capacités, des pointeurs particuliers formés en concaténant l'indice de segment avec les droits d'accès à ce segment. Si un programme veut accéder à une adresse, il fournit une capacité de la forme "sélecteur:droits d'accès", et un décalage qui indique la position de l'adresse dans le segment.
Il est impossible d'accéder à un segment sans avoir la capacité associée, c'est là une sécurité importante. Un accès mémoire demande que l'on ait la capacité pour sélectionner le bon segment, mais aussi que les droits d'accès en permettent l'accès demandé. Par contre, les capacités peuvent être passées d'un programme à un autre sans problème, les deux programmes pourront accéder à un segment tant qu'ils disposent de la capacité associée.

Mais cette solution a deux problèmes très liés. Au niveau des sélecteurs de segment, le problème est que les sélecteur ont une portée globale. Avant, l'indice de segment était interne à un programme, un sélecteur ne permettait pas d'accéder au segment d'un autre programme. Sur les architectures à capacité, les sélecteurs ont une portée globale. Si un programme arrive à forger un sélecteur qui pointe vers un segment d'un autre programme, il peut théoriquement y accéder, à condition que les droits d'accès le permettent. Et c'est là qu'intervient le second problème : les droits d'accès ne sont plus protégés par l'espace noyau. Les droits d'accès étaient dans la table de segment, accessible uniquement en espace noyau, ce qui empêchait un processus de les modifier. Avec une capacité, il faut ajouter des mécanismes de protection qui empêchent un programme de modifier les droits d'accès à un segment et de générer un indice de segment non-prévu.
La première sécurité est qu'un programme ne peut pas créer une capacité, seul le système d'exploitation le peut. Les capacités sont forgées lors de l'allocation mémoire, ce qui est du ressort de l'OS. Pour rappel, un programme qui veut du rab de mémoire RAM peut demander au système d'exploitation de lui allouer de la mémoire supplémentaire. Le système d'exploitation renvoie alors un pointeurs qui pointe vers un nouveau segment. Le pointeur est une capacité. Il doit être impossible de forger une capacité, en-dehors d'une demande d'allocation mémoire effectuée par l'OS. Typiquement, la forge d'une capacité se fait avec des instructions du processeur, que seul l'OS peut éxecuter (pensez à une instruction qui n'est accessible qu'en espace noyau).
La seconde protection est que les capacités ne peuvent pas être modifiées sans raison valable, que ce soit pour l'indice de segment ou les droits d'accès. L'indice de segment ne peut pas être modifié, quelqu'en soit la raison. Pour les droits d'accès, la situation est plus compliquée. Il est possible de modifier ses droits d'accès, mais sous conditions. Réduire les droits d'accès d'une capacité est possible, que ce soit en espace noyau ou utilisateur, pas l'OS ou un programme utilisateur, avec une instruction dédiée. Mais augmenter les droits d'accès, seul l'OS peut le faire avec une instruction précise, souvent exécutable seulement en espace noyau.
Les capacités peuvent être copiées, et même transférées d'un processus à un autre. Les capacités peuvent être détruites, ce qui permet de libérer la mémoire utilisée par un segment. La copie d'une capacité est contrôlée par l'OS et ne peut se faire que sous conditions. La destruction d'une capacité est par contre possible par tous les processus. La destruction ne signifie pas que le segment est effacé, il est possible que d'autres processus utilisent encore des copies de la capacité, et donc le segment associé. On verra quand la mémoire est libérée plus bas.
Protéger les capacités demande plusieurs conditions. Premièrement, le processeur doit faire la distinction entre une capacité et une donnée. Deuxièmement, les capacités ne peuvent être modifiées que par des instructions spécifiques, dont l'exécution est protégée, réservée au noyau. En clair, il doit y avoir une séparation matérielle des capacités, qui sont placées dans des registres séparés. Pour cela, deux solutions sont possibles : soit les capacités remplacent les adresses et sont dispersées en mémoire, soit elles sont regroupées dans un segment protégé.
La liste des capacités
modifierAvec la première solution, on regroupe les capacités dans un segment protégé. Chaque programme a accès à un certain nombre de segments et à autant de capacités. Les capacités d'un programme sont souvent regroupées dans une liste de capacités, appelée la C-list. Elle est généralement placée en mémoire RAM. Elle est ce qu'il reste de la table des segments du processus, sauf que cette table ne contient pas les adresses du segment, qui sont dans la table globale. Tout se passe comme si la table des segments de chaque processus est donc scindée en deux : la table globale partagée entre tous les processus contient les informations sur les limites des segments, la C-list mémorise les droits d'accès et les sélecteurs pour identifier chaque segment. C'est un niveau d'indirection supplémentaire par rapport à la segmentation usuelle.

La liste de capacité est lisible par le programme, qui peut copier librement les capacités dans les registres. Par contre, la liste des capacités est protégée en écriture. Pour le programme, il est impossible de modifier les capacités dedans, impossible d'en rajouter, d'en forger, d'en retirer. De même, il ne peut pas accéder aux segments des autres programmes : il n'a pas les capacités pour adresser ces segments.
Pour protéger la C-list en écriture, la solution la plus utilisée consiste à placer la C-list dans un segment dédié. Le processeur gère donc plusieurs types de segments : les segments de capacité pour les C-list, les autres types segments pour le reste. Un défaut de cette approche est que les adresses/capacités sont séparées des données. Or, les programmeurs mixent souvent adresses et données, notamment quand ils doivent manipuler des structures de données comme des listes chainées, des arbres, des graphes, etc.
L'usage d'une C-list permet de se passer de la séparation entre espace noyau et utilisateur ! Les segments de capacité sont eux-mêmes adressés par leur propre capacité, avec une capacité par segment de capacité. Le programme a accès à la liste de capacité, comme l'OS, mais leurs droits d'accès ne sont pas les mêmes. Le programme a une capacité vers la C-list qui n'autorise pas l'écriture, l'OS a une autre capacité qui accepte l'écriture. Les programmes ne pourront pas forger les capacités permettant de modifier les segments de capacité. Une méthode alternative est de ne permettre l'accès aux segments de capacité qu'en espace noyau, mais elle est redondante avec la méthode précédente et moins puissante.
Les capacités dispersées, les architectures taguées
modifierUne solution alternative laisse les capacités dispersées en mémoire. Les capacités remplacent les adresses/pointeurs, et elles se trouvent aux mêmes endroits : sur la pile, dans le tas. Comme c'est le cas dans les programmes modernes, chaque allocation mémoire renvoie une capacité, que le programme gére comme il veut. Il peut les mettre dans des structures de données, les placer sur la pile, dans des variables en mémoire, etc. Mais il faut alors distinguer si un mot mémoire contient une capacité ou une autre donnée, les deux ne devant pas être mixés.
Pour cela, chaque mot mémoire se voit attribuer un certain bit qui indique s'il s'agit d'un pointeur/capacité ou d'autre chose. Mais cela demande un support matériel, ce qui fait que le processeur devient ce qu'on appelle une architecture à tags, ou tagged architectures. Ici, elles indiquent si le mot mémoire contient une adresse:capacité ou une donnée.

L'inconvénient est le cout en matériel de cette solution. Il faut ajouter un bit à chaque case mémoire, le processeur doit vérifier les tags avant chaque opération d'accès mémoire, etc. De plus, tous les mots mémoire ont la même taille, ce qui force les capacités à avoir la même taille qu'un entier. Ce qui est compliqué.
Les registres de capacité
modifierLes architectures à capacité disposent de registres spécialisés pour les capacités, séparés pour les entiers. La raison principale est une question de sécurité, mais aussi une solution pragmatique au fait que capacités et entiers n'ont pas la même taille. Les registres dédiés aux capacités ne mémorisent pas toujours des capacités proprement dites. A la place, ils mémorisent des descripteurs de segment, qui contiennent l'adresse de base, limite et les droits d'accès. Ils sont utilisés pour la relocation des accès mémoire ultérieurs. Ils sont en réalité identiques aux registres de relocation, voire aux registres de segments. Leur utilité est d'accélérer la relocation, entre autres.
Les processeurs à capacité ne gèrent pas d'adresses proprement dit, comme pour la segmentation avec plusieurs registres de relocation. Les accès mémoire doivent préciser deux choses : à quel segment on veut accéder, à quelle position dans le segment se trouve la donnée accédée. La première information se trouve dans le mal nommé "registre de capacité", la seconde information est fournie par l'instruction d'accès mémoire soit dans un registre (Base+Index), soit en adressage base+offset.
Les registres de capacités sont accessibles à travers des instructions spécialisées. Le processeur ajoute des instructions LOAD/STORE pour les échanges entre table des segments et registres de capacité. Ces instructions sont disponibles en espace utilisateur, pas seulement en espace noyau. Lors du chargement d'une capacité dans ces registres, le processeur vérifie que la capacité chargée est valide, et que les droits d'accès sont corrects. Puis, il accède à la table des segments, récupère les adresses de base et limite, et les mémorise dans le registre de capacité. Les droits d'accès et d'autres méta-données sont aussi mémorisées dans le registre de capacité. En somme, l'instruction de chargement prend une capacité et charge un descripteur de segment dans le registre.
Avec ce genre de mécanismes, il devient difficile d’exécuter certains types d'attaques, ce qui est un gage de sureté de fonctionnement indéniable. Du moins, c'est la théorie, car tout repose sur l'intégrité des listes de capacité. Si on peut modifier celles-ci, alors il devient facile de pouvoir accéder à des objets auxquels on n’aurait pas eu droit.
Le recyclage de mémoire matériel
modifierLes architectures à capacité séparent les adresses/capacités des nombres entiers. Et cela facilite grandement l'implémentation de la garbage collection, ou recyclage de la mémoire, à savoir un ensemble de techniques logicielles qui visent à libérer la mémoire inutilisée.
Rappelons que les programmes peuvent demander à l'OS un rab de mémoire pour y placer quelque chose, généralement une structure de donnée ou un objet. Mais il arrive un moment où cet objet n'est plus utilisé par le programme. Il peut alors demander à l'OS de libérer la portion de mémoire réservée. Sur les architectures à capacité, cela revient à libérer un segment, devenu inutile. La mémoire utilisée par ce segment est alors considérée comme libre, et peut être utilisée pour autre chose. Mais il arrive que les programmes ne libèrent pas le segment en question. Soit parce que le programmeur a mal codé son programme, soit parce que le compilateur n'a pas fait du bon travail ou pour d'autres raisons.
Pour éviter cela, les langages de programmation actuels incorporent des garbage collectors, des morceaux de code qui scannent la mémoire et détectent les segments inutiles. Pour cela, ils doivent identifier les adresses manipulées par le programme. Si une adresse pointe vers un objet, alors celui-ci est accessible, il sera potentiellement utilisé dans le futur. Mais si aucune adresse ne pointe vers l'objet, alors il est inaccessible et ne sera plus jamais utilisé dans le futur. On peut libérer les objets inaccessibles.
Identifier les adresses est cependant très compliqué sur les architectures normales. Sur les processeurs modernes, les garbage collectors scannent la pile à la recherche des adresses, et considèrent tout mot mémoire comme une adresse potentielle. Mais les architectures à capacité rendent le recyclage de la mémoire très facile. Un segment est accessible si le programme dispose d'une capacité qui pointe vers ce segment, rien de plus. Et les capacités sont facilement identifiables : soit elles sont dans la liste des capacités, soit on peut les identifier à partir de leur tag.
Le recyclage de mémoire était parfois implémenté directement en matériel. En soi, son implémentation est assez simple, et peu être réalisé dans le microcode d'un processeur. Une autre solution consiste à utiliser un second processeur, spécialement dédié au recyclage de mémoire, qui exécute un programme spécialement codé pour. Le programme en question est placé dans une mémoire ROM, reliée directement à ce second processeur.
L'intel iAPX 432
modifierVoyons maintenat une architecture à capacité assez connue : l'Intel iAPX 432. Oui, vous avez bien lu : Intel a bel et bien réalisé un processeur orienté objet dans sa jeunesse. La conception du processeur Intel iAPX 432 commença en 1975, afin de créer un successeur digne de ce nom aux processeurs 8008 et 8080.
La conception du processeur Intel iAPX 432 commença en 1975, afin de créer un successeur digne de ce nom aux processeurs 8008 et 8080. Ce processeur s'est très faiblement vendu en raison de ses performances assez désastreuses et de défauts techniques certains. Par exemple, ce processeur était une machine à pile à une époque où celles-ci étaient tombées en désuétude, il ne pouvait pas effectuer directement de calculs avec des constantes entières autres que 0 et 1, ses instructions avaient un alignement bizarre (elles étaient bit-alignées). Il avait été conçu pour maximiser la compatibilité avec le langage ADA, un langage assez peu utilisé, sans compter que le compilateur pour ce processeur était mauvais.
Les segments prédéfinis de l'Intel iAPX 432
modifierL'Intel iAPX432 gére plusieurs types de segments. Rien d'étonnant à cela, les Burrough géraient eux aussi plusieurs types de segments, à savoir des segments de programmes, des segments de données, et des segments d'I/O. C'est la même chose sur l'Intel iAPX 432, mais en bien pire !
Les segments de données sont des segments génériques, dans lequels on peut mettre ce qu'on veut, suivant les besoins du programmeur. Ils sont tous découpés en deux parties de tailles égales : une partie contenant les données de l'objet et une partie pour les capacités. Les capacités d'un segment pointent vers d'autres segments, ce qui permet de créer des structures de données assez complexes. La ligne de démarcation peut être placée n'importe où dans le segment, les deux portions ne sont pas de taille identique, elles ont des tailles qui varient de segment en segment. Il est même possible de réserver le segment entier à des données sans y mettre de capacités, ou inversement. Les capacités et données sont adressées à partir de la ligne de démarcation, qui sert d'adresse de base du segment. Suivant l'instruction utilisée, le processeur accède à la bonne portion du segment.
Le processeur supporte aussi d'autres segments pré-définis, qui sont surtout utilisés par le système d'exploitation :
- Des segments d'instructions, qui contiennent du code exécutable, typiquement un programme ou des fonctions, parfois des threads.
- Des segments de processus, qui mémorisent des processus entiers. Ces segments contiennent des capacités qui pointent vers d'autres segments, notamment un ou plusieurs segments de code, et des segments de données.
- Des segments de domaine, pour les modules ou librairies dynamiques.
- Des segments de contexte, utilisés pour mémoriser l'état d'un processus, utilisés par l'OS pour faire de la commutation de contexte.
- Des segments de message, utilisés pour la communication entre processus par l'intermédiaire de messages.
- Et bien d'autres encores.
Sur l'Intel iAPX 432, chaque processus est considéré comme un objet à part entière, qui a son propre segment de processus. De même, l'état du processeur (le programme qu'il est en train d’exécuter, son état, etc.) est stocké en mémoire dans un segment de contexte. Il en est de même pour chaque fonction présente en mémoire : elle était encapsulée dans un segment, sur lequel seules quelques manipulations étaient possibles (l’exécuter, notamment). Et ne parlons pas des appels de fonctions qui stockaient l'état de l'appelé directement dans un objet spécial. Bref, de nombreux objets système sont prédéfinis par le processeur : les objets stockant des fonctions, les objets stockant des processus, etc.
L'Intel 432 possédait dans ses circuits un garbage collector matériel. Pour faciliter son fonctionnement, certains bits de l'objet permettaient de savoir si l'objet en question pouvait être supprimé ou non.
Le support de la segmentation sur l'Intel iAPX 432
modifierLa table des segments est une table hiérarchique, à deux niveaux. Le premier niveau est une Object Table Directory, qui réside toujours en mémoire RAM. Elle contient des descripteurs qui pointent vers des tables secondaires, appelées des Object Table. Il y a plusieurs Object Table, typiquement une par processus. Plusieurs processus peuvent partager la même Object Table. Les Object Table peuvent être swappées, mais pas l'Object Table Directory.
Une capacité tient compte de l'organisation hiérarchique de la table des segments. Elle contient un indice qui précise quelle Object Table utiliser, et l'indice du segment dans cette Object Table. Le premier indice adresse l'Object Table Directory et récupère un descripteur de segment qui pointe sur la bonne Object Table. Le second indice est alors utilisé pour lire l'adresse de base adéquate dans cette Object Table. La capacité contient aussi des droits d'accès en lecture, écriture, suppression et copie. Il y a aussi un champ pour le type, qu'on verra plus bas. Au fait : les capacités étaient appelées des Access Descriptors dans la documentation officielle.
Une capacité fait 32 bits, avec un octet utilisé pour les droits d'accès, laissant 24 bits pour adresser les segments. Le processeur gérait jusqu'à 2^24 segments/objets différents, pouvant mesurer jusqu'à 64 kibioctets chacun, ce qui fait 2^40 adresses différentes, soit 1024 gibioctets. Les 24 bits pour adresser les segments sont partagés moitié-moitié pour l'adressage des tables, ce qui fait 4096 Object Table différentes dans l'Object Table Directory, et chaque Object Table contient 4096 segments.
Le jeu d'instruction de l'Intel iAPX 432
modifierL'Intel iAPX 432 est une machine à pile. Le jeu d'instruction de l'Intel iAPX 432 gère pas moins de 230 instructions différentes. Il gére deux types d'instructions : les instructions normales, et celles qui manipulent des segments/objets. Les premières permettent de manipuler des nombres entiers, des caractères, des chaînes de caractères, des tableaux, etc.
Les secondes sont spécialement dédiées à la manipulation des capacités. Il y a une instruction pour copier une capacité, une autre pour invalider une capacité, une autre pour augmenter ses droits d'accès (instruction sécurisée, éxecutable seulement sous certaines conditions), une autre pour restreindre ses droits d'accès. deux autres instructions créent un segment et renvoient la capacité associée, la première créant un segment typé, l'autre non.
le processeur gérait aussi des instructions spécialement dédiées à la programmation système et idéales pour programmer des systèmes d'exploitation. De nombreuses instructions permettaient ainsi de commuter des processus, faire des transferts de messages entre processus, etc. Environ 40 % du micro-code était ainsi spécialement dédié à ces instructions spéciales.
Les instructions sont de longueur variable et peuvent prendre n'importe quelle taille comprise entre 10 et 300 bits, sans vraiment de restriction de taille. Les bits d'une instruction sont regroupés en 4 grands blocs, 4 champs, qui ont chacun une signification particulière.
- Le premier est l'opcode de l'instruction.
- Le champ reference, doit être interprété différemment suivant la donnée à manipuler. Si cette donnée est un entier, un caractère ou un flottant, ce champ indique l'emplacement de la donnée en mémoire. Alors que si l'instruction manipule un objet, ce champ spécifie la capacité de l'objet en question. Ce champ est assez complexe et il est sacrément bien organisé.
- Le champ format, n'utilise que 4 bits et a pour but de préciser si les données à manipuler sont en mémoire ou sur la pile.
- Le champ classe permet de dire combien de données différentes l'instruction va devoir manipuler, et quelles seront leurs tailles.

Le support de l'orienté objet sur l'Intel iAPX 432
modifierL'Intel 432 permet de définir des objets, qui correspondent aux classes des langages orientés objets. L'Intel 432 permet, à partir de fonctions définies par le programmeur, de créer des domain objects, qui correspondent à une classe. Un domain object est un segment de capacité, dont les capacités pointent vers des fonctions ou un/plusieurs objets. Les fonctions et les objets sont chacun placés dans un segment. Une partie des fonctions/objets sont publics, ce qui signifie qu'ils sont accessibles en lecture par l'extérieur. Les autres sont privées, inaccessibles aussi bien en lecture qu'en écriture.
L'exécution d'une fonction demande que le branchement fournisse deux choses : une capacité vers le domain object, et la position de la fonction à exécuter dans le segment. La position permet de localiser la capacité de la fonction à exécuter. En clair, on accède au domain object d'abord, pour récupérer la capacité qui pointe vers la fonction à exécuter.
Il est aussi possible pour le programmeur de définir de nouveaux types non supportés par le processeur, en faisant appel au système d'exploitation de l'ordinateur. Au niveau du processeur, chaque objet est typé au niveau de son object descriptor : celui-ci contient des informations qui permettent de déterminer le type de l'objet. Chaque type se voit attribuer un domain object qui contient toutes les fonctions capables de manipuler les objets de ce type et que l'on appelle le type manager. Lorsque l'on veut manipuler un objet d'un certain type, il suffit d'accéder à une capacité spéciale (le TCO) qui pointera dans ce type manager et qui précisera quel est l'objet à manipuler (en sélectionnant la bonne entrée dans la liste de capacité). Le type d'un objet prédéfini par le processeur est ainsi spécifié par une suite de 8 bits, tandis que le type d'un objet défini par le programmeur est défini par la capacité spéciale pointant vers son type manager.
Conclusion
modifierPour ceux qui veulent en savoir plus, je conseille la lecture de ce livre, disponible gratuitement sur internet (merci à l'auteur pour cette mise à disposition) :
Voici un document qui décrit le fonctionnement de l'Intel iAPX432 :
La pagination
modifierAvec la pagination, la mémoire est découpée en blocs de taille fixe, appelés des pages mémoires. La taille des pages varie suivant le processeur et le système d'exploitation et tourne souvent autour de 4 kibioctets. Mais elles sont de taille fixe : on ne peut pas en changer la taille. C'est la différence avec les segments, qui sont de taille variable. Le contenu d'une page en mémoire fictive est rigoureusement le même que le contenu de la page correspondante en mémoire physique.
L'espace d'adressage est découpé en pages logiques, alors que la mémoire physique est découpée en pages physique de même taille. Les pages logiques correspondent soit à une page physique, soit à une page swappée sur le disque dur. Quand une page logique est associée à une page physique, les deux ont le même contenu, mais pas les mêmes adresses. Les pages logiques sont numérotées, en partant de 0, afin de pouvoir les identifier/sélectionner. Même chose pour les pages physiques, qui sont elles aussi numérotées en partant de 0.

Pour information, le tout premier processeur avec un système de mémoire virtuelle était le super-ordinateur Atlas. Il utilisait la pagination, et non la segmentation. Mais il fallu du temps avant que la méthode de la pagination prenne son essor dans les processeurs commerciaux x86.
Un point important est que la pagination implique une coopération entre OS et hardware, les deux étant fortement mélés. Une partie des informations de cette section auraient tout autant leur place dans le wikilivre sur les systèmes d'exploitation, mais il est plus simple d'en parler ici.
La mémoire virtuelle : le swapping et le remplacement des pages mémoires
modifierLe système d'exploitation mémorise des informations sur toutes les pages existantes dans une table des pages. C'est un tableau où chaque ligne est associée à une page logique. Une ligne contient un bit Valid qui indique si la page logique associée est swappée sur le disque dur ou non, et la position de la page physique correspondante en mémoire RAM. Elle peut aussi contenir des bits pour la protection mémoire, et bien d'autres. Les lignes sont aussi appelées des entrées de la table des pages

De plus, le système d'exploitation conserve une liste des pages vides. Le nom est assez clair : c'est une liste de toutes les pages de la mémoire physique qui sont inutilisées, qui ne sont allouées à aucun processus. Ces pages sont de la mémoire libre, utilisable à volonté. La liste des pages vides est mise à jour à chaque fois qu'un programme réserve de la mémoire, des pages sont alors prises dans cette liste et sont allouées au programme demandeur.
Les défauts de page
modifierLorsque l'on veut traduire l'adresse logique d'une page mémoire, le processeur vérifie le bit Valid et l'adresse physique. Si le bit Valid est à 1 et que l'adresse physique est présente, la traduction d'adresse s'effectue normalement. Mais si ce n'est pas le cas, l'entrée de la table des pages ne contient pas de quoi faire la traduction d'adresse. Soit parce que la page est swappée sur le disque dur et qu'il faut la copier en RAM, soit parce que les droits d'accès ne le permettent pas, soit parce que la page n'a pas encore été allouée, etc. On fait alors face à un défaut de page. Un défaut de page a lieu quand la MMU ne peut pas associer l'adresse logique à une adresse physique, quelque qu'en soit la raison.
Il existe deux types de défauts de page : mineurs et majeurs. Un défaut de page majeur a lieu quand on veut accéder à une page déplacée sur le disque dur. Un défaut de page majeur lève une exception matérielle dont la routine rapatriera la page en mémoire RAM. S'il y a de la place en mémoire RAM, il suffit d'allouer une page vide et d'y copier la page chargée depuis le disque dur. Mais si ce n'est par le cas, on va devoir faire de la place en RAM en déplaçant une page mémoire de la RAM vers le disque dur. Dans tous les cas, c'est le système d'exploitation qui s'occupe du chargement de la page, le processeur n'est pas impliqué. Une fois la page chargée, la table des pages est mise à jour et la traduction d'adresse peut recommencer. Si je dis recommencer, c'est car l'accès mémoire initial est rejoué à l'identique, sauf que la traduction d'adresse réussit cette fois-ci.
Un défaut de page mineur a lieu dans des circonstances pas très intuitives : la page est en mémoire physique, mais l'adresse physique de la page n'est pas accessible. Par exemple, il est possible que des sécurités empêchent de faire la traduction d'adresse, pour des raisons de protection mémoire. Une autre raison est la gestion des adresses synonymes, qui surviennent quand on utilise des libraires partagées entre programmes, de la communication inter-processus, des optimisations de type copy-on-write, etc. Enfin, une dernière raison est que la page a été allouée à un programme par le système d'exploitation, mais qu'il n'a pas encore attribué sa position en mémoire. Pour comprendre comment c'est possible, parlons rapidement de l'allocation paresseuse.
Imaginons qu'un programme fasse une demande d'allocation mémoire et se voit donc attribuer une ou plusieurs pages logiques. L'OS peut alors réagir de deux manières différentes. La première est d'attribuer une page physique immédiatement, en même temps que la page logique. En faisant ainsi, on ne peut pas avoir de défaut mineur, sauf en cas de problème de protection mémoire. Cette solution est simple, on l'appelle l'allocation immédiate. Une autre solution consiste à attribuer une page logique, mais l'allocation de la page physique se fait plus tard. Elle a lieu la première fois que le programme tente d'écrire/lire dans la page physique. Un défaut mineur a lieu, et c'est lui qui force l'OS à attribuer une page physique pour la page logique demandée. On parle alors d'allocation paresseuse. L'avantage est que l'on gagne en performance si des pages logiques sont allouées mais utilisées, ce qui peut arriver.
Une optimisation permise par l'existence des défauts mineurs est le copy-on-write. Le but est d'optimiser la copie d'une page logique dans une autre. L'idée est que la copie est retardée quand elle est vraiment nécessaire, à savoir quand on écrit dans la copie. Tant que l'on ne modifie pas la copie, les deux pages logiques, originelle et copiée, pointent vers la même page physique. A quoi bon avoir deux copies avec le même contenu ? Par contre, la page physique est marquée en lecture seule. La moindre écriture déclenche une erreur de protection mémoire, et un défaut mineur. Celui-ci est géré par l'OS, qui effectue alors la copie dans une nouvelle page physique.
Je viens de dire que le système d'exploitation gère les défauts de page majeurs/mineurs. Un défaut de page déclenche une exception matérielle, qui passe la main au système d'exploitation. Le système d'exploitation doit alors déterminer ce qui a levé l'exception, notamment identifier si c'est un défaut de page mineur ou majeur. Pour cela, le processeur a un ou plusieurs registres de statut qui indique l'état du processeur, qui sont utiles pour gérer les défauts de page. Ils indiquent quelle est l'adresse fautive, si l'accès était une lecture ou écriture, si l'accès a eu lieu en espace noyau ou utilisateur (les espaces mémoire ne sont pas les mêmes), etc. Les registres en question varient grandement d'une architecture de processeur à l'autre, aussi on ne peut pas dire grand chose de plus sur le sujet. Le reste est de toute façon à voir dans un cours sur les systèmes d'exploitation.
Le remplacement des pages
modifierLes pages virtuelles font référence soit à une page en mémoire physique, soit à une page sur le disque dur. Mais l'on ne peut pas lire une page directement depuis le disque dur. Les pages sur le disque dur doivent être chargées en RAM, avant d'être utilisables. Ce n'est possible que si on a une page mémoire vide, libre. Si ce n'est pas le cas, on doit faire de la place en swappant une page sur le disque dur. Les pages font ainsi une sorte de va et vient entre le fichier d'échange et la RAM, suivant les besoins. Tout cela est effectué par une routine d'interruption du système d'exploitation, le processeur n'ayant pas vraiment de rôle là-dedans.
Supposons que l'on veuille faire de la place en RAM pour une nouvelle page. Dans une implémentation naïve, on trouve une page à évincer de la mémoire, qui est copiée dans le swapfile. Toutes les pages évincées sont alors copiées sur le disque dur, à chaque remplacement. Néanmoins, cette implémentation naïve peut cependant être améliorée si on tient compte d'un point important : si la page a été modifiée depuis le dernier accès. Si le programme/processeur a écrit dans la page, alors celle-ci a été modifiée et doit être sauvegardée sur le swapfile si elle est évincée. Par contre, si ce n'est pas le cas, la page est soit initialisée, soit déjà présente à l'identique dans le swapfile.
Mais cette optimisation demande de savoir si une écriture a eu lieu dans la page. Pour cela, on ajoute un dirty bit à chaque entrée de la table des pages, juste à côté du bit Valid. Il indique si une écriture a eu lieu dans la page depuis qu'elle a été chargée en RAM. Ce bit est mis à jour par le processeur, automatiquement, lors d'une écriture. Par contre, il est remis à zéro par le système d'exploitation, quand la page est chargée en RAM. Si le programme se voit allouer de la mémoire, il reçoit une page vide, et ce bit est initialisé à 0. Il est mis à 1 si la mémoire est utilisée. Quand la page est ensuite swappée sur le disque dur, ce bit est remis à 0 après la sauvegarde.
Sur la majorité des systèmes d'exploitation, il est possible d'interdire le déplacement de certaines pages sur le disque dur. Ces pages restent alors en mémoire RAM durant un temps plus ou moins long, parfois en permanence. Cette possibilité simplifie la vie des programmeurs qui conçoivent des systèmes d'exploitation : essayez d'exécuter l'interruption pour les défauts de page alors que la page contenant le code de l'interruption est placée sur le disque dur ! Là encore, cela demande d'ajouter un bit dans chaque entrée de la table des pages, qui indique si la page est swappable ou non. Le bit en question s'appelle souvent le bit swappable.
Les algorithmes de remplacement des pages pris en charge par l'OS
modifierLe choix de la page doit être fait avec le plus grand soin et il existe différents algorithmes qui permettent de décider quelle page supprimer de la RAM. Leur but est de swapper des pages qui ne seront pas accédées dans le futur, pour éviter d'avoir à faire triop de va-et-vient entre RAM et swapfile. Les données qui sont censées être accédées dans le futur doivent rester en RAM et ne pas être swappées, autant que possible. Les algorithmes les plus simples pour le choix de page à évincer sont les suivants.
Le plus simple est un algorithme aléatoire : on choisit la page au hasard. Mine de rien, cet algorithme est très simple à implémenter et très rapide à exécuter. Il ne demande pas de modifier la table des pages, ni même d'accéder à celle-ci pour faire son choix. Ses performances sont surprenamment correctes, bien que largement en-dessous de tous les autres algorithmes.
L'algorithme FIFO supprime la donnée qui a été chargée dans la mémoire avant toutes les autres. Cet algorithme fonctionne bien quand un programme manipule des tableaux de grande taille, mais fonctionne assez mal dans le cas général.
L'algorithme LRU supprime la donnée qui été lue ou écrite pour la dernière fois avant toutes les autres. C'est théoriquement le plus efficace dans la majorité des situations. Malheureusement, son implémentation est assez complexe et les OS doivent modifier la table des pages pour l'implémenter.
L'algorithme le plus utilisé de nos jours est l'algorithme NRU (Not Recently Used), une simplification drastique du LRU. Il fait la différence entre les pages accédées il y a longtemps et celles accédées récemment, d'une manière très binaire. Les deux types de page sont appelés respectivement les pages froides et les pages chaudes. L'OS swappe en priorité les pages froides et ne swappe de page chaude que si aucune page froide n'est présente. L'algorithme est simple : il choisit la page à évincer au hasard parmi une page froide. Si aucune page froide n'est présente, alors il swappe au hasard une page chaude.
Pour implémenter l'algorithme NRU, l'OS mémorise, dans chaque entrée de la table des pages, si la page associée est froide ou chaude. Pour cela, il met à 0 ou 1 un bit dédié : le bit Accessed. La différence avec le bit dirty est que le bit dirty est mis à jour uniquement lors des écritures, alors que le bit Accessed l'est aussi lors d'une lecture. Uen lecture met à 1 le bit Accessed, mais ne touche pas au bit dirty. Les écritures mettent les deux bits à 1.
Implémenter l'algorithme NRU demande juste de mettre à jour le bit Accessed de chaque entrée de la table des pages. Et sur les architectures modernes, le processeur s'en charge automatiquement. A chaque accès mémoire, que ce soit en lecture ou en écriture, le processeur met à 1 ce bit. Par contre, le système d'exploitation le met à 0 à intervalles réguliers. En conséquence, quand un remplacement de page doit avoir lieu, les pages chaudes ont de bonnes chances d'avoir le bit Accessed à 1, alors que les pages froides l'ont à 0. Ce n'est pas certain, et on peut se trouver dans des cas où ce n'est pas le cas. Par exemple, si un remplacement a lieu juste après la remise à zéro des bits Accessed. Le choix de la page à remplacer est donc imparfait, mais fonctionne bien en pratique.
Tous les algorithmes précédents ont chacun deux variantes : une locale, et une globale. Avec la version locale, la page qui va être rapatriée sur le disque dur est une page réservée au programme qui est la cause du page miss. Avec la version globale, le système d'exploitation va choisir la page à virer parmi toutes les pages présentes en mémoire vive.
La protection mémoire avec la pagination
modifierAvec la pagination, chaque page a des droits d'accès précis, qui permettent d'autoriser ou interdire les accès en lecture, écriture, exécution, etc. La table des pages mémorise les autorisations pour chaque page, sous la forme d'une suite de bits où chaque bit autorise/interdit une opération bien précise. En pratique, les tables de pages modernes disposent de trois bits : un qui autorise/interdit les accès en lecture, un qui autorise/interdit les accès en écriture, un qui autorise/interdit l'éxecution du contenu de la page.
Le format exact de la suite de bits a cependant changé dans le temps sur les processeurs x86 modernes. Par exemple, avant le passage au 64 bits, les CPU et OS ne pouvaient pas marquer une page mémoire comme non-exécutable. C'est seulement avec le passage au 64 bits qu'a été ajouté un bit pour interdire l'exécution de code depuis une page. Ce bit, nommé bit NX, est à 0 si la page n'est pas exécutable et à 1 sinon. Le processeur vérifie à chaque chargement d'instruction si le bit NX de page lue est à 1. Sinon, il lève une exception matérielle et laisse la main à l'OS.
Une amélioration de cette protection est la technique dite du Write XOR Execute, abréviée WxX. Elle consiste à interdire les pages d'être à la fois accessibles en écriture et exécutables. Il est possible de changer les autorisations en cours de route, ceci dit.
La traduction d'adresse avec la pagination
modifierComme dit plus haut, les pages sont numérotées, de 0 à une valeur maximale, afin de les identifier. Le numéro en question est appelé le numéro de page. Il est utilisé pour dire au processeur : je veux lire une donnée dans la page numéro 20, la page numéro 90, etc. Une fois qu'on a le numéro de page, on doit alors préciser la position de la donnée dans la page, appelé le décalage, ou encore l'offset.
Le numéro de page et le décalage se déduisent à partir de l'adresse, en divisant l'adresse par la taille de la page. Le quotient obtenu donne le numéro de la page, alors que le reste est le décalage. Les processeurs actuels utilisent tous des pages dont la taille est une puissance de deux, ce qui fait que ce calcul est fortement simplifié. Sous cette condition, le numéro de page correspond aux bits de poids fort de l'adresse, alors que le décalage est dans les bits de poids faible.
Le numéro de page existe en deux versions : un numéro de page physique qui identifie une page en mémoire physique, et un numéro de page logique qui identifie une page dans la mémoire virtuelle. Traduire l'adresse logique en adresse physique demande de remplacer le numéro de la page logique en un numéro de page physique.

Les tables des pages simples
modifierDans le cas le plus simple, il n'y a qu'une seule table des pages, qui est adressée par les numéros de page logique. La table des pages est un vulgaire tableau d'adresses physiques, placées les unes à la suite des autres. Avec cette méthode, la table des pages a autant d'entrée qu'il y a de pages logiques en mémoire virtuelle. Accéder à la mémoire nécessite donc d’accéder d'abord à la table des pages en mémoire, de calculer l'adresse de l'entrée voulue, et d’y accéder.

La table des pages est souvent stockée dans la mémoire RAM, son adresse est connue du processeur, mémorisée dans un registre spécialisé du processeur. Le processeur effectue automatiquement le calcul d'adresse à partir de l'adresse de base et du numéro de page logique.

Les tables des pages inversées
modifierSur certains systèmes, notamment sur les architectures 64 bits ou plus, le nombre de pages est très important. Sur les ordinateurs x86 récents, les adresses sont en pratique de 48 bits, les bits de poids fort étant ignorés en pratique, ce qui fait en tout 68 719 476 736 pages. Chaque entrée de la table des pages fait au minimum 48 bits, mais fait plus en pratique : partons sur 64 bits par entrée, soit 8 octets. Cela fait 549 755 813 888 octets pour la table des pages, soit plusieurs centaines de gibioctets ! Une table des pages normale serait tout simplement impraticable.
Pour résoudre ce problème, on a inventé les tables des pages inversées. L'idée derrière celles-ci est l'inverse de la méthode précédente. La méthode précédente stocke, pour chaque page logique, son numéro de page physique. Les tables des pages inversées font l'inverse : elles stockent, pour chaque numéro de page physique, la page logique qui correspond. Avec cette méthode table des pages contient ainsi autant d'entrées qu'il y a de pages physiques. Elle est donc plus petite qu'avant, vu que la mémoire physique est plus petite que la mémoire virtuelle.
Quand le processeur veut convertir une adresse virtuelle en adresse physique, la MMU recherche le numéro de page de l'adresse virtuelle dans la table des pages. Le numéro de l'entrée à laquelle se trouve ce morceau d'adresse virtuelle est le morceau de l'adresse physique. Pour faciliter le processus de recherche dans la page, la table des pages inversée est ce que l'on appelle une table de hachage. C'est cette solution qui est utilisée sur les processeurs Power PC.

Les tables des pages multiples par espace d'adressage
modifierDans les deux cas précédents, il y a une table des pages unique. Cependant, les concepteurs de processeurs et de systèmes d'exploitation ont remarqué que les adresses les plus hautes et/ou les plus basses sont les plus utilisées, alors que les adresses situées au milieu de l'espace d'adressage sont peu utilisées en raison du fonctionnement de la pile et du tas. Il y a donc une partie de la table des pages qui ne sert à rien et est utilisé pour des adresses inutilisées. C'est une source d'économie d'autant plus importante que les tables des pages sont de plus en plus grosses.
Pour profiter de cette observation, les concepteurs d'OS ont décidé de découper l'espace d'adressage en plusieurs sous-espaces d'adressage de taille identique : certains localisés dans les adresses basses, d'autres au milieu, d'autres tout en haut, etc. Et vu que l'espace d'adressage est scindé en plusieurs parties, la table des pages l'est aussi, ele est découpée en plusieurs sous-tables. Si un sous-espace d'adressage n'est pas utilisé, il n'y a pas besoin d'utiliser de la mémoire pour stocker la table des pages associée. On ne stocke que les tables des pages pour les espaces d'adressage utilisés, ceux qui contiennent au moins une donnée.
L'utilisation de plusieurs tables des pages ne fonctionne que si le système d'exploitation connaît l'adresse de chaque table des pages (celle de la première entrée). Pour cela, le système d'exploitation utilise une super-table des pages, qui stocke les adresses de début des sous-tables de chaque sous-espace. En clair, la table des pages est organisé en deux niveaux, la super-table étant le premier niveau et les sous-tables étant le second niveau.
L'adresse est structurée de manière à tirer profit de cette organisation. Les bits de poids fort de l'adresse sélectionnent quelle table de second niveau utiliser, les bits du milieu de l'adresse sélectionne la page dans la table de second niveau et le reste est interprété comme un offset. Un accès à la table des pages se fait comme suit. Les bits de poids fort de l'adresse sont envoyés à la table de premier niveau, et sont utilisés pour récupérer l'adresse de la table de second niveau adéquate. Les bits au milieu de l'adresse sont envoyés à la table de second niveau, pour récupérer le numéro de page physique. Le tout est combiné avec l'offset pour obtenir l'adresse physique finale.

On peut aussi aller plus loin et découper la table des pages de manière hiérarchique, chaque sous-espace d'adressage étant lui aussi découpé en sous-espaces d'adressages. On a alors une table de premier niveau, plusieurs tables de second niveau, encore plus de tables de troisième niveau, et ainsi de suite. Cela peut aller jusqu'à 5 niveaux sur les processeurs x86 64 bits modernes. Dans ce cours, la table des pages désigne l'ensemble des différents niveaux de cette organisation, toutes les tables inclus. Seules les tables du dernier niveau mémorisent des numéros de page physiques, les autres tables mémorisant des pointeurs, des adresses vers le début des tables de niveau inférieur. Un exemple sera donné plus bas, dans la section suivante.
L'exemple des processeurs x86
modifierPour rendre les explications précédentes plus concrètes, nous allons prendre l'exemple des processeur x86 anciens, de type 32 bits. Les processeurs de ce type utilisaient deux types de tables des pages : une table des page unique et une table des page hiérarchique. Les deux étaient utilisées dans cas séparés. La table des page unique était utilisée pour les pages larges et encore seulement en l'absence de la technologie physical adress extension, dont on parlera plus bas. Les autres cas utilisaient une table des page hiérarchique, à deux niveaux, trois niveaux, voire plus.
Une table des pages unique était utilisée pour les pages larges (de 2 mébioctets et plus). Pour les pages de 4 mébioctets, il y avait une unique table des pages, adressée par les 10 bits de poids fort de l'adresse, les bits restants servant comme offset. La table des pages contenait 1024 entrées de 4 octets chacune, ce qui fait en tout 4 kibioctet pour la table des pages. La table des page était alignée en mémoire sur un bloc de 4 kibioctet (sa taille).

Pour les pages de 4 kibioctets, les processeurs x86-32 bits utilisaient une table des page hiérarchique à deux niveaux. Les 10 bits de poids fort l'adresse adressaient la table des page maitre, appelée le directoire des pages (page directory), les 10 bits précédents servaient de numéro de page logique, et les 12 bits restants servaient à indiquer la position de l'octet dans la table des pages. Les entrées de chaque table des pages, mineure ou majeure, faisaient 32 bits, soit 4 octets. Vous remarquerez que la table des page majeure a la même taille que la table des page unique obtenue avec des pages larges (de 4 mébioctets).

La technique du physical adress extension (PAE), utilisée depuis le Pentium Pro, permettait aux processeurs x86 32 bits d'adresser plus de 4 gibioctets de mémoire, en utilisant des adresses physiques de 64 bits. Les adresses virtuelles de 32 bits étaient traduites en adresses physiques de 64 bits grâce à une table des pages adaptée. Cette technologie permettait d'adresser plus de 4 gibioctets de mémoire au total, mais avec quelques limitations. Notamment, chaque programme ne pouvait utiliser que 4 gibioctets de mémoire RAM pour lui seul. Mais en lançant plusieurs programmes, on pouvait dépasser les 4 gibioctets au total. Pour cela, les entrées de la table des pages passaient à 64 bits au lieu de 32 auparavant.
La table des pages gardait 2 niveaux pour les pages larges en PAE.

Par contre, pour les pages de 4 kibioctets en PAE, elle était modifiée de manière à ajouter un niveau de hiérarchie, passant de deux niveaux à trois.

En 64 bits, la table des pages est une table des page hiérarchique avec 5 niveaux. Seuls les 48 bits de poids faible des adresses sont utilisés, les 16 restants étant ignorés.

Les circuits liés à la gestion de la table des pages
modifierEn théorie, la table des pages est censée être accédée à chaque accès mémoire. Mais pour éviter d'avoir à lire la table des pages en mémoire RAM à chaque accès mémoire, les concepteurs de processeurs ont décidé d'implanter un cache dédié, le translation lookaside buffer, ou TLB. Le TLB stocke au minimum de quoi faire la traduction entre adresse virtuelle et adresse physique, à savoir une correspondance entre numéro de page logique et numéro de page physique. Pour faire plus général, il stocke des entrées de la table des pages.

Les accès à la table des pages sont gérés de deux façons : soit le processeur gère tout seul la situation, soit il délègue cette tâche au système d’exploitation. Sur les processeurs anciens, le système d'exploitation gère le parcours de la table des pages. Mais cette solution logicielle n'a pas de bonnes performances. D'autres processeurs gèrent eux-mêmes le défaut d'accès à la TLB et vont chercher d'eux-mêmes les informations nécessaires dans la table des pages. Ils disposent de circuits, les page table walkers (PTW), qui s'occupent eux-mêmes du défaut.
Les page table walkers contiennent des registres qui leur permettent de faire leur travail. Le plus important est celui qui mémorise la position de la table des pages en mémoire RAM, dont nous avons parlé plus haut. Les PTW ont besoin, pour faire leur travail, de mémoriser l'adresse physique de la table des pages, ou du moins l'adresse de la table des pages de niveau 1 pour des tables des pages hiérarchiques. Mais d'autres registres existent. Toutes les informations nécessaires pour gérer les défauts de TLB sont stockées dans des registres spécialisés appelés des tampons de PTW (PTW buffers).
L'abstraction matérielle des processus : une table des pages par processus
modifier
Il est possible d'implémenter l'abstraction matérielle des processus avec la pagination. En clair, chaque programme lancé sur l'ordinateur dispose de son propre espace d'adressage, ce qui fait que la même adresse logique ne pointera pas sur la même adresse physique dans deux programmes différents. Pour cela, il y a plusieurs méthodes.
L'usage d'une table des pages unique avec un identifiant de processus dans chaque entrée
modifierLa première solution n'utilise qu'une seule table des pages, mais chaque entrée est associée à un processus. Pour cela, chaque entrée contient un identifiant de processus, un numéro qui précise pour quel processus, pour quel espace d'adressage, la correspondance est valide.
La page des tables peut aussi contenir des entrées qui sont valides pour tous les processus en même temps. L'intérêt n'est pas évident, mais il le devient quand on se rappelle que le noyau de l'OS est mappé dans le haut de l'espace d'adressage. Et peu importe l'espace d'adressage, le noyau est toujours mappé de manière identique, les mêmes adresses logiques adressant la même adresse mémoire. En conséquence, les correspondances adresse physique-logique sont les mêmes pour le noyau, peu importe l'espace d'adressage. Dans ce cas, la correspondance est mémorisée dans une entrée, mais sans identifiant de processus. A la place, l'entrée contient un bit global, qui précise que cette correspondance est valide pour tous les processus. Le bit global accélère rapidement la traduction d'adresse pour l'accès au noyau.
Un défaut de cette méthode est que le partage d'une page entre plusieurs processus est presque impossible. Impossible de partager une page avec seulement certains processus et pas d'autres : soit on partage une page avec tous les processus, soit on l'alloue avec un seul processus.
L'usage de plusieurs tables des pages
modifierUne solution alternative, plus simple, utilise une table des pages par processus lancé sur l'ordinateur, une table des pages unique par espace d'adressage. À chaque changement de processus, le registre qui mémorise la position de la table des pages est modifié pour pointer sur la bonne. C'est le système d'exploitation qui se charge de cette mise à jour.
Avec cette méthode, il est possible de partager une ou plusieurs pages entre plusieurs processus, en configurant les tables des pages convenablement. Les pages partagées sont mappées dans l'espace d'adressage de plusieurs processus, mais pas forcément au même endroit, pas forcément dans les mêmes adresses logiques. On peut placer la page partagée à l'adresse logique 0x0FFF pour un processus, à l'adresse logique 0xFF00 pour un autre processus, etc. Par contre, les entrées de la table des pages pour ces adresses pointent vers la même adresse physique.

La taille des pages
modifierLa taille des pages varie suivant le processeur et le système d'exploitation et tourne souvent autour de 4 kibioctets. Les processeurs actuels gèrent plusieurs tailles différentes pour les pages : 4 kibioctets par défaut, 2 mébioctets, voire 1 à 4 gibioctets pour les pages les plus larges. Les pages de 4 kibioctets sont les pages par défaut, les autres tailles de page sont appelées des pages larges. La taille optimale pour les pages dépend de nombreux paramètres et il n'y a pas de taille qui convienne à tout le monde. Certaines applications gagnent à utiliser des pages larges, d'autres vont au contraire perdre drastiquement en performance en les utilisant.
Le désavantage principal des pages larges est qu'elles favorisent la fragmentation mémoire. Si un programme veut réserver une portion de mémoire, pour une structure de donnée quelconque, il doit réserver une portion dont la taille est multiple de la taille d'une page. Par exemple, un programme ayant besoin de 110 kibioctets allouera 28 pages de 4 kibioctets, soit 120 kibioctets : 2 kibioctets seront perdus. Par contre, avec des pages larges de 2 mébioctets, on aura une perte de 2048 - 110 = 1938 kibioctets. En somme, des morceaux de mémoire seront perdus, car les pages sont trop grandes pour les données qu'on veut y mettre. Le résultat est que le programme qui utilise les pages larges utilisent plus de mémoire et ce d'autant plus qu'il utilise des données de petite taille. Un autre désavantage est qu'elles se marient mal avec certaines techniques d'optimisations de type copy-on-write.
Mais l'avantage est que la traduction des adresses est plus performante. Une taille des pages plus élevée signifie moins de pages, donc des tables des pages plus petites. Et des pages des tables plus petites n'ont pas besoin de beaucoup de niveaux de hiérarchie, voire peuvent se limiter à des tables des pages simples, ce qui rend la traduction d'adresse plus simple et plus rapide. De plus, les programmes ont une certaine localité spatiale, qui font qu'ils accèdent souvent à des données proches. La traduction d'adresse peut alors profiter de systèmes de mise en cache dont nous parlerons dans le prochain chapitre, et ces systèmes de cache marchent nettement mieux avec des pages larges.
Il faut noter que la taille des pages est presque toujours une puissance de deux. Cela a de nombreux avantages, mais n'est pas une nécessité. Par exemple, le tout premier processeur avec de la pagination, le super-ordinateur Atlas, avait des pages de 3 kibioctets. L'avantage principal est que la traduction de l'adresse physique en adresse logique est trivial avec une puissance de deux. Cela garantit que l'on peut diviser l'adresse en un numéro de page et un offset : la traduction demande juste de remplacer les bits de poids forts par le numéro de page voulu. Sans cela, la traduction d'adresse implique des divisions et des multiplications, qui sont des opérations assez couteuses.
Les entrées de la table des pages
modifierAvant de poursuivre, faisons un rapide rappel sur les entrées de la table des pages. Nous venons de voir que la table des pages contient de nombreuses informations : un bit valid pour la mémoire virtuelle, des bits dirty et accessed utilisés par l'OS, des bits de protection mémoire, un bit global et un potentiellement un identifiant de processus, etc. Étudions rapidement le format de la table des pages sur un processeur x86 32 bits.
- Elle contient d'abord le numéro de page physique.
- Les bits AVL sont inutilisés et peuvent être configurés à loisir par l'OS.
- Le bit G est le bit global.
- Le bit PS vaut 0 pour une page de 4 kibioctets, mais est mis à 1 pour une page de 4 mébioctets dans le cas où le processus utilise des pages larges.
- Le bit D est le bit dirty.
- Le bit A est le bit accessed.
- Le bit PCD indique que la page ne peut pas être cachée, dans le sens où le processeur ne peut copier son contenu dans le cache et doit toujours lire ou écrire cette page directement dans la RAM.
- Le bit PWT indique que les écritures doivent mettre à jour le cache et la page en RAM (dans le chapitre sur le cache, on verra qu'il force le cache à se comporter comme un cache write-through pour cette page).
- Le bit U/S précise si la page est accessible en mode noyau ou utilisateur.
- Le bit R/W indique si la page est accessible en écriture, toutes les pages sont par défaut accessibles en lecture.
- Le bit P est le bit valid.

Comparaison des différentes techniques d'abstraction mémoire
modifierPour résumer, l'abstraction mémoire permet de gérer : la relocation, la protection mémoire, l'isolation des processus, la mémoire virtuelle, l'extension de l'espace d'adressage, le partage de mémoire, etc. Elles sont souvent implémentées en même temps. Ce qui fait qu'elles sont souvent confondues, alors que ce sont des concepts sont différents. Ces liens sont résumés dans le tableau ci-dessous.
| Avec abstraction mémoire | Sans abstraction mémoire | |||||
|---|---|---|---|---|---|---|
| Relocation matérielle | Segmentation en mode réel (x86) | Segmentation, général | Architectures à capacités | Pagination | ||
| Abstraction matérielle des processus | Oui, relocation matérielle | Oui, liée à la traduction d'adresse | Impossible | |||
| Mémoire virtuelle | Non, sauf émulation logicielle | Oui, gérée par le processeur et l'OS | Non, sauf émulation logicielle | |||
| Extension de l'espace d'adressage | Oui : registre de base élargi | Oui : adresse de base élargie dans la table des segments | Physical Adress Extension des processeurs 32 bits | Commutation de banques | ||
| Protection mémoire | Registre limite | Aucune | Registre limite, droits d'accès aux segments | Gestion des droits d'accès aux pages | Possible, méthodes variées | |
| Partage de mémoire | Non | Segment partagés | Pages partagées | Possible, méthodes variées | ||
Les différents types de segmentation
modifierLa segmentation regroupe plusieurs techniques franchement différentes, qui auraient gagné à être nommées différemment. La principale différence est l'usage de registres de relocation versus des registres de sélecteurs de segments. L'usage de registres de relocation est le fait de la relocation matérielle, mais aussi de la segmentation en mode réel des CPU x86. Par contre, l'usage de sélecteurs de segments est le fait des autres formes de segmentation, architectures à capacité inclues.
La différence entre les deux est le nombre de segments. L'usage de registres de relocation fait que le CPU ne gère qu'un petit nombre de segments de grande taille. La mémoire virtuelle est donc rarement implémentée vu que swapper des segments de grande taille est trop long, l'impact sur les performances est trop important. Sans compter que l'usage de registres de base se marie très mal avec la mémoire virtuelle. Vu qu'un segment peut être swappé ou déplacée n'importe quand, il faut invalider les registres de base au moment du swap/déplacement, ce qui n'est pas chose aisée. Aucun processeur ne gère cela, les méthodes pour n'existent tout simplement pas. L'usage de registres de base implique que la mémoire virtuelle est absente.
La protection mémoire est aussi plus limitée avec l'usage de registres de relocation. Elle se limite à des registres limite, mais la gestion des droits d'accès est limitée. En théorie, la segmentation en mode réel pourrait implémenter une version limitée de protection mémoire, avec une protection de l'espace exécutable. Mais ca n'a jamais été fait en pratique sur les processeurs x86.
Le partage de la mémoire est aussi difficile sur les architectures avec des registres de base. L'absence de table des segments fait que le partage d'un segment est basiquement impossible sans utiliser des méthodes complétement tordues, qui ne sont jamais implémentées en pratique.
Segmentation versus pagination
modifierPar rapport à la pagination, la segmentation a des avantages et des inconvénients. Tous sont liés aux propriétés des segments et pages : les segments sont de grande taille et de taille variable, les pages sont petites et de taille fixe.
L'avantage principal de la segmentation est sa rapidité. Le fait que les segments sont de grande taille fait qu'on a pas besoin d'équivalent aux tables des pages inversée ou multiple, juste d'une table des segments toute simple. De plus, les échanges entre table des pages/segments et registres sont plus rares avec la segmentation. Par exemple, si un programme utilise un segment de 2 gigas, tous les accès dans le segment se feront avec une seule consultation de la table des segments. Alors qu'avec la pagination, il faudra une consultation de la table des pages chaque bloc de 4 kibioctet, au minimum.
Mais les désavantages sont nombreux. Le système d'exploitation doit agencer les segments en RAM, et c'est une tâche complexe. Le fait que les segments puisse changer de taille rend le tout encore plus complexe. Par exemple, si on colle les segments les uns à la suite des autres, changer la taille d'un segment demande de réorganiser tous les segments en RAM, ce qui demande énormément de copies RAM-RAM. Une autre possibilité est de laisser assez d'espace entre les segments, mais cet espace est alors gâché, dans le sens où on ne peut pas y placer un nouveau segment.
Swapper un segment est aussi très long, vu que les segments sont de grande taille, alors que swapper une page est très rapide.
La micro-architecture
modifierDans le chapitre sur le langage machine, on a vu notre processeur comme une espèce de boite noire contenant des registres qui exécutait des instructions les unes après les autres et pouvait accéder à la mémoire. Mais on n'a pas encore vu comment celui-ci était organisé et comment celui-ci fait pour exécuter une instruction. Pour cela, il va falloir nous attaquer à la micro-architecture du processeur. C'est le but de ce chapitre : montrer comment les grands circuits de notre processeur sont organisés et comment ceux-ci permettent d’exécuter une instruction. On verra que notre processeur est très organisé et est divisé en plusieurs grands circuits qui effectuent des fonctions différentes.
L'exécution d'une instruction
modifierLe but d'un processeur, c'est d’exécuter une instruction. Cela nécessite de faire quelques manipulations assez spécifiques et qui sont toutes les mêmes quel que soit l'ordinateur. Pour exécuter une instruction, notre processeur va devoir faire son travail en effectuant des étapes bien précises.
Le cycle d'exécution d'une instruction
modifier
Pour exécuter une instruction, le processeur va effectuer trois étapes :
- le processeur charger l'instruction depuis la mémoire : c'est l'étape de chargement (Fetch) ;
- ensuite, le processeur « étudie » la suite de bits de l'instruction et en déduit quelle est l'instruction à éxecuter : c'est l'étape de décodage (Decode) ;
- enfin, le processeur exécute l'instruction : c'est l'étape d’exécution (Execute).
On verra plus tard dans le cours qu'une quatrième étape peut être ajoutée : l'étape d'interruption. Celle-ci permet de gérer des fonctionnalités du processeur nommées interruptions. Nous en parlerons dans le chapitre sur la communication avec les entrées-sorties.
Les micro-instructions
modifierCes trois étapes ne s'effectuent cependant pas d'un seul bloc. Chaque de ces étapes est elle-même découpée en plusieurs sous-étapes, qui va échanger des données entre registres, effectuer un calcul, ou communiquer avec la mémoire. Pour l'étape de chargement, on peut être sûr que tous les processeurs vont faire la même chose : il n'y a pas 36 façons pour lire une instruction depuis la mémoire. Même chose pour la plupart des processeur, pour l'étape de décodage. Mais cela change pour l'étape d’exécution : toutes les instructions n'ont pas les mêmes besoins suivant ce qu'elles font ou leur mode d'adressage. Voyons cela avec quelques exemples.
Commençons par prendre l'exemple d'une instruction de lecture ou d'écriture en mode d'adressage absolu. Vu son mode d'adressage, l'instruction va indiquer l'adresse à laquelle lire dans sa suite de bits qui la représente en mémoire. L’exécution de l'instruction se fait donc en une seule étape : la lecture proprement dite. Mais si l'on utilise des modes d'adressages plus complexes, les choses changent un petit peu. Reprenons notre instruction Load, mais en utilisant une mode d'adressage utilisé pour des données plus complexe. Par exemple, on va prendre un mode d'adressage du style Base + Index. Avec ce mode d'adressage, l'adresse doit être calculée à partir d'une adresse de base, et d'un indice, les deux étant stockés dans des registres. En plus de devoir lire notre donnée, notre instruction va devoir calculer l'adresse en fonction du contenu fourni par deux registres. L'étape d’exécution s'effectue dorénavant en deux étapes assez différentes : une implique un calcul d'adresse, et l'autre implique un accès à la mémoire.
Prenons maintenant le cas d'une instruction d'addition. Celle-ci va additionner deux opérandes, qui peuvent être soit des registres, soit des données placées en mémoires, soit des constantes. Si les deux opérandes sont dans un registre et que le résultat doit être placé dans un registre, la situation est assez simple : la récupération des opérandes dans les registres, le calcul, et l'enregistrement du résultat dans les registres sont trois étapes distinctes. Maintenant, autre exemple : une opérande est à aller chercher dans la mémoire, une autre dans un registre, et le résultat doit être enregistré dans un registre. On doit alors rajouter une étape : on doit aller chercher la donnée en mémoire. Et on peut aller plus loin en allant cherche notre première opérande en mémoire : il suffit d'utiliser le mode d'adressage Base + Index pour celle-ci. On doit alors rajouter une étape de calcul d'adresse en plus. Ne parlons pas des cas encore pire du style : une opérande en mémoire, l'autre dans un registre, et stocker le résultat en mémoire.
Bref, on voit bien que l’exécution d'une instruction s'effectue en plusieurs étapes distinctes, qui vont soit faire un calcul, soit échanger des données entre registres, soit communiquer avec la RAM. Chaque étape s'appelle une micro-opération, ou encore une micro-instruction. Toute instruction machine est équivalente à une suite de micro-opérations exécutée dans un ordre précis. Dit autrement, chaque instruction machine est traduite en suite de micro-opérations à chaque fois qu'on l’exécute. Certaines µinstructions font un cycle d'horloge, alors que d'autres peuvent prendre plusieurs cycles. Un accès mémoire en RAM peut prendre 200 cycles d'horloge et ne représenter qu'une seule µinstruction, par exemple. Même chose pour certaines opérations de calcul, comme des divisions ou multiplication, qui correspondent à une seule µinstruction mais prennent plusieurs cycles.

La micro-architecture d'un processeur
modifierConceptuellement, il est possible de segmenter les circuits du processeur en circuits spécialisés : des circuits chargés de faire des calculs, d'autres chargés de gérer les accès mémoires, etc. Ces circuits sont eux-mêmes regroupés en deux entités : le chemin de données et l'unité de contrôle. Le tout est illustré ci-contre.
- Le chemin de données est l'ensemble des composants où circulent les données, là où se font les calculs, là où se font les échanges entre mémoire RAM et registres, etc. Il contient un circuit pour faire les calculs, appelé l'unité de calcul, les registres et un circuit de communication avec la mémoire. On l'appelle ainsi parce que c'est dans ce chemin de données que les données vont circuler et être traitées dans le processeur.
- L’unité de contrôle charge et interprète les instructions, pour commander le chemin de données. Elle est en charge du chargement et du décodage de l'instruction. Elle regroupe un circuit chargé du Fetch, et un décodeur chargé de l'étape de Decode.
Le chemin de données
modifierPour effectuer ces calculs, le processeur contient un circuit spécialisé : l'unité de calcul. De plus, le processeur contient des registres, ainsi qu'un circuit d'interface mémoire. Les registres, l'unité de calcul, et l'interface mémoire sont reliés entre eux par un ensemble de fils afin de pouvoir échanger des informations : par exemple, le contenu des registres doit pouvoir être envoyé en entrée de l'unité de calcul, pour additionner leur contenu par exemple. Ce groupe de fils forme ce qu'on appelle le bus interne du processeur. L'ensemble formé par ces composants s’appelle le chemin de données.

L'unité de contrôle
modifierSi le chemin de données s'occupe de tout ce qui a trait aux donnés, il est complété par un circuit qui s'occupe de tout ce qui a trait aux instructions elles-mêmes. Ce circuit, l'unité de contrôle va notamment charger l'instruction dans le processeur, depuis la mémoire RAM. Il va ensuite configurer le chemin de données pour effectuer l'instruction. Il faut bien contrôler le mouvement des informations dans le chemin de données pour que les calculs se passent sans encombre. Pour cela, l'unité de contrôle contient un circuit : le séquenceur. Ce séquenceur envoie des signaux au chemin de données pour le configurer et le commander.
Il est évident que pour exécuter une suite d'instructions dans le bon ordre, le processeur doit savoir quelle est la prochaine instruction à exécuter : il doit donc contenir une mémoire qui stocke cette information. C'est le rôle du registre d'adresse d'instruction, aussi appelé program counter. Cette adresse ne sort pas de nulle part : on peut la déduire de l'adresse de l'instruction en cours d’exécution par divers moyens plus ou moins simples. Généralement, on profite du fait que le programmeur/compilateur place les instructions les unes à la suite des autres en mémoire, dans l'ordre où elles doivent être exécutées. Ainsi, on peut calculer l'adresse de la prochaine instruction en ajoutant la longueur de l'instruction chargée au program counter.

Mais sur d'autres processeurs, chaque instruction précise l'adresse de la suivante. Ces processeurs n'ont pas besoin de calculer une adresse qui leur est fournie sur un plateau d'argent. Sur de tels processeurs, chaque instruction précise quelle est la prochaine instruction, directement dans la suite de bit représentant l'instruction en mémoire. Les processeurs de ce type contiennent toujours un registre d'adresse d'instruction, pour faciliter l’interfaçage avec le bus d'adresse. La partie de l'instruction stockant l'adresse de la prochaine instruction est alors recopiée dans ce registre, pour faciliter sa copie sur le bus d'adresse. Mais le compteur ordinal n'existe pas. Sur des processeurs aussi bizarres, pas besoin de stocker les instructions en mémoire dans l'ordre dans lesquelles elles sont censées être exécutées. Mais ces processeurs sont très très rares et peuvent être considérés comme des exceptions à la règle.

Des processeurs vendus en kit aux premiers microprocesseurs
modifierUn processeur est un circuit assez complexe et qui utilise beaucoup de transistors. Avant les années 1970, il n'était pas possible de produire un processeur en un seul morceau. Impossible de mettre un processeur dans un seul boitier. Les tout premiers processeurs étaient fabriqués porte logique par porte logique et comprenaient plusieurs milliers de boitiers reliés entre eux. Par la suite, les progrès de la miniaturisation permirent de faire des pièces plus grandes. L'invention du microprocesseur permis de placer tout le processeur dans un seul boitier, une seule puce électronique.
Avant l'invention du microprocesseur
modifierAvant l'invention du microprocesseur, les processeurs étaient fournis en pièces détachées qu'il fallait relier entre elles. Le processeur était composé de plusieurs circuits intégrés, placés sur la même carte mère et connectés ensemble par des fils métalliques. Un exemple de processeur conçu en kit est la série des Intel 3000. Elle regroupe plusieurs circuits séparés : l'Intel 3001 est le séquenceur, l'Intel 3002 est le chemin de données (ALU et registres), le 3003 est un circuit d'anticipation de retenue censé être combiné avec l'ALU, le 3212 est une mémoire tampon, le 3214 est une unité de gestion des interruptions, les 3216/3226 sont des interfaces de bus mémoire. On pourrait aussi citer la famille de circuits intégrés AMD Am2900.
Les ALUs en pièces détachées de l'époque étaient assez simples et géraient 2, 4, 8 bits, rarement 16 bits. Et il était possible d'assembler plusieurs ALU pour créer des ALU plus grandes, par exemple combiner plusieurs ALU 4 bits afin de créer une unité de calcul 8 bits, 12 bits, 16 bits, etc. Il s'agit de la méthode du bit slicing que nous avions abordée dans le chapitre sur les unités de calcul.
L'intel 4004 : le premier microprocesseur
modifierPar la suite, les progrès de la miniaturisation ont permis de mettre un processeur entier dans un seul circuit intégré. C'est ainsi que sont nés les microprocesseurs, à savoir des processeurs qui tiennent tout entier sur une seule puce de silicium. Les tout premiers microprocesseurs étaient des processeurs à application militaire, comme le processeur du F-14 CADC ou celui de l'Air data computer.
Le tout premier microprocesseur commercialisé au grand public est le 4004 d'Intel, sorti en 1971. Il comprenait environ 2300 transistors, avait une fréquence de 740 MHz, et manipulait des entiers de 4 bits. De plus, le processeur manipulait des entiers en BCD, ce qui fait qu'il pouvait manipuler un chiffre BCD à la fois (un chiffre BCD est codé sur 4 bits). Il pouvait faire 46 opérations différentes. C'était au départ un processeur de commande, prévu pour être intégré dans la calculatrice Busicom calculator 141-P, mais il fut utilisé pour d'autres applications quelque temps plus tard. Son successeur, l'Intel 4040, garda ces caractéristiques et n'apportait que quelques améliorations mineures : plus de registres, plus d'opérations, etc.
Immédiatement après le 4004, les premiers microprocesseurs 8 bits furent commercialisés. Le 4004 fut suivi par le 8008 et quelques autres processeurs 8 bits extrêmement connus, comme le 8080 d'Intel, le 68000 de Motorola, le 6502 ou le Z80. Ces processeurs utilisaient là encore des boitiers similaires au 4004, mais avec plus de broches, vu qu'ils étaient passés de 4 à 8 bits. Par exemple, le 8008 utilisait 18 broches, le 8080 était une version améliorée du 8008 avec 40 broches. Le 8086 fut le premier processeur 16 bits.
L'évolution des processeurs dans le temps
modifierLa miniaturisation a eu des conséquences notables sur la manière dont sont conçus les processeurs, les mémoires et tous les circuits électroniques en général. On pourrait croire que la miniaturisation a entrainé une augmentation de la complexité des processeurs avec le temps, mais les choses sont à nuancer. Certes, on peut faire beaucoup plus de choses avec un milliard de transistors qu'avec seulement 10000 transistors, ce qui fait que les puces modernes sont d'une certaine manière plus complexes. Mais les anciens processeurs avaient une complexité cachée liée justement au faible nombre de transistors.
Il est difficile de concevoir des circuits avec un faible nombre de transistors, ce qui fait que les fabricants de processeurs devaient utiliser des ruses de sioux pour économiser des transistors. Les circuits des processeurs étaient ainsi fortement optimisés pour économiser des portes logiques, à tous les niveaux. Les circuits les plus simples étaient optimisés à mort, on évitait de dupliquer des circuits, on partageait les circuits au maximum, etc. La conception interne de ces processeurs était simple au premier abord, mais avec quelques pointes de complexité dispersées dans toute la puce.
De nos jours, les processeurs n'ont plus à économiser du transistor et le résultat est à double tranchant. Certes, ils n'ont plus à utiliser des optimisations pour économiser du circuit, mais ils vont au contraire utiliser leurs transistors pour rendre le processeur plus rapide. Beaucoup des techniques que nous verrons dans ce cours, comme l’exécution dans le désordre, le renommage de registres, les mémoires caches, la présence de plusieurs circuits de calcul, et bien d'autres ; améliorent les performances du processeur en ajoutant des circuits en plus. De plus, on n'hésite plus à dupliquer des circuits qu'on aurait autrefois mis en un seul exemplaire partagé. Tout cela rend le processeur plus complexe à l'intérieur.
Une autre contrainte est la facilité de programmation. Les premiers processeurs devaient faciliter au plus la vie du programmeur. Il s'agissait d'une époque où on programmait en assembleur, c'est à dire en utilisant directement les instructions du processeur ! Les processeurs de l'époque utilisaient des jeu d'instruction CISC pour faciliter la vie du programmeur. Pourtant, ils avaient aussi des caractéristiques gênantes pour les programmeurs qui s'expliquent surtout par le faible nombre de transistors de l'époque : peu de registres, registres spécialisés, architectures à pile ou à accumulateur, etc. Ces processeurs étaient assez étranges pour les programmeurs : très simples sur certains points, difficiles pour d'autres.
Les processeurs modernes ont d'autres contraintes. Grâce à la grande quantité de transistors dont ils disposent, ils incorporent des caractéristiques qui les rendent plus simples à programmer et à comprendre (registres banalisés, architectures LOAD-STORE, beaucoup de registres, moins d'instructions complexes, autres). De plus, si on ne programme plus les processeurs à la main, les langages de haut niveau passe par des compilateurs qui eux, programment le processeur. Leur interface avec le logiciel a été simplifiée pour coller au mieux avec ce que savent faire les compilateurs. En conséquence, l’interface logicielle des processeurs modernes est paradoxalement plus minimaliste que pour les vieux processeurs.
Tout cela pour dire que la conception d'un processeur est une affaire de compromis, comme n'importe quelle tâche d'ingénierie. Il n'y a pas de solution parfaite, pas de solution miracle, juste différentes manières de faire qui collent plus ou moins avec la situation. Et les compromis changent avec l'époque et l'évolution de la technologie. Les technologies sont toutes interdépendantes, chaque évolution concernant les transistors influence la conception des puces électroniques, les technologies architecturales utilisées, ce qui influence l'interface avec le logiciel, ce qui influence ce qu'il est possible de faire en logiciel. Et inversement, les contraintes du logiciel influencent les niveaux les plus bas, et ainsi de suite. Cette morale nous suivra dans le reste du cours, où nous verrons qu'il est souvent possible de résoudre un problème de plusieurs manières différentes, toutes utiles, mais avec des avantages et inconvénients différents.
Fonctionnement d'un ordinateur/Le chemin de données
Fonctionnement d'un ordinateur/L'unité de chargement et le program counter
Fonctionnement d'un ordinateur/L'unité de contrôle
Les jeux d’instructions spécialisés
modifierLes DSP, les processeurs de traitement du signal, sont des jeux d'instructions spécialement conçus pour travailler sur du son, de la vidéo, des images… Le jeu d'instruction d'un DSP est assez spécial, que ce soit pour le nombre de registres, leur utilisation, ou la présence d'instructions insolites.
Les registres des DSP
modifierPour des raisons de couts, tous les DSP utilisent un faible nombre de registres spécialisés. Un DSP a souvent des registres entiers séparés des registres flottants, ainsi que des registres spécialisés pour les adresses mémoires. On peut aussi trouver des registres spécialisés pour les indices de tableau ou les compteurs de boucle. Cette spécialisation des registres pose de nombreux problèmes pour les compilateurs, qui peuvent donner lieu à une génération de code sous-optimale.
De nombreuses applications de traitement du signal ayant besoin d'une grande précision, les DSP sont dotés de registres accumulateurs très grands, capables de retenir des résultats de calcul intermédiaires sans perte de précision.
De plus, certaines instructions et certains modes d'adressage ne sont utilisables que sur certains types de registres. Certaines instructions d'accès mémoire peuvent prendre comme destination ou comme opérande un nombre limité de registres, les autres leur étant interdits. Cela permet de diminuer le nombre de bits nécessaire pour encoder l'instruction en binaire.
Les instructions courantes des DSP
modifierLes DSP utilisent souvent l'arithmétique saturée. Certains permettent d'activer et de désactiver l'arithmétique saturée, en modifiant un registre de configuration du processeur. D'autres fournissent chaque instruction de calcul en double : une en arithmétique modulaire, l'autre en arithmétique saturée. Les DSP fournissent l'instruction multiply and accumulate (MAC) ou fused multiply and accumulate (FMAC), qui effectuent une multiplication et une addition en un seul cycle d'horloge, ce calcul étant très courant dans les algorithmes de traitement de signal. Il n'est pas rare que l'instruction MAC soit pipelinée.
Pour accélérer les boucles for, les DSP ont des instructions qui effectuent un test, un branchement et une mise à jour de l'indice en un cycle d’horloge. Cet indice est placé dans des registres uniquement dédiés aux compteurs de boucles. Autre fonctionnalité : les instructions autorépétées, des instructions qui se répètent automatiquement tant qu'une certaine condition n'est pas remplie. L'instruction effectue le test, le branchement, et l’exécution de l'instruction proprement dite en un cycle d'horloge. Cela permet de gérer des boucles dont le corps se limite à une seule instruction. Cette fonctionnalité a parfois été améliorée en permettant d'effectuer cette répétition sur des suites d'instructions.
Les DSP sont capables d'effectuer plusieurs accès mémoires simultanés par cycle, en parallèle. Par exemple, certains permettent de charger toutes leurs opérandes d'un calcul depuis la mémoire en même temps, et éventuellement d'écrire le résultat en mémoire lors du même cycle. Il existe aussi des instructions d'accès mémoires, séparées des instructions arithmétiques et logiques, capable de faire plusieurs accès mémoire par cycles : ce sont des déplacements parallèles (parallel moves). Notons qu'il faut que la mémoire soit multiport pour gérer plusieurs accès par cycle. Un DSP ne possède généralement pas de cache pour les données, mais conserve parfois un cache d'instructions pour accélérer l’exécution des boucles. Au passage, les DSP sont basés sur une architecture Harvard, ce qui permet au processeur de charger une instruction en même temps que ses opérandes.

Les modes d’adressage sur les DSP
modifierLes DSP incorporent pas mal de modes d'adressages spécialisés. Par exemple, beaucoup implémentent l'adressage indirect à registre avec post- ou préincrément/décrément, que nous avions vu dans le chapitre sur l'encodage des instructions. Mais il en existe d'autres qu'on ne retrouve que sur les DSP et pas ailleurs. Il s'agit de l'adressage modulo et de l'adressage à bits inversés.
L'adressage « modulo »
modifierLes DSP implémentent des modes d'adressages servant à faciliter l’utilisation de files, des zones de mémoire où l’on stocke des données dans un certain ordre. On peut y ajouter de nouvelles données, et en retirer, mais les retraits et ajouts ne peuvent pas se faire n'importe comment : quand on retire une donnée, c'est la donnée la plus ancienne qui quitte la file. Tout se passe comme si ces données étaient rangées dans l'ordre en mémoire.
Ces files sont implémentées avec un tableau, auquel on ajoute deux adresses mémoires : une pour le début de la file et l'autre pour la fin. Le début de la file correspond à l'endroit où l'on insère les nouvelles données. La fin de la file correspond à la donnée la plus ancienne en mémoire. À chaque ajout de donnée, on doit mettre à jour l'adresse de début de file. Lors d'une suppression, c'est l'adresse de fin de file qui doit être mise à jour. Ce tableau a une taille fixe. Si jamais celui-ci se remplit jusqu'à la dernière case, (ici la cinquième), il se peut malgré tout qu'il reste de la place au début du tableau : des retraits de données ont libéré de la place. L'insertion continue alors au tout début du tableau. Cela demande de vérifier si l'on a atteint la fin du tableau à chaque insertion. De plus, en cas de débordement, si l'on arrive à la fin du tableau, l'adresse de la donnée la plus récemment ajoutée doit être remise à la bonne valeur : celle pointant sur le début du tableau. Tout cela fait pas mal de travail.
Le mode d'adressage « modulo » a été inventé pour faciliter la gestion des débordements. Avec ce mode d'adressage, l'incrémentation de l'adresse au retrait ou à l'ajout est donc effectué automatiquement. De plus, ce mode d'adressage vérifie automatiquement que l'adresse ne déborde pas du tableau. Et enfin, si cette adresse déborde, elle est mise à jour pour pointer au début du tableau. Suivant le DSP, ce mode d'adressage est géré plus ou moins différemment. La première méthode utilise des registres « modulo », qui stockent la taille du tableau. Chaque registre est associé à un registre d'adresse pour l'adresse/indice de l’élément en cours. Vu que seule la taille du tableau est mémorisée, le processeur ne sait pas quelle est l'adresse de début du tableau, et doit donc ruser. Cette adresse est souvent alignée sur un multiple de 64, 128, ou 256. Cela permet ainsi de déduire l'adresse de début de la file : c'est le multiple de 64, 128, 256 strictement inférieur le plus proche de l'adresse manipulée. Autre solution : utiliser deux registres, un pour stocker l'adresse de début du tableau et un autre pour sa longueur. Et enfin, dernière solution, utiliser un registre pour stocker l'adresse de début, et un autre pour l'adresse de fin.
L'adressage à bits inversés
modifierL'adressage à bits inversés (bit-reverse) a été inventé pour accélérer les algorithmes de calcul de transformée de Fourier (un « calcul » très courant en traitement du signal). Cet algorithme va prendre des données dans un tableau, et va fournir des résultats dans un autre tableau. Seul problème, l'ordre d'arrivée des résultats dans le tableau d'arrivée est assez spécial. Par exemple, pour un tableau de 8 cases, les données arrivent dans cet ordre : 0, 4, 2, 6, 1, 5, 3, 7. L'ordre semble être totalement aléatoire. Mais il n'en est rien : regardons ces nombres une fois écrits en binaire, et comparons-les à l'ordre normal : 0, 1, 2, 3, 4, 5, 6, 7.
| Ordre normal | Ordre Fourier |
|---|---|
| 000 | 000 |
| 001 | 100 |
| 010 | 010 |
| 011 | 110 |
| 100 | 001 |
| 101 | 101 |
| 110 | 011 |
| 111 | 111 |
Comme vous le voyez, les bits de l'adresse Fourier sont inversés comparés aux bits de l'adresse normale. Nos DSP disposent donc d'un mode d’adressage qui inverse tout ou partie des bits d'une adresse mémoire, afin de gérer plus facilement les algorithmes de calcul de transformées de Fourier. Une autre technique consiste à calculer nos adresses différemment. Il suffit, lorsqu'on ajoute un indice à notre adresse, de renverser la direction de propagation de la retenue lors de l’exécution de l'addition. Certains DSP disposent d'instructions pour faire ce genre de calculs.
Fonctionnement d'un ordinateur/Les architectures actionnées par déplacement
Les entrées-sorties et périphériques
modifierFonctionnement d'un ordinateur/Les méthodes de synchronisation entre processeur et périphériques Fonctionnement d'un ordinateur/L'adressage des périphériques Fonctionnement d'un ordinateur/La mémoire virtuelle des périphériques Fonctionnement d'un ordinateur/La carte mère, chipset et BIOS Fonctionnement d'un ordinateur/Les périphériques et les cartes d'extension
Les mémoires de masse
modifierFonctionnement d'un ordinateur/Les mémoires de masse : généralités Fonctionnement d'un ordinateur/Les disques durs Fonctionnement d'un ordinateur/Les solid-state drives Fonctionnement d'un ordinateur/Les disques optiques Fonctionnement d'un ordinateur/Les technologies RAID
La mémoire cache
modifierFonctionnement d'un ordinateur/Les mémoires cache Fonctionnement d'un ordinateur/Le préchargement Fonctionnement d'un ordinateur/Le Translation Lookaside Buffer
Le parallélisme d’instructions
modifierFonctionnement d'un ordinateur/Le pipeline Fonctionnement d'un ordinateur/Les pipelines de longueur fixe et dynamiques Fonctionnement d'un ordinateur/Les exceptions précises et branchements Fonctionnement d'un ordinateur/La prédiction de branchement Fonctionnement d'un ordinateur/Les optimisations du chargement des instructions Fonctionnement d'un ordinateur/L'émission dans l'ordre des instructions Fonctionnement d'un ordinateur/Les dépendances de données et l'exécution dans le désordre Fonctionnement d'un ordinateur/Le renommage de registres Fonctionnement d'un ordinateur/Le scoreboarding et l'algorithme de Tomasulo Fonctionnement d'un ordinateur/Les unités mémoires à exécution dans l'ordre Fonctionnement d'un ordinateur/Les unités mémoires à exécution dans le désordre Fonctionnement d'un ordinateur/Le parallélisme mémoire au niveau du cache Fonctionnement d'un ordinateur/Les processeurs superscalaires Fonctionnement d'un ordinateur/Les processeurs VLIW et EPIC Fonctionnement d'un ordinateur/Les architectures dataflow
Les architectures parallèles
modifierFonctionnement d'un ordinateur/Les architectures parallèles Fonctionnement d'un ordinateur/Architectures multiprocesseurs et multicœurs Fonctionnement d'un ordinateur/Architectures multithreadées et Hyperthreading Fonctionnement d'un ordinateur/Les architectures à parallélisme de données Fonctionnement d'un ordinateur/Les architectures parallèles exotiques Fonctionnement d'un ordinateur/La cohérence des caches Fonctionnement d'un ordinateur/Les sections critiques et le modèle mémoire
Annexes
modifierFonctionnement d'un ordinateur/Les mémoires historiques Fonctionnement d'un ordinateur/Le matériel réseau Fonctionnement d'un ordinateur/Les architectures neuromorphiques Fonctionnement d'un ordinateur/La tolérance aux pannes Fonctionnement d'un ordinateur/Les circuits réversibles
























































































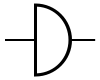





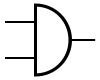





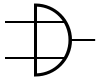


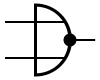


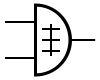

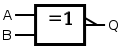



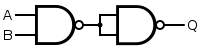
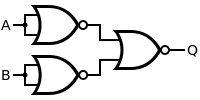

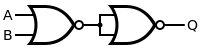



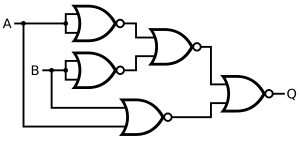

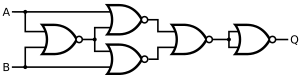









































































![{\displaystyle e0.[({\overline {e2}}.e1)+(e2.{\overline {e1}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95a5d00477a179e003e1d4d6dd3fa79137262380)










![{\displaystyle \left[{\overline {E_{c}}}.[(a.{\overline {b}})+(a.b)]\right]+\left[E_{c}.[({\overline {a}}.b)+(a.b)]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c010205967d4c3b4c86e7b3e084fd7c79f5e986)

![{\displaystyle \left[{\overline {E_{c}}}.a.({\overline {b}}+b)\right]+\left[E_{c}.b.({\overline {a}}+a)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8bb81a210e532d26d6d848493334a608fc207a7)


![{\displaystyle \left[{\overline {E_{c}}}.a.1\right]+\left[E_{c}.b.1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48d7dfbe7b01f36cafe9f8dd3a872998c83f8e48)
























































































![{\displaystyle [2R-D]-[2R-3D]=2D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/737c3e7c3902ef0b9083b7546c82aeaaa0bd41b9)















































![{\displaystyle \log _{2}(x+y)=\log _{2}\left(x+x\times {\frac {y}{x}}\right)=\log _{2}\left[x\times \left(1+{\frac {y}{x}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70719c9b06db25ff7931cd8b804844e46167096e)

















![{\displaystyle (A>B)+\left[E(>).{\overline {(A<B)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cb0d026dae50ef7883b549a872f6d07dd732e90)
![{\displaystyle (A<B)+\left[E(<).{\overline {(A>B)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7abb9ad9ed51feaa4b880ff01ec0a498fb3ee4fe)